Teoría de Máquinas y Mecanismos: Esquemas Cinemáticos
Anuncio

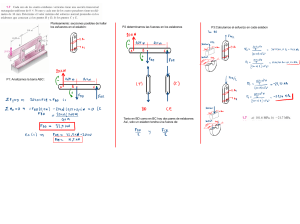
UNIVERSIDAD NACIONAL JORGE BASADRE GROHMANN Facultad de INGENIERÍA Escuela profesional de INGENIERÍA MECÁNICA -Curso: Teoría de Máquinas y Mecanismos -Docente: Ing. Williams Sergio Almanza Quispe -Tema: Trabajo de Investigación -Año: 3er año -Alumno: Pedro Ricardo Tejada Armendáriz Tacna-2020 Capítulo 1. ESQUEMAS CINEMÁTICOS 1.1 INTRODUCCIÓN Para comprender los esquemas cinemáticos primero tenemos que definir qué es la cinemática, podemos definir a la cinemática como ciencia que estudia la geometría del movimiento, su análisis determina la posición, desplazamiento, rotación, velocidad y aceleración de un mecanismo. Notaremos que en la mayoría de los casos, los mecanismos muestran un movimiento en un plano paralelo al que se encuentran, estos mecanismos se encuentran limitados a un espacio de 2 dimensiones y se conocen como mecanismos planares. Estos sistemas o mecanismos también tienen una propiedad importante que debemos tomar en cuenta, la cual es el número de grados de libertad en el eslabonamiento y puede ser definido también como el número de actuadores requeridos para operar el mecanismo. Más adelante podremos ver que la movilidad o grados de libertad se podrán determinar por medio de la ecuación de Gruebler. teniendo siempre en cuenta algunas excepciones que no ejercerán movimiento del eslabonamiento. 1.2 TEORÍA DE ESQUEMAS CINEMÁTICOS Un diagrama cinemático o esquema cinemático ilustra la conectividad entre los eslabones y uniones de un mecanismo o maquinaria, en lugar de usar dimensionamiento de piezas, alguna distancia o la forma de las piezas, utiliza objetos geométricos como líneas, triángulos, círculos, estos enlaces representan las articulaciones del mecanismo o máquina. un esquema cinemático también puede ser llamado como mapa conjunto o diagrama esquelético 1.3 TERMINOLOGÍA DE MECANISMOS Eslabonamiento o enlace. Es un mecanismo donde partes rígidas están conectadas para formar una cadena. Hay eslabonamientos simples y eslabonamientos complejos. Marco. Es la parte del eslabonamiento que sirve como marco de referencia para el movimiento de todas las otras partes y que típicamente no exhibe movimiento (está en reposo). Eslabones. Son las partes individuales del mecanismo. Son considerados cuerpos rígidos y están conectados entre sí para transmitir movimiento y fuerzas. Teóricamente, un cuerpo rígido no cambia de forma durante el movimiento, y a pesar de que en nuestra realidad física los cuerpos rígidos no existen, en vista de que los eslabones están diseñados para deformación mínima; se puede considerar que son rígidos. Las partes elásticas, resortes por ejemplo, no son rígidos y consecuentemente no son considerados eslabones. Estos dispositivos no tienen efecto sobre la cinemática de un mecanismo y usualmente son ignorados durante el análisis cinemático más no durante el análisis dinámico. Junta. Es una conexión entre los eslabones que permite un movimiento relativo entre ellos. Hay dos juntas primarias o completas, estas son las juntas de revolución y las de deslizamiento. Junta de revolución o de bisagra. Permite rotación pura entre los eslabones que conecta. Junta de deslizamiento o prismática. Sólo permite deslizamiento lineal entre los eslabones que conecta. Eslabón simple. Es un cuerpo rígido que solo tiene dos juntas, las cuáles le permite conectarse a otros eslabones. Juntas de orden superior o medias juntas. Estas son juntas de movimiento complejo que generalmente involucran tanto rotación como deslizamiento. Ejemplo de ellas son las juntas curvilíneas o de levas y las conexiones de engranes. Manivela. Es un eslabón simple que es capaz de completar una rotación completa sobre un centro fijo. Balancín. Es un eslabón simple que oscila hasta un determinado ángulo de amplitud, revirtiendo su dirección a ciertos intervalos. Eslabón complejo. Es un cuerpo rígido que contiene más de dos juntas. Un brazo de balancín es un eslabón complejo (contiene tres juntas y esta pivotado cerca de su centro). Actuador. Es el componente que opera o que da energía al mecanismo. Actuadores comunes incluyen: motores eléctricos, motores hidráulicos, máquinas reciprocantes, cilindros hidráulicos y neumáticos, solenoides, y movimiento humano. Cadenas cerradas. Eslabonamientos en donde cada eslabón está conectado a dos o más eslabones. Punto de interés. Es un punto en un eslabón donde el movimiento es de interés especial. Una vez el análisis cinemático es efectuado, el desplazamiento, velocidad, y aceleración de ese punto son determinados. MOVILIDAD: La Movilidad que se encuentra en cualquier mecanismo es un método que nos sirve para cuantificar cuántas Variables de Par deben definirse antes de poder localizar o ubicar todos los puntos de todos los componentes del mecanismo en función del tiempo. Por lo tanto podemos decir; que la movilidad de un mecanismo representa la cantidad de movimientos de entrada de forma independiente para que el mecanismo pueda llegar a las posiciones deseadas; por ejemplo, en la Figura, mecanismo biela-manivelacorredera para que esta última pueda llegar al punto l+r , y suponiendo que tenemos un control completo de la biela, entonces al completar la distancia deseada; la corredera deberá alinearse con la manivela de modo que el ángulo (Ø)debe ser de cero, Mecanismo Biela-Manivela-Corredera (en el plano) Mecanismo Biela-Manivela-Corredera (en 3D) Representación gráfica de movimiento de corredera Observe que controlando el ángulo de la biela puedo llegar llevar a la corredera a cualquier punto a lo largo de x. Ahora vamos a establecer que estamos tratando con un mecanismo en 2D es de un mecanismo plano; es decir todo los mecanismos posibles están determinados dentro de un plano de acción, como es el caso de la figura anterior (biela-manivela-corredera). Si retiramos la biela del mecanismo (pero no del plano) ella va a tener libertad de moverse arriba-abajo, derecha-izquierda y rotar, por tal razón se dice que este mecanismo tiene tres grados de libertad. Partiendo del hecho de que cada elemento dentro de un mecanismo plano tiene tres grados de libertad y estableciendo que uno de los eslabones debe ser fijo se puede decir que, para n eslabones el grado de libertad será 3(n-1), pero una vez ensamblado el mecanismo, la movilidad se verá afectada por la restricción que imponga el par cinemático, disminuyendo por cada pareja de eslabones la posibilidad de un movimiento en cada uno, es decir, si el par tiene un grado de libertad disminuye un movimiento en cada uno (dos en total) y si tiene dos grados de libertad se genera una restricción. De este modo la movilidad (m) será: m=3(n-1)-(2 *J1)-J2 donde: J1= cantidad de juntas o pares de un grado de libertad J2= cantidad de juntas o pares de dos grados de libertad. A esta fórmula presentada se le denomina criterio de Kutzbach para la movilidad de un mecanismo plano. Si m=1, entonces si nosotros un solo movimiento de entrada al mecanismo, tendremos la capacidad de impulsarlo y controlarlo; en caso de que m=2 para poder controlar el mecanismo vamos a requerir dos movimientos independientes. Si se dal el caso de que m=0 entonces no existirá movilidad en el mecanismo y este no se podrá considerar como tal sino como una estructura. Para que un conjunto de elementos sea llamado como Mecanismo, este tiene que tener como Grado de Libertad uno o superior. De manera tradicional los diferentes mecanismos que podíamos encontrar tenían sólo un Grado de Libertad. Sin embargo, actualmente gracias a los diferentes avances tecnológicos, es usual encontrar diseños mecánicos con dos o más grados de libertad. Como contraparte si vemos que un mecanismo tiene una movilidad de cero, o inferior a ella (negativa), como resultado de aplicar las ecuaciones de movilidad presentadas más adelante, podemos decir que no se trata de un Mecanismo, sino más bien de una Estructura. Así mismo es válido aclarar que para efectos de diseño y poder determinar fuerzas actuantes en un mecanismo, si nos encontramos que la movilidad es cero, la estructura es Estáticamente Determinada, en el caso de que nuestro resultado sea una movilidad menor a cero (negativa), la estructura es Estáticamente Indeterminada. MOVILIDAD EN MECANISMOS: ESLABONES UBICADOS EN UN PLANO: Cualquier eslabón en un plano tiene tres Grados de Libertad. Por consiguiente un sistema de L eslabones no conectados en el mismo plano tendrá 3L*GDL, como se muestra en la figura, donde los eslabones no conectados tienen un total de 6 Grados de Libertad. ESLABONES UNIDOS POR UNA JUNTA COMPLETA: Cuando estos eslabones están conectados por un Junta Completa como en la siguiente figura �y1 y �y2se combinan como �y,�x1 y �x2. Por consiguiente esto elimina 2 Grados de Libertad y deja 4 ESLABONES UNIDOS POR UNA SEMIJUNTA: En la figura mostrada la semijunta elimina solo 1 Grado de Libertad del sistema (porque un semijunta tiene 2 Grados de Libertad) y deja el sistema de dos eslabones conectados por una semijunta con un total de cinco Grados de Libertad. EJEMPLO DE APLICACIÓN DE CRITERIO DE KUTZBACH *En la siguiente figura se muestra un pequeño montacarga frontal. Dibuje el diagrama cinemático del mecanismo y determine la movilidad del mismo aplicando el criterio de Kutzbach. SOLUCIÓN: capitulo 2 (junior) movilidad capítulo 3(iván) grados de libertad capítulo 4(brandon) ecuación de gruebler Ecuación de Grübler Sirve para encontrar los grados de libertad o grado de movilidad, de esta manera identificamos si estamos trabajando con un mecanismo o estructura Grado de libertad: es la posibilidad de cualquier estructura o mecanismo para desplazarse o girar . Mecanismo: es un conjunto de piezas o elementos ajustados entre si y aplicando energía mecánica, cumplen una función. Fórmula de Grübler: m-GDL: Son los grados de libertad n: Número de miembros de un mecanismo P1: Pares binarios de un grado de libertad P2: Pares binarios de dos grados de libertad EJEMPLOS: Posibilidades y limitaciones G < 0 Estructura hiperestática. G = 0 Estructura isostática. G = 1 Mecanismo desmodrómico. Dada la posición de un elemento, se conoce la del resto. ● G = 2 Mecanismo diferencial. ● G > 2 Mecanismo con el número de grados de libertad. ● ● ● Limitaciones: 1. Los pares terciarios se consideran binarios y se introducen dos veces: 2. La aplicación del criterio indica que se trata de una estructura isostática, pero en realidad se mueve 3. Pero los elementos 7, 8 y 9 sí se mueven Reglas prácticas para aplicar el criterio de Grübler: ❖ Evitar usar barras de la misma longitud. ❖ Identificar qué partes del mecanismo actúan como sólido rígido y tratarlos como elementos n-arios. Inconsistencias del criterio Grübler: ➔ El mecanismo posee un par inferior que puede ser sustituido por uno superior sin alterar el movimiento. ➔ El mecanismo posee un par cinemáticamente redundante. Si se elimina la articulación A, el sistema se moverá exactamente igual. ➔ El mecanismo posee una restricción redundante. capítulo 5 (fanny) excepciones conclusiones(2 conclusiones por capítulo) bibliografía anexos