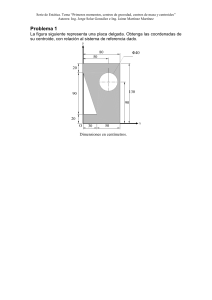
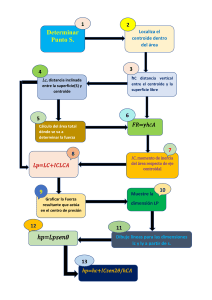
UNIVERSIDAD NACIONAL DEL ALTIPLANO FACULTAD DE INGENIERÍA MECÁNICA ELÉCTRICA, ELECTRÓNICA Y SISTEMAS ESCUELA PROFESIONAL DE INGENIERIA DE SISTEMAS FISICA TRABAJO ENCARGADO: INVESTIGACIÓN SOBRE CENTRO DE MASA Y CENTROIDE PRESENTADO POR: MAMANI CONDEMAYTA SANDRA DOCENTE: MAMANI CUTIPA JUAN PERCY SEMESTRE: II GRUPO: A PUNO-PERÚ RESUMEN El propósito de este trabajo es describir la comprensión del centro de masa y el centroide a partir de un estudio de caso. La descripción se apoya en el análisis del procedimiento cuando se resuelven algunas tareas planteadas en una muestra representativa de contextos, un contexto mecánico estático o dinámico, en los que el centro de masa y el centroide son importantes para su resolución. La comparación entre la configuración epistémica, organizada por un docente, y las configuraciones cognitivas de los estudiantes, muestra que el contexto estático deberá incluir situaciones en las que se favorezca el proceso de idealización, que el uso competente de dicha noción en una tarea concreta provee al alumno de un conocimiento parcial y, por otro lado, que la transferencia del conocimiento de un contexto a otro no es inmediata, pues los alumnos no consideran la complejidad del contexto dinámico. OBJETIVO La investigación plantea el objetivo de caracterizar el proceso de comprensión del centro de masa y centroide, a partir de las resoluciones de una muestra representativa de situaciones físicas en un contexto mecánico estático o dinámico donde interviene el centro de masa y centroide donde se organizan, mediante ciertos procesos cognitivos, un conjunto de objetos físico-matemático. APLICACIÓN DE CENTRO DE MASA EN LA FÍSICA: Encontrar la posición del centro de masa para una placa metálica de densidad uniforme, la cual mide 4cm de ancho por 10cm de largo. 4cm Simétrico Simétrico 10cm Si la densidad es uniforme (la masa en la placa está distribuida de forma homogénea) y la placa es simétrica entonces el centro de masa coincide con el centro geométrico (5,4) anillo Notación de la estructura de un anillo: Notamos que el CM no está dentro de la estructura del anillo entonces, consideremos al XM mas que todo como una simplificación matemática que permite la descripción del movimiento o de las fuerzas sobre los cuerpos mas alla de si el CM se ubica o no en la estructura de los cuerpos (0,3) Para una placa triangular el CM coincide con el centroide o baricentro debido a que tiene una densidad uniforme 3 X1 + X2 + X3 𝑌𝐶𝑀 = 𝑋𝐶𝑀 = 3 Y1 + Y2 + Y3 3 CM para un triángulo (4,0) (0,0) 𝑋𝐶𝑀 = 0+4+0 3 𝑌𝐶𝑀 = 0+0+3 3 𝑋𝐶𝑀 = 4 3 𝑌𝐶𝑀 = 3 3 4 𝑋𝐶𝑀 = 1,3 𝑌𝐶𝑀 = 1 8 Para la siguiente placa, el CM de una densidad uniforme A2 3 (3,2.5) A1 (1,1.5) 2 2 A3 𝑋𝐶𝑀 = A1X1 + A2X2 + A3X3 A1 + A2 + A3 𝑋𝐶𝑀 = 6 ∗ 1 + 2 ∗ 3 + 12 ∗ 6 20 𝑋𝐶𝑀 = 84 20 (6,1.5) 4 𝑋𝐶𝑀 =4,2 𝑌𝐶𝑀 = A1Y1 + A2Y2 + A3Y3 A1 + A2 + A3 𝑌𝐶𝑀 = 6 ∗ 1,5 + 2 ∗ 2,5 + 12 ∗ 1,5 20 𝑌𝐶𝑀 = 32 20 𝑌𝐶𝑀 =1,6 APLICACIÓN DEL CENTROIDE EN LA FÍSICA: El grosor del marco es adimensional en el cual podemos encontrar coordenadas en cuerpos con grosor despreciable, donde a la mitad de la base encontraremos el centroide de línea, considerando la longitud de distancia. Una figura homogénea así que a la mitad de la base como a la mitad de la altura encontraremos la ubicación del centroide. En este caso podemos determinar áreas y coordenadas donde las coordenadas son las del centride En este caso tendremos a un volumen gracias a sus unidades cubicas, ya que lleva base, altura y profundidad. Mecánica vectorial, aplicación de centroides a cargas distribuidas, obtener una fuerza equivalente que se obtiene por el cálculo del área de la figura geométrica correspondiente. el muro de contención a gravedad esta hecho de concreto, determine la ubicación x, y del centro de masa para el muro. Para calcular centroides lo que se hace es encontrar las coordenadas que nos indican para el problema Área negativa figura 1 2 3 4 suma Área(m2) 1.44 3.6 2.7 -0.9 6.84 X(m) 1.8 3 1.8 3.4 Y(m) 0.2 1.9 1.4 1.4 xA(m3) 2.592 10.8 4.86 -3.06 15,192 yA(m3) 0.288 6.84 3.78 -1.26 9.648 𝑿= ∑𝑿𝑨 𝟏𝟓. 𝟏𝟗𝟐 = ∑𝑨 𝟔. 𝟖𝟒 𝑿= ∑𝑿𝑨 = 𝟐. 𝟐𝟐𝒎 ∑𝑨 𝒀= 𝒀= ∑𝒀𝑨 𝟗. 𝟔𝟒𝟖 = ∑𝑨 𝟔. 𝟖𝟒 ∑𝒀𝑨 = 𝟏. 𝟒𝟏𝒎 ∑𝑨 CONCLUSIONES La conclusión de este trabajo es que el uso competente de la noción de centro de masa en un determinado contexto puede significar una interpretación estática y otra dinámica. En el contexto de las situaciones físicas planteadas, el paso de la concepción material a la concepción abstracta del centro de masa solo se logró a través de la reflexión. Cada situación física mostró una propiedad específica del centro de masa, la cual hubiese sido imposible observar en otras situaciones, en otras palabras, el centro de masa en una situación concreta es interpretada de manera distinta a como pudiese ser interpretado en otros contextos debido a que se relaciona con otros conceptos. Por otro lado podemos concluir que el centro de gravedad es un punto imaginario que se ubica en la posición promedio del peso de un cuerpo. REFERENCIAS http://neel.fis.puc.cl/cncm/Fis1503/Apuntes_files/capitulo_04.pdf https://repositorio.pucp.edu.pe/index/handle/123456789/7139 http://www.cesparza.org/usach/publicaciones_pdfs/esparza_sochedi2009_pesajebarra.pdf https://upcommons.upc.edu/bitstream/handle/2117/133357/1400856343.pdf?seque nce=1 http://ri.uaemex.mx/bitstream/handle/20.500.11799/34516/secme18599.pdf?sequence=1 https://d1wqtxts1xzle7.cloudfront.net/57058997/ensayoaplicacionesdecentos-degravedadcentroidesprimermomentoymomentodeinerciaenlaingenieriacivil160217233952-with-cover-pagev2.pdf?Expires=1658211493&Signature=QWBYB8QhN1X7eB1Rz5ODApMMgXGOzYV~s magpjMMWA~rW-eiO~dlzZXwKCjF4VX8RuGohLI4T3eE6Ja08WicsAQNLGzGz9NeC~1ADb1nzZLZsX~hhX64YgVW3fPUGOk5UHrpJdDhJquS8kb9lWuTT37WYosdwvPHwzHwlKcvd3Ecx43~IDy05Ka hLBM0ygsfSSt9KxP6R8MHnPtd4LufvG91hUWb2JUYiRqBavAzPfhJGQgYMtraHs2QSFdp GjWa-662PONvfbSSwRVJG5sdyPMgs6fRTx-1GPwNvC3hv072ByEM2DaaikyD7eY37OI7ed8vSDNNAF~rpx3JedQ__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA