Centroides y centros de masa - jorge

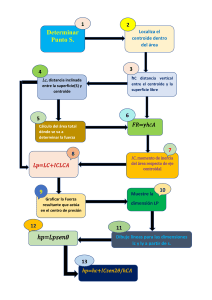
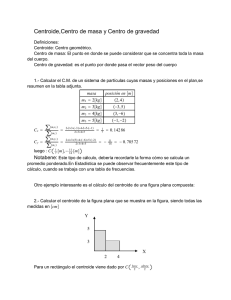
Preparado por:
Mtro. Jorge Eduardo Aguilar Rosas
Centroides y centros de gravedad
1 Centroides
El centroide de un objeto, compuesto de un número de partes, es la posición del promedio
ponderado por los factores de peso ,
̅ =
∑ ,
∑ ∑ , ̅
∑ =
=
∑ ∑ Los factores de peso pueden ser áreas, volúmenes o segmentos de línea asociados con la
distribución de masa del objeto.
Áreas
Consideremos un objeto “plano”, con su área total, y sean con = 1,2, … , , las áreas de las
partes “simples” que componen al objeto con posiciones ( , ), respectivamente. El centroide
del objeto plano está dado por:
̅ =
∑ , =
∑ Para un objeto en donde su forma es muy irregular, se puede trabajar con elementos de área ,
y “sumar” sobre toda la superficie , quedando:
̅ =
, =
siendo el área total:
= .
Si la densidad de masa es constante, la posición del centroide de objetos de forma simple
corresponde al centro geométrico. Por ejemplo, para un disco circular o un rectángulo, el
centroide es el centro de la pieza. Para un triángulo rectángulo, el centroide está localizado a ,
"
siendo ! la longitud de la base y , siendo ℎ la longitud de la altura, tomados a partir del ángulo
recto del triángulo. Para media circunferencia el centroide se encuentra a
centro de la circunferencia, sobre el eje de simetría.
$%
,
&
desde el punto
Volúmenes
En el caso de un objeto en el espacio (3 dimensiones), las coordenadas del centroide son:
̅ =
( '
'
, =
( '
'
, ̅ =
( '
'
siendo ) el volumen total:
) = ' ).
El centroide de un cono circular de radio R y altura h se encuentra a 1/4 de la altura (medida desde
la base), sobre su eje.
1
Preparado por:
Mtro. Jorge Eduardo Aguilar Rosas
Líneas
En el caso de un objeto en forma de una “línea” en el espacio (3 dimensiones), las coordenadas del
centroide son:
̅ =
+ *
*
, =
+ *
*
, ̅ =
+ *
*
siendo L la longitud total:
, = * ,.
Centros de masa
El centro de masa de un objeto es su centroide considerando a la masa como el factor de peso:
̅ =
. -
. -
-
-
, =
, ̅ =
. -
siendo / la masa total:
/ = - /.
Los elementos de masa pueden estar en líneas, superficies o volúmenes, por lo que se pueden
asociar a la distribución de masa correspondiente:
Para una línea con densidad lineal de masa 0, los elementos de masa son: / = 0,
Para una superficie con densidad superficial de masa 1, los elementos de masa son: / = 1
Para un volumen con densidad volumétrica de masa 2, los elementos de masa son: / = 2)
En cualquiera de los casos, si la densidad es constante, se dice que tiene distribución de masa
homogénea y el centro de masa es igual al centroide.
La importancia del centro de masa de un objeto (centroide), es que el peso del objeto se
representa como una sola fuerza equivalente que actúa en esta posición.
2 Elementos compuestos
Una línea, una superficie o un volumen compuesto es una combinación de partes simples.
Para determinar las coordenadas del centroide (centro de masa) se encuentran las coordenadas
de los centroides (centros de masa) de cada parte y se toma el promedio ponderado (como se
indicó el inicio).
3 Teoremas de Pappus-Guldinus
Primer teorema
Sea , una línea en el plano − , sean ̅ , las coordenadas del centroide. Sea S la superficie de
revolución que se genera al girar , alrededor del eje . El área de la superficie de revolución es
igual a: = 24,.
Segundo teorema
Sea el área en el plano − , y sean ̅ , las coordenadas del centroide. Sea V el volumen de
revolución que se genera al girar alrededor del eje . El volumen del sólido de revolución es
igual a: ) = 24.
2