CENTROIDES DE SUPERFICIES PLANAS

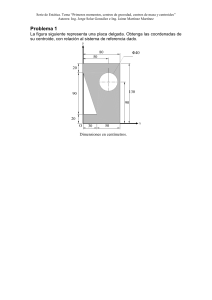
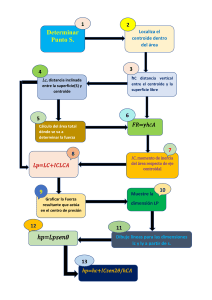
CENTROIDES DE
SUPERFICIES PLANAS
MARTINEZ GUZMAN ELIZABETH
CALCULO II
GUSTAVO ROCHA
CENTROIDE
• Constituye el Centro Geométrico de una superficie o
•
•
•
cuerpo.
Su ubicación puede determinarse por medio de
integrales que relacionan fuerzas que actúan en el.
(gravedad, dimensiones, correspondencia, etc.)
Los términos que pertenecen constantes en el cuerpo
en estudio se cancela dentro de la integral, tanto en
numeradores como en denominadores.
Las formulas (integrales) resultantes definen el
centroide del cuerpo, siendo independientes del peso
y dependiendo solo de la geometría del cuerpo.
CASOS DE CENTROIDES
• VOLUMEN
– Si un cuerpo se subdivide en elementos de volumen
dv; la ubicación del centroide C(x,y,z) del volumen
de un objeto, puede determinarse calculando “Los
momentos” de los elementos con respecto a los
ejes coordenados con las integrales:
x
v
x
dv

vdv

;y 
v
y
dv

vdv

;z 
v
z
dv

vdv

AREA
• Si un área se subdivide en
elementos de volumen dA; la
ubicación del centroide C(x,y,z)
del área de un cuerpo, puede
determinarse calculando los
momentos de estos elementos de
área con respecto a los ejes
coordenados llamados:
x

x
d



d


;y 

y
d



d


;z 

z
d



d


LINEA
• Si la geometría de un objeto, toma la forma de
una línea (varilla, o alambre), entonces la forma
de encontrar su centroide es idéntica al
procedimiento mencionado para los casos
anteriores.
x
L
x
dL

LdL

;y 
L
y
dL

LdL

;z 
L
z
dL

LdL

PROCEDIMIENTO PARA EL
ANALISIS DE PROBLEMAS
METODO DE INTEGRACION SIMPLE
• ELEMENTO DIFERENCIAL
1. Selección de un sistema de coordenadas de
referencia.
2. Escoger un elemento diferencial para
integración, utilizando un rectángulo de
longitud finita dA y un ancho diferencial,
ubicando el área de tal forma que este se
intersecte en un punto arbitrario (x,y,z)
PROCEDIMIENTO PARA EL
ANALISIS DE PROBLEMAS
METODO DE INTEGRACION SIMPLE
• Tamaño y brazos de momento
3. Expresar el área del elemento en términos
de las coordenadas utilizadas para definir el
contorno de la figura.
4. Determine las coordenadas del brazo de
momento (x,y,z) para el centro del área.
PROCEDIMIENTO PARA EL
ANALISIS DE PROBLEMAS
METODO DE INTEGRACION SIMPLE
• Integraciones:
5. Sustitución de datos y evaluación de integrales,
NOTA: Las integrales solo pueden realizarse cuando la
función en el integrando esta expresada en
términos de la misma variable (área).
6. El intervalo debe tomarse el limite entre los 2
puntos extremos del espesor diferencial, para así
abarcar la región completa.
EJEMPLO:
SOLUCION
• ELEMENTOS DIFERENCIAL
– Considerando un dy = rectángulo con longitud “x”;
por triangulo semejantes:
b
x
b

; x  h  y 
h h  y 
h
El elemento intersecta los lados del triangulo a
una altura “h” y base sobre el eje de las “x”
SOLUCION
• AREA Y BRAZO DE MOMENTO:
– El área del elemento es:
b
dA  xdy; x  h  y dy
h
Y su centroide se ubica a una distancia
yy
Del eje x
SOLUCION
• INTEGRACIONES:
b


y
y

h
dy
A
y
dA
0 h

y
 H
b
AdA



h

y
dy
0 h
1 bh 2
h
6


1 bh 3
2
H
Gracias