Subido por
KEVIN ALEXANDER MAIQUIZA TITUANA
Sistemas de Control: Función de Transferencia y Respuesta en Frecuencia
Anuncio

UNIVERSIDAD TÉCNICA DE COTOPAXI
FACULTAD DE CIENCIAS DE LA INGENIERÍA Y APLICADAS
CARRERA INGENIERÍA EN ELECTRICIDAD
SISTEMAS DE CONTROL
DATOS INFORMATIVOS:
NOMBRE: GUISELA CASTAÑEDA
DOCENTE: PHD. SECUNDINO MARRENO
CICLO: QUINTO “A”
FECHA: 28/11/2021
LATACUNGA – ECUADOR
2021
TEMA1.- FUNCIÓN DE TRANSFERENCIA Y RESPUESTA EN FRECUENCIA DE
MODELOS FÍSICOS
MODELACIÓN Y SIMULACIÓN DE SISTEMAS EN MATLAB – FUNCIÓN DE
TRANSFERENCIA
INTRODUCCIÓN
En todos los sistemas de control se usan con frecuencia componentes de distintos tipos, por
ejemplo, componentes mecánicos, eléctricos, hidráulicos, neumáticos y combinaciones de
estos. Un ingeniero que trabaje con control debe estar familiarizado con las leyes físicas
fundamentales que rigen estos componentes. Sin embargo, en muchos casos y principalmente
entre los ingenieros, los fundamentos existen como conceptos aislados con muy pocos lazos
de unión entre ellos. El estudio de los controles automáticos puede ser de gran ayuda para
establecer lazos de unión entre los diferentes campos de estudio haciendo que los distintos
conceptos se usen en un problema común de control.
El estudio de los controles automáticos es importante debido a que proporciona una
comprensión básica de todos los sistemas dinámicos, así como una mejor apreciación y
utilización de las leyes fundamentales de la naturaleza.
El problema de control consiste en seleccionar, de un conjunto específico o arbitrario de
elementos (o parámetros, configuraciones, funciones, etc), aquellos que aplicados a un
sistema fijo, hagan que este se comporte de una manera predeterminada. Así un problema de
control es seleccionar el punto de apoyo de la palanca de un regulador de nivel para que la
altura del líquido en el recipiente se mantenga constante a pesar de las variaciones del caudal
de salida.
OBJETIVOS
Obtener la respuesta dinámica de sistemas con el uso de las funciones de transferencia
Identificar los diferentes elementos que forman parte de un sistema de control.
FUNDAMENTACIÓN TEÓRICA
Sistemas de control
Es un arreglo de componentes físicos conectados de tal manera que el arreglo pueda
comandar, dirigir o regular, asimismo o a otro sistema. Estos sistemas comandan dirigen o
controlan dinámicamente.
Un sistema de control automático es una interconexión de elementos que forman una
configuración denominada sistema, de tal manera que el arreglo resultante es capaz de
controlarse por sí mismo.
Un sistema o componente del sistema susceptible de ser controlado, al cual se le aplica una
señal r(t ) a manera de entrada para obtener una respuesta o salida y(t ), puede representarse
mediante bloques. [1]
Figura 1: Sistema de control en lazo cerrado
Fuente: [2]
Entrada de un sistema de control
Es una variable del sistema controlado que se elige de modo tal que mediante su
manipulación se logra que el sistema cumpla un objetivo determinado.
Las variables de entrada, son variables que ingresan al sistema y no dependen de ninguna
otra variable interna del mismo.
No solo la señal de referencia (valor deseado de la salida del sistema) conforma una variable
de entrada, también hay ciertas señales indeseadas, como son algunas perturbaciones
externas, que se generan fuera del sistema y actúan sobre la planta, afectando
desfavorablemente la salida del sistema, comportándose también como una variable de
entrada, cuyo valor no dependen de ninguna otra variable interna al sistema
Salida de un sistema de control
Es una variable del sistema controlado que se elige de modo tal que mediante su estudio se
analiza si el sistema cumple o no con los objetivos propuestos, en los sistemas realimentados
esta señal de salida contribuye a realizar el control propuesto. [3]
Variable manipulada
Es la cantidad o condición modificada por el controlador a fin de afectar la variable
controlada. Estas afectan el curso del proceso y pueden ser medidas y cambiadas a voluntad.
Es la que se modifica para afectar directamente a la variable controlada, es la herramienta
para modificar la variable directa en el proceso. Es la cantidad que se encarga de variar los
instrumentos finales de control. Es el mensaje del controlador que transmite modificaciones
para lograr lo esperado de la variable controlada. [4]
Lazo abierto
La acción de control se calcula conociendo la dinámica del sistema, las consignas y
estimando las perturbaciones. Esta estrategia de control puede compensar los retrasos
inherentes del sistema anticipándose a las necesidades del usuario. Sin embargo, el lazo
abierto generalmente es insuficiente, debido a los errores del modelo y a los errores en la
estimación de las perturbaciones. Por ello, es común la asociación de lazo cerrado-lazo
abierto, de modo que el lazo cerrado permite compensar los errores generados por el lazo
abierto. [4]
Figura 2: lazo abierto
Fuente: [4]
Lazo cerrado
La acción de control se calcula en función del error medido entre la variable controlada y la
consigna deseada. Las perturbaciones, aunque sean desconocidas son consideradas
indirectamente mediante sus efectos sobre las variables de salida. Este tipo de estrategia de
control puede aplicarse sea cual sea la variable controlada. La gran mayoría de los sistemas
de control que se desarrollan en la actualidad son en lazo cerrado. [4]
Figura 3: lazo cerrado
Fuente: [4]
Resultados
Obtener la respuesta en régimen dinámico y estacionario de los sistemas representados a
continuación:
1. Utilizar en la entrada del sistema las funciones escalón e impulso unitario para obtener
la respuesta dinámica del sistema y obtener la gráfica de respuesta de sistema teniendo
en cuenta el tiempo necesario de simulación para que el sistema llegue al nuevo
régimen estacionario.
1000
a) 𝐺 (𝑠) = (𝑠+1000)
Función escalón
Respuesta en régimen dinámico y estacionario.
Impulso unitario.
Respuesta en régimen dinámico y estacionario.
(2𝑠+3)
b) 𝐺 (𝑠) = (𝑠 3 +3𝑠+4)
Función escalón
Respuesta en régimen dinámico y estacionario.
Impulso unitario.
Respuesta en régimen dinámico y estacionario.
1
1
c) 𝐺 (𝑠) = 𝑠 3 − 𝑠 2 (𝑠+1)
Función escalón
Respuesta en régimen dinámico y estacionario.
Impulso unitario.
Respuesta en régimen dinámico y estacionario.
d) 𝐺 (𝑠) =
𝑠 2 +5𝑠+1
𝑠 2+𝑠+4
Función escalón
Respuesta en régimen dinámico y estacionario.
Impulso unitario.
Respuesta en régimen dinámico y estacionario.
e)
Función escalón.
Respuesta en régimen dinámico y estacionario.
Impulso unitario.
Respuesta en régimen dinámico y estacionario.
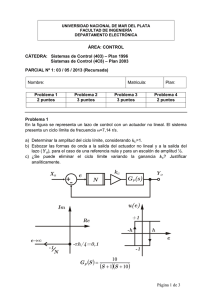
2. Analizar el sistema del inciso 1(e) cuando existe una perturbación de tipo sinusoidal
en el proceso con período de 100 segundos y amplitud de 2.
ANÁLISIS._ como se puede observar en la figura el régimen estacionario tiene una amplitud
constante en todo el tiempo de los 100 segundos que se ha designado para la simulación,
además de ellos en el régimen dinámico al inicio se observa que tiene una amplitud menor
comparado con el régimen estacionario, pero cuando sigue aumentando el tiempo las dos
amplitudes tienen una igualdad.
3. Obtener la función de transferencia equivalente del sistema representado en el
diagrama de bloquea del inciso 1(e).
4. Determinar con las instrucciones de MATLAB los polos y ceros de la función de
transferencia siguiente y evaluar estos polinomios para el valor de las raíces
obtenidas.
𝐺 (𝑠 ) =
2𝑠 3
2𝑠 + 8
+ 3𝑠 2 + 2
Función a utilizar: Se utiliza la función “r = roots( p )” que es la que devuelve las
raíces del polinomio representado por p como vector columna. En este ejercicio se
obtendrá los ceros y polos tanto del numerador como del denominador.
Ceros: -4 (parte de la gráfica que se representa por un círculo)
Polos:
[-0.750000000000000
+
0.661437827766148i;-0.750000000000000
0.661437827766148i] (parte de la gráfica que se representa por un cruce)
Instrucciones del programa:
%4. Determinar con las instrucciones de MATLAB los polos
% y ceros de la función de transferencia siguiente
% y evaluar estos polinomios para el valor de las raíces obtenidas.
num=[2 8];
den=[2 3 2];
ceros=roots(num);
polos=roots(den);
rlocus(num,den)
(a) Utilizar la instrucción step para aplicar un escalón unitario a la función G(s)
-
5. Construir el modelo dinámico del motor de corriente directa controlado por la tensión de
armadura.
Las ecuaciones dinámicas del motor se dan a continuación:
𝑖𝑅 + 𝐿
𝑑𝑖
+ 𝐾𝑒 𝑤 = 𝑉𝑔
𝑑𝑡
𝐾𝑡 𝑖 = 𝐽
𝑑𝑤
+ 𝐵𝑤 + 𝑇𝐿
𝑑𝑡
Donde:
R- Resistencia de armadura
Ke = Ke - Constante electromotriz
J = Inercia del motor
w- velocidad
L = Inductancia de armadura
B = Coeficiente de fricción
Vg – Tensión de la fuente de entrada
TL = Torque de la carga
Θ – Ángulo (posición)
Ke=KT=0.05 Nm/A, R=2 Ω, L=5.2 mH., Vg=-60..60 V, B=6e-6 (Nm)/(rad/s), J=1e-3
Nms2/rad
El sistema obtenido se representa en el diagrama de bloques siguiente:
Fig 1: Diagrama de bloques del motor de corriente continúa
Para el diagrama de bloques de la figura 1:
(a) Determinar la función de transferencia G(s), si la variable de entrada es la fuente de
tensión Vg y la salída el ángulo θ. (Considere que la perturbación no existe TL = 0.)
(b) Determinar con la ayuda del Simulink las respuestas del sistema utilizando el diagrama
de bloques:
Cuando la tensión Vg = 40V y se incrementa en un 10%.
Cuando existe una perturbación en el torque TL que varía 0.05Nm hasta 0.15Nm.
Mostrar las gráficas de variación de velocidad w
En el programa de MATLAB R2017b, se utilizó el siguiente programa para de esta manera
poder observar la onda para poder construir el modelo dinámico del motor de corriente
directa controlado por la tensión además de que se obtiene una recta constante hasta un cierto
punto para luego seguir creciendo y observar una forma de onda respecto al ejercicio
propuesto.
Instrucciones del programa:
%% Ejercicio 5: Construir el modelo dinámico del motor de corriente
directa
% controlado por la tensión de armadura.
% R- Resistencia de armadura
% Ke = Ke - Constante electromotriz
% J = Inercia del motor
% w- velocidad
% L = Inductancia de armadura
% B = Coeficiente de fricción
% Vg – Tensión de la fuente de entrada
% TL = Torque de la carga
% ? – Ángulo (posición)
% Ke=KT=0.05 Nm/A, R=2 ?, L=5.2 mH., Vg=-60..60 V, B=6e-6 (Nm)/(rad/s),
% J=1e-3 Nms2/rad
Vg=60;
Kt=0.05;
Ke=Kt;
R=2;
L=5.2e-03;
B=6e-06;
J=1e-03;
Tls=0;% carga
Tms=Vg*Kt/(R+L*s);
Ws=1/(B+J*s);
Ts=Tms-Tls;
Gps=Ts*Ws;
Gfs=feedback(Gps,Ke)
Theta_s=Gfs*1/s;
figure
step(Theta_s)
Vg=(w/(s^2+w^2));%con funa fuente variable sinusoidal
Tls=0;% carga
Tms=Vg*Kt/(R+L*s);
Ts=Tms-Tls;
Gps=Ts*Ws;
Gfs=feedback(Gps,Ke);
disp('Funcion de transferencia: ')
Theta_s=Gfs*1/s
figure
step(Theta_s)
title('fuente variable sinusoidal')
Preguntas de control
1. Diga cuando tenemos un sistema de malla abierta?
Cuando la salida no tiene efecto sobre el sistema de control, es decir que la salida sensada
del proceso no es comparada con la señal de referencia.
2. Diga cuál es la definición de la variable controlada y la variable de control o
manipulada?
Variable controlada: una variable controlada es una variable del proceso que se quiere
mantener a un valor constante, es decir que si esta varia su variación alteraría las condiciones
requeridas en el sistema, su monitoreo a través de un sensor es una condición importante para
dar inicio al control.
Variable de control o manipulada: variable del proceso que se modifica para corregir el
efecto de la desviación provocada por la perturbación la variable manipulada es la cantidad
o condición que es variada por el controlador de tal manera que afecte el valor de la variable
controlada.
3. Definir qué se entiende por función de transferencia de un sistema?
Se entiende por función de transferencia de un sistema a aquella función matemática lineal
que emplea a la transformada de Laplace y que a la vez permite representar el
comportamiento dinámico y estacionario de cualquier sistema.
Se obtiene a partir de la representación de un sistema LTI por medio de ecuaciones
diferenciales con coeficientes constantes, en un sistema en lazo cerrado es aquel en el que la
salida es realimentada y tiene efecto sobre la señal de control mientras que en un sistema de
lazo abierto es la relación entre la señal del sensor y la señal de error actuante.
4. Explique cuando tenemos un modelo lineal?
Se tiene un modelo lineal cuando se requiere hacer un análisis de regresión simple en dónde
se pretende estudiar y explicar el comportamiento de una variable que notamos y y que se
denominará variable respuesta, variable dependiente o variable de interés a partir de otra
variable, que notamos x y que se denomina variable explicativa, variable independiente,
covariable o regresor, en dónde el principal objetivo de la regresión es encontrar la función
que mejor explique la relación entre la variable dependiente y las independientes, además el
modelo lineal se los utiliza cuando se quiere predecir o explicar una variable dependiente a
partir de una o más variables independientes.
5. Diga cómo es utilizado el principio de superposición en el análisis de los sistemas de
control lineal?
Se puede aplicar el principio de superposición en los sistema que son esencialmente lineales
es decir que cuando las magnitudes de las señales en un sistema de control están limitadas en
intervalos en los cuales los componentes del sistema exhiben una característica lineal, pero
cuando las magnitudes de las señales se extienden más allá del intervalo de porción lineal,
dependiendo de la severidad de la no linealidad, el sistema no se debe seguir considerando
lineal.
Conclusiones
Se obtuvo las respuestas dinámicas de los sistemas que se presentaron en esta práctica
mediante Matlab y con el uso de las funciones de transferencia teniendo así las respuestas en
régimen dinámico y estacionario para de esta manera dar una respuesta gráfica a cada
enunciado.
Con ayuda del programa Matlab y que tiene como herramienta Simulink se pudo simular la
respuesta en el tiempo de los sistemas físicos propuestos en la práctica del laboratorio número
1 y así se entiende que con ayuda de esta simulación cuando un sistema es estable o inestable
además de aplicar nuevas instrucciones para poder obtener los ceros y poder observar los
polos de un sistema de control.
Referencia bibliográfica
[1]
R. Hernández, «Conceptos Generales,» de Introducción a los sistemas de control,
México, Prentice Hall, 2010, pp. 18-22.
[2]
S. Moya, «www.isamex.org,» 24 Diciembre 2018. [En línea]. Available:
https://www.isamex.org/intechmx/index.php/2018/12/24/conceptos-basicossistemas-de-control/.
[3]
A. P. &. E. P. Mario Pérez, «La planta junto con el proceso, conforman un sistema,»
de “INTRODUCCION A
LOS SISTEMAS DE CONTROL Y MODELO
MATEMÁTICO PARA SISTEMAS LINEALES INVARIANTES EN EL TIEMPO.”, San
Juan, Prentice Hall, 2007, pp. 22-25.
[4]
Glosario, «glosarios.servidor-alicante.com,» 12 Junio 2017. [En línea]. Available:
https://glosarios.servidor-alicante.com/instrumentacion/variablemanipulada#:~:text=La%20variable%20manipulada%20es%20la,la%20salida%20de
%20un%20sistema.&text=en%20el%20proceso.,Es%20la%20cantidad%20que%20se%20encarga,los%20instrumentos%20finales%
20de%20.
[5]
J.
Jiménez,
«upcommons.upc.edu,»
2017.
[En
línea].
Available:
https://upcommons.upc.edu/bitstream/handle/2099.1/3330/34059-5.pdf?sequence=5.