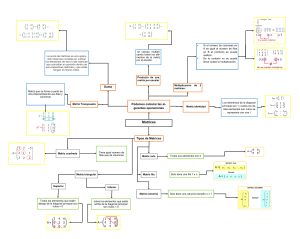
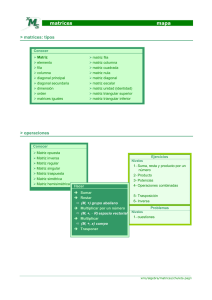
FACULTAD DE CIENCIAS ECONÓMICAS Y EMPRESARIALES PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Matrices PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Matrices Considérese, por ejemplo, un inventario de camisetas en una sección de un gran almacén. Se tienen camisetas de tres diferentes tamaños y cinco colores, y cada noche el supervisor de la sección prepara un inventario de las existencias para la gestión. Un párrafo de dicho inventario podría tener la forma siguiente: “Camisetas.... Nueve amarillas de talla S y cinco amarillas de talla M; ocho S de color verde y seis M verdes; las de tamaño L casi se han agotado pues sólo quedan tres rojas, una rosa y dos negras; también tenemos tres M rosas, cinco M rojas, una M negra y siete S negras...". Rosa Amarillo Verde Rojo negro S 0 9 8 0 7 M 3 5 6 5 1 L 1 0 0 3 2 PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Definición de una matriz Una matriz en ℝ es un arreglo rectangular de números reales distribuidos en filas y columnas. En general, una matriz real 𝐴 que tiene 𝑚 filas y 𝑛 columnas es un ordenamiento de números reales de la forma: 𝐴= 𝑎11 𝑎21 ⋮ 𝑎𝑚1 𝑎12 𝑎22 ⋮ 𝑎𝑚2 ⋯ ⋯ ⋱ ⋯ 𝑎1𝑛 𝑎2𝑛 ⋮ 𝑎𝑚𝑛 Donde 𝑎𝑖𝑗 ∈ ℝ, ∀ 𝑖, 𝑗 ∈ ℕ con 1 ≤ 𝑖 ≤ 𝑚, 1 ≤ 𝑗 ≤ 𝑛. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Notación de una matriz • Si una matriz 𝐴 tiene 𝑚 filas y 𝑛 columnas se dice que 𝐴 es de tamaño 𝑚 × 𝑛 o que 𝐴 es de orden 𝑚 × 𝑛 𝐴𝑚×𝑛 . Si 𝑚 = 𝑛, se dice que 𝐴 es de orden 𝑛 (𝐴𝑛 ). • Cada número real 𝑎𝑖𝑗 del ordenamiento es llamado elemento de 𝐴 o entrada de 𝐴. Este elemento significa que está en la 𝑖-ésima fila y en la 𝑗-ésima columna de 𝐴. Ejercicio: Dadas las siguientes matrices: 1 2 𝑒2 𝐴 = −1 −2 −4 0 ln 2 −4 2 3 0 cos 450 𝐵= 0 0 −1 2 𝐶 ∈ 𝑀2×2 𝑡𝑎𝑙 𝑞𝑢𝑒 𝑐𝑖𝑗 = 𝑖 − 2𝑗 𝑝𝑎𝑟𝑎 𝑡𝑜𝑑𝑜 𝑖, 𝑗 a. ¿Cuál es la dimensión de las matrices? b. ¿Cuál es el elemento? 𝑎22 , 𝑎32 , 𝑏41 , 𝑏22 . Determinar: 𝑎22 ∙ 𝑎23 + 𝑏11 /4. c. Construya la matriz 𝐶. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Ejercicios 1. Escribir la matriz 𝐴 = 𝑎𝑖𝑗 2×3 , donde 𝑎𝑖𝑗 = −1 𝑖+𝑗 . 2. Hallar 𝐴 ,𝐵 𝑦 𝐶 𝐴 = 𝑎𝑖𝑗 𝐵 = 𝑏𝑖𝑗 𝐶 = 𝑐𝑖𝑗 3×3 PROGRAMA ACADÉMICO DE ECONOMÍA 0 𝑠𝑖 𝑖 < 𝑗 tal que: 𝑎𝑖𝑗 = ቐ−1 𝑠𝑖 𝑖 = 𝑗 5×5 𝑖 𝑠𝑖 𝑖 > 𝑗 8 𝑠𝑖 𝑖 ≠ 𝑗 tal que 𝑏𝑖𝑗 = ቊ 6×2 7 + 𝑗 𝑠𝑖 𝑖 = 𝑗 −1 𝑗+1 2𝑖 = ൞ 𝑖 −1 𝑖+𝑗 𝑖+𝑗−1 𝑠𝑖 𝑖 = 1,2,3 , 𝑠𝑖 𝑖 = 1,2,3, 𝑗=1 𝑗 = 2,3 E1MR1 Tipos especiales de matrices 1. Matriz Nula: Todos sus elementos son ceros, 𝑎𝑖𝑗 = 0 ∀ 𝑖, 𝑗 Ejemplo: 0 0 0 𝐴= 0 0 0 0 0 0 2. Matriz vector: Conjunto ordenando de elementos dispuestos o en una fila o en una columna • Vector fila: matriz de una sola fila Ejemplo : 𝐴 = 1 −2 3 • Vector columna: matriz de una sola columna Ejemplo: PROGRAMA ACADÉMICO DE ECONOMÍA 0 𝐵= 5 4 E1MR1 Tipos especiales de matrices 3. Matriz cuadrada: Matriz que tienen el número de filas igual al número de columnas Caracteristicas de una matriz cuadrada: Si tenemos una matriz cuadrada A, donde 𝑎11 ⋯ 𝑎1𝑛 ⋱ ⋮ 𝐴= ⋮ 𝑎𝑛1 𝑎𝑛𝑛 Podemos hablar de la diagonal principal formada por los elementos 𝑎11 , 𝑎22 , ⋯ , 𝑎𝑛𝑛 . La suma de los elementos de la diagonal principal recibe el nombre de traza 𝑛 𝑇𝑟𝑎𝑧𝑎 𝐴 = 𝑎𝑖𝑖 𝑖=1 Una matriz cuadrada 𝐴𝑛×𝑛 también se puede representar como 𝐴𝑛 . PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Tipos especiales de matrices 4. Matriz diagonal : es una matriz cuadrada, cuyos elementos son todos iguales a cero excepto los que pertenecen a la diagonal principal. 2 0 0 𝑃= 0 4 0 0 0 7 5. Matriz escalar: matriz diagonal, cuyos elementos de la diagonal principal son todos iguales 3 0 𝐴= 0 3 6. Matriz identidad: matriz diagonal muy útil, cuyos elementos de la diagonal principal son iguales a la unidad 1 0 0 𝐼= 0 1 0 0 0 1 7. Matriz triangular superior: matriz cuadrada, cuyos elementos que se encuentran debajo de la diagonal principal son iguales a cero. 𝐴𝑖𝑗 = 0 si 𝑖 > 𝑗 2 4 7 𝐵= 0 4 9 0 0 5 PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Tipos especiales de matrices 8. Matriz triangular inferior: cuyos elementos que se encuentran encima de la diagonal principal son iguales a cero. 𝐴𝑖𝑗 = 0 si 𝑖 < 𝑗. 4 0 0 𝐶= 8 2 0 1 9 1 9. Matriz simétrica: matriz cuadrada, donde los elementos simétricos , son iguales, es decir cada 𝑎𝑖𝑗 = 𝑎𝑗𝑖 . (𝐴 = 𝐴𝑡 ). 3 9 7 𝐸= 9 5 2 7 2 7 10. Matriz antisimétrica: matriz cuadra que cumple con 𝑎𝑖𝑗 = −𝑎𝑗𝑖 . (𝐴 = −𝐴𝑡 ). 4 1 3 𝐺 = −1 8 6 −3 −6 2 11. Matriz rectangular : matriz donde el número de filas no coincide con el número de columnas. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Ejercicios 1. ¿Para qué valores de 𝑎, la matriz 𝐵 es simétrica? 𝑎 𝑎2 − 1 −3 𝐵 = 𝑎+1 2 𝑎2 + 4 −3 4𝑎 −1 2. Calcule 𝑥 e 𝑦 para que la matriz 𝐴 sea antisimétrica: 0 2𝑥 1 0 −4𝑥 𝐴 = 𝑥2 𝑦+1 𝑥 0 3. Si 𝐵 es una matriz antisimétrica cuyos elementos de la diagonal principal son ceros y que cumple que: −4 0 2 𝐵 = 0 −4 Hallar los elementos de la matriz 𝐵. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Operaciones con matrices PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Operaciones con Matrices 1. Igualdad de Matrices: Las matrices 𝐴 y 𝐵 son iguales, si y sólo si tienen la misma dimensión y cada elemento de 𝐴 es igual al correspondiente de 𝐵. 𝐴 = 𝐵 si y sólo si 𝑎𝑖𝑗 = 𝑏𝑖𝑗 para todo 𝑖, 𝑗 2. Suma de matrices: Las matrices se pueden sumar, si y sólo si tienen la misma dimensión y el resultado se obtiene sumando los elementos que ocupan el mismo lugar en las matrices, 3. Producto de un número real por una matriz: El producto de un número real 𝑘 por una matriz 𝐴𝑚×𝑛 es una matriz que resulta de multiplicar el escalar por cada uno de los elementos de la matriz. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Ejercicios 1. Encontrar 𝑎, 𝑏, 𝑐 y 𝑑 para que satisfaga la igualdad: −𝑎 2 3 𝑏−𝑎 𝑎 𝑏 2 = + 1 3𝑑 𝑐+𝑑 4 𝑐 𝑑 2. Determine, de ser posible, valores para 𝑥, 𝑦, 𝑧 ∈ ℝ. De manera que se cumpla la igualdad de matrices. −5 −7 𝑦 0.5 , 𝐵 = • 𝐴= − 16 𝑥 − 1 𝑧+1 1 − 49 𝜋 cos − ln 𝑒 4 𝑦 − 2𝑥 𝑥2 − 1 92 •𝐶 = 𝑦 𝑧+𝑦 3 2 ,𝐷 = −1 𝑦 PROGRAMA ACADÉMICO DE ECONOMÍA −52 −3 3 −3 2 4 −25 𝑦 + 𝑧 𝑦𝑧 −1 E1MR1 Multiplicación de matrices Dos matrices sólo se pueden multiplicar sin son multiplicativamente conformes, y esto se verifica cuando el número de columnas del multiplicando coincide con el número de filas del multiplicador. 𝐴𝑚×𝑛 × 𝐵𝑛×𝑝 = 𝐶𝑚×𝑝 Cuando se multiplican 2 matrices, el elemento 𝑐𝑖𝑗 de la matriz producto, es el producto del i-ésimo vector fila de la primera matriz con el j-ésimo vector columna de la segunda (producto interior). 𝑛 𝑛 𝑎1𝑗 𝑏𝑗1 ⋯ 𝑗=1 𝐴𝑚×𝑛 × 𝐵𝑛×𝑝 = 𝐶𝑚×𝑝 = 𝑐𝑖𝑗 𝑚×𝑝 = ⋱ 𝑎𝑚𝑗 𝑏𝑗1 ⋯ 𝑗=1 PROGRAMA ACADÉMICO DE ECONOMÍA 𝑗=1 ⋮ 𝑛 𝑎1𝑗 𝑏𝑗𝑝 𝑛 ⋮ 𝑎𝑚𝑗 𝑏𝑗𝑝 𝑗=1 E1MR1 Propiedades de la multiplicación matricial • 𝐴𝑚×𝑛 × 𝐵𝑛×𝑝 × 𝐶𝑝×𝑞 = 𝐴𝑚×𝑛 × 𝐵𝑛×𝑝 × 𝐶𝑝×𝑞 : Asociativa • 𝐴𝑚×𝑛 × 𝐵𝑛×𝑝 + 𝐶𝑝×𝑞 = 𝐴𝑚×𝑛 × 𝐵𝑛×𝑝 + 𝐴𝑚×𝑛 × 𝐶𝑝×𝑞 Distributiva : • 𝑎 𝐵𝑛×𝑝 × 𝐶𝑝×𝑞 = 𝑎𝐵𝑛×𝑝 × 𝐶𝑝×𝑞 = 𝐵𝑛×𝑝 × 𝑎𝐶𝑝×𝑞 • 𝐼 × 𝐴 = 𝐴 × 𝐼 = 𝐴 ( 𝐴 es una matriz cuadrada): Identidad multiplicativa • 0 × 𝐴 = 𝐴 × 0 = 0 (𝐴 y 0 son matrices cuadradas) PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Multiplicación de matrices Tres asesores en redes, Alan, María y Esteban, recibieron un bono a fin de año, de $10000 para cada uno, y decidieron invertir en un plan de retiro 401K auspiciado por su empresa. Bajo este plan, cada empleado puede colocar sus inversiones en tres fondos, un fondo accionario I, un fondo de desarrollo II, y un fondo global III. Las distribuciones de las inversiones de los tres empleados al principio del año se resumen en la siguiente matriz: Alan A= María Esteban I II III 4000 3000 3000 2000 5000 3000 2000 3000 5000 B= I 0.18 II 0.24 III 0.12 Los reditos de los tres fondos después de un año están dados por la matriz B. ¿Cuál empleado obtuvo los mejores réditos en su inversión para el año en cuestión? PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Matriz transpuesta: La matriz transpuesta de una matriz 𝐴, designada por 𝐴𝑡 , se obtiene creando una matriz cuya 𝑘-ésima fila es la 𝑘-ésima columna de la matriz original. Propiedades de las matrices transpuestas, siendo 𝑨 y 𝑩 matrices: a) Si A es de orden 𝑚 × 𝑛 entonces 𝐴𝑡 es de orden 𝑛 × 𝑚 𝐴 + 𝐵 𝑡 = 𝐴𝑡 + 𝐵𝑡 . 𝐴𝑡 𝑡 = 𝐴. 𝑘𝐴 𝑡 = 𝑘𝐴𝑡 , 𝑘 es un esclar. 𝐴 × 𝐵 𝑡 = 𝐵𝑡 × 𝐴𝑡 , siempre y cuando 𝐴 y 𝐵 sean multiplicativamente conformes. f) Si 𝐴 es simétrica 𝐴 = 𝐴𝑡 b) c) d) e) PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Potenciación de una matriz Para poder efectuarla, la matriz tiene que ser cuadrada. Se obtiene al multiplicar 𝑛 veces la matriz por si misma. Es decir: 𝐴𝑛 = 𝐴 × 𝐴 × ⋯ × 𝐴 En caso que 𝑛 = 0 entonces 𝐴0 = 𝐼 (matriz identidad). Propiedades de la potenciación que son válidas para cualquier entero positivo 𝒎 y 𝒏. a) 𝐴𝑛 × 𝐴𝑚 = 𝐴𝑛+𝑚 . b) 𝐴𝑛 𝑚 = 𝐴𝑛×𝑚 . c) 𝑐𝐴 𝑛 = 𝑐 𝑛 𝐴𝑛 . PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Otras matrices especiales Sea 𝐴 una matriz cuadrada: • La matriz 𝐴 es una matriz periódica si y solo si, ∃ 𝑝 ∈ ℤ+ , tal que 𝐴𝑝+1 = 𝐴. El menor entero positivo 𝑝 con el que satisfaga 𝐴𝑝+1 = 𝐴 se llama periodo de 𝐴. • La matriz 𝐴 es una matriz idempotente si y solo si, 𝐴2 = 𝐴. • La matriz 𝐴 es una matriz nilpotente si y solo si, ∃ 𝑛 ∈ ℤ+ , tal que 𝐴𝑛 = 𝑂𝑚 . El menor entero positivo 𝑛 con el que se satisfaga la igualdad 𝐴𝑛 = 𝑂𝑚 se llama índice de nilpotencia. • La matriz 𝐴 es una matriz involutiva si cumple que 𝐴2 = 𝐼. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Ejercicios 1. Halla una matriz 𝐵, sabiendo que su primera fila es 1 0 , y que verifica 1 0 −1 2 2 𝐴𝐵 = , 𝑠𝑖𝑒𝑛𝑑𝑜 𝐴 = 1 0 2 1 0 2. Sea la matriz 1 0 1 𝐴= 0 1 0 0 0 1 Determine 𝐴𝑛 , para 𝑛 ∈ ℕ. 2 −2 −4 3. Pruebe que la matriz 𝐴 = −1 3 4 es idempotente. 1 −2 −3 PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Ejercicios Rpta: 1 1. 𝐵 = −1 2 1 2. 𝐴𝑛 = 0 0 0 0 0 0 𝑛 1 0 0 1 PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Polinomio de matrices Con las matrices también se pueden evaluar funciones polinómicas. La matriz resultante se halla efectuando todas las operaciones antes descritas. Generalmente se usan matrices cuadradas 3 7 y los siguientes polinomios: 5 1 𝑃 𝑥 = 𝑥 3 − 𝑥 + 𝑥 2 y 𝑄 𝑥 = 𝑥 2 + 3𝑥 + 1 Hallar 𝑃(𝐵) y 𝑄(𝐵). Ejercicio: Sea 𝐵 = PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Problema Cindy realiza llamadas regulares de larga distancia a Londres, Tokio y Hong Kong. Las matrices 𝐴 y 𝐵 dan las longitudes (en minutos) de sus llamadas en horas pico y no pico, respectivamente, a cada una de estas ciudades durante el mes de junio A= Londres Tokio Hong Kong 86 66 78 B= Londres Tokio Hong Kong 345 151 356 Los costos de llamadas para los periodos pico y no pico en el mes en cuestión están dados, respectivamente, por las matrices: Londres 𝐶 = Tokio Hong Kong 0.44 0.32 0.68 Londres 𝐷 = Tokio Hong Kong 0.14 0.51 0.75 Calcule la matriz 𝐴 × 𝐶 + 𝐵 × 𝐷 y explique lo que representa. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Problema En la sala de un hospital dedicado al tratamiento de diabéticos se administra insulina de tres clases: Semilenta, lenta y ultralenta. El número de unidades diarias que se aplica a los 5 pacientes ingresados viene dado por la siguiente tabla. A= Paciente I II II IV V Semilenta 15 15 20 30 10 Lenta 20 20 15 5 20 Ultralenta 10 5 10 10 15 Número de días (𝑁) que ha estado internado cada paciente 𝐵= Paciente I II III IV V N días 3 7 5 12 20 Calcule con la ayuda de producto de matrices, las unidades de cada clase que fueron administradas a los pacientes. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Problema La matriz 𝐴 da el porcentaje de votantes elegibles en la ciudad de Alewton, clasificados según su afiliación partidista y grupo de edad. Dem. 𝐴= Rep. Ind. Menores de 30 0.50 0.30 0.20 De 30 a 50 0.45 0.40 0.15 Mayor a 50 0.40 0.50 0.10 La matriz 𝐵 representa la población de votantes elegibles en la ciudad por grupo de edad. Menor de 30 𝐵 = 30000 De 30 a 50 Mayor de 50 40000 20000 Halle la matriz que proporcione el número total de votantes elegibles en la ciudad que votarán por un candidato demócrata, repúblicano o independiente. PROGRAMA ACADÉMICO DE ECONOMÍA E1MR1 Bibliografía 1. Bazán, C.; Fernández, R. Álgebra lineal para administración y economía. Publicaciones. Universidad de Piura, 2006. 2. Larson, Ron y Falvo, David. Fundamentos de Álgebra Lineal. Sexta edición 2010. CENGAGE Learning. Editores, S.A. 3. Stanley L. Grossman. Álgebra Lineal. Séptima Edición. 2012. McGrawHill/INTERAMERICANA EDITORES S.A DE C.V. PROGRAMA ACADÉMICO DE ECONOMÍA ÁLGEBRA LINEAL