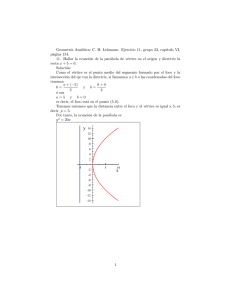
1 REPÚBLICA DE PANAMÁ MINISTERIO DE EDUCACIÓN DIRECCIÓN REGIONAL DE BOCAS DEL TORO INSTITUTO PROFESIONAL Y TÉCNICO EL SILENCIO UNDÉCIMO GRADO SEGUNDO TRIMESTRE 2021 (Del 14 de junio al 3 de septiembre) MÓDULO DE MATEMÁTICA PROFESORA: 𝑬𝒍𝒊𝒂𝒏𝒂 𝑺𝒆𝒓𝒓𝒂𝒏𝒐 𝑪𝒐𝒆̂𝒍𝒉𝒐 CONTACTO: 6465-9719 CORREO ELECTRÓNICO: [email protected] GRADO: 11° (A,B,C,D,E,F,) BACHILLER EN AGROPECUARIA NOMBRE DEL ESTUDIANTE: ______________________________________ GRUPO: ___________________________ N° CÉDULA: _______________________ CORREO ELECTRÓNICO: ________________________________ NÚMERO DE TELÉFONO: _______________________ 2 MENSAJE Respetado participante El COVID-19 ha golpeado la sociedad, la economía, el comercio, el deporte, y muchas cosas más. Que no golpee nuestra fe y nuestros deseos de superarnos en la vida, por lo tanto, mantengámonos firmes en cumplir todas y cada una de nuestras metas. Bienvenidos a este curso de Matemática 2021, de undécimo grado bachiller en Agropecuaria. El módulo que se pone a su disposición tiene como meta lograr que usted tenga las destrezas y habilidades básicas para solucionar problemas de manera autónoma, usando conocimientos matemáticos firmes, estrategias y modelos de representaciones diversas basadas en sus habilidades de pensamientos lógicos - creativo y con una actitud de apertura favorable para solucionar situaciones, además, es prescindible lograr que usted, joven estudiante logre desarrollar conocimientos, habilidades y destrezas del pensamiento geométrico a través de la identificación, investigación, planteamientos y resolución de problemas basados en los conceptos, formas y espacios geométricos sobresalientes, observables y aplicables en el contexto para representar y describir geométricamente a partir de modelos concretos, su realidad. Claro está, es necesario que se familiarice con la terminología, el procedimiento y las aplicaciones según el caso. Espero que las instrucciones, el desarrollo de los ejercicios y las actividades de aprendizaje, sean de su comprensión y contribuyan a fortalecer sus conocimientos en Matemática, materia fundamental para el crecimiento cognitivo y la destreza del pensamiento lógico deductivo. A continuación, se presenta una serie de actividades correspondientes a las temáticas a desarrollar durante este segundo trimestre del año lectivo 2021, las mismas deberán ser desarrolladas y entregadas en la plataforma classroom tratando de respetar las fechas límites de entrega para cada una. 3 ÍNDICE Mensaje para los estudiantes…………………………………………………….3 Geometría Analítica……………………………………………………..…….…5 Tema 1. Ecuación de la recta……………………………………..………..……5 Formas de la ecuación de la recta y pendiente…………………………….…...5 Forma pendiente ordenada al origen……………………………………………7 Actividad # 1…………………………………….…………………………..…….9 Forma punto pendiente…………………………………………………..……..11 Forma estándar de la recta………………………………………………….….14 Actividad # 2……………………………………………………………………..17 Forma general de la recta…………………………………………………….…19 Actividad # 3……………………………………………………………………..21 Tema 2. Las secciones cónicas…………………………………………………..23 La parábola……………………………………………………….……………...24 Ecuaciones de la parábola………………………………………….……………24 Actividad # 4……………………………………………………………………...28 Cronograma de Actividades……………………………………………………..30 Sugerencias e información importante………………………………..………...31 4 GEOMETRÍA ANALÍTICA Tema # 1: ECUACIÓN DE LA RECTA Formas de las Ecuaciones de una Recta y Pendiente La pendiente de una recta es una medida de su inclinación. Matemáticamente, la pendiente se calcula como "desplazamiento vertical entre el desplazamiento horizontal", es decir cambio en “𝑦” dividido entre cambio en “𝑥” Se dice que la recta que pasa por 𝐴 (𝑥1, 𝑦1) y 𝐵 (𝑥2, 𝑦2) donde 𝑥1 ≠ 𝑥2, se define la pendiente “𝑚” de esta recta como: 𝑃𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒 = 𝐷𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 ∆𝑦 = 𝐷𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 ∆𝑥 𝑚= 𝐸𝑙𝑒𝑣𝑎𝑐𝑖ó𝑛 𝑦2 − 𝑦1 = 𝐴𝑣𝑎𝑛𝑐𝑒 𝑥2 − 𝑥1 Para profundizar, en la definición de la pendiente, te recomendamos que observes el siguiente video. Accede aquí o copia la dirección https://youtu.be/jpIOnLHIxrg EJEMPLO 1: Dada la gráfica de una recta, determine su pendiente. Observar la figura 1 Figura 1 5 Solución: Para determinar la pendiente, marquemos dos puntos por donde pasa la recta, pueden ser 𝐴(2,5) y 𝐵(8,2). Observar la figura 2 Figura 2 𝑃𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒 = 𝑚= 𝐷𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝐷𝑒𝑠𝑝𝑙𝑎𝑧𝑎𝑚𝑖𝑒𝑛𝑡𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 ∆𝑦 𝑦2 − 𝑦1 = ∆𝑥 𝑥2 − 𝑥1 6 𝑚= 2−5 8−2 𝑚=− Figura 3 3 3 6 Observar en la figura 3, que por cada seis unidades que se mueve horizontalmente hacia la derecha en la recta, se mueve tres unidades verticalmente hacia abajo en la recta. 6 Forma pendiente ordenada al origen Ahora que se hizo el repaso del concepto de pendiente veremos las diferentes formas de la ecuación de la recta: La forma pendiente-ordenada al origen es una representación específica de las ecuaciones lineales y tiene la siguiente estructura: 𝒚 = 𝒎𝒙 + 𝒃 En la ecuación anterior, 𝒎 y 𝒃 pueden ser números reales cualesquiera. Por ejemplo, las siguientes ecuaciones lineales corresponden a la forma pendiente-ordenada al origen: 𝒚 = 𝟒𝒙 − 𝟔 𝒚 = −𝟖𝒙 + 𝟑, 𝟓 𝒚 = 𝟏𝟐 − 𝟏𝟒𝟒𝒙 La forma pendiente-ordenada al origen es la más destacada de las representaciones que hay para las ecuaciones lineales. Por las siguientes razones a mencionar: La forma pendiente-ordenada al origen tiene la ventaja de que exhibe las dos características principales de la recta que representa: La pendiente es 𝒎 La coordenada 𝒚 de la intersección con el eje 𝒚 es 𝒃. Es decir, la recta se interseca con el eje en (0, 𝒃) Por ejemplo, la recta 𝒚 = 𝟒 𝒙 – 𝟔 tiene pendiente 𝟒 y se interseca con el eje 𝒚 en: (0, −6). Como podemos ver, en la Figura 4, esta representación da la pendiente y la ordenada al origen (es decir, la intersección de la recta con el eje y) y es la razón por la cual se llama forma pendienteordenada al origen. Figura 4 7 EJEMPLO 2: ¿Cuál es la pendiente de la recta representada por 𝒚 = 𝟑 𝒙 + 𝟓? Solución: Recuerda que en la forma 𝒚 = 𝒎 𝒙 + 𝒃, la pendiente está dada por 𝒎. Por lo tanto, 𝒚 = 𝟑 𝒙 + 𝟓 tiene una pendiente de 3. EJEMPLO 3: ¿Cuál es la ordenada al origen de la recta representada por 𝒚 = −𝟓 𝒙 − 𝟖? Solución: En la forma 𝒚 = 𝒎 𝒙+𝒃, la ordenada al origen está dada por 𝒃. En la intersección con el eje 𝒚, 𝒙 siempre es igual a cero. Por lo tanto, 𝒚 = −𝟓 𝒙 – 𝟖 se interseca con el eje 𝒚 en el punto (0, −8) EJEMPLO 4: ¿Cuál es la ordenada al origen de la recta representada por 𝒚 = 𝟕𝒙? Solución: Recuerde que en la forma 𝒚 = 𝒎 𝒙 + 𝒃 la ordenada al origen está dada por 𝒃. Si el término 𝒃 no aparece, eso quiere decir que 𝒃 es igual a cero. De otra manera, podemos escribir la ecuación dada como: 𝒚 = 𝟕 𝒙 + 𝟎. Por lo tanto, 𝒚 = 𝟕 𝒙 + 𝟎 se interseca con el eje 𝒚 en el punto (0,0). EJEMPLO 5: ¿Cuál es la pendiente de la recta representada por 𝒚 = 𝟐 − 𝟒 𝒙? Solución: Recuerda que en la forma 𝒚 = 𝒎 𝒙 + 𝒃, la pendiente está dada por 𝒎. Por lo tanto, 𝒚 = 𝟐 − 𝟒 𝒙 tiene una pendiente de −𝟒. 8 Al enviar su actividad, cada hoja del documento, o cada imagen que envía, debe ser identificado con su nombre y grado, escrito con bolígrafo azul o negro; además debe desarrollar toda la actividad a mano. De lo contrario, no se evaluará. I Parte. Seleccione con un gancho la respuesta correcta. 1) ¿Cuáles rectas se intersecan con el eje y en el punto (0, 3)? 𝒚=−𝟒𝒙+𝟑 𝒚=𝟑𝒙+𝟐 𝒚=𝟔+𝟑𝒙 𝒚=𝟑–𝒙 2) ¿Cómo encontramos la pendiente de una recta que está dada en forma pendiente- ordenada al origen? La pendiente es el primer número que aparece en la ecuación La pendiente es el coeficiente que multiplica a 𝒙, sin importar el orden en el que aparece. 3) ¿Cuáles de las siguientes rectas, su pendiente es -8? 𝒚=8𝒙−8 𝒚=−8𝒙+8 𝒚=−8−8𝒙 𝒚 = 8 + 8𝒙 II Parte. Responda de acuerdo con lo solicitado. 1) Escriba la ecuación de una recta cuya pendiente es 9 y se interseca con el eje 𝒚 en (0, −12). Solución: 2) ¿Cuál es el punto de intersección de la recta 𝑦 = −7 𝑥 − 2 con el eje 𝑦? Solución: 3) ¿Cuál es la pendiente de 𝑦 = −15? Solución: 4) ¿Cuál es la pendiente de 𝑦 = 6𝑥 − 11? Solución: 9 RÚBRICA PARA EVALUAR ACTIVIDAD# 1 Grado que cursa: Fecha de entrega: 25 de junio de 2021 Tema: Formas de la ecuación de la recta y pendiente ordenada al origen. Valor: 35 puntos Objetivo: Utiliza razonamiento, en sus conclusiones y síntesis y es coherente al resolver las actividades propuestas. CRITERIOS A EVALUAR/PUNTAJE Detalles Excelente (7) Muy bien (de 5 a 6) Bien (de 2 a 4) Regular (1) Total Falta mucho más de Falta la mitad de Desarrollo Completo Casi completo la mitad de los los ejercicios ejercicios En sus respuestas se En casi todas sus En algunas Sus respuestas nota que distingue respuestas se nota respuestas se nota demuestran la claramente el que distingue que distingue confusión que tiene Respuestas procedimiento claramente el claramente el para distinguir los adecuado para cada procedimiento procedimiento procedimientos caso. adecuado para cada adecuado para adecuados para cada caso. cada caso. caso. Todas las Casi todas las La mitad de las Mucho más de la actividades son actividades son actividades son mitad de las Conclusión resueltas resueltas resueltas actividades son correctamente correctamente correctamente resueltas incorrectamente. Presenta cada Presenta cada Presenta cada Presenta cada ejercicio en forma ejercicio en forma ejercicio r en ejercicio en forma ordenada, clara y ordenada y clara forma ordenada, descuidada y Claridad y organizada; de pero u poco pero muy difícil de desorganizada, de organización manera que es desorganizada; de evaluar, por falta manera que es muy sencillo evaluar. manera que es un de claridad y difícil evaluar. poco difícil de organización. evaluar. Entrega en la fecha Entrega un día Entrega dos días Entrega tres o más Puntualidad indicada después de la fecha. después de la días después de la fecha. fecha. Total: 10 Forma punto pendiente. La forma punto-pendiente es una forma específica de ecuaciones lineales en dos variables: 𝒚 − 𝒃 = 𝒎 (𝒙 – 𝒂) Cuando una ecuación está escrita en la forma punto-pendiente, 𝑚 da la pendiente de la recta y el punto (𝒂, 𝒃) es un punto por donde pasa la recta. Esta forma se deriva de la fórmula de la pendiente. Para profundizar, en la definición punto-pendiente, le recomendamos observar el siguiente video2. Acceda aquí o copie la dirección https://youtu.be/tsv4KJ-9ais EJEMPLOS: En este ejemplo se obtiene como dato la pendiente y un punto de la recta. 1. En este ejemplo se obtiene como dato la pendiente y un punto de la recta. Determinar la ecuación de la recta que pasa por (𝟐, 𝟕) y cuya pendiente es –𝟑 Solución: Para ello sustituimos 𝑚 = −3, 𝑎 =2 y 𝑏 = 7 en la forma puntopendiente y graficamos. 𝒚 − 𝒃 = 𝒎(𝒙– 𝒂) 𝒚 − 𝟕 = −𝟑(𝒙– 𝟐) 𝒚 − 𝟕 = −𝟑𝒙 + 𝟔 𝒚 = −𝟑𝒙 + 𝟔 + 𝟕 𝒚 = −𝟑𝒙 + 𝟏𝟑 Figura 5 11 2. En este ejemplo se obtiene como dato dos puntos de la recta. Determinar la recta que pasa por los puntos (𝟒, 𝟑) y (𝟓, 𝟕). Solución: Para hallar la solución, primero usamos los dos puntos para encontrar la pendiente: 𝑚= ∆𝑦 ∆𝑥 𝑚= 𝑦2 − 𝑦1 𝑥2 − 𝑥1 𝑚= 7−3 5−4 𝒎= 𝟒 =𝟒 𝟏 Figura 6 Ahora usamos uno de los puntos, tomaremos (4,3), y escribimos la ecuación en la forma puntopendiente. 𝑦 − 𝑏 = 𝑚(𝑥– 𝑎) 𝑦 − 3 = 4(𝑥– 4) 𝑦 − 3 = 4𝑥 − 16 𝑦 = 4𝑥 − 16 + 3 𝒚 = 𝟒𝒙 − 𝟏𝟑 3. Observe la gráfica y determine la ecuación en la forma punto-pendiente a partir de dos puntos. 12 Figura 7 Solución: Para realizar esta actividad necesitamos un punto y la pendiente que encontraremos a través de la representación gráfica que nos dan. Para ello seleccionamos un punto por donde pasa la recta, escogeremos (4, 3) y la pendiente la determinamos de forma gráfica seleccionando dos puntos por donde pasa la gráfica, escogeremos (4,3) y (2, −1) como muestra la Figura 8 A partir de dos puntos. Seleccionaremos los puntos (4, 3) y (2, −1) para determinar la pendiente de forma algorítmica: 𝑚= 𝑚= ∆𝑦 ∆𝑥 𝑦2 − 𝑦1 𝑥2 − 𝑥1 𝑚= −1 − 3 2−4 𝒎= −𝟒 =𝟐 −𝟐 Figura 8 ∆𝒚 = −𝟒 ∆𝒙 = −𝟐 Ahora usamos uno de los puntos, tomaremos (4,3), y escribimos la ecuación en la forma puntopendiente. 𝑦 − 𝑏 = 𝑚(𝑥– 𝑎) 𝑦 − 3 = 2(𝑥– 4) 𝑦 − 3 = 2𝑥 − 8 𝑦 = 2𝑥 − 8 + 3 𝒚 = 𝟐𝒙 − 𝟓 13 Forma estándar de la recta. La forma estándar de las ecuaciones lineales de dos variables es: 𝑎𝑥 + 𝑏𝑦 = 𝑐 Generalmente en esta forma, 𝑎, 𝑏 y 𝑐 son todos enteros. Para profundizar, en la forma estándar de la recta, le recomendamos observar el siguiente video2. Acceda aquí o copie la dirección https://youtu.be/utUMbgmOm30 Cuando tenemos una ecuación lineal en forma estándar, podemos encontrar sus intersecciones con los ejes 𝑥 y 𝑦. Esto también nos permite graficarla. Observemos la ecuación 2𝑥 + 3𝑦 = 12. Si hacemos 𝑥 = 0, obtenemos la ecuación 3𝑦 = 12, y rápidamente podemos decir que: 𝑦 = 4, lo que significa que la intersección con el eje y es (0,4). De manera similar, podemos hacer 𝑦 = 0 para obtener 2𝑥 = 12 y encontrar que la intersección con el eje 𝑥 es (6,0). Ahora podemos graficar la recta. Lo dicho anteriormente se resume en la siguiente tabla: Ecuación Valor para x Valor para y Sustitución Punto 𝟐(𝟎) + 𝟑𝒚 = 𝟏𝟐 𝟎 + 𝟑𝒚 = 𝟏𝟐 𝟑𝒚 = 𝟏𝟐 0 4 𝟏𝟐 (𝟎, 𝟑) 𝒚= 𝟑 𝒚=𝟒 𝟐𝒙 + 𝟑𝒚 = 𝟏𝟐 𝟐𝒙 + 𝟑(𝟎) = 𝟏𝟐 𝟐𝒙 + 𝟎 = 𝟏𝟐 𝟐𝒙 = 𝟏𝟐 6 0 (𝟔, 𝟎) 𝟏𝟐 𝒙= 𝟐 𝒙=𝟔 La gráfica que resulta es la siguiente: 14 Figura 9 EJEMPLOS: 1. ¿Cuál es la intersección de la recta 𝟑𝒙 – 𝟔𝒚 = 𝟏𝟐 con el eje 𝒙? Solución: Para encontrar la intersección con el eje 𝑥 haremos 𝑦 = 0, podemos decir: 𝟑𝒙 − 𝟔𝒚 = 𝟏𝟐 𝟑𝒙 − 𝟔(𝟎) = 𝟏𝟐 𝟑𝒙 − 𝟎 = 𝟏𝟐 𝟑𝒙 = 𝟏𝟐 𝒙= 𝟏𝟐 𝟑 𝒙=𝟒 Lo que significa que la intersección con el eje 𝑥 es (4,0). ¿Cuál es la intersección con el eje y? Para encontrar la intersección con el eje y haremos 𝑥 = 0, podemos decir: 𝟑𝒙 − 𝟔𝒚 = 𝟏𝟐 𝟑(𝟎) − 𝟔𝒚 = 𝟏𝟐 𝟎 − 𝟔𝒚 = 𝟏𝟐 −𝟔𝒚 = 𝟏𝟐 𝒚= 𝟏𝟐 −𝟔 𝒚 = −𝟐 Lo que significa que la intersección con el eje 𝑦 es (0, −2). Figura 10 15 2. ¿Qué es 𝒚 − 𝟓 = 𝟏𝟑 (𝒙 – 𝟐) escrito en forma estándar? Solución: En algunos casos, como al resolver sistema de ecuaciones, podríamos querer convertir una ecuación escrita de manera distinta para ponerla en la forma estándar. Convertiremos la ecuación 𝑦 − 5 = 13 (𝑥 – 2) a la forma estándar: 𝒚 − 𝟓 = 𝟏𝟑(𝒙 − 𝟐) 𝒚 − 𝟓 = 𝟏𝟑𝒙 − 𝟐𝟔) 𝒚 = 𝟏𝟑𝒙 − 𝟐𝟔 + 𝟓) 𝒚 − 𝟏𝟑𝒙 = −𝟐𝟏 −𝟏𝟑𝒙 + 𝒚 = −𝟐𝟏 3. Convierta la ecuación 𝒚 = 𝟐 𝟕 𝒙 + 𝟗 a la forma estándar. Solución: Convertiremos la ecuación 𝒚 = 𝟐 𝟐 𝟕 𝒙 + 𝟗 a la forma estándar: 𝒚= 𝒙+𝟗 𝟕 𝟕𝒚 = 𝟐𝒙 + 𝟔𝟑 𝟕𝒚 − 𝟐𝒙 = 𝟔𝟑 −𝟐𝒙 + 𝟕𝒚 = 𝟔𝟑 16 Al enviar su actividad, cada hoja del documento, o cada imagen que envía, debe ser identificado con su nombre y grado, escrito con bolígrafo azul o negro; además debe desarrollar toda la actividad a mano. De lo contrario, no se evaluará. 1. Determine la ecuación de la recta que pasa por los puntos (5, −2) y (1, −3) en la forma puntopendiente. 2. Dada la siguiente gráfica, figura 11, determine la ecuación de la recta de la forma punto- pendiente. Figura 11 3. Tenemos la ecuación de la forma punto-pendiente 𝑦 − 9 = −4 (𝑥 – 4) identifique el punto (𝑎, 𝑏) y la pendiente. 4. Necesitamos determinar la ecuación de la recta en la forma punto-pendiente que pasa por (5, −3) y tiene pendiente −7. ¿Cómo lo haría? 5. ¿Cuál es la pendiente de la recta 𝑦 − 8 = 11 (𝑥 – 1)? Y ¿Por cuál punto pasa la recta? Seleccione con un gancho la respuesta correcta. (8,1) (−1, −8) (1, 8) (−8, −1) (8, 11) (11, 1) 17 6. ¿Cómo se escribe 𝒚 = −𝟑𝒙 − 3𝑥 + 𝑦 = −3 9 𝑦 = −18 𝑥 − 3 27 𝑥 + 9 𝑦 = −2 9 𝑥+ 9 𝑦 = 3 𝟐 𝟗 en la forma estándar? 7. ¿Cuál es la intersección de la recta 7𝑥 – 3𝑦 = −21 con el eje 𝑥 y con el eje 𝑦? 8. ¿Qué es 𝑦 + 8 = −3(𝑥 + 5) escrito en forma estándar? 4. Grafique −5𝑥 + 3 𝑦 = 15 RÚBRICA PARA EVALUAR ACTIVIDAD# 2 Grado que cursa: Fecha de entrega: 15 de julio de 2021 Tema: Forma punto pendiente y estándar de la recta. Valor: 35 puntos Objetivo: Utiliza razonamiento, en sus conclusiones y síntesis y es coherente al resolver las actividades propuestas. CRITERIOS A EVALUAR/PUNTAJE Detalles Excelente (7) Muy bien (de 5 a 6) Bien (de 2 a 4) Regular (1) Total Desarrollo Respuestas Conclusión Claridad y organización Puntualidad Completo Casi completo En sus respuestas se nota que distingue claramente el procedimiento adecuado para cada caso. En casi todas sus respuestas se nota que distingue claramente el procedimiento adecuado para cada caso. Todas las actividades son resueltas correctamente Casi todas las actividades son resueltas correctamente Presenta cada ejercicio en forma ordenada, clara y organizada; de manera que es sencillo evaluar. Presenta cada ejercicio en forma ordenada y clara pero u poco desorganizada; de manera que es un poco difícil de evaluar. Entrega un día después de la fecha. Entrega en la fecha indicada Falta la mitad de los ejercicios Falta mucho más de la mitad de los ejercicios En algunas respuestas se nota que distingue claramente el procedimiento adecuado para cada caso. La mitad de las actividades son resueltas correctamente Sus respuestas demuestran la confusión que tiene para distinguir los procedimientos adecuados para cada caso. Mucho más de la mitad de las actividades son resueltas incorrectamente. Presenta cada ejercicio r en forma ordenada, pero muy difícil de evaluar, por falta de claridad y organización. Presenta cada ejercicio en forma descuidada y desorganizada, de manera que es muy difícil evaluar. Entrega dos días después de la fecha. Entrega tres o más días después de la fecha. Total: 18 De estos temas, se va a desarrollar una prueba en classroom. La misma se habilitará el día 16 de julio de 2021. Forma general de la recta. La forma general de la recta es 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 donde 𝑎, 𝑏 y 𝑐 son números reales. La forma general de la ecuación de una recta contempla tanto a las rectas verticales como a las que no lo son. De la ecuación general se puede despejar 𝑦 de tal manera que se puede determinar la forma pendiente-ordenada al origen así: 𝒂𝒙 + 𝒃𝒚 + 𝒄 = 𝟎 𝒃𝒚 = − 𝒂𝒙 − 𝒄 −𝒂𝒙 − 𝒄 𝒚 = 𝒃 𝒂 𝒄 𝒚=− 𝒙− 𝒃 𝒃 Por lo tanto, la pendiente de la recta sería, 𝒎 = − 𝒂 𝒃 𝒄 y la intersección con el eje 𝑦 sería; (𝟎, − ) 𝒃 EJEMPLOS: 1. ¿Cuál es la forma general de la ecuación 𝒚 = 𝟓𝒙 + 𝟑? Solución: Para expresar 𝑦 = 5𝑥 + 3 en la forma general de la recta basta con pasar todos los términos a un lado de la ecuación: 𝒚 = 𝟓𝒙 + 𝟑 − 𝟓𝒙 + 𝒚 − 𝟑 = 𝟎 𝟓𝒙 − 𝒚 + 𝟑 = 𝟎 2. ¿Cuál es la forma general de la ecuación de la recta que pasa por (−𝟒, 𝟐) y tiene pendiente 𝟔? Solución: Con los datos que nos proporcionan podemos escribir la ecuación de la recta en la forma puntopendiente para luego escribirla en su forma general así: 𝒚 − 𝒃 = 𝒎(𝒙 − 𝒂) 𝒚 − 𝟐 = 𝟔(𝒙 + 𝟒) 𝒚 − 𝟐 = 𝟔𝒙 + 𝟐𝟒 𝒚 − 𝟐 − 𝟔𝒙 − 𝟐𝟒 = 𝟎 −𝟔𝒙 + 𝒚 − 𝟐𝟔 = 𝟎 𝟔𝒙 − 𝒚 + 𝟐𝟔 = 𝟎 19 3. ¿Cuál es la pendiente y la ordenada al origen de la recta 𝒙 + 𝟑𝒚 – 𝟗 = 𝟎? De la ecuación general se puede despejar 𝑦 de tal manera que se puede determinar la forma pendienteordenada al origen así: 𝒙 + 𝟑𝒚 − 𝟗 = 𝟎 𝟑𝒚 = − 𝒙 + 𝟗 −𝒙 + 𝟗 𝒚 = 𝟑 𝟏 𝟗 𝒚=− 𝒙+ 𝟑 𝟑 Por lo tanto, la pendiente de la recta sería, 𝒎 = − simplificar 𝟗 𝟑 𝟏 𝟑 𝟗 y la intersección con el eje 𝑦 sería; (𝟎, ) que al 𝟑 queda (𝟎, 𝟑) 20 Al enviar su actividad, cada hoja del documento, o cada imagen que envía, debe ser identificado con su nombre y grado, escrito con bolígrafo azul o negro; además debe desarrollar toda la actividad a mano. De lo contrario, no se evaluará. 1. ¿Cómo se escribe 𝑦 = −9𝑥 + 15 en la forma general? Escoja una respuesta: 9𝑥 + 𝑦 = 15 −9𝑥 + 𝑦 + 15 = 0 −9𝑥 + 𝑦 − 15 = 0 9𝑥 + 𝑦 − 15 = 0 2. ¿Cuál es la forma general de la ecuación 3𝑦 = −8𝑥 − 11? 3. ¿Qué es 𝑦 + 12 = −7(𝑥 − 6) escrito en forma general? 4. ¿Cuál es la forma general de la ecuación de la recta que pasa por (7, −8) y tiene pendiente 9? 21 RÚBRICA PARA EVALUAR ACTIVIDAD# 3 Grado que cursa: Fecha de entrega: 30 de julio de 2021 Tema: Forma general de la recta. Valor: 35 puntos Objetivo: Utiliza razonamiento, en sus conclusiones y síntesis y es coherente al resolver las actividades propuestas. CRITERIOS A EVALUAR/PUNTAJE Detalles Excelente (7) Muy bien (de 5 a 6) Bien (de 2 a 4) Regular (1) Total Falta mucho más de Falta la mitad de Desarrollo Completo Casi completo la mitad de los los ejercicios ejercicios En sus respuestas se En casi todas sus En algunas Sus respuestas nota que distingue respuestas se nota respuestas se nota demuestran la claramente el que distingue que distingue confusión que tiene Respuestas procedimiento claramente el claramente el para distinguir los adecuado para cada procedimiento procedimiento procedimientos caso. adecuado para cada adecuado para adecuados para cada caso. cada caso. caso. Todas las Casi todas las La mitad de las Mucho más de la actividades son actividades son actividades son mitad de las Conclusión resueltas resueltas resueltas actividades son correctamente correctamente correctamente resueltas incorrectamente. Presenta cada Presenta cada Presenta cada Presenta cada ejercicio en forma ejercicio en forma ejercicio r en ejercicio en forma ordenada, clara y ordenada y clara forma ordenada, descuidada y Claridad y organizada; de pero u poco pero muy difícil de desorganizada, de organización manera que es desorganizada; de evaluar, por falta manera que es muy sencillo evaluar. manera que es un de claridad y difícil evaluar. poco difícil de organización. evaluar. Entrega en la fecha Entrega un día Entrega dos días Entrega tres o más Puntualidad indicada después de la fecha. después de la días después de la fecha. fecha. Total: 22 TEMA # 2. LAS SECCIONES CÓNICAS. Hagamos un poco de historia: En el siglo XVI el filósofo y matemático René Descartes (1596-1650) desarrolló un método para relacionar las curvas con ecuaciones. Este método es la llamada Geometría Analítica. En la Geometría Analítica las curvas cónicas se pueden representar por ecuaciones de segundo grado en las variables 𝒙 e 𝒚. El resultado más sorprendente de la Geometría Analítica es que todas las ecuaciones de segundo grado en dos variables representan secciones cónicas.3 Las secciones cónicas son curvas que pueden obtenerse como la intersección de un cono circular recto con un plano que no contenga el vértice del cono. Una superficie cónica de revolución o cono de doble hoja se obtiene al girar una recta alrededor de una recta fija llamada eje. Figura 12 El punto de corte de ambas rectas es el vértice de la superficie cónica. Las diferentes cónicas se obtienen al intersecar una superficie cónica con un plano. Las curvas obtenidas pueden ser: una parábola, una circunferencia, una elipse o una hipérbola. Figura 13 El plano es paralelo a la generatriz de la superficie cónica El plano corta de forma perpendicular a la superficie cónica. El plano corta transversalmente a la superficie cónica. El plano es paralelo al eje de la superficie cónica. Si desea aprender más sobre las secciones cónicas, le recomendamos mirar con detenimiento el video que aparece en el enlace debajo de la figura 13. Para profundizar, en la forma estándar de la recta, le recomendamos observar el siguiente video4. Acceda aquí o copie la dirección https://www.youtube.com/watch?v=a26ErrkU_-M 23 Iniciaremos con el estudio de las secciones cónicas, en particular con la parábola como recomienda el Currículo priorizado del MEDUCA para el área de Profesional y Técnica. La parábola: Las parábolas se conocen comúnmente como las gráficas de funciones cuadráticas. Pueden también verse como el conjunto de todos los puntos cuya distancia desde un punto determinado (el foco) es igual a su distancia desde una línea determinada (la directriz)4. Elementos de una parábola: 𝐹𝑜𝑐𝑜 (𝑓): 𝐸𝑠 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑓𝑖𝑗𝑜. 𝑉é𝑟𝑡𝑖𝑐𝑒 (𝑣): 𝐸𝑠 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑚𝑒𝑑𝑖𝑜 𝑒𝑛𝑡𝑟𝑒 𝑒𝑙 𝑓𝑜𝑐𝑜 𝑦 𝑙𝑎 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑧. 𝐷𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑧 (𝑑): 𝐸𝑠 𝑙𝑎 𝑟𝑒𝑐𝑡𝑎 𝑓𝑖𝑗𝑎. 𝑃𝑎𝑟á𝑚𝑒𝑡𝑟𝑜 (𝑝): 𝐸𝑠 𝑙𝑎 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑒𝑛𝑡𝑟𝑒 𝑒𝑙 𝑓𝑜𝑐𝑜 𝑦 𝑒𝑙 𝑣é𝑟𝑡𝑖𝑐𝑒 𝑑𝑒 𝑢𝑛𝑎 𝑝𝑎𝑟á𝑏𝑜𝑙𝑎. 𝐿𝑎𝑑𝑜 𝑟𝑒𝑐𝑡𝑜 (𝐿𝑟): 𝑐𝑢𝑒𝑟𝑑𝑎 𝑞𝑢𝑒 𝑝𝑎𝑠𝑎 𝑝𝑜𝑟 𝑒𝑙 𝑓𝑜𝑐𝑜 𝑦 𝑒𝑠 𝑝𝑎𝑟𝑎𝑙𝑒𝑙𝑎 𝑎 𝑙𝑎 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑧. 𝐸𝑠 𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡𝑒 𝑎 4 𝑣𝑒𝑐𝑒𝑠 𝑒𝑙 𝑝𝑎𝑟á𝑚𝑒𝑡𝑟𝑜 (4𝑝). Foco (f) Vértice (v) Directriz (d) Parámetro (p) Lado recto (Lr) Figura 14 Ecuaciones de la parábola: Veremos cómo se grafica una parábola cuando se conoce el foco y la directriz. Es importante comprender la siguiente tabla para la resolución de ejercicios. Abre hacia arriba (𝑥 − ℎ)2 = 4𝑝(𝑦 − 𝑘) Abre hacia abajo Abre hacia la derecha (𝑥 − ℎ)2 = −4𝑝(𝑦 − 𝑘) (𝑦 − 𝑘)2 = 4𝑝(𝑥 − ℎ) Figura 15 Abre hacia la izquierda (𝑦 − 𝑘)2 = −4𝑝(𝑥 − ℎ) 24 EJEMPLOS: 1. ¿Cuál es la ecuación de la parábola con foco en (6, -4) y directriz en 𝑦 = −7? Solución: Para encontrar la ecuación de la parábola usaremos la siguiente parrilla o tabla, donde ubicaremos primeramente los valores que nos da el enunciado del problema para luego de acuerdo con las definiciones ir buscando el resto. Le recomendamos antes de iniciar tener a mano su plano coordenado para que represente primeramente los valores que le facilita el enunciado y luego los que va obteniendo en el transcurso de la solución. De acuerdo con los datos que nos proporciona la directriz (𝑦 = −7), nuestra parábola puede abrir hacia arriba o hacia abajo, ya que al extenderse la parábola no toca la directriz. Cuando graficamos y=-7 se comprende mejor hacia dónde abre la parábola y se complementa cuando ubicamos el foco. Recuerde que el vértice se encuentra entre la directriz y el foco. Elemento Foco (f) Procedimiento (6, -4) Observación Me lo facilita el enunciado Calculamos la distancia entre el foco y un punto en la directriz usando la fórmula de la distancia entre dos puntos, que corresponde al teorema de Pitágoras. El punto (6,-7) lo obtenemos de la gráfica. Es el punto medio entre el foco y la directriz. Se puede calcular con la fórmula de la distancia entre dos puntos o identificar gráficamente. Cuando representamos el punto f en el plano y la directriz (d) nos damos cuenta de que entre ambos hay una distancia de 3 unidades. Como el vértice es el punto medio entre el foco y la directriz podemos calcularlo dividiendo 3÷2=1,5 𝑥1 𝑦1 𝑥2 𝑦2 ⏞ ) 𝑦 (⏞ ⏞) (⏞ 6 , −4 6 , −7 Vértice (v) 𝑑 = √(𝑦2 − 𝑦1 )2 + (𝑥2 − 𝑥1 )2 𝑑 = √(−7 − (−4))2 + (6 − 6)2 𝑑 = √(−7 + 4)2 + (0)2 𝑑 = √(−3)2 + 0 𝑑 = √9 𝑑=3 Luego 𝟑 ÷ 𝟐 = 𝟏, 𝟓 Por lo tanto, el vértice tiene coordenadas (𝟔, −𝟓. 𝟓) Directriz (d) 𝒚 = −𝟕 Parámetro (p) 𝒑 = 𝟏, 𝟓 Me lo facilita el enunciado. Su representación en el plano coordenado nos facilita entender hacia dónde puede abrir nuestra parábola. En este caso abre hacia arriba. Es la distancia entre el foco y el vértice de la parábola. El cálculo anterior nos permite encontrar esa distancia, la cual es de 1,5 (una unidad con cinco décimas). También se puede obtener a través de la distancia entre dos puntos. 25 Lado recto (Lr) 𝑳𝒓 = 𝟒𝒑 = 𝟒(𝟏, 𝟓) = 𝟔 unidades El lado recto indica la abertura de la parábola Coordenadas del vértice: ℎ 𝑘 ⏞) ⏞ , −5,5 (6 Ecuación Cuerda que pasa por el foco y es paralela a la directriz. Es equivalente a 4 veces el parámetro (4p). Puede realizar las operaciones con la ayuda de una calculadora. 𝑝 = 1,5 (𝑥 − ℎ)2 = 4𝑝(𝑦 − 𝑘) (𝑥 − 6)2 = 4(1,5)(𝑦 + 5,5) (𝑥 − 6)2 = 6(𝑦 + 5,5) (𝑥 − 6)2 = 6𝑦 + 33 (𝑥 − 6)2 − 33 = 6𝑦 6𝑦 = (𝑥 − 6)2 − 33 (𝑥 − 6)2 33 𝑦= − 6 6 (𝒙 − 𝟔)𝟐 𝟏𝟏 𝒚= − 𝟔 𝟐 Figura 16 2. ¿Cuál es la ecuación de la parábola con foco en (-4, 8) y directriz en 𝑥 = −6? Solución: Para encontrar la ecuación de la parábola usaremos la parrilla o tabla parecida al ejemplo 1. De acuerdo con los datos de la directriz 𝑥 = −6 nuestra parábola puede abrir hacia la derecha o hacia la izquierda, para su mejor comprensión se recomienda graficar la recta. Elemento Procedimiento Observación Me lo facilita el enunciado Foco (f) (−𝟒, 𝟖) Vértice (v) Calculamos la distancia entre el foco y un punto en la directriz usando la fórmula de la distancia entre dos puntos, que corresponde al teorema de Pitágoras. El punto (6,-7) lo Es el punto medio entre el foco y la directriz. Se puede calcular con la fórmula de la distancia entre dos puntos o identificar gráficamente. 26 obtenemos de la gráfica. 𝑥1 𝑦1 𝑥2 𝑦2 ⏞,⏞ ⏞,⏞ (−4 8 ) 𝑦 (−6 8) 𝑑 𝑑 𝑑 𝑑 𝑑 𝑑 = √(𝑦2 − 𝑦1 )2 + (𝑥2 − 𝑥1 )2 = √(8 − 8)2 + (−6 − (−4))2 = √(0)2 + (−6 + 4)2 = √0 + (−2)2 = √4 =2 Cuando representamos el punto f en el plano y la directriz (d) nos damos cuenta de que entre ambos hay una distancia de 2 unidades. Como el vértice es el punto medio entre el foco y la directriz podemos calcularlo dividiendo 2÷2=1 Luego 2 ÷ 𝟐 = 1 Por lo tanto, el vértice tiene coordenadas (−𝟓, 𝟖) Directriz (d) 𝒙 = −𝟔 Parámetro (p) 𝒑=𝟏 𝑳𝒓 = 𝟒𝒑 = 𝟒(𝟏) = 𝟒 unidades El lado recto indica la abertura de la parábola Lado recto (Lr) Coordenadas del vértice: ℎ 𝑘 ⏞ ,⏞ (−5 8) Ecuación Me lo facilita el enunciado. Su representación en el plano coordenado nos facilita entender hacia dónde puede abrir nuestra parábola. En este caso abre hacia la derecha. Es la distancia entre el foco y el vértice de la parábola. El cálculo anterior nos permite encontrar esa distancia, la cual es de 1 (una unidad). También se puede obtener a través de la distancia entre dos puntos. Cuerda que pasa por el foco y es paralela a la directriz. Es equivalente a 4 veces el parámetro (4p). Puede realizar las operaciones con la ayuda de una calculadora. 𝑝=1 (𝑦 − 𝑘)2 = 4𝑝(𝑥 − ℎ) (𝑦 − 8)2 = 4(1)(𝑥 + 5) (𝑦 − 8)2 = 4(𝑥 + 5) (𝑦 − 8)2 = 4𝑥 + 20 (𝑦 − 8)2 − 20 = 4𝑥 4𝑥 = (𝑦 − 8)2 − 20 (𝑦 − 8)2 20 𝑥= − 4 4 𝟐 (𝒚 − 𝟖) 𝒙= −𝟓 𝟒 Si necesita ver más ejemplos desarrollados sobre cómo encontrar la ecuación de la parábola le recomendamos ver el video que se encuentra en el siguiente enlace: https://www.youtube.com/watch?v=5Vgy7tdMC2k O ingrese aquí Figura 17 27 Al enviar su actividad, cada hoja del documento, o cada imagen que envía, debe ser identificado con su nombre y grado, escrito con bolígrafo azul o negro; además debe desarrollar toda la actividad a mano. De lo contrario, no se evaluará. 1. Determine la ecuación de las parábolas con los siguientes elementos: a. Foco (−2,5) y directriz en 𝑦 = 3 5 5 b. Foco (0, − 2) y directriz en 𝑦 = − 2 c. Foco (−5,0) y directriz en 𝑥 = 5 d. Foco (0, −2) y directriz en 𝑥 = 5 Puede usar como guía la siguiente tabla: Elementos Foco (f) Vértice (v) Directriz (d) Parámetro (p) Lado recto (Lr) Ecuación Procedimiento 2. ¿Cuáles son los elementos (foco, vértice y parámetro), la longitud del lado recto, la directriz y la ecuación de la siguiente parábola de la figura 18? Figura 18 28 3. Dada la siguiente parábola de la figura 19, encuentre: a. Coordenada del foco: b. Coordenada del vértice: c. Longitud del parámetro: d. Longitud del lado recto: e. Ecuación de la parábola: Figura 19 RÚBRICA PARA EVALUAR ACTIVIDAD# 4 Grado que cursa: Fecha de entrega: 19 de agosto de 2021 Tema: Ecuación de la parábola. Valor: 35 puntos Objetivo: Utiliza razonamiento, en sus conclusiones y síntesis y es coherente al resolver las actividades propuestas. Detalles Desarrollo Respuestas Conclusión Claridad y organización Puntualidad CRITERIOS A EVALUAR/PUNTAJE Excelente (7) Muy bien (de 5 a 6) Bien (de 2 a 4) Regular (1) Completo Casi completo Falta la mitad de los ejercicios Falta mucho más de la mitad de los ejercicios En sus respuestas se nota que distingue claramente el procedimiento adecuado para cada caso. En casi todas sus respuestas se nota que distingue claramente el procedimiento adecuado para cada caso. En algunas respuestas se nota que distingue claramente el procedimiento adecuado para cada caso. Todas las actividades son resueltas correctamente Casi todas las actividades son resueltas correctamente La mitad de las actividades son resueltas correctamente Sus respuestas demuestran la confusión que tiene para distinguir los procedimientos adecuados para cada caso. Mucho más de la mitad de las actividades son resueltas incorrectamente. Presenta cada ejercicio en forma ordenada, clara y organizada; de manera que es sencillo evaluar. Presenta cada ejercicio en forma ordenada y clara pero u poco desorganizada; de manera que es un poco difícil de evaluar. Presenta cada ejercicio r en forma ordenada, pero muy difícil de evaluar, por falta de claridad y organización. Presenta cada ejercicio en forma descuidada y desorganizada, de manera que es muy difícil evaluar. Entrega en la fecha indicada Entrega un día después de la fecha. Entrega dos días después de la fecha. Entrega tres o más días después de la fecha. Total Total: 29 De la ecuación de la parábola, se va a desarrollar una prueba en classroom. La misma se habilitará el día 20 de julio de 2021. CRONOGRAMA DE ACTIVIDADES Actividad a evaluar Formas de la ecuación de la recta y pendiente ordenada al origen Forma punto pendiente y estándar de la recta Evaluación sumativa # 1 (Vía Classroom) Forma general de la recta La parábola Evaluación sumativa # 2 (Vía Classroom) Prueba trimestral (Vía Classroom) Fecha de entrega 25 de junio de 2021 15 de julio de 2021 16 de julio de 2021 30 de julio de 2021 19 de agosto de 2021 20 de agosto de 2021 31 de agosto de 2021 30 SUGERENCIAS E INFORCACIÓN IMPORTANTE Las actividades deben ser entregadas en formato de PDF por medio de la plataforma de Classroom. Para su apreciación se tomará en cuenta la entrega puntual de las actividades y pruebas, además de su responsabilidad al cumplir con la entrega de todo. Todas las actividades deben ser resueltas a mano y cada hoja o imagen que envíe debe tener su nombre y grado. Deben estar pendiente de entregar las actividades en las fechas indicadas en el cronograma. Cada actividad tiene una rúbrica que detalla lo que se le va a tomar en cuenta, asegúrese de cumplir con cada punto. Cada estudiante debe comunicarse con mi persona al número 6465 9719, para facilitarle el código de clase en Classroom (Al comunicarse, poner su nombre completo y el grupo al que pertenece) Estar pendientes a las fechas de evaluaciones sumativas. Este trimestre se va a llevar a cabo la prueba trimestral. 31 32