mcgraw-hill - solucionario fisica-quimica 4º eso -sin contraseña

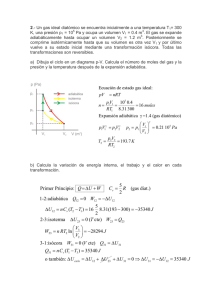
4
Física y química
Solucionario
MADRID • BARCELONA • BUENOS AIRES • CARACAS • GUATEMALA • LISBOA • MÉXICO
NUEVA YORK • PANAMÁ • SAN JUAN • SANTAFÉ DE BOGOTÁ • SANTIAGO • SÃO PAULO
AUCKLAND • HAMBURGO • LONDRES • MILÁN • MONTREAL • NUEVA DELHI • PARÍS
SAN FRANCISCO • SIDNEY • SINGAPUR • ST. LOUIS • TOKIO • TORONTO
http://www.mcgraw-hill.es
crÉDiToS
Física y química · 4.o Eso
solucioNario
no está permitida la reproducción total o parcial de este libro, ni su tratamiento informático, ni la transmisión de ninguna forma o por cualquier medio, ya sea electrónico,
mecánico, por fotocopia, por registro u otros métodos, sin el permiso previo y por escrito
de los titulares del copyright.
Derechos reservados © 2008, respecto a la primera edición en español, por:
McGraw-Hill/interamericana de España, S.a.u.
Edificio Valrealty, 1.ª planta
Basauri, 17
28023 aravaca (Madrid)
isbN: 978-84-481-6298-6
Depósito legal:
autores del libro del alumno: Ángel r. cardona, José antonio García,
Ángel Peña, antonio Pozas, antonio José Vasco
autor de la Guía Didáctica: antonio José Vasco
autora de atención a la Diversidad: reyes de la Vega
Equipo Editorial: Bernardino Pérez, Daniel Zarazaga, anna Katarina Victoria,
Sergio nombela
Equipo Preimpresión: Javier aranda, Eduardo Márquez, luis Hernández,
María de los Ángeles ramírez, Patricia Fernández
Diseño de cubierta: islagrafica.com
Diseño de interior: Germán alonso
maquetación: artedís Producción Gráfica, S.l.l.
ilustraciones: Pilar Bermejo, Mamen canalda
Fotografías: Getty images, cover, age Fotostock, Prisma archivo Fotográfico
impresión:
imPrEso EN EsPaÑa - PriNTED iN sPaiN
2
SuMario
Libro del alumno . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
Introducción: Medidas y método científico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
Unidad 1.
El movimiento de los cuerpos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
Unidad 2.
Las fuerzas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
Unidad 3.
Las fuerzas y el movimiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
Unidad 4.
Estática de fluidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
Unidad 5.
Fuerzas gravitacionales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
Unidad 6.
Trabajo, potencia y energía mecánica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
Unidad 7.
Calor y energía térmica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
Unidad 8.
La energía de las ondas: luz y sonido . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
Unidad 9.
Los elementos químicos y sus enlaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
Unidad 10. Las reacciones químicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
Unidad 11. Reacciones químicas de interés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
Unidad 12. La química de los compuestos del carbono . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
Unidad 13. La Física y la Química en el mundo en que vivimos . . . . . . . . . . . . . . . . . . . .
76
Anexo. Formulación y nomenclatura de los compuestos inorgánicos . . . . . . . . . . . . . . . .
80
Guía didáctica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Introducción: Medidas y método científico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
Unidad 1.
El movimiento de los cuerpos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
Unidad 2.
Las fuerzas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
96
Unidad 3.
Las fuerzas y el movimiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99
Unidad 4.
Estática de fluidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
104
Unidad 5.
Fuerzas gravitacionales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
111
Unidad 6.
Trabajo, potencia y energía mecánica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
114
Unidad 7.
Calor y energía térmica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
120
Unidad 8.
La energía de las ondas: luz y sonido . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
124
Unidad 9.
Los elementos químicos y sus enlaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
128
Unidad 10. Las reacciones químicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
131
Unidad 11. Reacciones químicas de interés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
136
Unidad 12. La química de los compuestos del carbono . . . . . . . . . . . . . . . . . . . . . . . . . . .
138
Unidad 13. La Física y la Química en el mundo en que vivimos . . . . . . . . . . . . . . . . . . . .
142
3
Atención a la diversidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
4
Unidad 1.
El movimiento de los cuerpos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
146
Unidad 2.
Las fuerzas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
147
Unidad 3.
Las fuerzas y el movimiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
148
Unidad 4.
Estática de fluidos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
149
Unidad 5.
Fuerzas gravitacionales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
150
Unidad 6.
Trabajo, potencia y energía mecánica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
152
Unidad 7.
Calor y energía térmica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
153
Unidad 8.
La energía de las ondas: luz y sonido . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
154
Unidad 9.
Los elementos químicos y sus enlaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
156
Unidad 10. Las reacciones químicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
158
Unidad 11. Reacciones químicas de interés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
159
Unidad 12. La química de los compuestos del carbono . . . . . . . . . . . . . . . . . . . . . . . . . . .
162
Unidad 13. La Física y la Química en el mundo en que vivimos . . . . . . . . . . . . . . . . . . . .
166
Solucionario
libro
nI
inTroDucciÓn:
MEDiDaS Y MÉToDo ciEnTÍFico
EJErcicios
1 Cita 10 magnitudes derivadas y escribe el nombre
de la unidad que tienen en el SI.
Respuesta libre. Ejemplos: velocidad (m/s), aceleración (m/s2),
cantidad de movimiento (kg m/s), impulso (N s), fuerza (N
—newton—), energía (J —julio—), calor (J), trabajo (J), potencia (W —vatio—), cantidad de electricidad (C —culombio—), diferencia de potencial (V —voltio—), resistencia
(Ω —ohmio—) que ya conozcan y velocidad angular (rad/s),
aceleración angular (rad/s2), frecuencia (Hz —hercio o hertzio—), etcétera.
2 Busca en Internet o en libros el valor de 10 constantes físicas y escríbelas en notación científica con unidades del Sistema Internacional.
Respuesta libre.
3 Escribe el valor de π y de 3 con 5 cifras significativas, redondeando el número si es preciso. Recuerda que
lo puedes hacer con la calculadora.
π ≈ 3,141 592 653 589 793 238 462 643 383 279 502 884 197
169 399 375 105 820 974 944 592 307 816 406 286 208 998
628 034 825 342 117 067 982 148 086 … ≈ 3.141 59
3 ≈ 1,732 050 807 568 877 293 527 446 341 505 872 366
942 805 253 810 380 628 055 806 979 451 933 016 908 800
037 081 146 186 757 248 575 675 626… ≈ 1,732 05
4 Si tengo un reloj preciso puesto en hora perfectamente (es exacto) en Valencia y me voy volando a Tenerife, ¿sigue siendo correcta la hora que marca el reloj si
no lo cambio de hora? ¿Sigue siendo exacto el reloj? ¿Y
preciso? ¿Cuánto vale el sesgo que tiene el reloj?
6
La hora ya no es correcta puesto que, por convenio, la hora en
Canarias es una unidad anterior a la de la Península. El reloj ha
dejado de ser exacto, pues no marca la hora correcta, aunque
sigue siendo igual de preciso que era en Valencia. Lo que ha
variado es que antes tenía un sesgo nulo y ahora tiene un
sesgo de una hora de adelanto sobre la hora correcta.
5 Haz un trabajo buscando en Internet o en libros el
nombre de 10 aparatos de medida, quién los fabricó por
primera vez (si es posible), qué magnitud miden, si existe
la versión analógica y/o digital y cómo se utilizan.
Respuesta abierta. Hay multitud de aparatos de medida que
pueden contestar como respuesta. Enunciar aquí todas las
posibilidades excede el espacio del que disponemos. En
Wikipedia, «instrumento de medición», hay una enumeración exhaustiva de aparatos de medida con su historia, en
la mayoría de los casos (http://es.wikipedia.org/wiki/Instrumento_de_medici%C3%B3n).
6 Intenta averiguar por qué, si pesamos un objeto con
una balanza y una báscula en la Tierra, da el mismo valor, mientra que si lo hacemos en la Luna da valores distintos.
En la Tierra, una balanza compararía el objeto con una serie
de pesas que equivalen a su peso y a su masa, ya que se
ven atraídas por la Tierra de igual forma (objeto y pesas). Lo
mismo sucede en la Luna, aunque ahora la fuerza de atracción sea menor, pero lo es por igual para los dos conjuntos
(objeto y pesas). En la Tierra, una báscula compara el peso
del objeto con la compresión que produce en un muelle, que
se ha calibrado para medir pesos en la Tierra, por lo que el
valor que se obtendrá será el correcto. En la Luna, el objeto
pesa menos, comprime o estira menos el muelle y el valor
obtenido será menor al del peso del objeto en la Tierra (la
sexta parte).
El MoViMiEnTo DE loS cuErPoS
EJErcicios
1 Coloca las siguientes posiciones en el sistema cartesiano y dibuja una posible trayectoria para el móvil:
a) (1, 2); b) (2, 4); c) (5, 7); d) (8, 9); e) (11, 11); f) (12, 15) y
g) (14, 20).
1
dolo en el velocímetro, ¿por qué empleamos la representación gráfica y el cálculo de la pendiente para obtener
la velocidad? ¿Qué ventajas tiene resolver el problema
mediante el método gráfico? ¿Crees que es importante el
número de datos que se obtengan a la hora de emplear
este método?
Se trata, simplemente, de colocar los puntos señalados en
un diagrama de coordenadas.
2 ¿Tiene el mismo valor el desplazamiento que el espacio recorrido?
El desplazamiento no tiene por qué coincidir con el espacio
recorrido (ver libro de texto).
3 ¿En qué caso coinciden el desplazamiento y el espacio recorrido?
Cuando la trayectoria seguida por el móvil coincide con el
desplazamiento.
4 Representa gráficamente la velocidad frente al tiempo de los datos recogidos en la Tabla 1.1. Ten en cuenta
que la velocidad debes expresarla en m/s.
a) ¿Qué conclusiones obtienes de la gráfica?
b) ¿Cuánto vale el área encerrada entre la línea que has
obtenido, el valor de tiempo t = 60 s y el eje de abscisas?
c) Calcula matemáticamente, aplicando la correspondiente ecuación, el espacio recorrido por el corredor
en los primeros 60 s del movimiento.
d) ¿Qué conclusiones obtienes de los resultados obtenidos en los apartados b) y c)?
v (m/s)
Porque la representación gráfica ajusta de forma correcta y
lo más aproximada posible los datos de una experimentación, ya que es difícil que los datos experimentales se ajusten
exactamente a rectas. Para evitar esos pequeños errores se
hace el ajuste por el método de mínimos cuadrados de los
puntos experimentales que en principio se ajustan a una recta. De esa forma, eliminamos el posible error experimental.
Por ello, el número de datos ha de ser el máximo posible.
Al calcular la pendiente de la gráfica ajustada a los puntos
se obtiene el valor medio e igualmente se minimizan los
errores.
6 El guepardo puede llegar a correr a 30 m/s. Calcula:
a) Cuál es su velocidad en km/h.
b) Cuánto tiempo tardaría en recorrer 1 km.
a) 30
b) t =
m 1 km 3 600 s
km
⋅
⋅
= 108
s 1000 m 1 h
h
e
1 km
=
= 0,00925 horas = 33,3 s
v 108 km
h
7 Calcula la velocidad media del ejemplo anterior
empleando unidades del SI.
6,6
225
t (s)
a) Estamos ante un movimiento rectilíneo uniforme.
e 300
700
v= =
= 6, 6 ⋅m s −1 ;
= 6, 6 ⋅m s −1
t
45
105
1100
1500
= 6, 6 ⋅m s −1 ;
= 6, 6 ⋅m s −1
165
225
b) A = 6,6 · 225 = 1 485 m2
c) e = 6,6 · 60 = 396 m
d) Que, al ser el mismo, el área contenida debajo de la recta
y la ecuación e = v t representan lo mismo.
5 Si se puede calcular la velocidad del coche mediante
una simple división entre el espacio y el tiempo o leyén-
88
km 1000 m
1h
m
⋅
⋅
= 24, 4
h 27, 81 km 3 600 s
s
8 ¿Puede ser la velocidad instantánea diferente de la
velocidad media?
Sí, pues la velocidad media es el cociente entre el espacio
recorrido y el tiempo empleado en recorrerlo, mientras que
la velocidad instantánea es la velocidad del móvil en un instante dado.
9 ¿Podrías decir en qué tipo de movimiento coincide
siempre la velocidad media con la velocidad instantánea?
En el movimiento uniforme constante.
7
1
10 ¿Únicamente con el dato de la velocidad de un coche
puedes saber si tiene aceleración?
Sí, pues la velocidad va variando con el tiempo, su cociente
es la aceleración. Si la velocidad del móvil fuera constante la
aceleración sería cero.
11 ¿Qué conclusiones obtienes de la gráfica representada en la Fig. 1.10?
Que el movimiento en la primera parte del recorrido lleva
velocidad variable y, por lo tanto, es uniformemente variado
y en la segunda parte del recorrido lleva velocidad constante,
lo que implica aceleración cero y responde a un movimiento
rectilíneo uniforme.
12 Compara las gráficas v-t de los movimientos MRU y
MRUA. ¿Qué diferencias observas?
b)
e (m)
t (s)
15 Con los conocimientos que has adquirido, completa
la siguiente tabla y deduce las ecuaciones que faltan.
Velocidad
v = f(v0 , a, t)
v f = v0 + a t
Aceleraciones
Espacio
a = f(v0 , e, t)
e = f(v0 , a, e)
a=
e=
Tiempo
t = f(v0 , v, a)
t=
v = f(v0 , e, t)
2e
vf =
– v0
t
a = f(v0 , v, e)
e = f(v0 , v, a)
t = f(v0 , v, e)
a=
e=
t=
v = f(v0 , a, e)
a = f(v0 , v, t)
vf = √v + 2 a e
a=
e = f(v0 , a, t)
t = f(v0 , e, a)
1 2
e = v0 t + 2 at t =
( )
2
0
 v + v0
a = f (v 0 , e , t ) sabemos que v = v 0 + at y e =  f
 2
MRU
MRUA
Aunque en ambos casos la representación gráfica es una recta, en un caso (MRU) la pendiente es cero, y en el otro (MRUA)
la pendiente es ≠ 0.
13 Obtén la gráfica de «a» frente a «t» de la Fig. 1.10.
¿Qué conclusiones obtienes?
a
(0-20)
(20-30)
0
20
30
t (s)
a=
vf − v0
=
t
27, 8 −13,9
m
=
= 1,39 2
10
s
a = 0 ya que v = cte
14 Con los datos de la Tabla 1.2:
a) Calcula el espacio recorrido por el móvil en cada intervalo.
b) Representa en una gráfica el espacio recorrido frente
al tiempo.
a) en el intervalo t = 0s a t = 20s se produce un MRUA, así
1
1,39 ⋅ 202
e1 = e0 + v 0t + a t 2 =
= 278 m
2
2
en el intervalo t = 20s a t = 30s el movimiento es MRU, así
e2 = v · t = 27,8 · 10 = 278 m
eT = e1+ e2 = 278 + 278 = 556 m
 v + at + v0 
 2v0 + at 
por tanto: e =  0
 ⋅t = 
 ⋅t =
2
2




2
= v0t + 1/2 at
despejamos a tenemos: a =
a = f (v 0 , v , e ); t =
=
v 2 − v 02
2a
;e =
v −v0
a
v 2 − v 02
;e =
2e − 2v 0t
t2
v +v0 v −v0
⋅
=
2
a
2a
de donde: a =
v − v 02
2
2e
a = f (v 0 , v , t ) directamente a =
v −v0
t
Con el espacio actuamos de la misma forma:
e = f(v0, v, a), ya lo hemos calculado cuando se hizo la a = f(v0,
v, t) y por tanto:
e=
v 2 − v 02
2a
1 22
ee == ff (v,
(v ,a,
a, t);
t );ee==vv00tt++1/2atat
2
Con el tiempo procedemos de la misma forma:
t = f (v0, v, e) directamente; t =
2e
v + v0
t = f (v0, a, e) directamente; 1/2 at2 + v0 f – e = 0
ecuación de 2.o grado que habría que resolver; t = f (v0, v, a)
directamente t =
8

 ⋅t

v −v0
a
16 Expresa en radianes la equivalencia de los siguientes
ángulos: a) 30º ; b) 60º ; c) 240º ; d) 320º y e) 3 vueltas.
EJErcicios ProPuEsTos
πrad
πrad
= 0,166π;
b) 60º⋅
= 0,33π
180 o
180º
πrad
πrad
c) 240º⋅
=1,33π;
d) 320º⋅
=1,77π
180º
180º
2πrad
d) 3 vueltas ⋅
= 6πrad
1 vuelta
Para rEPasar
17 Expresa la velocidad angular de un CD que gira a 45
rpm. Asimismo, calcula la velocidad lineal de los puntos
situados a 5 y 8 cm del centro.
2 Define qué es desplazamiento y qué es el espacio
recorrido por un móvil. Di qué diferencias encuentras
entre ellos.
a) 30º⋅
rev 2 π rad 1 min
45 rpm = 45
⋅
= 1,5 π rad/s
min 1 rev 60 s
rad
v = R ⋅ω = 1,5π
⋅0, 05 m = 0, 075 m/s
s
rad
v = R ⋅ω = 1,5 m
⋅0, 08 m = 0,12 m/s
s
18 En la experiencia de laboratorio Movimiento circular
uniforme, mide la distancia de las fichas roja, amarilla,
verde y azul y calcula la velocidad de cada una. Posteriormente, representa en una gráfica las velocidades lineales
en ordenadas y las distancias al centro del microondas de
cada ficha, en abscisas. ¿Qué deduces de esa ecuación?
Realizar la experiencia.
— La velocidad angular de todas las fichas es la misma y,
por tanto, constante.
1 Explica qué es la trayectoria de un móvil.
Trayectoria es la línea que une todos los puntos por los que
ha pasado el móvil.
Desplazamiento es la distancia más corta entre dos puntos,
mientras que el espacio recorrido es la trayectoria seguida
por el móvil.
3 ¿Qué es lo que mide la aceleración?
La variación de la velocidad con el tiempo.
4 ¿Cómo definirías el movimiento uniforme? ¿Cuánto
vale la aceleración en el movimiento rectilíneo uniforme?
Es el movimiento que lleva un móvil cuando su velocidad
permanece constante respecto al tiempo. La aceleración
es 0.
5 Hay una magnitud que permanece constante en el
movimiento rectilíneo uniforme. ¿Cuál es?
La velocidad.
6 ¿Siempre son iguales la velocidad media y la velocidad instantánea?
— La velocidad lineal dependerá de la distancia al eje de
giro, pero la gráfica que debemos obtener será una recta
cuya pendiente es la velocidad angular (ω).
19 Expresa el periodo y la frecuencia, en función de la
velocidad lineal, de un punto situado a una distancia r
del centro.
Velocidad media es el cociente entre el espacio recorrido y
el tiempo empleado en recorrerlo. Es igual a la velocidad
instantánea cuando la aceleración es 0.
7 ¿Qué magnitud permanece constante en un movimiento uniformemente acelerado?
La aceleración.
r
2π 2 / v 2πr
=
=
v
ω
v
r
1
v
f= =
T 2πr
T=
8 ¿Cómo varía la velocidad de caída de un cuerpo que
se deja caer desde una azotea? ¿Qué variación sufre la velocidad vertical del mismo cuerpo cuando se lanza hacia
arriba?
La caída es un movimiento uniformemente acelerado, cuya aceleración adquiere un valor que coincide con el de la
gravedad.
a = g = 9,8 m/s2
9
1
El movimiento hacia arriba —contra el sentido de la gravedad— hará que el móvil sufra una aceleración exactamente
igual que en el caso anterior, cuyo valor será:
Horaria → ω =
1 vuelta 2π rad
1h
⋅
⋅
=
12 h 1 vuelta 3600 s
=1, 45 ⋅10 −4 rad/s
a = –g = –9,8 m/s2
9 ¿Qué indica el velocímetro de un vehículo que se
mueve con movimiento circular uniforme? ¿Qué ocurre
con la dirección hacia la que se dirige el coche? ¿Es siempre la misma?
El velocímetro se mantiene inmóvil.
Que cambia continuamente, siendo tangente a la trayectoria
que es una circunferencia.
10 Si desde un barco te comunicaras por teléfono con
otra persona, ¿cómo le indicarías tu posición exacta en
ese instante?
Lo correcto sería preguntar por las coordenadas de situación
al capitán, así como el rumbo a seguir y la velocidad que
llevamos en ese instante.
Otra forma menos precisa sería contestar, una vez conocida
la velocidad media que lleva el barco, que la posición de éste respecto al muelle del que partió será la recorrida a esa
velocidad multiplicada por el tiempo transcurrido desde la
salida hasta que realizamos la llamada, suponiendo que el
rumbo del barco es conocido.
11 ¿Por qué cuando vuelas en avión sobre el océano no
puedes demostrar que el avión está en movimiento?
Porque el punto de referencia, el azul del océano, es siempre
igual y no existe ningún elemento que nos haga saber que
estamos en movimiento; igual ocurrirá si volamos en un cielo
limpio de nubes.
12 Expresa en rad/s la velocidad angular de las manecillas de un reloj.
13 Indica cuerpos o sistemas materiales que se muevan
a tu alrededor continuamente, desde las nubes hasta el
mar.
Se mueven: las nubes, el agua de lluvia, la nieve en su deshielo hacia los ríos, el agua de los ríos en su recorrido hacia el
mar, el agua que se evapora del mar y vuelve a formar nubes,
las personas, los coches, etcétera.
14 La representación gráfica del movimiento de un cuerpo es la que aparece en la figura siguiente.
e (m)
30
20
10
t (s)
0 1 2 3 4 5 6 7 8 9 10
a) Explica razonadamente los movimientos que el móvil
ha seguido desde el principio.
b) ¿Cuál ha sido la velocidad que ha llevado el móvil en
el primer y tercer tramo?
c) ¿Qué distancia ha recorrido mientras ha durado el
movimiento?
d) ¿Cuál es el desplazamiento final del móvil?
a) De (0-2) segundos, MRU; de (2-3) segundos, marcha atrás
con MRU; de (3-5) segundos, el móvil está parado; de
(5-10) segundos, marcha atrás hasta llegar al punto de
partida con MRU.
e 30
m
b) Primer tramo → v = = =15
t 2
2
La aguja del segundero da una vuelta cada minuto:
1 vuelta 2π rad 1 min
⋅
⋅
=
min 1 vuelta 60 s
π rad
rad
=
= 0,10
30 s
s
Segundero → ω =
La aguja del minutero da una vuelta cada hora, y por tanto:
Minutero → ω =
1 vuelta 2π rad
1h
⋅
⋅
=
h
1 vuelta 3600 s
=1,74 ⋅10 −3 rad/s
Tercer tramo → v =
∆e 0
m
= = 0 ; está parado durante 2 s.
∆t 2
2
c) eT = e1 + e2 + e3 + e4 = 30 + 10 + 0 + 20 = 60 m.
d) Desplazamiento cero, pues el móvil vuelve al punto de
origen.
15 De las gráficas siguientes correspondientes a movimientos rectilíneos, ¿cuáles corresponden a un MRU
y cuáles a un MRUA? ¿Hay alguna gráfica que no corresponda a ninguno de los movimientos? Razona tus respuestas.
e
e
v
v
La aguja horaria da una vuelta cada 12 horas, y por tanto:
(a)
10
t
(b)
t
(c)
t
(d)
t
Gráfica (a): MRU v = cte.
Gráfica (b): el móvil está parado.
Gráfica (c): MRUA con velocidad inicial vo (a = cte).
Gráfica (d): MRU v = cte.
a) Aplicamos la ecuación:
v = 2 a e = 2 · 2 · 36 = 12 m/s
16 Un cuerpo lleva un movimiento correspondiente a
la tabla adjunta:
Tiempo (s)
Espacio (m)
0
0
10
25
20
50
30
75
40
100
50
125
60
150
a) ¿Cuál ha sido la velocidad media del móvil a lo largo
del recorrido?
b) Representa gráficamente los valores de la tabla. ¿Qué
significado tiene esa gráfica?
a) v m =
b)
b) Dividimos el tiempo en el tramo A, que es un MRUA y en
el tramo B, que es un MRU

v 12 m/s
=
= 6 s
2
a 2 m/s

 tT = t A + t B = 2 s + 6 s = 8 s
e
24 m
tB = =
= 2 s

v 12 m/s
tA =
c)
t (s)
e (m)
60
36
∆e 150− 0
m
=
= 2,5
∆t 60− 0
s
e (m)
v (m/s)
12
La gráfica es la representación de una recta cuya pendiente es la velocidad, única
magnitud que se mantiene
constante.
17 En una prueba de aceleración, una moto de carreras
alcanza los 240 km/h en 14 s. Calcula la velocidad que ha
alcanzado, en unidades del SI, así como su aceleración y
el espacio recorrido.
6
8
t (s)
6
8 t (s)
19 Nos vamos a la playa, que se encuentra a 1,3 km de
casa. Tardamos 15 minutos en llegar, estamos en ella durante dos horas y volvemos a casa en 20 minutos. Dibuja
las gráficas e-t y v-t que representan nuestro movimiento
a lo largo de la mañana.
e (m)
a)
km 1000 m
1h
v = 240
·
·
= 66, 6 m/s
h
1km 3 600 s
1300
v 66,6 m/s
b) a = =
= 4,7 m/s 2
t
14
c)
e=
v · t 66,6 m/s · 14 s
=
= 466,2 m
2
2
t (s)
18 Una esfera se deja caer con una aceleración de
2 m/s2 por un plano inclinado de 36 m de longitud. Posteriormente, continúa moviéndose sobre un plano horizontal con MRU, hasta que choca y se detiene en una
pared que hay a 24 m de distancia del plano inclinado.
a) Calcula la velocidad final con la que el móvil llega al
final del plano inclinado.
b) ¿Cuánto tiempo ha estado el cuerpo en movimiento?
c) Dibuja las gráficas v – t y e – t del movimiento completo.
8 100
9 300
v (m/s)
1,4
1,1
t (s)
900
8 100
9 300
Hemos pasado los kilómetros a metros: 1,3 km = 1 300 m
Las horas a segundos: 2 h = 7 200 s
Y los minutos a segundos: 15 min = 900 s y 20 min = 1 200 s
vo = 0 m/s
36 m
MRUA
900
vf = 12 m/s
MRU
24 m
20 Un ciclista recorre una semicircunferencia cuyo diámetro son 300 metros. Si situamos el origen de coordenadas en el punto de la salida (véase la figura), contesta
las siguientes preguntas:
11
1
b) ¿Qué representa el número 10? ¿Y el 20?
c) El tiempo que debe transcurrir hasta que el móvil se
encuentre a 500 metros de distancia.
d) ¿Cuál es la velocidad del móvil?
e) Representa la gráfica del movimiento.
D = 300 m
O (salida)
P (llegada)
a) ¿Cuál es el espacio recorrido por el ciclista?
b) ¿Cuál ha sido su desplazamiento desde el origen de
coordenadas?
D = 300 m
L = 2πr
a)
e = 10 + 20 t
a) t = 30 s → e = 10 + 20 · 30 = 610 m
b) El espacio inicial → t = 0; e = eo
c) 500 = 10 + 20 t → t = 24,5 s
d) 20 m/s es la pendiente de la recta e = eo + v t
e) e (m)
40
2πr
= πr = 3,14 · 150 = 471 m
e=
2
b) Desplazamiento = 300 m
10
21 El movimiento de un cuerpo responde a la gráfica
de la figura siguiente:
v (m/s)
Pte. = 20
2 t (s)
0
24 La representación gráfica de un movimiento viene
dada por la figura adjunta. Responde a las siguientes
cuestiones:
40
v (m/s)
40
30
20
20
10
0
10
20
30
40
a) ¿Qué movimiento lleva en cada tramo de la gráfica?
b) Calcula el espacio recorrido cuando el tiempo transcurrido ha sido 30 s.
a) (0 – 20) segundos = MRUA
(20 – 30) segundos = MRU
(30 – 40) segundos = MRUA
v t 40 ⋅ 20
b) e = e1 + e2 ; e1 = =
= 400 m;
2
2
e2 = v · t = 40 · 10 = 400 m
e = 400 + 400 = 800 m
22 Calcula la velocidad media de un ciclista que tarda
15 minutos en recorrer 12 km. Calcula su velocidad y exprésala en km/h y en m/s.
e 12 000
=
= 13,3 m/s ;
t
900
m 1 km 3 600s
13,3 ⋅
⋅
= 48 km/h
s 1000 m 1 hora
v=
23 El movimiento sobre una línea horizontal correspondiente a un móvil viene dado por la expresión
e = 10 + 20 t, donde el espacio viene en metros y el tiempo, en segundos. Calcula:
a) La posición del objeto cuando han transcurrido 30
segundos.
12
t (s)
t (s)
0
10
20
30
40
50
a) ¿En qué tramos el movimiento es uniforme? ¿En algún
tramo el cuerpo está parado?
b) ¿Cuál ha sido la aceleración durante el primer y cuarto
tramos?
c) ¿Qué espacio total ha recorrido el móvil?
a) (0 – 10) segundos → MRU
(10 – 20) segundos → MRUA aceleración positiva
(20 – 30) segundos → MRU
(30 – 50) segundos → MRUA aceleración negativa
∆v 0
b) Primer tramo a = 0 → a =
= =0
∆t 10
v −v
0 − 40
4
Cuarto tramo a = f 0 =
= − m/s 2
∆t
5
5
c) e1 = 200 m; e2 = 300 m; e3 = 400 m; e4 = 400 m
et = 1 300 m
25 Razona cuál de las gráficas de la figura siguiente
responden a un MRUA. ¿Cuáles de ellas no? Razona tus
respuestas.
v
a
(a)
t
e
(b)
t
a
(c)
La a) y la c) corresponden a un MRUA.
t
(d)
v
— La a) responde a una gráfica de la forma:
y = mx + n; donde la pendiente es la aceleración, v = v0 +
at
— La c) corresponde a una gráfica de la forma
y = 1/2 a x2 → e = 1/2 a t2
26 Dos familias, en coche, van a visitar una ciudad que
se encuentra a 450 km de su lugar de origen. Una de
ellas va a 100 km/h de media, mientras que la otra va a
120 km/h.
a) ¿Cuál debe salir primero para que al cabo de cierto
tiempo se puedan encontrar en una gasolinera a
240 km del punto de partida?
b) Si el coche que marcha a mayor velocidad sale 15 minutos más tarde, ¿cuánto tiempo tardará en alcanzar
al otro?
c) ¿Qué distancia han recorrido ambos en ese momento?
d) Representa ambos movimientos en la misma gráfica.
}
v1 = 100 km/h = 27,77 m/s
v2 = 120 km/h = 33,33 m/s
a) Debe salir primero la familia que va a menor velocidad.
b) Cuando la segunda familia alcance a la primera, ambas
habrán realizado el mismo recorrido, la distancia desde
el inicio al punto P.
xm
0
e1 = v1t 

e2 = v2t 2 
P
700 = 1/2 · 8 · t2 → t = 13,2 s;
v = at = 8 · 13,2 = 105,6 m/s
b) a =
c)
vf − v0
t
=
80 − 0
= 8 m/s 2
10
v (m/s)
e (m)
t (s)
t (s)
a (m/s2)
8
t (s)
28 Un nadador en una competición de saltos compite
desde el trampolín de 20 m. Calcula:
a) Con qué velocidad llegará al agua si se deja caer libremente.
b) Cuánto tiempo tardará en efectuar el recorrido.
c) Cómo sería la representación gráfica del espacio frente al tiempo y de la velocidad frente al tiempo a lo
largo de toda la trayectoria.
d) Dibuja también la gráfica de la aceleración frente al
tiempo en todo el movimiento.
a) h = 20; v = 2gh = 2 ⋅9, 8 ⋅20 =19, 8 m/s
b) v f = v 0 a t; t =
v1t1 = v2t2; t2 = t1 – 900
27,77 · t1 = 33,33 (t1 – 900); t1 = 5 395,14 s
t2 = 5 395,14 – 900 = 4 495,14 s
c) e1 = 27,77 · 5 395,1 = 149 822 m
e2 = 33,33 · 4 495,1 = 149 822 m
d) Solución gráfica no incluida.
c)
vf − v0
a
=
19, 8 − 0
=2 s
9, 8
v (m/s)
e (m)
t (s)
27 Los datos de e, v y t correspondientes al inicio de
un recorrido que ha realizado un coche con MRUA en el
transcurso de una carrera, se han recogido en la siguiente tabla de forma incompleta.
d)
t (s)
a (m/s2)
9,8
t (s)
Tiempo (s)
Velocidad (m/s)
Espacio (m)
0
0
0
5
40
10
80
400
700
a) Completa los datos de la tabla.
b) Calcula la aceleración del coche.
c) Representa las gráficas e – t, v – t y a – t del movimiento hasta el punto final.
a) e =
v f2 − v 02
2a
=
402
v t 40 ⋅5
100 m; e =
=
=100 m;
2 ⋅8
2
2
1
1
e = a t 2 = ⋅8 ⋅52 =100 m
2
2
29 La ecuación de velocidad de un móvil viene dada
por la siguiente expresión:
v = 30 + 3t
donde la velocidad está expresada en m/s y el tiempo, en
segundos. Contesta a las siguientes cuestiones:
a)
b)
c)
d)
e)
f)
Cuál es la velocidad inicial del móvil.
El tipo de movimiento que lleva.
Cuál será su velocidad a los 5 segundos.
Cuál es su aceleración.
El espacio que recorrerá el móvil en 50 segundos.
El tiempo necesario para que el móvil tenga una velocidad de 35 m/s.
13
1
g) Construye una gráfica v – t que represente el movimiento.
a) v0 = 30 m/s responde a la recta de la forma:
vf = v0 + a t
b) MRUA
c) v = 30 + 3 · 5 = 45 m/s
d) a = 3 m/s2 es la pendiente de la recta
e) Aplicamos e = v0t + 1/2 a t2 =
1
= 30 ⋅50 + ⋅3 ⋅502 = 5250 m
2
f) 35 = 30 + 3t → t = 1,66 s
g)
t2 =
333,52 km
= 1,33 horas
250 km/h
31 Un camión que se desplaza a velocidad constante de
90 km/h adelanta a un coche que se encuentra parado en
la carretera. Si éste arranca 5 segundos después con una
aceleración constante de 3 m/s2, calcula:
a) El tiempo que tardará el coche en alcanzar al camión.
b) La velocidad del coche cuando alcanza al camión.
c) El espacio que recorre el camión antes de ser alcanzado.
v = 90 km/h = 25 m/s
v (m/s)
v1 = 25 m/s
a = 3 m/s2
x
v = 30 + 3 t
30
t (s)
30 Dos trenes salen al mismo tiempo de Madrid y de
Sevilla. El tren que sale de Madrid hacia Sevilla es un tren
de mercancías que circula a una velocidad media de 110
km/h, mientras que el que sale de Sevilla hacia Madrid es
el AVE, que circula a una velocidad media de 250 km/h.
Sabiendo que la distancia Madrid-Sevilla es de 480 km,
calcula:
a) El tiempo que tardan en cruzarse.
b) El espacio recorrido por cada tren en ese momento.
M
P
v1 = 30,5 m/s
x
S
v2 = 69,4 m/s
480 km
480 - x
P
Cuando el coche alcance al camión se ha de cumplir que el
espacio recorrido por ambos ha de ser el mismo.
1
a) e1 = v1t1 
v1t1 = at 2
 e1 = e 2
2
1 
1
e 2 = at 2 t 2 = t1 − 5
25t1 = ⋅ 3 ⋅ (t − 5)2
2 
2
De donde: t1 = 25,7 s ; t2 = 20,7 s
b) v2 = at2 = 3 · 20,7 = 62,1 m/s
c) e1 = v1t1 = 25 ⋅ 25,7 = 642 m;
1
e2 = ⋅ 3 ⋅ 20,72 = 642 m
2
32 El conductor de un vehículo tarda en pararse 5 segundos después de frenar con una deceleración de 3 m/s2.
Calcula:
Cuando se encuentren los dos trenes habrán tardado el
mismo tiempo desde que partieron, lo que ocurre es que el
más rápido habrá recorrido más espacio; por tanto, se debe
cumplir:
a) La velocidad inicial del automóvil antes de comenzar
a frenar.
b) El espacio recorrido durante la frenada.
c) Dibuja una gráfica e – t que represente el movimiento
de frenada descrito.
e
e

et = 30,5 ⋅ t1  t1 = t2 ; 1 = 2

30,5 69,44 

e2 = 69,44 ⋅ t2 
e1 = x ; e2 = 480 000 − x 
5m
/s
a) vf = v0 + at ; v0 = vf − at = 0 − ( −3 ⋅ 5) = 115
m/s
480 000 − x
x
=
30,5
69,44
x = 146,48 ⋅ 103 m = 146,48 km
1
1
b) e = v0 t + at 2 = 15 ⋅ 5 − ⋅ 3 ⋅ 52 = 37,5 m
2
2
c) v (m/s)
15
El móvil 1 recorre 146,48 km.
146, 48 km
t1 =
= 1,33 horas
110 km/h
El móvil 2 recorre 333,52 km.
14
5
t (s)
33 Un neumático de coche de 55 cm de diámetro gira
a razón de 800 rpm. ¿Qué velocidad lineal lleva el
coche?
En este caso el tiempo que tardarán en encontrarse es el
mismo, y por tanto:
R = 55 cm = 0,55 

ω = 800 rpm

rev 2πrad 1 min
⋅
⋅
= 83, 8 rad/s
min 1 rev 60 s
v = ω · R = 83,8 rad/s · 0,55 m = 46,09 m/s
800
34 Un punto material situado en un volante de 1 m de
radio gira a razón de 30 vueltas/minuto. Calcula: el periodo, la frecuencia, la velocidad angular y la velocidad
lineal.
t1 =
e1
v1
t1 =
t2 =
e2
v2
t2 =
150 000 − x
22,2
a) Los tiempos serán: t1 =
83 400
= 3 000 s
27,8
equivalentes a 50 min.
vueltas 2πrad 1 min
⋅
⋅
= πrad
min 1 vuelta 60 s
2π 2π
1 1
T=
=
= 2 s; f = = = 0,5 s
ω π
T 2
ω = 30
t2 =
b)
Para rEForZar
35 Un pasajero camina hacia popa a 5 km/h por la cubierta de un barco que se mueve a 15 km/h. Se para y se
le cae un objeto. Todo esto lo observa una persona en
reposo desde una playa cercana. Describe qué tipo de
movimiento tienen las dos personas y el objeto, utilizando todos los sistemas de referencia posibles.
El pasajero que circula por la cubierta del barco se mueve
con MRU a:
v=5
x
27,8
66 600
= 3000 s
22,2
150 000 − x
x
=
27,8
22,2
de donde x = 83 400 m
El móvil A recorrerá 83 400 m y el móvil B recorrerá
150 000 – 83400 = 66 600 m
c) El reloj marcará las 12:50 h
37 Estás asomado a una ventana de tu casa y observas que pasa por delante de ti una pelota que ha caído
desde la azotea. Si la diferencia de altura entre tu casa
y la azotea es de 7 m, ¿a qué velocidad pasará la pelota
por delante de tu ventana?
km
1h
1000 m
·
·
= 1,38 m/s
h 3 600 s 1km
7m
respecto a la propia cubierta del barco y a una velocidad
suma de la suya propia y de la del barco con respecto al observador que está en reposo en la playa, es decir:
15
km
1h
1000 m
·
·
= 4 ,16 m/s
h 3 600 s 1km
4,16 m/s + 1,38m/s = 5,54 m/s
36 Dos coches están separados por una distancia de
150 km. A las 12 de la mañana salen uno al encuentro del
otro; uno lo hace a una velocidad constante de 100 km/h
y el otro lo hace a una velocidad de 80 km/h. Calcula:
a)
b)
c)
d)
¿Cuánto tiempo tardarán en encontrarse?
¿Qué distancia ha recorrido cada uno de ellos?
¿Qué hora marcará el reloj cuando se encuentren?
Dibuja las gráficas que creas oportuno.
v1 = 100 km/h
v1 = 27,8 m/s
A
x
v2 = 80 km/h
v2 = 22,2 m/s
P 150 000 - x B
150 · 103 m
v = 2gh = 2 ⋅ 9,8 ⋅ 7 = 11,7 m/s
38 Calcula la profundidad de un pozo sabiendo que cuando tiras una piedra al fondo tardas 4 segundos en oír
el ruido que ésta hace al chocar contra el agua.
(Dato: velocidad del sonido 340 m/s.)
h
Bajada (MRUA): h = 1/ 2gt12 

Subida (MRU): h = v2t 2

t1 + t 2 = 4
v2 = 330 m/s ya que v sonido = v2
Por tanto: 1/ 2 ⋅9, 8 ⋅t12 = 330 ⋅t 2 ;
4,9 t12 = 330 (4 − t1 )
De donde: t1 = 3,787 s y t2 = 0,212 s
1
h = ⋅ 9,8 ⋅ 3,3872 = 70 m y h = 330 ⋅ 0,212 = 70 m
2
= 70 m
15
1
EValuaciÓN
d) En los movimientos acelerados la velocidad siempre
aumenta.
1 Un ciclista va por delante de un motorista. Para que
el motorista alcance al ciclista:
Respuesta correcta: b).
a)
b)
c)
d)
Basta que vaya con la velocidad que tiene el ciclista.
Debe ir con más velocidad que el ciclista.
No le alcanzará nunca.
Sólo le alcanzará si el ciclista se cae.
Respuesta correcta: b).
2 El movimiento representado en la figura se corresponde a un móvil que:
a)
b)
c)
d)
Sube una cuesta en línea recta.
Posee un movimiento rectilíneo y uniforme.
Está parado.
Lleva velocidad constante y, por tanto, recorre espacios iguales en tiempos iguales.
4 El movimiento representado en la figura corresponde al de un móvil:
a) Con movimiento rectilíneo y uniforme.
b) Que va cuesta abajo.
c) Con aceleración positiva, o sea, que aumenta su velocidad a medida que pasa el tiempo.
d) Con aceleración negativa, es decir, que disminuye su
velocidad a medida que pasa el tiempo.
v
e
t
Respuesta correcta: b).
t
Respuesta correcta: d).
3 Indica las respuestas que creas correctas:
a) En un movimiento rectilíneo uniforme el móvil se
desplaza en línea recta.
b) En un movimiento rectilíneo uniforme el móvil va
siempre con velocidad constante.
c) El móvil va con velocidad constante en los movimientos llamados «de tipo uniforme».
16
5 Contesta cuáles de los siguientes movimientos corresponden a un movimiento circular con velocidad constante:
a) La rueda de un coche que circula con aceleración
constante.
b) Las manecillas de un reloj.
c) Una pelota que dejamos caer por una pendiente.
d) La cuchilla de una batidora cuando hacemos un batido.
Respuestas correctas: b) y d).
laS FuErZaS
EJErcicios
3N
1 Indica, mediante un ejemplo, cada uno de los tipos
de efectos que pueden ocasionar las fuerzas.
c)
6N
6N
2
3N
6,7 N
Por ejemplo, si detienes una pelota con la mano has cambiado su velocidad.
Si coges esa pelota y la aplastas has cambiado su forma.
2 Pon ejemplos de materiales de los tres tipos que existen, en función del efecto que las fuerzas ejercen sobre
ellos.
Rígidos: un lápiz, una silla, una mesa.
Elásticos: una goma de borrar, una regla de plástico.
Plásticos: una hoja de papel, plastilina.
3 Se ejerce una fuerza sobre un muelle y se observa que
se alarga 5 cm. ¿Cuánto se alargará si se le somete a una
fuerza cinco veces mayor?
F = k ∆l, el alargamiento es proporcional a la fuerza, si la fuerza es cinco veces mayor también lo será el alargamiento, es
decir, serán 25 cm.
3N

FR =
2 
F1 + F2
2
= (6 N)2 + (3 N)2 = 6,7 N
7 Dibuja dos fuerzas concurrentes que formen ángulo
de 30°, de manera que una tenga su intensidad tres veces
la de la otra, y calcula el valor de su resultante gráficamente.
FR
8 Halla gráficamente la resultante de cada uno de estos grupos de fuerzas y calcula su intensidad.
4 Se tiene un muelle de 20 cm que se alarga 10 cm
cuando se le aplica una fuerza de 2 N. ¿Cuánto vale su
constante elástica?
Aplicando directamente la ley de Hooke queda
F = k ∆ l ⇒ 2 N = k · 0,10 m; k = 20 N/m.
FR
5 Dibuja a escala 2 N : 1 cm, dos fuerzas de 3 N y 6 N
que forman 30° y 60° con el eje Ox y cuyo punto de aplicación es el origen de coordenadas.
y
FR
FR
6N
9 Se tiene una fuerza de 10 N en ángulo de 30° con la
horizontal. Calcula y dibuja las componentes de dicha
fuerza.
3N
x
6 Halla la fuerza resultante, numérica y gráficamente,
de dos fuerzas de 3 N y 6 N cuando:
a) Se ejercen en la misma dirección y sentido.
b) Se ejercen en la misma dirección, pero sentidos opuestos.
c) Se ejercen formando un ángulo de 90°.
a) FR = 3 N + 6 N = 9 N
3N
6N
b) FR = 6 N – 3 N = 3 N
Y
FY
10 N
FX
X
Fx = F cos α = 10 N ⋅ cos 30° = 8,7 N
Fy = F sen α = 10 N ⋅ sen 30° = 5 N
9N
10 Imagina que dejas caer un cuerpo por su propio peso
por una pendiente. Dibuja las fuerzas que actúan y obtén
la componente útil de manera gráfica.
17
2
F1
F2
P
F1 es la componente útil, la que hace descender al cuerpo.
11 ¿Cuál debería de ser la inclinación óptima que debe
tener una cuerda con la que estás arrastrando un cuerpo
atado a ella para que sea mínima la fuerza que se desaprovecha?
La fuerza debe hacerse en horizontal, para que no haya
componente perpendicular al desplazamiento, lo que no
ocasionaría trabajo.
Si el coeficiente de rozamiento fuera muy grande, a veces
resulta interesante tirar con un cierto ángulo hacia arriba,
para que la componente vertical disminuya parte de la normal y el rozamiento sea menor, pero eso excede sus conocimientos.
12 Dadas dos fuerzas de 10 N y 15 N que forman un ángulo de 90°, aplicadas sobre el punto (0, 0) de los ejes cartesianos, dibuja y calcula el valor de la fuerza necesaria
para equilibrar ambas.
FR
10 N
FR =
2
2
F1 + F2 =
= (10)2 + (15)2 =18 N
15 N
Fequilibrante
Luego, la fuerza equilibrante será también de 18 N, pero su
dirección y sentido es tal y como se muestra en la figura.
13 Se tienen tres fuerzas de 5 N, 8 N y 10 N que forman, respectivamente, ángulos de 30°, 45° y 60° con la
horizontal, y que se aplican sobre un mismo punto. Calcula gráfica y numéricamente la fuerza que provocará el
equilibrio de las tres sobre el punto de aplicación.
Fresultante total
y
FR1
x
— F1X = F1 · cos α1 = 5 · cos 30 = 4,33 N
— F1Y = F1 · sen α1 = 5 · sen 30 = 2,50 N
— F2X = F2 · cos α2 = 8 · cos 45 = 5,66 N
— F2Y = F2 · sen α2 = 8 · sen 45 = 5,66 N
— F3X = F3 · cos α3 = 10 · cos 60 = 4,99 N
— F3Y = F3 · sen α3 = 10 · sen 60 = 8,66 N
Podemos sacar una componente X total y una componente
Y total.
FXT = 4,33 + 5,66 + 4,99 = 14,98 N
FYT = 2,50 + 5,66 + 8,66 = 16,82 N
Ahora se pueden sumar las dos componentes:
F1 = (14,98)2 + (16,82)2 = 22,52 N
La fuerza equilibrante será también de 13,7 N, pero su dirección y sentido es tal y como se muestra en la figura.
EJErcicios ProPuEsTos
Para rEPasar
1 Indica el tipo de fuerza, a distancia o contacto, que
se aplica cuando:
a)
b)
c)
d)
Cae un coco de una palmera.
Golpeas el balón con el pie.
Coges un libro.
El viento mueve las hojas de un árbol.
a) Fuerza a distancia;
c) Fuerza de contacto;
2 Cuando se le aplica a un muelle una fuerza de 10 N se
observa que se alarga 4 cm. Calcula la constante elástica
del muelle.
k = 10 N/0,04 m = 250 N/m
3 De las siguientes magnitudes, indica cuáles son
escalares y cuáles vectoriales: velocidad, temperatura,
volumen y energía. Explícalo.
Velocidad: vectorial; temperatura: escalar; volumen: escalar;
energía: escalar.
4 Se aplican en dirección horizontal fuerzas de 5 N, 6 N y
8 N sobre un cuerpo. Calcula con qué fuerza y hacia dónde
se moverá éste si dos van hacia la derecha y una hacia la
izquierda (estudia todas las posibilidades).
8N
Fequilibrante
Un método fácil es la descomposición de las fuerzas en sus
componentes normales:
18
b) Fuerza de contacto;
d) Fuerza de contacto.
5N
6N
5N
6N
6N
5N
8N
8N
3N
PARA REFORZAR
9N
7N
Estas posibilidades y sus correspondientes en sentido contrario.
5 Una barca atraviesa un río empujada por el remero
con una fuerza de 350 N y por la corriente que la arrastra
perpendicularmente con otra fuerza de 100 N. ¿Cuál es
la fuerza que hace avanzar la barca?
Se aplica la ecuación:

FR =
 2  2
F 1 + F 2 = (350)2 + (100)2 = 364 N
En dirección 45° con la horizontal del río.
F > 100 N + 30 N > 130 N
7 Calcula la resultante de las siguientes fuerzas:
6N
2N
11 En un experimento con un dinamómetro se reflejaron las siguientes medidas:
F (N)
0
2
4
10
14
18
Alargamiento (cm)
0
3
6
15
21
27
a) La constante elástica del muelle del dinamómetro en
N/m.
b) Cuánta fuerza se aplica cuando se estira 30 cm.
c) Cuánto se estirará el muelle cuando se apliquen
25 N.
a) Se dibuja en un papel milimetrado la recta dada por los
puntos.
Su pendiente es la constante K:
∆y/∆x = 0,67 N/cm
0,67 100 cm
⋅
= 67 N/m
1 cm 1 m
b) F = 67 N/m · 0,30 m = 20,1 N
c) 25 N = 67 N/m · ∆l; ∆l = 0,37 m
5N
FRH = 7 N – 2 N = 5 N;
FRV = 6 N – 5 N = 1 N;

 2  2
F R = F1 + F 2 =
F = k · ∆l; 40 N = 100 N/m · ∆l; ∆l = (l – l0) = 0,4 m; l = 0,15 +
0,40 = 0,55 m
No se romperá porque 0,55 m < 0,80 m.
Calcula:
6 ¿Cuál será la fuerza mínima que se debe aplicar para
conseguir mover una mesa que pesa 100 N por un suelo
cuyo rozamiento —fuerza que se opone al movimiento— tiene su misma dirección, sentido contrario y vale
30 N?
2N
10 Se tiene un muelle de 15 cm de longitud cuya constante de elasticidad vale 100 N/m. Calcula la longitud que
tendrá el muelle cuando se cuelgue de él un objeto que
pesa 40 N. Si el máximo estiramiento que soporta es de
80 cm, ¿se romperá el muelle al colgar este peso?
5N
= (5 N)2 + (1 N)2 = 5,1 N
FR
12 Tres remolcadores tiran de una barcaza tal y como se
ve en la figura. ¿Cuál es la fuerza real que hace avanzar
la barcaza?
1N
12 000 N
8 Un caballo tira de un carromato con una fuerza de
2 000 N y le ayuda el carretero con una fuerza de 250 N.
Si el suelo opone una fuerza de rozamiento de 150 N,
calcula la fuerza que realmente impulsa al carromato.
30°
30°
15 000 N
12 000 N
FR = 2 000 N + 250 N – 150 N = 2 100 N
9 Vas empujando una bola con una fuerza de 2 N por un
suelo barnizado. ¿Qué fuerza de rozamiento hará éste si la
bola se desplaza con velocidad constante?
Frozamiento = 2 N
La forma más fácil de realizar este ejercicio es descomponer
las fuerzas de 12 000 N en sus componentes x e y. Sólo nos
interesa la componente x.
Fx1 = 12 000 · cos 30 = 10 392,3 N
19
2
Sumando las dos componentes de 12 000 N tenemos una
componente x que es 2 · Fx1. La fuerza total que hace avanzar
la barcaza es:
F2 + 2 · F1x = 15 000 + 2 · 10 392,3 = 25 392,3 N
13 Dos chicos aplican sendas fuerzas de 30 N y 40 N
hacia arriba y con un ángulo de 30° a fin de conseguir
sacar de un pozo un saco de 50 N de peso. Indica si lo
conseguirán.
EVALUACIÓN
1 Cuando acercas un imán a un clavo observas que
éste es atraído por aquél. Esto ocurre porque:
= (30 N)2 + (10 N)2 + 2 ⋅30 N⋅ 40 N⋅cos30º =
a) No ocurre. El imán no atrae al clavo hasta que no contacta con él.
b) El imán ejerce una fuerza sobre el clavo atrayéndolo
a pesar de estar a una distancia de él.
c) El clavo ejerce una fuerza sobre el imán atrayéndolo
a pesar de estar a una distancia de él.
d) Ambos ejercen fuerzas atractivas, cada uno sobre el
otro.
= 67, 4 N
Respuesta correcta: d).

FR =
 2  2
 
F 1 + F 2 + 2 F 1 F 2 cos α =
Como la fuerza resultante es mayor de 50 N que pesa el saco,
lo podrán arrastrar.
14 Se aplican las siguientes fuerzas sobre un objeto:
10 N en la dirección de la horizontal, 15 N en dirección
30° sobre la horizontal y 25 N en dirección vertical ascendente. Calcula la fuerza resultante que actúa sobre
el objeto y dibuja su vector a escala.
Y
2 Si colocas un papel encima de una mesa y soplas,
observarás que el papel se mueve. Esto ocurre porque:
a) Ejerces una fuerza a distancia con tu boca sobre el
papel.
b) El papel se mueve porque al girar la Tierra se desplaza
sobre la mesa.
c) El aire que sale de tu boca al contactar con el papel
ejerce una fuerza que lo mueve.
d) En realidad el papel nunca se moverá sólo porque
soples hacia él.
Respuesta correcta: c).
X

F R1 =
 2  2
 
F 1 + F 2 + 2 F 1 F 2 cos α =
= (10 N)2 + (15 N)2 + 2 ⋅10 N⋅15 N⋅cos30º = 24,1 N

 2  2
 
F T = F R1 + F 3 + 2 F R1 F 3 cos α =
= (24,1 N)2 + (25 N)2 + 2 ⋅24,1 N⋅25 N⋅cos71,9º =
= 39, 8 N
15 Dibuja una fuerza de 20 N con escala 4 N: 2 cm inclinada 30° sobre la horizontal. Calcula gráfica y numéricamente cuáles son sus componentes sobre los ejes cartesianos.
Y
30°
X

 
FY = F sen 30º = 20 N ⋅1/ 2 =10 N;

 
FX = F cos 30º = 20 N 3 / 2 =17,3 N
3 Coges varios objetos: un lápiz, un trozo de plastilina
y una goma elástica, e intentas doblarlos.
a) Todos se doblarán con facilidad; son objetos elásticos.
b) Ninguno se puede doblar porque son objetos rígidos.
c) El lápiz no se doblará, es rígido; la plastilina y la goma
sí, porque son elásticos.
d) El lápiz no se doblará, es rígido; la goma sí, porque es
elástica; la plastilina aunque se dobla no recupera su
forma inicial, es plástica.
Respuesta correcta: d).
4 Aplicas una fuerza de estiramiento de 4 N sobre un
objeto elástico y observas que se alarga 2 cm.
a) Si se aplica una fuerza de 8 N se observará un alargamiento de 3 cm.
b) Si se aplica una fuerza de 2 N se observará un alargamiento de 0,5 cm.
c) Si se aplica una fuerza de 6 N se observará un alargamiento de 3 cm.
d) Si se aplica una fuerza de 15 N se observará un alargamiento de 6 cm.
Respuesta correcta: c).
20
5 Al aplicar sobre un mismo punto de un cuerpo varias
fuerzas de la misma dirección pero diferentes sentidos,
la resultante será:
a) La suma de todos los módulos de las fuerzas aplicadas.
b) La resta de todos los módulos de las fuerzas aplicadas.
c) La suma algebraica de todos los módulos de las fuerzas aplicadas.
d) Es imposible de calcular sólo con esta información.
6 Una fuerza puede descomponerse:
a) Sólo en dos únicas fuerzas concurrentes.
b) En dos fuerzas de la misma dirección y sentidos
opuestos.
c) En dos fuerzas de la misma dirección y el mismo sentido.
d) En infinitas parejas de fuerzas concurrentes.
Respuesta correcta: d).
Respuesta correcta: c).
21
3 LAS FUERZAS Y EL MOVIMIENTO
EJERCICIOS
1 En las siguientes figuras se representan ejemplos
de fuerzas de contacto (C) y de acción a distancia (D).
Clasifícalas con las letras C y D. Indica el agente que las
origina y marca el sistema en cada una punteando una
circunferencia.
El peso depende de la gravedad, por tanto, varía de un planeta a otro. En cambio, la masa es una propiedad característica de los cuerpos y es independiente del planeta en que
se encuentren.
5 Dibuja la fuerza de rozamiento en los siguientes
casos:
m
a)
b)
Movimiento
Fr
a) Fr
b)
6 Cuando tenemos frías las manos, instintivamente
las frotamos entre sí presionándolas con energía. ¿Por
qué hacemos esto?
a) Fuerza de contacto entre el sistema (el muelle) y el agente
(la mano).
b) Fuerza de contacto entre el pie del futbolista (agente) y
el balón (sistema).
c) Fuerza a distancia entre la Tierra (agente) y la masa (sistema).
d) Fuerza de contacto entre la cuerda (agente) y el cubo
(sistema).
e) Fuerza a distancia entre el imán (agente) y el tornillo (sistema).
f) Fuerza a distancia que ejerce la varilla electrizada (agente)
y el péndulo (sistema).
2 Calcula el peso que corresponde a una persona de
masa 50 kg, a una bicicleta de masa 6 kg y a un filete de
120 g. Dato: g = 9,8 m/s2.
El peso de un cuerpo viene dado por P = mg:
— Para la persona: P = 50 kg · 9,8 m/s2 = 490 N
— Para la bicicleta: P = 6 kg · 9,8 m/s2 = 58,8 N
— Para el filete: P = 0,12 kg · 9,8 m/s2 = 1,2 N
3 ¿Qué pesa más, un libro de 12,5 N de peso o un paquete de naranjas de 1,3 kg de masa? Dato: g = 9,8 m/s2.
El paquete es más pesado que el libro, porque su peso es:
P = 1,3 kg · 9,8 m/s2 = 12,7 N
4 En los demás planetas también existe el peso. Busca en Internet o en una enciclopedia los valores de la
aceleración de la gravedad en los distintos planetas del
Sistema Solar. ¿El que sea distinto significa que los objetos cambian de peso según el planeta en el que estén?
¿Cambiarían los objetos de masa?
22
La presión de las manos aumenta el rozamiento entre ellas.
Cuanto mayor sea el rozamiento, mayor será el calor que se
origina en el movimiento.
7 Cuando las calles están cubiertas de hielo se echa
sal y se ponen cadenas en las ruedas de los automóviles.
Justifica estas operaciones.
Las cadenas se usan para aumentar la adherencia y aumentar,
así, el rozamiento.
8 Dibuja el diagrama de cuerpo libre de las fuerzas
que actúan sobre un libro en cada uno de los siguientes
casos:
a) Apoyado en tu mano.
b) Que lanzas a lo largo de una mesa.
c) Que arrastras por la mesa tirando de él con una
cuerda.
d) Que empujas contra la mesa.
N
N
N
Fr
b)
a)
P
P
NN N
Fr
P
N
NN N
Fr FrFr Fr
c)
PP
P
P
PP
FrT
P
N
FTr
P
NN N
T
F
P
P
N
N
F
P
F
P
T
d)
F
P
9 Los cuerpos a y b de la siguiente figura están unidos con una cuerda que pasa por una polea. El cuerpo
a se desliza subiendo por la rampa.
Dibuja el diagrama de las fuerzas,
a
incluida la de rozamiento, que acb
túan sobre cada cuerpo.
P
mente, pero la inercia de los pasajeros los lanza hacia adelante hasta que una fuerza los detiene; esta fuerza, si no usamos
el cinturón de seguridad, suele ser el volante, el tablero de
mandos o el cristal del parabrisas.
10 Dibuja el diagrama de las fuerzas, incluida la de rozamiento, que
intervienen en la figura.
15 La Segunda Ley de Newton nos permite conocer la
causa de cada uno de los movimientos fundamentales.
Completa en tu cuaderno los siguientes enunciados:
N
a
Fr
T
P
N
Fr
T
b
a) Si un cuerpo tiene MRU, la resultante de las fuerzas
que actúan sobre él es
b) Una fuerza instantánea produce un movimiento
F
F'
P
11 Una niña se desliza con velocidad constante por un
tobogán, como se ve en el dibujo.
a) ¿Qué diagrama es correcto, a o b?
b) Indica el nombre de las fuerzas que intervienen.
c) ¿Falta alguna fuerza en el dibujo? En caso afirmativo,
indica su nombre y dibújala.
a)
b)
c) Una fuerza constante produce un movimiento
d) Una fuerza constante en intensidad, pero que cambia
continuamente de dirección produce un movimiento
a)
b)
c)
d)
Cero.
Rectilíneo y uniforme.
Rectilíneo y uniformemente acelerado.
Circular uniforme.
16 Completa las tablas siguientes aplicando la Segunda
Ley de Newton:
a) Es correcto el diagrama a).
b) La normal (N) debe ser perpendicular a la superficie de
deslizamiento.
c) Falta la fuerza de rozamiento: paralela a la superficie de
deslizamiento y opuesta al movimiento.
12 ¿Qué cuerpo tiene más inercia?
a)
b)
c)
d)
3 kg
2 kg
20 kg
1 kg
v = 100 m/s
v = 20 m/s
v = 0 m/s
v = 300 m/s
La inercia es una propiedad que depende solamente de la
masa. Por tanto, tiene más inercia el cuerpo c).
13 La limitación de velocidad en los vehículos pesados
¿está relacionada con la inercia? ¿Por qué?
La inercia de un cuerpo es tanto mayor cuanto mayor sea su
masa. Por tanto, los vehículos pesados tienen mayor tendencia a mantener su velocidad y por ello es más difícil frenarlos.
De ahí la limitación de velocidad.
14 La inercia es la causa principal de los accidentes mortales en los choques frontales de dos vehículos. Explica
por qué. ¿Qué objetivo tiene el cinturón de seguridad?
La inercia es la causa fundamental de los accidentes en el
choque frontal de dos vehículos. Éstos se detienen brusca-
F
m
2F
m
F
2m
a/2
4F
m
3F
F
2m
F
m
a
3F
m
2m
a
2F
m
2a
F
3m
a
3F
m
3a
2F
2m
a
5F
m
4F
m
4a
3F
3m
a
5F
m
5a
F
3m
a/3
17 Una fuerza F aplicada sobre un libro produce una
aceleración a. Cuando esa fuerza se duplica sobre un
segundo libro, la aceleración es tres veces mayor. ¿Qué
relación existe entre las masas de los dos libros?
Si m1 es la masa del primer libro, se cumple:
m1 = F1/a1.
Si m2 es la masa del segundo libro, se cumple que:
m2 =
F2 2 ⋅ F1 2
=
= ⋅m
a2 3 ⋅ a1 3 1
23
3
La relación anterior también se puede escribir:
2 m1 = 3 m2.
Aplicando la segunda ley de Newton se deduce que:
18 El movimiento de un automóvil viene dado por la
gráfica:
v
m=
100 N
= 4 kg
25 m s −2
b) m =
50 N
= 5 kg
10 m s −2
a)
c)
m=
25 N
= 12,5 kg
2 m s −2
Por tanto, el cuerpo c) tiene mayor masa.
A
21 ¿Qué cuerpo puede moverse con movimiento rectilíneo y uniforme si las únicas fuerzas que actúan son
las que se indican a continuación?
B
10 N
t
0
5N
4N
Indica las afirmaciones correctas:
a) En el tramo OA el coche no está sometido a ninguna
fuerza.
b) En el tramo OA la resultante de las fuerzas es constante.
c) En el tramo AB el coche está parado.
d) En el tramo AB la resultante de las fuerzas sobre el
coche es cero.
a) Es falso. En el tramo OA la velocidad aumenta uniformemente con el tiempo, como indica la pendiente de la
gráfica. El automóvil, pues, está sometido a una fuerza
constante.
b) Es verdadero. Por lo expuesto anteriormente.
c) Es falso. En el tramo AB el coche tiene velocidad constante, ya que la pendiente del diagrama v-t, que representa
la aceleración, es cero.
d) Es verdadero. Porque en ese tramo la aceleración es
nula.
19 Completa la siguiente tabla en tu cuaderno:
F = 45 N
F = 15 N
m=
m = 400 g
m = 15 kg
m=
a = 0,2 m/s2
a = 2 m/s2
a=
a = 0,5 m/s2
F = 10 N
F = 0,8 N
F = 45 N
F = 15 N
a = 0,2 m/s
m = 15 kg
m = 30 kg
a = 2 m/s
a = 3 m/s
a = 0,5 m/s2
2
20 ¿Cuál de los siguientes cuerpos tiene mayor masa?
F = 100 N
a = 25 m/s2
24
F = 50 N
a = 10 m/s2
F = 25 N
a = 2 m/s2
3N
10 N
Se moverá con movimiento rectilíneo y uniforme aquel cuerpo en el que la resultante de las fuerzas que actúan sobre
él sea cero. Esta condición la cumple el cuerpo que está en
segundo lugar.
22 Para que el cuerpo de la figura se mueva hacia la
derecha con una aceleración de 2 m/s2, la fuerza F debe
valer:
a) 10 N; b) 15 N; c) 20 N; d) 25 N
20 N
F
a = 2 m/s2
m = 400 g
2
3N 2N
4N
15 kg
F=
2
3N 5N
2N
15 N
F = 10 N
m = 50 kg
3N
Aplicamos la segunda ley de Newton.
Fresultante = m a ⇒ F + 20 N – 15 N = 15 kg · 2 m/s2
De donde, F = 30 N + 15 N – 20 N = 25 N
En consecuencia, es correcta la afirmación d).
23 Un hombre está de pie sobre una barca. Salta hacia la orilla y la barca se desplaza hacia atrás. Explica los
movimientos que tienen lugar.
Para poder saltar, el hombre debe ejercer una fuerza (acción)
sobre la barca, la cual ejerce otra fuerza igual (reacción) sobre
el individuo. Esto hace que los dos cuerpos, el hombre y la
barca, se muevan en sentido contrario.
24 El Barón de Munchausen, en una de sus inverosímiles
aventuras, explica cómo salió de un pantano en el que
había caído, agarrándose por los cabellos y tirando de
ellos con todas sus fuerzas. Demuestra con las Leyes de
Newton en la mano que el Barón no dice la verdad.
Si un hombre intenta elevarse tirándose de los cabellos, la
acción estaría sobre la cabeza y la reacción, sobre la mano. Así
que las dos fuerzas son internas, aplicadas al mismo sistema,
por lo que producirán sobre él un efecto nulo.
3 El cuerpo de la figura tiene una aceleración de:
a)
b)
c)
d)
1 m/s2
2 m/s2
3 m/s2
4 m/s2
30 N
5 kg
20 N
40 N
EJERCICIOS PROPUESTOS
De la segunda ley de Newton se deduce que:
30 N + 20 N – 40 N = 5 kg · a ⇒ a = 2 m/s2
Es correcta la afirmación b).
PARA REPASAR
1 Completa en tu cuaderno las siguientes afirmaciones:
a) La Ciencia que estudia las relaciones que existen entre las fuerzas y el movimiento recibe el nombre de
b)
es la propiedad de un cuerpo según la cual
éste se resiste a cambiar su estado de movimiento.
c) Un cuerpo está
cuando una fuerza no
equilibrada actúa sobre él.
d) La aceleración de un cuerpo es inversamente proporcional a
de dicho cuerpo.
a) La ciencia que estudia las relaciones que existen entre las
fuerzas y el movimiento recibe el nombre de Dinámica.
b) Inercia es la propiedad de un cuerpo según la cual éste
se resiste a cambiar su estado de movimiento.
c) Un cuerpo está acelerado cuando una fuerza no equilibrada actúa sobre él.
d) La aceleración de un cuerpo es inversamente proporcional a la masa de dicho cuerpo.
2 La fuerza de la figura vale:
a)
b)
c)
d)
10 N
20 N
30 N
40 N
4 La fuerza F de la figura vale:
a)
b)
c)
d)
10 N
30 N
50 N
70 N
a = 4 m/s2
10 N
5 kg
20 N
F
Es correcta la afirmación a), porque se cumple:
20 N + 10 N – F = 5 kg · 4 m/s2
F = 30 N – 20 N = 10 N
5 La masa m de la figura vale:
a)
b)
c)
d)
2 kg
4 kg
5 kg
8 kg
m
25 N
a = 0 m/s2
9N
20 kg
F
20 N
10 N
20 N
8 kg
Al no haber aceleración, la resultante de las fuerzas es cero.
Se debe cumplir, pues, que:
10 N + 20 N – F = 0 ⇒ F = 30 N
Por tanto, es correcta la afirmación c).
a = 1,5 m/s2
Aplicamos la segunda ley de Newton:
20 N + 25 N – 9 N = (20 kg + m) · 1,5 m/s2
36 N – 30 N = 1,5 m/s2 · m
6N
m=
= 4 kg
1,5 ms −2
Es correcta, pues, la afirmación b).
25
3
6 Para que el cuerpo de la figura se mueva hacia la
derecha con una aceleración de 0,5 m/s2, la masa m del
cuerpo debe valer:
a)
b)
c)
d)
10 kg
15 kg
20 kg
25 kg
20 N
m
a=
vt − v 0
20 m s −1 − 5 m s −1
=
t
10 s
15 m s −1
=
=1,5 m/s 2
10 s
=
De la segunda ley de la Dinámica se obtiene que:
F – Fr = m a ⇒ Fr = F – m a =
= 15 N – 8 kg · 1,5 m/s2 = 3 N
a = 0,5 m/s2
15 N
En primer lugar calculamos la aceleración:
5N
12 Calcula la masa de un autobús que se mueve a 90
km/h sabiendo que para detenerlo en 20 s se precisa una
fuerza de 12 000 N.
Aceleración del autobús mientras frena:
Es correcta la afirmación d), como se deduce de la aplicación
de la segunda ley del Movimiento.
5 N + 20 N – 15 N = m · 0,5 m/s2
10 N
m=
= 20 kg
0,5 m/s −2
7 Un objeto tiene 55 kg de masa y es acelerado con
una fuerza de 82,5 N. ¿Qué aceleración tiene?
La aceleración viene dada por:
a=
F 82,5 N
=
=1,5 m/s 2
m 55 kg
8 Un estudiante tiene una masa de 64 kg. ¿Cuánto
pesa este estudiante?
P = m g = 64 kg · 9,8 m/s2 = 627,2 N
9 ¿Qué masa debe tener un objeto para que adquiera
una aceleración de 0,5 m/s2 bajo la acción de una fuerza
de 135 N?
m=
F
135 N
=
= 270 kg
a 0,5 ms −2
10 Calcula la fuerza que debes aplicar a un cuerpo de
4 kg para que en 5 s cambie su velocidad de 2 m/s a
5 m/s.
Hallamos primero la aceleración:
a=
vt − v 0
t
=
5 m s −1 − 2 m s −1
= 0, 6 m/s 2
5s
La fuerza que se debe aplicar se obtiene de la segunda ley
de la Dinámica.
F = m a = 4 kg · 0,6 m/s2 = 2,4 N
11 Un cuerpo de 8 kg se desplaza por el suelo bajo la
acción de una fuerza horizontal de 15 N y pasa de 5 m/s
a 20 m/s en 10 s. ¿Cuánto vale la fuerza de rozamiento?
26
a=
vt − v 0
t
=
20 m s −1 − 25 m s −1
= −1,25 m/s 2
20 s
La masa se obtiene de la segunda ley de la Dinámica:
m=
F
12 000 N
=
= 9 600 kg
a −12,5 m s −2
13 Dibuja las fuerzas que intervienen en las siguientes
situaciones:
a) Un globo que asciende verticalmente con velocidad
constante (se supone despreciable el rozamiento con
el aire).
b) Un paracaidista que desciende con velocidad constante.
c) Un coche que se mueve, por una carretera horizontal,
con velocidad constante.
d) Un bañista
E (empuje)que flota en el agua.
E
a)
b)
E (empuje)
P
P
P
P
c)
d)
N
Fr
Fr
E
N
P
Fm
Fm
E
E
P
P
P
14 Una motora tiene una masa de 500 kg y ha recorrido
60 m en 5 s con aceleración constante, partiendo del reposo.
¿Cuál es la fuerza resultante sobre la motora?
De la ecuación e = 1/2 a t2 del movimiento obtenemos la
aceleración:
a=
2e 120 m
=
= 4, 8 m/s 2
t 2 (25 s)2
La fuerza motriz será:
F = m a = 500 kg · 4,8 m/s2 = 2 400 N
15 Un alpinista de 65 kg de masa pesa en la cumbre de
una montaña 636 N. ¿Cuánto vale la gravedad en la cima
de la montaña? ¿Cuánto pesa el alpinista al nivel del mar
si la gravedad aquí vale 9,80 m/s2?
g=
P 636 N
=
= 9,78 m s −2
m 65 kg
Operamos igual que en elE (empuje)
problema anterior.
a=
vt − v 0
t
=
25 m s −1
= 3,125 m/s 2
P
8s
Si la velocidad es constante, la resultante de las fuerzas ha
de ser cero:
F – Fr = 0 ⇒ Fr = F = 5,8 N
17 Una piedra pesa 5,4 N. ¿Qué fuerza se debe aplicar
sobre la piedra para que ésta ascienda verticalmente con
una aceleración de 2 m/s2?
N
Fr
P
5, 4 N
=
= 0, 6 kg
g 9, 81 m s −2
La fuerza se obtiene de la segunda ley de la Dinámica:
F–P=ma⇒F=P+ma=
= 5,8 N + 0,6 kg · 2 m/s2 = 7 N
18 Un ladrillo de 0,400 kg de masa se desplaza por una
superficie horizontal con una aceleración de 0,25 m/s2. Si
la fuerza de rozamiento vale 0,8 N, ¿qué fuerza se aplica
sobre el ladrillo?
Hallamos primero la aceleración:
a=
vt − v 0
t
=
25 m s −1 − 20 m s −1
= 0,5 m/s 2
10 s
La fuerza se obtiene de la segunda ley de la Dinámica:
F = Fr + m a = 200 N + 800 kg · 0,5 m/s2 = 600 N
20 Un automóvil de 1 000 kg acelera durante 8 s partiendo del reposo. Al cabo de dicho tiempo la velocidad
del coche es de 90 km/h. Calcula:
a) La aceleración del vehículo.
b) La fuerza resultante que ha originado dicha aceleración.
P
PARA REFORZAR
21 Una pelota alcanza una velocidad de 12 m/s en un
recorrido de 0,5 m cuando se le aplica una fuerza constante. Si la pelota tiene una masa de 0,050 kg, ¿cuánto
vale la fuerza aplicada?
La aceleración se obtiene aplicando la expresión:
v 2 = 2 a e; a =
v 2 144 m2 /s 2
=
=144 m/s 2
2 ⋅e
1m
La fuerza aplicada será:
F = m a = 0,050 kg · 144 m/s2 = 7,2 N
22 Un ciclista y su bicicleta tienen una masa de 85 kg.
Cuando el ciclista se mueve a 15 m/s observa un árbol en
medio del camino a 20 m de distancia. ¿Con qué fuerza
debe frenar para parar justamente delante del árbol?
Operando de la misma manera que en el problema anterior
tenemos:
Aplicando la ley de Newton tenemos:
F – Fr = m a
F = Fr + m a = 0,400 kg · 0,25 m/s2 + 0,8 N = 0,9 N
19 Un coche de 800 kg pasa de 72 km/h a 90 km/h en
10 s. Si la fuerza de rozamiento vale 200 N, ¿qué fuerza
desarrolla el motor?
E
Fm
P
Hallamos la masa de la piedra:
m=
P
F = m a = 1 000 kg · 3,125 m/s2 = 3 125 N
P = m g = 65 kg · 9,80 m/s2 = 637 N
16 Una caja de masa 1,4 kg se mueve por el suelo con
velocidad constante por la acción de una fuerza de 5,8 N.
¿Cuánto vale la fuerza de rozamiento?
E
a=
v 2 225 m2 /s 2
=
= 5, 625 m/s 2
2 ⋅e
40 m
F = m a = 85 kg · 5,625 m/s2 = 478 N
23 Una pelota de béisbol de 180 g de masa se dirige
hacia un bateador con una velocidad de 30 m/s, quien, al
golpearla, le imprime una velocidad de 45 m/s en sentido
contrario. Si la pelota y el bate estuvieron en contacto
durante 2 · 10 –2 s:
a) ¿Qué fuerza ejerció el bate sobre la pelota?
b) ¿Qué fuerza ejerció la pelota sobre el bate?
a=
=
vt − v 0
t
=
45 m/s − (−30 m/s)
=
2, 0 ⋅10 −2 s
75 m/s
= 3 750 m/s 2
2, 0 ⋅10 −2 s
a) F = m a = 0,180 kg · 3 750 m/s2 = 675 N
b) F = – 675 N, de acuerdo con la tercera ley de la Dinámica.
27
3
24 El cable de un montacargas soporta una tensión
máxima de 10 000 N. ¿Con qué aceleración máxima puede subir el montacargas una masa de 800 kg?
d) Si la fuerza se hace el doble, la aceleración también se duplica. Por tanto, la pendiente de la gráfica será el doble.
V
Sobre el sistema actúan dos fuerzas: la tensión del cable y el
peso del montacargas. La resultante de estas fuerzas produce
la aceleración, de acuerdo con la ley de la Dinámica.
T–mg=ma
a=
20
15
10
T − m g 10 000 N − 800 kg ⋅9, 81 m/s 2
=
= 2,7 m/s 2
m
800 kg
25 Un hombre quiere huir de un edificio en llamas
descolgándose por una cuerda que sólo soporta un peso
de 400 N. El hombre pesa 800 N.
a) ¿Le sirve esa cuerda para abandonar el edificio?
b) En caso afirmativo, ¿con qué aceleración lo puede
hacer?
Aplicamos la ley de la Dinámica teniendo en cuenta que la
aceleración es negativa, porque tiene el mismo sentido que
la aceleración de la gravedad:
T – m g = m (–a)
T −mg
a=
=
m
400 N − 800 N
800N
= −4,9 m/s 2
9, 81 m/s 2
5
1
2
3
4
t
27 La figura siguiente es la gráfica v–t del movimiento
rectilíneo de un coche de 1 200 kg. Tacha en tu cuaderno
las afirmaciones falsas:
a)
b)
c)
d)
e)
La velocidad del coche es constante.
La aceleración del coche vale 5 m/s2.
La velocidad del coche a los 2 s vale 8 m/s.
Para t = 0, la aceleración es cero.
Cuando han transcurrido 4 s la velocidad del coche
es 72 km/h.
f) La fuerza constante que actúa sobre el coche es 4 000
N.
v (m/s)
26 Un automóvil de 1 000 kg se mueve según la gráfica:
v (m/s)
20
15
20
10
15
5
t (s)
10
0
1
2
3
4
5
5
t (s)
0
a)
b)
c)
d)
1
2
3
4
5
¿Cuánto vale la aceleración del coche?
¿Qué fuerza actúa sobre él?
¿Qué velocidad tendrá el coche al cabo de 10 s?
Dibuja la gráfica v – t en el caso de que la fuerza fuera
el doble.
a) La aceleración viene dada por la pendiente de la gráfica:
a=
vt − v 0
t
=
10 m/s − 0 m/s
= 2,5 m/s 2
4s
b) F = m a = 1 000 kg · 2,5 m/s2 = 2 500 N
c) v = v0 + a t = 0 + 2,5 m/s2 · 10 s = 25 m/s
28
a) Afirmación falsa. Porque el coche tiene aceleración.
b) La aceleración vale a =
15 m/s
= 5 m/s 2 . Por tanto, la afir3s
mación es verdadera.
c) La velocidad es: v = a t = 5 m/s2 · 2 s = 10 m/s. Por tanto,
la afirmación es falsa.
d) Afirmación falsa. El móvil ha tenido una aceleración constante desde el instante inicial.
e) La velocidad toma el valor de:
v = a t = 5 m/s2 · 4 s = 20 m/s = 72 km/h
Por tanto, se trata de una afirmación verdadera.
f) La afirmación es falsa, porque el valor de la fuerza es:
F = 1 200 kg · 5 m/s2 = 6 000 kg
28 Un móvil de 4 kg se desplaza de acuerdo con la gráfica v–t de la figura.
a) El recipiente A está lleno de agua.
b) El recipiente C contiene clavos de hierro.
c) El recipiente B está lleno de serrín.
v (m/s)
20
15
10
5
t (s)
0
1
2
3
4
5
a) ¿En qué intervalos de tiempo está sometido a una
fuerza?
b) ¿En qué intervalos de tiempo la fuerza es nula?
c) ¿Cuánto vale la aceleración en el intervalo de 4 a 5 s?
d) ¿Cuánto vale la velocidad en el intervalo comprendido entre 2 y 3 s?
e) ¿Cuánto vale la fuerza durante los dos primeros segundos?
a) Estará sometido a una fuerza en aquellos intervalos en
los que el móvil tenga aceleración. Es decir, en aquellos
intervalos en los que la pendiente del diagrama no sea
cero. Estos intervalos son: de 0 a 2 s y de 4 a 5 s.
b) La fuerza deja de actuar en el intervalo de 2 a 4 s. Porque
en este intervalo no hay aceleración.
c) La aceleración vale en ese intervalo:
a=
vt − v 0
t
=
0 m/s −15 m/s
= −15 m/s 2
1s
d) En el intervalo de 2 a 3 s la velocidad es constante y vale
15 m/s.
e) En el intervalo indicado la aceleración vale
a=
15 m/s
= 7,5 m/s 2
2s
Por tanto, la fuerza será: F = 4 kg · 7,5 m/s2 = 30 N
29 Tenemos tres recipientes iguales. El primero está
lleno de clavos de hierro. El segundo está lleno de agua
y el tercero, de serrín. En la figura se muestra cómo varía
la fuerza aplicada sobre cada recipiente y la aceleración
con que se mueven éstos. Responde falso o verdadero:
La pendiente de las gráficas representa la masa del cuerpo
correspondiente. De acuerdo con esto:
— El recipiente C tiene clavos de hierro, por ser la pendiente
mayor.
— El recipiente B contiene agua, pendiente intermedia.
— El recipiente A tiene serrín, porque es el recipiente que
tiene la pendiente más pequeña.
Por tanto, a) Falso; b) Verdadero; c) Falso.
30 Calcula la masa de un automóvil que se mueve a 70
km/h sabiendo que para detenerlo en 16 segundos es
precisa una fuerza de 4 000 N.
La velocidad en el SI vale v = 19,4 m/s
La aceleración es a = 19,4/16 = 1,2 m/s2
Y la masa m = F/a = 4 000/1,2 = 3 333 kg
31 ¿Qué fuerza debes aplicar sobre un cuerpo de 200 g
de masa para que en 2 s aumente la velocidad desde 10
m/s a 20 m/s?
La aceleración vale a =
20 −10
= 5 m/s 2
2
Y la fuerza se obtiene por F = m a = 0,2 · 5 = 1 N
32 Un automóvil de 1 000 kg se mueve con una velocidad
de 60 km/h. Si dicho automóvil acelera uniformemente
durante 8 s hasta alcanzar una velocidad de 100 km/h,
¿cuánto vale la fuerza aceleradora?
Hallamos las velocidades en m/s:
v = 60 km/h = 16,7 m/s
v = 100 km/h = 27,8 m/s
La aceleración será a =
27, 8 −16,7
=1,39 m/s 2
8
F = 1 000 · 1,39 = 1 390 N
EVALUACIÓN
1 Indica si las siguientes afirmaciones son verdaderas
o falsas.
Re c
ip i e
nte
C
fuerza
Re
cip
B
te
i en
Recip
iente
A
aceleración
a) Las fuerzas constantes no producen movimiento.
b) Las fuerzas constantes producen movimiento uniforme.
c) Si un cuerpo se mueve en línea recta y con velocidad
constante no está sometido a ninguna fuerza.
d) Si la resultante de las fuerzas que actúan sobre un
cuerpo es cero, dicho cuerpo puede estar en movimiento.
29
3
a) Falso.
b) Falso. Porque una fuerza constante origina un movimiento uniformemente acelerado.
c) Falso. Lo correcto sería «… no está sometido a ninguna
fuerza neta».
d) Verdadero. Porque puede estar parado o puede tener
movimiento rectilíneo y uniforme, como se deduce de
la ley de la inercia.
2 Indica la respuesta correcta en el siguiente texto:
una furgoneta que transporta un paquete frena bruscamente. Como consecuencia de esto:
a)
b)
c)
d)
El paquete no experimenta ningún cambio.
El paquete tiende a irse hacia adelante.
El paquete tiende a irse hacia atrás.
El paquete salta hacia arriba.
Es correcta la respuesta b), porque el paquete, por inercia,
tiende a conservar el movimiento que tenía. Por esto tiende
a irse hacia delante.
3 Un automóvil se desplaza por una carretera recta
con una velocidad constante de 120 km/h. Indica si las
siguientes afirmaciones son verdaderas o falsas.
a) Sobre el coche no actúa ninguna fuerza porque no
existe aceleración.
b) Sobre el coche actúan dos fuerzas que se equilibran:
la fuerza que ejerce el motor y el peso del coche.
c) La resultante de todas las fuerzas que actúan sobre
el coche es cero.
d) Sobre el coche solamente actúa una fuerza: la que
ejerce el motor.
a) Falso. Lo correcto sería «Sobre el coche no actúa ninguna
fuerza neta».
b) Falso. La fuerza del motor y el peso no pueden equilibrarse en este caso, porque no tienen la misma dirección.
c) Verdadero. Como dice la Ley de la inercia.
d) Falso. Además de la fuerza del motor, actúan sobre el
coche el peso, la normal y la fuerza de rozamiento.
30
4 Señala la afirmación correcta. Si solamente existiera
la Tierra en el Universo:
a) Estaría necesariamente en reposo.
b) Se movería necesariamente en línea recta y sin aceleración.
c) Podría estar en reposo o moviéndose en línea recta
y sin aceleración.
d) Seguiría con el mismo movimiento que actualmente
posee.
Es correcta la afirmación d). De acuerdo con la Ley de la
inercia, un cuerpo que está aislado se mueve con velocidad
constante o está parado.
5 Las siguientes afirmaciones están referidas a las
fuerzas de acción y reacción. Indica cuáles son verdaderas:
a)
b)
c)
d)
Las dos fuerzas son iguales.
Las dos fuerzas actúan sobre el mismo cuerpo.
Si la acción es F, la reacción es –F.
Siempre se equilibran porque tienen la misma dirección y sentido contrarios.
Respuesta correcta: c).
6 Señala la respuesta verdadera. Cuando dos cuerpos
interaccionan:
a) La fuerza que ejerce el primero es igual a la fuerza
que ejerce el segundo, incluso con la misma dirección
y sentido.
b) La masa de los dos cuerpos es la misma.
c) La variación de la cantidad de movimiento del primero
es igual y opuesta al cambio en el segundo cuerpo.
d) La cantidad de movimiento total de los dos cuerpos
permanece constante.
Respuesta correcta: c).
ESTÁTICA DE FLUIDOS
EJERCICIOS
1 Aplica la Teoría cinética de la materia, estudiada el
curso anterior, a fin de explicar las características básicas
que acabamos de mencionar para los fluidos.
La teoría cinético-molecular se basa en dos postulados:
a) Las partículas que componen la materia están en movimiento continuo.
b) Cuanto mayor es la temperatura, mayor es su movimiento.
Los sólidos se caracterizan por partículas muy juntas y en posiciones fijas; por eso tienen forma y volumen constantes.
En los líquidos, las fuerzas son más débiles, lo que permite
cierta libertad de rotación y traslación; por ello los líquidos
adoptan la forma del recipiente. Tienen volumen constante.
Los gases presentan movilidad casi total de vibración, rotación y traslación, por lo que no tienen ni volumen ni forma
definidos.
2 Intenta explicar por qué al ponernos unos esquís
nos hundimos menos en la nieve, aunque ahora pesamos
más.
Porque al ponernos los esquíes aumenta nuestra superficie
de contacto y como nuestro peso no cambia, la presión ejercida sobre la superficie de contacto es menor y, por ello, nos
hundimos menos.
3 ¿A qué crees que se debe el que, con una persona «a
caballito» en la espalda te hundas más?
Porque al aumentar el peso aumenta la presión sobre la superficie de contacto (nuestros pies) que no ha variado.
4 ¿Existe alguna relación entre el peso y la presión que
haces sobre la nieve?
F
Sí, a mayor peso, mayor presión: p =
S
↑F→↑p
4
7 ¿Por qué los clavos se clavan por la punta en lugar
de hacerse por la cabeza?
Porque la punta tiene mucha menor superficie de contacto.
8 ¿Cómo te hace más daño un libro al caerte en el pie:
si te cae de punta o si cae plano? ¿Por qué?
Hace mucho más daño si cae de punta, puesto que, al caer el
mismo peso sobre menor superficie, el valor de la presión es
mucho mayor por lo que puede incrustarse o por lo menos
incidir de forma mucho más evidente sobre el pie.
9 Calcula la presión a la que se ve sometido el nadador
de la Fig. 4.3 cuando está a 2 y a 3 metros de profundidad.
p(2m) = d g h = 1000 kg/m3 ⋅9, 8 m/s 2 ⋅2 m =
= 16 900 Pa
p(3m) = d g h = 1000 kg/m3 ⋅9, 8 m/s 2 ⋅3 m =
= 29 400 Pa
10 Si en otra botella, también llena de agua, practicas dos
orificios a la misma altura, pero en sitios diferentes, ¿qué
ocurrirá? ¿Por qué?
Que el alcance del agua será el
mismo en ambos lados, porque
la presión ejercida en ambos
puntos es la misma, ya que la h
es igual.
h
x
x
11 Según el esquema de la Fig. 4.7, ¿qué pozo artesiano
dejará antes de suministrar el agua?
El que está a mayor altura.
12 Indica otras situaciones de la vida cotidiana en
donde se emplee el Principio de Pascal.
5 ¿A qué crees que se debe el hecho de que se corten
mejor las cosas con cuchillos afilados que con cuchillos
romos?
En cualquier situación en que se usen pistones de presión
(sillones de peluqueros, de dentistas, en las plataformas elevadoras de los garajes de coches, etcétera).
A que la superficie de contacto es menor y al realizar la misma
fuerza la presión aumenta.
13 Calcula la densidad de la piedra de la experiencia
anterior en unidades del SI.
6 ¿Por qué a veces nos cortamos en los dedos al pasar
una página de un libro?
Porque están muy afiladas, es decir, la superficie de contacto
es muy pequeña, con lo que al realizar una mínima fuerza,
la presión ejercida sobre nuestra piel es muy elevada y nos
cortamos.
La densidad hay que darla en el SI en kg/m3, por tanto:
x
g
1 kg 10 6 cm3
kg
⋅
⋅
= x ⋅ 103 3
cm3 1000 g 1 m3
m
Habrá que multiplicar por 1 000 el valor que nos salga en
g/cm3 para pasarlo al SI.
31
4
14 Si introduces una pelota de goma en el interior de
un río a 0,5 m de profundidad, ¿sufrirá un empuje igual
o diferente que si la introducimos a 1,5 m?
El empuje a una profundidad de 1,5 m será exactamente igual
que a 0,5 m, ya que el empuje es una fuerza y, por tanto, no
dependerá de la altura sino del volumen del líquido desalojado, que será igual al volumen del cuerpo que introducimos
en el agua, pero una vez introducido da igual que lo hagamos
a 0,5 m o a 1,5 m: E = Vc dl g.
15 ¿Por qué el empuje de los gases es menor que el de
los líquidos para un mismo cuerpo?
Porque la densidad de los gases es del orden de 1 000 veces
menor.
16 ¿Por qué crees que hay cuerpos que flotan y otros
que se hunden en algunos líquidos? ¿A qué puede ser
debido?
A que la densidad del cuerpo sea mayor que la del líquido y,
por tanto, la presión ejercida sea mayor que el empuje.
17 Sabiendo que la densidad de la madera es 6/10 de la
densidad del agua líquida, ¿cuál será la parte emergente
de un bloque de madera?
Utilizamos la expresión:
Vc
Vsumergido
Vc
Vs
=;
Vc
Vs
=
=
dlíquido
dcuerpo
;
10
6
Del volumen total de la madera, 6 partes estarán sumergidas
y 4 estarán emergidas.
18 ¿Dónde existirá mayor presión, en una montaña a
2 000 m de altitud o en la superficie terrestre?
Existirá mayor presión en la superficie
terrestre, ya que el aire ejerce presión;
aunque sea gas igualmente se cumple
que: p = d g h.
(1)
(2)
En la superficie terrestre existirá la misma presión que en la
cima de la montaña más la debida a la altura, es decir:
Psuperficie = pmontaña + d g h
19 La densidad del aire es unas 800 veces menor que
la densidad del agua, ya que su valor aproximado es
1,29 g/L, mientras que para el agua es 1 000 g/L. Teniendo en cuenta estos valores, explica qué diferencias se
apreciarán en ambos medios cuando se ascienda 10 m en
su seno. ¿Qué le ocurre a la presión en uno y otro caso?
32
Como p = d g h, la gravedad es constante en ambos casos y la
altura exactamente igual: 10 m.
La única magnitud diferente es la densidad, que en un caso
es 800 veces mayor, por lo que la presión a los 10 m en ambos
casos valdrá:
a) paire = 1,3 kg/m3 · 9,8 m/s2 · 10 m = 127 Pa, ya que 1,3 g/L
= 1,3 kg/m3.
b) pagua = 1 000 kg/m3 · 9,8 m/s2 · 10 m = 98 000 Pa.
Mientras que a 1 m de altura los valores serán:
p = 1,3 kg/m3 · 9,8 m/s2 · 1 m = 12,7 Pa
p = 1 000 kg/m3 · 9,8 m/s2 · 1 m = 9 800 Pa
Es decir, la presión en ambos casos ha aumentado 10 veces.
20 Si succionas, con ayuda de una pajita, el batido contenido en un vaso, el líquido asciende hacia tu boca. Esto
es también consecuencia de la existencia de la presión
atmosférica. ¿Puedes explicarlo? Los globos que venden
en las ferias, cuando se escapan, aumentan de tamaño
a medida que ascienden. ¿Tiene que ver también con la
presión atmosférica?
Evidentemente, pues si ponemos la pajita en el
vaso observaremos que el líquido no sale por
la pajita hasta que no vencemos la presión atmosférica que se ejerce sobre la superficie del
líquido.
Para vencer esa presión hay que succionar, que es exactamente lo mismo que hacemos cuando bebemos un batido
con una pajita.
21 Sabiendo que la presión atmosférica al nivel del mar
equivale a 0,76 m de mercurio y que la densidad de éste
es 13 600 kg/m3, ¿cuál será la altura de una columna de
agua, cuya densidad es 1 000 kg/m3 equivalente a la presión atmosférica?
d g h = d’ g’ h’
13 600 kg/m3 · 9,8 m/s2 · 0,76 m =
= 1 000 kg/m3 · 9,8 m/s2 · h’
de donde: h’ = 10,33 m
22 Recuerda el experimento de los hemisferios de Otto de Guericke. Si en lugar de ellos se acoplan dos cajas
cilíndricas de 15 cm de diámetro, ¿qué fuerza habría que
realizar para separarlas en un día de presión atmosférica
normal?
Habrá que vencer la presión atmosférica, suponemos 1 atm
= 101 300 Pa
F = p S = 101300 N/m2 ⋅πR 2 = 101300 N/m2 ⋅
2
 0,15 
⋅ 3,14 ⋅ 
= 1789,2 N
 2 
EJERCICIOS PROPUESTOS
7 ¿Dónde pesa más un cuerpo, en una habitación con
aire o en una en donde se ha hecho el vacío? Explícalo.
PARA REPASAR
Donde se ha hecho el vacío la masa del cuerpo sería la misma,
ya que al hacer el vacío se eliminaría el efecto de la gravedad y, como el peso del cuerpo es p = m g, el cuerpo pesaría más en una habitación donde no se hubiera realizado el
vacío.
1 ¿Cuál será la presión que ejercerá una vaca sobre el
suelo si la superficie inferior de cada una de sus patas es
aproximadamente de 50 cm2 y su masa es de 600 kg?
p=
F m g 600 ⋅9, 8
=
=
= 294 000 N
S
S
4 ⋅5010 −4
2 Compara el resultado anterior con la presión que
ejerce una chica, que tiene una masa de 50 kg, sobre el
suelo cuando está con zapatos de tacón, cuya superficie
es de 20 cm2.
p=
F mg
50 ⋅9, 8
=
=
=122 500 N
S
S
2 ⋅20 ⋅10 −4
3 Un automóvil tiene una masa de 1 500 kg y sus
neumáticos están hinchados a una presión de 175 · 103 Pa.
Calcula la superficie de contacto de cada neumático con
el suelo. Dato: g = 9,8 m/s2.
1500 ⋅9, 8
F mg
4
S= =
=
= 0, 02 m2
p
S
175 ⋅103
4 Habrás leído alguna vez que si un coche cae en el río
o en el mar, antes de abrir sus puertas se debe esperar a
que se haya llenado de agua su interior. ¿Por qué crees
que esto es así?
Para poder igualar la presión interior con la exterior.
5 ¿Qué presión deben aguantar los animales marinos
que viven a 5 000 m de profundidad? (Densidad del agua
del mar = 1,03 · 103 kg/m3, g = 9,8 m/s2.)
8 La presión máxima que puede soportar el ser humano es de 8 atm. ¿Hasta qué profundidad puede descender
en el mar sin peligro?
p
p=d gh⇒h=
=
gh
101300 Pa
1 atm = 80,3 m
m
kg
9, 8 2 ⋅1030 3
s
m
8 atm ⋅
9 Queremos levantar un peso de 1 000 kg con una
prensa hidráulica sabiendo que el émbolo pequeño es
un cuadrado de 10 cm de lado y el émbolo grande es un
cilindro de 10 cm de radio. ¿Cuál será la fuerza que deberemos realizar y en qué émbolo de los dos, si queremos
hacer la mínima fuerza?
Superficie del émbolo grande: S = l2; S = 0,102 = 0,01 m2
Superficie del émbolo pequeño: s = πR2 = 3,14 · (10 –2)2 =
= 3,14 · 10–4 m2
f =F
s
0, 000314
; f = 1000 kg ⋅9, 8 m/s 2 ⋅
= 307, 88 N
S
0, 01
10 Explica cómo calcularías la densidad de un objeto de
forma irregular con la ayuda de un dinamómetro, agua
y una probeta.
p = d g h = 1,030 kg/m3 · 9,8 m/s2 · 5 000 = 50 470 000 Pa
Con el dinamómetro calcularíamos la masa del objeto y con la
probeta calcularíamos el volumen del mismo, que sería equivalente al aumento de volumen dentro de la probeta. Finalmente se aplicaría la ecuación d = m/V en unidades del SI.
6 ¿Por qué las bombas manuales de extracción de
agua no pueden cumplir su cometido cuando el líquido
está a 11 o más metros de profundidad?
11 ¿Qué crees que pasa con la línea de flotación de un
barco cuando, durante su navegación, pasa de un río al
mar?
Porque para subir el agua había que vencer la presión atmosférica que sabemos que vale:
p = 13 600 kg/m3 · 9,8 m/s2 · 0,76 m = 101 293 Pa
y esa presión equivaldría a una altura de agua que es:
La densidad del agua de mar es mayor (1 030 kg/m3) que la
del agua de río (1 000 kg/m3); por tanto, la línea de flotación
subirá.
p
101293 Pa
h=
=
=10,33 m
d g 1000 kg/m2 ⋅9, 8 m/s 2
Por eso, a partir de una profundidad de más de 10,33 metros
haría falta una bomba con un motor y no serviría una bomba
manual.
12 Al sumergir dos cuerpos en agua uno desaloja 3 mL
y el otro, 12 cm3. ¿Qué podrías decir de sus densidades?
Si los dos cuerpos tienen el mismo volumen, el que desplaza
mayor volumen de agua debe tener mayor densidad, pues se
ha de sumergir más para que desplace más volumen; exactamente, la densidad ha de ser cuatro veces mayor.
33
4
13 ¿Qué fuerza ejerce la atmósfera un día en que el
barómetro marca 760 mm Hg sobre un objeto que tiene
una superficie de 2 m2? ¿Y si el barómetro marcara 700
mm Hg?
101300 Pa
⋅2 m2 = 202 600 N
760 mm Hg
101300 Pa
F = p S = 700 mm Hg ⋅
⋅2 m2 = 186 605 N
760 mm Hg
F = p S = 760 mm Hg ⋅
14 ¿Hubieran cambiado los resultados si el tubo que usó
Torricelli fuera la mitad de ancho que el que utilizó?
No, porque la presión depende exclusivamente de la altura
y no del volumen: p = d g h.
PARA REFORZAR
15 Calcula la diferencia entre las presiones que soportan dos peces en un pantano si uno está 5 m más arriba
que el otro.
La presión equivalente a una altura de 5 m de agua es:
p =1000
kg
m
⋅9, 8 2 ⋅5 m = 49 000 Pa
m3
s
16 ¿Cuántos metros deberíamos escalar en una montaña para que la diferencia de presiones fuera la misma
que la del apartado anterior? (Densidad media del aire
= 1,29 g/dm3.)
g
1 kg 103 dm3
⋅
⋅
⋅ 9, 8 m/s 2 h →
dm3 1000 g 1 m3
→ h = 3 875,9 m
49 000 = 1,29
En agua, la presión equivalente a 5 m es igual a 3 875,9 m
en el aire.
17 La ventana lateral de un batiscafo tiene 80 cm de
diámetro. Calcula la fuerza que se ejerce sobre ella cuando el batiscafo se halla a 8 km de profundidad. (Densidad
del agua de mar = 1,03 g/cm3.)
Si la ventana es circular, tenemos:
F = p S = d g h S = 1 030 kg/m3 · 9,8 m/s2 · 8 000 m · 3,14 ·
· 0,42 = 40 590 382 N
18 En el lateral de un depósito de 5 m de altura se produce un agujero de 4 cm de diámetro a una altura de
4 m por debajo de la superficie. Si el depósito se va a
llenar totalmente de agua, ¿cuál será la presión que deberá soportar el material que utilicemos para taponar el
agujero? ¿Y la fuerza?
34
p = d g h = 1 000 kg/m3 · 9,8 m/s2 · 4 m =
= 39 200 Pa
F = p S = 39 200 Pa · 3,14 · 0,042 = 197 N
5
4
19 Durante el mes de agosto de 2000 se hundió en el
mar de Barents, a 110 metros de profundidad, el submarino nuclear Kursk, de nacionalidad rusa. Para proceder
a su reflotación un equipo de buceadores noruegos tuvo
que sumergirse. Calcula la diferencia de presión que soportaron con respecto al nivel de mar.
p = d g h = 1 030 kg/m3 · 9,8 m/s2 · 110 m = 1 110 340 Pa
20 La torre Eiffel tiene una masa de 7,34 · 106 kg, y se
apoya en tierra descansando sobre los émbolos grandes
de 16 prensas hidráulicas de sección circular. Sabiendo que
el diámetro de las prensas hidráulicas grandes es de 6,2 m
y el de las pequeñas, 17,3 cm, calcula la fuerza que soporta
cada una de estas últimas.



2

 0,173 
2
2
S = πR = 3,14 ⋅ 
 = 0, 0235 m 
 2 

m
458 750 kg ⋅9, 8 2
F
s =1,9 ⋅10 8 Pa
p= =
S
0, 0235 m2
m=
7,34 ⋅10 6 kg
= 458 750 kg
16
F = p S = 1,9 · 108 Pa · 0,0235 m2 = 4 495 750 N
21 Una balsa de madera de 2 m de largo por 1 m de ancho y 15 cm de espesor soporta, antes de hundirse totalmente, una masa de 150 kg. Calcula la densidad de la
madera con la que se ha construido la balsa.
Vbalsa = 2 · 1 · 0,15 = 0,3 m3; la masa de la balsa será: mb = 0,3 m3 · db
y el peso de la balsa será: P = 0,3 m3 · db · 9,8 m/s2
El empuje que puede llegar a soportar es:
E = m g = 150 kg · 9,8 m/s2 = 1 470 N
Por tanto: 1 470 N = 0,3 m3 · db · 9,8 m/s2
De donde la densidad de la balsa será: d = 500 kg/m3
22 Sabiendo que la densidad del corcho es de 310 kg/m3,
calcula cuál será la relación entre su volumen emergido
y sumergido en agua.
v cuerpo
v sumergido
v cuerpo
v sumergido
=
dagua
;
v cuerpo
dcorcho v sumergido
=
1000 kg/m3
;
310 kg/m3
= 3,22
Esta relación es la existente entre el volumen total del objeto
de corcho y el que se encuentra sumergido. De 10 partes hay
3,1 sumergidas y 6,9 emergidas.
Dato: Cuando estaba en tierra, el manómetro marcaba
1 atmósfera; 1 atmósfera = 101 300 Pa.
Si el volumen del cuerpo fuera 10 m3:
vs =
10
= 3,1 m3
3,22
23 Se realiza la experiencia de Torricelli al pie de una
montaña y en su cima. Entre ambas experiencias existe
una diferencia de altura de la columna de mercurio del
barómetro de 2 cm. (Densidad del aire = 1,3 kg/m3.)
a) Calcula la altura de la montaña.
b) ¿Cuál sería la diferencia de altura si en lugar de emplear mercurio (d = 13 600 kg/m3) en el barómetro
hubiésemos utilizado agua?
a) La altura es equivalente a una diferencia de presión de
2 cm de Hg, por tanto, la presión equivalente a esa altura
de Hg será:
∆p = d g∆h =13 600
= 2 665, 6 P
kg
m
⋅9, 8 2 ⋅0, 02 m =
3
m
s
Como estamos en el aire, esa diferencia de presión equivaldrá a:
2 665,6 = 1,3 kg/m3 · 9,8 m/s2 · h
De donde h = 209,2 m.
La montaña pequeña tendrá aproximadamente 210 m
menos de altura.
b) 13 600 kg/m3 · 9,8 m/s2 · 0,02 m = 1 000 kg/m3 · 9,8 m/s2 ·
· h → h = 27,2 m
24 Indica el fondo de qué recipiente sufre mayor presión:
d = densidad
S = superficie
h = altura
d/2
d
h
2d
S/2
2S
1.a columna: p = d g h = d / 2 g h =
h
h/2
S
d gh
2
2.a columna: p = d g h
3.a columna: p = d g h = 2d g h/2 = d g h
25 Un paracaidista se lanza en caída libre con un barómetro de precisión en su muñeca. Calcula:
a) Si la caída comienza a los 3 000 m de altitud, cuál es
la lectura del manómetro.
b) Si el paracaidista quiere abrir su paracaídas cuando
esté a 500 m sobre el suelo, cuál será la lectura que
debe marcar su manómetro de muñeca.
A nivel terrestre la presión sería de 1 atmósfera o 760 mmHg
o 101 300 Pa; como el paracaidista está a 3 000 m de altura la
presión será menor y equivaldrá a:
a) p = 101 300 Pa – d g h = 101 300 – (1,3 kg/m3 · 9,8 m/s2 ·
· 3 000 m) = 63 080 Pa
63 080 Pa⋅
760 mm Hg
= 473,25 mm Hg
101300 Pa
b) A 500 m la altura que deberá marcar el manómetro será:
p = 101 300 Pa – d g h = 101 300 – (1,3 kg/m3 · 9,8 m/s2 ·
· 500 m) = 94 930 Pa
94 930 Pa⋅
760 mm Hg
= 712,2 mm Hg
101300 Pa
26 El tapón de una bañera es circular y tiene 4 cm
de radio. Si llenamos la bañera con agua hasta una
altura de 0,50 m, calcula la fuerza que habría que
hacer para levantar el tapón, si su masa es de 20 g.
F = mtapóng + d g h S = 0,020 kg · 9,8 m/s2 + 1 000 kg/m3 ·
· 0,50 m · 9,8 m/s2 = 49,5 N
27 La copa Jules Rimet que recibe el ganador del Mundial de fútbol es de oro. Sabiendo que pesa 2,50 kg y que
si la sumerges en agua su peso aparente es de 23,23 N,
calcula la densidad del oro de esa copa.
P = m g = 2,50 kg · 9,8 m/s2 = 24,5 N
El empuje que sufre es de: 24,5 – 23,23 = 1,27 N
Como sabemos que E = Vlíquido dlíquido g;
1,27 = Vlíquido · 1 000 kg/m3 · 9,8 m/s2
De donde Vlíquido = 129,6 · 10 –6 m3 que será el mismo que el
del cuerpo sumergido.
Por tanto Vlíquido = Vcuerpo; d = m/V = 2,50 kg/ /129,6 · 10 –6 m3 =
= 19 290 kg/m3
28 Queremos medir la densidad de un objeto esférico
de metal. Para ello disponemos de un dinamómetro que
nos señala 25 N cuando colgamos la esfera en el aire.
Si repetimos el mismo procedimiento sumergiendo el
objeto en agua, el dinamómetro señala 20 N. Calcula la
densidad del metal y su volumen.
El empuje realizado por el agua es:
E = P – Paparente = 25 – 20 = 5 N
5 = Vlíquido · 1 000 kg/m3 · 9,8 m/s2
Y como el volumen del líquido desalojado es igual al volumen
del cuerpo, tenemos:
Vcuerpo = 510 cm3 = 5,1 · 10 –4 m3; F = m g;
35
4
m = F/g = 25 N/9,8 m/s2 = 2,55 kg
d = m/V; d = 2,55 kg/5,1 · 10 –4 m3 = 5 000 kg/m3
29 ¿Cuánto hubiera marcado el dinamómetro del ejercicio anterior si en lugar de introducir la bola de metal en agua lo hubiéramos introducido en metanol o en
mercurio? Datos: dmetanol = 7,91 · 102 kg m –3; dHg = 13,6 ·
103 kg m–3.
Ealcohol = 5,1 · 10 –4 m3 · 7,91 · 102 kg/m3 · 9,8 m/s2 = 3,95 N
E = 25 – 3,95 = 21,05 N
Emercurio = 5,1 · 10 –4 m3 · 13,6 · 103 kg/m2 · 9,8 m/s2 = 67,97 N
No se habría hundido, pues el empuje es mayor que el peso.
Que también podía haberse calculado como:
PE + Paparente = 2,26 + 0,33 = 2,59 N
b) El empuje en ese caso será:
E = 2,59 – 2,38 = 0,21 N
Y la densidad del alcohol será: 0,21 = Vc dl g
dalcohol =
32 Calcula a qué altura hay que subir para que la presión
atmosférica disminuya en 5 mm Hg aproximadamente.
La altura equivalente a una presión de 5 mm Hg es:
101300 Pa
= 666, 6 Pa
760 mm Hg
∆p
∆p = d g ∆h; ∆h =
=
dg
666, 6
=
= 52,3 m
1,3 kg/m3 ⋅9, 8 m/s 2
5 mm Hg ⋅
30 Una esfera de madera tiene una masa de 200 g. La
densidad de la madera es 600 kg/m3.
a) Si se sumerge en agua, ¿qué fuerza hay que aplicarle
para mantenerla en equilibrio dentro de ella?
b) Si se deja en libertad, ¿cuál es la aceleración con la
que sube hacia la superficie?
El empuje que sufrirá la bola de madera cuando está dentro
del agua será:
a)
E = m/d dagua g =
0,200 kg
kg
m
⋅1000 3 ⋅9, 8 2 = 3,26 N
kg
m
s
600 3
m
Por tanto, la fuerza que deberíamos hacer será: 3,26 –
– 0,200 · 9,8 = 1,3 N
b) La fuerza con que la bola saldrá del agua una vez que la
soltamos será:
E – m g = 3,26 – 0,200 · 9,8 = 1,3 N
Y, por tanto, la aceleración con que la bola emergería es:
a = F/m = 1,3 N/0,200 = 6,5 m/s2
EVALUACIÓN
1 Dos esquiadores se encuentran sobre la nieve. Se
hundirán más o menos dependiendo:
a) De sus pesos y de la superficie de los esquís sobre los
que se encuentran.
b) De sus pesos y de la velocidad a la que se mueven.
c) Sólo de sus pesos.
d) De las características de la nieve (su dureza, lo compacta que esté, etcétera).
Respuesta correcta: a).
31 Se introduce, colgada de un dinamómetro, una bola
de hierro de 2 cm de radio en un vaso de agua.
a) ¿Qué empuje experimenta la bola? ¿Cuál será su peso
aparente?
b) Si en vez de en agua se introduce en alcohol, el peso
aparente observado es 2,38 N. ¿Cuál sería su densidad? (dhierro = 7 900 kg/m3.)
Suponemos que la bola se sumerge totalmente en el líquido.
a) E = Vlíquido desalojadod líquidog = 4/3 · 3,14 · 0,023 · 1 000 kg/m3 ·
· 9,8 m/s2 = 0,33 N
ya que el volumen del cuerpo es: V = 4/3 · 3,14 · 0,023 =
= 3,35 · 10–5 m3
E = P – Paparente; Paparente = P – E = mc · g – E = Vc · dc · g – E
El peso de la bola será: p = 3,35 · 10–5 m3 · 7,9 ·
· 103 kg/m3 · 9,8 m/s2 = 2,59 N
Paparente = 3,35 · 10–5 m3 · 7,9 · 103 kg/m3 · 9,8 m/s2 – 0,33 =
= 2,26 N
36
0,21
= 650 kg/m3
3,35 ⋅10 −5 9, 8
2 La presión en el interior de una piscina depende:
a)
b)
c)
d)
De la forma del vaso de la piscina.
Del volumen de agua que tengamos encima.
Sólo de la profundidad a la que estamos.
De la densidad, profundidad y gravedad del lugar.
Respuesta correcta: d).
3 El empuje sobre un objeto que se encuentra dentro
de un fluido es:
a) La masa del fluido desalojado.
b) La fuerza que ejerce el fluido sobre el cuerpo en sentido contrario al peso.
c) El volumen del fluido desalojado.
d) La profundidad a la que está sumergido.
Respuesta correcta: b).
4 ¿Dónde es mayor la presión?
a)
b)
c)
d)
En la cima del Everest.
En Barcelona.
En un puerto de montaña.
En el fondo de una piscina situada al nivel del mar.
Respuesta correcta: d).
5 De las siguientes afirmaciones, indica cuál es la
correcta:
a) La densidad de un objeto depende de su tamaño.
b) La densidad de un objeto depende de su forma.
c) La densidad de un objeto depende de su masa y de
su volumen.
d) La densidad de un objeto sólo depende de su peso.
Respuesta correcta: c).
7 1 atmósfera de presión equivale a:
a)
b)
c)
d)
900 mm Hg.
1 013 milibares.
100 000 Pa.
1 N/m2.
Respuesta correcta: b).
8 La tensión superficial es la causante de:
a) Que los líquidos se adapten al recipiente que los contiene.
b) Que los líquidos mojen los objetos que tocan.
c) La forma de las gotas de agua.
d) Que la mayoría de los troncos floten en el agua.
Respuesta correcta: c).
6 Un objeto flotará en el agua cuando:
a)
b)
c)
d)
Su densidad sea igual a la del agua.
Su densidad sea mayor que el agua.
El empuje sea mayor que su peso.
El empuje sea igual a su peso.
Respuesta correcta: c).
37
5 FUERZAS GRAVITACIONALES
EJERCICIOS
8 Si el radio de la Tierra fuera el doble y su masa también, ¿cuánto valdría la gravedad entonces?
1 Calcula a qué distancia equivale el año-luz.
365 días 24 h 3 600 s
⋅
⋅
= 31,536 ⋅10 6 s
1 año 1 día 1 h
e = 3⋅10 8 ms −1 ⋅31,536 ⋅10 6 s = 9,5⋅1015 m
e = v t; 1 año ⋅
2 La Vía Láctea tiene un diámetro de 100 000 añosluz y el Sol se encuentra a 30 000 años-luz del centro de
la galaxia. Calcula a cuántos kilómetros corresponden
estas distancias.
10 años-luz · 9,5 · 10 km año-luz = 9,5 · 10 km
3 · 104 años-luz · 9,5 · 1012 km año-luz–1 = 2,9 · 1017 km
5
12
–1
17
3 La Gran Nube de Magallanes se halla situada a 1,6 ·
1018 km. Calcula su distancia expresada en años-luz.
1,6 · 10 km/9,5 · 10 km años-luz = 168 421 años-luz.
18
12
–1
4 Sabemos que hay al menos diez mil millones de
galaxias. Si tuvieran cada una el mismo número de estrellas que la Vía Láctea, ¿cuántas estrellas habría en el
Universo?
1010 galaxias en el Universo · 2 · 1011 estrellas en la Vía Láctea
= 2 · 1021 estrellas en el Universo.
5 Nuestra galaxia tiene un radio de unos 50 000 añosluz. Suponiendo que el Sol no cambiara de posición respecto del centro de la galaxia durante el tiempo que la
circunvala, y que gira alrededor de ella a unos 225 km/s,
calcula cuánto tiempo tardará en hacerlo.
r = 5 · 104 años-luz · 9,5 · 1015 m años-luz–1 = 4,75 · 1020 m;
l = 2π r = 2π · 4,75 · 1020 m = 3 · 1021 m
t = e/v = 3 · 1021 m/2,25 · 105 m s–1 = 1,3 · 1016 s
t = 1,3 · 1016 s/31,536 · 106 s año–1 = 4,2 · 108 años
6 Calcula cuánto tiempo tarda la luz del Sol en llegar
a nosotros, si la distancia que le separa de la Tierra es de
150 · 106 km.
t = e/v = 150 · 109 m/3 · 108 m s–1 = 450 s; t = 450 s/60 min s–1 =
= 7,5 min
7 Calcula cuánto pesará un robot de 60 kg de masa en
la superficie de Marte. (Datos: masa de Marte = 6,40 · 1023
kg; radio de Marte = 3,39 · 106 m.)
M
6, 40 ⋅1023 kg
g = G 2 = 6, 67 ⋅10 −11 Nm2 kg−2
=
r
(3,39 ⋅10 6 m)2
= 3,7 m/s 2
P = m g = 60 kg⋅3,7 m/s 2 = 222 N
38
M
2M
2M
; g′ = G
=G 2 ;
r2
(2r )2
4r
M 2M
g/g′ = G 2 /G 2 = 2 ; g' = g/2 = 4,9 m s −2
r
4r
g=G
EJERCICIOS PROPUESTOS
PARA REPASAR
1 Indica el nombre de algunos de los principales científicos griegos que destacaron en el estudio del cosmos, comentando las ideas y aportaciones de dichos personajes.
Mirar en el texto (apartado 5.1).
2 Diferencia entre las teorías helio y geocentrista e
indica los nombres de los principales astrónomos que
promovieron la primera de ellas.
Teoría heliocentrista: indica que el Sol es el centro del sistema
alrededor del cual giran la Tierra y los otros planetas. Promovida por Copérnico, Kepler y Galileo.
Teoría geocentrista: indica que la Tierra es el centro del sistema alrededor del cual giran el Sol y los otros planetas.
3 Comenta las principales aportaciones científicas de
Isaac Newton y Galileo Galilei.
Mirar en el texto (apartado 5.1).
4 Indica las diferencias entre las teorías del Big Bang
y del Big Crunch.
La Teoría del Big Bang dice que la energía contenida en un
punto fue dispersándose por el Universo a medida que éste
se expansionaba, dando lugar a las primeras partículas componentes de la materia. Poco a poco, el Universo comenzó
a enfriarse y estas partículas, a unirse para formar otras más
complejas que, a su vez, constituyeron los átomos.
La Teoría del Big Crunch dice que si la materia que existe en
el Universo es lo suficientemente abundante, los objetos celestes se atraerán unos a otros por medio de su fuerza gravitacional, generando un retroceso que provocará la inversión
de la situación actual. El Universo se plegará de nuevo hasta
el punto original.
5 Comenta las principales diferencias entre galaxia,
estrella, planeta y agujero negro.
Galaxia. Agrupación de miles de millones de estrellas girando en torno a un eje común. Suelen ser, principalmente,
elípticas, espirales o irregulares.
Estrella. Cuerpo celeste compuesto principalmente por hidrógeno, cuyos átomos, al fusionarse para producir helio,
emiten luz y calor.
Planeta. Objeto celeste sin luz propia que gira en torno a una
estrella, formado por el material que no ha sido aglomerado
por ésta, y que a menudo tiene otros objetos menores, llamados satélites, girando a su vez en torno a él.
Agujero negro. Estado final de una estrella de masa al menos tres veces la del Sol. Su fuerza de atracción es tan enorme
que ni siquiera la luz puede escapar de él.
6 La galaxia Andrómeda se encuentra situada a 2,2
millones de años-luz. ¿Cuánto tiempo tarda su luz en
llegar a nosotros? ¿A qué distancia, expresada en km,
se halla?
Tarda 2,2 millones de años; distancia = 2,2 · 106 a.l. · 9,5 ·
· 1012 km a.l.–1 = 2,1 · 1019 km
7 La estrella Alfa Centauro es la más próxima a nosotros; se encuentra a 4,3 años-luz. Calcula en km a qué
distancia nos encontramos de ella.
4,3 a.l. · 9,5 · 1012 km a.l.–1 = 4,1 · 1013 km
8 Empleando la Ley de la Gravitación Universal, explica el fenómeno de las mareas producidas por la Luna
y el Sol sobre nuestro planeta.
El nivel del mar alcanza cada 24 h dos máximos (pleamar)
cuando la luna está situada frente a la Tierra, merced a su
fuerza gravitacional, y dos mínimos (bajamar) cuando se aleja.
Son vivas cuando el Sol y la Luna se hallan en línea con la
Tierra; en caso contrario se denominan muertas.
9 Calcula la fuerza centrípeta que hace que la Tierra
gire alrededor del Sol sabiendo que sus masas son de
5,98 · 1024 kg y 2 · 1030 kg, y que sus centros están separados por 150 · 106 km.

Mm
F = G 2 = 6, 67 ⋅10 −11 N m2 kg−2 ⋅
d
5,98 ⋅1024 kg ⋅2 ⋅1030 kg
⋅
= 3,5 ⋅1028 N
(150 ⋅10 6 m)2
10 Calcula con qué fuerza se atraerán dos personas
de 70 kg situadas a 1 m de distancia. ¿Apreciaremos esa
fuerza?

Mm
70 kg ⋅70 kg
F = G 2 = 6, 67 ⋅10 −11 N m2 kg−2
=
d
(1 m)2
= 3,3 ⋅10 −7 N
11 Sabiendo que la gravedad de la Luna es aproximadamente 1/6 de la de la Tierra, indica cuánto pesará un
cuerpo en la superficie del satélite sabiendo que pesa
686 N en la Tierra.
gL = gT/6 =1,63 m/s2; PT = 686 N = m · 9,8 ms–2; m = 70 kg;
PL = 70 kg · 1,63 m/s2 = 114,1 N
12 Calcula la diferencia entre el peso de una persona
cuando está en el Ecuador y el que tiene cuando se halla
en el Polo Norte, si su masa es 55 kg.
PE = m gE = 55 kg · 9,80 ms–2 = 539 N;
PP = m gP = 55 kg · 9,86 ms–2 = 542,3 N
∆P = 542,3 N – 539 N = 3,3 N
PARA REFORZAR
13 Indica algunos de los principales astrofísicos modernos que destacaron en el estudio del cosmos y comenta
las ideas y aportaciones de dichos científicos.
Mirar en el texto (apartado 5.1).
14 Si se dispara un rayo láser —que viaja a la velocidad
de la luz— contra la superficie de la Luna tarda 2,56 s
en volver reflejado a la Tierra. Calcula a qué distancia se
encuentra nuestro satélite.
e = v t = 3 · 108 ms–1 · 2,56 s = 7,7 · 108 m
15 La distancia entre la Tierra y el Sol, que es de unos
150 · 106 km, se denomina unidad astronómica (UA). Crea
el factor de conversión correspondiente y expresa en esta unidad (UA) las distancias de los planetas del siguiente
cuadro:
Planeta
Mercurio
Venus
Marte
Júpiter
Saturno
Distancia al Sol
(millones de km)
58
108
228
778
1 430
Mercurio: d = 58 · 106 km/150 · 106 km UA–1 = 0,39 UA
Venus: d = 108 · 106 km/150 · 106 km UA–1 = 0,72 UA
Marte: d = 228 · 106 km/150 · 106 km UA–1 = 1,52 UA
Júpiter: d = 778 · 106 km/150 · 106 km UA–1 = 5,2 UA
Saturno: d = 1 430 · 106 km/150 · 106 km UA–1 = 9,5 UA
16 A partir de los datos obtenidos en UA en el problema anterior, prepara una representación sobre papel
milimetrado cuya escala sea 1 UA: 5 cm.
Hacer la representación.
17 Se tienen dos cuerpos de masas iguales separados
una distancia de 2 m que se atraen con una fuerza de
4 · 10–6 N. Calcula cuánto vale la masa de cada uno.
39
5

Mm
M ⋅M
F = G 2 = 6, 67 ⋅10 −11 N m2 kg−2
=
d
(2 m)2
= 4 ⋅10 −6 N; M = 490 kg
18 Calcula cuánto vale la aceleración de la gravedad
cuando nos elevamos una distancia de la Tierra equivalente a su radio.
M
= 6, 67 ⋅10 −11 N m2kg−2 ⋅
r2
5,98 ⋅1024 kg
⋅
= 2, 45 m/s 2
(6,38 ⋅10 6 m + 6,38 ⋅10 6 m)2
g=G
M
= 4,9 m s −2 = 6, 67 ⋅10 −11 N m2kg−2 ⋅
r2
5,98 ⋅1024 kg
⋅
⇒ d = 9, 02 ⋅107 m
(d)2
h = 9, 02 ⋅107 m − 6,38 ⋅10 6 m = 8,38 ⋅107 m
g=G
20 Sabiendo que la masa de Júpiter es 318 veces la de la
Tierra, y que su radio es 11,2 veces el de nuestro planeta,
calcula cuánto valdrá la gravedad en Júpiter.
318MT
M
318
=G
=g
= 24, 8 m s −2
2
r
(11,2rT )2
(11,2)2
21 El radio del Sol es 100 veces mayor que el de la Tierra,
y su gravedad, 27 veces mayor que la nuestra. Si la masa
de la Tierra es 5,98 · 1024 kg, calcula la del Sol.
gT = G
MT
rT2
; gs = G
MS
rT2
; 27 gT = G
MS
(100rT )2
;
dividiendo ambas queda: 27 = MS/104 MT ; MS = 1,6 · 1030 kg.
EVALUACIÓN
1 ¿Quién propuso por vez primera que la Tierra y el resto
de los planetas giraban alrededor del Sol?
a)
b)
c)
d)
Respuesta correcta: b).
3 Una galaxia es:
a) Un conjunto de estrellas agrupadas.
b) Un conjunto de estrellas que giran en torno a un eje
central.
c) Una constelación.
d) Un método de observación del Universo.
Respuesta correcta: b).
19 ¿A qué altura de la superficie terrestre el valor de la
gravedad se reduce a la mitad?
(Dato: RT = 6,38 · 106 m)
g=G
d) Siempre ha existido, sin principio ni fin.
Un científico griego.
Cristóbal Colón.
Nicolás Copérnico.
Albert Einstein.
4 Las estrellas se forman:
a) Por unión de varias galaxias.
b) Por fusión de átomos de hidrógeno muy concentrados en una nebulosa.
c) Por explosión de un agujero negro.
d) Cuando otra estrella se apaga.
Respuesta correcta: b).
5 Vemos las imágenes de las estrellas:
a) Tal como son ahora.
b) Tal como eran cuando la luz salió de ellas.
c) Ambas son correctas porque la luz viaja a velocidad
infinita.
d) No sabemos de cuándo son las imágenes que vemos.
Respuesta correcta: b).
6 El Sistema Solar está formado por:
a)
b)
c)
d)
Respuesta correcta: d).
7 La gravedad:
a)
b)
c)
d)
a) A partir de las galaxias.
b) A partir de una gran explosión.
c) A partir de otro Universo anterior.
40
Es una propiedad de los cuerpos.
Es la fuerza de atracción de los planetas.
Es la misma en cualquier planeta.
Varía según el lugar de la Tierra en que nos encontremos.
Respuesta correcta: d).
8 Los cuerpos pesan:
Respuesta correcta: c).
2 El Universo se formó:
Planetas interiores y exteriores.
El Sol, planetas y asteroides.
El Sol, planetas, satélites y asteroides.
El Sol, planetas, satélites, asteroides y cometas.
a)
b)
c)
d)
Lo mismo aquí que en la Luna.
Más en la Tierra que en la Luna.
Menos en la Tierra que en la Luna.
No podemos saberlo.
Respuesta correcta: b).
TRABAJO, POTENCIA
Y ENERGÍA MECÁNICA
EJERCICIOS
1 Sujeta un resorte elástico, o una goma, por un extremo y del otro cuelga un peso.
a) ¿Hasta cuándo se estira el resorte?
b) Si, una vez establecido el equilibrio, desplazas el
cuerpo unos centímetros hacia abajo y lo sueltas,
¿qué movimiento experimenta el cuerpo?
c) ¿En qué posición el cuerpo está sometido a la máxima
fuerza?
d) ¿Existe algún punto en donde el cuerpo no tenga aceleración?
a) El resorte se estira hasta que la fuerza peso es equilibrada
por la fuerza elástica del resorte.
b) El cuerpo sube y baja desplazándose a ambos lados de
la posición de equilibrio. Este desplazamiento recibe el
nombre de movimiento oscilatorio.
c) El cuerpo está sometido a la máxima fuerza elástica en los
extremos de la trayectoria.
d) En la posición de equilibrio la fuerza elástica tiene valor
cero. Por tanto, en dicha posición no existe aceleración.
2 La energía puede tomar varias formas. ¿Cuántas formas de energía conoces?
Mecánica, térmica, eléctrica, etcétera.
3 La energía es necesaria para el movimiento. Cita tres
ejemplos de cuerpos dotados de movimiento e indica la
forma de energía que utilizan, así como la fuente de esa
energía.
Un velero: energía eólica (el viento); un automóvil: energía
térmica (gasolina); un ventilador: energía eléctrica (electricidad).
4 Nombra situaciones o actividades que tienen lugar en
un hogar que no se puedan realizar sin consumir energía.
Aspirar el polvo, afeitarse, ver la televisión, lavar la ropa, etcétera.
5 Propón ejemplos de ejercicios o experiencias que exijan esfuerzo e indica en cuáles de ellos se realiza trabajo.
Mantener unas pesas en alto, apretar los dientes, sujetar un
armario que se cae, etc., no realizan trabajo; apretar un muelle, subir escaleras, etc., sí lo realizan.
6 Cita tres ocupaciones que normalmente se consideran como trabajo, pero que no lo son desde el punto de
vista de la Física.
Estudiar, sostener la bolsa de la compra, empujar una pared,
etcétera.
6
7 Un hombre que rema en una barca río arriba está en
reposo con respecto a la orilla.
a) ¿Está realizando trabajo?
b) Si deja de remar y es arrastrado por la corriente, ¿se
hace trabajo sobre él?
a) No. Porque la barca adquiere energía cinética equivalente
al trabajo realizado por el agua.
b) Sí. Porque la barca adquiere energía cinética equivalente
al trabajo realizado por el agua.
8 En un concurso de soga-tira, los dos equipos están
equilibrados. ¿Las personas que tiran de la cuerda realizan trabajo? Si un equipo va perdiendo poco a poco,
¿qué trabajo se está haciendo y quién lo hace?
No, porque no hay desplazamiento.
El trabajo neto viene dado por el producto de la fuerza neta
por el desplazamiento.
Los dos equipos realizan trabajo:
• Positivo, el equipo que vence.
• Negativo, el equipo que va perdiendo.
9 Fíjate en la figura adjunta e indica si se trata de trabajo positivo, trabajo negativo o trabajo nulo si:
a) Sostenemos el libro.
b) Subimos el libro.
c) Bajamos el libro.
2
h1
1
0
h0
a) Trabajo nulo: no hay desplazamiento.
b) Trabajo positivo: la fuerza y el desplazamiento tienen la
misma dirección y sentido.
c) Trabajo negativo: la fuerza y el desplazamiento tienen la
misma dirección, pero sentido contrario.
10 Completa el siguiente enunciado:
Una mano comprime un resorte ___________ hace trabajo negativo sobre _____________ y _______________
hace trabajo positivo sobre _______________ .
41
6
Una mano comprime un resorte. La fuerza elástica hace trabajo negativo sobre la mano y la mano hace trabajo positivo
sobre el resorte.
11 Completa la tabla siguiente, sabiendo que las fuerzas tienen la misma dirección y sentido que el desplazamiento.
Fuerza
15 N
Desplazamiento
1,5 m
0,70 m
Trabajo
Desplazamiento
1,5 m
0,70 m
2,5 m
Trabajo
22,5 J
19,6 J
30 J
Fr
12 N
Fuerza
15 N
28 N
12 N
Fr
Fr
Fm
Fm
17 El pie de una persona cuando
está de puntillas es una palanca.
a) Localiza el punto de apoyo.
b) Identifica las fuerzas Fm y FR.
c) ¿De qué genero de palanca se
trata?
Palanca de primer género.
A
B
80 kg ⋅m
=
60 kg
= 1,3 m del punto de apoyo.
40 kg ⋅2 m = 60 kg ⋅d; d =
14 ¿Qué tipo de palanca son los cubiertos que utilizamos en la mesa? Señala el punto de apoyo y las fuerzas que intervienen en un cuchillo, un tenedor y una cuchara.
Cuchara: primer género. Tenedor y cuchillo: palancas de tercer género.
15 ¿Es posible que la fuerza motriz sea mayor que la
fuerza resistente? ¿En qué casos ocurre esto?
En las palancas de tercer género.
16 Dibuja las fuerzas Fm y FR que actúan cuando se utilizan las herramientas representadas en la siguiente figura:
42
Fr
Fm
12 La polea de la figura es una
palanca de brazos iguales. Dibuja
las fuerzas Fm y FR. ¿De qué género
de palanca se trata? ¿Cómo son
entre sí las fuerzas motriz y resistente? ¿Qué ventaja tiene esta máquina?
13 ¿Dónde se debe colocar el niño
A de 60 kg para columpiarse, si la
niña B de 40 kg está sentada en
un extremo de la barra de 4 m de
longitud apoyada en su punto medio?
Fm
19,6 J
30 J
a) Los huesos de los dedos.
b) Fm = contracción del músculo.
FR = peso del cuerpo.
c) Palanca de segundo género.
18 ¿Es posible que la energía cinética de un cuerpo pueda tener valor negativo? Razona la respuesta.
La energía cinética no puede ser negativa porque depende
de dos factores que son siempre positivos: la masa y el cuadrado de la velocidad.
19 Si se duplica la velocidad de un cuerpo, ¿qué le sucede a su energía cinética?
Se hace cuatro veces mayor.
20 ¿Qué puedes decir sobre la velocidad de un objeto
si el trabajo neto realizado sobre él es cero?
Que es constante. El cuerpo está en reposo o se mueve con
movimiento rectilíneo y uniforme.
21 Explica por qué es posible que la energía potencial
de un cuerpo tenga valor negativo.
La energía potencial es una energía de posición que depende
del punto de referencia que se tome. Si el cuerpo se encuentra en una posición negativa respecto del punto de referencia, la energía potencial será negativa.
22 Pon un ejemplo en el que existan simultáneamente
las dos energías: cinética y potencial gravitatoria.
Un cuerpo que desciende desde una cierta altura.
a)
b)
c)
d)
23 ¿En qué casos se almacena energía potencial elástica?
EJERCICIOS PROPUESTOS
a)
b)
c)
d)
e)
f)
g)
h)
PARA REPASAR
Al saltar sobre un trampolín.
Al saltar sobre una cama elástica.
Al doblar un alambre de hierro.
Al estirar una goma.
Al saltar con una pértiga.
Al disparar una flecha con un arco.
Al comprimir una pelota de tenis.
Al doblar ligeramente una goma de borrar.
En todos, excepto el caso de doblar un alambre de hierro,
puesto que ese metal no es elástico.
24 Lanzas por un suelo horizontal un objeto con una
cierta velocidad. Si no existe ningún obstáculo ni rozamiento:
Cinética y potencial.
Cinética y potencial.
Potencial.
Cinética.
1 Una persona de 80 kg que lleva un paquete de 35 N
sube por una escalera. ¿Qué trabajo realiza cuando asciende a una altura de 15 m?
El trabajo viene dado por el incremento que experimenta,
respecto del punto de referencia, la energía potencial.
W = m g h = 80,0 kg · 9,81 m/s2 · 15 m = 11 772 J
2 Ordena de mayor a menor la energía potencial de
los siguientes cuerpos:
8 kg
200 kg
80 kg
a)
b)
c)
d)
a)
b)
c)
d)
¿Se conserva la energía mecánica?
¿Qué ocurre con la velocidad del cuerpo?
¿Qué tipo de movimiento tiene el cuerpo?
¿Hay alguna ley de la Dinámica que permita llegar a
la misma conclusión?
Sí se conserva la energía mecánica.
Permanece constante.
Rectilíneo y uniforme.
La ley de la inercia.
15 m
25 m
35 m
1,5 m
a)
b)
c)
d)
e)
e), d), c), b), a).
3 ¿Qué objeto tiene mayor energía cinética?
v = 1 m/s
v = 15 m/s
25 Explica las transformaciones energéticas que tienen
lugar en las siguientes situaciones:
a) Lanzar verticalmente hacia arriba un objeto.
b) Un jugador de tenis golpea una pelota con una raqueta.
a) Cinética en el lanzamiento. Cinética y potencial en la subida y en la bajada.
b) Cinética al llegar al punto de partida.
26 Desde un acantilado lanzas verticalmente una pelota hacia arriba. ¿Qué tipo de energía posee la pelota respecto del nivel del mar?
a) En el punto A de lanzamiento.
b) Cuando pasa por el punto
B.
c) Cuando alcanza el punto C
más alto del recorrido.
d) Cuando llega al agua.
6 kg
5 kg
C
B
A
0
Nivel del mar
v = 3 m/s
v = 30 m/s
5 kg
2 kg
150 kg
a)
b)
c)
500 kg
d)
b), E = 900 J
4 Un objeto que pesa 15 N se deja caer desde una altura de 8 m. Este objeto llega al suelo con una energía
cinética de:
a) 8 J; b) 15 J; c) 120 J y d) 1 176 J
c), E = m g h = 15 N · 8 m = 120 J
5 Un objeto de 5 kg tiene una energía cinética de 250 J.
Este objeto se mueve con una velocidad de:
a) 5 m/s; b) 10 m/s; c) 250 m/s y d) 1 250 m/s
b), v = 10 m/s
6 Dejas caer un objeto de 2 kg en un pozo. ¿Con qué
energía potencial llega al nivel del agua si está a 10 m
43
6
por debajo del brocal que tomamos como nivel de referencia?
Ep = m g h = 2 kg · 9,8 m/s2 · (–10 m) = –196 J
7 Un objeto de 2 kg posee una energía potencial respecto del suelo de 400 J.
a) ¿A qué altura se encuentra?
b) ¿Con qué energía cinética llega al suelo?
c) ¿Con qué velocidad llega al suelo?
a) h =
Ep
mg
=
400 J
400 J
=
= 20, 4 m
2 kg ⋅9, 8 m/s 2 19, 6 N
b) Ec = Ep = 400 J
c)
1
800 J
m v 2 = 400 J; v =
= 20 m/s
2
2 kg
8 Clasifica las siguientes palancas:
a) Un remo.
b) Una pinza de tender la ropa (de las que tienen un
muelle en medio).
a) Palanca de segundo género.
b) Palanca de primer género.
9 ¿Cuánto mide una palanca de segundo género, cuya
fuerza motriz es de 215 N y 850 N la fuerza resistente, si
el brazo de esta última fuerza es 0,75 m?
215 N ⋅ = 850 N ⋅0,75 m;  =
850 N ⋅0,75 m
=3m
215 N
10 Un ascensor ha elevado una carga de 500 kg a un
piso que está a 25 m de altura y ha tardado 12 s. Halla la
potencia en CV del motor.
m g h 500 kg ⋅9, 8 m/s 2 ⋅25 m
=
=
t
12 s
=10 208,3 W =14 CV
P =W/t =
11 Se lanza por el suelo un cuerpo con una energía cinética de 270 J. Si el cuerpo recorre 20 m antes de pararse,
¿cuánto vale la fuerza de rozamiento?
1
1
270 J
Fr x = m v 2 ; Fr = m v 2 =
=13,5 N
2
2
20 m
12 ¿Qué variación de energía potencial experimenta un
ascensor de 800 kg cuando sube desde la planta cero
hasta el último piso de un rascacielos situado a 200 m
de altura?
Ep = m g h = 800 kg · 9,81 m/s2 · 200 m = 1,6 · 106 J
44
PARA REFORZAR
13 Un obrero lleva en una carretilla que pesa 150 N una
carga de 90 kg. Si el peso total se supone aplicado en un
punto de la carretilla y las distancias de éste al punto de
apoyo y a la fuerza motriz son, respectivamente, 0,40 m
y 0,90 m, ¿qué fuerza hará el obrero?
Fm · 0,90 = (150 N + 90 kg · 9,8 m/s2) · 0,40 m
Fm = 459 N
14 Unos mineros, para evitar la inundación de la mina, han
de sacar 1 500 L de agua cada 5 minutos de una profundidad de 85 m. ¿Qué potencia en CV debe tener la bomba?
Trabajo realizado: W = m g h = 1 500 kg · 9,8 m/s2 · 85 m =
= 1 249 500 J
Potencia desarrollada P =
W 1249 500 J
=
=
t
30 s
= 41 650 W = 57 CV
15 El martillo de esta figura tiene una masa de 3 kg y se
desplaza a 10 m/s en el instante que golpea el clavo. Si el
clavo se introduce 4 mm dentro de la pared, ¿qué fuerza
de resistencia ofrece la pared?
La energía cinética con que llega
el martillo al clavo se emplea en
el trabajo necesario para introducirlo.
1
1
⋅m v 2 = Fr x; Fr = m v 2 =
2
2
0,5 ⋅3 kg ⋅100 m2 /s 2
=
= 37 500N
4 ⋅10 −3 m
16 Una masa de 100 g cuelga de un hilo, como indica la
figura. Si esta masa la desplazamos hasta la posición B
y la soltamos, ¿con qué velocidad pasará por la posición
A? ¿Qué velocidad tendrá en la posición C, si está a 5 cm
de altura respecto de A?
En el movimiento del péndulo de
conserva la energía mecánica. Por
tanto, se cumple:
m g hB = 1/2 m v A2 ; v A = 2 g hB =
B
C
= 2 ⋅9, 81 m/s 2 ⋅0,15 m = 1,7 m/s
5 cm
En el punto C la masa tiene energía potencial y energía cinética.
En esa posición se cumple:
m g hB = 1/2 m vC2 + m g hC
De donde:
A
15 cm
vC = 2 ⋅ g ⋅(hB − hC ) =
= 2 ⋅9, 81 m/s 2 ⋅0,10 m =1, 4 m/s
EVALUACIÓN
a) Falso, porque la energía potencial también depende de
la masa, que es mayor en el caso de la bola de golf.
b) Falso. Llegan con la misma velocidad, pero con distinta
energía cinética.
c) Falso. Tiene mayor energía mecánica la bola de golf.
d) Verdadero.
1 Indica falso o verdadero. El trabajo mecánico es:
5 Indica en qué situaciones se realiza trabajo:
a)
b)
c)
d)
Una forma de crear energía.
Una forma de crear o consumir energía.
Una forma de transmitir energía.
Un sinónimo de esfuerzo.
a)
b)
c)
d)
a)
b)
c)
d)
Falso, porque la energía no se crea.
Falso, por la misma razón.
Verdadero, por definición de trabajo.
Falso.
Respuestas correctas: b) y d).
2 ¿Es correcta alguna de las siguientes afirmaciones?
a) Una fuerza siempre realiza trabajo.
b) Una fuerza realiza trabajo cuando hay desplazamiento.
c) Una fuerza realiza trabajo cuando produce un desplazamiento en la misma dirección en que actúa.
d) Las fuerzas no realizan trabajo.
Es correcta la afirmación c).
3 ¿Qué afirmaciones son falsas?
a) La energía cinética de un cuerpo no puede ser negativa.
b) La energía potencial de un cuerpo no puede ser negativa.
c) La energía cinética de un cuerpo depende del lugar
en donde esté situado dicho cuerpo.
d) La energía cinética depende de la velocidad.
Son falsas las afirmaciones b) y c). Porque la energía potencial
sí puede ser negativa, y porque la energía cinética no depende
de la posición, sino de la velocidad.
4 Desde el mismo punto de un puente sobre un río, dejas caer dos bolas del mismo tamaño, una de ping-pong
y la otra de golf. Indica falso o verdadero:
a) Las dos bolas tienen inicialmente la misma energía
potencial, porque están a la misma altura respecto
del agua.
b) Llegan al agua con la misma energía cinética.
c) Las dos tienen en el punto de partida la misma energía mecánica.
d) La bola de golf llega al agua con mayor energía mecánica.
Preparar un examen de Matemáticas.
Jugar al fútbol.
Sostener un cuerpo de 15 kg durante una hora.
Subir por una escalera.
6 La magnitud que determina la eficacia de un motor
es:
a)
b)
c)
d)
El trabajo que ha realizado.
La velocidad con que funciona.
La potencia que posee.
El tiempo que está funcionando.
Respuesta correcta: a).
7 El profesor te pide que empujes la pared de la clase
con el fin de derribarla. Tú respondes que te sientes incapaz de realizar tal cosa. Tu incapacidad es debida a que
no tienes:
a)
b)
c)
d)
Suficiente fuerza.
Suficiente potencia.
Suficiente energía.
Suficiente tiempo para realizarlo.
Suficiente fuerza. Para poder derribar una pared, haría falta
que fuéramos capaces de hacer una fuerza superior a la resistencia de la pared.
8 Un mecánico afloja una tuerca utilizando una llave
inglesa. ¿Realiza algún trabajo?
a) No, porque la tuerca gira pero, sin embargo, no se
desplaza.
b) Sí, porque el punto de aplicación de la fuerza se desplaza cuando gira la tuerca.
c) No, porque el punto de aplicación de la fuerza no se
ha desplazado.
d) Sí, porque el mecánico realiza un esfuerzo al aflojar
la tuerca.
La respuesta correcta es la b). Por pequeño que sea el desplazamiento, se hace un trabajo de rotación, ya que la tuerca
gira.
45
7 CALOR Y ENERGÍA TÉRMICA
EJERCICIOS
1 ¿Qué procedimientos conoces para transferir energía a un cuerpo? ¿Es correcto decir que el calor es energía
en movimiento?
Se puede transferir energía a un cuerpo mediante trabajo y
mediante calor.
El calor es energía que se transfiere, es energía en tránsito,
en movimiento.
9 Un termómetro calibrado en la escala Celsius marca
32 °C en un día caluroso de verano. ¿Qué temperatura indicaría un termómetro calibrado en la escala Fahrenheit?
¿Cuál sería su equivalencia en Kelvin?
2 ¿Es correcto decir que un cuerpo tiene calor? ¿Debemos considerar al calor como una forma de energía?
32 T − 32
=
; T = 89,6° F
100
180
T = 32 + 273 = 305 K
No. Los cuerpos no tienen ni calor ni trabajo.
El calor no es una forma de energía, sino energía que se
transfiere.
10 ¿Intercambian energía térmica entre sí dos cuerpos
que se encuentran en equilibrio térmico?
3 ¿Cómo varía la energía interna de un cuerpo: cuando
cede calor o cuando recibe trabajo?
Dos cuerpos están en equilibrio térmico cuando tienen la
misma temperatura. En estas condiciones, los cuerpos no
intercambian energía térmica.
Cuando un cuerpo recibe trabajo (energía), aumenta su energía interna. Si cede calor, disminuye su energía interna.
4 Define los conceptos de calor y temperatura.
El calor es energía que se transfiere, que pasa de un cuerpo a
otro como consecuencia de una diferencia de temperatura.
La temperatura es una medida de la velocidad media de las
partículas que forman un cuerpo.
5 ¿Podemos utilizar nuestro sentido del tacto para
medir la temperatura con precisión?
Nuestro sentido del tacto no permite medir la temperatura
de los cuerpos con precisión.
6 Si la temperatura del aula es la misma en todos los
puntos, ¿tienen la misma velocidad todas las moléculas
que forman el aire? ¿Es igual su energía cinética?
No. La temperatura es una medida de la velocidad media de
las moléculas que forman el aire, pero eso no significa que
todas las moléculas tengan la misma velocidad. Por tanto,
tampoco su energía cinética es la misma; además, las moléculas de oxígeno, nitrógeno, dióxido de carbono, etc., que
forman el aire tienen distinta masa.
11 Julius R. Mayer observó que la temperatura del mar se
había incrementado tras una gran tormenta; por ello, sugirió en 1842 que debía existir alguna relación entre calor
y trabajo. ¿Cómo explicas el pensamiento de Mayer?
Mayer pensó que el trabajo realizado por las olas habría incrementado la temperatura del agua al transferirle calor a
ésta por rozamiento.
12 Expresa en julios o en calorías (lo que proceda) las
siguientes cantidades de energía:
a)
b)
c)
d)
254 cal
316 kJ
12,5 kcal
8,9 · 106 J
a)
b)
c)
d)
254 cal · 4,18 J/cal = 1 060 J
316 kJ = 316 000 J · 0,24 cal/J = 75 840 cal
12,5 kcal = 12 500 cal · 4,18 J/cal = 52 250 J
8,9 · 106 J · 0,24 cal/J = 2,136 · 106 cal
13 El calor específico del agua es 4 180 J/kg K y el del
mercurio, 140 J/kg K. ¿Cuál de las dos sustancias se calienta más rápidamente al utilizar la misma fuente de
calor?
7 Un vaso contiene 100 g de agua a 15 °C. ¿Contiene
calor el agua? ¿Tiene energía interna?
El mercurio se calienta más rápidamente, pues su calor específico es menor que el del agua.
El agua no contiene calor; sí tiene energía interna.
14 ¿Cuánta energía se necesita para elevar la temperatura de 125 g de aluminio de 14 °C a 120 °C? El calor específico del aluminio es c = 898 J/kg K.
8 La temperatura máxima y la mínima de un día de
invierno fueron 14 °C y –2 °C. Expresa estas temperaturas
en la escala absoluta y calcula la variación de temperatura a lo largo del día en las escalas Celsius y Kelvin.
46
T1 = –2 + 273 = 271 K; T2 = 14 + 273 = 287 K
∆T = 14 ºC – (–2) = 16 ºC;
∆T = 287 K – 271 K = 16 K
En todos los casos, la variación de temperatura es la misma
en las escalas Celsius y Kelvin.
Q = m c (T2 – T1) = 0,125 kg · 898 J/kg K · (120 – 14) K =
= 1,19 · 104 J
15 Si mezclas 8,2 L de agua a 16 °C con 6,5 L de agua a
64 °C, ¿cuál es la temperatura de equilibrio de la mezcla?
El calor cedido por el agua caliente es igual al absorbido por
el agua fría:
mc cc (Tc– TF) = mf cf (TF – Tf )
6,5 kg · 4 180 J/kg ºC · (64 – TF) ºC =
= 8,2 kg · 4 180 J/kg ºC · (TF – 16) ºC
TF = 37,2 ºC
16 Un cilindro de cobre de 155 g de masa que está a una
temperatura de 322 °C se introduce en un recipiente que
contiene 496 mL de agua a 18,2 °C. ¿Cuál es la temperatura final de la mezcla?
mc cc (Tc– TF) = ma ca (TF – Ta)
0,155 kg · 385 J/kg ºC · (322 – TF) ºC =
= 0,496 kg · 4 180 J/kg ºC · (TF – 18,2) ºC
TF = 26,7 ºC
17 Los cambios de estado, ¿son cambios físicos o químicos? ¿Por qué?
Los cambios de estado son cambios físicos, porque no cambia la composición de las sustancias que intervienen.
18 Según la Teoría cinético-molecular, ¿por qué mientras el agua está hirviendo se mantiene constante su
temperatura?
La energía transferida aumenta la energía interna y permite
separar las moléculas, con lo que el líquido pasa al estado
de vapor.
19 Calcula la cantidad de energía que se desprende cuando se solidifican 1,5 kg de agua que se encuentra a 0 °C.
23 Describe las transformaciones energéticas que se
producen cuando una pila eléctrica hace funcionar una
bombilla, una calculadora o un reloj.
En la bombilla, la energía eléctrica se transforma en energía
luminosa, energía térmica y energía cinética del aire situado
encima de la bombilla y, en último término, toda la energía
se transforma en calor, que se dispersa en el aire.
En una calculadora o en un reloj, la energía eléctrica se transforma en energía luminosa y, al final, en calor que se dispersa
en el aire.
24 Describe las transformaciones energéticas que se
producen cuando un automóvil está en movimiento.
¿Se puede convertir íntegramente en trabajo la energía
térmica de los gases calientes que salen por el tubo de
escape?
La energía química del combustible se transforma en energía
mecánica, energía eléctrica al cargar la batería, energía acústica, energía térmica y, al final, todo en calor que se dispersa
en el aire.
La energía térmica de los gases calientes que salen por el tubo de escape no se puede convertir íntegramente en trabajo.
La energía se ha degradado, no es útil.
25 ¿Es posible fabricar una máquina térmica que intercambie energía con un solo foco calorífico?
No. Las máquinas térmicas requieren para su funcionamiento
dos focos a distinta temperatura.
A esa hipotética máquina se le denomina «móvil perpetuo
de segunda especie».
26 El motor de un automóvil produce 1 550 J de trabajo
por cada 1,15 kcal consumidas. ¿Cuál es el rendimiento
del motor?
Q = mL = 1,5 kg · 3,34 · 105 J/kg = 5 · 105 J
20 Determina la energía intercambiada mediante calor
al transformar 315 g de agua a una temperatura de 10,5 °C
en vapor de agua a 100 °C.
Q = m c (T2 – T1) = 0,315 kg · 4 180 J/kg ºC · (100 – 10,5) ºC =
= 11,8 · 104 J
Q2 = mL = 0,315 kg · 22,5 · 105 J/kg = 7,09 · 105 J
Q T = Q1 + Q2 = 8,27 · 105 J
21 Si la dilatación del agua fuera normal, ¿podría practicarse el patinaje sobre hielo? Razona tu respuesta.
η=
W
1550 J
=
= 0,322 ⇒ 32,2 %
Q1 1 150 cal⋅ 4,18 J/cal
27 ¿Qué factores influyen en el crecimiento continuo
del consumo de energía en el mundo?
El aumento de la población, el desarrollo industrial, el crecimiento económico de las sociedades modernas y el consumo
abusivo de energía que se produce en los países ricos.
28 ¿Qué inconvenientes encuentras en el uso de combustibles fósiles para producir energía? ¿Deberían utilizarse otras fuentes de energía?
No, porque el hielo se hundiría en el agua líquida.
22 ¿Conoces alguna aplicación de la dilatación en los
líquidos?
Los termómetros de mercurio, agua, alcohol, etcétera.
Los combustibles fósiles son perecederos, es decir, no durarán indefinidamente. Además, su combustión produce
dióxido de carbono, lo que propicia el cambio climático e
incrementa el efecto invernadero. También son los responsables de las lluvias ácidas.
47
7
Deberían sustituirse gradualmente por energías renovables
menos contaminantes: solar, eólica, mareomotriz, biomasa
e hidráulica.
EJERCICIOS PROPUESTOS
PARA REPASAR
1 ¿Es correcto decir que un cuerpo contiene más calor
que otro?
No, los cuerpos no contienen calor.
2 Explica la diferencia entre calor y temperatura.
El calor es energía que se transfiere, energía en tránsito, entre
dos cuerpos a distinta temperatura.
La temperatura es una medida de la velocidad media de las
partículas que forman un cuerpo.
3 En un día de invierno la temperatura mínima es de
–12 °C. ¿Cuál es su valor en la escala absoluta de temperaturas?
T = – 12 + 273 = 261 K
4 ¿A qué temperatura en grados Celsius equivale una
temperatura de 323 K?
T = 323 – 273 = 50 °C
5 ¿A cuántos julios equivalen 2,3 kcal? ¿Y a cuántas
calorías equivalen 2,3 kJ?
Q = 2 300 cal · 4,18 J/cal = 9,6 · 103 J
Q = 2 300 cal · 0,24 cal/J= 552 cal
mAlcAl(TAl – TF) = maca(TF – Ta)
0,425 kg · 898 J/kg °C · (182 – TF) °C =
= 0,368 kg · 4180 J/kg °C · (TF – 18) °C
TF = 50,6 °C
10 Si mezclas 5,2 L de agua a 22 °C con 8,6 L de agua a
46 °C, ¿cuál es la temperatura final de la mezcla?
El calor cedido por el agua caliente es igual al absorbido por
el agua fría:
5,2 kg · 4 180 J/kg °C · (TF – 22) °C =
= 8,6 kg · 4 180 J/kg °C · (46 – TF) °C
TF = 37 °C
11 Justifica la presión de los gases basándote en la Teoría cinético-molecular de la materia.
La presión se debe a los choques de las moléculas del gas
con las paredes del recipiente.
12 ¿Qué puedes decir acerca de la energía cinética de las
partículas que forman dos cuerpos en equilibrio térmico?
La energía cinética media de sus partículas es la misma. Dos
cuerpos en equilibrio térmico no intercambian energía cuando se ponen en contacto.
13 ¿A qué se debe el incremento de volumen que experimentan los cuerpos cuando aumenta su temperatura?
6 ¿Por qué la escala Kelvin de temperaturas no tiene
valores negativos?
Cuando aumenta la temperatura de un cuerpo, aumenta la
velocidad de sus partículas y la amplitud de sus movimientos.
La separación entre sus partículas se hace mayor y el cuerpo
aumenta su volumen: se dilata.
Porque en ella se asigna el valor cero a la temperatura más
baja.
14 Enuncia el Principio de conservación de la energía.
¿Por qué decimos que la energía se degrada?
7 ¿Qué cantidad de energía se transfiere cuando se
eleva la temperatura de 220 g de agua desde 15 °C hasta
55 °C?
La energía ni se crea ni se destruye, solamente se transforma.
Sin embargo, en todas las transformaciones de la energía
aparece calor por rozamiento que no puede utilizarse de
nuevo. La energía se degrada, cada vez es menos útil.
Q = m c (T2 – T1) = 0,220 kg · 4 180 J/kg °C (55 – 15) °C =
= 3,68 · 104 J
48
9 Un cubo de aluminio de 425 g de masa que está a una
temperatura de 182 °C se introduce en un recipiente que
contiene 368 g de agua a 18 °C. ¿Cuál es la temperatura
final de la mezcla? Calor específico del aluminio: c = 898
J/kg K.
PARA REFORZAR
8 Un kilogramo de agua y un kilogramo de cobre reciben la misma cantidad de energía. ¿En cuál de ellos se
produce un mayor incremento de la temperatura?
15 ¿Existe alguna temperatura a la que coincidan la
escala Celsius y la Fahrenheit?
En el cobre, porque su calor específico es menor.
x
x − 32
=
=; x = −40 º C = −40 ºF
100
180
16 ¿Por qué cuando nieva la temperatura ambiente
suele ser menos fría que después de la nevada?
Al solidificarse el agua, se desprende el calor latente de solidificación, que es igual al de fusión en valor numérico.
17 ¿Por qué el agua contenida en un botijo se mantiene
relativamente fría en verano?
Para evaporarse el agua de la superficie del botijo necesita
una cantidad elevada de energía (el calor latente de vaporización del agua es muy elevado: 2,25 · 106 J/kg), que obtiene,
en parte, del agua del botijo y, por tanto, ésta se enfría.
18 ¿Por qué en una olla a presión los alimentos se cuecen en menos tiempo?
Porque al aumentar la presión, aumenta la temperatura de
ebullición.
19 ¿Por qué en un día caluroso de verano la arena de la
playa quema y el agua del mar no?
Porque el calor específico del agua es mucho mayor que el
de la arena y ésta se calienta más.
20 ¿Qué cantidad de energía se desprende por medio
de calor cuando 72 g de vapor de agua a 100 °C se convierten en agua a 10 °C?
Q1 = m L = 0,072 kg · 2,25 · 106 J/kg = 1,62 · 105 J
Q2 = m c (T2 – T1) = 0,072 kg · 4 180 J/kg °C · (100 – 10) °C =
= 2,71 · 104 J
QT = Q1 + Q2 = 1,89 · 105 J
21 ¿Qué cantidad de energía hay que transferir por medio de calor a 82 g de agua a 15 °C para transformarla en
vapor a 100 °C?
Q1 = m c (T2 – T1) = 0,082 kg · 4 180 J/kg °C · (100 – 15) °C =
= 2,91 · 104 J
Q2 = m L = 0,082 kg · 2,25 · 106 J/kg = 1,85 · 105 J
QT = Q1 + Q2 = 2,14 · 105 J
22 Un cuerpo de 1 450 g de masa cae al suelo desde una
altura de 17,5 m. Si toda su energía potencial gravitatoria
se invierte en aumentar la temperatura del cuerpo, ¿cuánto varía su temperatura? Calor específico: c = 125 J/kg °C.
Ep = m g h = 1,45 kg · 9,8 m s–2 · 17,5 m = 249 J
Q = m c ∆T; 249 J = 1,45 kg · 125 J/kg °C · ∆T; ∆T = 1,37 °C
23 Calcula la energía intercambiada al transformar 120 g
de hielo a –12 °C en vapor de agua a 110 °C.
Q1 = m c (T2 – T1) = 0,120 kg · 2 050 J/kg °C · [0 – (–12)] °C =
= 2,95 · 103 J
Q2 = m Lf = 0,120 kg · 3,34 · 105 J/kg = 4,0 · 104 J
Q3 = m c (T2 – T1) = 0,120 kg · 4 180 J/kg °C · (100 – 0) °C =
= 5,02 · 104 J
Q4 = m Lv = 0,120 kg · 2,25 · 106 J/kg = 2,70 · 105 J
QT = Q1 + Q2 + Q3 + Q4 = 3,63 · 105 J
24 Basándote en la Teoría cinético-molecular, explica
por qué durante la fusión de una sustancia no varía su
temperatura.
Mientras se produce la fusión, la energía transferida sirve
para separar las moléculas del sólido, venciendo las fuerzas
que las unen, con lo que pasa al estado líquido, sin variar la
temperatura.
25 Calcula la energía necesaria para transformar 1,2 kg
de hielo a –14 °C en vapor de agua a 100 °C.
Q1 = m c ∆T = 1,2 kg · 2 050 J/kg · (100 –(–12) °C )= 2,8 · 105 J
Q2 = m Lf = 1,2 kg · 3,34 · 105 J/kg = 4,01 · 105 J
Q3 = m c ∆T = 1,2 kg · 4 180 J/kg °C · (100 – 0) °C = 5,02 · 105 J
Q4 = m Lv = 1,2 kg · 2,25 · 106 J/kg = 2,7 · 106 J
QT = Q1 + Q2 + Q3 + Q4 = 3,88 · 106 J
26 Determina la energía necesaria para fundir un bloque de aluminio de 23 kg de masa que se encuentra a
una temperatura de 45 °C. Calor específico del aluminio:
c = 898 J/kg K; calor latente de fusión: Lf = 3,42 · 105 J/kg;
temperatura de fusión del aluminio: T = 930 K.
Q1 = m c ∆T = 23 kg · 898 J/kg °C · (657 – 45) °C = 1,26 · 107 J
Q2 = m Lf = 23 kg · 3,42 · 105 J/kg = 7,87 · 106 J
QT = Q1 + Q2 = 2,05 · 107 J
27 Un calentador eléctrico de inmersión que tiene una
potencia de 250 W se sumerge en un recipiente que contiene 5,2 L de agua a 18 °C. Calcula el tiempo necesario
para que la temperatura del agua llegue hasta 62 °C.
Q = m c ∆T = 5,2 kg · 4 180 J/kg °C · (62 – 18) °C = 9,56 · 105 J
P=
W Q
Q 9,56 ⋅105 J = 3,28 · 103 s
= ; t= =
t
t
P
250 J s −1
EVALUACIÓN
1 ¿Cuál de las siguientes afirmaciones es falsa?
a) Las partículas que forman la materia están en constante movimiento.
b) El calor es una forma de energía.
c) La escala Celsius de temperaturas es una escala
centígrada.
d) La unidad de energía en el SI es el julio.
Respuesta correcta: b).
49
7
2 ¿Cuáles de las siguientes afirmaciones son correctas?
a) Cuando se transfiere energía a un cuerpo aumenta
su temperatura.
b) En la escala Kelvin de temperaturas no existen valores negativos.
c) El paso de sólido a líquido se denomina solidificación.
d) Algunas sustancias sólidas pasan directamente al
estado gaseoso.
Todas menos la c).
3 ¿Alguna de las siguientes afirmaciones es falsa?
¿Cuál?
a) El agua siempre hierve a 100 °C.
b) Si dos cuerpos tienen la misma temperatura están en
equilibrio térmico.
c) Un julio equivale aproximadamente a 0,24 calorías.
d) Encontrarse a una temperatura de 27 °C es lo mismo
que estar a 300 K.
Respuesta correcta: a).
4 ¿Cuáles de las siguientes transformaciones son cambios de estado?
a)
b)
c)
d)
El filamento de una bombilla se pone incandescente.
Se calienta un trozo de hielo desde –20 °C a –5 °C.
Un poco de aceite se mezcla con agua.
La nieve de la montaña se funde cuando llega la primavera.
Respuesta correcta: d).
50
5 Señala de forma razonada las respuestas correctas.
a) La unidad de calor latente en el SI es el J/kg.
b) En la ebullición, la vaporización se produce en toda
la masa del líquido.
c) Los gases se dilatan menos que los líquidos.
d) El rendimiento de las máquinas térmicas es muy grande.
Son correctas las respuestas:
a) El calor latente debe multiplicarse por la masa para obtener el calor total, por lo que su unidad es el J/kg.
b) Correcto. Es en la evaporación donde sólo se produce en
superficie.
6 Indica de forma razonada las afirmaciones incorrectas:
a)
b)
c)
d)
En el proceso de fusión se desprende energía.
La máquina de vapor es la primera máquina térmica.
El calor específico del agua es elevado.
La energía se conserva, pero se degrada.
La respuesta correcta es la a). La fusión absorbe energía para
poder transformar el sólido en líquido, por tener mayor movilidad sus partículas.
7 ¿Cuáles de las siguientes afirmaciones son falsas?
a)
b)
c)
d)
La unidad de calor específico en el SI es J/K.
1 kJ equivale a 0,24 kcal.
En el proceso de fusión se absorbe energía.
El uso de combustibles fósiles contribuye al cambio
climático.
Respuesta correcta: a).
LA ENERGÍA DE LAS ONDAS:
LUZ Y SONIDO
EJERCICIOS
1 ¿Qué es una onda? ¿Qué relación existe entre onda
y movimiento vibratorio?
Respuesta teórica ya incluida en el libro.
2 Explica por qué decimos que las ondas transportan
energía pero no materia.
Lo que se propaga es la perturbación no las partículas del medio, que sólo oscilan en torno a su posición de equilibrio.
Se propaga la energía, no la materia.
3 Describe las analogías y las diferencias existentes
entre las ondas mecánicas y las electromagnéticas.
Ambos tipos de ondas responden a las características fundamentales de las ondas, pero las ondas mecánicas se mueven
a través de la materia, necesitan un medio material para propagarse; en cambio, las ondas electromagnéticas también lo
hacen en el vacío.
4 ¿En qué medios se propagan las ondas mecánicas?
¿Qué ondas pueden propagarse en el vacío?
Las ondas mecánicas transversales se propagan en los sólidos
pero no en el interior de los líquidos o los gases.
En el vacío sólo se propagan las ondas electromagnéticas.
5 Calcula la longitud de onda y la frecuencia de las ondas emitidas por un radar cuyo periodo es de 1,5 · 10 –10 s .
La velocidad de propagación de las ondas en el aire es de
300 000 km/s.
1
1
=
=
−10
T 1,5 · 10
s/ciclo
= 6,7 · 109 ciclos/s = 6,7 · 109 Hz
f =
v=
λ
; λ = vT =
T
= 3 · 10 8m/s · 1,5 · 10 −10
s
m
= 4,5 · 10 −2
ciclo
ciclo
6 Calcula la longitud de onda y el periodo de un sonido
de frecuencia f = 1 200 Hz. La velocidad del sonido en el
aire es de 340 m/s.
v 340 m s −1
1
=
= 0,28 m; T = =
f 1200 s −1
f
1
=
= 8,3 ⋅ 10 −4 s
1200 s −1
8
Como el relámpago va tan rápido que prácticamente es instantáneo, sólo contamos el movimiento del sonido.
e = v t = 331 m/s · 2,16 s = 715 m
8 Se golpea en un extremo una barra de aluminio
de 1,25 m de longitud. ¿Cuánto tiempo tarda la perturbación en llegar al otro extremo? La velocidad del sonido
en el aluminio es v = 5 150 m/s.
t=
x
1,25 m
=
= 2,4 ⋅ 10 −4 s
v 5150 m s −1
9 ¿Por qué cuando gritas delante de un obstáculo no
siempre se produce el eco? Razona la respuesta.
El oído humano distingue dos sonidos consecutivos cuando
los percibe con una diferencia mínima de 0,1 s. En ese tiempo,
el sonido recorre 34 m, aproximadamente; por tanto, el obstáculo en el que se refleja debe estar situado a una distancia
mínima de 17 m.
10 ¿A qué distancia de una roca se halla un cazador si
oye el eco de la detonación de su escopeta 2,4 s después
de disparar?
x = v t = 340 m/s · 1,2 s = 408 m
11 ¿Los sonidos agudos tienen mayor o menor longitud
de onda que los graves? ¿De qué depende el timbre de
los sonidos?
Como la frecuencia de los sonidos es mayor, su longitud de
onda es más pequeña: λ = v /f. El timbre de dos sonidos es
diferente porque lo es la forma de la onda (en forma de sierra,
en forma de pico, con irregularidades, etcétera). Es debido a
la distinta forma en que se generan los sonidos en distintas
fuentes.
12 Un cantante tiene un tono de 2 200 Hz. ¿Cuál es la
longitud de la onda sonora en el aire si su velocidad es
de 340 m/s?
λ=
v 340 m s −1
=
= 0,155 m/ciclo
f 2 200 Hz
13 Calcula el periodo y la longitud de onda en el aire
de los ultrasonidos emitidos por un murciélago si su frecuencia es de 108 000 Hz. Suponemos que la velocidad
en el aire es de 340 m/s.
λ=
7 Un alpinista oye un trueno 2,16 s después de ver el
relámpago. ¿A qué distancia se encuentra la nube si la
temperatura en la montaña es de 0 ºC?
1
1
T= =
= 9,26 · 10 −6 s/ciclo
f 108 000 Hz
λ=
v 340 m s −1
=
= 3,15 · 10 −3 m/ciclo
f 108 000 Hz
51
8
14 Un sónar, que emite una onda ultrasónica, recibe la
onda reflejada en un obstáculo submarino 1,25 s después
de la emisión. ¿A qué profundidad se encuentra el obstáculo? Suponemos que la velocidad del sonido en el
agua del mar es de 1 500 m/s.
x = v t = 1 500 m/s · 0,625 s = 938 m
15 El índice de refracción de la luz en el agua es 1,33.
¿Cuál es la velocidad de la luz en el agua?
v=
c 3 ⋅10 8 m s −1
=
= 2,25 ⋅10 8 m s −1 = 225 000 km/s
n
1,33
16 ¿Por qué cuando miramos un río desde la orilla su
profundidad parece siempre menor de la que realmente es?
La luz procedente de los cuerpos sumergidos se refracta en
la superficie del agua, cambia de dirección y vemos el objeto
como si la luz viajara en línea recta, sin cambiar su dirección
de propagación.
17 Una chica de 1,72 m de altura se coloca delante de
un espejo plano, a 75 cm de ella. ¿Qué tamaño tiene su
imagen? ¿A qué distancia del espejo se forma?
La imagen tiene una altura de 1,72 cm y está situada 75 cm
detrás del espejo.
18 Haz en equipo una pequeña investigación sobre los
procedimientos que se utilizan para corregir los defectos
del ojo humano.
Un ojo miope no ve con nitidez los objetos lejanos.
Este defecto del ojo se corrige con lentes divergentes.
19 Describe el proceso mediante el cual se produce la
dispersión de la luz. ¿Qué luces forman el espectro visible?
La dispersión de la luz blanca en un prisma óptico se debe
a que las luces se propagan con distintas velocidades en el
vidrio del prisma.
Espectro visible: rojo, naranja, amarillo, verde, azul, añil y
violeta.
20 ¿Cómo se denominan las ondas cuya frecuencia es
mayor que la de la luz violeta? ¿Qué ondas electromagnéticas tienen la menor longitud de onda?
La luz ultravioleta tiene frecuencias mayores que la luz visible.
Las ondas electromagnéticas de menor longitud de onda
son los rayos gamma.
52
EJERCICIOS PROPUESTOS
PARA REPASAR
1 ¿Qué magnitud experimenta la perturbación cuando
se propagan las ondas sonoras?
La magnitud que experimenta la perturbación que se propaga en el espacio es la presión.
2 ¿Qué diferencias existen entre las ondas mecánicas
longitudinales y las transversales?
En las ondas mecánicas transversales la dirección de vibración
de las partículas es perpendicular a la dirección de propagación de la onda; en las ondas longitudinales ambas direcciones
coinciden. Las ondas mecánicas transversales sólo se propagan en los sólidos y en las superficies de separación entre
líquidos y líquido-gas, pero no se propagan en el interior de
los gases o de los líquidos. En cambio, las ondas longitudinales
pueden hacerlo en cualquier medio material.
3 ¿Qué tipo de perturbación se propaga en las ondas
electromagnéticas?
Las ondas electromagnéticas propagan su energía por medio
de perturbaciones eléctricas y magnéticas.
4 ¿Qué tipo de ondas se propagan en el vacío? ¿A qué
velocidad?
Las ondas electromagnéticas se propagan en el vacío a una
velocidad aproximada de 300 000 km/s.
5 Pon algún ejemplo de ondas transversales y de ondas longitudinales.
Ondas transversales: luz, ondas de radio y TV, rayos X, etcétera.
Ondas longitudinales: ondas sonoras.
6 Las ondas emitidas por una emisora de radio tienen
una longitud de onda de 45 cm. Calcula la velocidad con
que se propagan en el aire, su frecuencia y su periodo.
Todas las ondas electromagnéticas se propagan en el aire
con una velocidad aproximada de 300 000 km/s.
v 3 ⋅10 8 m s −1
=
= 6,7 ⋅10 8 Hz
λ
0, 45 m
1
1
T= =
= 1,5 ⋅10 −9 s
f 6,7 ⋅10 8 s −1
f=
7 La frecuencia de una onda sonora en el aire es de
1 450 Hz. Calcula su longitud de onda y su periodo.
v = 340 m/s.
λ=
−1
v 340 m s
=
= 0,23 m
f 1450 s −1
1
1
T= =
= 6,9 ⋅10 −4 s
f 1450 Hz
8 ¿Cuál es el origen de todos los sonidos? Pon algunos
ejemplos.
El sonido se produce por las vibraciones del foco emisor.
Ejemplos: altavoz, voz humana, tambor, guitarra, etcétera.
9 Calcula la distancia recorrida por una onda sonora
en el agua en 12 s. La velocidad del sonido en el agua es
de 1 450 m/s.
x = v t = 1 450 m/s · 12 s = 1,74 · 104 m
PARA REFORZAR
16 ¿De qué factores depende la energía transportada
por una onda?
Cuanto mayor es la energía transportada por una onda mayor
es la intensidad de ésta. Para una determinada frecuencia, la
intensidad de la onda, y, por tanto, la energía que transporta,
es directamente proporcional al cuadrado de la amplitud e
inversamente proporcional al cuadrado de la distancia al foco
emisor de la onda.
17 Si el número de Mach con que vuela un avión es
2,05, ¿cuál es su velocidad? Suponemos que la velocidad
del sonido en el aire en las mismas condiciones es de
310 m/s.
v = 310 m/s · 2,05 = 635,5 m/s
10 Un montañero recibe el eco de su voz 0,80 s después
de gritar. ¿A qué distancia se encuentra el obstáculo que
ha reflejado su voz?
18 Calcula la profundidad a la que se encuentra un
submarino si desde que el sónar emite la correspondiente onda ultrasónica hasta que recibe la onda reflejada
transcurren 0,24 s. La velocidad del sonido en el agua
del mar es igual a 1 500 m/s.
x = v t = 340 m/s · 0,40 s = 136 m
x = v t = 1 500 m/s · 0,12 s = 180 m
11 ¿Qué propiedad física distingue los sonidos fuertes
de los débiles?
19 Una antena de radar emite una onda electromagnética y recibe el eco 0,018 s después de emitir la señal. ¿A
qué distancia del radar se encuentra el obstáculo?
La sonoridad, que depende de la intensidad de la onda, es
decir, de la energía que transporta.
12 ¿Qué sonido es más grave, el que tiene una frecuencia de 1 400 Hz o aquel cuya frecuencia es de 8 000 Hz?
El de mayor frecuencia: el sonido de 1 400 Hz.
13 ¿Qué son los ultrasonidos? Indica algunas de sus
aplicaciones más importantes.
Los ultrasonidos son los sonidos con frecuencias superiores
a 20 000 Hz. Aplicaciones: medicina (ecografías), industria
(perforaciones, soldaduras, localización de defectos), sonar
(detección de objetos submarinos), etcétera.
x = v t = 3 · 108 m/s · 0,009 s = 2,7 · 106 m
20 Las naves que han explorado la superficie de Marte
se comunicaban con la Tierra mediante ondas electromagnéticas. ¿Cuánto tiempo tardaban en llegar sus señales si el planeta Marte se encontraba a 54 millones de
kilómetros de la Tierra?
t=
x 54 ⋅10 6 km
=
=180 s
v 3 ⋅105 km s −1
14 ¿Qué cualidad nos permite diferenciar dos sonidos
de la misma sonoridad e igual frecuencia?
21 Cuando presenciamos un amanecer y recibimos los
primeros rayos de sol, ¿realmente es en ese instante cuando el Sol aparece en el horizonte? ¿Con qué retraso recibimos su luz? La distancia del Sol a la Tierra es de 150
millones de kilómetros.
El timbre del sonido.
La luz del Sol tarda en llegar a la Tierra en el siguiente tiempo:
15 El índice de refracción del diamante es 2,41. ¿Cuál es
la velocidad de la luz en el diamante?
t=
v=
c 3 ⋅10 8 m s −1
=
=1,24 ⋅10 8 m s −1
n
2, 41
x 150 ⋅10 6 km
=
= 500 s ≅ 8,3 min
v 3 ⋅105 km s −1
22 ¿En qué consiste el fenómeno sonoro que denominamos reverberación? ¿Cómo puede evitarse?
53
8
Cuando las ondas sonoras se reflejan en obstáculos situados
a distancias inferiores a 17 m, el sonido directo y los reflejados
se superponen y la audición es confusa, los sonidos no se
perciben con nitidez. Este fenómeno se denomina reverberación. Se observa en locales vacíos y cerrados y en las salas con
malas condiciones acústicas. Se evita instalando materiales
absorbentes que impidan la reflexión de las ondas sonoras:
cortinas, alfombras, tapices, corcho, butacas, etcétera.
c) Las ecografías se realizan con sonidos de alta frecuencia llamados ultrasonidos.
d) El sonido no se propaga mediante ondas.
23 ¿Qué son los armónicos? ¿Qué cualidad del sonido
determinan?
a) La luz del Sol es una mezcla de varios tipos de luces.
b) El eco se produce cuando el sonido se refleja en ciertos obstáculos.
c) La velocidad de la luz en el aire es de 300 000 km/s,
aproximadamente.
d) La miopía se corrige con lentes divergentes.
Los focos sonoros no producen una vibración única, sino que
al sonido fundamental, de frecuencia definida, se superponen otros más débiles, de frecuencias múltiplos de la fundamental, que se denominan armónicos o sobretonos. Estos
armónicos determinan el timbre de cada sonido.
3 ¿Alguna de las siguientes afirmaciones es verdadera?
Respuesta correcta: Todas.
24 ¿Cómo son las lentes convergentes? ¿Qué defecto
del ojo se corrige con este tipo de lentes?
4 Indica de forma razonada las respuestas que son
correctas:
Hay que ver el apartado 8.6 del libro de texto. La hipermetropía se corrige con lentes convergentes.
a) El tono de un sonido depende de su frecuencia.
b) Los sonidos agudos tienen menor frecuencia que los
graves.
c) La intensidad física de una onda se mide en decibelios.
d) La energía transportada por las ondas sonoras es
siempre muy pequeña.
25 Ordena de mayor a menor frecuencia las distintas
luces que forman el espectro visible.
Violeta > añil > azul > verde > amarillo > naranja > rojo.
26 Realiza en equipo una pequeña investigación sobre
la contaminación acústica y lumínica. Utiliza revistas,
periódicos, Internet, etcétera.
Actividad abierta para realizar en grupo.
EVALUACIÓN
1 ¿Cuáles de las siguientes afirmaciones son verdaderas?
a) Las ondas que se forman en la superficie del agua
transportan agua y energía.
b) Las ondas transfieren energía sin transporte de masa.
c) El ruido excesivo produce contaminación acústica.
d) Las radiografías y las ecografías se realizan con rayos X.
Respuesta correcta: b) y c).
2 ¿Cuál de las siguientes afirmaciones sobre el sonido
es falsa?
a) No se propaga en el vacío, pero sí lo hace en el aire y
en el agua.
b) Se propaga a mayor velocidad en los sólidos que en
los gases.
54
Respuesta correcta: d).
Son correctas a (el tono, agudo o grave, está relacionado con
la frecuencia —mayor en los agudos—) y c (hay una equivalencia entre la energía radiada por unidad de superficie y la
escala en decibelios).
5 Indica las afirmaciones que son falsas, razonando la
respuesta:
a) Los ultrasonidos tienen frecuencias mayores que los
infrasonidos.
b) La luz que se refleja cambia de dirección y de velocidad.
c) El índice de refracción del aire es prácticamente igual
a uno.
d) El timbre de los sonidos depende de la amplitud de
la onda.
Son falsas b (la luz que se refleja cambia de dirección, pero
no de velocidad al mantenerse en el mismo medio) y d (el
timbre de los sonidos depende de la forma de la onda, no
de su amplitud).
6 ¿Cuáles de las siguientes afirmaciones son verdaderas?
a) Las lentes esféricas pueden ser convergentes y divergentes.
b) La dispersión de la luz se puede conseguir con un
prisma de vidrio.
c) La luz visible tiene mayor frecuencia que los rayos X.
d) Las ondas sonoras y las de la luz son ondas electromagnéticas.
Son correctas a (las lentes esféricas son convergentes o divergentes en función de hacia dónde está el centro de curvatura)
y b (la dispersión de la luz se consigue muchas veces en un
prisma de vidrio; es el fundamento de los espectroscopios
antiguos).
55
9
LOS ELEMENTOS QUÍMICOS
Y SUS ENLACES
EJERCICIOS
1 Nombra los siguientes elementos y la familia en que
se colocan: Li, N, Al, P, K, Ag, I, Hg, Ra, Pb y U. ¿Algunos
se hallan en el mismo periodo o en el mismo grupo?
Li: litio, alcalinos, grupo 1.
N: nitrógeno, nitrogenoideos, grupo 15.
Al: aluminio, térreos, grupo 13.
P: fósforo, nitrogenoideos, grupo 15.
K: potasio, alcalinos, grupo 1.
Ag: plata, elementos de transición, grupo 11.
I; yodo, halógenos, grupo 17.
Hg: mercurio, elementos de transición, grupo 12.
Ra: radio, alcalinotérreos, grupo 2.
Pb: plomo, carbonoideos, grupo 14.
U: uranio, elementos de transición interna.
En el mismo periodo están Li y N (periodo 2), Al y P (periodo 3),
Ag e I (periodo 5), Hg y Pb (periodo 6), Ra y U (periodo 7).
2 ¿Qué elemento es más metálico, el bario o el calcio?
¿Y cuál es más no metálico, el oxígeno o el yodo?
Más metálico cuanto más abajo y a la izquierda, luego el bario
es más que el calcio. Más no metálico cuanto más arriba y a
la derecha, luego el oxígeno es más que el yodo.
3 Indica la carga esperada para los iones que componen las siguientes sustancias basándote en el grupo al
que pertenecen y sus características como metales o no
metales: KBr ; CaCl2 ; MgS ; AlI3 y BaO.
KBr:
Potasio grupo 1 (1 electrón externo) metal ..
Bromo grupo 17 (7 electrones externos) no
metal ............................................................................
CaCl2: Calcio grupo 2 (2 electrones externos)
metal.............................................................................
Cloro grupo 17 (7 electrones externos) no
metal ............................................................................
MgS: Magnesio grupo 2 (2 electrones externos)
metal.............................................................................
Azufre grupo 16 (6 electrones externos) no
metal ............................................................................
AlI3: Aluminio grupo 13 (3 electrones externos)
semimetal ...................................................................
Yodo grupo 17 (7 electrones externos) no
metal.............................................................................
BaO: Bario grupo 2 (2 electrones externos) metal ..
Oxígeno grupo 16 (6 electrones externos)
no metal ......................................................................
K+
Br
5 ¿Por qué crees que las sustancias covalentes conducen mal la electricidad mientras que las metálicas son
buenas conductoras?
Porque en las sustancias metálicas los electrones no están
asociados a ningún átomo en particular, por lo que están
más o menos libres y pueden moverse fácilmente por la red
a poco que se les fuerce con una diferencia de potencial,
mientras que en las sustancias covalentes, los electrones
pertenecen a los átomos que los comparten y no pueden
escaparse de ellos con facilidad.
6 ¿Qué diferencias encuentras en la estructura de los
tres tipos de cristales estudiados, iónicos, covalentes y
metálicos?
Los cristales iónicos tienen cationes y aniones formando la
red; los covalentes carecen de cargas netas; y los metálicos
tienen cationes formando la red con los electrones intercalados entre ellos.
EJERCICIOS PROPUESTOS
PARA REPASAR
–
Ca2+
1 Indica las principales diferencias entre metales y no
metales.
Cl–
Ver texto, págs. 200 y 201.
Mg2+
2 Indica el nombre del grupo al que pertenecen los
siguientes elementos: Ca, Ni, Ag, P, He, Hg y U.
S2–
Al3+
I–
Ba2+
O2–
4 Indica los electrones externos que deben tener los
siguientes elementos, y cuáles crees que podrían actuar
como cationes y cuáles como aniones: Li, N, F, Sr y Zn.
Li: litio, grupo 1 (1 e – externo) que tiende a perder, será el
catión Li+.
56
N: nitrógeno, grupo 15 (5 e – externos) por lo que tiende a
ganar, será el anión N3–.
F: flúor, grupo 17 (7 e– externos) por lo que tiende a ganar,
será el anión F–.
Sr: estroncio, grupo 2 (2 e – externos) que tiende a perder,
será el catión Sr2+.
Zn: cinc, grupo 12 (e– externos) que tiende a perder, será el
catión Zn2+.
Ca, alcalinotérreos; Ni, elementos de transición; Ag, elementos de transición; P, nitrogenoideos; He, gases inertes; Hg,
elementos de transición; U, elementos de transición interna
(actínido).
3 El elemento 19 del Sistema Periódico:
a) ¿A qué grupo y periodo pertenece?
b) ¿Es metal o no metal?
c) Indica otros elementos de su grupo.
a) Grupo 1, Periodo 4.
b) Metal.
c) Litio, Sodio, Rubidio y Cesio.
4 Coloca los siguientes elementos en orden creciente
de carácter metálico: Zn, Ca, Ag, Rb y Cd.
Grupo
Elemento
Símbolo
1
Litio
Li
Electrones
externos
1
2
Berilio
Be
2
Me
13
Boro
B
3
Metaloid
14
Carbono
C
4
No Met
Bi < P < S < Cl< F.
15
Nitrógeno
N
5
No Met
6 Indica cuántos electrones externos tienen los átomos
de los siguientes elementos: Na, C, P, Mg y Cl.
16
Oxígeno
O
6
No met
17
Flúor
F
7
No Met
18
Neón
Ne
8
No Met
Zn < Cd < Ag < Ca < Rb.
5 Coloca los siguientes elementos en orden creciente
de carácter no metálico: F, Bi, S, P y Cl.
Na, 1 electrón; C, 4 electrones; P, 5 electrones; Mg, 2 electrones; Cl, 7 electrones.
7 ¿Cuáles son las diferencias que existen entre moléculas y cristales?
Las moléculas están formadas por un número no muy grande
de átomos enlazados sin formar estructuras, mientras que los
cristales están formados por macroestructuras de muchos
átomos enlazados y ordenados.
8 Indica el tipo de enlace que se puede esperar cuando
se unan los átomos o iones de los siguientes elementos:
sodio con nitrógeno, calcio con flúor, hierro con oxígeno
y fósforo con cloro.
Sodio con nitrógeno … iónico;
Calcio con flúor … iónico;
Fósforo con cloro … covalente;
Hierro con oxígeno … iónico.
9 ¿Por qué crees que los gases nobles se presentan
como átomos libres y no se enlazan unos con otros?
Porque no se estabilizan más por perder o ganar electrones.
Ya tienen 8 externos.
10 Completa la siguiente tabla referida al segundo
periodo:
Grupo
1
2
13
14
15
16
17
18
Li
Be
B
C
N
O
F
Ne
Elemento
Símbolo
Electrones externos
Carácter
Carácter
Me
11 El hidrógeno ni tiene propiedades metálicas ni no
metálicas. ¿Por qué crees que se le coloca en el grupo 1
del Sistema Periódico?
Porque tiene un electrón en la zona externa, como el resto
de los elementos que se encuentran en el grupo 1.
PARA REFORZAR
12 Explica si son ciertas o no las siguientes afirmaciones:
a) Un elemento químico puede estar formado por átomos de diferentes números atómicos y másicos.
b) Un átomo se transforma en su ion negativo cuando
gana electrones en la corteza, y en su ion positivo
cuando gana protones en el núcleo.
a) Los átomos de un elemento químico siempre tienen el
mismo número atómico, pueden tener distinto número
másico cuando se trata de isótopos.
b) Un átomo se transforma en su ion negativo cuando gana electrones en la corteza, y en su ion positivo cuando
pierde electrones.
13 Dados los átomos: X (A = 39; Z = 19), Y (A = 24; Z = 12)
y Z (A = 16; Z = 8), indica:
a)
b)
c)
d)
Protones, neutrones y electrones que poseen.
¿Cuáles serán metales y cuáles no metales?
Periodo en que se encuentra cada uno.
¿Qué tipos de enlace se dan en la unión de X con Z y
de Y con Z?
a) X tiene 19 protones, 19 electrones y 20 neutrones. Y tiene
12 protones, 12 electrones y 12 neutrones. Z tiene 8 protones, 8 electrones y 8 neutrones.
b) X e Y metales, Z no metal.
c) X en el tercer periodo, Y en el segundo y Z en el primero.
d) Iónico en ambos casos.
57
9
14 Clasifica las siguientes sustancias según el tipo de
enlace que presenten: KCl, CO, Ag, CuI2, SiO2 y NH3.
KCl, iónico (metal con no metal); CO, covalente (no metal con
no metal); Ag, metálico; CuI2, iónico (metal con no metal);
SiO2, covalente (no metal con no metal); NH3, covalente (no
metal con hidrógeno).
15 Indica el tipo de enlace esperado para una sustancia
que:
a) Cuando se disuelve conduce la corriente eléctrica.
b) No se puede disolver en agua ni conduce la corriente
eléctrica.
c) No se disuelve en agua, pero conduce la corriente
eléctrica.
a) Iónica.
b) Covalente.
c) Metálica.
Hielo … red; hierro … red; agua … molécula;
aceite … molécula; oxígeno … molécula;
vidrio … red.
17 A la vista de lo expresado en la tabla adjunta, indica
el tipo de enlace que presentan las sustancias A, B y C.
Punto
de fusión
Solubilidad
en agua
Conductividad
Dureza
A
Alto
Sí
Sólo disuelta
Alta
B
Bajo
No
No
Baja
C
Alto
No
No
Alta
Sustancia A … iónica; Sustancia B … covalente; Sustancia C
… covalente reticular.
18 Desarrolla una hipótesis que justifique por qué el
agua es capaz de disolver los compuestos iónicos y en
cambio no puede hacer lo propio con los sólidos covalentes reticulares.
Si puede disolver sólo sustancias que tengan cargas netas
como ocurre en los sólidos iónicos es porque debe poder
interaccionar con cargas tanto positivas como negativas, y
para ello debe tener partes de su molécula también con ciertas cantidades de carga, tanto positiva como negativa. Debe
tener polos eléctricos.
58
1 Los metales son:
a)
b)
c)
d)
Todos los elementos.
Sólo los elementos que brillan.
Elementos que conducen la corriente eléctrica.
Elementos aislantes.
Respuesta correcta: c).
2 Los no metales son:
a)
b)
c)
d)
Todos los elementos.
Sólo elementos sólidos.
Elementos que conducen la corriente eléctrica.
Elementos aislantes.
Respuesta correcta: d).
16 A partir de sus propiedades, clasifica las siguientes
sustancias como moléculas o redes: hielo, hierro, agua,
aceite, oxígeno y vidrio.
Sustancia
EVALUACIÓN
3 En el Sistema Periódico:
a) Los elementos se ordenan alfabéticamente.
b) Los elementos se ordenan en forma creciente de sus
masas atómicas.
c) Los elementos se ordenan en forma creciente de sus
números atómicos.
d) Los metales y los no metales están mezclados.
Respuesta correcta: c).
4 Indica cuál o cuáles de estas afirmaciones son
ciertas:
a)
b)
c)
d)
El sodio es un alcalino y el oxígeno, un halógeno.
El sodio es un carbonoideo y el oxígeno, un anfígeno.
El sodio es un alcalino y el oxígeno, un anfígeno.
Sodio y oxígeno son gases nobles.
Respuesta correcta: c).
5 La materia se puede presentar formada por:
a)
b)
c)
d)
Átomos juntos unos con otros desordenadamente.
Átomos unidos formando moléculas.
Átomos unidos formando moléculas y cristales.
Átomos unidos formando moléculas y cristales, pero
también como átomos individuales.
Respuesta correcta: d).
6 Los enlaces se forman:
a) Siempre que chocan átomos de dos elementos.
b) Sólo cuando los átomos que chocan conducen a sustancias con energía menor.
c) Muy raramente.
d) Cuando lo provocamos en un laboratorio.
Respuesta correcta: b).
7 Los compuestos iónicos se forman:
a) Entre un metal y un no metal que intercambian electrones.
b) Entre un metal y un no metal que comparten electrones.
c) Entre un metal que cede electrones a un no metal que
los toma.
d) Entre dos metales que ceden electrones.
Respuesta correcta: c).
8 Los compuestos covalentes se forman:
a) Entre un metal y un no metal que intercambian electrones.
b) Entre dos no metales que comparten electrones.
c) Entre un metal que cede electrones y un no metal que
los toma.
d) Entre dos metales que ceden electrones.
Respuesta correcta: b).
59
10 LAS REACCIONES QUÍMICAS
EJERCICIOS
50 g de N2 ⋅
1 La fusión del hielo o la disolución del sulfato de cobre en agua, ¿son transformaciones químicas? Explica el
porqué.
No, son transformaciones físicas. Las transformaciones químicas son procesos en los que se modifican las sustancias
iniciales denominadas reactivos para convertirse en otras
finales, denominadas productos.
En el caso de la fusión del hielo, lo que ocurre es un cambio de
estado de sólido a líquido.
En la disolución del sulfato de cobre en agua lo que ocurre es
que el sólido pasa a forma iónica por la acción del agua.
2 Clasifica las siguientes reacciones según los tres tipos citados y nombra las diferentes sustancias:
a)
b)
c)
d)
e)
f)
HBr + KOH
KBr + H2O
2 Na + 1/2 O2
Na2O
Ca(NO3)2 + Na2SO4
CaSO4 + 2 NaNO3
2 KClO3
2 KCl + 3 O2
N2 + 3 H2
2 NH3
CaCO3
CaO + CO2
a) HBr + KOH → KBr + H2O
b) 2 Na + 1/2 O2 → Na2O
c) Ca (NO3)2 + Na2SO4 →
CaSO4 + 2 NaNO3
d) 2 KClO3 → 2 KCl + 3 O2
e) N2 + 3 H2 → 2 NH3
f) CaCO3 → CaO + CO2
Sustitución
Síntesis o combinación
Sustitución
Descomposición
Síntesis o combinación
Descomposición
3 Completa y ajusta las siguientes reacciones:
a)
b)
c)
d)
e)
f)
g)
a)
b)
c)
d)
e)
f)
g)
H3PO4 + LiOH
Ca(OH)2 + HI
Al(OH)3 + H2SO4
CH4 + O2
CH3–CH2OH + O2
Zn(OH)2 + HCl
CaO + H2O
4 Se hacen reaccionar 50 gramos de N2 con H2 para
obtener amoniaco (NH3). Calcula cuánto NH3 se obtendrá.
Expresa el resultado en moles y en gramos.
N2 + 3 H2 → 2 NH3
50 g de N2 ⋅
2 ⋅ 17 g de NH3
28 g N2
= 60,7 g NH3
1 mol de N2 2 moles de NH3
⋅
=
28 g N2
1 mol de N2
= 3,57 moles NH3
28 g N2
= 60,7 g NH3
1 mol de N2 2 moles de NH3
⋅
= 3,57 moles NH3
28 g N2
1 mol de N2
5 En la descomposición térmica del carbonato de calcio se obtiene CO2 y CaO. ¿Es posible obtener 60 gramos
de óxido de calcio a partir de 100 gramos de carbonato
de calcio?
CaCO3 → CaO + CO2
CaCO3 → CaO + Co2
100 g de CaCO3 ⋅
56 g de CaO
= 56 g CaO
100 g CaCO3
No es posible, lo máximo que podríamos obtener con 100
gramos de CaCO3 son 56 gramos de CaO y no 60.
6 El gas ciudad es mayoritariamente metano (CH4),
que cuando se quema con O2 da CO2 y H2O. Calcula los
litros de O2, medidos a 1 atm y 20 °C, que serían necesarios para quemar completamente 2 kg de metano. Y si
lo que quemamos son 2 kg de butano (C4H10), ¿cuántos
litros de O2 se consumirían, también medidos a 1 atm y
20 °C? ¿Cuántos litros de CO2 se obtendrían en esas mismas condiciones?
CH4 + 2 O2 → CO2 + 2 H2 O
2 000 g CH4 ⋅
1 mol CH4 2 mol O2
⋅
= 250 moles de O2
16 g CH4 1 mol CH4
nRT
=
p
atm L
250 moles O2 ⋅ 0, 082
⋅ 293 K
mol K
=
= 6 000 L de O2
1 atm
2 C 4H10 + 13 O2 → 8 CO2 + 10 H2 O
pV = n R T ⇔ V =
2 000 g C 4H10 ⋅
H3 PO4 + 3 LiOH → 3 H2O + Li3PO4
Ca(OH)2 + 2 HI → CaI2 + 2 H2O
2 Al(OH)3 + 3 H2SO4 → Al2(SO4)3 + 6 H2O
CH4 + 2 O2 → CO2 + 2 H2O
CH3–CH2OH + 3 O2 → 2 CO2 + H2O
Zn(OH)2 + 2 HCl → ZnCl2 + 2 H2O
CaO + H2O → Ca (OH)2
60 50 g de N2 ⋅
50 g de N2 ⋅
2 ⋅17 g de NH3
nRT
V=
=
p
= 5 380 L O2
5 380 L O2 ⋅
1 mol C 4H10 13 mol O2
⋅
= 224 moles de O2
58 g C 4H10 2 mol C 4H10
224 moles O2 ⋅ 0, 082
1 atm
8 L de CO2
13 L de CO2
atm L
⋅ 293 K
mol K
=
= 3 300 L de CO2
7 ¿Cuántos litros de O2 se consumen en un día al cocinar
en tu casa (utiliza una presión de 1 atm y la temperatura
que consideres habitual en tu casa)? ¿A cuántos moles
equivale esa cantidad de O2? ¿Cuántos kilogramos de agua
se obtienen en la reacción de combustión anterior? Dato:
al cocinar se queman unos 8 kg de metano cada mes.
CH4 + 2 O2 → CO2 + 2 H2O;
8 000/30 = 266,7 g/día
266,7 g CH4 ⋅
2 ⋅32 g O2 1 mol O2
⋅
= 33,3 moles O2
16 g CH4 32 g O2
Suponiendo que las condiciones sean las anteriores, tenemos:
3 Indica a qué tipo de reacción se refiere la frase: «En
algunos procesos químicos los reactivos tienen menos
energía que los productos de reacción». Explica tu respuesta.
La frase se refiere a los procesos endotérmicos; ello implicará
que los enlaces formados son más débiles e inestables que
los reactivos de los que proceden.
4 Ajusta las reacciones siguientes:
pV = n RT;
n R T 33,3 ⋅ 0, 082 ⋅ 293
V=
=
= 800, 8 L O2
p
1
2 ⋅ 18 g H2 O
1 kg H2
266,7 g CH4 ⋅
⋅
= 0, 6 kg H2 O
16 g CH4
1000 g H2 O
8 Disuelve con agua un poco de cloruro amónico
(NH4Cl) y de ácido sulfúrico (H2SO4), depositados en sendos vasos. Comprueba las características energéticas de
los procesos de disolución realizados.
Es una actividad experimental para que los alumnos la comprueben en el laboratorio.
9 Cuando la gasolina hace explosión con el aire en el
motor de un automóvil, cada gramo de gasolina produce
44 kJ. Calcula los kJ que se producirían en la combustión
de 1 kg de gasolina. Considerando que la gasolina se
comporta, desde el punto de vista energético, como
si fuese heptano (C7H16), escribe su ecuación de combustión, indicando el calor de reacción.
C7 H16 + 11 O2 → 7 CO2 + 8 H2O
1g
1000 g
=
, de donde x = 44 000 kJ
44 kJ
x kJ
EJERCICIOS PROPUESTOS
PARA REPASAR
1 ¿Cuáles son las condiciones para que el choque entre
dos moléculas sea eficaz y produzca, por tanto, la reacción química?
Que tengan la orientación adecuada y la energía suficiente.
2 ¿Podría darse en m/s la velocidad de una reacción?
Razona tu respuesta.
No, la velocidad de reacción en Química no mide la relación
entre el espacio y el tiempo empleado en recorrerlo como
en Física. La velocidad de reacción mide la variación entre la
concentración de reactivo que desaparece o la de producto
que aparece en función del tiempo.
C2H4 + O2
HCl + Al(OH)3
CO2 + H2O
AlCl3 + H2O
C2H4 + 3 O2 → 2 CO2 + 2 H2O
3 HCl + Al(OH)3 → AlCl3 + 3 H2O
5 Dibuja el esquema de un proceso exotérmico. ¿Quién
tiene más energía en este proceso, el conjunto de los productos o el de los reactivos?
E
R
P
Tienen más energía los reactivos que los
productos.
6 ¿Por qué crees que cuando se trocea, la leña arde
mejor?
Porque la combustión se realiza mejor cuanto mayor sea la
superficie de contacto. Uno de los factores que aumenta la
velocidad de reacción es precisamente la superficie de contacto de los reactivos.
7 ¿Cómo crees que influye un catalizador en la velocidad de reacción? Razona la respuesta.
Un catalizador acelera la velocidad de reacción porque disminuye la Ea, aunque mantiene constantes los valores energéticos de reactivos y productos.
8 ¿Qué crees que le ocurre a la velocidad de una reacción cuando aumenta la temperatura?
Al aumentar T la velocidad de reacción se incrementa ya que
aumenta la energía de las moléculas y, por tanto, la probabilidad de que los choques sean efectivos también aumenta.
9 ¿Se pueden convertir 32 g de CH4 en 96 g de CO2 sin
añadir ni quitar carbono? ¿Cuántas moléculas hay de
cada uno de estos compuestos químicos?
CH4 + 2 O2 → CO2 + 2 H2O
La máxima cantidad de CO2 que se podría obtener a partir
de 32 gramos de CH4 es:
61
10
16 g CH4
44 g CO2
=
32 g CH4
x g CO2
de donde x = 88 g de CO2
Por tanto, para obtener 92 g de CO2 habría que aportar mayor
cantidad de CH4 o de C, ya que:
C + O2 → CO2
En 32 gramos de CH4 habrá:
32 g CH4 ⋅
1 mol CH4 6, 022 ⋅1023 moléculas CH4
⋅
= 1,2 ⋅1024
44 g CH4
1 mol CH4
1 mol CO2 6, 022 ⋅1023 moléculas CH4
⋅
= 1,3 ⋅1024
44 g CO2
1 mol CH4
10 Calcula el número de moles que hay en 318 g de carbonato sódico.
318 g Na2 CO3 ⋅
1 mol Na2 CO3
106 g NA2 CO3
= 3 moles
11 ¿A qué masa de HCl equivalen 3 moles de ácido clorhídrico?
3 moles de HCI ⋅
36,5 g HCI
= 109,5 gramos
1 mol HCI
12 Ajusta las siguientes reacciones químicas:
C2H6 + O2
C6H6 + O2
Na2CO3 + HCl
Fe2O3 + CO
CO2 + H2O
CO2 + H2O
NaCl + CO2 + H2O
Fe + CO2
C2H6 + 7/2 O2 → 2 CO2 + 3 H2O
C6 H6 + 15/2 O2 → 6 CO2 + 3 H2O
Na2 CO3 + 2 HCl → 2 NaCl + CO2 + H2O
Fe2O3 + 3 CO → 2 Fe + 3 CO2
13 Cuando quemamos 0,75 g de magnesio en presencia
de aire, el compuesto resultante tiene una masa de 1,25
g. ¿Por qué aumenta la masa?
Porque se forma la reacción: Mg + 1/2 O2 → MgO y, por tanto,
se adiciona oxígeno:
24,3 g MG 0,75 g MG
=
;
40,3 g MgO
x g MgO
40,3 g MgO
0,75 g de Mg ⋅
= 1,24 g MgO
24,3g Mg
62
CaCO3
CaO + CO2
a) ¿Cuántos moles de carbonato cálcico necesitamos
calentar para obtener 150 g de óxido de calcio?
b) ¿Cuántos gramos se obtendrían de óxido de calcio?
c) ¿Qué volumen de CO2 se obtendrá si la reacción tiene
lugar a 10 °C y 700 mm Hg de presión?
CaCO3 → CaO + CO2
1 mol de CaO
= 2, 68 moles de CaO
56 g CaO
1 mol de CaCO3
2, 68 moles de CaO .
= 2, 68 moles de CaCO3
1 mol de CaO
1 mol de CO2
2, 68 moles de CaCO3 .
= 2, 68 moles de CO2
1 mol de CaCO3
150 g de CaO ⋅
En 96 gramos de CO2 habrá:
96 g CO 4 ⋅
14 Al calentar carbonato cálcico tiene lugar la siguiente
reacción:
2, 68 moles de CaCO3 ⋅
pV = n RT; V =
1 mol de CO2
1 mol de CaCO3
= 2, 68 moles de CO2
n R T 2, 68 ⋅ 0, 082 ⋅ 283
=
= 675,5 L de CO2
700
p
760
15 El sulfuro ferroso se tuesta industrialmente con
oxígeno según el proceso siguiente:
2 FeS + 3 O2
2 SO2 + 2 FeO
a) ¿Cuántos moles de SO2 se obtienen con 3 moles de
FeS?
b) ¿Cuántos litros de O2 se consumen?
2 FeS + 3 O2 → 2 SO2 + 2 FeO
3 moles FeS ⋅
3 moles FeS ⋅
2 moles SO2
2 moles FeS
3 moles O2
= 3 moles de SO2
= 4,5 moles de O2
2 moles Fe S
22, 4 L O2 (c.n.)
4,5 moles O2 ⋅
=100, 8 L
1 mol O2
16 Se desprenden 2 200 kJ al quemar un mol de propano según la reacción:
C3H8 + 5 O2
3 CO2 + 4 H2O
Calcula la energía desprendida en la combustión de 13
kg de propano.
C3H8 + 5 O2 → 3 CO2 + 4 H2 O + 2 200 kJ
13 000 g C3H8 ⋅
2 200 kJ
= 6,5 ⋅105 kJ
44 g C3H8
5 000 g C 4H10 ⋅
= 7 758, 6 g H2 O ⋅
5 ⋅18 g H2 O
58 g C 4H10
1 mol H2 O
18 g H2 O
=
= 431 moles H2 O
6, 022 ⋅1023 moléculas
=
1 mol
= 5,2 ⋅1025 moléculas C 4H10
86,2 moles C 4H10 ⋅
6, 022 ⋅1023 moléculas
=
1 mol
= 3,3 ⋅1026 moléculas O2
560,3 moles O2 ⋅
6, 022 ⋅1023 moléculas
=
1 mol
= 2 ⋅1026 moléculas CO2
PARA REFORZAR
344, 8 moles CO2 ⋅
17 Al reaccionar el ácido clorhídrico con el óxido de
calcio se produce la reacción:
CaO + 2 HCl
6, 022 ⋅1023 moléculas
=
1 mol
= 2, 6 ⋅1026 moléculas H2 O
431 moles H2 O ⋅
CaCl2 + H2O
22, 4L
= 1930,9 L C 4H10 ;
1 mol
22, 4 L
560,3 moles O2 ⋅
= 12 544 L O2
1 mol
22, 4 L
344, 8 moles CO2 ⋅
= 7 723,5 L CO2 ;
1 mol
22, 4 L
431 moles H2 O ⋅
= 9 654, 4 L H2 O
1 mol
¿Se podrían obtener 111 g de CaCl2 si se parte de 73 g
de HCl? Calcula la masa de CaO que se necesita para obtenerlos.
86,2 moles C 4H10 ⋅
CaO + 2 HCI → CaCI2 + H2 O
73 g HCI ⋅
113 g CaCI2
= 113 g de CaCI2
2 ⋅36,5 g HCI
Se podrían obtener hasta 113 gramos de CaCI2
111 g CaCI2 ⋅
73 g HCI
= 71,7 g HCI
113 g CaCI2
18 La combustión del butano C4H10 con O2 da como productos CO2 y H2O. Completa la tabla adjunta si la reacción
se realiza en condiciones normales.
C4H10
Masa (g)
O2
CO2
H2O
5 000
C4H10
O2
CO2
H2O
Masa (g)
5 000
17 931
15 172
7 758,6
Volumen (L)
1 930,9
12 544
7 723,5
9 654,4
Moles
Moléculas
86,2
560,3
344,8
431
5,2 · 1025
3,3 · 1026
2 · 1026
2,6 · 1026
19 El zinc reacciona con ácido perclórico según la
siguiente reacción:
Zn + HClO4
Volumen (L)
Moles
Moléculas
C 4H10 +13/2 O2 → 4 CO2 + 5 H2 O
5 000 g C 4H10 ⋅
= 17 931 g O2 ⋅
13 ⋅16 g O2
58 g C 4H10
1 mol O2
32 g O2
5 000 g C 4H10 ⋅
= 15172, 4 g CO2 ⋅
13 ⋅16 g O2
58 g C 4H10
1 mol CO2
44 g Co2
5 000 g C 4H10 ⋅
= 7 758, 6 g H2 O ⋅
58 g C 4H10
1 mol H2 O
18 g H2 O
=
= 344, 8 moles CO2
5 ⋅18 g H2 O
=
= 431 moles H2 O
6, 022 ⋅1023 moléculas
=
1 mol
= 5,2 ⋅1025 moléculas C 4H10
86,2 moles C 4H10 ⋅
6, 022 ⋅1023 moléculas
=
1 mol
= 3,3 ⋅1026 moléculas O2
560,3 moles O2 ⋅
6, 022 ⋅1023 moléculas
=
1 mol
= 2 ⋅1026 moléculas CO2
344, 8 moles CO2 ⋅
431 moles H2 O ⋅
6, 022 ⋅1023 moléculas
=
1 mol
26
Después de ajustar la reacción, calcula los gramos de perclorato de zinc que se obtienen al hacer reaccionar 500 g
de zinc. ¿Qué volumen de H2 medido a 1 atm de presión y
25 °C de temperatura se recogerá? (Masas atómicas: Zn =
= 65,3; Cl =35,5; H = 1 y O = 16.)
=
= 560,3 moles O2
Zn(ClO4)2 + H2
Zn + 2 HCIO 4 → Zn (CIO 4 )2 + H2
500 g Zn ⋅
266, 4 g Zn (CIO 4 )2
= 2 036,7 g Zn (CIO 4 )2
65, 4 g Zn
2g H2
500 g Zn ⋅
= 15,3 g H2
65, 4 g Zn
n R T 15,3/2 ⋅0, 082 ⋅298
V=
=
= 186, 8 L de H2
p
1
20 El amoniaco reacciona con el ácido nítrico para dar
nitrato amónico, según la reacción:
NH3 + HNO3
NH4NO3
a) ¿Cuántos gramos de amoniaco deben reaccionar para
obtener 2 moles de nitrato amónico?
b) Sabiendo que el amoniaco es un gas, ¿qué volumen
ocupará el NH3 del apartado anterior si las condiciones
de reacción son de 20 °C y 700 mm Hg de presión?
c) ¿Cuántos gramos de ácido nítrico deben reaccionar
para obtener los dos moles de nitrato amónico?
63
10
NH3 + HNO3 → NH4NO3
a) 2 moles NH4NO3 ⋅
= 2 moles NH3 ⋅
1 mol NH3
1 mol NH4NO3
17 g NH3
1 mol NH3
=
= 34 g
700
b)
⋅V = 2 ⋅0, 082 ⋅293; V = 52,2 L NH3
760
1 mol NH3
c) 2 moles NH4NO3 ⋅
⋅
1 mol NH4NO3
⋅
63 g HNO3
1 mol HNO3
b) 350 g CaCO3 ⋅
= 154 g CO2 ⋅
44 g CO2
100 g CaCO2
22, 4 L CO2
44 g CO2
21 Al reaccionar 18 litros de O2, medidos en condiciones
normales, con CO en exceso, ¿cuántos litros de CO2 se
obtienen, si nos encontramos a T = 25 °C y p = 0,8 atm?
CO + 1/2 O2 → CO2
En condiciones normales, de 1/2 mol de O2 se obtiene 1 mol
de CO2; esto es lo mismo que decir:
22, 4
L de O2 18 L de O
2
2
=
22, 4 L de CO2 x L de CO2
100 g CaCO3 100
⋅
=
56 g CaO
70
= 255102 kg piedra caliza
d) 255102 g de piedra ⋅0,70 = 178 571 g CaCO3
P V P'V ' 1⋅20 0, 8 ⋅V
=
=
=
V = 27,3 L
T
T'
273
298
22 El principal componente de la roca caliza es el carbonato cálcico, que se utiliza para obtener la cal viva
(CaO). En un horno de cal descomponemos 500 g de piedra caliza de un 70 % de riqueza en carbonato cálcico,
según la siguiente reacción:
CaCO3
CaO + CO2
a) ¿Cuántos gramos de cal se obtendrán?
b) ¿Cuántos litros de CO2 medidos en condiciones normales se obtendrían?
c) ¿Cuántos gramos de piedra caliza harían falta para
obtener 100 kg de CaO?
d) ¿Cuántos moles de CaCO3 se han utilizado en el
apartado anterior?
CaCO3 → CaO + CO2
500 · 0,7 = 350 g de CaCO3 puros
a) 350 g CaCO3 ⋅
64
56 g CaO
= 196 g CaO
100 g CaCO3
1 mol CaCO3
100 g CaCO3
=
= 1785,7 moles CaCO3
23 Se queman 100 g de un azúcar según la siguiente
reacción sin ajustar:
C6H12O6 + O2
CO2 + H2O
a) Calcula los gramos de CO2 que se obtendrán.
b) ¿Cuántos gramos de O2 nos harán falta para que reaccione todo el azúcar?
c) Calcula los volúmenes de O2 y CO2 en cn.
C6H12O6 + 6 O2 → 6 CO2 + 6 H2O
x = 36 L de CO2
Ahora se pasa a las condiciones experimentales:
= 78, 4 L CO2
c) 100 000 g CaO
178 571 g de CaCO3 ⋅
= 126 g HNO3
=
a) 100 g C6H12 O 6 ⋅
b) 100 g C6H12 O 6 ⋅
c) 146, 6 g CO2 ⋅
106, 6 g O2 ⋅
6 ⋅ 44 g CO2
180 g C6H12 O 6
6 ⋅32 g O2
180 g C6H12 O 6
= 146, 6 g CO2
= 106, 6 g CO2
22, 4 L
= 74, 6 L CO2 ;
44 g CO2
22, 4 L
= 74, 6 L O2
32 g O2
Al existir el mismo número de moles de O2 y de CO2 los
volúmenes también serán iguales.
24 El ácido sulfúrico reacciona con el zinc dando sulfato de zinc e hidrógeno. Ajusta la reacción y calcula los
gramos de zinc que deben reaccionar para producir 100 g
de sulfato de zinc.
Zn + H2 SO 4 → ZnSO 4 + H2
1000 g ZnSO 4 ⋅
65, 4 g Zn
= 40,5 g Zn
161, 4 g ZnSO 4
25 En la reacción del carbonato de calcio con ácido clorhídrico se produce dióxido de carbono, cloruro de calcio
y agua. Calcula la cantidad de carbonato de calcio que se
necesita para obtener 250 g de cloruro de calcio.
CaCO3 + 2 HCI → CaCI2 + CO2 + H2 O
250 g CaCI3 ⋅
100 g CaCO3
113 g CaCI3
= 221,24 g CaCO3
26 El bario reacciona con HCl para dar cloruro de bario
e hidrógeno. Calcula:
a) La cantidad de bario que se necesita para que reaccionen 2 moles de HCl.
b) ¿Qué volumen de H2 se obtendrá si se mide a 700 mm
Hg y 23 °C?
Ba + 2 HCl → BaCl2 + H2
1 mol Ba
= 1 mol de Ba;
2 moles HCI
137,3 g Ba
1 mol de Ba ⋅
= 137,3 g Ba
1 mol Ba
a) 2 moles HCI ⋅
b) 2 moles HCI ⋅
1 mol H2
2 moles HCI
= 1 mol de H2  22, 4 L
27 Calcula la cantidad de O2 que puede reaccionar con
el H2 que se desprende al atacar 100 g de Al con exceso
de H2SO4.
2 Al + 3 H2 SO4 → Al2 (SO4)3 + 3 H2
100 g Al ⋅
3 ⋅2 g H2
2 ⋅27 g Al
H2 +1/2 O2 → H2 O;
11,11 g H2 ⋅
16 g O2
2 g H2
= 11,11 g H2
= 88,9 g O2
28 La fosfina (PH3) es un compuesto que se utilizó como
gas venenoso durante la Segunda Guerra Mundial y se
obtiene mediante la reacción:
Na3P + H2O
PH3 (g) + NaOH
¿Qué cantidad de fosfina se obtendrá al hacer reaccionar
150 gramos de Na3P con 250 g de H2O?
P + 3(g)
H2+O3→
PH3 (g) + 3 NaOH
Na3P + 3 H2O Na
→3PH
NaOH
3
M (Na3P) = 100
M(Na P) = 100
3
150 g Na3P ⋅
34 g PH3
100 g Na3P
= 51 g PH3
Si hubiéramos tomado como referencia los 250 g de H2O,
tendríamos:
250 g H2 O ⋅
100 g Na3P
3 ⋅18 g H2 O
= 462,9 g Na3P
Nos habrían hecho falta 462,9 gramos de fosfuro, cantidad
que no tenemos pues nuestra máxima cantidad de fosfuro
sódico es 150 gramos; ello quiere decir que existe agua en
exceso y que el fosfuro es el reactivo limitante.
29 Uno de los métodos más comunes de obtención de
sosa cáustica (NaOH) se basa en la reacción del carbonato
sódico con hidróxido cálcico, para obtener carbonato
cálcico e hidróxido sódico.
a) Escribe la ecuación ajustada.
b) ¿Cuántos gramos de hidróxido sódico se pueden obtener a partir de 1 kg de carbonato sódico?
c) Si el rendimiento de la reacción fuera del 80 %, ¿de
qué cantidad de carbonato sódico habríamos de partir para obtener los mismos gramos de NaOH que en
el apartado anterior?
a) Na2 CO3 + Ca(OH)2 → 2 NaOH + CaCO3
b) 1000 g Na2 CO3 ⋅
2 40 g NaOH
= 754,7 g NaOH
106 g Na2 CO3
c) 754,7 · 100/80 = 943,4 g Na2CO3
EVALUACIÓN
1 En un plato tenemos un hielo, que se está licuando y
un clavo que se está oxidando. Por lo tanto:
a) Se están produciendo dos reacciones químicas distintas.
b) No se produce ninguna reacción química.
c) El clavo se oxida mediante una reacción química y el
agua se licúa sin que se produzca reacción.
d) El clavo se oxida mediante un proceso físico que no
es una reacción, mientras que el agua obtenida se ha
formado en una reacción química.
Respuesta correcta: c).
2 En una reacción química:
a) La masa de los productos siempre es mayor que la de
los reactivos.
b) La masa de los reactivos es siempre mayor que la de
los productos.
c) Realizada en un recipiente abierto, la masa siempre
se mantiene constante aunque algunos de los productos formados sean gases.
d) Realizada en un recipiente cerrado, la masa siempre
se mantiene constante.
Respuesta correcta: d).
3 En la reacción de formación del dióxido de carbono:
a) Una molécula de carbono reacciona con una molécula
de oxígeno y se crean dos moléculas de CO2.
65
10
b) Un mol de carbono reacciona con 1 mol de oxígeno y
se forma 1 mol de CO2.
c) 12 g de carbono reaccionan con 16 g de oxígeno y se
obtienen 28 g de CO2.
d) 10 g de carbono reaccionan con 10 g de oxígeno y se
obtienen 20 g de CO.
Respuesta correcta: b).
4 Al hacer reaccionar hidrógeno con oxígeno para formar vapor de agua, se tiene que cumplir que:
a) La masa de hidrógeno ha de ser el doble que la de
oxígeno.
b) El volumen de hidrógeno ha de ser el doble que el del
oxígeno.
c) La masa de oxígeno ha de ser el doble que la del hidrógeno.
d) El volumen de oxígeno ha de ser el doble que el del
hidrógeno.
Respuesta correcta: b).
66
5 La velocidad de una reacción química se modifica
cuando:
a) La concentración de los reactivos permanece constante.
b) Añadimos cualquier otra sustancia.
c) Hacemos reaccionar una sustancia radioactiva.
d) Se aumenta la temperatura.
Respuesta correcta: d).
6 Respecto a la energía intercambiada en un proceso
químico se puede afirmar que:
a) Las combustiones siempre absorben calor.
b) En los procesos endotérmicos se desprende calor.
c) En los procesos exotérmicos siempre se desprende
calor.
d) Siempre se desprende calor.
Respuesta correcta: c).
rEaccionES QuÍMicaS DE inTErÉS
EJERCICIOS
1 Escribe tres propiedades características de los
ácidos.
11
9 Completa y ajusta las siguientes reacciones de neutralización:
a) HCl + KOH
b) H2SO3 + Ca(OH)2
Sabor ácido; reaccionan con la mayoría de los metales, sobre
todo con el Zn, desprendiendo hidrógeno; enrojecen el papel
azul de tornasol; con el mármol producen efervescencia.
a) HCl + KOH → KCl + H2O
b) H2SO3 + Ca(OH)2 → CaSO3 + 2 H2O
2 Indica las analogías existentes entre los ácidos y las
bases.
10 ¿Por qué las comidas copiosas provocan acidez de
estómago?
En disolución conducen la corriente eléctrica (son electrolitos); son corrosivos; reaccionan entre sí: neutralización.
La secreción de HCl en el estómago está en consonancia con
la cantidad de alimentos ingeridos. Si la comida es copiosa
la cantidad de ácido es grande, provocando la sensación de
acidez de estómago.
3 Describe el comportamiento de los ácidos y de las
bases frente al papel indicador y en su reacción con el
cinc.
Los ácidos enrojecen el papel de tornasol; las bases lo azulean. Los ácidos reaccionan con el Zn; las bases no reaccionan
con él.
4 Escribe la disociación acuosa de los siguientes ácidos: a) HI; b) HClO4 y c) H3PO4.
HI → H+ + I–
HClO4 → H+ + ClO4–
H3PO4 → 3 H+ + PO3–
4
11 En las farmacias también se venden como antiácidos
Mg(OH)2 (leche de magnesia) y Al(OH)3. Completa y ajusta
las siguientes reacciones de neutralización:
a) HCl + Mg(OH)2
b) HCl + Al(OH)3
a) 2 HCl + Mg(OH)2 → MgCl2 + 2 H2O
b) 3 HCl + Al(OH)3 → AlCl3 + 3 H2O
12 Escribe las semirreacciones correspondientes a los
procesos de oxidación y de reducción que se producen
en la siguiente reacción:
5 Escribe la disociación acuosa de las siguientes bases:
a) KOH; b) Ba(OH)2 y c) Cr(OH)3.
KOH → K+ + OH–
Ba(OH)2 → Ba2+ + 2 OH–
Cr(OH)3 → Cr3+ + 3 OH–
6 Al disolver una aspirina en un vaso de agua se obtiene una disolución cuyo pH es aproximadamente igual
a 3. ¿Se trata de una disolución ácida o básica?
Se trata de una sustancia ácida, puesto que el pH es inferior
a 7.
7 ¿Qué es un indicador? Pon algunos ejemplos.
Un indicador es una sustancia que tiene la propiedad de
adoptar un color distinto según esté en un medio ácido o
básico.
Por ejemplo: el papel de tornasol, la fenolftaleína y el rojo
de metilo.
8 El pH de dos disoluciones acuosas es 10,2 y 12,5, respectivamente. ¿Cuál de las dos es más básica?
Una sustancia es tanto más básica cuanto mayor es su pH. Por
tanto, la sustancia con pH = 12,5 es más básica.
Ca + Cl2
CaCl2
Ca → Ca2+ + 2e–
Cl2 + 2e– → 2 Cl–
13 Define los conceptos de oxidación, reducción,
agente oxidante y agente reductor.
Estos conceptos están explicados en el libro del alumno.
14 Enumera algunos ejemplos de pilas eléctricas. ¿Mediante qué tipo de procesos químicos producen energía
eléctrica?
Pilas alcalinas, pilas ácidas, pilas de botón (de mercurio), etc.
Las pilas funcionan basadas en los procesos de oxidación-reducción.
15 Escribe las características más significativas de las
reacciones de combustión.
Desprenden calor y son muy rápidas.
16 ¿Cómo se realiza el metabolismo de los alimentos?
Está explicado en el libro del alumno.
67
11
17 Haz una relación de combustibles sólidos, líquidos
y gaseosos.
7 Escribe y ajusta la reacción de combustión del metano (CH4).
Por ejemplo: carbón, leña, gasolina, alcohol, gasóleo, hidrógeno, propano, gas natural, etcétera.
CH4 + 2 O2 → CO2 + 2 H2O
EJERCICIOS PROPUESTOS
8 Haz una relación de combustibles de uso frecuente.
Por ejemplo: carbón, gasolina, propano, gas natural, etcétera.
PARA REPASAR
1 Indica las diferencias más importantes entre ácidos
y bases.
El sabor. Todos los ácidos tienen sabor agrio y todas las bases
tienen sabor a lejía (cáustico o amargo).
Reacción con los metales. Los ácidos reaccionan; las bases
no.
Reacción con los carbonatos. Los ácidos reaccionan produciendo efervescencia; las bases no reaccionan.
Reacción con las grasas. Los ácidos no reaccionan; las bases
sí, produciendo jabón.
2 Escribe las reacciones de disociación acuosa de las
siguientes sustancias: HBr, Cu(OH)2 y HIO4.
HBr → Br – + H+
Cu(OH)2 → Cu2+ + 2 OH–
HIO4 → IO4– + H+
3 Ajusta y completa la siguiente reacción de neutralización:
H2SO4 + NaOH
H2SO4 + 2 NaOH → Na2SO4 + 2 H2O
4 Indica el color que adquieren la fenolftaleína y el
tornasol en disoluciones ácidas o básicas.
Es un proceso de reducción, puesto que hay pérdida de oxígeno.
2 Fe2O3 + 3 C → 3 CO2 + 4 Fe
PARA REFORZAR
10 El pH de varias disoluciones es: 8,5; 2,3; 0,6; 7; 13,4;
1,2 y 14. Ordena estas disoluciones de mayor a menor
acidez.
0,6; 1,2; 2,3; 7; 8,5; 13,4; 14. El grado de acidez disminuye a
medida que aumenta el pH.
11 ¿Por qué se emplea el agua oxigenada (H2O2) como
desinfectante en las heridas?
El agua oxigenada es un gran oxidante. El oxígeno que desprende destruye muchos tipos de bacterias que pueden
originar infecciones.
12 En la combustión de los derivados del petróleo se
produce siempre dióxido de carbono (CO2). ¿Encuentras
algún inconveniente al uso de estos productos como
combustibles?
Fenolftaleína: en ácido (incolora); en base (roja).
Tornasol: en ácido (rojo); en base (azul).
El principal inconveniente es la contaminación que origina
la combustión de estos derivados, favoreciendo el efecto
invernadero.
5 ¿Por qué cuando el cobre se convierte en CuO se dice
que se ha oxidado?
13 Escribe y ajusta la reacción de combustión del propano (C3H8).
Porque ha ganado oxígeno en la reacción. Se ha combinado
con el oxígeno.
C3H8 + 5 O2 → 3 CO2 + 4 H2O
6 Haz una relación de oxidantes y reductores que
conozcas.
Por ejemplo: Oxidantes: el oxígeno, el agua oxigenada, el
ozono, el ácido sulfúrico, etc. Reductores: los metales en general, el gas hidrógeno, el carbón, el CO, etcétera.
68
9 El hierro puede obtenerse a partir de un mineral
(oligisto) rico en Fe2O3. ¿Es éste un proceso de oxidación
o de reducción?
14 Un oxidante cuando actúa como tal se reduce. Justifica este hecho.
La oxidación y la reducción son procesos inversos. Si una
sustancia hace de oxidante es que cede oxígeno a otra y
como consecuencia su proporción de oxígeno se reduce. El
oxidante se reduce, pues, al perder oxígeno.
15 Las personas que padecen úlcera de estómago no pueden tomar aspirina. ¿Cómo explicas esta circunstancia?
23 Escribe las reacciones de disociación de las siguientes sustancias: Fe(OH)2; Ag(OH) y H3BO3.
Una acidez de estómago prolongada desemboca en úlcera
de este órgano digestivo. La aspirina tiene carácter ácido. Por
tanto, aumenta la acidez de estómago acelerando la aparición de úlceras. Si ya se tiene úlcera de estómago, la aspirina
aumentará las molestias propias de ésta.
Fe(OH)2 → Fe2+ + 2(OH)–
Ag(OH) → Ag+ + (OH)–
H3BO3 → 3 H+ + (BO3)3–
16 Una disolución acuosa tiene un pH igual a 12. ¿Es
grande o pequeña la concentración de protones en la
disolución?
La sustancia es muy poco ácida. Por tanto, la concentración
de protones es muy pequeña.
17 Si un átomo metálico reacciona convirtiéndose en
un catión, ¿el metal se oxida o se reduce?
Para que el átomo metálico se convierta en catión debe perder electrones; por tanto, se oxida.
18 Explica por qué es necesario proteger los objetos
fabricados con hierro.
Porque el hierro se oxida con facilidad.
19 Cita los principales agentes contaminantes del aire
y explica cómo se originan.
Consultar el texto.
20 Explica en qué consiste el efecto invernadero.
Respuesta libre.
21 Explica el origen de la lluvia ácida.
Respuesta libre.
22 El recipiente de la figura contiene agua destilada.
Indica en qué casos se enciende la bombilla:
24 Escribe la reacción de combustión del alcohol etílico
sabiendo que la fórmula de esta sustancia es C2H6O.
C2H6O + 3 O2 → 2 CO2 + 3 H2O
25 Completa las reacciones e indica qué sustancias se
oxidan y cuáles se reducen.
a) FeO + CO
b) H2 + O2
c) Cu2O + H2
a) FeO + CO → Fe + CO2; se oxida CO y el FeO se reduce.
b) 2 H2 + O2 → 2 H2O; se oxida el H2.
c) Cu2O + H2 → 2 Cu + H2O; se oxida el H2, se reduce el Cu2O.
EVALUACIÓN
1 Indica falso o verdadero. Los ácidos, entre otras,
tienen las siguientes propiedades:
a)
b)
c)
d)
Se disuelven en agua.
Son de sabor cáustico.
Reaccionan con todas las sustancias.
Tienen sabor variable.
a) es verdadera y el resto falsas.
2 Señala la afirmación correcta. La reacción entre un
ácido y una base recibe el nombre de:
a)
b)
c)
d)
Corrosión.
Neutralización.
Oxidación.
Los ácidos no reaccionan con las bases.
Respuesta correcta: b).
3 De las siguientes afirmaciones sobre los ácidos y las
bases, tres son falsas. Indica cuáles son:
a)
b)
c)
d)
e)
Cuando se añade agua oxigenada.
Cuando se añade vinagre.
Cuando se añade sal.
Cuando se añade azúcar.
Cuando se añade alcohol.
La bombilla se enciende en los casos b) y c) porque el vinagre
y la sal son electrolitos.
a)
b)
c)
d)
Tienen propiedades semejantes.
Reaccionan entre sí algunas veces.
Reaccionan entre sí solamente en caliente.
Reaccionan siempre entre sí aun en frío.
Son falsas a), b) y c).
4 Señala la afirmación correcta. El pH es:
69
11
a) Un factor que sirve para distinguir los distintos tipos
de sangre humana.
b) Una escala que indica el número de hidrógenos que
tiene un ácido.
c) Una escala que mide la rapidez con que se desprende
hidrógeno en la reacción de un ácido con un metal.
d) Una escala que mide el grado de acidez de una sustancia.
Respuesta correcta: d).
5 Señala la afirmación correcta. La reacción contraria
a la oxidación recibe el nombre de:
a)
b)
c)
d)
Combustión.
Neutralización.
Reducción.
No existe esa reacción.
Respuesta correcta: c).
6 Los metales alcalinos, como el sodio y el potasio,
ceden electrones con facilidad. A la vista de esta propiedad indica qué afirmaciones son verdaderas. Los metales
alcalinos son:
a) Buenos oxidantes.
b) Buenos reductores.
70
c) Se oxidan fácilmente.
d) Se reducen con facilidad.
Son ciertas b) (son buenos reductores puesto que suministran electrones), y c) (se oxidan fácilmente puesto que pierden los electrones).
7 El hidrógeno arde con facilidad, formando agua.
¿Cuáles de las siguientes afirmaciones son verdaderas?
a)
b)
c)
d)
El hidrógeno es un oxidante.
El hidrógeno es un reductor.
El hidrógeno se oxida fácilmente.
El hidrógeno recibe electrones de otras sustancias.
Son correctas b) y c).
8 En los procesos de combustión, los combustibles:
a) Arden solos sin necesidad de otras sustancias.
b) Necesitan combinarse con otras sustancias como el
oxígeno.
c) Absorben una gran cantidad de energía.
d) Dan lugar a unos compuestos sólidos, llamados óxidos.
Respuesta correcta: b).
la QuÍMica DE loS coMPuESToS
DE carBono
CH3
1 Además del carbono, ¿qué otros elementos intervienen en la constitución de los seres vivos?
Los enlaces Si – Si son más débiles e inestables que los enlaces C – C.
Las uniones del silicio con el oxígeno forman cadenas tan
estables que prácticamente resultan inertes y no son aptas
para los procesos biológicos. A diferencia del dióxido de
carbono, el dióxido de silicio es sólido, insoluble en agua y,
por tanto, incapaz de realizar los procesos biológicos que sí
permite el CO2.
3 ¿Qué características del átomo de carbono hacen
posible la formación de un número tan elevado de compuestos orgánicos?
El átomo de carbono forma cuatro enlaces covalentes relativamente fuertes. Además, forma cadenas de átomos de
carbono unidos mediante enlaces simples, dobles y triples.
Las cadenas pueden ser lineales, ramificadas y cerradas. Por
último, muchas sustancias orgánicas presentan el fenómeno
denominado isomería.
4 Además de carbono, ¿qué otros elementos contienen principalmente los compuestos orgánicos?
Hidrógeno, oxígeno y nitrógeno.
5 Aunque las reacciones entre compuestos orgánicos
suelen ser lentas, generalmente no se puede elevar la
temperatura de reacción hasta valores muy altos para
aumentar la velocidad de reacción, ¿por qué?
Las sustancias orgánicas se descomponen a temperaturas
relativamente bajas.
6 ¿Por qué los compuestos orgánicos presentan, por lo
general, puntos de fusión y de ebullición bajos? ¿Suelen
ser solubles en agua?
Las fuerzas intermoleculares son débiles; por tanto, los puntos
de fusión y de ebullición de los compuestos orgánicos suelen
ser bajos.
Se disuelven preferentemente en disolventes orgánicos; en
cambio, muchos compuestos orgánicos son insolubles en
agua.
7 Nombra los siguientes hidrocarburos:
–
b)
c)
CH3 – CH – CH = CH2
–
2 ¿Por qué creemos que no es posible que pueda existir vida basada en el átomo de silicio?
CH2 – CH2 – CH3
CH2
–
Fundamentalmente, hidrógeno, oxígeno, nitrógeno, azufre
y fósforo.
CH3 – CH2 – CH2 – CH – CH3
–
a)
CH3
d)
a)
b)
c)
d)
CH2 – CH3
–
EJERCICIOS
12
– CH2 – CH3
2-metilpentano.
propilciclopentano.
3-metil-1-penteno.
1,2-dietilbenceno.
8 Utilizando los modelos moleculares de bolas y varillas construye las moléculas de diversos hidrocarburos.
Actividad manipulativa abierta.
9 Escribe la reacción de combustión del 1-buteno con
oxígeno.
CH2=CH–CH2–CH3 + 6 O2 → 4 CO2 + 4 H2O
10 Escribe la fórmula de los siguientes hidrocarburos:
a)
b)
c)
d)
e)
f)
g)
h)
Butano.
Propeno.
2-penteno.
1-butino.
Ciclohexano.
2-metilhexano.
Etilbenceno.
Ciclobuteno.
a)
b)
c)
d)
e)
CH3–CH2–CH2–CH3
CH2=CH–CH3
CH3–CH=CH–CH2–CH3
CH≡C–CH2–CH3
CH2
CH2
CH2
CH2
CH2
CH2
f) CH3–CH(CH3)–CH2–CH2–CH2–CH3
71
12
CH2
g)
CH3
h)
CH2
CH
CH2
CH
11 ¿Por qué el uso como combustibles de los derivados
del petróleo contribuye al incremento del efecto invernadero?
19 Averigua el nombre y la fórmula del ácido presente
en el aceite de oliva.
En la combustión de los derivados del petróleo se produce
dióxido de carbono.
Ácido oleico:
CH3 – (CH2)7 – CH = CH – (CH2)7 – COOH
12 Haz una relación de los productos más importantes
obtenidos por destilación fraccionada del petróleo.
20 Si lees la etiqueta de alguna botella de agua o de
otra bebida encontrarás las iniciales del plástico empleado en su fabricación. ¿De qué plástico se trata?
Ver el apartado 12.4 del libro de texto.
13 ¿Por qué los alcoholes con pocos átomos de carbono
son solubles en agua?
El grupo hidroxilo (–OH) característico de los alcoholes hace
que éstos sean polares y se disuelvan en agua.
Polietilentereftalato (PET).
21 ¿En qué consiste el vulcanizado del caucho? ¿Qué
propiedades del caucho mejoran con la vulcanización?
14 Haz una relación de productos que contienen etanol.
El caucho se vulcaniza tratándolo con azufre.
Es muy resistente al rozamiento, no se ablanda con el calor
y es prácticamente insoluble.
El etanol se encuentra en las bebidas alcohólicas: vino, cerveza, coñac, etcétera.
22 Haz una relación de grasas de origen animal y vegetal e indica cuáles son más beneficiosas para la salud.
15 Escribe la reacción de combustión del etanol.
CH3 – CH2OH + 3 O2
2 CO2 + 3 H2O
16 Nombra los siguientes alcoholes:
a)
b)
c)
d)
e)
CH3OH
CH3–CHOH–CH3
CH2OH–CH2–CH2OH
CH2OH–CH2–CHOH–CH2–CH2OH
CH2OH–CHOH–CHOH–CH2OH
a)
b)
c)
d)
e)
Metanol.
2-propanol.
1,3-propanodiol.
1,3,5-pentanotriol.
1,2,3,4-butanotetraol.
17 Formula los siguientes ácidos carboxílicos:
a) Ácido propanoico.
b) Ácido hexanoico.
c) Ácido pentanoico.
72
Ácido metanoico: picadura de insectos y ortiga.
Ácido etanoico: vinagre.
Ácido butanoico: mantequilla y queso.
Ácido láctico: leche.
Grasas de origen animal: mantequilla, manteca, sebo, la
grasa del queso, etcétera.
Grasas de origen vegetal: aceites de oliva, girasol, soja, etcétera.
Las grasas insaturadas son las más beneficiosas para la salud;
en general, los aceites.
23 Haz una relación de alimentos que contienen hidratos de carbono e indica en cada caso el hidrato de
carbono presente.
Frutas (glucosa), azúcar (sacarosa), patata (almidón), cereales
y legumbres (almidón), etcétera.
EJERCICIOS PROPUESTOS
PARA REPASAR
1 ¿Qué condiciones reúne nuestro planeta para que
fuera posible la aparición de la vida?
a) CH3 – CH2 – COOH
b) CH3 – CH2 – CH2 – CH2 – CH2 – COOH
c) CH3 – CH2 – CH2 – CH2 – COOH
La Tierra posee la masa gravitatoria suficiente para retener
su atmósfera; su distancia al Sol es idónea para mantener las
temperaturas adecuadas; existen grandes masas de agua; y
en su corteza se encuentran los cuatro elementos que constituyen el 98 por ciento de los tejidos vivos: carbono, hidrógeno, oxígeno y nitrógeno.
18 Escribe ejemplos de ácidos orgánicos que se encuentren en productos naturales.
2 Describe los enlaces covalentes de las siguientes
moléculas: CH4, C2H4 y C2H2.
Metano: enlace simple. Eteno: enlace doble
C = C. Etino: enlace triple C ≡ C.
3 Escribe tres cadenas carbonadas distintas formadas
por cuatro átomos de carbono.
Butano, metil-propano, ciclobutano.
4 ¿En qué consiste el fenómeno denominado isomería?
Pon algún ejemplo.
En numerosas ocasiones se encuentran sustancias orgánicas
que tienen la misma fórmula molecular (el mismo número de
átomos de cada elemento), pero poseen propiedades diferentes porque tienen distinta estructura. Este fenómeno se
denomina isomería. Por ejemplo: butano y 2-metil-propano.
5 Escribe las fórmulas de los siguientes hidrocarburos:
hexano, 2-penteno, 1-butino, ciclopropano y benceno.
a) CH3 – CH2 – CH2 – CH2 – CH2 – CH3
b) CH3 – CH = CH – CH2 – CH3
c) CH ≡ C – CH2 – CH3
d)
CH2
H2C
CH2
e)
10 ¿Conoces algún alcohol que se utilice para fabricar
cremas para la piel?
La glicerina (1,2,3-propanotriol).
11 Formula los siguientes ácidos orgánicos: ácido etanoico, ácido propanoico y ácido butanoico.
a) CH3 – COOH
b) CH3 – CH2 – COOH
c) CH3 – CH2 – CH2 – COOH
12 ¿Qué son los polímeros? ¿Por qué otro nombre se
conocen?
Los polímeros, o macromoléculas, son sustancias formadas
por moléculas de gran tamaño que se obtienen por la unión
de moléculas sencillas llamadas monómeros. Su masa molecular puede alcanzar millones de unidades de masa atómica.
13 Escribe los nombres de algunos polímeros naturales
y artificiales.
Naturales: almidón, celulosa, caucho natural, proteínas.
Artificiales: polietileno, poliestireno, policloruro de vinilo,
polipropileno, etcétera.
6 Nombra los siguientes hidrocarburos:
a) CH3–CH3
b) CH2=CH–CH2–CH3
c)
d)
a)
b)
c)
d)
a) CH3OH
b) CH3 – CHOH – CH2 – CH3
c) CH3 – CH2OH
Etano.
1-buteno.
Ciclopentano.
Ciclohexeno.
7 Escribe la reacción de combustión del butano.
C 4H10 +
13
O → 4 CO2 + 5 H2 O
2 2
8 ¿Cuál es la composición química de los alcoholes?
Son compuestos orgánicos oxigenados que contienen uno
o más grupos hidroxilo (–OH).
9 Escribe la fórmula de los siguientes alcoholes: metanol, 2-butanol y etanol.
14 Probablemente las persianas o las tuberías de desagüe de tu casa sean de PVC, ¿cuál es su composición
química? ¿Sabes qué es el teflón?
El PVC es policloruro de vinilo. Está formado por carbono,
hidrógeno y cloro. Su monómero es el cloruro de vinilo (cloro-eteno): CH2 = CHCl. El teflón es un material plástico que
contiene flúor. Es duro, inerte y resiste temperaturas muy
altas. Se utiliza como recubrimiento de sartenes y cacerolas
para proporcionarles antiadherencia.
15 Pon ejemplos de fibras textiles sintéticas.
Poliamidas (nailon) y poliésteres (tergal y terilene).
PARA REFORZAR
16 ¿Por qué el CO2 hace posible la vida y el SiO2 no?
El CO2 es gaseoso, estable y soluble en agua, por lo que puede ser absorbido por las plantas y expelido por los animales.
En cambio, el SiO2 es sólido e insoluble en agua y, por tanto, no puede realizar los procesos biológicos que permite
el CO2.
73
12
17 Escribe tres isómeros de fórmula molecular C4H8.
1-buteno; 2-buteno; ciclobutano.
18 Escribe las fórmulas de los siguientes hidrocarburos:
a)
b)
c)
d)
e)
f)
2-metilhexano
2,2,4-trimetilpentano
1,3-butadieno
3-propil-1,4-pentadiino
1,2-dietilciclopenteno
1-etil-4-metilbenceno
a) CH3 – CH – CH2 – CH2 – CH2 – CH3
|
CH3
b)
CH3
|
CH3 – C – CH2 – CH – CH3
|
|
CH3
CH3
c) CH2 = CH – CH = CH2
d) CH ≡ C – CH – C ≡ CH
|
CH2 – CH2 – CH3
e)
CH2 CH3
CH2
f)
CH2
CH3
CH3
CH3
19 Escribe el nombre de los siguientes alcoholes:
a) CH2OH–CHOH– CHOH–CH2–CH2OH
b) CH3 –CH=CH–CH2OH
a) 1,2,3,5-pentanotetraol
b) 2-buten-1-ol
20 Escribe la reacción de fermentación de la glucosa
(C6H12O6) para obtener el vino.
C6H12O6 → 2 CH3 – CH2OH + 2 CO2
21 Nombra los siguientes ácidos orgánicos:
–
a) H–COOH
b) HOOC–COOH
COOH
c)
a) Ácido metanoico.
74
b) Ácido etanodioico.
c) Ácido benzoico.
22 ¿Por qué se avinagra el vino contenido en una botella abierta?
El etanol se transforma en ácido etanoico por acción del oxígeno del aire.
23 ¿Cuáles son las propiedades más importantes de
los plásticos? ¿Cuál es la principal materia prima que se
emplea en su fabricación?
Generalmente los plásticos se obtienen a partir de derivados
del petróleo. Sus propiedades más importantes son las siguientes: son poco densos, muy inertes desde el punto de vista químico, flexibles y aislantes de la corriente eléctrica y del calor.
24 ¿Por qué las botellas de agua se fabrican con PET y
no con PVC?
Por los problemas medioambientales que puede presentar
el policloruro de vinilo (PVC).
25 ¿Qué propiedades tienen los cauchos vulcanizados?
Son resistentes al rozamiento, no se ablandan con el calor y
son prácticamente insolubles.
26 ¿Cuál es la composición química de una grasa? ¿Qué
diferencia una grasa saturada de otra insaturada?
Las grasas contienen carbono, hidrógeno y oxígeno. Se forman por la unión de la glicerina (1,2,3-propanotriol) con los
ácidos grasos. Las grasas insaturadas contienen uno o más
dobles enlaces.
27 ¿Cuál es la composición química de las proteínas?
¿Por qué existe una cantidad tan grande de proteínas
diferentes?
Las proteínas son macromoléculas naturales que contienen
carbono, hidrógeno, oxígeno, nitrógeno y, a veces, azufre
y fósforo. Algunas contienen otros elementos como hierro,
cobre y cinc.
Aunque todas las proteínas se forman por la unión de unos
veinte aminoácidos diferentes, existe una gran cantidad de
proteínas diferentes, que se diferencian en el número de aminoácidos que contienen, la secuencia con que se unen y la
estructura espacial de la proteína.
EVALUACIÓN
1 ¿Cuál de las siguientes afirmaciones es verdadera?
a) Generalmente, el carbono presenta valencia tres, por
eso forma tres enlaces covalentes.
b) La fórmula molecular del butano es C4H10.
c) El hidrógeno es un combustible orgánico de gran
importancia.
d) El papel se fabrica a partir de la madera; por tanto,
no contiene carbono.
Respuesta correcta: b).
2 ¿Cuál de las siguientes afirmaciones es falsa?
a) El gas natural está formado principalmente por metano.
b) El gas que origina explosiones en las minas de carbón
es el metano, también llamado «grisú».
c) Los alcoholes no contienen carbono.
d) La gasolina es un derivado del petróleo y, por tanto,
es un producto que contiene carbono.
5 ¿Cuál de las siguientes afirmaciones es falsa?
a) Los plásticos son productos obtenidos artificialmente.
b) Muchos de los tejidos utilizados para fabricar nuestras prendas de vestir están hechos con fibras sintéticas.
c) La fórmula del ácido etanoico es CH3–COOH.
d) Las grasas contienen C, H, O y N.
Respuesta correcta: d).
6 ¿Cuáles de los siguientes compuestos orgánicos contienen oxígeno?
Respuesta correcta: c).
a)
b)
c)
d)
3 ¿Cuáles de las siguientes afirmaciones referidas al
átomo de carbono son verdaderas?
Todos menos b).
a) Tiene seis electrones.
b) Se toma como referencia para definir la unidad de
masa atómica.
c) Forma cadenas al unirse a otros átomos de carbono.
d) Forma cuatro enlaces covalentes, es decir, es tetravalente.
Todas son correctas.
4 ¿Cuál de las siguientes afirmaciones es falsa?
a) La fórmula del 2-propanol es CH2OH–CH2–CH3.
b El butano, utilizado como combustible, es un hidrocarburo.
c) El vinagre contiene un ácido orgánico: ácido etanoico.
d) El alcohol que compramos en las farmacias se denomina etanol.
Los alcoholes.
Los hidrocarburos aromáticos.
Los ácidos carboxílicos.
Las proteínas, los ácidos nucleicos y los hidratos de
carbono.
7 Las siguientes afirmaciones están referidas a los
polímeros o macromoléculas. Indica cuáles son verdaderas:
a) Sus moléculas son de gran tamaño y su masa molecular puede alcanzar millones de unidades de masa
atómica.
b) Las proteínas son macromoléculas naturales.
c) El teflón se utiliza en la fabricación de botellas para
agua y bebidas de refresco.
d) Los polímeros sintéticos se obtienen por unión de
moléculas sencillas llamadas monómeros.
Todas menos c).
Respuesta correcta: a).
75
13
LA FÍSICA Y LA QUÍMICA
EN EL MUNDO EN QUE VIVIMOS
EJERCICIOS
1 Busca en Internet o en una enciclopedia actualizada
alguna noticia o información que demuestre la influencia que una acción humana ejerce en otro lugar del planeta.
Respuesta libre. Dentro de las posibles respuestas, y siempre
buscando consecuencias que puedan alejarse más de 1 000
km del lugar en el que se han producido, se encuentran la
lluvia ácida, las contaminaciones de ríos y lagos, las nubes de
sustancias tóxicas o contaminantes, los vertidos de petróleo
por limpieza o hundimiento de buques, el traslado incontrolado de sustancias radiactivas, la contaminación marina, la
pesca incontrolada de especies marinas, las pruebas nucleares (hoy en día prácticamente inexistentes) la contaminación
por material de desecho de satélites de órbitas estratégicas
(geoestacionarias), etcétera.
2 Localiza el nombre de 5 gases de efecto invernadero.
Compara su índice de efectividad con el del CO2.
Los gases más importantes de efecto invernadero (GEI) son el
vapor de agua (H2O), el dióxido de carbono (CO2), el metano
(CH4), los óxidos de nitrógeno (NOx), el ozono (O3) y los halocarbonos (entre los que destaca el CFC). Si tomamos como
índice de referencia 1 la acción correspondiente al CO2, la
del metano es unas 25 veces superior, el N2O alrededor de
200 y los CFC de unos 15 000. Esto significa que un gramo de
CFC contribuye al calentamiento global tanto como 15 000
gramos de CO2.
El Protocolo de Kyoto sólo regula la composición atmosférica
del CO2, N2O, CH4, hidrofluorocarburos, perfluorocarburos y
hexafluoruro de azufre.
3 Busca en Internet o en una enciclopedia actualizada
distintas maneras que se proponen para tratar los residuos radiactivos que se producen en las centrales nucleares. ¿Crees que eliminarlos mandándolos al espacio
puede ser la solución?
Evidentemente, la solución no puede ser mandarlos al espacio ya que el índice de lanzamientos erróneos de naves
espaciales es muy alto y produciríamos una contaminación
elevadísima en el caso de una explosión en un lanzamiento
espacial. Todo ello sin contar con la responsabilidad de mandar un paquete de alta radiactividad al espacio.
El método más usado hoy en día es el almacenamiento en
bidones sellados con paredes que impiden el escape radiactivo, manteniéndolos en piscinas que refrigeran el calor
producido en las reacciones nucleares que se producen en
el interior. Se prevén almacenamientos geológicos en minas
de sal (las zonas más geoestables del planeta), pero todavía
no se han resuelto los problemas que plantean.
También hoy en día se opta por vitrificar los residuos con lo
que conseguimos que la radiactividad que emiten hacia el
exterior sea menor.
76
4 Localiza el nombre químico completo del DDT y su
fórmula semidesarrollada. Compárala con la Fig. 13.4.
¿Qué conclusiones eres capaz de obtener? ¿Con qué nombre se conocía anteriormente a este compuesto para que
su nombre se simplificara y le llamaran DDT?
El nombre completo es 1,1,1–tricloro–2,2–bis(4–clorofenil)etano y la fórmula semidesarrollada es:
Cl
Cl
C
Cl
CH
Cl
Cl
Las conclusiones que se pueden obtener de comparar ambas
fórmulas es que es un compuesto formado única y exclusivamente por carbono, cloro e hidrógeno con una estructura
simétrica y que es un derivado halogenado de un compuesto
aromático.
El nombre antiguo, y del que provienen las siglas DDT, es
dicloro–difenil–tricloroetano que evidentemente es un nombre incorrecto puesto que no da información sobre la forma
en que se unen los átomos y la estructura de la molécula.
EJERCICIOS PROPUESTOS
PARA REPASAR
1 ¿Existía el efecto invernadero antes del desarrollo
industrial? ¿Ha sido siempre pernicioso el efecto invernadero sobre la vida animal y vegetal?
Sí. El efecto invernadero está provocado por la presencia de
gases de efecto invernadero en la atmósfera y siempre han
estado allí. En Venus ocasiona que el planeta sea un lugar
inhabitable, mientras que en Marte, al no existir apenas, su
ausencia hace que sea un lugar muy frío.
En la Tierra contribuye a que la temperatura superficial sea
más homogénea y esté unos 30 ºC por encima de lo que por
nuestra distancia al Sol nos corresponde, por lo que no sólo
no ha sido siempre pernicioso sino que ha sido fundamental
para el desarrollo de la vida, por lo menos al ritmo que se ha
producido.
2 ¿Cuál es la razón por la que las moléculas de metano,
dióxido de carbono, óxidos de nitrógeno, agua y otras,
creen efecto invernadero y sin embargo no lo produzcan
gases como el nitrógeno o el oxígeno?
Para poder absorber las radiaciones infrarrojas, las moléculas
del gas tienen que tener momento bipolar en los enlaces o
globalmente. Por esta razón, la mayoría de los gases de efecto
invernadero son gases heteroatómicos, es decir, tienen distintos elementos dentro de la molécula. Los homoatómicos,
como el nitrógeno y el oxígeno, no presentan efecto inver-
nadero, salvo los que pueden presentar momento bipolar
molecular como es el caso del ozono (O3).
3 Menciona varios proyectos que intenten evitar el
efecto invernadero.
Para evitar el efecto invernadero se llegó a los acuerdos del
Protocolo de Kioto y de la Conferencia de Río, así como algunas decisiones en tratados intergubernamentales como
el de Maastricht.
En algunos países se prevé la eliminación de dióxido de carbono en minas, en yacimientos petrolíferos, la absorción
del metano de la atmósfera, y proyectos locales como el
proyecto Castor (danés), el Hypogen (europeo), el Futuregen
(norteamericano), o el MDL (Mecanismo para un Desarrollo
Limpio, muy desarrollado en países de América Latina), que
persiguen el mismo fin.
Por último hay multitud de proyectos que pretenden «arrojar» menos gases a la atmósfera, en vez de tener que pasar
por su eliminación posterior. Entre ellos está la utilización
de fuentes de energía no agresivas y el no utilizar o fabricar
gases de efecto invernadero, como los clorofluorocarbonos
en las neveras.
4 Comenta dos razones por las que los incendios forestales contribuyen a incrementar el efecto invernadero.
Al arder los árboles emiten a la atmósfera cantidades ingentes de vapor de agua y dióxido de carbono que son gases
de efecto invernadero. Por otro lado, la deforestación que
se produce elimina árboles que podrían absorber el CO2 que
hay en la atmósfera.
5 ¿Qué fuentes de energía, entre las que conoces, no
crean gases de efecto invernadero?
Las más importantes son la energía solar, la eólica, la geomotriz (los gases emitidos en algunos casos no son imputables
a la generación de energía sino a que la Tierra los emite de
forma natural), la nuclear (salvo por una pequeña cantidad
de vapor de agua), la mareomotriz y la hidroeléctrica.
6 ¿Qué es el Principio de precaución? ¿Desde cuándo
se valora la precaución como un procedimiento a tener
en cuenta en la resolución de problemas relacionados
con el medio ambiente?
El Principio de precaución indica que se deben tomar medidas de protección aunque no se tenga una certeza científica
absoluta sobre la existencia de daños graves o irreversibles. Se
enuncia en Río en 1992, y en el año 2000 se desarrolla por parte
de la Unión Europea. En el enlace http://europa.eu/scadplus/
leg/es/lvb/l32042.htm se puede encontrar más información.
7 Menciona varios casos en los que se haya utilizado el
Principio de precaución o en los que se haya estudiado si sería conveniente su utilización.
En la prohibición de la utilización del DDT, en el uso de transgénicos, en el transporte de mercancía peligrosas por mar y
por carretera, etc. Hay casos donde sin llegar a enunciarse su
utilización, se han aprobado medidas en ese sentido, como en
la utilización de antenas de telefonía móvil, en la presencia de
líneas de alta tensión cerca de núcleos urbanos, etcétera.
8 ¿Cuáles crees que serán las fuentes de energía que
se utilizarán principalmente en los próximos años?
A corto plazo, las mismas que ahora, pero a largo plazo se
prevé que se vayan sustituyendo por energías más limpias
como son la energía solar, la eólica, la geomotriz, la mareomotriz y la hidroeléctrica.
La utilización de la energía nuclear de fusión se convertirá sin
duda en la principal fuente de energía en cuanto su generación sea posible y su comercialización sea rentable.
9 Cita las ventajas y los incovenientes que tiene la utilización de la energía eólica, la hidroeléctrica y la biomasa como fuentes de energía.
La energía hidroeléctrica y la eólica son de las más limpias y
de las que no plantean problemas en cuanto a su renovación
por ser inagotables —mientras el Sol nos caliente, se podrán
utilizar, ya que dependen de él—. Plantean como principal
problema el que ocupan mucha superficie contaminando
visualmente (aerogeneradores) o la inhabilita por completo
(presas).
10 ¿Qué ventajas e inconvenientes tiene la utilización
de la energía nuclear como fuente de energía?
La energía de fusión nuclear (todavía en una fase muy primaria
de investigación) marcará el futuro, puesto que es también
muy limpia y además sus recursos se miden en millones de
años. No genera radiactividad (aunque transmite bastante calor residual) y utiliza hidrógeno (un elemento muy abundante
en la Tierra, ya que es un componente básico del agua).
Como inconvenientes principales encontramos el que todavía
está muy lejos de poderse comercializar (se calcula que será
posible en unos 50 años) y el hecho de que la construcción
de las centrales requerirá indudablemente un desembolso
económico altísimo, por lo que, al menos al principio, sólo
estará en manos de los países económicamente más desarrollados.
Respecto a la energía nuclear de fisión, la principal ventaja
es que no contribuye apenas al efecto invernadero. Y entre
las desventajas más importantes se encuentran el que utiliza
un combustible escaso y que genera residuos altamente radiactivos que resulta muy complicado almacenar.
11 ¿Qué ventajas e inconvenientes tiene la utilización de
las centrales térmicas como fuente de energía?
Como única ventaja casi podríamos decir que se encuentra el
hecho de que la tecnología asociada a ellas está ya comple-
77
13
tamente desarrollada y de que hoy en día pueden utilizarse
en cualquier lugar, prácticamente.
Como inconvenientes se encuentran la contaminación, el
coste del combustible, el efecto invernadero, la lluvia ácida,
la pérdida de recursos naturales que supone quemar el gas
y el petróleo, etcétera.
PARA REFORZAR
12 Busca en Internet algo sobre la teoría Gaia y el «mundo de margaritas» y comenta lo que piensas sobre ambas
teorías. ¿Crees que realmente es una teoría que se debe
tener en cuenta?
En la página web http://es.wikipedia.org/wiki/Hip%C3%
B3tesis_de_Gaia, de Wikipedia, se encuentra una descripción
suficientemente extensa y correcta de la hipótesis Gaia. En
cuanto al «mundo de margaritas», también se puede recurrir
a Wikipedia, http://es.wikipedia.org/wiki/Mundo_de_margaritas, donde también está suficientemente descrito.
13 Busca en Internet o en enciclopedias actualizadas
los porcentajes de reducción de emisión de gases de
efecto invernadero a los que se comprometieron los
países firmantes del Protocolo de Kioto y su nivel de
cumplimiento actual.
En principio, todos los gobiernos que participaron en el acuerdo (básicamente los países desarrollados) se comprometieron,
para el periodo 2008-2012, a reducir las emisiones medias anuales un 5 % por debajo de las correspondientes al año 1990.
La Unión Europea, en función de su nivel de desarrollo, recalculó este porcentaje entre los países miembros de la siguiente manera: Luxemburgo (–28 %), Alemania (–21 %), Dinamarca
(–21 %), Austria (–13 %), Reino Unido (–12,5 %), Bélgica (–7,5 %),
Italia (–6,5 %), Países Bajos (–6 %), Finlandia (0 %), Francia (0 %),
Suecia (+4 %), Irlanda (+13 %), España (+15 %), Grecia (+25 %)
y Portugal (+27 %).
14 Haz una crítica sobre la película Una verdad incómoda comentando los aspectos que consideras que son
aciertos de la película y aquellos que crees que son exageraciones no demostradas. Consulta otras fuentes para
aclarar las cosas que te planteen dudas.
78
El problema parece que ha entrado en vías de solución desde
que se prohibió la utilización de CFC en los refrigeradores y
aparatos de aire acondicionado, además de como propelente
de sustancias en los «sprays». También se prohibieron algunos fungicidas, como el bromuro de metilo.
En el Protocolo de Montreal se desarrolla toda la información
correspondiente a esta pregunta.
La página Web que contiene el Protocolo y las enmiendas
relacionadas con él es: http://ozone.unep.org/spanish/Ratification_status/evolution_of_mp.shtml.
16 ¿Cómo y en qué lugares se desprende CH4 hacia la
atmósfera? ¿Cuáles son debidos a la influencia humana?
En muchas partes. Como factores no dependientes del hombre, son principalmente los gases emitidos por la descomposición de materia orgánica (animales y vegetales muertos,
pantanos, aguas estancadas, etc.), en la digestión de los animales, y en algunas emisiones del interior de la Tierra por
encontrarse embolsado en capas permeables (por lo que
escapan de ellas).
Entre los creados por el hombre están los que escapan de las
extracciones de gas y petróleo, los subproductos de algunas
fábricas (aunque en estos casos se suele quemar o reutilizar
como combustible) y en algunas plantas de reproceso de
residuos.
17 Halla tres casos de contaminación extensa que se
hayan producido en nuestro planeta. Comenta, en la
medida de lo posible, de qué manera se podían haber
evitado.
Algunos ejemplos pueden ser la emisión de radiación de la
central nuclear de Chernóbil, el chapapote del Prestige, la rotura del Exxon Valdez, las emisiones en el Mar Mediterráneo,
las pruebas nucleares en distintos archipiélagos, etcétera.
18 Averigua por qué se hizo la reunión de Río de Janeiro
de 1992 y qué países intervinieron en ella.
Todo lo concerniente a dicha reunión, también conocida como Cumbre para la Tierra, se encuentra en http://es.wikipedia.
org/wiki/Cumbre_de_la_Tierra aunque hay más datos en la
versión inglesa http://en.wikipedia.org/wiki/Earth_Summit.
Respuesta libre. Sería interesante haber visto la película con
todo el grupo e intentar que las contestaciones den lugar a
un debate entre ellos sobre la veracidad y la peligrosidad real
de los problemas planteados en la película.
19 Busca, utilizando las fuentes que creas conveniente,
cómo funciona una planta depuradora de aguas residuales. Averigua también el nombre y ubicación de las más
importantes de tu Comunidad Autónoma.
15 Consulta en Internet o en enciclopedias actualizadas
qué gases fabricados por el hombre crearon el agujero en
la capa de ozono, para qué se utilizaban, por qué otras
sustancias se han sustituido y si el problema se ha resuelto, se está agravando o está en vías de solución.
Una extraordinaria página que contiene una información
detalladísima sobre este tema es http://www2.cbm.uam.es/
jalopez/personal/SeminariosVarios/ERARtexto.htm.
EVALUACIÓN
1 Elige, entre los siguientes problemas del mundo
actual, cuál de ellos no ha sido creado por el desarrollo
tecnológico e industrial del hombre:
a) El agujero en la capa de ozono.
b) Las reservas de especies animales.
c) Los terremotos y tsunamis.
d) El incremento del efecto invernadero.
Respuesta correcta: c).
2 Elige de esta lista los gases que crean y los que no
crean efecto invernadero:
a)
b)
c)
d)
CO2, O2 y CH4 sí lo crean. N2 y NO2 no lo crean.
CO2, NO2 y CH4 sí lo crean. N2 y O2 no lo crean.
CO2 y CH4 no lo crean. N2 y O2 sí lo crean.
CO2, O2, CH4, N2 y NO2 sí lo crean.
Respuesta correcta: b).
3 El Protocolo de Kioto pretende evitar el cambio
climático mediante:
a) La prohibición de la emisión de gases de efecto invernadero.
b) La reducción en la emisión de gases de efecto invernadero por parte de todos los países.
c) La prohibición de la emisión de gases de efecto invernadero de los países subdesarrollados.
d) La reducción en la emisión de gases de efecto invernadero por parte de los países desarrollados.
Respuesta correcta: d).
4 El Protocolo de Kioto se está cumpliendo:
a) Por casi todos los países, y ya se notan sus efectos
positivos.
b) Sólo por los países europeos, pero puede que sea
suficiente.
c) No se está cumpliendo.
d) Se está cumpliendo aproximadamente y estamos
optimistas de cara al futuro.
Respuesta correcta: c).
5 La contaminación en el mundo actual:
a) Es un problema que se va globalizando.
b) Es un problema casi resuelto en todos los países.
c) Es un problema resuelto en los países industrializados.
d) Es un problema local, y la contaminación de cada país
es cosa suya.
Respuesta correcta: a).
6 Cuando se prohíbe la utilización de una sustancia:
a) Ya está todo dicho. Es mala y se evita su uso.
b) Debemos seguir estudiando si los problemas que
creaba eran mayores o menores que las ventajas que
aportaba.
c) Debemos volver a usarla, si así el país avanza económicamente.
d) Debemos dejar de fabricarla, pero utilizar la que
crean otros países.
Respuesta correcta: b).
7 El Principio de precaución consiste:
a) En no cruzar la calle si pasan vehículos.
b) En no arriesgar creando una central eléctrica si no se
tiene los recursos necesarios.
c) En prohibir la utilización de cualquier nuevo producto.
d) En poder restringir el uso de algún recurso o sustancia sobre la que existen dudas sobre sus posibles
riesgos.
Respuesta correcta: d).
79
A
ForMulaciÓn Y noMEnclaTura
DE coMPuESToS inorGÁnicoS
EJERCICIOS
1
Fórmula o nombre
80
Fórmula
Tradicional
Stock o sistemática
simplificada
Sistemática
1. Mn2O7
Mn2O7
óxido permangánico
óxido de manganeso(VII)
heptaóxido de dimanganeso
2. Yoduro de plomo(IV)
PbI4
yoduro plúmbico
yoduro de plomo(IV)
tetrayoduro de plomo
3. Óxido de potasio
K 2O
óxido potásico
óxido de potasio
óxido de potasio
4. BH3
BH3
borano
hidruro de boro(III)
hidruro de boro
5. Li2O
Li2O
óxido lítico
óxido de litio
henióxido de litio
6. KI
KI
yoduro potásico
yoduro de potasio
yoduro de potasio
7. Dióxido de carbono
CO2
óxido carbónico
óxido de carbono(IV)
dióxido de carbono
8. Cloruro de bario
BaCl2
cloruro bárico
cloruro de bario
cloruro de bario
9. CuO
CuO
óxido cúprico
óxido de cobre(II)
óxido de monocobre
10. Sulfuro de platino(IV)
PtS2
sulfuro platínico
sulfuro de platino(IV)
disulfuro de platino
11. PbO2
PbO2
óxido plúmbico
óxido de plomo(IV)
dióxido de plomo
12. CuH2
CuH2
hidruro cúprico
hidruro de cobre(II)
dihidruro de cobre
13. CuCl2
CuCl2
cloruro cúprico
cloruro de cobre(II)
dicloruro de cobre
14. NH3
NH3
amoniaco
hidruro de nitrógeno(III)
trihidruro de nitrógeno
15. Hg2O
Hg2O
óxido mercurioso
óxido de mercurio(I)
óxido de dimercurio
16. SnH2
SnH2
hidruro estañoso
hidruro de estaño(II)
dihidruro de estaño
17. Triyoduro de cromo
CrI3
yoduro crómico
yoduro de cromo(III)
triioduro de cromo
18. H2Se
H2Se
seleniuro de hidrógeno
19. SnH4
SnH4
hidruro estáñico
hidruro de estaño(IV)
tetrahidruro de estaño
20. Hidruro de magnesio
MgH2
hidruro magnésico
hidruro de magnesio
hidruro de magnesio
21. Fe3O4
Fe3O4
óxido ferroso-férrico
óxido de hierro(II)hierro(III)
tetraóxido de trihierro
22. FeH2
FeH2
hidruro ferroso
hidruro de hierro(II)
dihidruro de hierro
23. CaS
CaS
sulfuro cálcico
sulfuro de calcio
sulfuro de calcio
24. Tribromuro de fósforo
PBr3
bromuro fosforoso
bromuro de fósforo(III)
tribromuro de fósforo
25. SiH4
SiH4
silano
hidruro de silicio
tetrahidruro de silicio
26. Óxido de bario
BaO
óxido bárico
óxido de bario
óxido de bario
27. Ácido selenhídrico
H2Se(aq)
á. selenhídrico
28. P2O5
P2O5
óxido fosfórico
óxido de fósforo(V)
pentaóxido de difósforo
29. RbH
RbH
hidruro rubídico
hidruro de rubidio
hidruro de rubidio
30. Estibina
SbH3
estibina
hidruro de antimonio
trihidruro de antimonio
31. Bromuro de cadmio
CdBr2
bromuro cádmico
bromuro de cadmio
bromuro de cadmio
32. Ag2O
Ag2O
óxido argéntico
óxido de plata
óxido de plata
33. SO3
SO3
óxido sulfúrico
óxido de azufre(VI)
trióxido de azufre
34. Hidruro de estaño(IV)
SnH4
hidruro estáñico
hidruro de estaño(IV)
tetrahidruro de estaño
35. BaCl2
BaCl2
cloruro bárico
cloruro de bario(II)
cloruro de bario
36. Cu(OH)2
Cu(OH)2
hidróxido cúprico
hidróxido de cobre(II)
dihidróxido de cobre
37. NaI
NaI
yoduro sódico
yoduro de sodio
yoduro de sodio
38. AsH3
AsH3
arsina
hidruro de arsénico(III)
hidruro de arsénico
seleniuro de hidrógeno
seleniuro de hidrógeno
Fórmula o nombre
Fórmula
Tradicional
Stock o sistemática
simplificada
Sistemática
39. CoCl2
CoCl2
cloruro cobaltoso
cloruro de cobalto(II)
dicloruro de cobalto
40. Óxido de cromo(III)
Cr2O3
óxido crómico
óxido de cromo(III)
trióxido de dicromo
41. Cloruro de estroncio
SrCl2
cloruro estróncico
cloruro de estroncio
cloruro de estroncio
42. Sulfuro de hidrógeno
H2S
sulfuro de hidrógeno
43. PbH2
PbH2
hidruro plumboso
hidruro de plomo(II)
dihidruro de plomo
44. Dióxido de azufre
SO2
óxido sulfuroso
óxido de azufre(IV)
dióxido de azufre
45. Cr2O3
Cr2O3
óxido crómico
óxido de cromo(III)
trióxido de dicromo
46. Peróxido de rubidio
Rb2O2
peróxido rubídico
peróxido de rubidio
dióxido de dirubidio
47. MnBr2
MnBr2
bromuro manganoso
bromuro de
manganeso(II)
dibromuro de manganeso
48. CoO
CoO
óxido cobaltoso
óxido de cobalto(II)
monóxido de cobalto
49. Peróxido de hidrógeno
H2O2
agua oxigenada
peróxido de hidrógeno
dióxido de dihidrógeno
50. CoH3
CoH3
hidruro cobáltico
hidruro de cobalto(III)
trihidruro de cobalto
51. Ni2O3
Ni2O3
óxido niquélico
óxido de níquel(III)
trióxido de diníquel
52. Bromuro de hidrógeno
HBr
bromuro de hidrógeno
53. Peróxido de plata
Ag2O2
peróxido argéntico
peróxido de plata
dióxido de diplata
54. Óxido de estaño(IV)
SnO2
óxido estáñico
óxido de estaño(IV)
dióxido de estaño
55. Fluoruro de aluminio
AlF3
fluoruro alumínico
fluoruro de aluminio
fluoruro de aluminio
56. CaO2
CaO2
peróxido cálcico
peróxido de calcio
dióxido de calcio
57. BaH2
BaH2
hidruro bárico
hidruro de bario
dihidruro de bario
58. Sulfuro de magnesio
MgS
sulfuro magnésico
sulfuro de magnesio
sulfuro de magnesio
59. Pentabromuro de
fósforo
PBr5
bromuro fosfórico
bromuro de fósforo(V)
pentabromuro de fósforo
60. PbS2
PbS2
sulfuro plúmbico
sulfuro de plomo(IV)
disulfuro de plomo
61. Dióxido de selenio
SeO2
óxido selenioso
óxido de selenio(IV)
dióxido de selenio
62. HgO
HgO
óxido mercúrico
óxido de mercurio(II)
óxido de mercurio
63. Cu2Te
Cu2Te
telururo cuproso
telururo de cobre(I)
telururo de dicobre
64. Cl2O7
Cl2O7
óxido perclórico
óxido de cloro(VII)
heptaóxido de dicloro
65. ZnO
ZnO
óxido cíncico
óxido de cinc
monóxido de cinc
66. FeN
FeN
nitruro férrico
nitruro de hierro(III)
nitruro de hierro
67. As2O5
As2O5
óxido arsénico
óxido de arsénico(V)
pentaóxido de diarsénico
68. Óxido de calcio
CaO
óxido cálcico
óxido de calcio
óxido de calcio
69. ZnI2
ZnI2
yoduro cíncico
yoduro de cinc
diyoduro de cinc
70. Seleniuro de aluminio
Al2Se3
seleniuro alumínico
seleniuro de aluminio
sesquiseleniuro de aluminio
71. Monosulfuro de
dihidrógeno
H2S
sulfuro de hidrógeno
72. MgO
MgO
óxido magnésico
óxido de magnesio
óxido de magnesio
73. Ditelururo de platino
PtTe2
telururo platínico
telururo de platino(IV)
ditelururo de platino
74. CoS
CoS
sulfuro cobaltoso
sulfuro de cobalto(II)
monosulfuro de cobalto
75. CH4
CH4
metano
hidruro de carbono
tetrahidruro de carbono
76. ZnO2
ZnO2
peróxido cíncico
peróxido de cinc(II)
dióxido de cinc
77. Óxido cobaltoso
CoO
óxido cobaltoso
óxido de cobalto(II)
monóxido de cobalto
78. Óxido áurico
Au2O3
óxido áurico
óxido de oro(III)
trióxido de dioro
sulfuro de hidrógeno
bromuro de hidrógeno
sulfuro de hidrógeno
81
A
2
Fórmula o nombre
82
Fórmula
Tradicional
Stock o sistemática
simplificada
hidróxido de litio
Sistemática
1. Hidróxido lítico
LiOH
hidróxido lítico
hidróxido de litio
2. Telurito cuproso
Cu2TeO3
telurito cuproso
3. H3BO3
H3BO3
á. ortobórico
4. Oxoclorato(I) de calcio
Ca(ClO)2
hipoclorito cálcico
5. H2Cr2O7
H2Cr2O7
á. dicrómico
6. Trioxocarbonato de
plomo(II)
PbCO3
carbonato plumboso
trioxocarbonato de plomo(II)
7. Telurito cúprico
CuTeO3
telurito cúprico
trioxotelurato(IV) de cobre(II)
8. H2SO4
H2SO4
á. sulfúrico
9. Ni2P2O7
Ni2P2O7
pirofosfato niqueloso
10. Hidróxido de plomo(IV)
Pb(OH)4
hidróxido plúmbico
11. Cromato mercurioso
Hg2CrO4
cromato mercurioso
tetraoxocromato(VI) de mercurio(I)
12. Clorato cálcico
Ca(ClO3)2
clorato cálcico
trioxoclorato(V) de calcio
13. Zn(MnO4)2
Zn(MnO4)2
permanganato cíncico
tetraoxomanganato(VII) de cinc
14. Á. dicrómico
H2Cr2O7
á. dicrómico
á. heptaoxodicrómico(VI)
heptaoxodicromato(VI) de
hidrógeno
15. Á. selénico
H2SeO4
á. selénico
á. tetraoxoselénico(VI)
tetraoxoseleniato(VI) de
hidrógeno
16. Hipoclorito cálcico
Ca(ClO)2
hipoclorito cálcico
oxoclorato(I) de calcio
17. K2Cr2O7
K2Cr2O7
dicromato potásico
heptaoxodicromato(VI) de potasio
18. Á. hexaoxoyódico(VII)
H5IO6
á. ortoperyódico
á. hexaoxoyódico(VII)
hexaoxoyodato(VII) de hidrógeno
19. H4P2O7
H4P2O7
á. pirofosfórico
á. heptaoxodifosfórico(V)
heptaoxodifosfato(V) de
hidrógeno
20. Fe(ClO2)2
Fe(ClO2)2
clorito ferroso
21. Hidróxido de plata
AgOH
hidróxido argéntico
hidróxido de plata
hidróxido de plata
22. HClO
HClO
á. hipocloroso
á. oxoclórico(I)
oxoclorato(I) de hidrógeno
23. Perclorato plumboso
Pb(ClO4)2
perclorato plumboso
24. Á. trioxosulfúrico(IV)
H2SO3
á. sulfuroso
25. Hipoclorito bárico
Ba(ClO)2
hipoclorito bárico
oxoclorato(I) de bario
26. Ni3(PO4)2
Ni3(PO4)2
fosfato niqueloso
tetraoxofosfato(V) de níquel(II)
27. Cu2SO4
Cu2SO4
sulfato cuproso
tetraoxosulfato(VI) de cobre(I)
28. H2SO3
H2SO3
á. sulfuroso
29. Al4(As2O7)3
Al4(As2O7)3
piroarseniato alumínico
30. Ba(NO3)2
Ba(NO3)2
nitrato bárico
31. Hidróxido áurico
Au(OH)3
hidróxido áurico
32. Al2(SiO3)3
Al2(SiO3)3
silicato alumínico
trioxosilicato de aluminio
33. SnSeO3
SnSeO3
selenito estañoso
trioxoseleniato(IV) de estaño(II)
34. HClO4
HClO4
á. perclórico
35. Ortofosfato férrico
FePO4
fosfato férrico
tetraoxofosfato(V) de hierro(III)
36. Na2SiO3
Na2SiO3
silicato sódico
trioxosilicato(IV) de sodio
trioxotelurato(IV) de cobre(I)
á. trioxobórico(III)
trioxoborato(III) de hidrógeno
oxoclorato(I) de calcio
á. heptaoxodicrómico(VI)
á. tetraoxosulfúrico(VI)
heptaoxodicromato(VI) de
hidrógeno
tetraoxosulfato(VI) de hidrógeno
heptaoxodiarseniato(V) de
níquel(II)
hidróxido de plomo(IV)
tetrahidróxido de plomo
dioxoclorato(III) de hierro(II)
tetraoxoclorato(VII) de plomo(II)
á. trioxosulfúrico(IV)
á. trioxosulfúrico(IV)
trioxosulfato(IV) de hidrógeno
trioxosulfato(IV) de hidrógeno
heptaoxodiarseniato(V) de
aluminio(III)
trioxonitrato(V) de bario
hidróxido de oro(III)
á. tetraoxoclórico (VII)
trihidróxido de oro
tetraoxoclorato(VII) de hidrógeno
Fórmula o nombre
Fórmula
Tradicional
Stock o sistemática
simplificada
Sistemática
37. Arseniato sódico
Na3AsO4
arseniato sódico
tetraoxoarseniato(V) de sodio
38. Ba3(AsO4)2
Ba3(AsO4)2
arseniato bárico
tetraoxoarseniato(V) de bario
39. H3PO4
H3PO4
á. fosfórico
40. Telurito estannoso
SnTeO3
telurito estañoso
41. Á. sulfuroso
H2SO3
á. sulfuroso
42. Fosfato férrico
FePO4
fosfato férrico
43. Cu(OH)2
Cu(OH)2
hidróxido cúprico
hidróxido de cobre(II)
dihidróxido de cobre
44. Á. fosforoso
H3PO3
á. fosforoso
á. trioxofosfórico(III)
trioxofosfato(III) de hidrógeno
45. HNO3
HNO3
á. nítrico
á. trioxonítrico(V)
trioxonitrato(V) de hidrógeno
46. KOH
KOH
hidróxido potásico
hidróxido de potasio
hidróxido de potasio
47. Hg(OH)2
Hg(OH)2
hidróxido mercúrico
hidróxido de mercurio(II)
dihidróxido de mercurio
48. Á. trioxofosfórico(V)
HPO3
á. metafosfórico
á. trioxofosfórico(V)
trioxofosfato(V) de hidrógeno
49. Sn(OH)4
Sn(OH)4
hidróxido estáñico
hidróxido de estaño(IV)
tetrahidróxido de estaño
50. Sulfato de cinc
ZnSO4
sulfato cíncico
51. Á. trioxotelúrico(IV)
H2TeO3
á. teluroso
á. trioxotelúrico (IV)
trioxotelurato(IV) de hidrógeno
52. HBrO2
HBrO2
á. bromoso
á. dioxobrómico(III)
dioxobromato(III) de hidrógeno
53. Ca3(PO4)2
Ca3(PO4)2
fosfato cálcico
tetraoxofosfato(V) de calcio
54. Tetraoxoarseniato(V) de
cinc
Zn3(AsO4)2
arseniato cíncico
tetraoxoarseniato(V) de cinc
55. Permanganato lítico
LiMnO4
permanganato lítico
tetraoxomanganato(VII) de litio
56. Á. yodoso
HIO2
á. yodoso
57. Piroarsenito ferroso
Fe2As2O5
piroarsenito ferroso
58. Á. piroarsenioso
H4As2O5
á. piroarsenioso
59. Sulfito crómico
Cr2(SO3)3
sulfito crómico
trioxosulfato(IV) de cromo(III)
60. Trioxoseleniato(IV) de
cesio
Cs2SeO3
selenito césico
trioxoseleniato(IV) de cesio
á. tetraoxofosfórico(V)
tetraoxofosfato(V) de hidrógeno
trioxotelurato(IV) de estaño(II)
á. trioxosulfúrico(IV)
trioxosulfato(IV) de hidrógeno
tetraoxofosfato(V) de hierro(III)
tetraoxosulfato(VI) de cinc
á. dioxoyódico(III)
dioxoyodato(III) de hidrógeno
pentaoxodiarseniato(III) de
hierro(II)
á. pentaoxodiarsénico(III)
pentaoxodiarseniato(III) de
hidrógeno
3
Fórmula o nombre
Fórmula
Tradicional
Stock o sistemática
simplificada
Sistemática
1. Metafosfato plumboso
Pb(PO3)2
metafosfato plumboso
trioxofosfato(V) de plomo(II)
2. Á. sulfúrico
H2SO4
á. sulfúrico
á. tetraoxosulfúrico(VI)
tetraoxosulfato(VI) de hidrógeno
3. H3AsO3
H3AsO3
á. arsenioso
á. trioxoarsénico(III)
trioxoarseniato(III) de hidrógeno
4. CuOH
CuOH
hidróxido cuproso
hidróxido de cobre(I)
monohidróxido de cobre
5. H2SeO4
H2SeO4
á. selénico
á. tetraoxoselénico(VI)
tetraoxoseleniato(VI) de
hidrógeno
6. Á. trioxocarbónico
H2CO3
á. carbónico
á. trioxocarbónico
trioxocarbonato de hidrógeno
7. Carbonato crómico
Cr2(CO3)3
carbonato crómico
8. Pb(PO3)2
Pb(PO3)4
metafosfato plúmbico
9. Hidróxido bismútico
Bi(OH)3
hidróxido bismútico
10. Pb(SeO4)2
Pb(SeO4)2
seleniato plumboso
tetraoxoseleniato(VI) de plomo(II)
11. CuCrO4
CuCrO4
cromato cúprico
tetraoxocromato(VI) de cobre(II)
trioxocarbonato(IV) de cromo(III)
trioxofosfato(V) de plomo(IV)
hidróxido de bismuto
trihidróxido de bismuto
83
A
Fórmula o nombre
Fórmula
Tradicional
Stock o sistemática
simplificada
Sistemática
12. Tetraoxofosfato(V) de
aluminio
AlPO4
fosfato alumínico
tetraoxofosfato(V) de aluminio
13. Ba(OH)2
Ba(OH)2
hidróxido bárico
hidróxido de bario
hidróxido de bario
14. Á. pirofosfórico
H4P2O7
á. pirofosfórico
á. heptaoxodifosfórico(V)
heptaoxodifosfato(V) de
hidrógeno
15. Pb(OH)4
Pb(OH)4
hidróxido plúmbico
hidróxido de plomo(IV)
tetrahidróxido de plomo
16. AlPO4
AlPO4
fosfato alumínico
17. H3PO3
H3PO3
á. fosforoso
18. Carbonato potásico
K2CO3
carbonato potásico
trioxocarbonato(IV) de potasio
19. Sulfato de potasio
K2SO4
sulfato potásico
tetraoxosulfato(VI) de potasio
20. Fe2(SO4)3
Fe2(SO4)3
sulfato férrico
tetraoxosulfato(VI) de hierro(III)
21. ZnMnO4
ZnMnO4
manganato cíncico
tetraoxomanganato(VI) de cinc
22. Clorato mercúrico
Hg(ClO3)2
clorato mercúrico
trioxoclorato(V) de mercurio(II)
23. Perbromato plúmbico
Pb(BrO4)4
perbromato plúmbico
tetraoxobromato(VII) de plomo(IV)
24. Á. carbónico
H2CO3
á. carbónico
25. Perclorato potásico
KClO4
perclorato potásico
tetraoxoclorato(VII) de potasio
26. Telurato bismútico
Bi2(TeO4)3
telurato bismútico
tetraoxotelurato(VI) de bismuto
27. H2TeO4
H2TeO4
á. telúrico
á. tetraoxotelúrico(VI)
tetraoxotelurato(VI) de hidrógeno
28. Á. telúrico
H2TeO4
á. telúrico
á. tetraoxotelúrico(VI)
tetraoxotelurato(VI) de hidrógeno
29. Á. hipocloroso
HClO
á. hipocloroso
á. oxoclórico(I)
oxoclorato(I) de hidrógeno
30. Tetraoxomanganato (VI)
de sodio
Na2MnO4
manganato sódico
tetraoxomanganato(VI) de sodio
31. Metafosfato alumínico
Al(PO3)3
metafosfato alumínico
trioxofosfato(V) de aluminio
32. Ortoborato magnésico
Mg3(BO3)2
ortoborato magnésico
trioxoborato(III) de magnesio
33. Á. tetraoxoyódico(VII)
HIO4
á. peryódico
á. tetraoxoyódico(VII)
tetraoxoyodato(VII) de hidrógeno
34. Á. bromoso
HBrO2
á. bromoso
á. dioxobrómico(III)
dioxobromato(III) de hidrógeno
35. Hidróxido de bario
Ba(OH)2
hidróxido bárico
hidróxido de bario
hidróxido de bario
36. Á. fluorhídrico
HF(aq)
á. fluorhídrico
tetraoxofosfato(V) de aluminio
á. trioxofosfórico(III)
á. trioxocarbónico
trioxofosfato(III) de hidrógeno
trioxocarbonato de hidrógeno
fluoruro de hidrógeno
EJERCICIOS PROPUESTOS
Fórmula o nombre
84
Fórmula
Tradicional
Stock o sistemática
simplificada
óxido de arsénico(V)
Sistemática
As2O5
As2O5
óxido arsénico
Arseniato auroso
Au3AsO4
arseniato auroso
tetraoxoarseniato(V) de oro(I)
Sulfito crómico
Cr2(SO3)3
sulfito crómico
trioxosulfato(IV) de cromo(III)
ZnS
ZnS
sulfuro cíncico
Ag2SiO3
Ag2SiO3
silicato argéntico
Óxido de antimonio(III)
Sb2O3
óxido antimonioso
óxido de antimonio(III)
trióxido de diantimonio
Óxido de potasio
K 2O
óxido potásico
óxido de potasio
óxido de potasio
Tetrahidróxido de platino
Pt(OH)4
hidróxido platínico
hidróxido de platino(IV)
tetrahidróxido de platino
Yoduro de oro(III)
AuI3
yoduro áurico
yoduro de oro(III)
triyoduro de oro
Cloruro de hidrógeno
HCl
cloruro de hidrógeno
sulfuro de cinc(II)
pentaóxido de diarsénico
sulfuro de cinc
trioxosilicato de plata
cloruro de hidrógeno
Fórmula o nombre
Fórmula
Tradicional
Stock o sistemática
simplificada
yoduro de cobre(I)
Sistemática
CuI
CuI
yoduro cuproso
monoyoduro de cobre
Ni3(PO4)2
Ni3(PO4)2
fosfato niqueloso
tetraoxofosfato(V) de níquel(II)
Seleniato cobaltoso
CoSeO4
seleniato cobaltoso
tetraoxoseleniato(VI) de cobalto(II)
Sulfato de potasio
K2SO4
sulfato potásico
tetraoxosulfato(VI) de potasio
Monóxido de calcio
CaO
óxido cálcico
óxido de calcio(II)
óxido de calcio
ZnI2
ZnI2
yoduro cíncico
yoduro de cinc
diyoduro de cinc
Nitrato argéntico
AgNO3
nitrato argéntico
Á. nitroso
HNO2
á. nitroso
á. dioxonítrico(III)
dioxonitrato(III) de hidrógeno
HBrO4
HBrO4
á. perbrómico
á. tetraoxobrómico(VII)
tetraoxobromato(VII) de hidrógeno
CuClO3
CuClO3
clorato cuproso
FeN
FeN
nitruro férrico
Perclorato cádmico
Cd(ClO4)2
perclorato cádmico
tetraoxoclorato(VII) de cadmio
Carbonato cuproso
Cu2CO3
carbonato cuproso
trioxocarbonato(IV) de cobre(I)
Co(ClO)2
Co(ClO)2
hipoclorito cobaltoso
oxoclorato(I) de cobalto(II)
Ag2O
Ag2O
óxido argéntico
óxido de plata
óxido de plata
CaO
CaO
óxido cálcico
óxido de calcio
monóxido de calcio
H3AsO3
H3AsO3
á. arsenioso
á. trioxoarsénico(III)
trioxoarseniato(III) de hidrógeno
Sesquióxido de cobalto
Co2O3
óxido cobáltico
óxido de cobalto(III)
sesquióxido de cobalto
H2S2O7
H2S2O7
á. disulfúrico
á. heptaoxodisulfúrico(VI) heptaoxodisulfato(VI) de hidrógeno
PbS2
PbS2
sulfuro plúmbico
sulfuro de plomo(IV)
Dicromato plumboso
PbCr2O7
dicromato plumboso
Peróxido de hidrógeno
H2O2
agua oxigenada
peróxido de hidrógeno
dióxido de dihidrógeno
Hg(OH)2
Hg(OH)2
hidróxido mercúrico
hidróxido de mercurio(II)
dihidróxido de mercurio
HBrO3
HBrO3
á. brómico
á. trioxobrómico(V)
trioxobromato(V) de hidrógeno
Telururo de dihidrógeno
H2Te
telururo de hidrógeno
Ni2O3
Ni2O3
óxido niquélico
óxido de níquel(III)
trióxido de diníquel
ZnO
ZnO
óxido cíncico
óxido de cinc
monóxido de cinc
H2CrO4
H2CrO4
á. crómico
á. tetraoxocrómico(VI)
tetraoxocromato(VI) de hidrógeno
HBr
HBr
bromuro de hidrógeno
Óxido de calcio
CaO
óxido cálcico
Á. clorhídrico
HCl(aq)
á. clorhídrico
Peróxido de rubidio
Rb2O2
peróxido rubídico
peróxido de rubidio
dióxido de dirubidio
Tetrahidruro de plomo
PbH4
hidruro plúmbico
hidruro de plomo(IV)
tetrahidruro de plomo
Sn(OH)2
Sn(OH)2
hidróxido estañoso
hidróxido de estaño(II)
dihidróxido de estaño
Telurato bismútico
Bi2(TeO4)3
telurato bismútico
Á. pirofosfórico
H4P2O7
á. pirofosfórico
FeCO3
FeCO3
carbonato ferroso
Hidruro de níquel(II)
NiH2
hidruro niqueloso
Carbonato potásico
K2CO3
carbonato potásico
trioxocarbonato(IV) de potasio
Pb(SeO4)2
Pb(SeO4)2
seleniato plumboso
tetraoxoseleniato(VI) de plomo(IV)
trioxonitrato(V) de plata
trioxoclorato(V) de cobre(I)
nitruro de hierro(III)
nitruro de hierro
disulfuro de plomo
heptaoxodicromato(VI) de
plomo(II)
telururo de dihidrógeno
bromuro de hidrógeno
óxido de calcio
óxido de calcio
cloruro de hidrógeno
tetraoxotelurato(VI) de bismuto
á. heptaoxodifosfórico(V)
heptaoxodifosfato(V) de
hidrógeno
trioxocarbonato(IV) de hierro(II)
hidruro de níquel(II)
dihidruro de níquel
85
Solucionario
GUÍA
DIDÁCTICA
I
inTroDucciÓn:
MEDiDaS Y MÉToDo ciEnTÍFico
ACTIVIDAD DE
AMPLIACIÓN PÁG. 31
1 Comprueba que en los dos lados de la igualdad que
representa las siguientes fórmulas físicas, la ecuación de
dimensiones y por tanto las magnitudes que utilizamos,
es equivalente.
J
1 kg
· 4 180
· (–27,4 ºC) =
1000 g
kg ºC
a) e = e0 + v t
b) m g h = 1/2 m v2
c) ac = v2/R
Q = 200 g
a) [e] = L ; [v] = L/T = L T–1 ; [t] = T
[e] = [e0] + [v] · [t]
L = L + L T–1 · T = L + L ; es coherente.
b) [m] = M ; [g] = L/T2 = L T–2 ; [h] = L ; [v] = L/T = L T–1
[m] [g] [h] = [1/2] [m] [v]2
M · L T–2 · L = M · (L T–1)2 = M L2 T–2 ; es coherente.
c) [ac] = L/T2 = L T–2 ; [v] = L/T = L T–1 ; [R] = L
[a] = [v]2/[R]
L T–2 = (L T–1)2/L = L2 T–2 · L–1 = L T–2 ; es coherente.
ACTIVIDAD DE
AMPLIACIÓN PÁG. 35
= –22 906,4 J = –2,29 · 104 J
ACTIVIDAD DE REFUERZO
PÁG. 32
1 Escribe los siguientes números en notación científica, anulando siempre los ceros a la derecha. Luego di
cuántas cifras significativas tienen y redondéalos para
que tengan 4 cifras significativas: 2 348,457 046 00;
0,003 460 02; 13 800 000; 67,342 0182; 252 525,252 525 y
0,000 000 02.
2 348,457 046
2,348 457 046 · 103
10 CS
2 348
346 082 · 10
6 CS
0,003 461
13 800 000
1,38 · 107
3 CS
No se
puede
67,345 018 2
6,734 501 82 · 101
9 CS
67,35
252 525,252 525
2,525 252 525 25 · 105
12CS
2,525 · 105
0,000 000 02
2 · 10–8
1CS
No se
puede
0,003 460 82
–3
ACTIVIDAD DE REFUERZO
PÁG. 33
1 Calcula la cantidad de calor desprendido (Q) por un
recipiente con 200 g de agua, cuando desciende su temperatura desde 39,52 ºC hasta 12,1 ºC. Utiliza la fórmula
Q = m ce (Tf – T0) donde ce es una constante llamada calor
específico que para el agua vale 4 180,0 J/kg ºC. Hazlo utilizando los criterios de redondeo que has aprendido.
88
Primero hallamos la diferencia de temperaturas teniendo en
cuenta que la temperatura final sólo la sabemos con precisión a las décimas.
Tf – T0 = 12,1 ºC – 39,5 ºC = –27,4 ºC
A la hora de multiplicar y dividir, el número con menos cifras
significativas tiene 3 (la masa y la temperatura), por lo que
sólo debemos poner 4 cifras en el número que más tenga.
Q = m ce (Tf – T0)
1 Elige un aparato de medida de la lista anterior y busca en Internet o en una enciclopedia actualizada cómo
funciona, qué magnitud mide, si es analógico o digital,
cómo está hecho y una fotografía y haz un pequeño trabajo (no más de dos páginas) con lo que hayas encontrado.
Respuesta libre. El profesor debería comentar en clase los
aparatos más interesantes que hayan elegido.
ACTIVIDAD DE REFUERZO
PÁG. 36
1 Busca bibliografía que relacione la altura desde la
que cae un objeto y el tiempo que tarda en caer. Se trata
de que veas cómo un científico encuentra información.
Probablemente encuentres que ya está establecida la
ley que relaciona el tiempo que un objeto tarda en caer
con la altura desde la que cae.
Respuesta libre.
ACTIVIDAD DE REFUERZO
PÁG. 37
1 Observa un guión de prácticas de laboratorio y
propón qué cambiarías para que se ajustara más al modelo de informe científico.
Respuesta libre.
El MoViMiEnTo DE loS cuErPoS
1
ACTIVIDAD DE REFUERZO
PÁG. 41
ACTIVIDAD DE
AMPLIACIÓN PÁG. 44
1 Pon un ejemplo de movimiento que se dé en la vida
real que tenga una trayectoria:
1 Dos trenes salen al mismo tiempo de Madrid y de Sevilla. El tren que sale de Madrid hacia Sevilla es un correo
que circula a una velocidad media de 110 km/h, mientras
que el que sale de Sevilla hacia Madrid es el AVE, que
circula a una velocidad media de 250 km/h. Sabiendo
que la distancia Madrid-Sevilla es de 480 km, calcula:
a)
b)
c)
d)
e)
Rectilínea.
Circular.
Parabólica.
Elíptica.
Caótica.
a) El movimiento de un coche por una recta o el de caída
de una manzana desde un árbol.
b) El de una etiqueta pegada en el borde de un CD en movimiento.
c) La caída de una piedra lanzada en una dirección no vertical.
d) La de los planetas alrededor del Sol.
e) El movimiento de una mosca por la habitación.
ACTIVIDAD DE REFUERZO
PÁG. 42
1 En una hilera de árboles nos encontramos situados en el árbol número 5. Nos movemos llegando hasta
el árbol 20, volvemos al 8, nos alejamos hasta el 32 y
volvemos para terminar en el 6. ¿Cuántos árboles nos
hemos desplazado?
Damos tantos datos para comprobar que los alumnos han
entendido el concepto de desplazamiento, porque si al principio estábamos en el árbol 5 y terminamos en el 6 nos hemos
desplazado:
∆x = xf – x0 = 6 – 5 = 1 árbol.
Y no hace falta tener en cuenta ningún otro dato.
Para calcular el número de árboles recorridos, sí habría que
conocer cómo hemos ido de un sitio a otro. En nuestro
caso:
|20 – 5| + |8 – 20| + |32 – 8| + |6 – 32| = 77 árboles.
ACTIVIDAD DE REFUERZO
PÁG. 43
1 Un coche sale de Torrejón de Ardoz (Madrid) en el km
21 de la A2 y se dirige hacia Barcelona. El conductor comprueba que una hora después de haber salido se encuentra
en el kilómetro 117, a las dos horas en el 213, a las tres
horas en el 309 y a las tres horas y media en el 357.
Dibuja la gráfica posición-tiempo y calcula la velocidad
del movimiento.
Planteando y dibujando la gráfica se obtiene que la velocidad
es 96 km/h.
a) El tiempo que tardan en cruzarse.
b) El espacio recorrido por cada tren en ese momento.
M
P
v1 = 30,5 m/s
x
S
v2 = 69,4 m/s
480 km
480 - x
Cuando se encuentren los dos trenes habrán tardado el
mismo tiempo desde que partieron, lo que ocurre es que el
más rápido habrá recorrido más espacio; por tanto, se debe
cumplir:
e
e

et = 30,5 ⋅ t1  t1 = t2 ; 1 = 2

30,5 69,44 

e2 = 69,44 ⋅ t2 
e1 = x ; e2 = 480 000 − x 
480 000 − x
x
=
30,5
69,44
x = 146,48 ⋅ 103 m = 146,48 km
t1 =
146,48 km
= 1,33 horas
km
110
h
ACTIVIDAD DE REFUERZO
PÁG. 45
1 Dos coches están separados por una distancia de
150 km. A las 12 de la mañana sale uno al encuentro del
otro; uno lo hace a una velocidad constante de 100 km/h
y el otro lo hace a una velocidad de 80 km/h. Calcula:
a) ¿Cuánto tiempo tardarán en encontrarse?
b) ¿Qué distancia ha recorrido cada uno de ellos?
c) ¿Qué hora marcará el reloj cuando se encuentren?
Dibuja las gráficas que creas oportuno.
v1 = 100 km/h
v1 = 27,8 m/s
A
x
v2 = 80 km/h
v2 = 22,2 m/s
P 150 000 - x B
150 · 103 m
En este caso el tiempo que tardarán en encontrarse es el
mismo, y por tanto:
89
1
t1 =
e1
v1
t1 =
t2 =
e2
v2
t2 =
¿Está el coche en reposo después de los 6 s?
Si no es así, ¿a qué velocidad se mueve?
x
27,8
150 000 − x
22,2
a) Los tiempos serán: t1 =
83 400
= 3 000 s
27,8
equivalentes a 50 min.
t2 =
b)
9π
π R2
=
m/s y que eso es el incremento de la velocidad,
2
2
66 600
= 3 000 s
22,2
150 000 − x
x
=
27,8
22,2
de donde x = 83 400 m
El móvil A recorrerá 83 400 m y el móvil B recorrerá
150 000 – 83 400 = 66 600 m
c) El reloj marcará las 12:50 h.
ACTIVIDAD DE REFUERZO
PÁG. 47
1 Si la velocidad de un coche, después de arrancar
desde un semáforo, llega a valer 72 km/h después de 15 s,
¿cuál es el valor de la aceleración? ¿Eso significa que
siempre se ha movido con esa aceleración?
La aceleración es el cociente entre el incremento de la velocidad y el tiempo en el que se produce este incremento,
por lo que:
a=
∆v
=
t
72
km 1000 m
1h
·
·
h
1 km
3 600 s
= 1,33 m/s 2
15 s
Ésa es la aceleración media que resulta de calcular lo que
ha variado la velocidad a lo largo de todo el recorrido. Puede ser que haya ido siempre con esa aceleración o que en
ningún momento, salvo puntualmente, la haya tenido de
ese valor.
ACTIVIDAD DE
AMPLIACIÓN PÁG. 48
1 Un vehículo parte del reposo y acelera cada vez
más durante 3 s hasta llegar a un valor de 3 m/s2 y luego
va disminuyendo su aceleración durante otros 3 s de la
forma en que se ve en la gráfica:
a
t
90
Como la aceleración varía de una forma muy extraña (semicircular) es muy difícil hacer los cálculos analíticamente, pero
sí podemos decir que el área contenida debajo de la gráfica
es la de medio círculo (hemos dado a t y a los valores justos
para que así sea):
por lo que el vehículo va a 14,1 m/s.
La pregunta de si está en reposo es una pregunta trampa.
Muchos alumnos tenderán a decir que así es. Podemos «romperles» esa idea, y fomentar que «lean» bien las gráficas (es
una gráfica de aceleración, no de velocidad), comentando
que, si la aceleración es siempre positiva (aunque se reduzca
en algunos momentos) la velocidad no puede disminuir, por
lo que cada vez irá más rápido.
ACTIVIDAD DE
AMPLIACIÓN PÁG. 49
1 El conductor de un vehículo tarda en pararse 5 segundos después de frenar con una deceleración de 3
m/s2. Calcula:
a) La velocidad inicial del automóvil antes de comenzar
a frenar.
b) El espacio recorrido durante la frenada.
c) Dibuja una gráfica v-t que represente el movimiento
de frenada descrito.
a) vt = v 0 + a t; v 0 = vt − a t = 0 − (−3⋅5) =
= 15 m/s
1
1
b) e = v 0t + a t 2 = 15⋅5 + ⋅3⋅52 = 37,5 m
2
2
c)
v (m/s)
15
5
t (s)
ACTIVIDAD DE REFUERZO
PÁG. 49
1 Estás asomado a una ventana de tu casa y observas que pasa por delante de ti una pelota que ha caído
desde la azotea. Si la diferencia de altura entre tu casa
y la azotea es de 7 metros, ¿a qué velocidad pasará la
pelota por delante de tu ventana?
7m
v = 2 g h = 2 ⋅9, 8 ⋅7 = 11,7 m/s
ACTIVIDAD DE
AMPLIACIÓN PÁG. 50
1 Un camión que se desplaza a velocidad constante de
90 km/h adelanta a un coche que se encuentra parado
en la carretera. Si éste arranca 5 segundos después con
una aceleración constante de 3 m/s2, calcula:
ACTIVIDADES DE REFUERZO
PÁG. 52
1 Calcula el intervalo de tiempo con el que llegan al
suelo tres bolas lanzadas al mismo tiempo desde lo alto
de una torre de 50 m de altura, una con velocidad inicial
20 m/s hacia abajo, la segunda sin velocidad inicial y la
tercera con velocidad inicial 20 m/s hacia arriba.
Aplicando la ecuación
h = h0 + v0 t +
0 = 50 m + ( −20 m/s · t1 ) +
0 = 50 m +
t1 = 3,2 s
v = 90 km/h = 25 m/s
t3 = 5,83 s
P
Cuando el coche alcance al camión se ha de cumplir que el
espacio recorrido por ambos ha de ser el mismo.
1
( −9,8 m/s2 ) t12
2
t1 = 1,7 s
a) El tiempo que tardará el coche en alcanzar al
camión.
b) La velocidad del coche cuando alcanza al camión.
c) El espacio que recorre el camión antes de ser alcanzado.
v1 = 25 m/s
a = 3 m/s2
x
1 2
at
2
1
( −9,8 m/s2 ) t22
2
0 = 50 m + (20 m/s · t3 ) +
1
( −9,8 m/s2 ) t32
2
El primero llega 1,7 s después del lanzamiento, el segundo
1,5 s después y el tercero a 2,6 s de este último.
2 Lanzamos hacia arriba un objeto con una velocidad
inicial de 8 m s–1. Despreciando rozamientos, determina:
1
a) e1 = v1 t1  e = e
v1 t1 = a t 2
 1 2
2

1
1
e2 = a t 2  t 2 = t1 − 5
25 t1 = ⋅3⋅(t − 5)2
2

2
a) La máxima altura alcanzada.
b) La velocidad del objeto cuando se encuentra a 2 m
del suelo.
c) El tiempo que tarda en bajar desde el punto más alto
hasta el suelo.
De donde: t1 = 25,7 s; t2 = 20,7 s
b) v2 = a t2 = 3 · 20,7 = 62,1 m/s
c) e1 = v1 t1 = 25⋅25,7 = 642 m;
a)
1
e2 = ⋅3⋅20,72 = 642 m
2
ACTIVIDAD DE REFUERZO
PÁG. 51
1 Se deja caer desde lo alto de un acantilado un objeto que llega al suelo con una velocidad de 20 m/s. ¿Qué
altura tiene el acantilado? ¿Cuánto tiempo ha durado la
caída?
s=
t=
v f2 − v 02
2a
vf − v0
a
=
(20 m/s)2 − (0 m/s)2
= 20, 4 m
2 · 9,8 m/s 2
=
20 m/s − 0 m/s
= 2, 04 s
9,8 m/s 2
s=
vt2 − v 02
2a
b) v =
t
=
(0 m/s)2 − (8 m/s)2
= 3,3 m
2 ⋅(−9, 8) m/s 2
v 02 + 2 a s =
= (8 m/s)2 + 2 ⋅(−9, 8) m/s 2 ⋅2 m =
= 5 m/s
c) t =
vt − v0
a
=
−8 m/s − 0 m/s
= 0,8 s
−9,8 m/s2
ACTIVIDADES DE
AMPLIACIÓN PÁG. 53
1 Calcula cuánto tiempo tarda en caer un objeto lanzado en la superficie de la Tierra y en la superficie de la
Luna, si la velocidad inicial es de 10 m/s y se lanza desde
1 m de altura. Dato: gLuna = 1,6 m/s2.
91
1
Aplicando la ecuación: h = h0 + v0 t +
0 = 1 m + (10 m/s · tT ) +
tú el valor de la velocidad angular. t es el tiempo que
tarda el planeta en dar una vuelta alrededor del Sol (la
Luna es alrededor de la Tierra).
1 2
at
2
1
( −9,8 m/s2 ) tT2
2
Planeta
tT = 2,1 s
0 = 1 m + (10 m/s · tL ) +
1
( −1,6 m/s2 ) tL2
2
velocidad
angular
(rad/s)
Mercurio
Venus
tL = 7,9 s
Tierra
2 Calcula la profundidad de un pozo, sabiendo que
cuando tiras una piedra al fondo tardas en oír el ruido
que ésta hace al chocar contra el agua 4 segundos. Dato:
velocidad del sonido 340 m/s.
Marte
Júpiter
Saturno
Urano
1 2
gt 
2 1
Subida (MRU): h = v2 t 2 
t1 + t 2 = 4
Bajada (MRUA): h =
h
Neptuno
Luna*
ACTIVIDADES DE REFUERZO
PÁG. 56
v2 = 330 m/s ya que v sonido = v2
Por tanto:
1
⋅ 9, 8 ⋅ t12 = 330 ⋅ t 2 ;
2
4,9t12 = 330 (4 − t1 )
De donde: t1 = 3,787 s y t 2 = 0,212 s
1
⋅ 9, 8 ⋅3,3872 = 70 m y h = 330 ⋅ 0,212 == 70m
2
= 70 m
h=
ACTIVIDAD DE REFUERZO
PÁG. 54
1 Calcula a cuántos grados equivalen los siguientes
ángulos en radianes: 1; 1,57; 2; 3; 3,14; 4, 5, 6 y 6,28.
Como la longitud de la circunferencia es 2 π r y la longitud del
arco de un radián es r, en una circunferencia hay 2 π radianes,
por lo que el factor de conversión es
360º
º
, por lo que:
= 57,3
2 π radianes
rad
rad
1
1,57
º
57,3
90
rad
4
5
º
2
3
114,6 171,9
6
229,2 286,5 343,8
3,14
180
6,28
360
ACTIVIDAD DE
AMPLIACIÓN PÁG. 55
1 Buscando los datos en Internet o en una enciclopedia actualizada, completa la siguiente tabla, calculando
92
t (s)
1 Si la biela de un pistón de un motor de F1 gira a
19 000 rpm, calcula el ángulo que ha girado en 1 minuto.
Si la media de giro en una carrera es de 12 000 rpm, calcula cuánto ángulo, en grados, ha girado en una carrera
que dura una hora y media.
Como recorre 19 000 vueltas en un minuto, aplicando el factor de conversión:
19 000 vueltas
360 º
·
· 1 min == 6 840 000 º
1 min
1 vuelta
= 6 840 000 º
12 000 vueltas
360 º
·
· 90 min == 389 000 000 º
1 min
1 vuelta
= 389 000 000 º
2 Calcula la velocidad angular, en rad/s y en rpm, del
giro de la pala de un aerogenerador que da una vuelta
en 6 s.
1 vuelta
6s
1 vuelta
6s
2 π rad
= 1,05 rad/s
1 vuelta
60 s
·
= 10 rev/m
1 min
·
ACTIVIDADES
COMPLEMENTARIAS
1 Situamos un móvil en lo alto de un plano inclinado
por el que baja, con una aceleración de 3 m/s2, durante 5
segundos. Posteriormente se mueve por un plano horizontal, con velocidad uniforme, durante otros 10 segun-
dos, para concluir ascendiendo por otro plano inclinado
con una aceleración de –5 m/s2 hasta que se detiene.
Dibuja las gráficas velocidad-tiempo y espacio-tiempo
del movimiento completo. ¿Cuánto tiempo tarda en detenerse? ¿Qué espacio total recorre?
v0 = vf – a t ; 0 = 40 m/s – a · 10 s de donde a = 4 m/s2.
ec = v0 t + 1/2 a t2 = 0 + 1/2 · 4 m/s2 · (10 s)2 = 200 m
Recorren la misma distancia.
e(m)
200
Como el móvil desciende durante 5 s con una aceleración de
3 m/s2 (y v0 = 0), alcanza una velocidad:
vf = a t = 3 m/s2 · 5 s = 15 m/s y recorre un espacio
e1 = 1/2 a t2 = 1/2 · 3 m/s2 · (5 s)2 = 1/2 · 3 m/s2 · 25 s2 = 37,5 m
150
100
Se mueve con esa velocidad durante 10 segundos en los que
recorre:
e2 = v t = 15 m/s · 10 s = 150 m
Y posteriormente se frena con una aceleración de –5 m/s2
por lo que tarda:
v0 = vf – a t; 15 m/s = 0 + (–5 m/s2) · t de donde t = 3 s.
Recorre, en este tercer movimiento:
e3 = v0 t + 1/2 a t2 = 15 m/s · 3 s + 1/2 · (–5 m/s2) · (3 s)2 = 45 m +
+ (–22,5 m) = 22,5 m
Dibujamos las gráficas:
50
0
v(m/s)
210
200
10
100
Pasamos la velocidad de la rueda a m/s:
km 1 h 1000 m
⋅
⋅
= 5 m/s
h 3 600 s 1 km
120 m ⋅
10
15
18
t(s)
0
5
10
15
18
t(s)
El tiempo total de movimiento es 18 s, que es la suma del
tiempo utilizado en cada movimiento. El espacio total es la
suma de los tres:
e1 + e2 + e3 = 37,5 m + 150 m + 22,5 m = 210 m.
También coincide con el área de la figura formada por el eje
0x y la gráfica de la velocidad.
2 ¿Quién recorre más espacio en 10 segundos, una moto que se mueve con velocidad constante de 72 km/h o
un coche que, partiendo del reposo, llega a alcanzar una
velocidad de 40 m/s? Dibuja las gráficas espacio-tiempo
de ambos movimientos?
Pasamos la velocidad de la moto a m/s:
72
km 1 h 1000 m
⋅
⋅
= 20 m/s
h 3 600 s 1 km
La moto se mueve con un MRU:
em = v t = 20 m/s · 10 s = 200 m
El coche se mueve con un MRUA:
t(s)
3 Calcula el número de vueltas que da en un minuto
la rueda de una bicicleta de 35 cm de radio cuando ésta
se mueve a 18 km/h.
5
50
5
10
coche
La rueda se mueve con un MRU:
er = v t = 5 m/s · 60 s = 120 m
La longitud de una vuelta es l = 2 π r = 2 · π · 0,35 m ≈ 2,2 m
Dividiendo la longitud total recorrida entre la correspondiente a una vuelta obtenemos el número de vueltas:
15
150
0
5
moto
18
e (m)
1
1 vuelta
≈ 55 vueltas
2,2 m
También se puede hacer deduciendo la ω, ya que sabemos
v y r, y obtenemos el número de vueltas multiplicando ω
por el tiempo, y pasando la solución (que está en radianes)
a vueltas.
4 Lanzamos una pelota hacia arriba con una velocidad inicial de 25 m/s. ¿Hasta qué altura llegará? ¿Cuánto
tiempo tarda en subir? Dato: g = 9,8 m/s2
vf = v0 + a t ; 0 = 25 m/s + (–10 m/s2) · t de donde t = 2,5 s.
h = v0 t + 1/2 a t2 = 25 m/s · 2,5 s + 1/2 · (–10 m/s2) · (2,5 s)2 ≈
≈ 31 m
5 Una rueda, de 20 cm de diámetro, gira con una velocidad angular de 30 rpm. ¿Cuál es su velocidad angular
en rad/s? ¿Cuántas vueltas da en 15 segundos? ¿Cuánto
tiempo tarda un punto de su periferia en recorrer 10 m?
Convertimos la velocidad:
30
rev 1 min 2π rad
rad
⋅
⋅
≈ 3,14
min 60 s 1 rev
s
93
1
si se mueve con una velocidad de 18 km/h. ¿Cuánto vale
su frecuencia? ¿Y su periodo?
El número de vueltas se obtiene:
30
vueltas 1 min
⋅
⋅ 15 s = 7,5 vueltas
min
60 s
La velocidad lineal de un punto de la periferia, y dado que el
radio es la mitad del diámetro, se obtiene:
v = ω R ≈ 3,14 rad/s · 0,1 m/rad ≈ 0,31 m/s
Como el movimiento es uniforme se aplica la fórmula:
e = v t ; 10 m = 0,31 m/s · t de donde t ≈ 32 s.
6 ¿Hasta qué altura puede subir un objeto si se lanza
hacia arriba con una velocidad inicial de 15 m s–1 desde
20 m de altura?
v f2 − v 02
2a
=
(0 m/s)2 − (15 m/s)2
= 11,5 m
2 · ( − 9,8) m/s 2
km
1h
1000 m
⋅
⋅
= 5 m/s
h 3 600 s 1 km
v
5 m/s
ω
1 rad/s
=
=1 rad/s ⇒ v =
=
≈
R 5 m/rad
2π 2π rad/vuelta
1
1
≈ 0,16 vuelta/s ⇒ T = =
≈ 6,3 s/vuelta
v 0,16 vuelta/s
ω=
EVALUACIÓN
Datos conocidos: v0 = 0 m s–1; vf = 18 m s–1 y
g = 9,8 m s–2
Datos desconocidos: e = ? ; t = ?
1 Un tren que lleva una velocidad de 20 m/s recorre
150 m desde el momento que frena (con deceleración
constante) hasta que está parado. Calcula la aceleración
y el tiempo que tarda en pararse. Representa las gráficas
a–t, v–t y e–t.
h =1/2 g t 2
h =1/2 ⋅9,8 t 2
18 m/s
⇒
⇒t =
≈1,8 s ⇒
9,8 m/s 2
v = gt
18 = 9,8 t
Datos conocidos: v0 = 20 m s–1 ; vf = 0 m s–1 ; s = 150 m
Datos desconocidos: a = ? ; t = ?
e = v 0 t +1/2 a t 2
150 = 20 t +1/2 a t 2
⇒
v = v0 + a t
⇒t =
0 = 20 + a t
−20
⇒
a
−400 200
−200
⇒150 =
+
⇒⇒150 a = −200 ⇒ a =
≈
a
a
150
−20
≈ −1,3 m/s 2 y t =
= 15 s
−200
150
Representación a–t: una línea horizontal –1,3 unidades por
debajo del eje 0x.
Representación v–t: Una línea recta, oblicua descendente
desde el punto (0,20) hasta el punto (15,0).
Representación s–t: La rama izquierda de una parábola que
empieza ascendiendo rápidamente desde el punto (0,0) disminuyendo su pendiente hasta alcanzar su máximo en el
punto (15,150) donde acaba.
2 Calcula la velocidad angular que posee un móvil que
se mueve describiendo una circunferencia de radio 5 m,
94
v =18
3 ¿Desde qué altura debe caer un cuerpo libremente
para que al llegar al suelo su velocidad sea de 18 m/s?
¿Dónde hay que poner el origen del sistema de referencia
para poder resolver el problema?
Lo que sube es:
∆s =
Datos conocidos: v = 18 km h–1 ; R = 5 m
Datos desconocidos: v(m/s) = ? ; ν = ? ; T=?
⇒ h =1/2 ⋅9,8 t 2 =1/2 ⋅9,8 m/s 2 ⋅ (1,8 s)2 ≈16 m
El origen del sistema se puede poner en cualquier punto;
no va a cambiar el resultado. Si lo ponemos en el punto de
lanzamiento, el espacio inicial es cero y el espacio, h, nos da
la altura. Si lo ponemos en el punto de recepción, el espacio
inicial sería h y el espacio final, cero.
4 Si se hubiera lanzado desde el suelo un cuerpo en
vertical con una velocidad de 18 m/s, ¿cuál sería el desplazamiento cuando vuelve al suelo? ¿Cuál ha sido el espacio recorrido? Date cuenta de que los datos se parecen
a los del problema anterior.
El desplazamiento es cero, porque sale y llega al mismo
punto del sistema de referencia. El espacio recorrido es
32 m, aproximadamente (16 de subida y 16 de bajada), puesto
que es el doble del espacio que nos da el problema anterior,
puesto que los datos son similares.
5 Calcula la velocidad media de un objeto que se
mueve siguiendo un movimiento rectilíneo que está
representado en la figura adjunta:
a) En los primeros 4 segundos del movimiento.
b) En el intervalo entre los segundos 4 y 10 del movimiento.
c) Cuando se está moviendo entre el punto C y el D.
La velocidad media se obtiene dividiendo el desplazamiento
entre el tiempo empleado por lo que:
e (m)
C
12
A
8
F
B
a) v =
e(t f )− e(t 0 ) e(4)− e(0) 12 m− 8 m
=
=
=1 m/s
t f −t 0
4−0
4s
b) v =
e(t f )− e(t 0 ) e(10)− e(4) 12 m−12 m
=
=
= 0 m/s
t f −t 0
10− 4
6s
4
0
E
D
0
2
4
6
8
10
t (s)
c)
v=
e(t f )− e(t 0 ) e(8)− e(4) 2 m−12 m
=
=
= −2,5 m/s
t f −t 0
8− 4
4s
95
2 laS FuErZaS
ACTIVIDAD DE REFUERZO
PÁG. 73
1 Pretendemos estirar un muelle de constante recuperadora k = 10 N/m ejerciendo una fuerza de 1 N.
¿Cuánto se alargará? Si ahora aumentamos la fuerza en
1 N, ¿cuánta longitud más se habrá estirado el muelle?
Como F = k ∆l
1 N = 10 N/m · l de donde l = 0,1 m = 10 cm
Si aumentamos la fuerza en 1 N, la fuerza valdrá 2 N por lo
que:
2 N = 10 N/m· l de donde l = 0,2 m = 20 cm, con lo que se
habrá alargado otros 10 cm.
Evidentemente podríamos haberlo calculado:
∆F = k ∆l ; 1 N = 10 N/m · ∆l de donde ∆l = 0,1 m = 10 cm
y aprovechamos para explicarles lo que hemos comentado
anteriormente en la recomendación didáctica.
ACTIVIDAD DE REFUERZO
PÁG. 74
1 Calcula el valor de la resultante de dos fuerzas de 60 y
80 N cuando forman un ángulo de 0º. Hazlo también en los
casos de que formen 60º, 90º y 180º, pero siempre utilizando la fórmula de la resultante de fuerzas concurrentes.
Aplicando en todos los casos la fórmula:

FR =
2  2
 
F1 + F2 + 2 F1 F2 cos α
obtenemos:

FR = 602 + 802 + 2 · 60 · 80 · cos 0º =
= 3 600 + 6 400 + 2 · 60 · 80 · 1 =140 N

FR = 602 + 802 + 2 · 60 · 80 · cos 60º =
= 3 600 + 6 400 + 2 · 60 · 80 · 0,5 ≈122 N

FR = 602 + 802 + 2 · 60 · 80 · cos 90º =
= 3 600 + 6 400 + 2 · 60 · 80 · 0 =100 N

FR = 602 + 802 + 2 · 60 · 80 · cos 180º =
= 3 600 + 6 400 + 2 · 60 · 80 · ( −1) = 20 N
Es el momento de hacerles ver que el primer caso coincide
con el caso de fuerzas en la misma dirección y sentido, el
tercero la de fuerzas perpendiculares y el cuarto fuerzas en la
misma dirección y sentidos contrarios, por lo que la fórmula
96
que se les ha dado para el caso de fuerzas concurrentes vale
para todos los casos.
ACTIVIDADES
COMPLEMENTARIAS
1 Indica el tipo de fuerza, a distancia o contacto, que
se aplica cuando:
a)
b)
c)
d)
e)
El peine pone de punta los pelos al peinarnos.
Un objeto se frena al rozar con el suelo.
Cae el agua de un grifo abierto.
Se mueve la tapa de una olla con el agua hirviendo.
Un barquito de plástico que soltamos en el fondo de
una bañera asciende.
La fuerza del apartado a) es una fuerza a distancia (fuerza
electrostática) puesto que pone de punta los pelos sin llegar
a estar en contacto el peine con el pelo. La fuerza del apartado
b) que es la fuerza de rozamiento es de contacto, ya que si
no hay contacto no se puede rozar. La fuerza del apartado c)
es el peso del agua y es una fuerza a distancia. La fuerza del
apartado d) es una fuerza de contacto entre el vapor de agua
y la tapa. La fuerza del apartado e) es el empuje, una fuerza de
contacto que estudiaremos en la Unidad 4. Al intentar volver el
agua que ha elevado su posición a causa de haber sumergido
el barco, «empuja» literalmente el barco hacia arriba.
2 Si ejercemos una fuerza de 30 N oprimiendo un
muelle de constante recuperadora k = 150 N/m, ¿cuánto
se acortará éste? Si aumentamos la fuerza hasta 50 N sin
soltarlo, ¿cuánto más se comprimirá?
Aplicando la Ley de Hooke F = k x
30 N = 150 N/m · x de donde x = 0,2 m = 20 cm.
En el segundo caso, y aplicando la misma ley:
50 N = 150 N/m · x de donde x ≈ 0,33 m = 33 cm.
Como ya se había comprimido 20 cm, se comprimirá 33 cm –
– 20 cm = 13 cm más.
También se puede calcular teniendo en cuenta sólo el incremento de fuerza que realizamos:
50 N – 30 N = 20 N = 150 N/m · x de donde x ≈ 0,13 m =
= 13 cm.
3 Si empujamos una caja hacia el este con una fuerza
de 60 N y otra persona tira de ella hacia el sur con otra
fuerza de 80 N, ¿cuál es la fuerza total que se ejerce sobre
la caja? ¿Y si en vez de tirar de ella hacia el sur lo hiciera
hacia el oeste? Dibuja el diagrama de las fuerzas que actúan en ambos casos.
Puesto que ambas fuerzas son perpendiculares, la resultante
vale:
R = F12 + F22 = (60 N)2 +(80 N)2 =
= 10 000 N2 =100 N
3
2
5
E
R
5
R
4
1
2
4
3
S
En el segundo caso las dos fuerzas son paralelas y de sentido
contrario por lo que se restan. El sentido de la resultante es
hacia el oeste, ya que hacia ese punto se dirige la mayor de
ambas fuerzas.
R
O
EE
4 ¿Cuál será la fuerza mínima que debo hacer para
conseguir levantar del suelo una caja que pesa 150 N,
sobre la que reposa un libro de 30 N, si al mismo tiempo
otra persona la empuja en dirección horizontal con una
fuerza de 100 N?
La fuerza que hemos de ejercer sólo tiene que compensar las
fuerzas verticales, puesto que la fuerza horizontal la moverá
pero no influye en su subida o bajada, por lo que tendremos
que hacer:
R = 150 N + 30 N = 180 N
5 Calcula gráficamente la resultante de las fuerzas
de la figura adjunta. Si cada cuadro mide de lado 1 N,
¿cuánto valdrían dos fuerzas, una vertical y otra horizontal, equivalentes a la resultante? ¿Cuánto vale la fuerza
resultante?
6 Calcula la suma de tres fuerzas, una de 40 N horizontal, otra de 30 N que forma un ángulo de 30º sobre
la horizontal y otra de 20 N vertical.
Descomponemos las tres fuerzas:
F1x = 40 N · cos 0º = 40 N
F1y = 40 N · sen 0º = 0 N
F2x = 30 N · cos 30º = 26 N
F2y = 30 N · sen 30º = 15 N
F3x = 20 N · cos 90º = 0 N
F3y = 20 N · sen 90º = 20 N
Sumamos las componentes verticales y las horizontales:
Σ Fy = F1y + F2y + F3y = 35 N
Σ Fx = F1x + F2x + F3x = 66 N
Por lo que la resultante será:

FR = 352 + 662 ≈ 75 N
7 ¿Por qué se cae una lámpara a la que se le rompe el
cable del que cuelga?
La lámpara está en equilibrio ya que sobre ella actúan dos
fuerzas: el peso, hacia abajo y la fuerza que el cable hace
sobre ella reteniéndola, hacia arriba. Como son iguales, permanece la lámpara en equilibrio. Cuando éste desaparece, al
romperse el cable, sólo queda una, el peso, por lo que cae.
Cuando da en el suelo, éste hace una fuerza hacia arriba que
impide que la lámpara lo atraviese. Al cabo de un instante
ésta equilibra al peso y la lámpara se vuelve a quedar quieta,
esta vez en el suelo.
EVALUACIÓN
La fuerza horizontal vale 8 N hacia la izquierda, la vertical 9
N hacia arriba y la resultante:
R = F + F = (8 N) + (9 N) = 141 N ≈12 N
2
x
2
y
2
2
2
1 Enuncia la Ley de Hooke. Cuando colgamos un peso
de 0,04 N de un muelle de k = 8 N/m, ¿cuánto se alarga?
Pregunta teórica explicada en el libro del alumno.
F = k ∆l
97
2
Despejando ∆l de la fórmula con F = 0,04 N y k = 8 N/m, el
alargamiento es de 0,005 m = 5 mm.
2 Tres fuerzas de 20, 30 y 40 N tienen el mismo punto
de aplicación formando, entre las dos primeras, un ángulo de 30º, mientras que la primera y la tercera son opuestas. Calcula analítica y gráficamente la resultante.
Sumamos primero la de 20 N y 40 N, ya que son opuestas
y por lo tanto es más fácil. La resultante vale 20 N y forma
un ángulo de 180º – 30º = 150º con la de 30 N. Aplicando la
fórmula de la resultante a las dos fuerzas que nos quedan,
ésta vale:
FR = 302 +202 +2 · 30 · 20 · cos 150º ≈
≈ 900+ 400+( −1040) = 260 ≈16 N
Ahora lo hacemos gráficamente:
Las características básicas de una magnitud vectorial que
la diferencian de las magnitudes escalares son el punto de
aplicación, dirección y sentido. El módulo es el equivalente
al valor de la magnitud escalar.
4 Una fuerza de 26 N forma un ángulo de 30º bajo la
horizontal. ¿Cuánto vale su componente vertical? ¿Y la
horizontal?
La componente vertical vale:
Fy = F sen α = 26 N · sen (–30º) = –13 N
La componente horizontal vale:
Fx = F cos α = 26 N · cos (–30º) = 22,5 N
5 Una niña tira de una cuerda atada a un trineo, que
forma un ángulo de 45º sobre la horizontal. Si la fuerza
que hace la niña es de 50 N, ¿cuánto vale la fuerza útil
que hace que el trineo avance?
El trineo avanza en dirección horizontal, por lo que la fuerza
útil es Fx.
R
Resultante
3 Decimos que la fuerza es una magnitud ………
………… a diferencia del tiempo que es una magnitud
………………… ¿Qué significa eso? ¿Qué características
básicas son necesarias para definir una fuerza que no
tiene el tiempo?
Decimos que la fuerza es una magnitud vectorial a diferencia
del tiempo que es una magnitud escalar.
98
La componente útil (horizontal) vale:
Fx = F cos α = 50 N · cos 40º ≈ 38 N
laS FuErZaS Y El MoViMiEnTo
3
ACTIVIDAD DE REFUERZO
PÁG. 92
ACTIVIDAD DE REFUERZO
PÁG. 94
1 En un cajón tenemos varias canicas metálicas. Si consideramos el sistema formado únicamente por las bolas,
di si son externas o internas las siguientes fuerzas:
1 Se les puede pedir a los alumnos que en un buscador de Internet (en concreto en Google aparecen más de
5 000) pongan «diagrama cuerpo libre» en la búsqueda
de imágenes, y que luego vayan mirándolos despacio.
El ejercicio de ver cómo son varios diagramas de cuerpo libre les ayudará a entender mucho mejor este concepto.
a)
b)
c)
d)
e)
Una bola empuja a otra.
El peso de cada una de las bolas.
Una bola choca con las paredes del cajón.
Un imán atrae a una bola.
Una pequeña carga explosiva, en el centro de una
bola, hace que ésta explote en dos trozos.
f) Una bola roza con el suelo del cajón.
a) Cada una de las bolas ejerce una fuerza interna sobre la
otra.
b) Es externa. Se ejerce entre la bola y la Tierra.
c) También es externa. El cajón no lo consideramos sistema.
d) Externa. El imán ejerce una fuerza de atracción a distancia
y pertenece al entorno.
e) Interna. Todo lo que se encuentre en el interior de la bola
es parte de la bola y de hecho no crea variación en el
movimiento total del conjunto de bolas.
f) Externa. Al no ser el cajón parte del sistema, la fuerza es
externa.
Resulta muy interesante hacerles ver que el movimiento global de todas las canicas permanece igual, si las fuerzas aplicadas son todas internas, mientras que cambia si alguna es
externa. Posteriormente, lo vamos a utilizar cuando veamos
el concepto de cantidad de movimiento.
ACTIVIDAD DE
AMPLIACIÓN PÁG. 93
1 Apretamos una mano contra otra con una fuerza
de 70 N. Al intentar separarlas horizontalmente, la fuerza de rozamiento vale 22 N. Por otro lado, un alumno de 600 N de peso, lleva unas zapatillas de deporte
que, al deslizar por el suelo crean una fuerza de rozamiento de 135 N. ¿Cuál de los dos pares de superficies
piel-piel o zapatilla-suelo tiene mayor coeficiente de
rozamiento?
Como el coeficiente es el cociente entre la fuerza de rozamiento y la fuerza que les mantiene unidos los valores serán:
µ1 =
22 N
135 N
= 0,31 y µ2 =
= 0,22
70 N
600 N
Por lo que hay más rozamiento entre piel y piel.
Respuesta libre.
ACTIVIDADES DE REFUERZO
PÁG. 101
1 Calcula la aceleración con la que se mueve un coche,
de masa 1 225 kg, si el motor ejerce una fuerza de 3 800 N
y consideramos despreciable el rozamiento.
Sería muy interesante que dibujaran el diagrama de cuerpo libre, donde se vea que actúa una fuerza horizontal de 3 800 N,
se vea también el peso (que deberían calcular previamente
y que vale 1 225 kg · 9,8 m/s2 ≈ 12 000 N), y la normal que
ejerce el suelo que vale otros 12 000 N. Como N y P se anulan
podemos poner F = m a de donde:
a=
F 3 800 N
=
= 3,10 m/s 2
m 1225 kg
2 La resultante de las fuerzas que actúan sobre un cuerpo vale 15 N y es horizontal. Si el cuerpo, por la acción
de esta fuerza ha recorrido, en 5 segundos, 30 metros
partiendo del reposo, calcula la masa del cuerpo.
Con los datos de espacio recorrido y de tiempo calculamos la
aceleración del movimiento rectilíneo uniformemente acelerado. Posteriormente aplicamos la Segunda Ley de Newton
y obtenemos la masa:
2 s 2 · 30 m
=
= 2, 4 m/s 2
t2
(5 s)2
F
15 N
m= =
= 6,25 kg
a 2,4 m/s 2
a=
ACTIVIDAD DE
AMPLIACIÓN PÁG. 101
1 Podemos añadir una pequeña ampliación al Ejercicio de aplicación 2 preguntándoles cuánto vale el coeficiente de rozamiento en los dos casos del ejercicio.
La solución evidentemente es que es cero en el caso a) (puesto que les hemos enseñado que el coeficiente de rozamiento
99
3
es el cociente entre la fuerza de rozamiento y la fuerza que
hace que las superficies estén en contacto y que en este caso
es el peso), ya que la fuerza de rozamiento es nula.
En el caso b) valdría: µ = 5 N/70 N ≈ 0,07
ACTIVIDAD DE REFUERZO
PÁG. 102
1 Calcula la aceleración con la que se mueve, y hacia
dónde, una caja de 200 kg de masa, sobre la que actúan
las siguientes fuerzas:
a) Una fuerza de 300 N que ejerce en horizontal un trabajador empujándola hacia la derecha.
b) Otra fuerza de 200 N que ejerce otro, también en horizontal, y también hacia la derecha.
c) Una fuerza de 120 N que ejerce otro individuo en vertical y hacia arriba.
d) Una fuerza que ejerce un niño empujando hacia la
izquierda de 30 N.
e) La fuerza de rozamiento que vale 100 N.
Σ Fx = 300 N + 200 N + (–30 N) + (-100 N) = 370 N
Σ Fy = 120 N + (–1 960 N) + Normal = 0
Les explicamos que la resultante de las dos fuerzas verticales
(120 N y –1 960 N) es una fuerza dirigida hacia abajo que haría
que la caja fuera en ese sentido.
Eso no sucede mientras debajo de ella haya un suelo rígido
que se resiste a «ser atravesado» por la caja, por lo que ejerce
una fuerza (a la que llamamos normal) que compensa y anula
la resultante de las otras dos.
La caja, en cuanto a movimientos verticales, está en equilibrio
estático.
Por lo tanto existe una aceleración horizontal y hacia la derecha que vale:
2 A la fuerza con la que la Tierra atrae a los cuerpos se
le llama peso. ¿Se cumple el Principio de acción y reacción? Si es así, ¿por qué no lo percibimos? Compruébalo
con una persona de masa 50 kg, sabiendo que la Tierra
tiene una masa de 6 · 1024 kg.
Si consideramos acción la fuerza que la Tierra ejerce sobre la
persona, la reacción es una fuerza real, igual y sentido contrario que la persona ejerce sobre la Tierra. El peso vale unos
500 N, por lo que la reacción vale lo mismo.
Si aplicamos a la Tierra una fuerza de 500 N, podemos obtener la aceleración correspondiente, aplicando la Segunda
Ley de Newton:
F = 500 N = m a = 6 · 1024 kg · a
La aceleración, a, vale 8,3 · 10 –23 ms–2 que es una aceleración
tan pequeña que es absolutamente indetectable.
Pero que no se pueda detectar, no significa que no exista.
ACTIVIDAD DE
AMPLIACIÓN PÁG. 105
1 Un deportista, de 70 kg de masa, que se mueve a
una velocidad de 3 km/h choca durante 0,2 s con un niño,
de 30 kg, que se encontraba en reposo y que termina
moviéndose a 3 km/h. ¿A qué velocidad se mueve ahora
el deportista?
ACTIVIDADES DE REFUERZO
PÁG. 104
Con las fórmulas del MRUA se puede conocer la aceleración
que actúa sobre el niño. Aplicando el Principio de acción y
reacción
F12 = –F21 ; 30 kg · 4,2 m/s2 = –70 kg · ad de donde obtenemos
ad que es –1,8 m/s2
aplicando vf = v0 + a t obtenemos:
vf = 3/3,6 m/s + (–1,8 m/s2) · 0,2 s = 0,47 m/s = 1,7 km/h
Este problema nos sirve para recordar conversión de unidades y Cinemática.
1 Un jugador de béisbol golpea una bola con su bate.
¿En quién actúa la acción y en quién actúa la reacción?
¿Qué magnitudes cambian de valor y en qué medida?
ACTIVIDADES DE
AMPLIACIÓN PÁG. 106
Aunque se pueden intercambiar los nombres y decirlo al
contrario vamos a situar la acción, que la ejerce el bateador,
sobre la bola. Se manifiesta en que sobre la bola, durante
el contacto con el bate, actúa una aceleración en sentido
contrario a la velocidad inicial de ésta que consigue, en muy
poco tiempo, invertir su sentido de movimiento.
La reacción la ejerce la bola sobre el bate. Se manifiesta en
una aceleración que actúa sobre éste disminuyendo la velocidad a la que se mueve. Evidentemente es menor que la
1 Una fuerza de 5 N actúa durante 10 segundos sobre
un objeto de 15 kg de masa que inicialmente se encuentra en reposo. ¿Con qué velocidad final se mueve el objeto?
a=
100
aceleración que actúa sobre la bola, ya que la masa de ésta
es menor que la del bate.
Ambas fuerzas cumplen así con el principio. Son iguales, opuestas, simultáneas y actúan sobre cuerpos diferentes pero
nunca sobre el que las ejerce.
Σ F 370 N
=
=1,85 m/s 2
m 200 kg
Conviene que se les explique que no es necesario calcular la
aceleración para posteriormente calcular la velocidad final, sino que se puede hacer en un solo paso aplicando la igualdad
entre impulso y variación en la cantidad de movimiento.
I = F ∆t = ∆p = m ∆v de donde:
∆v =
F ∆t 5 N · 10 s
= 3,3 m/s
=
m
15 kg
Como originalmente parte del reposo, también ésta es la
velocidad final.
También puede resultar muy útil para resolver problemas
de objetos que se separan y que se parten, dado que en ese
caso el sistema está aislado y las fuerzas externas al sistema
son nulas, al igual que el impulso.
2 Calcula el retroceso de un fusil de 5 kg que dispara
balas de 25 g de masa a velocidades de 200 m/s.
Teniendo en cuenta que la cantidad de movimiento total del
sistema bala-fusil es la suma de las cantidades de movimiento
de la bala por un lado y el fusil por el otro, por cada bala que
dispare éste experimenta un retroceso que en velocidad se
puede calcular como:
I = F ∆t = ∆p = mf ∆vf + mb ∆vb de donde:
I = 0 = 5 kg · (vf – 0) + 0,025 kg · (200 m/s – 0) y
vf =
−0,025 kg · 200 m/s
= –1 m/s
5 kg
Debemos aprovechar para contarles que el signo es negativo
puesto que la velocidad es una magnitud vectorial y eso significa que la velocidad es en sentido contrario a la de la bala.
Los problemas de Dinámica que no exijan el cálculo de aceleraciones, siempre son más sencillos de resolver por cantidades de movimiento e impulso.
actividades
cOMPleMentarias
Dato común a todos los ejercicios: g = 9,80 m s–2
1 Sobre un objeto actúan dos fuerzas de la misma dirección y sentido contrario de 30 y 12 N. Si el objeto se
mueve con una aceleración igual a 3 m/s2,
a) ¿Cuál de las dos fuerzas es responsable del movimiento del objeto?
b) ¿Cuánto vale la masa del objeto?
c) ¿En qué sentido se mueve?
d) ¿Con qué aceleración se movería si las dos fuerzas
tuvieran la misma dirección y sentido?
e) ¿Y si fueran perpendiculares?
a) Todas las fuerzas que actúan sobre un objeto son responsables del movimiento de éste, puesto que, la modificación de cualquiera de ellas, repercute en la resultante
y por lo tanto en el movimiento del objeto.
b) La masa del objeto se obtiene aplicando la Segunda Ley
de Newton:
Σ F = m a; 30 N + (–12 N) = m · 3 m/s2 ; m = 6 kg
c) La masa se moverá en el sentido de la mayor de ambas
(30 N) porque ése es el sentido de la resultante.
d) Aplicando, una vez más, la Segunda Ley de Newton:
Σ F = m a; 30 N + 12 N = 6 kg · a; a = 7 m/s2
e) Si son perpendiculares, obtenemos la resultante aplicando el Teorema de Pitágoras:
R = F12 + F22 = (30 N)2 +(12 N)2 = 1 044 N2 ≈ 32 N
por lo que la aceleración sería:
Σ F = m a; 32 N = 6 kg · a; a ≈ 5,3 m/s2
2 ¿Cuál es la masa en la superficie de la Tierra de un
filete de ternera de 220 g? ¿Y su peso?
La primera pregunta tiene el fin de comprobar que no se
lanzan automáticamente a multiplicar por g. La masa es un
dato del problema: 220 g. Es admisible que contesten la conversión a kilogramos: 0,22 kg.
El peso se obtiene directamente de la fórmula:
P = m g = 0,22 kg · 9,8 m/s2 ≈ 2,2 N
3 Si logramos frenar en 6 segundos un camión de
12 500 kg que inicialmente se movía a 108 km/h, ¿qué
fuerza han ejercido los frenos?
Como el camión ha pasado de 108 km/h a 0 en 6 segundos
podemos calcular la aceleración:
v 0 =108
km
1h
1000 m
⋅
⋅
= 30 m/s
h
3 600 s
1 km
vf = v0 + a t;
0 = 30 m/s + a · 6 s; a = –5 m/s2
Aplicando la Segunda Ley de Newton, y teniendo en cuenta
que la única fuerza que actúa es la de frenado:
Σ F = m a; Ffrenado = 12 500 kg · (–5 m/s2); Ffrenado ≈ –61 000 N
= 61 kN
4 Desde lo alto de una terraza situada a 20 m del suelo
unos obreros sujetando una cuerda consiguen que un
bulto con 100 kg de escombros, inicialmente en reposo,
llegue al nivel de la calle con una velocidad de 9 km/h.
Si suponemos el movimiento del bulto uniformemente
acelerado, calcula la fuerza ejercida por los obreros. ¿A
qué velocidad llegaría el bulto al suelo si los obreros hicieran la mitad de la fuerza anterior?
La velocidad final es:
v0 = 9
km
1h
1000 m
⋅
⋅
= 2,5 m/s
h
3 600 s
1 km
Sobre el bulto actúan dos fuerzas: su propio peso: P = m g
= 100 kg · 9,8 m/s2 = 980 N y la fuerza que ejercen los obreros.
101
3
La aceleración con la que desciende el bulto la hallamos
aplicando las fórmulas del movimiento uniformemente
acelerado:
h = h0 + v0 t + 1/2 a t2 y vf = v0 + a t
20 m =1/2a t 2
20 m =1/2 ⋅ (a t)t ⇒ 20 m =1/2 ⋅ 2,5 m/s ⋅ t
2,5 m/s = a t
de donde t =16 s y a ≈ 0,16 m/s 2
Aplicando la Segunda Ley de Newton, y teniendo en cuenta
las dos fuerzas que actúan:
Σ F = m a; P + (– Fobreros) = 980 N – Fobreros = 100 kg · 0,16
m/s2 = 16 N
Fobreros = 980 N – 16 N = 964 N
Para el segundo caso, la fuerza aplicada por los obreros es la
mitad, o sea, 482 N.
Aplicando la Segunda Ley de Newton, y teniendo en cuenta
las dos fuerzas que actúan:
Σ F = m a; P + (– Fobreros) = 980 N – 482 N ≈ 500 N = 100 kg · a
a = 5 m/s2
Aplicando las fórmulas del movimiento uniformemente acelerado:
2 ⋅20 m
20 m =1/2 ⋅ 5 m/s 2 ⋅ t 2 ⇒ t =
= 8 s 2 ≈ 2,8 s
5 m/s 2
v f = 5 m/s 2 ⋅ 2,8 s =14 m/s ≈ 50 km/h
5 Calcula el peso aparente (equivale a la tensión de
la cuerda del ascensor sin contar el peso de éste) de una
chica de 50 kg de masa dentro de un ascensor que:
a)
b)
c)
d)
Asciende con una aceleración de 2 m/s2.
Desciende con una velocidad de 12 m/s.
Desciende con una aceleración de 3 m/s2.
Se encuentra parado.
Calculamos el peso de la chica:
P = m g = 50 kg · 9,8 m/s2 = 490 N
Aplicando la Segunda Ley de Newton, y teniendo en cuenta
las dos fuerzas que actúan:
a) Σ F = m a; Fasc + (– P) = Fasc – 490 N = 50 kg · 2 m/s2 =
= 100 N de donde Fasc = 590 N
b) Σ F = m a; Fasc + (– P) = Fasc – 490 N = 50 kg · 0 m/s2 =
= 0 N de donde Fasc = P = 490 N
c) Σ F = m a; Fasc + (– P) = Fasc – 490 N = 50 kg · (–3 m/s2) =
= –150 N de donde Fasc = 340 N
d) Σ F = m a; Fasc + (– P) = Fasc – 490 N = 50 kg · 0 m/s2 =
= 0 N de donde Fasc = P = 490 N
evalUaciÓn
1 Tenemos un libro, de 2 kg de masa, situado en una
mesa. Lo empujamos con la mano según la horizontal y
102
notamos que se mueve aunque percibimos la existencia
de rozamiento entre la mesa y el libro. Dibuja un esquema donde aparezcan todas las fuerzas que actúan sobre
el libro. Si éste se mueve con una velocidad uniforme de
3 m/s, al aplicarle una fuerza horizontal de 4 N, ¿cuánto
vale la fuerza de rozamiento?
Sobre el libro actúan las siguientes fuerzas: peso (vertical y
hacia abajo); resistencia de la mesa (vertical y hacia arriba
con el mismo módulo que el peso); fuerza que ejercemos
(horizontal y en un sentido) y rozamiento del libro con la
mesa (horizontal y en sentido contrario).
Si se mueve con velocidad uniforme es que el módulo del
rozamiento y el de la fuerza que aplicamos son iguales por
lo que la fuerza de rozamiento vale 4 N.
Nota: Los datos de masa y velocidad del libro se dan para
poder discernir si el alumno considera o no que la masa y la
velocidad tienen que ver con el rozamiento.
2 Un coche de 1 000 kg que se encuentra detenido en
un semáforo, y que consideramos no roza con la carretera, se pone en movimiento cuando sobre él actúa una
fuerza de 5 000 N. ¿Cuál es la velocidad que tiene al cabo
de 10 segundos?
Al no haber rozamientos, de F = m a ⇒ 5 000 N = 1 000 kg · a
obtenemos que el valor de a es 5 m s–2.
Aplicando la ecuación del MRUA v = v0 + a t y al no haber
velocidad inicial nos da:
v = 5 m/s2 · 10 s = 50 m/s = 180 km/h
3 Tenemos un sistema formado por una caja metálica
en la que se encuentran tres bolas de plástico. Rellena en
el siguiente cuadro todas las celdas que se encuentran
vacías:
Contacto
Fuerza de la
o acción a
que hablamos
distancia
Externa
o
interna
Agente de
la fuerza
Peso de las
bolas
Acción a
distancia
Externa
Atracción gravitatoria
(Tierra-bola)
Rozamiento de
las bolas con
la caja
Contacto
Interna
Rozamiento entre superficies (bola-caja)
Choques entre
bolas
Contacto
Interna
Impenetrabilidad de
las bolas (no pueden
ocupar el mismo sitio;
se empujan)*
Sacamos con
la mano una
bola de la caja
Contacto
Externa
Nosotros (ejercemos
una fuerza cogiendo
la bola)
Atraemos la
caja acercando
un imán
Acción a
distancia
Externa
Fuerza magnética
(atracción entre imán
y caja)
En el apartado de agentes de la fuerza, y con mayor motivo
en el marcado por un asterisco, se puede permitir una cierta
flexibilidad ya que les puede ser difícil identificar el agente.
De todas maneras, puede utilizarse como repaso del concepto de agente.
4 Una motocicleta de 150 kg de masa, que circula a
20 m/s, frena y se detiene después de recorrer 50 m. El
rozamiento, ¿ayuda o perjudica a que la moto frene en
poco espacio? Si la fuerza de rozamiento con el suelo
vale de 100 N, ¿cuál ha sido la fuerza que han ejercido los
frenos si al frenar se movía con un movimiento rectilíneo
uniformemente acelerado?
La fuerza de rozamiento siempre contribuye a que un objeto
se detenga en menos espacio, ya que se opone al movimiento en todos los casos.
Al detenerse en 50 m, teniendo una velocidad inicial de 20
m/s, podemos aplicar la ecuación del MRUA:
2 a s = v2 – v02 ⇒ 2 · a · 50 m = (0 m/s)2 – (20 m/s)2 de donde
despejamos a = –4 m/s2
Aplicando la Segunda Ley de Newton: Σ F = m a nos queda
que:
Ffrenado + Froz = m a ⇒ Ffrenado = m a – Froz ⇒ Ffrenado =
150 kg · (–4 m/s2) – (–100 N) = –500 N
Es importante que los alumnos resuelvan bien el concepto de
que la fuerza de frenado se opone a la velocidad, al igual que
la de rozamiento. La consideración de positiva o negativa es
secundaria porque depende del convenio utilizado.
5 Un ascensor posee, al arrancar, una aceleración de
2,0 m/s2. Si una persona de 80 kg de masa sube en él,
¿cuánto vale la fuerza que actúa sobre el suelo del ascensor mientras éste tiene aceleración?
Dato: g0 = 9,80 m/s2
Como la persona sube con una determinada aceleración,
aplicamos la Segunda Ley de Newton:
Σ F = m a; P + Fsuelo ascensor = m a ⇒ (–m g) + Fsuelo ascensor =
= m a de donde
Fsuelo ascensor = m a – (–m g) = m (g + a) = 80 kg · (9,8 m/s2 + 2
m/s2) ≈ 940 N.
Es positiva la que actúa sobre la persona (va hacia arriba)
y negativa la que la persona ejerce sobre el suelo del ascensor.
Es importante que descubran que la aceleración final y el
peso tienen signos contrarios (hacia arriba y hacia abajo).
103
4 ESTÁTica DE FluiDoS
actividad de reFUerZO
PÁG. 118
1 ¿Qué ventaja tiene para un tanque tener cadenas en
las ruedas?
Cuando un vehículo se apoya para avanzar en una carretera,
o simplemente está estacionado, carga el peso de todo el
vehículo sobre cuatro pequeñas bandas rectangulares que
son las superficies de contacto rueda-suelo.
Si montamos el vehículo sobre cadenas, sobre todo en el
caso de que sea muy pesado, como un tanque, la superficie
de contacto es mayor, por lo que la presión no es tan grande
y el suelo no se hunde tanto como se hundiría si fuera sobre
ruedas.
actividad de reFUerZO
PÁG. 119
1 Calcula la presión que ejerce una pirámide cuadrada
de cristal de 3 kg de masa, sobre su cara inferior, que
tiene 20 cm de lado.
F m g 3 kg · 9,8 m/s 2
=
=
= 730 Pa
2
S 2
( 0,2 m)
actividad de
aMPliaciÓn PÁG. 119
1 Calcula la presión que ejerce la pirámide anterior
sobre otra cara si su altura también es 20 cm.
Tenemos que calcular el área de la cara. Para ello calculamos
la altura de la cara sabiendo que es la hipotenusa de un triángulo rectángulo formado por ella, la altura de la figura y la
mitad de un lado inferior de la pirámide.
h=
(0,2 m) + (0,1 m)
2
2
= 0,24 m
La presión será:
p=
F m g 2 · 3 kg · 9,8 m/s 2
=
=
=1200 Pa
S h
0,2 m · 0,24 m
2
actividad de reFUerZO
PÁG. 121
1 Calcula la presión a la que se ve sometido un objeto
cilíndrico de 20 cm de altura, cuando se introduce en el
104
No, la presión no es igual en todos los puntos del cilindro porque no todos tienen encima la misma columna de
agua.
La cara inferior experimenta una presión:
p = h d g = 4 m · 1 000 kg/m3 · 9,8 m s–2 = 39 200 Pa
La cara superior se encuentra a:
p = h d g = 3,8 m · 1 000 kg/m3 · 9,8 m s–2 = 37 600 Pa
actividad de
aMPliaciÓn PÁG. 121
1 ¿A qué profundidad debe bajar un objeto en un
océano para recibir una presión igual a la que tiene en
una piscina de mercurio de 1 m de profundidad? Dato:
dHg = 13 600 kg/m3.
La presión en el interior del mercurio es:
p = h d g = 1 m · 13 600 kg/m3 · 9,8 m s–2 = 1,33 · 105 Pa
Por lo tanto, en el interior del agua:
h=
La presión es:
p=
interior de una piscina de 4,00 m de profundidad. ¿Es
igual la presión en todos los puntos del cilindro?
p
1,33 ⋅ 105 Pa
=
= 13,6 m
d g 1000 kg/m3 ⋅ 9,8 m/s2
Evidentemente es la misma proporción que hay entre sus
densidades.
actividad de
aMPliaciÓn PÁG. 122
1 Sabiendo que la presión atmosférica vale 101 300 Pa,
calcula la presión total que actúa sobre un pulpo que se
encuentra a 7 m de profundidad en el mar.
Dato: dagua-mar = 1 035 kg/m3.
La presión debida a la profundidad a la que se encuentra es:
p = h d g = 7 m · 1 035 kg/m3 · 9,8 m s–2 = 71 000 Pa
Hay que añadir la atmosférica
pT = 71 000 Pa + 101 300 Pa = 172 300 Pa
actividad de
aMPliaciÓn PÁG. 123
1 Introducimos un tubo con una tapa inferior despegada de él en un recipiente con agua hasta una profundidad de 30 cm. Empezamos a añadir lentamente alcohol
en el tubo hasta que vemos que incluso supera el límite
del agua exterior sin que la tapa se separe. Cuando la
columna de alcohol mide 37 cm, la tapa se despega y se
va al fondo, mezclándose agua y alcohol. ¿Cómo puede
ser posible que la columna de alcohol fuera más alta que
la de agua? ¿Cuánto vale la densidad del alcohol?
La altura de la columna no es un dato ni importante, ni significativo. La columna tiene que tener la altura necesaria para
que la presión hacia abajo, producida por el alcohol, empiece
a ser mayor que la presión hacia arriba debida al agua.
La tapa se separará cuando se cumpla que:
palc = halc dalc g = pagua = hagua dagua g
de donde halc dalc = hagua dagua
0,37 m · dalc = 0,30 m · 1 000 kg/m3
dalc =
0,30 m · 1 000 kg/m3
= 810 kg/m3
0,37 m
actividad de
aMPliaciÓn PÁG. 126
1 Si al presionar el líquido contenido en un vaso comunicante con una presión de 5 000 Pa el nivel del líquido
desciende hasta estar 30 cm por debajo del nivel del otro
vaso, ¿cuál es el valor de la densidad del líquido?
La presión en cualquier punto al mismo nivel tiene que ser
la misma, por lo que la presión que ejercemos tiene que
ser igual a la presión del exceso de líquido, por lo que:
p = 5 000 Pa = h d g = 0,3 m · d · 9,8 m/s2
De donde d = 1 700 kg/m3
actividad de reFUerZO
PÁG. 126
1 Si en un lado de un vaso comunicante con otros tres
empujamos con un pistón el líquido hacia abajo, ¿qué sucede en el resto de los vasos comunicados? ¿Cómo puede
ser que el nivel del líquido sea distinto en los vasos?
Sucederá que el líquido asciende por igual en los otros tres
vasos, ya que la presión ejercida se transmite por igual a todos los vasos.
El vaso donde estamos haciendo la presión tiene el nivel
de líquido menor que los demás porque tiene una sobrepresión (la ejercida por nosotros) que equivale a la presión
ejercida por el exceso de columna de líquido que tienen los
demás.
actividad de reFUerZO
PÁG. 127
1 Una prensa hidráulica para levantar automóviles
tiene una superficie en la bomba de 30 cm2 en la que se
pueden ejercer fuerzas de hasta 850 N. Si la superficie
del otro pistón de la prensa es de 0,4 m2, ¿hasta cuánto
puede pesar el automóvil que pongamos encima para
poder levantarlo?
Aplicando:
Fb
Sb
=
=
Fauto
Sauto
; Fauto =
Fb Sauto
Sb
=
850 N · 0,4 m2
= 110 000 N
1 m2
2
30 cm ·
10 000 cm2
Como Fauto = mauto g despejamos mauto y obtenemos:
mauto = 11 500 kg
actividad de
aMPliaciÓn PÁG. 128
1 Busca en Internet o en enciclopedias actualizadas
en qué consiste y por qué funciona el ludión.
El funcionamiento es muy simple: cuando presionamos las
paredes de la botella, al estar ésta cerrada, estamos transmitiendo una presión extra a todo el líquido y todo lo contenido
en su interior, cumpliendo el Principio de Pascal.
El aire contenido dentro de la bolsa de tomate disminuye su
volumen debido a esta presión por lo que ahora el empuje
que el agua ejerce sobre la bolsa es menor, como predice
el Principio de Arquímedes, y, como el peso es el mismo, la
bolsa desciende.
Al dejar de presionar, el aire interior vuelve a su volumen inicial, el empuje aumenta y la bolsa asciende hasta su posición
inicial.
La sal tiene la utilidad de equiparar la densidad global de la
bolsa con la del agua que la rodea.
Se puede jugar a mantener la presión de forma que la bolsa
se mantenga en el centro del líquido.
Evidentemente es uno de los mejores ejemplos de líquido y
sólido de la misma densidad y por tanto de empuje idéntico
al peso.
actividad de reFUerZO
PÁG. 129
1 Dentro del mismo recipiente, ¿qué empuje será
mayor, el que se ejerce sobre un anillo de oro o el que se
ejerce sobre un anillo de plata del mismo tamaño? Datos:
doro = 19 300 kg/m3 y dplata = 10 500 kg/m3.
Éste es un problema trampa con el que pretendemos que los
alumnos fijen bien los conceptos.
Evidentemente, el empuje será el mismo puesto que sólo depende del volumen del cuerpo (en este caso igual), de
la densidad del líquido (la misma) y del valor de g (idéntico).
Lo que cambia es el porcentaje de peso que se ve reducido
por efecto del empuje que es mayor en el caso de la plata
que ve reducido su peso en un 10 % mientras que el anillo
de oro sólo experimenta un 5 % de reducción.
105
4
actividad de
aMPliaciÓn PÁG. 129
1 Calcula cuál será el peso aparente de un cuerpo de
densidad igual a 3 200 kg/m3 que en el aire pesa 35 N.
Calculamos el volumen del cuerpo.
m P/g
P
=
; de donde V =
=
V
V
dg
35 N
=
= 1,1 · 10 −3 m3
3 200 kg/m3 · 9,8 m/s 2
actividad de
aMPliaciÓn PÁG. 131
El empuje será:
E = d V g = 1 000 kg/m3 · 1,1 · 10 –3 m3 · 9,8 m/s2 = 11 N
Por lo que el peso aparente será:
Pap = P – E = 35 N – 11 N = 24 N
1 Si llenamos un vaso de agua hasta el borde y le añadimos unos hielos, evidentemente parte del volumen de
agua desbordará y caerá por los bordes.
Si en ese momento secamos la parte exterior del vaso,
¿volverá a desbordarse el agua, se mantendrá en el máximo nivel o descenderá de ese máximo?
d=
actividades de reFUerZO
PÁG. 130
1 Una balsa de madera se hunde cuando la introducimos en un recipiente con alcohol pero flota cuando la
introducimos en un recipiente con agua. ¿Qué conclusión
podemos sacar de ello?
Dejamos a la libertad del profesor el aportarles los datos de
densidad de agua y alcohol (800 kg/m3) que preferimos no
dar para no darles pistas de la solución.
La respuesta es que la densidad de la madera ha de estar
entre 800 y 1 000 kg/m3.
2 ¿Existe algún cuerpo que pueda permanecer encima
de un líquido sin que nada del cuerpo esté sumergido?
No. Es absolutamente imposible ya que para que se mantenga flotando sobre el líquido tiene que haber un empuje
que compense el peso del cuerpo y para que haya empuje tiene que haber una parte del cuerpo sumergida.
Hasta el corcho blanco (poliestireno expandido) tiene
una parte sumergida como pueden comprobar en casa.
La densidad del poliestireno expandido es de las menores
de los sólidos conocidos llegando a ser incluso inferior a
10 kg/m3.
actividad de reFUerZO
PÁG. 131
1 Tenemos, en una isla de la que queremos salir,
herramientas, cuerda y grandes troncos de madera de
densidad 1 200 kg/m3. No hay ningún objeto que flote.
¿Podríamos hacer algo para poder salir de la isla?
106
Evidentemente la solución es libre pero pretendemos que
los alumnos lleguen a la conclusión de que ahuecando el
interior de los troncos conseguimos que el peso sea menor
mientras que el empuje seguirá siendo el mismo (supuesto
el mismo nivel de hundimiento).
Es una forma de introducirles el concepto de que barcos
hechos de metal pesado flotan, puesto que tienen grandes
zonas llenas de aire que van por debajo del nivel del mar por
lo que, sin apenas peso, experimentan un gran empuje.
Se mantendrá en el mismo nivel sin desbordarse ni bajar.
Aunque les parezca que esto no tiene que ver con el Principio
de Arquímedes, la verdad es que es una demostración más
de dicho principio.
El hielo mantiene una parte por encima del nivel del agua y
por lo tanto por encima del nivel del vaso. Pero, por Arquímedes, sabemos que en ese momento el empuje es igual al
peso del volumen de agua desalojada, que es igual al peso
del hielo. Por lo tanto, el hielo al deshacerse ocupará el volumen que tenía el hielo sumergido, por lo que no aumentará
ni disminuirá el nivel de agua en el vaso.
En el siguiente enlace puede ver tres animaciones con las
posibles respuestas, para que elijan una:
http://webphysics.davidson.edu/physletprob/ch8_problems/ch8_11_fluids/default.html
actividad de reFUerZO
PÁG. 132
1 Cuatro prismas de la misma forma y tamaño, pero de
distintos materiales, se introducen en un recipiente con
agua de forma que el prisma C se va al fondo, el prisma
A se queda entre dos aguas (totalmente hundido pero
sin tocar el fondo), el B flota casi hundido y el D flota
claramente. ¿Qué conclusión podemos sacar de ello? ¿Y
si el prisma C fuera el doble de grande que el A, éste el
doble que el B y éste el doble que el D?
La conclusión es que las densidades de los cuerpos tienen el
siguiente orden creciente:
dD = dB = dA = dC
En el segundo supuesto no cambiaría nada, puesto que la
flotabilidad sólo depende de las densidades del agua y de
los cuerpos, y nunca de su forma ni tamaño.
actividad de
aMPliaciÓn PÁG. 132
actividad de
aMPliaciÓn PÁG. 137
1 Un prisma de 20 cm de altura flota cuando se introduce en el agua, dejando sumergidos 18 cm de su altura.
Si se introduce en alcohol, ¿flotará o se hundirá? Si en
otro líquido desconocido, de apariencia metálica, flota
dejando fuera del líquido 18,7 cm, ¿qué podemos decir
de ese líquido? ¿De qué líquido se trata (consulta en Internet o en enciclopedias actualizadas)?
1 Hemos construido un barómetro con un líquido de
densidad 3 000 kg/m3 y descubrimos que la columna de
líquido alcanza una altura de 3 m. ¿A qué presión nos
encontramos? Contesta en Pa, en atmósferas y en mm de
Hg. Si el barómetro lo hubiésemos hecho de mercurio,
¿qué altura alcanzaría la columna de mercurio en él?
Como flota se cumple que:
E = Vh dagua g = P = V dp g = S hagua dagua g = S h dp g
por lo que hagua dagua = h dp
dp =
hagua dagua
h
=
0,18 m · 1000 kg/m3
= 900 kg/m3
0,20 m
Aplicando el mismo razonamiento tenemos que:
d =
h dp
h
=
La presión valdrá:
p = h d g = 3 m · 3 000 kg/m3 · 9,8 m/s2 =
0,2 m · 900 kg/m3
= 13 800 kg/m3
0,013 m
El único líquido con apariencia metálica y esa densidad es el
mercurio, por lo que ése será el líquido.
No es necesario que contesten a esto, pero sí que calculen
la densidad.
actividad de reFUerZO
PÁG. 136
1 Suponiendo que la densidad del aire fuera constante
e igual a 1,29 kg/m3, calcula qué altura tiene la atmósfera.
Como la presión atmosférica es 101 300 Pa, aplicando la ecuación de la presión hidrostática:
p = h d g ; 101 300 Pa = h · 1,29 kg/m3 · 9,8 m/s2
de donde h = 8 000 m
Hay que explicar a los alumnos que este valor no es, ni con
mucho, cierto. La densidad del aire varía con la altitud, haciéndose menor a medida que ascendemos.
Por otro lado, en altura la temperatura desciende mucho y
ya que la densidad de cualquier gas aumenta rápidamente
con menores temperaturas, también este dato experimenta
una gran variación.
El valor de g para alturas de unos cuantos kilómetros no varía
apreciablemente.
= 88 000 Pa ·
1 atm
= 0,87 atm
101300 Pa
= 88 000 Pa ·
760 mm Hg
= 660 mm Hg
101300 Pa
La altura que alcanza es 66 cm (660 mm Hg).
actividad de reFUerZO
PÁG. 138
1 Con un barómetro que tenga una raya cada 5 mm de
Hg, ¿qué diferencia de altura se puede detectar? Dato:
daire = 1,29 kg/m3.
Utilizando la ecuación p = h d g y despejando la altura nos
queda:
101300 Pa
p
760 mm Hg
h=
=
= 53 m
dg
1,29 kg/m3 · 9,8 m/s 2
5 mm Hg ·
actividad de
aMPliaciÓn PÁG. 138
1 Con un barómetro medimos la presión en la base de
una montaña, obteniendo el valor 103 000 Pa. Ascendemos la montaña, de 850 m de altura, y observamos que
en la cumbre la presión es de 690 mm de Hg. ¿Cuál es la
densidad del aire?
Aplicamos ∆p = ∆h d g y despejamos d:
d=
∆p
=
∆h g
103 000 Pa − 690 mm Hg ·
=
850 m · 9,8 m/s 2
101 300 Pa
760 mm Hg
= 1,32 kg/m3
107
4
actividades
cOMPleMentarias
Datos comunes a todos los problemas: g = 9,80 m s–2 y
1 atm = 101 300 Pa.
1 Un acróbata de 80 kg de masa se encuentra realizando un ejercicio en el que está apoyado en el suelo
sólo con la palma de la mano. Si la presión que ejerce
sobre el suelo es de 58 000 Pa, ¿cuánto vale la superficie
de su mano? Compara dicha presión con la presión atmosférica.
Partiendo de la definición de presión:
2
 1m 
1500 kg ⋅ 9,8 m/s 2 ⋅ 100 cm2 ⋅ 
 100 cm 
=
=14 ,7 N
10 m2
Para elevar 1 m una superficie de 10 m2 el volumen que se
ocupa es 1 m · 10 m2 = 10 m3
El mismo volumen, sobre un émbolo de 100 cm2, equivale
a una altura de:
h=
V
=
S
10 m3
 1m 
100 cm2 ⋅ 
 100 cm 
2
=100 m
F
F m g 80 kg ⋅ 9,8 m/s 2
; S= =
=
≈1,35 ⋅ 10 −2 m2 =
S
p
p
58 000 Pa
=135 cm2
que se consiguen después de:
La presión que ejerce sobre el suelo es equivalente a:
1 000 m⋅
p=
58 000 Pa ⋅
1 atm
≈ 0,57 atm
101300 Pa
poco más de la mitad de la atmosférica.
2 Un batiscafo está preparado para aguantar una presión de 8 · 107 Pa. Sabiendo que la densidad del agua
marina es 1 035 kg/m3, ¿hasta qué profundidad puede
descender? ¿Y si descendiera en un mar de mercurio?
Aplicando la fórmula de la presión en el interior de un fluido:
p=d hg ; h=
p
8 ⋅ 107 Pa
=
≈ 7 900 m
d g 1 035 kg/m3 ⋅ 9,8 m/s 2
En el caso del mercurio:
p=d hg ; h=
p
8 ⋅ 107 Pa
=
≈ 600 m
d g 13 600 kg/m3 ⋅ 9,8 m/s 2
También se podría haber descontado la presión atmosférica,
ya que en el interior del mar también nos afecta la presión
atmosférica, pero el resultado apenas varía (10 m en el caso
del agua y 76 cm en el caso del mercurio).
3 En un taller de automóviles hay una prensa hidráulica con un émbolo de 100 cm2 de superficie y recorrido
(distancia en vertical que baja el émbolo en cada impulsión) 50 cm. Sobre el émbolo grande, de 10 m2 de superficie, situamos un vehículo de 1 500 kg. ¿Qué fuerza debe
ejercer el operario para levantar el vehículo? ¿Cuántas
veces debe impulsar el émbolo para elevarlo 1 m?
Aplicando la ecuación fundamental de las prensas hidráulicas:
108
f F
F s mgs
p = p' = =
; f=
=
=
s S
S
S
1 impulsión
= 2 000 impulsiones
0,50 m
4 Un cubo (hexaedro) de plástico, de 30 cm de lado, se
encuentra flotando en una piscina, siendo su densidad
600 kg/m3. Calcula la altura del cubo que sobresale del
agua. ¿Cuál es la masa de un perro que, situado sobre el
plástico, lo hunde hasta que sólo sobresalen 2 cm?
Utilizando la igualdad entre empuje y peso que se produce
en un cuerpo que flota:
E = P ; V ' dagua g = V d plástico g ⇒ S h' dagua g =
= S h d plástico g ⇒ h' dagua = h d plástico
h' =
h d plástico
dagua
=
30 cm ⋅ 600 kg/m3
=18 cm
1000 kg/m3
Los 18 cm corresponden a la parte hundida, que está dentro
del agua, por lo que sobresalen
30 cm – 18 cm = 12 cm
El peso del perro tiene que ser compensado por los 10 cm
extras de cubo que se hunden en el agua por lo que:
E = P = magua g0 = dagua V g0 =
= 1 000 kg/m3 (0,2 m . 0,1 m . 0,06) 10 m/s2 = 12 N
5 Situamos un barómetro en el exterior de una avioneta que marca, en el momento del despegue, una presión de 740 mm de Hg. Nos elevamos y en un momento
determinado observamos que el barómetro marca 680
mm de Hg. ¿A qué altura nos encontramos sobre la pista
de aterrizaje? Datos: densidad del aire: 1,30 kg/m3. Puedes suponer que la variación en la presión sólo se debe
a la diferente altura.
Aplicando la fórmula de la presión en el interior de un
fluido:
∆p = d ∆h g ; ∆h =
∆p
=
dg
101 300 Pa
(740 mm Hg − 680 mm Hg) ⋅
760 mm Hg
=
≈ 630 m
1,30 kg/m3 · 9,8 m/s 2
6 ¿Qué sucederá en el interior de un vaso invertido
en el que hemos introducido una cerilla encendida que
flotaba sobre un plato con agua (la cerilla puede mantenerse flotando si la clavamos sobre un trozo de cáscara
de naranja)? El vaso tiene su borde por debajo del nivel
del agua.
El nivel del agua dentro del vaso sube elevándose aproximadamente la quinta parte de la altura del vaso. La razón es que
el oxígeno del interior del vaso se consume produciéndose
CO2 que ocupa el mismo volumen. Pero el CO2 es soluble en
agua, por lo que se disuelve en ésta y deja un vacío en su
interior que hace que la presión externa sea mayor y, para
compensar cumpliendo los principios de igualdad de presión
hidrostática, el agua se eleva.
evalUaciÓn
1 Un ladrillo macizo de 20 cm de largo, 10 cm de ancho
y 6 cm de alto, tiene una masa de 4 kg. Calcula la presión
que ejerce sobre una mesa cuando se coloca sobre su
cara:
a) Más pequeña.
b) Más grande.
Datos: g0 = 10 m/s2.
El valor de la presión viene dado por el cociente entre la
fuerza que se ejerce y la superficie sobre la que se ejerce:
p=
F
S
pg =
b) pp =
La densidad viene dada por el cociente entre la masa y el
volumen.
d=
4 kg
≈ 3,3 · 103 kg/m3
0,2 m ⋅ 0,1 m ⋅ 0,06 m
El empuje ocasionado por un líquido es igual al peso del
líquido desalojado (Principio de Arquímedes). En nuestro
caso:
E = P = magua g0 = dagua V g0 = 1 000 kg/m3 (0,2 m . 0,1 m . 0,06)
10 m/s2 = 12 N
3 Situamos un automóvil de 1 200 kg de masa en el
lado mayor de una prensa hidráulica de 10 m2 de superficie. ¿Qué fuerza debe ejercer el operario sobre el extremo menor, de superficie 100 cm2, para poder levantar
el automóvil? Datos: g0 = 10 m/s2.
La prensa hidráulica se rige por el Principio de Pascal, por
el cual:
p=
F1 =
=
F1
S1
=
F2 S1
S2
F2
S2
=
⇒
m gg S1
S2
=
1200 kg ⋅ 10 m/s 2 ⋅ 100 mm2 ⋅ 10 −4 m2 /cm2
=12 N
10 m2
4 En una montaña de tu localidad la presión atmosférica en su cumbre es de 0,98 atm. ¿Cuál es la presión en
unidades del SI? Si la presión en la base de la montaña
es de 1,10 atm, ¿cuál es la altura de la montaña? Datos:
g0 = 10 m/s2 y densidad del aire = 1,30 kg/m3.
Calculamos la presión en unidades del SI.
En nuestro caso la fuerza la produce el peso del ladrillo que
es igual a P = m g; P = 4 kg · 10 m/s2 = 40 N.
La superficie más grande del ladrillo es Sg = 0,2 m · 0,1 m =
0,02 m2, mientras que la menor viene dada por Sp = 0,1 m ·
0,06 m = 0,006 m2. Por lo tanto:
a)
2 Calcula la densidad del ladrillo del problema anterior. ¿Cuánto vale el empuje que sobre él ejerce el agua
cuando se sumerge totalmente en un cubo de agua? Datos: g0 = 10 m/s2 y densidad del agua = 1 000 kg/m3.
40
= 2 000 Pa
0,02 m2
40 N
≈ 6,7 ⋅103 Pa
0,006 m2
Se comprueba que es mayor la presión sobre la cara más
pequeña.
parriba = 0,98 atm ·
101 300 Pa
≈ 99 000 Pa
1 atm
Por otro lado, la diferencia de presión entre la cima y la base
es debida al peso de la columna de aire, por lo que:
∆ pcima-base = (1,10 atm− 0,98 atm) ·
∆ p = d h g0 ⇔ h =
h=
∆p
d g0
101 300 Pa
≈12 000 Pa
1 atm
12 000 Pa
≈ 920 m
1,3 kg/m3 · 10 m/s 2
109
4
5 Un recipiente para el agua tiene forma
de tronco de cono invertido. El diámetro en
la parte superior es de 50 cm y en la parte
inferior de 10 cm. La altura de la vasija es de
30 cm. Calcula la presión en el fondo del recipiente, si no tenemos en cuenta el efecto de
la presión atmosférica. Datos: g0 = 10 m/s2 y
densidad del agua = 1 000 kg/m3.
La forma del recipiente no influye en el valor de la presión
en el fondo del recipiente, que sólo depende de la altura de
la columna de agua.
p = d h g0 = 1 000 kg/m3 · 0,3 m · 10 m/s2 = 3 000 Pa ≈ 0,03
atm
110
FuErZaS GraViTacionalES
5
actividad de
aMPliaciÓn PÁG. 152
actividad de
aMPliaciÓn PÁG. 161
1 Busca en Internet o en enciclopedias actualizadas
logros relacionados con la Astronomía que tuvieran
lugar antes del periodo de los antiguos griegos.
1 Calcula la distancia al centro de la Tierra a la que se
tiene que encontrar un objeto en la línea Tierra-Luna para que las fuerzas con la que le atraen la Luna y la Tierra
sean iguales.
Datos: distancia Tierra-Luna = 384 000 km; masa de la
Tierra: 6,0 · 1024 kg y masa de la Luna = 7,1 · 1022 kg.
Respuesta libre, que se debe utilizar para atraer a los alumnos
hacia este campo de la Ciencia.
actividad de
aMPliaciÓn PÁG. 155
1 Busca en Internet o en enciclopedias actualizadas
distintas teorías que expliquen el comienzo y el fin del
Universo, y críticas a estas teorías. Haz un pequeño trabajo con lo que hayas encontrado.
F = G
MT
d
2
=
MT m
d2
(d
= G
ML
TL
−d
)
2
(
ML m
d TL − d
d TL − d
;
d
3,84 ⋅10 8 m − d
=
d
)
2
;
=
ML
MT
7,1⋅1022 kg
= 0,11
6,0 ⋅1024 kg
3,84 ⋅10 8 m
=
1,11
Respuesta libre, donde hay que fomentar el estudio crítico de
las teorías intentando aportar pruebas que validen o nieguen
las hipótesis.
3,84 ⋅10 8 m = 1,11 d ; d =
actividad de
aMPliaciÓn PÁG. 158
A 350 000 km, aproximadamente.
1 Busca en Internet o en enciclopedias actualizadas
información sobre planetas extrapolares.
Respuesta libre. Al menos deben haber encontrado que en
1992 se encontraron tres alrededor de un púlsar, aunque fue
en 1995 cuando se encontró el planeta 51 Pegasi b, el primero
alrededor de una estrella habitual.
También son importantes el Gliese 876 d (el primero de tipo
terrestre) y el Gliese 581 c (el más parecido a la Tierra).
actividad de reFUerZO
PÁG. 160
1 Calcula la fuerza de atracción gravitatoria entre el
Sol y Mercurio sabiendo que la masa del Sol es de 2,0·1030
kg, la de Mercurio 3,3 · 1023 kg y la distancia media entre
ambos de 5,8 · 1010 m.
Aplicando la Ley de Gravitación Universal:
F = G
·
2
Mm
-11 N m
=
6,67
·
10
·
d2
kg2
2 · 1030 kg · 3,3 · 1023 kg
(5,8 · 10
10
m)
2
= 1,3 · 1022 N
= 3,5⋅10 8 m
actividad de reFUerZO
PÁG. 162
1 Calcula el peso de un individuo de masa 70 kg en la
superficie de la Tierra. Compáralo con el peso del individuo calculado como m g. ¿Qué conclusiones sacas de
ello?
Datos: radio de la Tierra = 6 370 km y masa de la Tierra:
6,0 · 1024 kg.
F = G
·
Mm
N m2
= 6,67 · 10-11
·
2
d
kg2
5,98 · 1024 kg · 70 kg
(6,37 · 106 m)
2
P = m g = 70 kg · 9,8
= 688 N
m
= 686 N
s2
Evidentemente, nos estamos refiriendo a la misma fuerza
calculada de dos formas distintas.
actividades
cOMPleMentarias
Dato común a todos los problemas: G = 6,67 · 10 –11 N m2
kg–2.
1 Calcula la distancia, expresada en km, a la que se
encuentra de la Tierra:
111
5
F =G
a)
b)
c)
d)
e)
La Luna, que está a 1,25 segundos-luz.
El Sol, que está a 8,5 minutos-luz.
Júpiter, cuando está a 40 minutos-luz.
Plutón, cuando está a 6 horas-luz.
La estrella Betelgeuse, que está a 300 años-luz de la
Tierra (es una de las más grandes, su diámetro es la
tercera parte de la distancia Tierra-Sol).
Dato: velocidad de la luz c = 3 · 108 m s–1.
Las distancias en tiempo-luz se calculan teniendo en cuenta
que la luz se mueve con un movimiento uniforme por lo que
d=c t
a) dLuna = c t = 3 · 108 m/s · 1,25 s = 3,75 · 108 m = 375 000 km
b) dSol = c t = 3 · 10 8 m/s · 8,5 min ·
=150 000 000 km
c)
60 s
≈1,5 · 1011 m =
1 min
= 720 000 000 km
d) dPlutón = c t = 3 · 10 8 m/s · 6 h ·
= 6 500 000 000 km
60 s
= 7,2 · 1011 m =
1 min
3 600 s
≈ 6,5 · 1012 m =
1h
e) dBete lg euse = c t = 3 · 10 8 m/s · 300 años ·
365,25 días
·
1 año
24 h 3 600 s
·
≈ 2,8 · 1018 m =
1 día
1h
= 2 800 000 000 000 000 km
⋅
2 Calcula la fuerza de atracción gravitatoria entre la
Tierra y Marte, sabiendo que sus masas son 6,0 · 1024 kg
y 6,6 · 1023 kg, y que sus centros están separados, por
término medio, 225 · 106 km.
Aplicando la Ley de Gravitación Universal de Newton:
⋅
MT MM
d
2
T −M
= 6,67 · 10 −11
N m2
·
kg2
6,0 · 1024 kg · 6,6 · 1023 kg
≈ 5,2 · 1015 N
(2,25 · 1011 m)2
3 Conociendo el radio de su órbita (2,9 · 1012 m) y el
tiempo que tarda en dar una vuelta alrededor del Sol
(84 años), podemos calcular la fuerza de atracción entre
Urano y el Sol que es igual a 1,4 · 1021 N. Sabiendo que la
masa del Sol es 2 · 1030 kg, calcula la masa de Urano.
Aplicando la Ley de Gravitación Universal de Newton:
F =G
112 =
MU MS
2
dU−S
⇒ MU =
2
F dU−S
G MS
=
1, 4 · 1021 N · (2,9 · 1012 m)2
≈ 8,8 · 1025 kg
2
N
m
6,67 · 10 −11 2 · 2 · 1030 kg
kg
⇒ MU =
2
dU−S
2
F dU−S
G MS
=
1, 4 · 1021 N · (2,9 · 1012 m)2
≈ 8,8 · 1025 kg
2
−11 N m
30
6,67 · 10
· 2 · 10 kg
kg2
4 Calcula la altura sobre la superficie terrestre a la cual
un objeto de masa 1 kg pesa la décima parte que en la
superficie. ¿Y un objeto de masa 10 000 kg? Dato: RT =
6,38 · 106 m.
Aplicando la Ley de Gravitación Universal de Newton:
F′ = G
MT m
(RT + h)
2
=
Mm
1
1
·P=
· G T2 ⇒
10
10
RT
10 · RT2 = (RT + h)2 ⇒ RT · 10 = RT + h
h = RT ·
d Júpiter = c t = 3 · 10 8 m/s · 40 min ·
F =G
=
MU MS
(
)
10 −1 ≈ 6,38 · 10 6 m · (3,16−1) ≈1,38 · 107 m
Aproximadamente, 2,16 veces el radio de la Tierra. La altura
será siempre la misma puesto que no depende de la masa
del objeto.
5 Haz un trabajo de 3 folios como máximo, consultando enciclopedias o Internet, sobre uno de estos temas:
a)
b)
c)
d)
Estrellas de neutrones.
Agujeros negros.
Constelaciones.
Galaxias.
Respuesta libre. Se puede aprovechar para leer o recordar a la
clase entera los aspectos más sobresalientes (por didácticos
o entretenidos) que se hayan aportado en los trabajos.
evalUaciÓn
1 Define los siguientes conceptos, explicando someramente en qué consiste:
a)
b)
c)
d)
Galaxia.
Big-Bang.
Agujero negro.
Planeta.
a) Galaxia: agrupación de miles de millones de estrellas
girando en torno a un eje común. Pueden ser elípticas,
espirales e irregulares, principalmente.
b) Teoría del Big-Bang: modelo que intenta explicar la formación del Universo a partir de la energía contenida en
un punto que fue dispersándose por el Universo a medida que éste se expansionaba, dando lugar a las partículas
componentes de la materia.
c) Agujero negro: estado final de una estrella de masa al
menos tres veces la del Sol. Su fuerza de atracción es tan
enorme que ni siquiera la luz puede escapar de él.
d) Planeta: objeto celeste que gira en torno a una estrella,
formado por el material que no ha sido aglomerado por
ésta, y que a menudo tiene otros objetos menores, llamados satélites, girando a su vez en torno a él.
4 ¿Cuánto vale la aceleración de la gravedad en la superficie de Venus? Ten en cuenta que la masa de Venus
es 0,82 veces la masa de la Tierra y su radio 0,95 veces el
de la Tierra. Dato: g0 = 9,80 m s–2.
2 Explica, brevemente, las diferencias fundamentales
entre la teoría heliocéntrica y la teoría geocéntrica, añadiendo cuál es la más acertada y quiénes son las personas
que las han defendido a lo largo de la Historia.
Se puede resolver de muchas maneras, aunque es un problema bastante difícil para ellos. La más normal será despejar
G del valor de la g0 de la Tierra y sustituir en la expresión de
g de Venus. De todas maneras, y para que aprendan relaciones de magnitudes, conviene resolvérselo de la siguiente
forma:
Teoría geocéntrica: modelo planetario que suponía que la
Tierra era el centro del Universo, alrededor de la cual giraban los demás planetas y el Sol. Su principal defensor fue
Ptolomeo, aunque este modelo era muy anterior a él (ya lo
expuso Aristóteles). Fue defendido por la Iglesia Católica incluso acusando de herejía a Galileo que mejoró la teoría.
Teoría heliocéntrica: modelo planetario (enunciado por
Copérnico) que supone que el Sol es el centro de nuestro
sistema, alrededor del cual giran los demás planetas, incluida la Tierra. Es la teoría considerada como correcta en la actualidad.
3 Calcula la fuerza de atracción que experimentan
entre sí dos petroleros, de 3 000 000 kg cada uno, que
se encuentran en un puerto a 50 m de distancia. Dato:
G = 6,67 · 10 –11 N m2 kg–2.
La fuerza de atracción entre dos cuerpos viene dada por la
Ley de Gravitación Universal de Newton. En nuestro caso:
F =G
g=G
MV
RV2
=G
0,82 ⋅ MT
(0,95 ⋅ RT )
=G
0,82 MT
G
= 0,91g0 =
0,952 RT2
= 0,91 ⋅ 9,8 m/s 2 = 8,9 m/s 2
5 Calcula la distancia a la que se encuentra, en unidades del Sistema Internacional, la Estrella Polar, que está
a unos 300 años-luz de la Tierra. Dato: c = 3 · 108 m s–1.
La distancia viene dada por el producto de la velocidad a la
que se mueve la luz por el tiempo que emplea en recorrer el
camino entre la estrella y nosotros por lo que:
e = v t = 3 · 108 m s–1 · 300 años · 365,25 días/año · 24 horas/día ·
∙ 3 600 s/hora = 2,84 · 1018 m
No pasa nada porque consideren que un año son 365 días.
Daría lo mismo.
Mm
d2
F = 6,67 · 10 −11 N m2 kg−2 ⋅
(3 · 10 6 kg)2
= 0,24 N
(50 m)2
113
6
TraBaJo, PoTEncia
Y EnErGÍa MEcÁnica
actividad de reFUerZO
PÁG. 172
1 ¿Qué tipos de energía conoces? ¿Con qué magnitud
están relacionadas? Recuerda lo que aprendiste en el
curso anterior. ¿Cuáles son las fórmulas de esos tipos de
energía?
Al menos deben conocer la energía cinética (relacionada con
la velocidad), Ec = 1/2 m v2 y la energía potencial (relacionada
con la posición —vale que contesten altura—) Ep = m g h
actividad de reFUerZO
PÁG. 174
1 De entre las siguientes situaciones contesta en cuáles se realiza trabajo y por qué:
a) Una presa llena de agua.
b) Un péndulo oscilando.
c) Un helicóptero mantiene a una persona colgando 10 m
por encima del suelo.
d) Sacamos el agua de un pozo dando vueltas a la manivela.
e) Estoy colgado de una barra horizontal antes de hacer
flexiones.
a) En la presa hay mucha energía potencial almacenada,
ya que el agua pesa (sí hay fuerza), pero mientras no se
suelte agua o se rompa la presa no hay desplazamiento,
por lo que no hay trabajo.
b) En el péndulo hay fuerza (el peso) y desplazamiento, por
lo que sí hay trabajo. Además es un trabajo periódico,
porque el péndulo, por efecto de la velocidad que lleva,
vuelve a subir, y vuelve a iniciarse el proceso.
c) El helicóptero gastará mucho combustible, pero aunque
haga fuerza a través del cable que sujeta a la persona,
ésta no se desplaza. No hay trabajo.
d) Aunque parezca que en la manivela no hay desplazamiento (lo hay pero pequeño), sí lo hay en la cuerda, y
hay una fuerza que eleva el agua. Sí hay trabajo.
e) Hay peso pero no desplazamiento. Hasta que no empecemos con las flexiones, no hay trabajo.
actividad de reFUerZO
PÁG. 175
1 Calcula el trabajo que realiza una fuerza de 60 N cuando el objeto se desplaza 10 m en la dirección y sentido de
la fuerza. ¿Y si la fuerza es en el sentido opuesto al desplazamiento? ¿Y si es perpendicular al desplazamiento?
W = F d = 60 N · 10 m = 600 J
W = F d = –60 N · 10 m = –600 J
114
No se produce trabajo, ya que no hay fuerza en el sentido y
dirección del desplazamiento.
actividad de
aMPliaciÓn PÁG. 176
1 Calcula el trabajo que realiza una locomotora de
15 000 kg de masa, cuando, al impactar sobre un vagón,
reduce su velocidad de 15 m/s a 5 m/s a lo largo de diez
metros de vía (calcula la fuerza que ejerce).
Con este problema pretendemos que vean que éste es un
problema complejo que, cuando aprendan a resolverlo por
conservación de energía será mucho más fácil.
Calculamos la aceleración aplicando la fórmula:
2 a s = v2 – v02
a=
52 − 152 m2 /s2
= 10 m/s2
2 · 10 m
La fuerza será:
F = m a = 15 000 kg · 10 m/s2 = 150 000 N
El trabajo será:
W = F d = –150 000 N · 10 m = –1,5·106 J
Debemos aprovechar para hacerles ver que hubiera dado
igual cuál fuera la distancia que el resultado sería el mismo
(por conservación de la energía nos daría también el mismo resultado) y que la fuerza es negativa, porque es la reacción del vagón al ser impulsado por la máquina, por lo que
va en sentido contrario al movimiento.
actividad de reFUerZO
PÁG. 177
1 Comenta al menos el nombre de diez herramientas
que conozcas y la forma en que actúan.
Respuesta libre. Martillo, destornillador, alicates, tenazas,
mandíbula, abrelatas, remo, palanqueta, balanza, tijeras,
cortauñas, palanca, polea, plano inclinado, abrebotes triangular, brazo, bate de béisbol, cascanueces, puerta, trampa
para ratones, arado, guadaña, fregona, escoba, cuchillo, pala, carretilla, arco, ballesta, honda, caña de pescar, stick de
hockey, balancín, prensa hidráulica, manillar, volante, manija,
picaporte, grúa (cigüeño), palanca de salto de trampolín, tornillo, calzador, maneta de freno, pedal, tirachinas, catapulta,
grapadora, quitagrapas, llave de tuercas, llave inglesa, pinzas,
cuchara, cepillo de dientes, mondadientes, sierra, freno de
bicicleta, etcétera.
Es importante que destaquemos a los alumnos las herramientas «no habituales» (las que nadie a priori consideraría herramientas) para que descubran que casi cada minuto del día estamos utilizando herramientas, aunque no las llamemos así.
actividad de reFUerZO
PÁG. 178
de la mano 40 cm y somos capaces de levantar con esa
mano 30 kg de masa. El músculo puede contraerse con
una fuerza de 3 000 N.
1 Encuentra las palancas de primer género que se
muestran en la página anterior.
30 kg · 9,8 m s–2 · 0,4 m = 3 000 N · x
x = 0,039 m = 3,9 cm
El martillo (cuando sacamos un clavo), destornillador (cuando abrimos botes con él), alicates, tenazas, abrelatas, remo
(apoyado en la barca), palanqueta, balanza, tijeras, polea,
balancín, grúa (cigüeño), calzador, catapulta (algún tipo),
cuchara, mondadientes, freno de bicicleta, etcétera.
actividades de reFUerZO
PÁG. 180
actividad de
aMPliaciÓn PÁG. 178
1 Una bombilla marca que su potencia es 150 W. Calcula su potencia en CV y en kW h.
150 W ·
1 CV
= 0,20 CV
735,5 W
1 Apretamos unas tenazas, haciendo una fuerza de
100 N a una distancia de 20 cm del fulcro. ¿Qué fuerza
estaremos haciendo sobre la cabeza del clavo que se encuentra a 3 cm del fulcro?
No se puede calcular la potencia en kW h al ser una unidad
de energía. Pero sí podemos calcular la energía desprendida,
en kW h, por segundo.
100 N · 0,2 m = F · 0,03 m
F = 670 N
150 W ⋅
actividad de reFUerZO
PÁG. 179
2 Si la bombilla anterior está funcionando durante
media hora, y suponiendo que toda la energía que emite
se transforma en calor, calcula qué calor desprende, en
J y kW h.
1 Encuentra las palancas de segundo y tercer género
que se muestran dos páginas antes de ésta.
De segundo género: remo (cuando apoyamos en el agua y
movemos el remo hacia adelante), cascanueces, puerta (con
resistencia en el centro), carretilla, manija, picaporte, palanca
de salto de trampolín, maneta de freno, pedal, grapadora,
llave de tuercas, llave inglesa, etcétera.
De tercer género: mandíbula, cortauñas, brazo, bate de béisbol, puerta (con resistencia en el extremo), trampa para ratones, arado, guadaña, fregona, escoba, pala, honda, caña de
pescar, palo de hockey, catapulta (con punto de apoyo en el
extremo), quitagrapas, pinzas, cuchara, etcétera.
actividades de
aMPliaciÓn PÁG. 179
1 J/s 1 kW h
⋅
= 4,2 · 10 –5 kW h/s
1 W 3,6 ⋅ 10 6 J
W = P t = 150 W · 1 800 s = 2,7 · 105 J
2,7 ⋅ 105 J ⋅
1 kW h
= 0,075 kW h
3,6 ⋅ 10 6 J
actividad de reFUerZO
PÁG. 181
1 Indica si los siguientes objetos tienen algún tipo de
energía mecánica y de qué tipo es:
60 N · (0,1 + 0,04) m = F · 0,04 m
F = 210 N
a) Un muelle lanzado desde lo alto de un edificio y comprimido.
b) Un coche arrugado por un choque, detenido en la
carretera.
c) El mismo coche, que se ha quedado en lo alto de un
árbol, y con las ruedas dando vueltas.
d) Un muelle dejado libre en lo alto de una estantería
por la que va girando.
e) El agua retenida en una presa.
f) El café que gira por efecto de la cucharilla en un vaso.
g) Un balón que golpea en la escuadra de una portería.
2 Calcula a qué distancia del hueso se engancha el tendón del brazo, si el brazo mide desde el codo al centro
a) Tiene energía cinética, potencial gravitatoria y potencial
elástica.
1 Calcula la resistencia de una cáscara de nuez que se
rompe cuando ejercemos una fuerza de 60 N si la distancia desde el fulcro a la nuez es de 4 cm mientras que la
nuez está a 10 cm de la mano.
115
6
b) No tiene ninguna.
c) Tiene energía cinética (en las ruedas que giran) y potencial gravitatoria (puede caer del árbol).
d) Tiene potencial gravitatoria (está en alto) y cinética (ya
que gira) pero no tiene elástica mientras no se comprima
o estire.
e) Tiene energía potencial gravitatoria.
f) Tiene energía potencial (si se rompiera la taza se caería)
y cinética (el café gira).
g) Tiene energía potencial gravitatoria (está en alto) y tiene
energía cinética (salvo en el momento en que está más
comprimido contra el poste) y potencial elástica (mientras esté ligeramente deformado contra el poste por el
choque).
actividades de reFUerZO
PÁG. 182
1 Un coche de 1 200 kg de masa choca a 20 m/s con
una farola, quedándose detenido contra ésta. ¿Cuánto
trabajo ha realizado el coche?
Sin necesidad de saber en qué se ha convertido, toda la energía cinética se ha transformado en otro tipo, por lo que el
trabajo será:
W = ∆Ec = 1/2 m · (vf 2 – v02) = 1/2 · 1 200 kg · (02 – 202 m2/s2) =
= 2,4 · 105 J
2 Si la farola del problema anterior se encontrara
enganchada a un bloque de cemento que es capaz de
ejercer una fuerza constante de 100 000 N en oposición
al movimiento, ¿cuánto se habrá desplazado la farola?
2,4 ⋅ 105 J
= 2,4 m
W = F d de donde d =
100 000 N
actividades de reFUerZO
PÁG. 183
1 Calcula el trabajo que ha realizado un saco de cemento de masa 25 kg cuando cae desde lo alto de una
obra desde los 42 m hasta una repisa que se encuentra
a 8 m de altura.
W = m g h = 10 kg · 9,8 m s–2 ·5 m = 490 J
W = F d luego d = W/F = 490 J/20 N
W = 24,5 m
Los 20 N son el peso del cuerpo puesto que la energía que le
hemos comunicado mediante un trabajo hace que se mueva
hacia arriba y, si actúa una fuerza constante de 20 N hacia
abajo debe ser el peso.
Los 24,5 m son de altura, por el enunciado del problema.
actividades de reFUerZO
PÁG. 184
1 Calcula cuánto se alargará un muelle de constante recuperadora k = 300 N/m cuando se le suministran
1 300 J de energía en forma de trabajo.
W = 1/2 k x2 de donde
x=
2 Si una vez estirado, se comprime medio metro antes
de soltar otra vez al objeto, ¿qué trabajo habrá realizado
sobre él?
W = 1/2 k (xf 2 – x02) = 1/2 · 300 N/m · (1,22 – 1,72) m2 =
= 2,2 · 102 J
El trabajo es negativo para el muelle que lo hace, pero es
positivo para el cuerpo que lo recibe.
actividad de reFUerZO
PÁG. 185
1 Un objeto de 15 kg cae desde 15 m de altura sobre una
red elástica de constante recuperadora k = 40 000 N/m.
Calcula a qué velocidad toca la red y cuánto se hunde en
ella el objeto. No consideres que pierde energía potencial al hundirse.
Ep = Ec ; 15 kg · 9,8 m s–2 · 15 m = 1/2 · 15 kg · v2
v=
W = m g (hf – h0) = 25 kg · 9,8 m s–2 · (42 – 8) m = 8,3 · 103 J
2 Un objeto de 10 kg cae desde 5 m de altura sobre
un balancín que golpea y lanza hacia arriba un objeto
sobre el que actúa una fuerza de 20 N. ¿Cuánta distancia
es capaz de recorrer? Tal como está planteado el problema, ¿qué tipo de fuerza es la de 20 N y hacia dónde se
desplaza el objeto?
116
2W
2 · 1300 J
=
= 1,7 m
k
300 N/m
9,8 m/s2 ⋅ 15 m
= 17 m/s
12
Ep = Ee ; 15 kg · 9,8 m s–2 · 15 m =
= 1/2 · 40 000 N/m · x2
x=
9,8 m/s2 · 15 m · 15 kg
= 0,33 m
1/2 · 400000 N/m
∆E p = m g ∆h = −∆Ec =1/ 2 m v 2 ⇒ ∆h =
actividad de
aMPliaciÓn PÁG. 186
1 Un objeto de 300 g cae sin rozamiento por una rampa circular desde 5 m de altura y, cuando llega a la parte
baja horizontal, entra en una superficie rugosa donde
pierde 3 J por rozamiento, empotrándose contra un muelle de constante recuperadora 20 N/m. Calcula a qué velocidad llega a la parte inferior, qué velocidad lleva cuando
impacta con el muelle y cuánto se comprime éste.
Ep = Ec ; 0,3 kg · 9,8 m s–2 · 5 m = 1/2 · 0,3 kg · v2
v=
9,8 m/s2 · 5 m
= 9,9 m/s
1/2
Ep = Ee = Ec’ + 3 J ;
0,3 kg · 9,8 m s–2 · 5 m – 3 J = 1/2 · 0,3 kg · v’2
9,8 m/s2 · 5 m · 0,3 kg − 3 J
v' =
= 8,8 m/s
1/2 · 0,3 kg
0,3 kg · 9,8 m s–2 · 5 m – 3 J = 1/2 · 20 N/m · x2
x=
actividades
cOMPleMentarias
1 Dejamos caer un cubo de acero de 40 kg de masa por
el hueco interior de un pozo industrial. ¿Cuál ha sido la
variación de su energía potencial cuando ha descendido
15 m? ¿Qué velocidad lleva en ese momento? Si llega al
nivel del agua con una velocidad de 40 m/s, ¿cuál es la
profundidad del pozo?
Aplicamos la ecuación de la variación de energía potencial:
∆Ep = m g ∆h = 40 kg · 9,8 m/s2 · (15 m) ≈ 5 900 J
Como la energía potencial perdida se emplea en aumentar
la energía cinética:
∆E p = m g ∆h = −∆Ec =1/ 2 m v 2
v = −2 g ∆h = −2 · 9,8 m/s 2 · ( −15 m) ≈17 m/s
Aplicando el mismo principio de conservación de la energía:
=
( − 40 m/s)2
≈ −82 m
2 · 9,8 m/s 2
( − 40 m/s)2
≈ −82 m
2 · 9,8 m/s 2
2 ¿Qué fuerza hay que ejercer en una palanca de primer
género, si la fuerza resistente es 70 N y su brazo 15 cm?
El brazo de la fuerza que ejercemos es 45 cm. ¿Y si fuera
de segundo género? ¿Y de tercero?
Aplicamos la ecuación de la palanca:
Fm dm = FR dR de donde Fm · 0,45 m = 70 N · 0,15 m por
lo que Fm ≈ 23 N
Si la palanca fuera de segundo género daría lo mismo pero
la fuerza motriz sería en el sentido contrario de la fuerza resistente.
No puede existir una palanca de tercer género con esas características ya que, al estar la fuerza motriz entre la fuerza
resistente y el fulcro, su distancia debe ser menor que la distancia resistente.
3 Calcula la potencia que desarrolla una avioneta de
4 800 kg de masa, que acelera desde 0 hasta 100 km/h
en 20 s. Con esa potencia, y suponiendo que pudiera utilizarse para subir en vertical con velocidad constante,
¿qué altura podría subir la avioneta en esos 20 s?
Calculamos la velocidad en m/s:
9,8 m/s2 ⋅ 5 m · 0,3 kg − 3 J
= 1,08 m
1/2 · 20 N/m
∆E p = m g ∆h = −∆Ec =1/ 2 m v 2 ⇒ ∆h =
=
−v 2
=
2g
−v 2
=
2g
100
km 1 h 1000 m
≈ 28 m/s
h 3 600 s 1 km
Aplicamos la ecuación de la potencia:
P=
W ∆Ec 1/ 2 m v 2 1/ 2 ⋅ 4 800 kg ⋅ (28 m/s)2
=
=
=
≈ 94 kW
t
t
t
20 s
La potencia se invierte en incrementar la energía potencial
según:
∆E p
Pt
⇒ P t = m g ∆h ⇒ ∆h =
=
t
mg
94 000 W ⋅ 20s
=
≈ 40 m
4 800 kg ⋅ 9,8 m/s 2
P=
4 Lanzamos un objeto, de forma que se desplaza por
el suelo con una energía cinética de 270 J. Si la fuerza de
rozamiento entre el cuerpo y el suelo vale 45 N, ¿cuántos
metros recorre antes de pararse?
Aplicamos la ecuación de conservación de la energía, transformándose en trabajo de rozamiento:
Ec 0 + Wroz = 0 = Ec 0 + Froz d ⇒ d = −
Ec 0
Froz
=−
270 J
=6 m
−45 N
117
6
5 ¿Qué potencia teórica (en kW) puede llegar a generar una central hidroeléctrica donde se deja caer el agua
desde 35 m de altura por una tubería que permite el paso
de 30 m3 de agua cada minuto? ¿Y en CV? ¿Con esa potencia, qué número de automóviles, de 1 200 kg de masa,
podrían hacerse acelerar desde el reposo a 120 km/h en
1 minuto?
De todas estas situaciones describe, si transcurren a
velocidad constante de 1 m/s, cuáles realizan trabajo y
cuáles no y cuánto vale ese trabajo.
Calculamos la masa que cae en 1 minuto por la tubería:
W=Fd ⇒ W=0·1m=0
30 m3 de agua
1000 kg
= 30 000 kg de agua
1 m3
Aplicamos la ecuación de la potencia:
En el apartado a) no se realiza trabajo porque, para mover
una caja sobre ruedas con velocidad uniforme la fuerza que
hacemos es igual a la de rozamiento que es cero.
En el apartado b) se realiza trabajo porque, para levantar una
caja con velocidad uniforme la fuerza que hacemos es igual
al peso de la caja.
W = F d ⇒ W = 40 kg · 9,8 m/s2 · 1 m ≈ 390 N
W ∆Ep m g h 30 000 kg · 9,8 m/s 2 · 35 m
=
=
=
≈
t
t
t
60 s
≈170 kW
P=
Pasamos los kW a CV
1 CV
170 000 W ·
≈ 231 CV
735 W
La velocidad a la que va el coche al cabo de 1 minuto es:
120
km 1 h 1000 m
≈ 33 m/s
h 3 600 s 1 km
La potencia necesaria para acelerar un automóvil con las
condiciones pedidas es:
P=
W ∆Ec 1/2 m v 2 1/2 · 1 200 kg · (33 m/s)2
=
=
≈
≈11 kW
t
t
t
60 s
por lo que, con la potencia que tenemos nos sirve para acelerar:
170 kW ·
1 automóvil
≈15 automóviles
11 kW
evalUaciÓn
Dato para todos los problemas: g0 = 9,80 m/s2.
1 Un repartidor de bebidas coge una caja de botellas,
de 40 kg de masa, del suelo de su camión y:
a) La arrastra 1 m, sobre unas ruedas y sin rozamiento.
b) La levanta 1 m hacia arriba.
c) La saca 3 m fuera del camión manteniéndola a la misma altura;
d) La arrastra 10 m, empujándola con el pie, por el suelo
de la calle que sí presenta rozamiento (10 N) con la
caja.
118
En el apartado c) no se realiza trabajo porque, para sacar una
caja manteniendo la misma altura la fuerza que hacemos es
vertical (para compensar el peso) pero el desplazamiento es
horizontal.
W = F d cos α ⇒ W = 40 kg · 9,8 m/s2 · 3 m · cos 90º = 0
En el apartado d) se realiza trabajo porque, para mover una
caja a velocidad uniforme, la fuerza que hacemos es igual a
la de rozamiento que es 10 N.
W = F d ⇒ W = 10 N · 10 m = 100 J
2 Contesta cuáles de los siguientes aparatos son palancas y cuáles no y di de qué género son. Calcula también
el peso de un cuerpo que va en una carretilla, si el obrero
que la lleva hace una fuerza de 400 N. La distancia del
cuerpo a la rueda de la carretilla son 60 cm y la del punto
donde el obrero coge la carretilla a la rueda es 1,10 m.
Objeto
Palanca
o no
Prensa hidráulica
No es una
palanca
Balancín de un parque
Palanca
Plano inclinado
No es una
palanca
Cascanueces
Palanca
2.o género
Manilla de freno de una bici
Palanca
2.o género
Pinzas
Palanca
3.er género
En una palanca se cumple:
por lo que:
Género de la
palanca
1.er género
Fobrero robrero = Fcuerpo rcuerpo
400 N · 1,10 m = Pcuerpo · 0,60 m
⇒
⇒
Pcuerpo = 730 N
3 Aplicando el Principio de conservación de la energía
mecánica calcula desde qué altura se ha lanzado un objeto (hacia arriba con una velocidad inicial de 10 m/s) si
llega al suelo con una velocidad de 30 m/s, suponiendo
que no hay rozamiento con el aire.
Se cumple el Principio de conservación de la energía:
m g h + 1/2 m v02 = 1/2 m v2
Eliminando la masa de la ecuación obtenemos:
9,8 m/s2 · h = 1/2 · (30 m/s)2 – 1/2 · (10 m/s)2 ⇒ h ≈ 41 m
4 Calcula la potencia que ha de tener una bomba de
agua para levantar 1 000 L de agua por minuto hasta
una altura de 45 m. Dato: 1 L de agua tiene una masa de
1 kg.
Dado que P t = W = ∆E y ya que el trabajo que se produce
se invierte en incrementar la energía mecánica, que es sólo
energía potencial, nos queda:
P t = m g h ⇒ P · 60 s = 1 000 kg · 9,8 m/s2 · 45 m
de donde P = 7 350 W
5 Sobre un muelle de constante k = 1 000 N/m dejamos
caer un cuerpo de 5,2 kg desde 2,5 m de altura. ¿Cuánto se comprime el muelle? Una vez que se comprime, se
vuelve a expandir lanzando el objeto hacia arriba. ¿Con
qué velocidad sale despedido? No hay rozamientos ni
pérdidas de energía en todo el proceso.
En el primer paso, toda la energía potencial gravitatoria se
transforma en energía potencial elástica:
m g h = 1/2 k x2 ⇒ 5,2 kg · 9,8 m/s2 · 2,5 m =
= 1/2 · 1 000 N/m · x2
despejando x nos queda: x ≈ 0,5 m
En el segundo paso, toda la energía potencial elástica se
transforma en energía cinética:
1/2 k x2 = 1/2 m v2
= 1/2 · 5,2 kg · v2
⇒ 1/2 · 1 000 N/m · (0,5 m)2 =
despejando v nos queda: v ≈ 6,9 m/s
119
7 calor Y EnErGÍa TÉrMica
actividad de reFUerZO
PÁG. 196
actividad de
aMPliaciÓn PÁG. 200
1 Si tenemos un cuerpo que se encuentra en el espacio exterior, a –270 ºC, ¿podrá transmitir calor al espacio
alrededor suyo que se encuentra a –256 ºC?
1 Convierte en julios y en calorías las siguientes cantidades de energía (si desconoces la unidad busca su
equivalencia en Internet o en una enciclopedia).
No puede hacerlo, puesto que el proceso será al revés: el
espacio le transmitirá calor a él, pero en pequeña cantidad
porque tendrá muy poca energía térmica.
a)
b)
c)
d)
100 Mcal
100 GJ
100 eV
100 kW h
a)
b)
c)
d)
100 Mcal = 108 cal = 4,18 · 108 J
100 GJ = 1011 J = 2,4 · 1010 cal
100 eV = 6,25 · 10 –18 J = 1,5 · 10 –18 cal
100 kW h = 3,6 · 108 J = 8,64 · 107 cal
actividad de
aMPliaciÓn PÁG. 196
1 Si los alumnos están interesados, se les puede pedir
que busquen en Internet algún artículo que hable sobre
el calórico, para que descubran una teoría errónea sobre la transmisión de calor, que estuvo vigente hasta el
siglo XIX.
Respuesta libre.
actividad de
aMPliaciÓn PÁG. 198
1 Busca en Internet información sobre otras escalas
de temperatura que han existido o existen y comenta a
qué temperatura equivale el punto de fusión del hielo y
el punto de ebullición del agua.
Respuesta libre.
actividad de reFUerZO
PÁG. 199
1 Convierte en unidades de las otras dos escalas, las
siguientes temperaturas:
120
a)
b)
c)
d)
e)
f)
100 K
100 ºC
100 ºF
–100 ºC
–100 K
–100 ºF
a)
b)
c)
d)
e)
f)
100 K = –273 ºC = –459 ºF
100 ºC = 373 K = 212 ºF
100 ºF = 38 ºC = 311 K
–100 ºC = 273 K = –148 ºF
No se puede. No hay temperaturas negativas en kelvin.
–100 ºF = –73 ºC = 200 K
actividades de
aMPliaciÓn PÁG. 202
1 Calcula la temperatura final que alcanza el agua contenida en un recipiente (200 g) a 20 ºC cuando sobre ella
se añade un anillo de oro de 5 g que se encuentra a 150 ºC.
Utiliza los datos de la tabla de calores específicos.
Qabs = m2 c2 (Tf – T2) = Qced = m1 c1 (T1 – Tf)
0,2 kg · 4 180 J/kg K · (Tf – 20 ºC) =
= 0,005 kg · 130 J/kg K · (150 ºC – Tf)
Despejando:
836 Tf – 16 720 = 97,5 – 0,65 Tf
Tf = 16 817,5/836,65 = 20,1 ºC
2 ¿En cuánta cantidad de agua a 10 ºC hay que sumergir una barra de 5,0 kg de hierro a 1 000 ºC para que se
pueda coger con la mano sin que dé sensación de calor
(37 ºC)?
Qabs = m2 c2 (Tf – T2) = Qced = m1 c1 (T1 – Tf)
x · 4 180 J/kg K · (37 ºC – 10 ºC) = 5 kg · 440 J/kg K · (1 000 ºC
– 37 ºC)
Despejando:
112 860 x = 2 118 600
x = 2 118 600/112 860 = 18,8 kg
actividad de
aMPliaciÓn PÁG. 203
1 Busca, en enciclopedias o en Internet, las sustancias
que tengan los valores de calor latente de fusión y ebullición más extremos (mayor y menor) y compáralos con
los que han encontrado tus compañeros.
Comparamos los que han ido trayendo los alumnos, comprobamos posteriormente si son válidos (por ejemplo en
Internet) y podría ser interesante premiar a los alumnos que
hayan encontrado los valores más extremos con un «punto
positivo».
actividad de reFUerZO
PÁG. 204
Qabs = W + Qdes por tanto:
Qdes = 3 000 kcal – 3 000 000 J ·
1 kcal
1 cal
·
=
4,18 J 1000 cal
= 2 280 kcal
η=
Qabs − Qdes
Qabs
=
720 kcal
= 0,24 = 24 %
3 000 kcal
1 Compara la cantidad de calor que absorbe 1 kg de
agua al:
actividades de
aMPliaciÓn PÁG. 208
a)
b)
c)
d)
e)
1 Busca en Internet o en una enciclopedia actualizada
datos sobre el consumo y producción de energía en el
mundo y sobre el porcentaje de utilización de las distintas fuentes de energía. Haz un trabajo de recopilación
para entender si hay o no problema energético.
Aumentar un grado su temperatura.
Fundirse a 0 ºC.
Ebullir a 100 ºC.
Irse fundiendo desde los 10 ºC hasta los 20 ºC.
Compara los resultados.
a)
b)
c)
d)
Q = m ce (Tf – T0) = 4 180 J
Q = m cL = 334 000 J
Q = m cL = 2 250 000 J
El agua no se va fundiendo a lo largo de un intervalo, sino
que lo hace a una temperatura concreta; en este caso,
0 ºC.
e) Se necesita el mismo calor para convertir en vapor 1 kg
de agua a 100 ºC que para fundir 6,7 kg de hielo a 0 ºC
o que para elevar la temperatura de ¡80 kg de agua
80 ºC!
actividad de
aMPliaciÓn PÁG. 204
1 Una persona haciendo deporte suda y elimina el sudor evaporando un total de 100 g de agua. Si todo el calor
utilizado en la evaporación procede de la persona, y ésta
se encuentra a 37 ºC, ¿cuántas calorías ha eliminado por
este método?
El calor se utiliza en calentar el agua hasta 100 ºC y posteriormente en evaporarla con lo que:
Q = m ce (Tf –T0) + m cL = 0,1 kg · 4 180 J/kg K · (100 – 37) ºC +
0,1 kg · 22,5 · 105 J/kg = 26 334 + 225 000 = 2,5 · 105 J = 60 kcal
actividad de reFUerZO
PÁG. 207
1 Si una máquina térmica obtiene 3 000 kcal del foco
caliente y consigue transformar en trabajo 3 MJ, ¿cuánto
calor ha desprendido hacia el exterior (cuerpo frío)? ¿Con
qué rendimiento ha actuado?
Como la energía ni se crea ni se destruye, el calor que obtiene
del cuerpo caliente se emplea en parte en producir trabajo y
en parte se desprende hacia el exterior por lo que:
Respuesta libre.
2 En un mapamundi, colorea las zonas donde hay recursos energéticos importantes (gas, petróleo, etcétera).
Respuesta libre.
actividades
cOMPleMentarias
Datos comunes a todos los ejercicios: ce agua = 4 180 J/kg
K; ce hielo = 2 050 J/kg K; calor latente de fusión del agua =
= 334 kJ/kg.
1 Nos dicen que la temperatura en la superficie de un
planeta expresada en grados Fahrenheit es la mitad de
la temperatura en grados centígrados. ¿Es eso posible?
¿A qué temperatura? ¿Sería posible lo mismo en grados
Fahrenheit y en Kelvin? ¿A qué temperatura? ¿Sería posible lo mismo en grados centígrados y en Kelvin? ¿A qué
temperatura?
Como la fórmula que relaciona la temperatura en la escala
Fahrenheit con la escala centígrada es:
T (º C) T (º F)− 32
=
100
180
se tiene que cumplir que:
x x /2− 32
=
2
180
de donde 180 · x = 50 · x – 3 200 y x = –25. Sí es posible:
la temperatura es aproximadamente –25 ºC que equivalen
a –13 ºF.
La fórmula que relaciona la temperatura en la escala Fahrenheit con la escala Kelvin es:
121
7
T (K)− 273 T (º F)− 32
=
100
180
se tiene que cumplir que
x − 273 x /2− 32
=
100
180
2 ¿Cuántos gramos de agua podemos calentar desde
20 ºC a 30 ºC con la misma cantidad de energía que hemos suministrado a 1 kg de cobre al que hemos elevado
50 ºC su temperatura? Dato: ce cobre = 385 J/kg K.
Igualamos la energía absorbida en forma de calor por el cobre y por el agua:
Qcobre = mCu c e ∆T = Qagua = magua c e (T2 −T1 )
magua =
agua
mCu c e ∆T
1000 g ⋅ 385 J/kg K ⋅ 50 ºC
=
≈ 460 g
(T2 −T1 ) 4180 J/kg K ⋅ (30 ºC− 20 ºC)
Cu
ce
agua
3 Una bala de 20 g impacta a 450 m/s en un cilindro
que contiene 1 L de agua. Si toda la energía de la bala
pasa al agua, ¿a qué temperatura se encontrará el agua
al final, si estaba a 20,0 ºC? Dato: considera despreciable
el aumento de temperatura del metal de la bala.
Igualamos la energía cinética con la absorbida en forma de
calor por el agua:
∆Ec =1/ 2 mbala v = Qagua = magua c e
2
Tf =
1/ 2 mbala v 2
magua c e
agua
(T2 −T1 )
+T0
1 kg
· (450 m/s)2
1000 g
+ 20,0 ºC ≈ 20,5 ºC
1 kg · 4180 J
K kg
4 ¿Cuánto calor hay que suministrar a 100 g de hielo
a –15 ºC para convertirlos en 100 g de agua a 60 ºC?
Hay que calcular el calor necesario para llevar el hielo hasta
0 ºC, el calor necesario para fundirlo y el calor necesario para
llevarlo a 60 ºC y sumarlos, por lo que:
122
Q3 = magua c e (Tf − 0 ºC) = 0,06 kg · 4180 J/kg K ·
agua
⋅ (60ºC− 0ºC) ≈15 000 J
QT = Q1 + Q2 + Q3 ≈ 2 500 J+ 20 000 J+15 000 J = 37 500 J
5 ¿Qué potencia calorífica tiene una llama que es capaz, en una hora, de calentar y llevar desde –18 º C un
1 kg de hielo hasta los 20 ºC?
El calor que ha de captar el hielo es igual a:
Q1 = mhielo ce (0 ºC−T0 ) =1 kg · 2 050 J/kg K ·
hielo
⋅  0 ºC−( −18 ºC)  ≈ 37 000 J
Q2 = magua c L =1 kg · 334 000 J/kg K = 334 000 J
Q3 = magua ce (Tf − 0 ºC) =1 kg · 4180 J/kg K · (20 ºC− 0 ºC) ≈
agua
≈ 84 000 J
QT = Q1 + Q2 + Q3 = 37 000 J + 334 000 J + 84 000 J = 455 000 J
Por lo que la potencia será:
P=
Q
455 000 J
=
≈126 W
3 600 s
t
1h ⋅
1h
evalUaciÓn
1 Calcula la temperatura, expresada en grados Kelvin
y en grados Fahrenheit, a la que está ardiendo un libro,
si en la escala Celsius sucede a 233 ºC.
agua
1/ 2 · 20 g ·
Tf =
hielo
⋅  0ºC−( − 20ºC)  ≈ 2 500 J
Q2 = magua c L = 0,06 kg · 334 000 J/kg K ≈ 20 000 J
de donde 180 · x – 49 140 = 50 · x – 3 200 y x = 353. Sí
es posible: la temperatura es aproximadamente 353 K que
equivalen a 176 ºF.
La fórmula que relaciona la temperatura en la escala centígrada con la escala Kelvin es:
T (K) – 273 = T (ºC) se tiene que cumplir que: x – 273 = x/2
de donde x/2 – 273 = 0 y x = 546.
Sí es posible: la temperatura es aproximadamente 546 K que
equivalen a 273 ºC.
Cu
Q1 = mhielo c e (0 ºC−T0 ) = 0,06 kg · 2 050 J/kg K ·
Utilizando las ecuaciones de conversión:
180 ⋅ T (ºC)
180 ºF ⋅ 233 ºC
+ 32 =
+ 32 ºF ≈ 451 ºF ;
100
100 ºC
T (K) = T (ºC)+ 273 = 506 K
T (ºF) =
2 La energía potencial que tiene un objeto de plomo
de 0,2 kg es de 200 J. Si lo dejamos caer, toda su energía
cinética se emplea en subir la temperatura del plomo.
¿Cuánto calor, expresado en calorías, recibe el objeto?
¿Cuánto se incrementa su temperatura? Datos: 1 cal =
= 4,18 J; ce plomo = 130 J/ºC kg.
1 cal
≈ 48 cal
4 ,18 J
Q
200 J
Q = m c e ∆T ⇒ ∆T =
=
≈ 7,7 ºC
m c e 0,2 kg ⋅ 130 J/ºC kg
Q = 200 J ⋅
3 Si introducimos en 200 g de agua a 20 ºC una pieza
de aluminio de 50 g que se encuentra a 98 ºC, observamos que la temperatura final del conjunto es de 24 ºC.
¿Cuál es el calor específico del aluminio? Dato: ce agua =
= 4 180 J/ºC kg.
m c e (Tf −T0 ) = − m′ c e′ (Tf − T0′) ⇒
c e′ =
m c e (Tf −T0 )
− m′ (Tf − T0′)
=
0,2 kg · 4180 J/ºC kg (24 ºC− 20 ºC)
≈
−0,05 kg (24 ºC− 98 ºC)
plomo. ¿Qué diferencias se producen al calentar la misma
masa de agua y plomo con la misma cantidad de calor?
Que es más difícil convertir energía térmica en otro tipo de
energía que al revés. El rendimiento en esa conversión es
siempre muy bajo, por lo que la cantidad de energía térmica
del Universo va aumentando, mientras que las demás van
disminuyendo.
Al ser mayor el calor específico del agua, la temperatura de
ésta asciende más lentamente que en el caso del plomo.
5 Una máquina térmica aprovecha el vapor producido
en la combustión de carbón (se producen 50 kcal) para
conseguir el movimiento de un cuerpo, que parte del reposo. Si el cuerpo tiene de masa 1 000 kg y la velocidad
a la que se mueve al final es de 12 m/s, ¿cuál es el rendimiento de la máquina?
≈ 900 J/ºC kg
El rendimiento es igual a la proporción entre la energía cinética que se gana y la cantidad de energía térmica que aporta
la máquina:
4 Cuando decimos que la energía térmica es la forma
más degradada de la energía, ¿qué es lo que pretendemos indicar? A lo largo de la Unidad habrás podido comprobar que el calor específico del agua es mayor que el del
η=
1/2 m v 2 1/2 · 1 000 kg (12 m/s) 2
=
≈ 0,34 = 34 %
1 000 cal 4 ,18 J
Q
50 kcal
1 kcal 1 cal
123
8
la EnErGÍa DE laS onDaS:
luZ Y SoniDo
actividades de reFUerZO
PÁG. 221
Las vías del tren resultan un medio óptimo para trasladar
el sonido, porque canalizan las ondas a lo largo de grandes
distancias.
1 Calcula la frecuencia de un movimiento ondulatorio
con un periodo de 4 s.
actividad de
aMPliaciÓn PÁG. 222
Como la frecuencia y el periodo son inversos:
1
1
f= =
= 0,25 ciclos/s = 0,25 Hz
T 4 s/ciclo
2 Calcula la longitud de onda de un movimiento ondulatorio que avanza a razón de 1,5 km cada segundo si
la frecuencia es de 20 Hz.
Como la relación entre estas magnitudes es λ f = v
v 1500 m/s
λ= =
= 75 m/ciclo
f 20 ciclos/s
Como ambos sonidos salen al mismo tiempo y uno se mueve
a 5 050 m/s (a través de la vía) y otro a 330 m/s (a través del
aire), con movimiento uniforme se cumple que:
actividad de
aMPliaciÓn PÁG. 221
s = v t = 5 050 m/s · t y s = 330 m/s · (t + 20 s)
1 Al hacer una foto de una onda, podemos contar
que en un metro hay 350 longitudes de onda completas
mientras que con un detector de vibraciones hemos logrado contar hasta 1 000 000 de vibraciones en una hora.
¿A qué velocidad se desplaza la onda?
t = s/5 050 y s = 330 · (s/5 050 + 20)
5 050 s = 330 s + 33 330 000
4 720 s = 33 330 000 m ; s = 7 km
Si en un metro caben 350 longitudes de onda,
1 m = 350 λ ⇒ λ = 1 m/350 = 2,9 · 10 –3 m
Si se producen un millón de vibraciones en una hora,
f =
1000 000 ciclos
= 278 Hz
3 600 s
1h·
1h
Como v = λ f = 2,9 · 10 –3 m · 278 Hz = 0,8 m/s
actividad de reFUerZO
PÁG. 222
1 ¿Por qué los indios de Norteamérica ponían el oído
en el suelo para oír si llegaban los caballos del Séptimo
de Caballería? ¿Qué ventajas tiene ese método? ¿Era correcto entonces pegar el oído a las vías del tren?
El sonido se transmite mejor por el suelo o por el hierro de
la vía, ya que el medio portante es mejor para esa transmisión.
El sonido que se oye llega más rápido, más nítido y con mayor
energía, por lo que alcanza mayores distancias.
124
1 Queremos saber a qué distancia se encuentra una
estación de tren. Sabemos que en el mismo instante que
empieza a moverse suena la bocina. Ponemos el oído en
la vía de hierro y en cuanto percibimos el movimiento
del tren nos incorporamos y, al cabo de 20 s, oímos el
silbato.
¿A qué distancia se encuentra la estación? Obtén los datos que necesites de la Tabla 8.1 del libro del alumno.
Por lo que:
actividad de reFUerZO
PÁG. 223
1 Una persona grita en un desfiladero y oye el eco que
llega 1,2 s después de haber oído el sonido original. ¿A
qué distancia se encuentra de la pared rocosa?
Como el sonido va a una velocidad de 330 m/s, en 1,2 s
recorre:
s = v t = 330 m/s · 1,2 s = 396 m
Como este espacio se ha recorrido en que el sonido vaya y
venga de la pared rocosa, la distancia es la mitad por lo que
estamos a 198 m de la pared.
actividad de
aMPliaciÓn PÁG. 223
1 Una persona grita desde la ventanilla de un coche
que se dirige con velocidad uniforme hacia una montaña que se encuentra 400 m delante del vehículo y percibe
que el sonido le llega 2,2 s después de haberlo emitido.
¿A qué velocidad va el vehículo?
El sonido emitido tarda en llegar a la pared
t=
s
400 m
=
= 1,21 s
v 330 m/s
por lo que quedan 0,99 s
en esos 0,99 s el sonido recorre:
s = v t = 330 m/s · 0,99 s = 327 m
Por lo tanto, el relámpago realmente ha tardado:
s = v t ⇒t =
s
1,42 km
=
= 5⋅10 −6 s
v 300 000 km/s
por lo que el coche ha recorrido 400 – 327 m = 73 m en 2,2 s,
por tanto su velocidad es:
actividad de reFUerZO
PÁG. 227
3 600 s
s 73 m
m 1 km
v= =
= 33
·
·
== 120 km/h
t 2,2 s
s 1000 m
1h
= 120 km/h
1 Calcula la velocidad de la luz en el interior de un diamante. ¿Habrá algún medio en el que vaya más lento que
en el diamante?
actividad de
aMPliaciÓn PÁG. 224
1 Se les puede pedir a los alumnos que encuentren
en Internet o en enciclopedias, información sobre qué
es una ecografía y para qué se utiliza.
También pueden buscar la utilidad de los ultrasonidos
para romper cálculos renales y otras aplicaciones médicas.
Respuesta libre.
actividades de reFUerZO
PÁG. 226
1 Si la luz del Sol tarda 8,5 min en llegar a la Tierra y la
velocidad de la luz en el vacío es de 300 000 km/s, calcula
a qué distancia de la Tierra se encuentra el Sol.
Como la luz se mueve en línea recta y con un movimiento
uniforme se cumple que:
s = v t = 300 000 000 m/s · 510 s = 1,5 · 1011 m
2 Calcula cuánto tarda un rayo de luz en llegar de la
Tierra a la Luna, si la distancia entre ambas es de 380 000
km.
Como s = v t ⇒ t =
s
380 000 km
=
= 1,3 s
v 300 000 km/s
Como n =
v=
c
despejando v:
v
c 300 000 km/s
=
= 125 000 km/s
n
2,41
No, el diamante es la sustancia con el mayor índice de refracción.
actividades
cOMPleMentarias
Datos comunes a todos los problemas: velocidad del
sonido en el aire = 340 m/s; velocidad del sonido en el
agua = 1 450 m/s y velocidad de la luz en el vacío = 3 ·
· 108 m s–1.
1 Calcula la longitud de onda y la frecuencia de una
onda sonora que se mueve por el agua con un periodo
de 1 milésima de segundo.
Aplicando la fórmula de la velocidad de un movimiento uniforme:
e = v t de donde λ = 1 450 m/s · 0,001 s = 1,45 m
y la frecuencia
f=
1
1
=
=1000 Hz
T 0,001 s
actividad de
aMPliaciÓn PÁG. 226
2 Pegados a la pared de un lado de un cañón profundo
gritamos, percibiendo el eco que se produce al cabo de
0,25 segundos. ¿Cuál es la distancia al otro lado del cañón? Si en vez de estar al aire estuviéramos en una sima
marina, ¿tardaría más o menos o no se oiría eco?
1 Si oímos un trueno 4,3 s después de ver el relámpago, ¿cuánto ha tardado en llegarnos el relámpago?
En el tiempo que la onda vuelve a llegar a nuestros oídos, ésta
ha recorrido dos veces la anchura del cañón, por lo que:
Utilizamos la aproximación (en primera instancia) de que el
relámpago llega instantáneamente. Desde ese punto de vista
el rayo ha caído a:
2 d = v t = 340 m/s · 0,25 s
s = v t = 330 m/s · 4,3 s = 1 420 m
2 d ≈ 85 m = v t = 1 450 m/s · t
;
de donde
d ≈ 42 m
Si se moviera en el agua tardaría:
;
de donde t ≈ 0,06 s
125
8
Aunque en el agua las ondas se oyen mejor y alcanzan distancias mayores que en el aire, al tardar el eco sólo 0,06 s, no
se puede percibir ya que el oído sólo percibe sonidos que
lleguen con, al menos, 0,1 s de diferencia, No se oiría eco.
3 ¿Qué cualidad sonora distingue dos notas distintas
obtenidas al tocar una flauta? ¿Y dos notas obtenidas al
tocar distintos instrumentos musicales? ¿Y la nota de una
guitarra eléctrica que está conectada al amplificador de
la obtenida si no lo enchufamos al amplificador?
Las dos notas se distinguen por su frecuencia, por lo que son
de distinto tono.
Las de dos instrumentos musicales, aun siendo de la misma
frecuencia, se podrían distinguir por el timbre, esto es, la
composición de armónicos que la forman.
Las dos notas dadas en la guitarra se distinguirían por su
energía (su amplitud) lo que daría lugar a dos sonoridades
diferentes, con dos valores distintos en sus decibelios.
4 Si la velocidad de la luz en el interior de un cristal
es de 200 000 km/s, ¿cuál es el índice de refracción del
cristal?
El índice de refracción se calcula dividiendo la velocidad de
la luz en el vacío entre la velocidad de la luz en el medio,
por lo que:
c 3 ⋅ 10 8 m/s
n= =
=1,5
v 2 ⋅ 10 8 m/s
5 ¿Qué nota es más aguda en el aire, la que tiene una
longitud de onda de 77 cm o la que su longitud de onda
vale 50 cm? Calcula también la frecuencia de ambas.
Calculamos primero la frecuencia de ambas ondas:
λ
v 340 m/s
= λ f de donde f1 = =
= 440 Hz
T
λ 0,77 m
λ
v 340 m/s
v = = λ f de donde f2 = =
= 680 Hz
T
λ 0,50 m
v=
Como a mayor frecuencia más aguda es la onda, la onda más
aguda es la que tiene una longitud de onda de 50 cm.
6 Si el periodo de un movimiento ondulatorio es de
5 · 10 –5 s y su longitud de onda son 75 mm, ¿a qué velocidad se propaga?
Como la velocidad es v = λ f =
λ
v= =
T
126
λ
T
1m
1 000 mm =1 500 m/s
5 · 10 -5 s
75 mm ·
evalUaciÓn
1 Una onda sonora se propaga por el agua a una velocidad de 1 500 m/s. Si la longitud de onda es 1 cm, ¿cuál
es su frecuencia? ¿Cuál su periodo? ¿Sabrías decir si es
longitudinal o transversal?
Como vp = λ f ⇒ 1 500 m/s = 0,01 m · f
de donde f = 150 000 s–1 = 0,15 MHz
El periodo es la magnitud inversa de la frecuencia por lo
que T = 1/150 000 s–1 = 6,7 · 10 –6 s
Las ondas sonoras son ondas de presión que se transmiten
por las sustancias por lo que son ondas longitudinales. Las
ondas transversales no se pueden transmitir por el interior
de fluidos.
2 Habrás observado muchas veces que los auditorios
de música no tienen una forma habitual en otro tipo de
edificios. En los estudios de grabación de música las paredes están formadas, en toda su extensión, por una especie de cajas de las que contienen huevos. ¿Por qué? ¿A
qué fenómeno o fenómenos, relacionados con el sonido,
está asociado este hecho?
Las formas diferentes de los auditorios y las «cajas de huevos»
absorben la mayoría de las ondas sonoras que se dirigen a
ellas con lo que el sonido que se crea o se percibe en el interior del local sólo se dirige de forma directa a los oídos o
cintas de grabación, evitando ecos o reverberaciones que
impedirían la audición perfecta.
El ejemplo contrario sería una habitación vacía, donde percibimos el sonido que emitimos muy distorsionado por la
gran cantidad de ecos y reverberaciones que se mantienen
al chocar con las paredes las ondas sonoras y ser reflejadas
sin que sean absorbidas.
3 ¿Cuáles son las cualidades básicas de un sonido?
Defínelas.
Las cualidades básicas de un sonido son sonoridad, tono y
timbre.
La sonoridad es la cualidad que permite identificar los sonidos como fuertes o débiles. Depende de la intensidad de la
onda, es decir, de la energía transportada por la onda.
El tono es la cualidad del sonido que permite distinguir entre
sonido graves o bajos y agudos o altos.
El timbre es la cualidad por la que se distinguen dos sonidos
de la misma sonoridad y del mismo tono.
4 Sabemos que la velocidad de la luz en el vacío es
300 000 km/s, mientras que en el agua es 225 000 km/s.
¿Cuál es el índice de refracción del agua? ¿Cuál es la velocidad de la luz dentro de una lente, de índice de refracción 1,76?
El índice de refracción de un medio es el cociente entre la
velocidad de la luz en el vacío y la velocidad de la luz en dicho
medio por lo que:
nagua =
vvacío
v agua
300 000 km/s
=
=1,33
225 000 km/s
Para hallar el valor de la velocidad de la luz en la lente:
nlente =
vvacío
v lente
⇒ v lente =
vvacío
nlente
300 000 km/s
=
=170 000 km/s
1,76
5 Un submarino, que se encuentra a 200 m bajo la superficie del océano, emite una onda de sonar hacia abajo
que se refleja en el fondo marino. Si la onda se escucha
en el submarino 4,2 s después de ser emitida, ¿cuál es la
profundidad del océano en ese punto?
Dato: velocidad del sonido en el agua = 1 500 m/s.
La onda va hacia el fondo y vuelve en 4,2 s, por lo que en
bajar tarda la mitad, 2,1 s. Como el sonido se mueve con un
MRU, el espacio que recorre viene dado por:
e=vt ⇒
e = 1 500 m/s · 2,1 s = 3 150 m
Como ésa es la distancia desde el submarino, y éste se encuentra a 200 m de profundidad, la profundidad total será
de:
h = 200 m + 3 150 m = 3 350 m
127
9
loS ElEMEnToS QuÍMicoS
Y SuS EnlacES
actividad de reFUerZO
PÁG. 238
actividad de
aMPliaciÓn PÁG. 240
1 Recordando lo que aprendiste el curso pasado,
separa de esta lista los elementos de los compuestos o
mezclas: hierro, acero, cobre, latón, agua, oxígeno, hidrógeno, azufre, amoniaco, gasolina, leche, vino, cloro,
plástico, cerveza, mercurio, cristal, caliza, bario.
1 Comenta cuántos electrones tienen en la última capa los siguientes elementos:
H, Cl, K, Se, Mg, Bi, La, Sn, U, Al, Ti, Fe, Rn, Ag y Hg.
Elementos: hierro, cobre, oxígeno, hidrógeno, azufre, cloro,
mercurio y bario. Son elementos todas las sustancias que
están en la lista y que aparece su símbolo en el Sistema
Periódico.
actividad de
aMPliaciÓn PÁG. 238
Respuesta libre, pero sería interesante que hubieran encontrado información sobre el eka-aluminio y el eka-boro.
actividad de
aMPliaciÓn PÁG. 239
1 Dibuja el Sistema Periódico y sitúa dentro de él los
siguientes elementos: H, Cl, K, Se, Mg, Bi, La, Sn, U, Al, Ti,
Fe, Rn, Ag y Hg.
Colorea de azul los alcalinos, de rojo los térreos y de verde los elementos del periodo 6.
Proponemos la siguiente Tabla como muestra de los elementos que creemos deben aprender. La línea de transición y el
uranio tienen la utilidad de que no olviden las «cajitas» de
transición y transición interna. Dentro de ella, están, entre
otros, los elementos que hemos preguntado a los que se
pueden añadir más.
1
18
1
H
2
13
14
15
16
17
He
2
Li
Be
B
C
N
O
F
Ne
3
Na Mg
Al
Si
P
S
Cl
Ar
4
5
6
Sc
Ti
V
Cr Mn Fe
4
K
Ca
5
Rb
Sr
6
Cs
Ba
La
7
Fr
Ra
Ac
7
9
10
11
Co
Ni
Cu Zn
Ge As
Se
Br
Kr
Ag Cd
Sn Sb
Te
I
Xe
Au Hg
Pb
Pt
U
128
8
12
Bi
actividad de
aMPliaciÓn PÁG. 242
1 De entre la siguiente lista de compuestos, y basándote en lo que sabes sobre el Sistema Periódico y los enlaces iónico y covalente, rellena la siguiente tabla:
1 Busca en enciclopedias o en Internet todo lo que
encuentres sobre la predicción del elemento germanio
por Mendeleyev. Busca también si predijo la existencia
de otros elementos.
3
H (1), Cl (7), K (1), Se (6), Mg (2), Bi (5), La (2), Sn (4), U (2), Al (3),
Ti (2), Fe (2), Rn (8), Ag (2) y Hg (2).
Rn
Átomos a
combinar
H
O
Cs
CI
C
O
P
I
Ba
N
Al
S
S
CI
Átomos a
combinar
Tipo de
enlace
Posible
fórmula
Tipo de
enlace
Posible
fórmula
H
O
Covalente
H2O
Cs
CI
Iónico
CsCI
C
O
Covalente
CO2
P
I
Covalente
PI3
Ba
N
Iónico
Ba3N2
Al
S
Iónico
AI2S3
S
CI
Covalente
SCI2
Algunos compuestos no son así, pero preferimos «inventar» unos compuestos y que sepan razonar la posible molécula.
actividad de
aMPliaciÓn PÁG. 243
1 De los compuestos que se citan a continuación, busca el punto de fusión y ebullición y de los que puedas, el
índice de dureza: oro, oxígeno, bromuro de potasio, clo-
ruro de calcio, sulfuro de magnesio, ioduro de aluminio,
cloro, metano, butano, dióxido de nitrógeno, amoniaco,
óxido de bario, cloruro de hidrógeno, naftaleno, cloruro
de sodio, diamante y glucosa.
Haz una tabla donde aparezcan separados los compuestos iónicos y los covalentes y sus puntos de cambio de
estado. Añade posteriormente, si crees que conducirán
o no la corriente eléctrica.
actividades
cOMPleMentarias
Respuesta libre, puesto que se les pide encontrar lo que puedan. Se deben enfocar las soluciones que den a demostrar
que los puntos de fusión y ebullición más altos son de compuestos iónicos, así como el índice de dureza, si hacemos
excepción de compuestos cristalinos covalentes. Deben de
contestar que los metales conducen la corriente eléctrica y
los compuestos iónicos, si están fundidos o disueltos.
3
4
5
6
7
8
9
10
11
12
elementos de transición
13
14
15
C
Al
Ca
Cr
Co
16
17
18
gases nobles
2
anfígenos
1
halógenos
La tabla tiene la utilidad de que vean que hay bastante variación entre los puntos de cambio de estado de los metales
y que incluso tenemos conceptos erróneos de ellos. Casi
todos los alumnos contestarán, si no se les han dado datos
antes, que el oro funde a una temperatura superior a la del
hierro.
El wolframio aguanta las temperaturas elevadísimas que se
producen en el filamento cuando pasa la corriente eléctrica,
por lo que no se funde y no se estropea la bombilla.
Solución para las actividades 1, 2, 3 y 4:
carbonoideos
1 Construye una tabla con los puntos de fusión y ebullición de los metales. ¿Por qué se hacen los filamentos
de las bombillas de wolframio?
4 Señala con una estrella el elemento más metálico
de todo el Sistema Periódico y con un rombo el menos
metálico.
nitrogenoideos
actividad de
aMPliaciÓn PÁG. 244
3 En el Sistema Periódico en blanco que está arriba,
pinta de distintos colores los elementos metálicos, los
no metálicos y los gases nobles.
térreos
Se trata de que vean que en las dos primeras todos los átomos están unidos entre sí, lo que impide su separación,
mientras que en el hielo las uniones son mucho más lábiles
y cada molécula puede terminar «haciendo la guerra» por
su cuenta.
2 ¿A qué grupo pertenecen los elementos: C, Ca, Cd, Cl,
Co, Cr, Cs y Cu? Intenta situarlos en el Sistema Periódico
mudo que está arriba.
alcalinos
1 Busca en Internet o en enciclopedias la estructura
cristalina del diamante y la del cuarzo y compáralas con
la del hielo.
1 Pon encima del Sistema Periódico el nombre de todos los grupos que conozcas, y el número con el que se
les conoce.
alcalino-térreos
actividad de reFUerZO
PÁG. 243
±
Cl
Cu
Cd
Cs
*
elementos
tipo f (transición interna)
tierras raras
Pintamos en amarillo los metales, en rojo los no metales y en
azul los gases nobles. El hidrógeno lo dejamos en blanco al
ser intermedio entre metal y no metal.
129
9
El elemento más metálico del Sistema Periódico es el Fr
(francio), que está abajo a la izquierda y, por lo tanto, lo más
alejado posible de la separación entre metales y no metales.
Por la misma razón el más no metálico es el F (flúor) que
se encuentra arriba a la derecha —sin contar con los gases
nobles—.
5 Indica el tipo de enlace que se puede esperar cuando
se unan los átomos o iones de los siguientes elementos:
flúor con azufre, potasio con cloro, fósforo con magnesio
y aluminio con oxígeno.
El flúor con el azufre da compuestos básicamente covalentes
(SF2, SF4 y SF6).
El potasio con el cloro forma el KCl, compuesto netamente
iónico.
El fósforo con magnesio da Mg3P2, compuesto con un cierto
carácter iónico.
El aluminio con el oxígeno da un compuesto iónico, Al2O3.
evalUaciÓn
1 Tenemos tres compuestos diferentes:
a) Un compuesto blanco casi transparente, con apariencia de cristal, soluble en agua, que funde a baja
temperatura, que no conduce la electricidad ni en
estado sólido ni en estado líquido.
b) Un compuesto gris, con brillo, que conduce la corriente eléctrica, pero que no se disuelve en agua.
c) Un compuesto blanco, con apariencia de cristal, soluble en agua, que funde a una temperatura bastante
alta y que no conduce la electricidad en estado sólido, pero sí cuando está líquido.
Grupo
1
2
13
14
15
Elemento
Sodio
Magnesio
Aluminio
Silicio
Fósforo
Símbolo
Na
Mg
Al
Si
P
S
Cl
Ar
Electrones
externos
1
2
3
4
5
6
7
8
Carácter
Metal
No
metal
No
metal
No
metal
No
metal
Gas
noble
MeMetal taloide
16
17
AzuCloro
fre
Argon
3 El elemento 19 del Sistema Periódico:
a)
b)
c)
d)
¿A qué grupo y periodo pertenece?
¿Es metal o no metal?
Indica otros elementos de su grupo.
Cuando se combine con flúor, ¿qué ión formará? ¿Qué
tipo de compuesto se obtendrá?
El elemento 19 del Sistema Periódico es el potasio, K. Es un
metal que pertenece al grupo 1 ( I a ) del Sistema Periódico
por lo que es un alcalino, al igual que litio, sodio, rubidio,
cesio y francio.
Cuando se junte con flúor éste ganará un electrón que
perderá el potasio, transformándose en K+. El compuesto que
se forma, KF, es el fluoruro de potasio que es un compuesto
iónico.
4 Escribe el nombre por el que se conocen los grupos
1, 2, 13, 14, 15, 16, 17 y 18, añadiendo, en cada grupo, el
símbolo de todos los elementos que conozcas que pertenezcan a ese grupo. A los elementos de los grupos 3 al
12, ¿con qué nombre genérico se los conoce?
Di qué tipo de enlace presenta cada uno y añade, si conoces, alguna cualidad más que presente. Si uno es una
mezcla de aluminio y hierro, otro cloruro sódico y el otro
hielo, ¿cuál es cada uno?
Grupo
Nombre
1
Alcalinos
Li, Na, K, Rb, Cs, Fr
2
Alcalinotérreos
Be, Mg, Ca, Sr, Ba, Ra
El compuesto a) es el hielo, que es un compuesto con enlace
de tipo covalente. Se evapora también a temperatura relativamente baja. Es una sustancia relativamente blanda.
El compuesto b) es la mezcla de metales, que es un compuesto con enlace de tipo metálico. Se funde y evapora a
temperaturas bastante altas. Es dúctil y maleable.
El compuesto c) es el cloruro sódico, que es un compuesto
con enlace de tipo iónico. Se evapora también a temperaturas altas. Es duro pero frágil.
3 a 12
Transición
Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn,
La, Ac, ...*
13
Térreos
14
Carbonoideos
2 Completa la siguiente tabla referida al periodo tercero:
15
Elementos
B, Al (Ga, In, Tl)
C, Si, (Ge, Sn, Pb)
Nitrogenoideos N, P, As, Sb, (Bi)
16
Anfígenos
O, S, Se, Te, (Po)
17
Halógenos
F, Cl, Br, I, (At)
18
Gases nobles
He, Ne, Ar, Kr, Xe, Rn
5 Razona cómo se forma el enlace iónico.
Pregunta teórica cuya contestación está en el libro.
130
18
laS rEaccionES QuÍMicaS
actividad de reFUerZO
PÁG. 255
1 Un amigo me comenta que ha juntado agua (H2O)
con hierro metálico y que ha obtenido un compuesto que
ha analizado y resulta que es sulfato ferroso (FeSO4). ¿Es
eso posible? Si lo analizamos y resulta que el compuesto contiene de verdad sulfato ferroso, ¿qué conclusión
podemos obtener?
Que no es posible. No puede obtenerse sulfato sin que haya
azufre.
Si se confirma que hay sulfato ferroso es porque de entrada
había un compuesto con azufre que también ha reaccionado,
o se ha contaminado la muestra posteriormente.
En una reacción química no pueden aparecer átomos donde
no los había antes.
actividades de reFUerZO
PÁG. 258
1 Ajusta la siguiente reacción:
Hg + HCl + HNO3
HgCl2 + NO + H2O
Además, calcula cuántos gramos de monóxido de nitrógeno se formarán al consumirse 30 g de cloruro de hidrógeno. ¿Cuántos gramos de agua se obtienen?
Masas atómicas: N = 14 ; O = 16 ; Cl = 35,5 e H = 1
3 Hg + 6 HCl + 2 HNO3
3 HgCl2 + 2 NO + 4 H2O
1 mol HCl 2 mol NO 30 g NO
·
·
=
36,5 g HCl 6 mol HCl 1 mol NO
= 8,2 g de NO
10
1 mol S 3 mol PbS 239 g PbS
·
·
=
32 g S
3 mol S
1 mol PbS
= 370 g de PbS
50 g S ·
50 g S ·
63 g HNO3
1 mol S 8 mol HNO3
·
·
=
32 g S
3 mol S
1 mol HNO3
= 260 g de HNO3
actividad de reFUerZO
PÁG. 259
1 Calcula el número de moles y moléculas contenidas
en un gas que ocupa 5 L cuando se encuentra a 720 mm
de Hg de presión y una temperatura de 65 ºC.
Dato: R = 0,082
atm L
mol K
Aplicando p V = n R T
1 atm
·5L
760 mm Hg
n =
= 0,17 moles
atm L
0, 082
· 338 K
mol K
6,02 · 1023 moléculas
0,17 moles ·
= 1023 moléculas
1 mol
720 mm Hg ·
actividad de reFUerZO
PÁG. 260
1 Ajusta la reacción:
30 g HCl ·
KNO3 + C
30 g HCl ·
Calcula cuántos litros de dióxido de carbono, a 96 000
Pa y 68 ºF, se obtienen al juntar 32 g de nitrato potásico
con carbono en exceso.
Datos: Mat: K = 39,1; O = 16; C = 12 y N = 14
1 mol HCl 4 mol H2 O 18 g H2 O
·
·
=
36,5 g HCl 6 mol HCl 1 mol H2 O
= 9,8 g de H2 O
2 Ajusta la siguiente reacción:
PbS + HNO3
Pb(NO3)2 + NO + S + H2O
Calcula cuántos gramos de sulfuro de plomo (II) se han
necesitado para obtener 50 g de azufre. ¿Cuántos gramos de ácido nitrico harán falta para que tenga lugar la
reacción y no sobre nada de ningún reactivo?
Masas atómicas: Pb = 207; O = 16; S = 32; H = 1 y N = 14
3 PbS + 8 HNO3
3 Pb(NO3)2 + 2 NO + 3 S + 4 H2O
KNO2 + CO2
68 ºF − 32
T − 273
=
; T = 293 K
180
100
a KNO3 + b C
c KNO2 + d CO2
Potasio: a = c
Nitrógeno: a = c
Oxígeno: 3 a = 2 c + 2 d
Carbono: b = d
De O, 3 a = 2 a + 2 d ⇔ a = 2 d
Elijo a = 2, para que no dé el valor de d fraccionario:
a = 2; c = 2; d = 1; b = 1
2 KNO3 + C
2 KNO2 + CO2
131
10
1,3 atm · 20 L NH3
pV
1 mol CO2
=
= 0,80 mol NH3 ;
= 0,16 moles de CO2 n =
atm L
RT
101,1 g KNO3 2 mol KNO3
0,082
· 393 K
mol K
atm L
0,16
moles · 0,082
· 293 K
7
mol O2
= 0,16nmoles
de
CO
2
RT
mol K
0,80 mol NH3 ·
= 1,40 mol O2 ;
V =
=
= 4,1 L
4 mol NH3
1 atm
p
atm
L
96000
Pa ·
0,16 moles
· 0,082
· 293 K
101300
nRT
atm L
mol
K Pa = 4,1 L
V=
=
1,4 mol O2 · 0,082
· 393 K
n
R
T
1 atm
p
mol K
V=
=
= 35 L O2
96 000 Pa ·
p
1,3 atm
101 300 Pa
32 g KNO3 ·
1 mol KNO3
·
actividad de
aMPliaciÓn PÁG. 260
1 Si en un recipiente de 3 L de capacidad, a 35 ºC, tenemos yodo a 4 atmósferas de presión y un exceso de
tiosulfato sódico (que suponemos no ocupa volumen)
calcula cuántos gramos de ioduro sódico se obtienen,
después de que estos dos compuestos reaccionen.
La reacción que tiene lugar es: I2 + Na2S2O3
NaI +
+ Na2S4O6
Masas atómicas: I = 126,9; O = 16; Na = 23 y S = 32
(En estas condiciones el yodo no es un gas, pero se pone
este enunciado por interés estequiométrico.)
a I2 + b Na2S2O3
c NaI + d Na2S4O6
Yodo: 2 a = c
Sodio: 2 b = c + 2 d
Azufre: 2 b = 4 d ⇔ b = 2 d
Oxígeno: 3 b = 6 d
Elegimos a = 1:
a = 1; c = 2; b = 1 + d y como b = 2 d: d = 1; b = 2
I2 + 2 Na2S2O3
2 NaI + Na2S4O6
pV
=
RT
4 atm · 3 L
= 0, 48 mol
atm L
0, 082
· 308 K
mol K
2 mol NaI 149,9 g NaI
0, 48 mol I2 ·
·
= 144 g NaI
1 mol I2
1 mol NaI
n=
actividad de reFUerZO
PÁG. 261
1 El amoniaco reacciona con oxígeno para dar dióxido de nitrógeno y agua. Escribe la reacción, ajústala y
calcula cuántos moles y cuántos litros de oxígeno se
consumen al oxidar 20 L de amoniaco, a 120 ºC y 1,3 atm
de presión. ¿Cuántos litros de dióxido de nitrógeno se
obtienen? ¿Cuántos mililitros de agua se obtienen?
La reacción es:
4 NH3 + 7 O2
132
4 NO2 + 6 H2O
A este valor se podía haber llegado directamente como en:
20 L NH3 ·
4 L NO2
= 20 L NO2
4 L NH3
Es una pregunta trampa, para ver si los alumnos leen bien
los datos y razonan los problemas. Estamos a 120 ºC, por lo
que el agua es vapor:
20 L NH3 ·
6 L de H2 O
= 30 L de H2 O =
4 L de NH3
= 30 000 mL de H2 O vapor
actividades
cOMPleMentarias
1 Ajusta las siguientes reacciones:
C4H8 + O2
CO2 + H2O
HBrO3 + Cd(OH)2
Cd(BrO3)2 + H2O
K2CO3 + HNO3
KNO3 + CO2 + H2O
Cu + HNO3
Cu(NO2)2 + H2O
Las reacciones ajustadas son:
C4H8 + 6 O2
2 HBrO3 + Cd(OH)2
K2CO3 + 2 HNO3
Cu + 2 HNO3
4 CO2 + 4 H2O
Cd(BrO3)2 + 2 H2O
2 KNO3 + CO2 + H2O
Cu(NO2) 2 + H2O
2 Después de un proceso químico donde hacemos
reaccionar 16 g de SO2 con oxígeno y agua, hemos obtenido 49 g de una sustancia que creemos que es H2SO4. ¿Es
eso posible? ¿Cuántos moles de SO2 había inicialmente?
¿Y moléculas de SO2?
Masas atómicas: H = 1; O = 16 y S = 32.
La masa molecular del SO2 es: Mm = 1 · 32 + 2 · 16 = 64
La masa molecular del H2SO4 es: Mm = 2 · 1 + 1 · 32 + 4 ·
16 = 98
De cada molécula de SO2 obtenemos una molécula de H2SO4
ya que ambas tienen un azufre.
16 g de SO2 son:
16 g de SO2 ⋅
1mol de SO2
64 g de SO2
0,25 moles de SO2 ⋅
= 0,25 moles de SO2
6 ⋅ 1023 moléculas de SO2
1mol de SO2
=
=1,5 ⋅ 1023 moléculas de SO2
Con 0,25 moles de SO2 obtendríamos 0,25 moles de H2SO4
que son:
0,25 moles de H2 SO 4 ⋅
98 gramos de H2 SO 4
1mol de H2 SO 4
=
= 24,5 gramos de H2 SO 4
Es imposible por tanto obtener más de 24,5 gramos, por lo
que o no es H2SO4 o hemos añadido otras cantidades.
3 Al calentar clorato potásico en ausencia de aire tiene
lugar la siguiente reacción:
KClO3
KCl + O2
Ajusta la reacción y contesta:
¿Cuántos moles de clorato potásico teníamos inicialmente si hemos obtenido 100 gramos de cloruro potásico? ¿Y
moléculas? ¿Cuántos gramos de oxígeno se producen?
¿Qué volumen de O2, medido a 25 ºC y 730 mm Hg de
presión, se obtiene?
Masas atómicas: K = 39; O = 16 y Cl = 35,5.
La reacción ajustada es:
2 KClO3
2 KCl + 3 O2
Por lo tanto teníamos inicialmente:
4 Al añadir ácido nítrico en exceso sobre 30 g de zinc,
observamos que se desprende un gas, al mismo tiempo
que se disuelve el zinc, formando nitrato de zinc. ¿Qué
gas se desprende? ¿Qué masa de ácido nítrico hay que
añadir, como mínimo? ¿Qué volumen de gas se obtiene,
en condiciones normales?
Masas atómicas: Zn = 65,4; O = 16 y N = 14.
(Si necesitas algún dato más, obtenlo de la Tabla Periódica.)
La reacción que tiene lugar entre el zinc y el ácido es la de desprendimiento de hidrógeno puesto que éste es el elemento
desplazado cuando se forma nitrato de zinc.
Zn(NO3)2 + H2 ↑
2 HNO3 + Zn
La masa molecular del HNO3 es: Mm = 1 · 1 + 1 · 14 + 3 · 16 = 63.
Por lo tanto, habrá que añadir:
1 mol de átomos de Zn
⋅
65, 4 g de Zn
2 moles de HNO3
63 g de HNO3
⋅
⋅
≈ 58 g de HNO3
1 mol de átomos de Zn 1 mol de HNO3
30 g de Zn ⋅
De gas se obtienen:
1 mol de átomos de Zn
⋅
65, 4 g de Zn
1 mol de gas
⋅
≈ 0, 46 moles de gas
1 mol de átomos de Zn
30 g de Zn ⋅
1 mol de KCI 2 moles de KCIO3
⋅
≈
74 ,5 g de KCI
2 moles de KCI
≈ 1,34 moles de KCIO3
Aplicando Clapeyron: p V = n R T
Se obtienen:
de donde obtenemos, aproximadamente, 10 L de H2.
100 g de KCI ⋅
100 g de KCI ⋅
1 mol de KCI 3 moles de O2 32 gr de O2
⋅
⋅
≈
74 ,5 g de KCI 2 moles de KCI 1 mol de O2
≈ 64 gr de O2
Para hallar los litros calculamos los moles:
100 g de KCI ⋅
1 mol de KCI 3 moles de O2
⋅
≈ 2 moles de O2
74 ,5 g de KCI 2 moles de KCI
1 atm ⋅ V = 0, 46 mol ⋅ 0,082
atm L
⋅ 273 K
mol K
5 El amoniaco se obtiene a partir del hidrógeno y el
nitrógeno según la reacción:
N2 + H2
NH3
Ajusta la reacción y contesta:
Si partimos de 6 L de N2, en condiciones normales, y exceso de hidrógeno:
a) ¿Cuántos litros de hidrógeno se consumen?
b) ¿Cuántos litros de amoniaco se obtienen?
c) ¿Cuántas moléculas de amoniaco se han obtenido?
y aplicamos la ecuación de Clapeyron: p V = n R T
La reacción ajustada queda como:
1 atm
⋅V =
760 mm de Hg
atm L
= 2 mol 0,082 ⋅
⋅ 298 K
2 mol de K
N2 + 3 H2
730 mm de Hg ⋅
de donde obtenemos el volumen de 51 L de O2.
2 NH3
Como las proporciones pueden darse en volumen-volumen,
con 6 L de N2 y 18 L (3 · 6 L) de H2 obtendríamos 12 L (2 · 6 L)
de NH3.
133
10
Los 12 L de amoniaco, y aplicando Clapeyron son, aproximadamente: p V = n R T
atm L
1 atm ⋅ 12 L = n ⋅ 0,082
⋅ 273 K
mol K
0,54 moles de amoniaco que son:
0,54 moles de NH3 ⋅
6 ⋅ 1023 moléculas de NH3
1 mol de NH3
≈
≈ 3,2 ⋅ 1023 moléculas de NH3
6 Ajusta la siguiente reacción:
KMnO4 + H2SO4 + H2O2
MnSO4 +O2 +H2O + K2SO4
Calcula cuántos litros de oxígeno, medidos en condiciones normales, se formarán al consumirse 30 g de permanganato potásico. ¿Cuántos gramos de sulfato potásico
se obtienen?
Masas atómicas: Mn = 54,9; O = 16; K = 39,1 y S = 32
Ajustamos la reacción:
a KMnO4 + b H2SO4 + c H2O2
d MnSO4 + e O2 + f H2O +
+ g K2SO4
Y rehacemos las ecuaciones para cada elemento
Potasio: a = 2 g
Manganeso: a = d
Oxígeno: 4 a + 4 b + 2 c = 4 d + 2 e + f + 4 g
Hidrógeno: 2 b + 2 c = 2 f ⇔ b + c = f
Azufre: b = d + g´
Damos a a el valor 2 (para que g sea entero).
a = 2; g = 1 (K); d = 2 (Mn); b = 3 (S) y nos queda 8 + 2c = 2 e
+fy3+c=f
Como hay tres incógnitas y dos ecuaciones elegimos los valores más bajos de una de ellas que den valores naturales al
conjunto:
f = 4 (no puede ser menor que cuatro porque c sería nula o
negativa); c = 1; e = 3.
Si f fuera 6, c sería 3 y e, 4 y la reacción seguiría ajustada, y
así sucesivamente.
2 KMnO4 + 3 H2SO4 + H2O2
2 MnSO4 + 3 O2 + 4 H2O +
+ K2SO4
30 g KMnO 4 ⋅
⋅
134
158 g KMnO 4
22, 4 L de O2 en cn
1mol O2
30 g KMnO 4 ⋅
⋅
1mol KMnO 4
1mol KMnO 4
1mol K 2 SO 4
2 mol KMnO 4
⋅
= 6, 4 L de O2
158 g KMnO 4
174,2 g de K 2 SO 4
⋅
3 mol de O2
⋅
1mol K 2 SO 4
2 mol KMnO 4
= 16,5 g de K 2KO 4
⋅
evalUaciÓn
1 Ajusta las siguientes reacciones químicas y di a qué
tipo corresponden:
a) Aluminio + oxígeno
óxido de aluminio
b) Sulfato de plata + ácido clorhídrico
cloruro
de plata + ácido sulfúrico
c) Agua + trióxido de fósforo (III)
ácido trioxofosfórico (III) [ácido ortofosforoso]
d) Ácido carbónico
dióxido de carbono + agua
a)
b)
c)
d)
4 Al + 3 O2 ––→ 2 Al2O3 Síntesis
Ag2SO4 + 2 HCl ––→ 2 AgCl + H2SO4 Sustitución
3 H2O + P2O3 ––→ 2 H3PO3 Síntesis
H2CO3 ––→ CO2 + H2O Descomposición
Nota: Se les puede dar ya las reacciones escritas para simplificarles la tarea.
2 Escribe y ajusta la reacción que se produce entre
el ácido clorhídrico y el sodio metal en la que se forma
cloruro sódico y se desprende hidrógeno gas. Calcula la
cantidad de cloruro sódico que se obtiene al tratar, con
un exceso de clorhídrico, una muestra de 11,5 g de Na.
¿Qué volumen de hidrógeno se obtiene en condiciones
normales? Masas atómicas: H = 1; Na = 23 y Cl = 35,5.
Nota: Si se desea favorecer y simplificar el problema se puede
añadir la reacción sin ajustar.
2 Na + 2 HCl
2 NaCl + H2
11,5 g de sodio · 1 mol/23 g de Na = 0,5 moles de Na.
Con medio mol de sodio obtenemos medio mol de cloruro
sódico por lo que:
0,5 moles de NaCl · 58,5 g/mol de NaCl ≈ 29 g de NaCl
Con medio mol de sodio se obtiene 0,25 moles de H2. Aplicando la ecuación de Clapeyron:
p V = n R T ⇒ 1 atm · V = 0,25 moles · 0,082 atm L/mol K ·
· 273 K ⇒ de donde el volumen da: V ≈ 5,6 L.
También pueden suponer que, en condiciones normales se
obtienen 22,4 L por mol por lo que, a 0,25 moles, corresponden 5,6 L.
3 Para que tenga lugar una reacción hay que aportar
un calor de reacción muy grande. Contesta qué conclusión de las siguientes es verdadera y cuál falsa y por
qué.
a)
b)
c)
d)
La reacción transcurrirá muy lenta.
La reacción es exotérmica.
La reacción desprenderá muchísima energía.
Hay que aportar mucha energía para que la reacción
tenga lugar.
d) Un catalizador no sirve en esta reacción.
e) La reacción es endotérmica.
La a) es cierta porque aportar una cantidad de calor muy
grande es muy difícil (la energía de activación todavía sería
mayor) y la reacción tendrá que ir lenta.
La b) y la c) son falsas, por la misma razón que son verdaderas
la d) y la f). La reacción requiere aporte energético por lo que
es endotérmica.
La e) en principio es falsa puesto que un catalizador siempre
es útil en una reacción, ya sea para lentificarla, si es negativo,
como para acelerarla si es positivo. De todas maneras, sería
extraordinario que alguno se diera cuenta de que, en una
reacción fuertemente endotérmica es imposible disminuir la
energía de activación por debajo de unos límites, ya de por
sí muy altos, que «pone» el gran calor de reacción absorbido,
por lo que nunca sería una reacción muy rápida. Caso de que
alguno se diera cuenta, habría que primárselo.
4 ¿Qué factores influyen en la velocidad de reacción?
Los factores que influyen en la velocidad de una reacción
son:
• La naturaleza de los reactivos.
• La superficie de contacto de los reactivos.
• La concentración de los reactivos.
• La temperatura del proceso.
• Los catalizadores empleados.
5 Ajusta la siguiente reacción química:
C4H10 + O2
CO2 + H2O
Cuando quemamos 15 g de butano en aire, ¿cuántos gramos de agua se obtienen? ¿Cuántos litros de oxígeno (en
condiciones normales) se consumen por cada mol de CO2
que se forma? Masas atómicas: H = 1; O = 16 y C = 12.
Ajustamos la reacción:
2 C4H10 + 13 O2
8 CO2 + 10 H2O
Calculamos la masa de un mol de butano que es Mmol = 12 ·
· 4 + 1 · 10 = 58 g
Establecemos la relación entre butano y agua:
15 g de butano ⋅
⋅
1mol de butano 10 moles de agua
⋅
⋅
58 g de butano 2 moles de butano
18 g de agua
≈ 23 g de agua
1mol de agua
1mol de CO2 ⋅
13 moles de O2
8 moles de CO2
≈1,6 moles de O2
Aplicando la ecuación de Clapeyron:
p V = n R T ⇒ 1 atm · V = 1,6 moles · 0,082 atm L/mol K ·
· 273 K ⇒ de donde el volumen da: V ≈ 36 L.
También pueden suponer que, en condiciones normales se
obtienen 22,4 L por mol por lo que, a 1,6 moles, corresponden 36 L.
135
11 rEaccionES QuÍMicaS DE inTErÉS
actividad de
aMPliaciÓn PÁG. 282
1 Completa, ajusta y nombra las sustancias implicadas
en las siguientes reacciones de neutralización:
HF + Al(OH)3
H2SO4 + KOH
H3PO4 + Fe(OH)2
H2Te + NH3 (recuerda que el NH3 capta protones y no cede
OH–).
3 HF + Al(OH)3
AlF3 + 3 H2O
ácido fluorhídrico e hidróxido alumínico
fluoruro de aluminio y agua
H2SO4 + 2 KOH
K2SO4 + 2 H2O
ácido sulfúrico e hidróxido potásico
sulfato de potasio y agua
2 H3PO4 + 3 Fe(OH)2
Fe3(PO4)2 + 6 H2O
ácido (orto)fosfórico o e hidróxido de hierro (II)
(orto)fosfato ferroso y agua
H2Te + 2 NH3
(NH4)2Te
ácido telurhídrico y amoniaco
telururo de amonio
actividad de
aMPliaciÓn PÁG. 285
1 Comenta lo que pasa si juntamos:
a)
b)
c)
d)
Al3+ + Ca
Li + Au+
Sr + Fe2+
Cd2+ + H2
e)
f)
g)
h)
Cu2+ + Hg
Li+ + Na+
Zn + Cu
Mg + Be2+
En los casos d) y e) no pasaría nada, puesto que el que tiene
los electrones es el que más apetencia tiene ellos.
En el caso f) no pasa nada, porque a los dos les faltan los
electrones, igual que tampoco pasa nada en el caso g) puesto
que los dos tienen sus electrones.
En el caso a) se formará Ca2+ y Al.
En el caso b), Li+ y Au.
En el caso c) Sr2+ y Fe.
Por último, en el caso h) se formará Mg2+ y Be.
actividades
cOMPleMentarias
1 Añade si los hechos que se especifican a continuación corresponden al comportamiento de un ácido o de
una base, o al de ambos.
136
Hecho observado
Ácido y/o base
Reacciona con grasa produciendo jabón
Base
No reacciona con cinc
Base
Tiene sabor agrio (parecido al vinagre)
Ácido
Conduce la corriente eléctrica
Ambos
Azulea el papel de tornasol
Base
Tiene sabor amargo o caústico (a lejía)
Base
Es corrosivo para la piel
Ambos
Con el mármol produce efervescencia
Ácido
Tiene consistencia jabonosa o resbaladiza al
tacto
Base
Disuelve muchas sustancias
Ácido
Precipita muchas sustancias que son solubles
Base
2 ¿Qué es un electrolito? Menciona algún tipo de sustancias que se comporte como electrolito. ¿Quién es el
autor de esta teoría?
Un electrolito es una sustancia que, en disolución acuosa,
se disocia en iones con cargas de distinto signo. En disolución, por tanto, conducen la corriente eléctrica. Los ácidos,
las bases y las sales son electrolitos. Esta teoría la expuso
Arrhenius.
3 Escribe las disociaciones de los siguientes compuestos, mencionando si son ácidos o bases.
Disociación
Ácido o base
AI(OH)3
Al3+ + 3 OH–
Base
Ca(OH)2
Ca2+ + 2 OH–
Base
H2CO3
LiOH
HCIO4
Sn(OH)4
2 H + CO
+
Li + OH
+
2–
3
H+ + ClO4–
Ácido
Al3+ + 3 OH–
H4SiO4
4 H + SiO
H3PO4
3 H + PO
+
+
Ácido
Base
–
4–
4
3–
4
Base
Ácido
Ácido
4 Si tenemos una disolución de pH = 5, ¿qué tipo de
sustancia es? Tenemos otra disolución de pH = 3. ¿Cuál
de las dos es más fuerte? ¿Dónde se encuentra el punto
de neutralidad para el pH?
Una disolución de pH = 5 es una disolución ligeramente
ácida. Una disolución de pH = 3 es una disolución más ácida
que la anterior, ya que el punto de neutralidad se encuentra
a pH = 7 siendo ácidas las disoluciones por debajo de este
valor, y tanto más fuertes cuanto más bajo sea el valor.
5 Define oxidación y reducción. Escribe las semirreacciones de oxidación y reducción que se producen en las
siguientes reacciones químicas:
a) Cu + Br2
b) 3 S + 2 Al
CuBr2
Al2S3
Oxidación es la reacción en la que un átomo de un elemento
o de un compuesto pierde electrones.
Reducción es la reacción en la que un átomo de un elemento
o de un compuesto gana electrones.
a) La reacción Cu + Br2
Semirreacción de oxidación:
Cu
Cu2+ + 2 e–
Semirreacción de reducción:
Br2 + 2 e–
2 Br–
b) La reacción 3 S + 2 Al
Semirreacción de oxidación:
(Al
Al3+ + 3 e– ) · 2
Semirreacción de reducción:
(S + 2 e–
S2–) · 3
CuBr2 se produce por:
Al2S3 se produce por:
Nota: Si se les ha explicado principalmente la formulación
sistemática se les cambia los apartados por:
Ácido tetraoxosulfúrico (VI) e hidróxido de sodio.
Ácido clorhídrico e hidróxido de calcio.
Hidróxido de aluminio y ácido tetraoxobrómico (VII).
Hidróxido de cobre (II) y ácido tetraoxofosfórico (V).
Las soluciones son:
a)
b)
c)
d)
1 Ordena las siguientes sustancias, conocido su pH, según su grado de acidez, y añade si son ácidas o básicas.
Disociación
pH
Ácido o
base
Orden de
acidez
Disolución de amoniaco en
agua
10
Base
7.o
Disolución de cloruro de
hidrógeno en agua
2
Ácido
fuerte
1.o
Sangre
7,4
Base
débil
5.o
Gel de baño
5,5
Ácido
débil
2.o
Disolución de hidróxido
sódico
14
Base
fuerte
8.o
Disolución de carbonato
sódico
9
Base
6.o
Mezcla de ácido acético y
acetato sódico
7
Neutra
4.o
6,2
Ácido
débil
3.o
2 Escribe y ajusta la reacción que se produce entre:
a) Ácido sulfúrico e hidróxido sódico.
b) Ácido clorhídrico e hidróxido cálcico.
H2SO4 + 2 NaOH
2 HCl + Ca(OH)2
Al(OH)3 + 3 HBrO4
3 Cu(OH)2 + 2 H3PO4
Na2SO4 + 2 H2O
CaCl2 + 2 H2O
Al(BrO4)3 + 3 H2O
Cu3(PO4)2 + 6 H2O
3 Define qué es una reacción de reducción. Lo mismo
para una reacción de oxidación. Clasifica las siguientes
reacciones en reacciones de oxidación o reducción.
a)
b)
c)
d)
e)
evalUaciÓn
Orina
c) Hidróxido alumínico y ácido perbrómico.
d) Hidróxido cúprico y ácido ortofosfórico.
4 Ni + 3 O2
CuO + H2
Si + O2
FeO + C
4 K + O2
4 Ni + 3 O2
CuO + H2
Si + O2
FeO + C
4 K + O2
2 Ni2O3
Cu + H2O
SiO2
Fe + CO
2 K 2O
2 Ni2O3
Cu + H2O
SiO2
Fe + CO
2 K 2O
Oxidación
Reducción *
Oxidación
Reducción *
Oxidación
* Se debe valorar positivamente el que se den cuenta de que
el cobre o el hierro se reducen mientras que el hidrógeno
o carbono se oxidan. Si alguno pone que en las otras reacciones el oxígeno se reduce, también debe valorarse especialmente.
4 ¿Qué es una combustión? ¿Cuál es la diferencia entre
oxidación y combustión?
Una combustión es una oxidación rápida y violenta entre
un combustible y un comburente, normalmente oxígeno.
Se diferencia de la oxidación en la rapidez y el rápido incremento de temperatura que se produce en la combustión.
Además, normalmente la combustión necesita un agente que
ocasione el comienzo del proceso, mientras que la oxidación
se produce espontáneamente.
5 Explica en qué consiste el efecto invernadero.
Pregunta teórica que se encuentra en el libro del alumno.
137
12
la QuÍMica DE loS coMPuESToS
DE carBono
actividad de
aMPliaciÓn PÁG. 296
actividad de reFUerZO
PÁG. 300
1 Mira a tu alrededor y nombra 10 sustancias orgánicas y otras 10 inorgánicas que veas. ¿En qué te basas para
deducir si una sustancia es orgánica o no lo es?
1 ¿Por qué existe el propeno, el propino y sin embargo
no existe el pentino?
Respuesta libre, pero que es conveniente que descubran que
marcan como orgánica aquella sustancia que relacionan directamente con seres vivos. La mayoría de los alumnos nunca
incluyen una bolsa de plástico, la fibra de un borrador o la
suela de sus zapatillas de deporte.
actividad de
aMPliaciÓn PÁG. 298
1 Refiriéndonos a los tres compuestos de fórmula C5H12
que aparecen en el libro, di qué carbonos son primarios,
secundarios, terciarios y cuaternarios.
Primarios son los marcados con un punto, secundarios con
dos, terciarios con tres y cuaternarios con cuatro.
H
H H H H
H C. C: C: C. H H C.
H H H H
H
H
H
H C. H
H H H
H
H
C:. C: C. H H C. C:: C. H
H
H H
H
H C. H
C. H
H
H
actividad de
aMPliaciÓn PÁG. 300
1 Obtén la fórmula general de la combustión del hidrocarburo CaHb.
Prescindiendo de la energía, podemos obtener la fórmula
general de la combustión de un hidrocarburo de la siguiente
forma:
CaHb + x O2
y CO2 + z H2O
Como el número de átomos de cada elemento debe ser igual
en los dos lados nos queda:
C: a = y
H: b = 2z
O: 2x = 2y + z
de donde obtenemos que y = a ; z = b/2 y
2x = 2a + b/2 por lo que x = a + b/4
para evitar fracciones, multiplicamos todo por cuatro y nos
queda:
4 CaHb + (4a + b) O2
4a CO2 + 2b H2O
138
Si ningún alumno se da cuenta de que estamos planteando
una «trampa» puesto que sí existe el 1–pentino y el 2–pentino,
se les puede conducir a la pista de que pentinos hay dos.
Deben fijar como concepto a estas alturas la utilización de
números localizadores. Incluso puede ser aconsejable que
los pongan siempre y que aprendan a quitarlos cuando ya
dominen la técnica de nomenclatura.
actividades de reFUerZO
PÁG. 301
1 Dibuja la molécula, utilizando el criterio de línea
quebrada de los siguientes compuestos orgánicos: etano, eteno, etino, 1–buteno, 2–buteno y 1–butano.
Etano, eteno y etino se representan como están en la página,
puesto que todos los carbonos son terminales.
CH3
CH2
1-buteno
CH3
2-buteno
CH3
CH3
CH
1-butino
2 Dibuja moléculas orgánicas utilizando el criterio de
línea quebrada y nómbralas.
La solución es libre, puesto que son ellos los que eligen las
moléculas. Conviene dirigirles a que no sean muy complejas,
y hay que aprovechar para explicarles por qué las nombran
mal o bien, utilizando la opinión del resto de los alumnos.
actividad de reFUerZO
PÁG. 302
1 Representa, por el criterio de línea quebrada, todas las moléculas presentes en esta página del libro del
alumno, incluidas las de los ejercicios.
Ejercicio de aplicación 1
a)
CH3
CH3
b)
CH3 CH3
CH3
CH3
CH3
CH3
c)
CH3
CH3
a) 2,2–dimetilbutano, b) 3–etil–5–metil–2–hexeno y c) 1,3–dimetilbenceno.
Ejercicio 7
CH3 CH3
CH3
CH3
CH3
CH3
OH
CH3
CH2OH CH2OH
1,2-butanodiol 1,2,3-propanotriol
actividad de reFUerZO
PÁG. 305
CH3
CH3
CH2OH
2-propanol
CH3
CH3
CH2
OH
OH
1 Representa, por el criterio de línea quebrada, todas las moléculas presentes en esta página del libro del
alumno.
Ejercicio 9
CH3
Ejercicio de aplicación 2
CH2
1-buteno
CH2OH
CH3
CH2OH
CH2OH
OH
1-butanol 1,2,3-butanotriol
CH3
CH2
CH3
butano
CH3
propeno
CH3
CH
1-butino
OH
CH3
Ejercicio 10
ciclohexano
CH3
CH3
2-penteno
CH3
CH3
CH3
2-metilhexano
1,5-pentanodiol
Ejercicio 16
El metanol no tiene representación específica al ser el carbono terminal.
OH
CH3
CH3
etilbenceno
CH2OH
ciclobuteno
actividades de
aMPliaciÓn PÁG. 303
1 Busca en Internet o en enciclopedias actualizadas
la proporción de componentes que tiene el petróleo y el
consumo de esos componentes, para entender por qué
tiene que producirse el craqueo.
Respuesta libre.
2 Busca, en las mismas fuentes del problema anterior,
de dónde procede el gas natural y el petróleo consumidos en España.
Respuesta libre.
actividad de reFUerZO
PÁG. 304
1 Representa, por el criterio de línea quebrada, todas las moléculas presentes en esta página, del libro del
alumno, salvo la de glucosa.
Metanol, etanol y etanodiol se representan de la misma
manera, al ser los carbonos terminales.
CH2OH
CH3
CH2OH
1,3-propanodiol
2-propanol
El ácido metanoico y el etanoico se representan igual.
COOH
CH3
ácido butanoico
CH3
COOH
ácido propanoico
COOH
CH3
ácido hexanoico
actividad de
aMPliaciÓn PÁG. 306
1 Busca, en objetos de plástico que haya en tu casa,
el código de reciclado de cada uno, e intenta obtener
plásticos con los 7 números posibles.
Respuesta libre.
actividad de
aMPliaciÓn PÁG. 307
1 Busca la fórmula química del polietileno (PE), el poliestireno (PS), el policloruro de vinilo (PVC), el polipropileno (PP), el polimetilmetacrilato (PMMA), el polietilentereftalato (PET), el policarbonato (PC) y el teflón.
139
12
PE: (–CH2–CH2–)n
PS: (–CHC6H5–CH2–)n
PVC: (–CHCl–CH2–)n
PP: (–CHCH3–CH2–)n
PMMA: (–CH2–C(CH3)(COOCH3)–)n
PET: (–OOC–C6H4–COO– CH2– CH2–)n
PC: (–grupo functional–grupo carbonato–)n
Teflón: (–CF2–CF2–)n
actividades
cOMPleMentarias
1 Formula o nombra, según proceda, los siguientes
compuestos orgánicos:
Nombre
Fórmula
2–hexeno
CH3 – CH2 – CH2 – CH = CH – CH3
1,2–etanodiol
CH2OH – CH2OH
propino
CH – C – CH3
ácido heptanoico
CH3 – CH2 – CH2 – CH2 – CH2 – CH2 – COOH
2.3–dimetilbutano
2–etil–2–
metilpentano
1–propanol
CH
CH3–
CH3
CH–
CH –
– CH
– CH
– CH
CH33– CH – CH – CH33
CH
CH3 CH
CH3
CH33 CH33
CH
CH3
CH33
CH
CH2 –
CH3–
CH2 –
CH3
– CH
– CC –– CH
– CH
CH33– CH22– C – CH22– CH33
CH
CH
–
CH2 – CH3
CH22– CH33
CH3 – CH2 – CH2OH
CH
COOH
CH2 –
CH3–
CH –
– CH
– CH
– COOH
ácido 2–metil–bu- CH33– CH22– CH – COOH
CH
tanoico
CH33
CH3
2 ¿En qué consiste la diferencia entre alcanos, alquenos y alquinos? ¿Cuál es la característica más importante de los hidrocarburos aromáticos? Pon un ejemplo de
cada uno.
Los hidrocarburos son compuestos formados por carbono
e hidrógeno. Los alcanos son los hidrocarburos de cadena
abierta que tienen todos sus enlaces sencillos (saturados).
Los alquenos son los hidrocarburos de cadena abierta con,
al menos, un enlace doble y los alquinos los que tienen uno o
más enlaces triples. Los hidrocarburos aromáticos son hidrocarburos cíclicos formados por enlaces alternados sencillos y
dobles entre los carbonos que forman el anillo.
Ejemplos:
Alcanos: metano (CH4), etano (CH3 – CH3), propano (CH3–CH2–
CH3).
140
Alquenos: eteno (CH2=CH2), propeno (CH3–CH=CH2).
Alquinos: etino (CH≡CH), propino (CH3–C≡CH).
Aromáticos:
benceno naftaleno
antraceno
3 Escribe la reacción de combustión del propino. Ajústala.
La reacción de combustión del propino es:
CH3–C≡CH (ó C3H4) + O2
CO2 + H2O
Ajustándola nos queda:
C3H4 + 4 O2
3 CO2 + 2 H2O
4 ¿Qué es el petróleo? ¿De qué está formado? ¿Puedes
comentar el nombre de, al menos, dos componentes básicos del petróleo?
El petróleo es un producto natural, que consiste en una mezcla de muchos hidrocarburos.
Se produce por descomposición de materia orgánica en
condiciones de alta presión y temperatura en el interior de
la Tierra.
Está formado por hidrocarburos saturados e insaturados de
cadenas de longitud variable.
Los componentes más volátiles del petróleo, cadenas de
menor número de carbonos, forman las gasolinas, y aumentando el número de carbonos tenemos el gasóleo o
gasoil, el asfalto, ceras, etcétera.
5 ¿Qué son los glúcidos? ¿Se nombran de alguna otra
manera? ¿De qué elementos están formados? Nombra
dos glúcidos importantes para la vida.
Los glúcidos, o hidratos de carbono, son compuestos formados por carbono, hidrógeno y oxígeno (éstos en la misma
proporción 2:1 que se da en el agua) y son uno de los grupos
fundamentales constituyentes de los seres vivos.
Entre los glúcidos más importantes se encuentran los azúcares (de forma especial la glucosa) y el glucógeno que son
los combustibles principales de los seres vivos, y el almidón y
la celulosa, como compuestos estructurales y de almacenaje
de energía.
evalUaciÓn
1 Formula o nombra, según proceda, los siguientes
compuestos orgánicos:
Nombre
1–buteno
2–propanol
etanol
Fórmula
CH3–CH2–CH=CH2
CH3–CHOH–CH3
CH3–CH2OH
ácido metanoico
HCOOH
ácido pentanoico
CH3–CH2–CH2–CH2–COOH
3–etil–2–metilhexano
CH3– CH – CH – CH2 – CH2 – CH3
CH3– CH – CH – CH2 – CH2 – CH3
CH3 CH2
CH3 CH2
CH3
CH3
1,3–pentadiino
CH3–C≡C–C≡CH
OH
OH
ciclopentanol
3 ¿Qué es una macromolécula? Pon dos ejemplos de
macromoléculas artificiales comentando para qué sirven. ¿Cuáles son los principales constituyentes orgánicos
de los seres vivos?
Pregunta abierta en la que el número de posibles respuestas
es muy grande. Entre las macromoléculas más importantes
de las que pueden hacer mención están los plásticos, polietileno, poliestireno, policloruro de vinilo, polipropileno,
polietilentereftalato, teflón, caucho, fibras textiles sintéticas
y siliconas.
Los principales constituyentes de los seres vivos son lípidos,
glúcidos y proteínas. Pueden añadir las vitaminas.
4 ¿Por qué el carbono es el elemento fundamental a
partir del cual se crea la vida? ¿Por qué da lugar a tantos
compuestos?
Pregunta teórica que se encuentra en el libro del alumno.
2 Escribe y ajusta la reacción de combustión del octano.
5 Define qué es una cadena lineal, una ramificada, una
cerrada y un radical.
La reacción es:
2 C8H18 + 25 O2
Pregunta teórica que se encuentra en el libro del alumno.
16 CO2 + 18 H2O
141
13
la FÍSica Y la QuÍMica
En El MunDo En QuE ViViMoS
actividad de
aMPliaciÓn PÁG. 320
Respuesta libre en función de la localidad. Ha de corregirse
el planteamiento de al menos todos los puntos enumerados
en el enunciado.
1 Busca dónde se ha realizado las Conferencias de las
Partes sobre Cambio Climático y las fechas. Haz un resumen de los principales logros.
actividades de
aMPliaciÓn PÁG. 327
COP 1 - Berlín, 28 de marzo-7 de abril de 1995.
COP 2 - Ginebra, 8 -19 de julio de 1996.
COP 3 - Kioto, 1-10 de diciembre de 1997.
COP 4 - Buenos Aires, 2-13 de noviembre de 1998.
COP 5 - Bonn, 25 de octubre-5 de noviembre de 1999.
COP 6 - La Haya, 13-24 de noviembre de 2000.
COP 7 - Marrakesh, 29 de octubre-9 de noviembre de 2001.
COP 8 - N. Delhi, 23 de octubre-1 de noviembre de 2002.
COP 9 - Milán, 1-12 de diciembre de 2003.
COP 10 - Buenos Aires, 6-17 de diciembre de 2004.
COP 11 - Montreal, 28 de noviembre-9 de diciembre de
2005.
COP 12 - Nairobi, 6-17 de noviembre de 2006.
COP 13 - Nusa Dua (Bali), 3-14 de diciembre de 2007.
1 Busca en Internet o en enciclopedias actualizadas
noticias sobre las plantas transgénicas, los cultivos ecológicos, las centrales nucleares y las térmicas, las plantas
desaladoras y los transvases de ríos, y elige entre ellas
algún tipo de dato que te resulte sorprendente porque
esté lejos de la idea que tenías preconcebida sobre estos temas. Plantea un debate con tus compañeros para
aportar esa información.
Con respecto a los logros la respuesta es libre. En el enlace
que aparece en esta misma página se encuentran enlaces a
cada una de las Conferencias.
actividad de
aMPliaciÓn PÁG. 325
1 Busca en Internet o en enciclopedias actualizadas
las ventajas e inconvenientes que tienen para su utilización las distintas fuentes de energía que conoces, su
influencia en el medio ambiente y en el cambio climático
y la posibilidad de su desarrollo en cortos periodos de
tiempo que permitan la utilización en gran escala de este
recurso.
Respuesta libre. Deben utilizarse, si así se estima oportuno
y hay tiempo, las distintas respuestas de los alumnos para
concienciarles de la dificultad que tiene llegar a generalizar el
uso de fuentes de energía como la eólica o solar en un corto
periodo de tiempo y al mismo tiempo la falta de dependencia
de suministros exteriores que plantean en el caso español
donde serían unas fuentes de primer orden.
actividad de
aMPliaciÓn PÁG. 326
1 Haz un trabajo sencillo que contemple la gestión de
los residuos domésticos en tu localidad o zona: recogida
de basuras, selectividad en esta recogida, presencia de
contenedores especiales para papel, vidrio y envases,
gestión de aguas residuales, etcétera.
142
Respuesta libre, evidentemente, al depender de los preconceptos que el alumno tuviera. Puede ser un magnífico ejercicio para comprobar hasta qué punto la información que nos
llega está sesgada y cómo debemos esforzarnos en conseguir
información veraz para crear nuestra propia opinión, si queremos que ésta sea útil.
2 Investiga sobre las centrales productoras de energía y sobre las fábricas de tu entorno, haciendo una lista
de las ventajas que tiene la producción que en ellas se
obtiene y las desventajas para el medio ambiente de esta producción. Intenta encontrar posibles mejoras a los
inconvenientes que se planteen.
Respuesta libre. Debemos coordinar su atención en la línea
no de la crítica feroz a la producción de bienes de consumo
(energía, productos), sino en la de la mejora de la producción
creando una situación sostenible que mejore el desarrollo
de la zona.
actividad
cOMPleMentaria
1 Después de haber visto la película «La verdad incómoda», elabora un trabajo de unos cinco folios donde
desarrolles las ideas tanto negativas en cuanto a la situación actual del planeta, como positivas en cuanto a la
forma en que debemos proceder para mejorar el medio
ambiente, de forma que se pueda producir un debate
entre los compañeros para concienciarnos de los problemas actuales que penden sobre nuestro entorno.
El Ministerio o las Consejerías de Educación suministran la
película que conviene sea visionada en conjunto por la clase
para poder dirigir a los alumnos hacia los problemas básicos relacionados con el medio ambiente, siendo críticos a
la hora de evaluar los intereses de unos y otros, intentando
aprovechar las partes que nos permitan mejorar la opinión
de las alumnos sobre la Ciencia y su interés en aprovechar los
conocimientos que ésta nos aporta para mejorar el mundo
en que vivimos.
evalUaciÓn
Todas las contestaciones tienen una respuesta libre que se
valorará en mayor o menor medida en función del nivel de
explicación de los conceptos en clase.
No es necesario un rigor excesivo en las contestaciones
sino más bien un conocimiento lo suficientemente amplio
como para que el alumno conozca la existencia de un grave
problema medioambiental que debe ser resuelto por todos
y que se compruebe que es consciente de la importancia
de la Ciencia para resolver los problemas que ella misma o
terceros han creado.
1 Describe brevemente el contenido del Protocolo de
Kioto y cuáles son las medidas que propone para evitar el
calentamiento global. ¿Conoces algún país que se haya
negado a firmarlo o ratificarlo o que no se esté acercando
a las previsiones previstas en él?
El Protocolo va dirigido principalmente a reducir las emisiones de gases de efecto invernadero (GEI) en los países industrializados, comparando las emisiones a partir de 2012
con las que se hicieron en 1990. Pretende que a partir de ese
momento las emisiones de GEI cada vez sean menores con
el fin de evitar el calentamiento global.
Entre los países que no lo han ratificado se encuentran Australia y Estados Unidos, y uno de los países que está más lejos
de cumplirlo es España, que ha aumentado casi un 50 % sus
emisiones de 1990.
2 ¿En qué consiste el Principio de precaución? ¿Es una
norma de obligado cumplimiento o es sólo un concepto
teórico para intentar mejorar las agresiones que se cometen sobre el medio ambiente?
Es un Principio que pretende conseguir paralizar aquellas
supuestas agresiones al medio ambiente o a la salud de personas, animales o plantas cuando existe una duda razonable
sobre si son inocuas o no.
Desplaza la responsabilidad de demostrar si algo es negativo
o inocuo para el medio ambiente o para los individuos a la
persona, grupo de personas o empresas que ejercen la acción
que puede considerarse nociva.
No exime de la comprobación de si la agresión se produce o
no y de levantar las medidas precautorias si eran exageradas
o confirmar la prohibición en caso contrario.
No pretende ser una norma restrictiva sin más, sino estar
apoyada en estudios científicos donde se ponga en duda la
seguridad de una fábrica, método o cualquier otro tipo de
posible agresión sobre el medio ambiente.
Desde su aprobación por la Unión Europea es una norma de
obligado cumplimiento que los Estados deben ejercer con
responsabilidad y apoyados en consultores científicos y no
sólo en opiniones políticas.
3 De las siguientes fuentes de energía: eólica, solar,
hidroeléctrica, nuclear y térmica, comenta si influyen en
el efecto invernadero y cuáles son sus ventajas e inconvenientes a la hora de utilizarlas como fuentes de energía
en el futuro.
La eólica no influye en el efecto invernadero, es muy limpia y
barata, al ser renovable y no depender de fuentes externas,
por lo que no crea dependencia energética entre países.
Como problemas tiene el de la contaminación visual y sonora en su entorno, el que no siempre está en condiciones
de uso (puesto que depende del viento) y que se necesitan
zonas muy amplias dotadas de aerogeneradores para producir una cantidad significativa de energía. Además tiene el
inconveniente del tiempo que se tardaría en dotar grandes
zonas del planeta de los aerogeneradores necesarios para
ser autosuficientes con este tipo de energía.
La solar es similar a la eólica ya que no influye en el efecto
invernadero, es también muy limpia y barata, al ser renovable, y no depende de fuentes externas, por lo que tampoco
crea dependencia energética entre países, aunque su uso
está limitado a países con un número de días de sol al año
suficientemente alto. Es una de las fuentes de producción
de energía más individuales que existen, con lo que permite
una enorme autonomía y minimiza de forma importante los
cables y demás artilugios necesarios para el transporte de la
energía eléctrica.
Como problemas tiene el de la contaminación visual de
su entorno, el que no siempre está en condiciones de uso
(puesto que depende de la radiación solar) y que también
se necesitan zonas muy amplias dotadas de placas solares
para producir una cantidad significativa de energía. Tiene
al igual que la anterior el problema de que se necesitarían
muchos años para dotar grandes zonas del planeta de las
placas solares necesarias para ser autosuficientes con este
tipo de energía.
La hidroeléctrica también es muy limpia, barata y renovable,
además de que se puede utilizar la misma infraestructura
que para el almacenamiento de un recurso tan importante
como el agua.
Sin embargo, sólo determinadas zonas del planeta pueden
tenerla como fuente principal de energía, puesto que se
necesita una zona con desniveles del terreno y con la suficiente cantidad de lluvias al año para que permitan su explotación. Por otro lado anega numerosos valles impidiendo
su utilización con otros fines, y pueden plantear roturas de
presas que ocasionen problemas serios en caso de inundaciones no controladas.
La nuclear de fisión aporta energía barata sin contaminar con
gases de efecto invernadero y hay recursos para bastante
tiempo, y el precio del combustible, de momento, es plenamente asequible para casi todos los países.
Como inconvenientes tiene el de la gestión de los residuos
(que no está resuelta ni mucho menos), el de la contaminación durante miles de años de la zona donde la central
se ubica y la posible utilización con fines no pacíficos de la
tecnología y productos obtenidos con estas centrales.
143
13
Probablemente es el recurso a corto y medio plazo para evitar una crisis energética de gran calado evitando la emisión
de GEI, aunque debe debatirse en profundidad en cada zona.
Es la energía que genera el mayor problema de residuos a
largo plazo.
La nuclear de fusión está en estudio, por lo que todavía no
puede aplicarse, pero si se consiguiera es casi infinita en recursos y permitiría cantidades ingentes de energía a bajo
coste.
La dependencia tecnológica que tendrá su generación, en el
caso de que se consiga, incrementaría la brecha entre países
pobres y ricos y mantendría las distancias económicas entre
primer y tercer mundo, pero evitaría los conflictos relacionados con la generación de energía, ya que es la única forma de
generación masiva de energía que evitaría la dependencia
de las economías del primer mundo de recursos situados en
países en vías de desarrollo y en el tercer mundo.
La térmica tiene una tecnología perfectamente estudiada,
por lo que no exige ningún tipo de estudio ni desarrollo.
Es extremadamente contaminante, tanto en GEI como en
lluvia ácida, partículas, etc. Evidentemente debe ser el último
recurso para generar energía y debería evitarse su uso en la
medida de lo posible. Es prácticamente la única forma de
generación de energía en países no desarrollados, por lo que
es inevitable su utilización. Consume recursos tan preciados
como el gas natural y el petróleo.
4 Escribe al menos cinco medidas que te parezcan importantes relacionadas con la conservación del medio am-
144
biente y que puedas tú llevar a cabo en tu vida habitual.
¿Crees que el problema de degradación del medio ambiente tiene una solución global decidida por los Gobiernos de
los países o debe empezar a resolverlo cada individuo en
la medida de sus posibilidades en su entorno?
Respuesta libre pero que puede incluir no encender más luces de las necesarias, no generar ruidos innecesarios, reciclar
vidrios, envases y papel de forma selectiva, evitar el uso del
transporte privado, abrigarse con ropa disminuyendo la calefacción en invierno, quitarse ropa y ventilar a horas no solares
las casas en verano para evitar el uso de aire acondicionado,
consumir sólo el agua necesaria evitando el derroche de un
bien tan escaso, ducharse en vez de bañarse y hacerlo con
agua lo menos caliente posible dentro del confort necesario,
etcétera.
5 Enumera al menos tres problemas importantes que
tenga el mundo en este momento relacionados con el
medio ambiente y da una pequeña explicación de en qué
consisten.
Respuesta libre. Los más importantes son el calentamiento
global, la contaminación masiva, el agotamiento de los recursos y la mala gestión de éstos, la emisión de gases de efecto
invernadero, la deforestación y la lluvia ácida, etcétera.
Solucionario
atenciÓn
a la
diversidad
1 El MoViMiEnTo DE loS cuErPoS
1 Los datos de posición frente a tiempo para un determinado móvil son:
t (s)
0
0
0
0
r (m)
–4
0,5
2
5
a) Representa la gráfica posición frente a tiempo para
este móvil. ¿Qué tipo de movimiento es?
b) Calcula la velocidad entre los instantes 0 y 3 segundos. Comprueba que es la misma que entre los instantes 4 y 6 segundos.
c) Indica la posición del cuerpo en el instante inicial.
d) Escribe la ecuación de movimiento.
e) ¿Cuál será su posición a los 2 segundos?
f) ¿En qué instante se encontrará a 20 m a la derecha
del origen de coordenadas?
g) ¿En qué instante pasará por el origen de coordenadas?
a)
b)
c)
d)
e)
f)
g)
Movimiento Rectilíneo Uniforme.
v = 1,5 m/s
r0 = – 4 m
r = – 4 + 1,5 t
r(2) = – 1 m
t = 16 s
2,7 s
2 La ecuación de movimiento de un cuerpo es:
r = 9 – 3t.
a) Indica la posición inicial del móvil, así como la velocidad a la que se mueve.
b) ¿Qué nos indica el signo negativo de la velocidad?
c) ¿Cuál es su posición a los 2 segundos de empezar a
moverse? ¿Y a los 9 segundos?
d) ¿En qué momento se encontrará a 90 m a la izquierda
del origen?
e) ¿Para qué valor de t estará a 12 metros a la derecha
del origen? ¿Qué ocurre al tratar de resolver esta
ecuación?
a) r0 = 9 m v = –3 m/s
b) Que el cuerpo se desplaza en el sentido negativo del eje
x.
c) r(2) = 3 m; r(9) = –18 m
d) t = 27 s
e) Obtenemos un valor negativo para t. La solución no tiene
sentido desde un punto de vista físico.
3 La ecuación de movimiento de un cuerpo es:
r = –20 + 5t + t2.
a) Indica cuáles son la posición inicial del móvil, la velocidad inicial y la aceleración con la que se mueve.
b) ¿En qué instante se encuentra a 10 m a la izquierda
del origen? ¿Cuál es su velocidad en ese mismo instante?
146
c) ¿En qué momento pasa por el origen?
d) ¿Cuál es su posición a los 8 segundos de iniciarse el
movimiento?
e) ¿Para qué valor de t la velocidad es de 20 m/s?
f) ¿Cuál es el desplazamiento del móvil entre t = 1 y t = 4
segundos?
a)
b)
c)
d)
e)
f)
r0 = –20 m; v0 = 5 m/s; a = 2 m/s2
t = 1,5 s; v = 8 m/s
t = 2,6 s
r = 84 m
t = 7,5 s
Δx = 30 m
4 Un coche que se mueve con una velocidad de
100 km/h frena con una aceleración de 10 m/s2.
a) ¿Cuánto tiempo tarda en pararse?
b) ¿Qué espacio recorrerá hasta detenerse?
a) t = 2,8 s
b) Recorrerá 38,6 m
5 Dejamos caer un objeto desde una altura de 15 m.
a) Calcula el tiempo que tarda en llegar al suelo y su
velocidad en ese instante.
b) ¿Cuánto tiempo tarda en alcanzar una velocidad
de –8 m/s? ¿A qué altura se encuentra en ese momento?
a) t = 1,7 s; v = –16,7 m/s
b) t = 0,8 s; r = 11,9 m
6 Lanzamos hacia abajo un objeto desde una cierta
altura con una velocidad de 8 m/s. El objeto tarda 7 segundos en impactar contra el suelo. Calcula desde qué
altura se dejó caer y la velocidad con la que chocó contra
el suelo.
h = 296,1 m; v = –76,6 m/s
7 Lanzamos hacia abajo un objeto desde una altura de
100 m y con una velocidad inicial de –15 m/s. Calcula:
a) Tiempo que tarda en chocar contra el suelo y velocidad en ese mismo instante.
b) Posición y velocidad al segundo de lanzarlo.
c) Tiempo que tarda en hallarse a 5 m del suelo y velocidad en ese momento.
a) t = 3,2 s; v = –46,4 m/s
b) r = 80,1 m; v = –24,8 m/s
c) t =3,1 s; v = – 45,4 m/s
laS FuErZaS
1 Un muelle tiene una constante elástica k = 1 500
N/m.
a) Aplicamos una fuerza de 200 N, ¿Cuál será la elongación que experimente?
b) Colgamos del muelle un objeto y el muelle se estira
20 cm, ¿cuál es la fuerza aplicada?, ¿cuál es la masa
del objeto?
(Recuerda que el peso de un objeto es P = m g.)
a) ∆l = 1,33 m = 133,3 cm
b) F = 300 N; m = 30,6 kg
2 Un muelle mide 20 cm. Al colgarle un objeto de 300 g
pasa a medir 35 cm. Calcula la constante de elasticidad
del muelle y la fuerza aplicada.
(Recuerda que el peso de un objeto es P = m g.)
k = 19,6 N/m; F = 2,94 N
3 Sean los vectores:
FA = 3 N. Forma un ángulo de 0º con el eje X.
FB = 8 N. Forma un ángulo de 15º con el eje X.
FC = 2 N. Forma un ángulo de 45º con el eje X.
FD = 7 N. Forma un ángulo de 45º con el eje X.
FE = 1 N. Forma un ángulo de 180º con el eje X.
FG = 6 N. Forma un ángulo de 225º con el eje X.
Realiza las siguientes sumas de vectores, dibujando el
vector resultante y calculando el valor de su módulo.
 
FA + FB = 11 N
 
FB + FC = 9,8 N
 
FC + FD = 9 N
 
FC + FG = 4 N
 
FA + FD = 9,4 N
 
FA + FE = 2 N
 
FD + FG = 1 N
  
FA + FC + FD = 11,3 N;
  
FB + FD + FG = 8,9 N
Dibuja en cada caso sus componentes, calcula sus módulos y comprueba que la descomposición está bien
hecha.
FA = (11, 0)
FB = (3,5, 2)
FC = (6,4, 6,4)
FD = (3,5, 6,1)
FE = (0, 5)
FG =(–3, 5,2)
FH = (-8, 0)
FI = (–4,2, –4,2);
FK = (-3,5, –6,1)
Solución gráfica no incluida.


5 Sean los vectores FA (11 N, α = 0º) y FB (9 N, α = 60º).
a) Descompón ambos vectores en sus componentes X
e Y.
 
b) Calcula el vector resultante de la suma FA + FB .
a) FA = (11, 0); FB = (4,5, 7,8)
b) FR = (15,5, 7,8); FR = 17,4 N
6 Sean los vectores:
FA = 10 N. α = 0º
FB = 8 N. α = 30º
FC = 6 N. α = 45º
FD = 5 N. α = 45º
FE = 3 N. α = 60º
FG = 6 N. α = 90º
Realiza las siguientes sumas de vectores:
FA + FB = (16,9, 4)
FB + FC = (11,2, 8,2)
FA + FE = (11,5, 2,6)
FB + FE = (8,4, 6,6)
FA + FG = (10, 6)
FB + FG = (6,9, 10)
FA – FG + FB = (16,9, –2)
FC – FD + FG = (0,7, 6,7)
–FA + FG = (–10, 6)
FC – FE = (2,7, 1,6)
Solución gráfica no incluida.
4 Sean los vectores, definidos por su módulo y el ángulo que forman con el eje X.
FA = 11 N. α = 0º
FB = 4 N. α = 30º
FC = 9 N. α = 45º
FD = 7 N. α = 60º
FE = 5 N. α = 90º
2


7 Sean los vectores: FA (módulo de 4 N, α = 30º) y FB
(módulo de 12 N, α = 60º)
Ambos actúan sobre un mismo cuerpo. ¿Cómo debe ser
el vector que equilibre a estos dos vectores?
–FR = (–9,5, –12,4)
FG = 6 N. α = 120º
FH= 8 N. α = 180º
FJ = 6 N. α = 225º
FK = 7 N. α = 240º
147
3 laS FuErZaS Y El MoViMiEnTo
1 Sobre un cuerpo, inicialmente en reposo, actúa una
fuerza tal que, en 10 s el cuerpo se mueve a 30 m/s. Calcula:
4 Repite el ejemplo 2, calculando qué valor debe tener
la fuerza de rozamiento para que el cuerpo tarde en caer
4,8 segundos.
a) Aceleración del cuerpo.
b) Fuerza que actúa.
c) Espacio recorrido en esos 10 segundos. Masa del
cuerpo: 8 kg.
FR = 0,44 N
a) a = 3 m/s2
b) F = 24 N
c) s = 150 m
a) Dibuja las fuerzas que actúan sobre la lámpara.
b) ¿Qué valor tiene la tensión?
c) Si cortamos la cadena que une la lámpara al techo,
¿qué fuerza actuará sobre la lámpara?
d) ¿Cuánto tiempo tardará en llegar al suelo?
e) ¿Con qué velocidad chocará?
2 Un cuerpo de 9 kg de masa se mueve a 25 m/s. ¿Qué
fuerza de frenado lo detendrá en 15 segundos? ¿Qué espacio recorrerá hasta pararse? Repite el problema para
el caso de una masa de 18 kg.
F = 15 N; s = 183,8 m
Para un cuerpo de 18 kg: F = 306 N; s = 183,8 m
3 Un cuerpo de 54 kg de masa se mueve con una aceleración de 2 m/s2. Sobre él está actuando una fuerza de
200 N que favorece el movimiento y una fuerza de rozamiento. ¿Cuánto valdrá la fuerza de rozamiento? ¿Qué
valor tiene el coeficiente de rozamiento?
FR = 92 N; μ = 0,17
148
5 Una lámpara de 2 kg está colgada del techo a una
altura de 3,5 m.
a)
b)
c)
d)
e)
Solución gráfica no incluida.
T = 19,6 N
El peso = 19,6 N
t = 0,9 s
v = –8,3 m/s
6 Repite el ejemplo anterior, considerando que existe
una fuerza de rozamiento entre la mesa y el objeto que
está apoyado sobre ella de 0,6 N.
a) a = 4 m/s2
b) T = 40,6 N
ESTÁTica DE FluiDoS
1 Calcula la presión que ejerce un objeto de 15 kg de
masa que se apoya sobre una superficie de 3 m2. Repite
el problema si la superficie es de 60 dm2.
P = 49 Pa; P = 245 Pa
2 Calcula la presión que ejerce sobre el suelo un cilindro de 200 g de masa y 15 cm de radio. (Superficie del
círculo S = π r2.)
P = 27,7 Pa
3 Tenemos un bidón de 80 cm de altura lleno de aceite.
a) Calcula la presión que soporta la base.
b) ¿A qué profundidad, la presión es 100 000 Pa?
Dato: daceite =0,8 g/cm3.
4
4 Utilizando la misma prensa que en el ejemplo anterior, calcula la fuerza FA que habría que ejercer para
levantar un cuerpo de 700 kg de masa. (Dato: FB sería el
peso del cuerpo que queremos levantar.)
F = 668,85 N
5 Tenemos un cuerpo de 3 dm3 de volumen y densidad
1 050 kg/m3 y lo echamos al agua.
a) ¿Flotará?
b) Calcula su masa y su peso real.
c) Calcula el empuje que experimenta.
a) No. Su densidad es mayor que la del agua.
b) m = 3,15 kg; P = 30,87 N
c) E = 29,4 N
a) P = 6272 Pa; b) h = 12,75 m
149
5 FuErZaS GraViTacionalES
1 ¿Qué lugar ocupaba la Tierra en el Universo según
Aristóteles?
El centro del Universo.
2 ¿Quién fue el primero en afirmar que la Tierra giraba
en torno a sí misma y alrededor del Sol?
Aristarco de Samos fue el primero en afirmar que la Tierra
gira sobre sí misma cada 24 h, al mismo tiempo que, junto
con los otros planetas, lo hace alrededor del Sol.
3 ¿Qué eran los epiciclos según Claudio Tolomeo?
¿Qué dos fallos presentaba esta teoría?
Claudio Tolomeo postulaba que la Tierra era el centro del Universo, y que el Sol, la Luna y los planetas giraban alrededor
de ella describiendo a su vez pequeñas circunferencias —que
llamó epiciclos—, cuyo centro giraba también alrededor de la
Tierra. Esta teoría es errónea porque considera que el Sol gira
alrededor de la Tierra y porque recurre al concepto erróneo
de los epiciclos.
4 ¿En qué sentido la teoría de Kepler perfecciona la de
Copérnico?
Kepler sustituye las órbitas circulares de Copérnico por órbitas elípticas.
5 ¿Es correcta la afirmación de Kepler acerca de la
fuerza con la que el Sol atrae a los planetas?
Sí. Él afirma que la atracción que el Sol ejerce sobre otros
cuerpos disminuye al aumentar la distancia.
6 Señala la diferencia entre las concepciones heliocentrista y geocentrista del Universo. Elabora sendas listas
de los científicos que las defendieron.
En la concepción heliocentrista el Sol es el centro del Universo y en la geocentrista lo es la Tierra.
Defensores de la geocentrista: Eudoxo, Aristóteles, Claudio
Tolomeo.
Defensores de la heliocentrista: Aristarco de Samos, Copérnico, Kepler.
7 ¿Cómo explica el origen del Universo la teoría del
Big-Bang?
Considera que el Universo se formó a partir de una explosión inicial (Big-Bang). La energía contenida en un punto fue
dispersándose por el Universo a medida que éste se expandía, dando lugar a las primeras partículas componentes de
la materia.
8 ¿Qué rama de la Astronomía estudia la composición
de las estrellas?
150
La astrofísica.
9 ¿Qué diferencia hay entre la hipótesis del Universo
pulsante y la de la muerte térmica del Universo? ¿De qué
factor dependerá que el Universo evolucione en un sentido u otro?
La teoría que se denomina del Universo pulsante indica que,
si la materia que existe en el Universo es lo suficientemente abundante, la fuerza de atracción gravitacional entre los
objetos estelares conseguirá frenar la expansión, detenerla
e invertir el proceso, comenzando un acercamiento cada vez
más rápido. La teoría de la muerte térmica del Universo considera que si la materia no es lo suficientemente abundante el
Universo no frenará su expansión y las estrellas se apagarán
gradualmente. El que se siga uno u otro camino depende de
la cantidad de materia que exista en el Universo.
10 ¿Qué es el Big Crunch?
En la teoría de un Universo pulsante, en un primer momento
el Universo se expansionaría, para luego empezar a contraerse. El Universo se plegaría de nuevo hasta el punto original,
provocando lo que se denomina Gran Crujido (Big Crunch).
Esto generaría otro Big-Bang y así sucesivamente.
11 ¿A qué galaxia pertenece nuestro planeta? ¿En qué
cúmulo se encuentra? ¿Cuántas galaxias componen nuestro cúmulo?
Nuestro cúmulo se denomina Grupo Local, y contiene 28
galaxias. Nuestra galaxia es la Vía Láctea.
12 ¿Cómo tiene lugar el nacimiento de una estrella?
En ciertas zonas del Universo se produce una acumulación de
materia, lo que provoca un aumento de la temperatura. Hay
átomos de hidrógeno presentes que se fusionan generando
otros de helio y desprendiendo gran cantidad de energía.
13 Las estrellas pueden clasificarse de acuerdo con su
temperatura. ¿Cuáles son las estrellas más calientes?, ¿y
las más frías?
Las azules son las más calientes y las marrones las más frías.
14 ¿Qué tres tipos de estructuras puede originar una
estrella al extinguirse? ¿De qué depende que siga un
camino u otro? ¿Qué es un agujero negro?
Puede formar una enana negra, un púlsar o un agujero negro.
Depende de la masa de la estrella.
Un agujero negro es una acumulación muy densa de gran
cantidad de masa que deforma una zona del espacio, de
manera que nada que entre en su radio de acción puede
escapar, ni tan siquiera la luz, de ahí su nombre.
15 Un año luz es una unidad de a) tiempo b) longitud c)
volumen. ¿A cuántos años luz equivalen 1023 m?
De longitud. Equivale a 10,57 · 106 años luz.
16 ¿Qué espacio recorre la luz en 20 años? Expresa la
distancia en años luz y en km. vluz=3 · 105 km/s.
20 años luz = 1,9 · 1014 km
17 ¿Cuánto tiempo tarda la luz en recorrer 1015 km? Expresa la distancia en años-luz.
105,69 años-luz.; 3,3 · 109 s
18 ¿Por qué es difícil localizar un planeta en el espacio?
Porque el brillo de la estrella cercana nos impide verlo.
19 Sabiendo que la masa del Sol es 1,9891 · 1030 kg y la
masa de la Tierra es de 5,974 · 1024 kg. Calcula la fuerza
con que se atraen.
21 Sabiendo que la m de la Luna es 7,2 · 1022 kg y su r es
1,74 · 106 m, calcula la aceleración de la gravedad en la
superficie de ésta y compárala con la de la Tierra.
1,58 m/s2
22 ¿Cuál es el peso de un objeto de 25 kg de masa en la
Tierra? ¿Y en la Luna?
P(Tierra) = 245 N; P(Luna) = 39,5 N
23 ¿Cuál es la masa de un objeto que en la Luna tiene
un peso de 40 N? ¿Cuál sería su peso en la Tierra?
25,3 Kg; 248 N
24 Sabiendo que un objeto de 5 kg de masa tiene un
peso de 90 N en un determinado planeta, ¿cuál es el valor
de la gravedad en ese planeta? Si ese planeta tiene una
masa de 1023 kg, ¿cuánto mide su radio?
18 m/s2; 6,08 · 105 m
20 Sabiendo que la masa del Sol es 1,9891 · 1030 kg y la
masa de Júpiter es de 1,899 · 1027 kg. Calcula la fuerza
con que se atraen.
25 Calcula la fuerza con la que la Tierra atrae a un objeto de 50 g. ¿Qué aceleración actuará sobre ese cuerpo?
Por el Principio de Acción y Reacción el cuerpo ejerce sobre la Tierra una fuerza igual. ¿Qué aceleración produce
esta fuerza sobre la Tierra?
F = 4,16 · 1023 N
0,49 N; 9,8 m/s2; 8,2 · 10 -26 m/s2
F = 3,6 · 1022 N
151
6
TraBaJo, PoTEncia
Y EnErGÍa MEcÁnica
1 Sobre un cuerpo de 6 kg actúa una fuerza F. El cuerpo se desplaza verticalmente desde el suelo hasta una
altura de 20 m. Calcula el trabajo realizado por la fuerza
F y por la fuerza gravitatoria en los siguientes casos:
a) El cuerpo sube con velocidad constante.
b) El cuerpo sube con una aceleración de 4 m/s2.
a) WF = 1 176 J; WP = –1 176 J
b) WF = 1 656 J; WP = –1 176 J
2 Sobre un cuerpo de 6 kg de masa actúa una fuerza F paralela al suelo. El cuerpo se mueve 5 m con velocidad constante. Si el trabajo realizado por la fuerza de rozamiento es
de –20 J, calcula el valor de la fuerza F. Repite el problema
si el cuerpo se mueve con una aceleración de 3 m/s2.
F = 20 N; F = 38 N
3 Un cuerpo de 5 kg se desplaza con velocidad constante de 15 m/s a lo largo del eje X. Sobre él actúan una
Fx y una fuerza de rozamiento. El módulo de esta última
es de 20 N. Calcula:
a) Valor de Fx
b) Trabajo realizado por Fx y por la fuerza de rozamiento
si el cuerpo se desplaza 30 m.
c) Potencia desarrollada por Fx
a) Fx = 20 N; b) WF = 600 J; WR = –600 J; c) P=300 W
4 Una grúa funciona con una potencia de 10 CV. ¿Cuál
será el trabajo desarrollado por ella al cabo de 15 s?
Dicho trabajo se emplea en subir con velocidad constante un objeto desde el suelo hasta una altura de 12 m.
¿Cuál es la masa de dicho objeto?
W = 110 325 J; m = 938 kg
5 Dos coches de 1 500 y 2 000 kg de masa están parados. A los 6 s de iniciarse el movimiento el primero ha
alcanzado una velocidad de 30 km/h y el segundo se
mueve a 20 km/h.
¿Qué motor ha desarrollado una mayor potencia?
Expresa los resultados en CV.
PA = 70,8 CV; PB = 42,1 CV
El primer coche es el que ha desarrollado una mayor potencia.
6 Un cuerpo de 500 g de masa se desplaza con una
velocidad inicial de 20 m/s. La única fuerza externa que
actúa sobre él es la de rozamiento. El coeficiente de rozamiento es 0,18. Calcula:
a) Valor de la fuerza de rozamiento.
b) Aceleración con la que se mueve el cuerpo.
152
c) Tiempo que transcurre hasta que el cuerpo se para y
distancia recorrida hasta entonces.
d) Trabajo realizado por la fuerza de rozamiento.
a) FR = 0,88 N
b) a = –1,76 m/s2
c) t = 11,4 s; s = 113,6 m
d) W = –10 J
7 Desde una altura de 25 m se lanza un objeto de 30
g de masa. Contesta las siguientes preguntas para cada
uno de estos tres casos:
— Caso 1. El objeto se deja caer.
— Caso 2. Se lanza hacia arriba con una v = 5 m/s.
— Caso 3. Se lanza hacia abajo con una v = 5 m/s.
a) ¿La energía mecánica es igual en los tres casos?
b) ¿Chocarán contra el suelo a igual velocidad?
c) ¿Tardarán lo mismo en chocar contra el suelo?
d) ¿Qué tipo de energía (cinética, potencial gravitatoria)
tendrán en el instante en el que se dejan caer o son
lanzados?
e) ¿La velocidad a los 12,5 m es la mitad de la que tienen
al llegar al suelo?
a) Las energías mecánicas serán iguales en los casos 2 y 3 en
los que tenemos energía potencial y cinética. En el caso
1, al inicio, sólo hay energía potencial.
b) Igual que ocurre en la pregunta anterior, en los casos 2 y
3 chocarán con la misma velocidad, en el caso 1 lo hará
con una velocidad menor.
c) El tiempo en chocar es distinto en cada caso.
d) En el caso 1, energía potencial. En los casos 2 y 3, energías
cinética y potencial.
e) No. En los tres casos se trata de un movimiento uniformemente acelerado, por lo que la velocidad no crecerá
linealmente con el espacio recorrido.
8 Completa el siguiente cuadro para cada uno de los
casos anteriores:
Caso 1:
h (m)
Em (J)
Ec (J)
Ep (grav.) (J)
v (m/s)
25
7,35
0
7,35
0
12,5
7,35
3,67
3,68
15,64
10
7,35
4,41
2,94
17,15
5
7,35
5,88
1,47
19,80
0
7,35
7,35
0
22,14
h (m)
Em (J)
Ec (J)
Ep (grav.) (J)
v (m/s)
25
7,73
0,38
7,35
5
12,5
7,73
4,05
3,68
16,43
10
7,73
4,79
2,94
17,87
5
7,73
6,26
1,47
20,43
0
7,73
7,73
0
22,70
Casos 2 y 3:
calor Y EnErGÍa TÉrMica
7
1 Calcula la energía necesaria para elevar la temperatura de 250 g de hielo desde –20 ºC hasta 0 ºC. Dato:
c (hielo) = 2 050 J/kg K.
Observa: En este caso el agua tomará energía del cobre,
quedándose ambos a una temperatura intermedia entre
60 ºC y 10 ºC. Solución: 10,3 ºC.
Q = 10 250 J
Tf = 10,34 ºC
2 Calcula la energía que desprenderá un clavo de hierro de 15 g de masa que pasa desde 60 ºC hasta 25 ºC.
c(hierro) = 440 J/kg K
6 Repite la actividad 5 si el clavo está a 85 ºC. ¿Qué
ocurriría si en lugar de agua empleáramos un líquido con
un calor específico más pequeño? Repite la actividad 5
usando en lugar de agua un líquido con un calor específico de 400 J/kg K.
Q = 231 J
3 Sabiendo que el agua condensa a 100 ºC, calcula la
energía puesta en juego cuando 30 g de vapor de agua
a 100 ºC pasan a estado líquido.
Dato: LV (agua) = 22,5 · 105 J/kg. ¿Se trata de una energía
cedida al vapor o desprendida por éste?
Q = 67 500 J; Calor desprendido por el cuerpo.
4 Calcula el calor puesto en juego cuando 20 g de vapor
de agua a 100 ºC se transforma en agua líquida a 15 ºC. ¿El
vapor toma energía del entorno o se la cede a éste?
Dato: c(agua) = 4 180 J/kg K; LV = 2,2 · 106 J/kg
Q = 52 106 J; El vapor cederá energía a su entorno.
5 Tenemos 200 g de agua a 10 ºC. Introducimos una
pieza de cobre de 15 g de masa que está a 60 ºC.
¿Cuál será la temperatura final de la mezcla?
c(agua) = 4 180 J/kg K; c(cobre) = 385 J/kg K.
Caso 1: Tf = 10,51ºC
Caso 2: Tf = 13,37ºC
7 Repite el ejemplo 5, suponiendo ahora que la mezcla
final debe estar a 13 ºC.
Proceso 1: Hielo –18 ºC → Hielo 0 ºC → Agua 0 ºC →
Agua 13 ºC
Proceso 2: Agua 70 ºC → Agua 13 ºC
m = 0,268 kg
8 ¿A qué temperatura deben encontrarse 200 g de
agua para que sean capaces de fundir en su totalidad
70 g de hielo que inicialmente se encuentran a –8 ºC?
T = 41,57 ºC
153
8
la EnErGÍa DE laS onDaS:
luZ Y SoniDo
1 ¿En una onda se traslada materia de un punto a
otro? ¿Y energía? Explícalo para el caso de las ondas sísmicas.
Se traslada energía de un punto a otro sin que exista transporte de materia. En un terremoto, las ondas no desplazan
el suelo pero transportan mucha energía.
2 ¿Qué tipo de movimiento experimentan las partículas de un medio a través del cual se propaga una onda?
Un movimiento vibratorio.
3 ¿Qué diferencia hay entre una onda mecánica y otra
electromagnética? Pon un ejemplo.
Las ondas mecánicas precisan de un medio material para
desplazarse. Ejemplo: el sonido. Las ondas electromagnéticas pueden propagarse en el vacío. Ejemplo: la luz.
4 ¿Qué diferencia hay entre una onda transversal y
otra longitudinal? Pon un ejemplo.
En las ondas longitudinales la dirección de vibración de las
partículas y la de propagación de la onda coinciden. En las
transversales son perpendiculares. El sonido es una onda
longitudinal. La luz es una onda transversal.
5 Indica en cada caso si se trata de una onda longitudinal o transversal y si es mecánica o electromagnética:
onda en una cuerda, luz, onda de radio, rayos X, ondas
sonoras, ondas en la superficie del agua, ondas sísmicas,
ondas de un muelle.
Onda en una cuerda (mecánica y transversal),
luz (electromagnética y transversal),
onda de radio (electromagnética y transversal),
rayos X (electromagnética y transversal),
ondas sonoras (mecánica y longitudinal),
ondas en el agua (mecánica, longitudinal y transversal),
ondas sísmicas (mecánica, longitudinal y transversal),
ondas de un muelle (mecánica y longitudinal).
6 ¿Una onda transversal puede propagarse en un líquido? ¿Por qué?
Si es transversal y mecánica, sólo en los sólidos. El movimiento transversal requiere que cada partícula arrastre a las partículas contiguas a las que debe estar unida rígidamente, esto
sólo ocurre en los sólidos.
7 a) ¿Cómo se llama a la distancia sucesiva entre dos
crestas? b) ¿Cómo se llama al tiempo necesario para que
una partícula de un medio atravesado por una onda pase
por dos estados de vibración iguales? c) ¿Cómo se llama a
la altura de una cresta? d) En una onda, ¿todos los valles
tienen la misma profundidad?
154
a) Longitud de onda; b) Periodo; c) Amplitud; d) Sí.
8 ¿Cómo se ve afectada la energía transportada por
una onda si:
a) disminuye la amplitud de una onda?
b) aumenta la frecuencia de una onda?
c) aumenta el periodo de una onda?
(Consejo: Piénsalo gráficamente haciendo dibujos de las
ondas)
La energía transportada es directamente proporcional al cuadrado de su amplitud y al cuadrado de su frecuencia.
a) Disminuye la energía.
b) Aumenta la energía.
c) Disminuye la energía.
9 Un cantante emite un sonido que posee una longitud de onda de 3,9 m. Calcula:
a) frecuencia del sonido,
b) periodo del sonido.
Dato: velocidad del sonido en el aire = 340 m/s.
a) 87,2 Hz; b) 0,011 s
10 ¿En qué medio se propagan más rápido las ondas
sonoras (sólido, líquido, gas)?
Se propaga con mayor velocidad en este orden, primero en
los sólidos, luego en los líquidos, y en los gases.
11 ¿Qué es un aislante? Pon un ejemplo.
Son materiales cuyas partículas no vibran con la suficiente
energía como para transmitirla a las partículas vecinas. No
transmiten el sonido. Ejemplo: el corcho.
12 ¿Podemos variar la velocidad de propagación de una
onda modificando su longitud de onda o su frecuencia?
En la velocidad de las ondas sonoras no influye ni su frecuencia, ni su longitud de onda, ni su amplitud.
13 ¿Podemos aumentar la velocidad de propagación
del sonido en los gases? ¿Cómo?
La temperatura influye en la velocidad de propagación del
sonido en los gases. La velocidad de propagación aumenta
si lo hace la temperatura o la humedad.
14 ¿Con qué velocidad (en km/h) se desplaza un avión
que tiene un número de Mach de 1,6? Haz el problema
considerando que la temperatura ambiente es a) 15 ºC,
b) –55 ºC.
a) 1 958,4 km/h; b) 1 520,6 km/h
15 En el ejemplo anterior, si el tiempo que tarda en volver el sonido es 1,54 s, ¿cuál es la temperatura del aire?
(Consulte la tabla 8.1)
Tabla 8.1. Velocidad del sonido en el aire
T (ºC)
V (m/s)
-55
264
0
299
15
331
25
340
T = 15 ºC
16 ¿Cuál es la velocidad del sonido en el interior de un
lago si un submarino que está en su interior tarda 0,7 segundos en volver a escuchar un sonido que él ha emitido
y que se ha reflejado en un obstáculo situado a 500 m?
v = 1 429 m/s
17 ¿Qué es la sonoridad? ¿De qué depende? ¿En qué se
mide?
La sonoridad es la cualidad que permite identificar los sonidos como fuertes o débiles. Depende de la intensidad de la
onda, es decir, de la energía transportada por la onda, que
siempre es muy pequeña. Se mide en decibelios.
18 ¿Qué es el tono? ¿Qué diferencia hay entre los sonidos graves y los agudos?
El tono es la cualidad del sonido que permite distinguir entre
sonidos graves o bajos y agudos o altos. El tono está relacionado con su frecuencia: los sonidos graves son los de baja
frecuencia y los agudos los de alta.
19 Las longitudes de onda correspondientes a un bajo y
a un violín son, respectivamente, 5,23 m y 1,73 m. Calcula
la frecuencia correspondiente a cada instrumento. ¿Cuál
tiene un sonido más grave?
Dato: vsonido = 340 m/s
Bajo: F = 65 Hz; Violín: F = 196,5 Hz; Es más grave el bajo.
20 ¿Qué son los ultrasonidos? Indica alguna aplicación
de los mismos.
Los sonidos con frecuencias superiores a 20 000 Hz se denominan ultrasonidos. Tienen aplicación en Medicina, para
realizar ecografías en circunstancias en las que no se aconseje
el uso de rayos X.
21 ¿Qué es el timbre?
El timbre es la cualidad por la que se distinguen dos sonidos
de la misma sonoridad y del mismo tono.
22 ¿En qué consiste el fenómeno de la reflexión de la
luz? ¿Hay cambio en la velocidad de propagación de
la luz?
Cuando la luz incide sobre la superficie de un medio no transparente, opaco, vuelve al mismo medio en que se propagaba.
Este fenómeno se denomina reflexión. La luz que se refleja
cambia de dirección pero conserva la misma velocidad.
23 En la reflexión, ¿cómo son los ángulos incidente y
reflejados entre sí? Haz un dibujo.
Iguales. Solución gráfica no incluida.
24 ¿En qué medio es máxima la velocidad de propagación de la luz?
En el vacío.
25 En la refracción, ¿cambia la velocidad de la luz? ¿Y
su dirección?
Cambian la velocidad de propagación y la dirección.
26 Sabiendo que el índice de refracción del diamante
es 2,41, calcula la velocidad de propagación de la luz en
ese medio.
v = 1,24 · 108 m/s
27 Sabiendo que la energía transportada por una onda
es proporcional a su frecuencia, ordena en orden creciente de energía las siguientes radiaciones electromagnéticas: rayos X, ondas de radio, luz roja, luz azul y rayos
infrarrojos.
Ondas de radio, rayos infrarrojos, luz visible, rayos X.
155
9
loS ElEMEnToS QuÍMicoS
Y SuS EnlacES
1 Todos los átomos de un mismo elemento tienen el
mismo número de: a) protones, b) electrones, c) neutrones.
8 ¿Qué diferencia hay entre las moléculas y los cristales? ¿Son elementos, compuestos o pueden ser ambos?
Pon ejemplos.
Protones.
En las moléculas existe un número limitado de átomos enlazados. En los cristales no. Un ejemplo de cristal sería el cloruro
de sodio y de molécula, el agua (H2O).
2 ¿Qué es el número atómico de un elemento?
El número de protones que tiene en su núcleo.
3 Preguntas sobre la Tabla Periódica:
a) ¿Qué dos criterios se siguen para ordenar los elementos en el Sistema Periódico?
b) ¿Cuántos grupos y periodos tiene el Sistema Periódico actual?
c) ¿Qué nombre reciben los elementos de los grupos 1,
17 y 18?
d) ¿Qué grupos constituyen los elementos de transición?
e) ¿Qué son las tierras raras?
f) ¿Qué elemento pesa más el titanio o la plata? ¿Por
qué?
g) Ordena los siguientes elementos en orden creciente
de carácter metálico: Cl, Ge, Na, Al, F, Cs.
a) Se ordenan según el número atómico creciente, pero procurando que los elementos con propiedades semejantes
caigan en la misma columna.
b) 18 grupos y 7 periodos.
c) Alcalinos, halógenos y gases nobles.
d) Los comprendidos entre los grupos 3 y 12 (inclusives).
e) Los lantánidos y los actínidos. Son elementos que llenan
sus orbitales f.
f) La plata. Su peso molecular es más del doble.
g) F2, Cl2, Ge, Al, Na, Cs.
4 ¿Por qué los elementos de un mismo grupo suelen
tener propiedades químicas parecidas?
Porque tienen la misma configuración en su última capa.
5 ¿Por qué se enlazan entre sí los elementos químicos?
Un metal y un no metal.
10 Explica detenidamente los pasos que tienen lugar
en la formación de un compuesto iónico.
El metal cede sus electrones al no metal. Se forman un anión y
un catión y entre ellos aparecen interacciones electrostáticas.
11 Repite el ejemplo anterior para el caso de: a) F y Li,
b) Ca y Br, c) Al y Cl, d) K y I, e) Mg y S.
a)
b)
c)
d)
e)
Iones: Li+ F–; Compuesto: LiF
Iones: Ca2+ Br–; Compuesto: CaBr2
Iones: Al3+ Cl– ; Compuesto: AlCl3
Iones: K+ I–; Compuesto: KI
Iones: Mg2+ S2–; Compuesto: MgS
12 ¿Entre qué elementos se forma un enlace covalente?
Entre dos no metales.
13 ¿Cómo alcanzan los elementos unidos por un enlace
covalente la configuración de gas noble o de máxima
estabilidad? ¿Qué ocurre con los electrones?
Por compartición de electrones.
14 ¿Qué dos tipos de estructuras forman las sustancias
covalentes?
Pueden formar moléculas o redes cristalinas.
Porque compartiendo, ganando o perdiendo electrones pueden adquirir la configuración electrónica de un gas noble,
que es especialmente estable.
15 ¿Por qué las sustancias covalentes no conducen la
electricidad y las iónicas, cuando están disueltas o fundidas sí?
6 ¿Qué papel desempeñan los electrones en el enlace
químico?
Porque para que una sustancia conduzca la electricidad debe
poseer partículas cargadas (por ejemplo, iones o electrones)
capaces de moverse. En las sustancias covalentes no las hay.
En las sustancias iónicas los iones pueden moverse si disolvemos el sólido o lo fundimos.
El enlace químico entre dos elementos se establece por compartición o cesión de los electrones de valencia.
7 ¿Qué elementos del Sistema Periódico no suelen
enlazarse?
Los gases nobles.
156
9 ¿Qué elementos se enlazan en los compuestos iónicos?
16 Explica cómo es la estructura de un metal.
En los metales los átomos ceden algunos de sus electrones
al conjunto de la estructura. Los cationes que se forman se
disponen siguiendo una estructura cristalina.
17 ¿Por qué los metales conducen bien la electricidad?
Porque tienen electrones libres.
18 ¿Qué significa dúctil? ¿Y maleable?
Dúctiles: se pueden estirar en hilos. Maleables: cambian su
forma.
19 ¿Qué son las aleaciones?
Mezclas de metales, que poseen propiedades diferentes a las
de los metales por separado. Ejemplo: acero.
20 ¿Los compuestos iónicos forman moléculas o redes
cristalinas? Pon un ejemplo de un compuesto iónico
Redes cristalinas. Cloruro de sodio.
21 ¿Por qué los compuestos iónicos son duros?
Porque romperlos supone romper fuerzas electrostáticas,
que son grandes.
22 ¿Por qué los compuestos iónicos sólo conducen la
electricidad cuando están disueltos?
Porque para conducir la electricidad deben existir partículas
cargadas libres para moverse, y eso en el sólido cristalino no
sucede.
23 Señala en cada caso qué tipo de enlace presentaría
una sustancia que:
a)
b)
c)
d)
e)
Conduce bien la electricidad en estado sólido.
Es un gas a temperatura ambiente.
Es un sólido que se disuelve fácilmente en agua.
Conduce bien el calor.
No conduce la electricidad en estado sólido, pero sí
lo hace fundido.
f) Es un sólido que no se disuelve en agua y no conduce
la electricidad.
g) Es un líquido volátil que se disuelve bien en agua.
h) Es un sólido blando, que se puede estirar en hilos y
conduce bien la electricidad.
a) Metálico; b) Covalente; c) Iónico; d) Metálico;
e) Iónico; f) Covalente; g) Covalente; h) Metálico.
24 Señala en cada caso si nos encontramos frente a una
sustancia iónica, metálica o covalente. Explica qué iones
formaría y cuál sería la fórmula del compuesto si formara
enlace iónico. Dibuja su estructura de Lewis si es covalente: NaBr, Fe, AsH3, CaCl2, Na, Al2S3, SiH4, I2, Ni, H2.
Covalentes: AsH3, SiH4, I2, H2
Metálicas: Fe, Na, Ni
Iónicas: NaBr, CaCl2, Al2S3. Los iones que se formarían serían:
Na+, Br–, Ca2+, Cl–, Al3+, S2–
H +
I
As + H
+
H
+
++
+
I +
++
H + H
H
+
+
H
Si
+
H
+
H
157
10 laS rEaccionES QuÍMicaS
1 En 25 g de ácido sulfúrico (H2SO4), calcula:
a) El número de moles de sulfúrico que hay.
b) El número de moléculas de sulfúrico.
c) La masa de H que tenemos.
d) La masa de O que tenemos.
e) Los átomos de O que hay.
f) Los átomos de S presentes.
Datos: Masas atómicas: S: 32; O: 16; H: 1.
a) 0,26 moles; b) 1,54 · 1023 moléculas;
c) 0,51 g; d) 16,3 g;
e) 6,16 · 1023 átomos; f) 1,54 · 1023 átomos.
2 En 3 moles de cloruro de calcio (CaCl2), calcula:
a) La masa de compuesto que tenemos.
b) La masa de Cl presente.
c) Los átomos de Ca y Cl que hay.
a) 333 g; b) 213 g;
c) 1,8 · 1024 átomos de Ca; 3,6 · 1024 átomos de Cl.
3 Tenemos una cierta cantidad de agua que contiene
28 g de oxígeno. Calcula:
a)
b)
c)
d)
Los moles de agua que tenemos.
Las moléculas de agua presentes.
La masa de agua que hay.
El número total de átomos presentes en la muestra.
a) 1,75 moles de H2O; b) 1,05 · 1024 moléculas de H2O;
c) 31,5 g; d) 3,15 · 1024 átomos.
4 Tenemos una cierta cantidad de ácido nítrico (HNO3)
que contiene 5 · 1024 moléculas del ácido. Calcula:
158
a)
b)
c)
d)
La masa de ácido que tenemos.
Los moles de ácido.
La masa de oxígeno en la muestra.
Los átomos de oxígeno, nitrógeno e hidrógeno.
a) 523 g; b) 8,3 moles; c) 398,4 g;
d) 1,5 · 1025 átomos de O; 5 · 1024 átomos de N; 5 · 1024 átomos
de H.
5 Hacemos reaccionar 21 g de hidróxido de sodio
(NaOH) con la suficiente cantidad de ácido clorhídrico
(HCl), formándose cloruro de sodio (NaCl) y agua.
a)
b)
c)
d)
Escribe y ajusta la reacción.
¿Cuántos moles de ácido se necesitan?
¿Cuántos gramos de sal se forman?
¿Cuántos moles de agua obtendremos?
a) NaOH + HCl
NaCl + H2O; b) 0,52 moles;
c) 30,71 g; d) 0,52 moles.
6 Sea la reacción de formación del cloruro de hidrógeno:
H2(g) + Cl2 (g)
HCl (g).
Ajústala. Si se desean obtener 2 l de HCl, medidos a 30 ºC
y 0,5 atm,
a) ¿de qué masa de hidrógeno debemos partir?
b) ¿qué volumen ocuparán los moles de cloro que necesitemos, medidos en las mismas condiciones de
presión y temperatura?
H2 + Cl2
2 HCl
a) 0,04 g; b) 1 litro.
rEaccionES QuÍMicaS DE inTErÉS
1 ¿De qué color tiñen el papel de tornasol los ácidos?
¿Y las bases?
Los ácidos de rojo, las bases de azul.
Porque en medio ácido se presenta en su forma asociada
HIn y en medio básico lo hace como In-. Estas dos especies
presentan colores distintos. Como ejemplo, la fenolftaleína,
que en medio básico es rosa y en medio neutro incoloro.
2 ¿Cómo podemos neutralizar la acción de un ácido?
Con una base.
3 Indica en cada caso si se trata de un ácido o una base,
nombra el compuesto y escribe reacción de ionización:
H2SO3, Be(OH)2, H2S, KOH, Al(OH)3, H2CO3, Pb(OH)2, HBrO4,
Mg(OH)2, HNO2.
11
8 ¿Cuántos colores presenta un indicador universal?
Presenta varios colores. Es una mezcla de varios indicadores.
9 ¿De qué color se pondría una disolución de ácido
sulfúrico a la que añadiéramos unas gotas de rojo de
metilo?
Ácido sulfuroso H2SO3
SO32– + 2 H+
Hidróxido de berilio Be(OH)2
Be2+ + 2 OH–
2–
Ácido sulfhídrico H2S
S + 2 H+
Hidróxido de potasio KOH
K+ + OH–
Hidróxido de aluminio Al(OH)3
Al3+ + 3 OH–
2–
Ácido carbónico H2CO3
CO3 + 2 H+
Hidróxido de plomo (II) Pb(OH)2
Pb2+ + 2 OH–
–
Ácido perbrómico HBrO4
BrO4 + H+
Hidróxido de magnesio Mg(OH)2
Mg2+ + 2 OH–
–
+
Ácido nitroso HNO2
NO2 + H
Roja.
4 Tenemos dos disoluciones, una de ácido clorhídrico
y otra de ácido acético. Ambas tienen la misma concentración, 0,5 M. ¿En qué disolución será mayor la concentración de protones?
a) ¿De qué color es? Y si le añadimos unas gotas de fenolftaleína, ¿qué color adquiere?
b) ¿Qué hemos de hacer para decolorarla de nuevo?
En la de clorhídrico.
5 Ordena por orden creciente de pH:
a)
b)
c)
d)
e)
f)
Disolución 0,5 M de ácido nítrico.
Disolución 0,2 M de ácido nítrico.
Agua destilada.
Disolución 0,5 M de hidróxido sódico.
Disolución 0,2 M de ácido acético.
Disolución 0,2 M de hidróxido sódico.
a), b), e), c), f), d)
6 Indica, para cada ejemplo anterior, si la concentración de protones es mayor, menor o igual que la de los
iones OH –. Señala si se trata de una disolución ácida,
neutra o básica.
Las a, b y e son ácidas, la c es neutra y las f y d son básicas.
En las ácidas, hay más protones que aniones hidroxilo, en las
básicas ocurre al revés.
7 ¿Por qué cambia de color un indicador ácido-base?
Pon un ejemplo de un indicador, señalando cuáles son
los colores de sus formas ácida y básica.
10 ¿Podemos distinguir entre un ácido fuerte y otro
débil con ayuda del indicador fenolftaleína? ¿Y con el
papel indicador universal?
Con la fenolftaleína no, con el indicador universal, sí.
11 Tenemos una disolución de hidróxido de sodio
0,2 M.
a) Inicialmente es incolora. Al añadirle el indicador, rosa.
b) Si le añadimos un ácido volverá a ser incolora.
12 Escribe la reacción de neutralización entre:
a)
b)
c)
d)
ácido clorhídrico e hidróxido de calcio,
ácido nítrico e hidróxido de potasio,
ácido sulfúrico e hidróxido de aluminio,
ácido perclórico e hidróxido de hierro (III).
a)
b)
c)
d)
2 HCl + Ca(OH)2
HNO3 + KOH
3 H2SO4 + 2 Al(OH)3
3 HClO4 + Fe(OH)3
CaCl2 + 2 H2O
KNO3 + H2O
Al2(SO4)3 + 6 H2O
Fe(ClO4)3 + 3 H2O
13 Escribe la reacción de neutralización que produce:
a)
b)
c)
d)
bromuro de potasio,
sulfito de calcio,
sulfuro de cobalto (III),
perclorato de sodio.
a)
b)
c)
d)
HBr + KOH
H2SO3 + Ca(OH)2
3 H2S + 2 Co(OH)3
HClO4 + NaOH
KBr + H2O
CaSO3 + 2 H2O
Co2S3 + 6 H2O
NaClO4 + H2O
159
11
14 ¿Qué función cumplen los fertilizantes, desde el
punto de vista del pH del suelo?
Corregir los excesos de acidez o de basicidad que presentan
algunas tierras.
15 ¿Qué ácido segrega nuestro estómago? ¿Cómo podemos neutralizar su exceso? Escribe la correspondiente
reacción si la base utilizada es bicarbonato. ¿Qué gas se
libera?
Ácido clorhídrico. Bicarbonato de sodio. El gas que se libera
es dióxido de carbono.
HCl + NaHCO3
NaCl + H2O + CO2
16 ¿Cómo sería la reacción de neutralización que ocurriría en nuestro estómago si en lugar de bicarbonato
tomáramos hidróxido de aluminio?
3 HCl + Al(OH)3
AlCl3 + 3 H2O
17 Desde el punto de vista de los electrones, ¿qué es
oxidación?, ¿qué es reducción?
Oxidación es pérdida de electrones, reducción es ganancia
de los mismos.
18 Señala en cada caso si el hierro sufre una oxidación
o una reducción. Justifica tu respuesta:
a) de Fe a FeO
b) de Fe2O3 a FeO
c) de FeO a Fe
a) Pasamos de Fe0 a Fe2+, perdemos dos electrones, oxidación.
b) Pasamos de Fe3+ a Fe2+, ganamos un electrón, reducción.
c) Pasamos de Fe2+ a Fe0, ganamos dos electrones, reducción.
19 Repite lo mismo que en el ejercicio anterior, en este
caso para el carbono:
a) de C a CO
b) de CO2 a CO
c) de C a CO2
a) De C0 a C2+, oxidación. b) De C4+ a C2+, reducción. c) De C0
a C4+, oxidación.
20 Señala, en cada una de las siguientes reacciones,
qué elemento se oxida y cuál se reduce:
a) ZnO + C
b) Fe2O3 + C
160
Zn + CO
2 FeO + CO
c) Fe2O3 + 3 CO
2 Fe + 3 CO2
d) Cr2O3 + 2 Al
Al2O3 + Cr
e) ¿Qué elemento es el oxidante? ¿Y el reductor?
a) Zn se reduce, C se oxida. b) Fe se reduce, C se oxida. c) Fe se
reduce, C se oxida. d) Cr se reduce, Al se oxida. e) El oxidante
es, en cada caso, el elemento que se reduce. Reductor es el
elemento que reduce al otro, oxidándose él.
21 Asigna el número de oxidación de cada elemento en
los siguientes casos:
a)
b)
c)
d)
FeO
HCl
H2SO4
NaOH
e)
f)
g)
h)
HNO3
Ni
Ca(OH)2
H2CO3
i) CuO
j) HClO4
k) LiH
a) Fe:+ 2; O: –2; b) H: +1 Cl: –1; c) H: +1 S:+6 O: –2;
d) Na :+1 O: –2 H: +1; e) H:+1 N: +5 O: –2; f) Ni: 0;
g) Ca: +2 O: –2 H: +1; h) H: +1 C: +4 O: –2; i) Cu: +2 O: –2;
j) H: +1 O: –2 Cl: +7; k) Li: +1 H: –1
22 ¿De dónde sale la energía eléctrica de una pila?
De una reacción química espontánea.
23 Dadas las siguientes reacciones, asigna números de
oxidación a los elementos que en ellas aparecen. Señala
qué elementos se oxidan y cuáles se reducen.
2 HCl + Zn
ZnCl2 + H2
4 HCl + MnO2
MnCl2 + Cl2 + H2O
HNO3 + 3 Cu
3 Cu (NO3)2 + NO + H2O
KMnO4 + NH3
KNO3 + MnO2 + KOH + H2O
5 H2S + 2 KMnO4 + 6 HCl
5 S + 2 MnCl2 + 2 KCl + 8 H2O
2 H+ Cl– + Zn0
Zn2+ Cl2– + H20
Zn: Pasa de 0 a +2. H: de +1 a 0. Zn se oxida y H se reduce
4 HCl + MnO2
MnCl2 + Cl2 + H2O
Cl: Pasa de –1 a 0. Se oxida. Mn: de +4 a +2. Se reduce
HNO3 + 3 Cu
3 Cu (NO3)2 + NO + H2O
N: Pasa de +5 a +2. Se reduce.
Cu: Pasa de 0 a +2. Se oxida.
KMnO4 + NH3
KNO3 + MnO2 + KOH + H2O
Mn: Pasa de +7 a +4. Se reduce.
N: Pasa de –3 a +5. Se oxida.
5 H2S + 2 KMnO4 + 6 HCl
5 S + 2 MnCl2 + 2 KCl + 8 H2O
S: Pasa de –2 a 0. Se oxida.
Mn: Pasa de +7 a +4. Se reduce.
24 ¿Qué es la corrosión? Pon un ejemplo.
Es una oxidación. Por ejemplo, cuando el hierro se combina
con el oxígeno del aire y se transforma en óxido de hierro. En
el proceso el hierro pierde electrones (se oxida) y el oxígeno
los gana (se reduce).
25 ¿Cómo se suelen encontrar los metales en la naturaleza?
No es frecuente encontrarlos en su forma reducida. Lo habitual es hallarlos oxidados, combinados con otros elementos.
26 ¿Qué es una mena?
Los minerales cuya concentración de metal es suficiente
para que su extracción sea rentable reciben el nombre de
menas.
27 ¿Qué tres procedimientos existen para reducir una
mena?
Reducción por calentamiento en presencia de aire. Reducción con carbón. Reducción electrolítica.
28 En la reducción por calentamiento en presencia de
aire, ¿qué elemento actúa como reductor? En las siguientes reacciones, indica qué elemento se oxida, cuál se reduce, cuál es el oxidante y cuál el reductor:
a) Cu2S + O2
b) HgS + O2
2 Cu +SO2
Hg + SO2
Oxidante: Es el elemento que oxida al otro, reduciéndose
él.
Reductor: Es el elemento que reduce al otro, oxidándose él.
a) Cu2S + O2
2 Cu +SO2
Cu: Se reduce. O: Se reduce. S: Se oxida.
b) HgS + O2
Hg + SO2
Hg: Se reduce. S: Se oxida. O: Se reduce.
29 En la reducción con carbón, ¿qué compuesto actúa
como reductor? En las siguientes reacciones, indica qué
elemento se oxida, cuál se reduce, cuál es el oxidante y
cuál el reductor:
a) Fe2O3 + 3 CO
2 Fe + 3 CO2
b) CoO + CO
Co + CO2
Oxidante: El elemento que oxida al otro, reduciéndose él.
Reductor: El elemento que reduce al otro, oxidándose él.
a) Fe2O3 + 3 CO
2 Fe + 3 CO2
Fe: Se reduce. C: Se oxida.
b) CoO + CO
Co + CO2
Co: Se reduce. C: Se oxida.
30 ¿Qué es una reacción exotérmica?
Aquella que libera calor.
31 ¿Qué es un comburente?
El comburente es un agente oxidante, necesario para la combustión.
32 Dadas las siguientes reacciones, escribe cuáles serían los productos de la combustión. Ajusta la reacción:
C + O2
CO2
H2 + 1/2 O2
H2O
CH4 + 2 O2
CO2 + 2 H2O
CO + 1/2 O2
CO2
C2H2 + 5/2 O2
2 CO2 + H2O
C6H12O6 + 6 O2
6 CO2 + 6 H2O
C2H6 + 7/2 O2
2 CO2 + 3 H2O
C2H4 + 3 O2
2 CO2 + 2 H2O
33 ¿Qué es el punto de ignición?
Temperatura a partir de la cual una sustancia arde sin aporte
de energía externo.
34 ¿Por qué se dice que la respiración es una combustión lenta? ¿Qué sustancia sería el combustible? ¿Y el
comburente?
La respiración consiste en una serie de reacciones químicas
de las cuales el organismo obtiene la energía que necesita.
El combustible serían los alimentos que ingerimos. El comburente el oxígeno procedente de la respiración.
35 ¿Qué es el metabolismo?
El conjunto de reacciones químicas que ocurren en un organismo, de las cuales se obtiene la energía que ese ser necesita
y se sintetizan nuevas sustancias.
36 En los transbordadores espaciales, ¿qué sustancia
actúa como combustible? ¿Y como comburente? Escribe
y ajusta la reacción de combustión que tiene lugar.
El hidrógeno es el combustible y el oxígeno el comburente.
La reacción que tiene lugar es:
H2 + 1/2 O2
H2O
161
12
la QuÍMica DE loS coMPuESToS
DEl carBono
1 ¿Qué diferencia hay entre los enlaces Si-Si y C-C? ¿Es
posible formar largas cadenas de Si?
Los enlaces entre átomos de silicio son más débiles que los
que se forman entre los átomos de carbono. Por ello no es
posible formar largas cadenas de silicio, y sí de carbono.
2 Las burbujas de las bebidas gaseosas se deben a la
presencia de CO2 disuelto. ¿Podríamos hacer lo mismo
con SiO2?
No, el compuesto análogo al del carbono, SiO2 es insoluble
en agua y es sólido.
3 ¿Cita los 6 elementos que forman principalmente la
materia viva?
C, H, O, N, P y S.
4 De acuerdo con Oparin, ¿cuáles fueron las moléculas
inorgánicas precursoras de la vida? ¿De dónde salió la
energía necesaria para sintetizar, a partir de ellas, otras
moléculas más complejas?
Metano, amoníaco, vapor de agua e hidrógeno. La energía
se obtuvo gracias a las descargas eléctricas de los rayos, las
radiaciones solares, las sustancias radiactivas de la superficie
terrestre y el calor generado en zonas volcánicas.
5 La teoría de Oparin, ¿ha sido verificada experimentalmente?
Sí, en 1953 por Stanley Miller, en la Universidad de Chicago.
6 ¿La teoría de Oparin es la única para explicar cómo
aparecieron las primeras biomoléculas en la Tierra?
Existen otras teorías, según las cuales la vida se originó en
las proximidades de los volcanes submarinos o gracias a sustancias procedentes del espacio que llegaron a la Tierra en
asteroides y meteoritos.
7 Señala una explicación para la aparición del agua
en la Tierra.
Parece ser que el agua que existe en nuestro planeta llegó a
la Tierra transportada por cometas.
8 ¿Qué es la Química Orgánica? ¿Son orgánicos los siguientes compuestos: CH4, CaCO3, CH3CH3, CO2?
La Química Orgánica o Química del carbono estudia las sustancias que contienen carbono en su molécula, con excepción de sus óxidos y de los carbonatos.
Son orgánicas: CH4, CH3CH3
162
9 Escribe la configuración electrónica del C. ¿Tiene el octeto
completo? El enlace en la molécula de metano (CH4) es
iónico o covalente? Escribe la estructura de Lewis correspondiente.
C: 1s22s2p2. No tiene el octeto completo.
Se trata de un enlace covalente.
.H.
H : .C. : H
H
H
H C H
H
10 Escribe las estructuras de Lewis para las moléculas
etano, eteno y etino. ¿Qué tipo de enlace aparece, metálico, iónico o covalente?
Son enlaces covalentes.
H
.. H
..
:
H : .C. : C
.. H
H H
H
.. H
..
H : C :: C : H
C : C :. :. C : C
H H
H C C H
H H
H H
H C C H
H C C H
11 ¿Qué son los isómeros? Escribe los isómeros de los
siguientes compuestos: C4H10, C5H12.
Compuestos con la misma fórmula molecular pero distintas
estructuras.
C4H10 butano e isobutano (2-metilpropano).
C5H12 pentano; 2,2-dimetilpropano; 2-metilbutano.
12 ¿Conducen la electricidad los compuestos orgánicos?
No.
13 Escribe la reacción de combustión de los siguientes
hidrocarburos y ajústala: CH4, C6H6, C5H10.
CH4 + 2 O2
C6H6+ 15/2 O2
C5H10+ 15/2 O2
CO2 + 2 H2O
6 CO2 + 3 H2O
5 CO2 + 5 H2O
14 ¿A qué llamamos hidrocarburos? ¿De dónde se obtienen?
Son compuestos orgánicos formados exclusivamente por
carbono e hidrógeno. Están presentes en el petróleo y el gas
natural.
15 ¿Qué diferencia hay entre los hidrocarburos saturados y los insaturados?
En los saturados los enlaces carbono-carbono son sencillos
y en los insaturados son dobles o triples.
16 Dados los siguientes compuestos, escribe su fórmula
desarrollada, indicando si se tratan de alcanos, alquenos
o alquinos: CH4, C2H2, C3H6, C4H10, C4H8, C3H8.
CH4 alcano
HC ≡ CH alquino
CH2=CH–CH3 alqueno
CH3CH2CH2CH3 alcano
CH3CH2CH=CH2 alqueno
CH3CH2CH3 alcano
17 Realiza un esquema clasificando los términos: hidrocarburos, alifáticos, aromáticos, alcanos, alquenos,
alquinos, saturados e insaturados. Escribe un ejemplo
de cada.
a) Hidrocarburos alifáticos:
a1) Saturados: etano.
a2) Insaturados: alquenos (eteno) alquinos (etino).
b) Hidrocarburos aromáticos: benceno.
18 ¿Cómo varía el estado de agregación de los hidrocarburos conforme aumenta el peso molecular de los
mismos?
Los hidrocarburos de menor masa molecular son gases o
líquidos, los de mayor masa son sólidos.
19 ¿Qué hidrocarburos son más reactivos, los saturados
o los insaturados? ¿A qué se debe?
Los más reactivos son los insaturados. Esto se debe a la presencia de los enlaces dobles y triples, más inestables que
los simples.
20 ¿Qué compuestos orgánicos son los principales componentes del petróleo y el gas natural?
Los hidrocarburos.
21 ¿Qué hidrocarburos son los más abundantes en el
petróleo y el gas natural?
Gas natural: metano, etano, propano y butano.
Petróleo: hidrocarburos de tamaño variable.
22 ¿Qué carburante contiene hidrocarburos de cadena
más larga, el gasóleo o la gasolina?
El gasóleo.
23 ¿Qué carburante de los dos anteriores es más volátil?
La gasolina es más volátil.
24 ¿Existe alguna relación entre el número de carbonos
que posee un hidrocarburo y su volatilidad?
Cuanto mayor es el número de carbonos, mayor es la masa
molecular y menor la volatilidad.
25 Cita cuatro aplicaciones de los destilados del petróleo.
Como combustible para coches, para la calefacción, como
disolventes, y para la fabricación de pomadas.
26 ¿La vaselina es un hidrocarburo de cadena larga?
Sí, es de cadena larga.
27 Cita dos procedimientos para obtener la gasolina.
Por destilación del petróleo o por rotura de hidrocarburos
de cadena larga.
28 ¿Qué es el craqueo?
El craqueo es la ruptura de las cadenas de los hidrocarburos
más pesados, calentándolos bajo presión en presencia de
catalizadores.
29 Indica un residuo de la combustión del gas natural
que contribuye al aumento del efecto invernadero.
Dióxido de carbono.
30 Indica cuatro productos que fabrica la industria petroquímica.
Plásticos, cauchos, fibras textiles y herbicidas.
31 ¿Cuál es el grupo funcional característico de los alcoholes?
El grupo hidroxilo. –OH
32 Formula y nombra tres posibles isómeros del pentanal.
Pentanal 3-metilbutanal 2-metilbutanal
33 ¿Por qué los alcoholes se suelen disolver bien en
agua?
Por la formación de enlaces por puente de hidrógeno entre
las moléculas de agua y los grupos hidroxilo.
34 ¿Es peligrosa la ingesta de metanol?
Es tóxico. Puede provocar ceguera y muerte.
35 ¿Qué alcohol hay en las bebidas alcohólicas?
El etanol. Se obtiene por fermentación de los azúcares.
163
12
36 ¿Por qué ni el vino ni la cerveza contienen más del
16 % de alcohol?
límero está sustituyendo al PVC porque elimina posibles
problemas medioambientales?
Porque las levaduras que llevan a cabo la fermentación mueren en concentraciones superiores al 16 %.
Policloruro de vinilo (PVC). Como contiene cloro, su combustión libera compuestos clorados a la atmósfera que pueden
destruir la capa de ozono.
El polietilentereftalato (PET) se emplea en la fabricación de
botellas para agua y bebidas gaseosas o de refresco. Ha desplazado de este uso al PVC.
37 Escribe la fórmula y el nombre de un anticongelante.
Etanodiol (CH2OH–CH2OH), también llamado etilenglicol.
38 Escribe la fórmula de la glicerina y cita una de sus
aplicaciones.
Propanotriol (glicerina) (CH2OH–CHOH–CH2OH); se utiliza
para fabricar cremas para la piel.
39 ¿Cuál es el grupo funcional característico de los ácidos orgánicos?
El grupo carboxilo, –COOH.
40 ¿A partir de qué compuesto orgánico que has estudiado se pueden obtener los ácidos? Por ejemplo, ¿cómo
podrías obtener el ácido fórmico?
Por oxidación de los alcoholes. A partir del metanol.
41 ¿Cuál es el alcohol presente en el vino? ¿Y el ácido
presente en el vinagre?
El etanol. El ácido acético (etanoico).
42 ¿Cómo se llaman las unidades que forman un polímero?
El enlace carbono-flúor es muy fuerte, lo que hace que el
teflón sea duro, inerte y resista temperaturas muy altas.
48 Cita dos halógenos presentes en polímeros sintéticos.
Cloro (PVC) y flúor (teflón).
49 ¿Qué es el látex? ¿De dónde se extrae? El látex que
se emplea, ¿tiene un origen natural?
El caucho natural se encuentra en un fluido blanco lechoso,
llamado látex, que se extrae del árbol Hevea brasiliensis. Como la demanda de caucho es muy alta, también se sintetiza
caucho artificial a partir de butadieno.
50 Aplicaciones del látex.
El látex es fundamental en la fabricación de colchones y almohadas por su adaptabilidad y su resistencia.
51 ¿Qué es la vulcanización?
Monómero.
Las propiedades del caucho mejoran tratándolo con azufre (vulcanización). El caucho vulcanizado es muy resistente al rozamiento, no se ablanda con el calor y es prácticamente insoluble.
43 Indica cuál es el monómero constituyente en cada
caso: polietileno, poliestireno, PVC.
52 Señala un polímero artificial que se emplee en la
industria textil. ¿Qué ventaja presenta?
Polietileno: eteno. Poliestireno: estireno. PVC: cloroeteno.
Poliamida (nailon). Son fibras resistentes y que aceptan bien
los tintes.
44 Cita algunos polímeros que se sinteticen en la industria. Indica tres posibles usos de un polímero sintético.
Polipropileno, teflón, polimetacrilato de metilo.
Policloruro de vinilo (PVC). Se emplea en la fabricación de
tuberías, carpintería y envases.
45 ¿A partir de qué sustancia se obtienen los plásticos?
Del petróleo.
46 ¿Qué polímero libera, tras su combustión, cloro? ¿En
qué sentido perjudica esto al medio ambiente? ¿Qué po-
164
47 ¿Qué hace que el teflón sea un material duro?
53 Nombra los 4 tipos de biomoléculas que constituyen
la materia viva.
Glúcidos, lípidos, prótidos y ácidos nucleicos.
54 Cita dos ejemplos de hidratos de carbono.
Glucosa y sacarosa.
55 ¿En qué alimentos podemos encontrar hidratos de
carbono?
Azúcar y cereales.
56 Cita dos ejemplos de lípidos.
Grasas y colesterol.
57 ¿En qué alimentos están presentes los lípidos?
Queso y carne.
58 ¿Qué diferencias hay entre las grasas saturadas y las
insaturadas?
Las grasas saturadas son de origen animal, las insaturadas
vegetal. Las insaturadas disminuyen el nivel de colesterol.
60 ¿Qué son los aminoácidos?
Compuestos orgánicos que contienen un grupo amino y un
ácido orgánico.
61 Pon un ejemplo de una proteína.
La hemoglobina.
62 ¿Qué alimentos nos proporcionan proteínas?
Carne, pescado, leche.
59 ¿Qué elementos forman las proteínas?
Los aminoácidos.
165
13
la FÍSica Y la QuÍMica
En El MunDo En QuE ViViMoS
1 ¿Qué efecto tiene la capa de ozono sobre las radiaciones UVA?
Filtra radiaciones ultravioleta.
Reducir la emisión de gases de efecto invernadero. Nosotros fuimos un país favorecido, ya que no se nos exigió una
reducción tan drástica como a otros. A pesar de ello, hoy en
día emitimos por encima del nivel permitido.
2 ¿Qué problemas puede acarrear el no eliminar adecuadamente los metales pesados?
10 Pon dos ejemplos de métodos que se están estudiando para eliminar el CO2.
Que sean ingeridos por los animales y éstos mueran.
Nuevas fuentes de energía no emisoras de gases. Uso de
cianobacterias.
3 ¿Por qué no es aconsejable el uso de los fosfatos como fertilizantes?
Porque se degradan muy lentamente y al llegar a un lago o
un río favorecen la proliferación de algas que dificultan el
desarrollo de otras especies. Además, la presencia de fosfatos
hace que disminuya la cantidad de oxígeno en el agua.
A partir del petróleo se sintetizan muchos productos químicos y también es un combustible. Si lo usamos como esto
último perderemos una fuente de productos químicos.
4 ¿En qué consiste el fenómeno conocido como «lluvia
ácida»? Escribe las reacciones que tienen lugar.
12 ¿Qué significa la expresión «reducción de la biodiversidad»?
En la atmósfera hay óxidos de azufre y nitrógeno emitidos
por el hombre. Cuando estos óxidos se combinan con el agua
de la lluvia se forman los ácidos nítrico y sulfúrico.
SO3 + H2O
H2SO4
2 NO2 + H2O
HNO2 + HNO3
Hace referencia a la desaparición de muchas especies en
nuestro planeta.
5 ¿En qué consiste el efecto invernadero?
El efecto invernadero se debe al exceso de algunos compuestos gaseosos (CO2, metano, óxidos de nitrógeno) emitidos por
el hombre. Estos compuestos hacen que parte de la radiación
procedente del Sol que la Tierra devolvería al espacio quede
retenida, lo que provoca que la temperatura en la superficie de
la Tierra se incremente.
6 ¿Qué gases son los responsables del efecto invernadero?
Dióxido de carbono, metano, óxidos de nitrógeno.
7 ¿Es el efecto invernadero en parte beneficioso? ¿Por qué?
Sí. El efecto invernadero ha permitido que la temperatura en
la superficie de la Tierra fuera lo suficientemente alta como
para que la vida fuera posible. El problema es que, como consecuencia de la contaminación, este efecto se ha acentuado
y ahora la temperatura es excesiva.
8 Cita algunas fuentes emisoras de CO2.
La quema de combustible y los incendios forestales.
9 ¿En qué consiste el Protocolo de Kioto? ¿Qué compromiso adquirió España en Kioto?
Es un compromiso que adquirieron algunos países de reducir
la emisión de gases de efecto invernadero.
166
11 ¿Por qué dos razones nos es necesario el petróleo?
¿Por qué no es aconsejable usarlo como combustible?
13 ¿Puedes poner algún ejemplo de un producto químico cuyo empleo tuviera simultáneamente consecuencias
positivas y negativas? Explica cuáles fueron sus efectos.
El DDT es un insecticida cuyo uso se eliminó porque ocasionaba la muerte de los animales. Pero en muchos países en los
que se usó contribuyó a la erradicación de la malaria.
14 Cita dos efectos beneficiosos que haya tenido el
uso de productos químicos y farmacéuticos. ¿Por qué es
importante tomar un antibiótico el número exacto de días
indicados por el médico aunque pensemos que ya estamos
curados?
Prolongar la esperanza de vida del hombre y obtener mejores
cosechas.
Porque ése es el plazo de tiempo que nos garantiza que el
agente patógeno ha sido eliminado totalmente. Si no lo hacemos, lo que conseguiremos es que se haga resistente al
antibiótico.
15 ¿Qué elementos forman la molécula de DDT? ¿Puedes escribir su fórmula?
C, Cl, H. Es el diclorodifeniltricloroetano.
16 ¿Puedes explicar en qué consiste el «Principio de
precaución o de cautela»? Señala dos documentos en los
que se recoja este principio.
Este principio tiene como objetivo preservar el medio ambiente incluso en los casos en los que no se tengan todas las
certezas científicas. Esto es, si existe la posibilidad de que el
medio ambiente puede resultar irreversiblemente dañado,
hay que tomar medidas preventivas, aun sin tener la seguridad absoluta de que el riesgo existe. Este principio se recoge
en la Declaración de Río y en el artículo 130R del Tratado de
Maastricht.
17 ¿Qué son los transgénicos?
Especies cuyo material genético ha sido modificado.
18 Explica un problema medioambiental que te preocupe o te interese.
Respuesta libre.
19 ¿Qué es una energía limpia? ¿Y renovable?
Que no contribuye a la contaminación. Que no existe riesgo
de que se agote.
20 Pon un ejemplo de una energía no renovable.
La que usa el petróleo como fuente de energía.
21 ¿El uso del maíz como biocombustible es un caso
de energía renovable? ¿Qué inconveniente tiene su uso
como fuente de energía?
Es renovable, pero su uso como combustible encarece el
producto, lo que perjudica a países del Tercer Mundo cuyos
habitantes se alimentan de maíz.
22 Cita dos fuentes de energías limpias y renovables.
La energía solar y la eólica.
23 Ventajas e inconvenientes de la fusión nuclear como
fuente de energía.
Ventajas: es limpia y como fuente usa hidrógeno, muy abundante en la Tierra. El inconveniente es que se necesita más
tiempo para poner a punto la técnica.
24 ¿Qué significa la expresión in situ?
En el lugar.
25 ¿Qué problemas acarrean las centrales nucleares de
fisión? ¿Qué ventajas tiene este tipo de energía?
Los inconvenientes son su alta peligrosidad en caso de catástrofe y que genera muchos residuos radiactivos. Las ventajas
son que no emite gases y tiene un bajo impacto ambiental.
26 ¿Qué tarea se lleva a cabo en las depuradoras de
aguas residuales?
Se recoge el agua de desecho procedente de una ciudad o
una industria y se eliminan los contaminantes que pueda
llevar antes de devolverla al río.
27 Señala un ejemplo de cómo se puede:
a)
b)
c)
d)
Reciclar material.
Ejercer un consumo responsable de la energía.
No desperdiciar recursos naturales.
Ayudar a un país en vías de desarrollo.
Ejemplos que ponga el alumno: reciclar latas, apagar las luces
de casa, colaborar con ONGs…
167