Interés Compuesto y Anualidades: Ejercicios MAT 242
Anuncio

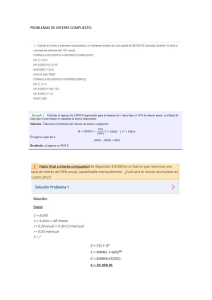
PRACTICA CONOCIMIENTOS PREVIOS MAT 242 Interés Compuesto Conclusiones a) Interés compuesto es mayor que el interés simple. b) A mayor frecuencia de conversión mayor será el interés siendo igual la tasa anual nominal. Ej. Un depósito que obtenga intereses mensualmente tendrá mayor rendimiento que uno que los obtenga trimestralmente. EJERCICIOS 1) Cuál es la tasa de interés por periodo de: a) 60% anual capitalizable mensualmente b) 36% semestral capital trimestralmente c) 12% trimestral d) 18% anual capital semestralmente e) 18% capitalizar mensualmente I. Se depositan US$ 500.00 en un banco a una tasa de interés del 48% anual capitalizable mensualmente. ¿Cuál será el monto acumulado en 2 años? II. Se obtiene un préstamo bancario de US$ 15,000 a plazo de un año y con interés del 52% convertible trimestralmente ¿Cuál será el monto a liquidar? III. Se decide liquidar el préstamo del ejemplo anterior en forma anticipada habiendo transcurrido 7 meses y ½. ¿Cuál es la cantidad que debe pagarse? IV. Se contrata un préstamo bancario por US$ 50,000 el plazo a pagar es 3 años, la tasa de interés es del 60% a, c s. ¿Qué cantidad debe pagarse si se decide cancelarlo en forma anticipada a los 15 meses. V. Determine el interés que gana en un año un depósito de US$ 1000.00 en: a) Una cuenta que paga el 20% de interés anual convertible trimestralmente. b) 20% a c diariamente VI. Determine el monto acumulado de US$ 5,000.00 que se depositan en una cuenta de valores que paga el 24% anual convertible mensualmente? a) Al cabo de un año b) Al cabo de dos años. VII. Cuánto dinero debe pagarse a un banco que hizo un préstamo de US$ 30,000 si se reembolsa al año capital e interés y la tasa aplicada es del 0.44 anual convertible trimestralmente? VIII. Qué cantidad deberá liquidarse en caso de que el préstamo del Ejemplo anterior se pagará al cabo de 10 meses? Tasa nominal tasa efectiva y tasa equivalente.-Cuando se utiliza una operación financiera, se pacta una tasa de interés anual que rige durante el lapso que dure la operación. Tasa Nominal de Interés.- Tasa de interés anual que rige durante el lapso que dure la operación. Tasa efectiva anual.- Si el interés se capitaliza en forma trimestral, semestral, mensual, la cantidad efectivamente pagada o ganada es mayor que si se compone en forma anual. Tasas equivalentes.- Dos tasas con diferentes periodos de capitalización serán equivalentes, si al cabo de un año producen el mismo interés compuesto. EJERCICIOS 1.¿Cuál es la tasa efectiva de interés que se recibe de un depósito bancario de US$ 1,000.00 pactado al 48% de interés anual convertible mensualmente? 2. Cuál es la tasa efectiva que se paga por un préstamo bancario de US$ 5,000.00 que se pactó al 55% de interés anual convertible trimestralmente? Anualidades En general se denomina anualidad a un conjunto de pagos iguales realizados a intervalos iguales de tiempo. Se conserva el nombre de anualidad por estar ya muy arraigado en el tema, aunque no siempre se refieran a periodos anuales de pago. Algunos ejemplos de anualidades son: Pagos mensuales por renta Cobro quincenal o semanal por sueldo Abonos quincenales o mensuales a una cuenta de crédito Pagos anuales de primas de pólizas de seguro de vida. Intervalo o periodo de pago.-Se conoce como intervalo o periodo de pago al tiempo que transcurre entre un pago y otro. Plazo de una anualidad.- es el tiempo que transcurre entre el inicio del primer pago y el final o ultimo. Renta.- es el nombre que se da al pago periódico que se hace. También hay ocasiones en que se habla de anualidades que no tienen pagos iguales, o no se realizan todos los pagos a intervalos iguales. Estos casos se manejan de forma especial Clasificación de las anualidades: Anualidad cierta.- Sus fechas son fijas y se estipulan de antemano. Por ejemplo : a) Al realizar una compra a crédito se fija tanto la fecha en que se debe hacer el primer pago, como la fecha para efectuar el ultimo. Anualidad contingente.- La fecha del primer pago, la fecha del ultimo pago, o ambas, no se fijan de antemano; dependen de algún hecho que se sabe que ocurrirá, pero no se sabe cuando. Un caso común de este tipo de anualidad son las rentas vitalicias que se otorgan a un cónyuge tras la muerte del otro. El inicio de la renta se da al morir el cónyuge y se sabe que este morirá, pero no se sabe cuando. Anualidad simple.- Cuando el periodo de pago coincide con el de capitalización de los intereses. Anualidad vencida.- También se le conoce como anualidad ordinaria y, como su primer nombre lo indica, se trata de casos en los que los pagos se efectúan a su vencimiento, es decir, al final de cada periodo. Anualidad inmediata.- Es el caso mas común. La realización de los cobros o pagos tiene lugar en el periodo inmediatamente siguiente a la formalización del trato : se compra a crédito hoy un articulo que se va a pagar con mensualidades, la primera de las cuales habrá de realizarse en ese momento o un mes después de adquirida la mercancía (anticipada o vencida). Formulas para calcular el monto y valor actual de anualidades simples, ciertas, vencidas e inmediatas: Monto Valor Actual Sn= a[(1+i)n - 1] -----------i Vn = R[(1+i)n -1] ----------i(1+i)n Donde: R= renta o pago por periodo a= anualidad o pago por periodo Sn= monto o valor en el momento de su vencimiento, es el valor de todos los pagos al final de las operaciones. n = numero de anualidades o pagos. Vn = valor actual o capital de la anualidad. Valor total de los pagos en el momento presente. Formulas de Anualidades Vencidas F = A [¨ (1 + i )n -1] =Valor futuro i P = A [¨ 1 – (1+ i )-n ]= Valor presente i F = Valor futuro; A = anualidad; n = tiempo 1. Calcular el valor futuro y el valor presente de las siguientes anualidades ciertas ordinarias. (a) $2.000 semestrales durante 8 ½ años al 8%, capitalizable semestralmente. (b) $4.000 anuales durante 6 años al 7,3%, capitalizable anualmente. (c) $200 mensuales durante 3 años 4 meses, al 8% con capitalización mensual. 2. Calcular el valor de contado de una propiedad vendida en las siguientes condiciones: $20.000 de contado; $1.000 por mensualidades vencidas durante 2 años y 6 meses y un último pago de $2.500 un mes después de pagada la última mensualidad. Para el cálculo, utilizar el 9% con capitalización mensual. 3. ¿Cuál es el valor de contado de un equipo comprado con el siguiente plan: $14.000 de cuota inicial; $1.600 mensuales durante 2 años 6 meses con un último pago de $2.500, si se carga el 12% con capitalización mensual? 4. Una mina en explotación tiene una producción anual de $8’000.000 y se estima que se agotará en 10 años. Hallar el valor presente de la producción, si el rendimiento del dinero es del 8%. 5. En el momento de nacer su hija, un señor depositó $1.500 en una cuenta que abona el 8%; dicha cantidad la consigna cada cumpleaños. Al cumplir 12 años, aumento sus consignaciones a $3.000. Calcular la suma que tendrá a disposición de ella a los 18 años. 6. Una persona deposita $100 al final de cada mes en una cuenta que abona el 6% de interés, capitalizable mensualmente. Calcular su saldo en la cuenta, al cabo de 20 años. Problemas de Anualidades Anticipadas Formulas de Anualidades Anticipadas F = A [¨ (1 + i )n + 1 -1 - 1] =Valor futuro i P = A [¨1 + 1 – (1+ i )-n + 1]=Valor presente i F = Valor futuro; A = anualidad; n = tiempo 1. Calcular el valor de Contado de una propiedad vendida a 15 años de plazo, con pagos de $3.000 mensuales por mes anticipado, si la tasa de interés es del 12% convertible mensualmente. 1. Una persona recibe tres ofertas parea la compra de su propiedad: (a) $400.000 de contado; (b) $190.000 de contado y $50.000 semestrales, durante 2 ½ años (c) $20.000 por trimestre anticipado durante 3 años y un pago de $250.000, al finalizar el cuarto año. ¿Qué oferta debe escoger si la tasa de interés es del 8% anual? 2. ¿Cuál es el valor presente de una renta de $500 depositada a principio de cada mes, durante 15 años en una cuenta de ahorros que gana el 9%, convertible mensualmente? 3.¿Qué suma debe depositarse a principio de cada año, en un fondo que abona el 6% para proveer la sustitución de los equipos de una compañía cuyo costo es de $2.000.000 y con una vida útil de 5 años, si el valor de salvamento se estima en el 10% del costo? 4. Sustituir una serie de pagos de $8.000 al final de cada año, por el equivalente en pagos mensuales anticipados, con un interés del 9% convertible mensualmente. 5. Un empleado consigna $300 al principio de cada mes en una cuenta de ahorros que paga el 8%, convertible mensualmente. ¿En cuánto tiempo logrará ahorrar $30.000? Problemas de Anualidades Diferidas Formulas para anualidades diferidas Son las mismas que las anualidades vencidas y anticipadas salvo que estas tienen un periodo de gracia. 1. Una compañía adquiere unos yacimientos de mineral; los estudios de ingeniería muestran que los trabajos preparatorios y vías de acceso demoraran 6 años. Se estima que los yacimientos en explotación rendirán una ganancia anual de $2.400.000. Suponiendo que la tasa comercial es del 8% y que los yacimientos se agotarán después de 15 años continuos de explotación, hállese el valor futuro de la renta que espera obtenerse. 2. En el problema anterior, hállese el valor de utilidad que espera obtener, en el momento de la adquisición de los yacimientos. 3. Una compañía frutera sembró cítricos que empezaran a producir dentro de 5 años. La producción anual se estima en $400.000 y ese rendimiento se mantendrá por espacio de 20 años. Hallar con la tasas del 6% el valor presente de la producción. 4. Alguien deposita $100.000 en un banco, con la intención de que dentro de 10 años se pague, a él o a sus herederos, una renta de $2.500, a principio de cada mes. ¿Durante cuántos años se pagará esta renta, si el banco abona el 6% convertible mensualmente? 5. Una deuda contraída al 8% nominal, debe cancelarse con 8 cuotas semestrales de $20.000 c/u, con la primera obligación por pagar dentro de 2 años. Sustituirla por una obligación equivalente pagadera con 24 cuotas trimestrales, pagándose la primera de inmediato.