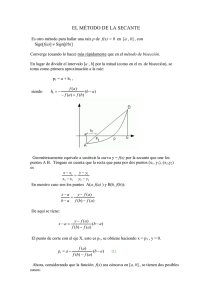
LOCALIZACIÓN DE RAICES En ciencias así como la ingeniería comúnmente se nos presenta ecuaciones que resultan algo más complejas de resolver que las estudiadas. Por ejemplo una ecuación del tipo polinomial como 𝑥 2 − 2𝑥 + 1 = 0 nos resulta sencilla de resolver pero una ecuación donde no nos sea posible factorar o despejar la variable buscada ingresa en el grupo de las denominadas ecuaciones no lineales, por ejemplo 𝑥 + 𝑒 𝑥 − cos 𝑥 − 4 = 0 Sea una función y=f(x) la cual es continua en [a,b] dentro del cual se encuentra por lo menos una raíz o cero para f(x)=0. Para localizar los 0 de la función debe tener en cuenta lo siguiente: La función considerar f(x)=0 se descompone en otros dos y puede expresarse: 𝑓1 𝑥 = 𝑓2 𝑥 . 1) La elección de estas dos funciones dependerá de la conveniencia ya sea por su rapidez de cálculo o por su similitud por sus formas geométricas conocidas. 2) Teniendo en cuenta la exactitud que tenga el gráfico y las escalas usadas podrá ubicarse un cierto intervalo [a,b] dentro del cual se intersectan las gráficas. Sea y=f(x) la cual es continua en todo el intervalo para el cual se ha definido. Del gráfico: Si f(a) es negativo f(a)<0 Si f(b) es positivo f(b)>0 Entonces f(a)xf(b)<0 • Pasos 1. Partimos de un valor inicial A, escogiendo además una determinada longitud H para el intervalo que se está buscando estos valores son escogidos por criterio personal. 2. Calculamos B, que es la suma de A+H. B=A+H 3. Evaluamos la función en los valores A y B. f(A) y f(B) 4. Se efectúa el producto f(A) x f(B), se resultara negativo, entonces el intervalo [A,B] es el intervalo buscado; en caso contrario es decir que el producto sea positivo el nuevo valor de A será el que tenía anteriormente B, siendo el nuevo valor de éste último su valor anterior incrementado en h, repitiéndose anteriormente el proceso hasta obtener el producto negativo. • Ejemplo: 𝐹 = 𝑥 2 +2x-4 Solución 𝑥 2 +2x−4=0 𝑥 2 =4-2x f(x1)=f(x2) Valor inicial A=0, H=1 i A B f(A) f(B) f(A).f(B) 1 0 1 -4 -1 (+) 2 1 2 -1 4 (-) [1,2] es el intervalo buscado Para H=-1 i A B f(A) f(B) f(A).f(B) 1 0 -1 -4 -5 (+) 2 -1 -2 …. … (+) …. … …. …. …. (+) …. … …… …. …. (+) ….. -4 -3 … …. (-) [-4,-3] es el otro intervalo buscado MÉTODO DE BISECCIÓN • Este método , que se utiliza para resolver ecuaciones de una variable, está basado en el “Teorema de los Valores Intermedios” (TVM), en el cual se establece que toda función continua f, en un intervalo cerrado [a,b], toma todos los valores que se hallan entre f(a) y f(b), de tal forma que la ecuación f(x)=0 tiene una sola raíz que verifica f(a).f(b)<0. MÉTODO DE BISECCIÓN • Es el método más elemental y antiguo para determinar las raíces de una ecuación. Está basado directamente en el teorema de Bolzano. Consiste en partir de un intervalo [x0,x1]tal que f(x0)f(x1) < 0, por lo que sabemos que existe, al menos, una raíz real. A partir de este punto se va reduciendo el intervalo sucesivamente hasta hacerlo tan pequeño como exija la precisión que hayamos decidido emplear. MÉTODO DE BISECCIÓN • El método de bisección es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz. Esto se logra llevar a cabo a través de varias interacciones que son aplicadas en un intervalo para por medio de ello encontrar la raíz de la función. MÉTODO DE BISECCIÓN • Este es uno de los métodos más sencillos de fácil intuición para resolver ecuaciones en una variable, también conocido como método del intervalo medio, este se basa en el teorema del valor intermedio, el cual establece que toda función continua f en un intervalo cerrado [a,c] toma todos los valores que se hallan entre f(a) y f(b). Esto es que todo valor entre f(a) y f(b) es la imagen de al menos un valor del intervalo [a,b].En caso de que f(a) y f(b) tengan signos opuestos, el valor cero seria un valor intermedio entre f(j)y f(e), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(a)=0. MÉTODO DE BISECCIÓN Sea y=f(x) continua [a,b] x→f(x)=0 f(a).f(b)<0 1) Calcular el valor C, punto medio del intervalo [a,b] por ello: (𝑎 + 𝑏) 𝑐= 2 MÉTODO DE BISECCIÓN 2) Evaluar la función en el valor c, anteriormente calculado, hallando así f(c). 3) Reemplazar uno de los extremos del intervalo inicial de solución, por el valor c, verificando que dentro del nuevo intervalo se enuentra la solución buscada. Para ello considerese: b=c, siempre que f(a).f(c)<0 a=c, siempre que f(a).f(c)>0 4) Repetir el proceso del 1er paso hasta obtener el solución deseada. Nótese que el producto de f(a)xf(b) es negativo. Determinamos el valor c correspondiente a evaluar la función en C. Como se observa el nuevo intervalo a considerarse será [a,b] puesto que el producto de f(a)xf(b) es menor que cero. • Ejemplo: Hallar la raíz positiva de la ecuación, con 4 cifras decimales exactas. 𝑥 2 + 2𝑥 − 4 = 0 A=0, H=1, se llegó a [1,2] i a b c F(a) F(c) Producto 1 1.00000 2.00000 1.50000 -1.00000 1.25000 -1.25000 2 1.00000 1.50000 1.25000 -1.00000 0.0625 -0.0625 3 1.00000 1.25000 1.12500 -1.00000 -0.4844 +0.4844 4 1.12500 1.25000 1.18750 -0.48440 -0.2148 +0.1041 5 1.18750 1.25000 1.21875 -0.21480 -0.0771 +0.0166 6 1.21875 1.25000 1.23438 -0.07710 -0.0075 +0.0006 7 1.23438 1.25000 1.24219 -0.00760 0.0274 -2.11E-04 i a b c F(a) F(c) Producto 8 1.23438 1.24219 1.23828 -0.0076 0.0099 -7.5E-05 9 1.23438 1.23828 1.23633 -0.00765 0.0012 -8.8E-06 10 1.23438 1.23633 1.23535 -0.0076 -0.0032 +2.4E-05 11 1.23535 1.23633 1.23584 -0.00320 -0.0010 +3.3E-06 12 1.23584 1.23633 1.23608 -0.0010 0.0001 -7.3E-08 13 1.23584 1.23608 1.23596 -0.0010 -0.0005 +4.8E-07 14 1.23596 1.23608 1.23602 -0.0005 -0.0002 +9.5E-08 15 1.23602 1.23608 • Hallar la raíz positiva de: 𝑥2. 𝑒 𝑥 − 1 = 0 MÉTODO DE LA FALSA POSICIÓN • Aun cuando la bisección es una técnica perfectamente válida para determinar raíces, su método de aproximación por "fuerza bruta" es relativamente ineficiente. La falsa posición es una alternativa basada en una visualización gráfica. • Un inconveniente del método de bisección es que al dividir el intervalo de x1 a xu en mitades iguales, no se toman en cuenta las magnitudes de f(x1) y f(xu). Por ejemplo, si f(x1) está mucho más cercana a cero que f(xu), es lógico que la raíz se encuentre más cerca de x1 que de xu. Un método alternaticvo que aprovecha esta visualización gráfica consiste en unir f(x1) y f(xu) con una línea recta. MÉTODO DE LA FALSA POSICIÓN La intersección de esta línea con el eje de las x representa un mejor aproximación de la raíz. El hecho de que se reemplace la curva por una línea recta de una "falsa posición" de la raíz; de aquí el nombre de método de la falsa posición, o en latín, regula falsi. También se le conoce como método de interpolación lineal. • MÉTODO DE LA FALSA POSICIÓN 𝑎. 𝑓 𝑏 − 𝑏. 𝑓(𝑎) 𝑐= 𝑓 𝑏 − 𝑓(𝑎) • Ejemplo: Hallar la raíz positiva de: 𝑥 2 + 5𝑥 − 12 = 0 Localizando los intervalos de las raíces: [1,2] y [-7,-6] a=1 →f(a) = -6 b=2→f(b)=2 1 2 − 2 −6 𝑐= = 1.75 2 − (−6) F(c)= 1.752 + 5 1.75 − 12 = −0.1875 Como: f(a).f(c)= (-6)x(-0.1875)>0 Entonces: a= 1.75 →f(a)=-0.1875 b=2 →f(b)=2 1.75 2 − 2 −0.1875 𝑐= = 1.77 2 − (−0.1875) f(c) = -0.0171 f(a).f(c) = 0.003>0 Entonces: a= 1.77 y b=2 i a b c F(a) F(b) F(c) 1 1 2 1.75 -6 2 -0.1875 2 1.75 2 1.77 -0.1875 2 -0.0171 3 1.77 2 • Ejemplo: F(x)=𝑥 2 -2, en intervalo [0,2] i a b c F(a) F(b) F(c) 1 0 2 1 -2 2 -1 2 1 2 1.333 -1 2 -0.223 3 1.333 2 1.399 -0.223 2 -0.043