Pruebas No Paramétricas
Material elaborado por: Dr. Jorge Valera
Junio, 2019.
Pruebas de Hipótesis No Paramétricas o de Distribución Libre
Introducción
La mayoría de las pruebas de hipótesis tradicionales conocidas, como la de comparación
de medias o varianzas requieren que las muestras aleatorias a ser utilizadas en los
procedimientos de prueba de hipótesis provengan de poblaciones normales, de tal manera que
los resultados y conclusiones que se obtengan sean confiables. Por otra parte, en las pruebas no
paramétricas no se necesita hacer suposiciones acerca de la distribución de la población y por
ello en ocasiones se denominan pruebas libres de distribución.
En ocasiones requerimos llevar a cabo un procedimiento de prueba de hipótesis
relacionadas con la media poblacional μ, una diferencia de medias poblacionales o pruebas
relacionadas con las varianzas de la población donde el supuesto de normalidad no se cumple.
En estos casos las pruebas no paramétricas o de distribución libre representan una alternativa a
las pruebas tradicionales.
Por ejemplo supongamos que deseamos probar la hipótesis de que el tiempo promedio
para obtener un título profesional en una universidad reconocida no es de 5 años como se cree
sino que este tiempo es superior a los 5 años. Para ello deseamos contrastar las hipótesis
Ho: μ=5 años vs Ha: μ>5 años
Si se deseara aplicar la prueba tradicional para contrastar estas hipótesis tendríamos que
probar que la muestra aleatoria de los tiempos para obtener el título profesional, obtenida de la
población de graduandos de la universidad proviene de una población normal o bien apelar al
teorema del límite central en caso que el tamaño de la muestra sea grande (n>30) así como a
otros supuestos como si la varianza de la población es o no conocida.
En general, los contrastes de pruebas de hipótesis tradicionales exigen el cumplimiento
de supuestos relacionados tanto con la distribución de los datos como de algunos parámetros
para que los resultados de las mismas sean considerados válidos. Parte fundamental de estos
requerimientos es que las poblaciones de donde provienen los datos que conforman las
muestras aleatorias utilizadas en los contrastes sean poblaciones normales, así como supuestos
relativos a las varianzas poblacionales, de allí que a estas se les conozcan como pruebas de
hipótesis paramétricas. En contraparte, los métodos de contraste de distribución libre o no
paramétricos a menudo no requieren suponer conocimiento alguno de las distribuciones de
probabilidad de las poblaciones de donde se obtienen las muestras, excepto tal vez que estas
distribuciones sean continuas.
Cuando se utilizan pruebas no paramétricas para realizar un contraste de hipótesis hay
situaciones donde los datos disponibles son medidos en una escala ordinal y en estos casos se
asignan rangos a los datos a fin de aplicar las pruebas no paramétricas, como veremos más
adelante. En cambio las pruebas paramétricas requieren que los datos analizados sean producto
de una medición por lo menos en una escala de intervalo.
Una gran ventaja de las pruebas no paramétricas es que son una excelente alternativa de
las paramétricas en los casos donde no es posible justificar las suposiciones de normalidad o en
casos donde la escala de medición de la variable es ordinal y no de razón. Por otro lado, para
grandes desviaciones del supuesto de la normalidad de los datos el método no paramétrico es
mucho más eficiente que el procedimiento paramétrico. Claramente es preferible utilizar las
pruebas paramétricas sobre las no paramétricas en los casos donde sea posible verificar las
condiciones de normalidad ya que los contrastes paramétricos son más eficientes.
En resumen, las pruebas no paramétricas junto a las pruebas paramétricas constituyen
todo un conjunto de herramientas estadísticas para adaptar a una gran variedad de situaciones
experimentales.
La Prueba del Signo.
Prueba de signo para comparar una mediana.
Es una alternativa no paramétrica a la prueba paramétrica empleada para realizar el contraste
de hipótesis de la media μ de una población. Si en determinado estudio se requiere contrastar
la hipótesis
Ho: μ=μ0 vs
{
Ha: μ ≠ μ 0
Ha :μ < μ0 ,
Ha :μ > μ0
según sea el caso, pero no se cumple que la población de donde proviene la muestra es normal,
esta prueba es una alternativa para contrastar las hipótesis.
Metodología
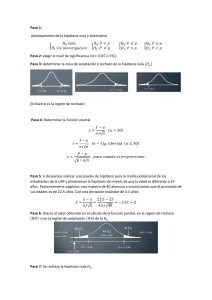
De la teoría estadística se sabe que cuando una población posee una distribución de
probabilidad simétrica como la que se presenta en la figura 1 se cumple que la media μ y la
μ son iguales.
mediana ~
En este sentido, al no poder verificarse los supuestos requeridos por la prueba
paramétrica tradicional, se opta por la prueba del signo la cual en lugar de la media μ emplea a
μ como parámetro de tendencia central.
la mediana ~
μ es
Dado que la distribución es simétrica, llevar a cabo la prueba sobre la mediana ~
equivalente a realizarla sobre la media μ ya que en este caso la media y la mediana poblacional
son iguales.
μ estadísticamente se define como el valor para el cual la mitad de los valores de la
La mediana ~
población son menores o iguales a él y la otra mitad son mayores o iguales a él. En términos de
μ se define como el valor para el cual se cumple:
probabilidad ~
P( X > ~
μ)=P(X < ~
μ)=0.5.
La manera correcta de plantear las hipótesis cuando decidimos utilizar la prueba del signo
es
Ho: ~
μ=~
μ0 versus
{
Ha: ~
μ ≠~
μ0
~
~
Ha : μ < μ0 ,
Ha : ~
μ >~μ0
De esta manera, la prueba del signo en esencia consiste en determinar cuántos de los
μ . En este sentido, para
valores de la muestra aleatoria se encuentran arriba y abajo del valor ~
0
μ=~
μ0 contra alguna de las alternativas según se al caso, lo que se
contrastar la hipótesis Ho: ~
hace es asignar un símbolo positivo (“+”) a los valores de la muestra que se encuentran por
μ 0 y uno negativo (“-“) a los que se encuentren por debajo del valor ~
μ 0. Cuando un
arriba de ~
μ se asigna el valor cero y no se considera para la aplicación
valor en la muestra es igual al valor ~
0
de la prueba.
Por ejemplo, supóngase que en una muestra de tamaño n=11 se obtuvieron los siguientes
μ =1.8, entonces se
valores 1.5, 2.2, 0.9, 1.3, 2.0, 1.6, 1.8, 1.5, 2.0, 1.2, 1.7 y que el valor ~
0
obtendría el resultado
Donde el valor cero se corresponde con el valor 1.8 en los datos que al ser igual a μ0=1.8
no se le asigna signo y por lo tanto no se tomaría en cuenta para llevar a cabo el contraste de las
hipótesis de la prueba del signo. En este caso para la prueba se dispone de tres signos más ( “+”)
y siete signos menos (“-“) para un total de 10 signos.
El sentido lógico de la prueba.
Si la hipótesis nula Ho es verdadera, lo lógico es que estadísticamente la proporción de
signos positivos sea igual a la de signos negativos, ya que en este caso es de esperar que el 50%
μ y el otro 50% se encuentre
de los datos en la muestra se encuentren por arriba del valor ~
0
μ 0 como se muestra en las figuras 2. de allí que se espere que la proporción de signos
debajo de ~
positivos y negativos estadísticamente sean iguales.
μ=~
μ0 es verdadera, la cantidad de valores que se espera
De esta manera, si Ho: ~
μ 0 debe ser igual tal y como se muestra
estadísticamente se hallen arriba y abajo de la mediana ~
en la Figura N° 3.
Claramente entonces una cantidad mayor de alguno de los signos reflejaría que la
hipótesis nula es falsa y en consecuencia se rechazaría que el verdadero valor de la mediana es
~
μ . En la figura N° 4 se presenta el caso donde la cantidad de signos positivos es
0
estadísticamente significativamente menor que los positivos, indicando que el verdadero valor
μ sino un valor menor a este
de la mediana no es ~
0
Por otra parte, si la cantidad de signos positivos es estadísticamente mayor a la cantidad
μ> ~
μ
de signos negativos como se presenta en la Figura N° 5, es evidencia que la hipótesis Ho: ~
0
es cierta.
Basamento estadístico.
En la prueba del signo se toman en cuenta son los signos positivos y el estadístico de
prueba que se utiliza para contrastar las hipótesis sigue una distribución binomial con parámetro
μ=~
μ es verdadera, indicando en este caso, que las
p=1 /2 cuando la hipótesis nula Ho: ~
0
probabilidades de obtener un signo positivo o negativo son iguales.
Formalmente, la variable aleatoria
X = Número de signos positivos encontrados en la muestra aleatoria de tamaño n.
X =0 , 1, 2 , … , n.
posee distribución de probabilidad binomial con parámetro p=1 /2. En consecuencia la
distribución de probabilidad de X esta dada por:
1
f ( x )= n
x 2
x
1
2
n−x
1
= n
x 2
( )( ) ( ) ( )( )
n
Casos Particulares.
μ0
Caso 1. El valor verdadero de la mediana posiblemente es menor a ~
μ 0 las hipótesis a probar
Si se sospecha que el valor verdadero de la mediana es menor a ~
son:
Ho: ~
μ=~
μ0
Ha: ~
μ< ~
μ0
vs
Si la cantidad de signos positivos y negativos es similar, es de esperarse que no se rechace
la hipótesis nula. Por el contrario, la presencia de pocos signos positivos (en otras palabras hay
estadísticamente mas signos negativos que positivos), es un indicativo de que la hipótesis nula
no es cierta y en la medida que la cantidad de signos positivos disminuyan y aumenten los signos
μ< ~
μ.
negativos es más probable que se rechace la hipótesis nula a favor de la alternativa Ha: ~
0
En términos de probabilidad significa que se rechaza Ho a favor de Ha si la proporción de
signos positivos es estadísticamente menor a 1/2 y por lo tanto la cantidad x de signos positivos
observados en la muestra será pequeño y entonces el valor P dado por
x
x
P=P r ( X ≤ x cuando p=1 /2 ) =∑ P ( X=i )=∑ n 1/2n
i=0
i=0 i
será menor a α, el nivel de significancia establecido.
()
μ=~
μ0
Pasos para llevar a cabo el contraste de hipótesis Ho: ~
vs
Ha: ~
μ< ~
μ 0.
1. Establezca las hipótesis nula Ho y alternativa Ha.
μ=~
μ
Ha: ~
μ< ~
μ.
a. Ho: ~
vs
0
μ=~
μ0
b. Ho: ~
μ=~
μ
c. Ho: ~
0
0
vs
Ha: ~
μ> ~
μ 0.
vs
Ha: ~
μ ≠ ~μ0.
2. Elija un nivel de significancia α fijo.
3. Calcule el valor P con base en el valor x = número de signos positivos.
a. P=Pr ( X ≤ x cuando p=1/2 )
(
b. P=Pr X ≥ x cuando p=
1
2
)
n
1
c. Si x < ; P=2 Pr X ≤ x cuando p=
2
2
(
)
n
1
S i x > ; P=2 Pr ( X ≥ x cuando p= )
2
2
4. Rechace Ho a favor de Ha si P ≤ α
5. Conclusiones.
μ 0.
Caso 2. El valor verdadero de la mediana posiblemente es mayor a ~
μ 0 las hipótesis a
Cuando se sospecha que el valor verdadero de la mediana es mayor a ~
probar son:
Ho: ~
μ=~
μ0 vs Ha: ~
μ> ~
μ0
Equivalente al caso 1, si la cantidad de signos positivos es estadísticamente
significativamente mayor al número de signos negativos encontrados a partir de los valores de la
muestra, la hipótesis nula será rechazada a favor de la hipótesis alternativa. En este caso, para
llevar a realizar el contraste de hipótesis el valor P se calcula a partir de la expresión
(
n
n
1
1 n
=∑ P ( X =i )=∑ n
P
2 i= x
2
i=x i
( )( )
1
1
P ( X ≥ x cuando p= )=1−∑ ( n) ( )
2
i 2
P=P r X ≥ x cuando p=
)
x−1
n
i=0
y si este valor de P es menor o igual al nivel de significancia α seleccionado, se rechazaría la
μ> ~
μ.
hipótesis nula a favor de la alternativa Ha: ~
0
Los pasos a seguir son similares al caso 1 solo que la expresión para calcular el valor P es
diferente.
μ=~
μ0
Pasos para llevar a cabo el contraste de hipótesis Ho: ~
vs
Ha: ~
μ> ~
μ 0.
1. Establezca las hipótesis nula Ho y alternativa Ha.
2. Elija un nivel de significancia α fijo.
3. Calcule el valor P con base en el valor x = número de signos positivos obtenidos a partir
de la muestra de tamaño n.
4. Rechace Ho a favor de Ha si P ≤ α.
5. Conclusiones.
μ 0.
Caso 3. El valor verdadero de la mediana posiblemente es diferente a ~
μ 0, pero
En el caso que se sospecha que el valor verdadero de la mediana es diferente a ~
no se está seguro si es mayor o menor, las hipótesis a probar son:
Ho: ~
μ=~
μ vs Ha: ~
μ ≠ ~μ
0
0
Rechazaremos la hipótesis nula si la cantidad de signos positivos obtenidos a partir de la
muestra es estadísticamente menor o bien mayor a la cantidad de signos negativos. Como de
antemano no conocemos la proporción de signos positivos a encontrar respecto a los negativos,
para llevar a cabo el procedimiento de prueba de hipótesis lo primero que debemos hacer es
determinar si el número de signos positivos x <n/2 o si x >n/2.
En caso de que x <n/2; es decir, si la cantidad de signos positivos es menor a la mitad del
tamaño de muestra y por ende menor a la cantidad de signos negativos, el valor P a calcular esta
dado por
x
x
n
1
Si x < ; P=2 P r ( X ≤ x cuando p=1/2 )=2 ∑ P r ( X=i )=2 ∑ n
2
i
2
i=0
i=0
n
( )( )
pero si la cantidad de signos positivos es mayor a la mitad del tamaño de la muestra ( x >n/2 )y
por lo tanto mayor a la cantidad de signos negativos, el valor P a encontrar es
n
1
Si x < ; P=2 Pr X ≤ x cuando p=
2
2
(
)
n
1
Si x > ; P=2 Pr ( X ≥ x cuando p= )
2
2
1
1
P=2 P r ( X ≥ x cuando p= )=2 ∑ P r ( X =i )=2 ∑ ( n ) ( )
2
i 2
(
P=2 P r X ≥ x cuando p=
(
n
n
i=x
i=x
n
1
1
=2 1−P r X ≤ x−1 cuando p=
2
2
)
[ (
P=2 P X ≥ x cuando p=
x−1
1
1
=2 1−∑ n
2
i
2
i=0
)
[
n
( )( ) ]
)]
μ=~
μ0 a favor de Ha: ~
μ ≠ ~μ0 si el valor P obtenido
y una vez encontrado el valor P, se rechaza Ho: ~
es menor o igual al nivel de significancia α seleccionado.
μ=~
μ0 vs Ha: ~
μ ≠ ~μ0.
Pasos para llevar a cabo el contraste de hipótesis Ho: ~
1. Establezca las hipótesis nula Ho y alternativa Ha.
2. Elija un nivel de significancia α fijo.
3. Calcule el valor P con base en el valor x = número de signos positivos obtenidos a partir
de la muestra de tamaño n. Tome en consideración para el cálculo del valor P si x <n/2 o
bien si x >n/2.
4. Rechace Ho a favor de Ha si P ≤ α.
5. Conclusiones.
Ejemplo de Aplicación.
Ejemplo1. Prueba de hipótesis sobre una mediana. Equivalente No Paramétrico de la prueba
de la media μ de una población normal.
Los siguientes datos representan el número de horas de entrenamiento de vuelo que reciben 18
estudiantes para piloto de cierto instructor antes de su primer vuelo solos:
9 12 18 14 12 14
12 10 16 11 9 11
13 11 13 15 13 14
Realice una prueba del signo al nivel de significancia de 0.02 para probar la afirmación del
instructor de que la mediana del tiempo que se requiere antes de que sus estudiantes vuelen
solos es 12 horas de vuelo de entrenamiento.
Solución.
Lo primero a hacer es plantear las hipótesis a contrastar.
Ho: ~
μ=12 vs Ha: ~
μ ≠ 12
1) Establecer el nivel de significancia α =0.02 para este caso.
2) Determinar el número de signos + y – y obtener el valor de P.
1
9 2
- 0
En este caso hay 9
1 1
8 4 12
+ + 0
signos “+”,
1 1 1
4 2 0 16
+ 0 - +
6 signos “-“y 3
muestra pasa de 18 datos inicialmente a n=15
1
1 9
- ceros
1
1 1
1 13 1 3
- + - +
(sin signo). Por
1
5 13 14
+ + +
lo tanto el tamaño de la
(
P=2 P X ≥ 9 cuando p=
8
1
1
=2 1−∑ 15
2
i
2
i=0
)
[
15
( )( ) ]=0.6072
μ=12.
3) Dado que α =0.02 y P=0.672 se cumple que P>α y por lo tanto no se rechaza Ho: ~
4) Conclusiones: Los datos no arrojan evidencia que contradiga la afirmación del instructor de
vuelo.
μ1 , ~
μ2 de dos poblaciones.
Prueba del signo para comparar la medianas ~
Ejemplo 2. Una empresa de taxis intenta decidir si al utilizar neumáticos radiales en vez de
neumáticos regulares con cinturón le serviría para ahorrar combustible. Para ello se equipan 16
automóviles con neumáticos radiales y se conducen por un recorrido de prueba previamente
establecido. Después los mismos automóviles se equipan con neumáticos regulares con cinturón
y los mismos conductores vuelvan a realizar el mismo recorrido de prueba. Se midió el
rendimiento de gasolina, en kilómetros por litro, y la data se muestra en la tabla más adelante.
¿Podemos concluir a un nivel de significancia de 0.05 que los autos equipados con neumáticos
radiales ahorran más combustible que los equipados con neumáticos regulares con cinturón?
Auto
Radiales
1
2
3
4.2 4.7 6.6
4
7
Cinturó
n
4.1 4.9 6.2 6.9
5
6.
7
6.
8
6
7
4.5 5.7
8
6
9 10 11
7.4 4.9 6.1
4.4 5.7 5.8 6.9 4.9
6
12
5.
2
4.
9
13 14 15 16
5.7 6.9 6.8 4.9
5.3 6.5 7.1 4.8
Solución.
Planteamiento de las Hipótesis.
H 0 :~
μ R −~
μC =0 vs H a : ~μR −~
μC >0
Nivel de Significancia. α =5 %.
Determinar el número de signos + y – y obtener el valor de P.
Auto
Radiales
1
4.2
Cinturó
n
Signo
Signo
4.1
1
+
2
4.
7
4.
9
-1
-
3
6.6
4
7
6.2
6.9
1
+
1
+
5
6.
7
6.
8
-1
-
6
4.5
4.4
1
+
7
5.
7
5.
7
0
8
6
9
7.4
5.8
6.9
1
+
1
+
10
4.
9
4.
9
0
11
6.1
6
1
+
12
5.
2
4.
9
1
+
13
5.7
14
6.9
5.3
6.5
1
+
1
+
15
6.
8
7.
1
-1
-
16
4.9
4.8
1
+
Hay 11 signos “+”, 3 signos “-“ y 2 ceros (sin signo). Por lo tanto el tamaño de la
muestra pasa de 16 datos inicialmente a n=14 datos.
10
1
1
P=P r X ≥11cuando p= =2 1−∑ 14
2
i 2
i=0
(
)
[
14
( )( ) ]=0.0287
Regla de Decisión. Rechazar Ho si P<α =0.05
Conclusiones. Dado que P=0.0287<0.05=α se concluye que efectivamente
los cauchos radiales ahorran más combustible.
μC ≠ 0. Para obtener el valor de P para la hipótesis
El SPSS produce la salida para el caso H a : ~μR −~
μC >0 se divide entre dos el valor P que da el programa; esto es,
alternativa unilateral H a : ~μR −~
μC >0 .
0.057 /2=0.0285 obteniéndose así el valor de P para la alternativa H a : ~μR −~
Prueba del Signo en Investigación de Mercados para estudiar la preferencia de los clientes.
La aplicación de la prueba en este caso consiste en determinar la preferencia hacia una
de dos marcas de un cierto producto utilizando una muestra de n opiniones de potenciales
clientes. En este sentido el objetivo es determinar si existen diferencias en las preferencias de los
clientes por algún producto como leche, refrescos, salsas, cafés, etcétera.
Para llevar a cabo la prueba del signo en este caso lo que se hace en preguntar a un
grupo de n clientes cual de los dos artículos prefieren. La variable que se mide entonces es del
tipo nominal y a través de la aplicación de esta prueba se determina si existen o no diferencias
entre las preferencias hacia los dos artículos que se comparan.
Ejemplo 3. Una empresa desea lanzar al mercado una nueva marca de mayonesa y por ello
decide llevar a cabo una prueba para comparar la preferencia de su producto con la mayonesa
de mayor popularidad que se encuentra en el mercado. Para ello se selecciona a 12 personas a
las que se les da a probar ambos productos de manera aleatoria. Los datos se muestran a
continuación:
Individuo
1
2
3
4
Preferenci
a
N E N E
5
6
7
8
9
10
N N E N N
N
1
1
E
12
N
donde N significa que se a la persona le gusta más el producto nuevo y E que le gusto la
mayonesa existente en el mercado.
Solución. En este caso la asignación del signo positivo es arbitraria, pudiendo asignarse el
signo”+” a la preferencia por la mayonesa nueva o a la mayonesa existente en el mercado. Para
efecto de este ejemplo se le asignara el signo “+” a la nueva mayonesa. De esta manera los
datos disponibles para aplicar la prueba del signo son:
Individuo
Preferenci
a
SPSS
Ref SPSS
1
+
2
-
3
+
4
-
5
+
6
+
7
-
8 9 10 11 12
+ + +
+
1 -1 1
0 0 0
-1
0
1
0
1 -1 1 1
0 0 0 0
1
0
-1
0
1
0
Planteamiento de las Hipótesis.
H o : No existe diferencias en la preferencia de los clientes por los dos articulos
H a :Si existe diferencia en la preferencia de los clientes por uno de los articulos
Nivel de Significancia. α =5 %.
Determinar el número de signos + y – y obtener el valor de P. Es este caso se obtuvieron x=8
signos '+' y 4 signos '-' para un total de n=12 elementos (individuos). Dado que x >n/2 se
calcula el valor de P a partir de la expresión:
7
1
1
P=2 P X ≥ 8 cuando p= =2 1−∑ 12
2
i 2
i=0
(
)
[
12
( )( ) ]=2 [ 1−0.8062]=0.3877
Conclusiones. Consérvese la hipótesis nula. No existen diferencias en la preferencia de los
clientes por los dos artículos.
Para realizar esta prueba con el SPSS se procede de acuerdo a lo que muestra las imágenes a
continuación, teniendo en cuenta el orden a la hora de seleccionar las variables.
Obsérvese que la variable Preferencia está compuesta por 1 y -1 y la variable RefPref está
compuesta de puros ceros. Esta codificación permite que la diferencia 1-0 de positiva y la
diferencia -1-0 un resultado negativo, coincidiendo estos resultados con los símbolos más y
menos.
Al seleccionar las variables primero se selecciona la variable RefPref y luego la variable
Preferencia.
Se selecciona el nivel de significancia
Y finalmente se ejecuta el procedimiento.
Resultado
Conclusiones. Consérvese la hipótesis nula. No existen diferencias en la preferencia de los
clientes por los dos artículos.
Prueba del Signo para medir si existen diferencias al comparar dos Tratamientos donde la
valoración de cada tratamiento se mide en una escala ordinal como es el caso de las escalas de
likert.
El siguiente ejemplo muestra como la prueba del signo se puede emplear para determinar si
existen diferencias significativas entre dos estrategias de enseñanza en las cuales en una un
profesor con experiencia se ocupa de instruir a un grupo numeroso de estudiantes y en la otra
un asistente de profesor ya graduado se encarga de instruir a un grupo más pequeño de
estudiantes.
Ejemplo 4. El rector de una universidad desea medir la eficiencia de dos estrategias de
enseñanza. La primera consiste en impartir clase a grupos numerosos de estudiantes a cargo de
profesores de tiempo completo y la segunda que las clases sean dadas por asistentes graduados
a grupos pequeños de alumnos. Para medir la calidad de la enseñanza se pidió a 40 profesores
con experiencia que evaluaran la Transmisión del conocimiento en la siguiente escala: excelente,
4; muy bueno, 3; bueno, 2, y deficiente. ¿Existen diferencias entre los métodos de enseñanza?.
Los resultados obtenidos se presentan en la siguiente tabla:
Evaluado
r
Puntaje a Grupo
Pequeño
Puntaje a Grupo
Grande
Evaluado
r
Puntaje a Grupo
Pequeño
Puntaje a Grupo
Grande
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
1
4
4
3
3
4
2
4
1
3
3
4
4
4
1
1
2
2
4
3
2
2
3
4
2
2
1
3
1
2
3
4
4
3
2
3
2
3
3
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
4
4
4
3
3
2
3
4
3
4
3
1
4
3
2
2
2
1
3
3
1
4
3
3
2
2
1
1
1
3
2
2
4
4
3
3
1
1
4
2
Solución. En este caso los signos positivos y negativos se obtienen a partir de las diferencias
Puntaje a Grupos Pequeños - Puntaje a Grupos Grandes
Planteamiento de las Hipótesis.
H o : No existe diferencias en la preferencia calidad de la enseñanza
H a : Noexiste diferencias en la preferencia calidad de laenseñanza
Nivel de Significancia. α =5 %.
Determinar el número de signos + y – y obtener el valor de P. Es este caso se obtuvieron x=19
signos “+” y 11 signos “-“ y 10 neutros para un total de n=30 elementos (mediciones). Dado
que x >n/2 se calcula el valor de P a partir de la expresión:
(
P=2 P X ≥ 19 cuando p=
18
1
1
=2 1−∑ 30
2
i 2
i=0
)
[
30
( )( ) ]
P=2 [ 1−0.8998 ] =0.2005
Conclusiones. Dado que el valor de P=0.2005>0.05=α no se rechaza la hipótesis nula y por
tanto no existen diferencias significativas en la calidad de enseñanza de ambos grupos.
Aproximación Normal para la Prueba del Signo.
Siempre que n > 10, las probabilidades binomiales con p = 1/2 se pueden aproximar a partir de la
curva normal, ya que np = nq > 5. En este caso μ=np=n/2 y σ =√ n∗p∗(1− p)=√ n/4= √n /2 y
para el ejemplo anterior por aproximación normal se tendría que
1
19−0.5−μ
≤
(
)2 =2 P ( X −μ
)
σ
σ
1
18.5−n /2
18.5−15
P=2 P ( X ≥ 19 cuando p= ) =2 P ( Z ≥
=2 P ( Z ≥
)
2
√ n/2
√30 /2 )
1
P=2 P ( X ≥ 19 cuando p= ) =2 P ( Z ≥1.2780 )=2∗ [ 0.1006 ] =0.2012
2
P=2 P X ≥ 19 cuando p=
Dado que el valor de P=0.2012> 0.05=α no se rechaza la hipótesis nula y por tanto no
existen diferencias significativas en la calidad de enseñanza de ambos grupos. Obsérvese que
0.201 es el valor aproximado que da el SPSS ya que la muestra es grande.
En general para muestras grandes los valores de P se obtienen a partir de la aproximación
binomial al modelo normal.
Casos
μ> ~
μ0
Caso 1: Cuando Ha: ~
P=P ( X ≤ x cuando p=1/2 )=P
x +0.5−μ
≤
( X −μ
)
σ
σ
(
P=P X ≤ x cuando p=
1
x +0.5−n/2
=P Z ≤
2
√ n/2
) (
)
μ< ~
μ0
Caso 2: Cuando Ha: ~
x−0.5−μ
≤
( X −μ
)
σ
σ
1
x−0.5−n /2
P=P ( X ≥ x cuando p= ) =P ( Z ≥
2
√ n/2 )
P=P ( X ≥ x cuando p=1/2 )=P
μ ≠ ~μ0
Caso 3: Cuando Ha: ~
Si x <n/2 el valor de P se obtiene a partir de la expresión
1
x +0.5−μ
≤
(
)2 =2 P ( X−μ
)
σ
σ
1
x +0.5−n/2
P=2 P ( X ≤ x cuando p= )=2 P ( Z ≤
2
√ n/2 )
P=2 P X ≤ x cuando p=
Si x >n/2 el valor de P se obtiene de la expresión
1
x−0.5−μ
≥
(
)2 =2 P ( X−μ
)
σ
σ
1
x−0.5−n /2
P=2 P ( X ≥ x cuando p= )=2 P ( Z ≥
2
√ n /2 )
P=2 P X ≥ x cuando p=
En las expresiones anteriores el valor de 0.5 que se suma y resta es un factor de corrección por
continuidad de la aproximación binomial a la normal que hace mas precia la aproximación.
Obsérvese que en el caso 3 las probabilidades que se obtienen son iguales a las de los caso 1 y 2
solo que multiplicadas por 2.
Pruebas U de Mann Whitney y de Kruskall-Wallis
A estas pruebas se les conoce como pruebas de suma de rangos porque dependen de los
rangos o clasificaciones de las observaciones de muestra.
La prueba de Mann-Whitney se utiliza cuando se quiere comparar sólo dos poblaciones La
prueba de Kruskal-Wallis es la generalización de la prueba u de Mann Whitney para más de dos
poblaciones.
En ambas pruebas las muestras se obtienen de manera independiente.
Ambas permiten determinar si las muestras independientes se obtuvieron de la misma
población o de poblaciones distintas con la misma distribución de probabilidad.
Estas pruebas consideran la magnitud de las observaciones a diferencia de la prueba de los
signos que solo toma en cuenta los signos más y menos y no la magnitud de los datos.
La ventaja de este tipo de pruebas en relación a la prueba de los signos es que a través de los
rangos
Ejemplo 5. Asignación de rangos a un conjunto de datos.
Un ingeniero civil dispone de n=20 mediciones de tensión a la fractura de asfalto mezclado
caliente (en megapascales) producidos por una planta de asfalto para analizarlos. Los datos a
continuación:
Tensión a la fractura
8
0
12
6
17
9
8
0 30
10
5
17
5
13
8
17
9
17
9
13
8
17
5
17
9
17
9
17
9
17
9
17
9
17
9
Solución.
Lo primero es ordenar los datos.
Tensión a la fractura
3
0 80 80
10
5
12
6
Una vez ordenados se asignan los rangos.
Tensión a la fractura
Rango
3
0
10
5
80 80
2.
1 5
2.5 3
12
6
4
13
8
5
17
5
6
8
8
8
Al valor 80 le corresponde como rango 2.5=( 2+ 3 ) /2 y al valor 179 le corresponde el rango
8=(7+ 8+9)/3, los promedios de los rangos que les corresponderían si ellos fueran diferentes.
Prueba U de Mann - Whitney
El principio lógico en que se basa esta prueba consiste en lo siguiente. Si se tienen dos muestras
aleatorias tomadas de manera independientes y si las dos muestras provienen de dos
poblaciones idénticas, al mezclarse las muestras y asignarse los rangos al conjunto combinado de
datos, entonces rangos altos y bajos deben caer de manera similar entre las dos muestras. Si por
el contrario, los rangos bajos se relacionan de forma predominante en una de las muestras y los
rangos altos se encuentran de forma mayoritaria en la otra muestra, es de sospechar que las
muestras provengan de poblaciones con similar distribución de probabilidad pero con medianas
diferentes. En otras palabras, cuando los datos no provienen de distribuciones idénticas, a una
de las muestras le corresponderán en general los rangos más altos y a la otra muestra le serán
asignados de forma mayoritaria los rangos bajos y en consecuencia las sumas de los rangos
correspondientes a cada una de las muestras serán estadísticamente bastante diferentes en
magnitud.
La prueba U de Mann Whitney es la alternativa no paramétrica a la prueba paramétrica t de
Student en dos muestras cuando esta última no sea aplicable por no cumplirse todos las
suposiciones estrictas de que las muestras sean independientes y elegidas de poblaciones con
comportamiento normal, con variancias iguales conocidas y que los datos se midan cuando
menos en una escala de intervalo.
Notación:
n1 = número de elementos en la muestra 1.
n2 = número de elementos en la muestra 2.
R1 = suma de los rangos de los elementos en la muestra 1
R2 = suma de los rangos de los elementos en la muestra 2.
U = estadístico de la prueba
Para el cálculo del estadístico de prueba U debemos calcular
U 1=n1 n 2+
n1 ( n1 +1 )
−R1
2
y
U 2=n1 n 2+
n2 ( n2 +1 )
−R 2
2
Escogencia del estadístico U .
Si la hipótesis alterna es Ha: ~μ1 < ~μ2 , U ¿ min (U ¿ ¿1 , U 2 )¿
Si la hipótesis alterna es Ha: ~μ1 > ~μ2, U ¿ máx ( U ¿ ¿ 1, U 2 )¿
En caso de que Ha: ~μ1 ≠ ~μ 2 podemos escoger a cualquiera
de los dos como valor del estadístico U .
Aproximación Normal
Cuando la hipótesis nula que las n +n observaciones provienen
de poblaciones idénticas es cierta y tanto n como n son mayores
que 8, entonces la distribución muestral del estadístico U tiene a
distribuirse normalmente con una media de
1
2
1
μU =
2
n1 n2
2
y desviación estándar
n 1 n2 ( n1 +n2 +1 )
12
√
en la medida que
σU =
zc=
U−μU
σU
n1
y
n2
son mayores y entonces la estadística
tiende a la distribución normal estándar.
Reglas de decisión. Dado que la estadística de prueba z c es normal la región crítica depende de
la forma de la hipótesis alternativa:
μ 2, se rechaza H 0 a favor de H a si el valor de P=Pr ( Z < z c ) <α .
Caso 1. Si H a : ~μ1< ~
μ 2, se rechaza H 0 a favor de H a si el valor de P=Pr ( Z > z c ) <α .
Caso 2. Si H a : ~μ1> ~
μ2, se rechaza H 0 a favor de H a cuando para z c < 0 el valor de
Caso 3. Si H a : ~μ1 ≠ ~
P=2 Pr ( Z < z c ) <α ó si z c > 0 el valor de P=2 Pr ( Z > z c ) <α .
En todos los casos cuando el valor de P es menor al valor de alfa se rechaza la hipótesis nula.
Ejemplo 6. Comparación de dos poblaciones.
Un profesor tiene dos grupos de psicología: uno en la mañana, con 9 alumnos, y otro en la tarde
con 12 alumnos. En el examen final, que es el mismo para ambos grupos, las calificaciones
obtenidas son las que se muestran en la tabla a continuación. ¿Puede concluirse a un nivel de
significancia de 0.05 que el grupo de la mañana posee un rendimiento menor al del grupo de la
tarde? Resolver el problema, primero a mano, dando todos los y luego utilizando el SPSS.
Grupo Mañana
Grupo Tarde
7
3
8
6
87
81
7
9
8
4
7
5
8
8
82
90
6
6
8
5
9
5
8
4
75
92
7
0
8
3
9
1
53 84
Solución.
Planteamiento de las hipótesis
Las hipótesis a probar son
Ho: ~
μ M =~
μ T vs
Ha: ~
μ M <~
μT
Ho : Calificaciones del grupo de la mañana son iguales a las calificaciones del grupo de la Tarde
vs
Ha: Calificaciones del grupo de la mañana son menores a las calificaciones del grupo de la Tarde
Establecer el nivel de significancia. α =0.05 .
Calculo del estadístico de prueba U .
n1 = numero de observaciones en la muestra 1 (mañana) = 9
n2 = numero de observaciones en la muestra 2 (tarde) = 12
R1 = suma de los rangos de la muestra 1 = 2+3+4+5.5+5.5+7+9+16+21 = 73
R2 = suma de los rangos de la muestra 2 = 1+8+10+12+12+12+14+15+17+18+19+20 = 158
Calificación
53
66
70
73
75
75
79
81
82
83
84
Grupo Rango Calificación Grupo Rango
Tarde
1
84
Tarde
12
Mañana
2
84
Tarde
12
Mañana
3
85
Tarde
14
Mañana
4
86
Tarde
15
Mañana
5.5
87
Mañana
16
Mañana
5.5
88
Tarde
17
Mañana
7
90
Tarde
18
Tarde
8
91
Tarde
19
Mañana
9
92
Tarde
20
Tarde
10
95
Mañana
21
Tarde
12
-
U 1=n1 n 2+
n1 ( n1 +1 )
9 ( 9+1 )
−R1 =9∗12+
−73=80
2
2
n2 ( n2 +1 )
12 ( 12+ 1 )
−R 2=9∗12+
−158=28
2
2
μ <~
μ , entonces U ¿ 28 ¿ ¿.
Dado que Ha: ~
U 2=n1 n 2+
M
T
Aproximación Normalón.
Dado que ambos tamaños de muestra son mayores a 8 se puede utilizar la aproximación normal.
Para ello calculamos la media y desviación estándar del estadístico U
Media
μU =
n1 n2 9∗12
=
=54
2
2
Desviación estándar
σU =
√
n 1 n2 ( n1 +n2 +1 )
9∗12 ( 9+ 12+1 )
=
= √198=14.07
12
12
√
luego obtenemos el valor de
zc=
U−μU 28−54
=
=−1.8477
σU
14.07
Regla de Decisión.
Dado que el valor de P=Pr ( Z ≤−1.8477 ) =0.0323,
se cumple que P<α y en consecuencia se rechaza la
μ =~
μ a favor de la alternativa
hipótesis nula H : ~
0
M
T
H a : ~μM < ~
μT .
Conclusión. Efectivamente el rendimiento de los
alumnos del grupo de la mañana es menor en
promedio al de los alumnos del grupo de la tarde.
Resultados obtenidos con el SPSS
Afortunadamente el uso de la tecnología nos facilita los cálculos. En este caso la manera como se
introducen los datos en el SPSS se muestra en la imagen a continuación. En ella se refleja la
codificación necesaria para realizar el análisis de Manny – Witney.
Esta codificación es necesaria para indicar al SPSS cuales datos pertenecen al grupo de la
mañana y cuales al grupo de la tarde. En este caso las primeras 9 observaciones de la variable
rendimiento son las del grupo de la mañana y se les asigna el código 1. El resto de los datos
pertenecen al grupo de la tarde y se les asigno el código cero.
Esta codificación es importante para que el signo del estadístico de prueba que calcula el SPSS
sea el correcto. En el caso del problema la hipótesis alternativa es posible plantearla de dos
maneras equivalentes:
Ha: ~
μ <~
μ que indica que la mediana del grupo de la mañana es menor al de la tarde
M
T
Ha: ~
μT > ~
μ M que indica que la mediana del grupo de la tarde es mayor al de la mañana
y ambas maneras significan lo mismo.
Regla para la codificación: Asignar el código 1 al grupo de datos que se encuentra a la izquierda
de la desigualdad.
μ M <~
μT el código 1 se debe asignar a los datos del grupo de la mañana y para
En el caso de Ha: ~
Ha: ~
μ >~
μ se debe asignar el 1 a los datos del grupo de la tarde.
T
M
En el caso del problema las hipótesis que se plantearon fueron
Ho: ~
μ =~
μ vs Ha: ~
μ <~
μ
M
T
M
T
μ M se
y por ello el código 1 se asignó a las observaciones del grupo de la mañana ya que ~
encuentra a la izquierda de la desigualdad.
Dado que por defecto el valor de P que genera el SPSS es para la hipótesis alterna de dos colas
Ha: ~
μ ≠~
μ para obtener el valor de P para la hipótesis unilateral simplemente se divide entre
1
2
dos el valor de P que produce el SPSS. En este caso el valor de P esta dado por
P=0.064/2=0.032 el cual coincide con nuestro valor calculado anteriormente.
Importante. El uso de la prueba de suma de rangos de Mann - Whitney no se restringe a
poblaciones no normales. Se puede utilizar en vez de la prueba t de dos muestras cuando las
poblaciones son normales, aunque la potencia será menor. La prueba de suma de rangos
siempre es superior a la prueba t para poblaciones definitivamente no normales.
Prueba de Kruskall-Wallis
Se le conoce también como la prueba H de Kruskal-Wallis.
Es la generalización de la prueba de Mann - Whitney para más de dos muestras.
Es la alternativa no paramétrica a la prueba F del análisis de la varianza para probar la
igualdad de k ≥ 2 medias poblacionales.
No requiere que todas las k muestras provengan de poblaciones normales con varianzas
iguales.
Notación.
k = número total de grupos = número total de muestras .
n1 = número de elementos en la muestra 1.
n2 = número de elementos en la muestra 2.
…
n k = número de elementos en la muestra k.
n = número total de datos disponible.
n=n1 +n2 +n 3+ …+nk .
R1 = suma de los rangos de todos los elementos en la muestra 1.
R3 = suma de los rangos de todos los elementos en la muestra 2.
…
Rk = suma de los rangos de todos los elementos en la muestra k.
Planteamiento de las Hipótesis. Las hipótesis a contrastar con esta prueba son
H 0 :μ 1=μ2=μ3 vs H a :al menosuna de las μi es diferente
mismas del análisis de la varianza para determinar si dos o más muestras provienen de
poblaciones normales idénticas.
El estadístico de prueba es
k
2
Rj
12
H=
−3 ( n+1 )
∑
n ( n+1 ) j=1 n j
cuya distribución se aproxima a una distribución ji-cuadrada con k −1 grados de libertad cuando
los tamaños de todas las muestras son mayores o iguales a 5.
Regla de decisión. Dado que H posee distribución ji-cuadrada con k −1 grados de libertad, la
regla de decisión es rechazar la hipótesis nula de que todas las medias son iguales a favor de la
alternativa si
H > χ 2k −1 ;α
Ejemplo 7. La tienda “Styles boutique” tiene tres establecimientos en centros comerciales.
“Styles boutique” mantiene un registro diario del número de clientes que realmente compran en
cada establecimiento. La siguiente es una muestra de esos datos. Utilizando la prueba de
Kruskal-Wallis, ¿puede decir, al nivel de significancia de 0.05, que sus tiendas tienen el mismo
número de clientes que compran?
Centro Comenrcial
Plaza Mayor
San Diego
El Tesoro
Número de Clientes
99
64 101 85 79 88 97 95 90
83 102 125 61 91 96 94 89 93
89 98 56 105 87 90 87 101 76
100
75
89
Solución.
Planteamiento de las Hipótesis.
H 0 :μ 1=μ2=μ3 vs H a :al menosuna de las μi es diferente
En palabras las hipótesis para el caso del ejemplo son
H 0 : El número promedio de compradores es igual en las tres tiendas
vs
H a : Para al menos una de las tiendas el número promedio de compradores diferente.
Establecer el nivel de significancia. α =0.05 .
Lo primero es combinar los datos, ordenarlos de menor a mayor y asignar rangos. Luego se
obtiene las sumas de los rangos por tienda en cada centro comercial. En este caso hay k =3
grupos.
R1 = La suma de los rangos de la tienda en Plaza Mayor.
R2 = La suma de los rangos de la tienda en San Diego.
R3 = La suma de los rangos de la tienda en El Tesoro.
Centro
comercial
El Tesoro
El Tesoro
El Tesoro
El Tesoro
El Tesoro
El Tesoro
El Tesoro
El Tesoro
El Tesoro
El Tesoro
Clientes
Rango
56
76
87
87
89
89
90
98
101
105
1
5
9.5
9.5
13
13
15.5
23
26.5
29
R1=¿
145
Centro
comercial
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Plaza Mayor
Clientes
Rango
64
79
85
88
90
95
97
99
100
101
3
6
8
11
15.5
20
22
24
25
26.5
R1=¿
161
Centro
comercial
San Diego
San Diego
San Diego
San Diego
San Diego
San Diego
San Diego
San Diego
San Diego
San Diego
Clientes
Rango
61
75
83
89
91
93
94
96
102
125
2
4
7
13
17
18
19
21
28
30
R1=¿
159
Obtenidas las sumas de los rangos se procede a obtener el valor del estadístico H Kruskall-Wallis
con n=30, n1 =n2=n 3=10, R1=145 , R2=161 , R3=159 .
H=
3
R2j
12
∑ −3 ( n+1 )
n ( n+1 ) j=1 n j
H=
12
1452 1612 1592
+
+
−3∗31
30∗31 10
10
10
(
)
H=0.19613
Regla de Decisión.
Dado que el estadístico H tiene distribución aproximadamente ji-cuadrada, se rechaza la
2
hipótesis nula si H > χ 22 ;α =0.05=5.991, o bien si P=Pr ( χ 2 >0.19613 ) <α
Conclusión. En la grafica se aprecia
que
el valor H no cae en la región
crítica.El
valor
de
P=Pr ( χ 22 >0.19613 ) =0.9066> 0.05
por
lo tanto la hipótesis nula no se
rechaza, lo que significa que el
número de compradores promedio
las tres tiendas no son significativamente diferentes.
en
Prueba de Kolmogorov – Smirnov para ajuste de distribuciones.
El objetivo de esta prueba es determinar si los datos de una muestra aleatoria fueron obtenidos
de una distribución de probabilidad en específico. Se utiliza más a menudo cuando la variable
aleatoria que representan los datos es de tipo continuo. Se basa en la comparación de la función
de distribución de probabilidad teórica de la que se considera provienen los datos de la muestra
con la función de distribución empírica obtenida a partir de los datos.
Si X 1 , X 2 , X 3 ,… , X n es una muestra de una variable aleatoria X , F (x) representa a la función
de distribución de probabilidad teórica del modelo propuesto y por Sn (x ) a la función de
distribución empírica de la muestra, el estadístico que se utiliza para llevar a cabo el contraste de
hipótesis viene dado por
Dn =¿ x |F ( x )−S n( x)|
La hipótesis nula a contrastar es entonces
H 0 : Los datos de la muestra se ajustan a la distribución dada por F (x).
vs
H a : Los datos de la muestra no se ajustan a la distribución dada por F (x).
Para un valor de α de significancia, Se rechazará la hipótesis nula en favor de la alternativa
cuando el valor P asociado al estadístico de prueba Dn sea menor que el valor de α.
Pasos para realizar el contraste.
1. Planteamiento de las hipótesis.
2. Especificación del nivel de significancia α.
3. Obtención des estadístico de la prueba.
Para ello se ordenan los valores de la muestra de menor a mayor.
Se obtiene la función de distribución empírica Sn ( x i )=i /n en cada valor de la muestra;
esto es, para cada dato x i en la muestra.
Se calcula el valor
{
}}
d n=max max |F ( x(i) )−S n ( x (i ) )|;|F ( x (i ) )−Sn ( x (i−1) )|
1≤ i ≤n
{
x
4. Regla de decisión. Si el valor de la tabla para el nivel de significancia elegido es mayor
que el valor calculado de d n, entonces aceptaremos la hipótesis nula, o tambien en
base al valor P se rechazará la hipótesis nula en favor de la alternativa si el valor de
P=P ( D n > d n) < α .
La distribución de probabilidad de DN, necesaria para calcular el p-valor, no es muy conocida.
Para evaluar esta probabilidad hay que consultar tablas de dicha distribución.
Tablas estadísticas para la prueba de Kolmogorov – Smirnov.
Ejemplo 8. Los datos que aparecen en la tabla a continuación representan el tiempo necesario
para que un individuo sea atendido en una cafetería. Nos planteamos si una distribución normal
es adecuada para su ajuste.
Tiempo para 3.35 3.69 3.76 3.81 3.85 3.86 3.99 4.03 4.04 4.16
se atendido 4.17 4.22 4.23 4.23 4.31 4.42 4.46 4.6 4.66 5.12
Solución.
Planteamiento de las hipótesis.
H 0 : Los datos de la muestra se ajustan a la distribución normal
vs
H a : Los datos de la muestra no se ajustan a la distribución normal
Nivel de significancia. α =0.05
Obtención de estadístico de prueba.
Tiempo
Fi
3.35
1
3.69
2
3.76
3.81
3
4
F(x)
0.0216
3
0.1230
2
0.1628
7
0.1959
Fr(i) Fr(i-1)
0.05
0.10
0.15
0.20
di
0.00 0.0284
0.05 0.0230
0.10 0.0129
0.15 0.0040
di-1
-0.0216 Max dn= 0.1177
-0.0730 Min dn= -0.0730
-0.0629
-0.0460
d20 = 0.1177
3.85
5
3.86
6
3.99
7
4.03
8
4.04
9
4.16
10
4.17
11
4.22
12
4.23
13
4.23
14
4.31
15
4.42
16
4.46
17
4.6
18
4.66
19
5.12
20
Media
=
Desv =
7
0.2251
9
0.2328
6
0.3445
1
0.3825
2
0.3922
2
0.5121
2
0.5222
2
0.5723
5
0.5822
7
0.5822
7
0.6592
1
0.7545
7
0.7853
1
0.8738
6
0.9026
5
0.9930
9
0.25
0.20 0.0248 -0.0252
0.30
0.25 0.0671 0.0171
0.35
0.30 0.0055 -0.0445
0.40
0.35 0.0175 -0.0325
0.45
0.50
0.40 0.0578 0.0078
0.45 0.0121 -0.0621
0.55
0.50 0.0278 -0.0222
0.60
0.55 0.0276 -0.0224
0.65
0.60 0.0677 0.0177
0.70
0.65 0.1177 0.0677
0.75
0.70 0.0908 0.0408
0.80
0.75 0.0454 -0.0046
0.85
0.80 0.0647 0.0147
0.90
0.85 0.0261 -0.0239
0.95
0.90 0.0473 -0.0027
1.00
0.95 0.0069 -0.0431
4.148
0.395
Regla de decisión Dado que el valor de la tabla 0.294 es mayor que el valor calculado de
d 20=0.118 , entonces no se rechaza la hipótesis nula.
Si se utiliza el valor de P que da el SPSS se tiene que dado P=0.2> 0.05 se concluye que no se
rechaza la hipótesis nula.
Conclusión. Dado que el valor de P es 0.2 > 0.05 se concluye que los tiempos para ser atendidos
en la cafetería siguen una distribución normal con media μ=4.148y desviación estándar
σ =0.395.
Salida en SPSS
Obsérvese que el Max dn = 0.118 y Min dn = -0.073 coinciden con los valores arrojados por el
SPSS.
Prueba ji-cuadrada de independencia(datos categóricos)
Una tabla de contingencia de 2 x 2 es una tabla donde se organizan los datos de dos variables
categóricas, de tal manera que en ella se exhibe la cantidad de elementos en la muestra que
tienen en común dos características, una por cada variable asociada a la tabla.
Si la tabla tiene r filas y c columnas se denomina tabla r ×c (“ r ×c ” se lee “r por c ”). En una
tabla de contingencia los totales de las filas y columnas se denominan frecuencias marginales.
A continuación se presenta un ejemplo de una tabla de contingencia de 3 x 4; es decir tres filas y
cuatro columnas. En esta tabla A, B, C son las categorías de la variable Municipio y Asalto, Robo
de casas, Hurto, Homicidio las categorías de la variable Tipo de crimen. El valor 162 significa que
de los 2532 casos investigados 162 fueron asaltos que se cometieron en el Municipio A. El valor
919 significa que de los 2532 casos investigados 919 crímenes ocurrieron en el Municipio B. De
similar manera se interpretan el resto de los valores en la tabla.
Municipi
o
A
B
C
Total
Asalt
o
162
258
280
700
Tipo de crimen
Robo de casas Hurto
118
193
175
486
451
458
390
1299
Homicidio
Total
18
10
19
47
749
919
864
2532
La prueba ji cuadrada de independencia tiene como objetivo probar si existe alguna relación de
dependencia entre dos variables categóricas. Para el caso de la tabla anterior la prueba busca
determinar si el tipo de crimen que se comete y el municipio donde ocurre el delito guardan o
no
alguna
relación.
Para
este
ejemplo
las
hipótesis
a
contrastar
serian:
H 0 : El tipo de delito que se comete es independiente del municipio donde ocurre eldelit o
H a : E ltipo de delito que se comete y el municipio donde ocurre el delit o son dependientes
Si al llevar a cabo el proceso de prueba de hipótesis la evidencia estadística (contenida en la
muestra) la hipótesis nula no es rechazada, significa que no existe relación alguna entre el
Municipio y el tipo de robo cometido. Por otra parte, el rechazo de H 0 a favor de H a implica que
si hay algún tipo de relación entre el municipio donde ocurre el crimen y ei tipo de crimen.
Los pasos a seguir para llevar a cabo el contraste ji cuadrado de independencia son muy
sencillos.
1. Plantear las hipótesis a contrastar. Para el ejemplo serian
H 0 : El tipo de delito que se comete es independiente del municipio donde ocurre eldelit o
H a : E ltipo de delito que se comete y el municipio donde ocurre el delit o son dependientes
2. Elegir el nivel de significancia α. Para este ejemplo elegiremos α =0.02.
3. Obtener el valor del estadístico de la prueba. El estadístico de prueba a calcular se obtiene a
partir de la expresión:
r
2
c
χ =∑ ∑ c
i=1 j=¿¿
( O ij −Eij )
2
Eij
donde la sumatoria se extiende a todas las r ×c celdas en la tabla de contingencia y donde a
Oij y Eij se les conoce como las frecuencias observadas y esperadas. Lo complicado de la
formula no nos debe de preocupar ya que como veremos los cálculos son muy sencillos de
realizar.
Las frecuencias observadas O ij son sencillamente las frecuencias que se presentan en la
tabla de frecuencia que se obtienen a partir de los datos de la muestra. En nuestro ejemplo
las frecuencias observadas son O11 =162, O 12=118, O 13=451 y así sucesivamente hasta
O34=19.
De manera equivalente E11 se refiere a la frecuencia esperada correspondiente a la celda
que se encuentra en al interceptar la fila 1 con la columna 1, la cual se obtiene a partir de
multiplicar el total de las fila 1 (749) por el total de la columna 1 (700) y luego dividiendo este
producto por el GranTotal=n=2352; es decir a partir de la expresión:
E11 =
Total de la fila 1 x Total de la columna 1
GranTotal
E11 =
749∗700
=207.07
2532
y de esta manera para las demás frecuencias esperadas.
Obtenidas las frecuencias esperadas se calcula el aporte a la suma ji-cuadrado a través de la
expresión
( Oij −Eij )
2
Eij
que para el caso del Municipio A y tipo de crimen Asalto seria
( O11−E 11 )
2
E 11
(162−207.07 )2
=
=9.81
207.07
A continuación la tabla con las frecuencias observadas, esperadas y el aporta a la suma jicuadado
Tipo de crimen
Municipi
o
Asalto
A
162 207.07
9.81
B
258 254.07
0.06
C
280 238.86
7.08
Total
700
700
16.955
Robo de casas
11
8 143.77 4.62
19
3 176.40 1.56
17
5 165.84 0.51
48
6.68
6 486.00
7
Hurto
Homicidio
Total
451
384.26
11.59
18
13.90
1.21
749
458
471.48
0.39
10
2.92
919
390
129
9
443.26
6.40
19
17.06
238.8
6
269.8
2
0.55
4.67
5
864
1299
18.376 47
2532
Una vez realizados los cálculos se procede a obtener el valor del estadístico de prueba jicuadrado
r
2
c
χ =∑ ∑ c
i=1 j=¿¿
2
( Oij −Eij )
Eij
=16.955+6.687+18.376+ 4.675=46.693
El estadístico de prueba χ 2c posaee distribución ji-cuadrado con
4. Regla de decisión.
v=( r−1 ) ( c−1 ) grados de libertad
r
2
c
χ =∑ ∑ c
i=1 j=¿¿
2
( Oij −Eij )
Eij
2
χv
En consecuencia, para un nivel de significancia α se rechaza la hipótesis nula de
independencia de las variables categóricas si χ 2c > χ 2v; α; es decir, si el valor calculado χ 2c cae en
la región critica como se muestra en la figura.
Para el ejemplo, los grados de libertad son v=( r−1 ) ( c−1 ) =( 3−1 ) ( 4−1 )=6 grados de libertad.
En consecuencia como χ 2v; α = χ 26 ;0.05=12.592 y χ 2c =46.693 se sigue que χ 2c > χ 2v; α (46.693>12.592),
en consecuencia se rechaza la hipótesis nula de independencia; esto es, la ocurrencia de estos
tipos de delitos depende del Municipio.
Salida del SPSS
Resumen de procesamiento de casos
Casos
Válido
N
Municipio * Crimen
2532
Perdidos
Total
Porcentaje N Porcentaje
100.0% 0
N
0.0% 2532
Porcentaje
100.0%
Municipio*Crimen tabulación cruzada
Crimen
Asalto Robo de casas
Municipio A Recuento
Recuento esperado
B Recuento
Recuento esperado
C Recuento
Recuento esperado
Total
Recuento
Recuento esperado
Total
Hurto
Homicidio
162
118
451
18
749
207.1
143.8
384.3
13.9
749.0
258
193
458
10
919
254.1
176.4
471.5
17.1
919.0
280
175
390
19
864
238.9
165.8
443.3
16.0
864.0
700
486
1299
47
2532
700.0
486.0 1299.0
47.0 2532.0
Pruebas de chi-cuadrado
Valor
gl
Sig. asintótica (2 caras)
46.693a
6
.000
Razón de verosimilitud
47.405
6
.000
Asociación lineal por lineal
34.255
1
.000
Chi-cuadrado de Pearson
N de casos válidos
2532
a. 0 casillas (0.0%) han esperado un recuento menor que 5. El recuento mínimo esperado es
13.90.
Nota: Obsérvese que los resultados obtenidos con el SPSS coincides con los obtenidos
anteriormente