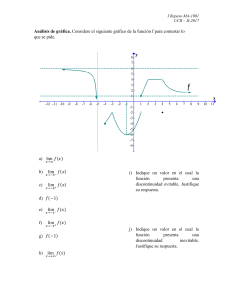
Actividad 3. Ejercicios colaborativos Iniciamos con la unidad 2 Límites y continuidad. De nuevo vamos a resolver ejercicios de forma colaborativa asumiendo un rol distinto al que ya has tenido en las actividades anteriores. Sigue las instrucciones atentamente: 1. Tu tutor te asignará el equipo al que perteneces 2. Elije el rol que deseas de acuerdo a la siguiente tabla: Roles en el equipo Descripción 1. El jefe de equipo* Coordina los esfuerzos de todos, es disciplinado, centrado y equilibrado. Habla, pero sobre todo, es capaz de escuchar a los demás. 2. El director de las tareas En caso de que falte el jefe, él asumirá esa función. Su gran valor añadido es su impulso, su pasión por el trabajo, y su calidad para estimular acciones. Desarrolla contactos. 3. El creativo Es la fuente de ideas originales y de las propuestas. Es un miembro del grupo que necesita expresarse o si no es muy probable que se desconecte y se aísle. 4. El evaluador* Es una persona más analítica que el creativo. Suele estar menos comprometido, está un poco en la sombra, pero es muy necesario para el control de calidad. Es una persona de confianza pero puede resultar fría. 5. El generador de recursos* Es el miembro más extrovertido del grupo, el más sociable, el que aporta contactos y desarrollos; pero no es una persona con gran iniciativa y por eso necesita del equipo. 6. El práctico Es el que transforma las ideas en realización de trabajos. Es metódico, es eficiente, no es un gran director, pero es un gran administrador. 7. El motivador* Es el “alma” del equipo, el que mantiene al grupo unido, da apoyo a los demás, los escucha, infunde coraje al equipo; es una persona que no destaca mucho cuando está, pero se nota mucho cuando no está. 8. El finalizador* En todo equipo de trabajo debe existir una persona que sea la que se ocupe por los tiempos, los objetivos; debe llevar a cabo un continuo seguimiento y comprobación de detalles; es un miembro importante pero no suele ser muy popular. 9. El especialista Es un integrante entregado, independiente con intereses limitados, aporta cualidades y conocimientos específicos en el contenido a trabajar por el alto dominio de los mismos. Notas: Establece una comunicación efectiva entre tus compañeros para no duplicar roles Pueden aprovechar las herramientas de comunicación de la plataforma *Son roles obligatorios a cubrirse durante la actividad por lo tanto no deben descuidarse. 3. Resuelve los siguientes ejercicios de forma colaborativa a partir de la gráfica que se presenta y entrega todos los resultados en un documento en Word. 1. lim 𝑓(𝑥) = 𝑥→−3− A) B) C) D) 8 No existe -5 0 La recta roja es la que cumple con la función, pero justo en el -3, hay un espacio en blanco por lo cual no hay continuidad, entonces el límite no existe en este caso. 2. lim 𝑓(𝑥) = 𝑥→−3+ A) 8 B) No existe C) -5 D) 0 Para este caso, tomamos en cuenta la parábola verde, cuya lectura se toma de derecha a izquierda y su límite termina justo en el -3. 3. lim 𝑓(𝑥) = 𝑥→−3 A) 8 B) No existe C) -5 D) 0 En este caso se nos indica que tiende a -3, más no si por la derecha o por la izquierda, por tanto su imagen será 8 nuevamente. 4. (−3) = A) 8 B) No existe C) -5 D) 0 En este caso es prácticamente lo mismo del inciso anterior, tiende a -3; su imagen es 8. 5. lim− 𝑓(𝑥) = 𝑥→2 A) -7 B) No existe C) -8 D) Vacío En este caso, observamos que justo en el punto -2, tiene una discontinuidad entre la parábola y la recta roja. 6. lim+ 𝑓(𝑥) = 𝑥→2 A) -7 B) No existe C) -8 D) Vacío En este caso se toma la lectura desde la derecha, pero se repite lo mismo que el inciso anterior, tiene discontinuidad. 7. lim (𝑥) = 𝑥→2 A) -7 B) No existe C) -8 D) Vacío Es el mismo caso que en los incisos anteriores, no existe. 8. (2) = A) -7 B) No existe C) -8 D) Vacío Sigue siendo el mismo caso. 9. lim+ 𝑓(𝑥) = 𝑥→6 A) B) C) D) -7 No existe -8 0 Tomando la recta morada desde la derecha, su límite será -7. 10. lim− 𝑓(𝑥) = 𝑥→6 A) -7 B) No existe C) -8 D) 0 En este caso viniendo desde la izquierda, el caso sigue siendo el mismo, su imagen es en -7. 11. lim (𝑥) = 𝑥→6 A) B) C) D) -7 No existe -8 0 Necesitamos encontrar el valor de f (x) cuando x = 6. Podemos observar que para cuando x=6+ el valor de y= -7 12. (6) = A) -7 B) No existe C) -8 D) 0 Necesitamos encontrar el valor de f (x) cuando x = 6. Entonces, la línea, x = 6 es el eje y. A continuación, averiguamos dónde se encuentra la gráfica con el eje y (x = 0) y leemos el valor de y = f (6) = - 7. 13. Dominio de 𝑓(𝑥) = A) (-∞, ∞) B) (-∞, 2) U (2, ∞) C) (-∞, -3) U (-3, ∞) D) (-∞, -3) U (-3, 2) U (2, ∞) El dominio de la expresión es todos los números reales excepto aquellos donde la expresión esta indefinida, en este caso no hay números reales que hagan que la expresión este indefinida 14. Rango de 𝑓(𝑥) = A) (-∞, ∞) B) (-∞, -7) U (-7, ∞) C) (-∞, 8] D) (-∞, -7) U (-7, -5) U (5, ∞) Tal como se ve, no tiene fin hacia abajo, pero sí lo tiene en el punto 8. 15. (0) = A) -7 B) No existe C) -8 D) 0 La parábola verde toca -7 cuando esta cruza por 0, entonces su imagen será -7.