Estadistica

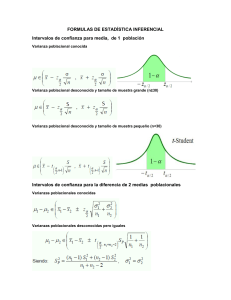
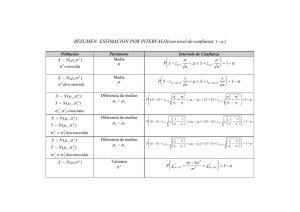
9.43 Una empresa de taxis trata de decidir si comprará neumáticos de la marca A o de la
marca B para su flotilla de taxis. Para estimar la diferencia entre las dos marcas realiza un
experimento utilizando 12 neumáticos de cada marca, los cuales utiliza hasta que se
desgastan.
Los resultados son:
Estimador
1 y2
S1 y 2
Marca A
36,300 km
5,000 km
Marca B
38,100 km
6,100 km
a) Calcule un intervalo de confianza del 95 % para suponiendo que las
poblaciones se distribuyen de forma aproximadamente normal.
b) Calcule un intervalo de confianza del 95 % para suponiendo que las
poblaciones se distribuyen de forma aproximadamente normal. Puede no suponer
que las varianzas son iguales.
Solución inciso a.
a) Calcule un intervalo de confianza del 95 % para suponiendo que las
poblaciones se distribuyen de forma aproximadamente normal.
Marca A
n1 =12
1 = 36,000
S1= 5,000
Marca B
n2 =12
2 = 38,100
S2= 6,100
Abstracción:
𝑃(𝐿𝑖 < 𝜇𝐴 − 𝜇𝐵 < 𝐿𝑠 ) = 95%
De las fórmulas empleamos:




Diferencia de medias
Con varianzas poblacionales desconocidas
Con muestra: n < 30
No se sabe sin 𝜎12 = 𝜎22 o bien 𝜎12 ≠ 𝜎22
Al desconocer si son iguales o no las varianzas poblacionales debemos sacar un intervalo de
confianza al 95 % para la razón de varianzas poblacionales:
𝑃 (𝐿𝑖 <
𝜎𝐴2
< 𝐿𝑠 ) = 95%
𝜎𝐵2
Aplicando fórmula Nº 10:
𝑃 ((
𝑆12
1
𝜎𝐴2
𝑆12
)
<
<
(
)𝑓∝ (𝑣1 , 𝑣2 )) = 95%
𝑆22 𝑓∝ (𝑣1 , 𝑣2 ) 𝜎𝐵2
𝑆22 2
2
Donde:
El nivel de confianza es al 95%
𝛾+𝛼 =1
Por lo tanto, despejando 𝛼 tenemos:
𝛼 =1−𝛾
𝛼 = 1 − 0.95 = 0.05
Para sustituir valores en la fórmula necesitamos 𝑓∝ y grados de libertad 𝑣1 , 𝑣2
2
Para 𝑓∝ tenemos lo siguiente:
2
𝑓∝ = 𝑓0.05 = 𝑓0.025
2
2
Para 𝑣1 , 𝑣2 tenemos lo siguiente:
𝑣1 = 𝑛1 − 1 , 𝑣2 = 𝑛2 − 1
Considerando que la muestra (n) es igual para ambas marcas n= 12, por tanto:
𝑣1 = 𝑣2 = 𝑛 − 1 = 12 − 1= 11 G.L
Buscando el valor en tablas con distribución Fisher y grados de libertad (11,11), tenemos:
𝑓0.025 = 3.474
Sustituyendo valores:
𝑃 ((
5,0002
1
𝜎𝐴2
5,0002
)
<
<
(
) 3.474) = 95%
6,1002 3.474 𝜎𝐵2
6,1002
𝑃 (0.193397 <
𝜎𝐴2
< 2.334050) = 95%
𝜎𝐵2
Al tener nuestro intervalo de confianza para la razón de varianzas poblaciones, como
siguiente paso es analizar cada escenario que se pueda presentar:
Si 𝜎𝐴2 = 𝜎𝐵2 ; entonces
Si 𝜎𝐴2 ≠ 𝜎𝐵2 ; entonces
2
𝜎𝐴
2
𝜎𝐵
𝜎𝐴
𝜎𝐵
=1
≠1
Si 𝜎𝐴2 < 𝜎𝐵2 ; entonces
Si 𝜎𝐴2 > 𝜎𝐵2 ; entonces
2
𝜎𝐴
2
𝜎𝐵
2
𝜎𝐴
2
𝜎𝐵
<1
>1
Partiendo de los datos generados en el intervalo de confianza para la razón de varianzas
poblaciones :
(0.193397,2.334050)
Concluimos que el valor numérico 1 cae dentro de este intervalo, por lo tanto, las varianzas
poblacionales son iguales.
Partiendo de esta conclusión, utilizaremos la fórmula Nº 6 con las siguientes características:



Diferencia de medias poblacionales
Varianzas poblacionales desconocidas e iguales
Muestra menor a 30: n < 30
1
1
1
1
𝑃 ((x̅1 − x̅2 ) − (𝑡∝ , 𝑣)(𝑠𝑝)√ +
< 𝜇𝐴 − 𝜇𝐵 < (x̅1 − x̅2 ) + (𝑡∝ , 𝑣)(𝑠𝑝)√ + )
𝑛1 𝑛2
𝑛1 𝑛2
2
2
= 95%
Fórmula compactada:
1
1
(x̅1 − x̅2 ) ± (𝑡∝ , 𝑣)(𝑠𝑝)√ +
𝑛1 𝑛2
2
Error:
1
1
𝑒 = (𝑡∝ , 𝑣)(𝑠𝑝)√ +
𝑛1 𝑛2
2
Para sustituir valores en la fórmula compactada necesitamos (𝑡∝ , 𝑣) y 𝑠𝑝; recordando que
∝
2
2
= 0.025 ; 𝑛1 = 𝑛2 = 12
Para los grados de libertad:
𝑣 = 𝑛1 + 𝑛2 − 2
𝑣 = 12 + 12 − 2 = 22 𝐺. 𝐿
Por tanto, buscando el valor en tablas con distribución student y grados de libertad 22
tenemos:
𝑡∝ = 𝑡0.025= 2.074
2
Para Sp, tenemos:
𝑠𝑝 = √
𝑠𝑝 = √
(𝑛1 − 1)𝑠12 + (𝑛2 − 1)𝑠22
𝑛1 + 𝑛2 − 2
(12 − 1)(5,000)2 + (12 − 1)(6,100)2
684,310,000
= √
= 5,577.185670
12 + 12 − 2
22
Sustituyendo valores:
1
1
(36,300 − 38,100) ± (2.074)(5,577.185670)√ +
12 12
(−1,800) ± 4,722.241893
𝑒 = 4,722.241893
Al tener estos valores sólo queda operar para encontrar el límite inferior y límite superior y
con ello estaríamos generando nuestro intervalo de confianza para diferencia de medias
poblacionales (
𝑃(−6,522.241893 < 𝜇𝐴 − 𝜇𝐵 < 2,922.241893) = 95%
Solución inciso b.
b) Calcule un intervalo de confianza del 95 % para suponiendo que las
poblaciones se distribuyen de forma aproximadamente normal. Puede no suponer
que las varianzas son iguales.
Abstracción:
𝑃(𝐿𝑖 < 𝜇𝐴 − 𝜇𝐵 < 𝐿𝑠 ) = 95%
De las fórmulas empleamos:




Diferencia de medias
Con varianzas poblacionales desconocidas
Se sabe que 𝜎12 ≠ 𝜎22
Con muestra: n < 30
Fórmula Nº 7
𝑆12 𝑆22
𝑆12 𝑆22
√
√
)
(
)
𝑃 ((x̅1 − x̅2 − (𝑡∝ , 𝑣)
+
< 𝜇𝐴 − 𝜇𝐵 < x̅1 − x̅2 + (𝑡∝ , 𝑣)
+ ) = 95%
𝑛1 𝑛2
𝑛1 𝑛2
2
2
Fórmula compactada:
𝑆2 𝑆2
(x̅1 − x̅2 ) ± (𝑡∝ , 𝑣)√ 1 + 2
𝑛1 𝑛2
2
Error:
𝑆12 𝑆22
𝑒 = (𝑡∝ , 𝑣)√ +
𝑛1 𝑛2
2
Para sustituir valores en la fórmula compactada necesitamos grados de libertad y 𝑡∝
2
𝑣=
𝑆2 𝑆2
(𝑛1 + 𝑛2 )2
1
2
2
2
𝑆12
𝑆2
1
1
(𝑛 ) (𝑛 − 1) + (𝑛2 ) (𝑛 − 1)
1
1
2
2
5,0002 6,1002
( 12 + 12 )2
𝑣=
2
2
5,0002
1
6,1002
1
( 12 ) (12 − 1) + ( 12 ) (12 − 1)
𝑣=
26,875,584,027,777.777
= 21.183948 ≅ 22
394,570,707,070.7071 + 874,106,123,737.3738
∝
Para 𝑡∝ , recordando que 2 = 0.025 y G.L= 21, buscamos el valor de tablas con distribución
2
student.
𝑡∝ = 𝑡0.025 =2.074
2
Sustituyendo valores:
5,0002
(36,300 − 38,100) ± 2.074 √
12
(−1,800) ± 4,722.241893
𝑒 = 4,722.241893
6,1002
+(
12
)
Al tener estos valores sólo queda operar para encontrar el límite inferior y límite superior y
con ello estaríamos generando nuestro intervalo de confianza para diferencia de medias
poblacionales (


𝑃(−6,522.24 < 𝜇𝐴 − 𝜇𝐵 < 2,922.241893) = 95%