RESUMEN: ESTIMACION POR INTERVALO(con nivel de confianza

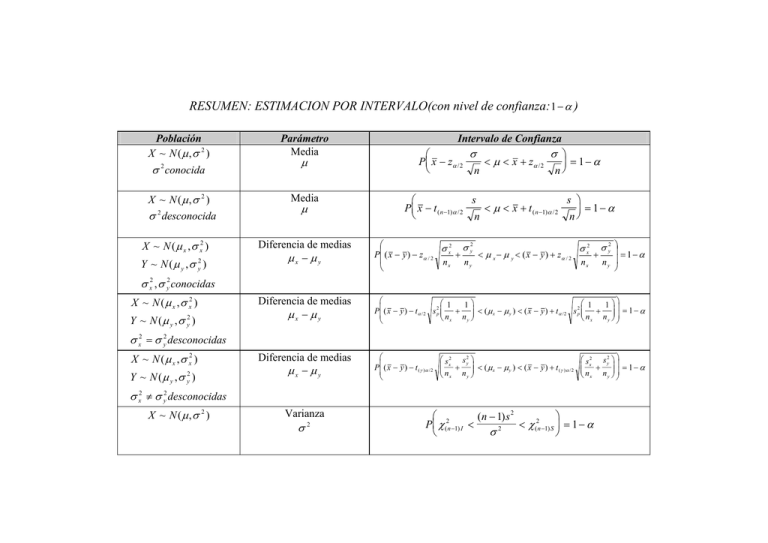
RESUMEN: ESTIMACION POR INTERVALO(con nivel de confianza: 1 − α )
Población
X ~ N (µ ,σ 2 )
σ conocida
2
X ~ N (µ ,σ 2 )
σ 2 desconocida
X ~ N ( µ x , σ x2 )
Y ~ N ( µ y , σ y2 )
Parámetro
Media
µ
Intervalo de Confianza
σ
σ ⎞
⎛
P ⎜ x − zα / 2
< µ < x + zα / 2
⎟ = 1− α
⎝
n
n⎠
Media
µ
s
s ⎞
⎛
P⎜ x − t ( n −1)α / 2
< µ < x + t ( n −1)α / 2
⎟ = 1− α
⎝
n
n⎠
Diferencia de medias
µx − µy
2
2
⎛
σ x2 σ y ⎞⎟
σ x2 σ y
+
< µ x − µ y < ( x − y ) + zα / 2
+
P ⎜ ( x − y ) − zα / 2
= 1−α
⎜
nx n y
nx n y ⎟
⎝
⎠
Diferencia de medias
µx − µy
⎛
⎛ 1
⎛ 1
1⎞
1 ⎞⎞
P⎜ ( x − y ) − t α / 2 s 2p ⎜⎜ + ⎟⎟ < ( µ x − µ y ) < ( x − y ) + t α / 2 s 2p ⎜⎜ + ⎟⎟ ⎟ = 1 − α
⎜
⎝ nx n y ⎠
⎝ n x n y ⎠ ⎟⎠
⎝
Diferencia de medias
µx − µy
⎛
P⎜ ( x − y ) − t ( γ )α / 2
⎜
⎝
σ x2 , σ y2 conocidas
X ~ N ( µ x , σ x2 )
Y ~ N ( µ y , σ y2 )
σ x2 = σ y2 desconocidas
X ~ N ( µ x , σ x2 )
Y ~ N ( µ y , σ y2 )
⎛ s x2 s y2 ⎞
⎜⎜ + ⎟⎟ < ( µx − µ y ) < ( x − y ) + t (γ )α / 2
⎝ nx n y ⎠
⎛ s x2 s y2 ⎞ ⎞⎟
⎜⎜ + ⎟⎟ = 1 − α
⎝ n x n y ⎠ ⎟⎠
σ x2 ≠ σ y2 desconocidas
X ~ N (µ ,σ 2 )
Varianza
σ
2
⎛ 2
⎞
(n − 1) s 2
2
P⎜ χ ( n −1) I <
<
χ
( n −1) S ⎟ = 1 − α
σ2
⎝
⎠
X ~ B(1, p )
X ~ B(1, p x )
Y ~ B 1, p y
(
)
⎛
P⎜⎜ pˆ − zα
⎝
Proporción
p
Diferencia de
proporciones
px − p y
⎛
P⎜ pˆ x − pˆ y − z( pˆ x − pˆ y )α
⎜
⎝
(
)
2
2
pq
< p < pˆ + zα
n
p x qx p y q y
+
nx
ny
(
pq ⎞
⎟ = 1−α
n ⎟⎠
2
)
< p x − p y < pˆ x − pˆ y + z pˆ x − pˆ yα
2
px q x p y q y ⎞⎟
=
+
nx
ny ⎟
⎠
= 1−α
Fuente: Llorente, F.; Marín, S.; Torra, S. (2001). “Inferencia estadística aplicada a la empresa”. Ed. Centro de Estudios Ramón Areces. Madrid.