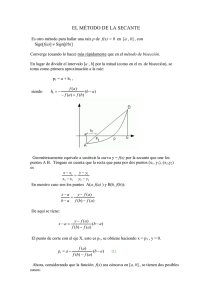
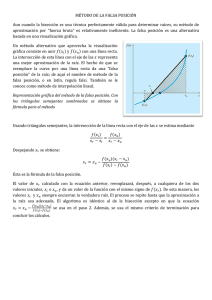
MÉTODOS DE BISECCIÓN, FALSA POSICIÓN Y NEWTON RAPSON INTEGRANTES: JUAN LUIS REYES MORALES JUAN PABLO GUTIERREZ AYALA STEVEN VELAZQUES BISECCION: • Este método , que se utiliza para resolver ecuaciones de una variable, está basado en el «Teorema de los Valores Intermedios» (TVM), en el cual se establece que toda función continua f, en un intervalo cerrado [a,b], toma todos los valores que se hallan entre f(a) y f(b), de tal forma que la ecuación f(x)=0 tiene una sola raíz que verifica f(a).f(b)<0. • si dicha función viaja del punto a al punto b, ha de pasar por m, que es cuando la función se hace cero. Ése es el punto que buscamos. FALSA POSICIÓN Es un método iterativo de resolución numérica de ecuaciones no lineales. El método combina el método de bisección y el método de la secante. El método de la falsa posición pretende conjugar la seguridad del método de la bisección con la rapidez del método de la secante. Este método, como en el método de la bisección, parte de dos puntos que rodean a la raíz f(x) = 0, es decir, dos puntos x0 y x1tales que f(x0)f(x1) < 0. La siguiente aproximación, x2, se calcula como la intersección con el eje X de la recta que une ambos puntos (empleando la ecuación del método de la secante). FALSA POSICIÓN La asignación del nuevo intervalo de búsqueda se realiza como en el método de la bisección: entre ambos intervalos, [x0,x2] y [x2,x1], se toma aquel que cumpla f(x)f(x2) < 0. FALSA POSICIÓN • Es claro que si en lugar de considerar el punto medio del intervalo, tomamos el punto donde cruza al eje esta recta, nos aproximaremos mucho más rápido a la raíz; ésta es en sí, la idea central del método de la regla falsa y ésta es realmente la única diferencia con el método de bisección, puesto que en todo lo demás los dos métodos son prácticamente idénticos. MÉTODO DE NEWTON-RAPHSON El método de Newton-Raphson es un algoritmo para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada. El método numérico de Newton fue descrito por Sir Isaac Newton. • la función f se muestra en azul y la línea de la tangente en rojo. Vemos que Xn+1 es una aproximación mejor que Xn para la raíz X de la función f NATURALMENTE ES NECESARIO QUE LA FUNCIÓN SEA DERIVABLE. SI LA RAÍZ ES MÚLTIPLE, EL MÉTODO ES INAPLICABLE, PUES LA DERIVADA SE ANULA. NÓTESE QUE EL MÉTODO DESCRITO ES DE APLICACIÓN EXCLUSIVA PARA FUNCIONES DE UNA SOLA VARIABLE CON FORMA ANALÍTICA O IMPLÍCITA CONOCIBLE. EXISTEN VARIANTES DEL MÉTODO APLICABLES A SISTEMAS DISCRETOS QUE PERMITEN ESTIMAR LAS RAÍCES DE LA TENDENCIA, ASÍ COMO ALGORITMOS QUE EXTIENDEN EL MÉTODO DE NEWTON A SISTEMAS MULTIVARIABLES, SISTEMAS DE ECUACIONES, ETCÉTERA. . Naturalmente es necesario que la función sea derivable. Si la raíz es múltiple, el método es inaplicable, pues la derivada se anula.