Derivada direccional y gradiente

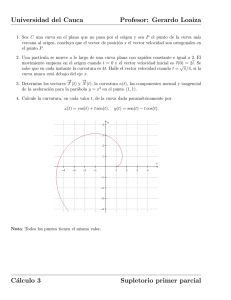
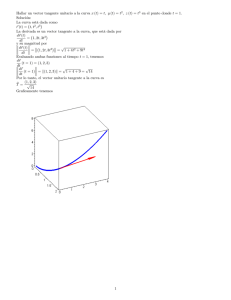
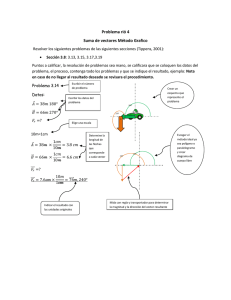
Derivada direccional y gradiente
Un estudio de la tasa instantánea de
variación de una función en una
dirección no paralela a los ejes x y y
Derivada parcial respecto a x
recta tangente a la curva en
P(a;b;f(a;b)); pendiente: fx(a;b)
f x (a; b)  lím
h 0
f (a  h; b)  f (a; b)
h
plano y = b
curva inters.
gráfica-plano
Puede pensarse como :
f x (a; b)  lím
h 0
f (( a; b)  h(1;0))  f (a; b)
h
f(x;y)
f x (a; b)  lím
h 0
a
f (( a; b)  hi )  f (a; b)
h
“Tasa de cambio en la
dirección del vector i”
i
Derivada parcial respecto a y
f y (a; b)  lím
h 0
recta tangente a la curva en
P(a;b;f(a;b)); pendiente: fx(a;b)
f (a; b  h)  f (a; b)
h
Puede pensarse como :
plano x = a
f y (a; b)  lím
h 0
f (( a; b)  h(0;1))  f (a; b)
h
f(x;y)
curva inters.
gráfica-plano
b
j
f y (a; b)  lím
h 0
f (( a; b)  hj)  f (a; b)
h
“Tasa de cambio en la
dirección del vector j”
¿Podremos determinar la tasa de
cambio en una dirección oblicua?
recta tangente a la curva en
Q(a;b;f(a;b)); su pendiente es la
tasa instantánea de cambio en la
dirección del vector u
f(x;y)
plano perpend.
al xy y paralelo
al vector u
a
Llamamos a dicha tasa de cambio Du f (a; b)
y proponemos para calcularla :
f (a  hu1 ; b  hu2 )  f (a; b)
h 0
h
f (( a; b)  h(u1 ; u2 ))  f (a; b)
Du f (a; b)  lím
h 0
h
Du f (a; b)  lím
b
Du f (a; b)  lím
h 0
u = (u1;u2) es un
vector unitario
curva inters.
gráfica-plano
f (( a; b)  hu)  f (a; b)
h
“Derivada direccional de f en
(a;b) en la dirección del
vector u”
Teorema
Sea f(x;y) diferenciable en (a;b). Sea u = (u1;u2) un vector unitario. Entonces la
derivada direccional de f en la dirección de u en (a;b) viene dada por:
Duf(a;b) = fx(a;b)u1 + fy(a;b)u2
DEMOSTRACIÓN
Definamos la función g (h)  f (a  hu1 ; b  hu2 ).
Notemos que cuando h  0 será x  a  0u1  a y y  b  hu2  b; luego g (0)  f (a; b)
Calcularem os ahora g (0) de dos maneras :
(1) Por definición
(2) Por la regla de la cadena
(1) Por definición
g (0)  lím
h 0
g ( h )  g ( 0)
f (a  hu1 ; b  hu 2 )  f (a; b)
 lím
h 0
h
h


Definición de
derivada direccional
(2) Por la regla de la cadena
g (h)  f x ( x; y ) x(h)  f y ( x; y ) y(h)


x  a  hu1
y b  hu2
f x ( x; y )u1  f y ( x; y )u2
En h  0 es x  a y y  b y
g (0)  f x (a; b)u1  f y (a; b)u 2
Igualando las expresione s para g (0) de (1) y (2) concluimos :
Du f (a; b)  f x (a; b)u1  f y (a; b)u2
Du f (a; b)
Observación
Podemos expresar el resultado que hemos obtenido para la derivada direccional:
Duf(a;b) = fx(a;b)u1 + fy(a;b)u2
como un producto escalar. En efecto:
Duf(a;b) = fx(a;b)u1 + fy(a;b)u2 = <fx(a;b); fy(a;b)>·(u1; u2)
Vector gradiente
DEFINICIÓN
Llamamos vector gradiente de f ( x; y ), y simbolizam os f ( x; y ), al vector integrado
por las derivadas parciales de la función.
f ( x; y )  f x ( x; y ); f y ( x; y )
De esa manera la expresión deducida para la derivada direcciona l queda :
Du f (a; b)  f x (a; b); f y (a; b) ·u1 ; u2   f (a; b)·u
Direcciones de máximo y mínimo
crecimiento
Hemos conseguido expresar la derivada direccional como un producto escalar:
Du f (a; b)  f x (a; b); f y (a; b) ·u1 ; u2   f (a; b)·u
Es fácil ver que este producto escalar será máximo cuando el gradiente y el vector u
tengan la misma dirección y sentido; y que será mínimo cuando tengan la misma
dirección y sentido opuesto. En efecto:
Du f (a; b)  f (a; b)·u  f (a; b) u cosf (a; b), u   f (a; b) cosf (a; b), u 

1
El máximo valor de ese coseno será 1 cuando el ángulo sea 0º (gradiente y vector u
con igual dirección y sentido), y el mínimo -1 cuando el ángulo sea 180º (gradiente
y vector u con igual dirección y sentido opuesto). De esa manera:
Du f (a; b)máx  f (a; b) en la dirección del gradiente
Du f (a; b)mín   f (a; b) en la dirección opuesta a la del gradiente
Propiedades del vector gradiente
f ( x; y ) diferencia ble
curva de nivel f ( x; y )  k
f ( x; y )  k es una curva de nivel en el plano; como toda
r (t )
curva, tambén admite una representa ción paramétric a,
r (t )  x(t ); y (t ) . Podemos componer ambas funciones
para obtener f (r (t ))  f ( x(t ); y (t ))  k . Derivando ahora
f
por regla de la cadena :
d
f ( x(t ); y (t ))  f x x(t )  f y y(t )  f ·r(t )  0 
dt
 f  r(t )
El gradiente es perpendicu lar al vector r(t ); y como este último es tangente a la curva, se
sigue que el gradiente f es normal a la curva f ( x; y )  k en cualquier punto.
Similarmente…
superficie de nivel f ( x; y; z )  k
f ( x; y; z ) diferencia ble
f
f ( x; y; z )  k es una superficie de nivel en el espacio; y por un
razonamien to similar al anterior, se tendrá que f es un vector
normal a esa superficie en cualquier punto.
Trayectorias de máximo incremento
curvas de nivel f ( x; y )  k
Trayectoria
aproximada de
máximo incremento
partiendo de P
Esta trayectoria no es
una de máximo
incremento
Como el gradiente es normal a
las curvas de nivel de una
función, y la dirección del
gradiente es a su vez la de
máximo crecimiento de una
función, se sigue que si
queremos desplazarnos en el
plano de las variables de manera
que el incremento de la función
sea en todo momento máximo,
debemos seguir una trayectoria
que en cada punto es normal a
la curva de nivel que pasa por
ese punto.