5. Convergencia de integrales impropias. Las funciones Γ y Β de Euler.

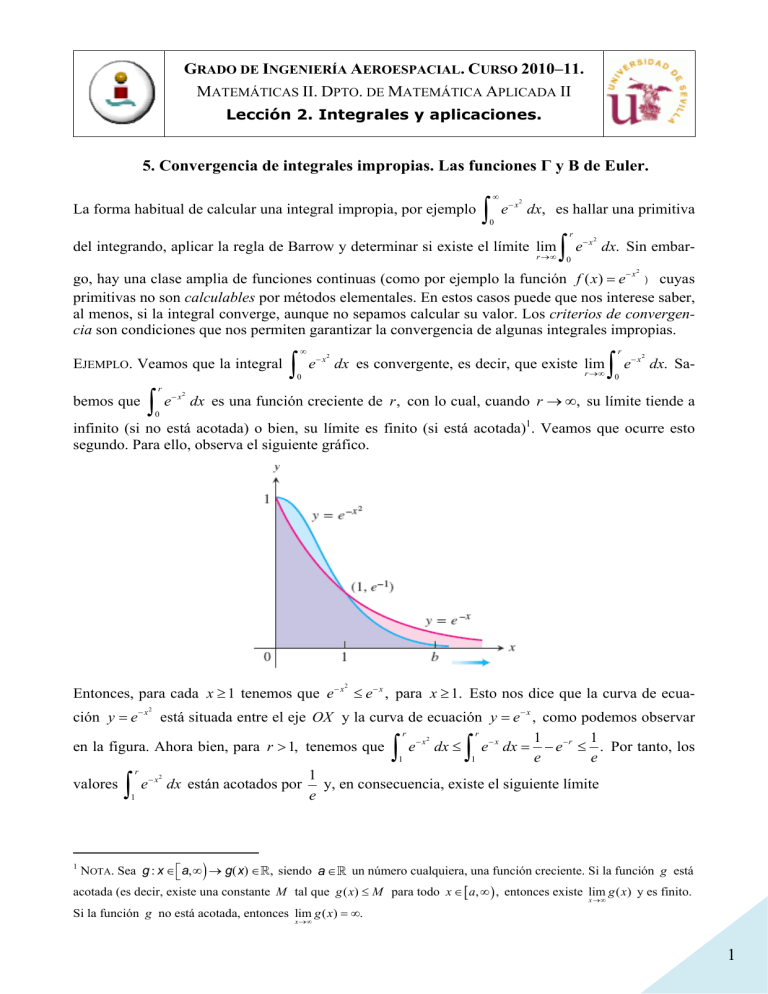
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
5. Convergencia de integrales impropias. Las funciones Γ y Β de Euler.
La forma habitual de calcular una integral impropia, por ejemplo
∫
∞
e − x dx, es hallar una primitiva
2
0
∫e
r
del integrando, aplicar la regla de Barrow y determinar si existe el límite lim
r →∞
− x2
dx. Sin embar-
0
go, hay una clase amplia de funciones continuas (como por ejemplo la función f ( x) = e − x ) cuyas
primitivas no son calculables por métodos elementales. En estos casos puede que nos interese saber,
al menos, si la integral converge, aunque no sepamos calcular su valor. Los criterios de convergencia son condiciones que nos permiten garantizar la convergencia de algunas integrales impropias.
2
EJEMPLO. Veamos que la integral
∫
∞
e − x dx es convergente, es decir, que existe lim
2
r →∞
0
∫e
r
bemos que
−x
2
∫
r
e − x dx. Sa2
0
dx es una función creciente de r , con lo cual, cuando r → ∞, su límite tiende a
0
infinito (si no está acotada) o bien, su límite es finito (si está acotada)1. Veamos que ocurre esto
segundo. Para ello, observa el siguiente gráfico.
Entonces, para cada x ≥ 1 tenemos que e − x ≤ e − x , para x ≥ 1. Esto nos dice que la curva de ecua2
ción y = e − x está situada entre el eje OX y la curva de ecuación y = e − x , como podemos observar
r
r
2
1
1
en la figura. Ahora bien, para r > 1, tenemos que
e − x dx ≤ e − x dx = − e − r ≤ . Por tanto, los
e
e
1
1
r
2
1
valores e − x dx están acotados por y, en consecuencia, existe el siguiente límite
e
1
2
∫
∫
∫
1
)
NOTA. Sea g : x ∈ ⎡⎣ a,∞ → g(x) ∈ , siendo a ∈
un número cualquiera, una función creciente. Si la función g está
acotada (es decir, existe una constante M tal que g ( x) ≤ M para todo x ∈ [ a, ∞ ) , entonces existe lim g ( x ) y es finito.
x →∞
Si la función g no está acotada, entonces lim g ( x ) = ∞.
x →∞
1
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
lim
r →∞
y la integral
∫
∞
∫
2
1
⎛1
⎞
e− x dx ≤ lim ⎜ − e − r ⎟ + 1 = + 1
r →∞ e
e
⎝
⎠
r
0
e − x dx es convergente.
2
0
La técnica empleada en este ejemplo sugiere el siguiente criterio.
PROPOSICIÓN (CRITERIO DE COMPARACIÓN). Sean f , g :[a,b) →
dos funciones continuas y positi-
∫
vas tales que f ( x) ≤ g ( x) para todo x ∈ [ a, b). Entonces, para las integrales impropias
b
f ( x) dx e
a
∫
b
g ( x) dx, se verifica que:
a
∫
(2) Si la integral
∫
∫
b
(1) Si la integral
g ( x) dx converge, entonces la integral
a
b
f ( x) dx también converge.
a
∫
b
f ( x) dx diverge, entonces la integral
a
b
g ( x) dx también diverge.
a
Es más, si la función f no es positiva, pero f ( x) ≤ g ( x) para todo x ∈ [a, b). Entonces, la integral
∫
b
f ( x) dx converge si la integral
a
LA
∫
b
g ( x) dx converge.
a
FUNCIÓN
Γ
EULER. Sea n un número natural. Entonces la integral impropia
DE
∫
∞
e − x x n −1 dx
0
converge y
∫
∞
e − x x n −1 dx = (n − 1)!. En lo que sigue, denotaremos por Γ(n) :=
0
∫
∞
e − x x n −1 dx. En
0
efecto, para n = 1 obtenemos que Γ(1) =
∫
∞
e − x dx = 1, como hemos visto en los ejemplos de la sec-
0
ción anterior. En general, tenemos que
Γ ( n) =
∫
∞
e− x x n −1 dx = lim
r →∞
0
r
⎛ − x xn ⎤
= lim ⎜ e
− lim
r →∞
n ⎥⎦ 0 r →∞
⎝
∫
r
∫
r
0
0
⎡u = e− x , du = −e− x dx ⎤
n ⎥
e− x x n −1 dx = ⎢
⎢ dv = x n −1dx, v = x ⎥
n ⎦⎥
⎣⎢
−e
−x
⎛ rn
xn
1
dx = lim ⎜ r +
n
n r →∞ ⎝ e
∫e
r
0
−x
⎞ 1
x n dx ⎟ = Γ(n + 1).
⎠ n
Entonces Γ(n + 1) = n Γ(n) para todo n = 1, 2,... Puesto que Γ(1) = 1 obtenemos que Γ(n) = (n − 1)!
para todo n = 1, 2,... De esta forma, tenemos definida la función Γ para números naturales. Usando
el criterio de comparación se puede extender la definición de la función Γ a números reales. Dado
un número real p consideramos la integral
∫
∞
e − x x p −1dx. Se trata de una integral impropia de pri-
0
2
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
mera y de segunda especie. Para estudiar su convergencia (debido a que el integrando puede que no
esté acotado en x = 0 ) dividimos esta integral en dos
∫
∞
∫
e− x x p−1 dx =
0
1
∫
e− x x p−1 dx +
0
∞
e− x x p−1 dx .
1
I1
I2
Comenzamos estudiando la integral I 2 . Supongamos que p − 1 ≥ 0 y consideremos un natural n tal
∫
que p − 1 ≤ n − 1. Entonces 0 ≤ e − x x p −1 ≤ e − x x n −1 para todo x ≥ 1. Como la integral
∞
e − x x n −1dx es
1
convergente, el criterio de comparación nos dice que la integral
∫
∞
e − x x p −1dx también es conver-
1
∫
gente. Si p − 1 < 0, entonces 0 ≤ e − x x p −1 ≤ e − x para todo x ≥ 1. Como la integral
∞
e − x dx es con-
1
vergente, el criterio de comparación nos dice que la integral
∫
∞
e − x x p −1dx también es convergente.
1
En definitiva, la integral I 2 converge para cualquier valor de p.
Ahora estudiamos la convergencia de la integral I1. Si 0 ≤ x ≤ 1, como la función exponencial e− x
1
1
1
dx
es decreciente, entonces ≤ e − x ≤ 1 y x p −1 ≤ e − x x p −1 ≤ x p −1. Como la integral
converge si
1− p
e
e
0 x
∫
1 − p < 1, es decir, si p > 0, el criterio de comparación asegura que la integral e x dx conver∫
dx
ge si p > 0. Por otra parte, como la integral
∫ x diverge si 1 − p ≥ 1, es decir si p ≤ 0, el criterio
de comparación asegura también que la integral e x dx diverge si p ≤ 0. En definitiva, la in∫
1
−x
p −1
0
1
0
1− p
1
−x
p −1
0
tegral I1 converge si, y sólo, si p > 0.
∞
∫e
p > 0 la función Γ( p ) := e
∫
En resumen, la integral
−x
x p −1dx converge si, y sólo, si p > 0. Esto nos permite definir, para
0
∞
−x
x p −1 dx que se llama función gamma de Euler.
0
EJEMPLO. Vamos a usar el criterio de comparación para establecer que la integral
∫
∞
0
x
dx es di1 + x2
x
para x ≥ 0 (o bien
vergente. Debemos encontrar una función f ( x) ≥ 0 de forma que f ( x) ≤
1 + x2
para x suficientemente grande, digamos x ≥ a ) y de manera que
∫
∞
f ( x)dx sea divergente. Para
a
encontrar esta función observemos que cuando x → ∞ la función
x
viene a ser parecida a la
1 + x2
3
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
x
x
2
2
1
1
función , en el sentido de que lim 1 + x = 1. Entonces, debe ocurrir que 1 + x ≥ , o equivalenx →∞
1
1
2
x
x
x
x
1
x
1
≥
para
≥
≥ 0, para x suficientemente grande. De hecho se verifica que
temente,
2
2
1+ x
2x
1+ x
2x
∞
∞
1
x
x ≥ 1. Como la integral
dx es divergente, entonces la integral
dx también es diver2
1 1+ x
1 2x
∞
x
gente. En consecuencia, la integral
dx es divergente. La técnica empleada en este ejemplo
2
0 1+ x
sugiere el siguiente criterio.
∫
∫
∫
PROPOSICIÓN (CRITERIO DE COMPARACIÓN POR PASO AL LÍMITE). Sean f , g :[a,b) ⊆ → dos funf ( x)
ciones continuas y positivas tales que existe L = lim−
. Entonces, para las integrales impropias
x →b g ( x )
∫
b
f ( x) dx e
a
∫
b
g ( x) dx, se verifica que:
a
(1) Si 0 < L < ∞, las dos integrales
∫
b
g ( x) dx y
a
integral
∫
∫
b
f ( x) dx tienen el mismo carácter, es decir, la
a
b
f ( x) dx converge si, y sólo, si la integral
a
∫
b
g ( x) dx converge.
a
∫
(3) Si L = ∞ y la integral
∫
(2) Si L = 0 y la integral
b
∫ f ( x) dx también converge.
g ( x) dx diverge, entonces la integral
∫ f ( x) dx también diverge.
b
g ( x) dx converge, entonces la integral
a
b
a
a
b
a
LA FUNCIÓN B DE EULER. Una compañera inseparable de la función gamma es la función beta de
Euler, definida para p > 0 y q > 0 por la igualdad B ( p, q ) :=
∫x
1
p −1
(1 − x) q −1 dx. Observemos que el
0
integrando no está acotado en los puntos x = 0 y x = 1. Vamos a comprobar, usando el criterio de
∫x
1
comparación por paso al límite, que la integral
p −1
(1 − x) q −1 dx es convergente si, y sólo si, p > 0
0
y q > 0. Para esto vamos a descomponer la integral en dos, de la siguiente forma
∫
1
0
p−1
x (1− x)
q−1
dx =
∫
1
2
x p−1 (1− x)q−1 dx +
0
I1
∫x
1
1
2
p−1
(1− x)q−1 dx .
I2
La integral I1 es impropia porque el integrando no está acotado en x = 0 y la integral I 2 es impropia porque el integrando no está acotado en x = 1. Comenzamos estudiando la convergencia de la
x p −1 (1 − x) q −1
integral I1. Observemos que lim
= 1. El criterio anterior nos dice que I1 tiene el misx →0
x p −1
4
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
mo carácter que
∫
1
2
x
p −1
dx =
∫
1
2
1
dx y ya sabemos que esta última integral converge si, y sólo,
x
si − p + 1 < 1, es decir, p > 0. Para estudiar la convergencia de la integral I 2 observemos que
0
0
− p +1
x p −1 (1 − x) q −1
= 1. El criterio de comparación por paso al límite nos dice que I 2 tiene el mismo
x →1
(1 − x) q −1
1
1
1
dx y ya sabemos que esta última incarácter que la siguiente integral 1 (1 − x) q −1 dx = 1
− q +1
−
x
(1
)
2
2
lim
∫
∫
tegral converge si, y sólo, si − q + 1 < 1, es decir, q > 0. En definitiva, tenemos que
B ( p, q ) =
∫x
1
p −1
(1 − x) q −1 dx
0
es convergente si, y sólo si, p > 0 y q > 0.
La funciones Γ( p ) =
∫
∞
e − x x p −1 dx y B ( p, q ) =
∫x
1
p −1
(1 − x) q −1 dx se llaman integrales eulerianas y
0
0
aparecen en varias áreas de la matemática aplicada. Existen muchas propiedades interesantes que
verifican las funciones eulerianas, así como relaciones entre ellas. Quizá la más relevante sea que
Γ( p ) ⋅ Γ(q )
para todos p > 0 y q > 0. A veces esta igualdad permite calcular integrales
B ( p, q ) =
Γ( p + q )
trigonométricas. Por ejemplo, si hacemos el cambio x = sen 2θ en la integral
∫x
1
p −1
(1 − x) q −1 dx ob-
0
tenemos
⎡ x = sen 2θ , dx = 2sen θ cosθ ⎤
⎥
x p−1 (1− x)q−1 dx = ⎢
π ⎥=
⎢
0
x = 0,θ = 0; x = 1,θ =
⎢⎣
2 ⎥⎦
∫
1
=2
∫
∫
π
2
sen 2 p−2θ cos 2q−2 θ 2sen θ cosθ dθ
0
π
2
sen 2 p−1θ cos 2q−1 θ dθ .
0
π
1
Γ( p) ⋅ Γ(q)
B( p,q) =
. Puesto que la función gamma está tabu2
2 ⋅ Γ( p + q)
0
lada, muchas de estas integrales se pueden calcular o aproximar de esta manera. Observa que la
∫
Entonces
integral
∫
2
sen 2 p−1θ cos 2q−1 θ dθ =
π
4
sen 2 p −1θ cos 2 q −1 θ dθ puede ser una integral impropia de segunda especie, puesto que la
0
función seno se anula en θ = 0 y la función coseno se anula en θ =
π
2
.
EJEMPLO. En la sección anterior calculamos el valor de esta integral impropia
∫
∞
dx
. Ahora
x (1 + x)
vamos a establecer la convergencia de dicha integral sin calcularla. Usaremos el criterio de comparación por paso al límite. Sabemos que esta integral es impropia porque el intervalo de integración
0
1
3
5
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
es infinito y también porque el integrando f ( x) =
1
(que es positivo en el intervalo de intex (1 + x)
gración) no está acotado en x = 0. Separamos la integral en dos, por ejemplo, ponemos
∫
∞
0
dx
1
3
=
x (1+ x)
∫
1
0
1
3
dx
+
1
3
x (1+ x)
∫
∞
1
dx
.
1
3
x (1+ x)
I1
I2
1
1
3
La integral I1 es de segunda especie. Además se verifica que lim
x →0
1
x (1 + x)
= lim
= 1. El critex →0 (1 + x )
1
1
x3
rio de comparación por paso al límite nos dice que I1 tiene el mismo carácter que
∫
1
dx
0
x3
1
. Como
1
< 1, esta integral es convergente, luego I1 también lo es. La integral I 2 es de primera especie.
3
1
4
1
3
x3
x (1 + x)
= lim 1
= 1. El criterio de comparación por paso al
Además se verifica que lim
x →∞
x →∞ 3
1
x (1 + x)
4
x3
límite nos dice que I 2 tiene el mismo carácter que
∫
∞
1
te, luego I 2 también lo es. Entonces la integral
∫
∞
0
1
dx
x
dx
4
3
. Como
x 3 (1 + x)
4
> 1, esta integral es convergen3
es convergente.
EJEMPLO. Vamos a usar ahora el criterio de comparación por paso al límite para establecer que la
∞
x
integral
dx es divergente. Observemos que esta integral es de primera especie. Además, el
2
0 1+ x
x
1
se comporta como
cuando x → ∞. Esto significa exactamente que
integrando
2
1+ x
x
∫
x
2
x2
= 1.
lim 1 + x = lim
x →∞
x →∞ 1 + x 2
1
x
El criterio de comparación por paso al límite nos dice, por ejemplo, que las integrales
∫
∞
1
∫
∫
∞
dx
tienen el mismo carácter. Como
x
1
∞
x
dx también es divergente.
2
0 1+ x
∫
∞
1
dx
es divergente, entonces
x
∫
∞
1
x
dx e
1 + x2
x
dx diverge, luego
1 + x2
6
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
EJEMPLO. En este último ejemplo analizaremos la convergencia de la integral
∫
∞
2
dx
, siendo
log p x
1
x
log x
p > 0. Comenzaremos con el caso p = 1. Observemos que lim
= lim
= ∞. El criterio de
x →∞
x →∞ log x
1
x
∞
∞
dx
dx
comparación por paso al límite nos dice que, puesto que
es divergente, entonces
x
1 log x
1
también es divergente. En el caso general ocurre algo similar puesto que sabemos que
∫
∫
1
x
log p x
= lim
=∞
lim
→∞
x →∞
x
1
log p x
x
para todo p > 0. La conclusión de que
∫
∞
1
dx
es divergente se hace igual que en el caso p = 1.
log p x
EJERCICIO 1. Determina si las siguientes integrales impropias convergen y, en su caso, calcula su
valor.
1
∞
∞
∞
log x
1
log x
.
(1)
dx
.
(3)
dx
(4)
dx.
( a sen x + b cos x ) e− x dx. (2)
2
x3
0 1+ x
1
0
0
x
∫
∫
∫
∫
x
, con x ∈ [0, ∞). Dibuja la
x + 3x + 2
gráfica de la curva de ecuación y = f ( x) y calcula el volumen generado al girar dicha curva alrededor del eje OX .
EJERCICIO 2. Consideremos la función definida por f ( x) =
2
EJERCICIO 3. Estudia la convergencia de las siguientes integrales impropias y, en su caso, calcula
su valor:
4
+∞
0
3
1
1
ex
1
(1)
dx.
dx
,
dx
dx
,
(2)
(3)
,
(4)
2x
1/ 3
0
−∞ 1 − x
−∞ 1 + e
2 (4 − x ) x
x (1 + x)
∫
∫
∫
∫
EJERCICIO 4. Usando el criterio de comparación por paso al límite, comprueba que la integral im-
propia
∫
∞
e − x log x dx es convergente.
0
EJERCICIO 5. Comprueba que la integral impropia
∫
π
0
4
dx
es convergente y expresa su valor
cos(2 x)
en función de la función Γ de Euler.
7
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 2010–11.
MATEMÁTICAS II. DPTO. DE MATEMÁTICA APLICADA II
Lección 2. Integrales y aplicaciones.
EJERCICIO 6. Establece la convergencia de la integral impropia
∫
∞
1
x log x
(x
2
+ 1)
2
dx, sin calcularla y,
posteriormente, calcula el valor de dicha integral.
EJERCICIO 7. Comprueba que la integral impropia
∫
∞
1
convergente la integral impropia
∫
∞
0
dx
es convergente y calcula su valor. ¿Es
senh x
dx
?
senh x
( )
EJERCICIO 8. Considera la función f : x ∈ 0,1 ⊆
→ f (x) =
1
∈ .
1
xlog
x
(1) Dibuja (de forma esquemática) la gráfica de la función y = f ( x).
(2) Calcula los siguientes límites lim−
1− x
y lim x f ( x).
x log x x→0+
(3) Justifica que la integral impropia
∫
x →1
1
f ( x)dx es convergente.
0
∫
∞
sen x
dx para estux
0
diar su convergencia? Razona la respuesta. A continuación, integra por partes para obtener la igualr
r
sen x
cos r
cos x
dad
−
dx = cos1 −
dx para todo r ≥ 1. A partir de aquí, determina si la integral
x
r
x2
1
1
∞
sen x
impropia
dx es convergente o divergente. Razona la respuesta.
x
0
EJERCICIO 9. ¿Es posible aplicar algún criterio de convergencia a la integral
∫
∫
∫
8