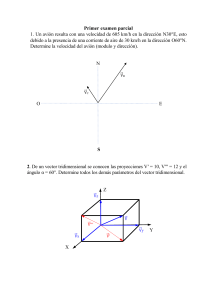
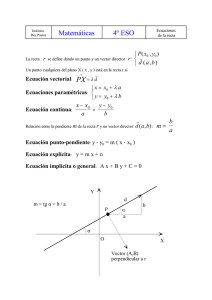
una-introduccion-al-computo-neuronal-artificial-ricardo-perez-aguila compress

Una Introducción
al Cómputo
Neuronal Artificial
Ricardo Pérez Aguila
Profesor Investigador Titular
Universidad Tecnológica de la Mixteca (UTM)
Dedicatorias
Con todo amor
a mi hija Diana,
mi esposa Kenia
y mi(s) hij@(s) que aún está(n)
por llegar a este mundo.
Con todo cariño
a mi sobrina Lucy,
mi mamá María de la Luz,
mi hermana Edna
y mi cuñada Fernanda
A quien me introdujo en el
mundo de las Redes Neuronales:
Dra. María del Pilar Gómez Gil
A mis amigos
Thelma García,
Gabriel Gerónimo,
Luis Javier Martínez,
Omar Ramírez,
Ricardo Ruiz,
Aisa Santiago
y Paola Soto
Una introducción al cómputo neuronal artificial.
24
!"#978-1-4135-2424-6
$%&'(Septiembre)
!"#* +&' +(978-1-4135-2424-6
!"#* +&',(978-1-4135-2434-5
Una Introducción al Cómputo Neuronal Artificial
Acerca del Autor
Ricardo Pérez Aguila es originario de la ciudad de Tehuacán, Puebla, México.
Es egresado de la Universidad de las Américas Puebla (UDLAP, Cholula, Puebla, México)
donde obtuvo los Títulos de Ingeniero en Sistemas Computacionales (2001),
Maestro en Ciencias con Especialidad en Ingeniería en Sistemas Computacionales (2003)
y Doctor en Ciencias de la Computación (2006). Durante el periodo 2003-2007 se
desempeñó como Profesor de Tiempo Parcial en el Departamento de Actuaría, Física y
Matemáticas de la UDLAP. En Otoño de 2007 se incorporó de Tiempo Completo como
Profesor-Investigador Titular del Instituto de Computación en la Universidad Tecnológica
de la Mixteca (UTM, Huajuapan de León, Oaxaca, México). Desde el año 2009 ostenta el
nombramiento de Candidato a Investigador Nacional por parte del Sistema Nacional de
Investigadores (Conacyt-SNI, México). En 2011 se le otorgó el Reconocimiento a
Perfil Deseable y Apoyo por parte del Programa de Mejoramiento del Profesorado
(PROMEP, México). Como docente ha impartido en varias ocasiones los cursos de
Matemáticas Discretas, Análisis de Algoritmos, Redes Neuronales Artificiales, Teoría de
Autómatas, Algoritmos Genéticos, Visión por Computadora, entre otros. Sus intereses de
investigación consideran la visualización, geometría, topología, representación y
aplicaciones de los Politopos n-Dimensionales. En el campo de las Redes Neuronales
Artificiales ha tenido particular interés en las arquitecturas basadas en entrenamiento no
supervisado. Cuenta en su haber con más de 30 artículos publicados, internacionalmente y
con arbitraje, en congresos y revistas.
Ricardo Pérez Aguila
Instituto de Computación
Universidad Tecnológica de la Mixteca (UTM)
Carretera Huajuapan-Acatlima Km. 2.5
Huajuapan de León, Oaxaca 69000, México
E-mails: [email protected], [email protected]
Web site: http://ricardo.perez.aguila.googlepages.com
iii
Una Introducción al Cómputo Neuronal Artificial
iv
Una Introducción al Cómputo Neuronal Artificial
También del Autor
El objetivo principal de este texto es el de proporcionar las bases formales y
fundamentales para que el alumno sea capaz de estudiar sus algoritmos y determinar si
éstos son, desde un punto de vista de la Complejidad Temporal, eficientes o no. Este trabajo
cuenta con cinco capítulos en donde se abordan tópicos como Preliminares Matemáticos
(Logaritmos, Series, Sucesiones, Inducción Matemática, Teorema del Binomio), Notación
Asintótica, Técnicas para el Análisis de Complejidad Temporal, Solución de Recurrencias
(Método de Extensiones, Teorema Maestro), Teoría de Grafos, enfoques de diseño de
algoritmos bajo Memoización, Bottom-Up y Voracidad. Finalmente, se presenta una
introducción informal a las Clases de Problemas P y NP, Problemas NP-Completos y
Reducción Polinomial. Las técnicas y conceptos son aplicados sobre los bien conocidos
algoritmos de ordenamiento Insertion Sort, Quick Sort, Merge Sort, Counting Sort y Bucket
Sort. También se estudia la Complejidad Temporal de algunos algoritmos que dan solución
a problemas clásicos de Teoría de Grafos: Búsquedas por Profundidad y Amplitud,
Algoritmos de Dijkstra, Bellman-Ford, Fleury y Kruskal. La forma de presentar los temas
está dirigida a estudiantes que estén cursando el segundo año de las Licenciaturas en
Computación, Sistemas Computacionales, Informática, Ciencias de la Computación y
Matemáticas Aplicadas.
Una Introducción a las Matemáticas para el Análisis y Diseño de Algoritmos
Ricardo Pérez Aguila
El Cid Editor, Argentina, 336 páginas, Primera Edición, 2012
ISBN Edición Impresa: 978-1-4135-7661-0, ISBN Edición Digital: 978-1-4135-7647-4
Registro SEP-INDAUTOR (México): 03-2011-111412410000-01
Web Site de Difusión y Distribución: http://www.e-libro.net/libros/libro.aspx?idlibro=6525
v
Una Introducción al Cómputo Neuronal Artificial
vi
Una Introducción al Cómputo Neuronal Artificial
Abstract
En este trabajo se presenta una introducción al estudio y análisis de las Redes
Neuronales Artificiales. Se hace mención de las bases neurofisiológicas que inspiran a
algunas de las Arquitecturas Neuronales más populares y se plantean de manera formal sus
procedimientos correspondientes haciendo uso de herramientas provenientes de áreas como
el Álgebra Lineal y el Cálculo Diferencial de Varias Variables. Se estudian inicialmente las
neuronas de tipo Adaline y Perceptrón. En el caso del Perceptrón se presentan el Problema
de Representación y el Teorema de Convergencia a fin de plantear los alcances y
limitaciones que se tiene con este tipo de Neurona Artificial. Posteriormente se aborda el
estudio de la Red Madaline a fin de establecer los retos que surgen para el aprendizaje en
una red formada por varias neuronas. Se da un especial énfasis a las redes compuestas por
Perceptrones al estudiar los fundamentos de su popular mecanismo de aprendizaje, definido
por el Algoritmo de Retropropagación. También se presentarán a las Redes de Kohonen
como un ejemplo de Arquitectura Neuronal cuyo aprendizaje no requiere de supervisión. A
lo largo del texto se desarrollan aplicaciones de las Redes Neuronales en los contextos del
Modelado y Predicción de Señales, Modelado de Funciones Booleanas y Clasificación
Automática de Imágenes.
vii
Una Introducción al Cómputo Neuronal Artificial
viii
Una Introducción al Cómputo Neuronal Artificial
Prólogo
"I propose we build a robot child, who can love.
A robot child who will genuinely love the parent or
parents it imprints on, with a love that will never end ...
But a mecha with a mind, with neuronal feedback.
You see what I'm suggesting is that live will be the key
by which they acquire a kind of subconscious never
before achieved. And inner world of metaphor,
of intuition, of self motivated reasoning. Of dreams."
Profesor Hobby en
A.I. Artificial Intelligence,
Dirigida por Steven Spielberg,
Warner Bros. Pictures, 2001
Tuve la oportunidad de conocer el área de las Redes Neuronales Artificiales gracias
a que formé parte, primero como alumno de Licenciatura y posteriormente como alumno de
Posgrado, de dos interesantes cursos impartidos por la Dra. María del Pilar Gómez Gil. Fue
en esas ocasiones en las que tuve acceso por primera vez a ese paradigma cuyo fundamento
radica en tomar el poder del procesamiento cerebral y tratar de llevarlo a la implementación
mediante nuestras computadoras actuales. Al incorporarme como Profesor Titular de la
Universidad Tecnológica de la Mixteca (UTM) me fue asignada la impartición del curso de
Redes Neuronales Artificiales. Se me presentó entonces la oportunidad de expandir mis
conocimientos en el área, nuevamente con la ayuda de la Dra. Gómez Gil, y de ganar un
poco más de experiencia. Desde entonces he tenido la oportunidad de transmitir lo que sé al
respecto a alumnos tanto de nivel Licenciatura como de Posgrado. Hasta el día de hoy,
teniendo identificadas las limitaciones teóricas de nuestras computadoras, no me ha dejado
de ser sumamente interesante que mediante esas Redes Neuronales y sus sencillas
implementaciones se han logrado resultados que han dado importantes soluciones a
problemas tan variados como de Optimización, Predicción y Clasificación. Inclusive, se
han dado soluciones aproximadas, pero muy cercanas a las exactas, a problemas que yacen
en la frontera de las Ciencias de la Computación, como son los bien conocidos Problemas
NP-Completos. Hemos de mencionarlo también, las Redes Neuronales Artificiales tienen
sus limitaciones, pero éstas a su vez forman un gran panorama de Investigación y
Desarrollo que ha de ser enfrentado y cubierto en los próximos años.
ix
Una Introducción al Cómputo Neuronal Artificial
Muchas de mis experiencias como Docente y como Investigador en el área de Redes
Neuronales Artificiales las he englobado en este texto, el cual se divide en siete Capítulos y
cuyos contenidos enuncio brevemente:
• Capítulo 1: Introducción. En donde se estudian las bases neurofisiológicas de las que
toma su inspiración el Computo Neuronal. También se hace una breve visita a los
principios de los que parte el diseño y expectativas de las Redes Neuronales Artificiales
y sus mecanismos de aprendizaje. Finalmente, se mencionan las estructuras básicas de
Neuronas y Redes más utilizadas en la actualidad.
• Capítulo 2: Preliminares Matemáticos. Se hace un repaso de algunas herramientas
Matemáticas que serán requeridas para la formalización de los Algoritmos de
Aprendizaje a abordar en el texto. Se estudian los vectores gradientes desde el punto de
vista del Cálculo Diferencial y su relación con los Máximos y Mínimos en una función
de varias variables. También se aborda a la Regresión Lineal y en particular al Método
de Mínimos Cuadrados. Finalmente se discutirá a la Desigualdad de Cauchy-Schwarz.
• Capítulo 3: La Neurona Adaline. En donde se utiliza a tal neurona para introducir los
métodos de Aprendizaje neuronal basados primeramente en el método de Mínimos
Cuadrados, y posteriormente en el método de Descenso Escalonado. Los métodos serán
formalizados desde un punto de vista que los analiza como procesos de búsqueda de
gradientes.
• Capítulo 4: El Perceptrón. En donde se abordará el estudio de la que quizás es la
Neurona Artificial más popular. Se analizará su estructura y principios funcionales.
También nos introduciremos en el Problema de Representación que se encarga de
establecer de manera formal los alcances y limitaciones que presenta la neurona de tipo
Perceptrón desde el punto de vista de los problemas a los que puede dar solución. Se
hará mención de una aplicación orientada al Modelado de Señales.
• Capítulo 5: La Red Madaline. En este Capítulo se introduce a esta red, formada por
neuronas de tipo Adaline, como un primer ejemplo de una arquitectura de neuronas
interconectadas. También se establecen los retos y consideraciones referentes al
aprendizaje. En particular, se discuten los aspectos relacionados con la eficiencia de los
métodos de aprendizaje desde el punto de vista de la solución que se encuentre para un
problema dado, así como el tiempo requerido para llegar a ésta. Finalmente, se presenta
una aplicación dirigida al Modelado de Funciones Booleanas.
• Capítulo 6: Redes de Perceptrones. Se estudian las redes formadas por neuronas de
tipo Perceptrón. Se retomará el estudio de la neurona de tipo Perceptrón al abordar la
Regla de Aprendizaje de Rosenblatt. También se demostrará y discutirá el Teorema de
Convergencia de Perceptrón, el cual formaliza la mencionada regla. Esta regla
representa el punto de partida e inspiración para el popular Algoritmo de
Retropropagación. Se estudiarán también las bases formales detrás de la
Retropropagación tanto para redes formadas por una capa oculta así también para redes
formadas por varias capas ocultas. Ubicaremos formalmente al Algoritmo de
Retropropagación como un método de búsqueda de gradiente por medio de Descenso
Escalonado. Por último, se presentará una aplicación de las redes de Perceptrones en la
Predicción de Señales.
x
Una Introducción al Cómputo Neuronal Artificial
•
Capítulo 7: Redes de Kohonen. En este último Capítulo se abordará el modelo
propuesto por el finlandés Teuvo Kohonen. Estas redes son un ejemplo de arquitectura
basada en aprendizaje no supervisado, es decir, aprendizaje no sustentado en la
presencia de un “maestro” o “evaluador”. Veremos como es que las Redes de Kohonen
toman inspiración de la forma en la cual la corteza cerebral procesa y administra
información proveniente de los sentidos. Se discutirá una aplicación para la
Clasificación Automática de Imágenes.
Este texto está pensado principalmente para estudiantes de nivel Licenciatura en las
carreras de Ciencias de la Computación, Informática, Física, Matemáticas Aplicadas y
afines. Desde el punto de vista Matemático se asume que el alumno se encuentra habilitado
con las nociones básicas de Álgebra Lineal y Cálculo Diferencial de Varias Variables.
Como se apreciará a lo largo del texto, desde el punto de vista Computacional sólo se
requiere un buen manejo de algún lenguaje de programación de alto nivel. Nuestros
algoritmos serán especificados utilizando únicamente estructuras de datos estáticas
(arreglos y matrices).
Reconozco que el área de las Redes Neuronales Artificiales no es mi principal nicho
de Investigación. Pero mi objetivo es transmitir las nociones que forman a este campo tal y
cómo las veo y las entiendo. Pero además, como se verá a través de este trabajo, lo haremos
desde la perspectiva de la aplicación intensa del Cálculo Diferencial de Varias Variables.
Esta es un área de estudio de la cual los estudiantes, sobre todo de Ingeniería (incluido el
Autor), han renegado en su momento. Quiero hacerles ver a los alumnos como es que el
Cálculo Diferencial es una poderosa herramienta que permite establecer los fundamentos
detrás de los mecanismos de Aprendizaje para algunos modelos de Redes Neuronales.
Veremos que términos como Derivada Parcial, Regla de la Cadena, Vector Gradiente,
Máximos y Mínimos de una Función tendrán una gran relevancia en el estudio que
presentamos. Espero haber cumplido con mis objetivos.
Quiero agradecer, en primer lugar y como mi siempre, a mi hermosa hija Diana y a
mi esposa Kenia. Ustedes han sido, y serán, mi motor y mi inspiración. Gracias por todos
los ánimos, cariño y amor que me han dado para poder concluir este trabajo. También
quiero dar las gracias a la Dra. María del Pilar Gómez Gil por ser, como ya mencioné antes,
quien me introdujo a este maravilloso campo de estudio y con quien además he tenido el
gran de honor de colaborar en varios artículos científicos. También agradezco
profundamente a mis amigos por todo su apoyo. Cualquier comentario, sugerencia o
corrección serán siempre bienvenidos. Éstos se podrán hacer llegar a través del e-mail
[email protected]. Finalmente, solo me basta hacer saber que a final del
texto se cuenta con una Sección de Referencias. Todas han sido utilizadas en la elaboración
de este trabajo y además el lector interesado puede consultarlas para profundizar más aún
en el área de Redes Neuronales Artificiales. Una buena opción, desde mi punto de vista,
sería comenzar por lo excelentes textos de Graupe, Haykin, Hilera & Martínez, y Rojas.
Ricardo Pérez Aguila
Agosto de 2012
xi
Una Introducción al Cómputo Neuronal Artificial
xii
Una Introducción al Cómputo Neuronal Artificial
Índice General
Índice de Ecuaciones
Índice de Algoritmos
Índice de Figuras
Índice de Tablas
1. Introducción
1.1 Redes Neuronales Biológicas
1.2 Principios del Diseño de Redes Neuronales Artificiales
1.3 Principios del Aprendizaje o Entrenamiento de una
Red Neuronal Artificial
1.4 Estructuras Básicas de Neuronas y Redes
2. Preliminares Matemáticos
2.1 Gradientes y Búsquedas de Máximos y Mínimos
2.2 Regresión Lineal
2.3 Regresión Lineal con Múltiples Variables
2.4 La Desigualdad de Cauchy-Schwarz
3. La Neurona Adaline
3.1 Estructura
3.2 Ajuste de Pesos de la Neurona Adaline por Mínimos Cuadrados
3.3 Ajuste de Pesos de la Neurona Adaline por Descenso Escalonado
3.3.1 Descenso Escalonado: Caso una entrada – una salida
3.3.2 Descenso Escalonado: Caso varias entradas – una salida
4. El Perceptrón
4.1. Estructura Básica y Funciones de Activación
4.2 El Problema de Representación
4.3 Aplicación: Identificación de Parámetros Autorregresivos
en una Señal
5. La Red Madaline
5.1 Estructura Básica
5.2 Ajuste de Pesos en una Red Madaline
5.3 Modelado de Funciones Booleanas
Página
xv
xxix
xxxi
xxxix
1
8
13
15
17
21
23
30
38
44
47
49
52
57
58
69
83
85
90
103
121
123
125
133
xiii
Una Introducción al Cómputo Neuronal Artificial
6. Redes de Perceptrones
6.1 La Regla de Rosenblatt
6.2 Teorema de Convergencia del Perceptrón
6.2.1 Discusión
6.3 Retropropagación
6.3.1 Retropropagación en una Red de una Sola Capa Oculta
6.3.2 Justificación del Algoritmo de Retropropagación
6.4 Retropropagación en una Red con Múltiples Capas Ocultas
6.5 Aplicación: Predicción de Señales
7. Redes de Kohonen
7.1 Redes Neuronales Auto-Organizadas
7.2 La Corteza Cerebral
7.3 El Modelo de Kohonen
7.4 Aplicación: Clasificación Automática de Imágenes
7.4.1 Redistribución del Conjunto de Entrenamiento
7.4.2. Clasificación de Imágenes mediante una
Red de Kohonen 1D
Referencias
xiv
153
155
159
168
173
174
184
201
227
243
245
246
248
262
263
268
279
Una Introducción al Cómputo Neuronal Artificial
Índice de Ecuaciones
Página
Ecuación 2.1.1
Ecuación 2.1.2
Ecuación 2.1.3
Ecuación 2.2.1
Ecuación 2.2.2
Ecuación 2.2.3
Ecuación 2.2.4
Ecuación 2.2.5
Ecuación 2.2.6
Ecuación 2.2.7
Ecuación 2.2.8
Ecuación 2.2.9
Ecuación 2.2.10
Ecuación 2.2.11
Ecuación 2.2.12
ªδ f º
«δ x »
« 1»
«δ f »
∇f ( x1 ,..., xn ) = «« δ x2 »»
« # »
«
»
«δ f »
«¬ δ xn »¼
δf
δf
δf
Du f ( x1 ,..., xn ) =
u1 +
u2 + ... +
u
δ x1
δ x2
δ xn n
Duf(x1, …, xn) = ||∇f(x1, …, xn)|| cos θ
di = wx1,i + b + εi
di = x2,i + εi
εi = di – (wx1,i + b)
εi = di – di’
1 N 2
J=
¦εi
2 N i =1
N x
N
δJ
b N d
= w¦ 1,i + ¦ − ¦ i
δb
i =1 N
i =1 N
i =1 N
N x2
N x
N d x
δJ
= w¦ 1,i + b¦ 1,i − ¦ i 1,i
N
δw
i =1 N
i =1 N
i =1
N x
N
N
d
b
w¦ 1,i + ¦ − ¦ i = 0
i =1 N
i =1 N
i =1 N
2
N x
N x
N d x
w¦ 1,i + b¦ 1,i − ¦ i 1,i = 0
N
i =1 N
i =1 N
i =1
wx + b − d = 0
wx 2 + bx − xd = 0
xd − d ⋅ x
w=
2
x2 − x
()
23
26
28
30
30
31
31
32
33
33
34
34
34
34
35
xv
Una Introducción al Cómputo Neuronal Artificial
Ecuación 2.2.13
d ⋅ x 2 − xd ⋅ x
b=
()
x2 − x
2
35
Ecuación 2.3.1
di' = b + ¦ wk xi ,k
38
Ecuación 2.3.2
ε i = di − (b + w1 xi ,1 + w2 xi ,2 + ... + wP xi , P )
38
P
k =1
Ecuación 2.3.3
P
ε i = di − ¦ wk xi ,k
39
k =0
Ecuación 2.3.4
1
2N
J=
§
N
P
¦ ¨© d − ¦ w x
i
k i ,k
i =1
k =0
·
¸
¹
2
39
Ecuación 2.3.5
δJ
1
§
·
= − ¦ xi , j ¨ di − ¦ wk xi ,k ¸
δ wj
N i =1
k =0
©
¹
Ecuación 2.3.6
§
·
di = ¦ ¨ xi , j ¦ wk xi ,k ¸
i =1
i =1 ©
k =0
¹
N
P
P
N
§
·
¦
¨ xi , j ¦ wk xi , k ¸ = ¦ wk ¦ xi , j xi , k
i =1 ©
k =0
¹ k =0 i =1
N
N
P
N
¦x
i, j
Ecuación 2.3.7
Ecuación 2.3.8
N
¦x
i, j
i =1
Ecuación 2.3.9
Ecuación 2.3.10
Ecuación 2.3.11
Ecuación 2.3.12
Ecuación 2.3.13
xvi
1
N
P
k =0
¦x
i, j
i =1
di = ¦ wk
k =0
N
N
1
¦ xi, j di
N i =1
ª℘0 º
«℘ »
℘= « 1 »
« # »
« »
¬℘P ¼
℘j =
41
42
i =1
P
1
N
N
¦x
x
i , j i,k
i =1
1
¦ xi, j xi,k
N i =1
ª R0,0 R0,1 " R0, P º
«R
R1,1 " R1, P »»
1,0
«
R=
« #
# %
# »
«
»
¬ RP ,0 RP ,1 " RP , P ¼
Rk , j =
41
N
di = ¦ wk ¦ xi , j xi ,k
N
40
P
k = 0,1, 2,..., P
j = 0,1, 2,..., P
42
42
42
j = 0,1, 2,..., P
42
43
Una Introducción al Cómputo Neuronal Artificial
Ecuación 2.3.14
Ecuación 2.3.15
Ecuación 2.3.16
Ecuación 3.1.1
Ecuación 3.2.1
ª w0 º
«w »
W =« 1»
« # »
« »
¬ wP ¼
℘ = RW
R-1℘ = W
P
§
·
y = sign ¨ w0 + ¦ wi xi ¸
i =1
©
¹
43
43
43
49
P
zi = ¦ wk xi ,k
54
54
k =0
Ecuación 3.2.2
Ecuación 3.2.3
Ecuación 3.3.1
Ecuación 3.3.2
Ecuación 3.3.3
Ecuación 3.3.4
Ecuación 3.3.5
Ecuación 3.3.6
Ecuación 3.3.7
Ecuación 3.3.8
Ecuación 3.3.9
Ecuación 3.3.10
εi = di - zi
1 N 2
¦εi
2 N i =1
Wm+1 = Wm + Δwm
Δwm = μ(-∇J(W)m)
J(W)m = (dm – zm)2 = (dm – (wm,0xm,0 + wm,1xm,1))2
ª xm ,0 º
∇J (W ) m = −2(d m − ( wm,0 xm ,0 + wm,1 xm ,1 )) «
»
¬ xm ,1 ¼
J (W ) =
§
·
J (W ) m = (d m − Wm ⋅ X m ) 2 = ¨ d m − ¦ wm ,k xm ,k ¸
k =0
©
¹
ª δ J (W ) m º
« δw
»
m ,0
«
»
« δ J (W ) m »
«
»
∇J (W ) m = « δ wm ,1 »
«
»
#
«
»
« δ J (W ) m »
« δw
»
m,P ¼
¬
P
54
58
63
63
64
2
δ J (W ) m
= −2 xm , j (d m − Wm ⋅ X m )
δ wm , j
ª xm,0 º
«x »
m ,1 »
∇J (W ) m = −2(d m − Wm ⋅ X m ) «
« # »
«
»
¬ xm , P ¼
SDO(T, N, P) = TN(7P + 8)
LSO(N, P) =
(P + 1)2(2N + 1) + (P + 1)(2N + 1) + (P + 1)3 + (P + 1)2
70
71
71
72
75
77
xvii
Una Introducción al Cómputo Neuronal Artificial
Ecuación 3.3.11
« 2P2 + 6P + 4 »
T ( P) = «
»
¬ 7P + 8 ¼
Ecuación 4.1.1
z = ¦ wi xi
Ecuación 4.1.2
Ecuación 4.1.3
Ecuación 4.1.4
z =W ⋅ X
y = fN(z)
79
n
85
85
86
i =1
Ecuación 4.1.5
Ecuación 4.1.6
Ecuación 4.1.7
Ecuación 4.1.8
Ecuación 4.1.9
Ecuación 4.1.10
Ecuación 4.1.11
Ecuación 4.2.1
Ecuación 4.2.2
Ecuación 4.2.3
Ecuación 4.2.4
Ecuación 4.2.5
1
=y
1 + e− z
e− z
fN ' =
(1 + e − z ) 2
§z·
f N ( z ) = Tanh ¨ ¸ = y
©2¹
2
§z·
f N ( z ) = Tanh ¨ ¸ =
−1
−z
© 2 ¹ 1+ e
2e− z
fN ' =
2
(1 + e− z )
fN ( z ) =
f N ( z ) = Tanh ( z ) =
fN ' =
fN ' =
4e
1− e
=y
1 + e−2 z
2z
Ecuación 4.3.2
xviii
89
89
89
2z
(1 + e )
2z
2
z(x1, x2) = w1 x1 + w2 x2
w1x1 + w2x2 = v⋅x = ||v||⋅||x|| cos θ
z(x1, x2, x3) = w1x1 + w2x2 + w3x3
z(x1, x2,…, xn) = w1x1 + w2x2 + … + wnxn = 0
2⋅ 2 ⋅ ... ⋅ 2 = 2n
2⋅ 2 ⋅ ... ⋅ 2 = 2
­
ck
si n = k , k ∈ {1, 2,..., M }
°M
xn = ®
n>M
°¦ ak xn − k + noise(n) si
¯ k =1
M
x 'n = ¦ a 'k xn − k
εn = xn – x 'n
90
92
92
94
95
99
(2n )
N ≥n>M
k =1
Ecuación 4.3.3
88
2
2n
Ecuación 4.3.1
88
−2 z
n
Ecuación 4.2.6
87
2z
(1 + e )
2e
86
N≥n>M
99
103
105
106
Una Introducción al Cómputo Neuronal Artificial
Ecuación 4.3.4
1
MSE =
N −M
Ecuación 4.3.5
§
·
MSEn = ¨ xn − ¦ a 'n ,k xn − k ¸
k =1
©
¹
δ MSEn
= −2ε n xn − j
δ a 'n , j
Ecuación 4.3.6
M
§
·
¦
¨ xn − ¦ a 'k xn − k ¸
n = M +1 ©
k =1
¹
N
M
2
107
2
N ≥n>M
107
108
ª xn −1 º
«x »
∇MSEn = −2ε n « n − 2 »
« # »
«
»
¬ xn − M ¼
108
ª a 'n ,1 º
«
»
a 'n ,2 »
«
a 'n =
« # »
«
»
¬« a 'n , M ¼»
109
Ecuación 4.3.9
a 'n +1 = a 'n + Δa'n
109
Ecuación 4.3.10
ª xn −1 º
«x »
Δa'n = μ2εn « n − 2 »
« # »
«
»
¬ xn − M ¼
ck
si n = k , k ∈ {1, 2,..., M }
­
°M
x 'n = ®
N ≥n>M
°¦ a 'k xn − k si
¯ k =1
109
Ecuación 4.3.7
Ecuación 4.3.8
Ecuación 4.3.11
Ecuación 5.1.1
CM ( n, p, m, q, n1 , …, nm ) = np + pn1 + ¦ nA ⋅nA +1 + nm q
A =1
Ecuación 5.2.1
Ecuación 5.2.2
2
­
½
S = ® w j ,0 + ¦ w j ,i yi : j = 3, 4 ¾
i =1
¯
¿
A( j ) = w j ,0 + ¦ w j ,i yi
i =1
Ecuación 5.2.3
Ecuación 5.2.5
124
127
129
m
M = q + ¦ nA
A =1
Ecuación 5.2.4
115
m −1
§M ·
M!
¨ ¸=
© k ¹ k !( M − k )!
§M · §M ·
§M ·
§M · M §M ·
+
+
...
+
+
...
+
¨ ¸ ¨ ¸
¨ ¸
¨ ¸ = ¦¨ ¸
©1¹ ©2¹
©k ¹
© M ¹ k =1 © k ¹
131
131
131
xix
Una Introducción al Cómputo Neuronal Artificial
Ecuación 5.2.6
Ecuación 5.2.7
Ecuación 5.3.1
Ecuación 5.3.2
Ecuación 5.3.3
Ecuación 5.3.4
Ecuación 5.3.5
Ecuación 5.3.6
Ecuación 5.3.7
Ecuación 5.3.8
Ecuación 5.3.9
Ecuación 5.3.10
Ecuación 5.3.11
Ecuación 5.3.12
Ecuación 5.3.13
Ecuación 5.3.14
Ecuación 5.3.15
Ecuación 5.3.16
Ecuación 6.1.1
Ecuación 6.1.2
M
§M ·
( a + b) M = ¦ ¨ ¸ a M − k b k
k =0 © k ¹
M
§ M · § M · M § M · M −k k
M
¦
¨ ¸ − ¨ ¸ = ¦ ¨ ¸1 1 − 1 = 2 − 1
0
k
k
k =1 ©
¹ © ¹ k =1 © ¹
f(x1, x2, x3) =
(¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3)
x1 ⊗ x2 = (¬x1 ∧ x2) ∨ (x1 ∧ ¬x2)
Z1(x1, x2) = w1,0 + x1w1,1 + x2w1,2
x1 − x2 − 1 = 0
Z2(x1, x2) = w2,0 + x1w2,1 + x2w2,2
x1 − x2 + 1 = 0
− x1 + x2 − 1 = 0
− y1 − y2 − 1 = 0
Z3(y1, y2) = y1 + y2 + 1
− x1 − x2 + x3 − 2 = 0
x1 − x2 + x3 + 2 = 0
− x1 + x2 − x3 − 2 = 0
− x1 − x2 − x3 + 2 = 0
x1 + x2 + x3 − 2 = 0
y1 + y2 + y3 + 2 = 0
§ 2n ·
(2n )!
=
¨ ¸
n
© n ¹ (2 − n)!n !
ª I1 º
«I »
E = « 2»
«#»
« »
¬ In ¼
ent = ¦ w j I j
xx
135
136
137
137
138
138
138
139
140
144
145
145
145
145
146
149
155
156
Ecuación 6.1.5
Ecuación 6.2.1
§
·
O = g(ent) = g ¨ ¦ w j I j ¸
© j =1
¹
§ n
·
Err = T – O = T – g ¨ ¦ w j I j ¸
© j =1
¹
wj = wj + α⋅Err⋅Ij
j = 1, 2, …, n
γ 1 = min {W * ⋅Ek }
Ecuación 6.2.2
Wk+1 = Wk + Ek = (E1 + E2 + … + Ek-1) + Ek
Ecuación 6.1.4
132
n
j =1
Ecuación 6.1.3
132
n
156
156
157
162
162
Una Introducción al Cómputo Neuronal Artificial
Ecuación 6.2.3
Ecuación 6.2.4
Ecuación 6.2.5
Ecuación 6.2.6
Ecuación 6.2.7
W*⋅Wk+1 = W*⋅(E1 + E2 + … + Ek-1 + Ek)
W*⋅Wk+1 = W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek
||Wk+1||2 = ||Wk||2 + 2Wk⋅Εk + ||Εk||2
||Wk+1||2 – 2Wk⋅Εk = ||Wk||2 + ||Εk||2
2
Wk
+ Ek
2
{
Ecuación 6.2.8
γ 2 = max Ek
Ecuación 6.2.9
(k ) γ
2
W*
Ecuación 6.2.10
Ecuación 6.2.11
Ecuación 6.2.12
Ecuación 6.2.13
Ecuación 6.3.1
k =
2
1
2
k
2
j =1
j =1
}
Ecuación 6.3.7
Ecuación 6.3.8
Ecuación 6.3.10
166
167
1
N
168
N
¦ (T
− Ok ) 2
k
170
k =1
2
§
§ n
··
MEk = (Tk – Ok)2 = ¨ Tk − g ¨ ¦ w j I j ¸ ¸
¨
¸
© j =1
¹¹
©
W*⋅Wk+1 =
W*⋅W1 + W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek
170
172
n2
enti = ¦ w j ,i a j
Oi = g(enti)
wj,I = wj,I + α⋅aj⋅Δi
Δi = Erri ⋅ g’(enti)
Erri = Ti – Oi
§ n2
·
g '(enti ) = g ' ¨ ¦ w j ,i a j ¸
© j =1
¹
wk,j = wk,j + α⋅Ik⋅Δj
176
176
176
176
176
177
177
n3
Δ j = g '(ent j ) ⋅ ¦ w j ,i Δ i
i =1
Ecuación 6.3.9
165
2
j =1
Ecuación 6.3.2
Ecuación 6.3.3
Ecuación 6.3.4
Ecuación 6.3.5
Ecuación 6.3.6
2
= kγ 2
γ2 W *
γ 12
ME =
k −1
= ¦ 2W j ⋅ E j + ¦ E j
162
163
164
164
177
n1
ent j = ¦ wk , j I k
E=
k =1
n3
1
(Ti − Oi ) 2
¦
2 i =1
177
184
xxi
Una Introducción al Cómputo Neuronal Artificial
Ecuación 6.3.11
Ecuación 6.3.12
§ n3
·
SSE = ¦ ¨ ¦ (Ti ,A − Oi ,A ) 2 ¸
A =1 © i =1
¹
n3
1
E = ¦ (Ti − g (enti )) 2
2 i =1
N
Ecuación 6.3.13
E=
Ecuación 6.3.14
Ecuación 6.3.15
Ecuación 6.3.16
xxii
§ n2
··
1 n3 §
T
g
w
a
−
¨
¨
¦ i ¦
j ,i j ¸ ¸
¸
2 i =1 ¨©
© j =1
¹¹
185
185
2
185
∂E
= −a j Δi
∂w j ,i
∂E
= −Δ j ⋅ I k
∂wk , j
189
ª δE º
« δw »
1,1
«
»
« # »
«
»
« δE »
« δ wn ,1 »
2
«
»
« # »
« δE »
«
»
« δ w1,n3 »
«
»
« # »
« δE »
«
»
« δ wn2 , n3 »
∇E = «
δ E »»
«
« δ w1,1 »
«
»
« # »
« δE »
«
»
« δ wn1 ,1 »
« # »
«
»
« δE »
« δw »
« 1, n2 »
« # »
«
»
« δE »
« δ wn ,n »
¬
1 2 ¼
190
187
Una Introducción al Cómputo Neuronal Artificial
Ecuación 6.3.17
ª − a1Δ1 º
« # »
«
»
« −an2 Δ1 »
«
»
« # »
« −a Δ »
« 1 n3 »
« # »
«
»
« −an2 Δ n3 »
∇E = «
»
« − I1Δ1 »
« # »
«
»
« − I n1 Δ1 »
« # »
«
»
« − I1Δ n2 »
«
»
« # »
« −I Δ »
¬ n1 n2 ¼
Ecuación 6.3.18
2
1
E = §¨ T12 − 2 ⋅ T1 ⋅ g w1,1 g ( w1,1 x1 ) + ª g w1,1 g ( w1,1 x1 ) º ·¸
¬
¼ ¹
2©
−2( w1,1x1 ) ·
§
1− e
§
¸ ·
−2¨ w1,1 ⋅
−2 ( w1,1x1 ) ¸
¨
1+ e
¨
©
¹ ¸
1− e
¨ T12 − 2 ⋅ T1 ⋅
¸
−2 ( w1,1x1 ) ·
§
1− e
¸ ¸
¨
−2¨ w1,1 ⋅
−2( w1,1x1 ) ¸
¨
¹ ¸
1 + e © 1+ e
1¨
E= ¨
¸
2
−2( w1,1x1 ) ·
§
1− e
2¨ ª
º
¸
¸
−2¨ w1,1 ⋅
−2( w1,1x1 ) ¸
¨
¹ »
¨ «1 − e © 1+ e
¸
»
¨+«
¸
−2( w1,1x1 ) ·
§
1− e
¸ »
−2¨ w1,1 ⋅
¨ «
¸
−2 ( w1,1x1 ) ¸
¨
¹ »
¨ «1 + e © 1+ e
¸
¼
© ¬
¹
−2 ( w1,1⋅0.2) ·
§
1− e
§
¸ ·
−2¨ w1,1 ⋅
−2 ( w1,1⋅0.2) ¸
¨
1+ e
¨
©
¹ ¸
1− e
¨ (0.5) 2 − 2 ⋅ (0.5) ⋅
¸
−2( w1,1⋅0.2 ) ·
§
1− e
¸ ¸
¨
−2¨ w1,1 ⋅
−2( w1,1⋅0.2 ) ¸
¨
¹ ¸
1 + e © 1+ e
1¨
E= ¨
¸
2
−2( w1,1⋅0.2) ·
§
1− e
2¨ ª
¸
¸ º
−2¨ w1,1 ⋅
−2( w1,1⋅0.2) ¸
¨
¹ »
¨ «1 − e © 1+ e
¸
»
¨+«
¸
−2 ( w1,1⋅0.2 ) ·
§
1− e
¸»
−2¨ w1,1 ⋅
¨ «
¸
−2 ( w1,1⋅0.2 ) ¸
¨
¹»
¨ «1 + e © 1+ e
¸
¼
© ¬
¹
1
2
2 2
E = (T12 − 2T1w1,1w1,1 x1 + w1.1
w1,1
x1 )
2
Ecuación 6.3.19
Ecuación 6.3.20
Ecuación 6.3.21
191
(
)
(
)
193
193
194
195
xxiii
Una Introducción al Cómputo Neuronal Artificial
Ecuación 6.3.22
2
2
E = 0.125 − 0.1w1,1w1,1 + 0.02 w1.1
w1,1
Ecuación 6.3.23
δE
2
= −0.1w1,1 + 0.04w1,1w1,1
δ w1,1
δE
2
= −0.1w1,1 + 0.04w1,1
w1,1
δ w1,1
Ecuación 6.3.24
195
196
196
Ecuación 6.3.25
w1,1 =
2.5
, w1,1 ≠ 0
w1,1
197
Ecuación 6.3.26
2.5
w1,1 =
, w1.1 ≠ 0
w1,1
197
Ecuación 6.4.1
enti =
nm
¦w
km =1
Ecuación 6.4.2
Ecuación 6.4.3
Ecuación 6.4.4
Ecuación 6.4.5
⋅ am,km
km ,i
204
§
·
Oi = g (enti ) = g ¨ ¦ wkm ,i ⋅ am ,km ¸
© km =1
¹
nm
entkA ,A =
nA −1
¦w
kA−1 =1
kA−1 , kA ,A
⋅ aA −1, kA .−1
§
·
aA , kA = g (entkA ,A ) = g ¨ ¦ wkA−1 ,kA ,A ⋅ aA −1,kA−1 ¸
© kA−1 =1
¹
Ecuación 6.4.7
Ecuación 6.4.8
Ecuación 6.4.10
Ecuación 6.4.11
xxiv
204
p
entk1 ,1 = ¦ wk ,k1 ,1 ⋅ I k
a1,k1
204
§ p
·
= g (ent1,k1 ) = g ¨ ¦ wk ,k1 ,1 ⋅ I k ¸
© k =1
¹
q
E = ¦ (Ti − Oi )
δE
δ wk
Ecuación 6.4.9
204
nA−1
k =1
Ecuación 6.4.6
204
204
2
205
i =1
= − (Ti − Oi ) g ' ( enti ) am,km
m ,i
207
§
·
Erri = Ti − Oi = Ti − g ¨ ¦ wkm ,i ⋅ am,km ¸
© km =1
¹
Δ i = Erri ⋅ g '(enti )
207
§
§ nm
· · § nm
·
= ¨ Ti − g ¨ ¦ wkm ,i ⋅ am ,km ¸ ¸ ⋅ g ' ¨ ¦ wkm ,i ⋅ am,km ¸
¨
¸
© km =1
¹ ¹ © km =1
¹
©
δE
= −Δ i ⋅ am ,km
δ wkm ,i
207
nm
207
Una Introducción al Cómputo Neuronal Artificial
δE
Ecuación 6.4.12
δ wk
Ecuación 6.4.13
(
i =1
(
Δ km ,m = ¦ Δ i ⋅ wkm ,i ⋅ g ' entkm , m
δE
δ wk
)
= −¦ Δ i wkm ,i g ' entkm ,m am −1,km−1
m−1 , km , m
q
Ecuación 6.4.14
Ecuación 6.4.15
q
i =1
)
210
210
= −Δ km , m ⋅ am −1, km−1
211
m−1 , k m , m
nA+1
Δ kA ,A = g '(entkA ,A ) ¦ Δ kA+1,A +1 ⋅ wkA ,kA+1 ,A +1
kA+1 =1
δE
Ecuación 6.4.16
δ wk
A −1 , kA , A
δE
Ecuación 6.4.17
δ wk ,k ,1
= −Δ kA ,A aA −1,kA−1
215
1< A < m
= −Δ k1 ,1 ⋅ I k
1
220
224
Ecuación 6.4.18
wkm ,i = wkm ,i + α⋅Δi⋅ am,km
225
Ecuación 6.4.19
wkm−1 ,km , m = wkm−1 ,km , m + α⋅ Δ km ,m ⋅ am −1, km−1
225
Ecuación 6.4.20
wkA−1 ,kA ,A = wkA−1 ,kA ,A + α⋅ Δ kA ,A ⋅ aA −1,kA−1
225
Ecuación 6.4.21
wk ,k1 ,1 = wk ,k1 ,1 + α⋅ Δ k1 ,1 ⋅Ιk
225
Ecuación 6.5.1
1
1+ t
ª x1 º
«x »
X = « 2»
«#»
« »
¬ xn ¼
Wj = Wj + α⋅ϕ(j, k, r)⋅(E – Wj)
H = [0,1]
× [0,1] × ... × [0,1]
Ecuación 7.3.1
Ecuación 7.3.2
Ecuación 7.4.1
α (t ) =
n
Ecuación 7.4.2
min
xi
­
½
ª # º
°
°
«
»
= min ® x j ,i : E j = « x j ,i » , j = 1, 2,..., N ¾
°
°
«¬ # »¼
¯
¿
233
248
250
263
264
xxv
Una Introducción al Cómputo Neuronal Artificial
Ecuación 7.4.3
Ecuación 7.4.4
Ecuación 7.4.5
ª x1min º
« min »
x
Pmin = « 2 »
« # »
« min »
«¬ xn »¼
ª x1max º
« max »
x
Pmax = « 2 »
« # »
« max »
¬« xn ¼»
­
½
ª # º
°
°
«
»
xi = max ® x j ,i : E j = « x j ,i » , j = 1, 2,..., N ¾
°
°
«¬ # »¼
¯
¿
min
ª x j ,1 º ª x1 º ª x ' j ,1 º
» «
« » «
»
E j ' = E j − Pmin = « # » − « # » = « # »
« x j ,n » « xnmin » « x ' j ,n »
¬ ¼ ¬
¼
¼ ¬
max
min
ª x1 º ª x1 º ª x1max 'º
«
» «
» «
»
Pmax ' = Pmax − Pmin = « # » − « # » = « # »
« xnmax » « xnmin » « xnmax '»
¬
¼ ¬
¼ ¬
¼
min
min
ª x1 º ª x1 º ª0 º
«
» «
»
Pmin ' = Pmin − Pmin = « # » − « # » = «« # »»
« xnmin » « xnmin » «¬0 »¼
¬
¼ ¬
¼
max
xi '⋅ Si = 1, i = 1, 2,..., n
1
Si = max , i = 1, 2,..., n
xi '
264
265
max
Ecuación 7.4.6
Ecuación 7.4.7
Ecuación 7.4.8
Ecuación 7.4.9
Ecuación 7.4.10
Ecuación 7.4.11
xxvi
ª
·º
1
min §
« ( x j ,1 − x1 ) ¨ max
min ¸ »
© x1 − x1 ¹ »
«
ª x*j ,1 º «
»
#
« » «
»
#
« » «
»
§
·
1
E j * = « x*j ,i » = « ( x j ,i − ximin ) ¨ max
min ¸ »
« » «
© xi − xi ¹ »
« # » «
»
#
« x* » «
»
,
j
n
¬ ¼
·»
«
1
min §
« ( x j ,n − xn ) ¨ max
min ¸ »
© xn − xn ¹ ¼
¬
265
266
266
266
267
267
268
Una Introducción al Cómputo Neuronal Artificial
Ecuación 7.4.12
Ecuación 7.4.13
Ecuación 7.4.14
G normalized
=
j
Gj
256
1
α (t ) =
t +1
« d
»
GW = «
⋅ 255»
¬ d max
¼
268
270
274
xxvii
Una Introducción al Cómputo Neuronal Artificial
xxviii
Una Introducción al Cómputo Neuronal Artificial
Índice de Algoritmos
Página
Algoritmo 3.1.
Algoritmo 3.2.
Algoritmo 3.3.
Algoritmo 3.4.
Algoritmo 4.1.
Algoritmo 6.1.
Algoritmo 6.2.
Algoritmo 6.3.
Algoritmo 6.4.
Algoritmo 6.5.
Algoritmo 7.1.
Algoritmo 7.2.
Cálculo del mínimo de la función J(W) mediante búsqueda
del vector gradiente ∇J(W) = 0 y actualización iterativa del
vector de pesos.
Método de Descenso Escalonado para la búsqueda de un
mínimo: caso de una única entrada.
Método de Descenso Escalonado para la búsqueda de un
mínimo: caso de una única entrada y T presentaciones del
conjunto de entrenamiento.
Método de Descenso Escalonado para la búsqueda de un
mínimo: caso de varias entradas y T presentaciones del
conjunto de entrenamiento.
Implementación del método de Descenso Escalonado para el
entrenamiento de un Perceptrón y determinación de
Parámetros Autorregresivos en una señal.
Implementación de la Regla de Rosenblatt para el
entrenamiento de un Perceptrón.
Propagación de un vector de entrada en una red de
Perceptrones con una única capa oculta.
Método de Retropropagación para el entrenamiento de una
Red de Perceptrones con una única capa oculta.
Propagación de un vector de entrada en una red de
Perceptrones con dos capas ocultas.
Entrenamiento por Retropropagación para una Red de
Perceptrones con dos capas ocultas.
Entrenamiento de una Red de Kohonen Unidimensional.
Determinando la neurona asociada a un vector de entrada E
en una Red de Kohonen Unidimensional.
61
65
69
72
110
158
180
182
230
233
251
253
xxix
Una Introducción al Cómputo Neuronal Artificial
xxx
Una Introducción al Cómputo Neuronal Artificial
Índice de Figuras
Figura 1.1.
Figura 1.2.
Figura 1.3.
Figura 1.4.
Figura 1.5.
Figura 1.6.
Figura 2.1.
Figura 2.2.
Figura 2.3.
Figura 2.4.
Figura 2.5.
Figura 3.1.
Figura 3.2.
Figura 3.3.
Figura 3.4.
Figura 3.5.
Figura 3.6.
Componentes principales de una Neurona Biológica.
Componentes de la Unión Sináptica entre dos neuronas.
Porción de una Red Neuronal Biológica.
Representación esquemática de una neurona (biológica o
artificial).
Ejemplo de Representación Esquemática de un
fragmento de Red Neuronal.
Un Red formada por 6 neuronas tipo Adaline.
Interpretación del signo de las pendientes de las Rectas
Tangentes a una función f. a) Una pendiente positiva
señala la dirección de crecimiento de f. b) Una pendiente
negativa indica que f decrece en la dirección positiva del
eje X1.
Ajuste de la recta wx1 + b.
Disposición en el plano cartesiano de los puntos
presentados en la Tabla 2.1.
La recta d = 2.9818x1 + 3.9545 como el mejor estimador
lineal para el conjunto de datos presentado en la Tabla
2.1.
El paraboloide asociado a la función de error
J = 5w2 + 0.5b2 – 29.81w – 3.95b + 52.397
Representación esquemática de una neurona Adaline.
Gráfica de la función sign.
Esquema de una neurona Adaline para dar solución al
modelado de la compuerta lógica OR.
Estructura de la neurona Adaline omitiendo el uso de la
función sign.
Sección transversal del paraboloide definido por J(W). El
vector gradiente nos indica la dirección de máximo
crecimiento de J(W).
Sección transversal del paraboloide definido por J(W).
La dirección opuesta del vector gradiente indica la
dirección en donde se ubica el mínimo de J(W).
Página
9
10
11
12
13
18
25
31
36
37
38
49
49
51
53
58
59
xxxi
Una Introducción al Cómputo Neuronal Artificial
Figura 3.7.
Figura 4.1.
Figura 4.2.
Figura 4.3.
Figura 4.4.
Figura 4.5.
Figura 4.6.
Figura 4.7.
Figura 4.8.
Figura 4.9.
Figura 4.10.
Figura 4.11.
xxxii
Sección transversal del paraboloide definido por J(W).
Dado un (punto) vector de pesos inicial W1 y -∇J(W1) se
obtiene el nuevo (punto) vector de pesos W2. Usando a
W2 y -∇J(W2) se obtiene el (punto) vector de pesos W3.
Se procede de manera sucesiva hasta obtener un vector
de pesos Wm tal que ∇J(Wm) = 0 o tan cercano a éste
como sea posible.
Representación esquemática de un Perceptrón.
Algunas Funciones de Activación para el Perceptrón:
a) Función Sigmoide; b) Tangente Hiperbólica con
z
argumento ; c) Tangente Hiperbólica; d) La función
2
1 + Tanh( z )
.
2
Una neurona de tipo Perceptrón con dos entradas.
El umbral z(x1, x2) = w1 x1 + w2 x2 = 0 asociado a un
Perceptrón de 2 entradas.
El vector normal v del umbral z(x1, x2) = w1 x1 + w2 x2 = 0
asociado a un Perceptrón de 2 entradas. Los componentes
de v son precisamente los valores de los pesos w1 y w2.
Caracterización de los puntos en el Espacio Euclidiano
Bidimensional en función del signo de su evaluación con
la función z(x1, x2) = w1 x1 + w2 x2. Si w1 x1 + w2 x2 > 0
entonces el punto está en la misma región hacia la que
apunta el vector normal v. Si w1 x1 + w2 x2 < 0 entonces
el punto está en la región hacia la que apunta –v. Si
w1 x1 + w2 x2 = 0 entonces el punto está sobre la recta
z(x1, x2) = 0.
\2
mediante
el
umbral
Partición
de
z(x1, x2) = w1 x1 + w2 x2 = 0 y su vector normal v. R12 se
forma por los puntos por encima de la recta z(x1, x2) = 0.
R22 se forma por los puntos debajo de la recta
z(x1, x2) = 0. R32 es el conjunto de puntos sobre la recta
z(x1, x2) = 0.
Una neurona de tipo Perceptrón con tres entradas.
El lugar geométrico asociado a z(x1, x2, x3) = 0.
Visualización en el plano de los cuatro posibles estados
de la compuerta lógica AND (Véase el texto para
detalles).
Una recta que separa los estados con salida 0 del estado
con salida 1 en la compuerta lógica AND.
60
85
87
91
91
92
93
94
94
95
96
97
Una Introducción al Cómputo Neuronal Artificial
Figura 4.12.
Figura 4.13.
Figura 4.14.
Figura 4.15.
Figura 4.16.
Figura 4.17.
Figura 4.18.
Figura 4.19.
Figura 4.20.
Figura 4.21.
Figura 4.22.
Figura 4.23.
Figura 5.1.
Figura 5.2.
Figura 5.3.
Visualización en el plano de los cuatro posibles estados
de la compuerta lógica XOR (Véase el texto para
detalles).
a) Una recta que agrupa, para la compuerta lógica XOR,
a los estados con salida 0 pero que también incluye a un
estado con salida 1. b) Una recta que agrupa a los estados
con salida 1 pero que también incluye a un estado con
salida 0.
Ejemplos de regiones convexas: a) Región Convexa
Cerrada; b) Región Convexa Abierta.
Separación de los estados de la compuerta lógica AND
mediante dos regiones cerradas convexas disjuntas
(véase el texto para detalles).
Dos regiones convexas no disjuntas que agrupan, cada
una, a los estados negros y a los estados blancos de la
función XOR.
Separación de los estados negros y los estados blancos de
la función XOR. Se tienen dos regiones disjuntas, pero
una de ellas es no convexa.
Una serie de tiempo de 7 parámetros autorregresivos
(véase el texto para detalles).
Representación esquemática del Perceptrón que se
utilizará para determinar los Parámetros Autorregresivos
en una Señal de Séptimo Orden (Véase el texto para
detalles).
Evolución del valor MSE (Ecuación 4.3.4) a lo largo de
las T = 100 presentaciones del conjunto de entrenamiento
para un Perceptrón entrenado mediante el Algoritmo 4.1
(Véase el texto para detalles).
Evolución del Coeficiente de Aprendizaje μ a lo largo de
las T = 100 presentaciones del conjunto de entrenamiento
para un Perceptrón entrenado mediante el Algoritmo 4.1
(Véase el texto para detalles).
Serie de tiempo de 7 parámetros autorregresivos
generada por un Perceptrón bajo la Ecuación 4.3.11
(véase el texto para detalles).
En color gris, la serie de tiempo presentada en la Figura
4.22. En color negro, la serie de tiempo presentada en la
Figura 4.18 (véase el texto para detalles).
Una red Madaline formada por 5 neuronas.
Una red Madaline formada por 5 neuronas que efectúa un
mapeo de vectores en \ 2 a vectores (escalares) en \ .
El umbral Z1(x1, x2) = 0 asociado a la neurona que
modelará la función Booleana x1 ∧ ¬x2.
98
99
100
101
102
102
106
114
116
117
118
119
123
126
138
xxxiii
Una Introducción al Cómputo Neuronal Artificial
Figura 5.4.
Figura 5.5.
Figura 5.6.
Figura 5.7.
Figura 5.8.
Figura 5.9.
Figura 5.10.
Figura 5.11.
Figura 6.1.
Figura 6.2.
Figura 6.3.
Figura 6.4.
Figura 6.5.
Figura 6.6.
xxxiv
El umbral Z2(x1, x2) = 0 asociado a la neurona que
modelará la función Booleana ¬x1 ∧ x2.
El umbral Z3(y1, y2) = 0 asociado a la neurona que
modelará la función Booleana OR.
Una red Madaline formada por 3 neuronas que resuelve
el problema del modelado de la compuerta XOR.
a), b) y c) En gris: Regiones del plano por encima de los
umbrales asociados a las neuronas que modelan las
funciones Booleanas x1 ∧ ¬x2, ¬x1 ∧ x2 y OR. d) Las tres
regiones anteriores sobrepuestas. En gris obscuro: sus
intersecciones.
Partición del plano inducida por la Red Neuronal de la
Figura 5.6 (Véase el texto para detalles).
Visualización en el espacio 3D de los estados y las
salidas de las funciones Booleanas a) ¬x1 ∧ ¬x2 ∧ x3, b)
¬x1 ∧ x2 ∧ ¬x3, c) x1 ∧ x2 ∧ x3, y d) y1 ∨ y2 ∨ y3. Los
triángulos en gris están inmersos en los planos que
separan a los estados negros de los estados blancos. Sus
vértices son utilizados para determinar sus
correspondientes ecuaciones y orientaciones (véase el
texto para detalles).
Red Madaline que modela a la función Booleana
f(x1, x2, x3) = (¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨
(x1 ∧ x2 ∧ x3).
Los estados de las funciones Booleanas de 1 a 4 variables
vistos como los vértices de hipercubos. a) Un hipercubo
1D: un segmento (2 vértices/estados). b) Un hipercubo
2D: un cuadrado (4 vértices/estados). c) Un hipercubo
3D: un cubo (8 vértices/estados). d) Un Hipercubo 4D
(16 vértices/estados).
Representación Esquemática de un Perceptrón.
Una red de Perceptrones con una única capa oculta
(Véase el texto para detalles).
Una Red de Perceptrones de una sola capa oculta con una
neurona en cada una de sus capas.
Gráfica de la función de Error asociada a la red de
Perceptrones de la Figura 6.3 (véase el texto para
detalles).
Gráfica de la Ecuación
2
2
E = 0.125 − 0.1w1,1w1,1 + 0.02 w1.1
w1,1
.
El conjunto de puntos, resaltados en negro, para los
cuales el vector gradiente de la función
2
2
E = 0.125 − 0.1w1,1w1,1 + 0.02 w1.1
w1,1
es el vector cero.
139
140
141
143
143
147
148
150
156
175
192
194
195
199
Una Introducción al Cómputo Neuronal Artificial
Figura 6.7.
Figura 6.8.
Figura 6.9.
Figura 6.10.
Una Función de Error E con un único punto crítico: un
máximo (punto remarcado).
Una de red de Perceptrones formada por m capas ocultas,
m ≥ 2 (Véase el texto para detalles).
En color gris se muestran las neuronas involucradas en la
actualización del peso wkm ,i . Tal peso se encuentra
únicamente en la i-ésima neurona de la capa de salida.
En color gris se muestran las neuronas involucradas en la
actualización del peso wkm−1 ,km ,m el cual reside en la
km-ésima neurona de la última capa oculta. Las
actualizaciones aplicadas sobre las neuronas en la capa
de salida influyen también en la actualización del peso
wkm−1 ,km ,m .
Figura 6.11.
Figura 6.15.
Figura 6.16.
205
208
211
En color gris se muestran las neuronas involucradas en la
actualización del peso wk , k1 ,1 . Este peso se ubica
específicamente en la k1-ésima neurona de la primera
capa oculta. Las correcciones aplicadas sobre todas las
neuronas de la red, a excepción de las neuronas en la
capa de entrada y de las neuronas en la primera capa
oculta (salvo la k1-ésima), influyen sobre la actualización
del peso wk ,k1 ,1 .
Figura 6.13.
Figura 6.14.
202
En color gris se presentan a las neuronas involucradas en
la actualización del peso wkA−1 , kA ,A . Éste se encuentra
localizado específicamente en la kO-ésima neurona en la
O-ésima capa oculta. Las actualizaciones aplicadas sobre
las neuronas en las capas ocultas O+1, O+2, …, m y la capa
de salida influyen sobre la actualización de wkA−1 ,kA ,A .
Figura 6.12.
201
Una serie de tiempo formada por K = 2000 muestras.
La serie de tiempo originalmente presentada en la Figura
6.13. En color negro, las muestras utilizadas para formar
el conjunto de entrenamiento. En color gris, las muestras
que conformarán al conjunto de evaluación.
1
a
Evolución del Coeficiente de Aprendizaje α (t ) =
1+ t
lo largo de 500 presentaciones del conjunto de
entrenamiento. En la última instancia se tiene
α(500) ≈ 0.0019.
Una Red de Perceptrones con dos capas ocultas. Se
utilizará para modelar a la serie de tiempo presentada en
la Figura 6.13.
221
229
229
237
238
xxxv
Una Introducción al Cómputo Neuronal Artificial
Figura 6.17.
Figura 6.18.
Figura 7.1.
Figura 7.2.
Figura 7.3.
Figura 7.4.
Figura 7.5.
Figura 7.6.
Figura 7.7.
xxxvi
Evolución del Error Global de la Red de Perceptrones de
la Figura 6.16 durante la aplicación del Algoritmo de
Retropropagación. Se efectuaron 500 presentaciones del
conjunto de entrenamiento.
En color gris, serie de tiempo producida por la Red de
Perceptrones de la Figura 6.16. En color negro, la serie
de tiempo original. La recta punteada separa las muestras
que conformaron al conjunto de entrenamiento
(n = 1, …, 1000) de las muestras que dieron lugar al
conjunto de evaluación (n = 1001, …, 2000).
El conjunto A es particionado en 20 regiones. Una Red
de Kohonen implementa a la función f de manera que los
vectores en el conjunto A son asociados a su
correspondiente clase.
Una Red Unidimensional de Kohonen para la
clasificación de vectores en \ n .
La vecindad de radio r para la k-ésima neurona en una
Red de Kohonen 1D. La vecindad se extiende r
posiciones hacia la izquierda y r posiciones hacia la
derecha.
Una Red de Kohonen Bidimensional para la clasificación
de puntos en \ n . Las neuronas son posicionadas en
renglones y columnas. El vector de entrada X es enviado
a todas las neuronas.
La vecindad bidimensional de radio r para la k-ésima
neurona en una Red de Kohonen 2D. La vecindad se
extiende r posiciones cubriendo una región cuadrangular.
Todas las neuronas dentro de esta región son vecinas de
la neurona k.
Evolución del ajuste de pesos para una Red de Kohonen
1D en la primeras 10 presentaciones del conjunto de
entrenamiento. Los triángulos denotan las posiciones de
los Centros de Gravedad (vectores de pesos) asociados a
las neuronas que forman la red (véase el texto para
detalles).
Algunas fases de la evolución del ajuste de pesos para
una Red de Kohonen 1D. Los triángulos denotan las
posiciones de los Centros de Gravedad (vectores de
pesos) asociados a las neuronas que forman la red (véase
el texto para detalles).
240
241
246
249
250
254
255
257
258
Una Introducción al Cómputo Neuronal Artificial
Figura 7.8.
Figura 7.9.
Figura 7.10.
Figura 7.11.
Figura 7.12.
Figura 7.13.
Figura 7.14.
Figura 7.15.
Figura 7.16.
Partición de la región [0, 1] × [0, 1] inducida por los
centros de gravedad (vectores de pesos, triángulos en la
figura) asociados a las 10 neuronas que conforman a una
Red de Kohonen 1D. La región ha sido subdividida en 10
clases después de 100 presentaciones del conjunto de
entrenamiento (véase el texto para detalles).
Evolución del ajuste de pesos para una Red de Kohonen
1D en la primeras 10 presentaciones de un conjunto de
entrenamiento inmerso en un cubo unitario
[0, 1] × [0, 1] × [0, 1]. Los círculos mayores denotan las
posiciones de los Centros de Gravedad (vectores de
pesos) asociados a las neuronas que forman la red (véase
el texto para detalles).
Algunas fases de la evolución del ajuste de pesos para
una Red de Kohonen 1D. Se mapea un conjunto de
entrenamiento inmerso en un cubo unitario
[0, 1] × [0, 1] × [0, 1]. Los círculos mayores denotan las
posiciones de los Centros de Gravedad (vectores de
pesos) asociados a las neuronas que forman la red (véase
el texto para detalles).
Un conjunto de vectores inmersos en el cubo
[0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6] ⊆ [0,1] × [0,1] × [0,1].
La
diagonal
principal
asociada
al
cubo
[0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6].
Traslación de los vectores originalmente inmersos en el
cubo [0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6] de manera que
Pmin ' es ahora el origen del espacio 3D.
Aplicación de factores de escalamiento de manera que el
conjunto de vectores originalmente inmerso en el cubo
[0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6] (Figura 7.11) se
redistribuya a lo largo del cubo [0, 1] × [0, 1] × [0, 1].
Una imagen correspondiente a una sección cerebral
capturada mediante Tomografía Computada.
Mapa de Falso Color que muestra las distancias entre los
vectores de pesos asociados a una Red de Kohonen 1D
formada por 20 neuronas.
259
260
261
264
265
266
267
269
276
xxxvii
Una Introducción al Cómputo Neuronal Artificial
xxxviii
Una Introducción al Cómputo Neuronal Artificial
Índice de Tablas
Tabla 2.1.
Tabla 3.1.
Tabla 3.2.
Tabla 3.3.
Tabla 3.4.
Tabla 3.5.
Tabla 4.1.
Tabla 4.2.
Tabla 4.3.
Tabla 4.4.
Tabla 4.5.
Tabla 5.1.
Tabla 5.2.
Tabla 5.3.
Tabla 5.4.
Un conjunto de 11 observaciones.
Una compuerta lógica a ser modelada por una neurona
Adaline.
Un conjunto de entrenamiento al que se le aplicará el
método de Descenso Escalonado a fin de que una
neurona Adaline lo modele.
Aplicación del método de Descenso Escalonado para el
ajuste de pesos de una neurona Adaline con el conjunto
de entrenamiento de la Tabla 3.2.
Aplicación del método de Descenso Escalonado para el
ajuste de pesos de una neurona Adaline presentando por
segunda vez el conjunto de entrenamiento de la Tabla 3.2
ª1.2432 º
y usando como vector de pesos iniciales W1 = «
».
¬3.4485¼
Vectores de pesos obtenidos al final de la t-ésima
presentación, t = 1, 2, …, 10, mediante Descenso
Escalonado, para el conjunto de entrenamiento de la
Tabla 3.2.
Tabla de verdad de la compuerta lógica AND.
Tabla de verdad de la compuerta lógica XOR.
Conteo de funciones Booleanas de 1 a 6 entradas
linealmente separables.
Las primeras 15 muestras asociadas a una serie de tiempo
de 7 parámetros autorregresivos (véase el texto para
detalles).
Desempeño del aprendizaje de un Perceptrón entrenado
mediante Descenso Escalonado y el Algoritmo 4.1 (véase
el texto para detalles).
Conjunto de entrenamiento a presentar a una red
Madaline.
Pesos iniciales de las neuronas en la red Madaline
presentada en la Figura 5.2.
Pesos de las neuronas en la red Madaline presentada en
la Figura 5.2 una vez que se ha aplicado un ajuste sobre
la neurona 4 (Véase el texto para detalles).
Estados y salidas para una función Booleana de 3
variables.
Página
36
55
67
67
68
70
96
98
100
105
115
125
126
128
133
xxxix
Una Introducción al Cómputo Neuronal Artificial
Tabla 5.5.
Tabla 5.6.
Tabla 5.7.
Tabla 5.8.
Tabla 5.9.
Tabla 5.10.
Tabla 6.1.
Tabla 7.1.
Tabla 7.2.
Tabla 7.3.
Tabla 7.4.
Tabla 7.5.
Tabla 7.6.
Tabla 7.7.
xl
Estados para los cuales la función Booleana de la Tabla
5.4 tiene salida 1.
Tabla de verdad asociada la función Booleana
(¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3).
Estados y salidas para la función Booleana XOR.
Estados y salidas para la función Booleana x1 ∧ ¬x2
(el valor 0 ha sido sustituido por -1).
Estados y salidas para la función Booleana ¬x1 ∧ x2
(el valor 0 ha sido sustituido por -1).
Estados y salidas para la función Booleana OR (el valor
0 ha sido sustituido por -1).
Pesos asociados a la Red de Perceptrones de la Figura
6.16 una vez que se aplicó el Algoritmo de
Retropropagación con 500 presentaciones del conjunto
de entrenamiento.
Distribución de los 100 elementos del conjunto de
entrenamiento en las 10 clases obtenidas mediante una
Red de Kohonen 1D. Se muestran también las
coordenadas finales de los centros de gravedad de cada
clase una vez efectuadas 100 presentaciones del conjunto
de entrenamiento (véase el texto para detalles).
Distribución de los 100 elementos del conjunto de
entrenamiento, inmerso en un cubo unitario
[0, 1] × [0, 1] × [0, 1], en las 10 clases obtenidas
mediante una Red de Kohonen 1D. Se muestran también
las coordenadas finales de los centros de gravedad de
cada clase una vez efectuadas 100 presentaciones del
conjunto de entrenamiento (véase el texto para detalles).
Clasificación de las 340 imágenes en el conjunto de
entrenamiento de acuerdo a una Red de Kohonen 1D con
20 neuronas (véase el texto para detalles).
Los 16 miembros de la clase 17 asociada a un conjunto
de entrenamiento formado por 340 imágenes y
clasificado mediante una Red de Kohonen 1D.
Los 25 miembros de la clase 12 asociada a un conjunto
de entrenamiento formado por 340 imágenes y
clasificado mediante una Red de Kohonen 1D.
Visualización de las imágenes asociadas a los vectores de
pesos de una Red de Kohonen 1D formada por 20
neuronas (Véase el texto para detalles).
Distancias que tienen los vectores de pesos asociados a
las clases 12 y 17 con todos los demás vectores de pesos
que conforman a una Red de Kohonen 1D.
133
135
135
137
139
140
239
259
262
271
271
272
275
277
Una Introducción al Cómputo Neuronal Artificial
1. Introducción
Una Introducción al Cómputo Neuronal Artificial
2
Capítulo 1. Introducción
Las Redes Neuronales Artificiales son Redes Computacionales cuya finalidad es la
de simular, en su totalidad, las redes de células nerviosas (neuronas) del sistema nervioso
central (biológico) de humanos o mamíferos. Usamos el término totalidad para referirnos al
hecho de que la simulación efectivamente es total: se detalla cada neurona a utilizar, la
forma en que procesa la información, y también se especifican las conexiones entre las
neuronas. Estas simulaciones se derivan del conocimiento neurofisiológico de las neuronas
biológicas y las redes formadas por éstas. Se dice que el proceso de solución de problemas
mediante Redes Neuronales, ya sean Biológicas o Artificiales, es llamado Cómputo
Neuronal. Esta distinción tiene la intención también de diferenciarlo del Cómputo Digital
“Convencional”, es decir, aquel cómputo que se sustenta en nuestras computadoras
digitales actuales. También diremos que el Cómputo Neuronal Artificial es el proceso de
solución de problemas pero utilizando específicamente Redes Neuronales Artificiales.
El Cómputo Neuronal Artificial aspira a reemplazar, mejorar o acelerar el cómputo
que se efectúa en el cerebro humano. Sabemos que la velocidad de procesamiento del
cerebro es lenta comparada con la velocidad de procesamiento presente en las
computadoras actuales. Operaciones simples pero en grandes volúmenes, como las
aritméticas por ejemplo, en los inicios del siglo XX le requerían interminables horas de
trabajo a un ser humano. Además, habría que tener en cuenta las posibilidades de cometer
errores, que por lo regular eran considerables. Con la llegada de las primeras computadoras
electrónicas de propósito general, como la ENIAC en 1946, cuyo poder de procesamiento
es hoy comparable al de una calculadora de bolsillo, esas mismas operaciones aritméticas
podían ser efectuadas con unos pocos segundos de procesamiento y con nulas
probabilidades de error. Ahora bien, imaginemos lo que se puede lograr al proporcionar la
misma velocidad de cómputo que nos da la electrónica al incorporarla a nivel neuronal y
combinarla con el poder de solución de problemas con que cuenta nuestro cerebro.
Tomemos en cuenta que hay una gran cantidad de problemas en los cuales el cerebro
humano supera, por su capacidad para formar y proporcionar soluciones, a las
computadoras digitales. La velocidad que nos da la electrónica junto con las capacidades
del Cómputo Neuronal deja abiertas grandes posibilidades de contar con soluciones
correctas a problemas realmente difíciles en tiempos sumamente cortos.
Otro punto interesante es que el Cómputo Neuronal no considera explícitamente la
organización de sus elementos de cómputo, las neuronas, y las redes que éstas forman. El
cerebro se estructura en una red de neuronas realmente enorme. Se tiene un conteo
aproximado de 1011 = 100,000,000,000 células nerviosas en el caso del cerebro humano.
Esta red neuronal se encuentra trabajando activamente incluso en los periodos de sueño. Es
la misma red que utilizamos para la solución de problemas. Sin embargo, es claro que
ningún ser humano está consciente de que partes de esa red fueron utilizadas para dar
solución a una Ecuación Diferencial, por ejemplo. Es decir, para solucionar problemas, no
requerimos, a priori, determinar a que subred neuronal hay que dirigir nuestro razonamiento
o bien cual de todas las subredes disponibles se adapta mejor para solucionarlo. Tampoco
estamos conscientes de los mensajes transmitidos por cada neurona involucrada en la
generación de la solución. Contamos con una arquitectura de Red Neuronal de la cual no
necesitamos conocer su organización y funcionamiento internos. En el caso de las Redes
3
Una Introducción al Cómputo Neuronal Artificial
Neuronales Artificiales veremos que si es necesario especificar una arquitectura y la
manera en que las neuronas se conectan. También es necesario especificar puntos en los
cuales proporcionaremos una entrada a la red y puntos en donde debemos esperar la salida
que ésta dará para nuestro problema. Pero aparte de ello, veremos que los mecanismos de
aprendizaje a utilizar no son dependientes en ninguna manera de la estructura de red.
También veremos que si el aprendizaje fue exitoso, entonces realmente sólo nos
preocuparemos de dar la entrada y obtener la salida correspondiente sin prestar mayor
consideración a la organización interna, tal y como sucede con el procesamiento cerebral.
Una Red Neuronal Artificial es computacionalmente y algorítmicamente muy
simple. Si bien sabemos que se tienen contabilizadas aproximadamente 1011 neuronas en el
cerebro humano, en la práctica, la implementación de una Red Neuronal Artificial sólo
requiere, a lo más, unos cientos de neuronas. Pero, por otro lado, se verá que existen
aplicaciones en las cuales una decena de neuronas basta para dar solución a un problema.
Ello implica que los requerimientos espaciales (memoria primaria y secundaria) son en
realidad pequeños. Adicionalmente, una Red Neuronal, y particularmente cada una de las
neuronas que la componen, usan únicamente operaciones computacionales elementales
tales como sumas, multiplicaciones y operadores lógicos. Esto tiene como consecuencia
que la implementación, ya sea en software o en hardware, es en realidad sencilla y además
cuenta con tiempos de ejecución, o respuesta, reducidos que de hecho dependen
directamente del tamaño de la entrada que recibirá la red y el número de neuronas que la
forman.
En el sistema nervioso central miles de neuronas mueren al año. La perdida de
neuronas inicia a partir del nacimiento y nunca se detiene. También hay que tomar en
cuenta que las neuronas tienen entre una de sus características la de no reproducirse. Por lo
tanto, la pérdida neuronal puede verse como un daño irreparable. Pero en este punto surge
un aspecto sumamente interesante y que forma parte del gran poder del Cómputo Neuronal:
las funciones del cerebro no se ven afectadas por daños menores (al menos bajo
condiciones normales y durante los primeros dos tercios de vida del ser humano). Esta
insensibilidad a daños menores se debe a tres propiedades trascendentales de las Redes
Neuronales Biológicas: su Alto Paralelismo, su Adaptabilidad y la capacidad de
Auto-Organización.
El Alto Paralelismo se refiere al hecho de que una vez que se recibe una entrada,
ésta es manipulada al mismo tiempo por varias neuronas. Cada neurona proporcionará su
correspondiente aportación a la solución del problema la cual es enviada a su vez como
entrada a otras neuronas que la procesarán también en paralelo. El punto trascendental es
que la pérdida de neuronas no implica necesariamente que la red quede desconectada o bien
que reduzca su eficiencia. La ventaja del paralelismo es que siempre existirán rutas
disponibles para procesar la entrada y producir la salida correspondiente. Sólo para hacer
un contraste: una computadora digital “convencional” es una máquina secuencial, ello
implica que si un transistor falla entonces la máquina por completo se hace inservible.
4
Capítulo 1. Introducción
El alto paralelismo presente en las Redes Neuronales permite siempre encontrar
rutas alternas para procesar una entrada. Sin embargo, es probable que el daño neuronal
reduzca la eficiencia de la red. Es cuando las propiedades de la Adaptabilidad y
Auto-Organización entran en acción. Puede que se tengan neuronas especializadas en
alguna tarea particular. Sin embargo, la pérdida neuronal puede obligar a éstas a
especializarse en otras nuevas tareas. Ello implica que deben adaptarse a un nuevo
ambiente e inclusive estar preparadas para recibir y procesar nuevos tipos de entradas y
proporcionar las salidas correspondientes a esas nuevas tareas. La auto-organización toma
lugar cuando se crean u omiten conexiones entre neuronas a fin de reforzar el proceso de
adaptación. Son las mismas neuronas las que controlan las modificaciones a la estructura de
la Red Neuronal a la que están asociadas. Los procesos de auto-organización y adaptación
toman lugar a lo largo de toda la vida, dado que ya mencionamos que a lo largo de ésta se
pierden neuronas, y además, se encuentra sumamente ligado a los procesos de aprendizaje.
Para su estudio y análisis, el cerebro humano, y en particular la corteza cerebral, se
dividen en regiones. Cada una de estas regiones es de hecho una Red Neuronal con una
tarea específica. Una de estas zonas es la llamada Área de Broca la cual está asociada con
el proceso de la comunicación oral. Mencionamos antes que bajo condiciones normales las
pérdidas neuronales pueden ser controladas sin percibir los daños o efectos provocados por
la ausencia de tales neuronas. Sin embargo, la adaptabilidad y auto-organización neuronales
también actúan bajo situaciones más dramáticas. Un accidente cerebrovascular puede ser
causado al incidir sobre una región del tejido cerebral un repentino bloqueo de la irrigación
sanguínea o bien, por el contrario, una hemorragia. Como consecuencia, la región afectada
queda por completo dañada. Si esta condición se presentara en el Área de Broca, el paciente
entonces perdería la capacidad del habla. En la Literatura Médica se tienen identificados
casos de pacientes con esta situación y que han regenerado su capacidad de comunicación
gracias a los procesos de auto-organización y adaptabilidad. En estos casos se requieren
intervalos de tiempo más largos para la recuperación, del orden de meses, debido a que son
millones las neuronas involucradas. Las regiones en la corteza cerebral que son vecinas del
Área de Broca deben adaptarse a la nueva función y al mismo tiempo continuar dando
seguimiento a las tareas que ya tienen asignadas. En consecuencia, se tiene que una Red
Neuronal, gracias a los procesos de adaptación y auto-organización, cuenta con un amplio
potencial para abordar una gran cantidad de problemas.
Aunque la base algorítmica sobre la que se sustentan Redes Neuronales Artificiales
es muy simple, veremos que éstas efectivamente cuentan con las características del
paralelismo, adaptabilidad y auto-organización. Dado un problema a ser resuelto,
plantearemos una topología de red neuronal: se establecen las neuronas a utilizar, su
posición dentro de la red y sus conexiones. Los algoritmos de aprendizaje ajustarán los
elementos de cómputo de cada neurona a fin de maximizar su eficiencia de manera que la
topología elegida se adapte tanto como sea posible para proporcionar una solución al
problema y procesar adecuadamente las entradas y producir las salidas correctas. Inclusive,
si la red es sometida en el futuro a cambios respecto a la naturaleza del problema, será
posible esperar que mediante reajustes mínimos de sus elementos, ésta tenga la capacidad
de responder exitosamente a tales cambios.
5
Una Introducción al Cómputo Neuronal Artificial
Todos los puntos anteriores nos conducen a pensar que una Red Neuronal puede
verse de hecho como una arquitectura novedosa a nivel computacional y algorítmico. Ello
quiere decir que incluso podríamos pensar en una arquitectura computacional adicional a la
arquitectura de Cómputo Digital “Convencional”. El cómputo “Convencional” debe
entenderse, de manera concreta y formal, como aquel basado en las Máquinas de Turing y
la electrónica. Las Máquinas de Turing proporcionan la Teoría y Fundamentos detrás de la
Computación. Una Máquina de Turing expresa a nivel elemental la lógica detrás de un
algoritmo. Una Máquina de Turing Universal T es aquella que es capaz de recibir como
entrada una Máquina de Turing M y las entradas para M de manera que T simula la
ejecución de M. Es decir, una Máquina de Turing Universal puede verse como el modelo
matemático de una computadora de escritorio y de manera más específica, de su Unidad
Central de Procesamiento (CPU). La electrónica nos proporciona los elementos para la
materialización y aceleración de nuestras Máquinas de Turing.
Ya hicimos mención de que el Cómputo Neuronal podría verse como un modelo
adicional al Cómputo “Convencional”. Sin embargo, en realidad las Redes Neuronales
Artificiales pueden simularse sin problema alguno en las computadoras convencionales.
Ello implica que las herramientas algorítmicas que utilizamos comúnmente nos serán útiles
para resolver problemas bajo el enfoque neuronal. El hardware y software que requiere el
Cómputo Neuronal Artificial es el mismo que utilizamos hoy en día. Además, hemos de
recalcar que una Red Neuronal usa únicamente operaciones computacionales elementales,
como sumas, multiplicaciones y lógica elemental, para dar solución a una amplia gama de
problemas. En este punto es posible plantearse una observación: Si el Cómputo Neuronal
Artificial no requiere hardware y software específicos y además se basa en operaciones
básicas, las mismas presentes en los CPUs, entonces, ¿qué ventajas puede tener sobre el
Cómputo “Convencional”? Parte de la respuesta a ello viene de las características del Alto
Paralelismo, Adaptabilidad y la capacidad de Auto-Organización que forman en sí una
porción de la base de los procesos de razonamiento y aprendizaje en el cerebro. La otra
parte de la respuesta surge al considerar las propiedades anteriores y su impacto en la
solución de algunos de los problemas a los cuales el Cómputo Neuronal Artificial ha dado
soluciones exitosas:
• Problemas Mal Definidos: Todo problema a ser resuelto computacionalmente debe
tener bien definidos sus conjuntos de entrada y de salida. Es decir, se debe especificar
claramente las propiedades de las entradas y las propiedades de las salidas y cómo es
que éstas pueden ser validadas como correctas o incorrectas. Sin embargo, no todos los
problemas presentan estas propiedades. Considérese por ejemplo el reconocimiento de
voz. Supongamos que se desean clasificar oraciones en general. Si bien los idiomas
cuentan con reglas para definir la estructura de una oración, sujeto-verbo-predicado por
ejemplo, la realidad es que muchas de las oraciones en ocasiones no se sujetan a una y
sólo una estructura ya definida. Por lo regular una oración puede ajustarse a varias
reglas o estructuras al mismo tiempo. Ello se debe a que si se busca clasificar oraciones
es necesario tomar en cuenta su semántica o intención. Una misma oración puede ser
entendida como una declaración, interrogación, exclamación, etc. Es claro que los
conjuntos de entrada y salida, en este caso, oraciones y su clasificación esperada, no
6
Capítulo 1. Introducción
•
•
•
están bien delimitados y estructurados. Pero por otro lado, como seres humanos somos
capaces de comunicarnos de manera oral y también somos capaces de entender y actuar
en función de los mensajes recibidos y su intención. En este sentido, existen
aplicaciones exitosas de Redes Neuronales Artificiales, bajo dominios restringidos, en
el Área de Reconocimiento de Voz.
Problemas No Lineales: Analicemos el caso particular de la Optimización
Matemática. Aquí se tienen conjuntos de entradas y salidas bien especificadas. Por lo
regular, se cuenta con una función objetivo y un conjunto de restricciones. La idea es
Maximizar o Minimizar la función al encontrar los valores de sus variables que la
optimicen y que además satisfagan las restricciones dadas. La instancia en la cual la
función objetivo y las restricciones son todas funciones lineales está sumamente
estudiada y se cuenta con soluciones algorítmicas “convencionales” eficientes. Sin
embargo, la gran mayoría de los problemas de optimización no son de naturaleza lineal.
Una búsqueda exhaustiva es no factible ya que el conjunto de los posibles valores de
que pueden tomar las variables es por lo regular infinito. Actualmente la Optimización
No Lineal es un área de Investigación de desarrollo intenso. Hay una gran cantidad de
Investigadores involucrados en la búsqueda de metodologías y soluciones para este tipo
de problemas. El campo de las Redes Neuronales Artificiales ha logrado aportar guías
respecto a la manera en la que problemas particulares podrían ser abordados al
proporcionar información geométrica y/o topológica respecto al espacio de búsqueda de
posibles soluciones, o bien al proporcionar soluciones bastante cercanas a las soluciones
óptimas.
Problemas de Predicción: Consideremos la situación en la cual contamos con una
serie de eventos dependientes del tiempo y para los cuales se desea saber como se
comportará esa serie pero en el futuro. Este tipo de estudios han encontrado nichos de
trascendencia vital para los seres humanos tales como la predicción de sismos, tornados,
actividad volcánica, el clima, e incluso en cuestiones de salud como análisis de
electrocardiogramas para predicción de infartos o bien en el diagnóstico de algunos
tipos de cáncer. El “Santo Grial” de los Economistas es un modelo que les permita
predecir el comportamiento futuro de las Bolsas de Valores. Es bien sabido que en este
tipo de situaciones la sola medición de los factores involucrados directos por lo regular
no es suficiente. Es decir, por ejemplo, el comportamiento de la Bolsa de Valores no
sólo se rige por el intercambio de divisas o por el mercado accionario, también se puede
ver afectado por factores externos como las declaraciones de un mandatario, por
movimientos sociales, o hasta actividades como el terrorismo. Estos factores por lo
regular son muy difíciles de modelar y predecir, pero influyen y están presentes de
manera intrínseca en las mediciones. Las Redes Neuronales Artificiales han encontrado
un nicho de aplicación exitoso al efectuar predicciones sobre series de tiempo o bien al
identificar predictores dentro de éstas: subsecuencias dentro de una serie de tiempo que
sirven como patrones para identificar eventos futuros como las devaluaciones de las
monedas, por ejemplo.
Problemas computacionalmente complejos: Dentro de la Teoría de la Computación
existe la llamada Completez NP. Un problema caracterizado como NP-Completo se
entiende, informalmente, como aquel para el cual no se ha encontrado una solución
7
Una Introducción al Cómputo Neuronal Artificial
algorítmica eficiente, es decir, no se ha determinado un algoritmo ejecutado sobre una
computadora convencional que lo resuelva en un tiempo razonable. Es importante
mencionar también que para este tipo de problemas tampoco se ha demostrado que no
puedan ser resueltos de manera eficiente. La clase de problemas NP-Completos tiene en
su haber a algunos bien conocidos como el Problema del Agente Viajero (PAV), el
Problema de la Satisfactibilidad de una Proposición en Forma Normal Conjuntiva
(SAT-CNF), el Problema del Cliqué de Orden k (k-Cliqué), el Problema del Circuito
Hamiltoniano, etc. De hecho, hasta el día de hoy se han caracterizado a millares de
problemas como NP-Completos, y la cuenta sigue en aumento al publicarse en la
literatura, año con año, nuevos problemas identificados. El consenso mayoritario entre
los expertos de la Teoría de la Computación, y basado únicamente en las experiencias e
información con que se cuenta, apunta a que para los problemas NP-Completos no
existirán soluciones algorítmicas eficientes. Ello quiere decir que existiría una noción
clara de lo que es un problema computacional “fácil” y un problema computacional
“difícil”. Lo importante es que entonces se estaría reconocimiento la ausencia de
soluciones eficientes para éstos últimos. Otra cuestión relevante es que existen una gran
cantidad de problemas prácticos que a final de cuentas se reducen a un problema
NP-Completo. Por lo tanto, tampoco podemos ignorarlos debido a que efectivamente,
bajo tales instancias, se requiere solucionarlos. Nuevamente, se tienen arquitecturas de
Redes Neuronales Artificiales que han proporcionado soluciones aproximadas a
instancias de entrada para algunos problemas NP-Completos. Lo mejor es que de hecho
estas arquitecturas proporcionan en algunos casos soluciones con rangos de error muy
bajos, usando pocos elementos de Cómputo Neuronal y con un tiempo de ejecución
sumamente corto.
1.1 Redes Neuronales Biológicas
Como bien sabemos una Red Neuronal Biológica se forma por células nerviosas, las
neuronas, las cuales se encuentran interconectadas. En el cuerpo de una neurona, el cuál
contiene su Núcleo, es donde la mayor parte de la Computación Neuronal se efectúa. Véase
la Figura 1.1. Las Dentritas son ramificaciones a través de las cuales una neurona recibe
las señales de entrada. Por otro lado, el Axón es una ramificación que puede llegar a tener
cientos o hasta miles de veces la longitud del diámetro del núcleo y su objetivo es propagar
una señal. Por lo regular la propagación es en un único sentido pero de hecho es posible
encontrar axones bidireccionales. El axón en su parte final se ramifica. A estas
ramificaciones se les llama en conjunto Región Pre-Sináptica. Por último, cada
ramificación termina en una Sinapsis. Es en las sinapsis donde precisamente una neurona
transmite su señal al propagarla con todas aquellas neuronas con las cuales tiene
conexiones. Nótese que la descripción que acabamos de presentar es muy similar a la
clasificación comúnmente usada para presentar los componentes de una computadora
digital “convencional”: tenemos entonces a las dentritas como los dispositivos de entrada,
el núcleo de la neurona como su CPU y finalmente las sinapsis como los dispositivos de
salida. De allí la razón de considerar a la neurona como la unidad básica del Cómputo
Neuronal.
8
Capítulo 1. Introducción
Dentritas
(Entradas)
Axón
Región
Pre-sináptica
(Salidas)
Núcleo
Figura 1.1. Componentes principales de una Neurona Biológica.
Las neuronas pueden ser clasificadas en 3 tipos de acuerdo al rol que cumplen
dentro de una Red Neuronal:
• Neuronas aferentes:
o Transmiten mensajes al interior del organismo los cuales proceden de los receptores
sensoriales (vista, tacto, olfato, etcétera).
• Neuronas eferentes:
o Llevan mensajes a las estructuras ejecutoras haciendo que los músculos se
contraigan o relajen y también al ordenar a las glándulas la secreción de hormonas.
• Interneuronas:
o Sirven como puntos de conexión entre otras neuronas dentro del sistema nervioso
central y constituyen aproximadamente el 97% de todas las células nerviosas.
Veremos en secciones posteriores como que es que esta clasificación es sumamente útil, ya
que en una Red Neuronal Artificial efectivamente identificaremos a las neuronas aferentes
(la entrada de la red), las interneuronas y a las neuronas eferentes (la salida de la red). De
acuerdo a su rol es como los algoritmos de aprendizaje aplican cambios y ajustes.
Parte del poder del Cómputo Neuronal radica en la capacidad de las neuronas para
transportar y transmitir mensajes. A esta propiedad se le conoce como Excitabilidad.
Analicemos de manera superficial como que es que una neurona transmite un mensaje.
Como cualquier célula, una neurona es delimitada por su membrana. La membrana de la
neurona se encuentra Polarizada. Es decir, en el exterior se presenta una baja
concentración de iones de potasio mientras que en su interior esta concentración es alta. Por
otro lado, se tiene una alta concentración de iones de sodio en el exterior y una baja
concentración en el interior. Estas concentraciones no se equilibran gracias a que la
membrana tiene diferencias de permeabilidad lo que impide el paso de iones del interior al
exterior y viceversa.
9
Una Introducción al Cómputo Neuronal Artificial
Sin embargo, es posible que la permeabilidad de la membrana de una neurona se
altere momentáneamente permitiendo que las concentraciones de los iones se equilibren.
Este fenómeno provoca entonces un súbito incremento de actividad eléctrica lo cual da
lugar a un Impulso Nervioso que se propaga a lo largo de la membrana. Una vez que la
neurona se ha Despolarizado, es decir, se ha liberado del impulso nervioso, inicia un
proceso rápido que la coloca en un estado de Reposo. En esta fase se reacomodan y
redistribuyen los iones de sodio y potasio en el interior/exterior de la membrana, así como
las moléculas que la forman para retornar a su estado de permeabilidad original. Durante
esta fase a la neurona se le llama Refractaria ya que no es capaz de transmitir impulsos
nerviosos.
Los impulsos nerviosos, dentro de una neurona, se mueven de las dentritas al
núcleo, del núcleo al axón y finalmente del axón a la región pre-sináptica. Cuando el
impulso llega a los extremos finales de las ramificaciones en la región pre-sináptica, es
decir, a las sinapsis, se encuentra con una discontinuidad. A este espacio, junto con una
sinapsis de la neurona que porta el impulso y la dentrita de una neurona a la cual se le
transmitirá el impulso, se le denomina Espacio Sináptico o Unión Sináptica. Véase la
Figura 1.2.
Dentrita
(Entrada)
Uni ón
Sin áptica
Neurotransmisor
Sinapsis
(Salida)
Figura 1.2. Componentes de la Unión Sináptica entre dos neuronas.
Cuando el impulso nervioso alcanza a una sinapsis provoca la liberación de una
sustancia química denominada Neurotransmisor. Los neurotransmisores están alojados en
vesículas adheridas a las terminaciones del axón. Al día de hoy se tienen identificados
decenas de tipos de neurotransmisores entre los que se encuentran, por ejemplo, la
adrenalina o la acetilcolina. La secreción ocupa el espacio sináptico y provoca los cambios
de permeabilidad en la membrana de la neurona receptora. De esta manera el impulso
nervioso pasa de una neurona a la siguiente y de hecho continúa su camino a través del
nervio correspondiente. Finalmente, el neurotransmisor es destruido por la acción de
enzimas con lo que se deja nuevamente libre el espacio sináptico.
Dado que una neurona puede tener miles de sinapsis, entonces ésta se puede
conectar, y por tanto transmitir su impulso, a otros miles de neuronas. Véase la Figura 1.3.
Es más, una neurona puede conectarse consigo misma. En otras palabras, al procesar la
10
Capítulo 1. Introducción
señal que ella misma generó se tiene un proceso que en ocasiones es llamado de
Retroalimentación. No todas las conexiones entre neuronas tienen los mismos valores o
pesos. Y de hecho esos valores o pesos determinan si la membrana de la neurona que recibe
el impulso lo transmitirá o no. Ello se debe a la existencia de Sinapsis Excitadoras y
Sinapsis Inhibidoras. Estas diferencias de pesos o prioridades son moduladas
precisamente por los neurotransmisores involucrados, los cuales en ocasiones son
clasificados en Neurotransmisores Excitadores y Neurotransmisores Inhibidores. Un
neurotransmisor excitador incrementa las probabilidades de que la neurona receptora
continúe con la transmisión del mensaje, mientras que un neurotransmisor inhibidor puede
encargarse de bloquear su transmisión.
Región
Pre-sináptica
Neurona i+1
Neurona i+1
Dentritas
Neurona i+1
Dentritas
Neurona i
Axón i+1
Región
Pre-sináptica
Neurona i+3
Neurona i
Dentritas
Neurona i+2
Axón i
Axón i+3
Región
Pre-sináptica
Neurona i
Región
Pre-sináptica
Neurona i+2
Neurona i +3
Neurona i+2
Axón i+2
Dentritas
Neurona i+3
Figura 1.3. Porción de una Red Neuronal Biológica.
A partir de este punto nos será más conveniente representar a las neuronas
(biológicas o artificiales) en términos esquemáticos. Véase la Figura 1.4. A toda neurona
se le visualizará como una entidad que cuenta con n entradas (las dentritas). En cada
entrada se recibirá un valor proveniente de otra neurona, o bien, tales valores pueden
formar también una entrada proveniente del mundo exterior. En el primer caso estaríamos
modelando una interneurona, mientras que en el segundo nuestra neurona sería del tipo
11
Una Introducción al Cómputo Neuronal Artificial
aferente. Ello implica que el conjunto de las entradas de una neurona puede ser
representado como un vector con n componentes. Cada entrada i, i = 1, 2, …, n, tendrá
asociada un peso wi. Este peso tendrá la función de neurotransmisor. El peso wi se asociará
al valor recibido en la entrada i. La combinación de ambos puede caracterizar a la conexión
como excitadora o como inhibidora. Todo par (entrada i, peso wi) es llevado al núcleo en
donde se efectuará el Cómputo Neural. El resultado obtenido es un único valor el cual es
distribuido en m salidas (las sinapsis). Estas salidas pueden conectarse con el mundo
exterior, en donde por instancia tenemos una neurona de tipo eferente. Si, por otro lado,
cada salida se conecta con otra neurona entonces tenemos una interneurona. Nótese que de
hecho podemos tener las siguientes caracterizaciones de neuronas en función de su relación
con otras neuronas y con el mundo exterior:
• Aferente/Eferente: entradas provenientes del exterior, salidas enviadas al exterior.
• Aferente/Interneurona: entradas provenientes del exterior, salidas enviadas a otras
neuronas.
• Interneurona/Eferente: entradas provenientes de otras neuronas, salidas enviadas al
exterior.
• Interneurona: entradas provenientes de otras neuronas, salidas enviadas a otras
neuronas.
W1
W2
Salida 1
Núcleo
Salida 2
Wn
Salida m
Figura 1.4. Representación esquemática de una neurona (biológica o artificial).
Con base en los puntos anteriores, también contamos con los elementos para una
representación esquemática de Red Neuronal (biológica o artificial). En la Figura 1.5 se
presenta un ejemplo de fragmento de esquema de Red Neuronal. Se puede apreciar
claramente la presencia de 3 neuronas y la manera en que se encuentran conectadas sus
respectivas entradas y salidas. A cada neurona le es asignado un índice. Por lo tanto, para
diferenciar los pesos a estos se les asignan dos índices de manera que wi,j denota al j-ésimo
peso de la i-ésima neurona.
12
Capítulo 1. Introducción
W i+2,1
W i+2,2
Neurona i+2
W i,1
W i+2,n
W i,2
Neurona i
W i,n
W i+1,1
W i+1,2
Neurona i+1
W i+1,n
Figura 1.5. Ejemplo de Representación Esquemática de un fragmento de Red Neuronal.
1.2 Principios del Diseño de Redes Neuronales Artificiales
A partir de este punto nos adentraremos en los aspectos teóricos detrás de las Redes
Neuronales Artificiales. También seremos más concretos y formales al especificar los
principios detrás de su funcionamiento e interacción con su “mundo exterior” y sus
procesos de aprendizaje. Finalmente, haremos mención de los modelos básicos de neuronas
y también de las estructuras básicas de Redes Neuronales.
Los principios básicos de las Redes Neuronales Artificiales fueron formulados por
Warren McCulloch y Walter Pitts en 1943 al proponer la idea de analizar el Cómputo
Neuronal (Biológico) por medio de operaciones elementales (sumas, multiplicaciones y
lógica básica). Establecieron cinco principios como punto de partida:
• La actividad de una neurona es “Todo o Nada”. Se refiere al hecho de que las salidas
proporcionadas por la neurona son binarias: 0 o 1. La neurona proporcionará un 1 (el
“todo”) si las entradas que recibe, y al ser “sumadas” de alguna manera, proporcionan
un valor lo “suficientemente alto” precisamente para proporcionar la salida 1. De lo
contrario, se proporciona la salida 0 (la “nada”). Es claro que entonces contamos con
Neurona Binaria.
• Un cierto número fijo de sinapsis, mayor a 1, deben ser estimuladas dentro de un
intervalo de tiempo para que una neurona sea excitada. Entenderemos a la excitación de
la neurona como el simple hecho de que inicia el procesamiento de su entrada. Es decir,
sólo se ha planteado un criterio para “encender” una neurona.
13
Una Introducción al Cómputo Neuronal Artificial
•
El único retraso no despreciable dentro de la Red Neuronal es el retraso sináptico. En
otras palabras, para efectuar Cómputo Neuronal se deben tomar en cuenta los tiempos
de espera para que las sinapsis proporcionen su salida.
• La actividad de cualquier sinapsis inhibidora impide por completo la excitación de la
neurona en ese momento. De hecho, la activación de una sola sinapsis inhibidora
“apagará” a la neurona durante un tiempo, independientemente de las sinapsis
excitadoras que se hayan activado en ese mismo momento.
• La estructura de las conexiones entre las neuronas de la red nunca cambia.
Estos cinco principios aún se aplican (no necesariamente todos al mismo tiempo) en el
diseño de Redes Neuronales Artificiales. Además cimentaron las bases a partir de las
cuales, de acuerdo a McCulloch y Pitts, las neuronas y las Redes Neuronales deberían ser
modeladas y estudiadas.
Por otro lado, en 1949, Donald Hebb estableció un principio que también es
utilizado en la actualidad: la Ley de Aprendizaje Hebbiano (Hebbian Rule, Hebbian
Learning Law). Esta ley se cita de la siguiente manera:
“Cuando un axón de una célula P está lo suficientemente cerca de una célula Q
y cuando P de manera repetida y persistente toma parte en la excitación de Q,
entonces algún proceso de crecimiento o cambio metabólico ocurre en una o
ambas células tal que la eficiencia de P es incrementada.”
¿Qué significa que la eficiencia de una neurona sea incrementada? Veamos primero
un ejemplo clásico que se utiliza para visualizar el proceso de Aprendizaje Hebbiano.
a) Supóngase que una célula S causa salivación y es excitada por una célula F la cual, a su
vez, es excitada por el avistamiento de comida.
b) Supóngase además que una célula L, la cual es excitada al escuchar una campana,
también se conecta con S, pero L no es capaz de encender o excitar, por sí sola, a S:
necesita a F.
c) Ahora, cada vez que S es excitada por F, también recibe estimulación proveniente de L.
Sin embargo, la conexión entre S y L es débil o no cuenta con prioridad suficiente de
manera que S no detecta o ignora el impulso proveniente de L. Como ya comentamos,
para excitar a S, L necesita excitar a F y ésta a su vez excita a S.
d) Eventualmente, por repetición sucesiva y por cambios metabólicos o de algún otro tipo,
L será capaz de excitar a S sin que F intervenga. Es decir, tales cambios incrementan el
peso (o prioridad) de la entrada de L hacia S.
e) L ha aprendido a estimular a S y a su vez S ha aprendido a detectar y responder a las
señales de L (sin intervención alguna de F).
De acuerdo al ejemplo anterior, es claro que el la Ley de Aprendizaje Hebbiano
implica la modificación de las sinapsis para controlar la memoria a largo plazo a través de
la generación de nuevas conexiones entre neuronas o a través del refuerzo de las
conexiones existentes entre éstas. Este tipo de modificaciones pueden incluso requerir el
que las neuronas se desplacen.
14
Capítulo 1. Introducción
Desde el punto de vista de las Redes Neuronales Artificiales se plantea la existencia
de un proceso de modificación de pesos en las entradas de cualquier neurona a fin de
mejorar su eficiencia. Esta variación de pesos es un evento que ocurre en todo modelo de
Red Neuronal Artificial. En la siguiente Sección veremos los principios de los que parte el
proceso de aprendizaje neuronal.
1.3 Principios del Aprendizaje o Entrenamiento
de una Red Neuronal Artificial
Considérese un conjunto formado por N vectores:
{X1, X2, …, XN}
Donde:
ª xi ,1 º
« # »
« »
X i = « xi ,k »
« »
« # »
« xi , P »
¬ ¼
i = 1, 2, …, N
xi,k ∈ \
k = 1, 2, …, P
A tal conjunto se le llamará el Conjunto de Vectores de Entrada para una Red
Neuronal. Ahora considérese un segundo conjunto de N vectores:
{D1, D2, …, DN}
Donde:
ª di ,1 º
« # »
«
»
«
d
Di = i ,k »
«
»
« # »
« di ,m »
¬
¼
i = 1, 2, …, N
di,k ∈ \
k = 1, 2, …, m
15
Una Introducción al Cómputo Neuronal Artificial
Al conjunto {D1, D2, …, DN} se le llamará el Conjunto de Vectores de Salida Esperada
para una Red Neuronal.
Se asumirá que dado un vector de entrada Xi, la salida que se espera proporcione la
Red Neuronal será el vector Di. El conjunto de vectores de entrada y el conjunto de
vectores de salida esperada forman el Conjunto de Entrenamiento de la Red Neuronal.
Nótese que de hecho la Red Neuronal efectuará un mapeo de vectores de entrada en \ P a
vectores de salida en \ m .
El conjunto de entrenamiento se utiliza para ajustar a las neuronas que forman una
Red Neuronal. El procedimiento de ajuste trata de modificar los pesos de las neuronas de
manera que para cualquier vector de entrada Xi el vector de salida Si proporcionado por la
red sea igual a Di. De hecho, en la práctica sólo se espera que Si sea tan cercano como sea
posible a Di. Ello implica que las salidas proporcionadas por la red tendrán un error
respecto a las esperadas. Por lo tanto, el procedimiento de ajuste en estos casos también
tratará de minimizar los errores. El procedimiento de ajuste de las neuronas de una red es
llamado Procedimiento de Aprendizaje o Procedimiento de Entrenamiento.
Aquellas arquitecturas de Redes Neuronales que requieren un conjunto de
entrenamiento formado por los vectores de entrada y por los vectores de salida esperada son
agrupadas en una clase denominada Redes Neuronales Supervisadas. El término
“Supervisado” surge del hecho de que los procedimientos de entrenamiento cuentan con un
parámetro para supervisar el desempeño actual de la red. Tal parámetro es usado para
determinar las mejores modificaciones a aplicar con la finalidad de mejorar el desempeño.
En las Redes Supervisadas el desempeño por lo regular se mide numéricamente con la
magnitud del Error de Aprendizaje, es decir, mediante la diferencia entre Di y Si. En
función de la magnitud obtenida se deciden los cambios a aplicar.
En ocasiones, sólo se cuenta con el conjunto de vectores de entrada. Estas
situaciones por lo regular se presentan en problemas relacionados con la agrupación de
tales vectores en clases de equivalencia. Un ejemplo clásico de un problema con este
enfoque es el del Reconocimiento Automático de Caracteres Manuscritos. Tenemos
conocimiento previo respecto a cuantas clases necesitamos para clasificar a los caracteres:
deseamos que aquellos caracteres que corresponden a la letra x, por ejemplo, estén
agrupados en la misma clase. Las arquitecturas de Redes Neuronales que parten de la
hipótesis de que el conjunto de entrenamiento únicamente se forma por los vectores de
entrada, forman parte de las denominadas Redes Neuronales No Supervisadas. Es claro
que los procedimientos de entrenamiento de las Redes No Supervisadas no pueden medir
numéricamente la magnitud del error de aprendizaje. Por lo tanto, estos procesos tratan de
determinar la estructura que forman los vectores de entrada al tomar en cuenta las
similitudes entre éstos. Para determinar en que clase debe ser colocado un vector, el
proceso de análisis de similitud se puede apoyar, por ejemplo, en evaluación y comparación
de características topológicas o geométricas.
16
Capítulo 1. Introducción
1.4 Estructuras Básicas de Neuronas y Redes
Dentro de las neuronas artificiales básicas en primer lugar debemos mencionar al
Perceptrón. Es quizás la neurona artificial más popular. Su mecanismo de aprendizaje está
basado en un entrenamiento supervisado y fue propuesta en 1958 por el psicólogo Frank
Rosenblatt. Por otro lado contamos con el Adaline (Adaptive Linear Neuron, Neurona
Lineal Adaptiva), la cual fue propuesta por Bernard Widrow en 1960. Esta neurona es
también conocida como ALC (Combinador Lineal Adaptivo). Si bien el Perceptrón,
históricamente, precede al Adaline, la última será estudiada en primer lugar en el
Capítulo 3 y posteriormente el Perceptrón en el Capítulo 4. Ello se debe a que el Adaline
cuenta en su especificación con parte de la estructura básica del Perceptrón. También
veremos que los mecanismos para entrenar a una neurona Adaline forman una serie de
preliminares para comprender mejor los procedimientos para entrenar a un Perceptrón, y
posteriormente, en el Capítulo 6, a una red formada por Perceptrones.
En las décadas de los 50s y 60s se conjeturaba que una sola neurona sería capaz de
representar una amplia gama de problemas. Desgraciadamente, veremos que una neurona,
como único elemento de Cómputo Neural, no es capaz de aprender cualquier problema y de
hecho el número de problemas que puede aprender es en realidad limitado. Sin embargo
notaremos posteriormente que estas restricciones son superadas al utilizar una Red
Neuronal. Entre los primeros problemas para los cuales se encontraron soluciones exitosas
al considerar redes de varias neuronas podemos mencionar, por ejemplo, al Modelado de
Funciones Booleanas de n variables, Reconocimiento de Patrones y Clasificación
Automática. Sin embargo, ante tales éxitos, también es natural plantearnos las siguientes
preguntas:
• ¿Qué problemas pueden ser modelados mediante una Red Neuronal?
• ¿Cuántas neuronas se requieren para garantizar que una red aprenderá un problema
dado?
• ¿Existe algún criterio que permita determinar el tiempo que requerirá el proceso de
entrenamiento de manera que se asegure el contar con un modelo apropiado del
problema y su solución?
Si bien el campo de las Redes Neuronales Artificiales ha logrado importantes
contribuciones, tal y como veremos a lo largo del texto, estas preguntas, de carácter
fundamental, aún siguen abiertas.
Las neuronas que forman parte de una red estarán interconectadas y agrupadas en
Capas. Se tendrán 3 diferentes tipos de capas:
• Capa de Entrada: el conjunto de neuronas que recibe información proveniente del
exterior.
• Capa de Salida: el conjunto de neuronas que proporciona la salida final proporcionada
por la red.
• Capas Ocultas: conjuntos de neuronas ubicadas entre las capas de entrada y salida.
Todas las neuronas, independientemente de la capa en que se encuentren, contribuyen al
Cómputo Neural. Por otro lado, es claro que el rol de las neuronas de acuerdo a su posición
17
Una Introducción al Cómputo Neuronal Artificial
en una red es consistente con la clasificación que se tiene para las neuronas biológicas en
Aferentes, Eferentes, e Interneuronas. Considérese por ejemplo la Red Neuronal presentada
en la Figura 1.6. Se tiene una red formada por 6 neuronas de tipo Adaline. Las neuronas 1,
2 y 3 forman la capa de entrada y pueden ser caracterizadas como las neuronas aferentes.
Sólo se cuenta en este caso con una neurona eferente, aquella etiquetada como la neurona 6.
De hecho, la capa de salida de la red se forma exclusivamente por esta neurona.
Finalmente, se tiene sólo una capa oculta formada por las neuronas 4 y 5. Si bien estas
neuronas funcionan como puntos de conexión entre las capas de entrada y salida, lo que las
caracterizaría como interneuronas, veremos que juegan un papel importante durante los
procesos de aprendizaje.
W1,1
Adaline 1
W 1,2
z =w +
1,1
1,0
¦
z 1,1
sign(z )
y1,1
1,1
W 4,1
W1,n
X1
W 4,2
Adaline 4
z =w +
4,1
W2,1
X2
¦
z 4,1
sign(z )
y4,1
4,1
Adaline 6
W 4,3
W 2,2
z =w +
2,1
2,0
¦
z 2,1
sign(z )
W6,1
y2,1
2,1
W 5,1
W2,n
W 5,2
Xn
4,0
Adaline 2
Adaline 5
z =w +
5,1
W3,1
Adaline 3
5,0
¦
z 5,1
sign(z )
W6,2
z =w +
6,1
6,0
¦
z 6,1
sign(z )
6,1
y 6,1
Network
output
y5,1
5,1
W 5,3
W 3,2
z =w +
3,1
3,0
¦
z 3,1
sign(z )
y3,1
3,1
W3,n
Figura 1.6. Un Red formada por 6 neuronas tipo Adaline.
•
•
•
18
Entre las Redes Neuronales más populares podemos mencionar:
Red Madaline (Many Adaline): También propuesta por Bernard Widrow en 1962. Es
una Red Neuronal basada en neuronas tipo Adaline. Esta red ha proporcionado
soluciones a problemas asociados a la Predicción de Señales y el Reconocimiento de
Patrones.
Red de Retropropagación (Back-Propagation Network): Quizás la más popular dentro
del área de las Redes Neuronales. Se trata de una red multicapa formada por
Perceptrones. Esta red, y de hecho el área misma de las Redes Neuronales Artificiales,
adquieren relevancia científica al ser presentado en 1986, por David Rumelhart,
Geoffrey Hinton y Ronald Williams, el Algoritmo de Retropropagación. Este
algoritmo describe un método eficiente para el entrenamiento de este tipo de redes. Se
tienen reportadas aplicaciones exitosas de la Red de Retropropagación en áreas
relacionadas a la Predicción de Señales, Reconocimiento de Patrones, Reconocimiento
de Caracteres Manuscritos y Búsqueda de Soluciones Aproximadas para problemas
como la Identificación de Secuencias Proteínicas y el Problema del Agente Viajero,
entre otras muchas más.
Red de Hopfield: Propuesta por John Hopfield en 1982. Es una Red Neuronal que se
diferencia de las anteriores debido a que permite retroalimentación recurrente entre
neuronas. Es decir, cada neurona cuenta con una salida que a su vez se conecta con
Capítulo 1. Introducción
•
alguna de sus propias entradas. En las áreas de Reconocimiento de Patrones,
Reconocimiento de Caracteres Manuscritos y Clasificación Automática de Imágenes es
donde la Red de Hopfield ha encontrado un nicho de aplicación.
Red de Kohonen (Kohonen Network): Una aportación del finlandés Teuvo Kohonen.
Se trata de redes basadas en aprendizaje no supervisado y cuya finalidad es resolver el
problema de la clasificación automática. Esta red ha proporcionado soluciones a
problemas asociados al Reconocimiento de Patrones, Reconocimiento de Caracteres
Manuscritos, Clasificación Automática de Imágenes y Búsqueda de Soluciones
Aproximadas para problemas como el del Agente Viajero.
La solución de un problema mediante una única neurona o bien mediante una red de
neuronas impone importantes diferencias en cuanto a los mecanismos de aprendizaje a usar.
Intuitivamente se debe entender que entrenar a una Red Neuronal requiere procedimientos
más sofisticados que aquellos para el ajuste de una única neurona, aunque no por ello éstos
últimos son menos importantes. De hecho, por ejemplo, veremos como es que el
mecanismo de aprendizaje del Perceptrón guarda una relación profunda con el mecanismo
de entrenamiento de una Red de Retropropagación. En realidad, existe una gama de
métodos de entrenamiento disponibles para redes como la Madaline o la de Perceptrones.
Entre éstos podemos mencionar:
• Aprendizaje basado en Solución por Mínimos Cuadrados
• Madaline Rule I
• Madaline Rule II
• Madaline Rule III
• Retropropagación (Back-Propagation)
En los Capítulos 2, 5 y 6 describiremos a detalle algunas de estas metodologías.
19
Una Introducción al Cómputo Neuronal Artificial
20
Una Introducción al Cómputo Neuronal Artificial
2. Preliminares
Matemáticos
Una Introducción al Cómputo Neuronal Artificial
22
Capítulo 2. Preliminares Matemáticos
El objetivo de este Capítulo es el de describir algunas de las herramientas
Matemáticas necesarias para abordar el estudio de las Redes Neuronales Artificiales. En la
Sección 2.1 efectuaremos un breve repaso relacionado con el Gradiente de una Función y
su relación con sus Máximos y Mínimos. En la Sección 2.2 comentaremos los fundamentos
del Método de Mínimos Cuadrados, una popular metodología de Regresión Lineal.
Abordaremos primero el caso del ajuste con una recta en el plano y posteriormente, en la
Sección 2.3, el ajuste con un hiperplano multidimensional. Finalmente, en la Sección 2.4
efectuaremos la demostración de la Desigualdad de Cauchy-Schwarz. Nuestro estudio de
las Redes Neuronales Artificiales iniciará formalmente a partir del Capítulo 3, por lo que
aquellos lectores que ya se encuentren familiarizados con los temas antes mencionados
pueden sin problema alguno omitir el presente Capítulo.
2.1 Gradientes y Búsquedas de Máximos y Mínimos
Consideremos una función f tal que f: \ n → \ . Es decir, nuestra función recibirá
como entrada un vector n-Dimensional y producirá como salida un escalar. El Vector
Gradiente de f en el punto (x1, …, xn), denotado por ∇f(x1, …, xn), se define como:
ªδ f º
«δ x »
« 1»
«δ f »
∇f ( x1 ,..., xn ) = «« δ x2 »»
« # »
«
»
«δ f »
«¬ δ xn »¼
(Ecuación 2.1.1)
δf
denota a la derivada parcial de f respecto a la variable xi, i = 1, 2, …, n.
δ xi
δf
no es más que la derivada “convencional”, aquella estudiada en los
Recordemos que
δ xi
Donde
cursos de Cálculo de una Única Variable, en donde las variables x1, x2, …, xn, excepto la
variable xi, son todas asumidas como constantes.
Sean e1, e2, …, en los vectores que forman la base canónica de \ n . Entonces el
vector gradiente de f puede ser descrito como la combinación lineal:
23
Una Introducción al Cómputo Neuronal Artificial
ªδ f º
«δ x »
« 1»
«δ f »
∇f ( x1 ,..., xn ) = «« δ x2 »»
« # »
«
»
«δ f »
«¬ δ xn »¼
δf
δf
δf
δf
⇔ ∇f ( x1 ,..., xn ) =
e1 +
e2 +
e3 + ... +
e
δ x1
δ x2
δ x3
δ xn n
ª1 º
«0»
δf « » δf
«0» +
=
δ x1 « » δ x2
«# »
«¬ 0 »¼
ª0 º
«1 »
« » δf
«0 » +
« » δ x3
«# »
«¬0 »¼
ª0º
«0»
« »
δf
«1 » + ... +
δ xn
« »
#
« »
«¬0 »¼
ª0 º
«0 »
« »
«0 »
« »
«# »
«¬1 ¼»
El i-ésimo componente de ∇f nos proporciona la razón de cambio de f en la dirección del
vector unitario ei, i = 1, 2, …, n.
ªδ f º
Analicemos primero el caso con n = 1. Ello implica que ∇f(x1) = «
» = [ f '( x1 ) ] .
¬ δ x1 ¼
Es decir, el único componente del gradiente de f, f: \ → \ , no es más que la derivada
“convencional”. Ese único componente nos proporciona la razón de cambio de f en la
dirección del eje X1. La evaluación de la derivada de f en el punto x0, f '( x0 ) , desde un
punto de vista geométrico, nos proporciona la pendiente de la recta tangente a f en el punto
(x0, f(x0)). Véase la Figura 2.1. El signo de la pendiente nos proporciona también
información acerca de la dirección hacia la cual f crece más rápido. Una pendiente positiva
nos informa que la función, partiendo de x0, crece más rápido en la dirección positiva del
eje X1 (Figura 2.1.a). Una pendiente negativa es indicativo de que, partiendo de x0, f
decrece en la dirección positiva del eje X1 (Figura 2.1.b). O de manera equivalente, una
pendiente negativa nos indica que f crece cuando nos movemos en la dirección negativa del
eje X1. Cuando f '( x0 ) = 0 entonces se ha encontrado un punto crítico que bien puede ser un
máximo, un mínimo, o un punto de inflexión.
24
Capítulo 2. Preliminares Matemáticos
f
f
x0
X1
x0
X1
a)
b)
Figura 2.1. Interpretación del signo de las pendientes de las Rectas Tangentes a una función f.
a) Una pendiente positiva señala la dirección de crecimiento de f.
b) Una pendiente negativa indica que f decrece en la dirección positiva del eje X1.
Ahora bien, consideremos una función f tal que f: \ 2 → \ . Por ejemplo, sea f la
función f(x1, x2) = x22 − x12 . Su vector gradiente estará dado por
ª −2 x1 º
∇f = «
»
¬ 2 x2 ¼
Al evaluar el vector gradiente en el punto (-2,3), y al expresarlo como combinación lineal
de la base canónica {e1, e2}, obtenemos:
ª 4 º ª 4 º ª0 º
∇f (−2,3) = « » = « » + « » = 4e1 + 6e2
¬ 6 ¼ ¬ 0 ¼ ¬6 ¼
El primer componente de ∇f(-2,3) nos indica que la razón de cambio en dirección
ª 4º
del vector « » , el cual es paralelo al eje X1, es 4. El segundo componente de ∇f(-2,3) nos
¬0¼
ª0º
indica que la razón de cambio en dirección del vector « » , paralelo al eje X2, es 6. De
¬6¼
hecho, las razones de cambio al ser ambas positivas denotan que la función crece al
moverse en cualquiera de esas dos direcciones partiendo del punto (-2,3). Es más, se tiene
ª0º
mayor crecimiento en la dirección « » .
¬6¼
Los dos ejemplos anteriores nos permiten observar como es que efectivamente cada
componente del vector gradiente nos informa acerca de la razón de cambio de una función
en las direcciones de los ejes principales de \ n . En el caso particular de n = 1 de hecho no
tenemos otras maneras de movernos más a que a lo largo del eje X1. Sin embargo, cuando
25
Una Introducción al Cómputo Neuronal Artificial
n > 1 es claro que podemos considerar direcciones no necesariamente paralelas a los ejes
principales. Y además, nos interesará conocer las razones de cambio de una función cuando
nos movemos a lo largo de tales direcciones. Por ejemplo, ¿qué tanto crece o decrece la
función f(x1, x2) = x22 − x12 cuando nos movemos, a partir de un punto dado, en la dirección
ª −3
del vector «
¬ 18
T
−3 º
» ?
18 ¼
Si se requiere la razón de cambio de f en la dirección del vector arbitrario y unitario
u, entonces se debe recurrir a la Derivada Direccional de f en la Dirección de u. Se le
denota por Duf(x1, …, xn) y se calcula mediante el producto punto del vector gradiente de f
(Ecuación 2.1.1) y el vector u:
Du f ( x1 ,..., xn ) = ∇f ⋅ u
ª u1 º
«u »
= ∇f ⋅ « 2 »
«#»
« »
¬un ¼
δf
δf
δf
u1 +
u2 + ... +
u
=
δ x1
δ x2
δ xn n
(Ecuación 2.1.2)
A diferencia del gradiente, la derivada direccional nos proporciona un escalar. Ello
se debe a que describe únicamente la razón de cambio de f cuando nos movemos, a partir
del punto (x1, …, xn), en la dirección del vector u (nuestro vector de dirección arbitraria). El
signo de tal escalar nos informará si la función crece o decrece al tomar la dirección u y
partiendo del punto (x1, …, xn).
Sea el vector unitario
ª
«
u1 = «
«
«
¬
−3 º
18 »
»
−3 »
18 »¼
Ahora deseamos conocer la derivada direccional de f(x1, x2) = x22 − x12 en el punto (-2,3) en
la dirección de u1. Por lo tanto, al aplicar la Ecuación 2.1.2, se tiene:
26
Capítulo 2. Preliminares Matemáticos
Du1 f (−2,3) = ∇f (−2,3) ⋅ u1
−3 º
§ −3 · § −3 ·
18 »
» = 4¨
¸ + 6¨
¸
−3 »
© 18 ¹ © 18 ¹
18 »¼
ª
ª4º «
=« »⋅«
¬6 ¼ «
«
¬
=−5 2
Ello implica que partiendo del punto (-2,3) y moviéndose en la dirección del vector u1, la
función f tiene una razón de cambio −5 2 . Tal razón, al ser negativa, nos indica que de
hecho la función decrece al moverse en esa dirección.
Consideremos el vector unitario
ª −1º
u2 = « »
¬0¼
La derivada direccional de f en el punto (-2,3) en la dirección de u2 es:
Du2 f (−2,3) = ∇f (−2,3) ⋅ u2
ª 4 º ª −1º
=« »⋅« »
¬6¼ ¬ 0 ¼
=−4
Partiendo del punto (-2,3) y moviéndose en la dirección del vector u2, la función f tiene una
razón de cambio -4. Nuevamente, la función decrece al moverse en esa dirección.
Ahora sea el vector unitario
ª
«−
u3 = «
«
«
¬
2 º
13 »
»
3 »
13 »¼
27
Una Introducción al Cómputo Neuronal Artificial
La derivada direccional de f en el punto (-2,3) en la dirección de u3 es:
Du3 f (−2,3) = ∇f (−2,3) ⋅ u3
ª
−
ª 4º «
=« »⋅«
¬6¼ «
«
¬
10
=
13
2 º
13 »
»
3 »
13 »¼
Concluimos que partiendo del punto (-2,3) y moviéndonos en la dirección u3, la función f
10
tiene una razón de cambio
. Aunque la razón es positiva, es menor que la obtenida
13
ª 4º
para la dirección « » , con valor 4. Ello implica que en la dirección dada por u3 la función
¬0¼
ª4º
crece aunque más “lento” que usando la dirección « » .
¬0¼
•
•
Plantearemos dos observaciones:
Dado un punto (x1, …, xn) es claro que es posible determinar una cantidad enorme de
derivadas direccionales de f en ese punto.
¿Cómo encontrar aquel vector cuya dirección, y partiendo del punto (x1, …, xn), nos
indique la máxima razón de cambio de f? La dirección de ese vector será también la
dirección de máximo crecimiento de f.
Por la teoría del Algebra Lineal se sabe que el producto punto entre ∇f y el vector
unitario u también puede ser expresado como:
Duf(x1, …, xn) = ∇f(x1, …, xn)⋅u
= ||∇f(x1, …, xn)|| ||u|| cos θ
= ||∇f(x1, …, xn)|| cos θ
(Por la Ecuación 2.1.2)
(recuérdese que ||u|| = 1)
(Ecuación 2.1.3)
Donde θ es el ángulo formado por los vectores ∇f y u.
El valor máximo del coseno se da cuando θ = 0. Ello implica que u y el vector
gradiente, ∇f, tienen la misma dirección. En ese caso la derivada direccional tendrá un
valor Duf(x1, …, xn) = ||∇f(x1, …, xn)||, que de hecho es también su valor máximo. Ello
implica que la dirección del vector gradiente nos indica hacia donde f tiene su máxima
razón de cambio. En este punto recalcamos que los componentes del vector gradiente, cada
uno por separado, proporcionan las razones de cambio en dirección de los ejes principales.
28
Capítulo 2. Preliminares Matemáticos
Pero en sí, el vector gradiente indica una dirección y es en esa dirección donde f tiene su
máximo crecimiento. Esta propiedad es sumamente útil si se requieren identificar máximos
en la función f.
Previamente establecimos que para f(x1, x2) = x22 − x12 su vector gradiente en el
ª 4º
punto (-2, 3) era ∇f(-2,3) = « » . La magnitud del vector gradiente está dada por:
¬6¼
||∇f(-2,3)|| =
42 + 62 = 52
ª 4º
Por lo tanto, partiendo del punto (-2, 3) y en la dirección dada por el vector « » , el vector
¬6¼
gradiente, se tiene la máxima razón de cambio de f, 52 , y en consecuencia su dirección
de máximo crecimiento. Cualquier derivada direccional en el punto (-2, 3) indicará una
razón de cambio menor o igual a la proporcionada por el vector gradiente.
Ahora nos plantearemos una nueva pregunta: ¿Cómo encontrar aquel vector cuya
dirección, y partiendo del punto (x1, …, xn), nos indique la mínima razón de cambio de f?
Sabemos por la Ecuación 2.1.3 que:
Duf(x1, …, xn) = ||∇f(x1, …, xn)|| cos θ
La función coseno tiene su valor mínimo cuando θ = π. Ello implica que los vectores u y ∇f
apuntan en direcciones opuestas. Por lo tanto, en ese caso, se tendrá que
Duf(x1, …, xn) = -||∇f(x1, …, xn)||
Entonces, es claro que la dirección opuesta a la del vector gradiente nos indica hacia donde
f tiene su mínima razón de cambio. Esta propiedad es sumamente útil si se requieren
identificar mínimos en la función f.
ª 4º
Para f(x1, x2) = x22 − x12 su vector gradiente en el punto (-2, 3) era ∇f(-2,3) = « » con
¬6¼
magnitud ||∇f(-2, 3)|| = 52 . Por lo tanto, partiendo del punto (-2, 3) y en la dirección dada
ª 4º
por el vector (-1) « » se tiene la mínima razón de cambio de f, - 52 . Cualquier otra
¬6¼
derivada direccional en el punto (-2, 3) indicará una razón de cambio mayor o igual a la
proporcionada por la dirección opuesta del vector gradiente.
29
Una Introducción al Cómputo Neuronal Artificial
2.2 Regresión Lineal
En ocasiones se requiere inferir un modelo o sistema a partir de datos
experimentales. La importancia y finalidad de tal inferencia radica en que entonces podrá
ser posible entender, predecir y controlar al sistema que generó tales datos. En esta Sección
aplicaremos razonamientos Matemáticos a fin de presentar una bien conocida metodología
de estimación: la Regresión Lineal. Primero, presentaremos el caso particular cuando los
datos son pares de la forma (x, d), donde x es la única variable de entrada y d el valor que se
espera genere el sistema para tal entrada. Posteriormente, en la Sección 2.3 discutiremos el
fundamento matemático detrás del caso general, en el cual se tienen varias variables.
Existen tres condiciones a las cuales los datos experimentales deben sujetarse y que
de hecho asumiremos se cumplen:
• Deben ser suficientes en cantidad.
• Deben capturar los principios fundamentales del sistema o modelo de origen.
• Y finalmente, deben ser libres, tanto como sea posible, de ruido.
Como ya comentamos previamente, se tendrán pares de observaciones (x1,i, di) tal
que x1,i se asume es libre de errores y di está contaminado por ruido. El objetivo es buscar
una relación lineal entre las variables x1 y d tal que
d ≈ wx1 + b
Es decir, buscaremos valores para las variables w y b de manera que contemos con un
modelo lineal tal que dado un valor para la variable x1, obtengamos, tan justa como sea
posible, la correspondiente predicción d. O de manera más específica, dado un valor de
entrada particular x1,i y el correspondiente ruido o error εi, el cual se agrega a wx1,i + b,
entonces podemos garantizar una predicción exacta di:
di = wx1,i + b + εi
(Ecuación 2.2.1)
Sea x2,i = wx1,i + b. Entonces al sustituir en la Ecuación 2.2.1 se tendrá:
di = x2,i + εi
(Ecuación 2.2.2)
Donde εi es ahora el error agregado a x2,i, w es una pendiente y b es una intersección con el
eje X2. Al valor b también se le llama sesgo. Es claro que se buscará entonces una recta en
el plano que se ajuste a las observaciones (x1,i, di). Véase la Figura 2.2. Es bien sabido que
cualquier recta se ajusta perfectamente a dos observaciones, pero ésta no necesariamente se
ajustará al resto de las observaciones. Nuestro problema a resolver se plantea en el
siguiente cuestionamiento: ¿Cuál es la mejor elección de w y b tal que la recta wx1 + b esté
tan “cerca” como sea posible a todas las observaciones?
30
Capítulo 2. Preliminares Matemáticos
(x1,i, di)
(x1,4, d4)
(x1,5, d5)
(x1,2, d2)
wx1 + b
(x1,3, d3)
(x1,1, d1)
X1
Figura 2.2. Ajuste de la recta wx1 + b.
Una solución muy popular para nuestro problema es el método de Mínimos
Cuadrados. Se trata de un método sistemático que permite determinar los mejores valores
para las constantes b y w. El método parte de la consideración de que todo di contiene
ruido, de manera que no será posible ajustar la relación sin error, por lo tanto se tiene que:
di = wx1,i + b + εi
⇔ εi = di – (wx1,i + b)
(Ecuación 2.2.3)
Sea di’ = wx1,i + b. Entonces al sustituir en la Ecuación 2.2.3:
εi = di – di’
(Ecuación 2.2.4)
Es claro que εi es el error o diferencia que existe entre el valor experimental di y el valor
predicho por la recta, es decir di’.
A fin de encontrar aquella recta que mejor se ajuste a los datos, se requerirá de un
criterio para determinar que tan bueno es un estimador lineal. Para este fin, se tiene que el
Promedio de los Errores al Cuadrado es un criterio bastante recurrido. Básicamente
considera, para cada una de las observaciones, y dada una recta candidata, la diferencia εi
entre la predicción que ésta proporciona y el valor esperado. Nótese que εi puede ser
positivo o negativo. Por ello es posible, en un caso extremo, que la suma de todas las
diferencias sea cero. Ello implica que la sola suma de diferencias puede no proporcionarnos
información real de cómo se comporta el estimador lineal con el conjunto de observaciones.
Por ello, a fin de que los signos de las diferencias no afecten la elección de la mejor recta,
31
Una Introducción al Cómputo Neuronal Artificial
es que estas diferencias son todas elevadas al cuadrado y posteriormente sumadas.
Claramente el Promedio de los Errores al Cuadrado queda definido como:
J=
1
2N
N
¦ε
2
i
(Ecuación 2.2.5)
i =1
Donde N es el número de observaciones.
J nos proporciona, para una recta candidata, el error total que ésta tiene con el
conjunto de observaciones. Ahora el objetivo será minimizar a J. La Sección anterior nos
proporcionó herramientas para lograr este objetivo. J puede ser vista como una Función de
Error para la cual se quiere determinar su mínimo global. Se garantiza la existencia de un
único mínimo ya que si se observan las Ecuaciones 2.2.3 y 2.2.5, se tiene que J describe un
paraboloide en el espacio tridimensional debido a que depende de las variables w y b. Es en
este mínimo donde el vector gradiente de J es precisamente el vector cero. Por lo tanto, el
primer paso es determinar ∇J. Ello implica encontrar las derivadas parciales de J respecto
a las variables w y b. Posteriormente, el segundo paso consistirá en igualar a las
expresiones resultantes a cero. Esto genera un sistema de ecuaciones:
­δ J
°° δ b = 0
®
°δ J = 0
°̄ δ w
La solución del sistema de ecuaciones nos proporcionará los valores óptimos de b y w de tal
forma que la función de error J sea minimizada tanto como sea posible. De esta forma,
habremos encontrado a la mejor recta para ajustar nuestros datos.
Procedamos a determinar la derivada parcial de J respecto a la variable b:
δJ δ 1 N 2
=
¦ε
δ b δ b 2 N i =1 i
1 N δ 2
=
¦ εi
2 N i =1 δ b
2
1 N δ
=
d i − wx1,i − b )
(
¦
2 N i =1 δ b
1 N
δ
=
2 ( di − wx1,i − b ) ( di − wx1,i − b )
¦
δb
2 N i =1
=
32
1
N
N
¦(d
i =1
i
− wx1,i − b ) (−1)
(Por la Ecuación 2.2.3)
(Regla de la Cadena)
§ di y wx1,i son constantes ·
¨
¸
© respecto a b
¹
Capítulo 2. Preliminares Matemáticos
=
1
N
N
¦ ( wx
1,i
i =1
+ b − di )
§ wx
b d ·
= ¦ ¨ 1,i + − i ¸
N N¹
i =1 © N
N x
N
b N d
= w¦ 1,i + ¦ − ¦ i
i =1 N
i =1 N
i =1 N
N
Por lo tanto tenemos que:
N x
N
δJ
b N d
= w¦ 1,i + ¦ − ¦ i
δb
i =1 N
i =1 N
i =1 N
(Ecuación 2.2.6)
Ahora determinaremos la derivada parcial de J respecto a la variable w:
δJ δ 1 N 2
=
¦ε
δ w δ w 2 N i =1 i
1 N δ 2
=
¦ εi
2 N i =1 δ w
2
1 N δ
di − wx1,i − b )
=
(
¦
2 N i =1 δ w
1 N
δ
2 ( di − wx1,i − b )
=
( d − wx1,i − b )
¦
2 N i =1
δw i
=
1
N
1
=
N
N
¦(d
− wx1,i − b ) (− x1,i )
i
i =1
N
¦ ( wx
2
1,i
i =1
(Por la Ecuación 2.2.3)
(Regla de la Cadena)
§ di y b son constantes ·
¨
¸
© respecto a w
¹
+ bx1,i − di x1,i )
§ wx1,2i bx1,i di x1,i ·
= ¦ ¨¨
+
−
¸
N
N ¹¸
i =1 © N
N x2
N x
N d x
= w¦ 1,i + b¦ 1,i − ¦ i 1,i
N
i =1 N
i =1 N
i =1
N
Es decir:
N x
N x
N d x
δJ
= w¦ 1,i + b¦ 1,i − ¦ i 1,i
δw
N
i =1 N
i =1 N
i =1
2
(Ecuación 2.2.7)
33
Una Introducción al Cómputo Neuronal Artificial
Ahora tanto
δJ
δJ
como
son igualadas a cero y se cuenta con el siguiente
δb
δw
sistema de ecuaciones:
­ N x1,i N b N di
+¦ −¦ = 0
° w¦
°° i =1 N i =1 N i =1 N
®
° N x2
N
N
° w¦ 1,i + b¦ x1,i − ¦ di x1,i = 0
°̄ i =1 N
N
i =1 N
i =1
(Ecuación 2.2.8)
(Ecuación 2.2.9)
Hagamos:
N
x1,i
i =1
N
x=¦
N
x1,2i
i =1
N
x2 = ¦
N
d =¦
i =1
di
N
N
di x1,i
i =1
N
xd = ¦
Entonces al sustituir en las Ecuaciones 2.2.8 y 2.2.9 el sistema se reescribe como:
­ wx + b − d = 0
°
®
° 2
¯ wx + bx − xd = 0
(Ecuación 2.2.10)
(Ecuación 2.2.11)
Procedemos a resolver el sistema de ecuaciones lineales. Para la Ecuación 2.2.10
tenemos:
wx + b − d = 0
⇔ b = d − wx
Sustituyendo el valor de b en la Ecuación 2.2.11:
wx 2 + (d − wx) x − xd = 0
()
2
⇔ wx 2 + d ⋅ x − w x − xd = 0
34
Capítulo 2. Preliminares Matemáticos
()
⇔ wx 2 − w x
⇔ w=
2
= xd − d ⋅ x
xd − d ⋅ x
()
x2 − x
(Ecuación 2.2.12)
2
Al sustituir el valor de w (Ecuación 2.2.12) en la Ecuación 2.2.10 tenemos finalmente:
b = d − wx
=d−
=d−
(
xd − d ⋅ x
=
2
x
()
x − ( x)
− ( x ) ) − xd ⋅ x + d ⋅ ( x )
x − ( x)
xd ⋅ x − d ⋅ x
d x2
=
()
x − x
2
2
2
2
2
2
2
2
d ⋅ x 2 − xd ⋅ x
()
x2 − x
2
Es decir:
b=
d ⋅ x 2 − xd ⋅ x
()
x − x
2
2
(Ecuación 2.2.13)
Las Ecuaciones 2.2.12 y 2.2.13 representan los valores óptimos para las variables w
y b respectivamente. Ello se debe a que se determinó para qué valores precisamente de w y
b el vector gradiente de la función de error J es el vector cero.
Analicemos un ejemplo práctico simple. En la Tabla 2.1 se presenta un conjunto de
observaciones para las cuales deseamos obtener un estimador lineal que se ajuste lo mejor
posible. En Figura 2.3 se puede apreciar la disposición de los puntos (x1,i, di).
35
Una Introducción al Cómputo Neuronal Artificial
Tabla 2.1. Un conjunto de 11 observaciones.
di
x1,i
-5
-10.5
-4
-8.5
-3
-4.5
-2
-2.5
-1
0.5
0
4.5
1
6.5
2
10.5
3
12.5
4
16.5
5
18.5
È
15
È
10
5È
4
2
È
È
È
È
È
È
È
È
2
4
5
10
Figura 2.3. Disposición en el plano cartesiano
de los puntos presentados en la Tabla 2.1.
•
Para el conjunto de datos en cuestión tenemos:
x=0
• x 2 = 10
• d = 3.9545
• xd = 29.8182
Que al sustituir en las Ecuaciones 2.2.12 y 2.2.13 obtenemos respectivamente:
w = 2.9818
b = 3.9545
Ello implica que la recta que mejor se ajusta a nuestro conjunto de datos está dada por:
d = 2.9818x1 + 3.9545
En la Figura 2.4 se muestra al conjunto de datos y la recta obtenida.
36
Capítulo 2. Preliminares Matemáticos
È
È
15
È
È
10
È
5È
4
2
È
2
È
È
È
È
4
5
10
Figura 2.4. La recta d = 2.9818x1 + 3.9545 como el mejor estimador lineal
para el conjunto de datos presentado en la Tabla 2.1.
Ahora bien, sustituiremos el conjunto de datos de la Tabla 2.1 en la Ecuación 2.2.5,
es decir, aquella correspondiente al Promedio de los Errores al Cuadrado:
J = 5w2 + 0.5b2 – 29.81w – 3.95b + 52.397
Como ya mencionamos, J describe un paraboloide inmerso en el espacio tridimensional. En
la Figura 2.5 se puede apreciar la gráfica de J. Cada punto sobre la superficie es de la
forma (w, b, J(w,b)) y describe el error total que se obtiene al usar los valores de w y b
como parámetros para una recta candidata. Es claro que al visualizar la superficie contamos
con una descripción gráfica del desempeño de todos los posibles estimadores lineales para
nuestro conjunto de datos. Sustituyendo w = 2.9818 y b = 3.9545, los valores encontrados
previamente, al aplicar directamente las Ecuaciones 2.2.12 y 2.2.13, obtenemos el error
total J = 0.122314. Por la Teoría antes presentada, sabemos que el punto
(w = 2.9818, b = 3.9545, J = 0.122314)
es precisamente el mínimo global de la función de error y es donde también el vector
gradiente de J es precisamente el vector cero. Es claro, observando la Figura 2.5, que
cualquier otro valor para w y b nos proporcionará un error total J mayor a 0.122314.
37
Una Introducción al Cómputo Neuronal Artificial
Figura 2.5. El paraboloide asociado a la función de error
J = 5w2 + 0.5b2 – 29.81w – 3.95b + 52.397
2.3 Regresión Lineal con Múltiples Variables
Sea el vector xi en \ P una medición libre de ruido y sea di un escalar posiblemente
P
contaminado con ruido. Sea b + ¦ wk xi ,k un hiperplano multidimensional. Este hiperplano
k =1
modelará la correlación lineal entre el vector xi y el escalar di. Sea di’ el valor
proporcionado por nuestro estimador:
P
di' = b + ¦ wk xi ,k
(Ecuación 2.3.1)
k =1
Sea εi el error que existe entre di y di’:
ε i = di − di'
P
§
·
= di − ¨ b + ¦ wk xi ,k ¸
k =1
©
¹
= di − (b + w1 xi ,1 + w2 xi ,2 + ... + wP xi , P )
(Ecuación 2.3.2)
El término b es llamado término de sesgo. A fin de incorporarlo en la sumatoria haremos
w0 = b y agregaremos un 0-ésimo componente a nuestros vectores xi de manera que xi,0 = 1.
Entonces al sustituir en la Ecuación 2.3.2 ahora tendremos:
38
Capítulo 2. Preliminares Matemáticos
P
ε i = di − ¦ wk xi ,k
(Ecuación 2.3.3)
k =0
El Promedio de los Errores al Cuadrado tiene la forma:
1
J=
2N
P
§
·
d
−
¦
¨ i ¦ wk xi ,k ¸
i =1 ©
k =0
¹
N
2
(Ecuación 2.3.4)
Donde N es el número de mediciones. J será minimizada al resolver el sistema de
ecuaciones formado precisamente al igualar a cero sus derivadas parciales respecto a las
variables w0, w1, w2, …, wP:
­ δJ
°δ w = 0
° 0
° δJ
=0
°
® δ w1
° #
°
° δJ
°δ w = 0
¯ P
Es decir, se buscará la solución de ∇J = 0.
En términos geométricos, lo que buscamos son los valores de los coeficientes w0,
w1, …, wP de manera que el hiperplano multidimensional
w0 xi ,0 + w1 xi ,1 + w2 xi ,2 + w3 xi ,3 + ... + wP xi , P
se ajuste lo mejor posible a nuestro conjunto de mediciones (xi, di), xi ∈ \ P +1 , di ∈ \ ,
i = 1, 2, 3, …, N. Por otro lado, la función de error J describe a una hipersuperficie, en
particular, un hiperparaboloide multidimensional. La ecuación de tal lugar geométrico está
dada en función de las variables w0, w1, …, wP. Por lo tanto, el hiperparaboloide asociado a
J está inmerso en un espacio Euclidiano (P+2)-Dimensional. Sin embargo, demostraremos
que, tal como sucede en el caso bidimensional (véase la Sección anterior), J cuenta con un
único mínimo. En ese punto el vector gradiente es el vector cero. Es precisamente en esa
localidad donde encontramos los valores óptimos para w0, w1, …, wP.
Considérese la j-ésima variable wj, 0 ≤ j ≤ P. Obtendremos la correspondiente
derivada parcial de la función de error J respecto a wj:
39
Una Introducción al Cómputo Neuronal Artificial
P
δJ
δ 1 N §
·
di − ¦ wk xi ,k ¸
=
¦
¨
δ w j δ w j 2 N i =1 ©
k =0
¹
·
di − ¦ wk xi , k ¸
¦
¨
i =1 δ w j ©
k =0
¹
N
1
=
2N
=
δ §
2
P
(Por la Ecuación 2.3.4)
2
P
§
· δ
2
−
d
¦
¨ i ¦ wk xi ,k ¸ δ w
i =1 ©
k =0
¹
j
N
1
2N
1
=
N
P
§
·§ δ
¦
¨ di − ¦ wk xi ,k ¸ ¨¨ − δ w
i =1 ©
k =0
¹©
j
1
=
N
P
§
·
−
d
¦
¨ i ¦ wk xi ,k ¸ ( − xi , j )
i =1 ©
k =0
¹
=−
N
P
§
·
−
d
¨ i ¦ wk xi ,k ¸
k =0
©
¹
P
¦w x
k i ,k
k =0
·
¸¸
¹
N
1
N
(di es constante respecto a w j )
§ Todas las variables wk son
¨
¨ constantes respecto a w j excepto
¨ aquella para la cual k = j
©
·
¸
¸
¸
¹
P
§
·
−
x
d
wk xi ,k ¸
¦
¦
i, j ¨ i
i =1
k =0
©
¹
N
Concretizando:
P
δJ
1 N
§
·
= − ¦ xi , j ¨ di − ¦ wk xi , k ¸
δ wj
N i =1
k =0
©
¹
(Ecuación 2.3.5)
Nótese que la Ecuación 2.3.5 define la derivada parcial de wj para todo valor de j
desde 0 hasta P. Ello implica que efectivamente hemos encontrado los valores de los
componentes del vector gradiente de J, ∇J. Como ya comentamos antes, resolver la
ecuación ∇J = 0 es equivalente a resolver el sistema de ecuaciones:
­ 1
®−
¯ N
P
§
·
x
d
−
wk xi ,k ¸ = 0
¦
¦
i, j ¨ i
i =1
k =0
©
¹
N
j = 0,1, 2,...P
Consideremos la j-ésima ecuación:
−
1
N
N
¦x
i, j
i =1
P
§
·
−
d
wk xi ,k ¸ = 0
¦
i
¨
k =0
©
¹
P
§
·
⇔ ¦ xi , j ¨ di − ¦ wk xi ,k ¸ = 0
i =1
k =0
©
¹
N
P
§
·
⇔ ¦ ¨ xi , j di − xi , j ¦ wk xi ,k ¸ = 0
i =1 ©
k =0
¹
N
40
(Al multiplicar ambos lados
por - N ).
Capítulo 2. Preliminares Matemáticos
N
N
P
§
·
⇔ ¦ xi , j di − ¦ ¨ xi , j ¦ wk xi , k ¸ = 0
i =1
i =1 ©
k =0
¹
N
N
P
§
·
⇔ ¦ xi , j di = ¦ ¨ xi , j ¦ wk xi , k ¸
i =1
i =1 ©
k =0
¹
(La sumatoria principal es
expresada como dos sumatorias)
(Ecuación 2.3.6)
Considérese el lado derecho de la Ecuación 2.3.6. En primer lugar desarrollaremos
la sumatoria principal y posteriormente cada sumatoria con índice de suma k:
P
P
P
P
P
§
·
=
+
+
+
+
x
w
x
x
w
x
x
w
x
x
w
x
...
x
¦
N , j ¦ wk xN , k
2, j ¦ k 2, k
3, j ¦ k 3, k
¨ i , j ¦ k i ,k ¸ 1, j ¦ k 1,k
i =1 ©
k =0
k =0
k =0
k =0
k =0
¹
N
P
P
P
P
k =0
k =0
k =0
k =0
= ¦ wk x1, j x1,k + ¦ wk x2, j x2, k + ¦ wk x3, j x3,k + ... + ¦ wk xN , j xN ,k
= ( w0 x1, j x1,0 + w1 x1, j x1,1 + w2 x1, j x1,2 + ... + wP x1, j x1, P
(w x
(w x
x
+ w1 x2, j x2,1 + w2 x2, j x2,2 + ... + wP x2, j x2, P
x
+ w1 x3, j x3,1 + w2 x3, j x3,2 + ... + wP x3, j x3, P
0 2, j 2,0
0 3, j 3,0
(w x
0 N, j
)+
)+
)+
#
xN ,0 + w1 xN , j xN ,1 + w2 xN , j xN ,2 + ... + wP xN , j xN , P )
Es claro que los términos entre paréntesis, con factor común xi , j , corresponden al
P
desarrollo “horizontal” de cada suma xi , j ¦ wk xi ,k . Pero nótense los recuadros punteados
k =0
que hemos agregado. Los términos en cada uno de estos recuadros pueden ser vistos como
N
el desarrollo “vertical” de una sumatoria de la forma wk ¦ xi , j xi , k , donde evidentemente sus
i =1
términos cuentan con el factor común wk. Reagrupando los términos de las sumatorias en
forma “vertical” tenemos ahora:
N
N
N
N
i =1
i =1
i =1
= w0 ¦ xi , j xi ,0 + w1 ¦ xi , j xi ,1 + w2 ¦ xi , j xi ,2 + ... + wP ¦ xi , j xi , P
i =1
P
N
k =0
i =1
= ¦ wk ¦ xi , j xi ,k
Es decir, el lado derecho de la Ecuación 2.3.6 queda ahora expresado como:
P
§
·
x
¦
¨ i , j ¦ wk xi , k ¸ =
i =1 ©
k =0
¹
N
P
N
k =0
i =1
¦ wk ¦ xi, j xi,k
(Ecuación 2.3.7)
41
Una Introducción al Cómputo Neuronal Artificial
Igualamos con el lado izquierdo de la Ecuación 2.3.6:
N
P
N
i =1
k =0
i =1
¦ xi, j di = ¦ wk ¦ xi, j xi ,k
(Ecuación 2.3.8)
Se dividen ambos lados de la Ecuación 2.3.8 por N:
N
¦ xi, j di
i =1
N
=
P
N
k =0
i =1
¦ wk ¦ xi, j xi,k
=
N
1
N
P
N
k =0
i =1
¦ wk ¦ xi, j xi,k
P
1 N
¦ xi, j xi,k
N i =1
k =0
P
1 N
1 N
⇔ ¦ xi , j di = ¦ wk ¦ xi , j xi ,k
N i =1
N i =1
k =0
= ¦ wk
(Ecuación 2.3.9)
Consideraremos ahora, del lado derecho de la Ecuación 2.3.9 la sumatoria con
1
. Sea Rk,j definido como:
índice i y su factor
N
Rk , j =
1 N
¦ xi, j xi,k
N i =1
k = 0,1, 2,..., P
j = 0,1, 2,..., P
(Ecuación 2.3.10)
Ahora, sea R la matriz de (P+1) × (P+1) dada por:
ª R0,0
«R
1,0
R=«
« #
«
¬ RP ,0
R0,1 " R0, P º
R1,1 " R1, P »»
# %
# »
»
RP ,1 " RP , P ¼
(Ecuación 2.3.11)
Sea ℘j igual al lado izquierdo de la Ecuación 2.3.9:
℘j =
42
1
N
N
¦x
i, j
i =1
di
j = 0,1, 2,..., P
(Ecuación 2.3.12)
Capítulo 2. Preliminares Matemáticos
Definimos a ℘ como un vector de P+1 elementos:
ª℘0 º
«℘ »
℘= « 1 »
« # »
« »
¬℘P ¼
(Ecuación 2.3.13)
Y sea W el vector de P+1 elementos dado por:
ª w0 º
«w »
W =« 1»
« # »
« »
¬ wP ¼
(Ecuación 2.3.14)
El sistema de ecuaciones que se obtuvo originalmente al calcular las derivadas
parciales de la función de error J
­ 1
®−
¯ N
P
§
·
x
d
−
wk xi ,k ¸ = 0
¦
¦
i, j ¨ i
i =1
k =0
©
¹
N
j = 0,1, 2,...P
Ahora puede ser reescrito como el producto matricial:
℘ = RW
(Ecuación 2.3.15)
Supongamos la existencia de la matriz inversa de R, es decir R-1, entonces tendremos
manera de determinar al vector W (Ecuación 2.3.14), cuyos componentes son precisamente
los valores de las variables w0, w1, …, wP:
℘ = RW
⇔ R-1℘ = R-1RW
⇔ R-1℘ = I W
⇔ R-1℘ = W
(I: matriz identidad)
(Ecuación 2.3.16)
La Ecuación 2.3.16 expresa de manera sumamente concreta, en términos de un
producto matricial, el procedimiento de Mínimos Cuadrados. Nótese que la existencia de la
solución depende precisamente de que se cuente con la inversa de la matriz R (Ecuación
2.3.11).
43
Una Introducción al Cómputo Neuronal Artificial
Consideremos el caso particular cuando P = 1, entonces la matriz R tendrá la forma:
ª R0,0
«R
¬ 1,0
R0,1 º
R1,1 »¼
Específicamente, por la Ecuación 2.3.10 y dado que xi,0 = 1, i = 1, 2, …, N:
ª1 N
« N ¦ xi ,0 xi ,0
i =1
R=«
«1 N
« N ¦ xi ,0 xi ,1
¬ i =1
1 N
º ª
xi ,1 xi ,0 » « 1
¦
N i =1
»=«
» «1 N
1 N
x
x
xi ,1
¦ i,1 i,1 »¼ «¬ N ¦
N i =1
i =1
1 N
º
xi ,1 »
¦
ª1
N i =1
»=«
1 N 2 » «¬ x
¦x
N i =1 i ,1 »¼
xº
»
x 2 »¼
Por las Ecuaciones 2.3.12 y 2.3.13, y haciendo xi,0 = 1, i = 1, 2, …, N, el vector ℘ estará
dado por:
ª1 N
º ª 1 N
º
x
d
di »
¦
¦
i ,0 i »
«
«
ªd º
N i =1
N i =1
ª℘ º
»=«
»=« »
℘= « 0 » = «
N
» «1 N
» ¬« xd ¼»
¬℘1 ¼ « 1
x
d
« N ¦ i ,1 i » « N ¦ xi ,1di »
¬ i =1
¼ ¬ i =1
¼
Suponiendo que el sistema ha de ser resuelto usando la Regla de Crammer, se tiene que
los valores para w0 y w1 están dados por:
w0 =
d
x
xd
x2
1
x
x
x2
1
=
d ⋅ x 2 − xd ⋅ x
()
x2 − x
2
w1 =
d
x xd
1
x
x
x2
=
xd − d ⋅ x
()
x2 − x
2
Es claro que las expresiones encontradas para w0 y w1 corresponden con las Ecuaciones
2.2.12 y 2.2.13 presentadas en la Sección anterior.
2.4 La Desigualdad de Cauchy-Schwarz
Sean u y v cualesquiera vectores en \ n . Su producto punto puede ser calculado
mediante
u ⋅ v = u ⋅ v ⋅ cos θ
44
Capítulo 2. Preliminares Matemáticos
Donde θ es el ángulo que forman u y v. Es bien sabido que cos θ ∈ [-1,1] y que por tanto el
valor absoluto aplicado sobre la función coseno hará que ésta tenga sus valores en [0, 1].
Por ello se plantea entonces la siguiente desigualdad:
u ⋅v =
u ⋅ v ⋅ cos θ ≤
u ⋅ v ⋅ cos θ
Es claro que el término |cos θ| puede interpretarse como un factor de escalamiento que
puede reducir el valor del producto de las magnitudes de u y v, u ⋅ v . Por lo tanto, se
tiene que:
u ⋅ v = u ⋅ v ⋅ cos θ ≤
u ⋅ v ⋅ cos θ
≤
u ⋅ v
Ÿ u ⋅v ≤ u ⋅ v
Precisamente la última desigualdad, u ⋅ v ≤ u ⋅ v , es conocida como la Desigualdad de
Cauchy-Schwarz.
45
Una Introducción al Cómputo Neuronal Artificial
46
Una Introducción al Cómputo Neuronal Artificial
3. La Neurona
Adaline
Una Introducción al Cómputo Neuronal Artificial
48
Capítulo 3. La Neurona Adaline
3.1 Estructura
Sea X = [x1, x2, …, xP]T un vector en \ P . La neurona Adaline procesará a X y
producirá su salida, un escalar, de la siguiente manera (véase la Figura 3.1):
P
§
·
y = sign ¨ w0 + ¦ wi xi ¸
i =1
©
¹
(Ecuación 3.1.1)
Donde:
• w0 es llamado término de Predisposición o Sesgo (Bias Term).
• wi es el peso en la entrada xi, i = 1, 2, …, P.
P
•
w0 + ¦ wi xi es llamada Sumatoria de Salida.
•
La función sign se define como (Véase la Figura 3.2):
i =1
sign : \ → {−1,1}
­−1 si
z sign( z ) = ®
¯ 1 si
z<0
z≥0
W1
#
Wi
Xi
#
P
z = w0 + ¦ wi xi
z
y
y = sign( z )
i =1
Salida
Entradas
X1
WP
XP
Figura 3.1. Representación esquemática de una neurona Adaline.
sign(z)
1
0
-1
Figura 3.2. Gráfica de la función sign.
49
Una Introducción al Cómputo Neuronal Artificial
Ahora bien, considérese un conjunto compuesto por N vectores de entrada a
presentar a la neurona:
{X1, X2, …, XN}
Como ya se comentó en la Sección 1.3, cada vector será de la forma:
ª xi ,1 º
« # »
« »
X i = « xi ,k »
« »
« # »
« xi , P »
¬ ¼
También considérese un segundo conjunto compuesto por N vectores:
{D1, D2, …, DN}
Tales vectores formaran la salida esperada para la neurona. Cada vector será de la forma:
ª di ,1 º
« # »
«
»
Di = « di ,k »
«
»
« # »
« di ,m »
¬
¼
La relación entre el conjunto de vectores de entrada y el conjunto de vectores de
salida está dada por el objetivo de que para un vector de entrada Xi se espera que la neurona
proporcione la salida Di. El entrenamiento de una neurona tipo Adaline tiene por finalidad
encontrar los pesos w0, w1, w2, …, wP tales que para todo vector de entrada Xi se
proporcione como salida un vector Si tal que Si = Di o bien la diferencia Si - Di sea
aceptable. De acuerdo a la Ecuación 3.1.1 tanto Di como Si tendrán únicamente un
componente.
•
Por ejemplo, considérese el siguiente conjunto de entrenamiento:
Se tienen los vectores de entrada:
ª0 º
ª1 º
ª0º
ª1º
X1 = « » , X 2 = « » , X 3 = « » , X 4 = « »
¬0 ¼
¬0 ¼
¬1 ¼
¬1¼
50
Capítulo 3. La Neurona Adaline
•
El conjunto de vectores de salida se forma por:
D1 = [ 0] , D2 = [1] , D3 = [1] , D4 = [1]
•
De manera que se espera que dado el vector de entrada
ª0º
o « » , la neurona proporcione [0]
¬0¼
ª1 º
o « » , la neurona proporcione [1]
¬0¼
ª0º
o « » , la neurona proporcione [1]
¬1 ¼
ª1º
o « » , la neurona proporcione [1]
¬1¼
En este punto debe ser claro que nuestro objetivo es modelar la compuerta lógica
OR. En la Figura 3.3 se presenta la correspondiente representación esquemática de la
neurona para este problema en particular. Se tendrán 2 entradas y se proporcionará un
escalar como salida. Dado que la función sign tiene por dominio el conjunto {-1, 1}
entonces el conjunto de entrenamiento, y en particular el conjunto de vectores de salida,
deberá ser ajustado de manera que sus valores estén precisamente en {-1, 1}. Es evidente
que la única modificación a aplicar tiene que ver con el valor cero y ésta no altera el
problema original:
• D1 = [ −1] , D2 = [1] , D3 = [1] , D4 = [1]
W1
2
z = w0 + ¦ wi xi
i =1
z
y = sign( z )
y
Salidas
Entradas
X1
W2
X2
Figura 3.3. Esquema de una neurona Adaline
para dar solución al modelado de la compuerta lógica OR.
Por el momento sólo verificaremos la existencia de los pesos w0, w1 y w2 de manera
que se obtienen siempre las salidas correctas. Considérense los pesos:
• w1 = 0.5
• w2 = 0.5
• w0 = -0.25
51
Una Introducción al Cómputo Neuronal Artificial
Ello implica que la Sumatoria de Salida tendrá la forma:
z = 0.5x1 + 0.5x2 – 0.25
Aplicando cada vector de entrada a la sumatoria se obtiene:
• 0.5(0) + 0.5(0) – 0.25 = -0.25
• 0.5(1) + 0.5(0) – 0.25 = 0.25
• 0.5(0) + 0.5(1) – 0.25 = 0.25
• 0.5(1) + 0.5(1) – 0.25 = 0.75
Finalmente, a cada salida z se le aplica la función sign. Con lo que se obtiene
respectivamente:
• sign(-0.25) = -1
• sign(0.25) = 1
• sign(0.25) = 1
• sign(0.75) = 1
Por lo tanto, hemos demostrado la existencia de pesos tales que una neurona
Adaline es capaz de aprender y modelar la compuerta lógica OR. Evidentemente surge la
pregunta de cómo es posible determinar tales pesos. Un mecanismo obvio, pero sumamente
ineficiente en la práctica, es mediante prueba y error. Es claro que se requiere una
metodología sistemática que nos permita encontrar los pesos. En las siguientes Secciones
presentaremos dos métodos a fin de lograr tal objetivo.
3.2 Ajuste de Pesos de la Neurona Adaline
por Mínimos Cuadrados
En la Sección 2.3 describimos al Método de Mínimos Cuadrados como una solución
al problema de la Correlación Lineal. Al observar la estructura interna de la neurona
Adaline y en particular su Sumatoria de Salida
P
w0 + ¦ wi xi
i =1
es claro que el objetivo es el ajuste de los pesos w0, w1, w2, … wP de manera que para cada
vector de entrada se obtenga la salida correcta o tan cercana como sea posible al valor
correcto. Además, tal como nos indica la misma sumatoria, el ajuste debe ser de manera
que todo valor de salida proporcionado por la neurona es una combinación lineal de su
correspondiente vector de entrada y el conjunto de pesos. Es por ello que el Método de
Mínimos Cuadrados resultará ser una primera metodología para el ajuste de pesos en una
neurona Adaline. El mismo método, y la Teoría que lo sustenta, nos garantiza que este
ajuste será el mejor posible.
52
Capítulo 3. La Neurona Adaline
Establezcamos primero puntos de conexión con la Teoría presentada en la Sección
2.3. Contaremos con N pares (Xi, di) en donde Xi es un vector en \ P+1 tal que
ª xi ,0 = 1º
« x »
« i ,1 »
X i = « xi ,2 »
«
»
« # »
« xi , P »
¬
¼
y di es un escalar que corresponde a la salida que se espera proporcione la neurona cuando
Xi le es enviado como entrada, i = 1, 2, 3, …, N.
Sea W el vector de pesos de la neurona. Éste también estará en \ P+1 :
ª w0 º
«w »
« 1»
W = « w2 »
« »
« # »
«¬ wP »¼
En este punto haremos una leve modificación a la estructura de la neurona en el
sentido de que no será requerido el uso de la función sign. Por lo tanto tendremos una
estructura neuronal como la presentada en la Figura 3.4.
W1
#
#
P
z = w0 + ¦ wk xi ,k
z
k =1
Salida
Entradas
Xi,1
WP
Xi,P
Figura 3.4. Estructura de la neurona Adaline
omitiendo el uso de la función sign.
53
Una Introducción al Cómputo Neuronal Artificial
Sea zi el escalar que produce la neurona como salida cuando se le envía como
entrada el vector Xi. De hecho:
P
zi = ¦ wk xi ,k
(Ecuación 3.2.1)
k =0
Nótese que hemos incorporado al peso w0 a la sumatoria haciendo xi,0 = 1 para todo vector
de entrada.
Se define al Error de Entrenamiento para el i-ésimo par (Xi, di) como:
εi = di - zi
(Ecuación 3.2.2)
Ahora se define al Costo de Entrenamiento para el vector de pesos W como:
J (W ) =
1
2N
N
¦ε
2
i
(Ecuación 3.2.3)
i =1
Es claro que el Costo de Entrenamiento no es más que la fórmula para el Promedio de los
Errores al Cuadrado originalmente presentada en la Sección 2.3 (Ecuación 2.3.4). Es
precisamente en este punto en que tenemos ya una conexión directa entre el objetivo de
ajustar los pesos de la neurona Adaline y el método de Mínimos Cuadrados.
Evidentemente, el costo de entrenamiento se minimiza al resolver la ecuación
matricial (Véase la Sección 2.3, Ecuación 2.3.15):
℘ = RW
El vector W contiene, una vez resuelta la ecuación, los pesos que deben ser aplicados a la
Sumatoria de Salida
P
zi = ¦ wk xi ,k
k =0
54
Capítulo 3. La Neurona Adaline
Consideremos el caso del ajuste de pesos de manera que una neurona Adaline
modele a la función Booleana presentada en la Tabla 3.1. Recuérdese que se agrega un
0-ésimo componente a los vectores de entrada: xi,0. Su valor es siempre igual a 1 y tiene la
finalidad de incorporar al peso w0 en la Sumatoria de Salida. Tenemos entonces el conjunto
de entrenamiento:
ª1 º
ª1 º
ª1 º
ª1º
«
»
«
»
«
»
• X 1 = «0 » , X 2 = «1 » , X 3 = «0 » , X 4 = ««1»»
«¬0 »¼
«¬0 »¼
«¬1 »¼
«¬1»¼
•
•
d1 = 1, d 2 = 0, d3 = 1, d 4 = 0
N=4
Tabla 3.1. Una compuerta lógica
a ser modelada por una neurona Adaline.
i xi,1 xi,2 di
1
2
3
4
0
1
0
1
0
0
1
1
1
0
1
0
Definimos en primer lugar a la matriz R. En este caso será de tamaño 3 × 3. De
acuerdo a la Ecuación 2.3.10 (Sección 2.3) sus elementos están dados por:
1 4
1 4
• R0,0 = ¦ xi ,0 xi ,0 = ¦1 = 1
4 i =1
4 i =1
1 4
1 4
1
• R0,1 = ¦ xi ,1 xi ,0 = ¦ xi ,1 =
4 i =1
4 i =1
2
4
4
1
1
1
• R0,2 = ¦ xi ,2 xi ,0 = ¦ xi ,2 =
4 i =1
4 i =1
2
1 4
1 4
1
• R1,0 = ¦ xi ,0 xi ,1 = ¦ xi ,1 =
4 i =1
4 i =1
2
4
4
1
1
1
• R1,1 = ¦ xi ,1 xi ,1 = ¦ xi2,1 =
4 i =1
4 i =1
2
1 4
1
1
• R1,2 = ¦ xi ,2 xi ,1 = ( 0 + 0 + 0 + 1) =
4 i =1
4
4
4
4
1
1
1
• R2,0 = ¦ xi ,0 xi ,2 = ¦ xi ,2 =
4 i =1
4 i =1
2
1 4
1
1
• R2,1 = ¦ xi ,1 xi ,2 = ( 0 + 0 + 0 + 1) =
4 i =1
4
4
4
4
1
1
1
• R2,2 = ¦ xi ,2 xi ,2 = ¦ xi2,2 =
4 i =1
4 i =1
2
55
Una Introducción al Cómputo Neuronal Artificial
Por lo tanto:
ª
«1
«
1
R=«
«2
«1
«
¬« 2
1
2
1
2
1
4
1º
2»
»
1»
4»
1 »»
2 »¼
La inversa de la matriz R está dada por:
ª 3 −2 −2 º
R = «« −2 4 0 »»
«¬ −2 0 4 »¼
−1
Al aplicar la Ecuación 2.3.12 (Sección 2.3) tenemos que los elementos del vector
℘ están dados por:
1 4
1 4
1
• ℘0 = ¦ xi ,0 di = ¦ di =
4 i =1
4 i =1
2
1 4
• ℘1 = ¦ xi ,1di = 0
4 i =1
1 4
1
• ℘2 = ¦ xi ,2 di =
4 i =1
4
Entonces:
ª1º
«2»
« »
℘= «0»
«1»
« »
¬4¼
Encontramos los valores del vector W mediante el producto matricial W = R-1℘
(Ecuación 2.3.16, Sección 2.3):
ª1º
−
−
3
2
2
ª
º «2» ª 1 º
« »
«
W = « −2 4 0 »» « 0 » = «« −1»»
« »
¬« −2 0 4 ¼» « 1 » ¬« 0 ¼»
¬4¼
56
Capítulo 3. La Neurona Adaline
•
•
•
Por lo tanto se han identificado los siguientes pesos:
w0 = 1
w1 = -1
w2 = 0
La Ecuación 3.2.3, correspondiente al costo de entrenamiento, describe, para este
ejemplo en particular, a un hiperparaboloide inmerso en el espacio Euclidiano
tetradimensional. La ecuación específica de tal lugar geométrico se obtiene al sustituir con
los valores del conjunto de entrenamiento:
w02 w12 w22 w0 w1 w0 w2 w1w2 w2 w0 1
J (W ) =
+
+
+
+
+
−
−
+
2
4
4
2
2
4
4
2 4
Calculemos el error de entrenamiento asociado a los pesos identificados al sustituirlos
precisamente en la ecuación anterior:
(1) 2 (−1) 2 (0) 2 (1)(−1) (1)(0) (−1)(0) 0 1 1
J (W ) =
+
+
+
+
+
− − +
2
4
4
2
2
4
4 2 4
=0
El punto (w0 = 1, w1 = -1, w2 = 0, J(W) = 0) es el único mínimo en la hipersuperficie
de nuestro hiperparaboloide, lo que nos garantiza que los pesos encontrados son los
mejores. De hecho estamos en la mejor de las situaciones al tener un error cero. Contamos
entonces con una neurona Adaline óptima para el modelado de la compuerta lógica
presentada en la Tabla 3.1.
3.3 Ajuste de Pesos de la Neurona Adaline
por Descenso Escalonado
A continuación describiremos al método de Descenso Escalonado. Se trata de un
método de búsqueda de mínimos en una función f usando información proporcionada por el
vector gradiente. Un punto interesante de esta metodología es que los gradientes usados no
necesariamente se obtienen de la función a optimizar f, sino que éstos se calculan a partir de
funciones auxiliares construidas a partir de f. Veremos que de hecho algunas definiciones
asociadas al método de Mínimos Cuadrados son el punto de partida para la definición del
Descenso Escalonado. Sin embargo, se observará que éste último proporciona un método
más eficiente en términos del número de operaciones efectuadas. En la siguiente Sección se
abordará primero el caso del Descenso Escalonado en el contexto de una neurona Adaline
con una única entrada. Posteriormente, en la Sección 3.3.2 comentaremos el caso con
múltiples entradas. En ambas situaciones se asume que la neurona proporciona como salida
un único escalar.
57
Una Introducción al Cómputo Neuronal Artificial
3.3.1 Descenso Escalonado: Caso una entrada – una salida
Sea N el número de elementos en el conjunto de entrenamiento, N > 2. Supóngase
que se cuenta con un método iterativo para el entrenamiento de la neurona Adaline de
manera que su vector de pesos es actualizado en cada iteración. Para la m-ésima iteración,
sea Wm el vector de pesos actual de la neurona. El vector Wm es entonces actualizado de
manera que se obtendrá un nuevo vector de pesos Wm+1. La actualización se efectuará
mediante la siguiente regla:
Wm+1 = Wm + Δwm
(Ecuación 3.3.1)
Donde Δwm es el llamado el Término de Variación o Cambio en Wm.
Por otro lado, la instancia particular de la Ecuación 3.2.3 que describe el error de
entrenamiento cuando se ajustan dos pesos está dada por:
J (W ) =
1
2N
N
¦ ε i2 =
i =1
1
2N
N
¦ (d
i
− ( w0 xi ,0 + w1 xi ,1 )) 2
i =1
Sabemos que la función J(W) define un paraboloide ya que sólo depende de las variables w0
y w1, y por tanto sólo tiene un mínimo. También sabemos que este mínimo puede ser
determinado por el método de Mínimos Cuadrados.
J(W)
∇J(W)
Figura 3.5. Sección transversal del paraboloide definido por J(W).
El vector gradiente nos indica la dirección de máximo crecimiento de J(W).
Ahora bien, la teoría presentada en la Sección 2.1 nos dejó claro que un vector
gradiente de J(W), es decir ∇J(W), es un vector que apunta a la dirección de máximo
crecimiento. Este vector nos indica la dirección hacia la cual el error se maximiza (Véase la
58
Capítulo 3. La Neurona Adaline
Figura 3.5 en la cual se presenta una sección transversal del paraboloide definido por
J(W)). Sin embargo, el vector gradiente ∇J(W) también puede ser usado para buscar el
mínimo de J(W). ∇J(W) puede ser calculado de manera local al ubicarnos en un punto dado
(w0, w1). Dado que la meta es alcanzar al mínimo de J(W) entonces partiendo de (w0, w1), la
dirección a tomar para efectuar la búsqueda debe ser la opuesta al gradiente, es decir, usar
la dirección dada por -∇J(W) (Véase la Figura 3.6).
-∇J(W)
∇J(W)
J(W)
Figura 3.6. Sección transversal del paraboloide definido por J(W).
La dirección opuesta del vector gradiente indica la dirección
en donde se ubica el mínimo de J(W).
Ahora conectaremos estos últimos puntos para definir de manera más precisa el
proceso iterativo que mencionamos al inicio de esta Sección y hacer uso de la Ecuación
3.3.1 para la actualización del vector de pesos de la neurona. Véase la Figura 3.7. Dado un
vector de pesos iniciales W1, se calcula el gradiente de J(W) en W1: ∇J(W1). Nótese que la
función J(W) está definida para cualquier punto, por lo tanto, W1 podría ser inicializado con
valores aleatorios. Se inicia la búsqueda del mínimo en dirección opuesta a ∇J(W1). Para
ello, se requiere que nos desplacemos a otro punto. Entonces, modificamos
proporcionalmente al vector W1 usando -∇J(W1) de tal forma que obtenemos un nuevo
vector de pesos W2. Ya ubicados en el punto W2, se calcula nuevamente el gradiente de
J(W) en W2, es decir, se obtiene ∇J(W2). Ahora debemos continuar la búsqueda en
dirección opuesta a ∇J(W2). Se modifica al vector W2 de manera proporcional usando a
∇J(W2) de tal forma que se obtiene un nuevo vector de pesos W3. Este proceso continúa de
manera iterativa de tal forma que en la m-ésima iteración estaremos ubicados en el punto
Wm. Se calcula el gradiente de J(W) en Wm: ∇J(Wm). Se continúa la búsqueda en dirección
opuesta a ∇J(Wm). Se modifica al vector Wm de manera proporcional usando -∇J(Wm) de
donde se obtiene un nuevo vector de pesos Wm+1. Este proceso terminará cuando el vector
59
Una Introducción al Cómputo Neuronal Artificial
gradiente en el punto actual sea el vector cero o esté tan cerca como sea posible al vector
cero. La idea es que en cada iteración nos acerquemos cada vez más al mínimo de la
función J(W). El punto final (w0, w1) es donde precisamente los valores de los pesos se
optimizan.
∇J(W1)
J(W)
W1
∇J(W3)
∇J(W2)
W2
W3
...
Wm+1
Wm
∇J(Wm)
Figura 3.7. Sección transversal del paraboloide definido por J(W).
Dado un (punto) vector de pesos inicial W1 y -∇J(W1) se obtiene el nuevo (punto) vector de pesos W2.
Usando a W2 y -∇J(W2) se obtiene el (punto) vector de pesos W3. Se procede de manera sucesiva hasta
obtener un vector de pesos Wm tal que ∇J(Wm) = 0 o tan cercano a éste como sea posible.
El Algoritmo 3.1 presenta la codificación del proceso que acabamos de definir.
Nuestro procedimiento recibe al conjunto de vectores de entrada en la forma de una matriz
de tamaño N × 2 de manera que la primer columna contiene únicamente el valor 1 = xi,0. En
la columna 2 se tendrán los valores xi,1, i = 1, 2, …, N. El algoritmo recibe como entrada
también 3 constantes: δ, α y maxIt. La constante δ ∈ \ + ∪ {0} representa el valor mínimo
aceptable para la magnitud del vector gradiente de la función J(W). Mientras la magnitud
de ∇J(W) sea mayor a δ el ciclo while del algoritmo seguirá efectuando iteraciones.
Mencionamos previamente que el vector de pesos actual es actualizado de manera
proporcional con el negativo del vector gradiente de J(W). La dirección opuesta del vector
gradiente nos indica hacia donde mover al vector de pesos mientras que la constante de
entrada α ∈ \ + servirá para establecer la magnitud de tal movimiento. Por lo regular, α es
un valor en el intervalo (0,1). Por último, tenemos a la constante maxIt ∈ ` . Nótese que el
número de iteraciones que efectuará el Algoritmo 3.1 depende del valor de las constantes δ
y α. En un caso ideal se haría δ = 0. Sin embargo, es posible, debido a errores de redondeo
o punto flotante, que se requiera un gran número de iteraciones para efectivamente lograr
alcanzar el punto en la función J(W) tal que el vector gradiente sea el vector cero. Por lo
tanto, maxIt simplemente indicará el número máximo de iteraciones que el algoritmo
60
Capítulo 3. La Neurona Adaline
efectuará. Si tal número de iteraciones es alcanzado entonces el algoritmo retorna como
salida al último vector de pesos calculado. Nótese que en consecuencia el Algoritmo 3.1
nos proporcionará como salida el punto donde J(W) tiene su mínimo o bien punto cercano a
éste.
Algoritmo 3.1. Cálculo del mínimo de la función J(W) mediante búsqueda del vector
gradiente ∇J(W) = 0 y actualización iterativa del vector de pesos.
Procedure FindMinimum
(Matrix x[1, …, N][0,1], Array d[1, …, N], Real δ, Real α, Integer maxIt)
// Se asignan valores aleatorios al vector de pesos iniciales.
W = new Array[0,1]
W[0] = Random( )
W[1] = Random( )
m=0
while (m < maxIt) do
// Se calcula el vector gradiente en el punto dado por W.
∇J_W = GetGradientVector(x, d, W, N)
// Se obtiene la magnitud del vector gradiente.
∇J_W[0]2 + ∇J_W[1]2
// Si la magnitud del vector gradiente es menor o igual a δ
// entonces se retorna como salida el vector de pesos actual.
if (mag ≤ δ) then
return W
end-of-if
// Se obtiene la variación o cambio a aplicar al vector de pesos W.
Δwm = new Array[0,1]
Δwm[0] = α ∗ (−1) ∗ ∇J_W[0]
Δwm[1] = α ∗ (−1) ∗ ∇J_W[1]
// Se actualiza el vector de pesos.
W[0] = W[0] + Δwm[0]
W[1] = W[1] + Δwm[1]
m=m+1
end-of-while
// Si se alcanzó el número máximo de iteraciones entonces se retorna como
// salida al último vector de pesos calculado.
return W
end-of-procedure
Real mag =
Hace falta especificar a la función GetGradientVector la cual es invocada en el
Algoritmo 3.1. Ésta recibe como entrada el conjunto de entrenamiento de la neurona y el
vector de pesos actual. Tal como indica su nombre, su objetivo es calcular al vector
61
Una Introducción al Cómputo Neuronal Artificial
gradiente en el punto dado por el vector de pesos. Ello implica que entonces implementa las
Ecuaciones 2.2.6 y 2.2.7 (Sección 2.2) que corresponden a las derivadas parciales de J(W):
N x
N
d
δ J (W )
•
= w1 ¦ 1,i + w0 − ¦ i
δ w0
i =1 N
i =1 N
N x
N x
N d x
δ J (W )
= w1 ¦ 1,i + w0 ¦ 1,i − ¦ i 1,i
δ w1
N
i =1 N
i =1 N
i =1
2
•
Nótese que las sumatorias dependen únicamente del conjunto de entrenamiento. Por lo que
éstas podrían ser precalculadas y pasadas también como entrada al Algoritmo 3.1 y en
consecuencia a la función GetGradientVector.
El procedimiento de búsqueda de mínimo que acabamos de describir e implementar
en el Algoritmo 3.1 es precisamente el método de Descenso Escalonado. La idea, como se
puede apreciar, es ir descendiendo sobre la función de error J(W) usando “pasos
escalonados” cuya dirección y longitud vienen dados por el vector de pesos actual Wm y la
dirección opuesta del vector gradiente de J(W) en el punto Wm. Se espera que por cada paso
ejecutado, el vector gradiente se acerque cada vez más al vector cero. Entre más nos
aproximemos al vector cero, el vector de pesos se aproximará cada vez más a sus valores
óptimos ubicados en el mínimo de la función J(W).
El método de Descenso Escalonado que acabamos de describir requiere contar con
el gradiente de la función J(W). Ello implica que todos los elementos del conjunto de
entrenamiento son considerados en cada iteración en la forma de las sumatorias
2
N
N d x
di N x1,i N x1,i
i 1,i
,
,
,
y
. En el caso particular que estamos tratando en esta
¦
¦
¦
¦
N
i =1 N
i =1 N
i =1 N
i =1
Sección, neurona con una entrada-una salida, pueden que se detecten situaciones con la
eficiencia si el conjunto de entrenamiento es muy grande. Sin embargo, cuando tomamos
en cuenta el caso una neurona varias entradas-una salida veremos que el cálculo del
gradiente se vuelve ineficiente debido a que se deben considerar P+1 pesos. Para cada uno
de éstos tendremos que obtener la derivada parcial de J(W) respecto al j-ésimo peso
(Ecuación 2.3.5, Sección 2.3), j = 0, 1, 2, …, P, la cual a su vez requiere tomar en cuenta a
todo el conjunto de entrenamiento para su cálculo:
P
N
P
δ J (W )
1 N
1§ N
§
·
·
= − ¦ xi , j ¨ di − ¦ wk xi ,k ¸ = − ¨ ¦ xi , j di − ¦ xi , j ¦ wk xi ,k ¸ , j = 0, 1, …, P
N i =1
N © i =1
δ wj
k =0
i =1
k =0
©
¹
¹
N
Es posible precalcular la sumatoria
¦x
i, j
di ya que únicamente depende del conjunto de
i =1
N
entrenamiento. Sin embargo no es así con la sumatoria doble
i, j
i =1
depende también de los pesos w0, w1, …, wP.
62
P
¦x ¦w x
k i ,k
k =0
debido a que
Capítulo 3. La Neurona Adaline
Toda la problemática impuesta por la cuestión de la eficiencia encuentra una
solución al simplificar los cálculos cuando consideremos en cada iteración sólo una parte
de la función J(W). Es decir, formaremos funciones auxiliares a partir de J(W) que
mejorarán la eficiencia de la búsqueda del mínimo al calcular gradientes que no dependen
de todo el conjunto de entrenamiento en cada iteración: usarán únicamente una parte de
éste.
Sea N el número de elementos en el conjunto de entrenamiento, N > 2. Nuevamente
partimos del hecho de que contamos con un método iterativo para el entrenamiento de la
neurona Adaline de manera que su vector de pesos es actualizado en cada iteración. Para la
m-ésima iteración, sea Wm el vector de pesos actual de la neurona. En esta misma iteración
se le presentará a la neurona únicamente el m-ésimo elemento del conjunto de
entrenamiento: (xm, dm), xm, dm ∈ \ . Recordemos que xm es el escalar de entrada y dm es el
escalar que se espera proporcione la neurona como salida. El vector Wm es entonces
actualizado de manera que se obtendrá un nuevo vector de pesos Wm+1. La actualización se
efectuará mediante la regla dada por la Ecuación 3.3.1:
Wm+1 = Wm + Δwm
Sin embargo el Término de Variación o Cambio del vector de pesos, Δwm, ahora estará dado
por:
Δwm = μ(-∇J(W)m)
(Ecuación 3.3.2)
Para la m-ésima iteración se tendrá la función J(W)m. A ésta se le llama Error al
Cuadrado Local y es precisamente el error que existe entre la salida esperada dm y la
salida zm proporcionada por la neurona cuando se le equipa con el vector de pesos actual
Wm y usando únicamente el m-ésimo elemento del conjunto de entrenamiento (xm, dm). El
error al cuadrado local se define entonces como:
J(W)m = (dm – zm)2 = (dm – (wm,0xm,0 + wm,1xm,1))2
(Ecuación 3.3.3)
Recordemos que wm,0 es el término de sesgo o predisposición de la neurona Adaline y que
xm,0 = 1 y xm,1 = xm, m = 1, 2, …, N. Nótese que J(W)m es también un paraboloide inmerso
en el espacio tridimensional y que por lo tanto cuenta con un único mínimo.
63
Una Introducción al Cómputo Neuronal Artificial
Ahora determinaremos al vector gradiente de la función J(W)m. Entonces
calculamos las derivadas parciales de J(W)m respecto a las variables wm,0 y wm,1:
δ J (W ) m
δ
ª(d − ( wm,0 xm ,0 + wm,1 xm ,1 )) 2 º¼
=
δ wm,0
δ wm,0 ¬ m
= 2(d m − ( wm,0 xm ,0 + wm,1 xm ,1 ))
δ
δ wm ,0
(d m − wm ,0 xm ,0 − wm,1 xm ,1 )
= 2(d m − ( wm,0 xm ,0 + wm,1 xm ,1 ))(− xm ,0 )
δ J (W ) m
δ
ª¬ (d m − ( wm ,0 xm ,0 + wm,1 xm ,1 )) 2 º¼
=
δ wm ,1
δ wm,1
= 2(d m − ( wm,0 xm ,0 + wm,1 xm ,1 ))
δ
δ wm ,1
(d m − wm ,0 xm,0 − wm,1 xm,1 )
= 2(d m − ( wm,0 xm ,0 + wm,1 xm ,1 ))(− xm ,1 )
δ J (W ) m
δ J (W ) m
y
tienen como factor común a −2(d m − ( wm,0 xm ,0 + wm,1 xm,1 ))
δ wm ,0
δ wm ,1
entonces se tendrá finalmente que el vector gradiente de J(W)m esta dado por:
Dado que
ª xm ,0 º
∇J (W ) m = −2(d m − ( wm,0 xm ,0 + wm,1 xm ,1 )) «
»
¬ xm ,1 ¼
(Ecuación 3.3.4)
Nótese que ∇J(W)m es uno de los términos presentes en la variación o cambio del
vector de pesos, Δwm, (Ecuación 3.3.2). Es claro que ∇J(W)m maximiza el error de la
función J(W)m, por lo tanto, si nuestro objetivo es buscar su mínimo, usaremos la dirección
opuesta: -∇J(W)m.
El m-ésimo término de la sumatoria presente en la función de error J(W) es
precisamente (d m − ( w0 xm,0 + w1 xm,1 ))2 . Ello implica que de hecho la función de error al
cuadrado local J(W)m puede ser vista como obtenida a partir de J(W). En consecuencia,
∇J(W)m puede ser visto también como un estimador de ∇J(W) el cual se usará para
aproximarnos también al mínimo global de J(W).
La idea ahora es reespecificar el método de Descenso Escalonado para entrenar una
neurona Adaline haciendo uso de las Ecuaciones 3.3.2 y 3.3.3. Se tendrá un proceso
iterativo en el cual por cada elemento del conjunto de entrenamiento (xm, dm) se considerará
una función de error J(W)m y el vector de pesos actual Wm. Específicamente se calculará el
vector gradiente de J(W)m en el punto dado por Wm. Nótese que el cálculo de ∇J(W)m
(Ecuación 3.3.4) es mucho más sencillo, en términos de eficiencia, que el cálculo del
64
Capítulo 3. La Neurona Adaline
vector gradiente de la función J(W) (Ecuaciones 2.2.6 y 2.2.7, Sección 2.2) precisamente
porque ∇J(W)m sólo requiere del m-ésimo par del conjunto de entrenamiento. Como ya se
comentó antes, ∇J(W)m servirá como un estimador para ∇J(W).
Algoritmo 3.2. Método de Descenso Escalonado para la
búsqueda de un mínimo: caso de una única entrada.
Procedure SteepestDescent(Matrix x[1, …, N][0,1], Array d[1, …, N], Real μ)
// Se asignan valores aleatorios al vector de pesos iniciales.
W = new Array[0,1]
W[0] = Random( )
W[1] = Random( )
for m = 1 until N do
Real ε_m = d[m] – (W[0] * x[m][0] + W[1] * x[m][1])
// Se calcula el vector gradiente de J(W)m en el punto dado por W.
∇J_Wm = new Array[0,1]
∇J_Wm[0] = -2 * ε_m * x[m][0]
∇J_Wm[1] = -2 * ε_m * x[m][1]
// Se obtiene la variación o cambio a aplicar al vector de pesos W.
Δwm = new Array[0,1]
Δwm[0] = μ ∗ (−1) ∗ ∇J_Wm[0]
Δwm[1] = μ ∗ (−1) ∗ ∇J_Wm[1]
// Se actualiza el vector de pesos.
W[0] = W[0] + Δwm[0]
W[1] = W[1] + Δwm[1]
end-of-for
// Se retorna como salida al último vector de pesos calculado.
return W
end-of-procedure
La implementación del proceso anterior requiere un vector de pesos inicial W1. Por
lo regular sus valores son inicializados aleatoriamente. Para cada iteración m,
m = 1, 2, 3, …, N, primero se selecciona al m-ésimo elemento del conjunto de
entrenamiento. Posteriormente se calcula el valor de εm = [dm – (wm,0xm,0 + wm,1xm,1)] y
entonces se obtiene el vector gradiente de J(W)m en el punto Wm mediante
ª xm ,0 º
∇J (W ) m = −2ε m «
»
¬ xm,1 ¼
Finalmente se actualiza proporcionalmente al vector de pesos Wm al sumarle el negativo de
∇J (W ) m . La proporción a aplicar viene dada por la constante μ ∈ \ + . De esta manera se
obtiene el vector de pesos actualizado Wm+1. El Algoritmo 3.2 presenta entonces el
procedimiento de entrenamiento de una neurona Adaline de una entrada y una salida
mediante el método de Descenso Escalonado. Nótese que hemos establecido que el
Algoritmo 3.2 efectúa en total N iteraciones, una por cada elemento del conjunto de
65
Una Introducción al Cómputo Neuronal Artificial
entrenamiento. Sin embargo, y dependiendo del problema que se esté modelando, es
posible que se requiera presentar en más de una ocasión al todo el conjunto de
entrenamiento. Analizaremos esta situación en los siguientes párrafos.
Considérese el conjunto de entrenamiento presentado en la Tabla 3.2. Veamos que
resultados nos proporciona el método de Descenso Escalonado usando al vector inicial de
pesos
ª0.5º
W1 = « »
¬0.5¼
y la constante μ = 0.02. Efectuaremos en total N = 11 actualizaciones del vector de pesos.
Véase la Tabla 3.3. En la iteración m = 11 se tiene el vector de pesos
ª1.2432 º
W12 = «
»
¬3.4485¼
El conjunto de entrenamiento de la Tabla 3.2 ya había sido presentado en la Sección 2.2
(Tabla 2.1) para ejemplificar el método de Mínimos Cuadrados. En ese caso se obtuvieron
los pesos finales y óptimos w0 = 3.9545 y w1 = 2.9818. Después de 11 iteraciones el método
de Descenso Escalonado nos ha proporcionado las aproximaciones w12,0 = 1.2432 y
w12,1 = 3.4485 la cuales pueden considerarse un tanto alejadas de las óptimas. Sin embargo,
comentamos previamente que es posible efectuar una presentación más del conjunto de
entrenamiento si se considerase necesario, es decir, efectuar otras 11 iteraciones. En este
caso aplicaríamos nuevamente el Algoritmo 3.2 pero usando como vector inicial W1 al
vector de pesos final que se obtuvo en la presentación anterior del conjunto de
entrenamiento, es decir, el vector W12. La Tabla 3.4 muestra los resultados obtenidos al
aplicar nuevamente el método de Descenso Escalonado usando ahora como vector inicial
ª1.2432 º
W1 = «
»
¬3.4485¼
En este caso se obtuvo la aproximación w12,0 = 2.1486 y w12,1 = 3.2661. Nótese que se ha
obtenido una mejora bastante considerable respecto a los pesos obtenidos en la primer
presentación del conjunto de entrenamiento. En realidad, es posible efectuar tantas
presentaciones sean necesarias. El Algoritmo 3.3 es una versión modificada del Algoritmo
3.2. Recibe una entrada adicional T que indica el número de veces que el conjunto de
entrenamiento será presentado. Nótese que hemos especificado que para la primer
presentación, t = 1, el vector W1 es inicializado aleatoriamente. En las posteriores
presentaciones, t ≥ 2, el vector W1 es el último vector de pesos que se obtuvo en la
presentación anterior.
66
Capítulo 3. La Neurona Adaline
Tabla 3.2. Un conjunto de entrenamiento al que se le aplicará
el método de Descenso Escalonado a fin de que una neurona Adaline lo modele.
di
i
x1,i
1
-5
-10.5
2
-4
-8.5
3
-3
-4.5
4
-2
-2.5
5
-1
0.5
6
0
4.5
7
1
6.5
8
2
10.5
9
3
12.5
10
4
16.5
11
5
18.5
Tabla 3.3.Aplicación del método de Descenso Escalonado para el ajuste de pesos
de una neurona Adaline con el conjunto de entrenamiento de la Tabla 3.2.
ª xm,0 º
Iteración m εm = [dm – (wm,0xm,0 + wm,1xm,1)] ∇J (W ) m = −2ε m «
» Wm+1 = Wm + μ(- ∇J (W ) m )
¬ xm,1 ¼
1
ε1 = −8.5
2
ε2 = 0.14
3
ε3 = 1.8672
4
ε4 = 1.667
5
ε5 = 2.0732
6
ε6 = 4.1301
7
ε7 = 4.1876
8
ε8 = 5.9078
9
ε9 = 4.3088
10
ε10 = 3.6508
11
ε11 = −0.3503
17 º
∇J (W )1 = ª«
»
¬ −85¼
−0.28º
∇J (W ) 2 = ª«
»
¬ 1.12 ¼
W2 = ª0.16 º
« 2.2 »
¬
¼
= ª 0.1656 º
W3
« 2.1776 »
¬
¼
−3.7344 º
∇J (W )3 = ª«
»
¬11.2032 ¼
−2.3335º
∇J (W ) 4 = ª«
»
¬ 4.6671 ¼
W4 = ª0.2402 º
«1.9535 »
¬
¼
−4.1464 º
∇J (W )5 = ª«
»
¬ 4.1464 ¼
−8.2602 º
∇J (W )6 = ª«
»
¬ 0 ¼
−8.3752 º
∇J (W )7 = ª«
»
¬ −8.3752 ¼
−11.8157 º
∇J (W )8 = ª«
»
¬ −23.6314 ¼
−8.6177 º
∇J (W )9 = ª«
»
−
¬ 25.8533¼
−7.3017 º
∇J (W )10 = ª«
»
¬ −29.207 ¼
0.7006 º
∇J (W )11 = ª«
»
¬3.5032 ¼
W5 = ª0.2869 º
«1.8601 »
¬
¼
= ª 0.3698 º
W6
«1.7772 »
¬
¼
W7 = ª0.5350 º
«1.7772 »
¬
¼
= ª 0.7025 º
W8
«1.9447 »
¬
¼
W9 = ª 0.9389 º
« 2.4174 »
¬
¼
= ª1.1112 º
W10
« 2.9344 »
¬
¼
W11 = ª1.2573 º
«3.5186 »
¬
¼
W12 = ª1.2432 º
«3.4485»
¬
¼
67
Una Introducción al Cómputo Neuronal Artificial
Tabla 3.4. Aplicación del método de Descenso Escalonado para el ajuste de pesos
de una neurona Adaline presentando por segunda vez el conjunto de entrenamiento de la Tabla 3.2
y usando como vector de pesos iniciales W = ª1.2432 º .
1
«3.4485»
¬
¼
Iteración m
εm = [dm – (wm,0xm,0 + wm,1xm,1)]
1
ε1 = 5.4994
2
ε2 = −0.5686
3
ε3 = 1.3784
4
ε4 = 0.5528
5
ε5 = 1.2122
6
ε6 = 2.9337
7
ε7 = 2.6348
8
ε8 = 4.1371
9
ε9 = 2.6918
10
ε10 = 2.6741
11
ε11 = −0.513
ª xm,0 º
∇J (W ) m = −2ε m «
»
¬ xm,1 ¼
−10.9988º
∇J (W )1 = ª«
»
¬ 54.9941 ¼
Wm+1 = Wm + μ(- ∇J (W ) m )
W2 = ª1.4632 º
« 2.3486 »
¬
¼
1.1372 º
∇J (W ) 2 = ª«
»
¬ −4.549 ¼
−2.7567 º
∇J (W )3 = ª«
»
¬ 8.2703 ¼
W3 = ª1.4405 º
« 2.4396 »
¬
¼
= ª1.4956 º
W4
« 2.2742 »
¬
¼
−1.1056 º
∇J (W ) 4 = ª«
»
¬ 2.2112 ¼
−2.4244 º
∇J (W )5 = ª«
»
¬ 2.4244 ¼
W5 = ª1.5177 º
« 2.23 »
¬
¼
−5.8674 º
∇J (W )6 = ª«
»
¬ 0 ¼
−5.2697 º
∇J (W )7 = ª«
»
¬ −5.2697 ¼
−8.2743 º
∇J (W )8 = ª«
»
−
¬ 16.5487 ¼
−5.3837 º
∇J (W )9 = ª«
»
¬ −16.1511¼
−5.3484 º
∇J (W )10 = ª«
»
¬ −21.3936 ¼
1.026 º
∇J (W )11 = ª«
»
¬5.1303¼
W6 = ª1.5662 º
« 2.1815»
¬
¼
= ª1.6836 º
W7
« 2.1815»
¬
¼
W8 = ª 1.789 º
« 2.2869 »
¬
¼
W9 = ª1.9544 º
« 2.6178»
¬
¼
W10 = ª 2.0621º
« 2.9409 »
¬
¼
= ª 2.1691º
W11
«3.3687 »
¬
¼
W12 = ª 2.1486 º
« 3.2661»
¬
¼
En la Tabla 3.5 se presentan los vectores de pesos W12 en la t-ésima presentación,
t = 1, 2, …, 10. Los vectores de pesos obtenidos en la primera y segunda presentación son
los mismos que se habían descrito en las iteraciones m = 11 de las Tablas 3.3 y 3.4. En la
última presentación, t = 10, se obtuvo la aproximación de pesos w12,0 = 3.7717 y
w12,1 = 2.9389. Nótese que en este punto contamos ya con valores bastante cercanos a los
óptimos w0 = 3.9545 y w1 = 2.9818. En el método de Descenso Escalonado es posible
efectuar tantas presentaciones del conjunto de entrenamiento sean requeridas. En este punto
es muy probable que no se aprecie una diferencia sustancial comparando con el método de
Mínimos Cuadrados respecto al número de operaciones efectuadas. En la siguiente Sección
se retomará este tópico, sin embargo, hemos de recalcar que parte la valía del Descenso
Escalonado radica en la simplicidad de las operaciones utilizadas.
68
Capítulo 3. La Neurona Adaline
Algoritmo 3.3. Método de Descenso Escalonado para la
búsqueda de un mínimo: caso de una única entrada y T presentaciones
del conjunto de entrenamiento.
Procedure SteepestDescent(Matrix x[1,…,N][0,1], Array d[1, …, N], Real μ, Integer T)
// Se asignan valores aleatorios al vector de pesos iniciales.
W = new Array[0,1]
W[0] = Random( )
W[1] = Random( )
for t = 1 until T do
for m = 1 until N do
Real ε_m = d[m] – (W[0] * x[m][0] + W[1] * x[m][1])
// Se calcula el vector gradiente de J(W)m en el punto dado por W.
∇J_Wm = new Array[0,1]
∇J_Wm[0] = -2 * ε_m * x[m][0]
∇J_Wm[1] = -2 * ε_m * x[m][1]
// Se obtiene la variación o cambio a aplicar al vector de pesos W.
Δwm = new Array[0,1]
Δwm[0] = μ ∗ (−1) ∗ ∇J_Wm[0]
Δwm[1] = μ ∗ (−1) ∗ ∇J_Wm[1]
// Se actualiza el vector de pesos.
W[0] = W[0] + Δwm[0]
W[1] = W[1] + Δwm[1]
end-of-for
end-of-for
return W // Se retorna como salida al último vector de pesos calculado.
end-of-procedure
3.3.2 Descenso Escalonado: Caso varias entradas – una salida
Consideremos ahora el caso de una neurona de tipo Adaline con P entradas y una
única salida. Sea N el número de elementos del conjunto de entrenamiento tal que N > P+1.
Formalmente, la neurona recibirá como entrada un vector Xm en \ P +1 , 1 ≤ m ≤ N:
ª xm,0 = 1º
« x
»
« m,1 »
X m = « xm ,2 »
«
»
« # »
« xm , P »
¬
¼
Recordemos que el componente agregado xm,0 = 1 se relacionará con el término de sesgo o
predisposición de la neurona.
69
Una Introducción al Cómputo Neuronal Artificial
Ahora retomaremos algunos conceptos ya presentados en la Sección anterior. Sea
Wm el vector de pesos obtenido al presentar a la neurona el m-ésimo par del conjunto de
entrenamiento (Xm, dm), dm ∈ \ . A partir de Wm y (Xm, dm) se actualiza al vector de pesos
mediante la regla (Ecuación 3.3.1):
Wm+1 = Wm + Δwm
Donde Δwm es el Término de Variación o Cambio en Wm dado por (Ecuación 3.3.2):
Δwm = μ(-∇J(W)m)
J(W)m es el error entre la salida proporcionada por la neurona y el valor esperado dm al usar
los pesos en Wm y el vector de entrada Xm. J(W)m se define ahora como (nótese la similitud
con la Ecuación 3.3.3):
P
§
·
J (W ) m = (d m − Wm ⋅ X m ) = ¨ d m − ¦ wm ,k xm ,k ¸
k =0
©
¹
2
2
(Ecuación 3.3.5)
Tabla 3.5. Vectores de pesos obtenidos al final de la t-ésima presentación,
t = 1, 2, …, 10, mediante Descenso Escalonado, para el conjunto
de entrenamiento de la Tabla 3.2.
Presentación t Vectores de Pesos en m = 11
ª1.2432 º
1
«3.4485»
¬
¼
ª 2.1486 º
2
« 3.2661»
¬
¼
ª 2.7364 º
3
«3.1476 »
¬
¼
ª 3.1181º
4
«3.0707 »
¬
¼
ª3.3659 º
5
«3.0207 »
¬
¼
ª3.5268º
6
« 2.9883»
¬
¼
ª3.6312 º
7
« 2.9672 »
¬
¼
ª 3.6991º
8
« 2.9535»
¬
¼
ª 3.7431º
9
« 2.9447 »
¬
¼
ª3.7717 º
10
« 2.9389 »
¬
¼
70
Capítulo 3. La Neurona Adaline
De acuerdo a la Ecuación 3.3.2, se requiere calcular el vector gradiente de J(W)m, es
decir, ∇J(W)m:
ª δ J (W ) m º
« δw
»
m ,0
«
»
« δ J (W ) m »
«
»
∇J (W ) m = « δ wm ,1 »
«
»
#
«
»
« δ J (W ) m »
« δw
»
m,P ¼
¬
(Ecuación 3.3.6)
Consideremos el j-ésimo componente de ∇J(W)m. Entonces:
P
δ J (W ) m
δ §
·
d m − ¦ wm ,k xm ,k ¸
=
¨
δ wm , j
δ wm , j ©
k =0
¹
2
P
§
· δ
= 2 ¨ d m − ¦ wm ,k xm ,k ¸
k =0
©
¹ δ wm , j
P
§
·
d
−
¨ m ¦ wm ,k xm ,k ¸
k =0
©
¹
P
δ
§
·§
= 2 ¨ d m − ¦ wm ,k xm ,k ¸ ¨ −
k =0
©
¹ ¨© δ wm, j
P
¦w
m,k
k =0
·
xm ,k ¸
¸
¹
P
·
δ
§
·§
= 2 ¨ d m − ¦ wm ,k xm ,k ¸ ¨ −
wm , j xm , j ¸
¸
k =0
©
¹ ¨© δ wm, j
¹
P
§
·
= 2 ¨ d m − ¦ wm ,k xm ,k ¸ ( − xm , j )
k =0
©
¹
= −2 xm , j (d m − Wm ⋅ X m )
Es decir:
δ J (W ) m
= −2 xm , j (d m − Wm ⋅ X m )
δ wm , j
(Ecuación 3.3.7)
71
Una Introducción al Cómputo Neuronal Artificial
Para cada m, m = 0, …, P, la Ecuación 3.3.7 nos proporciona el m-ésimo
componente de ∇J (W ) m . Es claro que todos los componentes del vector gradiente de
J (W ) m tienen el factor común −2(d m − Wm ⋅ X m ) . Por lo tanto ∇J (W ) m queda como:
ª −2 xm ,0 (d m − Wm ⋅ X m ) º
ª xm,0 º
« −2 x (d − W ⋅ X ) »
«x »
m ,1
m
m
m »
m ,1 »
«
«
∇J (W ) m =
= −2(d m − Wm ⋅ X m )
«
»
« # »
#
«
»
«
»
¬ −2 xm , P (d m − Wm ⋅ X m ) ¼
¬ xm , P ¼
(Ecuación 3.3.8)
Algoritmo 3.4. Método de Descenso Escalonado para la
búsqueda de un mínimo: caso de varias entradas y T presentaciones
del conjunto de entrenamiento.
Procedure SteepestDescent
(Matrix x[1,…,N][0,…,P], Array d[1, …, N], Real μ, Integer T)
// Se asignan valores aleatorios al vector de pesos iniciales.
W = new Array[0,…,P]
for i = 0 until P
W[i] = Random( )
end-of-for
for t = 1 until T do
for m = 1 until N do
Real ε_m = 0
for i = 0 until P
ε_m = ε_m + W[i] * x[m][i]
end-of-for
ε_m = d[m] − ε_m
// Se calcula el vector gradiente de J(W)m en el punto dado por W.
∇J_Wm = new Array[0,…,P]
for i = 0 until P
∇J_Wm[i] = -2 * ε_m * x[m][i]
end-of-for
// Se obtiene la variación o cambio a aplicar al vector de pesos W.
Δwm = new Array[0,…,P]
for i = 0 until P
Δwm[i] = μ ∗ (−1) ∗ ∇J_Wm[i]
end-of-for
for i = 0 until P
W[i] = W[i] + Δwm[i] // Se actualiza el vector de pesos.
end-of-for
end-of-for
end-of-for
return W // Se retorna como salida al último vector de pesos calculado.
end-of-procedure
72
Capítulo 3. La Neurona Adaline
Contamos ya con los elementos para definir el método de Descenso Escalonado en
el caso de una neurona con P entradas y una salida. La Ecuación 3.3.5,
J (W ) m = (d m − Wm ⋅ X m ) 2 , determina el error al cuadrado existente entre la salida actual de
la neurona y el m-ésimo elemento del conjunto de entrenamiento (Xm, dm). Es claro que la
función J (W ) m es uno de los términos que forman a la función J(W) de Costo de
Entrenamiento para el vector de pesos W (Ecuación 3.2.3):
J (W ) =
1
2N
N
¦ ε i2 =
i =1
1
2N
N
¦ (d
i
− Wi ⋅ X i ) 2
i =1
En este sentido el método de Descenso Escalonado utiliza a J (W ) m para obtener gradientes
que pueden ser vistos como estimaciones o aproximaciones de los vectores gradientes de
J(W). La ventaja es que ∇J (W ) m se calcula únicamente en función de (Xm, dm) y Wm,
mientras que el gradiente de J(W) requiere a todo el conjunto de entrenamiento (véase la
Ecuación 2.3.5).
Entonces, el procedimiento de Descenso Escalonado para actualizar a Wm es el
siguiente:
• Seleccionar al vector de entrada Xm y la salida esperada dm.
• Se calcula el error de entrenamiento para los pesos en Wm mediante
P
ε m = d m − Wm ⋅ X m = d m − ¦ wm ,k xm ,k
k =0
•
Se aplica la Ecuación 3.3.8 de manera que se obtiene:
ª xm,0 º
«x »
m ,1 »
∇J (W ) m = −2ε m «
« # »
«
»
¬ xm , P ¼
73
Una Introducción al Cómputo Neuronal Artificial
•
La dirección de ∇J (W ) m maximiza a la función de error J (W ) m , ello implica que el
cambio o variación a aplicar al vector de pesos deberá ir en el sentido contrario a
∇J (W ) m . Por lo tanto, de la Ecuación 3.3.2, tenemos:
Δwm = μ(-∇J(W)m)
Donde μ es una constante positiva que definirá la proporción de -∇J(W)m a aplicar
sobre Wm. Recordemos, por la Sección anterior, que μ determina que tanto se moverá
Wm para obtener su correspondiente versión actualizada Wm+1.
•
Por último, el vector Wm+1 es obtenido mediante (Ecuación 3.3.1):
Wm+1 = Wm + Δwm
El proceso anterior ha de ser efectuado por cada uno de los elementos en el conjunto
de entrenamiento. Ello implica que una vez terminada la presentación del conjunto de
entrenamiento se contará con un vector de pesos aproximados WN+1. Si así se requiere, es
posible efectuar más presentaciones a fin de mejorar al vector de pesos. A partir de la
segunda presentación, el vector de pesos inicial es el último que se obtuvo en la
presentación anterior.
El Algoritmo 3.4 implementa el proceso de Descenso Escalonado. Recibe como
entrada una matriz de tamaño N × (P+1) que contiene los vectores de entrada; un arreglo de
N elementos con los escalares de salida esperada; la constante positiva μ para establecer la
proporcionalidad de la actualización del vector de pesos y finalmente el número T de veces
que el conjunto de entrenamiento será presentado. Es claro que el Algoritmo 3.4 es sólo
una generalización de la especificación dada en el Algoritmo 3.3 al considerar que los
vectores de entrada son ahora de tamaño P+1. Cuando P = 1 entonces el Algoritmo 3.4
cubre la misma instancia que el Algoritmo 3.3.
Ahora efectuaremos una serie de conteos relacionados con el número de
operaciones ejecutadas por el Algoritmo 3.4. Estos conteos irán de la mano con los valores
de P (dimensionalidad de los vectores de entrada), N (número de elementos en el conjunto
de entrenamiento) y T (número de veces que el conjunto de entrenamiento será presentado).
Para calcular
P
ε m = d m − Wm ⋅ X m = d m − ¦ wm ,k xm ,k
k =0
74
Capítulo 3. La Neurona Adaline
Se requieren P + 1 multiplicaciones, P + 1 sumas y una resta. Es decir, 2P + 3 operaciones.
Por otro lado, para obtener
ª xm,0 º
«x »
m ,1 »
∇J (W ) m = −2ε m «
« # »
«
»
¬ xm , P ¼
se deben efectuar, por cada componente de ∇J (W ) m , 2 multiplicaciones. Entonces tenemos
en total 2(P+1) operaciones. Cada componente de ∇J (W ) m debe ser además multiplicado
por -1 y por la constante μ. Tenemos entonces que para calcular al Término de Variación o
Cambio Δwm = μ(-∇J(W)m) se requieren 2(P+1) operaciones. Finalmente, para la
actualización del vector de pesos
Wm+1 = Wm + Δwm
Se deberán realizar P+1 sumas. Agrupando los conteos anteriores tenemos, que para
obtener un vector de pesos actualizado, el número de operaciones requeridas en total es:
(2P+3) + 2(P+1) + 2(P+1) + (P+1) = 7P + 8
Dado que en una presentación se efectúan N actualizaciones del vector de pesos entonces
tenemos que se realizan N(7P + 8) operaciones. Por último, el conjunto de entrenamiento
completo es presentado en T ocasiones. Entonces el número total de operaciones efectuadas
por el Algoritmo 3.4 será representado por la función SDO(T, N, P) (Steepest Descent
Operations) y la cual está dada por:
SDO(T, N, P) = TN(7P + 8)
(Ecuación 3.3.9)
Ahora bien, tenemos pleno conocimiento de que el problema que estamos tratando
puede ser debidamente resuelto mediante el método de Mínimos Cuadrados. Recordemos
algunos puntos. Sea la matriz R de (P+1) × (P+1) dada por (Ecuación 2.3.11):
ª R0,0
«R
1,0
R=«
« #
«
¬ RP ,0
R0,1 " R0, P º
R1,1 " R1, P »»
# %
# »
»
RP ,1 " RP , P ¼
75
Una Introducción al Cómputo Neuronal Artificial
Donde cada uno de sus elementos está dado por (Ecuación 2.3.10):
Rk , j =
1
N
k = 0,1, 2,..., P
N
¦x
x
j = 0,1, 2,..., P
i , j i ,k
i =1
Tenemos también al vector de P+1 elementos ℘ (Ecuación 2.3.13):
ª℘0 º
«℘ »
℘= « 1 »
« # »
« »
¬℘P ¼
Donde (Ecuación 2.3.12):
℘j =
1
N
N
¦x
i, j
j = 0,1, 2,..., P
di
i =1
Por la Ecuación 2.3.15 tenemos que el método de Mínimos Cuadrados queda expresado
como el producto matricial:
℘ = RW
Donde W es precisamente nuestro vector de pesos. Dada la inversa de R, R-1, entonces la
Ecuación 2.3.16 nos dice que el vector de pesos óptimo esta dado por:
R-1℘ = W
Para abordar la búsqueda de los pesos óptimos mediante Mínimos Cuadrados y
usando el enfoque matricial es claro que tendremos tres fases:
• La fase de inicialización de la matriz R y el vector ℘.
• La fase de obtención de la matriz inversa de R.
• Y finalmente, la fase donde efectuamos el producto matricial R-1℘.
Calcularemos el número de operaciones efectuadas en cada una de estas fases. Cada
1 N
elemento de la matriz R, Rk , j = ¦ xi , j xi ,k , es calculado al ejecutar una multiplicación que
N i =1
involucra dos componentes por cada elemento del conjunto de entrenamiento. Los
resultados de estas multiplicaciones son sumados y la suma total se divide por N. Entonces
tenemos en total N multiplicaciones, N sumas y una división: 2N + 1 operaciones. Dado que
R es de tamaño (P + 1) × (P + 1) entonces en total, para inicializar a R, se efectúan
(P + 1)2(2N + 1) operaciones. Ahora bien, para inicializar al vector ℘, se debe obtener para
76
Capítulo 3. La Neurona Adaline
1 N
¦ xi, j di . Esta suma depende de
N i =1
multiplicar un componente de cada vector de entrada en el conjunto de entrenamiento por
su correspondiente escalar de salida esperada. Los resultados de cada multiplicación son
sumados y la suma total dividida por N. Entonces se efectúan N productos, N sumas y una
división: 2N + 1 operaciones. Este ultimo resultado se multiplica por (P + 1) de manera que
para inicializar al vector ℘ se requieren (P + 1)(2N + 1) operaciones. Por lo tanto, la fase
de inicialización de la matriz R y el vector ℘ requiere en total ejecutar
(P + 1)2(2N + 1) + (P + 1)(2N + 1) operaciones.
cada uno de sus P+1 componentes la suma ℘j =
Ahora bien, la segunda fase requiere encontrar la matriz inversa de R. Supongamos
que se aplica el bien conocido método de Eliminación de Gauss-Jordan. Es bien sabido que
se requieren un número de operaciones de orden cúbico, respecto al número de renglones
de la matriz, para encontrar su inversa. Tomemos tal cota justa. Por lo tanto, dado que R es
de tamaño (P + 1) × (P + 1) entonces el número total de operaciones a ejecutar para
encontrar su inversa es (P + 1)3.
Por último, debemos determinar el número de operaciones requeridas para calcular
los valores óptimos de los pesos. Estos dependen del resultado del producto matriz/vector
R-1℘. Recordando el algoritmo clásico de multiplicación matricial, cada elemento de cada
renglón de R-1 será multiplicado por cada elemento correspondiente en el vector ℘. Ello
implica que se efectuarán (P + 1)2 operaciones para finalmente obtener al vector de pesos
W. Entonces el número total de operaciones efectuadas por el método de Mínimos
Cuadrados, a fin de entrenar a una neurona Adaline, será representado por la función
LSO(N, P) (Least Squares Operations) la cual está dada por:
LSO(N, P) = (P + 1)2(2N + 1) + (P + 1)(2N + 1) + (P + 1)3 + (P + 1)2
(Ecuación 3.3.10)
Ahora efectuaremos una comparación entre el costo del entrenamiento bajo
Descenso Escalonado contra el método de Mínimos Cuadrados. De hecho, partiremos de
suponer que efectivamente el método de Descenso Escalonado es más eficiente, en
términos del número de operaciones efectuadas, que el método de Mínimos Cuadrados.
Para ello, verificaremos para qué valores de T (número de presentaciones), N (tamaño del
conjunto de entrenamiento) y P (dimensionalidad de los vectores de entrada) la siguiente
desigualdad se hace válida:
SDO(T, N, P) < LSO(N, P)
⇔ TN(7P + 8) < (P + 1)2(2N + 1) + (P + 1)(2N + 1) + (P + 1)3 + (P + 1)2
77
Una Introducción al Cómputo Neuronal Artificial
La idea ahora es acotar a T en función de N y P (lo cual en realidad será muy sencillo):
TN (7 P + 8) < ( P + 1) 2 (2 N + 1) + ( P + 1)(2 N + 1) + ( P + 1)3 + ( P + 1) 2
( P + 1) 2 (2 N + 1) + ( P + 1)(2 N + 1) + ( P + 1)3 + ( P + 1) 2
ŸT <
N (7 P + 8)
P 3 + 2 NP 2 + 5 P 2 + 6 NP + 8 P + 4 N + 4
=
7 NP + 8 N
Nótese que el denominador 7 NP + 8 N nunca se hace cero ya que N > 0 y P > 0. De hecho,
el cociente, para cualquier valor de N y P, ambos positivos, proporciona siempre un valor
positivo (todos los términos que lo conforman son positivos). Lo interesante es que
contamos con una formulación tal que dados los valores de N y P determinaremos el
número máximo de presentaciones del conjunto de entrenamiento que se deben efectuar de
manera que el número de operaciones del método de Descenso Escalonado sea
estrictamente menor al número de operaciones requeridas por el método de Mínimos
Cuadrados. Por ejemplo, supongamos que se cuenta con un conjunto de entrenamiento de
tamaño N = 100 y dimensionalidad P = 20. Entonces al sustituir en la cota superior para T
tenemos que:
(20)3 + 2(100)(20) 2 + 5(20) 2 + 6(100)(20) + 8(20) + 4(100) + 4
= 6.93
7(100)(20) + 8(100)
Ello implica que con el método de Descenso Escalonado se deben efectuar a lo más T = 6
presentaciones del conjunto de entrenamiento antes de que sea más conveniente utilizar el
método de Mínimos Cuadrados. Supongamos ahora que N = 1,000 y P continúa con su
valor 20. Nuevamente, al sustituir en la cota superior para T obtenemos:
(20)3 + 2(1, 000)(20) 2 + 5(20) 2 + 6(1, 000)(20) + 8(20) + 4(1, 000) + 4
= 6.3119
7(1, 000)(20) + 8(1, 000)
En esta situación concluimos, de nueva cuenta, que a lo más se deben efectuar T = 6
presentaciones. Ahora si N = 10,000 y P = 20:
(20)3 + 2(10, 000)(20) 2 + 5(20) 2 + 6(10, 000)(20) + 8(20) + 4(10, 000) + 4
= 6.25
7(10, 000)(20) + 8(10, 000)
Nuevamente determinamos que cómo máximo T = 6 presentaciones son las convenientes.
Surge entonces la observación de que quizás quien realmente determina el número máximo
de presentaciones del conjunto de entrenamiento es la dimensionalidad P de los vectores de
entrada. Veamos qué sucede cuando N → ∞ mientras P permanece constante. Para ello
calculamos el siguiente límite asumiendo por el momento a N y P como reales positivos:
78
Capítulo 3. La Neurona Adaline
P 3 + 2 NP 2 + 5P 2 + 6 NP + 8P + 4 N + 4
N →∞
7 NP + 8 N
(2 NP 2 + 6 NP + 4 N ) + ( P 3 + 5 P 2 + 8 P + 4)
= lim
N →∞
7 NP + 8 N
2
(2 NP + 6 NP + 4 N )
P3 + 5P 2 + 8P + 4
= lim
+ lim
N →∞
N →∞
N (7 P + 8)
N (7 P + 8)
lim
=
2P2 + 6P + 4
N P3 + 5P 2 + 8P + 4
1
lim +
lim
N →∞ N
N →∞
7P + 8 7P + 8
N
=
2P + 6P + 4
7P + 8
1
0
2
2P2 + 6P + 4
nos proporciona el número máximo
7P + 8
de veces que el conjunto de entrenamiento puede ser presentado, bajo Descenso
Escalonado, suponiendo que su tamaño N es suficientemente grande. Entonces, sea T(P)
definido como el número máximo de presentaciones de un conjunto de entrenamiento,
de tamaño suficientemente grande, y con vectores de dimensionalidad P, de manera que el
método de Descenso Escalonado requiera efectuar un número de operaciones menor que el
método de Mínimos Cuadrados:
Ello quiere decir que la expresión
« 2P2 + 6P + 4 »
T ( P) = «
»
¬ 7P + 8 ¼
(Ecuación 3.3.11)
Donde ¬«⋅»¼ denota a la Función Piso ( ¬« x ¼» = max{m ∈ ] : m ≤ x} ).
Por lo tanto, retomando nuestro ejemplo con P = 20 y aplicando la Ecuación 3.3.11:
« 2(20) 2 + 6(20) + 4 »
T (20) = «
»=6
7(20) + 8
¬
¼
Tenemos entonces que el número máximo de presentaciones a efectuar, para conjuntos de
entrenamiento de tamaño N suficientemente grande, es 6.
79
Una Introducción al Cómputo Neuronal Artificial
Supongamos, por ejemplo, que se requiere entrenar a una neurona Adaline usando
un conjunto de imágenes con resolución 320 × 240. Supongamos también, y de hecho en
ocasiones así se procede en la práctica, que tales imágenes son representadas como vectores
en \ P +1 de manera que P = 320⋅240 = 76,800. Entonces tenemos que, por la Ecuación
3.3.11, el número máximo de presentaciones a efectuar es:
« 2(76,800) 2 + 6(76,800) + 4 »
T (76,800) = «
» = 21,943
7(76,800) + 8
¬
¼
Tenemos entonces un margen bastante considerable de presentaciones a aplicar de manera
que se satisfaga la eficiencia del método de Descenso Escalonado sobre el método de
Mínimos Cuadrados, siempre y cuando se asuma al conjunto de entrenamiento como de un
tamaño suficientemente grande (N → ∞). En términos más concretos, suponiendo que se
contase con N = 1,000 imágenes y sustituyendo con P = 76,800 y T = 21,943 en las
Ecuaciones 3.3.9 y 3.3.10 tenemos:
• SDO(21943, 1000, 76800) = (21,943)(1, 000)(7(76,800) + 8) = 11,796,732,344,000
ª((76,800 + 1) 2 )(2(1, 000) + 1) + º
«
»
• LSO(1000, 76800) = «(76,800 + 1)(2(1, 000) + 1) + » = 464,811,264,618,404
«(76,800 + 1)3 + (76, 800 + 1) 2 »
¬
¼
LSO(1000, 76800)
464,811,264,618,404
=
= 39.4016
•
SDO(21943, 1000, 76800) 11,796,732,344,000
Es decir, el método de Mínimos Cuadrados, para esta situación, requiere efectuar casi 40
veces más operaciones que el método de Descenso Escalonado. Ahora bien, consideremos
el caso en que P = 1, tal como sucede con el conjunto de entrenamiento presentado en la
Sección anterior (Tabla 3.2). Tenemos entonces, por aplicación de la Ecuación 3.3.11:
« 2(1) 2 + 6(1) + 4 »
T (1) = «
»=0
7(1) + 8
¬
¼
El valor T(1) = 0 es indicativo de que de hecho, para este caso, el método de Descenso
Escalonado no es más eficiente que el método de Mínimos Cuadrados. Es más, este
comentario ya había sido hecho en su momento en la Sección anterior.
Cuando se tienen vectores de entrada de dimensionalidad P ≥ 2 se presentan los
casos en los cuales el método de Descenso Escalonado es más eficiente que el método de
Mínimos Cuadrados:
« 2(2) 2 + 6(2) + 4 »
T (2) = «
» =1
7(2) + 8
¬
¼
80
Capítulo 3. La Neurona Adaline
Recordemos que usando la desigualdad SDO(T, N, P) < LSO(N, P) acotamos el
valor de T en función de N y P. Simplemente debemos hacer la aclaración de que la
desigualdad anterior es válida para todo N y todo P positivos (P ≥ 1) mientras que T(P)
efectivamente acota a T pero bajo la suposición de que el tamaño del conjunto de
entrenamiento es suficientemente grande, o en otras palabras, cuando N → ∞. Es
precisamente por la última hipótesis que T(P) arroja valores positivos a partir de P ≥ 2
aparentemente dejando excluido el caso P = 1. Sin embargo, debe ser claro que para
algunos valores pequeños de N y con P = 1 es posible que el método de Descenso
Escalonado sea más eficiente que el método de Mínimos Cuadrados.
Por último, y para concluir esta sección, debemos hacer notar que mientras que la
Ecuación 3.3.9 nos indica el número de operaciones requeridas por el método de Descenso
Escalonado y la Ecuación 3.3.11 nos proporciona el número máximo de presentaciones del
conjunto de entrenamiento a efectuar, es importante tener en cuenta que la diferencia entre
el vector de pesos final y el vector de pesos óptimo va también en función de μ, de que tan
representativos son los elementos del conjunto de entrenamiento y del vector inicial W1.
Ello quiere decir que el efectuar T(P) presentaciones no garantiza de ninguna manera que el
vector de pesos final sea el vector óptimo o que incluso se encuentre sumamente cerca de
éste. Podemos encontrar situaciones en las cuales se requieren presentaciones adicionales
del conjunto de entrenamiento. Sin embargo, en la práctica se verá que el método de
Descenso Escalonado por nada deja de ser un muy buen mecanismo para una aproximación
rápida del vector de pesos. De hecho, es recurrente contar únicamente con un vector de
pesos lo suficientemente cercano al vector óptimo, pero que de igual manera produce una
solución bastante aceptable al problema que la correspondiente neurona Adaline esté
modelando. Por otro lado, debe ser claro que conforme la dimensionalidad P de los
vectores de entrada aumenta, la Ecuación 3.3.11 nos indica que el número de
presentaciones del conjunto de entrenamiento crece de manera significativa y satisfaciendo
el hecho de que se requieren menos operaciones que el método de Mínimos Cuadrados. En
conclusión, la eficiencia del método de Descenso Escalonado mejora conforme P → ∞.
81
Una Introducción al Cómputo Neuronal Artificial
82
Una Introducción al Cómputo Neuronal Artificial
4. El Perceptrón
Una Introducción al Cómputo Neuronal Artificial
84
Capítulo 4. El Perceptrón
4.1. Estructura Básica y Funciones de Activación
La estructura del Perceptrón se basa en la estructura fundamental de una célula
nerviosa, es decir, se cuenta con varias entradas cada una asociada a un peso y se tiene una
única salida la cual puede ser direccionada a otras neuronas (véase la Figura 4.1). Es claro
también que otras neuronas pueden conectarse a las entradas del Perceptrón.
W1
W2
n
X2
z = ¦ wi xi
i =1
z
y = f N ( z)
y
Salidas
Entradas
X1
Wn
Xn
Figura 4.1. Representación esquemática de un Perceptrón.
Considérese el Perceptrón de la Figura 4.1. Éste cuenta con n entradas cada una
asociada con su correspondiente peso wi, i = 1, 2, …, n. De acuerdo a la Figura, el escalar z
es claramente producido por la Sumatoria de Salida del Perceptrón:
n
z = ¦ wi xi
(Ecuación 4.1.1)
i =1
La Ecuación anterior puede ser escrita en forma vectorial como:
z =W ⋅ X
(Ecuación 4.1.2)
Donde:
ª w1 º
W = «« # »»
«¬ wn »¼
ª x1 º
X = «« # »»
«¬ xn »¼
Hasta este punto nótese la similitud de la estructura del Perceptrón con la de la
neurona Adaline (descrita en el Capítulo 3). La primera diferencia surge en el sentido de
que el Perceptrón no cuenta con un término de sesgo o predisposición tal como sucede en el
Adaline. La segunda diferencia es el uso, en el Perceptrón, de una Función de Activación.
85
Una Introducción al Cómputo Neuronal Artificial
Como se aprecia en la Figura 4.1 la salida final de un Perceptrón no está dada por la
ecuación z = W ⋅ X . El escalar z es sometido a la acción de una función fN cuyo resultado es
efectivamente la salida final de la neurona:
y = fN(z)
(Ecuación 4.1.3)
El objetivo de la Función de Activación es el de mantener la salida dentro de ciertos
límites: una situación, tal como se describió en el Capítulo 1, que se da, desde un principio,
en las neuronas biológicas. Es decir, la Función de Activación hará el papel de un
neurotransmisor.
Si bien mencionamos a la presencia de la Función de Activación como una
diferencia entre el Perceptrón y la neurona Adaline, es claro que ésta última cuenta de
hecho con una función que podría considerarse como de activación. En este caso, y tal
como se comentó en el Capítulo 3, se trata de la función sign. Sin embargo, veremos que
para efectos del proceso de entrenamiento del Perceptrón no se puede hacer fN(z) = sign(z)
debido a que ésta no es diferenciable de -∞ a ∞. En Secciones posteriores justificaremos el
porqué de la necesidad de que fN(z) sea diferenciable en el intervalo (-∞, ∞). De hecho,
cualquier función diferenciable en el intervalo (-∞, ∞) puede ser utilizada como Función de
Activación para el Perceptrón. Sin embargo, en la literatura son comúnmente mencionadas
cuatro funciones. En primer lugar tenemos a la Función Sigmoide la cual está dada por:
fN ( z ) =
1
=y
1 + e− z
(Ecuación 4.1.4)
Véase la Figura 4.2.a. Algunas de sus propiedades son:
• fN: \ → (0, 1)
y→0
• z → -∞ ⇔
⇔
y = 0.5
• z=0
⇔
y→1
• z→∞
• Dado que para todo z ∈ \ se tiene que e − z ≠ -1 entonces la función no se indefine en
ningún punto.
Determinemos la derivada de la Función Sigmoide:
d
d
1
fN =
dz
dz 1 + e − z
d
= (1 + e − z ) −1
dz
d
= − (1 + e − z ) −2 (1 + e − z )
dz
86
Capítulo 4. El Perceptrón
d −z
e
dz
d
= − (1 + e− z ) −2 e− z (− z )
dz
−z
e
=
(1 + e− z )2
= − (1 + e− z ) −2
Concretizando:
fN ' =
e− z
(1 + e − z ) 2
(Ecuación 4.1.5)
Nótese que e− z ≠ -1 para todo valor de z. Por lo tanto es posible calcular la derivada de fN
en cualquier punto z, con lo cual concluimos que efectivamente es diferenciable en el
intervalo (-∞, ∞).
1.0
1.0
0.8
0.5
0.6
5
5
0.4
0.5
0.2
5
1.0
5
a)
b)
1.0
1.0
0.8
0.5
0.6
10
5
5
10
0.4
0.5
0.2
1.0
10
5
5
10
c)
d)
Figura 4.2. Algunas Funciones de Activación para el Perceptrón: a) Función Sigmoide;
b) Tangente Hiperbólica con argumento z ; c) Tangente Hiperbólica; d) La función 1 + Tanh( z ) .
2
2
87
Una Introducción al Cómputo Neuronal Artificial
Otra función a considerar es la Tangente Hiperbólica con Argumento z
2
(Véase
la Figura 4.2.b):
§z·
f N ( z ) = Tanh ¨ ¸ = y
©2¹
(Ecuación 4.1.6)
La correspondiente expresión algebraica para la Ecuación 4.1.6 está dada por:
2
§z·
−1
f N ( z ) = Tanh ¨ ¸ =
−z
© 2 ¹ 1+ e
(Ecuación 4.1.7)
Al dar un vistazo a la gráfica de la Tangente Hiperbólica con argumento z
2
serán
evidentes las siguientes propiedades:
• fN: \ → (-1, 1)
• z → -∞ ⇔
y → -1
• z=0
⇔
y=0
• z→∞
⇔
y→1
−z
• e ≠ -1, ∀z ∈ \ : por lo tanto no se indefine en ningún punto.
§z·
Determinemos la derivada de la función Tanh ¨ ¸ usando su correspondiente
©2¹
expresión algebraica:
d
§z· d § 2
·
Tanh ¨ ¸ = ¨
− 1¸
−z
dz
© 2 ¹ dz © 1 + e
¹
−1
d
= 2 1 + e− z
dz
(
)
(
= 2(−1) 1 + e− z
(
=
88
−2
(1 + e )
−z
2
2e − z
(1 + e )
−z
2
−2
(
d
1 + e− z
dz
d −z
e
dz
d
e− z (− z )
dz
= − 2 1 + e− z
=
)
)
−2
)
Capítulo 4. El Perceptrón
Es decir:
fN ' =
2e− z
(1 + e )
−z
2
(Ecuación 4.1.8)
Dado que para todo valor de z se tiene que e− z ≠ -1 entonces concluimos que la función es
también diferenciable en el intervalo (-∞, ∞).
Consideremos también a la Tangente Hiperbólica junto con su correspondiente
expresión algebraica (Véase la Figura 4.2.c):
f N ( z ) = Tanh ( z ) =
1 − e −2 z
=y
1 + e−2 z
(Ecuación 4.1.9)
Algunas de sus propiedades están dadas por:
• fN: \ → (-1, 1)
• z → -∞ ⇔
y → -1
• z=0
⇔
y=0
• z→∞
⇔
y→1
−2 z
• e ≠ -1, ∀z ∈ \ .
La derivada de la Tangente Hiperbólica está dada por:
fN ' =
4e2 z
(1 + e2 z )
2
(Ecuación 4.1.10)
Tenemos que su denominador no se indefine, por lo tanto la función Tangente Hiperbólica
es diferenciable en (-∞,∞).
La Tangente Hiperbólica se puede utilizar para construir otras funciones. Tal es el
caso de la siguiente Función de Activación (Figura 4.2.d):
fN ( z ) =
1 + Tanh( z )
e2 z
=
=y
2
1 + e2 z
Haciendo referencia a su gráfica, la cual se presenta en la Figura 4.2.d, se visualizan
claramente las siguientes propiedades:
• fN: \ → (0, 1)
• z → -∞ ⇔
y→0
• z=0
⇔
y = 0.5
• z→∞
⇔
y→1
2z
• e ≠ -1, ∀z ∈ \ .
89
Una Introducción al Cómputo Neuronal Artificial
Su derivada está dada por:
fN ' =
2e2 z
(1 + e )
2z
2
(Ecuación 4.1.11)
Analizando su denominador se concluye que es ésta diferenciable en el intervalo (-∞,∞).
1 + Tanh( z )
acotan la salida del Perceptrón a
2
valores únicamente dentro del intervalo (0, 1). Por otro lado las funciones Tangente
z
Hiperbólica y Tangente Hiperbólica con argumento
restringen las salidas a valores en
2
(-1, 1). La Función de Activación a utilizar, tal como veremos en secciones posteriores,
depende del problema a modelar. De hecho, mencionamos previamente, que cualquier
función puede ser utilizada. El único requerimiento es que ésta sea diferenciable de -∞ a ∞.
Por ejemplo, es válido considerar a la Función Identidad fN(z) = z. Ésta es diferenciable en
el intervalo (-∞, ∞) y además hace que las salidas del Perceptrón se distribuyan sobre todo
el conjunto de los números reales. De alguna manera ya habíamos considerado previamente
a la Función Identidad cuando efectuamos el análisis del entrenamiento de la neurona
Adaline mediante Mínimos Cuadrados (Sección 3.2) y Descenso Escalonado (Secciones
3.3.1 y 3.3.2). De allí identificamos otro punto de similitud entre ambos tipos de neuronas.
Sin embargo, una desventaja que puede presentar la Función Identidad es que en un
momento dado, y dependiendo del problema que se trate, se pueden generan valores cuyos
valores absolutos son de gran magnitud, lo cual puede dificultar los cálculos.
Nótese que las funciones Sigmoide y
4.2 El Problema de Representación
Hicimos mención en el Capítulo 1 (Sección 1.4) que el Perceptrón fue presentado
originalmente en 1958 por el psicólogo Frank Rosenblatt. Antes de proseguir debemos
aclarar que el término Perceptrón, para Rosenblatt y algunos otros autores, puede hacer
referencia a una única neurona o bien a una Red Neuronal formada por varios Perceptrones
agrupados en capas. En nuestro caso, sólo basta aclarar que cuando hacemos referencia a un
Perceptrón nos referimos a una única neurona de ese tipo. En los siguientes Capítulos,
cuando hagamos referencia a una red formada por más de una neurona entonces haremos
mención explícita del término Red de Perceptrones.
90
Capítulo 4. El Perceptrón
En 1961, Rosenblatt publicó un texto titulado Principles of Neurodynamics en el
cual, en referencia al Perceptrón, se establece:
Un Perceptrón puede aprender (resolver) cualquier cosa que éste pueda
representar (simular).
Esta proposición de inmediato conduce a preguntarse: ¿Qué cosas puede representar, y por
tanto, aprender un Perceptrón? La respuesta a esta pregunta está bien delimitada e
identificada. De hecho el mismo Rosenblatt la abordó. En esta Sección discutiremos
precisamente qué puede ser representado o simulado en un Perceptrón.
W1
2
z = ¦ wi xi
z
i =1
= w1 x1 + w2 x2
y = f N ( z)
Salidas
Entradas
X1
y
W2
X2
Figura 4.3. Una neurona de tipo Perceptrón con dos entradas.
X2
z(x1, x2) = w1x1 + w2x2 = 0
X
1
Figura 4.4. El umbral z(x1, x2) = w1 x1 + w2 x2 = 0
asociado a un Perceptrón de 2 entradas.
Considérese el Perceptrón de la Figura 4.3. Supongamos que ya se tienen
identificados los pesos w1 y w2 para tal neurona. La Sumatoria de Salida puede ser
91
Una Introducción al Cómputo Neuronal Artificial
considerada de hecho como una función de los componentes x1 y x2 de los vectores de
entrada. Entonces tenemos que:
z(x1, x2) = w1 x1 + w2 x2
(Ecuación 4.2.1)
Desde un punto de vista geométrico, cuando z(x1, x2) = 0 se tiene una recta que pasa por el
origen del espacio Euclidiano Bidimensional. A la recta z(x1, x2) = w1x1 + w2x2 = 0 se le
llamará Umbral. Véase la Figura 4.4.
X2
ªw º
v = « 1»
¬ w2 ¼
z(x1, x2) = w1x1 + w2x2 = 0
X
1
Figura 4.5. El vector normal v del umbral z(x1, x2) = w1 x1 + w2 x2 = 0
asociado a un Perceptrón de 2 entradas. Los componentes de v son precisamente
los valores de los pesos w1 y w2.
Ahora considérese cualquier punto (x1, x2) en \ 2 . Es claro que este punto puede ser
evaluado en la función z(x1, x2). Dependiendo del signo del valor arrojado por la evaluación
es posible ubicar al punto sobre la recta o bien por “encima” o por “debajo” de ésta.
Claramente si z(x1, x2) = 0 entonces el punto forma parte de la recta. Ahora bien, sólo
tenemos que precisar la noción de “encima” o “debajo” de la recta. De la Ecuación 4.2.1
tomaremos los coeficientes de x1 y x2, es decir, los valores de los pesos w1 y w2. Usando
estos valores formaremos un vector v = [w1 w2]T, también en \ 2 , el cuál tendrá la
propiedad de ser perpendicular a la recta y de hecho es llamado su Vector Normal. La
dirección del vector normal de la recta z(x1, x2) = 0 es precisamente la referencia que
usaremos para determinar cuando un punto está por “encima” o por “debajo” de ésta. Véase
la Figura 4.5. Nótese que la evaluación w1x1 + w2x2 puede ser vista como un producto
punto entre el vector v y el punto a evaluar x = [x1 x2]T. Por lo tanto w1x1 + w2x2 = v⋅x. A su
vez, el producto punto nos permite inferir el ángulo θ que forman los vectores v y x:
w1x1 + w2x2 = v⋅x = ||v||⋅||x|| cos θ
92
(Ecuación 4.2.2)
Capítulo 4. El Perceptrón
Dado que las magnitudes de los vectores son siempre no negativas entonces únicamente
ª π·
nos concentramos en el signo de cos θ. Es claro que si cos θ > 0 entonces θ ∈ «0, ¸ y por
¬ 2¹
§ π 3π ·
otro lado, si cos θ < 0 entonces θ ∈ ¨ , ¸ . Por lo tanto diremos que si w1x1 + w2x2 > 0
©2 2 ¹
entonces el punto (x1, x2) está por encima de la recta z(x1, x2) = 0 y por otro lado si
w1x1 + w2x2 < 0 entonces el punto está por debajo de la recta. Véase la Figura 4.6.
X2
w1x1 + w2x2 > 0
ªw º
v = « 1»
¬ w2 ¼
z(x1, x2) = w1x1 + w2x2 = 0
X
w1x1 + w2x2 < 0
1
w1x1 +
w2x2 = 0
Figura 4.6. Caracterización de los puntos en el Espacio Euclidiano Bidimensional en función del signo de su
evaluación con la función z(x1, x2) = w1 x1 + w2 x2. Si w1 x1 + w2 x2 > 0 entonces el punto está en la misma
región hacia la que apunta el vector normal v. Si w1 x1 + w2 x2 < 0 entonces el punto está en la región hacia la
que apunta –v. Si w1 x1 + w2 x2 = 0 entonces el punto está sobre la recta z(x1, x2) = 0.
Los razonamientos anteriores nos permiten establecer ahora que el umbral
z(x1, x2) = 0 divide al plano en tres regiones:
• Región 1: El conjunto de puntos por encima del umbral.
o R12 = {(x1, x2): w1 x1 + w2 x2 > 0}
• Región 2: El conjunto de puntos por debajo del umbral.
o R22 = {(x1, x2): w1 x1 + w2 x2 < 0}
• Región 3: El conjunto de puntos inmersos en el umbral.
o R32 = {(x1, x2): w1 x1 + w2 x2 = 0}
Evidentemente \ 2 = R12 ∪ R22 ∪ R32 . Véase la Figura 4.7.
93
Una Introducción al Cómputo Neuronal Artificial
X2
R12
ªw º
v = « 1»
¬ w2 ¼
z(x1, x2) = w1x1 + w2x2 = 0
X
2
3
1
R
R22
Figura 4.7. Partición de \ 2 mediante el umbral z(x1, x2) = w1 x1 + w2 x2 = 0 y su vector normal v.
R12 se forma por los puntos por encima de la recta z(x1, x2) = 0. R22 se forma por los puntos debajo
de la recta z(x1, x2) = 0. R32 es el conjunto de puntos sobre la recta z(x1, x2) = 0.
W1
W2
X2
3
z = ¦ wi xi
z
i =1
= w1 x1 + w2 x2 + w3 x3
y = f N ( z)
y
Salidas
Entradas
X1
W3
X3
Figura 4.8. Una neurona de tipo Perceptrón con tres entradas.
Ahora considérese el Perceptrón de la Figura 4.8. Su Sumatoria de Salida z puede
ser considerada como una función de las variables x1, x2 y x3:
z(x1, x2, x3) = w1x1 + w2x2 + w3x3
(Ecuación 4.2.3)
Cuando se tiene z(x1, x2, x3) = 0 entonces se describe a un plano que pasa por el origen del
Espacio Euclidiano Tridimensional (Figura 4.9). A este plano también se le denomina
umbral.
94
Capítulo 4. El Perceptrón
X3
X2
z(x1,x2,x3) = w1x1 + w2x2 + w3x3 = 0
X1
Figura 4.9. El lugar geométrico asociado a z(x1, x2, x3) = 0.
Siguiendo una serie de razonamientos similares a aquellos referentes al Perceptrón
de dos entradas, tenemos que para cualquier punto (x1, x2, x3) el signo de la evaluación
w1x1 + w2x2 + w3x3 nos indica si éste está encima, debajo o inmerso en el plano
z(x1, x2, x3) = 0. Se tiene entonces que el umbral z(x1, x2, x3) = 0 divide a \ 3 en tres
regiones:
• Región 1: El conjunto de puntos por encima del umbral.
o R13 = {(x1, x2, x3): w1x1 + w2x2 + w3x3 > 0}
• Región 2: El conjunto de puntos por debajo del umbral.
o R23 = {(x1, x2, x3): w1x1 + w2x2 + w3x3 < 0}
• Región 3: El conjunto de puntos inmersos en el umbral.
o R33 = {(x1, x2, x3): w1x1 + w2x2 + w3x3 = 0}
Debe ser claro que \ 3 = R13 ∪ R23 ∪ R33 .
En general tenemos que para un Perceptrón con n entradas, el umbral
z(x1, x2,…, xn) = w1x1 + w2x2 + … + wnxn = 0
(Ecuación 4.2.4)
describirá a un hiperplano que divide al Espacio Euclidiano n-Dimensional, \ n , en tres
regiones:
• La Región 1 contendrá a todos los puntos (x1, …, xn) que están ubicados por encima del
hiperplano z(x1, …, xn) = 0:
o R1n = {(x1, …, xn): w1x1 + … + wnxn > 0}
• La Región 2 contendrá a todos los puntos (x1, …, xn) que están ubicados por debajo del
hiperplano z(x1, …, xn) = 0:
o R2n = {(x1, …, xn): w1x1 + … + wnxn < 0}
• La Región 3 contendrá a todos los puntos (x1, …, xn) inmersos en el hiperplano
z(x1, …, xn) = 0:
o R3n = {(x1, …, xn): w1x1 + … + wnxn = 0}
95
Una Introducción al Cómputo Neuronal Artificial
Ahora analizaremos la relación que existe entre las particiones del espacio \ n
inducidas por el umbral z(x1, …, xn) = 0 (Ecuación 4.2.4) y el conjunto de problemas que
pueden ser representados por el Perceptrón. Precisamente la relación se establece de
manera textual mediante el planteamiento del Problema de Representación:
El Perceptrón únicamente puede resolver aquellos problemas que pueden ser
reducidos a un Problema de Separación (Clasificación) Lineal.
Por ejemplo, considérese la tabla de verdad de la compuerta lógica AND. Véase la
Tabla 4.1.
Tabla 4.1. Tabla de verdad
de la compuerta lógica AND.
Estado x1 x2 Z
A
0 0 0
B
1 0 0
C
0 1 0
D
1 1 1
El operador AND es una función Booleana de dos variables. Ello claramente
implica que contamos con 4 posibles estados o vectores de entrada. El objetivo es
determinar si existe un umbral z(x1, x2) = 0 tal que un Perceptrón proporcione siempre la
salida correcta z. Supongamos que la Función de Activación utilizada es la función
identidad. Grafiquemos en el plano a cada una de las 4 posibles entradas (x1, x2). Nótese
que para la entrada (1, 1) esperamos la salida z(1, 1) = 1. Para el resto de las entradas se
espera la salida 0. Entonces los puntos con salida 0 serán puntos negros mientras que el
punto (1, 1) será blanco. Véase la Figura 4.10.
x2
(0,1)
(0,0)
(1,1)
x1
(1,0)
Figura 4.10. Visualización en el plano de los cuatro posibles estados
de la compuerta lógica AND (Véase el texto para detalles).
96
Capítulo 4. El Perceptrón
Si la compuerta AND ha de ser modelada mediante un Perceptrón entonces se
deberán determinar los valores de los pesos w1 y w2 de manera que se verifique la
existencia de una recta z(x1, x2) = w1x1 + w2x2 = 0 tal que ésta separe a los estados con salida
0 (A, B y C) de los estados con salida 1 (D) (véase la Tabla 4.1). Es precisamente este
punto el que caracteriza a un problema como Linealmente Separable: se tiene un problema
en el cual para una entrada formada por n escalares (x1, …, xn) se espera una salida que
únicamente puede tomar uno de dos posibles valores, digamos, α1 y α2. Entonces, para
aquellas entradas con salida α1 se espera que éstas estén inmersas en el hiperplano
z(x1, …, xn) = 0 o bien por encima de éste. Las entradas con salida esperada α2 se ubicarán
estrictamente por debajo del hiperplano z(x1, …, xn) = 0.
Es claro que el modelado de la compuerta AND es un problema Linealmente
Separable ya que efectivamente existe una recta que separa a los estados con salida
esperada 0 del estado con salida esperada 1. Véase una posible recta en la Figura 4.11. Un
comentario a hacer respecto a la recta presentada en la figura es que ésta evidentemente no
pasa por el origen y por lo tanto no se ajusta a la Sumatoria de Salida del Perceptrón
(Ecuación 4.2.1). Sin embargo, es posible considerar este tipo de rectas al agregar un
término de sesgo o predisposición, tal como sucede en la neurona Adaline. Otra opción es
simplemente trasladar a los 4 estados de manera que su centroide se ubique en el origen. El
punto importante es que hemos verificado la existencia de una recta que permite
caracterizar a nuestro problema en cuestión como linealmente separable.
x2
(0,1)
(0,0)
(1,1)
x1
(1,0)
Figura 4.11. Una recta que separa los estados con salida 0
del estado con salida 1 en la compuerta lógica AND.
Ahora considérese la tabla de verdad de la compuerta lógica XOR (OR Exclusivo).
Véase la Tabla 4.2. Se tienen nuevamente dos variables y por tanto 4 estados. Ahora véase
la Figura 4.12. Para dos de los estados se espera una salida 0 (puntos negros) mientras que
para los dos restantes una salida 1 (puntos blancos).
97
Una Introducción al Cómputo Neuronal Artificial
Tabla 4.2. Tabla de verdad
de la compuerta lógica XOR.
Estado x1 x2 Z
A
0 0 0
B
1 0 1
C
0 1 1
D
1 1 0
x2
(0,1)
(0,0)
(1,1)
x1
(1,0)
Figura 4.12. Visualización en el plano de los cuatro posibles estados
de la compuerta lógica XOR (Véase el texto para detalles).
Es claro, en términos visuales, que cualquier recta en el plano no podrá separar a los
puntos blancos de los puntos negros en la Figura 4.12. Si bien es posible hacer que los
puntos blancos (negros) queden por encima o inmersos en la recta, siempre estará un punto
negro (blanco) en esa misma región (véase la Figura 4.13). Por lo tanto, concluimos que no
existe una recta o umbral z(x1, x2) = 0 tal que los estados A y D queden separados de los
estados C y B. En consecuencia se tiene que el problema del modelado, mediante un
Perceptrón, de la función XOR no es linealmente separable.
La situación con el XOR nos conduce entonces a aceptar que existirán problemas
para los cuales el Perceptrón no proporciona una solución o modelo. El siguiente
cuestionamiento que surge es entonces aquel relacionado a determinar cuantos problemas
linealmente separables existen, o bien, de manera complementaria, determinar la cantidad
de problemas no linealmente separables. Para ello, nos concentraremos en un particular tipo
de problemas: el Modelado de Funciones Booleanas. Sabemos que una función Booleana f
es aquella para la que formalmente se tiene:
f :{0,1}n = {0,1} × {0,1} × ... × {0,1} → {0,1}
n
98
Capítulo 4. El Perceptrón
x2
x2
(0,1)
(0,0)
(1,1)
(0,1)
x1
(1,0)
(0,0)
(1,1)
x1
(1,0)
a)
b)
Figura 4.13. a) Una recta que agrupa, para la compuerta lógica XOR, a los estados con salida 0 pero que
también incluye a un estado con salida 1. b) Una recta que agrupa a los estados con salida 1 pero que también
incluye a un estado con salida 0.
Donde ⋅×⋅ denota al Producto Cartesiano de conjuntos. Es claro que las funciones AND y
XOR (Tablas 4.1 y 4.2, respectivamente) son funciones Booleanas. Es más, la cardinalidad
del dominio de una función Booleana es 2n. Ello se debe a que cada estado se forma por n
componentes y a su vez cada componente puede tomar uno de 2 posibles valores: o el valor
0 o el valor 1. Por lo tanto se tienen en total
2⋅ 2 ⋅ ... ⋅ 2 = 2n
(Ecuación 4.2.5)
n
posibles estados. Para las compuertas AND y XOR se tiene que n = 2 lo que en
consecuencia nos indica que cuentan con 22 = 4 estados. Ahora bien, cada uno de los 2n
estados de una función Booleana está asociado a una salida que la función debe
proporcionar. Esta salida puede ser 0 o 1. Ello implica que se tienen en total
2⋅ 2 ⋅ ... ⋅ 2 = 2(2
n
)
(Ecuación 4.2.6)
2n
posibles funciones Booleanas con estados formados por n componentes. Retomando el caso
n = 2, tenemos entonces que el número total de compuertas lógicas con 2 entradas es
2
2(2 ) = 24 = 16 . Entre esas 16 compuertas encontramos, como ya sabemos, a las funciones
AND y XOR, pero también a otras bien conocidas como OR, NOR, NAND, NXOR, etc.
En la década de los 60s, investigadores como R. O. Winder y Michael A. Harrison,
el primero con su Tesis Doctoral Threshold Logic (1962) y el segundo con su artículo On
the Classification of Boolean Functions by the General Linear and Affine Groups (1964),
abordan estudios relacionados con la clasificación de funciones Booleanas. Entre sus
99
Una Introducción al Cómputo Neuronal Artificial
resultados resaltan los conteos correspondientes al número de funciones Booleanas que
efectivamente son linealmente separables. En la Tabla 4.3 se presentan los conteos para las
funciones de 1 a 6 entradas. Todas las funciones de una única entrada son linealmente
separables, mientras que de aquellas con dos entradas solo 14 son linealmente separables.
Precisamente las compuertas XOR y NXOR son las no linealmente separables. Ello implica
que para n = 2 el 87.5% de las funciones son linealmente separables lo cual puede
considerarse como un número bastante aceptable de problemas factibles de ser resueltos por
el Perceptrón. Sin embargo, nótese que para n = 3 únicamente el 40.62% de las funciones
pueden ser modeladas por el Perceptrón. La situación se torna más dramática conforme el
número de entradas aumenta. Cuando n = 5 tenemos que sólo 0.0022% de las funciones son
linealmente separables y por tanto modelables por un Perceptrón. Ello nos lleva a concluir,
de manera clara y evidente, que un número sumamente limitado de las posibles
n
2(2 ) funciones Booleanas de n entradas son funciones linealmente separables. En la
práctica se puede requerir el modelado de funciones con número de entradas realmente
grande. Por tanto, el Perceptrón cuenta con una capacidad limitada para la solución de este
tipo de problemas.
Número de
entradas n
1
2
3
4
5
6
Tabla 4.3. Conteo de funciones Booleanas
de 1 a 6 entradas linealmente separables.
Funciones con Estados
Número de posibles
n
Funciones Booleanas: 2(2 ) Linealmente Separables
4
4
16
14
256
104
65,536
1,882
4,294,967,296
94,572
18,446,744,073,709,551,616
15,028,134
b)
a)
Figura 4.14. Ejemplos de regiones convexas: a) Región Convexa Cerrada;
b) Región Convexa Abierta.
Desde otro punto de vista, el Problema de Representación puede ser replanteado
como el hecho de que un único Perceptrón sólo puede resolver problemas de clasificación
de puntos que yacen en dos regiones convexas disjuntas. Recuérdese que una región es
convexa si para cualesquiera dos puntos en ésta, el segmento de recta que los une está por
completo dentro de la región (véase la Figura 4.14). Estas regiones pueden ser abiertas o
cerradas. De manera más precisa, recordemos que tenemos problemas en los cuales para
100
Capítulo 4. El Perceptrón
una entrada formada por n escalares (x1, …, xn) se espera una salida que únicamente puede
tomar uno de dos posibles valores: α1 o α2. Cuando decimos que los puntos deben yacer en
regiones convexas hacemos referencia a que los puntos con salida α1 deben formar parte de
una región y los puntos con salida α2 deben estar en la otra región. Además, el que las dos
regiones sean disjuntas implica que su intersección es vacía.
Recordemos que la compuerta lógica AND es un problema linealmente separable ya
que existe un umbral o recta z(x1, x2) = 0 tal que el conjunto de puntos negros queda
separado del conjunto de puntos blancos (véase la Figura 4.11). Ahora bien, desde el
nuevo punto de vista el problema se soluciona por un Perceptrón ya que al considerar a los
puntos negros como los vértices de un polígono, en este caso un triángulo, se tiene que éste
evidentemente describe a una región convexa cerrada (véase la Figura 4.15). El punto
blanco por si mismo es un conjunto convexo cerrado. Nótese que no hay puntos comunes
entre las dos regiones lo que las hace disjuntas.
x2
(0,1)
(0,0)
(1,1)
x1
(1,0)
Figura 4.15. Separación de los estados de la compuerta lógica AND
mediante dos regiones cerradas convexas disjuntas (véase el texto para detalles).
Ahora bien, el mismo procedimiento aplicado sobre los estados de la compuerta
XOR claramente nos permite agrupar a los puntos blancos en una región convexa y a los
puntos negros en su correspondiente región convexa, ambas cerradas. Véase la Figura
4.16. El problema que surge es que tales regiones se intersectan. Si se busca que las
regiones cuenten con intersección vacía entonces claramente habrá que definir a una de
ellas como no convexa, tal como su sucede en el ejemplo presentado en la Figura 4.17.
Esta situación hace que el XOR sea caracterizado, desde el punto de vista del uso de
regiones convexas disjuntas como un problema no modelable mediante un Perceptrón. Si se
espera que una neurona modele al XOR es entonces que habrá que considerar, por
consecuencia, la formación de umbrales no lineales o bien regiones no convexas que
agrupen adecuadamente a los estados de la función. Ambas posibilidades quedan fuera del
alcance del Perceptrón debido a que precisamente su estructura interna, y en particular su
sumatoria de salida, únicamente modelan umbrales lineales (Ecuación 4.1.1).
101
Una Introducción al Cómputo Neuronal Artificial
x2
(0,1)
(1,1)
x1
(0,0)
(1,0)
Figura 4.16. Dos regiones convexas no disjuntas que agrupan, cada una,
a los estados negros y a los estados blancos de la función XOR.
x2
(0,1)
(0,0)
(1,1)
x1
(1,0)
Figura 4.17. Separación de los estados negros y los estados blancos
de la función XOR. Se tienen dos regiones disjuntas, pero una de ellas
es no convexa.
La discusión que hemos efectuado en esta Sección puede conducir a perspectivas
pesimistas para el área de Redes Neuronales Artificiales. Sin embargo, el mismo Rosenblatt
y otros investigadores como Warren McCulloch y Walter Pitts (véase la Sección 1.2), ya
tenían conocimiento de que redes formadas por más de un Perceptrón si eran capaces de
modelar exitosamente compuertas lógicas como el XOR y de hecho otras funciones
Booleanas no linealmente separables. Sin embargo, lo que no se tenía era un mecanismo
eficiente para el ajuste de sus pesos. No fue sino hasta 1986 que David Rumelhart,
Geoffrey Hinton y Ronald Williams presentan el Algoritmo de Retropropagación, lo cual
significó un reimpulso importante para el área. En los Capítulos 5 y 6 nos concentraremos
en estudiar a las redes formadas por más de una neurona artificial, y de manera particular,
en el Capítulo 6 es donde abordaremos al Algoritmo de Retropropagación.
102
Capítulo 4. El Perceptrón
4.3 Aplicación: Identificación de Parámetros Autorregresivos
en una Señal
En las dos Subsecciones anteriores hemos discutido ya varios aspectos detrás del
Perceptrón, sin embargo, no hemos planteado una metodología para el ajuste de sus pesos.
Precisamente ese será el objetivo de esta Sección. Pero además, aplicaremos tal mecanismo
de entrenamiento en el contexto del problema de Predicción de una Señal. Mencionábamos
en el Capítulo 1 que el objetivo es modelar una serie de tiempo de manera que sea posible
determinar como se comportará en el futuro. A continuación plantearemos algunas
nociones necesarias respecto al problema en particular y posteriormente veremos como
abordarlo a fin de que un Perceptrón nos proporcione una solución.
Existen una gran cantidad de modelos matemáticos para generar series de tiempo.
En particular nosotros trabajaremos con una Serie de Tiempo de M-ésimo Orden de
Parámetros Autorregresivos. Ésta se define como:
­
ck
si n = k , k ∈ {1, 2,..., M }
°M
xn = ®
n>M
°¦ ak xn − k + noise(n) si
¯ k =1
(Ecuación 4.3.1)
Donde:
• M: Orden del modelo.
• ak: k-ésimo parámetro autorregresivo, una constante, k = 1, 2, …, M.
• ck: k-ésima muestra, una constante, de la serie de tiempo para t = k, k ∈ {1, 2, …, M}.
• xn: muestra de la serie de tiempo en t = n.
• noise(n): ruido o perturbación a aplicar a la muestra de la serie de tiempo en t = n. Se
utiliza para simular el hecho de que las muestras fueron obtenidas experimentalmente,
sin embargo, por ello mismo, las mediciones efectuadas no pueden ser libres de errores.
De acuerdo a la Ecuación 4.3.1, el valor de xn, cuando n > M, es una combinación
lineal de los M valores previos, xn-1, xn-2, …, xn-M, y los parámetros autorregresivos
a1, a2, …, aM. Cuando 1 ≤ n ≤ M entonces el valor de xn es uno de los M valores iniciales
c1, c2, …, cM (o casos base) para la serie de tiempo. Es claro que el valor de cualquier
muestra xn, n > M, tiene influencia de los valores de las muestras que le preceden y tendrá
influencia sobre los valores que le prosiguen.
103
Una Introducción al Cómputo Neuronal Artificial
Consideremos un ejemplo. Sea la serie de tiempo generada al usar los siguientes
valores:
• M=7
• a1 = -0.15
• a2 = 0.1
• a3 = -0.3
• a4 = -0.2
• a5 = -0.1
• a6 = -0.5
• a7 = 0.3
• c1 = -3
• c2 = 1
• c3 = 6
• c4 = -8
• c5 = -1
• c6 = -4
• c7 = 2
• noise(n): una función de ruido que retornará aleatoriamente números enteros en el
conjunto {-7, -6, -5, …, 5, 6, 7}.
• N = 2,000 muestras.
La Tabla 4.4 muestra la aplicación de la Ecuación 4.3.1 utilizando la configuración dada
para obtener las primeras 15 muestras de la serie de tiempo. Nótese que las primeras 7
muestras corresponden con los valores c1 a c7. A partir de la octava muestra se aplica la
función de ruido. En la Figura 4.18 se muestra la gráfica de la serie de tiempo
considerando las N = 2,000 muestras.
El problema a tratar parte de que únicamente contamos con N muestras asociadas a
una serie de tiempo. Supondremos que tal serie puede ser modelada como una serie de
tiempo de M-ésimo orden de parámetros autorregresivos, N > M, es decir, que se ajusta la
Ecuación 4.3.1. El objetivo es determinar sus correspondientes M parámetros
autorregresivos a1, a2, …, aM. A fin de buscar una solución utilizaremos un Perceptrón que
recibirá un vector en \ M . Los componentes de un vector de entrada estarán dados por:
ª xn −1 º
«x »
« n−2 »
« xn −3 »
«
»
« # »
«¬ xn − M »¼
Donde los escalares xn-1, xn-2, …, xn-M son una subsecuencia de las muestras que forman la
serie de tiempo bajo estudio.
104
Capítulo 4. El Perceptrón
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Tabla 4.4. Las primeras 15 muestras asociadas a una serie de tiempo
de 7 parámetros autorregresivos (véase el texto para detalles).
noise(n)
Muestra xn
x1 = c1 = -3
x2 = c2 = 1
x3 = c3 = 6
x4 = c4 = -8
x5 = c5 = -1
x6 = c6 = -4
x7 = c7 = 2
x8 = a1 x7 + a2 x6 + a3 x5 + a4 x4 + a5 x3 + a6 x2 + a7 x1 + noise(8)
-2
= − 2.8
x9 = a1 x8 + a2 x7 + a3 x6 + a4 x5 + a5 x4 + a6 x3 + a7 x2 + noise(9)
-7
= − 6.88
x10 = a1 x9 + a2 x8 + a3 x7 + a4 x6 + a5 x5 + a6 x4 + a7 x3 + noise(10)
3
= − 9.852
x11 = a1 x10 + a2 x9 + a3 x8 + a4 x7 + a5 x6 + a6 x5 + a7 x4 + noise(11)
-5
= − 8.2258
x12 = a1 x11 + a2 x10 + a3 x9 + a4 x8 + a5 x7 + a6 x6 + a7 x5 + noise(12)
-7
= − 0.65693
x13 = a1 x12 + a2 x11 + a3 x10 + a4 x9 + a5 x8 + a6 x7 + a7 x6 + noise(13)
2
= − 2.22364
x14 = a1 x13 + a2 x12 + a3 x11 + a4 x10 + a5 x9 + a6 x8 + a7 x7 + noise(14)
0
= 3.45319
x15 = a1 x14 + a2 x13 + a3 x12 + a4 x11 + a5 x10 + a6 x9 + a7 x8 + noise(15)
-4
= − 1.2833
El Perceptrón producirá como salida un escalar x 'n generado precisamente por su
sumatoria de salida:
M
x 'n = ¦ a 'k xn − k
N ≥n>M
(Ecuación 4.3.2)
k =1
Donde a '1 , a '2 ,..., a 'M son tanto los pesos de la neurona como los parámetros
autorregresivos que se buscarán. Dado que el escalar producido por la sumatoria es la salida
de la neurona entonces podemos considerar que la Función de Activación usada es la
Función Identidad. Claramente x 'n es un estimado que proporciona el Perceptrón para la
muestra xn dado el vector de entrada [xn-1 xn-2 … xn-M]T. Durante el entrenamiento de la
neurona se buscará ajustar los pesos a '1 , a '2 ,..., a 'M de tal forma que el error existente entre
x 'n y xn se reduzca tanto como sea posible.
105
Una Introducción al Cómputo Neuronal Artificial
xn
n
500
1000
1500
2000
Figura 4.18. Una serie de tiempo de 7 parámetros autorregresivos (véase el texto para detalles).
Plantearemos ahora un método de entrenamiento basado en Descenso Escalonado
(Sección 3.3). Sea εn la diferencia existente entre el estimado de la muestra que proporciona
la neurona y el valor esperado, es decir:
εn = xn – x 'n
N≥n>M
(Ecuación 4.3.3)
Dado que tenemos N muestras entonces los vectores de entrada estarán dados por
ª xM = cM º
«x =c »
« M −1 M −1 »
« xM − 2 = cM − 2 » ,
«
»
#
«
»
«¬ x1 = c1 ¼»
106
ª xM +1 º
« x =c »
M »
« M
« xM −1 = cM −1 » ,
«
»
#
«
»
«¬ x2 = c2 ¼»
ª xM + 2 º
« x
»
« M +1 »
« xM = cM » ,
«
»
« #
»
«¬ x3 = c3 ¼»
ª xN −1 º
ª xM +3 º
« x
»
«x »
« M +2 »
« N −2 »
« xM +1 » , ..., « xN −3 »
«
»
«
»
« # »
« # »
¬« x4 = c4 ¼»
¬« xN − M ¼»
Capítulo 4. El Perceptrón
Por lo tanto el conjunto de entrenamiento para el Perceptrón tendrá un tamaño N – M. El
promedio de los errores al cuadrado ahora estará dado por
N
1
¦ ε n2
N − M n = M +1
N
1
=
¦ ( xn − x 'n )2
N − M n = M +1
MSE =
=
1
N −M
M
§
·
−
x
¦
¨ n ¦ a 'k xn − k ¸
n = M +1 ©
k =1
¹
N
2
(Ecuación 4.3.4)
Tenemos pleno conocimiento de que es posible utilizar Mínimos Cuadrados a fin de
minimizar la Ecuación 4.3.4, sin embargo el proceso será costoso ya que se requiere
manipular todas las muestras al mismo tiempo. Para ello, definiremos a una serie de
funciones que forman parte de la función de error MSE. Se define a la función MSEn como:
MSEn = ε n2
= ( xn − x 'n ) 2
M
§
·
= ¨ xn − ¦ a 'n ,k xn − k ¸
k =1
©
¹
2
N ≥n>M
(Ecuación 4.3.5)
Claramente esta función corresponde al error al cuadrado entre la muestra xn y su valor
estimado x 'n . En este caso, a 'n ,1 , a 'n ,2 ,..., a 'n , M son los valores actuales de los pesos, y
también los parámetros autorregresivos de la señal a estimar, en el Perceptrón al presentar
el vector de entrada cuyos componentes son las muestras xn-1, xn-2, …, xn-M.
Se calculará el vector gradiente de MSEn. Es decir, buscaremos:
ª δ MSE n º
« δa' »
n ,1
«
»
« δ MSE n »
«
»
∇MSEn = « δ a 'n ,2 »
« #
»
«
»
« δ MSE n »
« δa'
»
n,M ¼
¬
107
Una Introducción al Cómputo Neuronal Artificial
Determinemos la derivada parcial de la función MSEn respecto al j-ésimo parámetro
autorregresivo a 'n , j :
M
δ MSEn
δ §
·
x
a 'n ,k xn − k ¸
=
−
¦
n
¨
δ a 'n , j δ a 'n , j ©
k =1
¹
2
M
§
· δ
= 2 ¨ xn − ¦ a 'n ,k xn − k ¸
k =1
©
¹ δ a 'n , j
(Por la Ecuación 4.3.5)
M
§
·
x
−
¨ n ¦ a 'n, k xn − k ¸
k =1
©
¹
M
δ
§
·§
= 2 ¨ xn − ¦ a 'n ,k xn − k ¸ ¨ −
¨
k =1
©
¹ © δ a 'n , j
M
¦a'
n,k
k =1
·
xn − k ¸
¸
¹
§ Aplicación de Regla de ·
¨
¸
© la cadena
¹
§ El término xn es constante ·
¨¨
¸¸
© respecto a a 'n , j
¹
§ Todos los términos de la ·
¨
¸
¨ sumatoria son constantes ¸
¨ excepto el j -ésimo
¸
©
¹
M
§
· δ
= −2 ¨ xn − ¦ a 'n ,k xn − k ¸
a 'n , j xn − j
k =1
©
¹ δ a 'n , j
= −2 ( xn − x 'n ) xn − j
(Por la Ecuación 4.3.2)
= −2ε n xn − j
(Por la Ecuación 4.3.3)
Concretizando:
δ MSEn
= −2ε n xn − j
δ a 'n , j
(Ecuación 4.3.6)
Tenemos los elementos para definir de manera precisa al vector gradiente de la
función MSEn:
ª δ MSE n º
« δa' »
n ,1
«
» ª −2ε x º
ª xn −1 º
n n −1
« δ MSE n » «
»
«x »
−2ε n xn − 2 »
«
»
∇MSEn = « δ a 'n ,2 » = «
= −2ε n « n − 2 »
«
»
« # »
#
« #
» «
»
«
»
«
» ¬ −2ε n xn − M ¼
¬ xn − M ¼
« δ MSE n »
« δa'
»
n,M ¼
¬
(Ecuación 4.3.7)
De acuerdo a la Teoría presentada en la Sección 3.3, el objetivo es minimizar a la
función de error MSE (Ecuación 4.3.4) al determinar el punto en el cual su gradiente es el
vector cero, sin embargo, utilizaremos los estimadores, los vectores gradientes,
proporcionados por las funciones MSEn. Dado que para ello se requiere minimizar a MSEn
entonces, como ya sabemos, se utilizará la dirección opuesta de su gradiente.
108
Capítulo 4. El Perceptrón
Sea a 'n el vector en \ M formado por los M pesos del Perceptrón:
ª a 'n ,1 º
«
»
a 'n ,2 »
«
a 'n =
« # »
«
»
¬« a 'n , M ¼»
(Ecuación 4.3.8)
El vector de pesos a 'n será actualizado mediante la regla:
a 'n +1 = a 'n + Δa'n
(Ecuación 4.3.9)
Donde Δa'n es el Término de Variación o Cambio en el vector de pesos a 'n y está dado
por:
ª xn −1 º
«x »
Δa'n = μ2εn « n − 2 »
« # »
«
»
¬ xn − M ¼
(Ecuación 4.3.10)
Claramente el término Δa'n nos indica la dirección de mínimo crecimiento de MSEn. La
constante μ fue introducida en la Sección 3.3 como la proporción del vector gradiente de la
función MSEn que se utilizará para actualizar al vector de pesos. Su función es la acelerar el
acercamiento del vector de pesos actual, o en términos formales su convergencia, al vector
de pesos óptimos de la función MSE (Ecuación 4.3.4). Dado que la elección de μ tiene
influencia sobre el número de iteraciones que el método de entrenamiento efectuará, es que
a partir de ahora a éste se le llamará Coeficiente de Aprendizaje. Este nombre viene del
hecho de que buena elección de μ inducirá un rápido aprendizaje por parte de la neurona,
pero por otro lado, también puede provocar que ésta aprenda muy lentamente del conjunto
de entrenamiento y por tanto requiera un número considerable de presentaciones.
En el Algoritmo 4.1 se implementa el método de Descenso Escalonado para el
entrenamiento de una neurona de tipo Perceptrón. El algoritmo recibe 6 entradas:
• Un arreglo x que contiene las N muestras asociadas a la serie de tiempo.
• Un entero M que indica el número de parámetros autorregresivos a determinar en la
serie de tiempo dada.
• El Coeficiente de Aprendizaje μ. Por lo regular es un valor en el intervalo (0, 1).
• El número T de presentaciones del conjunto de entrenamiento a efectuar.
• Un entero nInt que se usará para actualizar al Coeficiente de Aprendizaje.
109
Una Introducción al Cómputo Neuronal Artificial
Algoritmo 4.1. Implementación del método de Descenso Escalonado
para el entrenamiento de un Perceptrón y determinación de Parámetros Autorregresivos en una señal.
Procedure TrainPerceptron
(Integer N, Array x[1, …, N], Integer M, Real μ, Integer T, Integer nInt)
// Se inicializa el vector de pesos con valores aleatorios en (-1, 1).
a = new Array[1,…,M]
for i = 1 until M do
a[i] = Random( )
end-of-for
for i = 1 until T do
Integer n = M + 1
while n ≤ N do
// Se calcula el valor proporcionado por la neurona
// usando los pesos actuales y las muestras xn-1, xn-2, …, xn-M.
Real x ' = 0
for k = 1 until M do
x’ = x’ + a[k] * x[n – k]
end-of-for
Real εn = x[n] – x '
// Se calcula el cambio o variación a aplicar
// sobre el vector de pesos.
Δ = new Array[1,…,M]
for k = 1 until M do
Δ[k] = 2 * μ ∗ εn * x[n - k]
end-of-for
// Se obtiene el nuevo vector de pesos.
for k = 1 until M do
a[k] = a[k] + Δ[k]
end-of-for
// Se determina si μ debe ser actualizado.
if n mod nInt = 0 then
μ = μ / 1.01
end-of-if
n=n+1
end-of-for
110
Capítulo 4. El Perceptrón
// Se calcula MSE.
Real MSE = 0
for n = M + 1 until N do
Real x ' = 0
for k = 1 until M do
x’ = x’ + a[k] * x[n – k]
end-of-for
MSE = MSE + Pow(x[n] – x ' , 2)
end-of-for
MSE = MSE / (N – M)
Print(MSE)
Print(μ)
end-of-while
// Se retorna el vector de pesos final.
return a
end-of-procedure
Veamos como es que procede el Algoritmo 4.1. En primer lugar, se inicializa el
vector de pesos a con valores aleatorios tomados del intervalo (-1, 1). Después se tiene el
ciclo for principal que se encarga de controlar las T presentaciones del conjunto de
entrenamiento. Dentro de esta estructura de repetición encontramos un ciclo while que
controla la presentación de los vectores de entrada al Perceptrón y de la actualización del
vector de pesos a. En párrafos anteriores mencionamos que a la neurona se le presentan
vectores de entrada de tamaño M. Sin embargo, nuestra implementación, por cada iteración
del ciclo while, forma una subsecuencia de M muestras consecutivas las cuales toma del
vector de entrada x. Cada una de esas M muestras es multiplicada por su correspondiente
peso, el cual se toma del vector a. Finalmente los M productos obtenidos se suman. Es claro
que hemos implementado la Ecuación 4.3.2. Contamos entonces con la salida
proporcionada por la neurona: x’. Se calcula el error εn mediante la diferencia de la salida
de la neurona con la muestra esperada, la cual se encuentra en el arreglo de entrada x en la
posición n. Ahora se calcula el cambio o variación a aplicar sobre el vector de pesos. Para
ello se requiere usar la misma subsecuencia de M muestras que se presentaron a la neurona.
Cada uno de sus componentes es multiplicado por 2, el coeficiente de aprendizaje y el error
εn. El resultado, en la implementación, es almacenado en el arreglo Δ. Por ultimo, a cada
elemento del vector de pesos a le es sumado su correspondiente elemento del vector Δ. Con
ello se obtiene un nuevo vector de pesos.
Mencionamos que el objetivo del Coeficiente de Aprendizaje μ es el de permitir la
aceleración de la convergencia del vector de pesos. Uno de los parámetros de entrada del
Algoritmo 4.1 es precisamente μ. Este valor de entrada se considerará de hecho un
111
Una Introducción al Cómputo Neuronal Artificial
Coeficiente de Aprendizaje inicial ya que conforme avance la ejecución de algoritmo éste
se irá modificando. Las modificaciones a aplicar harán que el valor de μ disminuya
progresivamente. Justifiquemos esta manera de proceder. Recordemos primeramente que el
lugar geométrico descrito por las funciones MSEn (Ecuación 4.3.5), y de hecho también por
la función MSE (Ecuación 4.3.4), es un hiperparaboloide inmerso en el espacio
(M+1)-Dimensional. El Algoritmo 4.1 genera en primer lugar un vector de pesos inicial
con valores aleatorios. Este vector de pesos puede verse como un punto en el dominio tanto
de MSEn como de MSE. Cuando éste se evalúa es que entonces nos colocamos en algún
punto del espacio \ M +1 y que de hecho forma parte de la hipersuperficie del
hiperparaboloide. Ahora bien, estableceremos la suposición de que el punto en el que nos
encontramos se encuentra alejado del único mínimo global. A partir de este momento, se
utiliza la regla de actualización de pesos (Ecuación 4.3.9). En el momento en que el vector
de pesos es actualizado es que entonces estamos posicionados en otro nuevo punto sobre la
hipersuperficie. La idea es que mientras supongamos que estamos alejados del mínimo
global tendremos que aplicar un coeficiente de aprendizaje con un valor inicial “alto” que
nos permita acercarnos rápidamente al mínimo. Es claro que después de varias iteraciones
podríamos suponer que llegamos a una situación en la que ya nos encontramos lo
suficientemente cerca del mínimo global. Sin embargo, el seguir usando el coeficiente de
aprendizaje inicial podría ser contraproducente ya que en lugar de permitir que nos
acerquemos cada vez más, podríamos estarnos alejando. Es aquí donde se debe actualizar a
μ, con un valor más pequeño que el que tenía inicialmente, a fin de que las actualizaciones
del vector de pesos, y por lo tanto los posicionamientos sobre el hiperparaboloide, sean
cada vez más precisos en términos de su progresivo acercamiento al mínimo global. El
Algoritmo 4.1 implementa el proceso antes mencionado utilizando también el valor de
entrada nInt. Este valor determina un intervalo, de acuerdo al número de iteraciones
efectuadas por el ciclo while, en el cual el valor de μ se conserva. Después de nInt
iteraciones del ciclo while éste se actualiza. Su valor se reduce al dividirlo, en nuestra
implementación, por 1.01.
Una vez que el Algoritmo 4.1 termina la ejecución del ciclo while, se procede a
calcular el valor de la función MSE (Ecuación 4.3.4) usando los pesos actuales en el vector
a y el conjunto de entrenamiento en el vector de entrada x. Este cálculo es únicamente con
fines de medir el desempeño de la neurona una vez que se ha efectuado una presentación
del conjunto de entrenamiento. Cuando las T presentaciones del conjunto de entrenamiento
han sido ejecutadas, el Algoritmo 4.1 finaliza su ejecución retornando los últimos valores
para los pesos, los cuales se encuentran en el vector a.
Aplicaremos el método de Descenso Escalonado, implementado en el Algoritmo
4.1, para entrenar a un Perceptrón de manera que sus pesos correspondan con los 7
parámetros autorregresivos de la serie de tiempo presentada en la Figura 4.18. Como
sabemos, tal serie fue generada usando la Ecuación 4.3.1 y los siguientes valores:
112
Capítulo 4. El Perceptrón
• M=7
• a1 = -0.15
• a2 = 0.1
• a3 = -0.3
• a4 = -0.2
• a5 = -0.1
• a6 = -0.5
• a7 = 0.3
• c1 = -3
• c2 = 1
• c3 = 6
• c4 = -8
• c5 = -1
• c6 = -4
• c7 = 2
• noise(n) ∈ {-7, -6, -5, …, 5, 6, 7}
• N = 2,000 muestras.
Las 2,000 muestras serán guardadas en el arreglo de entrada x. El Perceptrón únicamente
recibirá la información asociada a tales muestras (véase la Figura 4.19). Ahora bien, para
la ejecución del Algoritmo 4.1, establecemos los siguientes valores de entrada:
• μ = 0.0003
• nInt = 500
• T = 100
Es decir, el conjunto de entrenamiento será presentado 100 veces. Se tendrá un coeficiente
de aprendizaje inicial μ = 0.0003 el cual será actualizado cada 500 iteraciones del ciclo
while en el Algoritmo 4.1. Una vez finalizada la ejecución del algoritmo esperaremos,
idealmente, que para los pesos a '1 a a '7 en la neurona se tenga:
•
a '1 ≈ a1 = -0.15
•
a '2 ≈ a2 = 0.1
•
a '3 ≈ a3 = -0.3
•
a '4 ≈ a4 = -0.2
•
a '5 ≈ a5 = -0.1
•
a '6 ≈ a6 = -0.5
•
a '7 ≈ a7 = 0.3
La Tabla 4.5, junto con las Figuras 4.20 y 4.21, describen el desempeño de la
neurona y la evolución del coeficiente de aprendizaje conforme se van efectuando las
presentaciones del conjunto de entrenamiento. Recordemos que el desempeño se mide en
función del resultado proporcionado por la función MSE (Ecuación 4.3.4). Nótese como es
que de la primer a la quinta presentación los valores de MSE son bastante altos: se inicia
113
Una Introducción al Cómputo Neuronal Artificial
con 2.90865 × 1017 y se termina en 381,223. Para este intervalo el valor de μ inició en
0.0003 (el valor de entrada) y terminó en 0.000245863. En las presentaciones del conjunto
de entrenamiento 10 a 40 el desempeño del Perceptrón mejora considerablemente ya que
MSE se ubicó entre 30 y 20. En la presentación 40 el Coeficiente de Aprendizaje μ tiene
valor 0.0000610522, es decir, es 4.9138 veces más pequeño que su valor original de
entrada. Esto viene a sustentar el hecho de que las modificaciones aplicadas a μ permiten
un ajuste cada vez más preciso del vector de pesos. A partir de la presentación 50 se
observa que el error MSE está por debajo de 20. Una vez finalizada la presentación 100 del
conjunto de entrenamiento se tiene el error final MSE = 18.5939. El Coeficiente de
Aprendizaje termina con valor final μ = 0.00000560495: el cual es 53.5231 veces más
pequeño que el valor original 0.0003.
a1'
Xn-1
a2'
Xn-2
Xn-3
a4'
Xn-4
a5'
Xn-5
7
x = ¦ ak' xn − k
'
n
k =1
xn'
Salida
Entradas
a3'
a6'
Xn-6
a7'
Xn-7
Figura 4.19. Representación esquemática del Perceptrón que se utilizará para determinar los Parámetros
Autorregresivos en una Señal de Séptimo Orden (Véase el texto para detalles).
Una vez finalizada la ejecución del Algoritmo 4.1 tenemos los siguientes pesos en
la neurona que de hecho son los parámetros autorregresivos identificados:
• a '1 = -0.165747
•
a '2 = 0.0845436
•
a '3 = -0.27829
•
a '4 = -0.17541
•
a '5 = -0.116675
•
a '6 = -0.495401
• a '7 = 0.28155
Comparémoslos ahora con los parámetros utilizados para generar la serie de tiempo de la
Figura 4.18:
114
Capítulo 4. El Perceptrón
•
a1 - a '1 = -0.15 – (-0.165747) = 0.015747
•
a2 - a '2 = 0.1 – 0.0845436 = 0.0154564
•
a3 - a '3 = -0.3 – (-0.27829) = -0.02171
•
a4 - a '4 = -0.2 – (-0.17541) = -0.02459
•
a5 - a '5 = -0.1 – (-0.116675) = 0.016675
•
a6 - a '6 = -0.5 – (-0.495401) = -0.004599
• a7 - a '7 = 0.3 – 0.28155 = 0.01845
Lo que en consecuencia nos dice que el promedio de los errores al cuadrado existente entre
los parámetros reales y aquellos identificados durante el entrenamiento del Perceptrón es
0.000314638. Ello implica que hemos obtenido aproximaciones bastante cercanas a las
esperadas.
Tabla 4.5. Desempeño del aprendizaje de un Perceptrón entrenado
mediante Descenso Escalonado y el Algoritmo 4.1 (véase el texto para detalles).
T-ésima Presentación
N
1
MSE =
ε n2
del Conjunto
μ
¦
N − M n = M +1
de Entrenamiento
0.000288294
1
2.90865 × 1017
15
0.000277045
2
1.42666 × 10
12
0.000266235
3
7.17163 × 10
0.000255846
4
2.07356 × 108
5
381,223
0.000245863
10
26.2274
0.000201496
20
22.5903
0.000135335
30
20.9588
0.0000908984
40
20.0612
0.0000610522
50
19.5134
0.0000410059
60
19.1554
0.0000275418
70
18.9167
0.0000184985
80
18.7727
0.0000124246
90
18.6672
0.00000834501
100
18.5939
0.00000560495
Los pesos identificados a '1 a a '7 se utilizan para generar la señal correspondiente.
Para este fin se utilizará la siguiente fórmula:
ck
­
°M
x 'n = ®
°¦ a 'k xn − k
¯ k =1
si n = k , k ∈ {1, 2,..., M }
si
N ≥n>M
(Ecuación 4.3.11)
Nótese la similitud de ésta con la Ecuación 4.3.1, la cual fue utilizada para generar la serie
de tiempo original (Figura 4.18). En el caso actual, las M muestras, para obtener al
estimado x 'n , son tomadas del conjunto de entrenamiento. Ello implica que de hecho la
115
Una Introducción al Cómputo Neuronal Artificial
sumatoria usada para generar a x 'n es la sumatoria de salida del Perceptrón. Por esa misma
razón hemos omitido el término de ruido o perturbación ya que la neurona fue entrenada
con muestras a las cuales ya se les había aplicado la función noise(n). Finalmente,
agregamos el hecho de que la Función de Activación utilizada fue la Función Identidad. Por
tanto, el caso cuando N ≥ n > M en la Ecuación 4.3.11 no hace más que enviar como
entrada al Perceptrón el vector [xn-1 xn-2 xn-3 … xn-M]T y obtener la salida
correspondiente x 'n . La Figura 4.22 muestra la señal generada al aplicar el Perceptrón bajo
la Ecuación 4.3.11. En la Figura 4.23 se presenta la señal generada por el Perceptrón (en
gris) sobrepuesta con la señal original (en negro). Debido a que los parámetros
autorregresivos identificados cuentan con errores respecto a los originales, es que es fácil
detectar pequeñas diferencias entre las señales. Sin embargo, es también claro que el error
es en realidad pequeño.
MSE
28
26
24
22
20
20
40
60
80
100
T
Figura 4.20. Evolución del valor MSE (Ecuación 4.3.4) a lo largo de las T = 100
presentaciones del conjunto de entrenamiento para un Perceptrón entrenado mediante
el Algoritmo 4.1 (Véase el texto para detalles).
116
Capítulo 4. El Perceptrón
μ
0.0003
0.00025
0.0002
0.00015
0.0001
0.00005
20
40
60
80
100
T
Figura 4.21. Evolución del Coeficiente de Aprendizaje μ a lo largo de las T = 100
presentaciones del conjunto de entrenamiento para un Perceptrón entrenado mediante
el Algoritmo 4.1 (Véase el texto para detalles).
En la Sección 4.2 reconocimos a las limitaciones del Perceptrón en términos del
número de problemas que es capaz de modelar y resolver. Sin embargo, esta Sección ha
presentado una aplicación interesante para la cual se ha proporcionado una solución, la cual
si bien es aproximada, es bastante cercana a la óptima. Al mismo tiempo, hemos presentado
un mecanismo de ajuste de pesos basado en el método de Descenso Escalonado. Es
evidente que las operaciones aplicadas son realmente sencillas: sumas, restas y
multiplicaciones. Por ello contamos con una unidad de cómputo neuronal cuya
implementación algorítmica es realmente simple, tal como lo muestra el Algoritmo 4.1. En
los siguientes dos Capítulos comenzaremos a considerar el uso de más de una neurona, lo
cual da a lugar a la especificación de Redes Neuronales Artificiales y la solución de
problemas mediante éstas. Será en ese punto cuando veamos que las limitaciones de una
única neurona logran ser superadas al considerar varias neuronas para la solución de un
problema.
117
Una Introducción al Cómputo Neuronal Artificial
xn
n
500
1000
1500
2000
Figura 4.22. Serie de tiempo de 7 parámetros autorregresivos
generada por un Perceptrón bajo la Ecuación 4.3.11 (véase el texto para detalles).
118
Capítulo 4. El Perceptrón
xn
n
500
1000
1500
2000
Figura 4.23. En color gris, la serie de tiempo presentada en la Figura 4.22.
En color negro, la serie de tiempo presentada en la Figura 4.18
(véase el texto para detalles).
119
Una Introducción al Cómputo Neuronal Artificial
120
Una Introducción al Cómputo Neuronal Artificial
5. La Red Madaline
Una Introducción al Cómputo Neuronal Artificial
122
Capítulo 5. La Red Madaline
La Red Madaline (Many Adaline) es una Red Neuronal Artificial formada por varias
neuronas del tipo Adaline (Capítulo 3) las cuales se encuentran agrupadas en capas. En el
Capítulo 1 comentamos que fue propuesta por Bernard Widrow en 1960. Existen varios
mecanismos para el ajuste de los pesos de las neuronas que conforman a una red Madaline.
Uno de ellos es la Madaline Rule II, la cual fue originalmente propuesta por Widrow junto
con Rodney Winter en 1988. En la Sección 5.2 haremos mención de una metodología para
el ajuste de pesos que toma algunos elementos de la Madaline Rule II. Por lo mientras, en
la siguiente Sección describiremos las bases que forman el procesamiento de un vector de
entrada para producir la correspondiente salida.
5.1 Estructura Básica
Consideremos una red Madaline formada por 5 neuronas. Véase la Figura 5.1. Tal
como comentamos previamente las neuronas estarán organizadas en capas. En el caso de la
red que hemos definido en la Figura 5.1 tenemos la siguiente estructura:
• Las neuronas 1 y 2 forman la Capa de Entrada.
• Las neuronas 3 y 4 forman una Capa Interna o Capa Oculta.
• La neurona 5 forma la Capa de Salida.
z1 = w1,0 +
x1
3
¦w
x
1,i i
i =1
Adaline 1
y1 =
sign( z1 )
z3 = w3,0
+ w3,1 y1
+ w3,2 y2
Adaline 3
y3 =
sign( z3 )
z5 = w5,0
x2
x3
+ w5,1 y3
z2 = w2,0 +
3
¦w
x
2,i i
i =1
Adaline 2
y2 =
sign( z2 )
z4 = w4,0
+ w4,1 y1
+ w4,2 y2
Adaline 4
+ w5,2 y4
Adaline 5
y5 =
sign( z5 )
y5
y4 =
sign( z4 )
Figura 5.1. Una red Madaline formada por 5 neuronas.
La red de la Figura 5.1 recibirá como entrada un vector en \ 3 : [x1 x2 x3]T. Los
escalares x1, x2 y x3 se envían tanto a la neurona 1 como a la neurona 2. Sabemos, por la
Sección 3.1, que las neuronas 1 y 2 producirán como salida los escalares y1 y y2
respectivamente. Ahora bien, los valores y1 y y2 formarán a su vez en un vector en \ 2 :
[y1 y2]T. Este vector será enviado como entrada a las dos neuronas que forman la capa
oculta. Las neuronas 3 y 4 producen entonces las salidas y3 y y4 respectivamente. De nueva
cuenta formamos un vector en \ 2 cuyos componentes son los escalares y3 y y4. El vector
[y3 y4]T es enviado como entrada a la única neurona en la capa de salida, es decir, la
neurona 5. Finalmente, la neurona 5 procesa sus entradas y produce la salida y5. Este
escalar es de hecho la salida final que proporciona la red.
El proceso que acabamos de describir, para la red de la Figura 5.1, puede ser visto
como una serie de mapeos de vectores que inicia desde la capa de entrada. Ésta recibe un
123
Una Introducción al Cómputo Neuronal Artificial
vector en \ 3 el cual es mapeado, por las neuronas 1 y 2, en un vector en \ 2 .
Posteriormente este vector es mapeado en un nuevo vector, también en \ 2 , por la acción
de las neuronas en la capa oculta. Finalmente, la única neurona en la capa de salida mapea a
su vector de entrada en un vector en \ . En general, es claro entonces que la
dimensionalidad de los mapeos va directamente en función del número de neuronas
presentes en cada capa de la red. Consideremos una red formada por m capas ocultas. Sean:
• p: número de neuronas en la capa de entrada
• nO: número de neuronas en la O-ésima capa oculta, 1 ≤ O ≤ m.
• q: número de neuronas en la capa de salida.
Suponiendo que los vectores de entrada están en \ n tenemos entonces la siguiente
secuencia de mapeos entre las capas de neuronas:
Capa
de
entrada
Primer
capa
oculta
\ n 6 \ p 6\ n1
Segunda
capa
oculta
Tercer
capa
oculta
6\ 6
n2
"
m -ésima
capa
oculta
Capa
de
salida
6 \ 6\
nm
q
Considerando únicamente la dimensionalidad de los vectores de entrada y de los vectores
en la salida final, es que se dice también que una red mapea vectores de \ n a \ q .
Esta secuencia de mapeos de vectores entre las capas también nos permite
determinar el número de conexiones existentes en la red. Dado que los n componentes del
vector de entrada se propagan todos a las p neuronas en la capa de entrada es que entonces
tenemos np conexiones. Sabemos que cada neurona en la capa de entrada contribuye con un
escalar de salida de manera que en esta capa se forma un vector de p componentes. Este
vector es propagado hacia todas las n1 neuronas que forman a la primera capa oculta. Por lo
tanto se tienen pn1 conexiones entre la capa de entrada y la primera capa oculta. La O-ésima
capa oculta se forma por nO neuronas. Las salidas de estas neuronas forman un vector de nO
componentes el cual a su vez es propagado a la siguiente capa oculta la cual se forma por
nO+1 neuronas. El número de conexiones entre estas dos capas ocultas estará dado por nO⋅nO+1.
Por último, se tiene que la última capa oculta se formará por nm neuronas. Sus salidas
forman un vector de nm componentes los cuales son todos propagados hacia las q neuronas
en la capa de salida. Se tienen entonces nmq conexiones. Sea CM(n, p, m, q, n1, …, nm) el
número de conexiones presentes en una red Madaline. De acuerdo a la descripción anterior
tendremos que:
m −1
CM ( n, p, m, q, n1 , …, nm ) = np + pn1 + ¦ nA ⋅nA +1 + nm q
(Ecuación 5.1.1)
A =1
Por ejemplo, para la red Madaline de la Figura 5.1 tenemos que la Ecuación 5.1.1
nos indica que existen 12 conexiones:
0
CM ( 3, 2,1,1, 2 ) = 3 ⋅ 2 + 2 ⋅ 2 + ¦ nA ⋅nA +1 + 2 ⋅1 = 6 + 4 + 0 + 2 = 12
A =1
124
Capítulo 5. La Red Madaline
5.2 Ajuste de Pesos en una Red Madaline
En el Sistema Nervioso Central se tiene que los seres humanos no estamos
conscientes del funcionamiento de las neuronas en las “capas ocultas” de nuestra red
neuronal en procesos, por ejemplo, como el aprendizaje. Realmente no se conocen ni se
pueden interpretar las salidas proporcionadas por tales neuronas. En realidad, solo estamos
conscientes de las entradas que recibe nuestra red, que pueden provenir de los órganos
sensoriales por ejemplo, y de las salidas que ésta proporciona y que pueden percibirse al
final como una acción ejecutada. En el caso de una Red Neuronal Artificial se presenta una
situación similar ya que el aprendizaje de una red sólo se mide en términos de las entradas
y las salidas finales. Las salidas de las neuronas en las capas de entrada y las capas ocultas
no se interpretan, aunque si son accesibles y por ello mismo se aplican modificaciones a los
pesos de estas neuronas ya que sus salidas contribuyen a los valores de las salidas finales de
la red. Esta actualización de pesos es consistente, por ejemplo, con la Ley de Aprendizaje
Hebbiano (Sección 1.2), sin embargo, desde el punto de vista biológico, realmente no
sabemos de manera precisa en qué momento se dan las modificaciones entre las conexiones
de las neuronas ni tampoco que tanto se refuerzan o debilitan éstas.
A continuación describiremos una metodología, la cual está basada en la propuesta
de Widrow y Winter para el ajuste de pesos en una red Madaline. Se trata de un método de
entrenamiento inspirado en la Madaline Rule II. Veremos que en realidad es una
metodología bastante intuitiva y por tanto fácil de comprender. Sin embargo, también
veremos que pueden existir problemas con su eficiencia. Pero no por ello nos dejará de ser
útil para comprender los retos y perspectivas presentes al momento de entrenar una red
formada por más de una neurona. Por eso mismo la metodología a detallar es una buena
introducción antes de proceder al Algoritmo de Retropropagación, el cual se discutirá en el
siguiente Capítulo.
Considérese el conjunto de entrenamiento de la Tabla 5.1. Éste será presentado a la
red Madaline de la Figura 5.2. Tal red se forma por 5 neuronas tipo Adaline. Se reciben
como entrada vectores en \ 2 . La salida final de la red está dada por un escalar. Dado que
todas las neuronas envían el resultado de sus respectivas sumatorias de salida a la función
sign, es que entonces, a partir de la capa de entrada, todos los vectores generados tienen sus
componentes en {-1, 1}.
Tabla 5.1. Conjunto de entrenamiento
a presentar a una red Madaline.
Salida
Entrada
Esperada
x1 x2
d
-2
0
1
-1
0
-1
0
1
1
1
1
-1
2
3
1
125
Una Introducción al Cómputo Neuronal Artificial
z1 = w1,0
x1
+ w1,1 x1
+ w1,2 x2
Adaline 1
y1 =
sign( z1 )
z3 = w3,0
+ w3,1 y1
+ w3,2 y2
Adaline 3
y3 =
sign( z3 )
z5 = w5,0
+ w5,1 y3
x2
z2 = w2,0
+ w2,1 x1
+ w2,2 x2
Adaline 2
y2 =
sign( z2 )
z4 = w4,0
+ w4,1 y1
+ w4,2 y2
Adaline 4
+ w5,2 y4
Adaline 5
y5 =
sign( z5 )
y5
y4 =
sign( z4 )
Figura 5.2. Una red Madaline formada por 5 neuronas que efectúa
un mapeo de vectores en \ 2 a vectores (escalares) en \ .
Tabla 5.2. Pesos iniciales de las neuronas
en la red Madaline presentada en la Figura 5.2.
w j,1
w j,2
wj,0
-0.23 -0.3
Neurona 1 0.5
Neurona 2 -0.16 -0.46 -0.26
Neurona 3 0.75 0.22 0.78
Neurona 4 0.37 -0.59 -0.28
Neurona 5 0.76 -0.96 0.38
Supongamos que las neuronas de la red de la Figura 5.2 cuentan con los pesos
iniciales mostrados en la Tabla 5.2. Veamos que sucede cuando enviamos como entrada al
primer vector en el conjunto de entrenamiento de la Tabla 5.1: x1 = -2, x2 = 0. Para éste se
espera que la red proporcione la salida final d = 1. Como sabemos, el vector es recibido
inicialmente por las neuronas en la capa de entrada, es decir, los Adalines 1 y 2.
Determinemos sus correspondientes salidas:
• Neurona 1:
o z1 = -2(-0.23) + 0(-0.3) + 0.5 = 0.96
o y1 = sign(0.96) = 1
• Neurona 2:
o z2 = -2(-0.46) + 0(-0.26) – 0.16 = 0.76
o y2 = sign(0.76) = 1
ª y º ª1º
Esto da lugar a la generación del vector « 1 » = « » . Éste ahora es enviado como entrada a
¬ y2 ¼ ¬1¼
las neuronas 3 y 4 que forman la única capa oculta:
• Neurona 3:
o z3 = 1(0.22) + 1(0.78) + 0.75 = 1.75
o y3 = sign(1.75) = 1
• Neurona 4:
o z4 = 1(-0.59) + 1(-0.28) + 0.37 = -0.5
o y4 = sign(-0.5) = -1
126
Capítulo 5. La Red Madaline
ªy º ª 1 º
Por ultimo, el vector generado por las salidas de la capa oculta, « 3 » = « » , se envía a la
¬ y4 ¼ ¬ −1¼
única neurona en la capa de salida:
• Neurona 5:
o z5 = 1(-0.96) + -1(0.38) + 0.76 = -0.58
o y5 = sign(-0.58) = -1
En este punto nos es claro que la red proporciona una salida diferente a la esperada. Se
deberá efectuar un ajuste de pesos de manera que para el vector de entrada [-2 0]T se
obtenga la salida d = 1.
Veamos como es que nuestra metodología procede para ajustar los pesos de la red
de la Figura 5.2 de tal forma que para la entrada [-2 0]T se obtenga la salida d = 1. En
primer lugar debemos considerar que las neuronas a ajustar serán aquellas en las capas
ocultas y de salida, y en particular, se inicia con las neuronas en la capa oculta.
Considérense las neuronas 3 y 4 de la Figura 5.2, suponemos que sus pesos son los
presentados en la Tabla 5.2. Sea S el conjunto dado por:
2
­
½
S = ® w j ,0 + ¦ w j ,i yi : j = 3, 4 ¾
i =1
¯
¿
(Ecuación 5.2.1)
Es decir, S se forma por los valores absolutos de las Sumatorias de Salida, sin aplicar la
función sign, de las neuronas 3 y 4. El vector que se les envía es el vector generado por la
capa de entrada una vez que ha procesado al vector de entrada en cuestión, es decir, el
vector [-2 0]T. Por lo tanto, específicamente S tendrá los siguientes valores:
S = {1.75, 0.5}
Ahora bien, se seleccionará aquella neurona, de la capa oculta, cuyo valor en S sea el más
pequeño. Tenemos que, para nuestro ejemplo, se trata de la neurona 4. La idea es ajustar
primero los pesos a las neuronas cuyos valores absolutos de sus Sumatorias de Salida sean
cercanos al cero. Debido a que las Sumatorias de Salida de estas neuronas son pequeñas en
comparación con las de las neuronas restantes en la capa, también será más sencillo
modificar sus pesos. De hecho, el objetivo es que la neurona seleccionada invierta su salida.
Si la neurona proporcionó una salida 1 (-1), entonces se espera que su contribución a la
solución del problema mejore, y en particular a obtener la salida final de la red correcta, al
hacer que su salida ahora sea -1 (1). Asignemos los siguientes nuevos pesos a la neurona 4:
• w4,0 = -0.39
• w4,1 = 0.58
• w4,2 = -0.60
Veamos en primer lugar si la salida de la neurona se invierte, para ello le enviamos el
vector generado por la capa de entrada al procesar al vector en el Conjunto de
Entrenamiento [-2 0]T:
127
Una Introducción al Cómputo Neuronal Artificial
• z4 = 1(0.58) + 1(-0.60) - 0.39 = -0.41
• y4 = sign(-0.41) = -1
Es claro que la salida no se invirtió. Se asignan los nuevos pesos:
• w4,0 = 0.9017
• w4,1 = -0.71
• w4,2 = 0.97
Se verifica si la salida se ha invertido:
• z4 = 1(-0.71) + 1(0.97) + 0.9017 = 1.1617
• y4 = sign(1.16) = 1
Los nuevos pesos efectivamente permiten que la salida de la neurona 4 ahora sea igual a 1.
Usando a éstos, se recalcula la salida final de la red y se verifica si se obtiene la salida
correcta d = 1. El vector de entrada para la neurona 5 será ahora [1 1]T cuyo segundo
componente es precisamente la nueva salida de la neurona 4:
• z5 = 1(-0.96) + 1(0.38) + 0.76 = 0.18
• y5 = sign(0.18) = 1
Con el reajuste de pesos aplicado a la neurona 4 hemos obtenido la salida esperada para el
vector de entrada x1 = -2, x2 = 0. Por lo tanto esta neurona preserva sus nuevos pesos. En la
Tabla 5.3 se presentan los pesos actuales de la red Madaline de la Figura 5.2.
Tabla 5.3. Pesos de las neuronas
en la red Madaline presentada en la Figura 5.2
una vez que se ha aplicado un ajuste sobre la neurona 4
(Véase el texto para detalles).
w j,1
w j,2
wj,0
0.5
-0.23 -0.3
Neurona 1
Neurona 2 -0.16 -0.46 -0.26
0.75
0.22 0.78
Neurona 3
Neurona 4 0.9017 -0.71 0.97
0.76
-0.96 0.38
Neurona 5
La idea ahora es presentar a la red un nuevo vector de entrada. En el caso en que
dado un vector de entrada la red proporcione la salida correcta entonces es obvio que no se
aplicará ninguna modificación. Si por otro lado, se obtiene salida final incorrecta y a todas
las neuronas en la capa oculta se les ha invertido su salida sin obtener la salida final
esperada, entonces se procede a efectuar modificaciones de pesos en las neuronas de la
siguiente capa oculta. Si todas las capas ocultas han sido procesadas sin obtener la salida
final correcta, entonces se procede a modificar los pesos de las neuronas en la capa de
salida.
Procedamos a describir el mecanismo para el entrenamiento de una red Madaline.
Sea h un índice para enumerar las capas de la red de manera que tomará valores desde 1
hasta m+1, donde m es el número de capas ocultas. Si h = m+1 entonces estamos haciendo
referencia a la capa de salida; si 1 ≤ h ≤ m entonces hacemos referencia a la
h-ésima capa oculta. Sean los vectores X1, X2, …, XN los vectores de entrada en el conjunto
de entrenamiento. Considérese al i-ésimo vector de entrada, Xi, 1 ≤ i ≤ N. Xi es presentado a
128
Capítulo 5. La Red Madaline
la red y se obtiene la correspondiente salida final. Asumamos que la salida de la red con Xi
es incorrecta. Se procede a recorrer cada una de las capas de la red comenzando desde la
primer capa oculta, h = 1, hasta la capa de salida, h = m+1. Para cada Adaline j en la
h-ésima capa de la red actualmente procesada se calcula:
A( j ) = w j ,0 + ¦ w j ,i yi
(Ecuación 5.2.2)
i =1
Ahora, sea S el conjunto de valores A(j) ordenados de manera ascendente. Procesaremos a
cada elemento de S de manera secuencial. Consideremos a la neurona Adaline asociada al
elemento A(j) de S actualmente procesado. Se modifican los pesos de la neurona de manera
que su salida se invierta. Se recalcula nuevamente la salida de la red cuando Xi le es
presentado:
• Si la salida final de la red es ahora correcta entonces se fijan los nuevos pesos a la
neurona de manera definitiva, las restantes neuronas de la capa actual y las restantes
capas de la red ya no son consideradas. Se procede a presentar al siguiente vector de
entrada: Xi+1.
• Si la salida de la red sigue siendo incorrecta entonces a la neurona actual le son
reasignados sus pesos originales. Se analizan las restantes neuronas de la capa actual y
de las siguientes capas de la red hasta encontrar una neurona que al invertir su salida
permita que la red proporcione la salida correcta.
Veamos algunas propiedades y conceptos asociados al procedimiento que acabamos
de describir. En primer lugar, aquella neurona a la cual se le ha invertido su salida, y
además hace que la red proporcione la salida final correcta, se le denotará, tal y como
establecieron Windrow y Winter en la Madaline Rule II, Neurona de Disturbancia
Mínima. Nótese que es posible que al invertir la salida de una neurona se obtenga la salida
esperada para el vector de entrada actual. Pero también es posible que debido a este cambio
otros vectores en el conjunto de entrenamiento dejen de ser reconocidos. Consideremos
nuevamente a la red presentada en la Figura 5.2. Dados los pesos iniciales de la Tabla 5.2
y el vector de entrada [-2 0]T determinamos que la neurona de disturbancia mínima era la
neurona 4 ubicada en la primer, y única, capa oculta. Al invertir la salida de esta neurona
obtuvimos la salida correcta por parte de la red. Ahora bien, de acuerdo a la Tabla 5.1 el
siguiente vector a presentar es [-1 0]T. Para éste se espera que la red proporcione como
salida d = -1. Usando los pesos de la Tabla 5.3 tenemos que la red procesa a [-1 0]T como
sigue:
•
•
Neurona 1:
o z1 = -1(-0.23) + 0(-0.3) + 0.5 = 0.73
o y1 = sign(0.73) = 1
Neurona 2:
o z2 = -1(-0.46) + 0(-0.26) – 0.16 = 0.3
o y2 = sign(0.3) = 1
129
Una Introducción al Cómputo Neuronal Artificial
•
Neurona 3:
o z3 = 1(0.22) + 1(0.78) + 0.75 = 1.75
o y3 = sign(1.75) = 1
• Neurona 4:
o z4 = 1(-0.71) + 1(0.97) + 0.9017 = 1.1617
o y4 = sign(1.1617) = 1
• Neurona 5:
o z5 = 1(-0.96) + 1(0.38) + 0.76 = 0.18
o y5 = sign(0.18) = 1
Lo cual nos indica que se tiene una salida final incorrecta. De acuerdo a la manera de
proceder previamente establecida, la primera neurona cuyos pesos se modificarán será
nuevamente la neurona 4. Su salida debe ser invertida. Consideremos los siguientes nuevos
pesos (que no son más que aquellos presentados en la Tabla 5.3 pero con signo opuesto):
• w4,0 = -0.9017
• w4,1 = 0.71
• w4,2 = -0.97
Ahora se tiene que:
• z4 = 1(0.71) + 1(-0.97) - 0.9017 = -1.1617
• y4 = sign(-1.1617) = -1
Y para la neurona en la capa de salida:
• z5 = 1(-0.96) + (-1)(0.38) + 0.76 = -0.58
• y5 = sign(-0.58) = -1
Lo cual hace que para el vector de entrada [-1 0]T ya se cuente con su correspondiente
salida correcta. El problema ahora es que para el vector [-2 0]T la red ha dejado de
proporcionar la salida esperada d = 1.
El ejemplo anterior nos proporciona evidencia de que es factible que una Neurona
de Disturbancia Mínima pueda permitir el aprendizaje de algunos vectores de entrada, pero
también puede hacer que otros vectores que ya habían sido reconocidos por la red dejen de
serlo. Para ello, es posible, una vez identificada la Neurona de Disturbancia Mínima,
presentar cada uno de los vectores en el conjunto de entrenamiento a la red y contabilizar el
número de vectores de entrada para los que se obtiene una salida incorrecta. Si el número
de vectores no reconocidos aumenta respecto al número que se tenía antes de modificar los
pesos de la neurona, entonces los pesos originales de tal neurona son restaurados y se busca
otra neurona en la capa actual y en las capas restantes, si es necesario. La idea de esta
modificación es forzar a que se busque una Neurona de Disturbancia Mínima que permita
el mayor aprendizaje posible. Sin embargo se debe aceptar entonces un compromiso
respecto a la eficiencia del algoritmo. Sea nh el número de neuronas en la capa h,
1 ≤ h ≤ m + 1. Entonces, en el peor de los casos, para la h-ésima capa se tendrían que
determinar, a lo más, nh⋅N salidas finales de la red.
Nótese que el enfoque para lograr el aprendizaje que se ha planteado se basa en la
idea de identificar a una neurona “culpable”. Se parte del principio de que existe una
neurona en las capas ocultas o de salida que hace que para el vector de entrada actual la red
130
Capítulo 5. La Red Madaline
no proporcione la salida correcta. Precisamente la neurona “culpable” es la Neurona de
Disturbancia Mínima. Sin embargo este razonamiento abre las posibilidades de considerar
la existencia de más de una neurona “culpable”. Intuitivamente se entiende que pueden
existir problemas en los cuales para algunos vectores de entrada se deban aplicar
correcciones en los pesos de dos o más neuronas al mismo tiempo. Y de hecho, es posible
modificar el proceso antes descrito a fin de que se identifiquen a la vez dos neuronas
“culpables”. Cada neurona puede estar en una capa diferente. Una vez que dos neuronas
han sido seleccionadas se modifican sus pesos de manera que se inviertan sus salidas y se
verifica la salida final de la red. Esto abre más posibilidades ya que también es posible, por
lo tanto, identificar a la vez tripletas, cuartetos, quintetos, etc. de neuronas “culpables”. El
punto fundamental, al considerar tales subconjuntos de neuronas, es que debe elegirse de
todos los posibles subconjuntos aquel que maximice el aprendizaje de la red de manera que
al modificar sus pesos el número de vectores de entrada correctamente reconocidos
aumente respecto al número que se tenia previo a la modificación. Sea M el número total de
neuronas en las capas ocultas y de salida en una red Madaline:
m
M = q + ¦ nA
(Ecuación 5.2.3)
A =1
Recordemos que q es el número de neuronas en la capa de salida y nO es el número de
neuronas en la O-ésima capa oculta, 1 ≤ O ≤ m. El número de subconjuntos de k neuronas
tomadas del conjunto formado por las M neuronas en las capas ocultas y de salida está dado
§M ·
por el bien conocido Coeficiente Binomial ¨ ¸ :
©k ¹
§M ·
M!
¨ ¸=
© k ¹ k !( M − k )!
(Ecuación 5.2.4)
Supongamos la situación extrema en que analizamos primero si una única neurona
“culpable” es la que no permite proporcionar la salida correcta final de la red. Asumamos
que no hemos logrado identificar la única Neurona de Disturbancia Mínima. Entonces
procedemos a determinar si son dos las neuronas “culpables”. Asumamos nuevamente que
la red no proporciona la salida final correcta. Ahora determinemos si son tres las neuronas
“culpables”, y así sucesivamente. Ello implica que el número total de subconjuntos a
analizar es a lo más:
§M · §M ·
§M ·
§M · M §M ·
+
+
...
+
+
...
+
¨ ¸ ¨ ¸
¨ ¸
¨ ¸ = ¦¨ ¸
©1¹ ©2¹
©k ¹
© M ¹ k =1 © k ¹
(Ecuación 5.2.5)
131
Una Introducción al Cómputo Neuronal Artificial
El Teorema del Binomio nos dice que el desarrollo de (a + b)M, donde a, b ∈ \ y
M ∈ ] + ∪ {0} está dado por:
M
§M ·
( a + b) M = ¦ ¨ ¸ a M − k b k
k =0 © k ¹
(Ecuación 5.2.6)
Haciendo a = 1 y b = 1 en el Teorema del Binomio tenemos el valor de la suma presentada
en la Ecuación 5.2.5:
§ M · § M · M § M · M −k k
M
M
¦
¨ ¸ − ¨ ¸ = ¦ ¨ ¸1 1 − 1 = (1 + 1) − 1 = 2 − 1 (Ecuación 5.2.7)
k =0 © k ¹ © 0 ¹
k =0 © k ¹
M
El índice inferior de la sumatoria asociada al Teorema del Binomio es k = 0 y por tanto el
§M ·
coeficiente binomial correspondiente es ¨ ¸ el cual evidentemente denota al número de
©0¹
subconjuntos de 0 elementos: 1. Dado que este término no nos es de utilidad es por ello que
lo restamos al formar la Ecuación 5.2.7.
Por ejemplo, si contásemos con una red Madaline con M = 16 neuronas en sus capas
ocultas y de salida entonces tendríamos que analizar a los más 2M - 1 = 65,535
subconjuntos de neuronas “culpables” a fin de hacer que el vector de entrada actual sea
reconocido correctamente sin afectar el desempeño actual de la red. En general, suponiendo
que contamos con un conjunto de entrenamiento formado por N vectores de entrada
entonces el número total de evaluaciones a efectuar durante el entrenamiento de la Red
Madaline, en el peor de los casos, sería N⋅(2M – 1). Es claro que el enfoque basado en la
determinación de un subconjunto de neuronas “culpables” nos genera un problema de
índole combinatoria.
La metodología que hemos descrito en esta Sección para el entrenamiento de una
red Madaline, y la cual toma varios elementos de la Madaline Rule II, deja claros algunos
retos que se deben superar si efectivamente se desea un ajuste bastante bueno de los pesos
de las neuronas en la red a fin de que ésta solucione y modele un problema dado. Por el
momento adelantamos, tal como se verá en el siguiente Capítulo, que una de las novedades
del Algoritmo de Retropropagación radica en no buscar un subconjunto de neuronas
“culpables”, sino que asume desde un principio que si un vector de entrada no es
reconocido correctamente ello se debe a que todas las neuronas contribuyen a esa falla de
reconocimiento. El error que existe entre la salida final de la red y la salida esperada es
entonces distribuido y usado para ajustar los pesos de todas las neuronas. Pero antes de
presentar el Algoritmo de Retropropagación, veremos, en la siguiente Sección, como es que
una red Madaline es capaz de dar solución al problema del modelado de la compuerta
XOR.
132
Capítulo 5. La Red Madaline
5.3 Modelado de Funciones Booleanas
Antes de abordar el modelado de la función XOR mediante una red Madaline,
consideremos primero un procedimiento para determinar a una función Booleana al partir
únicamente de sus estados y de los valores que ésta arroja para cada uno. Por ejemplo, sea f
una función que depende de las tres variables x1, x2 y x3. Los valores que ésta proporciona
para cada uno de sus 8 posibles estados son presentados en la Tabla 5.4.
Tabla 5.4. Estados y salidas
para una función Booleana de 3 variables.
x1 x2 x3 f(x1, x2, x3)
1 1 1
1
1 1 0
0
1 0 1
0
1 0 0
0
0 1 1
0
0 1 0
1
0 0 1
1
0 0 0
0
La pregunta a plantear ahora es: ¿cómo se expresa a f en términos de las variables
x1, x2 y x3? El procedimiento a definir permitirá determinar a f como una función de las
variables dadas y los bien conocidos conectivos de conjunción, disyunción y negación.
Nótese que son tres los estados para las cuales f proporciona como valor 1. Éstos se
presentan en la Tabla 5.5.
Tabla 5.5. Estados para los cuales
la función Booleana de la Tabla 5.4 tiene salida 1.
x1 x2 x3 f(x1, x2, x3)
1 1 1
1
0 1 0
1
0 0 1
1
De la Tabla 5.5, considérese el estado (0, 0, 1). Los siguientes razonamientos deben
ser sumamente claros:
• Si x1 = 0 entonces ¬x1 = 1.
• Si x2 = 0 entonces ¬x2 = 1.
• Si x3 = 1 entonces (obviamente) x3 = 1.
Recordemos que buscamos que con el estado (0, 0, 1) la función f proporcione el valor 1.
Por lo tanto, si x1, x2 y x3 son iguales a 0, 0 y 1, respectivamente, entonces se tiene que la
función Booleana
¬x1 ∧ ¬x2 ∧ x3
arroja el valor 1. Esta función la construimos a partir de los consecuentes de las 3
condicionales que planteamos uniéndolas mediante el operador AND. De hecho, es fácil
133
Una Introducción al Cómputo Neuronal Artificial
comprobar que con cualquier otro estado diferente de (0, 0, 1), la función anterior siempre
proporciona el valor 0.
Ahora tomemos de la Tabla 5.5 el estado (0, 1, 0):
• Si x1 = 0 entonces ¬x1 = 1.
• Si x2 = 1 entonces x2 = 1.
• Si x3 = 0 entonces ¬x3 = 1.
Tomemos los consecuentes de las tres condicionales anteriores y unámoslos mediante el
operador de conjunción. Tenemos entonces la siguiente función Booleana:
¬x1 ∧ x2 ∧ ¬x3
Tal función proporciona el valor 1 únicamente con el estado (0, 1, 0).
Finalmente, consideremos el estado (1, 1, 1) de la Tabla 5.5. Procedemos tal y
como lo hicimos con los dos estados anteriores:
• Si x1 = 1 entonces x1 = 1.
• Si x2 = 1 entonces x2 = 1.
• Si x3 = 1 entonces x3 = 1.
Construimos en consecuencia la siguiente función Booleana:
x1 ∧ x2 ∧ x3
Claramente el estado (1, 1, 1) es el único que hace que la función proporcione el valor 1.
A partir de los 3 estados con los cuales la función f de la Tabla 5.4 arroja el valor 1
hemos obtenido 3 funciones Booleanas expresadas en términos de las variables x1, x2 y x3 y
los operadores NOT y AND:
• ¬x1 ∧ ¬x2 ∧ x3
• ¬x1 ∧ x2 ∧ ¬x3
• x1 ∧ x2 ∧ x3
Ahora uniremos a esas tres funciones Booleanas utilizado el operador OR, de manera que
obtenemos una nueva función Booleana:
(¬x1 ∧ ¬x2 ∧
x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3)
Recordemos que dos funciones Booleanas son Lógicamente Equivalentes si sus
correspondientes tablas de verdad son iguales. Para la función f su tabla de verdad es
precisamente la Tabla 5.4. Ahora calcularemos la tabla de verdad de la función que
acabamos de construir. Véase la Tabla 5.6.
134
Capítulo 5. La Red Madaline
x1
x2
x3
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
Tabla 5.6. Tabla de verdad asociada la función Booleana
(¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3).
(¬
¬x1 ∧ ¬x2 ∧ x3)
¬x1 ∧ ¬x2 ∧ x3 ¬x1 ∧ x2 ∧ ¬x3 x1 ∧ x2 ∧ x3 ∨ (¬
¬x1 ∧ x2 ∧ ¬x3)
∨ (x1 ∧ x2 ∧ x3)
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
1
0
0
1
0
0
0
0
Es claro que ambas funciones arrojan los mismos valores para los mismos estados.
Entonces podemos concluir que la función f (Tabla 5.4) es lógicamente equivalente a la
función Booleana (¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3). Por lo tanto:
f(x1, x2, x3) = (¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3)
(Ecuación 5.3.1)
Hemos ilustrado un procedimiento mediante el cual es posible obtener para
cualquier función Booleana, dada únicamente su tabla de verdad, aquella función Booleana
que le es lógicamente equivalente pero que estará dada en términos de sus variables
involucradas y las compuertas lógicas AND, OR y NOT. Ahora consideremos la compuerta
lógica XOR. Su correspondiente tabla de verdad se presenta en la Tabla 5.7.
Tabla 5.7. Estados y salidas
para la función Booleana XOR.
x1 x2 x1 ⊗ x 2
0 0
0
0 1
1
1 0
1
1 1
0
Determinemos su correspondiente expresión en términos de las compuertas AND,
OR y NOT. Son dos los estados para los cuales la función tiene valor 1 (Véase la Tabla
5.7):
• (0, 1): Si x1 = 0 entonces ¬x1 = 1. Si x2 = 1 entonces x2 = 1. Por lo tanto, para el estado
(0, 1) se tiene la función Booleana ¬x1 ∧ x2.
• (1, 0): Si x1 = 1 entonces x1 = 1. Si x2 = 0 entonces ¬x2 = 1. Para el estado (1, 0)
obtenemos la función Booleana x1 ∧ ¬x2.
Al conectar las dos funciones que obtuvimos mediante una disyunción se tiene:
(¬x1 ∧ x2) ∨ (x1 ∧ ¬x2)
135
Una Introducción al Cómputo Neuronal Artificial
Tal función Booleana no es más que la expresión de la compuerta XOR en términos de las
compuertas AND, OR y NOT. Por lo tanto:
x1 ⊗ x2 = (¬x1 ∧ x2) ∨ (x1 ∧ ¬x2)
(Ecuación 5.3.2)
En la Sección 4.2 comentamos que el modelado de la compuerta XOR representa el
ejemplo clásico de un problema que es caracterizado como linealmente no separable. Por
ello mismo, un único Perceptrón, e incluso una neurona tipo Adaline, no será capaz de
representarlo en términos de un umbral Z(x1, x2) = 0, geométricamente una recta en el
plano, que separe a los estados con salida 1 de los estados con salida 0. Sin embargo, la
Ecuación 5.3.2, que expresa al XOR en términos de las compuertas AND, OR y NOT es
interesante. Recordemos que las funciones Booleanas con una variable son todas
linealmente separables, mientras que de aquellas con dos variables únicamente el XOR y
XNOT no lo son. Es decir, la Ecuación 5.3.2 expresa a una compuerta lógica no
linealmente separable en términos de compuertas que si son linealmente separables. Para
tales compuertas podemos garantizar la existencia de sus correspondientes neuronas
artificiales que las modelan adecuadamente. Esto tiene como consecuencia que una función
Booleana puede ser modelada mediante una red neuronal usando neuronas que
implementen efectivamente las funciones Booleanas “básicas” AND, OR y NOT. La forma
en que se organizarán tales neuronas es especificada precisamente por el orden en que se
aplicarán las conjunciones, disyunciones y negaciones.
Ahora construiremos una red Madaline que modele a la compuerta lógica XOR. La
red recibirá un vector de entrada formado por dos componentes. El vector será enviado en
primer lugar a dos neuronas en la capa de entrada: una neurona implementa la función
Booleana ¬x1 ∧ x2 mientras que la otra implementa la función x1 ∧ ¬x2 (véase la Ecuación
5.3.2). Nótese que hemos omitido el usar neuronas que implementen el operador de
negación, sin embargo es posible hacerlo. Ahora bien, cuando las dos neuronas
proporcionan sus correspondientes salidas se forma un nuevo vector, también de dos
componentes, que es enviado a una neurona que modela al operador OR. Esta neurona de
hecho proporciona la salida final de la red. Ello implica, por un lado, que tenemos una
neurona en la capa de salida, y por otro lado, que nuestra red no cuenta con capas ocultas.
Utilizaremos entonces una red Madaline de 3 neuronas para modelar al operador XOR.
Dado que las neuronas a utilizar son de tipo Adaline, y por ende se utilizará la
función sign, entonces para los estados (x1, x2) y para las salidas proporcionadas por las
funciones Booleanas a utilizar reemplazaremos el valor 0 por el valor -1. Consideremos en
primer lugar a la función Booleana x1 ∧ ¬x2. La Tabla 5.8 muestra cada uno de los estados
de entrada y las salidas esperadas para éstos. En la Figura 5.3 se tiene la disposición de los
136
Capítulo 5. La Red Madaline
estados en el plano cuando sus valores son considerados coordenadas. Los puntos negros
representan estados con salida -1 mientras que el único punto blanco representa al estado
con salida 1. La sumatoria de salida de la neurona 1, que modelará la función x1 ∧ ¬x2, está
dada por
Z1(x1, x2) = w1,0 + x1w1,1 + x2w1,2
(Ecuación 5.3.3)
Nuestro objetivo es determinar los valores de sus pesos w1,0, w1,1 y w1,2 de tal forma que la
recta Z1(x1, x2) = 0 separe al punto blanco de los puntos negros. Además, queremos que
Z1(1, -1) sea un número positivo mientras que con el resto de los estados se obtenga un
valor negativo. Esto es con la finalidad de que al aplicar la función sign se obtengan las
salidas 1 o -1 tal como se tienen en la Tabla 5.8. En la Figura 5.3 se observa que una
opción razonable es que la recta Z1(x1, x2) = 0 sea aquella que pase por los puntos (0, -1) y
(1, 0). Por elementos bien conocidos de geometría analítica tenemos:
0 − (−1) 1(−1) − 0(0)
+
1− 0
1− 0
⇔ x2 = x1 − 1
x2 = x1
⇔ x1 − x2 − 1 = 0
(Ecuación 5.3.4)
Es decir, tenemos que los valores de los pesos de la neurona 1 están dados por w1,0 = -1,
w1,1 = 1 y w1,2 = -1. El vector normal de la recta Z1(x1, x2) = x1 − x2 − 1 = 0 es [1 -1]T. Éste
apunta precisamente al punto blanco por lo que se satisface que Z1(1, -1) > 0 mientras que
para los puntos negros se tendrá que Z1(1, -1) < 0. Contamos ya con una neurona Adaline
que modela la función Booleana x1 ∧ ¬x2.
Tabla 5.8. Estados y salidas
para la función Booleana x1 ∧ ¬x2
(el valor 0 ha sido sustituido por -1).
x1 x2 ¬x2 x1 ∧ ¬x2
-1 -1
1
-1
-1 1
-1
-1
1 -1
1
1
1 1
-1
-1
137
Una Introducción al Cómputo Neuronal Artificial
1
(-1,1)
(1,1)
-1
1
(-1,-1)
(1,-1)
-1
Z1 (x 1 , x 2 ) = 0
Figura 5.3. El umbral Z1(x1, x2) = 0 asociado a la neurona
que modelará la función Booleana x1 ∧ ¬x2.
Consideremos ahora a la función Booleana ¬x1 ∧ x2. Sus estados y salidas se
presentan en la Tabla 5.9. La Figura 5.4 presenta la disposición de los estados en plano
(puntos blancos: estados con salida 1, puntos negros: estados con salida -1). Buscaremos
los valores de los pesos para la sumatoria de salida de la neurona 2:
Z2(x1, x2) = w2,0 + x1w2,1 + x2w2,2
(Ecuación 5.3.5)
La Figura 5.4 muestra que una opción es buscar la ecuación de la recta Z2(x1, x2) = 0 que
pase por los puntos (-1, 0) y (0, 1):
0 − 1 −1(1) − 0(0)
+
−1 − 0
−1 − 0
⇔ x2 = x1 + 1
x2 = x1
⇔ x1 − x2 + 1 = 0
(Ecuación 5.3.6)
El vector normal de la recta obtenida es [1 -1]T. Éste apunta precisamente al estado (1, -1)
cuya salida es -1. Requerimos que el vector normal apunte al único estado blanco. Para ello
simplemente multiplicamos ambos lados de la ecuación de la recta por -1. Se tiene el nuevo
lugar geométrico:
− x1 + x2 − 1 = 0
(Ecuación 5.3.7)
De esta forma tenemos que los valores de los pesos de la neurona 2, que se encarga de
modelar la función Booleana ¬x1 ∧ x2, son w2,0 = -1, w2,1 = -1 y w2,2 = 1.
138
Capítulo 5. La Red Madaline
Tabla 5.9. Estados y salidas
para la función Booleana ¬x1 ∧ x2
(el valor 0 ha sido sustituido por -1).
x1 x2 ¬x1 ¬x1 ∧ x2
-1 -1
1
-1
-1 1
1
1
1 -1 -1
-1
1 1
-1
-1
1
(-1,1)
(1,1)
-1
1
(-1,-1)
(1,-1)
-1
Z 2 (x 1 , x 2) = 0
Figura 5.4. El umbral Z2(x1, x2) = 0 asociado a la neurona
que modelará la función Booleana ¬x1 ∧ x2.
Ahora requerimos una neurona Adaline que modele la compuerta lógica OR. Sus
estados y salidas se presentan en la Tabla 5.10 mientras que la Figura 5.5 muestra la
disposición de los estados en plano (puntos blancos: estados con salida 1, puntos negros:
estados con salida -1). De nueva cuenta requerimos un umbral Z3(y1, y2) que separe a los
estados blancos del único estado negro. Calculamos la ecuación de la recta que pasa por los
puntos (-1, 0) y (0, -1):
−1 − 0 0(0) − (−1)(−1)
+
0 − (−1)
0 − (−1)
⇔ y2 = − y1 − 1
y2 = y1
⇔ − y1 − y2 − 1 = 0
( Ecuación 5.3.8)
El vector normal de la recta está orientado hacia el punto negro, para el cual se desea una
salida negativa. Por lo tanto, multiplicamos la ecuación anterior por -1 y obtenemos la
139
Una Introducción al Cómputo Neuronal Artificial
orientación deseada de manera que para todo punto blanco Z3(y1, y2) proporciona un valor
positivo. Tenemos entonces que para la neurona 3 se tiene
Z3(y1, y2) = y1 + y2 + 1
(Ecuación 5.3.9)
Tabla 5.10. Estados y salidas
para la función Booleana OR
(el valor 0 ha sido sustituido por -1).
y1 y2 y1 ∨ y2
-1 -1
-1
-1 1
1
1 -1
1
1 1
1
1
(-1,1)
(1,1)
-1
1
(-1,-1)
(1,-1)
-1
Z 3 (y 1 , y 2 ) = 0
Figura 5.5. El umbral Z3(y1, y2) = 0 asociado a la neurona
que modelará la función Booleana OR.
Contamos con las tres neuronas requeridas para formar una red Madaline que
modele la compuerta XOR. En párrafos anteriores ya habíamos planteado la manera en la
cual estas deberían ser conectadas. Recordemos que x1 ⊗ x2 = (¬x1 ∧ x2) ∨ (x1 ∧ ¬x2)
(Ecuación 5.3.2). Véase la Figura 5.6. Las neuronas 1 y 2 reciben el vector de entrada
[x1 x2]T el cual es de hecho uno de los estados de la compuerta lógica. La primer neurona
calcula el valor correspondiente a x1 ∧ ¬x2 mientras que la segunda calcula ¬x1 ∧ x2. Se
tienen entonces las respectivas salidas y1 y y2. Lo único que resta es efectuar una disyunción
entre éstas. El operador OR está modelado por la neurona 3. En este punto tenemos que la
salida y3 es de hecho la salida final de la neurona.
140
Capítulo 5. La Red Madaline
Adaline 1
x1
z1 =
x1 − x2 − 1
y1 =
sign( z1 )
Adaline 3
z3 =
y1 + y2 + 1
y3 =
sign( z3 )
y3
Adaline 2
x2
z2 =
− x1 + x2 − 1
y2 =
sign( z2 )
Figura 5.6. Una red Madaline formada por 3 neuronas
que resuelve el problema del modelado de la compuerta XOR.
En la Sección 4.2 planteamos que si un problema es linealmente separable entonces
existe un umbral Z(x1, x2, …, xn) = 0 que particiona al espacio n-Dimensional en tres
regiones:
• El conjunto de puntos de \ n que están por encima del umbral.
• El conjunto de puntos de \ n que están por debajo del umbral.
• El conjunto de puntos de \ n que están sobre el umbral.
Para las tres neuronas que forman la red Madaline de la Figura 5.6 tenemos bien
identificados sus respectivos umbrales (Figuras 5.3, 5.4 y 5.5) los cuales particionan al
espacio bidimensional. En la Figura 5.7.a se muestra, en color gris, la región de \ 2 que
está por encima del umbral Z1(x1, x2) = x1 − x2 − 1 = 0. En tal región se ubica el estado (1, -1)
el cual tiene salida 1. La Figura 5.7.b muestra la región por encima del umbral
Z2(x1, x2) = − x1 + x2 − 1 = 0 . En ésta se localiza el estado (-1, 1), también con salida 1.
Finalmente, la Figura 5.7.c muestra la región por encima del umbral
Z3(y1, y2) = y1 + y2 + 1 = 0 en donde se localizan los estados de salida 1: (-1, 1), (1, 1) y
(1, -1). Lo que haremos ahora es presentar a las tres regiones que hemos descrito al mismo
tiempo en el plano. Véase la Figura 5.7.d. En esta misma figura presentamos los estados de
la compuerta XOR. La intersección entre las tres regiones, mostrada en gris obscuro en la
figura, forma dos conjuntos convexos disjuntos abiertos. El estado (-1, 1) se ubica en uno
de los conjuntos mientras que el estado (1, -1) se ubica en el otro. Ambos son estados con
salida 1. La unión de los dos conjuntos resultantes es evidentemente un conjunto no
convexo también abierto. Este conjunto en cuestión y los estados de la compuerta XOR se
presentan ahora en la Figura 5.8. En nuestra discusión respecto al Problema de
Representación (Sección 4.2) argumentábamos que si un elemento de cómputo neural daba
solución al problema del modelado de la función XOR entonces debíamos aceptar que los
estados con salida 1 deberían estar contenidos en un conjunto no convexo (abierto o
cerrado) que los separara de los estados con salida -1. Una neurona Adaline o Perceptrón no
puede generar este tipo de regiones. Pero acabamos de probar que mediante el uso de una
Red Neuronal es posible que los umbrales, y las regiones que éstos definen, den lugar
precisamente a las regiones no convexas requeridas para efectivamente dar solución al
141
Una Introducción al Cómputo Neuronal Artificial
problema en cuestión, en nuestro caso, el problema del XOR. La Figura 5.8 muestra que
los umbrales de las neuronas de la red Madaline de la Figura 5.6 permiten establecer las
condiciones bajo las cuales se particiona al plano en dos regiones no convexas.
Formalmente éstas son:
•
RC12 = {(a1 , a2 ) ∈ \ 2 : Z 3 (a1 , a2 ) ≥ 0 ∧ ( Z1 (a1 , a2 ) ≥ 0 ∨ Z 2 (a1 , a2 ) ≥ 0)}
•
RC22 = {(a1 , a2 ) ∈ \ 2 : Z 3 (a1 , a2 ) < 0 ∨ ( Z 3 (a1 , a2 ) ≥ 0 ∧ ( Z1 (a1 , a2 ) < 0 ∧ Z 2 (a1 , a2 ) < 0))}
Textualmente tenemos que un punto (a1, a2) estará en la región RC12 si en primer lugar éste
se ubica sobre o por encima del umbral Z3 (Ecuación 5.3.9). Si esta condición se cumple
entonces sólo se debe determinar si (a1, a2) satisface el estar sobre o por encima del umbral
Z1 (Ecuación 5.3.3) o bien sobre o por encima del umbral Z2 (Ecuación 5.3.5). El conjunto
de puntos que cumplen las condiciones que acabamos de describir están en la región gris de
la Figura 5.8. Es claro que los estados con salida 1 se ubicarán en la región RC12 . Por otro
lado, analizando las condiciones establecidas para que un punto (a1, a2) se ubique en la
región RC22 es claro que ésta es complementaria a la región RC12 . Aplicando Álgebra de
Conjuntos se puede demostrar sin problema que RC12 ∪ RC22 = \ 2 . Finalmente, los
estados con salida -1 estarán en RC22 .
Procedamos ahora a modelar, mediante una Red Madaline, a la función Booleana
descrita originalmente en la Ecuación 5.3.1:
f(x1, x2, x3) = (¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3)
Analizaremos en primer lugar a las funciones Booleanas que la componen:
•
•
•
¬x1 ∧ ¬x2 ∧ x3
¬x1 ∧ x2 ∧ ¬x3
x1 ∧ x2 ∧ x3
La idea es que si las tres son linealmente separables entonces la capa de entrada de la
correspondiente red Madaline se formará únicamente por tres neuronas. Cada una recibirá
un vector de entrada [x1 x2 x3]T que contiene el estado a procesar. Debido al uso de la
función sign y a fin de diferenciar adecuadamente los estados y sus salidas reemplazaremos
el valor Booleano 0 por el valor -1.
142
Capítulo 5. La Red Madaline
1
(-1,1)
1
(1,1)
-1
(-1,-1)
(-1,1)
1
-1
(1,-1)
(-1,-1)
-1
(1,1)
1
(1,-1)
-1
Z 1 (x1 ,x 2)=0
Z 2 (x1 ,x 2) = 0
a)
b)
1
(-1,1)
1
(1,1)
-1
(-1,-1)
(-1,1)
1
-1
(1,-1)
(-1,-1)
-1
(1,1)
1
(1,-1)
-1
Z 3 (y1 ,y 2)=0
c)
d)
Figura 5.7. a), b) y c) En gris: Regiones del plano por encima de los umbrales asociados a las neuronas que
modelan las funciones Booleanas x1 ∧ ¬x2, ¬x1 ∧ x2 y OR. d) Las tres regiones anteriores sobrepuestas. En
gris obscuro: sus intersecciones.
1
(-1,1)
(1,1)
-1
1
(-1,-1)
(1,-1)
-1
Figura 5.8. Partición del plano inducida por la Red Neuronal
de la Figura 5.6 (Véase el texto para detalles).
143
Una Introducción al Cómputo Neuronal Artificial
Consideremos en primer lugar a la función ¬x1 ∧ ¬x2 ∧ x3. Por la forma en la que
fue construida sabemos que el único estado con el cual proporciona la salida 1 es (-1, -1, 1).
En la Figura 5.9.a se presentan los estados de esta función caracterizados de manera que
un estado negro es un estado con salida -1 y un estado blanco (el único) es de salida 1. Esta
función es claramente linealmente separable. Requerimos un plano que separe al estado
(-1, -1, 1) de los restantes. Para ello determinaremos la ecuación del plano usando los tres
puntos no colineales (-1, -1, 0), (0, -1, 1) y (-1, 0, 1). Estos puntos, también en la Figura
5.9.a, forman un triángulo, presentado en gris, inmerso en el plano considerado. La
ecuación, por elementos bien conocidos de Álgebra Lineal, se obtiene al resolver el
siguiente determinante:
x1
x2
x3 1
−1 −1 0 1
=0
0 −1 1 1
−1 0 1 1
⇔ − x1 − x2 + x3 − 2 = 0
(Ecuación 5.3.10)
Verifiquemos si el plano está bien orientado. Al sustituir el estado (-1, -1, 1) en el lado
izquierdo de la Ecuación 5.3.10 tenemos que
−(−1) − (−1) + 1 − 2 = 1 > 0
Por lo tanto el vector normal del plano apunta en dirección del estado (-1, -1, 1) lo cual
indica que se cuenta con la orientación correcta. Recordemos que la orientación es
importante ya que el valor proporcionado por Z1(x1, x2, x3) = − x1 − x2 + x3 − 2 será después
sometido a la función sign, de manera que se busca que la neurona proporcione valores tal
y como se presentan en la tabla de verdad de la función que se está modelando. Tenemos
entonces que los pesos de la neurona 1, que representa a la función ¬x1 ∧ ¬x2 ∧ x3, están
dados por: w1,1 = -1, w1,2 = -1, w1,3 = 1 y w1,0 = -2.
Para el caso de la función ¬x1 ∧ x2 ∧ ¬x3 se tiene que únicamente con el estado
(-1, 1, -1) ésta proporciona la salida 1. Véase la Figura 5.9.b. La función es evidentemente
linealmente separable. Se requiere un plano que separe al estado blanco (-1, 1, -1) de los
restantes estados negros. Usaremos de nueva cuenta tres puntos no colineales: (-1, 0, -1),
(0, 1, -1) y (-1, 1, 0):
144
Capítulo 5. La Red Madaline
x1 x2
−1 0
0
−1
1
x3 1
−1 1
=0
−1 1
1
0
1
⇔ x1 − x2 + x3 + 2 = 0
(Ecuación 5.3.11)
Veamos si el plano obtenido está correctamente orientado. Para ello sustituimos el lado
izquierdo de la Ecuación 5.3.11 con los valores (-1, 1, -1):
−1 − 1 + (−1) + 2 = −1 < 0
Se ha obtenido un número negativo, por lo tanto únicamente multiplicamos ambos lados de
la ecuación por -1 a fin de que esté orientado tal como requerimos. Se obtiene entonces la
ecuación final del plano:
− x1 + x2 − x3 − 2 = 0
(Ecuación 5.3.12)
Tenemos entonces una neurona 2 tipo Adaline que modela correctamente a la función
Booleana ¬x1 ∧ x2 ∧ ¬x3 y cuyos pesos están dados por w2,1 = -1, w2,2 = 1, w2,3 = -1 y
w2,0 = -2.
Veamos ahora el caso de la función Booleana x1 ∧ x2 ∧ x3. La Figura 5.9.c permite
apreciar claramente que es linealmente separable. Los vértices del triángulo en gris, de la
Figura 5.9.c, muestran los puntos a utilizar para definir el plano que separará al estado
blanco (1, 1, 1) de los restantes estados negros. Los tres puntos a usar son: (0, 1, 1), (1, 1, 0)
y (1, 0, 1). Entonces tenemos:
x1
x2
0
1
1
1
1
0
x3 1
1 1
=0
0 1
1 1
⇔ − x1 − x2 − x3 + 2 = 0
(Ecuación 5.3.13)
Verifiquemos si el plano está orientado correctamente:
−1 − 1 − 1 + 2 = −1 < 0
El plano requiere ser reorientado. Al multiplicar por -1 en ambos lados de la Ecuación
5.3.13 tenemos el plano final:
x1 + x2 + x3 − 2 = 0
(Ecuación 5.3.14)
145
Una Introducción al Cómputo Neuronal Artificial
Por tanto, la neurona 3 que modela la función x1 ∧ x2 ∧ x3 tendrá por pesos: w2,1 = 1,
w2,2 = 1, w2,3 = 1 y w2,0 = -2.
Tenemos ya bien definidas las 3 neuronas que formarán la capa de entrada de
nuestra red Madaline. Las neuronas 1, 2 y 3 proporcionarán respectivamente como salida
los escalares y1, y2 y y3. Estos formarán un vector de entrada para una neurona que modela a
la función y1 ∨ y2 ∨ y3. La salida de esta neurona será la salida final de la red. Por lo tanto
es claro que no requeriremos de capas ocultas. Apreciando la Figura 5.9.d se tiene que la
función y1 ∨ y2 ∨ y3 es linealmente separable. Siete de sus estados son de salida 1 (blancos)
mientras que el estado (-1, -1, -1) es el único de salida -1 (negro). Por lo tanto, usaremos los
puntos (-1, 0, -1), (-1, -1, 0) y (0, -1, -1) para encontrar la ecuación del plano que separa al
único estado negro de los estados blancos:
y1
y2
y3 1
−1 0 −1 1
=0
−1 −1 0 1
0 −1 −1 1
⇔ y1 + y2 + y3 + 2 = 0
(Ecuación 5.3.15)
Verifiquemos si el plano determinado está correctamente orientado:
−1 + (−1) + (−1) + 2 = −1 < 0
Recordemos que el estado (-1, -1, -1) es de salida -1. Por lo tanto la Ecuación 5.3.15 no
requiere modificación alguna. Tenemos que los pesos de la única neurona de salida de
nuestra red Madaline son: w2,1 = 1, w2,2 = 1, w2,3 = 1 y w2,0 = 2. En la Figura 5.10 se
presenta la red que precisamente nos permite modelar la función de la Ecuación 5.3.1.
146
Capítulo 5. La Red Madaline
x2
(-1,1,-1)
(1,1,-1)
x2
x3
(-1,1,-1)
(0,1,-1)
(1,1,-1)
x3
(-1,1,0)
(1,1,1)
(-1,1,1)
(1,1,1)
(-1,1,1)
(-1,0,-1)
x1
(-1,0,1)
(1,-1,-1)
(-1,-1,-1)
x1
(-1,-1,-1)
(1,-1,-1)
(-1,-1,0)
(-1,-1,1)
(-1,-1,1)
(1,-1,1)
(0,-1,1)
(1,-1,1)
b)
a)
x2
(-1,1,-1)
(1,1,-1)
y2
x3
(-1,1,-1)
(1,1,-1)
y3
(1,1,0)
(1,1,1)
(-1,1,1)
(-1,-1,-1)
(1,1,1)
(-1,1,1)
(0,1,1)
(-1,0,-1)
(1,0,1)
x1
y1
(-1,-1,-1)
(1,-1,-1)
(0,-1,-1)
(1,-1,-1)
(-1,-1,0)
(-1,-1,1)
(1,-1,1)
(-1,-1,1)
(1,-1,1)
c)
d)
Figura 5.9. Visualización en el espacio 3D de los estados y las salidas de las funciones Booleanas
a) ¬x1 ∧ ¬x2 ∧ x3, b) ¬x1 ∧ x2 ∧ ¬x3, c) x1 ∧ x2 ∧ x3, y d) y1 ∨ y2 ∨ y3. Los triángulos en gris están inmersos en
los planos que separan a los estados negros de los estados blancos. Sus vértices son utilizados para determinar
sus correspondientes ecuaciones y orientaciones (véase el texto para detalles).
147
Una Introducción al Cómputo Neuronal Artificial
Adaline 1
x1
z1 = − x1 − x2
+ x3 − 2
y1 =
sign( z1 )
Adaline 4
Adaline 2
x2
z2 = − x1 + x2
− x3 − 2
y2 =
sign( z2 )
z4 = y1 + y2
+ y3 + 2
y4 =
y4
sign( z4 )
Adaline 3
x3
z3 = x1 + x2
+ x3 − 2
y3 =
sign( z3 )
Figura 5.10. Red Madaline que modela a la función Booleana
f(x1, x2, x3) = (¬x1 ∧ ¬x2 ∧ x3) ∨ (¬x1 ∧ x2 ∧ ¬x3) ∨ (x1 ∧ x2 ∧ x3).
En esta Sección hemos descrito una serie de pasos a seguir a fin de que, en primer
lugar, una función Booleana, dada su tabla de verdad, sea descrita en términos de las
variables involucradas y los conectivos lógicos AND, OR y NOT. Posteriormente, en
segundo lugar, y basado en el hecho de que tales conectivos son linealmente separables, es
que hemos establecido una metodología para construir una red Madaline que dé solución al
problema del modelado de funciones Booleanas no linealmente separables como el XOR.
En la Sección 4.2 determinamos que una función Booleana de n variables tiene
exactamente 2n posibles estados. Un punto interesante es que si estos estados son
considerados puntos en el espacio n-Dimensional entonces es fácil apreciar que tales puntos
corresponden con los vértices de un Hipercubo n-Dimensional. Véase la Figura 5.11.
Cuando n = 1 se tienen funciones Booleanas de una variable con 2 estados: -1 y 1. Estos
dos puntos sobre la línea recta definen a un hipercubo unidimensional, es decir, un
segmento. Véase la Figura 5.11.a. Cuando n = 2 estamos considerando funciones Boolenas
de dos variables con 4 posibles estados: (-1, -1), (1, -1), (-1, 1) y (1, 1). Estos cuatro puntos
describen a un hipercubo bidimensional, o mejor dicho, un cuadrado centrado en el origen
(Figura 5.11.b). Si ahora consideramos a las funciones Booleanas de n = 3 variables
entonces tenemos que los estados corresponden a los 8 vértices de un cubo centrado en el
origen (Figura 5.11.c). Nótese que en párrafos anteriores utilizamos elementos visuales
para determinar de manera inmediata las rectas o planos requeridos para separar a los
estados con salida 1 de los estados con salida -1. O de manera equivalente, buscábamos
rectas o planos que nos permitieran particionar de manera adecuada a nuestros cuadrados o
cubos, respectivamente.
Ahora consideremos el caso de una función Booleana con n = 4 variables. Ello
implica que debemos tomar en cuenta 24 = 16 posibles estados. Tales estados corresponden
a los vértices de un hipercubo tetradimensional. Véase la Figura 5.11.d. Si la
correspondiente función es linealmente separable debemos determinar un hiperplano
tridimensional inmerso en el espacio de 4 dimensiones que separe apropiadamente a los
148
Capítulo 5. La Red Madaline
estados. Cuando n = 5 entonces lidiamos con una función con 5 variables y 25 = 32 estados.
El objetivo en esta instancia es encontrar un hiperplano tetradimensional inmerso en el
espacio de 5 dimensiones. La situación que claramente surge es el hecho de que el número
de estados crece de manera exponencial conforme consideramos más variables. Una
función Booleana de 10 variables cuenta con 210 = 1,024 estados que corresponden a los
vértices de un hipercubo de 10 dimensiones. Conceptualmente el problema es claro, dada
una función de n variables determinar el hiperplano (n-1)-Dimensional inmerso en \ n que
demuestre que la función es efectivamente linealmente separable. Es claro que el uso de
auxiliares visuales también se complica. Existen metodologías variadas para visualizar
espacios hiperdimensionales, sin embargo, debe entenderse que lo que se “ve” son
únicamente proyecciones, “sombras”, de los elementos inmersos en tales hiperespacios, por
lo que existirá pérdida de información. Ahora bien, es posible dejar a un lado la
visualización y concentrarnos en una búsqueda de hiperplanos basada en el hecho de que
los vértices de un hipercubo serán siempre particionados en dos conjuntos: los vértices que
corresponden a estados con salida 1 y los vértices que corresponden a estados con salida -1.
Esto en un momento puede original un problema de índole combinatoria. En \ 2 se
requieren dos puntos para definir una recta (un hiperplano unidimensional), en \ 3 se
requieren tres puntos para definir un plano (un hiperplano bidimensional), en \ 4 se
requieren cuatro puntos para determinar la ecuación de un hiperplano tridimensional. Es
claro que, en general, en \ n se requieren exactamente n puntos para definir un hiperplano
(n-1)-Dimensional. Considerando que en nuestro caso los puntos se tomarían de los 2n
vértices de nuestros hipercubos, entonces tendríamos que el número de posibilidades
analizar es a lo más
§ 2n ·
(2n )!
¨ ¸= n
© n ¹ (2 − n)!n !
(Ecuación 5.3.16)
Retomando el caso n = 10, tendríamos en consecuencia que el número de subconjuntos de
10 vértices, para formar hiperplanos candidatos, tomados del conjunto de 1,024 vértices del
hipercubo de 10 dimensiones es:
§ 210 ·
(210 )!
1, 024!
=
=
= 334,265,867,498,622,145,619,456
¨ ¸
10
(2
10)!10!
(1,
024
10)!10!
−
−
10
© ¹
En la práctica es claro que hemos de considerar el modelado de funciones con cientos de
variables de entrada.
149
Una Introducción al Cómputo Neuronal Artificial
x2
(-1,1)
-1
(1,1)
x1
x1
1
(-1,-1)
a)
(1,-1)
b)
x2
(-1,1,-1)
x3
(1,1,-1)
(1,1,1)
(-1,1,1)
x1
(-1,-1,-1)
(1,-1,-1)
(-1,-1,1)
(1,-1,1)
c)
x2
x4
(1,1,-1,-1)
(-1,1,-1,-1)
x3
(-1,1,-1,1)
(-1,1,1,-1)
(1,1,-1,1)
(1,1,1,-1)
(1,1,1,1)
(-1,1,1,1)
(-1,-1,-1,-1)
(1,-1,-1,-1)
x1
(-1,-1,-1,1)
(1,-1,-1,1)
(-1,-1,1,-1)
(1,-1,1,-1)
(-1,-1,1,1)
(1,-1,1,1)
d)
Figura 5.11. Los estados de las funciones Booleanas de 1 a 4 variables vistos como los vértices de hipercubos.
a) Un hipercubo 1D: un segmento (2 vértices/estados). b) Un hipercubo 2D: un cuadrado (4 vértices/estados).
c) Un hipercubo 3D: un cubo (8 vértices/estados). d) Un Hipercubo 4D (16 vértices/estados).
150
Capítulo 5. La Red Madaline
Los resultados anteriores vienen a establecer que la metodología presentada en esta
Sección, si bien es sumamente intuitiva e ilustrativa en lo que concierne al problema del
ajuste de pesos de una red Madaline, en la práctica puede no ser muy recomendada. Lo que
si debemos reconocer es que nos ha proporcionado elementos contundentes para verificar
que efectivamente el uso de varias neuronas permite el modelado de funciones Booleanas
no linealmente separables, tales como el XOR. También nos ha permitido visualizar, al
menos en el caso 2D, las particiones del plano que inducen los umbrales asociados a cada
neurona y las correspondientes reglas de separación entre estados con salida 1 y estados con
salida -1.
Este Capítulo nos ha planteado claramente los retos a considerar en lo que atañe a
las metodologías para el ajuste de pesos en Redes Neuronales Multicapa. En el siguiente
Capítulo presentaremos por fin al Algoritmo de Retropropagación, que representa una
solución eficiente y fácil de implementar para el ajuste de pesos en redes formadas por
neuronas del tipo Perceptrón.
151
Una Introducción al Cómputo Neuronal Artificial
152
Una Introducción al Cómputo Neuronal Artificial
6. Redes de
Perceptrones
Una Introducción al Cómputo Neuronal Artificial
154
Capítulo 6. Redes de Perceptrones
Hemos llegado al punto en el cual estamos listos para abordar el estudio de las
Redes Neuronales formadas por Perceptrones. En particular, hemos de considerar el
análisis y justificación del popular Algoritmo de Retropropagación, el cual representa una
de las opciones más eficientes y fáciles de implementar para el entrenamiento de este tipo
de Redes Neuronales. Procederemos en primer lugar al reconsiderar, en la Sección 6.1, a la
neurona de tipo Perceptrón al describir la Regla de Rosenblatt para la actualización de sus
pesos. Posteriormente, en la Sección 6.2, presentaremos la Demostración del Teorema de
Convergencia del Perceptrón. Este importante resultado servirá como punto de partida para
entender los fundamentos detrás del proceso de ajuste de pesos por parte del Algoritmo de
Retropropagación. En la Sección 6.3 describiremos el mecanismo de corrección de pesos,
propiamente por el Algoritmo de Retropropagación, en una Red compuesta por
Perceptrones bajo la suposición de que ésta se forma por una única capa oculta. También
justificaremos de manera formal las reglas de actualización establecidas y analizaremos los
aspectos relacionados con la convergencia de los pesos de las neuronas que forman la red.
En la Sección 6.4 presentaremos la versión generalizada del Algoritmo de
Retropropagación en el sentido de dar solución al problema del ajuste de pesos para redes
formadas por más de dos capas ocultas. Será hasta la Sección 6.5 en donde haremos
mención de un ejemplo de aplicación del Algoritmo de Retropropagación para la
solución/modelado de un problema mediante redes formadas por Perceptrones.
6.1 La Regla de Rosenblatt
Mencionábamos en las Secciones 1.4 y 4.2, que en 1958 el psicólogo Frank
Rosenblatt presenta a la neurona tipo Perceptrón. De hecho, en ese mismo año, Rosenblatt
introdujo un mecanismo de aprendizaje, un algoritmo de entrenamiento, para el Perceptrón
que hoy en día se conoce como Regla de Rosenblatt. El punto fundamental es que la Regla
viene acompañada con un Teorema que sustenta el hecho de que los pesos correctos de la
neurona serán siempre encontrados bajo el supuesto de que efectivamente existen tales
pesos para resolver el problema dado. Planteamos en primer lugar la Regla de Rosenblatt y
posteriormente, en la siguiente Sección, efectuaremos la demostración de tal Teorema.
Considérese un Perceptrón que recibe como entrada un vector E en \ n dado por:
ª I1 º
«I »
E = « 2»
«#»
« »
¬ In ¼
(Ecuación 6.1.1)
Supongamos que la neurona proporciona como salida un escalar O ∈ \ . Sea g una función
continua y diferenciable en (-∞, ∞). Se tiene que g es de hecho la Función de Activación
(Véase la Sección 4.1). Cada uno de los componentes del vector de entrada E estará
155
Una Introducción al Cómputo Neuronal Artificial
asociado a un único peso de la neurona. La relación entre el vector E y los pesos, de manera
que se produce a partir de éstos un escalar ent, está dada por la ya conocida Sumatoria de
Salida del Perceptrón:
n
ent = ¦ w j I j
(Ecuación 6.1.2)
j =1
La salida O del Perceptrón se produce al aplicar la Función de Activación g sobre el escalar
ent:
§ n
·
O = g(ent) = g ¨ ¦ w j I j ¸
© j =1
¹
(Ecuación 6.1.3)
La Figura 6.1 presenta esquemáticamente a todos los elementos del Perceptrón que hemos
descrito.
W1
W2
I2
n
ent = ¦ w j I j
ent
j =1
In
O = g (ent )
O
Salida
Entradas
I1
Wn
Figura 6.1. Representación Esquemática de un Perceptrón.
Sea T la salida que se espera proporcione el Perceptrón para el vector de entrada E.
Sabemos que el proceso de ajuste de los pesos wj de la neurona busca minimizar la
diferencia entre la salida proporcionada por ésta y la salida esperada. Es decir, se busca
optimizar:
§ n
·
Err = T – O = T – g ¨ ¦ w j I j ¸
© j =1
¹
(Ecuación 6.1.4)
Ahora bien, definamos los elementos detrás de la Regla de Rosenblatt.
Primeramente, se debe contar con un conjunto de pesos iniciales para la neurona. Por lo
regular éstos son inicializados con valores aleatorios, comúnmente en el intervalo (-1, 1)
(Sección 4.3). Tenemos que el proceso de aprendizaje se dividirá en Épocas. En cada
Época se presentan a la neurona todos los vectores de entrada en el conjunto de
entrenamiento. Es claro que la noción de Época es la misma que la de Presentación del
156
Capítulo 6. Redes de Perceptrones
Conjunto de Entrenamiento que planteamos desde la Sección 3.3.1. Por cada vector de
entrada E, se determina la diferencia entre la salida generada por el Perceptrón O y la salida
esperada T (Ecuación 6.1.4). De acuerdo a esa diferencia es que los pesos son actualizados.
Nótese que el valor de Err = T – O puede ser positivo o negativo. Es claro que si el
error, Err, es positivo entonces la salida O de la neurona debe ser incrementada. Por otro
lado, si el error es negativo entonces la salida O de la neurona debe reducirse. De manera
más específica, y observando la Ecuación 6.1.2, se tiene que el escalar de entrada Ij se
multiplica con el j-ésimo peso wj. Tenemos entonces el siguiente par de observaciones:
• Si Ij es positivo y el peso wj aumenta su valor entonces la salida O también aumentará
su valor.
• Si Ij es negativo y el peso wj aumenta su valor entonces la salida O disminuirá su valor.
En ambos casos podemos concluir que para obtener el ajuste apropiado del peso wj se tiene
que precisamente el valor de wj debe ser incrementado. Esto es interesante porque ya sea
que la salida O se requiera aumentar o reducir, los pesos deben ser actualizados mediante
una suma. Para tal efecto Rosenblatt propuso la siguiente regla de actualización de pesos:
wj = wj + α⋅Err⋅Ij
j = 1, 2, …, n
(Ecuación 6.1.5)
Donde α es la bien conocida constante positiva denominada, en la Sección 4.3, Coeficiente
de Aprendizaje. La Ecuación 6.1.5 es de hecho la Regla de Rosenblatt. Nótese su similitud
con la regla de actualización presentada en la Sección 4.3 la cual estaba basada en
búsqueda del vector gradiente mediante Descenso Escalonado.
El Algoritmo 6.1 es una implementación de la Regla de Rosenblatt. Éste recibe
cuatro entradas:
• Una matriz E de tamaño N × n, donde N es el número de vectores de entrada en el
conjunto de entrenamiento y n su dimensionalidad. Cada renglón de la matriz es
precisamente un vector de entrada.
• Un arreglo T de N elementos. Contiene los escalares que se espera la neurona
proporcione como salida (dados los correspondientes vectores de entrada).
• El coeficiente de aprendizaje α.
• Un entero L que indica el número de épocas, o presentaciones del conjunto de
entrenamiento, que el algoritmo efectuará.
El Algoritmo 6.1 efectúa los procedimientos antes mencionados al inicializar un vector de
pesos W con valores aleatorios. Posteriormente, en cada presentación del conjunto de
entrenamiento, cada vector de entrada en la matriz E es enviado a la neurona donde se
calcula el valor de su sumatoria de salida el cual es guardado en la variable ent. Se invoca
entonces a la Función de Activación g la cual debe ser continua y diferenciable en (-∞, ∞)
por razones que clarificaremos en las siguientes Secciones. Se tiene entonces la salida O de
la neurona. Se aplica la Ecuación 6.1.4 para obtener el error existente entre la salida O y la
salida esperada T. Por último, se tiene la actualización del vector de pesos W haciendo uso
del valor actual en la variable Err, el coeficiente de aprendizaje α y cada uno de los
componentes del vector de entrada actual.
157
Una Introducción al Cómputo Neuronal Artificial
Algoritmo 6.1. Implementación de la Regla de Rosenblatt
para el entrenamiento de un Perceptrón.
Procedure RosenblattRule
(Matrix E[1, …, N][1, …, n], Array T[1, …, N], Real α, Integer L)
// Se asignan valores aleatorios en (-1, 1) al vector de pesos.
W = new Array[1,…,n]
for j = 1 until n do
W[j] = Random( )
end-of-for
// Se lleva a efecto la t-ésima época.
for t = 1 until L do
for k = 1 until N do
// El k-ésimo vector de entrada es enviado a la neurona.
Real ent = 0
for j = 1 until n do
ent = ent + W[j] * E[k][j]
end-of-for
// Se aplica la función de activación
// y se obtiene la salida de la neurona.
Real O = g(ent)
// Se calcula el error entre la salida esperada
// y la salida de la neurona.
Real Err = T[k] – O
// Se actualiza el vector de pesos.
for j = 1 until n do
W[j] = W[j] + α * Err * E[k][j]
end-of-for
end-of-for
end-of-for
// Se retorna como salida el vector de pesos obtenido.
return W
end-of-procedure
Como se podrá observar, la Regla de Rosenblatt es, desde el punto de vista
algorítmico, muy simple. Pero es más interesante el hecho de que precisamente Rosenblatt
demostró que un Perceptrón convergerá a un conjunto de pesos que modela adecuadamente
a los elementos del conjunto de entrenamiento siempre y cuando éstos representen una
función linealmente separable. A tal proposición se le conoce como el Teorema de
Convergencia del Perceptrón. En la siguiente Sección abordaremos precisamente la
demostración del enunciado.
158
Capítulo 6. Redes de Perceptrones
6.2 Teorema de Convergencia del Perceptrón
Teorema:
Si existe un vector de pesos W* tal que para todo vector de entrada E y su correspondiente
salida T, en el conjunto de entrenamiento, se tiene que g(W*⋅E) = T
entonces
para cualquier vector inicial de pesos se tiene que la regla de aprendizaje del Perceptrón
convergerá a un vector de pesos (no necesariamente W*) tal que la neurona proporcionará
la salida correcta para todo vector de entrada en el conjunto de entrenamiento. Además, la
convergencia se tendrá en un número finito de pasos.
El enunciado establece en primer lugar que debemos suponer la existencia de un
vector de pesos W* tal que mediante éste el Perceptrón siempre proporcionará la salida
correcta para todo vector de entrada en el conjunto de entrenamiento. Ahora bien, debemos
demostrar que para cualquier vector de pesos inicial W, y al aplicar la Regla de Rosenblatt
tal como lo especifica el Algoritmo 6.1, encontraremos un vector de pesos tal que con éste
la neurona proporcionará siempre la salida correcta para todo vector de entrada en el
conjunto de entrenamiento. También debemos probar que el número de pasos requeridos,
para encontrar a tal vector de pesos, es finito.
El enunciado nos dice también que el vector de pesos que encontremos no
necesariamente es igual al vector de pesos W* que presuponemos existe. Esto implica que
de hecho los vectores de pesos que se obtienen mediante la Regla de Rosenblatt no son
únicos, y en consecuencia, pueden existir vectores de pesos diferentes que nos permiten
resolver el mismo problema. Esto es consistente con el hecho de que los problemas con los
cuales puede lidiar un Perceptrón son únicamente los linealmente separables.
Efectivamente, esta es una presuposición que debemos tomar en cuenta ya que aunque no
se menciona de manera explícita en el enunciado del Teorema, si la requeriremos para
efectuar su demostración. La sumatoria de salida del Perceptrón, en términos geométricos,
describe a un hiperplano que separará a los vectores de entrada en dos conjuntos. En este
sentido, por ejemplo, vale la pena recordar el modelado de funciones Booleanas
linealmente separables. Nuestros hiperplanos separaban a los vectores de entrada que
correspondían a los estados con salida 1 de los vectores de entrada que correspondían a los
estados con salida -1. Nos debe ser claro entonces que es posible la existencia de diferentes
hiperplanos, y en consecuencia diferentes vectores de pesos, que nos permitan cumplir con
este mismo fin haciendo que la neurona proporcione siempre las salidas correctas.
Habiendo efectuado la mención de las consideraciones a tomar en cuenta, ahora
procederemos a demostrar el Teorema de Convergencia del Perceptrón.
159
Una Introducción al Cómputo Neuronal Artificial
En primer lugar asumamos que los vectores de entrada para la neurona fueron
originados por dos clases linealmente separables. Llamemos a estas clases C1 y C2. Sea χ1
el subconjunto de los vectores de entrada que pertenecen a la clase C1 y sea χ2 el
subconjunto de los vectores de entrada que pertenecen a la clase C2. Es claro que el
conjunto de entrenamiento estará dado por χ1 ∪ χ2.
Dados los conjuntos χ1 y χ2 para entrenar al Perceptrón, se tiene que el
entrenamiento se encarga de ajustar su vector de pesos W tal que C1 y C2 sean linealmente
separables, o en otras palabras, el hiperplano asociado a la sumatoria de salida de
Perceptrón separe apropiadamente a C1 y C2.
Se espera que, una vez finalizado el entrenamiento, el vector de pesos W, para todo
vector de entrada E, satisfaga las siguientes dos condiciones:
•
•
Si E ∈ C1 entonces W⋅E > 0.
Si E ∈ C2 entonces W⋅E < 0.
Es decir, que los vectores en la clase C1 serán aquellos hacia los cuales apunte el vector
normal del hiperplano definido por la sumatoria de salida del Perceptrón. O bien, los
vectores de entrada en C1 estarán por encima del hiperplano, y en consecuencia, los
vectores en C2 estarán por debajo de tal hiperplano.
Nótese que hemos establecido las propiedades que deberá cumplir el vector de
pesos W una vez finalizado el entrenamiento. Ahora se debe establecer una metodología
para su construcción. Considérese el siguiente procedimiento:
a) Sea Wk el vector de pesos que actualmente tiene la neurona.
b) Considérese al k-ésimo vector de entrada, Ek, en el conjunto de entrenamiento. Si Ek es
correctamente clasificado ello implica que la neurona determinó acertadamente que
Ek ∈ χ1 o bien que Ek ∈ χ2. Por lo tanto, se aplicará una “corrección” a Wk y se obtendrá
el vector de pesos “actualizado” Wk+1:
b.1) Wk+1 = Wk
c) De lo contrario, si Ek fue clasificado de manera incorrecta por el Perceptrón, entonces el
vector de pesos Wk debe ser apropiadamente corregido y se obtiene por lo tanto el
nuevo vector de pesos Wk+1. Debemos manejar dos posibilidades de acuerdo al signo de
la sumatoria de salida Wk⋅Ek:
c.1) Ek ∈ χ2 pero Wk⋅Ek > 0, lo que implica que el vector fue incorrectamente
ubicado en χ1. Entonces aplicamos la corrección:
ƒ Wk+1 = Wk – Ek
c.2) Ek ∈ χ1 pero Wk⋅Ek < 0, lo que implica que el vector fue incorrectamente
ubicado en χ2. Entonces:
ƒ Wk+1 = Wk + Ek
160
Capítulo 6. Redes de Perceptrones
Asúmase, sin pérdida de generalidad, que se tiene el vector inicial de pesos W1 = 0,
es decir, el vector cero. Es claro que para todo vector de entrada Ek,
k = 1, 2, 3, …, Card(χ1), contenido precisamente en la clase χ1, se tiene que el Perceptrón,
equipado con los pesos en W1, clasifica incorrectamente a los vectores en χ1 ya que para
todos éstos se esperaría que W1⋅Ek > 0, lo cual evidentemente no se cumple (lo mismo
sucede con los vectores en la clase χ2). Nótese que de hecho W1⋅E1 = 0, pero sabemos en
que clase E1 debe ser ubicado. Usaremos entonces la regla de corrección Wk+1 = Wk + Ek.
Lo que haremos es que a partir del vector de pesos inicial W1 = 0 obtendremos, usando los
vectores de entrada en χ1, un vector Wk+1 que permita que la neurona los clasifique
correctamente. El vector Wk+1 se obtiene de manera iterativa:
•
•
•
•
•
•
•
W1 = 0
W2
= W1 + E1
W3
= W2 + E2
W4
= W3 + E3
…
(k-1)-ésima corrección: Wk
= Wk-1 + Ek-1
k-ésima corrección:
Wk+1 = Wk + Ek
Vector de pesos inicial:
Primer corrección:
Segunda corrección:
Tercer corrección:
= (0) + E1 = E1
= (E1) + E2
= (E1 + E2) + E3
= (E1 + E2 + … + Ek-2) + Ek-1
= (E1 + E2 + … + Ek-2 + Ek-1) + Ek
Recordemos que se presupone la existencia del vector de pesos W* el cual garantiza
que la neurona clasificará correctamente a todos los vectores de entrada y que se asume que
las clases C1 y C2 son linealmente separables. Entonces, se tiene que para todo vector Ek en
el conjunto de entrenamiento el vector W* efectivamente satisface las siguientes dos
condiciones:
•
•
Si Ek ∈ χ1 entonces W*⋅Ek > 0.
Si Ek ∈ χ2 entonces W*⋅Ek < 0.
En un problema linealmente separable tenemos que las salidas del Perceptrón deben
permitir inferir a cual de las dos clases, C1 o C2, pertenece un vector de entrada. Por ello
mismo, la salida de la neurona nos dice si un vector E está en χ1 ⊂ C1 o bien si está en
χ2 ⊂ C2. En este punto cabe hacer la aclaración de que C1 y C2 son particiones del espacio
n-Dimensional de tal forma que cuentan con un número infinito de elementos. C1 es el
conjunto de todos los puntos en \ n que están por encima del umbral definido por la
sumatoria de salida del Perceptrón, y por otro lado, C2 es el conjunto de todos los puntos
que están por debajo del umbral. De allí que hemos establecido, incluso en párrafos
anteriores, que χ1 ⊂ C1 y χ2 ⊂ C2.
Ahora definamos al conjunto χ'2 de la siguiente manera:
χ'2 = {(-1)E ∈ \ n : E ∈ χ2}
161
Una Introducción al Cómputo Neuronal Artificial
Es claro que χ'2 se conforma por todos los vectores en χ2 pero con dirección opuesta. Es
entonces evidente que los vectores en χ'2 están en C1 (los vectores en χ2 están en C2). Esto
tiene como consecuencia que el conjunto de entrenamiento del Perceptrón puede ser
redefinido como:
χ1 ∪ χ'2
Recordemos que el vector pesos W* satisface las condiciones:
• W*⋅Ek > 0 si Ek ∈ χ1
• W*⋅Ek < 0 si Ek ∈ χ2
Pero ahora, con la redefinición del conjunto de entrenamiento como χ1 ∪ χ'2 tenemos
entonces que las condiciones anteriores son equivalentes a la única condición:
• W*⋅Ek > 0 si Ek ∈ χ1 ∪ χ'2
Ello se debe a que si Ek está en χ'2 entonces W*⋅Ek > 0, pero Ek = (-1)E’k donde E’k está en
χ2 y por tanto W*⋅E’k < 0. Entonces tenemos que únicamente se requiere una sola regla de
actualización, expresada en términos de una suma, para efectuar correcciones asociadas a
vectores ubicados en χ1 o bien en χ2. El objetivo del conjunto χ'2 es únicamente el de
permitir unificar las reglas de corrección especificadas en los pasos c.1 y c.2 del
procedimiento de actualización del vector de pesos presentado previamente. A partir de este
punto supondremos que todos los vectores de entrada están en χ1 ∪ χ'2.
Se usará al vector de pesos W* para asegurar que la regla de actualización de pesos,
efectivamente permite encontrar un vector de pesos tal que la neurona clasifique
correctamente a todos los vectores de entrada del conjunto de entrenamiento. Sea γ1
definido como:
γ 1 = min {W * ⋅Ek }
(Ecuación 6.2.1)
Es decir, γ1 es el mínimo escalar elegido a partir de todos los productos punto entre W* y
cada vector de entrada Ek en el conjunto de entrenamiento.
Previamente se verificó que dado el vector de pesos inicial W1 = 0 el vector Wk+1
estaba dado por:
Wk+1 = Wk + Ek = (E1 + E2 + … + Ek-1) + Ek
(Ecuación 6.2.2)
Al efectuar un producto punto con el vector W* en ambos lados de la Ecuación 6.2.2 se
tiene:
W*⋅Wk+1 = W*⋅(E1 + E2 + … + Ek-1 + Ek)
162
(Ecuación 6.2.3)
Capítulo 6. Redes de Perceptrones
En el lado derecho de la Ecuación 6.2.3 haremos uso de la propiedad distributiva del
producto punto de vectores. Por lo tanto obtenemos:
W*⋅Wk+1 = W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek
(Ecuación 6.2.4)
Por la definición de γ1 (Ecuación 6.2.1) se tiene que:
W*⋅Wk+1 = W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek ≥ γ1k
⇔ W*⋅Wk+1 ≥ γ1k
Ello se debe a que cada término del lado derecho de la Ecuación 6.2.4 es mayor o igual a
γ1. Se tienen en total k términos y en consecuencia W*⋅Wk+1 ≥ γ1k. Si elevamos al cuadrado
ambos lados de la desigualdad tenemos que ésta claramente se preserva:
W * ⋅W
k +1
≥ γ 1k
⇔ (W * ⋅W k +1 ) ≥ γ 12 k 2
2
Ahora bien, por la desigualdad de Cauchy-Schwarz (Sección 2.4) tenemos que:
||W*||2⋅||Wk+1||2 ≥ (W*⋅Wk+1)2
Entonces:
W * ⋅ W k +1 ≥ (W * ⋅W k +1 ) ≥ γ 12 k 2
2
2
2
Al aplicar la propiedad transitiva del operador ≥ relacionamos directamente al extremo
izquierdo con el extremo derecho de la desigualdad:
W * ⋅ W k +1 ≥ γ 12 k 2
2
2
Nótese que el vector de pesos W* es diferente del vector cero. De lo contrario, con
cualquier vector de entrada E se tendría que W*⋅E = 0, lo que contradice los supuestos
establecidos respecto a W* en párrafos anteriores. De la desigualdad anterior multiplicamos
1
ambos lados por
y obtenemos:
2
W*
2
W k +1 ≥
γ 12 k 2
W*
2
163
Una Introducción al Cómputo Neuronal Artificial
Esta desigualdad nos indica que la magnitud al cuadrado del vector de pesos que se está
calculando crece con un factor k2, donde k es el número de veces que éste ha sido
actualizado. La misma desigualdad es también una Cota Inferior. Ésta nos dice que una vez
efectuadas k actualizaciones del vector de pesos, su magnitud al cuadrado será mayor o
γ 2k 2
igual al cociente 1 2 .
W*
Ahora se debe establecer una Cota Superior para el vector de pesos a fin de verificar
que los valores de sus componentes no crecen indefinidamente. De la Ecuación 6.2.2
tenemos que, dado el vector de pesos inicial W1 = 0, el vector Wk+1 esta dado por:
Wk+1 = (E1 + E2 + … + Ek-1) + Ek
⇔ Wk+1 = Wk + Ek
Sabemos que Wk+1 surge de aplicar una corrección al vector de pesos Wk. Ello implica que
con el vector de entrada Ek se obtuvo Wk⋅Ek < 0 (recuérdese que si el vector hubiese sido
clasificado correctamente se habría obtenido Wk⋅Ek > 0). Tenemos entonces que:
Wk+1 = Wk + Ek
⇔ ||Wk+1||2 = ||Wk + Ek||2
⇔ ||Wk+1||2 = ||Wk||2 + 2Wk⋅Εk + ||Εk||2
(Ecuación 6.2.5)
La Ecuación 6.2.5 surge del hecho de que para cualesquiera vectores u y v en \ n el
cuadrado de la magnitud de su suma, ||u + v||2 es igual a ||u||2 + 2u⋅v + ||v||2 (nótese la
analogía existente entre esta expresión con el desarrollo del binomio
(a + b)2 = a2 + 2ab + b2, a, b ∈ \ ). Dado que presuponemos que Wk⋅Εk < 0 entonces es
claro que -2Wk⋅Εk > 0. Al sumar precisamente -2Wk⋅Εk en ambos lados de la Ecuación 6.2.5
se obtiene:
||Wk+1||2 - 2Wk⋅Εk = ||Wk||2 + ||Εk||2
(Ecuación 6.2.6)
Recalcamos que - 2Wk⋅Εk es un número positivo. Entonces debe ser claro que:
||Wk+1||2 ≤ ||Wk+1||2 - 2Wk⋅Εk = ||Wk||2 + ||Εk||2
Y por transitividad se tiene la siguiente desigualdad:
||Wk+1||2 ≤ ||Wk||2 + ||Εk||2
Recordemos que el vector Wk surge de la corrección aplicada al vector de pesos Wk-1 con el
vector de entrada Ek-1. Es más, Wk-1 surge de actualizar al vector Wk-2 con el vector de
entrada Ek-2, y así sucesivamente hasta llegar a la actualización del vector de pesos inicial
164
Capítulo 6. Redes de Perceptrones
W1 usando el vector de entrada E1. Tomando esto en cuenta, desarrollemos el lado derecho
de la desigualdad anterior:
Wk
2
+ Ek
2
2
2
= Wk −1 + Ek −1 + Ek
(Wk = Wk −1 + Ek −1 )
2
2
= Wk −1 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
2
2
2
= Wk − 2 + Ek − 2 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
2
2
2
(Wk −1 = Wk − 2 + Ek − 2 )
2
= Wk − 2 + 2Wk − 2 ⋅ Ek − 2 + Ek − 2 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
=
2
"
#
2
= W2 + E2 + ... +
2
2
2
2
2
2
2
2
2
2
Wk − 2 + 2Wk − 2 ⋅ Ek − 2 + Ek − 2 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
2
(W3 = W2 + E2 )
2
= W2 + 2W2 ⋅ E2 + E2 + ... +
2
2
Wk − 2 + 2Wk − 2 ⋅ Ek − 2 + Ek − 2 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
2
2
= W1 + E1 + 2W2 ⋅ E2 + E2 + ... +
2
2
Wk − 2 + 2Wk − 2 ⋅ Ek − 2 + Ek − 2 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
2
2
(W2 = W1 + E1 )
2
= W1 + 2W1 ⋅ E1 + E1 + 2W2 ⋅ E2 + E2 + ... +
2
2
Wk − 2 + 2Wk − 2 ⋅ Ek − 2 + Ek − 2 + 2Wk −1 ⋅ Ek −1 + Ek −1 + Ek
k −1
k
j =1
j =1
= W1 + ¦ 2W j ⋅ E j + ¦ E j
2
k −1
k
j =1
j =1
= ¦ 2W j ⋅ E j + ¦ E j
2
2
(Dado que W1 = 0)
Concretizando:
Wk
2
+ Ek
2
k −1
k
j =1
j =1
= ¦ 2W j ⋅ E j + ¦ E j
2
(Ecuación 6.2.7)
Ahora bien, supongamos que para todo vector de pesos Wj, j = 1, …, k, se obtuvo que éste
clasificaba incorrectamente al vector Ej, es decir, en su momento se detectó que Wj⋅Ej < 0
(si el vector hubiese sido clasificado correctamente se habría obtenido Wj⋅Ej > 0). Ello
165
Una Introducción al Cómputo Neuronal Artificial
implica por un lado que tuvo que aplicarse una corrección a Wj a fin de obtener su versión
actualizada Wj+1. Pero por otro lado tenemos que entonces en la Ecuación 6.2.7 la suma
k −1
¦ 2W
⋅ Ej
j
j =1
es de hecho un número negativo. Recordemos que la Ecuación 6.2.7 es el lado derecho de
la desigualdad:
||Wk+1||2 ≤ ||Wk||2 + ||Εk||2
2
⇔ Wk +1 ≤ Wk
2
2
+ Ek
k −1
k
= ¦ 2W j ⋅ E j + ¦ E j
j =1
j =1
k −1
k
j =1
j =1
⇔ Wk +1 ≤ ¦ 2W j ⋅ E j + ¦ E j
2
2
2
Ahora bien, incorporando la observación de que Wj⋅Ej < 0 para j = 1, 2, …, k, entonces
podemos establecer:
Wk +1
2
k −1
k
¦ 2W j ⋅ E j + ¦ E j
≤
j =1
2
j =1
≤
k
¦
Ej
2
j =1
Y aplicando la propiedad transitiva del operador ≤ tenemos:
k
Wk +1 ≤ ¦ E j
2
2
j =1
Sea γ2 una constante positiva definida como:
{
γ 2 = max Ek
2
}
(Ecuación 6.2.8)
Es decir, γ2 es la mayor magnitud al cuadrado presente en los vectores de entrada del
conjunto de entrenamiento.
La siguiente desigualdad es claramente evidente:
Wk +1
2
k
≤ ¦ Ei
≤ kγ 2
i =1
⇔ Wk +1
166
2
2
≤ kγ 2
Capítulo 6. Redes de Perceptrones
Tenemos entonces que la magnitud al cuadrado del vector de pesos Wk+1 crece linealmente
2
con el número de iteraciones. Y en otras palabras, tenemos que Wk +1 está acotada
superiormente por el producto kγ 2 . Dado que γ2 depende directamente de los vectores de
entrada y k es el número de iteración, entonces hemos demostrado que la magnitud del
vector de pesos no diverge y en consecuencia sus componentes tampoco divergen.
Contamos ya con una Cota Superior y una Cota Inferior para el vector de pesos del
Perceptrón en la k-ésima iteración:
k 2γ 12
W*
≤ Wk +1 ≤ kγ 2
2
2
La Cota Inferior nos dice el valor mínimo esperado para la magnitud al cuadrado del vector
k 2γ 12
. Mientras que la Cota Superior nos dice que el vector de
de pesos. En este caso es
2
W*
pesos no crece de manera indefinida y que de hecho su magnitud al cuadrado es a lo más
kγ 2 .
El último punto de la demostración de nuestro Teorema requiere determinar el
número de iteraciones k necesarias para que la magnitud al cuadrado del vector de pesos
del Perceptrón sea igual tanto a su Cota Superior como a su Cota Inferior. ¿Por qué
buscamos igualar a las Cotas? Ello se debe a que queremos encontrar en que iteración los
pesos han convergido. Si el número k existe entonces hemos probado que el entrenamiento
de la neurona requiere de un número finito de iteraciones de tal forma que se tiene la
convergencia del vector de pesos de manera que se da solución al correspondiente
problema linealmente separable. Para tal efecto sea k = k . Por lo tanto, al igualar las Cotas
2
Superior e Inferior para Wk +1 se tiene:
(k ) γ
2
W*
2
1
2
= kγ 2
(Ecuación 6.2.9)
Realmente sólo se requieren unas manipulaciones simples para encontrar el valor de k :
167
Una Introducción al Cómputo Neuronal Artificial
(k )
2
γ 12
W*
⇔
2
= kγ2
k γ 12
W*
2
= γ2
γ W*
⇔k = 2 2
γ1
2
(Ecuación 6.2.10)
Por la Ecuación 6.2.1 tenemos que γ 1 = min {W * ⋅Ek } . Sabemos que el producto punto si
puede proporcionar en un momento dado el valor 0. Sin embargo, en el inicio de nuestra
demostración planteamos la suposición de que el vector W*, que presuponemos existe,
corresponde a un hiperplano que está colocado de manera tal que W*⋅Ek > 0 si Ek ∈ C1 o
bien que W*⋅Ek < 0 si Ek ∈ C2. Por lo tanto podemos garantizar que para todo vector en el
conjunto de entrenamiento W*⋅Ek ≠ 0 y en consecuencia γ1 ≠ 0. Entonces, la Ecuación
6.2.10 nos indica el número de iteraciones requerido de manera que el vector de pesos
resultante permita que el Perceptrón proporcione la salida correcta para todo vector de
entrada en el conjunto de entrenamiento. Con este punto ya validado tenemos debidamente
probado el Teorema de Convergencia del Perceptrón.
6.2.1 Discusión
La Regla de Rosenblatt descrita en la Sección 6.1, y expresada en la Ecuación
6.1.5, nos dice que el j-ésimo peso de un Perceptrón, wj, debe ser actualizado en función de:
• Un Coeficiente de Aprendizaje α;
• El error Err existente entre la salida O proporcionada por la neurona y la salida T
esperada;
• Y finalmente, por el j-ésimo componente del vector de entrada E: Ij.
Es decir:
wj = wj + α⋅Err⋅Ij
j = 1, 2, …, n
O en términos vectoriales, donde W es el vector de pesos de la neurona:
W = W + α⋅Err⋅E
Donde, por la Ecuación 6.1.4, Err = T – O y a su vez, por la Ecuación 6.1.3, la salida O
está dada por:
O = g (W ⋅ E )
La Función de Activación g se asume continua y diferenciable en (-∞, ∞).
168
Capítulo 6. Redes de Perceptrones
Ahora bien, consideremos algunos puntos que se establecen en el Teorema de
Convergencia y que, de primera vista, pueden contrastar con lo previamente mencionado:
• El Teorema hace alusión a la Función de Activación g únicamente en su enunciado,
pero no la utilizamos en la demostración.
• Tampoco se hace mención del error existente entre la salida de la neurona y la salida
esperada, es decir, el valor Err.
• Nunca se menciona al Coeficiente de Aprendizaje α. Ni en el enunciado ni en la
demostración.
• El enunciado del Teorema establece que la convergencia se debe garantizar para
cualquier vector de pesos inicial, sin embargo, en la demostración utilizamos
únicamente como vector de pesos inicial a W1 = 0 (el vector cero).
El objetivo de esta Sección es el de analizar uno a uno los puntos antes enunciados a fin de
clarificar las aparentes diferencias entre lo que se enuncia y demuestra en el Teorema de
Convergencia y lo establecido por la Regla de Rosenblatt.
Analicemos en primer lugar la aparente ausencia de la Función de Activación g en
la demostración del Teorema de Convergencia. En la Sección 4.1 comentamos que el rol de
la Función de Activación es el de mantener las salidas de las neuronas dentro de ciertos
límites. O desde otra perspectiva, la Función de Activación simplemente aplica un
escalamiento al valor de W⋅E. Recordemos que el Perceptrón solo es capaz de resolver
problemas de clasificación binaria: el vector de entrada forma parte de una clase A o de una
clase B, donde A y B son disjuntas. El valor de W⋅E se debe interpretar de manera que se
determine en qué clase ha ubicado la neurona a su vector de entrada. Si la función g aplica
un escalamiento sobre W⋅E entonces el valor escalado, g(W⋅E), debe interpretarse también
de manera pueda inferirse correctamente a que clase pertenece el vector de entrada. La
elección de g depende del problema en consideración. Y de hecho g podría ser la Función
Identidad en donde tenemos que no se aplica escalamiento alguno al valor de W⋅E. En este
sentido, la demostración del Teorema podría asumirse que trabaja específicamente usando
como Función de Activación a la Función Identidad. Dado que el Teorema utiliza el signo
de W⋅E para decidir si un vector de entrada fue correctamente clasificado, entonces si se
deseara incorporar una Función de Activación g diferente a la Identidad simplemente habría
que considerar el rango de valores arrojados por g(W⋅E) y establecer los intervalos bajo los
cuales se determina una clasificación correcta o incorrecta del vector de entrada E.
Ahora veamos la razón por la cual la Ecuación 6.1.4, Err = T – O, no es
mencionada. El Teorema de Convergencia parte de la suposición de que el problema a
resolver es efectivamente linealmente separable. Por ello mismo se asume la existencia de
un vector de pesos W* que permite la separación lineal efectiva de los elementos del
conjunto de entrenamiento en dos clases. Recordemos, tal como se estableció en la Sección
6.1, que el valor de Err = T – O puede ser positivo o negativo. Si el error, Err, es positivo
entonces la salida O de la neurona debe ser incrementada. Por otro lado, si el error es
negativo entonces la salida O de la neurona debe reducirse. En concreto, el objetivo del
valor Err es simplemente indicarnos como deberán ser modulados los pesos de la neurona:
169
Una Introducción al Cómputo Neuronal Artificial
si éstos se aumentan o se reducen. En la demostración del Teorema de Convergencia
tenemos que precisamente por contar con el vector de pesos W* es que podemos determinar
si el vector de pesos actual W en el Perceptrón clasifica correcta o incorrectamente. De
acuerdo a la demostración tenemos que si, dado el vector de entrada E, W⋅E > 0 pero
W*⋅E < 0 o bien, en el otro caso posible, si W⋅E < 0 pero W*⋅E > 0, entonces un ajuste de
pesos era requerido. El ajuste simplemente consistía en aumentar o reducir los pesos.
Tenemos entonces que el vector W* hace precisamente la función del valor Err: nos indica
el criterio de actualización de pesos a utilizar. En la práctica realmente nunca contamos con
el vector de pesos W*, de lo contrario, no se requeriría entrenar al Perceptrón porque
precisamente ya contamos con su vector de pesos óptimo. Al no contar con W* es que
requerimos de un criterio para determinar si los pesos deben ser aumentados o reducidos
durante el entrenamiento y ese es precisamente el papel de la Ecuación 6.1.4. Para efectos
de la demostración del Teorema, y para enfatizar el hecho de que se están tratando
problemas linealmente separables, es que se presupone la existencia de W*, pero hemos
visto que su papel es equivalente al del valor Err.
¿Por qué está ausente el Coeficiente de Aprendizaje α en la demostración del
Teorema de Convergencia? Primeramente veamos algunas propiedades de la Regla de
Rosenblatt, tal como la planteamos en la Sección 6.1. Vectorialmente, ésta está dada por:
W = W + α⋅Err⋅E
Ya habíamos hecho patente la similitud de esta regla de actualización con la presentada en
la Sección 4.3, la cual estaba basada en búsqueda de vector gradiente mediante Descenso
Escalonado. Para la Regla de Rosenblatt consideremos la siguiente Función de Error:
ME =
1
N
N
¦ (T
k
− Ok ) 2
(Ecuación 6.2.11)
k =1
Donde Tk es la salida esperada para el k-ésimo vector de entrada Ek y Ok es la salida
proporcionada por la neurona al presentarle precisamente Ek. Nótese que el lugar
geométrico descrito por la Ecuación 6.2.11 es también dependiente de la Función de
Activación utilizada. Si g es la Función Identidad entonces sabemos que ME es un
hiperparaboloide. A partir de la función ME podemos obtener funciones de error que no
dependen de todo el conjunto de entrenamiento (formado por N vectores de entrada). Es
decir, y tal como lo hicimos en el método de Descenso Escalonado, podemos considerar
únicamente el k-ésimo término de la sumatoria de la Ecuación 6.2.11:
§
§ n
··
MEk = (Tk - Ok) = ¨ Tk − g ¨ ¦ w j I j ¸ ¸
¨
¸
© j =1
¹¹
©
2
170
2
(Ecuación 6.2.12)
Capítulo 6. Redes de Perceptrones
Donde los escalares wj e Ij forman parte del vector de pesos actual W y del vector de
entrada Ek, respectivamente. Es claro que la Ecuación 6.2.12 no es más que el cuadrado de
la función Err presentada originalmente en la Ecuación 6.1.4. La función MEk, o de
manera equivalente, Err2, es un estimador para la función ME (Ecuación 6.2.11). Por lo
tanto, la minimización de Err2 = MEk es también un estimador para la minimización de ME.
Ahora requerimos el vector gradiente de Err2. El vector gradiente, como bien sabemos, nos
indica la dirección para maximizar a Err2. En consecuencia, nos movemos en la dirección
opuesta para minimizarla. La Regla de Rosenblatt como tal no calcula un vector gradiente
para determinar hacia que región, del lugar geométrico asociado a la función ME, nos
debemos mover. Pero es claro que la interpretación que se da al signo de la función Err nos
indica precisamente como debemos movernos. Si Err > 0 entonces debemos movernos de
manera que la salida de la neurona aumente. Si Err < 0 entonces nos movemos de tal forma
que el valor de salida de la neurona se reduce. Ahora bien, Err es un escalar, mientras que
el gradiente es un vector. Tal vector, en el método de Descenso Escalonado, está dado, en
parte, en función del vector de entrada actual Ek. Por lo tanto, tenemos que el valor de Err
para tal fin, en la Regla de Rosenblatt, es multiplicado por el vector de entrada actual. Al
final es claro que el vector Err⋅E cumple con la misma función que el vector gradiente de
Err2. Ahora bien, en el entrenamiento del Perceptrón mediante Descenso Escalonado
(Sección 4.3) establecimos que la función del Coeficiente de Aprendizaje es la de
establecer la velocidad de aprendizaje por parte de la neurona. Sabemos que la elección de
este valor influye sobre el número de iteraciones que el método de entrenamiento efectuará.
Un número reducido de iteraciones puede verse como un rápido aprendizaje. En términos
geométricos, el Coeficiente de Aprendizaje define, en parte, el tamaño del desplazamiento
que efectuará el vector de pesos actual cuando es actualizado y por tanto colocado en otra
región del lugar geométrico definido por la función de error ME. El valor del Coeficiente
influye en gran medida en que tan rápido nos acercaremos, o alejaremos inclusive (si éste
fue mal elegido), de manera progresiva a la minimización de la función ME. Debe ser claro
que la función del Coeficiente α es la misma en la Regla de Rosenblatt: permitir la
aceleración de la convergencia del vector de pesos. Por tanto, hemos posicionado a la Regla
como un método de minimización de la función ME (Ecuación 6.2.11). La Regla no
calcula vectores gradientes a lo largo de la búsqueda pero se puede apreciar que el término
de actualización α⋅Err⋅E cumple precisamente con la función de ir dirigiéndola.
Ahora bien, retomemos el punto referente al rol del Coeficiente del Aprendizaje en
el Teorema de Convergencia. En párrafos anteriores mencionamos que en la práctica, a
diferencia de las presuposiciones del Teorema, sólo contamos con un vector de pesos
inicial, que por lo general es inicializado de manera aleatoria. Nótese que por lo regular
tampoco analizamos las propiedades geométricas y topológicas asociadas al lugar
geométrico relacionado con la función ME: la función que precisamente buscamos
minimizar. El Coeficiente de Aprendizaje representa un parámetro que se nos proporciona
para acelerar la convergencia de los pesos y también para modular la precisión con que se
explora a la función ME. El Teorema de Convergencia, contando ya desde un principio con
existencia del vector de pesos óptimo W*, únicamente establece que efectivamente se
puede lograr la convergencia del vector de pesos, y que el número de iteraciones requerido
171
Una Introducción al Cómputo Neuronal Artificial
es finito. El Teorema no considera el problema de minimizar tal número de iteraciones. Es
decir, no lidia con la cuestión de la velocidad de aprendizaje. Sin embargo, nótese que es
posible asumir que el Coeficiente de Aprendizaje utilizado en la demostración es α = 1. En
conclusión debemos entender que el rol del Coeficiente de Aprendizaje queda fuera de los
objetivos del Teorema de Convergencia, pero su importancia en la práctica se hace evidente
cuando se entrena al Perceptrón a fin de modelar problemas particulares.
Por último, hagamos mención de la cuestión relacionada al vector de pesos inicial.
El enunciado del Teorema indica claramente que la convergencia se alcanza partiendo de
cualquier vector de pesos inicial. Sin embargo, la demostración establece que el vector de
pesos inicial utilizado es W1 = 0: el vector cero. Pero precisamente al establecer el uso del
vector cero se hace mención que esta aplicación no produce pérdida de generalidad en la
demostración del Teorema. El vector cero, como vector de pesos inicial, permite que la
identificación de las cotas Superior e Inferior para el vector de pesos en la k-ésima iteración
sean fáciles de calcular e interpretar. Gracias a ello sabemos, por la Cota Inferior, que la
magnitud al cuadrado del vector de pesos crece con un factor k2, mientras que por otro lado,
la Cota Superior nos dice que el vector de pesos no crece de manera indefinida y que de
hecho su magnitud al cuadrado es a lo más kγ 2 . Si la prueba fuese efectuada considerando
cualquier vector de pesos W1, y debido a que W2 = W1 + E1, donde, recalcamos, W1 no
necesariamente es el vector cero, entonces la Ecuación 6.2.4 tendría la siguiente forma:
W*⋅Wk+1 = W*⋅W1 + W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek
(Ecuación 6.2.13)
Nótese que γ1k sigue acotando inferiormente a la suma
W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek
Por lo tanto ahora tendríamos:
W*⋅Wk+1 = W*⋅W1 + W*⋅E1 + W*⋅E2 + … + W*⋅Ek-1 + W*⋅Ek ≥ W*⋅W1 + γ1k
⇔ W*⋅Wk+1 ≥ W*⋅W1 + γ1k
Por la desigualdad de Cauchy-Schwarz:
W * ⋅ W k +1 ≥ (W * ⋅W k +1 ) ≥ ( γ 1 k + W * ⋅W1 )
2
2
2
⇔ W * ⋅ W k +1 ≥ ( γ 1 k + W * ⋅W1 )
2
⇔ W k +1
172
2
(γ
≥
1
k + W * ⋅W1 )
W*
2
2
2
=
2
2
γ 12 k 2 + 2γ 1 k (W * ⋅W1 ) + (W * ⋅W1 )
W*
2
2
Capítulo 6. Redes de Perceptrones
Se ha obtenido entonces la Cota Inferior para el cuadrado de la magnitud del vector de
pesos en la k-ésima iteración y partiendo de cualquier vector de pesos inicial W1. Es claro
que cuando W1 = 0 entonces
γ 12 k 2 + 2γ 1 k (W * ⋅0 ) + (W * ⋅0 )
W*
2
2
=
γ 12 k 2
W*
2
Que es precisamente la Cota Inferior presentada en la demostración del Teorema de
Convergencia. Es evidente que esta Cota Inferior, considerando cualquier vector de pesos
inicial, es tan válida como la que se proporcionó en la demostración del Teorema de
Convergencia. De manera similar podemos obtener la correspondiente Cota Superior. Pero
debe apreciarse que éstas, al contar con más términos, puede que dificulten su
manipulación y hagan que la demostración se extienda de manera innecesaria sobre todo si
se requiere que las cotas sean tan ajustadas como sea posible. Finalmente, ya sea que se use
únicamente el vector de pesos inicial W1 = 0 o bien que éste sea cualesquiera, se llega a la
misma conclusión: se tiene probada la convergencia de los pesos de la neurona, que éstos
están debidamente acotados para cada iteración y que el número de iteraciones requeridas
para alcanzar la convergencia es finito.
6.3 Retropropagación
El lector se debe estar cuestionando acerca de la razón para revisitar al Perceptrón al
considerar la Regla de Rosenblatt para su entrenamiento y su correspondiente Teorema de
Convergencia. La razón es sencilla: la Regla de Rosenblatt representa el punto de partida
para los fundamentos a adoptar en el Algoritmo de Retropropagación en lo que respecta al
ajuste de pesos en una red formada por Perceptrones. Contrastemos este punto con el
mecanismo de ajuste de pesos para una red Madaline presentado en la Sección 5.2. En tal
procedimiento establecimos el principio de búsqueda de una neurona o neuronas
“culpables”. Si éstas existían entonces modificábamos de manera “abrupta” sus pesos de tal
forma que su salidas permitan que la salida final de la red sea la correcta, es decir, la
esperada. ¿Qué queremos decir cuando usamos el término “abrupto”? Nos referimos a que
los pesos originales de una neurona eran desechados por completo y sustituidos por otros
nuevos. Sin embargo, la Regla de Rosenblatt, y también el método de Descenso Escalonado
(Sección 4.3), realizan una actualización de pesos, pero ésta es gradual. Los pesos
originales son en parte conservados al serles aplicada una modificación que no los
reemplaza por completo por otros. Dado que esta modificación se aplica por cada vector de
entrada en el conjunto de entrenamiento, es que entonces la modificación es gradual.
Precisamente el principio del ajuste gradual de pesos fue adoptado por Rumelhart,
Hinton y Williams al presentar, en 1986, al Algoritmo de Retropropagación
(Back-Propagation Algorithm). Como a cualquier otro método de entrenamiento, se le
presenta a la red un vector del conjunto de entrenamiento. Si ésta calcula una salida que
coincida con la esperada entonces no se hace nada. Pero, si existen diferencias entre la
173
Una Introducción al Cómputo Neuronal Artificial
salida de la red y la salida esperada entonces los pesos deben ser ajustados de manera que el
error sea disminuido. Pero Rumelhart y compañía dieron un paso más que resulta ser una de
las novedades del algoritmo. Cuando un error entre la salida de la red y la esperada ha sido
identificado, entonces éste se distribuye y se utiliza para ajustar a todos los pesos de todas
las neuronas que forman las capas ocultas y de salida de la red. El ajuste aplicado en ese
momento busca hacer más pequeño el error entre la salida esperada y la salida producida
por la red, pero tampoco busca eliminarlo por completo en ese momento. Es decir, se tiene
por un lado un ajuste gradual de pesos que en consecuencia también reduce gradualmente
los errores, y por otro lado, no se busca identificar una sola o varias neuronas culpables: a
todas las neuronas se les atribuye una contribución al error generado y es por ello que a
todas se les deben ajustar sus respectivos pesos.
Al mecanismo de entrenamiento se le llama de Retropropagación debido a que
inicialmente el error de salida de la red es identificado a nivel de su capa de salida. Se dice
entonces que las salidas de las neuronas en esta capa se interpretan al compararlas con las
salidas esperadas. Por ello mismo los pesos en la capa de salida son los primeros en ser
modificados. Previamente mencionamos que las salidas de las capas ocultas realmente no
se pueden interpretar, aunque si son accesibles y también contribuyeron en su momento a la
salida errónea de la red. Por ello mismo una vez modificados los pesos en la capa de salida
se procede a modificar los pesos en las neuronas de la última capa oculta, posteriormente
los pesos de las neuronas en la penúltima capa oculta y así sucesivamente hasta llegar a la
modificación de pesos en la primera capa oculta. Es decir, a diferencia de la propagación de
un vector de entrada de la capa de entrada hacia las ocultas y finalmente a la de salida, la
actualización de pesos implica una Retropropagación, que va en el sentido opuesto.
Analizaremos en primer lugar, en la siguiente Sección, la instancia del Algoritmo de
Retropropagación bajo redes de Perceptrones formadas únicamente por una única capa
oculta. Posteriormente, en la Sección 6.4, veremos el caso general con varias capas ocultas.
6.3.1 Retropropagación en una Red de una Sola Capa Oculta
Considérese la Red de Perceptrones, de una sola capa oculta, presentada en la
Figura 6.2. Sean:
• n1: el número de neuronas en la capa de entrada.
• n2: el número de neuronas en la capa oculta.
• n3: el número de neuronas en la capa de salida.
Por la Figura 6.2 es claro que la red recibirá un vector de entrada X en \ n1 y proporcionará
como salida un vector en \ n3 . Sea g la función de activación utilizada en todas las
neuronas. Se asume que ésta es continua y diferenciable en (-∞, ∞). En nuestro caso,
supondremos que el número de neuronas en la capa de entrada es el mismo que de
componentes de los vectores de entrada: n1. Nótese también que cada neurona en la capa de
entrada recibe únicamente un componente del vector de entrada y que la salida de cada una
de estas neuronas se propaga a todas las neuronas de la capa oculta. Debe ser claro que las
neuronas que forman la capa de entrada contarán con un único peso el cual se multiplica
por el único escalar que reciben y el resultado es sometido a la Función de Activación g.
174
Capítulo 6. Redes de Perceptrones
Por lo general, el rol de las neuronas de la capa de entrada es el de simplemente recibir su
correspondiente escalar y propagarlo de manera inmediata a todas las neuronas de la capa
oculta. Ello quiere decir que podría considerarse que el valor de su único peso es igual a 1 y
que estas neuronas, en particular, cuentan con la Función Identidad como Función de
Activación. Por lo mismo de que su función es la de recibir y propagar el vector de entrada,
sin alterar los valores de sus componentes, es que estas neuronas no serán consideradas en
el proceso de ajuste de pesos. Realmente nos interesará ajustar los pesos de las neuronas en
las capas oculta y de salida que son las que se encargan de dar solución al problema que se
esté considerando. Finalmente, y como bien sabemos, la salida de cada neurona en la capa
oculta se propaga a todas las neuronas en la capa de salida.
x1
I1
o1
ajj
oi
an2
o n3
I2
x2
Ik
xk
xn
a1
1
In1
Figura 6.2. Una red de Perceptrones con una única capa oculta
(Véase el texto para detalles).
Sea T un vector en \ n3 . El vector T será de hecho un vector de salida esperada, en
donde Ti será su i-ésimo componente. Sea Oi la salida proporcionada por la i-ésima neurona
en la capa de salida de la red.
Como ya mencionamos en la Sección anterior, la Retropropagación, para el ajuste
de los pesos, en este tipo de red comprende dos fases:
•
•
Fase 1: Actualización de los pesos en las Neuronas en la Capa de Salida.
Fase 2: Actualización de los pesos en las Neuronas en la Capa Oculta.
175
Una Introducción al Cómputo Neuronal Artificial
Describamos en primer lugar el ajuste de pesos en las Neuronas de la Capa de
Salida. Considérese a la i-ésima neurona en esta capa, i = 1, 2, …, n3. Dado que ésta es una
neurona de tipo Perceptrón tenemos que su Sumatoria de Salida está dada por:
n2
enti = ¦ w j ,i a j
(Ecuación 6.3.1)
j =1
Nótese que esta neurona recibe como entrada un vector de n2 componentes que se forma
precisamente por las salidas de las neuronas en la capa oculta (Véase la Figura 6.2). Por lo
tanto, cada j-ésimo peso de nuestra i-ésima neurona en consideración, wj,i, se multiplicará
por el j-ésimo componente del vector de entrada, es decir, por la salida generada por la
j-ésima neurona en la capa oculta: aj. La salida final Oi está dada por la aplicación de la
función de activación g sobre el valor enti de la Sumatoria de Salida:
Oi = g(enti)
(Ecuación 6.3.2)
Ahora bien, suponiendo que debemos aplicar una corrección a nuestro Perceptrón, tenemos
entonces que aplicar la siguiente regla a cada uno de sus n2 pesos. Es decir, la actualización
del j-ésimo peso, wj,i, j = 1, 2, …, n2, estará dada por:
wj,i = wj,i + α⋅aj⋅Δi
(Ecuación 6.3.3)
Donde:
• wj,i: j-ésimo peso de la i-ésima neurona de la capa de salida.
• α: Coeficiente de aprendizaje.
• aj: Salida de la j-ésima neurona en la capa oculta.
A Δi, llamado el Término de Variación o Cambio de la i-ésima neurona de la Capa de
Salida, se le define de la siguiente manera:
Δi = Erri ⋅ g’(enti)
(Ecuación 6.3.4)
Erri es la diferencia entre el i-ésimo componente del vector de salida esperada y la salida
proporcionada por la i-ésima neurona en la capa de salida. Es decir:
Erri = Ti - Oi
176
(Ecuación 6.3.5)
Capítulo 6. Redes de Perceptrones
Por otro lado, g’ no es más que la derivada de la función de activación. Dado que g se
asume continua y diferenciable en cualquier punto, es que g’ no tendrá problemas de
indefinición y por tanto el ajuste de pesos será posible para cualquier neurona de cualquier
capa. En particular, g’ será evaluada, en el caso de las neuronas en la capa de salida, tal
como lo indica la Ecuación 6.3.4, con el valor de la Ecuación 6.3.1:
§ n2
·
g '(enti ) = g ' ¨ ¦ w j ,i a j ¸
© j =1
¹
(Ecuación 6.3.6)
Ahora procedamos a describir la manera en que los pesos de las neuronas en la capa
oculta son actualizados. Consideremos a la j-ésima neurona en la capa oculta, 1 ≤ j ≤ n2.
Véase la Figura 6.2. Ahora bien, la actualización del k-ésimo peso en la j-ésima neurona,
wk,j, de la capa oculta se da mediante la aplicación de la regla:
wk,j = wk,j + α⋅Ik⋅Δj
(Ecuación 6.3.7)
Donde Ik es la salida de la k-ésima neurona en la capa de entrada y α es el Coeficiente de
aprendizaje (el mismo utilizado para actualizar a las neuronas en la capa de salida).
Recordemos que, en base a lo establecido en párrafos anteriores, el valor Ik no es más que el
valor del k-ésimo componente del vector de entrada X. Es decir, Ik = xk (véase la Figura
6.2). El término Δj, denominado Término de Variación o Cambio de la j-ésima neurona
en la Capa Oculta, está dado por:
n3
Δ j = g '(ent j ) ⋅ ¦ w j ,i Δ i
(Ecuación 6.3.8)
i =1
Se requiere la derivada de la Función de Activación g, es decir, g’. Está será evaluada con
el valor proporcionado por la sumatoria de salida de la neurona que se está actualizado:
n1
ent j = ¦ wk , j I k
(Ecuación 6.3.9)
k =1
Tomando como referencia a la Figura 6.2, la sumatoria se conforma por n1 términos debido
a que cada uno de éstos es la salida que proporciona cada una de las neuronas en la capa de
entrada. Es decir, cada neurona en la capa oculta recibe un vector de entrada en \ n1 . Ahora
bien, en Secciones y párrafos anteriores mencionábamos que uno de los principios del
Algoritmo de Retropropagación es el de distribuir el error de la red entre todas las neuronas
que la conforman y utilizarlo para el ajuste de sus pesos. Previamente vimos como tal error
era utilizado para actualizar los pesos de las neuronas en la capa de salida (Ecuaciones
6.3.3 a 6.3.5). Ahora debemos ver como es que el error de la red es también utilizado para
actualizar los pesos de las neuronas en la capa oculta. Es claro que para toda neurona en la
capa oculta su salida, el escalar aj, es enviado a todas las neuronas en la capa de salida
177
Una Introducción al Cómputo Neuronal Artificial
(véase la Figura 6.2) y en particular se relacionará específicamente con su j-ésimo peso:
w j ,i . Al final, el producto w j ,i ⋅ a j contribuye al valor de la Sumatoria de Salida de las
neuronas en la capa de salida (véase la Ecuación 6.3.1), y en consecuencia, a la salida final
de la red. Por tanto, es claro que las neuronas en la capa oculta son en parte responsables
por el error que se produce en cada uno de los Perceptrones de salida con los que se
conectan. Ahora observemos la sumatoria presente en el término Δj (Ecuación 6.3.8):
n3
¦w
j ,i
Δi
i =1
Δi es precisamente el Término de Variación o Cambio que se utilizó para actualizar a la
i-ésima neurona en la capa de salida y a su vez, tal como lo muestra la Ecuación 6.3.4,
cuenta con el error existente entre la salida Oi proporcionada por la neurona y la salida Ti
esperada. Es claro que entonces parte de la actualización, o corrección, aplicada sobre las
neuronas en la capa de salida será también aplicada a las neuronas en la capa oculta. Esto
también tiene como consecuencia que para aplicar la regla de actualización de la Ecuación
3.6.7 se requiere haber actualizado primeramente a las neuronas en la capa de salida
mediante la Ecuación 6.3.3 y preservar los valores Δi. De allí el término Retropropagación.
Dado que las Ecuaciones 6.3.4 y 6.3.8 requieren que la Función de Activación sea
continua y diferenciable en (-∞, ∞), resulta obvio que funciones como sign (Sección 3.1)
no pueden ser consideradas. En la Sección 4.1 comentamos que por lo regular se usan las
siguientes funciones y sus correspondientes derivadas:
•
Función Sigmoide:
•
Función
1 + Tanh( z )
:
2
•
Función Tanh(z/2):
•
Función Tanh(z):
g ( z) =
1
,
1 + e− z
e2 z
,
1 + e2 z
2
g ( z) =
−1 ,
1 + e− z
g ( z) =
g ( z) =
1 − e −2 z
,
1 + e −2 z
g '( z ) =
e− z
(1 + e − z ) 2
g '( z ) =
2e 2 z
(1 + e 2 z ) 2
2e − z
g '( z ) =
(1 + e − z ) 2
g '( z ) =
4e 2 z
(1 + e 2 z ) 2
Debido a que el Algoritmo de Retropropagación requiere en primer lugar obtener la
salida producida por la red cuando un vector de entrada le es presentado, entonces es que
debemos implementar el mecanismo mediante el cual precisamente tal vector de entrada es
procesado. El Algoritmo 6.2 implementa la propagación de un vector de entrada hacia cada
una de las capas de la red. El algoritmo recibe como entrada 6 parámetros:
178
Capítulo 6. Redes de Perceptrones
•
•
•
•
Tres enteros n1, n2 y n3 que denotan, respectivamente, el número de neuronas en la capa
de entrada, el número de neuronas en la capa oculta y el número de neuronas en la capa
de salida.
Una matriz W_hidden de tamaño n2 × n1. Esta matriz contiene los pesos de las neuronas
en la capa oculta. Recordemos que tal capa se forma por n2 neuronas y cada una de
estas cuenta con n1 pesos. Por ello mismo, la información referente a la j-esima neurona
está contenida en el j-ésimo renglón de la matriz.
Una matriz W_output de tamaño n3 × n2. Contiene la información referente a las n3
neuronas que forman la capa de salida. Los n2 pesos del i-ésimo Perceptrón están
localizados precisamente en el i-ésimo renglón de esta matriz.
Un vector X en \ n1 . Es el vector de entrada que se presentará a la red.
El Algoritmo 6.2 procede de la siguiente manera:
•
•
Cada componente del vector de entrada X es enviado a su respectiva neurona en la capa
de entrada. Dado que estamos considerando el hecho de que el rol de estas neuronas es
el de simplemente propagar a X hacia la capa oculta, entonces en consecuencia
tendremos que el vector I generado por la capa de salida no es más que una copia del
vector de entrada X.
El vector I es presentado a las neuronas en la capa oculta. Para la j-ésima neurona en
esta capa, j = 1, …, n2:
n1
o Se calcula su sumatoria de salida: ent j = ¦ wk , j I k .
k =1
o Se determina su salida aj = g(entj).
•
Las salidas de las neuronas en la capa oculta forman un vector a de n2 componentes.
Ahora el vector a será enviado como entrada a las neuronas en la capa de salida. Para la
i-ésima neurona en la capa de salida, i = 1, …, n3:
n2
o Se calcula su sumatoria de salida: enti = ¦ w j ,i a j .
j =1
o Se determina su salida Oi = g(enti).
•
Las salidas de las neuronas en la capa de salida forman un vector O de n3 componentes.
Este vector es precisamente la salida final que la red proporciona.
El Algoritmo 6.2 proporciona como salida el vector O y también al vector a, el vector
generado por la capa oculta, debido a que éste último es requerido por el Algoritmo de
Retropropagación. Nótese que nuestro algoritmo invoca a un procedimiento g, que no es
más que la implementación de la Función de Activación.
179
Una Introducción al Cómputo Neuronal Artificial
Algoritmo 6.2. Propagación de un vector de entrada
en una red de Perceptrones con una única capa oculta.
Procedure Propagation
(Integer n1, Integer n2, Integer n3, Matrix W_hidden[1,…,n2][1,…,n1],
Matrix W_output[1,…,n3][1,…,n2], Array X[1,…,n1])
I = new Array[1,…,n1]
a = new Array[1,…,n2]
O = new Array[1,…,n3]
// Cada componente del vector de entrada es enviado a su respectiva neurona
// en la capa de entrada.
for k = 1 until n1 do
I[k] = X[k]
end-of-for
// El vector I es enviado como entrada a cada neurona en la capa oculta.
for j = 1 until n2 do
n1
// Se calcula, para la j-ésima neurona en la capa oculta, ent j = ¦ wk , j I k .
k =1
Real ent_j = 0
for k = 1 until n1 do
ent_j = ent_j + W_hidden[j][k] * I[k]
end-of-for
// Se obtiene, para la j-ésima neurona en la capa oculta,
// su salida aj = g(entj).
a[j] = g(ent_j)
end-of-for
// El vector a es enviado como entrada a cada neurona en la capa de salida.
for i = 1 until n3 do
n2
// Se calcula, para la i-ésima neurona en la capa de salida, enti = ¦ w j ,i a j .
j =1
Real ent_i = 0
for j = 1 until n2 do
ent_i = ent_i + W_output[i][j] * a[j]
end-of-for
// Se obtiene, para la i-ésima neurona en la capa de salida,
// su salida Oi = g(enti).
O[i] = g(ent_i)
end-of-for
// Se retornan como salida el vector a generado por las salidas de las neuronas
// en la capa oculta y el vector O que corresponde a la salida final de la red.
return {a, O}
end-of-procedure
180
Capítulo 6. Redes de Perceptrones
El Algoritmo 6.3 representa la implementación del método de Retropropagación
para el entrenamiento de una red de Perceptrones con una única capa oculta. Se reciben en
total 8 entradas:
• Un entero N: el número de elementos en el conjunto de entrenamiento.
• Tres enteros n1, n2 y n3 que denotan, respectivamente, el número de neuronas en la capa
de entrada, el número de neuronas en la capa oculta y el número de neuronas en la capa
de salida.
• Un entero L: el número de veces que el conjunto de entrenamiento será presentado a la
red. O en otras palabras, el número de épocas a aplicar.
• Un número real positivo α: el Coeficiente de Aprendizaje.
• Una matriz X de N × n1: contiene los N vectores de entrada del conjunto de
entrenamiento. Cada vector cuenta con n1 componentes. Por tanto, el n-ésimo vector de
entrada estará localizado en el renglón n de X.
• Una matriz T de N × n3: contiene los vectores que se espera la red proporcione.
El n-ésimo vector de salida esperada se ubica en el renglón n de la matriz T y cuenta
con n3 componentes.
En esencia, y de acuerdo al mecanismo de Retropropagación descrito en los párrafos
anteriores, el Algoritmo 6.3 funciona de la siguiente manera:
• Se inicializan los pesos de todas las neuronas en las capas oculta y de salida. Por lo
regular los valores iniciales asignados están en el intervalo (-1, 1).
• Repetir en L ocasiones:
o Para cada vector X en el conjunto de entrenamiento:
ƒ Se obtiene el vector de salida O de la red al presentarle X.
ƒ Se obtiene el vector de salida esperada T asociado al vector X.
ƒ Para cada neurona i en la capa de salida, i = 1, 2, …, n3:
• Se calcula Erri = Ti - Oi.
n2
•
Se calcula la sumatoria de salida enti = ¦ w j ,i a j .
•
Se obtiene el término Δi = Erri ⋅ g’(enti). El valor de Δi deberá estar
disponible para la actualización de las neuronas en la capa oculta.
Para cada peso j en la neurona i, j = 1, 2, …, n2, se aplica la actualización:
j =1
•
wj,i = wj,i + α⋅aj⋅Δi
ƒ
Para cada neurona j en la capa oculta, j = 1, …, n2:
•
n1
Se calcula su sumatoria de salida: ent j = ¦ wk , j I k .
k =1
•
n3
Se obtiene el término Δ j = g '(ent j ) ⋅ ¦ w j ,i Δ i
i =1
•
Para cada peso k en la neurona j, k = 1, 2, …, n3, se usa la actualización:
wk,j = wk,j + α⋅ak⋅Δj
181
Una Introducción al Cómputo Neuronal Artificial
El Algoritmo 6.3 requiere la derivada de la Función de Activación evaluada en enti o entj,
dependiendo de la capa de neuronas procesada. Para ello se invoca a la función
g_derivative que precisamente implemente la derivada requerida. Por otro lado, dado que se
requiere el vector de salida O proporcionado por la red usando los pesos actuales, es que
entonces se invoca al Algoritmo 6.2 que se encarga de presentar al vector de entrada actual
a la red y obtener la correspondiente salida. El Algoritmo 6.2 también retorna el vector a
que se forma con las salidas de las n2 neuronas en la capa oculta. Recordemos que este
vector es requerido para el cálculo de las sumatorias de salida de las neuronas en la capa de
salida. El último punto a considerar es el relacionado a los valores de salida proporcionados
por las neuronas en la capa de entrada. Tal como comentamos previamente, estas neuronas
reciben únicamente un componente del vector de entrada actual. También sabemos que a
esta capa se le puede especificar o no un procesamiento de tales entradas. En nuestro caso,
vemos a la capa de entrada con la única función de recibir el vector de entrada y propagar
sus componentes, sin alterarlos, a todas las neuronas de la capa oculta. Es por ello que en la
especificación del Algoritmo 6.3, y particularmente al calcular las sumatorias de salida de
las neuronas de la capa oculta y al aplicar la regla de actualización sobre sus pesos, se usará
al k-ésimo componente del n-ésimo vector de entrada como el valor del término Ik.
Algoritmo 6.3. Método de Retropropagación para el entrenamiento
de una Red de Perceptrones con una única capa oculta.
Procedure BackPropagation
(Integer N, Integer n1, Integer n2, Integer n3, Integer L, Real α,
Matrix X[1,…,N][1,…,n1], Matrix T[1,…,N][1,…,n3])
W_hidden = new Matrix[1,…,n2][1,…,n1]
W_output = new Matrix[1,…,n3][1,…,n2]
Δ = new Array[1,…,n3]
// Los pesos de las neuronas en la capa oculta se inicializan
// aleatoriamente en (-1, 1).
for j = 1 until n2 do
for k = 1 until n1 do
W_hidden[j][k] = Random( )
end-of-for
end-of-for
// Los pesos de las neuronas en la capa de salida se inicializan
// aleatoriamente en (-1, 1).
for i = 1 until n3 do
for j = 1 until n2 do
W_output[i][j] = Random( )
end-of-for
end-of-for
182
Capítulo 6. Redes de Perceptrones
// Se efectuarán en total L épocas o presentaciones del conjunto de entrenamiento.
for t = 1 until L do
for n = 1 until N do
// El n-ésimo vector de entrada, Xn, es enviado a la red.
// Se utilizarán los pesos actuales de las neuronas.
{a, O} = Propagation(n1, n2, n3, W_hidden, W_output, X[n])
// El vector a corresponde a las salidas de las neuronas
// en la capa oculta, el vector O es la salida de las neuronas
// en la capa de salida.
for i = 1 until n3 do
// Se procede a actualizar los pesos de la i-ésima neurona
// de la capa de salida.
// Se obtiene la diferencia entre la salida esperada y la salida
// proporcionada por la neurona.
Real Err_i = T[n][i] – O[i]
n2
// Se calcula enti = ¦ w j ,i a j .
j =1
Real ent_i = 0
for j = 1 until n2 do
ent_i = ent_i + W_output[i][j] * a[j]
end-of-for
// Se obtiene el término Δi = Erri ⋅ g’(enti).
Δ[i] = Err_i * g_derivative(ent_i)
// Se aplica la regla de actualización wj,i = wj,i + α⋅aj⋅Δi
// a cada peso de la neurona.
for j = 1 until n2 do
W_output[i][j] = W_output[i][j] + α * a[j] * Δ[i]
end-of-for
end-of-for
for j = 1 until n2 do
// Se procede a actualizar los pesos de la j-ésima neurona
// de la capa oculta.
n1
// Se calcula ent j = ¦ wk , j I k .
k =1
Real ent_j = 0
for k = 1 until n1 do
ent_j = ent_j + W_hidden[j][k] * X[n][k]
end-of-for
n3
// Se calcula Δ j = g '(ent j ) ⋅ ¦ w j ,i Δ i .
i =1
Real Δ_j = 0
183
Una Introducción al Cómputo Neuronal Artificial
for i = 1 until n3 do
Δ_j = Δ_j + W_output[i][j] * Δ[i]
end-of-for
Δ_j = Δ_j * g_derivative(ent_j)
// Se aplica la regla de actualización wk,j = wk,j + α⋅Ik⋅Δj
// a cada peso de la neurona.
for k = 1 until n1 do
W_hidden[j][k] = W_hidden[j][k] + α * X[n][k] * Δ_j
end-of-for
end-of-for
end-of-for
end-of-for
// Se retornan como salida los pesos de las neuronas en las capas oculta
// y de salida.
return {W_output, W_hidden}
end-of-procedure
6.3.2 Justificación del Algoritmo de Retropropagación
La Sección anterior tuvo el objetivo de plantear algorítmicamente al método de
Retropropagación para el entrenamiento de una Red de Perceptrones con una única capa
oculta. Ahora proporcionaremos las bases Matemáticas que sustentan al Algoritmo de
Retropropagación. De hecho, lo ubicaremos como un método de búsqueda de vector
gradiente, y específicamente, como un método de Descenso Escalonado.
El Algoritmo de Retropropagación constituye un procedimiento para el cálculo del
vector gradiente de la siguiente Función de Error:
1 n3
E = ¦ (Ti − Oi ) 2
2 i =1
(Ecuación 6.3.10)
Cada término de la sumatoria en la Ecuación 6.3.10 contiene la diferencia entre la salida Oi
proporcionada por la i-ésima neurona de la capa de salida y el i-ésimo escalar, Ti, del vector
de salida esperada. Es claro que la función E calcula únicamente la suma de las diferencias
al cuadrado existentes entre los correspondientes escalares de un vector de salida esperada
particular y las salidas de las neuronas en la capa de salida. Nótese que esta función no
considera en su totalidad al conjunto de entrenamiento, el cual se forma por N elementos.
Únicamente considera al A -ésimo elemento, 1 ≤ A ≤ N, es decir, la pareja formada por el
184
Capítulo 6. Redes de Perceptrones
A -ésimo vector de entrada y su correspondiente vector de salida esperada. Es posible
definir a la Función de Error en términos de todo el conjunto de entrenamiento.
Propiamente tendríamos en esta instancia la suma de todos los errores al cuadrado, SSE
(Sum of Squared Errors), producidos por la red al presentarle todo el conjunto de
entrenamiento:
N
§ n3
·
SSE = ¦ ¨ ¦ (Ti ,A − Oi ,A ) 2 ¸
A =1 © i =1
¹
(Ecuación 6.3.11)
Donde Ti ,A es el i-ésimo escalar del A -ésimo vector de salida esperada y Oi ,A es la salida de
la i-ésima neurona en la capa de salida cuando se presenta a la red el A -ésimo vector de
entrada del conjunto de entrenamiento. Sin embargo, tenemos conocimiento de que si bien
es posible abordar la minimización de esta función, es claro que tendremos un proceso
ineficiente, dado que precisamente se requiere en todo momento considerar al conjunto de
entrenamiento por completo. Es claro que la función E de la Ecuación 6.3.10 forma parte
de la función SSE ya que calcula una suma de errores al cuadrado específica. Por lo tanto,
la función E puede verse como un estimador para la función SSE. Y en consecuencia, como
bien sabemos, el vector gradiente de la función E es a su vez un estimador para el vector
gradiente de la función SSE. La ventaja esencial de trabajar con la Ecuación 6.3.10 radica
en el número reducido de operaciones a efectuar comparado con el número de operaciones
requeridas al manipular la función SSE.
Dado que Oi = g(enti), por la Ecuación 6.3.2, entonces tenemos que la Función de
Error ahora tiene la forma:
E=
=
1 n3
¦ (Ti − Oi )2
2 i =1
1 n3
¦ (Ti − g (enti ))2
2 i =1
(Ecuación 6.3.12)
Dado que enti es la Sumatoria de Salida de la i-ésima neurona de la capa de salida ahora se
obtiene al aplicar la Ecuación 6.3.1 sobre la Ecuación 6.3.12:
§ n2
··
1 n3 §
E = ¦ ¨ Ti − g ¨ ¦ w j ,i a j ¸ ¸
¸
2 i =1 ¨©
© j =1
¹¹
2
(Ecuación 6.3.13)
Donde, como ya sabemos, g es la Función de Activación, wj,i es el j-ésimo peso de la
i-ésima neurona de la capa de salida y aj es la salida proporcionada por la j-ésima neurona
en la capa oculta. Podemos sustituir al término aj por la aplicación de la Función de
Activación g sobre entj, la sumatoria de salida de la j-ésima neurona en la capa oculta
(Ecuación 6.3.9). Sin embargo, por el momento debe ser claro que la Función de Error
185
Una Introducción al Cómputo Neuronal Artificial
tiene como variables a optimizar precisamente a todos los pesos de todas las neuronas que
conforman a nuestras capas de salida y oculta. El objetivo, como siempre, es minimizarla:
encontrar los valores de los pesos que hagan tan pequeño como sea posible el error
existente entre el vector de salida O y el vector de salida esperada T.
Ahora determinaremos al vector gradiente de la Función de Error. Recordemos que
los componentes de tal vector serán sus derivadas parciales respecto a cada una de sus
variables involucradas: los pesos en las neuronas de salida y los pesos en las neuronas en la
capa oculta. Sea wj,i el j-ésimo peso de la i-ésima neurona en la capa de salida. Inicialmente
∂E
calcularemos
:
∂w j , i
∂E
∂ 1 n3
=
¦ (Ti − Oi )2
∂w j ,i ∂w j ,i 2 i =1
La sumatoria considera a todas las neuronas en la capa de salida. Sin embargo, es sólo una,
en particular la i-ésima neurona, la que cuenta con el peso wj,i. Por lo tanto, todos los
términos de la suma, excepto el i-ésimo, son eliminados por ser constantes respecto a wj,i:
=
∂ 1
(Ti − Oi ) 2
∂w j ,i 2
=
2
∂ 1
Ti − g ( enti ) )
(
∂w j ,i 2
(Por la Ecuación 6.3.2)
2
§ n2
··
∂ 1§
=
−
T
g
¨¨ i
¨ ¦ w j ,i a j ¸ ¸¸
∂w j ,i 2 ©
© j =1
¹¹
n
2
ª
§
·º ∂ §
§ n2
··
T
g
= «Ti − g ¨ ¦ w j ,i a j ¸ »
−
¨¨ i
¨ ¦ w j ,i a j ¸ ¸¸
«¬
© j =1
¹ »¼ ∂w j ,i ©
© j =1
¹¹
n
n
2
2
ª
§
·º §
§
··
∂
g ¨ ¦ w j ,i a j ¸ ¸
= «Ti − g ¨ ¦ w j ,i a j ¸ » ¨ −
¨
¸
«¬
© j =1
¹ »¼ © ∂w j ,i © j =1
¹¹
ª
§ n2
·º
= «Ti − g ¨ ¦ w j ,i a j ¸ » ⋅
«¬
© j =1
¹ »¼
ª
§ n2
· ∂
« − g ' ¨ ¦ w j ,i a j ¸
© j =1
¹ ∂w j ,i
¬«
186
n2
¦w
j =1
º
a
j ,i j »
¼»
(Por la Ecuación 6.3.1)
§ Aplicación de la ·
¨
¸
© Regla de la Cadena ¹
(Ti es constante respecto a wj,i)
§ Aplicación de la ·
¨
¸
© Regla de la Cadena ¹
Capítulo 6. Redes de Perceptrones
ª
§ n2
·º
= «Ti − g ¨ ¦ w j ,i a j ¸ » ⋅
«¬
© j =1
¹ »¼
ª
º
§ n2
· ∂
w1,i a1 + ... + w j ,i a j + ... + wn2 ,i an2 »
« − g ' ¨ ¦ w j ,i a j ¸
«¬
»¼
© j =1
¹ ∂w j ,i
§ Todos los términos de la
¨
º
ª
§ n2
·º ª
§ n2
· ∂
¨ última sumatoria son
= «Ti − g ¨ ¦ w j ,i a j ¸ » « − g ' ¨ ¦ w j ,i a j ¸
w j ,i a j »
¨ constantes respecto a
«¬
© j =1
¹ »¼ ¬«
© j =1
¹ ∂w j ,i
¼»
¨¨
© w j ,i excepto el j -ésimo
(
)
·
¸
¸
¸
¸¸
¹
ª
§ n2
·º ª
§ n2
· º
= «Ti − g ¨ ¦ w j ,i a j ¸ » « − g ' ¨ ¦ w j ,i a j ¸ a j »
© j =1
¹ ¼» ¬«
© j =1
¹ ¼»
¬«
= ª¬Ti − g ( enti ) º¼ ª¬ − g ' ( enti ) a j º¼
= [Ti − Oi ] ª¬ − g ' ( enti ) a j º¼
= Erri ª¬ − g ' ( enti ) a j º¼
= −a j Δi
(Por la Ecuación 6.3.1)
(Por la Ecuación 6.3.2)
(Por la Ecuación 6.3.5)
(Por la Ecuación 6.3.4)
Concretizando tenemos entonces que:
∂E
= −a j Δi
∂w j ,i
(Ecuación 6.3.14)
Se ha obtenido la dirección de máximo crecimiento de la función de error E respecto a la
variable (peso) wj,i.
Sea wk,j el k-ésimo peso de la j-ésima neurona en la capa oculta. Ahora
procederemos a calcular la derivada parcial de la función E, Ecuación 6.3.10, respecto a
wk,j:
∂E
∂ 1 n3
=
(Ti − Oi ) 2
¦
∂wk , j ∂wk , j 2 i =1
Recordemos que cada término de la sumatoria corresponde al error producido por cada
neurona en la capa de salida. Ahora bien, obsérvese la Figura 6.2. El peso respecto al cual
estamos derivando a la función E está contenido únicamente en la j-ésima neurona de la
capa oculta. Sin embargo, este mismo peso es propagado hacia todas las neuronas en la
capa de salida. Ello se debe a que forma parte del j-ésimo escalar del vector producido
como salida en la capa oculta y el cual, a su vez, es enviado como entrada a todas las
187
Una Introducción al Cómputo Neuronal Artificial
neuronas en la capa de salida. Por lo tanto, el peso wk,j está presente en todos los términos
de la sumatoria que forma a la función E. Eso quiere decir que entonces ninguno de los
términos de tal sumatoria puede ser visto como constante respecto a wk,j:
=
1 n3 ∂
(Ti − Oi ) 2
¦
2 i =1 ∂wk , j
n3
= ¦ (Ti − Oi )
i =1
∂
(Ti − Oi )
∂wk , j
n3
= −¦ (Ti − Oi )
i =1
n3
= −¦ (Ti − Oi )
i =1
(Aplicación de la Regla de la Cadena)
∂
Oi
∂wk , j
(Ti es constante respecto a wk,j)
§ n2
·
∂
g ¨ ¦ w j ,i a j ¸
∂wk , j © j =1
¹
(Por la Ecuación 6.3.2)
n3
§ n2
· ∂ n2
(Aplicación de la Regla de la Cadena)
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸
w j ,i a j
¦
∂
w
1
1
=
=
i =1
j
j
,
k
j
©
¹
n3
n2
§
· ∂
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸
w1,i a1 + ... + w j ,i a j + ... + wn2 ,i an2
i =1
© j =1
¹ ∂wk , j
(
)
n2
El término
¦w
j ,i
a j corresponde a la Sumatoria de Salida de la i-ésima neurona de la capa
j =1
de salida. Para esta neurona en particular se tiene que la variable wk,j aparece únicamente en
uno de sus términos. Tal término es el que corresponde a la salida proporcionada, aj, por la
j-ésima neurona de la capa oculta, que es precisamente la neurona que nos interesa por
contener al peso wk,j (Véase la Figura 6.2). Por lo tanto, todos los términos de la sumatoria
n2
¦w
j ,i
a j son constantes respecto a wk,j excepto el j-ésimo. Ahora bien, recordemos que la
j =1
sumatoria con índice i es la que se encarga de procesar una a una las neuronas en la capa de
salida. En consecuencia, se garantiza que para toda neurona en la capa de salida el j-ésimo
término de su sumatoria de salida es debidamente preservado y el resto eliminado por ser
constante respecto a wk,j:
n3
§ n2
· ∂
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸
w j ,i a j
i =1
© j =1
¹ ∂wk , j
n3
§ n2
·
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸ w j ,i ⋅
i =1
© j =1
¹
§ n1
·
∂
g ¨ ¦ wk , j I k ¸
∂wk , j © k =1
¹
188
§
§ n1
··
Dado
que
a
=
g
¨¨
¨ ¦ wk , j I k ¸ ¸¸
j
© k =1
¹¹
©
Capítulo 6. Redes de Perceptrones
n3
§ n2
·
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸ w j ,i ⋅
i =1
© j =1
¹
n1
§
· ∂ n1
g ' ¨ ¦ wk , j I k ¸
¦ wk , j I k
© k =1
¹ ∂wk , j k =1
§ Aplicación de la regla ·
¨
¸
© de la cadena
¹
n3
§ n2
·
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸ w j ,i ⋅
i =1
© j =1
¹
n1
§
· ∂
g ' ¨ ¦ wk , j I k ¸
w1, j I1 + ... + wk , j I k + ... + wn1 , j I n1
© k =1
¹ ∂wk , j
(
n3
§ n2
·
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸ w j ,i ⋅
i =1
© j =1
¹
)
§ Todos los términos de la
¨
¨ última sumatoria son
¨ constantes respecto a
¨¨
© wk , j excepto el k -ésimo
§ n1
· ∂
g ' ¨ ¦ wk , j I k ¸
wk , j I k
© k =1
¹ ∂wk , j
·
¸
¸
¸
¸¸
¹
n3
§ n2
·
§ n1
·
= −¦ (Ti − Oi )g ' ¨ ¦ w j ,i a j ¸ w j ,i ⋅ g ' ¨ ¦ wk , j I k ¸ I k
i =1
© k =1
¹
© j =1
¹
n3
§ n1
·
= −¦ Erri ⋅g ' ( enti ) w j ,i ⋅ g ' ¨ ¦ wk , j I k ¸ I k
i =1
© k =1
¹
§ Por la Ecuación 6.3.5, Erri , ·
¨
¸
© y la Ecuación 6.3.1, enti
¹
n3
§ n1
·
= −¦ Δ i ⋅w j ,i ⋅ g ' ¨ ¦ wk , j I k ¸ I k
i =1
© k =1
¹
(Por la Ecuación 6.3.4)
n3
= −¦ Δ i ⋅w j ,i ⋅ g ' ( ent j ) I k
(Por la Ecuación 6.3.9)
= −Δ j ⋅ I k
(Por la Ecuación 6.3.8)
i =1
En resumen tenemos:
∂E
= −Δ j ⋅ I k
∂wk , j
(Ecuación 6.3.15)
Esta derivada parcial representa la dirección de máximo crecimiento de la función E
respecto a wk,j.
189
Una Introducción al Cómputo Neuronal Artificial
Las derivadas parciales de la función E (Ecuación 6.3.10) forman los componentes
de su vector gradiente:
ª δE º
« δw »
1,1
«
»
« # »
«
»
« δE »
« δ wn ,1 »
2
«
»
#
«
»
« δE »
«
»
« δ w1,n3 »
«
»
« # »
« δE »
«
»
« δ wn2 ,n3 »
∇E = «
δ E »»
«
« δ w1,1 »
«
»
« # »
« δE »
«
»
« δ wn1 ,1 »
« # »
«
»
« δE »
« δw »
« 1, n2 »
« # »
«
»
« δE »
« δ wn , n »
¬
1 2 ¼
½
° Derivadas parciales respecto
°°
¾ a los pesos de la primer
° neurona en la capa de salida
°
°¿
½
° Derivadas parciales respecto
°°
¾ a los pesos de la n3 -ésima
° neurona en la capa de salida
°
°¿
½
° Derivadas parciales respecto
°°
¾ a los pesos de la primer
° neurona en la capa oculta
°
°¿
(Ecuación 6.3.16)
½
° Derivadas parciales respecto
°°
¾ a los pesos de la última
° neurona en la capa oculta
°
°¿
Es precisamente su posición en el vector ∇E la que claramente nos indica si un componente
está asociado a una neurona en la capa de salida o pertenece a una neurona en la capa
oculta. Al sustituir en ∇E con las Ecuaciones 6.3.14 y 6.3.15 se obtiene:
190
Capítulo 6. Redes de Perceptrones
ª −a1Δ1 º
« # »
«
»
« − an2 Δ1 »
«
»
« # »
« −a Δ »
« 1 n3 »
« # »
«
»
« −an2 Δ n3 »
∇E = «
»
« − I1Δ1 »
« # »
«
»
« − I n1 Δ1 »
« # »
«
»
« − I1Δ n2 »
«
»
« # »
« −I Δ »
¬ n1 n2 ¼
(Ecuación 6.3.17)
El vector gradiente representa la dirección de máximo crecimiento de la función E.
Entonces, para actualizar adecuadamente los pesos de todas las neuronas en la capa de
salida y la capa oculta se requiere utilizar la dirección opuesta de ∇E tal que el error se
minimice, es decir, requerimos a -∇E.
Recordemos que las reglas de actualización de pesos wj,i = wj,i + α⋅aj⋅Δi y
wk,j = wk,j + α⋅Ik⋅Δj hacen que nos movamos a una posición en el dominio de la función E.
Tal dominio se forma por todos posibles valores que pueden tomar los pesos. Dado que en
cada actualización nos movemos en dirección contraria a la del gradiente de E, entonces el
objetivo es acercarnos cada vez más a aquella región, del lugar geométrico descrito por la
función E, en donde los pesos minimizan el error de la red tanto como sea posible. El
tamaño de los desplazamientos efectuados va también en función del Coeficiente de
Aprendizaje α. Por ello, su elección de es vital importancia. Sabemos que es una constante
positiva con valor por lo regular en (0, 1). Sin embargo, éste influye sobre la rapidez con la
que nos acerquemos, o alejemos inclusive, de las regiones de E en donde los pesos
permiten un buen aprendizaje.
Ahora bien, tenemos bien claro que el objetivo del Algoritmo de Retropropagación
es el de determinar aquellos pesos con que deben ser equipadas las neuronas que forman
una Red de Perceptrones a fin de que un problema dado sea modelado tan bien como sea
posible. El cuestionamiento que nos plantearemos ahora tiene que ver con determinar si
tales pesos existen o bien si es posible encontrarlos. En el caso de la neurona Adaline
(Capítulo 3), la función a optimizar describía, desde el punto de vista geométrico, a un
hiperparaboloide. La buena noticia era que para este lugar geométrico podíamos garantizar
191
Una Introducción al Cómputo Neuronal Artificial
la existencia de un único mínimo global. Por lo tanto, los pesos que optimizaban a la
neurona, de manera que se obtenía el mejor aprendizaje, existen. Realmente el problema, en
el caso de la neurona Adaline, era contar con una buena elección de pesos iniciales y un
buen coeficiente de aprendizaje. En las Secciones 6.1 y 6.2 analizamos como es que el
Teorema de Convergencia del Perceptrón nos garantiza que es posible encontrar un
conjunto de pesos, precisamente para el Perceptrón, de manera que un problema
linealmente separable es efectivamente modelado por la neurona. Ahora nos preguntamos:
¿existirá algún resultado similar para el caso de una Red de Perceptrones entrenada
mediante el Algoritmo de Retropropagación?
Consideremos a la más pequeña de todas las Redes de Perceptrones con una capa
oculta. Véase la Figura 6.3. Es claro que para esta red tenemos que n1 = n2 = n3 = 1. Por
ello mismo, solo debemos considerar el ajuste de dos pesos: el peso de la única neurona en
la capa de salida y el peso de la única neurona en la capa oculta. Como siempre, asumimos
que la función de la neurona en la capa de entrada es la de simplemente enviar el único
escalar de entrada, sin modificarlo, a la neurona de la capa oculta.
x1
I1
a1
o1
Figura 6.3. Una Red de Perceptrones de una sola capa oculta con
una neurona en cada una de sus capas.
Ahora procederemos a desarrollar tanto como sea posible a la Ecuación 6.3.10
considerando nuestra red de la Figura 6.3 (para distinguir al peso de la neurona en la capa
de salida del peso de la neurona en la capa oculta usaremos la notación w para la primera y
w para la segunda):
E=
1 1
(Ti − Oi ) 2
¦
2 i =1
§ Dado que únicamente se
·
¨
¸
¨ tiene una neurona en la capa ¸
¨ de salida
¸
©
¹
1
= (T1 − O1 ) 2
2
§ 1
··
1§
= ¨ T1 − g ¨ ¦ w j ,1a j ¸ ¸
¸
2 ¨©
© j =1
¹¹
(
2
(
192
§ Sólo se tiene una neurona ·
¨
¸
© en la capa oculta
¹
)
2
1
T1 − g ( w1,1a1 )
2
1
= T1 − g w1,1 ⋅ g ( w1,1 I1 )
2
=
(Por la Ecuación 6.3.2)
(
))
2
( Dado que a
1
= g ( w1,1 I1 )
)
Capítulo 6. Redes de Perceptrones
(
(
1
= T1 − g w1,1 ⋅ g ( w1,1 x1 )
2
))
§ I1 = x1 dado que la neurona en ·
¨
¸
¨ la capa de entrada no efectúa ¸
¨ ningun procesamiento
¸
©
¹
2
(
)
(
)
2
1
= ¨§ T12 − 2 ⋅ T1 ⋅ g w1,1 ⋅ g ( w1,1 x1 ) + ª g w1,1 ⋅ g ( w1,1 x1 ) º ·¸
¬
¼ ¹
2©
Resumiendo, tenemos para la red de la Figura 6.3:
(
)
(
)
2
1
E = ¨§ T12 − 2 ⋅ T1 ⋅ g w1,1 g ( w1,1 x1 ) + ª g w1,1 g ( w1,1 x1 ) º ·¸
¬
¼ ¹
2©
(Ecuación 6.3.18)
En este punto tenemos que el lugar geométrico descrito por la Ecuación 6.3.18 está en
relación directa con la Función de Activación g que se utilice. Por ejemplo, sea g = Tanh,
entonces la Ecuación 6.3.18 toma la forma:
(
)
(
)
2
1
E = §¨ T12 − 2 ⋅ T1 ⋅ g w1,1 g ( w1,1 x1 ) + ª g w1,1 g ( w1,1 x1 ) º ·¸
¬
¼ ¹
2©
(
§ T 2 − 2 ⋅ T1 ⋅ Tanh w1,1 ⋅ Tanh ( w1,1 x1 )
1¨ 1
=
2
2 ¨¨ + ªTanh w ⋅ Tanh ( w x ) º
1,1
1,1
1
¼
© ¬
(
)
−2( w1,1x1 ) ·
§
1− e
§
¸ ·
−2¨ w1,1 ⋅
−2 ( w1,1x1 ) ¸
¨
+
1
e
¨
©
¹ ¸
1− e
¨ T12 − 2 ⋅ T1 ⋅
¸
−2 ( w1,1x1 ) ·
§
1− e
¸ ¸
¨
−2¨ w1,1 ⋅
2
(
−
w
x
)
1,1 1 ¸
¨
¹ ¸
1 + e © 1+ e
1¨
¸
= ¨
2
−2 ( w1,1x1 ) ·
§
1− e
2¨ ª
¸
¸ º
−2¨ w1,1 ⋅
−2( w1,1x1 ) ¸
¨
¹ »
¨ «1 − e © 1+ e
¸
»
¨+«
¸
2(
)
w
x
−
1,1 1 ·
§
1− e
¸ »
−2¨ w1,1 ⋅
¨ «
¸
−2 ( w1,1x1 ) ¸
¨
¹ »
¨ «1 + e © 1+ e
¸
¼
© ¬
¹
) ·¸
¸
¸
¹
(Por la Ecuación 4.1.9)
(Ecuación 6.3.19)
Recordemos que para evaluar a la función E requerimos de un vector de entrada y su
correspondiente vector de salida esperada en el conjunto de entrenamiento. Por la estructura
193
Una Introducción al Cómputo Neuronal Artificial
de la red sabemos que el vector de entrada tiene sólo un componente, así también el vector
de salida esperada. Supongamos que para el vector de entrada x1 = 0.2 se espera que la red
proporcione la salida T1 = 0.5. Sustituyendo tales valores en la Ecuación 6.3.19 tenemos:
2
−2( w1,1⋅0.2 ) ·
−2( w1,1⋅0.2 ) ·
§
§
§
·
1− e
1− e
ª
¸
¨ w1,1 ⋅
¸ º
−2¨ w1,1 ⋅
−
2
−2( w1,1⋅0.2 ) ¸
−2( w1,1⋅0.2 ) ¸
¨
¨
¨
¸
¹
¹ »
«1 − e © 1+ e
1¨
1 − e © 1+ e
2
» ¸
E = (0.5) − 2 ⋅ (0.5) ⋅
+«
−2 ( w1,1⋅0.2) ·
−2 ( w1,1⋅0.2) ·
§
§
1− e
1− e
2¨
¸
¸ » ¸
−2¨ w1,1 ⋅
−2¨ w1,1 ⋅
«
−2 ( w1,1⋅0.2) ¸
−2 ( w1,1⋅0.2) ¸
¨
¨
1+ e
1+ e
¨
©
¹
©
¹
«¬1 + e
»¼ ¸
1+ e
©
¹
(Ecuación 6.3.20)
La Figura 6.4 muestra la correspondiente gráfica de la función E para el caso de la red de
la Figura 6.3 y con el vector de entrada x1 = 0.2 y con salida esperada T1 = 0.5.
Visualmente, debe ser evidente que no se aprecia un punto sobre la superficie que tenga la
propiedad de ser un único mínimo global. Mencionábamos previamente que la presencia de
un único mínimo global era una propiedad sumamente valiosa de las funciones de error
asociadas, por ejemplo, a la neurona Adaline.
Figura 6.4. Gráfica de la función de Error asociada a
la red de Perceptrones de la Figura 6.3 (véase el texto para detalles).
194
Capítulo 6. Redes de Perceptrones
Reconsideremos la Ecuación 6.3.18. Sustituyamos en ella a la Función Identidad.
Por lo tanto obtendremos:
(
)
(
)º¼
(
)
(
)º¼
1
E = ¨§ T12 − 2 ⋅ T1 ⋅ g w1,1 g ( w1,1 x1 ) + ª g w1,1 g ( w1,1 x1 )
¬
2©
1
= §¨ T12 − 2 ⋅ T1 ⋅ι w1,1 ⋅ι ( w1,1 x1 ) + ªι w1,1 ⋅ι ( w1,1 x1 )
¬
2©
2
1
= T12 − 2T1w1,1w1,1 x1 + ª¬ w1,1w1,1 x1 º¼
2
1
2
2 2
w1,1
x1 )
= (T12 − 2T1w1,1w1,1 x1 + w1.1
2
(
)
2
2
·
¸
¹
·
¸
¹
(Ecuación 6.3.21)
Utilizando nuevamente el vector de entrada x1 = 0.2 y la salida esperada T1 = 0.5 tenemos:
1
2
2
0.25 − 0.2w1,1w1,1 + 0.04w1.1
w1,1
(
)
2
2
2
= 0.125 − 0.1w1,1w1,1 + 0.02 w1.1
w1,1
E=
(Ecuación 6.3.22)
La gráfica de la Ecuación 6.3.22 se presenta en la Figura 6.5. Es claro que, al menos en
términos visuales, no se aprecia un punto sobre la función E que corresponda a un mínimo
global. Sin embargo, la ventaja de utilizar a la Función Identidad como Función de
Activación es que podemos manipular de manera más sencilla a la función de error y por
tanto analizar si este punto existe o no y si es el caso, determinar si es único.
2
2
Figura 6.5. Gráfica de la Ecuación E = 0.125 − 0.1w1,1w1,1 + 0.02w1.1
.
w1,1
195
Una Introducción al Cómputo Neuronal Artificial
Procedamos a calcular las dos derivadas parciales de la función E (Ecuación
6.3.22):
δE
δ
2
2
=
0.125 − 0.1w1,1w1,1 + 0.02 w1,1
w1,1
(
)
δ w1,1 δ w1,1
=
δ
δ w1,1
= − 0.1
( −0.1w
1,1
δ
δ w1,1
2
2
w1,1 + 0.02w1,1
w1,1
)
w1,1w1,1 + 0.02
δ
δ w1,1
2
2
w1,1
w1,1
2
= − 0.1w1,1 + 0.04 w1,1w1,1
(Ecuación 6.3.23)
δE
δ
=
( 0.125 − 0.1w1,1w1,1 + 0.02w1,12 w1,12 )
δ w1,1 δ w1,1
=
δ
δ w1,1
= − 0.1
( −0.1w
1,1
δ
δ w1,1
2
2
w1,1 + 0.02w1,1
w1,1
)
w1,1w1,1 + 0.02
δ
δ w1,1
2
2
w1,1
w1,1
2
= − 0.1w1,1 + 0.04 w1,1
w1,1
(Ecuación 6.3.24)
Las Ecuaciones 6.3.23 y 6.3.24 forman precisamente los componentes del vector gradiente
de la función de error E. Nuestro objetivo, y también el del algoritmo de Retropropagación,
es determinar aquellos valores de los pesos que hacen que el vector gradiente sea el vector
cero (o tan cerca como sea posible a éste). Por lo tanto, al igualar las derivadas parciales,
previamente obtenidas, a cero tenemos el siguiente sistema de ecuaciones no lineales:
2
­°−0.1w1,1 + 0.04 w1,1w1,1
=0
®
2
°̄−0.1w1,1 + 0.04 w1,1w1,1 = 0
Una solución obvia e inmediata es w1,1 = w1,1 = 0 . Al sustituir tales valores en la Ecuación
6.3.22 tenemos:
E (0, 0) = 0.125 − 0.1(0)(0) + 0.02(0) 2 (0) 2 = 0.125
196
Capítulo 6. Redes de Perceptrones
Veamos que de hecho la solución w1,1 = w1,1 = 0 no es la única. Nótese en el sistema que el
peso w1,1 puede ser expresado en términos del peso w1,1 usando la primer ecuación:
2
−0.1w1,1 + 0.04 w1,1w1,1
=0
2
⇔ 0.04 w1,1w1,1
= 0.1w1,1
⇔ w1,1 =
2.5
, w1,1 ≠ 0
w1,1
(Ecuación 6.3.25)
De hecho, si despejamos a w1,1 de la Ecuación 6.3.25 obtenemos la misma expresión que si
hubiésemos manipulado desde un principio la segunda ecuación de nuestro sistema:
2
−0.1w1,1 + 0.04w1,1
w1,1 = 0
2
⇔ 0.04 w1,1
w1,1 = 0.1w1,1
⇔ w1,1 =
2.5
, w1.1 ≠ 0
w1,1
(Ecuación 6.3.26)
En cualquier caso, hemos verificado que el conjunto de puntos, en los cuales la función E
tiene a su vector gradiente igual a cero, es infinito. Usemos la Ecuación 6.3.26 para generar
algunos pesos. Por ejemplo, sea w1,1 = 1, entonces w1,1 = 2.5. Al evaluar el punto (1, 2.5) en
la Ecuación 6.3.22, la función de error, se obtiene:
E (1, 2.5) = 0.125 − 0.1(1)(2.5) + 0.02(1) 2 (2.5) 2 = 0.125 − 0.25 + 0.125 = 0
Si w1,1 = -1 entonces w1,1 = -2.5 y la función E nos proporciona:
E (−1, −2.5) = 0.125 − 0.1(−1)(−2.5) + 0.02(−1) 2 (−2.5) 2 = 0.125 − 0.25 + 0.125 = 0
Se nos ha presentado una situación interesante para meditar. Previamente, con el
punto (0, 0) la función E nos proporcionó el valor 0.125. Sin embargo, acabamos de
encontrar dos puntos para los cuales la función E proporciona el valor cero. Los tres puntos
tienen la propiedad de que los correspondientes vectores gradientes son cero. Por la
comparación anterior podríamos hipotetizar entonces que el punto (0, 0) es en realidad un
mínimo local. Sin embargo, para caracterizarlo como tal, y de manera contundente, es que
tendríamos que recurrir al bien conocido análisis de puntos críticos. Del estudio, sabemos
que el punto además de poder ser caracterizado como mínimo local también podría ser un
máximo o inclusive un punto de ensilladura. Las tres caracterizaciones tienen en común que
el vector gradiente es el vector cero.
197
Una Introducción al Cómputo Neuronal Artificial
Ahora bien, por la manera en la que el método de Descenso Escalonado procede, y
en consecuencia también el algoritmo de Retropropagación, tenemos que si el punto (0, 0)
fuese caracterizado como mínimo local entonces es posible que el algoritmo dirija la
búsqueda hacia éste y que de hecho allí finalice. Ello se debe a que, bajo la suposición de
que (0, 0) fuese un mínimo local, es claro que dentro de cierta vecindad de este punto los
vectores gradientes apuntaran en dirección opuesta a éste, buscando maximizar a la función
E. Pero dado que utilizamos, para movernos sobre la función, a la dirección opuesta del
gradiente, es que entonces nos acercaremos más a (0, 0) el cual suponemos es un mínimo.
Claramente estamos minimizando a la función E, pero no de manera óptima. Esta
afirmación se sustenta en el hecho de que hemos demostrado que existen al menos otros
dos puntos, (1, 2.5) y (-1, -2.5), para los cuales la función puede ser minimizada aún más.
La Figura 6.6 muestra la grafica de la Ecuación 6.3.26 sobrepuesta en la superficie
definida por la Ecuación 6.3.22 (hemos resaltado también al punto (0, 0) para el cual
sabemos que E(0,0) = 0.25). Este es el conjunto de puntos, o más bien pesos, para los
cuales la función de error E retornará el valor cero. Ello se verifica algebraicamente al
§ 2.5
·
, w1,1 ¸ en la Ecuación 6.3.22:
sustituir con el punto ¨
¨w
¸
© 1,1
¹
2
§ 2.5
·
§ 2.5 · 2
2.5
, w1,1 ¸ = 0.125 − 0.1
E¨
w1,1 + 0.02 ¨
w
¨w
¸
¨ w ¸¸ 1,1
w
1,1
1,1
1,1
©
¹
©
¹
= 0.125 − 0.25 + 0.125
=0
Ello implica que entonces el algoritmo de Retropropagación debería dirigir su búsqueda a
alguno de estos pesos, y no hacia el punto (0, 0), ya que es en éstos donde precisamente se
tendrá el mejor aprendizaje posible.
Hemos señalado entonces un posible problema que se podría presentar durante el
ajuste de pesos mediante el algoritmo de Retropropagación: que éste se quede “estancado”
o “atrapado” en un mínimo local. Debe apreciarse con claridad que la función de error, y en
consecuencia su geometría y topología, dependen en gran medida de la red de Perceptrones
asociada. El número de neuronas en las capas oculta y de salida determina el número de
pesos a ajustar. Ello quiere decir que podemos contar con una amplísima variedad de
funciones de error, en muchas de las cuales es sumamente probable que exista más de un
mínimo local. Es también posible que las funciones cuenten con más de un mínimo global,
como es el caso de la Ecuación 6.3.22. Sin embargo, el problema radica en que la presencia
de mínimos locales aumenta la probabilidad de que los pesos se ajusten en términos de
éstos y no en términos de un mínimo global. También se debe tomar en cuenta que los
valores iniciales de los pesos, en el algoritmo de Retropropagación, establecen el punto de
partida de la búsqueda a efectuar sobre la función de error. Valores iniciales de pesos que
sean cercanos a un mínimo local también aumentan las expectativas de que éste sea
alcanzado. Pero también debe ser claro que valores iniciales de pesos que estén alejados de
198
Capítulo 6. Redes de Perceptrones
un mínimo local no garantizan que éste no sea alcanzado ya que entonces entra en
consideración la elección del Coeficiente de Aprendizaje. Recordemos que el coeficiente
define el tamaño de las traslaciones, o “saltos”, que efectuaremos sobre la función de error
y en consecuencia puede que nos lleve al mínimo local, o lo suficientemente cerca de éste,
para que la búsqueda sea atraída hacia él.
Figura 6.6. El conjunto de puntos, resaltados en negro, para los cuales el vector gradiente
2
2
de la función E = 0.125 − 0.1w1,1w1,1 + 0.02w1.1
es el vector cero.
w1,1
Sabemos que el lugar geométrico descrito por la Función de Error va en relación
directa con la dimensionalidad de los vectores de entrada y de los vectores de salida
esperada en el conjunto de entrenamiento, el número de neuronas en la capa oculta, la
Función de Activación elegida, y por último, los valores específicos de los componentes de
los vectores que forman al conjunto de entrenamiento. Entonces, es lógico suponer que
podemos encontrar un muy variado conjunto de posibles lugares geométricos asociados a
las Funciones de Error cada uno con sus propiedades particulares respecto a sus puntos
críticos: mínimos, máximos, puntos de ensilladura. Sin embargo, es también posible que
algunos de tales lugares geométricos no cuenten con puntos críticos, y de nuestro interés
particular, se tenga ausencia de mínimos. Por ejemplo, recordemos que la Función de Error
asociada a nuestra red con una única neurona en cada capa (Figura 6.3) y usando la
Función Identidad como Función de Activación está dada por la Ecuación 6.3.21:
E=
1 2
2
2 2
T1 − 2T1w1,1w1,1 x1 + w1,1
w1,1
x1 )
(
2
199
Una Introducción al Cómputo Neuronal Artificial
Ahora bien, si consideramos al vector de entrada x1 = 0 y a la salida esperada T1 = 1
entonces la Ecuación 6.3.21 toma la siguiente forma:
E=
1
2
La cual es evidentemente un plano. De manera inmediata se puede apreciar que su vector
gradiente en cualquier punto es precisamente el vector cero. Sin embargo, ninguno de sus
puntos es un punto crítico en el sentido de que no puede ser caracterizado como un mínimo,
máximo o punto de ensilladura. Aunque también debe ser claro que cualquier punto sobre
el plano sirve para minimizar de manera óptima a la Función de Error para los elementos en
consideración del conjunto de entrenamiento. En este sentido la búsqueda por Descenso
Escalonado, no importa hacia donde se mueva, siempre encontrará un punto que permite
minimizar a la Función de Error. Ahora consideremos la situación en la cual el lugar
geométrico descrito por la Función de Error es similar al presentado en la Figura 6.7.
Supongamos que el punto marcado es el único punto crítico, un máximo, con el que se
cuenta. Ahora bien, precisamente por esta última propiedad es que no importa en donde se
ubiquen los pesos iniciales ( w1,1 , w1,1 ) porque el Descenso Escalonado procederá
efectuando la búsqueda siempre en dirección contraria al máximo global dado que nuestro
objetivo es minimizar a la función. Por cada par de nuevos pesos encontrados se
determinará que el valor de E se reduce. El problema es que esta búsqueda no garantiza una
convergencia de los pesos. Ello se debe precisamente a que por cada nuevo par de pesos se
encontrará que es posible minimizar aún más a la Función de Error. Si se estableciera que
el algoritmo de Retropropagación itere sucesivamente y además que se detenga una vez que
un vector gradiente de valor cero haya sido encontrado, entonces tendremos que
teóricamente el algoritmo tendrá una ejecución que requerirá un número infinito de pasos.
Recordemos que la función de la Figura 6.7 si cuenta con un punto en donde el gradiente
es el vector cero, pero se trata de un máximo y por nuestra manera de proceder siempre nos
alejaremos de éste. Los puntos anteriores dan lugar a una segunda observación respecto al
ajuste de pesos mediante el algoritmo de Retropropagación. Es posible que regiones en las
funciones de error no cuenten con puntos críticos, y en particular que no tengan valores
mínimos. Hemos visto que existen casos de Funciones de Error en donde las búsquedas de
pesos conducirán a una situación en la cual precisamente los pesos no convergerán y el
Algoritmo de Retropropagación efectuará una búsqueda que en teoría podría no terminar.
En esta Sección hemos establecido, por un lado, los fundamentos detrás del
Algoritmo de Retropropagación para el ajuste de pesos en una red de Perceptrones. Pero
por otro lado, también hemos señalado los posibles problemas que se pueden presentar y
que en conjunto permiten establecer que la convergencia de los pesos de las neuronas, y en
específico, la convergencia hacia un mínimo global que permita obtener el mejor ajuste
posible, no está garantizada. En un caso es posible que los pesos obtenidos correspondan a
un mínimo local. En otro caso es probable que la función de error a optimizar, debido a sus
propiedades geométricas y topológicas, hagan que los pesos se ajusten continuamente de
200
Capítulo 6. Redes de Perceptrones
manera que no se tenga la convergencia. Estos dos escenarios deben ser tomados siempre
en cuenta al momento de entrenar a una red neuronal. Es por ello mismo que por lo regular
el ajuste de pesos se efectúa asignando pesos iniciales aleatorios y con un número fijo de
presentaciones del conjunto de entrenamiento. Una vez que tal número de presentaciones
ha sido alcanzado se evalúa a todo el conjunto de entrenamiento y se calcula el error total
de aprendizaje de la red. A este proceso se le llama Corrida. La idea es que una vez que
una corrida ha sido finalizada, se efectúe una nueva inicialización aleatoria de pesos y se
ejecuten las presentaciones establecidas del conjunto de entrenamiento con el
correspondiente cálculo del error total del aprendizaje de la red. Es decir, efectuar una
nueva corrida. Se procede de manera que se efectúan varias corridas y de todas éstas se
elige aquella que reporte el menor error total de aprendizaje. El fundamento detrás de este
proceder se sustenta en que por cada corrida se explora una región diferente de la Función
Error. El objetivo es que mediante estas exploraciones se pueda determinar, de manera
empírica, cuales corridas corresponden a ajustes basados en mínimos locales o qué corridas
corresponden a potenciales ajustes que no convergerán. Se espera que aquella corrida con el
menor error de aprendizaje sea la que más cerca está de un mínimo global.
Figura 6.7. Una Función de Error E con un único punto crítico:
un máximo (punto remarcado).
6.4 Retropropagación en una Red con Múltiples Capas Ocultas
Ahora consideraremos el caso del ajuste de pesos, mediante el Algoritmo de
Retropropagación, para una red de Perceptrones formada por dos o más capas ocultas.
Como veremos más adelante el principio para el ajuste de pesos sigue la misma idea para el
caso con una única capa oculta, ya que se ajustan en primer lugar los pesos de las neuronas
en la capa de salida. Posteriormente se ajustan los pesos de las neuronas en la última capa
oculta. Dado que estas neuronas son responsables por el error producido en la capa de
201
Una Introducción al Cómputo Neuronal Artificial
salida es que parte del ajuste aplicado en la capa de salida también les es aplicado. Después
se efectúa el ajuste de pesos en las neuronas en la penúltima capa oculta. Es claro que las
salidas de estas neuronas influyen sobre el error producido por las salidas de las neuronas
en la última capa oculta. Por lo tanto, parte del ajuste aplicado en la última capa oculta, y en
consecuencia también parte de la corrección efectuada en la capa de salida, es también
aplicado sobre las neuronas en la penúltima capa oculta. Se procede de esta forma hasta
considerar por último el ajuste de pesos en la primera capa oculta. Se deben tomar también
en cuenta las correcciones efectuadas a los pesos en las restantes capas ocultas ya que éstas
son aplicadas a estas neuronas. En concreto, tenemos que los errores producidos por la red,
y los ajustes de pesos aplicados, son distribuidos entre todas las neuronas en las capas
ocultas y de salida. El objetivo como siempre es minimizar el error tanto como sea posible.
x1
I1
x2
I2
a 1,1
Ik
xp
Ip
a m,1
O1
O2
a1,k1
xk
a O,1
a O,k O
a m,k m
Oi
a 1,n1
a O,n O
a m,n m
Oq
Figura 6.8. Una de red de Perceptrones formada por m capas ocultas, m ≥ 2
(Véase el texto para detalles).
A fin de establecer las reglas de actualización de pesos a utilizar para las neuronas
en cada capa hemos de introducir notación apropiada. En primer lugar consideremos los
términos básicos. Véase la Figura 6.8. Sean:
• p: número de neuronas en la capa de entrada.
• m: número de capas ocultas.
• nO: número de neuronas en la O-ésima capa oculta, 1 ≤ O ≤ m.
• q: número de neuronas en la capa de salida.
• Ik: salida de la k-ésima neurona en la capa de entrada, 1 ≤ k ≤ p.
• aA ,kA : salida de la kO -ésima neurona en la O-ésima capa oculta, 1 ≤ O ≤ m, 1 ≤ kO ≤ nO.
• Oi: salida de la i-ésima neurona en la capa de salida, 1 ≤ i ≤ q.
De acuerdo a la Figura 6.8, tenemos que el papel de las neuronas en la capa de entrada
sigue siendo el mismo que el que les dimos en las dos Secciones anteriores: simplemente
202
Capítulo 6. Redes de Perceptrones
cada una recibe un componente del vector de entrada y se encarga de propagarlo a todas las
neuronas en la primer capa oculta. Por ello mismo tenemos que estas neuronas pueden tener
a su único peso igualado a uno y como Función de Activación a la Función Identidad. Bajo
esta última suposición, la cual consideraremos también en esta Sección, el proceso de
actualización de pesos no considera a las neuronas en la capa de entrada. Por la notación
establecida tenemos que nuestra red recibirá un vector de entrada en \ p . Las neuronas en
la capa de entrada propagan sus componentes a todas las neuronas en la primera capa
oculta. En este punto se produce como salida un vector en \ n1 . Todos sus componentes son
propagados hacia todas las neuronas en la segunda capa oculta. Esta capa produce entonces
un vector de salida en \ n2 . Se prosigue de esta manera al propagar todos los componentes
del vector de salida en \ nA , producido por la O-ésima capa oculta, hacia todas las neuronas
de la (O +1)-ésima capa oculta. La última capa oculta producirá un vector en \ nm cuyos
componentes son enviados a todas las neuronas en la capa de salida. Finalmente esta capa
produce la salida de la red: un vector en \ q . Tenemos entonces la secuencia de mapeos:
Capa
de
entrada
Primer
capa
oculta
\ p 6 \ p 6\ n1
Segunda
capa
oculta
Tercer
capa
oculta
( A +1)ésima
capa
oculta
A -ésima
capa
oculta
Última
capa
oculta
Capa
de
salida
6 \ 6 " 6 \ 6 " 6\ 6\
n2
nA
nm
q
Como ya tenemos conocimiento, las salidas producidas por las capas ocultas, aunque son
accesibles, no se les puede dar una interpretación. Por ello, también se dice que
simplemente la red neuronal efectúa un mapeo de un vector en \ p hacia un vector en \ q .
Ahora redefinamos algunas notaciones previamente establecidas a fin de que éstas
reflejen el hecho de que se está bajo el contexto de una red neuronal formada por más de
una capa oculta. Sean:
• wkm ,i : km -ésimo peso de la i-ésima neurona en la capa de salida, 1 ≤ i ≤ q, 1 ≤ km ≤ nm.
•
Sea wkA−1 , kA ,A el kO-1-ésimo peso de la kO-ésima neurona en la O-ésima capa oculta,
1 ≤ kO-1 ≤ nO-1, 1 ≤ kO ≤ nO, 1 < O ≤ m.
En el caso de los pesos en las capas ocultas, tenemos que el uso de la notación en el primer
índice ( kA −1 ) obedece a que toda neurona en la O-ésima capa oculta recibe en sus entradas las
salidas de las neuronas en la capa oculta que le precede, la capa O-1. El número de tales
entradas está dado por el número de neuronas en la capa O-1: nO-1. Nótese la restricción
establecida para el tercer índice, O, ya que éste debe ser estrictamente mayor a 1. Ello se
debe a que la notación es válida para cualquier capa oculta excepto la primera. Esto es
porque estas neuronas reciben sus entradas provenientes no de una capa oculta sino de la
capa de entrada. Por lo tanto, para estas neuronas en particular tendremos:
• wk , k1 ,1 : el k-ésimo peso de la k1-ésima neurona en la primera capa oculta, 1 ≤ k ≤ p,
1 ≤ k1 ≤ n1.
203
Una Introducción al Cómputo Neuronal Artificial
La Sumatoria de Salida de la i-ésima neurona en la capa de salida está dada por:
enti =
nm
¦w
km =1
km ,i
⋅ am , k m
(Ecuación 6.4.1)
Por lo tanto, la salida de la i-ésima neurona en la capa de salida, Oi, ahora se define de
manera precisa como:
§ nm
·
Oi = g (enti ) = g ¨ ¦ wkm ,i ⋅ am ,km ¸
© km =1
¹
(Ecuación 6.4.2)
Donde g es la Función de Activación continua y diferenciable en (-∞, ∞). Por otro lado, la
Sumatoria de Salida de la kA -ésima neurona en la O-ésima capa oculta 1 ≤ kA ≤ nA , 1 < A ≤ m ,
estará dada por:
entkA ,A =
nA −1
¦w
kA−1 =1
kA−1 , kA ,A
⋅ aA −1, kA .−1
(Ecuación 6.4.3)
En consecuencia, la salida de la kA -ésima neurona en la O-ésima capa oculta, aA ,kA , donde
1 ≤ kA ≤ nA y 1 < A ≤ m , estará dada por:
§ nA−1
·
aA , kA = g (entkA ,A ) = g ¨ ¦ wkA−1 ,kA ,A ⋅ aA −1,kA−1 ¸
© kA−1 =1
¹
(Ecuación 6.4.4)
Nótese que la Ecuación 6.4.3 es válida para cualquier neurona en cualquier capa oculta
excepto la primera (y por instancia también la Ecuación 6.4.4) De allí la condición de que
1 < A ≤ m . Ello se debe, tal como comentamos previamente, a que estas neuronas en
particular reciben entradas provenientes de la capa de entrada. Para estas neuronas
manejamos su caso especial. La Sumatoria de Salida de la k1-ésima neurona en la primera
capa oculta está dada por:
p
entk1 ,1 = ¦ wk ,k1 ,1 ⋅ I k
(Ecuación 6.4.5)
k =1
Donde Ik es la salida de la k-ésima neurona en la capa de entrada. Finalmente tenemos que
la salida de la k1-ésima neurona en la primer capa oculta, a1,k1 , 1 ≤ k1 ≤ n1 , se define como:
§ p
·
a1,k1 = g (entk1 ,1 ) = g ¨ ¦ wk ,k1 ,1 ⋅ I k ¸
© k =1
¹
204
(Ecuación 6.4.6)
Capítulo 6. Redes de Perceptrones
Consideremos ahora a la siguiente Función de Error (la cual es prácticamente la
presentada en la Ecuación 6.3.10, excepto por la modificación en el índice superior de la
sumatoria, para hacerla consistente con la notación introducida en párrafos anteriores):
q
E = ¦ (Ti − Oi )
2
(Ecuación 6.4.7)
i =1
Ti es el i-ésimo componente del vector de salida esperada T y Oi es la salida de la
i-ésima neurona en la capa de salida cuando el vector de entrada asociado a T es presentado
a la red. Recordemos que esta función sólo nos proporciona el error respecto a un elemento
del conjunto de entrenamiento. La idea sigue siendo el efectuar la corrección de pesos al
considerar únicamente a un elemento del conjunto de entrenamiento a la vez. Esto con la
finalidad de simplificar los cálculos.
Como ya comentamos antes, la actualización de pesos inicia con la corrección a las
neuronas en la capa de salida. Posteriormente se efectúa la corrección de pesos en las
neuronas en la última capa oculta y así sucesivamente hasta efectuar la corrección de pesos
en las neuronas de la primera capa oculta. En consecuencia, cada componente del vector
gradiente de la función de error está asociado a cada peso de cada neurona en cada capa
considerada. Además, la actualización de los pesos en las neuronas de una capa oculta
requiere que también se le aplique parte de la corrección efectuada en las neuronas de las
capas que le siguen. En base a todo esto vamos a definir las reglas de actualización de pesos
en el siguiente orden:
• Etapa 1: Actualización de los pesos de las neuronas en la capa de salida.
• Etapa 2: Actualización de los pesos de las neuronas en la última capa oculta.
• Etapa 3: Actualización de los pesos de las neuronas en la O-ésima capa oculta, 1 < O < m.
• Etapa 4: Actualización de los pesos de las neuronas en la primer capa oculta.
x1
I1
x2
I2
a1,1
Ik
xp
Ip
am,1
O1
O2
a1,k1
xk
a O,1
aO,k O
am,k m
Oi
a1,n1
aO,n O
am,n m
Oq
Figura 6.9. En color gris se muestran las neuronas involucradas en la actualización del peso wk ,i .
m
Tal peso se encuentra únicamente en la i-ésima neurona de la capa de salida.
205
Una Introducción al Cómputo Neuronal Artificial
Determinemos entonces el valor de la derivada parcial de E, Ecuación 6.4.7,
respecto a wkm ,i , el km-ésimo peso de la i-ésima neurona en la capa de salida (Véase la
Figura 6.9):
δE
δ wk
=
m ,i
δ
δ wk
m ,i
1 q
2
(Ti − Oi )
¦
2 i =1
1 δ
=
2 δ wkm ,i
q
¦ (T − O )
i
(Por la Ecuación 6.4.7)
2
i
i =1
En este punto nótese que el peso wkm ,i está contenido únicamente en la i-ésima neurona de
la capa de salida. Por lo tanto, todos los términos de la sumatoria, excepto el i-ésimo, son
constantes respecto a wkm ,i :
=
1 δ
2
(Ti − Oi )
2 δ wkm ,i
= (Ti − Oi )
δ
δ wk
= − (Ti − Oi )
(Ti − Oi )
(Regla de la Cadena)
m ,i
δ
δ wk
Oi
(Ti es constante respecto a wkm ,i )
m ,i
§ nm
·
g ¨ ¦ wkm ,i ⋅ am, km ¸
δ wkm ,i © km =1
¹
nm
§
·
= − (Ti − Oi ) g ' ¨ ¦ wkm ,i ⋅ am ,km ¸ ⋅
© km =1
¹
= − (Ti − Oi )
δ
δ
δ wk
nm
¦w
k =1
m ,i m
k m ,i
(Por la Ecuación 6.4.2)
(Regla de la Cadena)
⋅ am,km
La i-ésima neurona en la capa de salida cuenta con nm pesos, uno de los cuales es
precisamente wkm ,i . Por lo tanto, todos los pesos, excepto el km-ésimo, son constantes
respecto a wkm ,i :
§ nm
· δ
= − (Ti − Oi ) g ' ¨ ¦ wkm ,i ⋅ am, km ¸
wkm ,i ⋅ am, km
δ
w
=
1
k
,
k
i
m
©
¹
m
206
Capítulo 6. Redes de Perceptrones
§ nm
·
= − (Ti − Oi ) g ' ¨ ¦ wkm ,i ⋅ am ,km ¸ am ,km
© km =1
¹
= − (Ti − Oi ) g ' ( enti ) am,km
(Por la Ecuación 6.4.1)
En concreto tenemos:
δE
δ wk
= − (Ti − Oi ) g ' ( enti ) am,km
(Ecuación 6.4.8)
m ,i
Sea Erri la diferencia existente entre la salida proporcionada por la i-ésima neurona
en la capa de salida y el i-ésimo componente, Ti, del vector de salida esperada:
§ nm
·
Erri = Ti − Oi = Ti − g ¨ ¦ wkm ,i ⋅ am,km ¸
© km =1
¹
(Ecuación 6.4.9)
Es claro que esta definición para Erri inicialmente coincide con la definición dada
originalmente en la Ecuación 6.3.5. La diferencia ahora es que estamos considerándola
bajo el contexto de una red de Perceptrones con al menos dos capas ocultas. El contraste
con la Ecuación 6.3.5 se hace claro al sustituir Oi por la Ecuación 6.4.2. Algo similar
sucede al definir inicialmente al Término de Variación o Cambio, Δ i , asociado a la i-ésima
neurona en la capa de salida, ya que éste lo establecemos como el producto entre Erri y
g’(enti). En este caso, la expresión resultante es igual a la presentada en la Ecuación 6.3.4,
la cual esta asociada al caso de una red con una única capa oculta. Sin embargo las
diferencias surgen al sustituir Erri y enti con las Ecuaciones 6.4.9 y 6.4.1, respectivamente:
§
§ nm
· · § nm
·
Δ i = Erri ⋅ g '(enti ) = ¨ Ti − g ¨ ¦ wkm ,i ⋅ am ,km ¸ ¸ ⋅ g ' ¨ ¦ wkm ,i ⋅ am,km ¸
¨
¸
© km =1
¹ ¹ © km =1
¹
©
(Ecuación 6.4.10)
Finalmente, tenemos los elementos para expresar de manera concisa a la derivada
parcial de la función de error E respecto a wkm ,i . Por la Ecuación 6.4.8 sabemos que:
δE
δ wk
= − (Ti − Oi ) g ' ( enti ) am,km
m ,i
Ahora, la sustituir con la Ecuación 6.4.10 tenemos finalmente:
δE
δ wk
= −Δ i ⋅ am ,km
(Ecuación 6.4.11)
m ,i
207
Una Introducción al Cómputo Neuronal Artificial
x1
I1
x2
I2
a1,1
a O,1
Ik
xp
Ip
am,1
O1
O2
a1,k1
xk
am-1,1
aO,k O
am-1,k m
m-1
am,k m
Oi
a1,n1
aO,n O
a
m-1,n m-1
am,n m
Oq
Figura 6.10. En color gris se muestran las neuronas involucradas en la actualización del peso wk ,k ,m el cual
m−1 m
reside en la km-ésima neurona de la última capa oculta. Las actualizaciones aplicadas sobre las neuronas en la
capa de salida influyen también en la actualización del peso wk ,k ,m .
m−1
m
El siguiente paso en que nos concentraremos es el determinar la derivada parcial de
la función de error E respecto a wkm−1 ,km , m . Es decir, respecto al km-1-ésimo peso de la
km-ésima neurona en la última capa oculta. Véase la Figura 6.10. Suponemos que el
número de capas ocultas en la red es al menos 2, es decir, asumimos m ≥ 2.
δE
δ wk
=
m−1 , k m , m
=
δ
δ wk
m−1 , km , m
1 q
2
(Ti − Oi )
¦
2 i =1
1
δ
2 δ wkm−1 , km , m
q
¦ (T − O )
i
(Por la Ecuación 6.4.7)
2
i
i =1
Recordemos que el peso wkm−1 ,km ,m está ubicado en la km-ésima neurona en la última capa
oculta. La salida de esta neurona es propagada hacia todas las neuronas en la capa de salida.
Por lo tanto, el peso wkm−1 ,km ,m forma parte de la salida de todas las neuronas en esa capa.
Ello implica que entonces todos los términos de la sumatoria deben ser considerados:
1 q
δ
2
= ¦
(Ti − Oi )
2 i =1 δ wkm−1 ,km , m
δ
q
= ¦ (Ti − Oi )
i =1
δ wk
δ
q
= − ¦ (Ti − Oi )
i =1
208
(Ti − Oi )
(Regla de la Cadena)
m−1 , km , m
δ wk
m −1 , k m , m
Oi
§ El término Ti es constante ·
¨
¸
© respecto a wkm−1 , km , m .
¹
Capítulo 6. Redes de Perceptrones
§ nm
·
g ¨ ¦ wkm ,i ⋅ am, km ¸
δ wkm−1 ,km ,m © km =1
i =1
¹
nm
q
§
·
= − ¦ (Ti − Oi )g ' ¨ ¦ wkm ,i ⋅ am, km ¸ ⋅
i =1
© km =1
¹
δ
q
= − ¦ (Ti − Oi )
δ
δ wk
nm
La sumatoria
¦w
k m ,i
km =1
nm
¦w
k =1
m−1 , k m , m m
km ,i
(Por la Ecuación 6.4.2)
(Regla de la Cadena)
⋅ am ,km
⋅ am ,km es precisamente la Sumatoria de Salida de cada una de las
neuronas en la capa de salida (Ecuación 6.4.1). De sus nm términos realmente sólo nos
ocupa aquel que se relaciona con la neurona en la última capa oculta que contiene al peso
de interés wkm−1 ,km ,m . Por lo tanto, todos los términos de la sumatoria son constantes respecto
wkm−1 ,km ,m excepto el antes mencionado:
q
§ nm
·
= − ¦ (Ti − Oi )g ' ¨ ¦ wkm ,i ⋅ am,km ¸ ⋅
i =1
© km =1
¹
δ
δ wk
wkm ,i ⋅ am ,km
m−1 , k m , m
q
§ nm
·
= − ¦ (Ti − Oi )g ' ¨ ¦ wkm ,i ⋅ am, km ¸ ⋅
i =1
© km =1
¹
wkm ,i
δ
δ wk
§ El término wkm ,i es constante
¨¨
© respecto a wkm−1 , km , m .
⋅ am ,km
m−1 , k m , m
q
§ nm
·
= − ¦ Erri ⋅g ' ¨ ¦ wkm ,i ⋅ am, km ¸ ⋅
i =1
© km =1
¹
wkm ,i
δ
δ wk
(Por la Ecuación 6.4.9)
⋅ am ,km
m−1 , km , m
δ
q
= − ¦ Erri ⋅g ' ( enti ) wkm ,i
i =1
δ
q
= − ¦ Δ i ⋅wkm ,i
i =1
·
¸¸
¹
δ wk
δ wk
⋅ am , k m
(Por la Ecuación 6.4.1)
m−1 , k m , m
⋅ am,km
(Por la Ecuación 6.4.10)
m −1 , k m , m
209
Una Introducción al Cómputo Neuronal Artificial
q
= − ¦ Δ i wkm ,i ⋅
i =1
§
·
g ¨ ¦ wkm−1 ,km , m ⋅ am −1,km−1 ¸
δ wkm−1 ,km ,m © km−1 =1
¹
q
§ nm−1
·
= − ¦ Δ i wkm ,i g ' ¨ ¦ wkm−1 , km ,m ⋅ am −1, km−1 ¸ ⋅
i =1
© km−1 =1
¹
δ
nm−1
δ
δ wk
nm−1
m−1 , k m , m
¦w
⋅ am −1,km−1
km−1 , km , m
⋅ am −1,km−1 corresponde a la neurona en la última capa
¦w
km−1 =1
(Regla de la Cadena)
km−1 , km , m
km−1 =1
nm−1
La Sumatoria de Salida
§ Por la Ecuación 6.4.4, ·
¨
¸
© haciendo A = m
¹
oculta en la cual está contenido el peso que nos interesa: wkm−1 ,km ,m . Ello implica que
respecto a wkm−1 ,km , m todos los términos son constantes excepto el km −1 -ésimo:
q
§ nm−1
·
= − ¦ Δ i wkm ,i g ' ¨ ¦ wkm−1 , km ,m ⋅ am −1, km−1 ¸ ⋅
i =1
© km−1 =1
¹
δ
δ wk
wkm−1 , km ,m ⋅ am −1,km−1
m −1 , k m , m
q
§ nm−1
·
= − ¦ Δ i wkm ,i g ' ¨ ¦ wkm−1 , km ,m ⋅ am −1, km−1 ¸ am −1,km−1
i =1
© km−1 =1
¹
q
(
§ Por la Ecuación 6.4.3, ·
¨
¸
© haciendo A = m
¹
)
= − ¦ Δ i wkm ,i g ' entkm ,m am −1, km−1
i =1
Resumiendo:
δE
δ wk
q
m−1 , k m , m
(
)
= −¦ Δ i wkm ,i g ' entkm , m am −1, km−1
i =1
(Ecuación 6.4.12)
Definamos ahora al Término de Variación o Cambio Asociado a la km-ésima
Neurona en la Última Capa Oculta como:
q
(
Δ km ,m = ¦ Δ i ⋅ wkm ,i ⋅ g ' entkm , m
i =1
)
(Ecuación 6.4.13)
El término Δ km ,m hace explícito el hecho de que los cambios o correcciones aplicados a las
neuronas en la capa de salida, el primer conjunto de neuronas ajustadas por el Algoritmo de
210
Capítulo 6. Redes de Perceptrones
Retropropagación, también influyen sobre las correcciones a aplicar sobre la km-ésima
neurona en la última capa oculta, 1 ≤ km ≤ nm.
Sustituyendo la Ecuación 6.4.13 sobre la Ecuación 6.4.12 tenemos entonces
expresada de manera concisa la derivada parcial de la Función de Error E respecto al
km-1-ésimo peso en la km-ésima neurona de la última capa oculta:
δE
δ wk
x1
I1
x2
I2
a1,1
Ik
xp
Ip
(Ecuación 6.4.14)
a O-1,1
a O,1
aO+1,1
am,1
O1
O2
a1,k1
xk
= −Δ km ,m ⋅ am −1, km−1
m−1 , km , m
a O-1,kO-1
aO ,kO
a O+1,kO+1
am,k m
Oi
a1,n1
a O-1,nO-1
aO,n O
a O+1,nO+1
am,n m
Oq
Figura 6.11. En color gris se presentan a las neuronas involucradas en la actualización del peso wk ,k ,A .
A−1 A
Éste se encuentra localizado específicamente en la kO-ésima neurona en la O-ésima capa oculta.
Las actualizaciones aplicadas sobre las neuronas en las capas ocultas O+1, O+2, …, m y la capa de
salida influyen sobre la actualización de wk ,k ,A .
A−1 A
Procedamos a determinar el valor de la derivada parcial de la Función de Error E
respecto al kO-1-ésimo peso de la kO-ésima neurona en O-ésima capa oculta, es decir, wkA−1 , kA ,A .
Suponemos que este peso corresponde a una neurona ubicada en cualquier capa oculta
excepto la primera y la última: 1 < O < m. Véase la Figura 6.11. Como en los casos
anteriores, partimos de la Ecuación 6.4.7:
δE
δ wk
A −1 , kA , A
=
δ
δ wk
A −1 , kA , A
1 q
2
(Ti − Oi )
¦
2 i =1
Recordemos que el peso wkA−1 , kA ,A es propagado, por medio de la salida de su neurona
correspondiente, hacia todas las neuronas en la (O+1)-ésima capa oculta. A su vez, este
mismo peso es propagado hacia todas las neuronas en la (O+2)-ésima capa oculta. Tal
propagación continúa hasta llegar a las neuronas en la capa de salida. En concreto, tenemos
que el peso wkA−1 ,kA ,A está presente en todas las neuronas de la red, excepto aquellas en la
211
Una Introducción al Cómputo Neuronal Artificial
capa de entrada, y las capas ocultas 1 a O-1. De la capa oculta O sólo nos interesa la kO-ésima
q
neurona. Por lo tanto, tenemos que para la sumatoria
¦ (T − O )
i
i
2
, que considera a todas
i =1
las neuronas en la capa de salida, ninguno de sus términos es constante respecto a wkA−1 ,kA ,A ,
por lo tanto éstos se preservan:
=
1 q
δ
2
(Ti − Oi )
¦
2 i =1 δ wkA−1 ,kA ,A
δ
q
= ¦ (Ti − Oi )
i =1
δ wk
A −1 , kA , A
δ
q
= −¦ (Ti − Oi )
i =1
(Ti − Oi )
δ wk
§ Ti es constante ·
¨
¸
© respecto a wkA−1 , kA ,A ¹
Oi
A−1 , kA , A
§ nm
·
g ¨ ¦ wkm ,i ⋅ am, km ¸
δ wkA−1 ,kA ,A © km =1
i =1
¹
nm
q
§
·
= −¦ (Ti − Oi ) ⋅ g ' ¨ ¦ wkm ,i ⋅ am, km ¸ ⋅
i =1
© km =1
¹
δ
q
= −¦ (Ti − Oi )
δ
δ wk
nm
¦w
km ,i
k =1
A −1 , kA , A m
(Regla de la Cadena)
(Por la Ecuación 6.4.2)
(Regla de la Cadena)
⋅ am ,km
q
= −¦ Erri ⋅ g ' ( enti ) ⋅
i =1
δ
δ wk
i =1
¦w
k m ,i
k =1
A −1 , kA , A m
δ
q
= −¦ Δ i
nm
δ wk
⋅ am ,km
nm
A −1 , kA , A
¦w
km =1
km ,i
⋅ am , k m
§ Por la Ecuación 6.4.9,
¨
¨ Erri , y por la Ecuación
¨ 6.4.1, ent
i
©
·
¸
¸
¸
¹
(Por la Ecuación 6.4.10)
Nótese que los pesos de las neuronas en la capa de salida, wkm ,i , son constantes respecto al
peso que nos ocupa, wkA−1 , kA ,A y además éste último forma parte de las salidas, am,km , de las
neuronas en la última capa oculta:
q
nm
i =1
km =1
= −¦ Δ i ¦ wkm ,i
212
δ
δ wk
A −1 , kA , A
am ,km
Capítulo 6. Redes de Perceptrones
q
nm
i =1
km =1
= −¦ Δ i ¦ wkm ,i ⋅
§ Por la Ecuación 6.4.4, ·
¨
¸
© haciendo A = m
¹
§ nm−1
·
g ¨ ¦ wkm−1 ,km ,m ⋅ am −1, km−1 ¸
δ wkA−1 ,kA ,A © km−1 =1
¹
nm
q
§ nm−1
·
= −¦ Δ i ¦ wkm ,i g ' ¨ ¦ wkm−1 ,km , m ⋅ am −1,km−1 ¸ ⋅
i =1
km =1
© km−1 =1
¹
δ
δ
δ wk
nm−1
A −1 , kA , A
q
nm
i =1
km =1
¦w
km−1 =1
km−1 , km , m
(
(Regla de la Cadena)
⋅ am −1,km−1
)
= −¦ Δ i ¦ wkm ,i g ' entkm , m ⋅
δ
δ wk
nm−1
¦w
k =1
A −1 , kA , A m−1
km−1 , km , m
§ Por la Ecuación 6.4.3, ·
¨
¸
© haciendo A = m
¹
⋅ am −1, km−1
Supongamos que existe más de una capa entre la última capa oculta y la capa en donde la
neurona con el peso wkA−1 , kA ,A reside. Por lo tanto, los pesos de todas las neuronas en la
última capa oculta son constantes respecto al peso en consideración wkA−1 , kA ,A ya que no
existen conexiones directas con la neurona que precisamente contiene a wkA−1 ,kA ,A . Pero el
peso wkA−1 , kA ,A está contenido en las salidas de las neuronas de la (m-1)-ésima capa oculta. En
nm−1
consecuencia, todos los términos de la sumatoria
¦w
km−1
q
nm
i =1
km =1
(
km−1 , km , m
⋅ am −1,km−1 se conservan:
)
= −¦ Δ i ¦ wkm ,i g ' entkm , m ⋅
nm−1
¦w
km−1 =1
nm
= − ¦ Δ km , m
km−1 , km , m
nm
nm−1
km−1 , km , m
¦w
km−1 =1
δ
δ wk
δ wk
¦w
km−1 =1
km =1
δ
nm−1
km =1
= − ¦ Δ km , m
⋅
A −1 , kA , A
km−1 , km , m
am −1, km−1
A −1 , kA , A
⋅
δ
δ wk
A −1 , kA , A
am −1, km−1
⋅
§ nm−2
·
g ¨ ¦ wkm−2 ,km−1 , m −1 ⋅ am − 2, km−2 ¸
© km−2 =1
¹
(Por la Ecuación 6.4.13)
§ Por la Ecuación 6.4.4, ·
¨
¸
© haciendo A = m − 1
¹
213
Una Introducción al Cómputo Neuronal Artificial
nm
= − ¦ Δ km , m
km =1
nm−1
¦w
km−1 =1
km−1 , km , m
⋅
§ nm−2
·
g ' ¨ ¦ wkm−2 ,km−1 ,m −1 ⋅ am − 2,km−2 ¸ ⋅
© km−2 =1
¹
δ
δ wk
nm−2
¦
=1
k
A−1 , kA , A m− 2
nm
= − ¦ Δ km , m
km =1
nm−1
δ
δ wk
wkm−2 ,km−1 , m −1 ⋅ am − 2,km−2
¦w
km−1 =1
km−1 , km , m
nm−2
¦
=1
k
A −1 , kA , A m− 2
(Regla de la Cadena)
(
)
⋅g ' entk m−1, m −1 ⋅
wkm−2 ,km−1 ,m −1 ⋅ am − 2,km−2
§ Por la Ecuación 6.4.3, ·
¨
¸
© haciendo A = m − 1
¹
Los pesos de todas las neuronas en la (m-1)-ésima capa oculta son todos constantes
respecto al peso wkA−1 , kA ,A ya que no existen conexiones directas con la neurona que
precisamente contiene a wkA−1 ,kA ,A . Pero el peso wkA−1 ,kA ,A está contenido en las salidas de las
neuronas de la (m-2)-ésima capa oculta. De nueva cuenta tenemos que todos los términos
nm−2
de la sumatoria
¦
km−2 =1
nm
= − ¦ Δ km , m
km =1
nm−2
¦
km−2 =1
wkm−2 , km−1 , m −1 ⋅ am − 2, km−2 se preservan:
nm−1
¦w
km−1 =1
km−1 , km , m
wkm−2 , km−1 ,m −1 ⋅
(
)
⋅ g ' entk m−1 ,m −1 ⋅
δ
δ wk
A −1 , kA , A
am − 2,km−2
En ese punto haremos una pausa ya que conviene introducir nueva notación.
Reconsideremos al Término de Variación o Cambio asociado a la km-ésima neurona en la
última capa oculta, presentado originalmente en la Ecuación 6.4.13:
q
Δ km ,m = ¦ Δ i ⋅ wkm ,i ⋅ g '(entkm ,m )
i =1
Este término representa parte de la corrección a aplicar a las neuronas en la última capa
oculta. Dado que las salidas de estas neuronas influyen sobre el error que tuvieron en su
momento las neuronas en la siguiente capa, en este caso la capa de salida, es que entonces
parte de la corrección que se les aplicó a éstas últimas también debe ser aplicada a la última
214
Capítulo 6. Redes de Perceptrones
capa oculta, de allí la presencia de los términos Δ i y wkm ,i . Ahora bien, obsérvense los
(
términos Δ km ,m , wkm−1 ,km , m y g ' entk m−1,m −1
)
en la última expresión que obtuvimos para la
derivada parcial de la Función de Error E respecto a wkA−1 , kA ,A :
δE
δ wk
nm
A −1 , kA , A
= − ¦ Δ km , m
km =1
nm−1
¦
km−1 =1
(
)
nm−2
wkm−1 ,km , m ⋅ g ' entk m−1,m −1 ⋅ ¦ wkm−2 ,km−1 ,m −1 ⋅
km−2 =1
δ
δ wk
A −1 , kA , A
am − 2,km−2
Recordemos que en este punto estamos procesando a las neuronas que forman a la
(m-1)-ésima capa oculta. Las salidas de estas neuronas influyen en el error que en su
momento tuvieron las salidas de la siguiente capa, es decir, las salidas de las neuronas en la
m-ésima capa oculta, la última capa oculta de hecho. Las neuronas de la última capa fueron
corregidas en su momento al usar su correspondiente Término de Variación o Cambio:
Δ km ,m . Además de Δ km ,m , debe ser claro que para corregir a las neuronas de la capa actual,
la (m-1)-esima, también requerimos de los pesos wkm−1 ,km , m (los cuales residen en la siguiente
(
)
capa) y de g ' entk m−1,m −1 . Todos estos términos pueden ser agrupados bajo la sumatoria
con índices inferior km y superior nm. Es decir tendríamos la sumatoria:
nm
¦Δ
km =1
km , m
(
⋅ wkm−1 , km ,m ⋅ g ' entk m−1, m −1
)
Nótese la similitud de ésta con la sumatoria de la Ecuación 6.4.13. Así como la sumatoria
q
¦Δ ⋅w
i
i =1
k m ,i
⋅ g '(entkm ,m ) se definió como el Término de Variación o Cambio Δ km ,m para la
km-ésima neurona en la última capa oculta, ahora podemos definir a la sumatoria
nm
¦Δ
km =1
km , m
(
)
⋅ wkm−1 ,km , m ⋅ g ' entk m−1 ,m −1 como el Término de Variación o Cambio Δ km−1 ,m −1 para la
km-1-ésima neurona en la penúltima capa oculta. Pero como veremos más adelante,
tendremos que definir para cada neurona en cada capa oculta su correspondiente Término
de Variación o Cambio. La buena noticia es que las expresiones que se obtienen serán
similares a las que hemos obtenido para Δ km−1 ,m−1 y para Δ km ,m . Por ello mismo, definiremos
al Término de Variación o Cambio para la kO-ésima Neurona en la O-ésima Capa
Oculta, 1 ≤ O < m, como:
nA +1
Δ kA ,A = g '(entkA ,A ) ¦ Δ kA+1,A +1 ⋅ wkA ,kA+1 ,A +1
(Ecuación 6.4.15)
kA+1 =1
215
Una Introducción al Cómputo Neuronal Artificial
El caso cuando O = m ya está cubierto por la Ecuación 6.4.13. Teniendo ya a la mano esta
nueva definición, podemos proseguir con nuestra derivada parcial de la Función de Error E
respecto al peso wkA−1 , kA ,A . Aplicaremos la Ecuación 6.4.15 cuando sea requerido:
δE
δ wk
A −1 , kA , A
nm
= − ¦ Δ km , m
km =1
nm−2
¦
km−2 =1
nm−1
¦w
km−1 , km , m
km−1 =1
wkm−2 , km−1 , m −1 ⋅
nm−1
nm−2
km−1 =1
km−2 =1
= − ¦ Δ km−1 ,m −1
δ
δ wk
A −1 , kA , A
¦
nm−2
km−1 =1
km−2 =1
δ
δ wk
A −1 , kA , A
¦
δ
δ wk
A −1 , kA , A
am − 2, km−2
wkm−2 ,km−1 ,m −1 ⋅
§ Por la Ecuación 6.4.15, ·
¨
¸
© haciendo A = m − 1
¹
wkm−2 , km−1 ,m −1 ⋅
§ nm−3
·
g ¨ ¦ wkm−3 ,km−2 , m − 2 ⋅ am −3,km−3 ¸
© km−3 =1
¹
nm−1
nm−2
km−1 =1
km−2 =1
= − ¦ Δ km−1 ,m −1
)
am − 2,km−2
nm−1
= − ¦ Δ km−1 ,m −1
(
⋅ g ' entk m−1 ,m −1 ⋅
¦
wkm−2 ,km−1 ,m −1 ⋅
§ nm−3
·
g ' ¨ ¦ wkm−3 ,km−2 ,m − 2 ⋅ am −3,km−3 ¸ ⋅
© km−3 =1
¹
δ
δ wk
nm−3
¦w
k =1
A −1 , kA , A m−3
nm−1
nm−2
km−1 =1
km−2 =1
= − ¦ Δ km−1 ,m −1
δ
δ wk
¦
§ Por la Ecuación 6.4.4, ·
¨
¸
© haciendo A = m − 2
¹
km−3 , km−2 , m − 2
(Regla de la Cadena)
⋅ am −3, km−3
(
)
wkm−2 ,km−1 ,m −1 ⋅g ' entkm−2 , m − 2 ⋅
nm−3
¦w
k =1
A −1 , kA , A m−3
km−3 , km−2 , m − 2
⋅ am −3,km−3
§ Por la Ecuación 6.4.3, ·
¨
¸
© haciendo A = m − 2
¹
Los pesos de todas las neuronas en la (m-2)-ésima capa oculta son todos constantes
respecto al peso wkA−1 ,kA ,A ya que no existen conexiones directas con la neurona que
precisamente contiene a wkA−1 , kA ,A . Pero el peso wkA−1 , kA ,A está contenido en las salidas de las
neuronas de la (m-3)-ésima capa oculta. De nueva cuenta, todos los términos de la
nm−3
sumatoria
¦w
km−3 =1
216
km−3 , km−2 , m − 2
⋅ am −3,km−3 se preservan:
Capítulo 6. Redes de Perceptrones
nm−1
nm−2
km−1 =1
km−2 =1
= − ¦ Δ km−1 ,m −1
¦
(
δ
nm−3
¦w
km−3 =1
=−
nm−2
¦
km−2 =1
k m −3 , k m − 2 , m − 2
Δ km −2 , m − 2
δ
δ wk
=−
nm−2
¦
km−2 =1
A −1 , kA , A
Δ k m− 2 , m − 2
δ
δ wk
=−
A −1 , kA , A
nm−2
¦Δ
km−2 =1
δ wk
A −1 , kA , A
nm−3
¦w
km−3 , km−2 , m − 2
km−3 =1
am −3,km−3
⋅
§ Por la Ecuación 6.4.15, ·
¨
¸
© haciendo A = m − 2
¹
am −3,km−3
nm−3
¦w
km−3 , km−2 , m − 2
km−3 =1
⋅
§ Por la Ecuación 6.4.4, ·
¨
¸
© haciendo A = m − 3
¹
§ nm−4
·
g ¨ ¦ wkm−4 ,kk −3 , m −3 ⋅ am − 4, km−4 ¸
© km−4 =1
¹
nm−3
km −2 , m − 2
)
wkm−2 , km−1 ,m −1 ⋅ g ' entkm−2 ,m − 2 ⋅
¦w
km−3 , km−2 , m − 2
km−3 =1
⋅
§ nm−4
·
g ' ¨ ¦ wkm−4 ,kk −3 ,m −3 ⋅ am − 4,km−4 ¸ ⋅
© km−4 =1
¹
δ
δ wk
=−
nm−2
¦
km−2 =1
¦
=1
k
A −1 , kA , A m− 4
Δ k m−2 , m − 2
δ
δ wk
nm−4
wkm−4 ,kk −3 ,m −3 ⋅ am − 4, km−4
nm−3
¦w
km−3 , km−2 , m − 2
km−3 =1
nm−4
¦
=1
k
A −1 , kA , A m− 4
(Regla de la Cadena)
(
)
⋅g ' entkm−3 ,m −3 ⋅
wkm−4 ,kk −3 ,m −3 ⋅ am − 4,km−4
§ Por la Ecuación 6.4.3, ·
¨
¸
© haciendo A = m − 3
¹
Los pesos de todas las neuronas en la (m-3)-ésima capa oculta son todos constantes
respecto al peso wkA−1 , kA ,A ya que asumimos no existen conexiones directas con la neurona
que contiene a wkA−1 ,kA ,A . Pero el peso wkA−1 ,kA ,A está contenido en las salidas de las neuronas de
la (m-4)-ésima capa oculta. Tal como hemos procedido en párrafos anteriores, todos los
nm−4
términos de la sumatoria
¦
km−4 =1
wkm−4 , kk −3 , m −3 ⋅ am − 4,km−4 se preservan:
217
Una Introducción al Cómputo Neuronal Artificial
=−
nm−2
¦Δ
km−2 =1
nm−3
k m−2 , m − 2
nm−4
¦
km−4 =1
=−
nm−3
¦
km−3 =1
km−3 , km−2 , m − 2
wkm−4 ,kk −3 ,m −3 ⋅
Δ km−3 ,m −3
δ
δ wk
¦w
km−3 =1
A −1 , kA , A
nm−4
¦
km−4 =1
δ
δ wk
(
)
⋅ g ' entkm−3 ,m −3 ⋅
A −1 , kA , A
am − 4,km−4
wkm−4 ,km−3 ,m −3 ⋅
§ Por la Ecuación 6.4.15, ·
¨
¸
© haciendo A = m − 3
¹
am − 4,km−4
En este punto de nuestro desarrollo debe ser claro que mientras la capa oculta que contiene
a la neurona en donde reside el peso wkA−1 ,kA ,A no haya sido alcanzada aún tendremos la
secuencia de aplicaciones de la Ecuación 6.4.4, Regla de la Cadena, Ecuación 6.4.3, Regla
de la Derivada de una Suma, y finalmente Ecuación 6.4.15 donde obtenemos el Término
de Variación o Cambio asociado a cada neurona en la capa oculta actualmente procesada.
Supongamos que la capa oculta donde se encuentra el peso wkA−1 ,kA ,A está suficientemente
alejada de la última capa oculta de la red. Por lo tanto, la secuencia de aplicaciones antes
descrita nos lleva a obtener una expresión que contiene los Términos de Variación o
Cambio asociados a la (m-4)-ésima capa oculta:
="
=−
nm−4
¦
km−4 =1
Δ k m− 4 , m − 4
nm−5
¦
km−5 =1
wkm−5 ,km−4 ,m − 4 ⋅
δ
δ wk
A −1 , kA , A
am −5, km−5
Nuevamente aplicamos a la expresión anterior, en este orden, la Ecuación 6.4.4, Regla de
la Cadena, Ecuación 6.4.3, Regla de la Derivada de una Suma y finalmente Ecuación
6.4.15. Por lo tanto obtenemos:
="
=−
nm−5
¦
km−5 =1
218
Δ k m −5 , m − 5
nm−6
¦
km−6 =1
wkm−6 ,km−5 ,m −5 ⋅
δ
δ wk
A −1 , kA , A
am −6,km−6
Capítulo 6. Redes de Perceptrones
Debe ser claro que cada vez estamos más cerca de la capa oculta en cuestión: aquella que
contiene al peso wkA−1 ,kA ,A . Supongamos que aplicamos sucesivamente la secuencia de pasos
antes mencionada hasta que llegamos al punto en donde estamos procesando a las neuronas
en la (O+1)-ésima capa oculta. Es decir, tenemos la siguiente expresión:
="
nA+2
= − ¦ Δ kA + 2 , A + 2
kA+ 2 =1
nA+1
¦w
kA+1 =1
kA+1 , kA+2 , A + 2
⋅
δ
δ wk
A −1 , kA , A
aA +1,kA+1
Tenemos entonces:
nA+ 2
= − ¦ Δ kA + 2 , A + 2
kA+2 =1
nA+1
¦w
kA+1 =1
δ
δ wk
A −1 , kA , A
nA+ 2
= − ¦ Δ kA + 2 , A + 2
kA+2 =1
kA+1 , kA+2 ,A + 2
⋅
§ Por la Ecuación 6.4.4, ·
¨
¸
¨ para la (A +1)-ésima ¸
¨ capa oculta
¸
©
¹
§ nA
·
g ¨ ¦ wkA , kA+1 ,A +1 ⋅ aA , kA ¸
© kA =1
¹
nA+1
¦w
kA+1 =1
kA+1 , kA+2 ,A + 2
⋅
§ nA
·
g ' ¨ ¦ wkA , kA+1 ,A +1 ⋅ aA ,kA ¸ ⋅
© kA =1
¹
δ
δ wk
nA
A −1 , kA , A
nA+2
= − ¦ Δ kA + 2 , A + 2
kA+ 2 =1
¦w
kA+1 =1
¦w
kA =1
⋅ aA ,kA
A −1 , kA , A
kA+1 , kA+2 , A + 2
nA
¦w
kA =1
nA
La sumatoria
kA , kA+1 , A +1
nA+1
δ
δ wk
¦w
kA =1
kA , kA+1 , A +1
kA , kA+1 , A +1
(Regla de la Cadena)
(
)
⋅g ' entkA+1 , A +1 ⋅
⋅ aA , kA
§ Por la Ecuación 6.4.3, ·
¨
¸
¨ para la (A +1)-ésima ¸
¨ capa oculta
¸
©
¹
⋅ aA ,kA considera a todas las neuronas en la O-ésima capa oculta. Sin
embargo, es sólo una la neurona la que contiene a nuestro peso de interés wkA−1 , kA ,A . Por lo
tanto, todos los términos de la sumatoria son constantes respecto a wkA−1 , kA ,A excepto el
kO-ésimo:
219
Una Introducción al Cómputo Neuronal Artificial
nA+ 2
= − ¦ Δ kA + 2 , A + 2
kA+2 =1
nA+1
δ
δ wk
A−1 , kA , A
kA+1 =1
kA+1 , kA+2 , A + 2
(
)
⋅ g ' entkA+1 ,A +1 ⋅
wkA ,kA+1 ,A +1 ⋅ aA , kA
δ
nA+1
= − ¦ Δ kA+1 ,A +1
¦w
kA+1 =1
δ wk
A −1 , kA , A
δ
nA+1
= − ¦ Δ kA+1 ,A +1wkA ,kA+1 ,A +1
kA+1 =1
wkA , kA+1 ,A +1aA ,kA
δ wk
A −1 , kA , A
aA ,kA
§ Por la Ecuación 6.4.15, ·
¨
¸
¨ para la (A +1)-ésima
¸
¨ capa oculta
¸
©
¹
§ El peso wkA , kA+1 ,A +1 es constante ·
¨¨
¸¸
© respecto a wkA−1 ,kA ,A
¹
nA+1
= − ¦ Δ kA+1 ,A +1wkA ,kA+1 ,A +1 ⋅
kA+1 =1
δ
δ wk
A −1 , kA , A
§ nA−1
·
g ¨ ¦ wkA−1 , kA ,A ⋅ aA −1, kA−1 ¸
© kA−1 =1
¹
( Por la Ecuación 6.4.4 )
nA+1
= − ¦ Δ kA+1 ,A +1wkA ,kA+1 ,A +1 ⋅
kA+1 =1
§ nA−1
·
g ' ¨ ¦ wkA−1 , kA ,A ⋅ aA −1,kA−1 ¸ ⋅
© kA−1 =1
¹
δ
δ wk
nA−1
¦w
k =1
A −1 , kA , A A −1
(Regla de la Cadena)
kA−1 , kA ,A
⋅ aA −1, kA−1
(
)
nA+1
= − ¦ Δ kA+1 ,A +1wkA ,kA+1 ,A +1 ⋅ g ' entkA ,A ⋅
kA+1 =1
δ
δ wk
A −1 , kA , A
wkA−1 ,kA ,A ⋅ aA −1, kA−1
nA+1
(
( Por la Ecuación 6.4.3 )
)
= − ¦ Δ kA+1 ,A +1wkA ,kA+1 ,A +1 ⋅ g ' entkA ,A ⋅ aA −1, kA−1
kA+1 =1
= −Δ kA ,A aA −1, kA−1
(Por la Ecuación 6.4.15)
Finalmente, y después de un largo camino, tenemos que:
δE
δ wk
220
A −1 , kA , A
= −Δ kA ,A aA −1,kA−1
1< A < m
(Ecuación 6.4.16)
Capítulo 6. Redes de Perceptrones
Nótese que la notación impuesta por los Términos de Variación o Cambio permite que las
derivadas parciales puedan ser expresadas de manera sumamente concisa. Sin embargo,
debe tenerse en cuenta, sobre todo al momento de la implementación algorítmica, que para
poder obtener el valor del término Δ kA ,A se requiere conocer al término Δ kA+1 ,A +1 . A su vez,
para conocer el valor del término Δ kA+1 ,A +1 se requiere conocer a Δ kA+2 ,A + 2 , y así
sucesivamente hasta llegar a requerir al término Δ km ,m y finalmente a Δi . Ello implica que
conforme estos términos son calculados, es sumamente conveniente guardarlos ya que
serán requeridos para la actualización de las capas ocultas que preceden a sus capas
correspondientes.
x1
I1
x2
I2
a1,1
Ik
xp
Ip
a O,1
am,1
O1
O2
a1,k1
xk
a 2,1
a 2,k2
aO ,kO
am,k m
Oi
a1,n1
a 2,n2
aO,n O
am,n m
Oq
Figura 6.12. En color gris se muestran las neuronas involucradas en la actualización del peso wk ,k ,1 .
1
Este peso se ubica específicamente en la k1-ésima neurona de la primera capa oculta.
Las correcciones aplicadas sobre todas las neuronas de la red, a excepción de las neuronas en la capa
de entrada y de las neuronas en la primera capa oculta (salvo la k1-ésima), influyen sobre la actualización
del peso wk ,k ,1 .
1
Abordemos el último paso concerniente a la determinación de las derivadas
parciales de la Función de Error E para la situación de una red de Perceptrones con al
menos 2 capas ocultas. Requerimos ahora conocer el valor de la derivada parcial de E
respecto al k-ésimo peso de la k1-ésima neurona en la primer capa oculta. Es decir,
δE
. Véase la Figura 6.12. Debe ser claro que la neurona que contiene al
buscaremos
δ wk ,k1 ,1
peso wk ,k1 ,1 únicamente envía sus salidas de manera directa a las neuronas en la segunda
capa oculta. Obviamente está desconectada del resto de las capas ocultas y la capa de
salida. Sin embargo, el peso wk ,k1 ,1 formará parte de todas las sumatorias de salida asociadas
a las neuronas en tales capas incluyendo también a la segunda capa oculta. Esta propiedad
es importante ya que por un lado nos dice que la manera de proceder para encontrar la
derivada parcial es, en un principio, la misma que se aplicó para encontrar, tal como lo
221
Una Introducción al Cómputo Neuronal Artificial
hicimos previamente, el valor de
δE
δ wk
(Ecuación 6.4.16). Esto tiene como
A −1 , kA , A
consecuencia que todos los términos de las sumatorias obtenidas deberán ser preservados.
La concisión en las expresiones que encontremos se da al utilizar las Ecuaciones 6.4.3 y
6.4.15. Sin embargo, por otro lado, la diferencia de proceder se da hasta el momento en que
nos ubiquemos en la segunda capa oculta, que es cuando tendremos acceso directo a las
neuronas en la primera capa oculta. Sabemos que tal acceso se expresa a través de una
sumatoria en la cual cada término está asociado a cada neurona de la primera capa oculta.
Dado que de todas estas neuronas sólo nos interesa la k1-ésima es que los demás términos
de la sumatoria son eliminados. Finalmente, nos encontraremos con la sumatoria de salida
de la neurona de interés, en la cual todos sus términos, excepto el k-ésimo, son eliminados
por ser constantes respecto a wk ,k1 ,1 .
Aplicaremos los pasos descritos anteriormente. Iniciaremos como siempre con la
1 q
2
sustitución de E por ¦ (Ti − Oi ) . Tal como se comentó previamente, se aplicarán las
2 i =1
derivaciones y Ecuaciones requeridas, de manera similar a como se hizo en la
δE
determinación de
(Ecuación 6.4.16). Para este conjunto de operaciones el lector
δ wkA−1 ,kA ,A
puede hacer referencia a los párrafos anteriores. Sin embargo, volveremos a ser específicos
al momento en que se llegue a la tercera capa oculta, donde efectuaremos las operaciones a
detalle.
δE
δ wk ,k ,1
1
=
δ
δ wk ,k ,1
1
1 q
2
(Ti − Oi )
¦
2 i =1
(Por la Ecuación 6.4.7)
= ...
δ
n3
= − ¦ Δ k3 ,3
k3 =1
n2
¦w
δ wk ,k ,1 k =1
1
k2 , k3 ,3
⋅ a2,k2
2
Recordemos que los pesos de todas las neuronas en la tercera capa oculta son constantes
respecto al peso wk , k1 ,1 ya que no existen conexiones directas con las neuronas en la primera
capa oculta. Pero el peso wk ,k1 ,1 está contenido en las salidas de las neuronas de la
segunda capa oculta:
222
Capítulo 6. Redes de Perceptrones
n3
n2
k3 =1
k2 =1
n3
n2
k3 =1
k2 =1
= − ¦ Δ k3 ,3 ¦ wk2 ,k3 ,3 ⋅
δ
δ wk ,k ,1
a2,k2
1
= − ¦ Δ k3 ,3 ¦ wk2 ,k3 ,3 ⋅
§ n1
·
g ¨ ¦ wk1 ,k2 ,2 ⋅ a1,k1 ¸
δ wk ,k1 ,1 © k1 =1
¹
n3
n2
§ n1
·
= − ¦ Δ k3 ,3 ¦ wk2 ,k3 ,3 ⋅ g ' ¨ ¦ wk1 ,k2 ,2 ⋅ a1,k1 ¸
k3 =1
k2 =1
© k1 =1
¹
δ
δ
n1
¦w
δ wk ,k ,1 k =1
1
n3
n2
k3 =1
k2 =1
k1 , k2 ,2
⋅ a1,k1
(
n1
¦w
δ wk ,k ,1 k =1
1
k2 =1
k1 , k2 ,2
)
⋅ a1,k1
§ Por la Ecuación 6.4.3 ·
¨
¸
© haciendo A = 2
¹
1
δ
n2
= − ¦ Δ k2 ,2
(Regla de la Cadena)
1
= − ¦ Δ k3 ,3 ¦ wk2 ,k3 ,3 ⋅ g ' entk2 ,2
δ
§ Por la Ecuación 6.4.4 ·
¨
¸
© haciendo A = 2
¹
n1
¦w
δ wk ,k ,1 k =1
k1 , k2 ,2
⋅ a1,k1
1
1
§ Por la Ecuación 6.4.15, ·
¨
¸
© haciendo A = 2
¹
Nótese que el peso wk ,k1 ,1 estará contenido únicamente en la salida de la k1-ésima neurona
n1
en la primera capa oculta. Por lo tanto, todos los términos de la sumatoria
¦w
k1 =1
k1 , k2 ,2
⋅ a1,k1
son constantes, excepto el k1-ésimo, respecto a wk ,k1 ,1 :
δ
n2
= − ¦ Δ k2 ,2 wk1 ,k2 ,2 ⋅
k2 =1
δ wk ,k ,1
a1,k1
1
δ
n2
= − ¦ Δ k2 ,2 wk1 ,k2 ,2 ⋅
k2 =1
δ wk ,k ,1
1
§ p
·
g ¨ ¦ wk , k1 ,1 ⋅ I k ¸
© k =1
¹
§
·
= − ¦ Δ k2 ,2 wk1 ,k2 ,2 ⋅ g ' ¨ ¦ wk ,k1 ,1 ⋅ I k ¸
k2 =1
© k =1
¹
n2
§ Por la Ecuación 6.4.6 ·
¨
¸
© haciendo A = 1
¹
p
δ
p
δ wk ,k ,1
1
¦w
k =1
k , k1 ,1
(Regla de la Cadena)
⋅ Ik
223
Una Introducción al Cómputo Neuronal Artificial
De todos los términos en la Sumatoria de Salida de la k1-ésima neurona en la primera capa
oculta únicamente nos interesa el k-ésimo, que es precisamente wk ,k1 ,1 ⋅ I k :
§ p
·
= − ¦ Δ k2 ,2 wk1 ,k2 ,2 ⋅ g ' ¨ ¦ wk , k1 ,1 ⋅ I k ¸ ⋅
k2 =1
© k =1
¹
n2
δ
δ wk ,k ,1
wk ,k1 ,1 ⋅ I k
1
n2
§ p
·
= − ¦ Δ k2 ,2 wk1 ,k2 ,2 ⋅ g ' ¨ ¦ wk , k1 ,1 ⋅ I k ¸ ⋅ I k
k2 =1
© k =1
¹
n2
(
)
= − ¦ Δ k2 ,2 wk1 ,k2 ,2 ⋅ g ' entk1 ,1 ⋅ I k
(Por la Ecuación 6.4.5)
= −Δ k1 ,1 ⋅ I k
§ Por la Ecuación 6.4.15, ·
¨
¸
© haciendo A = 1
¹
k2 =1
Concretizando:
δE
δ wk ,k ,1
= −Δ k1 ,1 ⋅ I k
(Ecuación 6.4.17)
1
Por fin, y después de un largo viaje matemático, contamos con las derivadas
parciales que forman al vector gradiente de la Función de Error E. Suponemos que el
número de capas ocultas es al menos 2, es decir, m ≥ 2:
•
•
•
•
δE
δ wk
= −Δ i ⋅ am, km
m ,i
δE
δ wk
= −Δ km ,m ⋅ am −1, km−1
m−1 , km , m
δE
δ wk
A −1 , kA , A
δ
δ wk ,k ,1
= −Δ kA ,A aA −1, kA−1 , 1 < A < m
= −Δ k1 ,1 ⋅ I k
1
Sabemos que estas derivadas parciales representan las direcciones de máximo crecimiento
de la Función de Error E. Por lo tanto, para actualizar los pesos de las neuronas en la capa
de salida y en las capas ocultas se requiere la dirección opuesta del gradiente a fin de
minimizar el error. En consecuencia tendremos las siguientes reglas de actualización, o
corrección, de pesos:
224
Capítulo 6. Redes de Perceptrones
•
Para los pesos de las neuronas en la capa de salida:
wkm ,i = wkm ,i + α⋅Δi⋅ am,km
•
Para los pesos de las neuronas en la última capa oculta:
wkm−1 ,km , m = wkm−1 ,km , m + α⋅ Δ km ,m ⋅ am −1, km−1
•
(Ecuación 6.4.19)
Para los pesos de las neuronas en la O-ésima capa oculta, 1 < O < m:
wkA−1 , kA ,A = wkA−1 , kA ,A + α⋅ Δ kA ,A ⋅ aA −1,kA−1
•
(Ecuación 6.4.18)
(Ecuación 6.4.20)
Para los pesos de las neuronas en la primera capa oculta:
wk ,k1 ,1 = wk ,k1 ,1 + α⋅ Δ k1 ,1 ⋅Ιk
(Ecuación 6.4.21)
Donde α es nuestro bien conocido Coeficiente de Aprendizaje.
Realmente lo que nos queda por hacer es especificar al Algoritmo de
Retropropagación para el ajuste de pesos en una Red Neuronal de Perceptrones con al
menos 2 capas ocultas. Como ya mencionamos al inicio de esta Sección, el proceso de
ajuste de los pesos se dividirá en 4 fases. Dado un vector de entrada, tenemos en primer
lugar que se ajustarán los pesos de las neuronas en la capa de salida, aplicando la Ecuación
6.4.18. Una vez finalizada esta etapa se procederá al ajuste de los pesos en las neuronas en
la última capa oculta. Se deberá utilizar la Ecuación 6.4.19. La fase 3 comprende el ajuste
de los pesos de las neuronas en las capas ocultas intermedias, comenzando a partir de la
penúltima capa oculta y terminando en la segunda capa oculta. Las neuronas de cada capa
son procesadas y actualizadas haciendo uso de la regla presentada en la Ecuación 6.4.20.
Por último, en la cuarta fase tendremos que ajustar los pesos de las neuronas en la primera
capa oculta aplicando la Ecuación 6.4.21. Como ya se comentó con anterioridad, es
sumamente importante, a fin de no afectar la eficiencia del Algoritmo de Retropropagación,
el guardar, conforme se van calculado, los valores de:
• Δi: al actualizar los pesos de las neuronas en la capa de salida.
• Δ km ,m : al actualizar los pesos de las neuronas en la última capa oculta.
•
Δ kA ,A : al actualizar los pesos de las neuronas en las capas ocultas intermedias, 1 < O < m.
Ya que, como se ha visto, éstos son requeridos para la actualización de los pesos en las
capas ocultas. Las 4 fases descritas se ejecutan por cada elemento del conjunto de
entrenamiento. A su vez, el conjunto de entrenamiento es presentado tantas veces se
requiera. Otra opción es establecer una Función de Error que permita medir el desempeño
de la red una vez que se ha efectuado una presentación del conjunto de entrenamiento y si
el error obtenido es menor o igual a un error mínimo aceptable entonces se finaliza el
entrenamiento.
225
Una Introducción al Cómputo Neuronal Artificial
De manera más específica tenemos entonces que la secuencia de pasos a efectuar
por el Algoritmo de Retropropagación es la siguiente:
•
•
Inicializar los pesos de todas las neuronas de manera aleatoria con valores en (-1, 1).
Repetir hasta que la red proporcione salidas con un error aceptable o bien hasta que el
número requerido de presentaciones del conjunto de entrenamiento haya sido
alcanzado:
o Para cada vector χ en el conjunto de entrenamiento:
ƒ
ƒ
ƒ
Obtener la correspondiente salida O de la red.
Obtener el vector de salida esperada T asociado al vector de entrada χ.
Para i = 1 hasta q:
• Calcular Erri = Ti – Oi
ƒ
Fase 1 - Actualización de pesos en las neuronas de la capa de salida:
• Para cada neurona i en la capa de salida, i = 1, 2, …, q:
o Obtener Δi.
o Para km = 1 hasta nm:
ƒ wkm ,i = wkm ,i + α⋅Δi⋅ am,km
ƒ
Fase 2 - Actualización de pesos en las neuronas de la última capa oculta:
• Para cada neurona km en la última capa oculta, km = 1, 2, …, nm:
o Obtener Δ km ,m .
o Para km-1 = 1 hasta nm-1:
ƒ wkm−1 ,km , m = wkm−1 ,km , m + α⋅ Δ km ,m ⋅ am −1, km−1
ƒ
Fase 3 - Actualización de pesos en las neuronas en la (m-1)-ésima capa oculta
hasta la segunda capa oculta:
• Para O = m-1 hasta 2:
o Para cada neurona kOen la O-ésima capa oculta, kO = 1, 2, …, nO:
ƒ Obtener Δ kA ,A .
ƒ
ƒ
226
Para kO-1 = 1 hasta nO-1:
• wkA−1 ,kA ,A = wkA−1 ,kA ,A + α⋅ Δ kA ,A ⋅ aA −1,kA−1
Fase 4 - Actualización de pesos en las neuronas de la primer capa oculta:
• Para cada neurona k1 en la primer capa oculta, k1 = 1, 2, …, n1:
o Para k = 1 hasta p:
ƒ wk , k1 ,1 = wk , k1 ,1 + α⋅ Δ k1 ,1 ⋅Ιk
Capítulo 6. Redes de Perceptrones
Sabemos que cuando el Algoritmo de Retropropagación ha finalizado es que se
cuenta con una Corrida. Debe tenerse en consideración, tal como comentamos en la
Sección anterior, que no es posible, aún en el caso de 2 o más capas ocultas, garantizar el
aprendizaje óptimo en términos de que los pesos encontrados efectivamente minimizan a
nuestra función de error. Es posible que éstos correspondan a un mínimo local. Otra
situación que puede presentarse es que el lugar geométrico descrito por la función de error
carezca de puntos críticos y en particular de mínimos. En este sentido la convergencia de
los pesos nunca tendrá lugar. Por ello mismo, es que por lo regular se recomienda efectuar
más de una corrida. La idea detrás de este proceder, como ya comentamos antes, es la de
efectuar una exploración en diferentes regiones de la función de error. Aunque ello no
garantiza que se encontrarán los pesos óptimos, es una manera empírica de identificar si los
resultados obtenidos para una corrida, es decir los pesos encontrados, corresponden a
mínimos locales o globales.
6.5 Aplicación: Predicción de Señales
Recordemos que en los Capítulos 1 y 4 establecimos al problema de la Predicción
de Señales como el modelado de una serie de tiempo de manera que sea posible determinar
cómo se comportará en el futuro. En la Sección 4.3 este problema fue abordado como una
aplicación de la Neurona tipo Perceptrón. En ese caso se asumía que la señal se ajustaba a
un modelo de Serie de Tiempo de M-ésimo Orden de Parámetros Autorregresivos. El
objetivo era determinar a los M parámetros que definían a la señal. Tales parámetros, como
se recordará, estaban representados por los pesos de la neurona. Una vez que se finalizaba
el entrenamiento es que recurríamos a inspeccionar tales pesos y éstos se utilizaban para
generar una nueva señal, junto con los vectores en el conjunto de entrenamiento, y
determinar si la aproximación obtenida era lo suficientemente buena al compararla con la
señal original. En esta Sección veremos como es que una Red de Perceptrones puede
proporcionarnos una solución interesante pero ahora partiremos de una suposición
diferente: no tenemos conocimiento alguno respecto a qué modelo se ajusta la señal. Sólo
contamos con las muestras que la forman y nada más. En particular, trabajaremos con un
Red formada por exactamente dos capas ocultas. En primer lugar recordaremos algunos
conceptos planteados en la Sección 4.3. Posteriormente aplicaremos las reglas de
actualización definidas en la Sección anterior, pero las haremos instancias de nuestro caso
con m = 2 capas ocultas. Definiremos entonces al Algoritmo de Retropropagación
específico para el entrenamiento de una Red formada por dos capas ocultas y lo
aplicaremos a fin de que nuestra red modele la señal dada.
Sea K el número de muestras que conforman a nuestra señal. Cada muestra es de
hecho un número xn que es el valor de la señal en el momento n. Supondremos que el valor
de cualquier muestra xn tiene influencia de los valores de las muestras que le preceden y
tendrá influencia sobre los valores que le prosiguen. Sabemos que este razonamiento parte
de hecho de que los elementos de una serie de tiempo no son independientes entre sí. Por
ejemplo, el comportamiento actual de la Bolsa de Valores depende en gran medida de los
comportamientos de la misma en días previos. O bien, tenemos conocimiento que por lo
227
Una Introducción al Cómputo Neuronal Artificial
regular un sismo de gran magnitud en un día dado incide sobre la actividad sísmica en días
posteriores, de donde se tienen las llamadas Réplicas. En este sentido tenemos que las K
muestras, a fin de formar el conjunto de entrenamiento, serán usadas para formar
subsecuencias de la serie de tiempo. Tales subsecuencias serán de tamaño M ≥ 1 y cada una
dará lugar a un vector de entrada para nuestra red neuronal:
ª xn −1 º
«x »
« n −2 »
« xn −3 »
«
»
« # »
«¬ xn − M »¼
La idea ahora es que dado un vector de entrada formado por la subsecuencia xn-M, …, xn-2,
xn-1, la Red Neuronal proporcione como salida un estimado para la muestra xn. A tal
estimado lo denotaremos por xn’. La idea, como siempre, es ajustar los pesos de la red de tal
forma que la diferencia entre xn y xn’ sea tan pequeña como sea posible.
Dado que tenemos K muestras entonces los vectores de entrada, en \ M , estarán
dados por:
ª xM º ª xM +1 º ª xM + 2 º
ª xK −1 º
«x » « x » «x »
«x »
« M −1 » « M » « M +1 »
« K −2 »
« xM − 2 » , « xM −1 » , « xM » , ! , « xK −3 »
«
» «
» «
»
«
»
« # » « # » « # »
« # »
«¬ x1 »¼ «¬ x2 »¼ «¬ x3 »¼
«¬ xK − M »¼
Los respectivos vectores de salida esperada, en este caso en \ , serán entonces:
[ xM +1 ] , [ xM +2 ] , [ xM +3 ] , ! , [ xK ]
La señal con la que trabajaremos se conforma por K = 2,000 muestras. Véase la
Figura 6.13. Dado que K = 2,000 entonces podemos formar K – M vectores de entrada. En
nuestro caso trabajaremos con M = 7. Ello implica que contaremos con 1,993 vectores de
entrada, pero nuestro conjunto de entrenamiento se conformará únicamente por los
primeros 1,000 vectores. Los restantes 993 vectores serán utilizados, una vez finalizado el
entrenamiento, como Conjunto de Evaluación. Un conjunto de evaluación es un conjunto
de vectores los cuales se “ocultan” a la red y que se utiliza para medir su desempeño
usando entradas que no fueron presentadas durante su entrenamiento. Para estas entradas
tenemos también identificadas las salidas esperadas. La idea es determinar la robustez de
nuestra red cuando información nueva le sea proporcionada. También sirve para establecer
si el ajuste pesos no se sesgó a favor de una simple “memorización” de los vectores en el
conjunto de entrenamiento. Véase entonces en la Figura 6.14 la sección de la señal que se
presentará a la red durante el entrenamiento y la sección que se utilizará para efectos de
evaluación.
228
Capítulo 6. Redes de Perceptrones
1.2
xn
1
0.8
0.6
0.4
0.2
n
0
0
200
400
600
800
1000
1200
1400
1600
1800
2000
1800
2000
Figura 6.13. Una serie de tiempo formada por K = 2,000 muestras.
1.2
xn
1
0.8
0.6
0.4
0.2
n
0
0
200
400
600
800
1000
1200
1400
1600
Figura 6.14. La serie de tiempo originalmente presentada en la Figura 6.13.
En color negro, las muestras utilizadas para formar el conjunto de entrenamiento.
En color gris, las muestras que conformarán al conjunto de evaluación.
229
Una Introducción al Cómputo Neuronal Artificial
Concentrémonos ahora en los aspectos particulares del Algoritmo de
Retropropagación bajo una red con dos capas ocultas. En primer lugar requerimos del
procedimiento para que, dado un vector de entrada, la red proporcione, utilizando los pesos
actuales, la salida correspondiente. Sabemos que entonces simplemente tenemos un proceso
de propagación. El vector de entrada se presenta a la capa de entrada la cual meramente
distribuye sus p componentes a la primer capa oculta. Las n1 neuronas en la primer capa
oculta procesan entonces su vector de entrada y producen como salida un vector en \ n1 .
Este nuevo vector es enviado como entrada a las n2 neuronas que forman a la segunda capa
oculta, produciéndose como salida un vector en \ n2 . Finalmente este vector es llevado a las
q neuronas que forman la capa de salida produciendo entonces la salida final de la red: un
vector en \ q . Este proceso es implementado de manera directa en el Algoritmo 6.4. El
procedimiento, aparte del vector de entrada X, recibe otras 7 entradas:
• p: dimensionalidad de los vectores de entrada.
• n1: número de neuronas en la primer capa oculta.
• n2: número de neuronas en la segunda capa oculta.
• q: número de neuronas en la capa de salida.
• W_HLayer1: una matriz de tamaño n1 × p que contiene los pesos de las neuronas en la
primer capa oculta.
• W_HLayer2: una matriz de tamaño n2 × n1 que contiene los pesos de las neuronas en la
segunda capa oculta.
• W_Output: una matriz de tamaño q × n2 que contiene los pesos de las neuronas en la
capa de salida.
El Algoritmo 6.4 retorna como salida 3 vectores: el vector a1 que corresponde a la salida
producida por la primer capa oculta, el vector a2 que corresponde a la salida producida por
la segunda capa oculta y el vector O que es la salida final de la red. Como bien sabemos
todos estos vectores son requeridos por el Algoritmo de Retropropagación.
Algoritmo 6.4. Propagación de un vector de entrada en una red de Perceptrones con dos capas ocultas.
Procedure TwoLayerPropagation(Integer p, Integer n1, Integer n2, Integer q,
Matrix W_HLayer1[1,…,n1][1,…,p], Matrix W_HLayer2[1,…,n2][1,…,n1],
Matrix W_Output[1,…,q][1,…,n2], Array X[1,…,p])
I = new Array[1,…,p]
a1 = new Array[1,…,n1]
a2 = new Array[1,…,n2]
O = new Array[1,…,q]
// Se obtiene la salida de la capa de entrada. El vector X se copia al arreglo I.
for k = 1 until p do
I[k] = X[k]
end-of-for
// El vector I es enviado como entrada a las neuronas en la primer capa oculta.
// Se produce como salida el vector a1.
230
Capítulo 6. Redes de Perceptrones
for k1 = 1 until n1 do
// Se procesa a la k1-ésima neurona.
p
// Se calcula entk1 ,1 = ¦ wk ,k1 ,1 ⋅ I k .
k =1
Real ent_k1_1 = 0
for k = 1 until p do
ent_k1_1 = ent_k1_1 + W_HLayer1[k1][k] * I[k]
end-of-for
// Se aplica la función de activación y se obtiene la salida.
a1[k1] = g(ent_k1_1)
end-of-for
// El vector a1 es enviado como entrada a las neuronas en la segunda capa oculta.
// Se produce como salida el vector a2.
for k2 = 1 until n2 do
// Se procesa a la k2-ésima neurona.
n1
// Se calcula entk2 ,2 = ¦ wk1 ,k2 ,2 ⋅ a1, k1 .
k1 =1
Real ent_k2_2 = 0
for k1 = 1 until n1 do
ent_k2_2 = ent_k2_2 + W_HLayer2[k2][k1] * a1[k1]
end-of-for
// Se aplica la función de activación y se obtiene la salida.
a2[k2] = g(ent_k2_2)
end-of-for
// El vector a2 es enviado como entrada a las neuronas en la capa de salida.
// Se produce como salida final de la red el vector O.
for i = 1 until q do
// Se procesa a la i-ésima neurona.
n2
// Se calcula enti = ¦ wk2 ,i ⋅ a2,k2
k2 =1
Real ent_i = 0
for k2 = 1 until n2 do
ent_i = ent_i + W_Output[i][k2] * a2[k2]
end-of-for
// Se aplica la función de activación y se obtiene la salida.
O[i] = g(ent_i)
end-of-for
// Se retornan los vectores a1, a2 y O.
return {a1, a2, O}
end-of-procedure
231
Una Introducción al Cómputo Neuronal Artificial
Veamos ahora la instancia del Algoritmo de Retropropagación bajo una red con dos
capas ocultas. Es claro que haremos referencia a las Ecuaciones presentadas en la Sección
anterior. Primero describamos textualmente los pasos que deberán ser efectuados:
• Inicializar los pesos de todas las neuronas de manera aleatoria con valores en (-1, 1).
• Repetir hasta que la red proporcione salidas con un error aceptable o bien hasta que el
número requerido de presentaciones del conjunto de entrenamiento haya sido alcanzado:
o Para cada vector χ en el conjunto de entrenamiento:
ƒ Obtener la correspondiente salida O de la red.
ƒ Obtener el vector de salida esperada T asociado al vector de entrada χ.
ƒ Para i = 1 hasta q:
• Calcular Erri = Ti – Oi
ƒ Fase 1 - Actualización de pesos en las neuronas de la capa de salida:
• Para cada neurona i en la capa de salida, i = 1, 2, …, q:
o Calcular (Ecuación 6.4.10, haciendo m = 2):
§
§ n2
· · § n2
·
Δ i = Erri ⋅ g '(enti ) = ¨ Ti − g ¨ ¦ wk2 ,i ⋅ a2,k2 ¸ ¸ ⋅ g ' ¨ ¦ wk2 ,i ⋅ a2,k2 ¸
¨
¸
© k2 =1
¹ ¹ © k2 =1
¹
©
o Para k2 = 1 hasta n2:
ƒ wk2 ,i = wk2 ,i + α⋅Δi⋅ a2,k2
(Ecuación 6.4.18, m = 2)
ƒ
Fase 2 - Actualización de pesos en las neuronas de la segunda capa oculta:
• Para cada neurona k2 en la segunda capa oculta, k2 = 1, 2, …, n2:
o Calcular (Ecuación 6.4.13, haciendo O = 2, m = 2)
q
q
§ n1
·
Δ k2 ,2 = ¦ Δi ⋅ wk2 ,i ⋅ g ' entk2 ,2 = ¦ Δ i ⋅ wk2 ,i ⋅ g ' ¨ ¦ wk1 ,k2 ,2 ⋅ a1,k1 ¸
i =1
i =1
© k1 =1
¹
o Para k1 = 1 hasta n1:
ƒ wk1 ,k2 ,2 = wk1 ,k2 ,2 + α⋅ Δ k2 ,2 ⋅ a1,k1
(Ecuación 6.4.19, m = 2)
(
ƒ
ƒ
)
(Fase 3 - Actualización de pesos en las neuronas en las capas ocultas
intermedias)
Fase 4 - Actualización de pesos en las neuronas de la primer capa oculta:
• Para cada neurona k1 en la primer capa oculta, k1 = 1, 2, …, n1:
o Calcular (Ecuación 6.4.15, haciendo O = 1)
n2
n2
§ p
·
Δ k1 ,1 = ¦ Δ k2, 2 ⋅ wk1 ,k2 ,2 ⋅ g '(entk1 ,1 ) = ¦ Δ k2, 2 ⋅ wk1 ,k2 ,2 ⋅ g ' ¨ ¦ wk ,k1 ,1 ⋅ I k ¸
k2 =1
k2 =1
© k =1
¹
o Para k = 1 hasta p:
ƒ wk , k1 ,1 = wk , k1 ,1 + α⋅ Δ k1 ,1 ⋅Ιk
(Ecuación 6.4.21)
De acuerdo al procedimiento de Retropropagación descrito en la Sección anterior tenemos
que considerar 4 fases: (1) actualización de los pesos la neuronas en la capa de entrada, (2)
actualización de los pesos en la última capa oculta, (3) actualización de los pesos en las
neuronas de las capas ocultas intermedias, y (4) actualización de los pesos en la primer capa
oculta. En la instancia para una red de dos capas ocultas hemos hecho mención de la fase 3,
sólo por consistencia con la Sección anterior, aunque es claro que realidad no se hace nada.
232
Capítulo 6. Redes de Perceptrones
Contamos ya con los elementos para presentar la instancia específica del Algoritmo
de Retropropagación para una Red de Perceptrones formada por dos capas ocultas. Véase el
Algoritmo 6.5. Nuestro procedimiento recibe 8 entradas:
•
•
•
•
•
•
•
•
Un entero N que denota al tamaño del conjunto de entrenamiento.
Un entero p que indica la dimensionalidad de los vectores de entrada.
Un entero n1 que corresponde al número de neuronas en la primer capa oculta.
Un entero n2 que corresponde al número de neuronas en la segunda capa oculta.
Un entero q que denota al número de neuronas en la capa de salida.
Una matriz X de tamaño N × p que contiene a los vectores de entrada.
Una matriz T de tamaño N × q que contiene a los vectores de salida esperada.
Un entero L que indica el número de presentaciones del conjunto de entrenamiento.
Nótese que el Algoritmo 6.5 no recibe un Coeficiente de Aprendizaje. Ello se debe a que
utilizaremos un coeficiente que cambiará a lo largo del tiempo y en función de la
presentación del conjunto de entrenamiento que se esté efectuando. La fórmula que
utilizaremos para obtener a nuestro coeficiente será:
α (t ) =
1
1+ t
(Ecuación 6.5.1)
Ello implica que en la primer presentación del conjunto (t = 1) el coeficiente a utilizar será
1 , en la segunda presentación (t = 2) tendremos α (2) = 1 y así sucesivamente. La
2
3
Figura 6.15 muestra la evolución del Coeficiente de Aprendizaje para una situación en la
que se efectúan 500 presentaciones del conjunto de entrenamiento. El Algoritmo 6.5
retorna como salida tres matrices:
•
•
•
W_HLayer1: una matriz de n1 × p que contiene los pesos de las neuronas en la primer
capa oculta.
W_HLayer2: una matriz de n2 × n1 que contiene los pesos de las neuronas en la segunda
capa oculta.
W_Output: una matriz de q × n2 que contiene los pesos de las neuronas en la capa de
salida.
Algoritmo 6.5. Entrenamiento por Retropropagación
para una Red de Perceptrones con dos capas ocultas.
Procedure TwoLayerPropagation(Integer N, Integer p, Integer n1, Integer n2, Integer q,
Matrix X[1,…,N][1,…,p], Matrix T[1,…,N][1,…q], Integer L)
W_HLayer1 = new Matrix[1,…,n1][1,…,p]
W_HLayer2 = new Matrix[1,…,n2][1,…,n1]
W_Output = new Matrix[1,…,q][1,…,n2]
233
Una Introducción al Cómputo Neuronal Artificial
// Los pesos de todas las neuronas se inicializan con valores aleatorios en (-1,1).
// Se inicializan los pesos de las neuronas en la capa de salida.
for i = 1 until q do
for k2 = 1 until n2 do
W_Output[i][k2] = Random( )
end-of-for
end-of-for
// Se inicializan los pesos de las neuronas en la segunda capa oculta.
for k2 = 1 until n2 do
for k1 = 1 until n1 do
W_HLayer2[k2][k1] = Random( )
end-of-for
end-of-for
// Se inicializan los pesos de las neuronas en la primer capa oculta.
for k1 = 1 until n1 do
for k = 1 until p do
W_HLayer1[k1][k] = Random( )
end-of-for
end-of-for
Δ_i = new Matrix[1,…,q]
Δ_k2_2 = new Matrix[1,…,n2]
Err = new Array[1,…,q]
for t = 1 until L do
// Se efectúa la t-ésima presentación del conjunto de entrenamiento.
// Se actualiza el coeficiente de aprendizaje.
Real α = 1 / (1 + t)
for m = 1 until N do
// Se envía a la red al m-ésimo vector de entrada.
{a1, a2, O} = TwoLayerPropagation
(p, n1, n2, q, W_HLayer1, W_HLayer2, W_Output, X[m])
// a1 es el vector de salida de la primer capa oculta.
// a2 es el vector de salida de la segunda capa oculta.
// O es el vector de salida final de la red.
// Se determina al error entre la salida esperada y la salida
// proporcionada por la red.
for i = 1 until q do
Err[i] = T[m][i] – O[i]
end-of-for
234
Capítulo 6. Redes de Perceptrones
// Se actualizan los pesos en las neuronas de la capa de salida.
for i = 1 until q do
// Se procesa a la i-ésima neurona.
n2
// Se calcula enti =
¦w
k2 =1
k 2 ,i
⋅ a2,k2 .
Real ent_i = 0
for k2 = 1 until n2 do
ent_i = ent_i + W_Output[i][k2] * a2[k2]
end-of-for
// Se calcula Δi = Erri ⋅ g '(enti ) .
Δ_i[i] = Err[i] * g_derivative(ent_i)
// Se actualiza cada peso de la i-ésima neurona.
for k2 = 1 until n2 do
W_Output[i][k2] = W_Output[i][k2] +
α * Δ_i[i] * a2[k2]
end-of-for
end-of-for
// Se actualizan los pesos en las neuronas de la segunda capa oculta.
for k2 = 1 until n2 do
// Se procesa a la k2-ésima neurona.
n1
// Se calcula entk2 ,2 = ¦ wk1 ,k2 ,2 ⋅ a1, k1 .
k1 =1
Real ent_k2_2 = 0
for k1 = 1 until n1 do
ent_k2_2 = ent_k2_2 + W_HLayer2[k2][k1] * a1[k1]
end-of-for
q
(
)
// Se calcula Δ k2 ,2 = ¦ Δ i ⋅ wk2 ,i ⋅ g ' entk2 ,2 .
i =1
Δ_k2_2[k2] = 0
for i = 1 until q do
Δ_k2_2[k2] = Δ_k2_2[k2] + Δ_i[i] * W_Output[i][k2]
end-of-for
Δ_k2_2[k2] = Δ_k2_2[k2] * g_derivative(ent_k2_2)
// Se actualiza cada peso de la k2-ésima neurona.
for k1 = 1 until n1 do
W_HLayer2[k2][k1] = W_HLayer2[k2][k1] +
α * Δ_k2_2[k2] * a1[k1]
end-of-for
end-of-for
235
Una Introducción al Cómputo Neuronal Artificial
// Se actualizan los pesos en las neuronas de la primer capa oculta.
for k1 = 1 until n1 do
// Se procesa a la k1-ésima neurona.
p
// Se calcula entk1 ,1 = ¦ wk ,k1 ,1 ⋅ I k .
k =1
Real ent_k1_1 = 0
for k = 1 until p do
ent_k1_1 = ent_k1_1 + W_HLayer1[k1][k] * X[m][k]
end-of-for
n2
// Se calcula Δ k1 ,1 = ¦ Δ k2, 2 ⋅ wk1 , k2 ,2 ⋅ g '(entk1 ,1 ) .
k2 =1
Real Δ_k1_1 = 0
for k2 = 1 until n2 do
Δ_k1_1 = Δ_k1_1 + Δ_k2_2[k2] * W_HLayer2[k2][k1]
end-of-for
Δ_k1_1 = Δ_k1_1 * g_derivative(ent_k1_1)
// Se actualiza cada peso de la k1-ésima neurona.
for k = 1 until p do
W_HLayer1[k1][k] = W_HLayer1[k1][k] +
α * Δ_k1_1 * X[k]
end-of-for
end-of-for
end-of-for
// Se determina el error global de la red.
// Se calcula el promedio de las distancias Euclidianas entre los vectores
// de salida esperada y los vectores proporcionados por la red.
Real error = 0
for m = 1 until N do
// Se envía a la red al m-ésimo vector de entrada.
{a1, a2, O} = TwoLayerPropagation
(p, n1, n2, q, W_HLayer1, W_HLayer2, W_Output, X[m])
Real d = 0
for i = 1 until q do
d = d + Pow(T[m][i] – O[i], 2)
end-of-for
error = error + d
end-of-for
error = error / N
Print(error)
end-of-for
// Se retornan como salida los pesos encontrados.
return {W_HLayer1, W_HLayer2, W_Output}
end-of-procedure
236
Capítulo 6. Redes de Perceptrones
α
1.2
1
0.8
0.6
0.4
0.2
0
1
50
100
150
200
250
300
350
400
450
500
t
Figura 6.15. Evolución del Coeficiente de Aprendizaje α (t ) = 1 a lo largo
1+ t
de 500 presentaciones del conjunto de entrenamiento. En la última instancia se tiene α(500) ≈ 0.0019.
Una inspección de la codificación del Algoritmo 6.5 permitirá apreciar que se
calcula un Error Global una vez que se ha efectuado una presentación del conjunto de
entrenamiento. El cálculo de este error requiere que se presente a todos los vectores en el
conjunto de entrenamiento utilizando los pesos actuales de las neuronas pero sin
modificarlos. Utilizando el Algoritmo 6.4, cada vector de entrada es presentado y se
obtiene el correspondiente vector de salida O proporcionada por la red. Posteriormente se
calcula la Distancia Euclidiana entre el vector O y el correspondiente vector T de salida
esperada. La idea es que si el error es mínimo entonces las distancias serán pequeñas. Las
distancias se suman y finalmente se dividen entre el tamaño N del conjunto del
entrenamiento. Es decir, nuestro Error Global no es mas que el promedio de las Distancias
Euclidianas entre de los vectores de salida esperada y los vectores proporcionados por la
red. Esta función de error se utiliza para medir el aprendizaje de la red conforme el proceso
de entrenamiento se efectúa.
Retornemos a nuestro caso de estudio, es decir, el modelado de la señal presentada
en la Figura 6.13. Sabemos que ésta se conforma por K = 2,000 muestras. El tamaño de las
subsecuencias a considerar, para formar los vectores de entrada, es M = 7. Ya comentamos
que tendremos un conjunto de entrenamiento formado por N = 1,000 vectores de entrada y
un conjunto de evaluación compuesto por 993 vectores. La estructura de la red que
237
Una Introducción al Cómputo Neuronal Artificial
consideraremos se presenta en la Figura 6.16. Tenemos p = 7 neuronas de entrada, las
cuales sabemos no efectúan ningún procesamiento y cuya finalidad es la de distribuir a los
vectores de entrada hacia todas las neuronas en la primer capa oculta. Se tienen n1 = 8
neuronas en la primer capa oculta y n2 = 5 neuronas en la segunda capa oculta. Recordemos
que la red recibirá un vector en \ 7 que contiene una subsecuencia de la señal
[xn-1 xn-2 xn-3 xn-4 xn-5 xn-6 xn-7]T y proporcionará como salida un escalar que corresponde
a la predicción xn’ para la muestra xn. Por ello mismo tendremos sólo una neurona en la
capa de salida, q = 1. Nótese como es que todos los valores de la señal se encuentran dentro
del intervalo [0, 1]. Por lo tanto la Función de Activación que utilizaremos será la Función
Sigmoide (Ecuación 4.1.4), la cual, como apreciamos en el Capítulo 4, tiene su codominio
en (0,1):
1
g ( z) =
1 + e− z
a1,1
x1
I1
x2
I2
x3
I3
x4
I4
a1,2
a2,1
a1,3
a2,2
a1,4
a2,3
O1
a1,5
x5
I5
x6
I6
x7
I7
a2,4
a1,6
a2,5
a1,7
a1,8
Figura 6.16. Una Red de Perceptrones con dos capas ocultas.
Se utilizará para modelar a la serie de tiempo presentada en la Figura 6.13.
Al aplicar el Algoritmo 6.5 con L = 500 presentaciones del conjunto de
entrenamiento se obtuvieron los pesos presentados en la Tabla 6.1. En la Figura 6.17 se
presenta una gráfica con la evolución del Error Global de la red conforme el entrenamiento
avanzaba. Nótese como es que en las primeras 50 presentaciones del conjunto de
entrenamiento se tuvieron los cambios más drásticos en cuanto a los errores obtenidos. Una
vez efectuada la primer presentación (t = 1) el error global fue de 0.1059. Después de la
segunda presentación (t = 2) éste fue de 0.0685. Recordemos que el Coeficiente de
238
Capítulo 6. Redes de Perceptrones
1
1
y , respectivamente. En la tercer presentación
2
3
(t = 3) del conjunto de entrenamiento se tuvo un error global de 0.0547. Al presentar al
conjunto por décima ocasión (t = 10) se contó con un error 0.0496. En la presentación
t = 20 el error fue de 0.0488. En la presentación t = 50, con un Coeficiente de Aprendizaje
1
α = ≈ 0.0196 , el error global obtenido fue de 0.0478. El error Global Final, una vez
51
efectuadas las 500 presentaciones del conjunto de entrenamiento, fue de 0.0458.
Recordemos que durante el entrenamiento, a la red le fue presentada únicamente
información referente a las primeras 1,000 muestras de 2,000 que forman la señal.
Aprendizaje en estos dos casos fue de
Tabla 6.1. Pesos asociados a la Red de Perceptrones de la Figura 6.16 una vez que se aplicó
el Algoritmo de Retropropagación con 500 presentaciones del conjunto de entrenamiento.
Pesos Neuronas Primer Capa Oculta
Neurona a1,1
w1,1,1 = -0.4341
w2,1,1 = -0.2744
w3,1,1 = 0.5131
w4,1,1 = -0.9535
w5,1,1 = 0.9207
w6,1,1 = 0.5544
w7,1,1 = 0.2594
Neurona a1,5
w1,5,1 = -0.5186
w2,5,1 = -0.1219
w3,5,1 = -0.9797
w4,5,1 = -0.8753
w5,5,1 = -0.7295
w6,5,1 = -0.7908
w7,5,1 = 0.42148
Neurona a1,2
w1,2,1 = 0.0079
w2,2,1 = 0.9458
w3,2,1 = -0.3605
w4,2,1 = 0.9001
w5,2,1 = -0.5173
w6,2,1 = 0.7269
w7,2,1 = 0.9532
Neurona a1,6
w1,6,1 = -0.5679
w2,6,1 = 0.7864
w3,6,1 = 0.8
w4,6,1 = -0.2862
w5,6,1 = -0.1438
w6,6,1 = 0.9134
w7,6,1 = 0.051
Neurona a1,3
w1,3,1 = 0.8405
w2,3,1 = 0.5505
w3,3,1 = 0.8631
w4,3,1 = -0.801
w5,3,1 = 0.8127
w6,3,1 = -0.2181
w7,3,1 = -0.8438
Neurona a1,7
w1,7,1 = 0.2224
w2,7,1 = 0.8087
w3,7,1 = -0.5434
w4,7,1 = -0.7691
w5,7,1 = 0.8699
w6,7,1 = 0.0232
w7,7,1 = -0.1974
Neurona a1,4
w1,4,1 = 0.9602
w2,4,1 = -0.6138
w3,4,1 = 0.943
w4,4,1 = -0.2488
w5,4,1 = 0.8756
w6,4,1 = -0.6935
w7,4,1 = 0.6746
Neurona a1,8
w1,8,1 = 0.1796
w2,8,1 = -0.771
w3,8,1 = -0.0713
w4,8,1 = -0.7065
w5,8,1 = 0.3666
w6,8,1 = -0.3936
w7,8,1 = 0.5881
Pesos Neuronas Segunda Capa Oculta
Neurona a2,1
w1,1,2 = -0.7518
w2,1,2 = 0.9695
w3,1,2 = -0.7666
w4,1,2 = 0.0777
w5,1,2 = 0.2479
w6,1,2 = -0.68
w7,1,2 = 0.2831
w8,1,2 = -0.0803
Neurona a2,2
w1,2,2 = 0.4526
w2,2,2 = 0.6757
w3,2,2 = -0.7583
w4,2,2 = 0.7111
w5,2,2 = 0.1109
w6,2,2 = 0.8059
w7,2,2 = 0.7904
w8,2,2 = 0.4877
Neurona a2,3
w1,3,2 = -0.8859
w2,3,2 = 0.8004
w3,3,2 = 0.9212
w4,3,2 = 0.5105
w5,3,2 = 0.1298
w6,3,2 = -0.6075
w7,3,2 = -0.5820
w8,3,2 = 0.2346
Neurona a2,4
w1,4,2 = 0.1984
w2,4,2 = 0.9973
w3,4,2 = 0.297
w4,4,2 = 0.2689
w5,4,2 = -0.1319
w6,4,2 = -0.119
w7,4,2 = -0.9137
w8,4,2 = -0.2268
Neurona a2,5
w1,5,2 = -0.9319
w2,5,2 = -0.6094
w3,5,2 = -0.8472
w4,5,2 = -0.506
w5,5,2 = -0.8761
w6,5,2 = -0.7347
w7,5,2 = -0.7275
w8,5,2 = 0.143
Pesos Neurona Capa de Salida
Neurona O1:
w1,1 = 0.3026
w2,1 = 0.0804
w3,1 = -0.0936
w4,1 = 0.5123
w5,1 = -0.1862
239
Una Introducción al Cómputo Neuronal Artificial
Error
0.12
0.1
0.08
0.06
0.04
0.02
0
1
50
100
150
200
250
300
350
400
450
500
t
Figura 6.17. Evolución del Error Global de la Red de Perceptrones de la Figura 6.16
durante la aplicación del Algoritmo de Retropropagación. Se efectuaron 500 presentaciones
del conjunto de entrenamiento.
El siguiente paso consiste en evaluar el desempeño de la red considerando a todos
los vectores disponibles: 1,000 de éstos forman el conjunto de entrenamiento mientras que
los restantes 993 forman el conjunto de evaluación. El desempeño lo mediremos utilizando
nuevamente nuestra Función de Error Global: el promedio de las Distancias Euclidianas
entre los vectores proporcionados por la red y los vectores de salida esperada. Para contar
con una apreciación visual es que con las salidas proporcionadas por la red formaremos una
serie de tiempo que no es más que el estimado proporcionado por nuestra red de
Perceptrones. En la Figura 6.18 se muestran tanto la serie de tiempo generada por la red
(en color gris) sobrepuesta a la serie de tiempo original (en color negro). El Error Global
que se obtuvo, considerando ya la totalidad de los 1,993 vectores de entrada, fue de 0.0895.
Si bien es mayor al Error Global que se obtuvo únicamente con el conjunto de
entrenamiento, después de 500 presentaciones, es claro que es menor que el Error Global
obtenido al haber efectuado sólo una presentación (t = 1): 0.1059. Apreciando visualmente,
en la Figura 6.18, es claro que nuestra Red de Perceptrones ha sido capaz de capturar en
gran medida las propiedades y comportamiento de la señal original. En áreas como la
Economía, las Ciencias de la Salud y Sismología es donde se cuenta con fuentes de señales
para las cuales se busca una solución que las pueda modelar, y más importante aún, que
permita efectuar predicciones de gran precisión. En la práctica, se tiene un gran nicho de
aplicación e Investigación de las redes formadas por Perceptrones en este contexto.
240
Capítulo 6. Redes de Perceptrones
xn
1.2
1
0.8
0.6
0.4
0.2
n
0
1
200
400
600
800
1000
1200
1400
1600
1800
2000
Figura 6.18. En color gris, serie de tiempo producida por la Red de Perceptrones de la Figura 6.16.
En color negro, la serie de tiempo original. La recta punteada separa las muestras que conformaron
al conjunto de entrenamiento (n = 1, …, 1000) de las muestras que dieron lugar al conjunto
de evaluación (n = 1001, …, 2000).
241
Una Introducción al Cómputo Neuronal Artificial
242
Una Introducción al Cómputo Neuronal Artificial
7. Redes de Kohonen
Una Introducción al Cómputo Neuronal Artificial
244
Capítulo 7. Redes de Kohonen
7.1 Redes Neuronales Auto-Organizadas
Una de las principales desventajas de las Redes Neuronales Supervisadas yace en el
hecho de que en algunos problemas las salidas correctas esperadas no pueden ser definidas
a priori. En consecuencia, únicamente se cuenta con el Conjunto de Vectores de Entrada.
Por lo tanto, en estos casos, no es posible medir numéricamente la magnitud del error de
aprendizaje. Recordemos que esta magnitud es esencial para el control del aprendizaje en
algoritmos como el de Retropropagación.
En una Red Neuronal Auto-Organizada el Conjunto de los Vectores de Entrada
constituyen lo que es llamado el Espacio o Ambiente de la Red. Con cada uno de estos
vectores de entrada es que se producirá una adaptación de los parámetros internos de la red,
es decir, un ajuste apropiado de los pesos de sus neuronas. Si tal adaptación es controlada
correctamente entonces la red producirá su Representación Interna del Espacio o
Ambiente. En este sentido, uno de los modelos más populares de Redes Neuronales
Auto-Organizadas es el propuesto por el finlandés Teuvo Kohonen.
De acuerdo a la Teoría planteada por Kohonen, si un espacio o ambiente será
procesado entonces el factor fundamental a tomar en cuenta, durante el proceso de
entrenamiento, es el relacionado a identificar la Estructura del Espacio. Por ejemplo,
considérese un conjunto no vacío A. De hecho, el conjunto A es el espacio o ambiente de la
red. Supongamos que A es particionado en 20 regiones disjuntas: a1, a2, …, a20. Véase la
Figura 7.1. La idea es que el conjunto A puede ser “cubierto” por una Red de Kohonen de
tal forma que cuando un vector de entrada inmerso, por ejemplo, en la región a1 es
evaluado con la red, entonces una y sólo una de sus neuronas se activará. Si un vector de
entrada sobre la región a13 es evaluado, entonces una neurona diferente se ha de activar.
Debido a que en nuestro ejemplo se particionó al conjunto A en 20 regiones, es que en
consecuencia nuestra Red de Kohonen debería contar con al menos 20 neuronas. Cada
neurona se especializará en una y sólo una región. Entendamos este proceso como el hecho
de que la Red de Kohonen actúa como una función f cuyo dominio es precisamente el
conjunto A. La función en sí toma forma cuando cada elemento del conjunto de vectores de
entrada es debidamente mapeado a la subregión que le corresponde. Dado que cada región
está asociada a una neurona, que es la que proporciona la salida final, es que entonces
tenemos un mapeo que va de un vector de entrada a una neurona correspondiente en la red.
En términos concretos, la función f, o mejor dicho, la Red de Kohonen, efectúan una tarea
de clasificación de los vectores de entrada. Las clases se conforman por las regiones
definidas. Estas clases precisamente definen una representación de la estructura del espacio
que forman los vectores de entrada. Obsérvese, en la Figura 7.1, que las clases a1 a a20
forman una malla sobre el conjunto A. Esta malla es llamada propiamente Mapa o
Esquema del Espacio. El punto importante a estudiar en este Capítulo es que una Red de
Kohonen es capaz de construir mapas para sus espacios o ambientes al utilizar un
mecanismo de entrenamiento no supervisado.
245
Una Introducción al Cómputo Neuronal Artificial
a1 a2
A
a4
a5
a6
a7 a8
a9
a10
a11
a12
a13
a 14
a16
a17
a3
f
a 15
a18
a19 a20
Figura 7.1. El conjunto A es particionado en 20 regiones. Una Red de Kohonen implementa
a la función f de manera que los vectores en el conjunto A son asociados a su correspondiente clase.
7.2 La Corteza Cerebral
Las Redes de Kohonen tienen su inspiración en bases neurofisiológicas. Es bien
sabido que muchas de las estructuras neuronales en los cerebros de los mamíferos tienen
topologías lineales (1D) o planares (2D). Entiéndase esto como que el hecho de que se
tienen identificados conjuntos de neuronas que se conectan de manera que se forma arreglo
unidimensional, o bien de manera que forma una superficie, un elemento bidimensional.
Estas importantes estructuras neuronales se localizan en la Corteza Cerebral. La corteza
cerebral es una capa de tejido nervioso que cubre exteriormente al cerebro. Esta formada
por interneuronas, dentritas y núcleos de neuronas eferentes; y axones de neuronas
aferentes. La corteza es la parte que se encarga de examinar, administrar, comparar y
seleccionar la información proveniente del exterior y que es capturada en mayor parte por
lo sentidos. La corteza ocupa una superficie de aproximadamente medio metro cuadrado y
está completamente contenida en el cráneo gracias a que está plegada en una serie de
Circunvoluciones. Además, su superficie está dividida en varias zonas las cuales se
diferencian por cortes o hendiduras.
Para su estudio, la corteza cerebral es dividida en cuatro regiones principales que
toman su nombre de la porción del cráneo que la cubre:
• Lóbulo Frontal
• Dos Lóbulos Parietales
• Lóbulo Occipital
• Dos Lóbulos Temporales
El Lóbulo Frontal se encarga de la actividad mental relacionada con la personalidad y la
inteligencia. También tiene a su cargo del control de los movimientos voluntarios tales
como las acciones de correr, caminar, sujetar algo, etc. En los Lóbulos Parietales se recibe
toda la información relacionada con el tacto y es en esta región donde se efectúan los
procesos de orientación espacial. En el Lóbulo Occipital se procesan todas las sensaciones
y señales provenientes de los ojos. Finalmente, en los Lóbulos Temporales se recoge toda
la información concerniente al sentido del oído. Estas regiones de ninguna manera se
246
Capítulo 7. Redes de Kohonen
encuentran aisladas ya que las Áreas de Asociación son los puntos en los cuales las
diferentes partes de la corteza intercambian información a fin de completar una visión
global de lo que ocurre en el exterior del cuerpo.
Como hicimos mención con anterioridad, muchas de las estructuras contenidas
precisamente en los lóbulos presentan organizaciones lineales (1D) o planares (2D). Sin
embargo, la experiencia sensorial es de hecho una experiencia multidimensional. Por
ejemplo, la percepción de color se basa en la interacción entre tres diferentes tipos de
receptores de luz. Pero además, es bien conocido que nuestros ojos también capturan
información adicional acerca de la textura, estructura y posición de los objetos. Es decir,
tenemos información que se transmite por el nervio óptico mediante una señal que contiene
información referente a al menos 6 propiedades. Esta señal llega, como ya comentamos
antes, a la corteza cerebral y en particular al lóbulo occipital donde se ubica la corteza
visual, la cual se sabe es una estructura 2D. La señal multidimensional es entonces
procesada y se generan las acciones o razonamientos correspondientes. Surgen de
inmediato dos preguntas fundamentales (y para las cuales aún estamos en búsqueda de la
respuesta):
• ¿Qué mecanismo
multidimensionales
bidimensionales?
utiliza
sobre
la corteza cerebral para proyectar tales señales
sus estructuras neuronales unidimensionales o
• ¿Qué mecanismo utilizan las estructuras neuronales lineales o planares en la corteza para
procesar las señales multidimensionales provenientes de los sentidos y proporcionar sus
salidas correspondientes?
Hemos también de considerar algunas propiedades sumamente interesantes
referentes a la relación entre la información multidimensional que llega a la corteza y las
neuronas involucradas en su procesamiento. Por ejemplo, en la primera mitad del Siglo XX
el neurólogo Gordon Morgan Holmes identificó algunas relaciones entre el campo visual,
lo que vemos con los ojos, y la corteza visual, la unidad de procesamiento de la
información visual:
• Regiones vecinas en el campo visual son procesadas por regiones también vecinas,
formadas por neuronas, en la corteza visual.
• Las señales provenientes del centro del campo visual son procesadas, por la corteza
visual, con mayor detalle y con mayor resolución que las señales provenientes de la
periferia del campo visual. Ello implica que la agudeza visual se incrementa de la
periferia hacia el centro del campo visual.
Es posible encontrar en la corteza cerebral otras representaciones topológicas ordenadas
para las sensaciones provenientes de órganos aparte del sistema ocular. Las áreas que son
responsables de procesar señales están distribuidas de manera que la topología del cuerpo
humano es debidamente preservada. Por ejemplo, la región responsable de procesar las
señales provenientes de un brazo será vecina de la región responsable de procesar las
247
Una Introducción al Cómputo Neuronal Artificial
señales provenientes de una mano. El punto interesante es que las relaciones espaciales
entre las partes que componen al cuerpo humano se conservan tanto como es posible en la
corteza cerebral. En concreto, la corteza cerebral cuenta, nada más y nada menos, con una
representación interna que describe un esquema de su espacio o ambiente, donde tal espacio
es precisamente el cuerpo humano.
El Modelo Auto-Organizado de Kohonen se sustenta en todos los elementos antes
descritos y establece tres puntos a tomar en cuenta para su implementación:
• Es posible definir a la vecindad de una neurona. Tal vecindad se compone por otras
neuronas.
• Las neuronas dentro de una vecindad tendrán conexiones con otras neuronas que
forman parte de la misma vecindad.
• Las Redes de Kohonen son de hecho arreglos de neuronas con topologías
unidimensionales, bidimensionales, o inclusive, multidimensionales. Por lo regular sólo
se implementan las versiones 1D o 2D de las Redes de Kohonen.
7.3 El Modelo de Kohonen
Consideremos el problema del mapeo de un Espacio n-Dimensional utilizando una
Red Unidimensional de Kohonen. Tenemos que las neuronas que forman a la red serán
enumeradas de 1 a m. Cada neurona recibirá un vector de entrada X conformado por n
componentes:
ª x1 º
«x »
X = « 2»
«#»
« »
¬ xn ¼
(Ecuación 7.3.1)
A la j-ésima neurona, j = 1, 2, …, m, le será asociado un vector de pesos Wj en \ n . Este
vector será utilizado para calcular la correspondiente salida de la neurona. Véase la Figura
7.2. El objetivo detrás del proceso de mapeo considera la especialización de cada neurona
al asignarle una región específica del espacio o ambiente de la Red. Recordemos que este
espacio se conforma por todos los vectores de entrada en el conjunto de entrenamiento. La
región que se asigna a cada neurona es, como comentamos en la Sección 7.1, una clase o
partición dentro del espacio de entrada. Se espera que al presentar un vector de entrada a la
red, la correspondiente neurona, asociada a la clase a la que pertenece el vector dado,
proporcione la salida con valor mínimo de entre todas las salidas proporcionadas por las
neuronas restantes. A esta neurona se le denomina Neurona Ganadora. Las regiones o
clases en que se particionará el espacio de la red son disjuntas, por lo tanto dado un vector
de entrada únicamente se tendrá a una única Neurona Ganadora. Esta propiedad es
conocida como “El ganador se lo lleva todo” (“The winner takes all”).
248
Capítulo 7. Redes de Kohonen
Neurona 1
Neurona 2
w1
w2
x1
Neurona j
Neurona 3
...
w3
x2
x3
Neurona m
wj
...
...
wm
xn
Figura 7.2. Una Red Unidimensional de Kohonen para la clasificación de vectores en \ n .
Ahora bien, tenemos que especificar de manera precisa cómo es que un vector de
entrada y una neurona son asociados. Comentamos previamente que cada neurona contará
con un vector de pesos. Tanto el vector de entrada como el vector de pesos están en \ n y
ambos representan posiciones en el espacio. Al vector de pesos Wj se le denomina Centro
de Gravedad de la región de \ n asociada a la j-ésima neurona en la red. Eso quiere decir
que todos los vectores de pesos son de hecho puntos esparcidos sobre el espacio de la red.
Para definir la asociación de un vector de entrada X con su correspondiente región
simplemente, y es parte de la genialidad del modelo de Kohonen, se calcula la Distancia
Euclidiana entre X y cada uno de los vectores de pesos. Aquella neurona cuyo vector de
pesos sea el más cercano al vector X es la Neurona Ganadora. De allí el tener que
identificar a la neurona con la salida mínima. En este sentido, la Distancia Euclidiana
funciona como un criterio de comparación entre el vector de entrada y el vector de pesos.
Decimos entonces que X y Wj son cada más parecidos, o similares, conforme su Distancia
Euclidiana se acerque a cero. Por otro lado, si el valor de la distancia aumenta entonces
tenemos que se presentarán cada vez más diferencias entre los vectores.
Ya tenemos conocimiento de cómo es que una Red de Kohonen nos ayudará a
resolver el problema de la clasificación y mapeo de un conjunto vectores de entrada, ahora
debemos abordar la situación referente al proceso de su entrenamiento. Para ello será
necesario introducir algunos conceptos a fin de que se presenten, tanto como sea posible,
relaciones de vecindad entre las regiones asociadas a las neuronas, y de hecho entre las
neuronas mismas, tal como sucede con las regiones vecinas que conforman a la corteza
cerebral. Definimos a una Vecindad de Radio r Asociada a la k-ésima Neurona,
1 ≤ k ≤ m, como el conjunto de neuronas localizadas hasta r posiciones de la neurona k
tanto hacia la izquierda como hacia la derecha (recordemos que estamos en el caso de una
Red Unidimensional, posteriormente definiremos la noción de vecindad para Redes de
Kohonen Multidimensionales). Véase la Figura 7.3. Aquellas neuronas localizadas en los
extremos de la red, y dependiendo del valor del radio r, contarán con vecindades
asimétricas. Sea ϕ(j, k, r) una función con codominio en [0, 1], que denota a la Fuerza de
Enlace entre la neurona j y la neurona k a lo largo del proceso de entrenamiento. Un punto
importante es que ϕ(j, k, r) será diferente de cero sí y sólo si j se encuentra dentro de la
249
Una Introducción al Cómputo Neuronal Artificial
vecindad de radio r de la neurona k. En caso contrario se tendrá que ϕ(j, k, r) = 0. Es
posible tener “vecindades” de radio r = 0. Ello implica que ϕ(j, k, 0) = 0 para todas las
neuronas en la red excepto cuando j = k.
r
r
neurona k-r
...
wk-r
...
neurona k-1
neurona k
neurona k+1
wk-1
wk
wk+1
neurona k+r
...
wk+r
...
Figura 7.3. La vecindad de radio r para la k-ésima neurona en una Red de Kohonen 1D.
La vecindad se extiende r posiciones hacia la izquierda y r posiciones hacia la derecha.
El método de entrenamiento está dado por el siguiente procedimiento:
• Se inicializan los pesos de todas las neuronas con valores aleatorios.
• Se efectúa un número dado de presentaciones del conjunto de entrenamiento.
o Para cada vector de entrada E en el conjunto de entrenamiento:
ƒ Se identifica a la neurona k con la salida mínima. O en otras palabras, se identifica
aquella neurona cuya distancia entre su vector de pesos y el vector E sea la menor de
todas.
ƒ Cada vector de pesos Wj, j = 1, 2, 3, …, m, es actualizado de acuerdo a la siguiente
regla:
Wj = Wj + α⋅ϕ(j, k, r)⋅(E – Wj)
(Ecuación 7.3.2)
La constante positiva α no es más que nuestro bien conocido coeficiente de
aprendizaje. Por lo regular α ∈ (0, 1). Tiene el mismo rol, por ejemplo, que en el Algoritmo
de Retropropagación: controlar la magnitud de la actualización de los pesos. La regla de
actualización de pesos presentada en la Ecuación 7.3.2, y específicamente el término
(E – Wj), tiene el objetivo de atraer a los vectores de pesos hacia el vector de entrada E. Al
repetir la actualización de los pesos en varias presentaciones del conjunto de entrenamiento,
se espera que los vectores de pesos se distribuyan uniformemente en el espacio o ambiente
de la red. En la práctica, que se obtenga tal distribución uniforme depende del conjunto de
entrenamiento y en particular de los vectores de entrada.
Ahora bien, nótese que el procedimiento antes descrito aplica una actualización a
todos los vectores de pesos, no sólo a la neurona ganadora. La idea es la siguiente: cuando
la neurona ganadora ha sido actualizada aquellas neuronas dentro de su vecindad de radio r
son también actualizadas. En particular se busca que si el vector de pesos de la neurona
ganadora es atraído hacia una región en el espacio de la red entonces los vectores de pesos
de sus neuronas vecinas sean también atraídos, pero con menor intensidad. Previamente
mencionamos que la función ϕ(j, k, r) tiene su codominio en el intervalo [0, 1]. Por lo tanto,
y de acuerdo a lo previamente establecido, ϕ(j, k, r) = 1 sí y sólo si j = k, ya que la máxima
Fuerza de Enlace entre dos neuronas se dará cuando éstas sean ambas la neurona ganadora.
Conforme una neurona dentro de la vecindad se aleje de la neurona ganadora k es que
250
Capítulo 7. Redes de Kohonen
entonces se espera que ϕ(j, k, r) → 0. Esta propiedad viene a sustentar la aseveración de
que los vectores de pesos de las neuronas vecinas a la ganadora son también atraídas hacia
E salvo que con menor intensidad. Ahora bien, estrictamente hablando no todos los
vectores de pesos son actualizados. Es el caso cuando nos referimos a las neuronas que
están fuera de la vecindad de radio r de la neurona ganadora. En esta situación ϕ(j, k, r) = 0.
Aunque el procedimiento especificado se aplica a todos los vectores de pesos, en esta
instancia tenemos que realmente no se efectúa modificación alguna. Debe ser claro que
entonces el ajuste de pesos en una Red Unidimensional de Kohonen no es más que un
proceso en el que se trasladan sucesivamente a los vectores de pesos a regiones del espacio
de la red. La magnitud de tales traslaciones depende del coeficiente de aprendizaje α y de la
función ϕ(j, k, r). Mencionábamos en Capítulos anteriores que el Coeficiente de
Aprendizaje α puede tomar un valor en función de la iteración que actualmente se esté
aplicando. Por ejemplo, sabemos que podemos iniciar el entrenamiento con un coeficiente
inicial α0 y que éste vaya disminuyendo conforme un cierto número de iteraciones se hayan
efectuado. La idea es suponer que los pesos cada vez están más cerca de un estado óptimo y
por tanto las actualizaciones requeridas deben ser de magnitud pequeña para asegurar la
precisión y no alejarnos de tal punto de optimalidad. Esta misma idea puede aplicarse al
entrenar a una Red de Kohonen. Pero además, también puede ser aplicada sobre la función
ϕ de Fuerza de Enlace. Es posible hacer que el radio r de una vecindad sea gradualmente
reducido conforme el proceso de entrenamiento avance. La idea es que inicialmente la
neurona ganadora tenga influencia fuerte sobre su vecindad, pero que ésta gradualmente se
vaya reduciendo a fin de no hacer que un peso asociado a una neurona vecina sea
desplazado de su posición óptima debido a la actualización de la neurona ganadora.
Algoritmo 7.1. Entrenamiento de una Red de Kohonen Unidimensional.
Procedure TrainKohonenNetwork1D(Integer N, Integer n, Matrix E[1,…,N][1,…,n],
Real α, Integer m, Integer r, Integer L)
W = new Matrix[1,…,m][1,…,n]
// Se asignan valores aleatorios a los vectores de pesos.
for j = 1 until m do
for i = 1 until n do
W[j][i] = Random( )
end-of-for
end-of-for
// Se lleva a efecto la t-ésima presentación del conjunto de entrenamiento.
for t = 1 until L do
for k = 1 until N do
// El k-ésimo vector de entrada es enviado a cada neurona.
// Las variables minD y minN se utilizan para identificar
// a la distancia mínima y a la neurona ganadora respectivamente.
Real minD = ∞
Integer minN = -1
251
Una Introducción al Cómputo Neuronal Artificial
for j = 1 until m do
// Se calcula la Distancia Euclidiana entre el k-ésimo vector
// de entrada y el vector de pesos de la j-ésima neurona.
Real d = 0
for i = 1 until n do
d = d + Pow(E[k][i] – W[j][i], 2)
end-of-for
d= d
if (minD > d) then
minD = d
minN = j
end-of-if
end-of-for
// minN contiene el índice de la Neurona Ganadora.
Integer winnerNeuron = minN
// Se actualizan los pesos de las neuronas.
// El valor de ϕ determina qué vectores de pesos se actualizan.
for j = 1 until m do
for i = 1 until n do
W[j][i] = W[j][i] +
α * ϕ(j, winnerNeuron, r) * (E[k][i] – W[j][i])
end-of-for
end-of-for
end-of-for
end-of-for
// Se retornan como salida los pesos identificados.
return W
end-of-procedure
El Algoritmo 7.1 corresponde a la implementación del entrenamiento para una Red
de Kohonen 1D. El Algoritmo recibe las siguientes entradas:
• Un entero N que denota al número de vectores de entrada.
• Un entero n que corresponde a la dimensionalidad de los vectores de entrada.
• Una matriz E de tamaño N × n que contiene a los vectores en el conjunto de
entrenamiento. Entonces es claro que el k-ésimo vector de entrada y sus n componentes
podrán localizarse precisamente en el k-ésimo renglón de la matriz E.
• Una constante α ∈ (0, 1) correspondiente al Coeficiente de Aprendizaje.
• Un entero m que indica el número de neuronas en la red.
• Un entero L que denota el número de veces que el conjunto de entrenamiento será
presentado.
En un principio el algoritmo inicializa una matriz W de tamaño m × n. Es en esta matriz
donde los vectores de pesos de las neuronas estarán contenidos. El j-ésimo vector de pesos
252
Capítulo 7. Redes de Kohonen
estará entonces localizado en el j-ésimo renglón de W. Los valores de los pesos son
inicialmente números aleatorios. Posteriormente se tiene que efectúan una a una las
presentaciones del conjunto de entrenamiento. Cada vector de entrada es presentado a todas
las neuronas en la red. A través de la Mínima Distancia Euclidiana es que se identifica a la
Neurona Ganadora. En este punto tenemos que se invoca a la función de Fuerza de Enlace
ϕ la cual se presupone está implementada. Recordemos que esta función deberá cumplir
con retornar ϕ(j, winnerNeuron, r) = 1 cuando j corresponde a la Neurona Ganadora. Por
otro lado, ϕ(j, winnerNeuron, r) ∈ (0, 1] para las neuronas que se encuentren dentro de la
vecindad de radio r de la Neurona Ganadora. Finalmente, ϕ(j, winnerNeuron, r) = 0 para
las neuronas que se encuentran fuera de la vecindad de la Neurona Ganadora. Sabemos que
r debe ser un entero no negativo. En el caso cuando r = 0 entonces tendremos que
ϕ(j, winnerNeuron, r) = 0 para toda neurona excepto cuando j = winnerNeuron. A final de
cuentas el valor de la Función de Enlace determinará que vectores de pesos son
actualizados. El Algoritmo termina su ejecución una vez que retorna como salida a la
matriz W que contiene los pesos identificados para las m neuronas.
Algoritmo 7.2. Determinando la neurona asociada a un vector de entrada E
en una Red de Kohonen Unidimensional.
Procedure QueryKohonenNetwork1D
(Integer n, Integer m, Array E [1,…,n], Matrix W[1,…,m][1,…,n])
// El vector de entrada E es enviado a cada neurona.
// Las variables minD y minN se utilizan para identificar
// a la distancia mínima y a la neurona ganadora respectivamente.
Real minD = ∞
Integer minN = -1
for j = 1 until m do
// Se calcula la Distancia Euclidiana entre el vector de entrada E
// y el vector de pesos de la j-ésima neurona.
Real d = 0
for i = 1 until n do
d = d + Pow(E[i] – W[j][i], 2)
end-of-for
d= d
if (minD > d) then
minD = d
minN = j
end-of-if
end-of-for
// minN contiene el índice de la Neurona Ganadora, este valor se retorna.
return minN
end-of-procedure
253
Una Introducción al Cómputo Neuronal Artificial
El Algoritmo 7.2 representa la implementación del proceso de consulta a una Red
de Kohonen 1D. Es decir, una vez que ya se cuenta con los pesos de las neuronas, al haber
aplicado el Algoritmo 7.1, es que entonces se procede a invocar a la red para determinar,
dado un vector de entrada E, cual es su región del espacio, o mejor dicho clase,
correspondiente. En este sentido el Algoritmo 7.2 recibe como parámetros los valores de n
y m, es decir, la dimensionalidad de los vectores y el número de neuronas en la red,
respectivamente. Se recibe también un arreglo E de n elementos que es precisamente el
vector de entrada. La matriz W de m × n contiene a los vectores de pesos. Nuestro
Algoritmo simplemente calcula la Distancia Euclidiana del vector de entrada E con todos
los vectores de pesos. Se identifica a la Neurona Ganadora, cuya distancia es la mínima, y
se retorna su correspondiente índice como salida.
...
...
...
...
...
...
...
...
X = [x 1 x 2 x 3 ... x n] T
Figura 7.4. Una Red de Kohonen Bidimensional para la clasificación de puntos en \ n . Las neuronas son
posicionadas en renglones y columnas. El vector de entrada X es enviado a todas las neuronas.
Ahora consideremos la cuestión del problema de mapear un Espacio n-Dimensional
utilizando una Red de Kohonen Bidimensional (Véase la Figura 7.4). La red 2D tendrá
ahora las siguientes propiedades:
• Cada neurona recibirá un vector de entrada X en \ n .
• Cada neurona cuenta con un vector de pesos también en \ n .
• La salida de cada neurona está dada por la Distancia Euclidiana entre el vector de
entrada X y su vector de pesos. La Neurona Ganadora es aquella cuyo vector de pesos
cuenta con la menor distancia con el vector X.
• Se tiene una función ϕ(j, k, r) que describe la fuerza de enlace entre dos neuronas.
Bajo estos criterios es natural preguntarse cuál es la diferencia con la Red Unidimensional.
En realidad las diferencias entre el caso 1D y el 2D yacen en la función ϕ(j, k, r). Ello se
debe a que en el caso 2D se deberá considerar una vecindad bidimensional. Una vecindad
de radio r para la neurona k en una red 2D se forma por el conjunto de neuronas localizadas
hasta r posiciones a la derecha, a la izquierda, por arriba y por debajo de la neurona k. Es
254
Capítulo 7. Redes de Kohonen
decir, la vecindad de la neurona k es una porción cuadrangular de la red (Véase la Figura
7.5). Respecto al mecanismo de entrenamiento se tiene que es el mismo que hemos descrito
con anterioridad. El siguiente paso lógico debe ser obvio: una Red de Kohonen
m-Dimensional es una red en la cual las neuronas están posicionadas en un arreglo de m
dimensiones. Cada neurona cuenta con su vector de pesos, recibe al vector de entrada y se
determina a la Neurona Ganadora mediante el uso de la Mínima Distancia Euclidiana. La
función de Fuerza de Enlace deberá describir vecindades que no son más que porciones
hipercúbicas m-Dimensionales de la red. Es claro que en realidad para los casos
multidimensionales de las Redes de Kohonen debemos tomar atención únicamente de la
función ϕ.
r
...
...
...
...
...
...
...
...
r
r
...
r
...
r
...
k
...
...
...
...
...
...
...
...
...
r
r
r
Figura 7.5. La vecindad bidimensional de radio r para la k-ésima neurona en una Red de Kohonen 2D.
La vecindad se extiende r posiciones cubriendo una región cuadrangular. Todas las neuronas dentro
de esta región son vecinas de la neurona k.
Abordemos ahora un par de ejemplos a fin de apreciar, desde un punto de vista
visual, cómo es que la regla de actualización definida en la Ecuación 7.3.2 efectivamente
permite obtener una partición, en clases, del ambiente de la red. Esta partición es apropiada
para efectos de tareas de clasificación de los elementos en el conjunto de entrenamiento.
Veamos primero el caso referente al uso de una Red de Kohonen 1D para el mapeo de la
región en el plano [0, 1] × [0, 1]. Se cuenta con un conjunto de entrenamiento formado por
100 vectores de entrada distribuidos en la región dada (los componentes de los vectores
están en [0, 1]). Comentamos en párrafos anteriores que los vectores de pesos deben ser
inicializados con valores aleatorios, pero a fin de apreciar con mayor claridad el ajuste, los
pesos serán inicializados todos con el valor 0.5, es decir, los centros de gravedad de las
clases a obtener se ubican en el punto (0.5, 0.5). Supongamos que deseamos particionar el
espacio [0, 1] × [0, 1] en 10 clases. Por lo tanto nuestra red se formada precisamente por 10
neuronas. Utilizaremos un coeficiente de aprendizaje α = 0.01 el cual se mantendrá
constante durante todo el entrenamiento. Por otro lado, el radio de las vecindades a
considerar será r = 0. Ello implica que la Ecuación 7.3.2 será aplicada únicamente a la
Neurona Ganadora sin influir de ninguna manera en sus neuronas vecinas en la red.
Efectuaremos en total 100 presentaciones del conjunto de entrenamiento. Procederemos tal
255
Una Introducción al Cómputo Neuronal Artificial
como lo indica el Algoritmo 7.1. En la Figura 7.6 podemos apreciar visualmente la fase de
inicialización cuando t = 0 (la 0-ésima presentación). En la misma Figura, en la
presentación t = 2, se puede comenzar a apreciar como es que algunos vectores de pesos
comienzan a desplazarse. Se pueden observar en este punto 4 vectores ya con coordenadas
diferentes de (0.5, 0.5). En la presentaciones t = 4, 6, 8 vemos como es que este
desplazamiento aleja cada vez más a los mismos cuatro vectores de pesos del centro del
espacio. Es en la presentación t = 10 cuando claramente se aprecia un quinto vector de
pesos que comienza a alejarse del centro de [0, 1] × [0, 1]. Ahora véase la Figura 7.7. En la
presentación t = 20 seis vectores de pesos se alejan del punto (0.5, 0.5). Recordemos que
las traslaciones aplicadas a estos vectores van en función de su cercanía con los vectores en
el conjunto de entrenamiento. En la presentación t = 40 ya es posible observar a siete
vectores de pesos en movimiento, mientras que en t = 50 tenemos a ocho vectores de pesos
con componentes diferentes de 0.5. Es en la presentación t = 80 que ya es posible apreciar a
los diez vectores de pesos distribuidos a lo largo del ambiente de la red. Nótese como es
que en la presentación t = 90 aún se siguen efectuado desplazamientos, aunque también
éstos ya son claramente dentro de regiones bien definidas. Llegamos a la presentación
t = 100 con la que la ejecución del Algoritmo 7.1 finaliza.
Ahora bien, comentábamos en párrafos anteriores que los vectores de pesos son los
centros de gravedad de las clases en que hemos particionado, durante el entrenamiento de la
red, a la región [0, 1] × [0, 1]. El punto ahora es identificar a las subregiones que forman a
tales clases. Para ello haremos uso del Algoritmo 7.2 utilizando los pesos encontrados
previamente. Recordemos que este Algoritmo, dado un vector de entrada, retorna como
salida el índice asociado a la Neurona Ganadora. Ese índice lo utilizaremos ahora para
enumerar a nuestras diez clases. Cada elemento del conjunto de entrenamiento será enviado
al Algoritmo 7.2 a fin de determinar de qué clase es miembro. Una vez identificadas todas
las membresías es que podremos acotar a las subregiones definidas por cada clase. La
Tabla 7.1 describe un resumen de este análisis de membresía. También se presentan las
coordenadas de los centros de gravedad de las clases, que no son más que los pesos
identificados. Véase en la Tabla, por ejemplo, que 8 elementos del conjunto de
entrenamiento fueron agrupados en la Clase 3. Esto quiere decir que tales vectores son los
más similares al correspondiente vector de pesos. Pero además, al estar en la misma clase
se dice que los 8 vectores comparten características comunes. Lo mismo se puede concluir,
en otro caso, con los 13 vectores contenidos en la clase 8. Estos 13 vectores son los más
similares al vector de pesos [0.17727, 0.26008]T y además, por formar parte de la misma
clase, comparten similitudes entre sí. Es posible que una vez finalizado un entrenamiento se
encuentre que existen clases con cero miembros. Ello quiere decir, por un lado, que ningún
elemento del conjunto de entrenamiento se relacionó con el correspondiente vector de
pesos, y por otro lado, que la correspondiente neurona puede ser omitida de la red sin
afectar la partición del espacio que se obtuvo durante el entrenamiento. En la Figura 7.8 se
muestra la partición del espacio de la red inducida por las 10 clases identificadas durante la
aplicación del Algoritmo 7.1. Se pueden apreciar tanto los elementos del conjunto de
entrenamiento, ya con sus correspondientes membresías, así como las posiciones finales de
los centros de gravedad (vectores de pesos) de las clases.
256
Capítulo 7. Redes de Kohonen
X2
(1,1)
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
X2
È
È È
È È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È
È
È
È
È
È
È
Ô
Ô
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
(0,0)
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
ÔÔ
ÈÈ
È
Ô
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
(0,0)
È
È
È
È
È
X1
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È È
È
È
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
X1
È
È
È
È
(1,1)
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
ÈÈ
È
È
X2
È
È È
È
È
(0,0)
È
È
È
t=6
È
È
È
È
È
È
È
È
Ô
È
È
(1,1)
È
È
È
È
È
È
X2
È
È
È
t=4
È
È
È
È
X1
È
È
È
È
È
(0,0)
È
È
È
È
Ô
È
È
È
È
È
È
ÈÈ
È
È
Ô
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
Ô
Ô
È
È
È
È
È
È
(1,1)
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
X1
È
È
È
È
È
È
È
È
t=2
È
È
È
È
È
È
È
(1,1)
È
È
È
È
X2
È
È
È
È
È
È
Ô
È
È
(0,0)
È
È
È
È
È
È
È
È
(0,0)
X1
t = 0 (fase de inicialización de pesos)
È
È
È
È
È
È
Ô
Ô
Ô
ÈÈ
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È È
È
È
È
È
È
(1,1)
È
È
È
È
È
X2
È
È
È
È
È
ÈÈ
È
È
È
È
X1
t=8
t = 10
Figura 7.6. Evolución del ajuste de pesos para una Red de Kohonen 1D en la primeras 10 presentaciones del
conjunto de entrenamiento. Los triángulos denotan las posiciones de los Centros de Gravedad
(vectores de pesos) asociados a las neuronas que forman la red (véase el texto para detalles).
257
Una Introducción al Cómputo Neuronal Artificial
X2
(1,1)
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
(1,1)
È
È
Ô
È
È È
È
È
È
È
È
È
Ô
È
È
È
È
È
Ô
ÔÔ
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
Ô
È
È
È
Ô
Ô
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
Ô
È
X1
(0,0)
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
Ô
È
È
È
Ô
ÈÈ
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È È
È
È
È
È
È
È
È
È
È È
È
È
È
ÈÈ
È
È
Ô
È
È
È
Ô
È
È
(0,0)
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
(1,1)
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È È
È
È
X1
È
È
È
È
È
X2
È
È È
È
È
È
ÈÈ
È
È
(0,0)
È
È
Ô
È
t = 80
È
È
È
È
È
È
È
È
Ô
È
È
(1,1)
È
È
È
È
È
È
X2
È
È
È
t = 50
È
È
È
È
È
È
X1
È
È
È
È
(0,0)
È
È
È
È
È
Ô
È
È
È
È
È
Ô
Ô Ô
ÈÈ
È
È
Ô
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
Ô
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È È
È
È
È
ÈÈ
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
(1,1)
È
È
È
È
È
È
È
È
È
È È
È
È
X1
È
È
È
È
ÈÈ
È
È
X2
È
È
È
È
È
Ô
(0,0)
È
È
È
È
t = 40
X2
È
È
È
È
È
t = 20
È
È
È
È
X1
È
È
È
È
È
(0,0)
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
Ô
È
È
È
ÈÈ
È
È
Ô
Ô
È
È
È
È
Ô
È
È
È
È
ÈÈ
È
È
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
Ô
È
È
È
È
È È
È
È
ÈÈ
È
È
È
È
È
È
ÔÔ
È
È
È
È
È
È
È
Ô
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È
È È
È È
È
È
È
È
È
(1,1)
È
È
È
È
È
X2
È
È
È
È
È
È
È
ÈÈ
È
È
È
È
X1
t = 90
t = 100
Figura 7.7. Algunas fases de la evolución del ajuste de pesos para una Red de Kohonen 1D. Los triángulos
denotan las posiciones de los Centros de Gravedad (vectores de pesos) asociados a las neuronas que forman
la red (véase el texto para detalles).
258
Capítulo 7. Redes de Kohonen
Tabla 7.1. Distribución de los 100 elementos del conjunto de entrenamiento en las 10 clases obtenidas
mediante una Red de Kohonen 1D. Se muestran también las coordenadas finales de los centros
de gravedad de cada clase una vez efectuadas 100 presentaciones del conjunto de entrenamiento
(véase el texto para detalles).
Centro de Gravedad (Vector de Pesos)
Clase (Neurona)
X1
X2
Miembros
1
0.48833
0.53633
2
2
0.42424
0.43497
3
3
0.62508
0.43863
8
4
0.56403
0.80818
10
5
0.20741
0.54386
12
6
0.60624
0.16832
12
7
0.86220
0.72777
12
8
0.17727
0.26008
13
9
0.16455
0.84476
14
10
0.91601
0.26776
14
X2
(1,1)
(0,0)
X1
Figura 7.8. Partición de la región [0, 1] × [0, 1] inducida por los centros de gravedad
(vectores de pesos, triángulos en la figura) asociados a las 10 neuronas que conforman
a una Red de Kohonen 1D. La región ha sido subdividida en 10 clases después de 100 presentaciones
del conjunto de entrenamiento (véase el texto para detalles).
259
Una Introducción al Cómputo Neuronal Artificial
(1,1,1)
(1,1,1)
X3
X3
(0,0,0)
(0,0,0)
X1
X1
t = 0 (fase de inicialización de pesos)
t=2
(1,1,1)
(1,1,1)
X3
X3
(0,0,0)
(0,0,0)
X1
X1
t=4
t=6
(1,1,1)
(1,1,1)
X3
X3
(0,0,0)
(0,0,0)
X1
X1
t=8
t = 10
Figura 7.9. Evolución del ajuste de pesos para una Red de Kohonen 1D en la primeras 10 presentaciones
de un conjunto de entrenamiento inmerso en un cubo unitario [0, 1] × [0, 1] × [0, 1]. Los círculos mayores
denotan las posiciones de los Centros de Gravedad (vectores de pesos) asociados a las neuronas que forman
la red (véase el texto para detalles).
260
Capítulo 7. Redes de Kohonen
(1,1,1)
(1,1,1)
X3
X3
(0,0,0)
(0,0,0)
X1
X1
t = 20
t = 30
(1,1,1)
(1,1,1)
X3
X3
(0,0,0)
(0,0,0)
X1
X1
t = 50
t = 60
(1,1,1)
(1,1,1)
X3
X3
(0,0,0)
(0,0,0)
X1
X1
t = 80
t = 100
Figura 7.10. Algunas fases de la evolución del ajuste de pesos para una Red de Kohonen 1D. Se mapea
un conjunto de entrenamiento inmerso en un cubo unitario [0, 1] × [0, 1] × [0, 1]. Los círculos mayores
denotan las posiciones de los Centros de Gravedad (vectores de pesos) asociados a las neuronas que forman
la red (véase el texto para detalles).
261
Una Introducción al Cómputo Neuronal Artificial
Veamos ahora el caso referente al uso de una Red de Kohonen 1D para el mapeo de
la región en el espacio [0, 1] × [0, 1] × [0, 1]. Este subespacio 3D corresponde a un cubo
unitario. Tenemos ahora 100 vectores de entrada distribuidos a lo largo de nuestro cubo.
Los condiciones de entrenamiento son las mismas que establecidos para el caso del mapeo
2D: 10 neuronas, 100 vectores de entrada, 100 presentaciones del conjunto de
entrenamiento, Coeficiente de Aprendizaje α = 0.01, el cual es constante durante todo el
proceso de ajuste de pesos, y vecindades de radio r = 0. Los vectores de pesos de las
neuronas tendrán, obviamente, 3 componentes. Todos los componentes son inicializados
con el valor 0.5. La Figura 7.9 muestra el ajuste de pesos desde la inicialización (t = 0)
hasta la décima presentación del conjunto de entrenamiento (t = 10). Nótese como es que
en esta fase se pueden apreciar al menos 5 vectores de pesos con posiciones diferentes a
[0.5 0.5 0.5]T. La Figura 7.10 muestra el resto del entrenamiento. En la presentaciones
t = 20 y t = 30 son al menos seis vectores de pesos los que se alejan de la posición
[0.5 0.5 0.5]T. En t = 60 tenemos a 9 vectores de pesos ya alejados de la posición central
del cubo. Estos desplazamientos continúan en t = 80. En la última presentación del
conjunto de entrenamiento, t = 100, tenemos a los diez vectores de pesos en sus posiciones
finales. De hecho, y como se puede apreciar en la Tabla 7.2, todas sus posiciones son
diferentes de [0.5 0.5 0.5]T. La misma Tabla nos presenta la distribución de los 100
vectores de entrada en las 10 clases definidas. La clase 1 cuenta con sólo un miembro,
mientras que la clase 8 cuenta con 18. La Tabla 7.2 así como la Figura 7.10, en particular
en el estado t = 100, nos muestran, de manera visual, como es que los vectores de pesos
terminaron con una buena distribución dentro del cubo [0, 1] × [0, 1] × [0, 1].
Tabla 7.2. Distribución de los 100 elementos del conjunto de entrenamiento, inmerso en un cubo unitario
[0, 1] × [0, 1] × [0, 1], en las 10 clases obtenidas mediante una Red de Kohonen 1D. Se muestran también
las coordenadas finales de los centros de gravedad de cada clase una vez efectuadas 100 presentaciones
del conjunto de entrenamiento (véase el texto para detalles).
Centro de Gravedad (Vector de Pesos)
Clase (Neurona)
X1
X2
X3
Miembros
1
0.45305
0.47843
0.47249
1
2
0.29893
0.45176
0.70130
11
3
0.47045
0.64149
0.43975
6
4
0.18590
0.77053
0.32384
16
5
0.44663
0.17516
0.38233
7
6
0.37887
0.91071
0.82416
8
7
0.85845
0.29124
0.66388
12
8
0.82900
0.76613
0.37098
18
9
0.18899
0.09757
0.78948
10
10
0.26443
0.29779
0.10249
11
7.4 Aplicación: Clasificación Automática de Imágenes
Una de las aplicaciones más populares de las Redes de Kohonen es en la
clasificación no supervisada de datos. En particular, en esta Sección haremos una breve
visita a lo que es la Clasificación No Supervisada de Imágenes. Esta aplicación juega un rol
importante en áreas como Visión por Computadora en donde se requiere que imágenes con
262
Capítulo 7. Redes de Kohonen
características similares sean agrupadas en clases. Algunas de las tareas de procesamiento e
indexación de imágenes dependen en gran medida de cómo éstas se encuentran agrupadas.
Como mencionábamos previamente, en esta Sección mostraremos como es que el
entrenamiento de una Red de Kohonen 1D proporciona una solución al Problema de la
Clasificación Automática de Imágenes. Algunos métodos y procedimientos que se
describirán a continuación fueron originalmente presentados y discutidos en las siguientes
publicaciones por algunos muy distinguidos y apreciados colegas junto con el Autor:
• Pérez-Aguila, Ricardo; Gómez-Gil, Pilar & Aguilera, Antonio. One-Dimensional
Kohonen Networks and Their Application to Automatic Classification of Images.
International Seminar on Computational Intelligence 2006, pp. 95-99. IEEE – CIS
Chapter Mexico. October 9 to 11, 2006. Tijuana, México.
• Pérez-Aguila, Ricardo, Gómez-Gil, Pilar & Aguilera, Antonio. Non-Supervised
Classification of 2D Color Images Using Kohonen Networks and a Novel Metric. 10th
Iberoamerican Congress on Pattern Recognition, CIARP 2005; Lecture Notes in
Computer Science, Vol. 3773, pp. 271-284. La Havana, Cuba.
• Pérez-Aguila, Ricardo. Automatic Segmentation and Classification of Computed
Tomography Brain Images: An Approach Using One-Dimensional Kohonen Networks.
IAENG International Journal of Computer Science, Vol. 37, Issue 1, pp. 27-35.
International Association of Engineers (IAENG), February 2010.
7.4.1 Redistribución del Conjunto de Entrenamiento
En Secciones anteriores mencionábamos que el mecanismo de ajuste de pesos para
una Red de Kohonen asume que los elementos del conjunto de entrenamiento se encuentran
uniformemente distribuidos en el espacio o ambiente de la red. Sin embargo, y en función
de la naturaleza de los vectores de entrada, esto no siempre se puede garantizar. Por
ejemplo, considérese un conjunto de vectores distribuidos en el subespacio 3D definido por
el cubo unitario [0,1] × [0,1] × [0,1]. Además, asúmase que este conjunto de vectores está
inmerso en una subregión delimitada por el cubo [0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6]. Véase la
Figura 7.11. Debido a que los puntos no están uniformemente distribuidos en el cubo
[0,1] × [0,1] × [0,1], el espacio de la red, es que entonces podemos esperar importantes
repercusiones durante el proceso de clasificación, es decir, en el entrenamiento. Ello se
debe a que los vectores de pesos no tendrán “suficiente” espacio para moverse ya que el
hecho de que los vectores de entrada se encuentren “anidados” en una subregión hará que
no sea clara la identificación de similitudes y diferencias entre los elementos del conjunto
de entrenamiento. En consecuencia, podemos esperar vectores de pesos cuyos componentes
casi coinciden con los de otros vectores de pesos, o por otro lado, vectores de pesos, que si
bien se han desplazado, no tendrán elementos asociados del conjunto de entrenamiento, es
decir, describen clases sin miembros.
Veamos una solución para el problema que acabamos de plantear. Considérese un
Hipercubo unitario n-Dimensional H, es decir:
H = [0,1] × [0,1] × ... × [0,1]
(Ecuación 7.4.1)
n
263
Una Introducción al Cómputo Neuronal Artificial
X3
(1,1,1)
(0.3, 0.3, 0.3)
(0.6, 0.6, 0.6)
(0,0,0)
X2
X1
Figura 7.11. Un conjunto de vectores inmersos en el cubo
[0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6] ⊆ [0,1] × [0,1] × [0,1].
Supongamos ahora que tenemos un conjunto de vectores E1, E2, E3, …, EN, inmersos
también en un Hipercubo n-Dimensional h, pero con la propiedad de que h está contenido
en H, es decir, h ⊆ H (en el ejemplo que planteábamos anteriormente tenemos que n = 3,
H = [0,1] × [0,1] × [0,1] y h = [0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6]). Ahora bien, con los
vectores inmersos en h formaremos dos nuevos vectores: Pmin y Pmax. Pmin es el vector cuyo
i-ésimo componente, ximin , está dado por:
min
xi
­
½
ª # º
°
°
«
»
= min ® x j ,i : E j = « x j ,i » , j = 1, 2,..., N ¾
°
°
«¬ # »¼
¯
¿
(Ecuación 7.4.2)
Es decir, de los i-ésimos componentes de cada uno de los vectores E1, E2, E3, …, EN se elije
al menor. En consecuencia el vector Pmin está dado por:
Pmin
264
ª x1min º
« min »
x
=« 2 »
« # »
« min »
¬« xn ¼»
(Ecuación 7.4.3)
Capítulo 7. Redes de Kohonen
Es claro entonces que el vector Pmin se conforma por los componentes mínimos tomados de
los vectores E1, E2, E3, …, EN. Por otro lado, y de manera similar, tenemos que el vector
Pmax está dado por:
Pmax
ª x1max º
« max »
x
=« 2 »
« # »
« max »
¬« xn ¼»
(Ecuación 7.4.4)
Donde:
max
xi
­
½
ª # º
°
°
«
»
= max ® x j ,i : E j = « x j ,i » , j = 1, 2,..., N ¾
°
°
«¬ # »¼
¯
¿
(Ecuación 7.4.5)
Resulta claro que el vector Pmax se conforma por los componentes máximos tomados de los
vectores E1, E2, E3, …, EN. Los vectores Pmin y Pmax describen entonces la diagonal
principal del Hipercubo h (en nuestro ejemplo anterior, con n = 3, tendríamos que
Pmin = [0.3 0.3 0.3]T y Pmax = [0.6 0.6 0.6]T, véase la Figura 7.12).
X3
(1,1,1)
P max =
(0.6, 0.6, 0.6)
X2
P min =
(0.3, 0.3, 0.3)
(0,0,0)
X1
Figura 7.12. La diagonal principal asociada
al cubo [0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6].
265
Una Introducción al Cómputo Neuronal Artificial
A cada uno de los vectores Ej = [xj,1 xj,2 … xj,n]T, j = 1, 2, …, N, y también a los
vectores Pmin y Pmax, se les aplicará ahora una traslación. Esta traslación, definida en
función de Pmin, producirá un nuevo conjunto de vectores y está dada por:
ª x j ,1 º ª x1min º ª x ' j ,1 º
» «
« » «
»
E j ' = E j − Pmin = « # » − « # » = « # »
« x j ,n » « xnmin » « x ' j ,n »
¬ ¼ ¬
¼
¼ ¬
max
min
ª x1 º ª x1 º ª x1max 'º
«
» «
» «
»
Pmax ' = Pmax − Pmin = « # » − « # » = « # »
« xnmax » « xnmin » « xnmax '»
¬
¼ ¬
¼ ¬
¼
Pmin ' = Pmin − Pmin
(Ecuación 7.4.6)
(Ecuación 7.4.7)
ª x1min º ª x1min º ª0 º
«
» «
»
= « # » − « # » = «« # »»
« xnmin » « xnmin » «¬0 »¼
¬
¼ ¬
¼
(Ecuación 7.4.8)
La Ecuación 7.4.8 es obvia, pero nos indica claramente que la traslación aplicada hace que
se cuente ahora con un Hipercubo h’, aún inmerso en el Hipercubo H, en el cual uno de sus
vértices es precisamente el vector cero, o bien, el origen. La diagonal principal de h’ está
escrita por Pmin ' = 0 y Pmax ' . El conjunto de vectores, trasladados, E1 ', E2 ',..., EN ' está
claramente contenido en h’ (Véase la Figura 7.13 donde se aplica la traslación a nuestro
caso ejemplificado con n = 3).
X3
(1,1,1)
P max' =
(0.3, 0.3, 0.3)
X2
P min' =
(0, 0, 0)
X1
Figura 7.13. Traslación de los vectores originalmente inmersos en el cubo
[0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6] de manera que Pmin ' es ahora el origen del espacio 3D.
266
Capítulo 7. Redes de Kohonen
La segunda parte del procedimiento de redistribución del conjunto de entrenamiento
consiste ahora en la extensión del Hipercubo h’ a fin de ocupe por completo el espacio
definido por el Hipercubo H. Para ello requerimos aplicar un escalamiento a todos nuestros
vectores. Es bien sabido que el escalamiento se da al multiplicar a todos los componentes
de un vector por los factores S1, S2, …, Sn, donde el i-ésimo factor, Si, se relacionará
únicamente con el i-ésimo componente del vector. Dado que nuestro objetivo es extender a
h’, y a los vectores E1 ', E2 ',..., EN ' , de manera que ahora ocupen a todo el Hipercubo H,
entonces tenemos que el escalamiento deberá mapear al vector Pmax ' en el vector
[1 1 … 1]T. En consecuencia se debe dar solución al conjunto de n ecuaciones:
ximax '⋅ Si = 1, i = 1, 2,..., n
(Ecuación 7.4.9)
Lo cual es en realidad muy sencillo y la solución nos proporciona los factores de
escalamiento a aplicar:
Si =
1
max
i
x
'
, i = 1, 2,..., n
(Ecuación 7.4.10)
(Retomando nuestro ejemplo con n = 3 tenemos que en la Figura 7.14 se puede apreciar el
resultado de aplicar el mencionado escalamiento).
X3
(1,1,1)
X2
(0,0,0)
X1
Figura 7.14. Aplicación de factores de escalamiento de manera que el conjunto
de vectores originalmente inmerso en el cubo [0.3, 0.6] × [0.3, 0.6] × [0.3, 0.6] (Figura 7.11)
se redistribuya a lo largo del cubo [0, 1] × [0, 1] × [0, 1].
267
Una Introducción al Cómputo Neuronal Artificial
En la práctica nuestro método asume que efectivamente el conjunto de
entrenamiento está inmerso en el Hipercubo H pero que necesita ser redistribuido.
Entonces, realmente solo se requieren identificar a Pmin y Pmax (Ecuaciones 7.4.3 y 7.4.4) y
aplicar de manera directa las Ecuaciones 7.4.6 y 7.4.10. Con lo que se tiene una fórmula
que engloba a todos los pasos antes mencionados:
ª x j ,1 º
« »
Ej = « # »
« x j ,n »
¬ ¼
→
ª
·º
1
min §
« ( x j ,1 − x1 ) ¨ max
min ¸ »
© x1 − x1 ¹ »
«
ª x*j ,1 º «
»
#
« » «
»
#
« » «
»
§
·
1
E j * = « x*j ,i » = « ( x j ,i − ximin ) ¨ max
min ¸ »
« » «
© xi − xi ¹ »
« # » «
»
#
« x* » «
»
j
n
,
¬ ¼
·»
«
1
min §
« ( x j ,n − xn ) ¨ x max x min ¸ »
© n − n ¹¼
¬
(Ecuación 7.4.11)
Donde E1*, E2 *,...EN * son los vectores en el conjunto de entrenamiento pero redistribuidos
× [0,1] × ... × [0,1] .
de manera que ocupan por completo el espacio [0,1]
n
7.4.2. Clasificación de Imágenes mediante
una Red de Kohonen 1D
Sean m1 (renglones) y m2 (columnas) las dimensiones de una imagen bidimensional.
Sea n = m1 ⋅ m2. Sabemos que el j-ésimo píxel en la imagen, j = 1, 2, …, n, tendrá asociado
un vector en \ 3 dado por [xj,1 xj,2 Gj]T, donde xj,1 y xj,2 son sus respectivos renglón y
columna en la imagen, mientras que Gj es su valor en el conjunto {0, 1, 2, …, 255}, el cual
representa su intensidad bajo escala de grises. En primer lugar tenemos que los valores de
intensidad de los píxeles deberán ser normalizados de manera que éstos se encuentren en el
intervalo [0, 1]. Tal normalización es en realidad simple y se implementa mediante:
G normalized
=
j
Gj
255
(Ecuación 7.4.12)
Ahora bien, sabemos que una imagen por lo regular es representada mediante una
matriz de píxeles. Sin embargo, nótese que hemos introducido a n y j para denotar al
número total de píxeles en una imagen y para referirnos mediante un único índice a un
píxel, respectivamente. Y es que básicamente lo que haremos será definir a un vector en el
Espacio n-Dimensional al concatenar a los m1 renglones en la imagen. Cada renglón
contiene los valores de intensidad de sus correspondientes píxeles. A fin de asegurarnos que
268
Capítulo 7. Redes de Kohonen
el vector se encuentre dentro del Hipercubo H = [0,1]
× [0,1] × ... × [0,1] (Ecuación 7.4.1) es
n
que consideraremos sus valores de intensidad normalizados (Ecuación 7.4.12). De esta
manera una imagen estará ahora asociada a un vector.
Consideraremos un conjunto de 340 imágenes en escala de grises. Estas imágenes
corresponden a secciones cerebrales capturadas mediante Tomografía Computada. Las
imágenes están asociadas a 5 pacientes, cuentan todas con una resolución de 512 × 512
píxeles y fueron capturadas utilizando el mismo equipo y bajo las mismas condiciones de
contraste y configuración. Véase en la Figura 7.15 una de las imágenes bajo consideración.
Figura 7.15. Una imagen correspondiente a una sección cerebral
capturada mediante Tomografía Computada.
Nuestras 340 imágenes son en primer representadas mediante vectores inmersos en
un Espacio conformado por n = 512 × 512 = 262,144 dimensiones. Además, mediante la
aplicación de la Ecuación 7.4.12 tenemos asegurado que nuestros vectores estarán
inmersos en el Hipercubo unitario [0,1] × [0,1] × ... × [0,1] . Estos 340 vectores formarán
262,144
precisamente el conjunto de entrenamiento. A este conjunto también se le aplicó la
Ecuación 7.4.11 a fin de asegurar que se encuentre completamente distribuido a lo largo de
nuestro Hipercubo.
Utilizaremos a una Red de Kohonen 1D a fin de obtener una clasificación para las
340 imágenes. Nótese que entonces efectuaremos un mapeo de un Espacio de 262,144
dimensiones hacia un arreglo de neuronas unidimensional. Consideraremos una partición
en 20 clases. Por lo tanto nuestra red se conformará por 20 neuronas. El vector de pesos en
cada neurona tendrá 262,144 componentes inicializados todos con valor 0.5. Tal como en
los ejemplos presentados en la Sección 7.3, utilizaremos vecindades de radio
r = 0. Por lo que nuestra función de Fuerza de Enlace tendrá valor 1 únicamente para la
269
Una Introducción al Cómputo Neuronal Artificial
Neurona Ganadora y cero para las restantes neuronas en la red. Ello también tiene como
consecuencia que la actualización de pesos será aplicada sólo a la Neurona Ganadora.
Consideraremos 30 presentaciones del conjunto de entrenamiento. Finalmente, sólo nos
basta establecer a nuestro Coeficiente de Aprendizaje α. En este caso utilizaremos:
α (t ) =
1
t +1
(Ecuación 7.4.13)
Donde t es la actual presentación del conjunto de entrenamiento. Ello quiere decir que en la
1
primer presentación (t = 1) tendremos un coeficiente α (1) = , en la segunda presentación
2
1
(t = 2) se usará α (2) = , y así sucesivamente. En la última presentación (t = 30) tendremos
3
1
≈ 0.0322. La idea, como siempre, es la de iniciar
un Coeficiente de Aprendizaje α (30) =
31
el entrenamiento con actualizaciones que nos permitan explorar inicialmente el Espacio de
la Red con “pasos”, propiamente ajustes de pesos, de tamaño “grande”. Posteriormente,
asumimos que mientras el entrenamiento avanza los pesos se acercarán cada vez más a sus
posiciones óptimas. Ello implica que en estas fases requeriremos “pasos” de tamaño
“pequeño” con el fin de asegurar la mayor precisión posible en los posicionamientos finales
de los vectores de pesos. El Algoritmo 7.1, encargado del entrenamiento de la red, recibe
como entrada nuestro conjunto de entrenamiento así como los parámetros apropiados.
Debemos simplemente tomar en cuenta que el Algoritmo debe ajustarse apropiadamente
para considerar nuestra función de Fuerza de Enlace y el Coeficiente de Aprendizaje tal y
como los hemos establecido.
Una vez efectuadas las 30 presentaciones de nuestro conjunto de entrenamiento
aplicamos el Algoritmo 7.2 a fin de determinar la membresía de cada una de las 340
imágenes. Véase la Tabla 7.3. El primer punto interesante surge del hecho de que la
neurona asociada a la clase 20 no cuenta con miembros. Ello quiere decir que en realidad,
bajo los parámetros de entrenamiento que establecimos, 19 clases son suficientes. La clase
5 es la que más miembros tiene: 43. Por otro lado tenemos que la clase 9 únicamente cuenta
con dos miembros. En este punto será natural preguntarse que tienen en común las
imágenes dentro de cada clase. Para ello véase, en primer lugar, la Tabla 7.4. Esta Tabla
muestra a los 16 miembros de la clase 17. Inicialmente tenemos que estas imágenes
agrupan secciones correspondientes a dos pacientes. Lo interesante es que tales secciones
corresponden a prácticamente las mismas regiones craneales. Recordemos que el
entrenamiento de la Red de Kohonen utiliza a la Distancia Euclidiana para determinar la
similitud entre los vectores de entrada. Es claro entonces que para esta clase los vectores
asociados a las imágenes correspondientes fueron caracterizados como los más similares
entre sí. Ahora véase la Tabla 7.5. En ésta tenemos a los 25 miembros que conforman a la
clase 12. Las imágenes están asociadas a 3 diferentes pacientes y corresponden a secciones
cerebrales donde se aprecia claramente, y únicamente, materia blanca, materia gris y la
porción ósea del cráneo que protege a esa región del cerebro.
270
Capítulo 7. Redes de Kohonen
Tabla 7.3. Clasificación de las 340 imágenes en el conjunto
de entrenamiento de acuerdo a una Red de Kohonen 1D
con 20 neuronas (véase el texto para detalles).
Clase Miembros Clase Miembros
4
27
1
11
8
25
2
12
28
12
3
13
15
14
4
14
43
17
5
15
12
21
6
16
4
16
7
17
30
38
8
18
2
19
9
19
5
0
10
20
Tabla 7.4. Los 16 miembros de la clase 17 asociada a un conjunto de entrenamiento
formado por 340 imágenes y clasificado mediante una Red de Kohonen 1D.
271
Una Introducción al Cómputo Neuronal Artificial
Tabla 7.5. Los 25 miembros de la clase 12 asociada a un conjunto de entrenamiento
formado por 340 imágenes y clasificado mediante una Red de Kohonen 1D.
272
Capítulo 7. Redes de Kohonen
Contamos con una Red de Kohonen 1D que nos ha proporcionado una solución al
Problema de la Clasificación Automática de Imágenes. En este punto es conveniente
establecer, y como ya debe ser claro, que la clasificación es estructurada únicamente por la
Red de Kohonen durante el proceso de entrenamiento el cual es un mecanismo no
supervisado. Ello quiere decir, por un lado, que no existe un “maestro” u “orientador” que
le indique a la red la existencia de un porcentaje de error o desacierto como sucede en, por
ejemplo, el Algoritmo de Retropropagación. Es la Red misma la que forma su propia
estructura de clasificación. Esta propiedad es sumamente atractiva, ya que hemos venido
mencionado que existen una gran variedad de aplicaciones en las cuales únicamente
contamos con el conjunto de vectores de entrada y nada más. Por lo tanto, modelos de
Redes No Supervisadas como el de Kohonen pueden llegar a ser muy útiles a fin de
determinar automáticamente una estructura o partición para tales conjuntos de vectores.
Pero por otro lado, debemos tomar en cuenta que la clasificación que nos proporciona una
Red de Kohonen puede llegar a ser puesta a prueba en términos de su utilidad. Las Tablas
7.4 y 7.5 nos proporcionan evidencia de una “buena” clasificación por parte de la Red para
nuestras imágenes. Pero por lo regular, una vez que se cuenta con una clasificación, ésta es
evaluada por un experto quien decide si es útil o no o bien si ha ayudado a encontrar
patrones y propiedades que no eran visibles a simple vista. En el contexto de la aplicación
que estamos presentando, un Médico Especialista es quien debería juzgar si la clasificación
es apropiada o no. Por ejemplo, se podría requerir que la clasificación proporcione un
mecanismo para agrupar casos médicos con diagnósticos y procedimientos comunes. De
manera que cuando un nuevo caso se presente se recurra a la Red Neuronal a fin de
determinar la clase que le corresponde y utilizar a los casos miembros de esa clase, y que en
consecuencia son similares, como una guía a fin de proceder apropiadamente con el
tratamiento del paciente. Si el Médico Especialista determina que la clasificación no es
apropiada entonces es que se recurre a utilizar otros parámetros de entrenamiento: se
modifican la inicialización de pesos, el número de clases, el número de presentaciones, el
coeficiente de aprendizaje, etc. Esto con el fin de obtener una nueva clasificación y
determinar si es útil o no.
Ahora bien, hemos establecido la posible necesidad de recurrencia a un experto para
determinar la utilidad de la clasificación. Pero también hemos mencionado que se busca
que los vectores de pesos, una vez terminado el entrenamiento, se encuentren
uniformemente distribuidos a lo largo del espacio de la red. Esta propiedad es también un
parámetro a tomar en cuenta para determinar si la clasificación fue apropiada o no. En la
Sección 7.3 vimos ejemplos de mapeos de espacios de 2 y 3 dimensiones. La ventaja era
que podíamos analizar la relación entre el conjunto de entrenamiento y los vectores de
pesos finales, y su distribución, mediante elementos visuales. El problema que tenemos
ahora tiene que ver con el hecho de que hemos trabajado con un conjunto de entrenamiento
formado por 340 vectores inmersos en un espacio de n = 262,144 dimensiones. ¿Cómo
podemos determinar o inferir si efectivamente los vectores de pesos están uniformemente
distribuidos? Para ello, debemos recurrir al uso de otras herramientas. Sabemos que existe
273
Una Introducción al Cómputo Neuronal Artificial
una relación directa entre los vectores de entrada y los vectores de pesos: ambos tienen el
mismo número de componentes y sus valores están en el intervalo [0, 1]. Existe una
relación uno a uno entre una imagen 2D y su correspondiente vector de entrada. Por lo
tanto, podemos pensar en que un vector de pesos es la representación de una imagen. Tal
imagen se forma poco a poco conforme el proceso de entrenamiento avanza y además
debería considerar las características que tienen en común las imágenes que se agrupan en
su correspondiente clase. Esta última aseveración tiene sustento en el hecho de que un
vector de pesos es actualizado utilizando a la imagen actualmente procesada. El punto
ahora es simplemente considerar que todo vector de pesos puede ser expresado como una
imagen en escala de grises. Visualizando todas las imágenes formadas, y asociadas a los
vectores de pesos, es que podremos apreciar que tan diferentes, o similares, son entre sí. De
esta manera podemos contar con un parámetro para inferir que tan bien distribuidos están
los pesos en el Espacio de la red. La Tabla 7.6 muestra precisamente las 20 imágenes
descritas por nuestros vectores de pesos. Mencionamos antes que la clase 20 no contaba
con miembros. Véase en la Tabla como es que su imagen correspondiente no contiene
información visual alguna. De hecho, todos sus componentes tienen valor 0.5, indicando
que durante el entrenamiento la neurona asociada nunca fue caracterizada como Ganadora.
Por otro lado, obsérvense las imágenes asociadas a los vectores de pesos para las clases 12
y 17. Este par de imágenes guardan una gran similitud con sus correspondientes imágenes
en el conjunto de entrenamiento (Tablas 7.4 y 7.5).
Como hemos podido apreciar, las Redes de Kohonen usan como parte fundamental
de su proceso de entrenamiento y clasificación a la Distancia Euclidiana sobre el espacio
n-Dimensional. Debido a que cada uno de los vectores de pesos asociados a las clases son
precisamente vectores en \ n , entonces es que podemos determinar también la Distancia
Euclidiana entre cualquier par de vectores de pesos. La idea ahora es definir un Mapa de
Falso Color que representará la distribución de los vectores de pesos en el subespacio
[0,1] × [0,1] × ... × [0,1] . Es claro que la Distancia Euclidiana máxima entre dos vectores será
n
dmax = n , mientras que la Distancia Euclidiana mínima será, obviamente, dmin = 0. Toda
Distancia Euclidiana d entre dos vectores de pesos será asociada con una intensidad G en la
escala de grises mediante:
« d
»
⋅ 255»
GW = «
¬ d max
¼
(Ecuación 7.4.14)
De esta manera si d = 0 entonces se tendrá asociada la intensidad correspondiente al color
negro. Por otro lado, si d = dmax = n entonces se tendrá al color blanco.
274
Capítulo 7. Redes de Kohonen
Tabla 7.6. Visualización de las imágenes asociadas a los vectores de pesos
de una Red de Kohonen 1D formada por 20 neuronas (Véase el texto para detalles).
Clase 1
Clase 2
Clase 3
Clase 4
Clase 5
Clase 6
Clase 7
Clase 8
Clase 9
Clase 10
Clase 11
Clase 12
Clase 13
Clase 14
Clase 15
Clase 16
Clase 17
Clase 18
Clase 19
Clase 20
275
Una Introducción al Cómputo Neuronal Artificial
Consideremos a nuestra Red de Kohonen 1D. En la Figura 7.16 se presenta el
Mapa de Falso Color asociado a las distancias entre nuestros 20 vectores de pesos.
Tenemos entonces una representación visual y planar de cómo es que están distribuidos los
vectores de pesos una vez finalizado el entrenamiento de la red. La diagonal principal tiene
asociado el color negro debido a que la distancia de un vector de pesos consigo mismo es
cero. Realmente son las regiones restantes del mapa las que nos interesan. Intuitivamente,
concluiríamos que la distribución es buena si los colores asociados a las distancias tienden
hacia el blanco. ¿Cómo deberíamos interpretar al mapa de manera más objetiva? Para ello
tendríamos que recurrir a los valores de las distancias.
Distancia Euclidiana Mínima
Distancia Euclidiana Máxima
Figura 7.16. Mapa de Falso Color que muestra las distancias entre los vectores
de pesos asociados a una Red de Kohonen 1D formada por 20 neuronas.
Consideremos únicamente las distancias que tienen los vectores de pesos asociados
a las clases 12 (Tabla 7.5) y 17 (Tabla 7.4) con todos los demás vectores de pesos. Véase
la Tabla 7.7. Veamos primero el caso de las distancias que tiene el vector de pesos
asociado a la clase 12. Evidentemente la distancia de un vector de pesos consigo mismo es
cero y por esa razón omitiremos esa instancia. La distancia mínima que tiene este vector es
con el vector de pesos asociado a la clase 8 (111.6704); mientras que la máxima es con el
vector correspondiente a la clase 10 (173.0801). En promedio se tiene una distancia de
132.7726. Son 15 los vectores de pesos con los que se tiene una distancia por encima del
promedio. Ahora bien, analicemos de igual forma al vector de pesos asociado a la clase 17.
La distancia máxima se da con el vector de pesos correspondiente a la clase 8 (159.4698);
mientras que la mínima se presenta con el vector de pesos asociado a la clase 19
276
Capítulo 7. Redes de Kohonen
(108.6999). El promedio de las distancias que tiene nuestro vector con los restantes es de
127.0818. Se tienen 16 vectores de pesos cuyas distancias están por encima de este valor.
Utilizando estas observaciones podemos entonces establecer que aquellos vectores de pesos
cuyas distancias estén por debajo del promedio sean caracterizados como los vectores más
similares, mientras que aquellos que estén por encima del promedio se les ha de denotar
como con los que más diferencias se tienen. Lo interesante es que para ambas clases bajo
estudio, la 12 y 17, tenemos que más del 75 % de los vectores de pesos que conforman a la
red presentan diferencias notables. Desde un punto de vista geométrico podemos decir
entonces que los vectores de pesos asociados a las clases 12 y 17 se encuentran bien
colocados en el espacio de la red. Si la mayoría de las clases para nuestra Red de Kohonen
hubiesen sido caracterizadas como similares a nuestros vectores de pesos, debido a que sus
distancias son menores a la distancia promedio, entonces hubiésemos podido inferir que el
vector de pesos bajo estudio está demasiado cerca de otros y por tanto no se logra
diferenciar adecuadamente, impactando con ello la partición obtenida para el Espacio de la
red. Finalmente, este tipo de análisis tienen el objetivo de proporcionar elementos para
establecer si la clasificación es apropiada. Pero como ya comentamos antes, la utilidad de la
clasificación también va en función del contexto del problema que se esté tratando.
Tabla 7.7. Distancias que tienen los vectores de pesos asociados a las clases 12 y 17
con todos los demás vectores de pesos que conforman a una Red de Kohonen 1D.
Clase 12
Clase 17
168.3854
139.3557
Clase 1
151.5977
141.7146
Clase 2
167.1622
158.2210
Clase 3
170.0472
150.0269
Clase 4
138.8657
146.1057
Clase 5
148.1818
127.6880
Clase 6
169.6480
143.1229
Clase 7
111.6704
159.4698
Clase 8
164.2003
144.7317
Clase 9
173.0801
148.6562
Clase 10
128.3436
110.4572
Clase 11
0.0
146.3194
Clase 12
131.3029
119.8285
Clase 13
138.4280
131.3952
Clase 14
133.6582
144.6634
Clase 15
138.4936
157.2248
Clase 16
146.3194
0.0
Clase 17
116.2553
136.6072
Clase 18
147.5144
108.6999
Clase 19
145.0719
154.4305
Clase 20
277
Una Introducción al Cómputo Neuronal Artificial
278
Una Introducción al Cómputo Neuronal Artificial
Referencias
Libros de Texto
•
Inteligencia Artificial: Sistemas Inteligentes con C#.
Nicolás Arrioja Landa Cosio.
Gradi, 2007.
•
Introduction to Algorithms.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest y Clifford Stein.
MIT Press, Segunda Edición, 2001.
•
Neural Networks.
Eric Davalo y Patrick Naïm.
The Macmillan Press Ltd, 1992.
•
Principles of Artificial Neural Networks.
Daniel Graupe.
Advanced Series on Circuits and Systems, Vol. 6. World Scientific, Segunda Edición,
2007.
•
Elementary Linear Algebra.
Stanley I. Grossman.
Brooks Cole, Quinta Edición, 1994.
•
Neural Networks: A Comprehensive Foundation.
Simon Haykin.
Prentice Hall; Segunda Edición, 1998.
•
Redes Neuronales Artificiales.
José Hilera y Victor Martínez.
Editorial Alfaomega, 2000.
•
Linear Algebra and Its Applications.
David C. Lay.
Addison Wesley, Tercera Edición, 2005.
•
Fuzzy-Neuro Approach to Agent Applications.
Raymond S. T. Lee.
Springer-Verlag Berlin Heidelberg, 2006.
279
Una Introducción al Cómputo Neuronal Artificial
•
La Mente Humana
C. Rayner
Ediciones Orbis, 1985.
•
El Cuerpo Humano (Tomos I y II)
C. Rayner
Ediciones Orbis, 1985.
•
Neural Computation and Self-Organizing Maps, An Introduction.
Helge Ritter, Thomas Martinetz y Klaus Schulten.
Addison-Wesley Publishing Company, 1992.
•
Neural Networks: A Systematic Introduction.
Raul Rojas.
Springer-Verlag, Berlin, New-York, 1996.
•
Artificial Intelligence: A Modern Approach.
Stuart Russell y Peter Norvig.
Prentice Hall Series in Artificial Intelligence, Segunda Edición, 2002.
•
Calculus On Manifolds: A Modern Approach To Classical Theorems Of Advanced
Calculus.
Michael Spivak.
Westview Press, 1971.
•
Calculus.
Michael Spivak.
Publish or Perish, Segunda Edición, 1980.
•
Calculus.
James Stewart.
Brooks/Cole Publishing Company, Tercera Edición, 1995.
Artículos
•
280
Automatic Segmentation and Classification of Computed Tomography Brain Images:
An Approach Using One-Dimensional Kohonen Networks.
Ricardo Pérez-Aguila.
IAENG International Journal of Computer Science, Vol. 37, Issue 1, pp. 27-35.
ISSN: 1819-9224 (online version), 1819-656X (print version).
International Association of Engineers (IAENG), February 2010.
Una Introducción al Cómputo Neuronal Artificial
•
Brain Tissue Characterization Via Non-Supervised One-Dimensional Kohonen
Networks.
Ricardo Pérez-Aguila.
Proceedings of the XIX International Conference on Electronics, Communications and
Computers CONIELECOMP 2009, pp. 197-201.
ISBN: 978-0-7685-3587-6.
IEEE Computer Society, February, 2009.
•
One-Dimensional Kohonen Networks and Their Application to Automatic
Classification of Images.
Ricardo Pérez-Aguila, Pilar Gómez-Gil y Antonio Aguilera.
Proceedings of International Seminar on Computational Intelligence 2006, pp. 95-99.
IEEE – CIS Chapter Mexico. Tijuana Institute of Technology.
October, 2006.
•
Non-Supervised Classification of 2D Color Images Using Kohonen Networks and a
Novel Metric.
Ricardo Pérez-Aguila, Pilar Gómez-Gil y Antonio Aguilera.
Progress in Pattern Recognition, Image Analysis and Applications; 10th Iberoamerican
Congress on Pattern Recognition, CIARP 2005; Proceedings. Lecture Notes in
Computer Science, Vol. 3773, pp. 271-284.
ISBN: 3-540-29850-9.
Springer-Verlag Berlin Heidelberg, 2005.
281