Solucion problemas Mecanica Vectorial Para Ingenieros Dinamica 9th : BEER

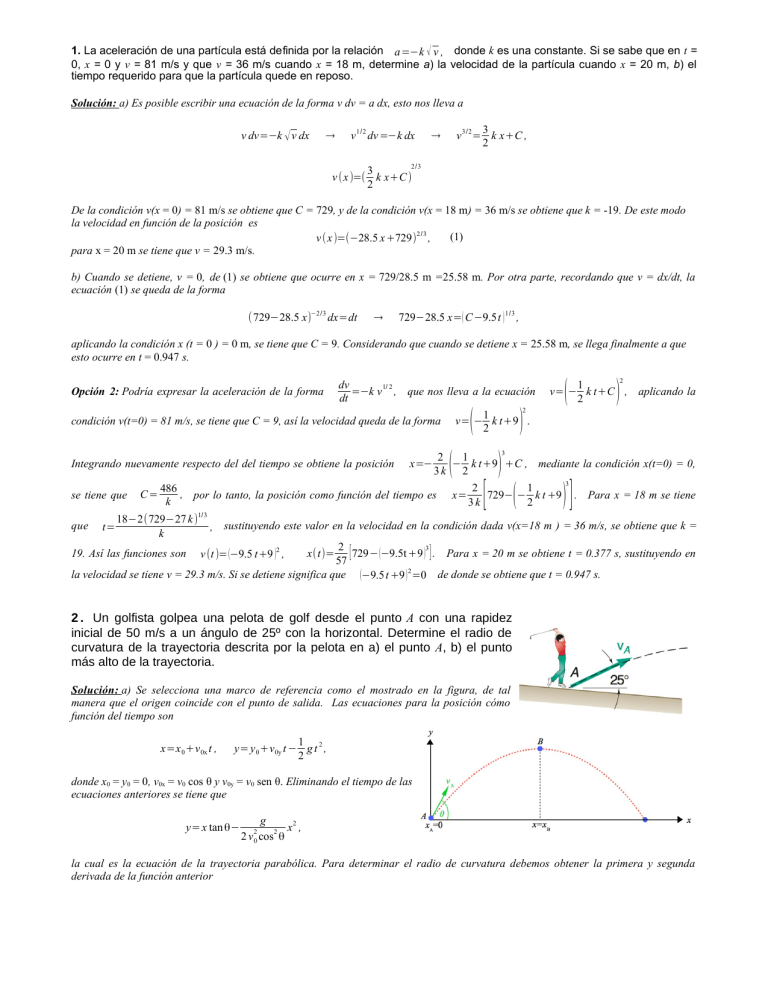
1. La aceleración de una partícula está definida por la relación a=−k √ v , donde k es una constante. Si se sabe que en t =
0, x = 0 y v = 81 m/s y que v = 36 m/s cuando x = 18 m, determine a) la velocidad de la partícula cuando x = 20 m, b) el
tiempo requerido para que la partícula quede en reposo.
Solución: a) Es posible escribir una ecuación de la forma v dv = a dx, esto nos lleva a
v dv=−k √ v dx
→
v 1/2 dv =−k dx
3
v 3/2 = k x+C ,
2
→
2/3
3
v (x )=( k x+C )
2
De la condición v(x = 0) = 81 m/s se obtiene que C = 729, y de la condición v(x = 18 m) = 36 m/s se obtiene que k = -19. De este modo
la velocidad en función de la posición es
(1)
v (x )=(−28.5 x +729)2/3 ,
para x = 20 m se tiene que v = 29.3 m/s.
b) Cuando se detiene, v = 0, de (1) se obtiene que ocurre en x = 729/28.5 m =25.58 m. Por otra parte, recordando que v = dx/dt, la
ecuación (1) se queda de la forma
(729−28.5 x)−2/3 dx=dt
→
729−28.5 x=( C −9.5t ) 1/3 ,
aplicando la condición x (t = 0 ) = 0 m, se tiene que C = 9. Considerando que cuando se detiene x = 25.58 m, se llega finalmente a que
esto ocurre en t = 0.947 s.
dv
=−k v 1/ 2 , que nos lleva a la ecuación
dt
2
1
condición v(t=0) = 81 m/s, se tiene que C = 9, así la velocidad queda de la forma v= − k t+9 .
2
Opción 2: Podría expresar la aceleración de la forma
(
que
t=
)
)
3
2
1
− k t+9 +C , mediante la condición x(t=0) = 0,
3k 2
3
2
1
486
C=
, por lo tanto, la posición como función del tiempo es x=
729− − k t +9 . Para x = 18 m se tiene
k
3k
2
Integrando nuevamente respecto del del tiempo se obtiene la posición
se tiene que
(
)
(
2
1
v= − k t+C , aplicando la
2
18−2(729−27 k )
k
x=−
1/3
[ (
)]
, sustituyendo este valor en la velocidad en la condición dada v(x=18 m ) = 36 m/s, se obtiene que k =
2
[729− (−9.5t +9 )3 ] . Para x = 20 m se obtiene t = 0.377 s, sustituyendo en
57
la velocidad se tiene v = 29.3 m/s. Si se detiene significa que (−9.5 t +9 ) 2 =0 de donde se obtiene que t = 0.947 s.
19. Así las funciones son
v (t )= (−9.5 t+9 )2 ,
x(t)=
2 . Un golfista golpea una pelota de golf desde el punto A con una rapidez
inicial de 50 m/s a un ángulo de 25º con la horizontal. Determine el radio de
curvatura de la trayectoria descrita por la pelota en a) el punto A, b) el punto
más alto de la trayectoria.
Solución: a) Se selecciona una marco de referencia como el mostrado en la figura, de tal
manera que el origen coincide con el punto de salida. Las ecuaciones para la posición cómo
función del tiempo son
x=x 0 +v 0x t ,
1
y= y 0 +v 0y t − g t 2 ,
2
donde x0 = y0 = 0, v0x = v0 cos θ y v0y = v0 sen θ. Eliminando el tiempo de las
ecuaciones anteriores se tiene que
y= x tan θ−
g
x2 ,
2 v 20 cos2 θ
la cual es la ecuación de la trayectoria parabólica. Para determinar el radio de curvatura debemos obtener la primera y segunda
derivada de la función anterior
dy
g
=tan θ− 2 2 x ,
dx
v 0 cos θ
d2 y
−g
=
,
dx 2 v 20 cos2 θ
así el radio de curvatura es
ρ( x)=
{1+[ f ' (x )]2 }3/2
=
∣ f ' ' (x )∣
{[
(1)
(2)
1+ tan θ−
g
x
v cos2 θ
2
0
g
v 20 cos 2 θ
]}
2 3/2
, (3)
para x = 0 se tiene que
3/2
ρ(0)=
{1+tan 2 θ } v 20 cos2 θ v 20 cos 2 θ sec3 θ
=
g
g
=
v 20
,
g cosθ
sustituyendo v0 = 50 m/s y θ = 25º, se tiene que ρ(0)=281m.
b) En el punto más alto corresponde al máximo de la función que describe la trayectoria, es decir, la primera derivada debe ser cero. De
la ecuación (1) se tiene que
v 20 senθ cosθ
g
tan θ− 2
x
=0
→
x
=
m
m
g
v 0 cos 2 θ
al sustituir esta expresión en la ecuación (3) se llega a
ρ( x m)=
v 20 cos 2 θ
=209m .
g
3. En la figura el punto P se mueve sobre la barra ranurada que tiene la forma
de un cuarto de circunferencia. Si se sabe que y = 150 mm, dy/dt = 300 mm/s y
d2y/dt2 = 0, ¿cuáles son las magnitudes de la velocidad y la aceleración del punto
P?
Solución: El movimiento del punto P se describe mediante la ecuación de una circunferencia
x 2+ y 2=r 2
→
x= √ r 2 − y 2 ,
derivando respecto del tiempo se tiene que
ẋ=−
sustituyendo r = 0.3 m, y = 0.15 m,
y ẏ
, (2)
√ r 2− y 2
ẏ=0.3 m/ s , se tiene que
ẋ=−0.173m / s , por lo tanto, la rapidez es
∣⃗v∣=√ ẋ 2 + ẏ 2 =0.346 m /s .
Para determinar la magnitud de la aceleración es necesario obtener la segunda derivada de x respecto del tiempo, así de la ecuación (2)
y tomando en cuenta que ẏ es constante, se tiene que
ẍ=−
así se tiene que
r2 ẏ 2
=−0.462 m/ s2 ,
(r − y 2 )3/2
2
∣⃗
a∣=√ ẍ 2 + ÿ 2 =0.462 m /s 2 .
4. Una furgoneta viaja a lo largo de una carretera recta con una velocidad descrita
por la gráfica. Subraye las respuestas correctas.
a) ¿Hacia dónde viaja en t = 5 s?
A) Izquierda
B) Está en reposo
C) Derecha
D) No se puede saber
b) Si en t = 2 s está en x = 10 pies, ¿dónde estará en t = 4 s?
A) x = 370 pies
B) x = 146 pies
C) x =140 pies
D) x = 74 pies
c) Su aceleración en t = 7 s es
A) a = -80 pies/s2
B) a = 80 pies/s2
C) a = -4 pies/s2
D) a = 4 pies/s2
Solución: a) La ecuación que describe la velocidad está dada por
v (t )=−4 t+80 ,
puesto que el signo de la velocidad nos indica la dirección, tenemos que v (5s)=[−4(5)+80] pies/ s=60 pies/ s , ya que es positiva,
significa que va hacia la derecha.
b) La posición es
x=∫ v dt=−2 t +80 t+C ,
2
de la condición
x(2s)=10pies , se tiene que C =−142pies , por lo tanto, se puede determinar que
x(4s)=146pies.
c) La aceleración es
a=
dv
=−4 m/ s 2 ,
dt
la cual es constante, por lo tanto, para cualquier tiempo la aceleración es -4 m/s2.
1. Cuando un corredor de relevos A ingresa a la zona de intercambio, de 20 m
de largo, con una rapidez de 12.9 m/s empieza a desacelerar. Entrega la
estafeta al corredor B 1.82 s despues, y su companero deja la zona de
intercambio con la misma velocidad. Determine a) la aceleracion uniforme de
cada uno de los corredores, b) el momento en el que el corredor B debe
empezar a correr.
Solución: a) Analizamos el movimiento del corredor A, para ello definimos un marco
de referencia cuyo origen coincide con el inicio de la zona de intercambio. Puesto
que la aceleración es constante, se tiene que
1
x A =x 0A +v 0A t + a A t 2
2
a A=−2.10 m/ s 2 ,
→
al terminar salir de la zona de intercambio tiene una velocidad dada por
v A=v 0A +a A t A =9.078 m/ s.
Para el corredor B, teniendo en cuenta de que parte del reposo hasta alcanzar la
misma velocidad que tiene el corredor A al momento de terminar la zona de
intercambio, por lo tanto,
v 2B =v 20B+2 a B ( x B − x 0B)
→
a B=2.06 m/ s 2 .
b) El tiempo que el corredor B le tomará recorrer los 20 metros para alcanzar la
misma velocidad que el corredor A es
v −v
t B = B 0B =4.4 s ,
aB
Así que que el corredor B debe empezar a correr 4.4 s – 1.82 s = 2.57 s antes de que el corredor A entre en la zona de intercambio.
2. Una partícula se mueve a lo largo de una trayectoria dada por
x(t )=a cos(ω t ) ,
y (t )=a sen(ω t ) ,
donde a es una constante que está en metros y ω es otra constantes cuyas unidades son rad/s. a) Demuestre
que la distancia de la partícula al origen es independiente del tiempo, esto es, que es una constante y por lo
tanto la trayectoria es una circunferencia de radio a. b) Demuestre que el vector velocidad es perpendicular al
vector posición en cualquier instante. c) Demuestre que la aceleración siempre está dirigida hacia el centro del
círculo, esto es, que su sentido es opuesto al vector posición, y que su magnitud está dada por a ω2. d)
Demuestre que la magnitud de la velocidad es una constante dada por aω. e) Combine los resultados de c) y d)
para demostrar que la aceleración de la partícula tiene una magnitud constante dada por v2/a.
Solución: a) El vector posición para la partícula es
⃗r (t)=a cos(ωt ) ̂i+a sen(ωt ) ̂j ,
cuya magnitud, esto es, la distancia del origen al punto donde se encuentra la partícula,
es
∣⃗r (t )∣= √ a 2 cos2 (ωt)+a2 sen2 (ωt )=a ,
la cual resulta ser constante, por lo tanto, la partícula se mueve en una trayectoria
circular de radio a.
b) La velocidad es
⃗v (t)=
d⃗
r (t)
=−a ω sen(ωt) ̂i+a ωcos(ωt) ̂j ,
dt
si dos vectores son perpendiculares su producto escalar debe ser cero en todo momento,
⃗r (t)⋅⃗
v (t)=−a 2 ω sen(ωt )cos(ωt )+a 2 ω cos(ωt) sen(ω t)=0 ,
como se observa para cualquier tiempo t, los vectores son perpendiculares.
c) La aceleración es
⃗a (t)=
d⃗
v (t)
=−a ω2 sen(ωt ) ̂i −a ω2 sen(ω t) ̂j=−a ω2 ⃗
r (t) ,
dt
note que la aceleración es igual al vector posición multiplicado por una constante negativa, -a ω2, por lo tanto, su dirección tiene sentido
contraria al vector posición para cada instante. La magnitud de la aceleración es
∣⃗
a (t )∣= √ a 2 ω4 sen 2 (ω t)+a2 ω4 sen2 (ωt)=a ω2 .
d) La magnitud de la velocidad es
∣⃗v (t )∣= √ a 2 ω2 sen 2 (ω t)+a 2 ω2 cos2 (ωt )=a ω.
e) Del resultado anterior se tiene que
ω=∣⃗v (t )∣/a , al sustituir en la magnitud de la aceleración se llega a
∣⃗
a (t )∣=
a∣⃗
v (t)∣2 ∣⃗
v (t)∣2
=
.
2
a
a
3. Suponga que el punto P se mueve hacia arriba por la ranura con forma de
un cuarto de circunferencia a una velocidad ⃗v (t)=(300 mm / s) ê t . Cuando y =
150 mm, ¿qué valor tienen ẏ y ÿ ?
Solución: El movimiento del punto P ocurre sobre una trayectoria circular, por lo tanto, el eje
tangencial es perpendicular al radio y el eje normal coincide con éste. De la figura se tiene que
θ=30º , y por lo tanto la componente vertical de la velocidad es
ẏ=v y =∣⃗v (t)∣cosθ=0.260 m/ s.
Observe que la rapidez es constante,
ṡ=∣⃗
v (t)∣= √ (0.3m/ s)2 +(0 m /s )2 =0.3m/ s ,
por lo tanto, la aceleración tangencial es cero,
la normal cuya magnitud es
at =
s̈=d ṡ /dt=0 , así la aceleración es igual a
ṡ 2
=0.3m /s 2 ,
r
donde la componente vertical es
ÿ=a y=−a t senθ=−0.150 m/ s 2 .
4 . Una bicicleta rueda por una carretera recta donde la gráfica mostrada
describe su velocidad como función de la posición. Subraye las respuestas
correctas
I. Su aceleración en s = 16 m es
A) -4 m/s2
B) - 1 m/s2
C) 1 m/s2
D) 4 m/s2
II. Si partió de s = 10 m, ¿donde estará en t = 4 s?
A) 2.72 m
B) 12 m
C) 27.2 m
D) 40 m
III. Considerando que partió de s = 10 m, ¿cuál será su velocidad en t = 4 s?
A) 2.72 m
B) 6.79 m/s
C) 13.6 m/s
D) 40 m/s
Solución: I) La ecuación de la gráfica mostrada es
1
v= s ,
4
así la aceleración es
a=
dv 1 ds 1
1
=
= v= s ,
dt 4 dt 4
16
para s = 16 m se tiene que a = 1 m/s2.
II) De la ecuación de la velocidad se puede obtener la posición como función del tiempo
ds 1
= s
dt 4
→
ds 1
= dt ,
s 4
integrando la ecuación diferencial se tiene que
1
ln∣s∣= t+C
4
→
1t
s(t)= Ae 4 ,
donde A = eC, la cual está determinada por la condición s(t=0) = 10m, esto implica que A = 10m, por lo tanto,
1t
para t = 4 s, se tiene que s = (10m) e1 = 27.2 m.
s (t )=(10m)e 4 ,
III) La velocidad como función del tiempo es
v (t )=
para t = 4 s, se tiene que v = (2.5m/s) e1 = 6.79 m/s.
(
)
1
t
ds 5
= m/ s e 4 ,
dt 2