operadores compactos 2

V. TEORÍA ESPECTRAL
EN ESPACIOS
NORMADOS
Damos comienzo en este capı́tulo a la llamada teorı́a espectral
de operadores en espacios normados. Toda la información acumulada hasta el momento se irá aplicando sucesivamente al estudio
de las propiedades espectrales de los operadores lineales y acotados. Con la mirada puesta en la situación finito-dimensional,
trataremos de generalizar los conceptos de resolvente y espectro y de obtener descomposiciones de los operadores compactos
mediante proyecciones sobre ciertos subespacios invariantes.
SECCIONES
1. Introducción. Definiciones previas.
2. Propiedades espectrales de los operadores lineales acotados. Funciones
de un operador.
3. Operadores compactos.
4. Descomposición espectral de los operadores compactos.
5. Ecuaciones lineales de operadores compactos. Ecuaciones integrales de
Fredholm.
6. Ejercicios.
197
1. INTRODUCCIÓN. DEFINICIONES PREVIAS.
Mucha información sobre el comportamiento de un operador lineal A se puede obtener estudiando la familia de operadores A−λI, con λ real o complejo
(obsérvese que todo subespacio invariante bajo A es también invariante bajo
A − λI y que todos los operadores de la forma A − λI conmutan entre sı́).
Por otra parte, a menudo el inverso de un operador es más importante que el
propio operador. En particular, la teorı́a espectral trata de las propiedades
del operador (A − λI)−1 , donde A ∈ L(X) con X espacio normado y λ un
escalar fijado (esto permitirá descomponer el operador A en el mayor número de componentes y, paralelamente, una descomposición del espacio X en
suma de subespacios invariantes bajo A). En las aplicaciones prácticas esto
permitirá resolver sistemas de ecuaciones lineales, ecuaciones diferenciales y
ecuaciones integrales.
En el caso de dimensión finita la situación es particularmente simple: dado
un operador lineal A : X → X en un espacio normado de dimensión finita,
dim X = n, fijado un escalar λ, o existe (A − λI)−1 o no existe; si no existe,
en cuyo caso λ recibe el nombre de autovalor de A, se prueba fácilmente
que existen como máximo n autovalores y son precisamente las raı́ces de la
ecuación caracterı́stica det(A − λI) = 0 (donde identificamos el operador A
con su matriz asociada respecto a cualquier base de X). En particular se
deduce que todo tal operador tiene al menos un autovalor. Además todas
las matrices que representan al mismo operador A ∈ L(X) con respecto a
distintas bases de X tienen los mismos autovalores.
Las cosas no son tan simples en dimensión infinita: aparte de que puede
haber infinitos valores de λ para los que (A − λI)−1 no existe, en los casos
de existencia debemos precisar los resultados, tanto el que (A − λI)−1 sea
lineal y acotado como el que el rango de (A − λI) sea denso en X. Nada de
esto tiene significado en dimensión finita.
El estudio de estas cuestiones nos conduce al análisis espectral y pretendemos
obtener los resultados que generalizan los conocidos en el caso de dimensión
finita. Un resultado fundamental en álgebra lineal es el siguiente:
Teorema. Si X es un espacio euclı́deo de dimensión n y A ∈ L(X) es un
operador autoadjunto, entonces existe una base ortonormal {ϕ1 , . . . , ϕn } de
X y unos números reales λ1 , . . . , λn tales que Aϕi = λi ϕi , i = 1, . . . , n.
Además, si llamamos Ei a la proyección ortogonal sobrePN (A − λi I), i =
n
1, . . . , n, entonces Ei 6= 0, ∀i,PEi Ej = 0 si i 6= j,
i=1 Ei = I y se
n
tiene la descomposición A =
λ
E
.
Como
consecuencia,
la matriz
i
i
i=1
de A asociada a dicha base es la matriz diagonal (hAϕi , ϕj i)i,j=1,...n =
198

λ1 . . .

..

.
0 ...
0


.
λn
Veamos un ejemplo de lo que puede pasar en dimensión infinita.
Ejemplo. Sea h una función real continua y 2π-periódica.
R πEntonces el operador K : L2 [−π, π] → L2 [−π, π], definido por (Kf )(t) = −π h(t−s)f (s)ds,
es lineal y acotado. Si elegimos la base ortonormal ϕn (t) = √12π eint , n ∈ Z,
resulta
Z π
Z t+π
1 ins
1
1
√
h(t−s)
h(s) √ ein(t−s) ds = √ eint λn ,
(Kϕn )(t) =
e ds =
2π
2π
2π
−π
t−π
donde λn =
Rπ
−π
h(s)e−ins ds, n ∈ Z, es decir, Kϕn = λn ϕn .
La matriz asociada al operador K respecto a la base {ϕn }n∈Z es la matriz
diagonal doblemente infinita








..

.
λ−1



.



0
λ0
0
λ1
..
.
En lo que sigue, mientras no se especifique lo contrario, supondremos que
X es un espacio normado complejo no trivial y A : X → X un operador
lineal.
1.1.- Definición. Diremos que λ ∈ C es un punto regular de A si existe
Rλ (A) = (A − λI)−1 y es un operador acotado definido en un subconjunto
denso de X. El conjunto resolvente de A es ρ(A) = {λ ∈ C : λ es punto
regular de A}.
El término resolvente se refiere a que la ecuación (A−λI)x = y tiene solución
x = (A−λI)−1 y. Además el estudio de las propiedades de (A−λI)−1 permite
obtener información sobre el propio A.
Llamaremos espectro de A al conjunto σ(A) = C \ ρ(A), es decir al conjunto
de puntos no regulares de A, que llamaremos puntos espectrales de A. En
particular los autovalores de A son puntos espectrales. El siguiente ejemplo
muestra que, en general, no todos los puntos espectrales son autovalores (a
diferencia de los espacios de dimensión finita donde la teorı́a espectral se
estudia a partir de los autovalores al ser estos los únicos puntos espectrales).
199
Ejemplo. En el espacio H = L2 (R) con la medida de Lebesgue se define
el operador (M f )(x) = eix · f (x). Como kM f k = kf k y (M −1 f )(x) =
e−ix · f (x), deducimos que M es unitario. Encontremos los autovalores de
M:
Dado λ ∈ C, existe fλ ∈ L2 (R) tal que M fλ = λfλ si y sólo si eix fλ (x) =
λfλ (x) c.s. Esto implica que fλ (x) = 0 c.s. de modo que kfλ k = 0 y M no
tiene autovalores.
Sea ahora ρ ∈ C tal que (M − ρI)f = g, es decir (eix − ρ)f (x) = g(x) c.s. o
bien f (x) = (eix − ρ)−1 g(x) c.s. y se define un operador lineal
[(M − ρI)−1 g](x) = (eix − ρ)−1 g(x).
El operador (M − ρI)−1 está acotado si y sólo si |ρ| =
6 1; esto quiere decir
que σ(M ) = {ρ ∈ C : |ρ| = 1} = T, lo que prueba que el espectro es no vacı́o
aunque el operador no posea autovalores.
Clasificaremos el espectro en tres grupos:
- Un punto λ ∈ C es autovalor de A o pertenece al espectro puntual de A,
λ ∈ σp (A), si no existe (A−λI)−1 . Cada vector x ∈ X tal que (A−λI)x = 0,
con λ ∈ σp (A) se llama autovector de A correspondiente a λ y el subespacio
de X que contiene al cero y a los autovectores correspondientes a un mismo
λ se llama autoespacio correspondiente a λ.
- Un punto λ ∈ C pertenece al espectro continuo de A, λ ∈ σc (A), si R(A−λI)
es denso en X y existe (A − λI)−1 pero no está acotado.
- Un punto λ ∈ C pertenece al espectro residual de A, λ ∈ σr (A), si existe
(A − λI)−1 pero está definido en un subconjunto no denso de X.
De las definiciones anteriores se deduce que
C = ρ(A) ∪ σ(A) = ρ(A) ∪ σp (A) ∪ σc (A) ∪ σr (A)
y que la unión es disjunta, obteniéndose ası́ una partición de C.
La siguiente tabla resume las caracterı́sticas de los distintos conjuntos:
λ
(A − λI)−1 (A − λI)−1
R(A − λI)
ρ(A)
existe
acotada
denso en X
σc (A)
existe
no acotada
denso en X
σr (A)
existe
–
no denso en X
σp (A)
no existe
–
–
Una propiedad básica de los autovectores es la siguiente:
200
1.2.- Proposición. Autovectores x1 , . . . , xn correspondientes a autovalores
λ1 , . . . , λn distintos de un operador lineal A sobre un espacio normado complejo X son linealmente independientes.
Demostración. Si {x1 , . . . , xn } fueran linealmente dependientes, denotamos
por xm el primero de ellos que es combinación lineal de los anteriores, es
decir xm = α1 x1 + · · · + αm−1 xm−1 .
Entonces
0
=
(A − λm I)xm =
m−1
X
αj (A − λm I)xj =
j=1
m−1
X
αj (λj − λm )xj
j=1
=⇒ αj (λj − λm ) = 0, ∀j = 1, . . . , m − 1
=⇒ αj = 0, ∀j = 1, . . . , m − 1 =⇒ xm = 0,
lo cual es absurdo.
♦
(A − λI)−1 ,
Es sabido que si X tiene dimensión finita y existe
entonces debe
ser acotado. Además R(A − λI) = X, con lo que se deduce que σc (A) =
σr (A) = ∅; de ahı́ que los puntos del espectro puntual se llamen también
autovalores de A.
Sin embargo en el caso de dimensión infinita tenemos puntos espectrales que
no son autovalores, como muestran los siguientes ejemplos.
1.3.- Ejemplos. 1) Sea T : `2 → `2 el operador traslación a la derecha,
definido por T (x1 , x2 , . . . ) = (0, x1 , x2 , . . . ). Este operador es acotado y tiene
norma uno. El operador inverso T −1 : T (X) → X es la traslación hacia la
izquierda T −1 (x1 , x2 , . . . ) = (x2 , x3 , . . . ). Como T (X) no es denso en X,
el punto λ = 0 es un valor espectral de T pero no es autovalor ya que
T x = 0 =⇒ x = 0 y el vector cero no puede ser autovector.
2) Sea X un espacio de Hilbert separable de dimensión infinita
P y {xn }n∈N
una base ortonormal de X. SiP
hacemos para cada x ∈ X, x = n∈N αn xn , y
definimos el operador Ax = n∈N αn λn xn , donde {λn }n∈N es una sucesión
de escalares distintos de uno pero con λn → 1, se prueba que
λn ∈ σp (A), ∀n;
1 ∈ σc (A);
Si λ 6= λn , ∀n y λ 6= 1 =⇒ λ ∈ ρ(A);
σr (A) = ∅.
3) Bajo las mismas condiciones del ejemplo anterior, definimos el operador
destrucción
∞
∞
X
X
αn
Ax =
xn+1 , para x =
αn xn .
n+1
n=1
n=1
201
Se comprueba aquı́ que 0 ∈ σr (A) y λ ∈ ρ(A), ∀λ 6= 0.
En el caso de dimensión infinita, los operadores cuyo comportamiento es el
más parecido al caso de dimensión finita son los operadores completamente
continuos o compactos pues, como veremos en el apartado 4, el conjunto de
autovalores es a lo sumo numerable y el cero es su único posible punto de
acumulación.
2. PROPIEDADES ESPECTRALES DE LOS OPERADORES LINEALES ACOTADOS. FUNCIONES DE UN OPERADOR.
Supondremos en esta sección que X es un espacio de Banach complejo y
no vacı́o y T : X → X un operador lineal y estudiaremos las principales caracterı́sticas del espectro y de la resolvente. Utilizaremos la notación
Rλ (T ) = (T − λI)−1 para indicar la resolvente de T (cuando no haya confusión escribiremos simplemente Rλ ).
Nota. Las propiedades que enunciamos en este apartado relativas a L(X)
se pueden fácilmente extender a cualquier álgebra de Banach con identidad;
pero el contexto en el que aquı́ se plantean es el que aplicaremos posteriormente en la teorı́a espectral (puede consultarse en [Ru] para el estudio de
estos conceptos).
2.1.- Lema. Sea X de Banach, T : X → X lineal y λ ∈ ρ(T ). Si T es cerrado o acotado, entonces Rλ (T ) está definido en todo X y es acotado.
Demostración. Si T es cerrado, también lo es T − λI. Por tanto, también
lo es (T − λI)−1 . Entonces, por el teorema del gráfico cerrado, su dominio
D(Rλ ) es cerrado, de modo que D(Rλ ) = D(Rλ ) = X, pues λ ∈ ρ(T ).
Si T fuera acotado, como D(T ) = X es cerrado, T es cerrado y se aplica el
razonamiento anterior.
♦
2.2.- Teorema. Sean T ∈ L(X) y λ, µ ∈ ρ(T ). Entonces:
(a) (Ecuación de la resolvente) Rµ − Rλ = (µ − λ)Rµ Rλ .
(b) Rλ S = SRλ , ∀S ∈ L(X) tal que ST = T S.
(c) Rλ Rµ = Rµ Rλ .
Demostración. (a) Teniendo en cuenta que Rλ y Rµ están definidas en todo
202
X, resulta:
Rµ − Rλ = Rµ (T − λI)Rλ − Rµ (T − µI)Rλ
= Rµ (T − λI − T + µI)Rλ = (µ − λ)Rµ Rλ .
(b) Si ST = T S, S(T − λI) = (T − λI)S. Entonces
Rλ S = Rλ S(T − λI)Rλ = Rλ (T − λI)SRλ = SRλ .
(c) Como Rλ conmuta con T , Rλ conmuta con Rµ , por (b).
♦
2.3.- Lema. Si T ∈ L(X), σ(T ) = σ(T ∗ ) y Rλ (T ∗ ) = Rλ (T )∗ si λ ∈
ρ(T ∗ ) = ρ(T ).
Demostración. Ver ejercicio 2 al final del capı́tulo.
A continuación enunciamos el teorema de la aplicación espectral que generaliza el resultado en dimensión finita de que si λ es autovalor de una
matriz A, entonces p(λ) = an λn + · · · + a1 λ + a0 es autovalor de la matriz
p(A) = an An + · · · + a1 A + a0 I. Utilizaremos la notación p(σ(T )) = {µ ∈ C :
µ = p(λ), λ ∈ σ(T )} y la notación análoga p(ρ(T )) para la resolvente.
2.4.- Teorema (aplicación espectral para polinomios). Si T ∈ L(X) y
p(λ) = an λn + · · · + a1 λ + a0 , an 6= 0, entonces p(σ(T )) = σ(p(T )).
Demostración. Supondremos que σ(T ) 6= ∅ (ver teorema 2.10).
Si n = 0, p(σ(T )) = {a0 } = σ(p(T )). Sea pues n > 0.
• Llamaremos S = p(T ) y Sµ = p(T ) − µI, µ ∈ C. Veamos que σ(S) ⊂
p(σ(T )).
Fijado µ ∈ C, el polinomio Sµ (λ) = p(λ) − µ se factoriza como
Sµ (λ) = αn (λ − γ1 ) . . . (λ − γn )
lo que corresponde a
Sµ = p(T ) − µI = αn (T − γ1 I) . . . (T − γn I).
Si cada γj está en ρ(T ), entonces existe Sµ−1 = (αn )−1 (T − γn I)−1 . . . (T −
γ1 I)−1 por lo que µ ∈ ρ(p(T )). Lo anterior prueba también que si µ ∈
σ(p(T )), entonces γj ∈ σ(T ) para algún j. Por lo tanto, Sµ (γj ) = p(γj )−µ =
0, de donde µ = p(γj ) ∈ p(σ(T )).
• Sea ahora µ ∈ p(σ(T )). Por definición µ = p(β) para algún β ∈ σ(T ).
Aquı́ se presentan dos posibilidades:
(∗) T − βI no tiene inversa.
Como β es un cero del polinomio Sµ (λ) = p(λ) − µ, entonces Sµ (λ) =
203
(λ − β)g(λ) y también Sµ = p(T ) − µI = (T − βI)g(T ). Ahora bien,
como todos los factores de g(T ) conmutan con T −βI, es cierto también
que Sµ = g(T )(T − βI).
Si Sµ tuviera inversa, podrı́amos poner
I = (T − βI)g(T )Sµ−1 = Sµ−1 g(T )(T − βI),
pero esto indica que T − βI tiene inverso, lo cual contradice nuestro
supuesto. Por tanto Sµ no tiene inverso, es decir µ ∈ σ(p(T )).
(∗) T − βI tiene inverso. Esto indica que R(T − βI) 6= X pues, en caso
contrario, β ∈ ρ(T ) por el teorema de la aplicación abierta.
Como Sµ = p(T ) − µI = (T − βI)g(T ), entonces R(Sµ ) 6= X, de donde
µ ∈ σ(p(T )).
♦
El teorema de la aplicación espectral es también cierto en espacios más
generales que los polinomios. Ası́, si definimos el espacio
F (T ) = {f : f es función analı́tica en algún entorno de σ(T )},
entonces se puede demostrar que f (σ(T )) = σ(f (T )), ∀f ∈ F (T ) (ver
[DS]).
El lema siguiente es un resultado básico que permitirá deducir las propiedades topológicas del espectro, ası́ como fórmulas de representación para la
resolvente.
2.5.- Lema. Sea X un espacio de Banach y T ∈ L(X). Si kT k < 1, entonces
∞
P
existe (I − T )−1 ∈ L(X) e (I − T )−1 =
T j , donde la serie converge en
j=0
la norma de L(X).
Demostración. Como kT j k ≤ kT kj y la serie geométrica
∞
P
kT kj converge
j=0
∞
P
para kT k < 1, la serie
T j converge absolutamente para kT k < 1.
j=0
Como X es de Banach, también lo es L(X) y la convergencia absoluta im∞
P
plica la convergencia de la serie
T j.
j=0
Llamemos S =
P∞
j=0 T
j.
Como
(I − T )(I + T + · · · + T n ) = (I + T + · · · + T n )(I − T ) = I − T n+1 , ∀n,
y T n+1 → 0 cuando n → ∞, pues kT k < 1, entonces (I −T )S = S(I −T ) = I
de donde S = (I − T )−1 .
♦
2.6.- Teorema. El espectro σ(T ) de un operador T ∈ L(X), donde X es de
Banach complejo, es un conjunto cerrado.
204
Demostración. Si ρ(T ) = ∅, es abierto. Sea pues ρ(T ) 6= ∅ y λ0 ∈ ρ(T ).
∀λ ∈ C, T − λI = (T − λ0 I) − (λ − λ0 )I = (T − λ0 I)[I − (λ − λ0 )(T −
λ0 I)−1 ].
Por el lema 2.1, (T − λ0 I)−1 ∈ L(X) y por el lema 2.5, si llamamos V =
∞
P
(λ − λ0 )j (T − λ0 I)−j , ∀λ tal que
(λ − λ0 )(T − λ0 I)−1 , existe (I − V )−1 =
j=0
kV k < 1, es decir cuando
|λ − λ0 | <
(∗)
1
.
k(T − λ0 I)−1 k
Esta desigualdad muestra que (T − λI)−1 ∈ L(X); por tanto, si λ verifica
(∗), existe (T − λI)−1 = [(T − λ0 I)(I − V )]−1 = (I − V )−1 (T − λ0 I)−1 .
Ası́ pues, la desigualdad (∗) representa un entorno de λ0 formado por puntos
regulares de T . Esto quiere decir que ρ(T ) es abierto, de modo que σ(T ) =
C \ ρ(T ) es cerrado.
♦
De la demostración del resultado anterior se obtiene inmediatamente el siguiente teorema de representación.
2.7.- Teorema. En las condiciones anteriores, si λ0 ∈ ρ(T ), se tiene la
representación para la resolvente
(∗∗)
Rλ = (T − λI)−1 =
∞
X
(λ − λ0 )j Rλj+1
,
0
j=0
donde la serie converge absolutamente en la bola |λ−λ0 | < k(T −λ0 I)−1 k−1 ,
la cual está contenida en ρ(T ).
2.8.- Corolario. Dado T ∈ L(X), la resolvente Rλ (T ), considerada como
función de λ con valores en L(X), es localmente holomorfa en ρ(T )1 .
Demostración. Para cualesquiera x ∈ X, f ∈ X 0 , definimos h(λ) = f (Rλ (T )x).
A partir de (∗∗) obtenemos el desarrollo en serie
h(λ) =
∞
X
cj (λ − λ0 )j con cj = f (Rλ0 (T )j+1 x)
j=0
que converge absolutamente en el disco |λ − λ0 | < kRλ0 k−1 .
♦
Además ρ(T ) es el mayor conjunto en el cual Rλ (T ) es localmente holomorfa por lo que podemos decir que es el dominio natural de analiticidad de
Rλ (T ).
1
Dado un conjunto Ω abierto en C, si S : Ω → L(X) es una función que toma valores
operadores en X (donde escribiremos S(λ) = Sλ ), decimos que S es localmente holomorfa en Ω
si ∀x ∈ X, f ∈ X 0 , la función h(λ) = f (Sλ x) es holomorfa en Ω.
205
2.9.- Teorema. Si T ∈ L(X), dado λ ∈ ρ(T ), entonces kRλ (T )k ≥ 1/δ(λ)
siendo δ(λ) = ı́nf s∈σ(T ) |λ−s| = d(λ, σ(T )). En consecuencia, kRλ (T )k → ∞
cuando δ(λ) → 0.
Demostración. Si λ ∈ ρ(T ), entonces {µ : |µ − λ| < kRλ k−1 } ⊂ ρ(T ) de
donde d(λ, σ(T )) ≥ 1/kRλ k si suponemos que σ(T ) 6= ∅.
♦
2.10.- Teorema. Si T ∈ L(X), σ(T ) 6= ∅.
Demostración. Si T = 0, evidentemente σ(T ) = {0} =
6 ∅.
Sea pues T 6= 0 y supongamos que σ(T ) = ∅. Entonces, ρ(T ) = C y existe
(T − λI)−1 ∈ L(X), ∀λ ∈ C. Por el corolario 2,8, la función h(λ) = f (Rλ x)
es holomorfa en C, ∀x ∈ X, f ∈ X 0 .
Probemos a continuación que h es acotada en todo el plano complejo.
a) En el cı́rculo |λ| ≤ 2kT k, h es continua y por tanto acotada.
b) Si λ > 2kT k, la serie
1
1
1X 1 n
(T − λI)−1 = − (I − T )−1 = −
T
λ
λ
λ
λn
n≥0
converge absolutamente, pues k(1/λ)T k < 1.
Además
k(T − λI)−1 k ≤
1
1
1
1
1 X 1
=
·
· kT kn =
·
<
.
1
n
|λ|
|λ|
|λ| 1 − |λ| kT k
|λ| − kT k
kT k
n≥0
Se prueba ası́ que h está acotada también en esta región pues
|h(λ)| ≤ kf k · kRλ k · kxk <
kf k · kxk
.
kT k
En definitiva, h es holomorfa y acotada en C y, por el teorema de Liouville, h
es constante. Esto implica que Rλ es independiente de λ, ası́ como también
lo es Rλ−1 = T − λI, lo cual es absurdo.
♦
El teorema anterior puede ser falso si se consideran espacios de Hilbert reales.
Ası́ por ejemplo,
si consideramos el operador T : R2 → R2 definido por la
0 −1
matriz A =
, entonces T − λI no es inyectiva si y sólo si λ es raı́z
1 0
de la ecuación det(A − λI) = 0. Como R2 tiene dimensión finita sobre R,
σ(T ) = ∅.
2.11.- Teorema. El espectro σ(T ) de T ∈ L(X) es compacto y está contenido en la bola cerrada B(0, kT k).
206
Demostración. Procediendo como en el teorema anterior, se tiene que
1X 1
(∗ ∗ ∗)
Rλ = −
· T n,
λ
λn
n≥0
donde la serie converge cuando |λ| > kT k. Esto implica que {λ ∈ C : |λ| >
kT k} está contenido en ρ(T ), con lo que el espectro σ(T ) debe estar en el
disco B(0, kT k). Como σ(T ) es además cerrado, es compacto.
♦
De este teorema se deduce en particular que ρ(T ) 6= ∅. El resultado motiva
además el siguiente concepto:
2.12.- Definición. Si T ∈ L(X), se llama radio espectral de T a
rσ (T ) = sup{|λ| : λ ∈ σ(T )},
es decir al radio del menor disco centrado en el origen que contiene a
σ(T ).
Del teorema 2.11 es claro que rσ (T ) ≤ kT k (la figura adjunta ilustra lo
dicho). El siguiente resultado permite refinar esta acotación.
σ(T )
rσ (T )
kT k
2.13.- Teorema (fórmula de Gelfand). Sea T ∈ L(X). Entonces
rσ (T ) = lı́m kT n k1/n = ı́nf kT n k1/n .
n
n≥1
Demostración. a) Probaremos en primer lugar que lı́m kT n k1/n = ı́nf kT n k1/n .
n→∞
n≥1
Fijado un entero positivo m, ∀n ∈ N, n = m · qn + rn con 0 ≤ rn < m. Esto
implica que
kT n k1/n = kT m·qn +rn k1/n ≤ kT m kqn /n · kT krn /n .
Como qn /n → 1/m y rn /n → 0 cuando n → ∞, resulta que
lı́m sup kT n k1/n ≤ kT m k1/m ,
n→∞
de donde
lı́m sup kT n k1/n ≤ ı́nf kT m k1/m ≤ lı́m inf kT n k1/n .
n→∞
n→∞
m≥1
207
b) Por el teorema de la aplicación espectral, σ(T n ) = [σ(T )]n ; es evidente
entonces que rσ (T n ) = [rσ (T )]n . Ahora bien, como rσ (T n ) ≤ kT n k, entonces
rσ (T ) = [rσ (T n )]1/n ≤ kT n k1/n , ∀n.
Por tanto, rσ (T ) ≤ lı́mn→∞ kT n k1/n y la demostración estará concluida si
lı́mn→∞ kT n k1/n = rσ (T ).
P
Recordando de nuevo la fórmula (∗ ∗ ∗), tenemos que Rλ = −κ n≥0 κn T n ,
donde llamamos κ = 1/λ.
Por la fórmula de Hadamard, la serie anterior converge absolutamente cuando |κ| < r, donde 1/r = lı́mn→∞ kT n k1/n .
Como Rλ es localmente holomorfa en el conjunto resolvente ρ(T ), si llamamos M al conjunto del plano que corresponde a ρ(T ) por la transformación
κ = 1/λ, sabemos que el radio de convergencia r es el radio del mayor disco
abierto alrededor de κ = 0 que está incluido completamente en M . Por tanto,
1/r es el radio del menor cı́rculo alrededor de λ = 0 cuyo exterior está completamente incluido en ρ(T ). Como esta es precisamente la definición de radio espectral de T , resulta en definitiva que rσ (T ) = 1/r = lı́mn→∞ kT n k1/n ,
lo que prueba el enunciado.
♦
3. OPERADORES COMPACTOS.
Los operadores compactos son aquellos cuyas propiedades más se asemejan
a las de los operadores lineales en espacios de dimensión finita de modo
que su teorı́a espectral será una extensión directa de aquellos y una forma
sencilla de introducirse en este estudio. Además muchos de los operadores
que aparecen en el estudio de ecuaciones integrales son compactos. Ası́, una
aplicación de dicha teorı́a espectral conduce a la teorı́a de Fredholm para
ecuaciones integrales.
Es sabido que un operador acotado transforma conjuntos acotados en conjuntos acotados. Si además dicho operador tiene rango finito, es decir la
imagen tiene dimensión finita, transforma conjuntos acotados en relativamente compactos. Esta propiedad nos lleva a introducir la siguiente clase de
operadores.
3.1.- Definición. Sean X e Y espacios normados. Un operador T : X → Y
es compacto o completamente continuo si es lineal y la imagen de todo subconjunto acotado en X es relativamente compacto (es decir, tiene clausura
208
compacta).
De la definición se deduce que un operador lineal T : X → Y es compacto si
y sólo si T (B1 ) es compacto, siendo B1 = {x ∈ X : kxk ≤ 1} la bola unidad
en X.
3.2.- Ejemplo. Una clase importante de operadores compactos la forman
ciertos operadores integrales.R Ası́, si X = L2 ([0, 1], dt), el operador T : X →
1
X definido por (T f )(s) = 0 k(s, t)f (t)dt, donde k ∈ C([0, 1] × [0, 1]), es
compacto. Para comprobarlo, veamos que T (B1 ) es compacto.
Es claro que si f ∈ B1 , T f ∈ C[0, 1] y
Z
1
|f (t)|dt ≤ kkk∞ · kf k2 ≤ kkk∞
kT f k∞ ≤ kkk∞
0
de modo que T (B1 ) es un conjunto acotado de (C[0, 1], k·k∞ ). Además T (B1 )
es un conjunto equicontinuo. En efecto, dado ε > 0, por ser k uniformemente
continuo en [0, 1] × [0, 1], existe δ > 0 tal que
|k(s1 , t) − k(s2 , t)| < ε, ∀t ∈ [0, 1], |s1 − s2 | < δ.
Por tanto, para todo f ∈ B1 ,
Z
|(T f )(s1 )−(T f )(s2 )| ≤
1
Z
|k(s1 , t)−k(s2 , t)|·|f (t)|dt < ε
0
1
|f (t)|dt ≤ εkf k2 ≤ ε.
0
Por el teorema de Arzelá-Ascoli, T (B1 ) es compacto en (C[0, 1], k · k∞ ).
Entonces, si (fn )n∈N ⊂ B1 , existe una subsucesión (fnk )k∈N y una función
f ∈ C[0, 1] tales que kT fnk − f k∞ → 0, de donde kT fnk − f k2 → 0 lo que
prueba la compacidad de T .
Incluso si k ∈ L2 ([0, 1] × [0, 1], dsdt), el operador integral arriba definido es
compacto (ver los ejercicios al final del capı́tulo). Tales operadores se llaman
operadores de Hilbert-Schmidt y juegan un papel importante en el estudio de
ecuaciones diferenciales e integrales. Ası́ por ejemplo, el operador T origina
la ecuación integral (T − λI)x(s) = y(s), donde λ ∈ C, es un parámetro,
y, k son funciones dadas y x es la función incógnita. Hilbert probó que la
solubilidad de la ecuación no depende de la existencia de la representación
integral de T sino de que T es un operador compacto.
Es fácil verificar que todo operador lineal acotado aplica conjuntos relativamente compactos en conjuntos relativamente compactos, de modo que la
propiedad de compacidad es más fuerte que la de continuidad. El término
de operador completamente continuo viene sugerido por el siguiente resultado, en donde se prueba además que no todo operador acotado es compacto.
209
3.3.- Lema. a) Todo operador compacto T : X → Y es acotado y, por tanto,
continuo.
b) Si dim X = ∞, el operador identidad I : X → X no es compacto.
Demostración. a) Como S = {x ∈ X : kxk = 1} es acotado, T (S) es
compacto y por tanto acotado. Ası́ pues sup kT xk < ∞, de donde T es
kxk=1
acotado.
b) La bola unitaria cerrada B = {x ∈ X : kxk ≤ 1} es acotada. Si dim X =
∞, B no puede ser compacto (teorema 5.3, capı́tulo II). De ahı́ que I(B) =
B = B no sea relativamente compacto.
♦
Las siguientes caracterizaciones son a veces usadas como definición de operador compacto.
3.4.- Teorema. Sea T : X → Y lineal. Son equivalentes:
i) T es compacto.
ii) Dada cualquier sucesión {xn }n∈N acotada en X, su imagen {T xn }n∈N
tiene alguna sub-sucesión convergente.
iii) Dada cualquier sucesión {xn }n∈N ⊂ B(0, 1), {T xn }n∈N tiene alguna subsucesión convergente.
Demostración. i) =⇒ ii): Si T es compacto y {xn }n∈N es acotada, la clausura del conjunto {T xn }n∈N es compacto. De aquı́ se deduce que {T xn }n∈N
contiene alguna subsucesión convergente.
ii) =⇒ iii): es trivial.
iii) =⇒ i): Sea M ⊂ X un conjunto acotado e {yn }n∈N una sucesión arbitraria
en T (M ). Entonces existe una sucesión {xn }n∈N en M tal que T xn = yn , ∀n.
Como {xn }n∈N está acotada, existe r > 0 tal que kxn k < r, ∀n. Por hipótesis, la sucesión {T (r−1 xn )}n∈N tiene una subsucesión convergente, digamos
{T (r−1 xnk )}k∈N . Como T xnk = rT (r−1 xnk ), la sucesión {T xnk } = {ynk }
también converge, lo que quiere decir que T (M ) es compacto.
♦
Un operador T : X → Y se dice de rango finito cuando dim T (X) < ∞.
El siguiente resultado prueba que todo operador acotado de rango finito es
compacto. (En particular los operadores de Cn en Cn , objeto del Algebra
Lineal, son siempre compactos.)
3.5.- Teorema. Sea T : X → Y lineal. Entonces
a) Si T es acotado y de rango finito, entonces T es compacto.
b) Si dim X < ∞, T es compacto.
210
Demostración. a) Sea {xn }n∈N una sucesión acotada en X. De la desigualdad
kT xn k ≤ kT k·kxn k, se deduce que {T xn }n∈N es acotada. Como dim T (X) <
∞, {T xn }n∈N es relativamente compacto, de modo que tiene una subsucesión
convergente.
El apartado b) es consecuencia de a), pues T es acotado si dim X < ∞, y
dim T (X) ≤ dim X < ∞.
♦
Observación. Todo operador compacto se puede descomponer en suma de
dos operadores donde uno tiene rango finito y el otro tiene norma menor
que cualquier número positivo (ver [LS]). Por eso, aunque el recı́proco de
3.5(a) no es cierto, los operadores compactos son casi de rango finito.
3.6.- Teorema. El conjunto {T : X → X : T lineal y compacto} es subespacio de L(X).
Demostración. Dados S, T compactos y α, β ∈ E, consideramos una sucesión {xn }n∈N acotada en X. Por hipótesis, {T xn }n∈N tiene una subsucesión, que llamaremos {T xnk }k∈N , convergente. Aplicando ahora S, también existe una subsucesión de {Sxnk }k∈N , {Sxnkj }j∈N , convergente. Como
ambas sucesiones, {T xnkj }j∈N y {Sxnk }k∈N , son convergentes, es claro que
{αT xnkj + βSxnkj }j∈N es convergente.
♦
3.7.- Teorema. Sean T : X → X un operador compacto y S : X → X un
operador lineal acotado. Entonces T S y ST son compactos.
Demostración. Sea B ⊂ X acotado; entonces S(B) es acotado y T (S(B)) =
T S(B) es relativamente compacto. Esto implica que T S es compacto.
Sea ahora {xn }n∈N una sucesión acotada en X; entonces {T xn }n∈N tiene
una subsucesión convergente {T xnk }k∈N y, por ser S continuo, {ST xnk }k∈N
también converge. Esto prueba que ST es compacto.
♦
Los dos últimos teoremas prueban que la clase de operadores compactos es
un ideal bilátero del anillo L(X).
Como consecuencia de lo anterior y del lema 3.3(b) se prueba que, en un
espacio de dimensión infinita, un operador compacto no admite inverso acotado.
El siguiente resultado prueba que la clase de los operadores compactos forma
un subconjunto cerrado de L(X, Y ).
3.8.- Teorema. Sea {Tn }n∈N una sucesión de operadores lineales y compactos de X en Y , donde Y es de Banach. Si {Tn }n∈N converge uniformemente,
es decir, ∃T : kTn − T k → 0, entonces T es compacto.
Demostración. Usaremos el llamado método diagonal, para lo cual sea {xm }m∈N
una sucesión acotada en X. Como T1 es compacto, existe una subsucesión
211
{x1m } tal que {T1 x1m } es de Cauchy. A su vez existe {x2m } subsucesión de
{x1m } tal que {T2 x2m } es de Cauchy. En general, existe una sub-sucesión
{xnm } tal que {Tn xnm } es de Cauchy.
Si elegimos ahora la sub-sucesión diagonal {ym }m∈N con ym = xmm , ∀m,
entonces {Tn ym }m∈N es de Cauchy para cada n fijo. Como {ym }m∈N es también acotada, ∃c > 0 : kym k ≤ c, ∀m. De la convergencia uniforme de la
sucesión {Tn }n∈N se deduce que
∀ε > 0, ∃n0 : kT − Tp k < ε/3c, ∀p ≥ n0 ,
y, como {Tp ym }m∈N es de Cauchy,
∃n1 : kTp yj − Tp yk k < ε/3, ∀j, k ≥ n1 .
Entonces
kT yj − T yk k ≤ kT yj − Tp yj k + kTp yj − Tp yk k + kTp yk − T yk k
≤ kT − Tp k · kyj k + ε/3 + kTp − T k · kyk k
< (ε/3c) · c + ε/3 + (ε/3c) · c = ε.
Como Y es completo, {T ym }m∈N converge, lo que prueba que T es compacto.
♦
Observación. El teorema es falso si sustituimos convergencia uniforme por
convergencia fuerte, como lo muestra el ejemplo de Tn : `2 → `2 definido por
Tn x = (x1 , . . . , xn , 0, . . . ). Como Tn es lineal y acotado y dim Tn (`2 ) < ∞,
es compacto para todo n. Además Tn x → x = Ix pero el operador identidad
no es compacto pues dim `2 = ∞.
Ejemplo. Para probar que el operador T : `2 → `2 definido por T x =
(xn /n)n≥1 es compacto, definimos Tn : `2 → `2 del siguiente modo:
x2
xn
Tn x = x1 , , . . . , , 0, . . . .
2
n
Ası́ Tn es lineal y acotado y como dim Tn (`2 ) < ∞, es también compacto.
Además
k(T − Tn )xk2 =
∞
∞
X
X
1
1
kxk2
2
2
|x
|
≤
|x
|
≤
.
j
j
j2
(n + 1)2
(n + 1)2
j=n+1
j=n+1
Tomando el supremo sobre todos los x de norma 1, vemos que kT − Tn k ≤
1
n+1 y el teorema anterior prueba que T es compacto.
Probaremos a continuación que los operadores compactos aplican sucesiones
débilmente convergentes en sucesiones fuertemente convergentes.
212
d
3.9.- Teorema. Sea T : X → Y un operador compacto. Si xn → x en X,
f
entonces T xn → T x.
Demostración. Llamamos yn = T xn e y = T x.
Sea g ∈ Y 0 y definimos f : X → E por f (z) = g(T z), ∀z ∈ X. Como T es
acotado, f ∈ X 0 y
|f (z)| = |g(T z)| ≤ kgk · kT zk ≤ kgk · kT k · kzk.
d
Por definición, si xn → x, entonces f (xn ) → f (x), es decir, g(T xn ) → g(T x),
d
o bien g(yn ) → g(y). Como g es arbitrario, yn → y.
f
Si no fuera cierto que yn → y, existirı́a {ynk }k∈N subsucesión de {yn }n∈N tal
que kynk − yk ≥ η, para algún η > 0. Como {xn }n∈N converge débilmente,
está acotada y también lo estará {xnk }k∈N . Como T es compacto, {T xnk }k∈N
tiene una subsucesión convergente, digamos {e
yj }j∈N y escribimos yej → ye.
d
Como también yej → y, entonces ye = y. En consecuencia ke
yj − yk → 0 pero
||e
yj − yk ≥ η > 0 lo cual es absurdo.
♦
Otra propiedad interesante es que los operadores compactos admiten clausura compacta.
3.10.- Teorema. Sean X un espacio normado, Y un espacio de Banach
y T : X → Y un operador lineal compacto. Entonces existe Te : X → Y
extensión lineal compacta.
Demostración. Como T es acotado (lema 3.3.a), tiene una extensión lineal
acotada Te : X → Y . Veamos que Te es compacto:
Sea {e
xn }n∈N una sucesión acotada en X. Por ser X denso en X, existe una
sucesión {xn }n∈N en X tal que x
en − xn → 0, ∀n. Evidentemente {xn }n∈N
está acotada, de modo que {T xn }n∈N tiene una sub-sucesión convergente,
T xnk → y ∈ Y . Como, en particular, x
enk − xnk → 0, entonces
Tex
enk − Texnk = Tex
enk − T xnk → 0,
de donde Tex
enk → y, lo que prueba la compacidad de Te.
♦
Un hecho fundamental en la resolución de ecuaciones que involucran operadores compactos es el de que el adjunto de un operador compacto es también
compacto.
3.11.- Teorema (Schauder). Si T : X → Y es compacto, entonces T ∗ es
también compacto.
Demostración. Basta ver que la imagen T ∗ (B 0 ) de la bola unidad B 0 de Y 0
es relativamente compacto.
213
Sea B = B(0, 1) en X. Como T es compacto, T ( B) es relativamente compacto. Dado f ∈ B 0 , para cualquier y ∈ T ( B), tenemos
|f (y)| ≤ kf k · kyk = kf k · kT xk ≤ kf k · kT k · kxk ≤ kT k,
pues kf k < 1 y kxk ≤ 1. Esto indica que los funcionales de B 0 están uniformemente acotados sobre T ( B). Por otra parte, dichos funcionales son
equicontinuos sobre T ( B) pues, si y1 , y2 ∈ T ( B) y f ∈ B 0 , |f (y1 ) − f (y2 )| =
|f (y1 − y2 )| ≤ ky1 − y2 k.
Una generalización del teorema de Arzelá-Ascoli (capı́tulo I, teorema 5.12)
prueba que B 0 es relativamente compacto para la convergencia uniforme
sobre T ( B).
Sea ahora una sucesión arbitraria (T ∗ fn )n∈N ⊂ T ∗ (B 0 ). Como B 0 es relativamente compacto, existe una subsucesión (fni )i∈N de (fn ), que converge
uniformemente sobre T ( B), es decir
sup |fni (T x) − fnj (T x)| = sup |T ∗ (fni − fnj )(x)| = kT ∗ (fni − fnj )k → 0.
x∈ B
x∈ B
Esto implica que la sucesión (T ∗ fni )i∈N converge en norma, de modo que
T ∗ (B 0 ) es relativamente compacto.
♦
4. DESCOMPOSICIÓN ESPECTRAL DE LOS OPERADORES
COMPACTOS.
Obtenemos en esta sección la descomposición espectral de los operadores
compactos en espacios normados. Es notable el hecho de que las propiedades espectrales de los operadores compactos son simples generalizaciones
de la teorı́a de autovalores de matrices finitas. Se deben a F. Riesz y J.
Schauder los resultados fundamentales de la teorı́a que desarrollamos a continuación.
En primer lugar veremos que si un operador compacto tiene infinitos autovalores, estos pueden disponerse en una sucesión que converge a cero (más
adelante se probará que el espectro de un operador compacto, a excepción
del cero, está formado únicamente por autovalores).
4.1.- Teorema. El conjunto de autovalores de un operador compacto T
sobre un espacio normado X es finito o numerable y su único posible punto
de acumulación es λ = 0.
214
Demostración. Basta probar que para todo real k > 0, el conjunto
Ak = {λ ∈ σp (T ) : |λ| ≥ k}
S
es finito pues σp (T ) = k∈N Ak . Supongamos por el contrario que ∃k0 > 0
tal que Ak0 es infinito. Existe entonces una sucesión {λn }n∈N de autovalores
distintos tal que |λn | ≥ k0 . Para cada λn , existe xn 6= 0 tal que T xn = λn xn
y el conjunto {x1 , . . . , xn } es linealmente independiente (proposición 1.2).
Llamamos Mn = h{x1 , . . . , xn }i.
Como los Mn tienen dimensión finita, son cerrados; por el lema de Riesz
(capı́tulo II, lema 5.1), existe una sucesión {yn }n∈N tal que
yn ∈ Mn , kyn k = 1, kyn − xk ≥ 1/2, ∀x ∈ Mn−1 .
Podemos pues escribir T yn − T ym = λn yn − x
e, donde x
e = λn yn − T y n + T y m .
Supongamos m < n y probemos que x
e ∈ Mn−1 :
ym ∈ Mm ⊂ Mn−1 = h{x1 , . . . , xn−1 }i =⇒ T ym ∈ Mn−1 pues T xj = λj xj .
Además, si yn =
Pn
i=1 αi xi ,
λn yn − T y n =
n
X
entonces
αi (λn xi − T xi ) =
i=1
n−1
X
αi (λn − λi )xi ∈ Mn−1 .
i=1
Ambos resultados conducen a que x
e ∈ Mn−1 ; por tanto, x = λ−1
e ∈ Mn−1
n x
ası́ que
1
1
1
kλn yn − x
ek = |λn | · kyn − xk ≥ |λn | ≥ k0 =⇒ kT yn − T ym k ≥ k0 .
2
2
2
Esto implica que {T yn }n∈N no tiene ninguna subsucesión convergente lo que
contradice la compacidad de T pues {yn }n∈N es acotado.
♦
Ejemplo. El conjunto de autovalores puede ser también vacı́o como muestra
el operador T : `2 → `2 definido por T (x) = (0, x1 , x2 /2, x3 /3, . . . ).
El siguiente teorema prueba que un operador compacto sólo tiene un número
finito de vectores propios linealmente independientes asociados a un mismo
autovalor no nulo, es decir el autoespacio correspondiente a cualquier autovalor no nulo tiene dimensión finita (utilizaremos la notación Tλ = T − λI,
para cualquier λ ∈ C).
4.2.- Teorema. Sea T : X → X un operador compacto. Entonces N (Tλ ) es
cerrado y tiene dimensión finita para todo λ 6= 0.
Demostración. La primera parte es evidente pues T es continuo y N (Tλ ) =
(T − λI)−1 ({0}) es la imagen inversa de un cerrado.
215
Por otra parte, debido al teorema 5.3 del capı́tulo II, la dimensión de N (Tλ )
es finita si la bola unitaria cerrada M en N (Tλ ) es compacta. Para ello sea
{xn }n∈N una sucesión en M . Entonces {xn }n∈N es acotada y {T xn }n∈N tiene
una subsucesión convergente {T xnk }k∈N . Pero Tλ xn = T xn − λxn = 0, de
modo que xn = λ−1 T xn . Entonces la sucesión {xnk }k∈N = {λ−1 T xnk }k∈N
también converge y su lı́mite está en M . Esto prueba que M es compacto.
♦
Observación. La hipótesis de compacidad es esencial pues, si T es el operador identidad y λ = 1, basta tomar el espacio X de dimensión infinita para
que N (Tλ ) = N (0) = X no tenga dimensión finita.
Por otra parte, en el caso λ = 0 tampoco se puede asegurar nada pues basta
tomar T = 0 para que dim N (T0 ) = dim N (T ) = dim X que puede no ser
finita.
4.3.- Corolario. En las condiciones del teorema anterior, dim N (Tλn ) < ∞,
∀n ∈ N y λ 6= 0.
Demostración. Del desarrollo
n n X
X
n k−1
n k
n−k
n
n
n
T
(−λ)n−k ,
T (−λ)
= (−λ) I + T
Tλ = (T − λI) =
k
k
k=1
k=0
se deduce que podemos escribir Tλn = W − µI, donde llamamos µ = −(−λ)n
n
k−1
P
n
y W = ST = T S, donde S =
(−λ)n−k , que es acotado por serlo
k T
k=1
T.
Como T es compacto, W también es compacto (teorema 3.7) y del teorema
anterior se deduce la tesis.
♦
Sabemos que el rango de un operador acotado no es necesariamente cerrado,
pero en el caso de operadores compactos tenemos lo siguiente.
4.4.- Teorema. Si T : X → X es compacto, el rango de Tλ es cerrado,
∀λ 6= 0.
Demostración. Supongamos que Tλ (X) no es cerrado. Entonces existe algún
elemento y ∈ Tλ (X), y 6∈ Tλ (X) y una sucesión {xn }n∈N en X tales que
yn = Tλ xn → y.
Como y 6= 0, existe N ∈ N tal que yn 6= 0, ∀n > N , con lo que xn 6∈ N (Tλ ).
Supondremos sin pérdida de generalidad que esto es cierto para todo n.
Como N (Tλ ) es cerrado, δn = ı́nf z∈N (Tλ ) kxn − zk > 0. Por definición de
ı́nfimo, existe alguna sucesión {zn }n∈N en N (Tλ ) tal que an = kxn − zn k <
2δn .
Ahora veamos que an = kxn − zn k → ∞ por reducción al absurdo.
216
Si lo anterior no es cierto, {xn − zn }n∈N tiene alguna subsucesión acotada.
Como T es compacto, {T (xn − zn )}n∈N tiene una subsucesión convergente.
De la igualdad I = λ−1 (T − Tλ ) y usando que Tλ zn = 0, tenemos
xn − zn = λ−1 (T − Tλ )(xn − zn ) = λ−1 [T (xn − zn ) − Tλ xn ].
Como {Tλ xn }n∈N converge, {xn −zn }n∈N tiene una subsucesión convergente,
digamos xnk − znk → v. Como T es compacto, es continuo y ası́ también Tλ .
Entonces
Tλ (xnk − znk ) = Tλ xnk → Tλ v,
de modo que Tλ v = y. Esto contradice el hecho de que y 6∈ Tλ (X).
Por último, si llamamos wn = a−1
n (xn − zn ), tenemos kwn k = 1. Debido a
que an → ∞, Tλ zn = 0 y {Tλ xn }n∈N converge a y 6= 0, entonces
Tλ wn = an −1 Tλ xn → 0.
Nuevamente, de I = λ−1 (T − Tλ ), deducimos que wn = λ−1 (T wn − Tλ wn ).
Como T es compacto y {wn }n∈N acotada, {T wn }n∈N tiene una subsucesión
convergente. Además, como hemos visto, {Tλ wn }n∈N converge. Por tanto
{wn }n∈N tiene una subsucesión convergente, wnk → w. Esto implica que
Tλ w = 0, es decir w ∈ N (Tλ ). Como también zn ∈ N (Tλ ), un = zn + an w ∈
N (Tλ ). Entonces
kxn − un k ≥ δn =⇒ δn ≤ kxn − zn − an wk
= kan wn − an wk = an kwn − wk < 2δn kwn − wk
=⇒ 1/2 < kwn − wk,
lo que es absurdo.
♦
4.5.- Corolario. En las condiciones del teorema anterior, el rango de Tλn
es cerrado, ∀n ∈ N y λ 6= 0.
Demostración. Basta observar que el operador W definido en la demostración del corolario 4.3 es compacto.
♦
Es evidente comprobar que
N (Tλ0 ) ⊂ N (Tλ ) ⊂ · · · ⊂ N (Tλn ) ⊂ . . .
y Tλ0 (X) ⊃ Tλ (X) ⊃ · · · ⊃ Tλn (X) ⊃ . . .
En el caso de operadores compactos, estas inclusiones pueden refinarse del
siguiente modo.
4.6.- Lema. Sea T : X → X compacto y λ 6= 0. Entonces existe un entero
positivo r tal que
N (Tλ0 ) ⊂ N (Tλ ) ⊂ · · · ⊂ N (Tλr ) = N (Tλr+1 ) = . . .
217
y las inclusiones son estrictas.
Demostración. Escribiremos por comodidad Nn = N (Tλn ).
*) Es evidente que Nm ⊂ Nm+1 . Supongamos que no hay ningún m para el
que Nm = Nm+1 . Como Nn es cerrado para todo n, por el lema de Riesz
(capı́tulo II, lema 5.1), existe una sucesión {yn }n∈N tal que
yn ∈ Nn , kyn k = 1, kyn − xk ≥ 1/2, ∀x ∈ Nn−1 .
De Tλ = T − λI, tenemos que T = Tλ + λI y T yn − T ym = λyn − x
e donde
x
e = Tλ ym + λym − Tλ yn .
Si m < n, claramente λym ∈ Nm ⊂ Nn−1 . Además,
0 = Tλm ym = Tλm−1 (Tλ ym ),
de donde Tλ ym ∈ Nm−1 ⊂ Nn−1 .
Análogamente, de yn ∈ Nn obtenemos Tλ yn ∈ Nn−1 . Lo anterior indica que
x
e ∈ Nn−1 y también x = λ−1 x
e ∈ Nn−1 . Entonces
kT yn − T ym k = kλyn − x
ek = |λ| · kyn − xk ≥ |λ|/2
y {T yn }n∈N no tiene ninguna subsucesión convergente pero T es compacto.
Esto quiere decir que existe m tal que Nm = Nm+1 .
*) Veamos ahora que Nm = Nm+1 =⇒ Nn = Nn+1 , ∀n > m.
Si x ∈ Nn+1 , entonces Tλn+1 x = 0. Si llamamos z = Tλn−m x, entonces
z ∈ Nm+1 . Por hipótesis z ∈ Nm , de modo que x ∈ Nn .
♦
Para los rangos el resultado análogo es el siguiente.
4.7.- Lema. Sea T : X → X compacto y λ 6= 0. Entonces existe un entero
positivo q tal que
Tλ0 (X) ⊃ Tλ (X) ⊃ · · · ⊃ Tλq (X) = Tλq+1 (X) = . . .
y las inclusiones son estrictas.
Demostración. La prueba es paralela a la anterior y escribiremos Rn =
Tλn (X).
*) Supongamos que para todo s, Rs 6= Rs+1 , es decir Rn+1 es subespacio
propio de Rn , para todo n. Por el lema de Riesz, existe una sucesión {xn }n∈N
tal que
xn ∈ Rn , kxn k = 1, kxn − xk ≥ 1/2, ∀x ∈ Rn+1 .
Como T = Tλ + λI, T xm − T xn = λxm − (−Tλ xm + Tλ xn + λxn ). Por un
lado, λxm ∈ Rm y como xm ∈ Rm , Tλ xm ∈ Rm+1 .
218
Además, si n > m, Tλ xn + λxn ∈ Rn ⊂ Rm+1 ; entonces existe x ∈ Rm+1 tal
que T xm − T xn = λ(xm − x), de donde
kT xm − T xn k = |λ| · kxm − xk ≥ |λ|/2 > 0.
Como T es compacto, {T xn }n∈N debe tener alguna subsucesión convergente,
lo que contradice la desigualdad anterior. Esto prueba que existe s ∈ Z+ tal
que Rs = Rs+1 .
*) Además Rq+1 = Rq significa que Tλ aplica Rq sobre sı́ mismo. Sucesivas
aplicaciones de Tλ dan lugar a Rn+1 = Rn , ∀n > q.
♦
Combinando los dos lemas anteriores llegamos al siguiente resultado.
4.8.- Teorema. Sea T : X → X un operador compacto y λ 6= 0. Entonces
existe r ∈ N tal que
N (Tλ0 ) ⊂ N (Tλ ) ⊂ · · · ⊂ N (Tλr ) = N (Tλr+1 ) = . . .
Tλ0 (X) ⊃ Tλ (X) ⊃ · · · ⊃ Tλr (X) = Tλr+1 (X) = . . .
y las inclusiones son propias.
Demostración. Debido a los dos lemas anteriores, sólo falta probar que q =
r.
a) Probemos que q ≥ r. Por el lema 4.7, Rq+1 = Rq . Ası́, si y ∈ Rq ,
∃x ∈ Rq : y = Tλ x.
Veamos en primer lugar que
(∗)
Tλ x = 0, x ∈ Rq =⇒ x = 0.
Si no fuera cierto, existirı́a x1 ∈ Rq , x1 6= 0, tal que Tλ x1 = 0.
En esta situación debe existir x2 ∈ Rq tal que x1 = Tλ x2 . Sucesivamente,
tenemos para todo n
0 6= x1 = Tλ x2 = · · · = Tλn−1 xn , pero 0 = Tλ x1 = · · · = Tλn xn .
Esto implica que xn ∈ Nn \ Nn−1 , de donde Nn−1 ⊂ Nn , Nn−1 6= Nn , ∀n,
lo que contradice el lema 4.6.
Veamos ahora que Nq+1 = Nq (esto implicará que q ≥ r pues r es el menor
entero que da la igualdad). Teniendo en cuenta (∗),
x ∈ Nq+1 =⇒ Tλq+1 x = 0 =⇒ Tλ (Tλq x) = 0 =⇒ Tλq x = 0 =⇒ x ∈ Nq .
Como siempre Nq ⊂ Nq+1 , se deduce la igualdad.
Queda probado entonces que q ≥ r.
219
b) Veamos ahora que q ≤ r. Para ello, basta ver que Nq−1 es subespacio
propio de Nq , pues r es el menor entero n para el que Nn = Nn+1 .
Por la definición de q, la inclusión Rq ⊂ Rq−1 es propia.
Sea y ∈ Rq−1 \ Rq . Entonces ∃x ∈ X : y = Tλq−1 x. Como Tλ y ∈ Rq = Rq+1 ,
existe z ∈ X : Tλ y = Tλq+1 z. Veamos que x − Tλ z ∈ Nq \ Nq−1 :
Tλq−1 (x − Tλ z) = y − Tλq z 6= 0 pues y 6∈ Rq y Tλq z ∈ Rq =⇒ x − Tλ z 6∈ Nq−1 ;
Tλq (x − Tλ z) = Tλ y − Tλ y = 0 =⇒ x − Tλ z ∈ Nq .
Resulta entonces que Nq−1 es subespacio propio de Nq .
♦
El siguiente teorema, aplicación del resultado anterior, es análogo al conocido
en el caso de dimensión finita y representa la principal herramienta en el
estudio de los operadores compactos.
4.9.- Teorema (descomposición espectral). Sean X, T, λ, r como en los teoremas previos. Entonces X tiene la descomposición
X = N (Tλr ) ⊕ Tλr (X).
Demostración. Dado x ∈ X, debemos encontrar una descomposición x =
y + z, con y ∈ N (Tλr ), z ∈ Tλr (X).
Si llamamos z = Tλr x, por el teorema 4.8, como z ∈ Rr , z ∈ R2r y existe
x1 ∈ X tal que z = Tλ2r x1 .
Llamamos ahora x0 = Tλr x1 ; entonces Tλr x0 = Tλ2r x1 = z = Tλr x, de donde
x − x0 ∈ Nr y x = (x − x0 ) + x0 con x − x0 ∈ Nr , x0 ∈ Rr .
Para comprobar que la descomposición es única, llamemos v0 ∈ Nr ∩ Rr .
Entonces existe v ∈ X : v0 = Tλr v y además Tλr v0 = 0, de donde Tλ2r v =
Tλr v0 = 0. Esto quiere decir que v ∈ N2r = Nr . Ası́ Tλr v = v0 = 0. ♦
1 −1
2
2
Ejemplo. Sea T : R → R el operador definido por T =
.
−1 1
Para λ = 2, se obtiene r = 1 y la descomposición R2 = N (T2 ) ⊕ T2 (R2 ),
donde N (T2 ) = h(1, −1)i y T2 (R2 ) = h(1, 1)i.
Para λ 6= 0 y λ 6= 2, la descomposición es trivial R2 = {0} ⊕ R2 .
Probaremos por último las siguientes sencillas propiedades espectrales.
4.10.- Teorema. Si X es un espacio de Banach de dimensión infinita y
T ∈ L(X) un operador compacto, entonces 0 ∈ σ(T ).
Demostración. Si 0 ∈ ρ(T ), existirı́a T −1 = T0−1 ∈ L(X). Como T es compacto, I = T −1 T es compacto, lo que no es posible pues dim X = ∞.♦
220
4.11.- Teorema (caracterización del espectro). Sea X un espacio de Banach
y T : X → X compacto. Todo punto espectral λ 6= 0 de T (si existe) es
autovalor.
Nota. El teorema también es cierto en espacios normados generales (ver
ejercicio 13).
Demostración. Si N (Tλ ) 6= {0}, λ es autovalor de T .
Si N (Tλ ) = {0}, entonces existe Tλ−1 : Tλ (X) → X. Como {0} = N (I) =
N (Tλ0 ) = N (Tλ ), se obtiene el valor r = 0 en el teorema 4.8. Entonces
X = Tλ0 (X) = Tλ1 (X) =⇒ Tλ es biyectiva y Tλ−1 es acotado por el teorema
de la aplicación abierta, ya que X es completo. En definitiva λ ∈ ρ(T ).
♦
5. ECUACIONES LINEALES DE OPERADORES COMPACTOS.
ECUACIONES INTEGRALES DE FREDHOLM.
La teorı́a espectral de operadores compactos fue desarrollada por Riesz para
estudiar las ecuaciones integrales lineales. Aquı́ la aplicaremos para probar
el teorema de alternativa de Fredholm, que relaciona el comportamiento
de los operadores compactos con la solubilidad de ciertas ecuaciones. Los
resultados que obtendremos extienden los resultados análogos de Algebra
Lineal.
Sean X un espacio normado y A : X → X un operador compacto y definimos
T = A−I. Damos a continuación una cadena de proposiciones que muestran
la estrecha relación que existe entre las soluciones de las ecuaciones
Tx = y
∗
T f
= g
(1)
(2)
y sus correspondientes ecuaciones homogéneas asociadas.
5.1.- Teorema. Dado y ∈ X, la ecuación (1) tiene solución si y sólo si
f (y) = 0, para todo funcional lineal f solución de la ecuación homogénea
T ∗ f = 0.
Demostración. Si T x = y tiene solución x0 ∈ X y f es un funcional lineal
tal que T ∗ f = 0, entonces
f (y) = f (Ax0 −x0 ) = f (Ax0 )−f (x0 ) = (A∗ f )(x0 )−f (x0 ) = (T ∗ f )(x0 ) = 0.
221
Recı́procamente, supongamos que f (y) = 0, para todo funcional lineal f
tal que T ∗ f = 0. Si y 6∈ T (X), entonces d(y, T (X)) = d > 0 pues, al ser
A compacto, T (X) es cerrado. Por el teorema de Hahn-Banach, existe f0
funcional lineal tal que f0 (y) = 1 y f0 (z) = 0, ∀z ∈ T (X). De esta igualdad
se deduce que
0 = f0 (Ax − x) = (A∗ f0 − f0 )(x) = (T ∗ f0 )(x), ∀x ∈ X =⇒ T ∗ f0 = 0.
Por hipótesis f0 (y) = 0 lo que contradice la construcción anterior.
♦
A∗ f
5.2.- Corolario. Si la ecuación homogénea adjunta
− f = 0 sólo tiene
la solución trivial f = 0, la ecuación Ax − x = y tiene solución para todo
y ∈ X.
Enunciamos a continuación un lema auxiliar que utilizaremos en la proposición siguiente (su demostración se propone en el ejercicio 7 al final del
capı́tulo).
5.3.- Lema. Si X es un espacio normado y A : X → X un operador lineal
compacto, entonces existe α > 0 tal que, para todo valor de y para el que
(1) tiene solución, al menos una de esas soluciones x
e satisface la acotación
ke
xk ≤ αkyk.
5.4.- Teorema. Para que la ecuación (2) con g ∈ X 0 dado tenga solución, es
necesario y suficiente que g(x) = 0 para todo x ∈ X solución de la ecuación
homogénea T x = 0.
Demostración. La necesidad se deduce inmediatamente de la igualdad
g(x) = (T ∗ f )(x) = f (T x) = f (0) = 0.
Para la suficiencia, definimos en L = T (X) un funcional f0 como f0 (y) =
g(x), donde y = T x. Dicho funcional está bien definido pues, si T x = T u,
entonces
A(x − u) − (x − u) = 0 =⇒ g(x − u) = 0 =⇒ g(x) = g(u).
Es fácil ver que f0 es lineal; para ver que está acotado, utilizamos el lema
anterior, es decir que kxk < αkyk para algún x tal que T x = y, y algún
α > 0. Entonces
|f0 (y)| = |g(x)| ≤ kgk · kxk ≤ kgk · α · kyk.
Por el teorema de Hahn-Banach, f0 se puede extender a f definido en X de
modo que
f (T x) = f (y) = f0 (y) = g(x) =⇒ (T ∗ f )(x) = g(x)
lo que produce una solución de (2).
♦
222
5.5.- Corolario. Si T x = 0 sólo admite la solución trivial x = 0, la ecuación
T ∗ f = g admite solución para todo g.
Además de lo anterior existe una estrecha relación entre la solubilidad de la
ecuación homogénea y la de la ecuación no homogénea asociada.
5.6.- Teorema. Si A es un operador compacto en un espacio normado X,
la ecuación (1) tiene solución para todo y ∈ X si y sólo si la ecuación
homogénea asociada T x = 0 sólo tiene la solución trivial. En este caso la
solución de (1) es única y el operador T = A−I tiene inverso acotado.
Demostración. a) Por hipótesis, para cada y ∈ X, existe x ∈ X tal que
T x = y. Supongamos sin embargo que existe x1 6= 0 tal que T x1 = 0.
Aplicando la hipótesis a x1 , existe x2 ∈ X tal que T x2 = x1 .
Procediendo por recurrencia, obtenemos una sucesión (xn )n∈N ⊂ X tal que
xn = T xn+1 , ∀n ∈ N. Tenemos ası́:
0 6= x1 = T x2 = · · · = T n−1 xn y 0 = T x1 = T 2 x2 = · · · = T n xn , ∀n ∈ N.
Esto implica que xn ∈ N (T n ) \ N (T n−1 ), ∀n ∈ N lo que contradice el lema
4.6 (recordemos que T = A − I = A1 ).
b) Supongamos ahora que x = 0 es la única solución de la ecuación homogénea T x = 0. Por el corolario 5.5, ∀g ∈ X 0 la ecuación T ∗ f = g tiene
solución.
Como A∗ también es compacto, podemos aplicar la implicación probada en
a) para concluir que T ∗ f = 0 sólo tiene la solución trivial.
Por el corolario 5.2, la ecuación T x = y tiene solución, ∀y ∈ X.
c) Para ver que la solución de (1) es única, supongamos que existen x1 , x2 ∈
X tales que T x1 = T x2 = y. Entonces T (x1 − x2 ) = 0. Ahora bien, como
T x = 0 sólo tiene la solución trivial, debe ser x1 = x2 .
d) Por último, como T x = y tiene solución única, se puede definir T −1 y = x,
∀y ∈ X. Además T −1 está acotado pues, por el lema 5.3, existe α > 0 tal
que kxk = kT −1 yk ≤ αkyk.
♦
5.7.- Corolario. La ecuación T ∗ f = g tiene solución para todo g ∈ X 0 si
y sólo si f = 0 es la única solución de la ecuación homogénea T ∗ f = 0. En
este caso, la ecuación T ∗ f = g tiene solución única.
Nuestro siguiente resultado se basa en el lema que enunciamos a continuación, y cuya demostración puede hacerse por inducción.
5.8.- Lema. Si X es un espacio normado y {f1 , . . . , fm } un conjunto linealmente independiente en X 0 , existe un conjunto {z1 , . . . , zm } ⊂ X tal
que fj (zk ) = δjk (j, k = 1, . . . m).
223
Un par de conjuntos como los que verifican el lema recibe el nombre de
sistema biortogonal.
5.9.- Teorema. Las ecuaciones T x = 0 y T ∗ f = 0 tienen el mismo número
de soluciones linealmente independientes.
Demostración. Debemos probar que dim N (T ) = dim N (T ∗ ). Al ser A y A∗
compactos, n = dim N (T ) < ∞ y m = dim N (T ∗ ) < ∞.
a) Si suponemos n = 0, la ecuación T x = 0 sólo tiene la solución trivial
x = 0. Por el corolario 5.5, la ecuación T ∗ f = g tiene solución ∀g ∈ X 0 .
Por el corolario 5.7, f = 0 es la única solución de T ∗ f = 0, con lo que
m = 0.
b) Sean ahora n > 0, m > 0 y consideremos una base de N (T ), {x1 , . . . , xn }.
Para cada k ∈ {1, . . . , n}, consideramos el subespacio Mk generado por el
conjunto {x1 , . . . , xk−1 , xk+1 , . . . , xn }. Como xk 6∈ Mk , d(xk , Mk ) = δk >
0.
Por una consecuencia del teorema de Hahn-Banach,
∃gk ∈ X 0 : kgk k = 1, gk (xk ) = 1, gk (xi ) = 0 (i 6= k).
Si consideramos también una base {f1 , . . . , fm } de N (T ∗ ), el lema anterior
afirma que existe un conjunto {z1 , . . . , zm } ⊂ X tal que fj (zk ) = δjk (j, k =
1, . . . , m).
c) Supongamos
Pn que n < m y definamos el operador S : X → X por
Sx = Ax + j=1 gj (x)zj . Es fácil comprobar que S es lineal y compacto. Veamos también que la ecuación homogénea Sx − x = 0 sólo tiene la
solución trivial.
En efecto, si suponemos que Sx0 −x0 = 0, entonces fk (Sx0 −x0 ) = fk (0) = 0
(k = 1, . . . , m), de donde
0 = fk (Sx0 − x0 ) = fk (T x0 +
n
X
gj (x0 )zj ) = fk (T x0 ) +
j=1
n
X
gj (x0 )fk (zj )
j=1
= fk (T x0 ) + gk (x0 ) = (T ∗ fk )(x0 ) + gk (x0 ) = gk (x0 ), k = 1, . . . , n.
P
Entonces Sx0 − x0 = T x0 + nj=1 gj (x0 )zj = T x0 . Como
P Sx0 − x0 = 0
por hipótesis, resulta que x0 ∈ N (T ); por tanto, x0 = nj=1 αj xj . Entonces
n
X
0 = gk (x0 ) =
αj gk (xj ) = αk , k = 1, . . . , n,
j=1
lo que implica que x0 = 0.
224
Aplicando el teorema 5.6, la ecuación Sx − x = y tiene solución ∀y ∈ X.
En particular, para y = zn+1 (recordamos que n < m), existe x = v tal que
Sv − v = zn+1 . De aquı́ obtenemos:
1 = fn+1 (zn+1 ) = fn+1 (Sv − v) = fn+1 T v +
n
X
gj (v)zj
j=1
= fn+1 (T v) +
n
X
gj (v)fn+1 (zj ) = (T ∗ fn+1 )(v).
j=1
Por otro lado, fn+1 ∈ N (T ∗ ) lo que lleva a una contradicción; deducimos
pues que n < m es imposible.
d) Supongamos ahora
que n > m. Definimos análogamente Se : X 0 → X 0
P
m
∗
e =A f+
por Sf
j=1 f (zj )gj .
Nuevamente, Se es lineal y compacto. Además f0 = 0 es la única solución de
e − f = 0 lo que se prueba de forma análoga al obtenido en c). Aplicando
Sf
e − f = g tiene solución para
nuevamente el teorema 5.6, deducimos que Sf
0
e
cualquier g ∈ X . En particular, para g = gm+1 existe f = h tal que Sh−h
=
gm+1 . Entonces
e − h)(xm+1 )
1 = gm+1 (xm+1 ) = (Sh
m
X
∗
= (T h)(xm+1 ) +
h(zj )gj (xm+1 ) = (T ∗ h)(xm+1 ) = h(T xm+1 ).
j=1
Ahora bien, como xm+1 ∈ N (T ), T (xm+1 ) = 0, de modo que h(T xm+1 ) = 0
lo que es absurdo.
De c) y d) se deduce que n = m.
♦
Observación. Debido a que la ecuación
(10 )
Ax − λx = y, λ 6= 0
se puede escribir como λ−1 Ax−x = λ−1 y y a que λ−1 A es compacto a la vez
que A, los teoremas anteriores son válidos para las ecuaciones (10 ) y
(20 )
A∗ f − λf = g, λ 6= 0
en lugar de (1) y (2).
Las relaciones obtenidas en las proposiciones anteriores motivan la adopción
del concepto de alternativa.
5.10.- Definición. Un operador A ∈ L(X) sobre un espacio normado X
satisface la alternativa de Fredholm si cumple alguna de las siguientes condiciones:
225
(I) Las ecuaciones no homogéneas Ax = y, A∗ f = g (donde A∗ representa
el adjunto de A) tienen soluciones x, f para cualesquiera y ∈ X, g ∈ X 0 ,
respectivamente, y dichas soluciones son únicas. En este caso las ecuaciones
homogéneas asociadas sólo tienen las soluciones triviales.
(II) Las ecuaciones homogéneas Ax = 0, A∗ f = 0, tienen el mismo número
finito de soluciones linealmente independientes {x1 , . . . , xn }, {f1 , . . . , fn },
n ≥ 1, respectivamente. En particular las ecuaciones no homogéneas Ax = y,
A∗ f = g tienen soluciones si y sólo si fk (y) = 0, g(xk ) = 0, k = 1, . . . , n,
respectivamente.
Con esta noción, todo lo anterior se puede agrupar enunciando el siguiente
resultado general de alternativa.
5.11.- Teorema (alternativa de Fredholm). Sea A : X → X un operador
lineal compacto sobre un espacio normado X y λ 6= 0. Entonces Aλ =
A − λI verifica la alternativa de Fredholm. Las soluciones generales
de las
P
ecuaciones P
(10 ) y (20 ) son respectivamente de la forma x = x0 + nk=1 αk xk ,
f = f0 + nk=1 λk fk , donde x0 , f0 son soluciones particulares y αk , λk
constantes arbitrarias.
Este resultado generaliza el obtenido por Fredholm sobre existencia de soluciones de ecuaciones integrales del tipo
b
Z
g(s) + µ
k(s, t)f (t)dt = f (s),
a
donde ahora X = C[a, b], el núcleo k es una función continua y g ∈ C[a, b]
es dado. La ecuación anterior puede escribirse como g = (I − µA)f , donde
Rb
el operador (Af )(s) = a k(s, t)f (t)dt es compacto. Aplicando el teorema de
alternativa, se deduce fácilmente el siguiente resultado:
5.12.- Teorema (Fredholm). Sea D = {(s, t) : a ≤ s, t ≤ b} y k : D → C
una función continua. Si µ es un número complejo no nulo, una de las
siguientes alternativas es cierta:
a) o bien cada una de las ecuaciones
Z
b
f (s) = g(s) + µ
k(s, t)f (t)dt, a ≤ s ≤ b, (3)
(3)
k(t, s)f (t)dt, a ≤ s ≤ b, (4)
(4)
a
Z
f (s) = g(s) + µ
b
a
tiene solución única f ∈ C[a, b] para cada g ∈ C[a, b],
226
b) o bien las dos ecuaciones homogéneas
Z b
f (s) = µ
k(s, t)f (t)dt, a ≤ s ≤ b, (5)
a
Z b
k(t, s)f (t)dt, a ≤ s ≤ b, (6)
f (s) = µ
(5)
(6)
a
tienen soluciones no nulas f ∈ C[a, b].
Si se cumple (b), las ecuaciones (5) y (6) tienen el mismo número de soluciones linealmente independientes en C[a, b]; la ecuación (3) tiene soRb
luciones f ∈ C[a, b] si y sólo si a g(s)h(s)ds = 0, ∀h ∈ C[a, b] solución de (6); y la ecuación (4) tiene soluciones f ∈ C[a, b] si y sólo si
Rb
a g(s)h(s)ds = 0, ∀h ∈ C[a, b] solución de (5).
Por último, el conjunto {µ ∈ C : se cumple (b)} es numerable y no tiene
puntos de acumulación.
Demostración. Definimos los operadores integrales K, K 0 : C[a, b] → C[a, b]
por
Z b
Z b
0
(Kf )(s) =
k(s, t)f (t)dt, (K f )(s) =
k(t, s)f (t)dt, ∀s ∈ [a, b].
a
a
Ası́ definidos, K y
escribir en la forma
K0
son compactos. Las ecuaciones (3) a (6) se pueden
(I − µK)f = g,
(I − µK 0 )f = g,
(I − µK)f = 0,
(I − µK 0 )f = 0.
Debido a que K 0 no es el adjunto de K no se puede aplicar el teorema de
alternativa 5.11. Sin embargo, veremos que K 0 y K ∗ están estrechamente
ligados.
Definimos para cada g ∈ C[a, b] el funcional Jg : C[a, b] → C por
Z b
Jg (f ) =
g(s)f (s)ds.
a
C[a, b]0
Es fácil comprobar que Jg ∈
definida por Jg = Jg es inyectiva.
y que la aplicación J : C[a, b] → C[a, b]0
Probaremos ahora que K ∗ ◦ J = J ◦ K 0 . En efecto, ∀f, g ∈ C[a, b],
Z b
∗
(K Jg )(f ) = Jg (Kf ) =
g(s)(Kf )(s)ds
a
Z b
Z b
Z b
Z b
=
g(s)
k(s, t)f (t)dt ds =
f (t)
k(s, t)g(s)ds dt
a
Z
=
a
b
a
f (t)(K 0 g)(t)dt = JK 0 g (f ).
a
227
a
De lo anterior se deduce que (I ∗ − µK ∗ ) ◦ J = J ◦ (I − µK 0 ) y, como J es
inyectiva, J[N (I − µK 0 )] = N (I ∗ − µK ∗ ) ∩ J(C[a, b]), de donde
dim N (I − µK 0 ) = dim J[N (I − µK 0 )] = dim[N (I ∗ − µK ∗ ) ∩ J(C[a, b])]
≤ dim N (I ∗ − µK ∗ ) = dim N (I − µK).
Como la relación entre K y K 0 es simétrica, podemos intercambiar K con
K 0 y obtener la desigualdad contraria, con lo que
dim N (I − µK 0 ) = dim N (I − µK) = dim(I ∗ − µK ∗ ).
(∗)
Como µK y µK 0 son compactos, se obtiene la tesis aplicando el teorema de
alternativa de Fredholm. En efecto:
- Supongamos que (I − µK)f = 0 sólo tiene la solución trivial. Debido a (∗),
la ecuación (I − µK 0 )f = 0 sólo tiene la solución trivial. Por el teorema 5.6,
las ecuaciones (I − µK)f = g, (I − µK 0 )f = g tienen soluciones únicas, con
lo que queda probado (a).
- Supongamos ahora que (I − µK)f = 0 tiene alguna solución f0 6= 0. Otra
vez, por (∗), la ecuación (I − µK 0 )f = 0 tiene alguna solución no nula, lo
que prueba el apartado (b).
- La misma condición (∗) muestra que (5) y (6) tienen el mismo número de
soluciones linealmente independientes.
Rb
- Veamos ahora que (I − µK)f = g tiene solución si y sólo si a g(s)h(s) = 0
para cualquier h solución de (I − µK 0 )h = 0.
Sean pues f y h tales que (I − µK)f = g y (I − µK 0 )h = 0. Entonces,
como
Z
b
g(s) = f (s) − µ
k(s, t)f (t)dt,
a
resulta
Z b
Z
b
h(s)f (s)ds − µ
g(s)h(s)ds =
a
Z b Z
a
Z b
a
a
b Z b
Z
h(s)f (s)ds−µ
=
a
Z
=
b
Z
a
b
h(s)f (s)ds−
a
b
k(s, t)f (t)dt h(s)ds
k(s, t)h(s)ds f (t)dt
a
h(t)f (t)dt = 0.
a
Recı́procamente, si h es solución de (I − µK 0 )h = 0, entonces J(I − µK 0 )h =
0, de donde (I ∗ − µK ∗ )(Jh) = 0, es decir Jh es solución de (I ∗ − µK ∗ )f = 0.
Como, por hipótesis, (Jh)g = 0, por el teorema 5.1, (I − µK)f = g tiene
solución.
Análogamente se procede con el caso dual.
228
♦
(Ver [BN] y [RN] para desarrollos similares y aplicaciones del mismo tema.)
229
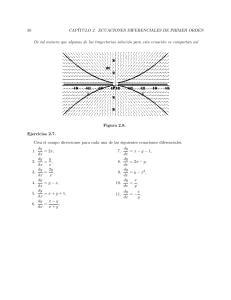
EJERCICIOS.
1. Sea T ∈ L(X).
a) Probar que el conjunto ∆ = {λ ∈ C : T − λI es biyectiva pero
(T − λI)−1 no es continua} es vacı́o.
b) Probar que σ(T ) \ σp (T ) = {λ ∈ C : T − λI es inyectivo pero no
sobre}.
Resp.: a) Es consecuencia directa del teorema de la aplicación abierta.
b) Teniendo en cuenta que
σp (T ) = {λ ∈ C : T − λI es no inyectiva}
resulta que σ(T ) \ σp (T ) = {λ ∈ C : T − λI inyectiva no sobre} ∪ ∆ y
el resultado es consecuencia del apartado a).
Observación. Este hecho sugiere la distinción hecha en la teorı́a entre
espectro puntual y espectro no puntual.
2. Sea T ∈ L(X). Probar que σ(T ) = σ(T ∗ ) y Rλ (T ∗ ) = Rλ (T )∗ ,
∀λ ∈ ρ(T ∗ ) = ρ(T ) (lema 2.3).
Resp.: Utilizaremos las siguientes propiedades:
(T − λI)∗ = T ∗ − λI
∃T −1 ∈ L(X) ⇐⇒ ∃(T ∗ )−1 ∈ L(X 0 ) y (T −1 )∗ = (T ∗ )−1 .
Ası́ pues,
λ ∈ ρ(T ) ⇐⇒ (T − λI)−1 ∈ L(X) ⇐⇒ ((T − λI)−1 )∗ ∈ L(X 0 )
⇐⇒ (T ∗ − λI) ∈ L(X 0 ) ⇐⇒ λ ∈ ρ(T ∗ ).
Como σ(T ) = C \ ρ(T ), se deduce que σ(T ) = σ(T ∗ ).
Por otra parte, ∀λ ∈ ρ(T ) = ρ(T ∗ ),
Rλ (T ∗ ) = (T ∗ − λI)−1 = ((T − λI)∗ )−1 = ((T − λI)−1 )∗ = (Rλ (T ))∗ .
230
3. Sea X normado. Probar que el conjunto de operadores invertibles
es abierto en L(X).
Resp.: Sea T ∈ L(X) invertible. Probemos que ∃r > 0 tal que la bola
B(T, r) está formada por operadores invertibles. Para ello elegimos
r = kT −1 k−1 ; si S ∈ B(T, r), entonces kS − T k < kT −1 k−1 . Veamos
que S es invertible:
kT −1 S − Ik
=
kT −1 (S − T )k ≤ kT −1 k · kS − T k < 1
=⇒ ∃(I − (T −1 S − I))−1 ∈ L(X)
=⇒ ∃(T −1 S)−1 ∈ L(X) =⇒ ∃S −1 ∈ L(X).
4. Sea X de Banach y T ∈ L(X). Probar que
lı́m kT n k1/n < 1 =⇒ (I − T )−1 =
n→∞
X
Tn
n≥0
y converge en la norma de L(X).
n 1/n
n
n
Resp.: Sea α < 1 tal que lı́mn→∞
PkT k n < α. Entonces kT k < α ,
∀n > N . De este modo, la P
serie n≥0 kT k es convergente y, por ser
L(X) de Banach, también n≥0 T n converge.
P
P
n
Llamamos S = n≥0 T n y Sm = m
n=0 T ; entonces S = lı́mm→∞ Sm
y
(I − T )Sn = Sn (I − T ) = I − T n+1 .
Como kT n k < αn , lı́mn→∞ kT n k = 0, de donde lı́mn→∞ Sn = (I −
T )−1 .
De este resultado se obtiene la fórmula de Neumann: si T ∈ L(X) y
λ ∈ C son tales que |λ|−1 > lı́mn kT n k1/n , entonces lı́mn k(λT )n k1/n <
1, de modo que I − λT es invertible y
(I − λT )−1 =
X
λn T n ,
n≥0
donde la serie converge en la norma de L(X).
231
5. Sea X un espacio de dimensión infinita y A : X → X un operador
compacto. Probar que A−1 , si existe, no es acotado.
Resp.: Supongamos que A−1 ∈ L(X). Por ser A compacto y la clase
de operadores compactos un ideal bilátero de L(X), se deduce que
I = AA−1 es compacto. Pero, como la dimensión del espacio es infinita,
el operador identidad no puede ser compacto.
6. Sea X un espacio normado, z ∈ X , f ∈ X 0 elementos fijos. Definimos A : X → X por Ax = f (x)z . Probar que A es compacto.
Resp.: Sea {xn }n∈N una sucesión acotada en X, kxn k ≤ M , ∀n. Veamos que {Axn }n∈N posee alguna subsucesión convergente.
Como f es acotado, |f (xn )| ≤ kf k · kxn k ≤ kf k · M , lo que prueba que
{f (xn )}n∈N es una sucesión uniformemente acotada. Por el teorema de
Bolzano-Weierstrass, tiene una subsucesión, {f (xnk )}k∈N , convergente,
digamos a λ. Como Axnk = f (xnk )z, resulta que Axnk → λz, lo que
prueba el enunciado.
7. Sea T : X → X un operador compacto. Probar que existe una
constante M > 0 tal que
∀y ∈ R(Tλ ), kTλ−1 yk ≤ M kyk.
Resp.: Sea y 6= 0 un elemento de R(Tλ ) y x0 ∈ X tal que (T −
λI)x0 = y. Como dim N (Tλ ) < ∞, N (Tλ ) es cerrado. Entonces existe
w ∈ N (Tλ ) tal que d(x0 , N (Tλ )) = kx0 − wk > 0. Si llamamos x =
x0 − w, entonces Tλ x = y y, si probamos que existe M > 0 tal que
d(x0 , N (Tλ )) ≤ M kTλ x0 k, entonces
kxk = kx0 − wk ≤ M kTλ x0 k = M kyk.
Supongamos por el contrario que no existe tal M , es decir que
(∗)
∀n > 0, ∃yn ∈ R(Tλ ) : kTλ−1 yn k > nkyn k.
Entonces existe una sucesión (xn )n∈N ⊂ X tal que Tλ xn = yn , ∀n y,
como yn 6= 0, xn 6∈ N (Tλ ), ∀n.
232
Como N (Tλ ) es cerrado, si llamamos dn = d(xn , N (Tλ )), entonces
dn > 0, ∀n. Por tanto, ∃wn ∈ N (Tλ ) tal que dn ≤ kxn −wn k < 2dn . Sea
ahora vn = kxn −wn k−1 (xn −wn ); ası́, kvn k = 1 y, por ser T compacto,
existe una subsucesión (vnk )k∈N tal que (T vnk )k∈N es convergente.
Por otra parte, de la igualdad
yn = Tλ xn = Tλ (xn − wn ) = Tλ (kxn − wn k · vn )
y teniendo en cuenta (∗), se deduce que kxn − wn k · kvn k > nkyn k, de
donde
kTλ vn k = kxn − wn k−1 · kyn k < 1/n, ∀n ∈ N.
Esto implica que Tλ vn → 0. Como además vn = −λ−1 (Tλ vn − T vn ),
deducimos que (vnk )k∈N también converge, en contradicción con la
definición de vn (ver prueba del teorema 4.4).
8. Dado un espacio vectorial X y un subespacio M de X , se llama
codimensión de M a codim M = dim X/M , cuando esta cantidad
es finita.
a) Probar que M tiene codimensión finita si y sólo si existe N
subespacio de X con dimensión finita tal que X = M ⊕ N .
b) Si X es un espacio normado y T : X → X es un operador compacto, probar que R(T − λI) tiene codimensión finita y
codim R(T − λI) = dim N (T − λI).
Resp.: a) Supongamos que {x1 +M, . . . , xn +M } es una base de X/M .
Es evidente que {x1 , . . . , xn } es linealmente independiente. Llamamos
N
Pnal espacio generado por dicho conjunto. Ası́, ∀x ∈ X, x + M =
k=1 αk (xk + M ), es decir x = y + z, con y ∈ M , z ∈ N , y la
descomposición es única.
Recı́procamente, si {y1 , . . . , yn } es una base de N , definimos ϕ : N →
X/M por ϕ(yk ) = yk + M (restricción a N de la aplicación canónica).
Como, por hipótesis, X = M ⊕ N , ϕ es biyectiva. Esto implica que
dim X/M = codim M = n.
b) Por el teorema espectral de operadores compactos,
(∗)
X = N (Tλr ) ⊕ R(Tλr ).
Por tanto, debido que que Tλ (R(Tλr )) = R(Tλr ), deducimos que
(∗∗)
R(Tλ ) = Tλ (X) = Tλ (N (Tλr )) ⊕ Tλ (R(Tλr )) = Tλ (N (Tλr )) ⊕ R(Tλr ).
233
Por otra parte, es fácil probar que Tλ (N (Tλr )) ⊂ N (Tλr ), lo que permite
definir S = Tλ |N (Tλr ) : N (Tλr ) → N (Tλr ).
Como N (Tλr ) tiene dimensión finita, dim N (Tλr ) = dim N (S)+dim R(S),
de donde dim N (S) = codim R(S).
Por el apartado a), existe N ⊂ N (Tλr ) tal que N (Tλr ) = R(S) ⊕ N ,
con dim N = codim R(S). Sustituyendo esta descomposición en (∗) y
aplicando (∗∗), resulta:
X = R(S) ⊕ N ⊕ R(Tλr ) = N ⊕ R(Tλ ),
de modo que codim R(Tλ ) = dim N = dim N (S) = dim N (Tλ ) pues
N (Tλ ) = N (S).
9. Sea k un núcleo continuo en el cuadrado [0, 1]×[0, 1]. Probar que el
Z 1
operador integral T : C[0, 1] → C[0, 1], definido por T x(s) =
k(s, t)x(t)dt,
0
es compacto.
Resp.: Sea M ⊂ C[0, 1] un conjunto acotado. Probemos que T (M ) es
relativamente compacto en la métrica de C[0, 1].
Por hipótesis, existe K > 0 tal que kxk∞ ≤ K, ∀x ∈ M .
• Veamos que T x es una función uniformemente acotada, ∀x ∈ M :
Si λ = máx0≤s,t≤1 |k(s, t)|, entonces |T x(s)| ≤ λ · K.
• Veamos además que T x es equicontinua, ∀x ∈ M :
Sea para ello ε > 0 arbitrario. Como k es uniformemente continuo,
existe δ > 0 tal que
|k(s1 , t) − k(s2 , t)| < ε/K, si |s1 − s2 | < δ, ∀t ∈ [0, 1].
Entonces
Z
|T x(s1 ) − T x(s2 )| ≤
1
|k(s1 , t) − k(s2 , t)| · |x(t)|dt < ε
0
si |s1 − s2 | < δ.
Aplicando ahora el teorema de Arzela-Ascoli, deducimos que el conjunto T (M ) es relativamente compacto.
234
10. Probar que el operador integral T : L2 [0, 1] → L2 [0, 1] definiZ 1
Z 1Z 1
do por Ax(s) =
k(s, t)x(t)dt, donde
k 2 (s, t)dsdt < ∞, es
0
compacto.
0
0
Resp.: Supongamos en primer lugar que k es continua en [0, 1] × [0, 1]
y llamemos λ = máx |k(s, t)|. Para ver que T es compacto, sea M
0≤s,t≤1
un conjunto acotado en L2 [0, 1] y kxk2 ≤ K, ∀x ∈ M .
Por la desigualdad de Hölder, ∀x ∈ M,
1
Z
|T x(s)| ≤
Z
|k(s, t)x(t)|dt ≤
0
1
1/2 Z
|k(s, t)| dt
1
2
0
2
|x(t)| dt
1/2
≤ λ·K,
0
de lo que se deduce que T (M ) es uniformemente acotado.
Además, T (M ) es equicontinua pues, si elegimos ε > 0 arbitrariamente, existe δ > 0 tal que
|k(s1 , t) − k(s2 , t)| < ε/K, si |s1 − s2 | < δ, t ∈ [0, 1].
Entonces
1
Z
2
|T x(s1 )−T x(s2 )| ≤
1/2 Z
|k(s1 , t) − k(s2 , t)| dt
0
1
1/2
|x(t)| dt
< ε.
2
0
Del teorema de Arzela-Ascoli se deduce que T es compacto.
Supongamos ahora que k es un núcleo arbitrario en L2 ([0, 1] × [0, 1]).
Consideramos una sucesión {kn }n∈N de núcleos continuos
convergente
R1
2
a k en L ([0, 1] × [0, 1]). Si definimos Tn x(s) = 0 kn (s, t)x(t)dt, se
obtiene que
2
kT x − Tn xk
Z
1
Z
2
1
[k(s, t) − kn (s, t)]x(t)dt ds
0
0
Z 1 Z 1
Z 1
2
≤
|k(s, t) − kn (s, t)| dt ·
|x(t)|2 dt ds
0
0
0
Z 1Z 1
= kxk22 ·
|k(s, t) − kn (s, t)|2 dtds.
=
0
0
R R
1/2
1 1
Esto implica que kT − Tn k ≤ 0 0 |k(s, t) − kn (s, t)|2 dsdt
y, en
consecuencia, que Tn → T . Por el teorema 3.8 se deduce que T es
compacto.
235
11. Sea T : `2 → `2 definido por T (x1 , x2 , . . . ) = (0, x2 , 0, x4 , . . . ). Calcular N (Tλn ), ∀n ∈ N. Deducir que T no es compacto.
Resp.: Por definición, Tλ (x1 , x2 , . . . , ) = (−λx1 , (1 − λ)x2 , −λx3 , (1 −
λ)x4 , . . . ).
Procediendo por recurrencia, obtenemos que
Tλn (x1 , x2 , . . . ) = ((−λ)n x1 , (1 − λ)n x2 , (−λ)n x3 , (1 − λ)n x4 , . . . ).
De este modo, x ∈ N (Tλn ) ⇐⇒ (−λ)n x2k−1 = 0, (1−λ)n x2k = 0, ∀k ∈
N.
En el caso λ = 0, resulta N (Tλn ) = {(x1 , 0, x3 , 0, . . . ) : xk ∈ C}.
Si λ = 1, N (Tλn ) = h{(0, x2 , 0, x4 , 0, . . . ) : xk ∈ C}i. Este espacio tiene
dimensión infinita, lo que implica que T no es compacto.
12. En el espacio `2 definimos los operadores compactos
A(x1 , x2 , . . . ) = (x2 , x3 /2, x4 /3, . . . ),
B(x1 , x2 , . . . ) = (0, x1 , x2 /2, x3 /3, . . . ),
C(x1 , x2 , . . . ) = (x1 , x2 /2, x3 /3, . . . ).
Probar que 0 ∈ σp (A), 0 ∈ σr (B), 0 ∈ σc (C).
Resp.: a) Por definición, λ ∈ σp (A) ⇐⇒ N (Aλ ) 6= {0}. Ahora bien,
como
Aλ (x1 , x2 , . . . ) = (x2 − λx1 , x3 /2 − λx2 , x4 /3 − λx3 , . . . ),
resulta que
x ∈ N (Aλ ) ⇐⇒ xn+1 /n − λxn = 0, ∀n ∈ N
⇐⇒ xn+1 = nλxn = · · · = n!λn x1 , ∀n ∈ N.
En particular, el elemento (1, λ, 2λ2 , . . . , n!λn , . . . ) ∈ N (Aλ ). Haciendo
λ = 0, e1 = (1, 0, 0, . . . ) ∈ N (A0 ) lo que indica que 0 ∈ σp (A).
b) Por definición, λ ∈ σr (B) ⇐⇒ (B − λI)−1 está definido en un
conjunto no denso de `2 , es decir R(Bλ ) 6= `2 .
En este caso,
y ∈ R(Bλ ) ⇐⇒ ∃x ∈ `2 : −λx1 = y1 , xn /n − λxn+1 = yn+1 , ∀n ∈ N.
236
Para λ = 0, B0 x = y ⇐⇒ 0 = y1 , xn /n = yn+1 , ∀n ∈ N, de modo
que el espacio generado por e1 = (1, 0, . . . ) 6∈ R(B0 ). Esto implica que
R(B0 ) 6= `2 y 0 ∈ σr (B).
c) Si llamamos (en )n∈N a la base canónica de `2 , es evidente que R(C) =
`2 , pues Cen = (1/n)en , ∀n ∈ N. Ası́ pues, existe el inverso C −1 y
está definido en todo el espacio; sin embargo, C −1 no está acotado
pues
C −1 en = nen =⇒ kC −1 en k2 = |n| · ken k2 = |n|.
Por definición, 0 ∈ σc (C).
13. Sean X un espacio normado y T ∈ L(X) un operador compacto.
Probar que todo punto espectral no nulo de T es autovalor.
Resp.: Sea λ ∈ σ(T ), λ 6= 0 y supongamos que existe Tλ−1 . Probemos
que λ ∈ ρ(T ):
Por hipótesis, la ecuación homogénea Tλ x = 0 sólo tiene la solución
trivial x = 0. Por el teorema 5.6, la ecuación Tλ x = y tiene solución
para cualquier y ∈ X. El mismo teorema prueba que el operador Tλ−1
está definido en todo X y está acotado, lo que significa que λ ∈ ρ(T ).
Z
1
14. Resolver la ecuación integral x(s) − µ
x(t)dt = 1, en el espacio
0
L2 [0, 1].
Resp.: Consideramos en primer lugar la ecuación homogénea
1
Z
x(s) − µ
x(t)dt = 0.
0
Z
De la igualdad x(s) = µ
1
x(t)dt, deducimos que
0
Z
x(s) = µ
1
Z
µ
0
1
2
Z
x(r)dr dt = µ
0
1
x(r)dr = µx(s),
0
de donde (1 − µ)x(s) = 0. Descomponemos pues el problema en dos
casos:
237
a) Si µ 6= 1, la única solución de la ecuación homogénea es la trivial.
Ası́ pues, la ecuación propuesta tiene solución
R 1 única.
Debido a que el operador asociado T x(s) = 0 x(t)dt tiene norma
uno, pues
Z 1 Z 1
2
x(t)dt ds = kxk22 ,
kT xk22 =
0
0
kT k−1
en el caso |µ| <
= 1 la solución puede expresarse mediante
la fórmula de Neumann
x = 1 + µT (1) + µ2 T 2 (1) + · · · =
1
,
1−µ
solución que también es válida cuando |µ| > 1.
b) Si µ = 1, cualquier función constante es solución de la ecuación
homogénea. Sabemos por elR teorema 5.12 que la ecuación dada
1
tiene solución si y sólo si 0 1 · h(s)ds = 0, para cualquier h
solución de la homogénea asociada (observar que T = T ∗ ). Ahora
bien, como la última igualdad no es cierta para las funciones
constantes, deducimos que la ecuación dada no tiene solución.
TEMAS COMPLEMENTARIOS
1. Propiedades espectrales de las álgebras de Banach ([Kr]).
2. Algebras-C ∗ ([Ru]).
3. Principio del punto fijo de Schauder y sus aplicaciones ([LS]).
4. Aplicaciones de las ecuaciones integrales a la teorı́a del potencial ([RN]).
238