Prof.Andrés Pérez
“La dignidad de la educación, reside en la promoción de la
verdadera perfección y la alegrı́a de los que han de ser formados”
Joseph Aloisius Ratzinger - Papa Benedicto XVI -
Matemáticas IV
“...Ense~
nar en la Universidad, no es impartir clases,
sino contagiar irreverencias...”
Prof. Jesús Alberto León
Universidad Nacional Experimental Politécnica
“Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Prácticas de Matemáticas IV
Prof.: Andrés Pérez
Caracas, Enero de 2014
“Después de escalar una monta~
na muy alta,
descubrimos que hay muchas monta~
nas por escalar”
Nelson Mandela
UNIDAD I
Ecuaciones de Primer Orden
•
•
•
•
•
•
•
Grados ∼ Ordenes ∼ Soluciones
Ecuaciones Separables
Ecuaciones reducibles a separables
Ecuaciones Exactas
Ecuaciones Lineales
Ecuaciones reducibles a lineales
Ecuaciones de Clairaut y Lagrange
“Existe al menos un rincón del universo que con toda seguridad
puedes mejorar...y eres tú mismo”
Aldous Huxley
4
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Práctica 1
2014
Prof. Andrés Pérez
E.D.O. de Primer Orden*
Parte I: Ordenes ∼ Grados ∼ Soluciones
1. En las siguientes ecuaciones diferenciales, determinar el orden, el grado (si es posible), si es lineal o no, la función incognita
y la variable independiente.
1.1) (y ′′ )2 − 3yy ′ + xy = 0
1.2) x4 y(4) + xy ′′′ = ex
1.3) t2 s̈ − tṡ = sen t
(4)
1.4) y
(
1.7)
+ xy
d2 y
dx2
′′′
(
+ x y − xy + sen y = 0
dn x
1.5)
= y2 + 1
dyn
1.6)
+y=x
1.8)
d7 b
= 3p
dp7
1.9)
2
′′
′
)3/2
(
1.10) s2
d2 t
dt
+ st
=8
ds2
ds
1.11) (y ′ )3 + 5xyy ′ − xy sen t = 0
1.13) t2
d2 y
dy
+t
+ 2y = sen t
dt2
dt
1.14)
d2 r
dy2
db
dp
)2
+
dr
d2 r
+y
=0
dy2
dy
)7
= 3p
(
)m
+ ay(n) + q(x)y = p(x)
1.12) y(n)
d2 y
+ sen(s + y) = sen s
ds2
1.15)
d3 y
dy
+t
+ (cos2 t)y = t3
dt3
dt
2. Verifique que las siguientes funciones (explı́citas o implı́citas) son soluciones de las correspondientes ecuaciones diferenciales:
2.1) y ′ = 2x
; y = x2 + C
2.2) xy ′ = 2y
; y = Cx2
2.3) yy ′ = e2x
; y2 = e2x + C
2.5) y = arcsen xy
; xy ′ + y = y ′
2.7) y + sen y = x
; (y cos y − sen y + x)y ′ = y
′′
2.9) y − y = 0
√
1 − x2 y2
x
; y1 (x) = e , y2 (x) = cosh x
2.4) xy ′ = y + x2 + y2
; y = x tan x
2.6) y ′ = y2 /(xy − x2 )
;
2.8) 1 + y2 + y2 y ′ = 0
; x + y = arctan y
y = Cey/x
∫x
′
2.10) xy = y + x sen x
; y=x
0
2.11) y ′ (x + y) = y ; x = y ln(Cy)
2.13) y ′′ + y = sec x, 0 < x <
π
2
;
sen t
dt
t
2.12) y(4) + 4y ′′′ + 3y = x
y(x) = cos(x) ln(cos x) + x sen x
; y1 (x) = x3 , ∫y2 (x) = e−x + x3
x
2
2
2
2.14) y ′ − 2xy = 1 ; y(x) = ex
e−t dt + ex
0
3. En cada una de las siguientes ecuaciones diferenciales, determine el o los valores de r, para el o los cuales la E.D.O. dada
tiene soluciones de la forma y = erx .
3.1) y ′ + 2y = 0
3.2) y ′′ − y = 0
3.3) y ′′ + y ′ − 6y = 0
3.4) y ′′′ − 3y ′′ + 2y ′ = 0
4. En cada una de las siguientes ecuaciones diferenciales, determine el o los valores de r, para el o los cuales la E.D.O. dada
tiene soluciones de la forma y = xr , para x > 0.
4.1) x2 y ′′ + 4xy ′ + 2y = 0
4.2) x2 y ′′ − 4xy ′ + 4y = 0
5. Pruebe que y = Cx4 , es solución general de xy ′ − 4y = 0. Además, Halle dos soluciones particulares y una solución
singular.
6. Considere la EDO, dada por: y ′ = y2 − 1. Demuestre que: y =
singular de la EDO?
1 + Ce2x
, es solución general. ¿Será y = −1 solución
1 − Ce2x
5
7. Demuestre que las siguiente s familias de funciones son soluciones generales de las EDO asociadas.
7.1) C(x + y)2 = xey/x
; (x2 + y2 )dx + x(x − y)dy = 0
7.2) x2 y + y2 = C
; 2xydx + (x2 + 2y)dy = 0
8. En los problemas dados a continuación, hallar C1 y C2 de tal forma que las funciones dadas satisfagan las condiciones
iniciales establecidas.
8.1) y(x) = C1 ex + C2 e−x + 4 sen x ; y(0) = 1, y ′ (0) = −1
8.2) y(x) = C1 x + C2 + x2 − 1
; y(1) = 1, y ′ (1) = 2
8.3) y(x) = C1 ex + C2 e2x + 3e3x
;
y(0) = 0, y ′ (0) = 0
8.4) y(x) = C1 sen x + C2 cos x + 1 ;
y(π) = 0, y ′ (π) = 0
8.5) y(x) = C1 ex + C2 xex + x2 ex
;
y(1) = 1, y ′ (1) = −1
8.6) y(x) = C1 sen x + C2 cos x
y( π4 ) = 0, y ′ ( π6 ) = 0
;
Parte II: Ecuaciones Separables
9. Hallar la solución general de cada una de las siguientes ecuaciones diferenciales a variables separadas:
9.1)
y ′ = e3x − x
9.2)
xy ′ = 1
9.3) y ′ = xex
9.4)
y ′ = arcsen x
9.5)
(1 + x)y ′ = x
9.6) (1 + x3 )y ′ = x
9.7)
(1 + x2 )y ′ = arctan x
9.8)
xyy ′ = y − 1
9.9) xy ′ = (1 − 2x2 ) tan y
9.10) (1 + x2 )
9.13)
dy
+ (1 + y2 ) = 0
dx
9.12)
y ′ + y tan x = 0
9.15)
2
9.18)
dy
(1 + x2 )−1/2
=
dx
(1 + y2 )1/2
dy
= e−y + e−y−2x
dx
9.21)
dx
1 + 2y2
=
dy
y sen x
dy
xy + 3y − x − 3
=
dx
xy − 2x + 4y − 8
9.24)
dy
= sen x(cos 2y − cos2 y)
dx
sen 3xdx + 2y cos3 3xdy = 0
9.27)
(y − yx2 )
9.11) y ln ydx − xdy = 0
xy + 2y − x − 2
dy
=
dx
xy − 3y + x − 3
9.16) (1 + x2 + y2 + x2 y2 )dy = y2 dx
2
9.14)
y
x
9.19) (4y + yx2 )dy − (2x + xy2 )dx = 0
dy
+ sen(x − y) = sen(x + y)
dx
sec2 xdy + cosec ydx = 0
9.17) y ln x
9.20) ex y
9.22)
sec y
9.25)
(
(
)
)
ey sen 2xdx + cos e2y − y dy = 0 9.26)
9.23)
dx
=
dy
(
y+1
x
)2
dy 1
2x
− =
dx y
y
dy
= (1 + y2 )
dx
10. Resuelva los siguientes Problemas de Valores Iniciales (P.V.I).
10.1) y ′ sen x = y ln y
; y( π2 ) = e
10.3) xex dx + (y5 − 1)dy = 0 ; y(0) = 0
10.5)
dy
= xy3 (1 + x2 )−1/2
dx
; y(0) = 1
10.2)
(x2 + 1)dx +
1
dy = 0 ; y(−1) = 1
y
10.4) x2 y ′ = y − xy
10.6)
dT
= k(T − 50)
dt
; y(−1) = −1
; T (0) = 200
11. Resuelva los siguientes problemas de valores iniciales (P.V.I) y determine el intervalo donde la solución es válida.
1 + 3x2
dy
3x2 + 4x + 2
11.1) y ′ = 2
; y(0) = 1 11.2) (3y2 − 4)dx = 3x2 dy ; x(−1) = 1 11.3∗ )
=
; y(0) = −1
3y − 6y
dx
2(y − 1)
dy
dx
Sugerencia: Para encontrar el intervalo de definición, busque los puntos en los que
= 0 ó
= 0.
dx
dy
6
12. Resuelva las ecuaciones
ax + b
dy
12.1)
=
dx
cx + d
[
]
dy
dy
12.2) a x
+ 2y = xy
dx
dx
12.3)
dy
ay + b
=
dx
cy + d
donde a, b, c y d son constantes.
13. Transformar las siguientes ecuaciones diferenciales en las formas diferenciales que sean separables y luego resolver.
y
xex
x2 y − y
13.1) y ′ = 2
13.2) y ′ =
13.3) y ′ =
x
2y
y+1
Parte III: Ecuaciones Reducibles a Ecuaciones Separables
14. Una ecuación diferencial de la forma
dy
= f(ax + by + c)
dx
siempre se puede reducir a una ecuación de variables separadas con la sustitución u = ax + by + c, b ̸= 0. En virtud de esta
sustitución, resuelva entonces las siguientes ecuaciones.
dy
dy
3x + 2y
14.1)
= (−5x + y)2 − 4
14.2)
=
; y(−1) = −1
14.3) (x + y)dx + (3x + 3y − 4)dy = 0
dx
dx
3x + 2y + 2
15. Para ecuaciones de la forma
yf(xy)dx + xg(xy)dy = 0
la sustitución xy = u, las transforma en una ecuación a variables separadas. Resuelva las siguientes ecuaciones diferenciales,
con la sustitución indicada.
15.1) y(xy + 1)dx + x(1 + xy + x2 y2 )dy = 0
15.2) (y − xy2 )dx − (x + x2 y)dy = 0
15.3) (1 − xy + x2 y2 )dx + (x3 y − x2 )dy = 0
⋆ Ecuaciones Homogéneas
16. Se dice que una función f : D ⊂ R2 → R, es homogénea de grado α ∈ R, si se verifica que f(tx, ty) = tα f(x, y), t > 0.
Determine si las funciones dadas son homogéneas. Si lo son, indique entonces su grado de homogeneidad.
√
y4
x3 y − x2 y2
16.1) f(x, y) = x3 + 2xy2 −
16.2) f(x, y) = x + y(4x + 3y)
16.3) f(x, y) =
x
(x + 8y2 )
16.4)
(
x
√
f(x, y) =
2
y + x4 + y4
16.5)
f(x, y) = cos
x2
x+y
)
16.6)
f(x, y) =
ln x3
ln y3
17. Suponga que M(x, y)dx + N(x, y)dy = 0 es una ecuación homogénea. Demuestre que alguna de las sustituciones x = vy
o y = ux, reducen la ecuación a una de variables separables.
18. Suponga que M(x, y)dx + N(x, y)dy = 0 es una ecuación homogénea. Demuestre que la sustitución x = r cos θ ;
y = r sen θ, reducen la ecuación a una de variables separables.
19. Resuelva las ecuaciones diferenciales homogéneas dadas, utilizando la sustitución adecuada.
19.1)
19.2) (y2 + yx)dx − x2 dy = 0
(
)
dx
−2x
19.5) y
= x + 4y exp
dy
y
(x − y)dx + xdy = 0
19.4) (x2 + xy − y2 )dx + xydy = 0
(
19.7)
y + x cotan
19.10) y ′ =
19.13) y ′ =
y)
dx − xdy = 0
x
19.8)
y−x
x
2xy
− x2
y2
19.16) (1 + 2ex/y )dx +
2
e−x/y
(
1−
x
y
dx
x + 3y
=
dy
3x + y
19.3) 2x2 ydx = (3x3 + y3 )dy
19.6)
dy
y (y)
= ln
dx
x
x
19.9)
dy
y x2
= + 2 +1
dx
x y
19.11) y ′ =
2y + x
x
19.12)
y′ =
x2 + 2y2
xy
19.14) y ′ =
y
√
19.15)
y′ =
x4 + 3x2 y2 + y4
x3 y
x+
xy
)
dy = 0
19.17) (x2 + y2 )dx + (x2 − xy)dy = 0 19.18)
dy
y3 y
= 3 −
dx
x
x
7
⋆ Ecuaciones Reducibles a Homogéneas
Existen ecuaciones reducibles a homogéneas y en consecuencia son también reducibles a separables, veamos
20. Para ecuaciones de la forma
dy
f(ax + by + c)
=
(1)
dx
g(mx + ny + p)
{
x=u+h
, transforma a la ecuación (1) en una ecuación homogénea.
con c y n no nulos (no ambos). La sustitución
y=v+k
Utilizando esta sustitución, resuelva las siguientes ecuaciones difereciales.
20.1)
dy
2x + 9y − 20
=
dx
6x + 2y − 10
20.2)
20.7)
x+y−2
dy
=
20.5)
dx
−x + y − 4
(2x + 2y − 1)dy − (x + y + 1)dx = 0
20.9)
(x − 2y + 1)dx + (2x − 4y + 3)dy = 0
20.4)
dy
(2x − y)2
=
dx
(4x − 2y − 1)2
20.3)
dy
3y − 2x − 3
=
dx
4x − 6y
dy
3x − 4y − 2
dy
2x + y + 7
=
20.6)
=
dx
3x + 4y − 3
dx
3y − x
20.8) (x − y + 1)dx + (2x + y − 2)dy = 0
20.11) (3y − 7x + 7)dx − (3x − 7y − 3)dy = 0
20.10)
(12x + 21y − 9)dx + (47x + 40y + 7)dy = 0
20.12)
(2x − 5y + 3)dx + (2x + 4y − 6)dy = 0
21. Demuestre que la EDO: (x2 y2 − 1)dy + 2xy3 dx = 0, se puede transformar en una Ecuación Homogénea, haciendo la
sustitución: y = zα . Halle α y resuelva esta ecuación.
22. Realice la sustitución, x = zα , para resolver la ecuación: (x + y3 )dx + (3y5 − 3y2 x)dy = 0.
23. Demuestre que la sustitución y = ux, resuelve la ecuación: xdy − ydx = (6x2 − 5xy + y2 )dx. ¿Es esta ecuación
homogénea?¿Por qué este cambio la resuelve?
⋆ Sustituciones Diversas
24. Algunas ecuaciones de la forma y ′ = f(x, y), que no son separables, se pueden transformar en tales haciendo alguna
sustitución adecuada. Realizar una sustitución adecuada en cada uno de los siguientes casos, siguiendo las indicaciones o
buscando dicha sustitución.
24.1) y ′ = sen(x − y)
hacer x − y = z
24.2) (x + y)2 y ′ = a2
(x + y)m
(x + y)n+1
hacer xy = z
24.4)
y′ + 1 =
24.5)
x6 − 2x5 + 2x4 − y3 + 4x2 y + (xy2 − 4x3 )y ′ = 0 hacer y = zx
24.6)
(x + y)2 y ′ = 2x + 2y + 5
24.7)
y cos xdx + (2y − sen x)dy = 0
24.8)
2(x2 y +
24.3) (x2 y2 + 1)dx + 2x2 dy = 0
√
1 + x4 y2 )dx + x3 dy = 0
hacer u = sen x
hacer y = zα
Parte IV: Ecuaciones Exactas
25. Las siguientes ecuaciones diferenciales de primer orden se dan en forma usual y en forma diferencial. Determine si las
ecuaciones en forma usual y/o diferencial (según sea el caso) son homogéneas y/o separables y/o exactas.
1
25.1) y ′ = xy
; xydx − dy = 0
25.2) y ′ = xy
; xdx − dy = 0
y
25.3)
y ′ = xy + 1
25.5)
y′ =
25.7)
y′ =
x2
y2
x2
dx − dy = 0
y2
; (xy + 1)dx − dy = 0
25.4) y ′ =
x2
y2
; −x2 dx + y2 dy = 0
25.6) y ′ = −
2y
x
; 2xydx + x2 dy = 0
xy2
x2 y + y3
; xy2 dx − (x2 y + y3 )dy = 0
25.8) y ′ = −
xy2
x2 y + y2
; xy2 dx − (x2 y + y2 )dy = 0
;
8
26. Compruebe si las siguientes ecuaciones diferenciales son exactas y resuelva las que lo sean.
(x + 3y)dx + (x − 2y)dy = 0
26.2)
(y + 3x)dx + xdy = 0
26.3) (x3 + 5xy2 )dx + (2y3 + 5x2 y)dy = 0
26.4)
(tan y − 3x2 )dx + x sec2 y dy = 0
26.5) (2xy − cos x)dx + (x2 − 1)dy = 0
26.6)
xexy dx + yexy dy = 0
26.7) (2xy + x)dx + (x2 + y)dy = 0
26.8)
3x2 y2 dx + (2x3 y + 4y3 )dy = 0
26.9) (sen xy + xy cos xy)dx + (x2 cos xy)dy = 0
26.10)
(2xy2 + yex )dx + (2x2 y + ex − 1)dy = 0
26.11) (tan x − sen x sen y)dx + cos x cos y dy = 0
26.12)
x2 cos xydy + (2x − y sen xy − 5y4 )dx = 0
26.13) (ex sen y − 2y sen x)dx + (ex cos y + 2 cos x)dy = 0
26.14)
(ex sen y + 3y)dx − (3x − ex sen y)dy = 0
26.15) (yexy cos 2x − 2exy sen 2x + 2x)dx + (xexy cos 2x − 3)dy = 0
26.16)
(y/x + 6x)dx + (log x − 2)dy = 0
26.17) (x log y + xy)dx + (y log x + xy)dy = 0
26.18)
26.19) (3x2 − 2xy + 2)dx + (6y2 − x2 + 3)dy = 0
26.20)
26.1)
(x2
y
x
dx + 2
dy = 0
2
3/2
+y )
(x + y2 )3/2
(2xy2 + 2y) + (2yx2 + 2x)y ′ = 0
27. Escriba cada ecuación en la forma M(x, y)dx + N(x, y)dy = 0, compruebe si es exacta y resuelva las que lo son.
y(y − ex )
27.1) 2xyy ′ = x2 − y2
27.2) y ′ = x
e − 2xy
27.3)
(
x − y cos x
dy
=
dx
sen x + y
27.4)
x2 +
y)
dx + (ln x + 2y)dy = 0
x
28. Resuelva los siguientes P.V.I.
28.1)
2xydx + (x2 + 1)dy = 0 ; y(1) = −3
(
28.3)
)
1
dy
+ cos x − 2xy
= y(y + sen x) ; y(0) = 1
2
1+y
dx
28.5) (9x2 + y − 1)dx − (4y − x)dy ; y(1) = 0
y − 2x
; y(1) = 2
2x − y
28.2)
y′ =
28.4)
(x2 + 2ye2x )y ′ + 2xy + 2y2 e2x = 0 ; y(0) = 1
28.6)
(2x − y)dx + (2y − x)dy = 0 ; y(1) = 3
29. Resuelva el siguiente P.V.I: (y2 cos x − 3x2 y − 2x)dx + (2y sen x − x3 + ln y)dy = 0 ;
2
30. Resuelva el siguiente P.V.I: x cos xy dy + (ye
xy
3
+ 4y )dx = 0 ;
y(0) = e.
y(0) = 2.
31. Determine la función M(x, y) para que la EDO
(
)
1
M(x, y)dx + xyex + 2xy +
dy = 0
x
sea Exacta. Resuélvala !!!
32. Determine la función N(x, y) para que la EDO
(
1
1
y 2 x− 2 +
x
x2 + y
)
dx + N(x, y) dy = 0
sea Exacta. Resuélvala !!!
33. Demuestre que cualquier ecuación separable de la forma: M(x) + N(y)y ′ = 0, también es exacta.
34. Encuentre el valor de b, para el cual la ecuación dada es exacta y luego resuélvala.
34.1) (xy2 + bx2 y)dx + (x + y)x2 dy = 0
34.2) (ye2xy + x)dx + bxe2xy dy = 0
9
⋆ Ecuaciones Reducibles a Exactas
35. Demuestre que las siguientes ecuaciones no son exactas, pero que se hacen exactas cuando se multiplican por el factor
de integración dado. Después resuelva las ecuaciones.
35.2) x2 y3 + x(1 + y2 )y ′ = 0 , µ(x, y) =
35.1) (x + 2) sen ydx + x cos ydy = 0 , µ(x, y) = xex
(
35.3)
)
(
)
sen y
cos y + 2e−x cos x
−x
− 2e sen x dx +
dy = 0 , µ(x, y) = yex
y
y
1
xy3
35.4) ydx + (2x − yey )dy = 0 , µ(x, y) = y
36. Utilice el Factor Integrante generalizado, para convertir las siguientes ecuaciones diferenciales en Exactas y resuélvalas.
36.1)
(2xy2 − 2y)dx + (3x2 y − 4x)dy = 0
36.2)
36.3) (3xy3 + 4y)dx + (3x2 y2 + 2x)dy = 0
(cos 2y − sen x)dx − 2 tan x sen 2y dy = 0
36.4) 2xy ln y dx + (x2 + y2
√
y2 + 1)dy = 0
36.5)
ex dx + (ex cotan y + 2y cosec y)dy = 0
36.6)
(xy − 1)dx + (x2 − xy)dy = 0
36.7)
y dx + (x2 y − x)dy = 0
36.8)
(2xy − e−2x )dx + x dy = 0
36.10∗ ) (y2 + xy + 1)dx + (x2 + xy + 1)dy = 0
36.9) (3x2 + 2xy + y3 )dx + (x2 + y2 )dy = 0
36.11)
[ 3
]
[
]
x
3
x
4 2+
dx + 3 2 + 4y dy = 0
y
y
y
(
36.12)
6
3x +
y
)
(
+
x2
y
+3
y
x
)
dy
=0
dx
37. Resuelva la ecuación diferencial: (3xy + y2 ) + (x2 + xy)y ′ = 0, encontrando el factor de integración adecuado. Luego, use
el factor de integración µ(x, y) = [xy(2x + y)]−1 y verifique que la solución en este caso coincide con la dada anteriormente.
Parte V: Ecuaciones Lineales
38. Encuentre la solución general de cada una de las ecuaciones diferenciales dadas:
38.1)
3y ′ + 12y = 4
38.2) x
38.4)
x ′ + 3xy2 = y3
dy
+ 2y = 3
dx
38.3)
xdy = (x sen x − y)dx
38.5) (x + 4y2 )dy + 2ydx = 0
38.6)
(1 + x2 )y ′ + (xy + x3 + x) = 0
dy
1
=
dx
cos y + xy2
38.9)
dy
1 − e−2x
+y= x
dx
e + e−x
38.7) (1 + ex )
dy
+ ex y = 0
dx
38.8)
38.10) (1 + x)
dy
− xy = x + x2
dx
34.11)
(x + 2)2 y ′ = 5 − 8y − 4xy
38.12) ydx + (x + 2xy2 − 2y)dy = 0
38.14)
xy ′ + 2y = ex + ln x
38.15) (x + 1)y ′ + (x + 2)y = 2xe−x
38.16) dy − (y + senh x)dx = 0
38.17)
x
38.19) y ′ − y cotan x = ex (1 − cotan x)
38.20)
y ′ x cos x + y(x sen x + cos x) = 1
38.13)
sec x
dy
y
+
=1
dx cos2 x
dy
+ (3x + 1)y = e−3x
dx
38.18) x
dy
+ y + xy = e−x sen 2x
dx
38.21) s ′ + s tan t = 2t + t2 tan t
10
dy
− 3y = (x + a)5
dx
38.23) x ln x
dy
+ y = 2 ln x
dx
dy
− y = (x − 1)ex
dx
38.22)
x+a
38.25)
(x + 1)y ′ + (2x − 1)y = e−2x
38.26) x(x − 1)y ′ + y = x2 (2x − 1) 38.27)
(6 − 2xy)
38.28)
(1 + t2 )y ′ + 4ty = (1 + t2 )−2
38.29) y ′ + 2ty = 2te−t
(6 − 2xy)y ′ + y = te−t + 1
38.24) x
2
38.30)
dy
+ y2 = 0
dx
39. Resuelva la ecuación diferencial lineal dada, sujeta a la condición inicial que se indica:
dy
39.1) y ′ + y tan x = cos2 x
; y(0) = −1
39.2) sen x
+ y cos x = 0
dx
dy
y
=
dx
y−x
;
(
)
y − π2 = 1
39.3)
cos2 xy ′ + y = 1
; y(0) = −3
39.4)
;
y(5) = 2
39.5)
dy
+ y tan x = sec x
dx
; y(0) = −1
39.6) xdy + (xy + 2y − 2e−x )dx = 0 ;
y(1) = 0
39.7) y ′ + 2y + x(e3x − e2x ) = 0 ; y(0) = 2
39.8)
39.9) ty ′ + (t + 1)y = t
39.10)
; y(log 2) = 1
2y
dy
−
= (x + 1)3
dx x + 1
dy 2
cos x
+ y= 2
dx x
x
;
y(0) = 1
;
y(π) = 0
40. Resuelva los dos siguientes problemas, como una aplicación de las ecuaciones diferenciales lineales.
2y + x + 1
.
x
y2 ln x − y
40.2) Hallar la ecuación de curva que pasa por el punto (1, 1) y cuya pendiente en un punto cualquiera es igual
.
x
41. Considere el PVI
1
y ′ + y = 2 cos x ,
y(0) = −1
4
Encuentre las coordenadas del primer punto máximo local para x > 0.
40.1) Hallar la ecuación de curva que pasa por el punto (1, 0) y cuya pendiente en un punto cualquiera es igual
42. Considere el PVI
2
1
y′ + y = 1 − t ,
y(0) = y0
3
2
Encuentre el valor de y0 , para el cual la solución toca al eje t sin cruzarlo.
43. Considere el PVI
1
y ′ + y = 3 + 2 cos 2x ,
y(0) = 0
4
Encuentre la solución de este PVI y determine su comportamiento para x grande y además, determine el valor de x, para el
cual la solución corta por primera vez a la recta y = 12.
44. Sea y = y1 (x), una solución de
y sea y = y2 (x), una solución de
y ′ + p(x)y = 0
y ′ + p(x)y = q(x)
(2)
Demuestre que y = y1 (x) + y2 (x), también es una solución de la ecuación (2).
45. Demuestre que si a y λ son constantes positivas y b es cualquier número real, entonces, toda solución de la ecuación
y ′ + ay = be−λx
tiene la propiedad de que y → 0, cuando x → ∞.
11
46. Considere la ecuación diferencial dada por:
dy
= ay − b
dt
e intentemos un método alternativo para resolver dicha ecuación. Método de los Coeficientes Indeterminados:
dy
46.1) Resuelva la ecuación mas sencilla:
= ay y llame a esta solución y1 (t).
dt
46.2) Observe que la diferencia entre la ecuación original y la resuelta es el término −b. Por tanto es razonable suponer que
las soluciones de ambas ecuaciones difieran en una constante. En base a esta suposición, encuentre una constante k, tal que
y(t) = y1 (t) + k, sea solución de la ecuación original.
47. Considere la ecuación diferencial lineal de primer orden general dada por:
dy
+ p(t)y = g(t)
dt
e intentemos un método alternativo para resolver dicha ecuación. Método de Variación de Parámetros:
∫
− p(t)dt
47.1) Demuestre que y(t) = Ae
, si hacemos g(t) = 0 en (3), donde A es una constante arbitraria.
47.2) Si g(t) no es nula en todo punto de I, entonces, suponga que la solución es de la forma
∫
− p(t)dt
y(t) = A(t)e
(4)
∫
donde A es ahora una función de t. Demuestre que A(t), debe satisfacer la ecuación: A ′ (t) = g(t)e
(3)
p(t)dt
.
47.3) Encuentre A(t) mediante la ecuación anterior, luego sustituya A(t) en la ecuación (4)y determine a y(t). Verifique que
la solución obtenida concuerda con la dada por el método del factor de integración.
47.3) Utilice el método descrito para resolver las ecuaciones siguientes:
(a)
ty ′ + 2y = sen t , t > 0
(b)
1
y ′ + y = 3 cos 2t , t > 0
t
(c) y ′ − 2y = x2 e2x
⋆ Ecuaciones Reducibles a Lineales
⋆ Ecuación de Bernoulli
48. Considere la ecuación diferencial:
dy
+ P(x)y = Q(x)yn
dx
(5)
donde n es cualquier número real.
48.1) Encuentre la solución para n = 0.
48.2) Encuentre la solución para n = 1.
48.3) Si n ̸= 0 y n ̸= 1. Demuestre que el cambio de variable u = y1−n , transforma dicha ecuación en una ecuación lineal
de primer orden no homogénea.
La ecuación (5), se conoce como ecuación de Bernoulli.
49. Resuelva la ecuación de Bernoulli dada:
1
dy
+y= 2
49.1) x
dx
y
49.4) x
dy
− (1 + x)y = xy3
dx
49.7) (2xt2 ln x + 1) =
49.10)
2xdt
tdx
dx
2y3 x2 + x2 y2 − 2x
=
dy
2y + 1
49.2)
dy
− y = ex y2
dx
49.5) x2
dy
+ y2 = xy
dx
49.6) 3(1 + x2 )
dy
=y
dx
49.9) x2 y − x3
49.8) (x + 2y3 )
49.11)
49.3) y ′ = y(xy3 − 1)
dy
3x2
= 3
dx
x +y+1
49.12)
dy
= 2xy(y3 − 1)
dx
dy
= y4 cos x
dx
dy
= (2 − y)(y − 5)
dx
12
50. Resuelva la ecuación diferencial de Bernoulli dada sujeta a la condición que se indica
dy
dy
50.1) x2
− 2xy = 3y4 ; y(1) = 1
50.2) y1/2
+ y3/2 = 1 ; y(0) = 4
dx
dx
50.3) xy(1 + xy2 )
dy
=1 ;
dx
y(1) = 0
50.4) 2
dy
y
x
= − 2
dx
x y
; y(1) = 1
51. Responda cada uno de los planteamientos dados a continuación.
(51.1) Demuestre que la función y(x) = C1 e−3x + C2 e2x , es solución de la EDO de segundo orden: y ′′ + y ′ − 6y = 0.
(51.2) Determine las constantes C1 y C2 del apartado anterior, considerando las condiciones iniciales y(0) = 15 y y ′ (0) = 5.
(51.3) Determine la solución de la EDO de primer orden: y ′ + ym − xyn = 0, donde m y n, satisfacen el sistema
{
C1 C2
= 10n
C1 + C2 = 15m
donde C1 y C2 , son las constantes obtenidas en (1.2).
52. Resuelva la ecuación: (x2 + y2 + 1)dy + xy dx = 0.
53. Resuelva la ecuación: 2y ′ sen x + y cos x = y3 (x cos x − sen x).
54. Resuelva la ecuación:
y′ + y
x + 12
(1 − x2 )y2
= 2
2
x +x+1
(x + x + 1)3/2
55. Resuelva la ecuación y ′ = ry − ky2 , con r, k > 0, Esta ecuación es importante en la dinámica de poblaciones.
56. Resuelva la ecuación y ′ = εy − σy3 , con ε, σ > 0. Esta ecuación se presenta en la estabilidad del flujo de fluidos.
57. Resuelva la ecuación y ′ = (Γ cos t + T )y − y3 , donde Γ y T son constantes. Esta ecuación también se presenta en la
estabilidad del flujo de fluidos.
⋆ Ecuación de Ricatti
58. La ecuación diferencial:
dy
= p(x)y2 + q(x)y + g(x)
dx
se denomina ecuación de Ricatti. Suponga que se conoce una solución particular y1 (x), de esta ecuación.
Demuestre que la sustitución
1
y = y1 (x) +
v(x)
(6)
dv
+ [q(x) + 2y1 (x)p(x)]v = −p(x).
dx
59. Utilice el método del problema 32, para resolver las siguientes ecuaciones diferenciales de Ricatti, dado que y1 , es una
solución conocida en cada una de las ecuaciones.
transforma la ecuación (6), en la ecuación lineal:
59.1)
y ′ + y2 = 1 + x2
;
y1 (x) = x
59.3)
4
1
dy
= − 2 − y + y2
dx
x
x
;
y1 (x) =
2
x
59.4)
dy
= e2x + (1 + 2ex ) + y2
dx
; y1 (x) = −ex
59.5)
dy
1
= 2x2 + y − 2y2
dx
x
;
y1 (x) = x
59.6)
dy
= sec2 x − y tan x + y2
dx
; y1 (x) = tan x
59.7)
dy
= 1 + x2 − 2xy + y2
dx
;
y1 (x) = x
59.8)
dy
1
y
= − 2 − + y2
dx
x
x
; y1 (x) =
59.9)
dy
2 cos2 x − sen2 x + y2
=
dx
2 cos x
;
y1 (x) = sen x
59.10) (1 + x3 )
;
y1 (x) =
59.11)
1 − x + y2
dy
√
=
dx
2 x
√
59.2) y ′ + 2xy = 1 + x2 + y2
x
; y1 (x) = x
1
x
dy
+ 2xy2 + x2 y + 1 = 0 ; y1 (x) = −x
dx
59.12) y ′ − ex = y2 − (1 + ex )y + ex
; y1 (x) = ?
13
60. Dada la E.D.O.
dy
+ 2x2 y − x3 = xy2 + 1
dx
60.1) Hallar los valores de a y b para que y1 = ax + b sea solución.
60.2) Hallar todas las soluciones de la ecuación dada.
61. La propagación de una acción particular en una población grande (por ejemplo que los conductores, enciendan las luces
de su automóvil al atardecer) a menudo depende en parte de circunstancias externas (la creciente oscuridad) y en parte de
una tendencia a imitar a otros que ya han realizado la acción en cuestión. En este caso, la proporción y(t) de personas que
han realizado la acción puede ser descrita por la ecuación:
dy
= (1 − y)[x(t) + by]
dt
donde x(t) mide el estı́mulo externo y b es el coeficiente de imitación. Entonces:
(a) Observe que la ecuación anterior es una ecuación de Ricatti. Encuentre la ecuación lineal que satisface v(t).
(b) Encuentre v(t) en el caso en que x(t) = at, donde a es constante. Exprese la respuesta en forma de una integral.
⋆ Otros casos
62. Considere la ecuación diferencial:
y ′ + p(x)y = q(x)y ln y
(7)
Demuestre que haciendo la sustitución u = ln y, en la ecuación (7), se obtiene la siguiente ecuación diferencial lineal
u ′ + p(x) = q(x)u
Use este hecho para resolver la siguiente ecuación diferencial
xy ′ − 4x2 y + 2y ln y = 0
63. Demuestre que la sustitución u = tan y, reduce la EDO: y ′ + x sen 2y = xe−x cos2 y, a una EDO lineal.
2
64. Demuestre que ∫la ecuación: x2 yy ′′ = (y − xy ′ )2 , se transforma en una ecuación lineal de primer orden si consideramos
la sustitución y = e z(x) dx , donde z es una función dependiente de x.
65. Realice una sustitución conveniente, para transformar la siguiente ecuación diferencial: y ′ + sen y + x cos y + x = 0, en
una ecuación lineal y resuélvala.
Parte VI: Ecuaciones de Clairaut y Lagrange.
66. Resolver las siguientes ecuaciones diferenciales de Clairaut.
a
2y ′
66.1)
y = xy ′ +
66.5)
x=
66.9)
xy ′ = y + ey
1
y
+
y ′ (y ′ )2
′
66.2) y = xy ′ +
a
(y ′ )2
66.6) y = (x + 4)y ′ + (y ′ )2
66.10) y = xy ′ +
√
1 + (y ′ )2
66.3) x(y ′ )2 − yy ′ − y ′ + 1 = 0
66.4) y = xy ′ + (y ′ )2
66.7) y = xy ′ − (y ′ )3
66.8) y = xy ′ + 1 − ln y ′
66.11) y = y ′ tan x − (y ′ )2 sec2 x
(u = sen x)
67. Resolver las siguientes ecuaciones diferenciales de Lagrange.
67.1)
y = 2xy ′ + ln y ′
67.2)
2y = xy ′ + y ′ ln y ′
67.5)
y = x(y ′ )2 + y ′
67.3) y = x(1 + y ′ ) + (y ′ )2
67.4)
y = x(y ′ )2
“Hay una fuerza motriz mas poderosa que el vapor, la electricidad
y la energı́a atómica: LA VOLUNTAD”
Albert Einstein
UNIDAD II
Aplicaciones de Ecuaciones de Primer Orden
•
•
•
•
•
•
•
Aplicaciones geométricas
Decaimiento radiactivo y poblaciones
Temperatura (Ley de enfriamiento de Newton)
Mecánica y Cinemática
Vaciado de Tanques (Ley de Torricelli)
Mezclas quı́micas
Circuitos eléctricos
“No le evitéis a vuestros hijos las dificultades de la vida, ense~
nadles a superarlas”
Louis Pasteur
15
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Práctica 2
2014
Prof. Andrés Pérez
Aplicaciones de las E.D.O. de Primer Orden
Parte I: Aplicaciones geométricas
⋆ Método de las Isoclinas
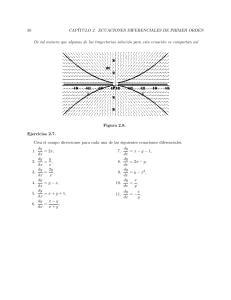
1. Si es necesario trazar manualmente el campo direccional de la ecuación diferencial y ′ = f(x, y), es útil observar que la
pendiente y ′ de la solución tiene el valor constante c en todos los puntos de la curva f(x, y) = c. Estas curvas se denominan
Isoclinas. Para ecuaciones relativamente simples, es posible trazar el campo direccional, dibujando unas cuantas isoclinas y
luego insertar los segmentos rectilı́neos tangentes a la solución en varios puntos de cada una. En cada uno de los problemas
dados a continuación, determine las isoclinas y después úselas para trazar el campo direccional.
1.1)
y ′ = 3 − 2y
1.2) y ′ = −y(1 + y2 )
1.3) y ′ = (1 − y)(2 − y)
1.5) y ′ = x2 + y2
1.6) y ′ = 1 − xy
1.4)
y ′ = 2x − 3y
⋆ Trayectorias Ortogonales
2. Halle las trayectorias ortogonales de las siguientes familias de curvas.
2.1) y2 = 4ax
2.2)
x2 − y2 = k
2.3)
xy = k
2.4) (x − 1)2 + y2 + kx = 0
2.5)
y2 = kx, pasa por P(−2, 3)
2.6)
x2 = y2 + ky3
2.7) y2 = x2 + ky, pasa por P(1, −2)
2.8)
x + y = key , pasa por P(0, 10)
2.9)
y = kx2
⋆ Trayectorias Isogonales
3. Halle la familia de curvas isogonales a la familia dad con el ángulo indicado.
3.1) y = kx, α = 30◦
3.2) y = kx, α = 45◦
3.3)
y2 = kx, α = 60◦
3.4) x2 + y2 = kx, α = 30◦
4. Halle la trayectoria isogonal que intercepta a la familia dada con un ángulo de 45◦ y que pasa por el punto indicado.
4.1) y = kex + 1, (−1, 1) 4.2)
y = ke−x , (1, −1) 4.3)
ex+y (1 − y) = k, (1, 1) 4.4) 2y3 + 3y = −3x + k, (1, 1)
Parte II: Decaimiento radiactivo y poblaciones ∼ epidemias
5. Un cultivo tiene una cantidad inicial N0 bacterias. Cuando ha transcurrido una hora la cantidad medida de bacterias
es 32 N0 . Si la razón de reproducción es proporcional a la cantidad de bacterias presentes, calcule el tiempo necesario para
triplicar la cantidad inicial de microorganismos.
6. Suponga que la tasa de crecimiento de determinada población varı́a a una razón equivalente a la quinta parte de r(t)y,
tal que r(t) = 21 + sen t. Entonces,
(a) Si y(0) = 1, calcule o estime el tiempo τ en que la población se duplica. Elija otras condiciones iniciales y determine
si el tiempo de duplicación τ depende de la población inicial.
(b) Suponga que en la tasa de crecimiento se sustituye el factor sen t por sen 2πt, es decir, la variación de la tasa de
crecimiento tiene una frecuencia sustancialmente mayor. ¿Qué efecto tiene esto en el tiempo de duplicación τ?
16
7. Suponga que determinada población satisface el problema con valor inicial
dy
= r(t)y − k
dt
donde la tasa de crecimiento r(t), está dada por r(t) = 51 (1 + sen t) y k representa la tasa de depredación. Determine el
tiempo τ en que la población tiende a la extinción , tomando k = 51 .
8. La transferencia de calor de un cuerpo a sus alrededores por radiación, con base en la ley de Stefan-Boltzmann, está
descrita por la ecuación diferencial
du
= −α(u4 − T 4 )
dt
donde u(t) es la temperatura absoluta del cuerpo en el instante t, T es la temperatura absoluta de los alrededores y α es una
constante que depende de los parámetros fı́sicos del cuerpo. Sin embargo, si u es mucho mayor que T , entonces las soluciones
de la ecuación anterior se aproximan con las soluciones de la ecuación mas simple
du
= −αu4
dt
Suponga que un cuerpo con temperatura inicial de 2000 K, está rodeado por un medio con temperatura de 300 K y que
α = 2 × 10−12 K−3 /seg. Determine la temperatura del cuerpo en cualquier instante de tiempo.
9. Cuando se produce cierto alimento, se estima en N el número de organismos de una cierta clase presentes en el paquete. Al
cabo de 60 dı́as el número N ha aumentado a 1000N. Sin embargo, el número 200N es considerado como el lı́mite saludable.
A los cuántos dı́as, después de elaborado, vence el alimento?.
10. Un material radiactivo como el isótopo torio 234, se desintegra a una razón proporcional a la cantidad presente del
isótopo. Entonces, si 100 mg de torio 234 decaen a 82.04 mg en una semana, determine la tasa de decaimiento k y encuentre
una expresión para la cantidad de torio presente en cualquier instante de tiempo t. Por último determine el tiempo necesario
para que el torio 234 decaiga a la mitad de su cantidad original.
11. La vida media o semivida de un material radiactivo se define como el tiempo requerido para que una cantidad de este
materia, decaiga a la mitad de su valor original. Demuestre que para cualquier material radiactivo que decae, la vida media
τ y la tasa de decaimiento k, satisfacen la ecuación kτ = log 2.
12. El radio 226, tiene una vida media de 1620 años. Encuentre el perı́odo durante el cual una cantidad dada de este isótopo
se reduce a una cuarta parte.
13. Un reactor de crı́a convierte el uranio 238, relativamente estable, en plutonio 239, un isótopo radioactivo. Al cabo de
15 años, se ha desintegrado el 0.043% de la cantidad inicial A0 de una muestra de plutonio. Calcule la vida media de este
isótopo, si la razón de desintegración es proporcional a la cantidad presente.
14. Se analizó un hueso fosilizado y se encontró que contenı́a la centésima parte de C-14. Determine la edad del fósil,
asumiendo que el perı́odo de vida media del C-14 es de aproximadamente 5600 años.
15. Suponga que un alumno es portador del virus de la gripe y regresa a su escuela donde hay 1000 estudiantes. Si se
supone que la razón con que se propaga el virus es proporcional no sólo a la cantidad de alumnos infectados, sino también a
la cantidad de alumnos sanos, determine la cantidad de alumnos infectados pasados seis dias, si se observa que a los cuatro
dias ya habı́an 50.
16. Hace algunos años (no precisaré cuantos, ya que podrı́an ser muchos), unos arqueólogos usaron unos trozos de madera
quemada (entiéndase chamuscada), es decir, de carbón vegetal (pero no para hacer parrilla), para fechar las pinturas prehistóricas y rupestres de las paredes y los techos de una caverna en Lacaux, Francia. Según estos tipos, las pinturas esas eran
“burda” de bonitas. Determine entonces, cuántos años tenı́an estos trozos de carbón, si ellos lograron observar que habı́an
perdido el 85.5% del carbono C − 14.
17. Muchos creen que el sudario de Turı́n que muestra el negativo de un cuerpo de un hombre crucificado es la mortaja de
Jesús de Nazareth. En 1988, el Vaticano otorgó autorización para que se fechara el carbono del manto. Tres laboratorios
cientı́ficos independientes llegaron a la conclusión de que el manto tiene unos 660 años. Edad que coincide con su aparición
histórica. Con ésta edad, determine qué porcentaje de la cantidad original de C − 14 le quedaba en 1988.
Ayuda: Recuerde que el periodo de vida media es de aproximadamente 5600 años.
18. El isótopo radiactivo I-131 se usa en el tratamiento de la hipertiroides. El I-131 administrado a un paciente se acumula
en forma natural en la glándula tiroides, en donde se desintegra y reduce parte de la glándula.
17
(a) Suponga que se requieren 72 horas para enviar el I-131 del productor al hospital. ¿Qué porcentaje de la cantidad
originalmente enviada llega al hospital?
(b) Si el I-131 es almacenado en el hospital 48 horas adicionales antes de ser utilizado, ¿qué tanto queda de la cantidad
original enviada por el productor cuando el material radioactivo se utilice?
(c) ¿Qué tiempo le tomará al I-131 para desintegrarse completamente, de manera que el hospital pueda deshacerse de los
residuos sin precauciones especiales?
Nota: La vida media del I-131 es de 8 dias.
19. Suponga que el modelo logı́stico de una población especı́fica, se reduce a la siguiente ecuación
(
)
dP
P
= 0.4 1 −
P
dt
230
(a) ¿Para qué valores de t está en equilibrio la población? (b) ¿Para qué valores está creciendo la población? (c) ¿Para qué
valores de t está decreciendo la población?. Realice un análisis gráfico de la situación.
20. Cuando se produce cierto alimento, se estima en N el número de organismos de una cierta clase presentes en el paquete.
Al cabo de 60 dı́as el número N ha aumentado a 1000N. Sin embargo, el número 200N es considerado como el lı́mite
saludable. A los cuántos dı́as, después de elaborado, vence el alimento?.
21. Para describir la rapidez con la que se adquiere una habilidad se usa una curva de aprendizaje. Por ejemplo, supongamos
que un fabricante estima que un nuevo operario producirá A objetos el primer dı́a de trabajo, y que a medida que va
adquiriendo experiencia, producirá los objetos más rápidamente hasta que produzca un máximo de M objetos por dı́a. Sea
f(t), la cantidad de artı́culos producidos el dı́a t, para t ≥ 1. Suponga que el ritmo de producción f ′ , es proporcional a
M − f(t). Entonces:
21.1) Deduzca una fórmula para calcular la cantidad de artı́culos producidos en un dı́a cualquiera.
21.2) Suponiendo que M = 30, f(1) = 5 y f(2) = 8. Estime el número de artı́culos producidos el vigésimo dı́a.
22. Suponga que se invierte una suma S0 a una tasa de rendimiento anual r que se compone de manera continua.
(a) Encuentre el tiempo T necesario para que la suma inicial duplique su valor como una función de r.
(b) Determine T , si r = 7%.
(c) Encuentre la tasa de rendimiento que debe obtenerse si la inversión inicial debe duplicarse en 8 años.
Parte III:Temperatura (Ley de enfriamiento de Newton)
23. Una pequeña barra de metal, cuya temperatura inicial es de 20◦ C, se deja caer en un recipiente con agua hirviendo.
Calcule el tiempo que dicha barra demorará en alcanzar los 90◦ C, si se sabe que aumentó 2◦ C en un segundo. ¿Cuánto
demorará la barra en alcanzar los 98◦ C?
24. Suponga que el dı́a de ayer fué al mercado con su respectiva madre y en el ajetreo, las bolsas y todas esas cosas, se le
ocurrió la brillante idea de comprarse un par de laticas para refrescarse como en las propagandas de T.V (cosa que nadie
cree que es malta). El portu de la esquina, le vendió una frı́a y la otra caliente, ya que se le daño la nevera. En realidad,
la caliente no estaba tan caliente, se encontraba a una temperatura de 23◦ C. Cuando usted llegó a su casa, lo primero que
hizo fué introducirla en el “freezer” (entiéndase parte superior de su nevera), que se encontraba como Dios manda a una
temperatura de envidiables 2◦ C bajo cero. Como usted tenı́a mucha sed, abrió la nevera a los 10 minutos y se percató que
la lata aún estaba en los 10◦ C. Determine el momento exacto en que debe abrir la nevera para tomarse la espumoza, si la
mejor temperatura para ingerirla es de 4◦ C.
25. Un termómetro que está en el interior de una habitación se lleva al exterior, en donde la temperatura del aire es de 5◦ F.
Después de un minuto el termómetro marca 55◦ F y al segundo minuto marca 30◦ F. ¿Cuál es la temperatura inicial de la
habitación?
26. Durante un dı́a claro y despejado, un forense llega a la escena de un crimen en un conocido barrio de Caracas. Al llegar,
inmediatamente observa su reloj (un casio altimeter bien pepeado) y escribe en su libreta de anotaciones que son las 3 : 45
pm. y que la temperatura se encuentra a 23◦ C. Seguidamente, toma los signos vitales del ya occiso y determina que estaba
18
muerto (que brillante descubrimiento!!!) y que su temperatura corporal era de 27◦ C. Interrogando a los curiosos del lugar
(que nunca faltan) encontró a la vieja bruja del barrio y esta que se la da de policı́a le dijo: “al pasar una hora de escuchar los
disparos salı́ con mi termómetro y Juansito tenı́a 35◦ C y la lengua afuera, no tenı́a zapatos y faltaba su cartera”. Al escuchar
el relato fué directamente donde el detective y le dijo: “ya sé a que hora murió el occiso”. Determine aproximadamente, a
qué hora murió Juansito.
27. Al sacar un pastel del horno, su temperatura es de 300◦ F. Tres minutos después, su temperatura es de 200◦ F. ¿Cuánto
demorará en enfriarse hasta una temperatura ambiente de 70◦ F?
28. Un termómetro que indica una temperatura de 70◦ F se coloca en un horno precalentado a temperatura constante. A
través de una ventana de vidrio del horno, un observador se percata que la temperatura que registra el termómetro después
de 21 minuto es de 110◦ F y al minuto de introducido registra una temperatura de 145◦ F. ¿A qué temperatura está el horno?
29. A las 9:00 am. un termómetro marca 70◦ F, se lleva al aire libre donde la temperatura es 15◦ F. A las 9:05 am. marca
45◦ F. A las 9:10 am. es llevado de nuevo al interior de la habitación donde la temperatura se mantiene a 70◦ F ¿Cuánto
marca a las 9:20 am.?
Parte IV:Mecánica ∼ Cinemática
30. En la escena de un accidente, el investigador de la policı́a determina que tan rápido iba el conductor a partir de las marcas
dejadas por los cauchos en el pavimento. Suponga que el carro frenó con una desaceleración de 15 sm2 . ¿A qué velocidad iba
el auto cuando aplicó los frenos, si recorrió 75 m antes de detenerse?
31. Un auto que va a 60 millas por hora, patina 176 pies cuando los frenos son aplicados. Si el sistema de frenado produce
una desaceleración constante, ¿cuál es esa desaceleración? ¿Durante cuántos segundos continuará el derrape?32. Un auto patina 15 metros cuando los frenos son aplicados y está moviéndose a 50 Km/h. Supongamos que el auto, tiene
la misma desaceleración constante. ¿cuánto patinará si se mueve a 100 Km/h, cuando los frenos son aplicados?
33. Se está remolcando una barca a una velocidad de 12 millas por hora. En el momento (t = 0) que se suelta la cuerda
de remolque, un hombre que está en la barca, comienza a remar siguiendo la dirección del movimiento y ejerciendo una
fuerza de 20 lb. Si el peso conjunto del hombre es de 480 lb y la resistencia en libras es de 1.75v, donde v está medido en
pies/segundo, hallar la velocidad de la barca después de 12 minuto.
Observación: Recuerde que el factor de conversión de millas a pies es 5280 y la aceleración en este sistema es 32 pies/seg2 .
34. Un resorte de peso despreciable está suspendido verticalmente. En su extremo libre se ha sujetado una masa de m
kilogramos. Si la masa se mueve con velocidad v0 m/seg, cuando el resorte está sin alargar, hallar la velocidad v como una
función del alargamiento x en metros.
Parte V:Mezclas quı́micas (mezclas homogéneas)
35. Cierto producto quı́mico se disuelve en agua a una velocidad proporcional a la cantidad aún no disuelta y a la diferencia
entre la concentración en una solución saturada y la concenración en la solución real. Se sabe que en 100 gramos de una
solución saturada están disueltos 50 gramos de la sustancia. Si se agitan 30 gramos del producto quı́mico con 100 gramos de
agua, en dos horas se disuelven 10 gramos. ¿Cuántos se disuelven en 5 horas?
36. Unos vagabundos estafadores en un barrio de Caracas, intentan embaucar a algunos incautos, vendiendo una panela de
papelón fantasma (recuerden que no hay azúcar), según nos informó una fuente que no quiso revelar su nombre. Para ello,
combinan dos sustancias que llamaremos A y B (ya que la ley RESORTE nos prohı́be colocar nombres exactos). Al principio
del negocio, comenzaron con 40 kilogramos de A y 50 kilogramos de B, en tanto que por cada kilo de B, se consumen 2 de
A (allı́ justamente es donde está la estafa, ya que A es de mucha menor calidad y se consigue a precio de gallina flaca en el
mercado de Catia). Se observa entonces, que a los diez minutos se han formado 10 kilos de la panela fraudulenta. ¿Cuántos
kilos de panela tendrán al cabo de 20 minutos de trabajo?
37. Cuando se combinan dos sustancias quı́micas A y B se forma un compuesto C. La reacción entre ambas es tal que, por
cada gramo de A, se usan 4 gramos de B. Se observa que a los 10 minutos se han formado 30 gramos del producto C, calcule
la cantidad de C, en función del tiempo si la velocidad de la reacción es proporcional a las cantidades de A y B que quedan
y al principio hay 50 gramos de A y 32 gramos de B. ¿Qué cantidad del compuesto C hay a los 15 minutos?. Analice la
situación cuando t → ∞.
38. Un tanque contiene originalmente 100 gal de agua dulce. Después en el tanque se vierte agua que contiene 12 lb de sal
por galón, con un gasto de 2 gal/min, y se permite que la mezcla salga con el mismo gasto. Luego de 10 min, el proceso
19
se detiene y se vierte agua dulce en el tanque con un gasto de 2 gal/min, la mezcla sale nuevamente con el mismo gasto.
Encuentre la cantidad de sal en el tanque luego de un lapso adicional de 10 min.
39. A un tanque de de 60 gal. de agua pura comienza a entrar salmuera con 1 libra de sal por galón a 2 gal/min y sale a 3
gal/min. ¿Qué cantidad de sal contiene cuando el volumen se ha reducido a la mitad? ¿Cuál es la máxima cantidad de sal
que llega a contener el tanque?
40. Un tanque de 100 litros, contiene 100 kg de sal disueltos en agua. Se bombea agua pura hacia adentro a 5 lib/seg y
la mezcla homogénea, se extrae con la misma razón. ¿Cuánto tiempo pasará antes que queden solamente 10 kg de sal en el
tanque?
41. Un tanque con capacidad de 500 gal, contiene originalmente 200 gal de agua con 100 lb de sal en solución. En él se vierte
agua con 1 lb de sal por galón con un gasto de 3 gal/min y la mezcla resultante se hace salir del tanque con un gasto de 2
gtal/min: Encuentre la cantidad de sal en el tanque en cualquier instante de tiempo, antes del instante en que la solución
comience a derramarse.
Parte VI: Circuitos Eléctricos (R − C ∼ L − R)
La segunda ley de Kirchhoff (circuito L − R − C), establece que las sumas de las caı́das de
di
1
voltaje a través del inductor (L dt
), del resistor (iR) y del capacitor C
q es igual al voltaje
aplicado (E(t)).
Si consideramos por L (henrys) a la inductancia, R (ohmios) la resistencia, a C (faradios)
a la capacitancia, i (amperios) la corriente, q (coulombs) a la carga y E (voltios) la fuerza
electromotriz (con R, C y L constantes), entonces lo anterior queda fielmente expresado,
como sigue
di
1
L + Ri + q = E(t)
(8)
dt
C
Entonces en un circuito L − R (no hay capacitor), la ecuación (8), nos queda
L
Sabemos que i(t) =
dq
dt ,
di
+ Ri = E(t)
dt
(9)
luego en un circuito R − C (no hay inductor), la ecuación (8), nos queda
R
dq
1
+ q = E(t)
dt
C
(10)
42. Resolver la ecuación (9), considerando E(t) = E0 y la corriente inicial i0 .
43. Resolver la ecuación (9) considerando, L = 3 henrys, R = 15 ohmios, y E(t) una
onda sinusoidal de amplitud 110 voltios y ciclo 60, e i = 0 para t = 0.
44. Utilice la ecuación (10), para hallar la corriente y la corriente de régimen estable a los 2 segundos si R = 8 Ω, q(0) = 0,
C = 16 f y la entrada de voltaje es sinusoidal con amplitud 10 y perı́odo π/64.
45. Un acumulador de 30 voltios, se conecta a un circuito en serie L − R con una inductancia de 0.1 henry y una resistencia
de 50 ohms. Determine la intensidad de corriente si la corriente inicial es cero. Halle la corriente cuando t → ∞.
46. Hallar el tiempo en que la corriente alcanza el 96 % de su valor lı́mite si la entrada de voltaje es constante, con R = 20 Ω,
L = 1 h y no hay corriente inicialmente.
47. Halle el voltaje constante aplicado a un circuito con R = 10 Ω y L = 2 h, de forma que la corriente alcance 97 % de su
valor lı́mite al segundo, si la corriente inicial es 2 amp. Calcule la corriente transitoria al cabo de medio segundo.
48. Hallar la corriente inicial tal que al medio segundo la corriente sea 6 amp, si R = 30 Ω, L = 4 h y se conecta a una
baterı́a de 110 voltios.
49. Hallar la resistencia, tal que, a los 2 segundos, la corriente alcanza el 0.6 % de su valor inicial, si C =
de voltaje es constante.
1
6
f y la entrada
20
50. Calcule la corriente de estado estable y la corriente a los 5 segundos, si R = 8 Ω, L = 6 h, i(0) = 0 y E(t) = 80 sen 100t.
Parte VII: Vaciado de tanques (Ley de Torricelli)
51. Un tanque cilı́ndrico de 5 pies de largo y 3 pies de radio, tiene un agujero en el fondo de 1 pie de radio y el tanque
inicialmente, contiene 3/4 partes de lı́quido. ¿Cuánto demorará en contener solamente 1/4 parte del lı́quido? (k = 0.62)
52. Un tanque tiene forma de cubo con arista de 2 metros y en su base hay un agujero de en forma de cuadrado de 1/10 de
unidad de diámetro. Si inicialmente el tanque está lleno en un 75 %, ¿cuándo contendrá la mitad de su capacidad? (k = 0.5)
53. A un tanque cónico invertido de 16 pies de altura que está lleno de agua se le hace un agujero de área 0.5 unidades en el
vértice. Hallar el tiempo de vaciado, si el ángulo entre dos generatrices cualesquiera sobre un mismo plano es 60◦ . (k = 0.6)
Parte VIII: Otra tanda mezcladita
54. Al final de un dı́a oscuro y lluvioso (6:30 pm aprox.), unas personas que se encontraban caminando por la Gran Avenida,
avistan a una persona que yace en el pavimento (Seguramente fue vı́ctima del hampa, a pesar del mega plan CARACAS
SEGURA murmuran los ociosos). Entre ellas, se encontraba el Dr. Yanohaguanto Chinkamiza, una eminencia en eso de la
anatomı́a patológica. Este le tomó la temperatura al cadáver y era de 29.4◦ C (recuerden que estos tipos siempre tienen unos
relojes ultrawao). A las dos horas que lo encontraron la temperatura del occiso era de 23.3◦ C, considerando una temperatura
ambiente de unos 20◦ C aproximadamente (según el super reloj del man este). Determine:
(a) La hora de la muerte del hombre, asumiendo que vivo tenı́a una temperatura de 37◦ C.
(b) Halle la temperatura del cuerpo en cualquier instante de tiempo, si asume que después cae un palo de agua que hace
t
variar la temperatura del ambiente de la forma: Tm (t) = 20 − e− 4 . (k es la misma)
55. El lago Erie (EEUU - Canadá) tiene un volumen de 458 km3 (¡¡ y una superficie igual a la República de Macedonia !!).
El flujo de entrada y salida se realizan ambos a razón de 175 km3 por año. Suponga que para el año 2000, su concentración
de contaminación era de 0.05% y que un tiempo después, la concentración de contaminantes que ingresa en el agua es de
0.01%. Suponiendo que el agua se mezcla perfectamente dentro del lago, calcule la fecha en la que la concentración de
contaminantes se reduce al 0.02%.
56. Hace poco, una comitiva de la ONU visitó la cárcel de Guantánamo en Cuba, donde se encontraban unas 587 personas,
entre presos y personal de custodia. La comitiva, estaba integrada por 15 personas (incluida Miss Universe -in English-). La
señorita en cuestión, mas roba cámara que polı́tico en campaña, estaba infectada con mononucleosis infecciosa (también
conocida como enfermedad del beso, fiebre glandular o enfermedad de Pfeiffer, causada por el virus Epstein-Barr - VEB
-). Al llegar la señorita en cuestión, empezó con su majaderı́a y su abrazadera (seguro pensaba que estaba haciendo su
entrada en el Teatro Kodak de Los Angeles) y por supuesto beso pa’ to el mundo. Determine cuántas personas estaban
infectadas hasta que los presos se molestaron y echaron a esa loca después de una hebdómada, conociendo el hecho de que
al dı́a siguiente de llegar, ya habı́an 158 enfermos.
57. Suponga que después de un caluroso partido de Softball, usted que se encuentra en envidiables condiciones fı́sicas (pero
hediondo a mono) se hallaba lo suficientemente sediento, como para tomarse el agua directamente de la botella (cosa por la
que su respectiva progenitora lo ha regañado toda la vida). Al llegar a la cocina y abrir la nevera, se da cuenta que el agua
que asumimos es filtrada, no estaba muy frı́a (unos 15◦ C), toma un poco e introduce la botella en la nevera con la intensión
de que otro beba su saliva. A los 5 minutos, vuelve a abrir la nevera e ingiere un sorbo del ya no tan preciado lı́quido, que
estaba un poco más frı́o (unos 10◦ C). Pasados otros cinco minutos, realiza un último intento y el agua ya se encontraba a
8◦ C. ¿A qué temperatura se encontraba la nevera?, asumiendo que la variación de la temperatura del agua durante el tiempo
que estuvo pegada a su boca es despreciable y el abre - cierra de la nevera, tampoco afectó la temperatura de la misma.
58. Cierto dı́a del mes de julio, la familia Zambrano se encontraba de picnic en el Junquito (vulgar atrangante de cochino
frito con hallaquitas). En el deguste de tan suculento manjar, se les olvido que no cerraron las llaves del fregadero y llegó el
agua cuando ellos estaban de paseo (a todo pobre .... le pasa eso). Al llegar a su hogar, se dieron cuenta que su cocina se
habı́a inundado, un espacio de unos 15 m2 , donde el agua alcanzó una altura de 20 cm. Procedieron a destapar el desagüe
(circular por supuesto!!!), cuyo diámetro, es de aproximadamente 10 cm. Determine el tiempo que tardó en vaciarse la cocina,
para proceder al coletazo final, suponiendo que la constante de fricción es 0.5.
59. Un acumulador de 30 voltios, se conecta a un circuito en serie L − R con una inductancia de 0.1 henrios y una resistencia
de 50 ohms. Determine la intensidad de corriente si la corriente inicial es cero. Halle la corriente cuando t → ∞.
21
60. Una cooperativa que se encarga de limpiar los vidrios de los edificios, contrata a una “matraca” de gordo de unos 160
Kg., donde, el arnés al cual estaba sujeto pesa 2.75 Kg. El gordo, después de un suntuoso almuerzo (aproximadamente 2250
gramos), se encontraba reposando la papita, y por supuesto, el andamio (que se encontraba colocado en el piso quince) se
partió en dos, ocasionando la posterior megacaida del gordo al vacı́o (una distancia considerable, ya que cada piso tiene unos
3.5 m). Determine aproximadamente, el tiempo que tardó el gordo en volverse papilla, considerando que la resistencia al
aire de tamaña humanidad es de 2 veces la velocidad instantánea.
61. Determine la corriente de estado estable, en un circuito cuya resistencia es de 5Ω, la capacitancia es de un sexto de
faradio (f ), la carga inicial es nula y la fuerza electromotriz, está dada por
E(t) = 15 sen 60t voltios
62. Sabemos que en las cárceles venezolanas hay un brutal e inhumano hacinamiento. Un dia haciendo una pesquisa en Yare
I, determinaron que en el pabellón de la muerte (Pabellón B - se le dice de la muerte, ya que por cualquier viento mal oliente
que sople mueren de asfixia -), se encontraba un recluso con una patulequera (chiripiorca según el chavo) y este decı́a, que le
habı́a pasado algo con la tensión. Midieron su temperatura y determinaron que se encontraba en los 39.5◦ C, lo cambiaron
al pabellón de las locas (Pabellón G) y al cabo de 2 minutos su temperatura disminuyó en 2◦ C. ¿A qé temperatura se
encontraba el Pabellón G?
63. Como siempre sucede en los barrios de Caracas, hay desadaptados sociales que llevan la marginalidad por dentro como
bandera. Un cierto dı́a, regresaba a su casa en el San Blas, un sujeto apodado “Er Chino” (se parecı́a a Yoshi Toshia - el de
la propaganda -). Este, venı́a de ese famoso lugar llamado Adrenalina (donde le tumbaron la moto, la cartera y la pechuga),
bueno, el asunto es que el tipo venı́a super amotinado y se encontro a Rin Tin Tin (el perro vagabundo del barrio) y le
ha metido la mamá de las patadas, por supuesto, el perro estiró la pata. Al tiempo, hizo acto de presencia “Er iluminao”
(no era Hermes por si acaso), el cual regresaba de Canadá (estuvo preso), subiendo las escaleras, miró al matorral y hallo
bien flaco y comido de ratas el cadaver del querido Rin Tin, decı́a: Chamo pana mio, te dieron bollo. Este antisocial, era
bien inteligente (acostumbraba hacer practicas forenses con los reclusos que quedaban de los motines) y se puso a medirle el
C1 4 al cánido en cuestión y determinó con sus equipos rudimentarios que habı́a perdido el 0.0015% del “C-catolce” (como el
decı́a). Adivine usted hace cuánto “Er Chino” le dió bollo al perro?
64. En este paı́s, últimamente hasta los chinos están pelando y nos damos cuenta, ya que, se está vendiendo una salsa de
soya “chimba” en un conocido mercado popular. Estos, utilizan un tanque que inicialmente contiene 200 litros de un lı́quido
al cual llaman, receta secreta (chin secleto) y donde se disuelven 40 gramos de un polvo granulado semejante a la sal (pero
de un aspecto poco agradable). Una mezcla que tiene un gramo del polvo por litro se bombea al tanque con una rapidez de
3 litros por minuto; la solución homogénea (salsa de soya medio rara) se bombea hacia afuera con la rapidez de 4 litros por
minuto. Encuentre la cantidad de gramos de polvo que parece sal, que hay en el tanque a los 30 minutos.
65. Erase una vez una famosa discoteca en un dı́a que es mejor no recordar, llegaron unos tipos limpios a rumbear. Estos
como no tenı́an dinero, compraban un trago y de cada trago tomaban cuatro personas, una de ellas (el que bebe y se rasca
primero - sólo bebió una vez -) tenı́a un extraño virus que comenzó a propagarse. A la media hora habı́an 10 limpios
infectados. Determine cuántos tragos habı́an comprado a la hora, cuando sacaron a ese poco de gente al hospital. Asuma,
que los tragos se compraban en forma progresiva, ya que la entrada a la discoteca se hace en grupos de cuatro, fueron
cuarenta limpios y uno de los infectados tomaba un trago del nuevo grupo.
66. Un obrero, sale de su casa a eso de las 6:30 am, como todos los dı́as. Para ir a la construcción, este señor debe abordar el
tren del metro en la estación Plaza Sucre (trayecto que le toma unos 15 minutos desde su casa) y desembarcar en la estación
Sabana Grande. Como todos sabemos, el metro es el gran desastre de Caracas y por supuesto estamos en una época del
año donde los calorones son propios de menopáusica prematura. El obrero, aborda el vagón en el que el aire no funciona y
con toda esa gente y los tufos respectivos, realmente hace calor. Al señor, le da una “yeyera” entre Colegio de Ingenieros
y Plaza Venezuela, debiendo accionar la alarma respectiva, muy a pesar de los insultos de los demás viajeros. Cuando es
atendido dentro del mismo vagón (aproximadamente a las 7:05 am), determinan que su temperatura corporal se encontraba
en los 39◦ C y el operador de la estación (irónico el muchacho) le manifiesta que realmente está enfermo, ya que el vagón se
encuentra a unos confortables 19◦ C. A los 5 minutos, ya el señor tenı́a 39.5◦ C. Determine si el señor estaba quebrantado de
salud al entrar al vagón.
67. Una persona infectada con un virus muy raro, ingresa al vagón del metro en Propatria y estornuda, volando gérmenes
por todo el vagón (como la mujer de la propaganda). Es de hacer notar, que según informaciones de la gente del metro en
un vagón caben aproximadamente 120 personas (yo creo que más -pregúntenle a la gente en Capitolio-) y este venı́a full. A
los seis minutos, el tren se detiene entre Plaza Sucre y Gato Negro y se escuchan 5 estornudos mas en diferentes puntos.
Asumiendo, que entre estaciones el tren se demora 2 minutos y nunca se bajó nadie, determine la cantidad de personas que
adquirieron una peste brutal al llegar a Chacaito.
“La educación consiste en que el hombre,
llegue a ser cada vez mas hombre”
Karol Wojtyla - Papa Juan Pablo II -
UNIDAD III
Ecuaciones de orden superior
•
•
•
•
•
•
•
•
Conjunto fundamental de soluciones
Reducción de orden
Ecuaciones homogéneas
Coeficientes indeterminados
Sistemas de Primer orden
Variación de paramétros
Ecuaciones de cauchy - Euler
Ejercicios adicionales
“Siempre sue~
na y apunta mas alto de lo que sabes que puedes lograr”
William Faulkner
23
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Práctica 3
2014
Prof. Andrés Pérez
Conjunto Fundamental de Soluciones
Comprobación e independencia de Soluciones
1. En los siguientes problemas, la familia de funciones dada es solución de la ecuación diferencial planteada. Halle las
constantes para escoger a un miembro de la familia que verifique el P.V.I.
1.1) y = c1 ex + c2 e−x
; (−∞, ∞) ;
y ′′ − y = 0
; y(0) = 0 ;
y ′ (0) = 1
1.2) y = c1 e4x + c2 e−x
; (−∞, ∞) ;
y ′′ − 3y ′ − 4y = 0
; y(0) = 1 ;
y ′ (0) = 2
1.3) y = c1 x + c2 x ln x
;
(0, ∞)
; x2 y ′′ − xy ′ + y = 0 ; y(1) = 3 ;
y ′ (1) = −1
2. Si y(t) = c1 cos ωt + c2 sen ωt, es la solución general de y ′′ + ω2 y = 0 en el intervalo (−∞, ∞), demuestre que una
solución que satisface las condiciones iniciales y(0) = y0 y y ′ (0) = y1 , es justamente
y(t) = y0 cos ωt +
y1
sen ωt
ω
3. Use la solución general del problema anterior para demostrar que la solución que satisfaga las condiciones iniciales
y(t0 ) = y0 y y ′ (t0 ) = y1 , es exactamente la solución del problema anterior desplazada t0 unidades.
4. Compruebe si los conjuntos de funciones son linealmente independientes (L.I.) en el intervalo (−∞, ∞).
4.1) f1 (x) = x
;
f2 (x) = x2
;
f3 (x) = 4x − 3x2
4.2) f1 (x) = 0
;
f2 (x) = x
;
f3 (x) = ex
4.3) f1 (x) = 5
;
f2 (x) = cos2 x
;
f3 (x) = sen2 x
4.4) f1 (x) = cos 2x ;
f2 (x) = 1
;
f3 (x) = cos2 x
4.5) f1 (x) = x
;
f2 (x) = x − 1
;
f3 (x) = x + 3
4.6) f1 (x) = 2 + x
;
f2 (x) = 2 + |x|
5. Responda las siguientes preguntas:
(a) Si el wronskiano W(f, g) es 3e4t y si f(t) = e2t , encuentre g(t).
(b) Si el wronskiano W(f, g) es t2 et y si f(t) = t, encuentre g(t).
(c) Si W(f, g) es el wronskiano de f y g y si u = 2f − g y v = f + 2g, encuentre el wronskiano W(u, v) de u y v en términos
de W(f, g).
(d) Si el wronskiano W(f, g) es t cos t − sen t y si u = f + 3g y v = f − g, encuentre W(u, v).
6. Verifique que y1 (t) = t2 y y2 (t) = t−1 , son soluciones de la ecuación diferencial t2 y ′′ − 2y = 0, para t > 0. Luego,
demuestre que C1 t2 + C2 t−1 , es también una solución de la ecuación diferencial para cualesquiera C1 y C2 .
√
′′
′ 2
7. Verifique que y1 (t) =
√ 1 y y2 (t) = t, son soluciones de la ecuación diferencial yy + (y ) = 0, para t > 0. Luego,
demuestre que C1 + C2 t, no es en general una solución de la ecuación diferencial. Explique por qué este resultado no
contradice el principio de superposición.
24
8. Compruebe que las funciones dadas forman un conjunto fundamental de soluciones de la ecuación diferencial dada en el
intervalo indicado. Forme la solución general.
8.1)
y ′′ − y ′ − 12y = 0
; e−3x
;
e4x
; (−∞, ∞)
8.2)
y ′′ − 4y ′ = 0
; cosh 2x
;
senh 2x
; (−∞, ∞)
8.3)
y ′′ − 2y ′ + 5y = 0
; ex cos 2x ;
ex sen 2x ; (−∞, ∞)
8.4)
4y ′′ − 4y ′ + y = 0
; ex/2
;
xex/2
; (−∞, ∞)
8.5)
x2 y ′′ − 6xy ′ + 12y = 0
; x3
;
x4
;
(0, ∞)
8.6)
x2 y ′′ + xy ′ + y = 0
; cos(ln x)
;
sen(ln x)
;
(0, ∞)
8.7)
y ′′ + 4y = 0
; cos 2t
;
sen 2t
; (−∞, ∞)
8.8)
y ′′ − 2y ′ + y = 0
; et
;
tet
; (−∞, ∞)
8.9)
x2 y ′′ − x(x + 2)y ′ + (x + 2)y = 0 ; x
;
xex
;
(0, ∞)
;
sen x
;
(0, π)
8.10) (1 − x cotan x)y ′′ − xy ′ + y = 0
; x
9. Considere la ecuación: y ′′ − y ′ − 2y = 0
(a) Demuestre que y1 (t) = e−t y y2 (t) = e2t , forman un conjunto fundamental de soluciones.
(b) Sean y3 (t) = −2e2t , y4 (t) = y1 (t) + 2y2 (t) y y5 (t) = 2y1 (t) − 2y3 (t). ¿Son también y3 (t), y4 (t) y y5 (t) soluciones de
la ecuación diferencial dada?
(c) Determine si cada uno de los siguientes pares, forma un conjunto fundamental de soluciones: {y1 (t), y3 (t)}, {y2 (t), y3 (t)},
{y1 (t), y4 (t)} y {y4 (t), y5 (t)}
10. Compruebe que cada una de las familias biparamétricas de funciones dadas en los siguientes problemas, sea la solución
general de la ecuación diferencial no homogénea en el intervalo indicado.
10.1) y ′′ − 7y ′ + 10y = 24ex
; y = c1 e2x + c2 e5x + 6ex
10.2) y ′′ + y = 2 sec x
; y = c1 cos x + c2 sen x + x sen x + cos x ln(cos x) ;
;
(−∞, ∞)
(− π2 , π2 )
10.3) y ′′ − 4y ′ + 4y = 2e2x + 4x − 12 ; y = c1 e2x + c2 xe2x + x2 e2x + x − 2
;
(−∞, ∞)
10.4) 2x2 y ′′ + 5xy ′ + y = x2 − x
;
(0, ∞)
; y = c1 x−1/2 + c2 x−1 +
1 2
15 x
− 16 x
11.
11.1) Compruebe que yp1 = 3e2x y yp2 = x2 + 3x son, respectivamente, soluciones particulares de
y ′′ − 6y ′ + 5y = −9e2x
y ′′ − 6y ′ + 5y = 5x2 + 3x − 16
y
11.2) Use la parte anterior para hallar soluciones particulares de
y ′′ − 6y ′ + 5y = 5x2 + 3x − 16 − 9e2x
y
y ′′ − 6y ′ + 5y = −10x2 − 6x + 32 + e2x
12.
12.1) Halle por simple inspección una solución particular de y ′′ + 2y = 10.
12.2) Halle por simple inspección una solución particular de y ′′ + 2y = −4x.
12.3) Halle una solución particular de y ′′ + 2y = 10 − 4x.
12.4) Determine una solución particular de y ′′ + 2y = 8x + 5.
25
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Práctica 4
2014
Prof. Andrés Pérez
E.D.O. de segundo orden homogéneas y no homogéneas
Parte I: Reducción de Orden
1. La función y1 (x) es una solución en los siguientes problemas. Use la reducción de orden para encontrar una segunda
solución y2 (x).
1.1)
y ′′ − 4y ′ + 4y = 0
; y1 = e2x
1.2)
y ′′ + 2y ′ + y = 0
;
y1 = xe−x
1.3)
y ′′ + 16y = 0
; y1 = cos 4x
1.4)
y ′′ + 9y = 0
;
y1 = sen 3x
1.5)
y ′′ − y = 0
; y1 = cosh x
1.6)
y ′′ − 25y = 0
;
y1 = e5x
1.7)
9y ′′ − 12y ′ + 4y = 0
; y1 = e2x/3
1.8)
6y ′′ + y ′ − y = 0
;
y1 = ex/3
1.9)
x2 y ′′ − 7xy ′ + 16y = 0 ; y1 = x4
1.10) x2 y ′′ + 2xy ′ − 6y = 0
;
y1 = x2
1.11)
xy ′′ + y ′ = 0
; y1 = ln x
1.12) 4x2 y ′′ + y = 0
;
y1 = x1/2 ln x
1.13)
x2 y ′′ − xy ′ + 2y = 0
; y1 = x sen(ln x)
1.14) x2 y ′′ − 3xy ′ + 5y = 0
;
y1 = x2 sen(ln x)
1.15)
xy ′′ − y ′ + 4x3 y = 0
; y1 = sen x2
1.16) x2 y ′′ − (x − 0.1875)y = 0 ;
√
y1 = x1/4 e2
x
2. La función y1 (x) indicada es una solución de la ecuación homogénea asociada. Aplique el método de reducción de
orden para determinar una segunda solución, y2 (x), de la ecuación homogénea y una solución particular de la ecuación no
homogénea dada.
2.1)
y ′′ − 4y ′ = 2
; y1 = e−2x
2.2) y ′′ + y ′ = 1
;
y1 = 1
2.3)
y ′′ − 3y ′ + 2y = 5e3x
; y1 = ex
2.4) y ′′ − 4y ′ + 3y = x
;
y1 = ex
Parte II: Ecuaciones Homogéneas
3. Encuentre la solución general de la ecuación diferencial dada.
3.1) 4y ′′ + y ′ = 0
3.2) 2y ′′ − 5y ′ = 0
3.3)
y ′′ − 36y ′ = 0
3.4) y ′′ + 8y ′ + 16y = 0
3.5) y ′′ − y ′ = 0
3.6) y ′′ + 9y ′ = 0
3.7)
3y ′′ + y ′ = 0
3.8) y ′′ − 4y ′ + 5y = 0
3.9) y ′′ − y ′ − 6y = 0
3.10)
y ′′ − 3y ′ + 2y = 0
3.11)
d2 y
dy
+8
+ 16y = 0 3.12) y ′′ + 9y = 0
dx2
dx
3.13)
y ′′ + 3y ′ − 5y = 0
3.14)
d2 y
dy
− 10
+ 25y = 0 3.15) y ′′ + 4y ′ − y = 0
2
dx
dx
3.16) y ′′ − 36y = 0
3.17)
12y ′′ − 5y ′ − 2y = 0
3.18)
3y ′′ + 2y ′ + y = 0
3.20) 3y ′′ + 2y ′ + y = 0
3.19) 2y ′′ + 2y ′ + y = 0
26
4. Resuelava los siguientes P.V.I.
4.1) y ′′ + 16y = 0 ;
y(0) = 2 ;
4.3) 4y ′′ − 4y ′ − 3y = 0 ; y(0)1 ;
y ′ (0) = −2
y ′ (0) = 5
(π)
4.2)
d2 y
+y=0 ;
dθ2
4.4)
d2 y
dy
−4
− 5y = 0 ; y (1) = 0 ;
dt2
dt
y
3
y′
=0;
(π)
3
=2
y ′ (1) = 2
5. Para cada una de las siguientes funciones, determine una ecuación diferencial de segundo orden con coeficientes constantes
cuya solución sea la función dada.
5.1)
y = c1 e3x + c2 e−4x
5.2) y = c1 senh 4x + c2 cosh 4x
5.3)
y = c1 sen 2x + c2 cos 2x
5.4) y = c1 ex + c2 xex
5.5)
y = e3x (c1 sen 4x + c2 cos 4x)
5.6) y = c1 e2x + c2 xe2x + c3 x2 e2x
Parte III: Ecuaciones no Homogéneas (Coeficientes Indeterminados)
6. Encuentre la solución general de cada una de las ecuaciones diferenciales dadas.
6.1)
y ′′ + y = cos 2x
6.2) 2y ′′ − 14y ′ = 10x − 6
6.3)
y ′′ − y = senh 2x
6.4)
y ′′ − 3y ′ + 2y = 2e−x
6.5) y ′′ + 2y ′ + 5y = 3 sen x
6.6)
y ′′ + 2y ′ + y = cos x + 3 sen 2x
6.7)
y ′′ − 4y ′ + 3y = xe2x
6.8) 2y ′′ + 4y ′ + 2y = e2x cos 2x
6.9)
y ′′ + 4y = xex − ex + 2e3x
6.12) y ′′ − 2my ′ + m2 y = sen mx
6.10)
y ′′ − 9y ′ = 5e−3x
6.11) y ′′ + 4y ′ + 5y = 10e−2x cos x
6.13)
y ′′ + 3y = x2 sen x
6.14) y ′′ + y = cos2 2x + sen2
6.16)
y ′′ + y = 4x cos x
6.17) y ′′ + 2y ′ + 5y = e−x (2x + sen 2x)
6.18) y ′′ + 5y ′ + 4y = 8x2 + 3 + 2 cos 2x
6.19)
y ′′ + 9y = x3 + 6
6.20) y ′′ + 2y ′ − 24y = 16 − (x + 2)e4x
6.21) y ′′ − 5y ′ = 2x3 − 4x2 − x + 6
x
2
6.15) y ′′ − 3y ′ + 2y = (x2 + x)e3x
Parte IV: Ecuaciones no Homogéneas (Variación de Parámetros)
7. Utilice el método de variación de parámetros para resolver las siguientes ecuaciones diferenciales.
7.1)
y ′′ + y = sec x
7.4)
y ′′ − 4y =
7.7)
3y ′′ − 6y ′ + 6y = ex sec x
e2x
x
7.10) y ′′ + 2y = sec x tan x
ex
1 + x2
7.2) y ′′ + y = tan x
7.3)
y ′′ − 2y ′ + y =
7.5) y ′′ + 3y ′ + 2y = sen ex
7.6)
y ′′ + 2y ′ + y = e−x ln x
√
7.8) 2y ′′ + 2y ′ + y = 4 x
7.9)
4y ′′ − 4y ′ + y = ex/2
7.11) y ′′ − 2y ′ + y = ex arctan x
7.12)
y ′′ − y = senh 2x
√
1 − x2
27
Parte V: Ecuaciones de Cauchy - Euler
8. Resuelva las siguientes ecuaciones diferenciales homogéneas de Cauchy - Euler.
8.1) x2 y ′′ − 2y = 0
8.2) 4x2 y ′′ + y = 0
8.3)
x2 y ′′ + xy ′ + 4y = 0
8.4) x2 y ′′ − 3xy ′ − 2y = 0
8.5) 3x2 y ′′ + 6xy ′ + 2y = 0
8.6)
2x2 y ′′ + 2xy ′ + y = 0
8.7) x2 y ′′ + 5xy ′ + 4y = 0
8.8) x2 y ′′ + 8xy ′ + 6y = 0
8.9)
x2 y ′′ − 7xy ′ + 41y = 0
9. Utilice el método de variación de parámetros para resolver las siguientes ecuaciones diferenciales de Cauchy - Euler.
9.1) x2 y ′′ − 4xy ′ = x4
9.2) 2x2 y ′′ + 5xy ′ + y = x2 − x
9.3) x2 y ′′ − xy ′ + y = 2x
9.4) x2 y ′′ − 2xy ′ + 2y = x4 ex
10. Use la sustitución x = et , para transformar la respectiva ecuación de Cauchy - Euler, en una ecuación con coeficientes
constantes. Resuelva la ecuación original a través de la nueva ecuación.
10.1)
x2 y ′′ + 9xy ′ − 20y = 0
10.2)
x2 y ′′ − 9xy ′ + 25y = 0
10.3)
x2 y ′′ + 10xy ′ + 8y = x2
10.4)
x2 y ′′ − 3xy ′ + 4y = ln x
10.5)
x2 y ′′ + 7xy ′ + 5y = x
Parte VI: Otra tanda de ecuaciones de orden dos
11. Ecuaciones en la que falta y: En una ecuación diferencial de segundo orden de la forma y ′′ = f(x, y), la sustitución
dy du
d2 y
du
u=
y
=
, genera una ecuación de primer orden de la forma
= f(x, u).
2
dx
dx
dx
dx
11.1)
x2 y ′′ + 2xy ′ − 1 = 0 ;
11.2)
xy ′′ + y ′ = 1
11.3)
y ′′ + x(y ′ )2 = 0
11.4)
2x2 y ′′ + (y ′ )3 = 2xy ′
; x>0
11.5)
y ′′ + y ′ = e−x
11.6)
x2 y ′′ = (y ′ )2
; x>0
x>0
12. Ecuaciones en la que falta x: Si una ecuación diferencial de segundo orden tiene la forma y ′′ = f(y, y ′ ), la variable
dy
independiente x no aparece explı́citamente, sólo a través de la variable dependiente y. Si se realiza la sustitución u =
,
dx
du
entonces se obtiene
= f(y, u).
dx
12.1) yy ′′ + (y ′ )2 = 0
12.2) y ′′ + y = 0
12.3) y ′′ + y(y ′ )3 = 0
12.4) 2y2 y ′′ + 2y(y ′ )2 = 1
12.5)
yy ′′ − (y ′ )3 = 0
12.6) y ′′ + (y ′ )2 = 2e−y
13. En los siguientes problemas de valor inicial, resuelva aplicando los métodos de los ejercicios (12) y (13).
13.1) y ′ y ′′ = 2
; y(0) = 1 ; y ′ (0) = 1
13.2) y ′′ − 3y2 = 0
; y(0) = 2 ; y ′ (0) = 4
13.3) (1 + x2 )y ′′ + 2xy ′ + 3x−2 = 0
; y(1) = 2 ; y ′ (1) = −1
13.4) y ′ y ′′ − x = 0
; y(1) = 2 ; y ′ (1) = 1
28
14. Resolver las siguientes ecuaciones diferenciales lineales homogéneas de segundo orden, con coeficientes constantes.
14.1)
y ′′ − y = 0
; y(0) = 1 ; y ′ (0) = 0
14.2) y ′′ − 7y = 0
; y(0) = 2 ; y ′ (0) = 0
14.3)
y ′′ − y ′ − 30y = 0
14.5)
y ′′ − 2y ′ + y = 0
14.7)
y ′′ + y = 0
14.8) y ′′ − 3y ′ − 5y = 0
14.9)
y ′′ + 2y ′ + 2y = 0
14.10)
14.4) y ′′ + 6y ′ + 9y = 0
; y(0) = 1 ; y ′ (1) = 1
14.6) y ′′ + 2y ′ + 3y = 0
y ′′ + y ′ + 41 y = 0 ; y(0) = 2 ; y ′ (1) = 1
15. En cada uno de los siguientes problemas, halle la solución de la ecuación diferencial dada.
15.1) y ′′ − 2y ′ − 3y = 3e2x
15.2) y ′′ + 2y ′ + 5y = 3 sen 2x
15.3) y ′′ − 2y ′ − 3y = 3xe−x
15.4) y ′′ + 2y ′ = 3 + 4ex sen 2x
15.5) y ′′ + 9y = x2 e3x + 6x
15.6) y ′′ + 2y ′ + y = 2e−x
15.7) 2y ′′ + 3y ′ + y = x2 + 3 cos x
15.8) y ′′ + y = 3 sen 2x + x cos 2x
16. En cada uno de los problemas, encuentre la solución general de la ecuación diferencial dada. En los problemas (16.7) y
(16.8), g(x) es una función continua arbitraria.
π
π
16.1) y ′′ + y ′ = tan x
; 0<x<
16.2) y ′′ + 9y = sec2 3x
; 0<x<
2
6
16.3) y ′′ + 4y ′ + 4y = x−2 e−2x
16.5) 4y ′′ + y = 2 sec
x
2
;
x>0
16.4) y ′′ + 4y = 3 cosec 2x
;
−π < x < π
16.6) y ′′ − 2y ′ + y =
16.7) y ′′ − 5y ′ + 6y = g(x)
;
0<x<
π
2
ex
1 + x2
16.8) y ′′ + 4y = g(x)
17. En cada uno de los problemas, compruebe que las funciones dadas y1 y y2 satisfacen la ecuación homogénea asociada;
entonces encuentre una solución particular de la ecuación no homogénea dada. En los problemas (17.7) y (17.8), g(x) es una
función continua arbitraria.
17.1)
x2 y ′′ − 2y = 3x2 − 1
; x>0
;
y1 (x) = x2
;
y2 (x) = x−1
17.2)
x2 y ′′ − x(x + 2)y ′ + (x + 2)y = 2x3
; x>0
;
y1 (x) = x
;
y2 (x) = xex
17.3)
xy ′′ − (1 + x)y ′ + y = x2 e2x
; x>0
;
y1 (x) = 1 + x
;
y2 (x) = ex
; 0<x<1
;
y1 (x) = x
;
y2 (x) = ex
17.4) (1 − x)y ′′ + xy ′ − y = 2(x − 1)2 e−x
17.5)
x2 y ′′ − 3xy ′ + 4y = x2 ln x
; x>0
;
y1 (x) = x2
;
y2 (x) = x2 ln x
17.6)
x2 y ′′ + xy ′ + (x2 − 41 )y = 3x3/2 sen x
; x>0
;
y1 (x) = x−1/2
;
y2 (x) = x−1/2 sen x
17.7)
x2 y ′′ + xy ′ + (x2 − 41 )y = g(x)
; x>0
;
y1 (x) = x−1/2 sen x ;
y2 (x) = x−1/2 cos x
; 0<x<1
;
y1 (x) = x
y2 (x) = ex
17.8) (1 − x)y ′′ + xy ′ − y = g(x)
;
29
18. Resuelva las siguientes ecuaciones de Cauchy - Euler.
18.1)
x2 y ′′ + 10xy ′ + 8y = x2
18.2)
x2 y ′′ − 4xy ′ + 6y = ln x2
18.3)
2x2 y ′′ − 3xy ′ − 3y = 1 + 2x + x2
18.4)
x2 y ′′ − 3xy ′ + 13y = 4 + 3x
18.5)
x2 y ′′ + 9xy ′ − 20y =
18.6)
x3 y ′′′ − 3x2 y ′′ + 6xy ′ − 6y = 3 + ln x3
18.7)
x2 y ′′ + xy ′ + 4y = sen(log x)
18.8)
x2 y ′′ − 2xy ′ + 2y = 3x2 + 2 log x
5
x3
Parte VII: Soluciones en series de potencias
19. Resuelva la ecuación diferencial dada por medio de una serie de potencia de x y verifique que a0 es arbitrario en cada
caso. Cuando sea posible compare la solución en serie con los métodos vistos en clase.
19.1)
y′ − y = 0
19.4) (1 − x)y ′ = y
19.2)
y ′ − xy = 0
19.3) y ′ = ex y
19.5)
y ′ − y = x2
19.6) y ′ + xy = 1 + x
2
20. En cada caso encuentre los cuatro primeros términos distintos de cero de cada una de las series de potencias LI alrededor
del origen. ¿Cuál espera sea el radio de convergencia para cada solución?
20.1)
y ′′ + (sen x)y = 0 20.2) ex y ′′ + xy = 0
20.3)
(cos x)y ′′ + xy ′ − 2y = 0 20.4) e−x y ′′ + log(1 + x)y ′ − xy = 0
21. Resuelva la ecuación diferencial dada por medio de una serie de potencias alrededor del punto x0 indicado. Encuentre
la relación de recurrencia; encuentre también los cuatro primeros términos de cada una de las soluciones LI (a menos que la
serie termine antes). De ser posible determine el término general de cada solución.
21.1) y ′′ − y = 0
x0 = 0
21.2)
y ′′ − xy ′ − y = 0
x=0
21.3) y ′′ − xy ′ − y = 0
x0 = 1
21.4)
(1 − x)y ′′ + y = 0
x0 = 0
21.5) (1 + x2 )y ′′ − 4xy ′ + 6y = 0
x0 = 0
21.6)
xy ′′ + y ′ + xy = 0
x0 = 1
21.7) 2y ′′ + xy ′ + 3y = 0
x0 = 0
21.8)
2y ′′ + (x + 1)y ′ + 3y = 0
x0 = 2
22. Encuentre todos los puntos singulares de la ecuación dada y en cada caso determine si son regulares o irregulares.
22.1) xy ′′ + (1 − x)y ′ + xy = 0
22.2) x2 (1 − x2 )y ′′ + 2xy ′ + 4y = 0
22.3) x2 (1 − x2 )y ′′ + (x − 2)y ′ − 3xy = 0
22.4) x2 (1 − x2 )y ′′ + x2 y ′ + 4y = 0
22.5) (1 − x2 )2 y ′′ + x(1 − x)y ′ + (1 + x)y = 0
22.6) 2x(x − 2)2 y ′′ + 3xy ′ + (x − 2)y = 0
22. Resuelva la siguiente EDO de segundo orden:
xy ′′ − (1 + x)y ′ + y = x2 e2x
para x > 0, siguiendo los siguientes pasos:
(a) Pruebe que x = 0, es punto singular regular de la EDO.
(b) Use el método de Frobenius, para encontrar un conjunto fundamental de soluciones de la ecuación diferencial (solución
transitoria).
(c) Halle la solución particular al caso no homogéneo (solución estable).
“Un individuo exitoso, es un so~
nador
que cree en sus sue~
nos”
Anónimo
UNIDAD IV
Aplicaciones de Orden dos:
•
•
•
Sistemas de Primer orden
Sistemas de Masa - Resorte
Circuitos LRC
“Todo aquel que tiene una razón para vivir, puede soportar cualquier forma de hacerlo”
Friedrich Nietzsche
31
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Práctica 5
2014
Prof. Andrés Pérez
Aplicaciones de E.D.O de Segundo Orden
Parte I: Sistemas de Primer orden
1. Resuelva el sistema de ecuaciones de Primer Orden dado, sujeto a las condiciones iniciales que se indican:
{
1.1)
{
1.3)
{
1.5)
{
1.7)
{
1.9)
{
x′1
x′2
= x1 + x2
= 4x1 − 2x2
x′1
x′2
= 2x1 − 5x2 − sen(2t),
= x1 − 2x2 + t,
x1 (0) = 0
x2 (0) = 0
1.4)
x′1
x′2
= 3x1 − 4x2 + et ,
= x1 − x2 − et ,
x1 (0) = 1
x2 (0) = −1
1.6)
x′1
x′2
= 3x1 − 2x2 − e−t sen(t)
= 4x1 − x2 + 2e−t cos(t)
x′1
x′2
= x1 + 2x2
= 4x1 + 3x2
1.2)
{
{
{
1.8)
{
1.10)
x′1 − x1 − x2 − 2et
x′2 − 4x1 + x2 + et
=
=
x′1
x′2
=
=
x1 − x2 − t2
x1 + 3x2 + 2t
x′1
x′2
=
=
4x1 − 2x2 + 2t
8x1 − 4x2 + 1
x′1
x′2
=
=
x1 − 5x2 ,
2x1 − 5x2 ,
x′1
x′2
0
0
x1 (0) = 1
x2 (0) = 0
= −4x1 + 2x2
= − 52 x1 + 2x2
Parte II: Aplicaciones de las ecuaciones de segundo orden
•
Sistemas de Masa - Resorte
Para los siguientes problemas debemos recordar que en el sistema inglés de medidas, la masa se mide en slugs, la distancia
pie
en pies y que un pie equivale a 12 pulgadas y la aceleración de gravedad está dada por 32 2 .
seg
2. Se suspende un peso de 10 libras de un resorte y lo alarga 2 pulgadas de su longitud natural. Halle la constante del
resorte.
3. Se cuelga de un resorte una masa de 41 de slug, con lo cual el resorte se alarga 6 pulgadas de su longitud natural. La masa
pie
se pone en movimiento de la posición de equilibrio con una velocidad inicial de 4 seg
, en la dirección hacia arriba. Halle el
movimiento resultante de la masa, si la fuerza debido a la resistencia del aire es −2x ′ libras.
4. Se suspende de un resorte una masa de 12 slug de tal manera que el resorte se alarga 2 pies de su longitud natural. La masa
se pone en movimiento sin velocidad inicial desplazándola 12 pie en dirección hacia arriba. Halle el movimiento resultante de
la masa , si el medio ofrece una de menos cuatro veces la velocidad instantánea en libras.
5. Se suspende un peso de 32 libras de un resorte, alargándolo 8 pies de su longitud natural. el peso se pone en movimiento
pie
hacia abajo. Halle el movimiento
desplazándolo 1 pie en dirección hacia arriba y dándole una velocidad inicial de 2 seg
resultante del peso si el medio ofrece una resistencia despreciable.
6. Se suspende una masa de 12 slug de un resorte que tiene una constante de 6 libra
pie . La masa se pone en movimiento
desplazándola 6 pulgadas por debajo de la posición de equilibrio sin velocidad inicial. Halle el movimiento resultante de la
masa, si la fuerza debido al medio es de menos cuatro veces la velocidad instantánea en libras.
32
7. Se suspende una masa de 1 slug de un resorte que tiene una constante de 8 libra
pie . La masa se pone en movimiento de la
posición de equilibrio sin velocidad inicial aplicándole una fuerza externa F(t) = 16 cos 4t. Halle el movimiento resultante de
la masa si la fuerza debida a la resistencia del aire es de menos cuatro veces la velocidad instantánea en libras.
8. Demuestre
que el perı́odo del movimiento de una vibración no amortiguada de una masa suspendida de un resorte vertical
√
L
es 2π g , en donde L es el alargamiento del resorte debido a la masa m y g es la aceleración de gravedad.
9. Una pesa de 4 libras se une a un resorte cuya constante es de 2 libra
pie . El medio presenta una resistencia al movimiento
numéricamente igual a la velocidad instantánea. Si la pesa se suelta de un punto a 1 pie arriba de la posición de equilibrio
pie
con una velocidad de 8 seg
hacia abajo, calcule el tiempo en que pasa por la posición de equilibrio. Encuentre el momento
en que la pesa llega a su desplazamiento extremo respecto a la posición de equilibrio. ¿Cuál es su posición en ese instante?
10. Un resorte de 4 pies√alcanza 8 pies al colgarle una pesa de 8 libras. El medio en el cual se mueve ofrece una resistencia
numéricamente igual a 2 veces su velocidad instantánea. Deduzca la ecuación del movimiento si la pesa se suelta de la
pie
posición de equilibrio con una velocidad de 5 seg
hacia abajo. Calcule el desplazamiento extremo y el tiempo en que lo
alcanza.
11. Una fuerza de 2 libras estira 1 pie un resorte. A este resorte se le une un contrapeso de 3.2 libras y el sistema se sumerge
en un medio que imparte una fuerza de amortiguamiento numéricamente igual al 40 % de su velocidad instantánea.
11.1) Deduzca la ecuación del movimiento si el contrapeso parte del reposo un pie arriba de la posición de equilibrio.
(√
)
11.2) Exprese la ecuación del movimiento en la forma x(t) = Ae−λt sen
ω 2 − λ2 t + ϕ
11.3) Calcule el primer momento en que el contrapeso pasa por la posición de equilibrio dirigiéndose hacia arriba.
12. Una pesa de 16 libras estira 83 de pie un resorte. Al principio, parte del reposo a 2 pies arriba de la posición de
equilibrio y el movimiento ocurre en un medio que presenta una fuerza de amortiguamiento numéricamente igual a la mitad
de la velocidad instantánea. Deduzca la ecuación del movimiento si la pesa está impulsada por una fuerza externa igual a
f(t) = 10 cos 3t.
•
Circuitos LRC
13. Un circuito LRC, con R = 6 Ω, C = 0.02 f y L = 0.1 h, tiene un voltaje aplicado de 6 volt. Suponiendo que no hay
corriente inicial y no hay carga inicial cuando se aplica por primera vez el voltaje, halle la carga resultante en el condensador
y la corriente del circuito.
14. Un circuito LRC, con R = 6 Ω, C = 10−2 f y L = 18 h, no tiene voltaje aplicado. Halle la corriente resultante en el
1
de coul y la corriente inicial es cero.
circuito si la carga inicial en el condensador es de 10
15. Un circuito LRC, con R = 5 Ω, C = 0.02 f y L = 0.1 h, no tiene voltaje aplicado. Halle la corriente resultante en
condiciones estables en el circuito.
16. Un circuito LRC, con R = 5 Ω, C = 0.02 f y L = 0.1 h, tiene un voltaje aplicado igual a E(t) = sen t volt. Halle la
corriente resultante en condiciones estables en el circuito.
17. Determine la carga y la corriente de estado estable en un circuito en serie LRC, cuando R = 2 Ω, C = 0.25 f y L = 1 h y
el voltaje está dado por E(t) = 50 cos t volt.
18. Determine la carga y la corriente de estado estable en un circuito en serie LRC, cuando R = 20 Ω, C = 0.001 f y L =
y el voltaje está dado por E(t) = 100 sen 60t + 200 cos 40t volt.
19. Determine la carga y la corriente de estado estable en un circuito en serie LRC, cuando R = 10 Ω, C =
el voltaje está dado por E(t) = 300 volt, donde q(0) = 0 coul e i(t) = 0 amp.
1
30
fyL=
5
3
1
2
h
hy
“Si quieres buscar la grandeza, olvı́dala y busca la verdad,
de ese modo hallarás ambas”
Johannes Eckhart
UNIDAD V
Transformada de Laplace:
•
•
•
•
Transformadas directas
Transformadas Inversas
Teoremas Relacionados
Aplicaciones
“La constancia quebranta los muros mas sólidos,
y vence los imposibles mas colosales”
Virgilio
34
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Práctica 6
2014
Prof. Andrés Pérez
Transformadas de Laplace y Aplicaciones
Transformadas de Laplace y Aplicaciones
1. Aplique la definición,
F(s) = L{f(t)} =
∫∞
e−st f(t) dt
0
para determinar directamente las transformadas de Laplace de las siguientes funciones
1.1) f(t) = t
1.2)
f(t) = t2
1.3)
f(t) = e3t+1
1.4)
f(t) = teat
1.5) f(t) = cos t
1.6)
f(t) = t2 senh at
1.7)
f(t) = sen2 t
1.8)
f(t) = t cos t
2. En los problemas siguientes trace la gráfica de la función dada. En cada caso, determine
trozos o ninguna de las dos cosas en el intervalo [0, 3].
2
, 0≤t≤1
t
t
2+t , 1<t≤2
(a) f(t) =
3−t
(b)
f(t)
=
6−t , 2<t≤3
1
2
2
t
, 0≤t≤1
t
1
(c) f(t) =
, 1<t≤2
1
(d)
f(t)
=
t−1
3−t
1
, 2<t≤3
si f es continua , continua por
, 0≤t≤1
, 1<t≤2
, 2<t≤3
, 0≤t≤1
, 1<t≤2
, 2<t≤3
3. Use los resultados de la tabla anexa a esta guı́a, para determinar las transformadas de Laplace de las siguientes funciones.
Ayuda: Tal vez necesite una integración por partes preliminar
3.3) f(t) = t − 2e3t
f(t) = t3/2 − 2e−10t
3.5) f(t) = 1 + cosh 5t
3.6) f(t) = sen 2t + cos 2t
f(t) = cos2 2t
3.8) f(t) = sen 3t cos 3t
3.9) f(t) = (1 + t)3
3.11) f(t) = t cos 2t
3.12)
f(t) = 3t +
3.4)
3.7)
3.10)
√
3.2) f(t) = 3t5/2 − 4t3
3.1)
t
f(t) = tet
f(t) = senh2 3t
4. Use los resultados de la tabla anexa a esta guı́a, para determinar las transformadas inversas de Laplace de las siguientes
transformadas.
1
2
3
4.2) F(s) = s−3/2
4.3) F(s) = − 5/2
4.1) F(s) = 4
s
s s
3s + 1
s2 + 4
4.4) F(s) =
1
s+5
4.5)
F(s) =
3
s−4
4.6)
F(s) =
4.7) F(s) =
2s − 3
s2 − 4
4.8)
F(s) =
10s − 3
25 − s2
4.9)
F(s) = 2s−1 e−3s
4.10)
F(s) =
s2
3s
−s−6
4.11) F(s) =
s2
2
+ 3s − 4
4.12)
F(s) =
2s2
2s − 1
+ 5s − 13
35
5. Utilice la fórmula
∫
eax cos bx dx =
eax
[a cos bx + b sen bx] + C
a2 + b2
para obtener L{cos kt}, directamente de la definición de la Transformada de Laplace.
6. Muestre que la función f(t) = sen(t2 ), es de orden exponencial cuando t → ∞, pero que su derivada no lo és.
7. En los problemas siguientes, trace la gráfica de la función dada en el intervalo [0, ∞)
(a) U(t − 1) + 2U(t − 3) − 6U(t − 4)
(b) (t − 3)U(t − 2) − (t − 2)U(t − 3)
(c) f(t − π)U(t − π) donde f(t) = t2
(d) f(t − 3)U(t − 3) donde f(t) = sen t
(e) f(t − 1)U(t − 2) donde f(t) = 2t
(f) (t − 1)U(t − 1) − 2(t − 2)U(t − 2) + (t − 3)U(t − 3)
8. Sea f(t) = 1 para 0 ≤ t ≤ a y f(t) = 0 si t > a (donde a > 0). Exprese a f en términos de funciones de paso unitario,
1 − e−as
para mostrar que L{f(t)} =
.
s
9. Sea f(t) = 1 para a ≤ t ≤ b y f(t) = 0 si t < a o t > b (donde b > a > 0). Exprese a f en términos de funciones de paso
e−as − e−bs
unitario, para mostrar que L{f(t)} =
.
s
10. En cada uno de los siguientes problemas, encuentre la transformada de Laplace de la función dada
, t≤2
, t<1
0
0
(a) f(t) =
(b) f(t) =
2
(t − 2)2 , t ≥ 2
t − 2t + 2 , t ≥ 1
,
t<π
0
t − π , π ≤ t ≤ 2π
(d) f(t) = U(t − 1) + 2U(t − 3) − 6U(t − 4)
(c) f(t) =
0
, 2 < t ≥ 2π
(e)
(f)
f(t) = (t − 3)U(t − 2) − (t − 2)U(t − 3)
f(t) = t − (t − 1)U(t − 1) ,
t≥0
11. En cada uno de los siguientes ejercicios, encuentre las transformadas de Laplace, haciendo uso de los Teoremas.
11.1)
11.4)
f(t) = t3 + 3 cos 2t
f(t) =
√
11.2)
f(t) = t2 sen 4t
11.3)
f(t) = 5e2t + 7e−t
∫t
2t
te
11.5)
2
f(t) = 2t cosh t
11.6)
x senh x dx
f(t) =
0
∫t
11.7)
f(t) = 2t2 e−t cosh t
11.8)
e3x cos x dx
f(t) =
0
12. En cada uno de los problemas, dibuje las funciones dadas y luego halle su transformada de Laplace.
{
1 si t ∈ [2k, 2k + 1)
t si 0 ≤ t ≤ 1
k = 0, 1, 2, 3, . . .
12.1) f(t) =
12.2) f(t) =
0 si
t>1
0 si t ∈ (2k − 1, 2k]
12.3)
12.5)
f(t) = t , si 0 ≤ t < 1 y además f(t + 1) = f(t)
f(t) = sen t , si 0 ≤ t < π y además f(t + π) = f(t)
1
12.4)
12.6∗ )
f(t) =
si
0≤t<1
−1 si
1≤t<2
f(t + 2) = f(t)
f(t) = 1 +
∞
∑
(−1)k U(t − k)
k=1
36
13. Usando la tabla anexa, halle la transformada inversa de Laplace de las siguientes transformadas.
13.1)
1
s+2
13.2)
2
(s − 2)2 + 9
13.3)
2s + 1
(s − 1)2 + 7
13.4)
1
s2 + 4
13.5)
s
(s + 1)2 + 5
13.6)
1
2s2 + 1
13.7)
4
(s − 1)3
13.8)
2s + 2
s2 − 2s + 2
13.9)
2s − 3
s2 + 2s + 10
14. Use completación de cuadrados, para hallar la transformada inversa de Laplace de las siguientes transformadas
14.1)
s2
1
− 2s + 2
14.2)
s2
s+3
+ 2s + 5
14.3)
s2
s
−s+
14.4)
17
4
s2
s+1
+ 3s + 5
15. Utilice la descomposición en fracciones simples para reescribir las siguientes transformadas y luego hallar la transformada
inversa de cada una.
15.1)
2s2
(s − 1)(s2 + 1)
15.2)
s2
1
−1
15.3)
2
(s +
1)2 (s
−
15.4)
1)2
(s −
s+1
+ 3s + 5)
3)2 (s2
16. Halle las transformadas inversas de Laplace de
16.1)
2s − 3
s(s2 − 4s + 13)
16.2)
2(s − 1)
s2 − s + 1
16.3)
s
2s2 + 4s +
16.4)
5
2
1
2(s − 1)(s2 − s + 1)
17. Determine f ∗ g(x) y g ∗ f(x), si f(x) = 4x y g(x) = e2x .
18. Use convoluciones para encontrar la transformada inversa de Laplace.
18.1)
1
(s − 1)(s − 2)
18.2)
1
s2
18.3)
2
s(s + 1)
{
}
1
1
s
19. Halle L
usando convoluciones, de dos maneras diferentes; Primero considere F(s) = 2 y G(s) = 2
s(s2 + 4)
s
s +4
1
1
y luego haciendo F(s) = y G(s) = 2
. Compare y concluya acerca de sus resultados.
s
s +4
20. Demuestre que para cualquier constante k, [kf] ∗ g(x) = k[f ∗ g](x).
−1
21. Halle L{g(x)}, para
{
21.1)
g(x) =
0
si
sen(x − 1) si
{
x<1
x≥1
21.2) g(x) =
0
si
x3 + 1 si
x<2
x≥2
22. Determine L−1 {F(s)} = f(t), para
22.1)
F(s) =
22.5)
F(s) =
s
e−πs
+4
22.2)
F(s) =
1 −s
e
s3
22.3)
F(s) =
2
e−2s
2
s −4
22.6)
F(s) =
s−2
e−s
2
s − 4s + 3
22.7)
F(s) =
s2
2(s − 1) −2s
e
− 2s + 2
s2
s
e−πs
2
s −9
22.4) F(s) =
22.8) F(s) =
s2
1
e−2s
+s−2
e−s + e−2s − e−3s
s
37
23. Supóngase que F(s) = L{f(t)}, existe para s > a ≥ 0. Entonces:
1 (s)
F
.
c
c
( )
1
t
(b) Demuestre que si k > 0, entonces, L−1 {F(ks)} = f
.
k
k
(a) Demuestre que si c > 0, entonces, L{f(ct)} =
(c) Demuestre que si a y b son constantes con a > 0, entonces, L−1 {F(as + b)} =
1 −bt/a
e
f
a
( )
t
.
a
24. En los siguientes problemas, use las propiedades del ejercicio anterior.
24.1)
F(s) =
2n+1 n!
sn+1
24.2)
F(s) =
2s + 1
2
4s + 4s + 5
24.3)
F(s) =
1
2
9s − 12s + 3
24.4)
F(s) =
e2 e−4s
2s − 1
25. Use las transformadas de Laplace para resolver los siguientes Problemas de Valor Inicial (P.V.I).
25.1)
y ′ + 2y = 0
y(0) = 1
25.2)
y ′ + 2y = 2
y(0) = 1
25.3)
y ′ + 2y = ex
y(0) = 1
25.4)
y ′′ − y = 0
y(0) = 1
y ′ (0) = 1
25.5)
y ′′ − y ′ − 6y = 0
y(0) = 1
y ′ (0) = −1
25.6)
y ′′ − y = sen x
y(0) = 0
y ′ (0) = 0
25.7)
y ′′ + 2y ′ − 3y = sen 2x
y(0) = 0
y ′ (0) = 0
25.8)
y ′′ + y ′ + y = 0
y(0) = 4
y ′ (0) = −3
25.9)
y ′′ + 2y ′ + 5y = 3e−2x
y(0) = 1
y ′ (0) = 1
25.10)
y ′′ + 5y ′ − 3y = U(x − 4)
y(0) = 0
y ′ (0) = 0
25.11)
y ′′′ − y = 5
y(0) = 0
y ′ (0) = 0
25.12)
y ′′ + ω2 y = cos 2t
y(0) = 1
y ′ (0) = 0 (ω2 ̸= 4)
25.12)
y ′′ − 2y ′ + 2y = cos t
y(0) = 1
y ′ (0) = 0
25.13)
y ′′ − 2y ′ + 2y = e−t
y(0) = 0
y ′ (0) = 1
25.14)
y ′′ + 2y ′ + y = 4e−t
y(0) = 2
y ′ (0) = −1
y(0) = 1
y ′ (0) = 0
y(0) = 0
y ′ (0) = 0
′′
{
25.15)
y + 4y =
25.16)
y ′′ + y =
{
1, 0 ≤ t < π
0,
t≥π
t,
0,
0≤t<1
t≥1
y ′′ (0) = 0
38
26. Use transformadas de Laplace para resolver los siguientes sistemas de ecuaciones.
′
y′ − z = 0
y +z=x
y − z′ = 0
z′ − y = 0
26.1)
26.2)
y(0) = 1
y(0) = 1
z(0) = 0
26.3)
26.5)
w ′ − w − 2y = 0
y ′ − 4w − 3y = −1
w(0) = 1
u ′′ + v = 0
u ′′ − v ′ = −2ex
u ′ (0) = 0
26.4)
y(0) = 2
u(0) = 0
v(0) = 0
26.6)
v ′ (0) = 2
z(0) = 1
w′ − y = 0
w + y′ + z = 1
w − y + z ′ = 2 sen x
u ′′ − 2v = 2
u + v ′′ = 5e2 x + 1
u ′ (0) = 2
w(0) = 1
y(0) = 1
z(0) = 1
u(0) = 2
v(0) = 1
27. Considere los siguientes circuitos cuyas funciones de entrada (o fuerza electromotriz), está dada por las gráficas adjuntas.
27.1)
27.3)
27.5)
• R = 10 Ω
• R = 5Ω
• C = 0.01 f
• C = 0.1 f
• L = 1h
27.2)
• L = 2h
• q(0) = 0 coul
• q(0) = 0.5 coul
• i(0) = 0 amp
• i(0) = 0.05 amp
• R = 8Ω
• R = 5Ω
• C = 0.01 f
• C = 0.02 f
• L = 4h
27.4)
• L = 2h
• q(0) = 0.2 coul
• q(0) = 0 coul
• i(0) = 0.3 amp
• i(0) =
• R = 10 Ω
• R = 6Ω
• C = 0.01 f
• C = 0.01 f
• L = 1h
27.6)
3
8
amp
• L = 4h
• q(0) = 0 coul
• q(0) = 0 coul
• i(0) = 0 amp
• i(0) = 0 amp
39
28∗∗ . Las transformadas de Laplace de determinadas funciones pueden hallarse de manera conveniente a partir de sus
desarrollos en series de Taylor.
(a) Usando la serie de Taylor para sen t
sen t =
∞
∑
(−1)n t2n+1
(2n + 1)!
n=0
y suponiendo que la transformada de Laplace de esta serie puede calcularse término a término, verifique que
L{sen t} =
(b) Sea
1
,
s2 + 1
sen t
t
f(t) =
1
s>1
,
t ̸= 0
,
t=0
Encuentre la serie de Taylor para f alrededor de t = 0. Suponiendo que la transformada de Laplace de esta función
puede calcularse término a término, verifique que
L{f(t)} = arctan
1
,
s
s>1
“Ten el coraje de hacer,
lo que te dice tu corazón y tu intuición”
Steve Jobs
Tabla de Transformadas
de Laplace
“No tengo talentos especiales, pero sı́ soy profundamente curioso”
Albert Einstein
41
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Tabla de TL
2014
Transformadas de Laplace
F(s)
f(t)
1
1
s
1
2
1
s2
t
3
1
, n = 1, 2, 3, . . .
sn
tn−1
(n − 1)!
4
1
,n>0
sn
tn−1
Γ (n)
5
1
s−a
eat
6
1
, n = 1, 2, 3, . . .
(s − a)n
tn−1 eat
(n − 1)!
7
1
,n>0
(s − a)n
tn−1 eat
Γ (n)
8
a
s2 + a2
sen at
s
+ a2
cos at
9
s2
10
a
(s − b)2 + a2
ebt sen at
11
s−b
(s − b)2 + a2
ebt cos at
12
s2
a
− a2
senh at
42
F(s)
f(t)
13
s
s2 − a2
cosh at
14
a
(s − b)2 − a2
ebt senh at
15
s−b
(s − b)2 − a2
ebt cosh at
16
1
, a ̸= b
(s − a)(s − b)
ebt − eat
b−a
17
s
, a ̸= b
(s − a)(s − b)
bebt − aeat
b−a
18
1
(s2 + a2 )2
sen at − at cos at
2a3
19
20
21
(s2
s
+ a2 )2
t sen at
2a
(s2
s2
+ a2 )2
sen at + at cos at
2a
(s2
s3
+ a2 )2
1
cos at − at sen at
2
22
s2 − a2
(s2 + a2 )2
t cos at
23
1
(s2 − a2 )2
at cosh at − senh at
2a3
24
s
(s2 − a2 )2
t senh at
2a
25
s2
(s2 − a2 )2
senh at + at cosh at
2a
43
F(s)
26
(s2
s3
− a2 )2
f(t)
1
cosh at + at senh at
2
27
s2 + a2
(s2 − a2 )2
t cosh at
28
1
2
(s + a2 )3
(3 − a2 t2 ) sen at − 3at cos at
8a5
29
30
(s2
s
+ a2 )3
t sen at − at2 cos at
8a3
(s2
s2
+ a2 )3
(1 + a2 t2 ) sen at − at cos at
8a3
31
s3
(s2 + a2 )3
3t sen at + at2 cos at
8a
32
aF1 (s) + bF2 (s)
af1 (t) + bf2 (t)
33
F
(s)
a
af(at)
34
F(s − a)
35
e−as F(s)
36
sF(s) − f(0)
f ′ (t)
37
s2 F(s) − sf(0) − f ′ (0)
f ′′ (t)
38
sn F(s) − sn−1 f(0) − sn−2 f ′ (0) − · · · − f(n−1) (0)
f(n) (t)
39
F ′ (s)
−tf(t)
40
F ′′ (s)
t2 f(t)
eat f(t)
{
f(t − a)U(t − a) =
f(t − a)
0
si
si
t>a
t<a
44
F(s)
f(t)
41
F(n) (s)
(−1)n tn f(t)
42
F(s)
s
∫t
f(u) du
0
∫t
F(s)
sn
43
···
∫t
0
∫t
0
0
∫t
F(s)G(s)
44
(t − u)n−1
f(u) du
(n − 1)!
f(u) dun =
f(u)g(t − u) du
0
∫∞
45
f(t)
t
F(u) du
s
46
1
1 − esT
1
F
s
48
( )
1
s
∫∞
t
∫∞
2
u−3/2 e−s
/4u
e−u
2
/4t
f(u) du
0
√
J0 (2 ut)f(u) du
n/2
∫∞
√
u−n/2 Jn (2 ut)f(u) du
0
(
)
F s + 1s
s2 + 1
1
√
2 π
∫∞
0
( )
1
F
sn+1
s
50
53
f(t) = f(t + T )
1
√
πt
1
49
52
e−su F(u) du
0
√
F( s)
s
47
51
∫T
∫t
√
J0 (2 u(t − u))f(u) du
0
F(u) du
f(t2 )
0
F(ln s)
s ln s
P(s)
Q(s)
P(s) = polinomio de grado inferior an
Q(s) = (s − a1 )(s − a2 ) . . . (s − an )
donde a1 , a2 , . . . , an son todas distintas
∫∞
0
tu f(u)
du
Γ (u + 1)
n
∑
P(ak ) ak t
e
Q ′ (ak )
k=1
“Las grandes expectativas, son la clave del éxito
Sam Walton
Apéndices
“La experiencia es algo que tenemos, después de haberla necesitado”
Gabriela Mistral
46
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Aplicaciones de las EDO’s de primer orden
Apéndice 1
2014
Prof. Andrés Pérez
Las aplicaciones de las ecuaciones diferenciales de primer orden, son muy diversas en situaciones fı́sicas y complejidad. En
este pequeño apartado, abordaremos algunas aplicaciones sumamente sencillas, sólo para ilustrar algunas de las situaciones
que podemos modelar, para ası́, incentivar el estudio de este campo de la matemática en cada una de sus respectivas áreas.
Al aplicar ecuaciones diferenciales en cualquiera de los numerosos campos en que son de utilidad, es necesario formular
primero la ecuación diferencial apropiada que describe, o modela, el fenómeno que se investiga, Cuando se construyen modelos
matemáticos, se debe reconocer que cada problema es distinto y que el modelado exitoso no es simplemente una habilidad
que pueda reducirse a una aplicación de una serie de reglas preestablecidas. Aunque la construcción del modelo en sı́ mismo
es algunas veces la parte mas difı́cil del problema, es posible enunciar algunos pasos de utilidad en el proceso de modelado:
1. Identificar las variables dependiente e independiente y asignar letras para representarlas, dejando claro el significado
de cada una de ellas. Muchas veces es útil asignar estos nombres en función del problema, donde a menudo la variable
independiente es el tiempo y por tanto, casi siempre está representada por t.
2. Elegir unidades de medición para cada variable, aunque estas son arbitrarias, usualmente se eligen por conveniencia, y
por pertinencia fı́sica. Al momento de elegir la medida debemos ser homogéneos.
3. Enunciar con claridad el principio básico que rige el problema que se investiga. Para ello es necesario el conocimiento
del objeto de estudio desde el punto de vista fı́sico (quı́mico, biológico, etc.), para ası́ manejar de forma óptima las
leyes y propiedades inherentes a él.
4. Expresar el principio o ley del paso 3, en términos de las variables que fueron declaradas en el paso 1. Es probable que
en algunos casos esto resulte difı́cil, en virtud de que se necesite introducir variables auxiliares o intermedias que luego
deban relacionarse con las variables primarias.
5. Asegurarse que cada término en la ecuación del modelo maneje las mismas unidades fı́sicas. Si las unidades concuerdan,
entonces, al menos la ecuación es dimensionalmente congruente, aunque esto no es prueba de veracidad para el modelo.
Las aplicaciones a estudiar las dividiremos en dos grupos, en función de su complejidad operacional:
• Aplicaciones que conducen a ecuaciones de variables separables.
• Aplicaciones que conducen a ecuaciones lineales.
0.1
Aplicaciones que conducen a ecuaciones de variables separables
• Decaimiento Radiactivo (Ley de Malthus)
Esta ley es justamente en honor al economista y polı́tico inglés Thomas Robert Malthus (1766-1834), quien fue uno
de los primeros en darse cuenta que la población crece como una razón geométrica, mientras que los medios de subsistencia
crecen de manera aritmética. Esta afirmación está plasmada en su ensayo sobre el Principio de Poblaciones, el cual, inspiró a
Darwin en la formulación de principio de selección natural. Malthus, muy religioso y creyente pensaba que esa diferencia en el
crecimiento de la población y las necesidades que ellas generaban, eran de procedencia divina y que forzarı́a a la humanidad a
ser más laboriosa e ingeniosa para lograr los medios de subsistencia. Darwin, no tan religioso, lo formuló como una situación
natural presente en todas las especies.
Básicamente los materiales radiactivos, obedecen a la siguiente ley.
“La variación de material radiactivo en cualquier instante de tiempo t, es proporcional a la cantidad de
material presente en el instante t”.
47
Si consideramos a R(t), como la cantidad de material radiactivo en el instante t, entonces, el modelo asociado a la ley
anterior queda expresado de la forma
dR
= kR
(11)
dt
donde k, es la constante de proporcionalidad y como el material radiactivo decae en el tiempo, podemos asumir que esta
constante es negativa. Este modelo sirve para muchos otros fenómenos, como por ejemplo los problemas de Interés Compuesto.
Separando variables en la ecuación (11), obtenemos que:
dR
dR
= kR =⇒
= kdt =⇒ ln(R(t)) = kt + ln C =⇒ ln
dt
R
(
R(t)
C
)
= kt
de donde
R(t) = Cekt ,
C>0
(12)
Si suponemos que existe una cantidad R0 en el instante t = 0, entonces, de (12) concluimos que, C = R0 y la gráfica asociada
al modelo está dada por
Observación 0.1.1. Quizá la única dificultad real en este tipo de problemas, radica en la comprensión de los datos, ya que,
las variables se definen casi siempre en tiempo presente y operacionalmente resulta sencilla de resolver.
Ejemplo 0.1.1. Inicialmente se tenı́an 100 mg de Torio 234. Al cabo de 6 horas, esa cantidad disminuyó en 3%. Calcule la
vida media de esa sustancia radiactiva.
Solución: Si T (t) representa la cantidad de Torio 234 en el instante de tiempo t, entonces, el problema que debemos resolver
es justamente
dT
= kT
(13)
dt
sujeto a las condiciones iniciales T (0) = 100 y T (6) = 97. Resolviendo (13), de la misma forma que se solucionó (11),
obtenemos que
T (t) = Cekt ,
C>0
(14)
y usando la primera condición inicial nos queda que C = 100 =⇒ T (t) = 100ekt , para hallar k usaremos la segunda condición
inicial, luego
1
97 = T (6) = 100e6k =⇒ e6k = 0.97 =⇒ k = ln(0.97) = k0 < 0
6
Ahora bien, calcular la vida media del material, significa que debemos encontrar el tiempo en el que la cantidad de material
inicial se reduce a la mitad, es decir, calcular un tiempo τ, tal que, T (τ) = 50. Entonces,
50 = T (τ) = 100ek0 τ =⇒ ek0 τ =
1
1
=⇒ τ =
ln(0.5) ≈ 137 horas z
2
k0
Ejemplo 0.1.2. Un reactor generativo transforma el Uranio 238, que es relativamente estable, en el isótopo radiactivo
Plutonio 239. Después de 15 años, se determina que el 0.043% de la cantidad inicial de Plutonio se ha desintegrado.
Determine la cantidad de Plutonio que queda al pasar 45 años.
Solución: Sea P(t) la cantidad de Plutonio en el instante t y además, consideremos que la cantidad inicial de Plutonio es
P0 , es decir, P(0) = P0 . Por consiguiente, al cabo de 15 años tenemos que P(15) = 99.957%P0 = 0.99957P0 . Entonces, el
problema que debemos resolver es el siguiente
dP
= kP
(15)
dt
48
sujeta a las condiciones anteriores. Bajo el mismo esquema de (11), la solución de (15) queda expresada por
P(t) = Cekt ,
(16)
C>0
y usando las condiciones iniciales obtenemos que
C = P0
y
k=
1
ln(0.99957) = k0 < 0
15
Luego, la cantidad de Plutonio a los 45 años, queda determinada por
P(45) = P0 e45k0 = P0 (0.99957)3 ≈ 0.9987105546P0 ≈ 99.87%P0
z
Un importante recurso en la investigación arqueológica es el fechado por radiocarbono, desarrollado por el quı́mico estadounidense Williard F. Libby (1908 - 1980), el cual nació en una zona rural de Colorado y asistió a la Universidad de California
en Berkeley. Desarrolló su método de fechado por carbono radiactivo en 1947 mientras se encontraba en la Universidad de
Chicago. Por su trabajo recibió el Premio Nobel en Quı́mica en 1960.
Este proceso se refiere a un medio para determinar la edad de restos de madera o vegetales y, en consecuencia de huesos
humanos o de animales o de artefactos encontrados enterrados a la misma profundidad. Esta técnica se basa en que los
restos de madera o vegetales contienen cantidades residuales de carbono 14, un isótopo radiactivo del carbono. Este isótopo
se acumula durante el lapso de vida de las plantas y comienza a decaer cuando mueren. Dado que la semivida del carbono es
larga (aproximadamente 5730 años - algunos usan 5600 o 5700 años - ), en un vegetal o animal quedan cantidades medibles
de carbono después de miles de años. Si sigue presente incluso una fracción diminuta de carbono 14, por medio de mediciones
de laboratorio es posible establecer con exactitud la proporción de la cantidad original que queda. Las técnicas actuales de
medición permiten el uso de este método para perı́odos de 50.000 años o más. Veamos un ejemplo
Ejemplo 0.1.3. Se analizó un hueso fosilizado y se determinó que contenı́a la centésima parte del Carbono 14. Determine
la edad del fósil.
Solución: Sea C(t) la cantidad de C14 en el instante t. Si C(0) = C0 , tenemos que por (12), nos queda
C(t) = C0 ekt
C0
1
, entonces, k = − 5600
ln 2 = k0 < 0.
2
1
Por tanto, para determinar la edad del fósil debemos encontrar un tiempo τ, tal que C(τ) = 100
C0 . Veamos
(
)
1
1
1
C0 = C(τ) = C0 ek0 τ =⇒ τ =
ln
≈ 37205.59466 años z
100
k0
100
donde, si usamos el hecho de que C(5600) =
• Interés Compuesto
Supóngase que se deposita una cantidad de dinero en un banco o en un fondo que paga intereses a una tasa anual r. El
valor S(t) de la inversión en cualquier instante de tiempo t, depende de la tasas de interés y de a frecuencia con que éste
se compone. Las instituciones financieras tienen diversas polı́ticas sobre la composición del interés: algunas lo componen
cada mes, otras cada semana e incluso algunas lo hacen a diario. Si se supone que la composición se da de manera continua,
entonces, es posible formular un problema con valor inicial que resulte sencillo y que describe el crecimiento de la inversión.
dS
La razón de cambio del valor de la inversión es
y esta cantidad es igual a la rapidez con que se acumula el interés, que
dt
es justamente la tasa de interés r multiplicada por el valor actual de la inversión S(t). Ası́
dS
= rS
dt
(17)
y supongamos además que conocemos el valor de la inversión en un momento dado, por ejemplo, S(0) = S0 . Entonces, la
solución del problema (17), da el saldo S(t) de la cuenta en cualquier momento t y este saldo tiene la forma
S(t) = S0 ert
(18)
Por tanto, una cuenta bancaria cuyo interés se compone continuamente, crece de manera exponencial. Ahora bien, comparemos este modelo con la situación que el interés se compone en intervalos de tiempo finitos. Si el interés se compone una vez
al año, entonces después de t años, se tiene que
S(t) = S0 (1 + r)t
49
Si se compone dos veces al año, entonces, luego de seis meses el saldo es S0 (1 + 2r ) y al final del año es S0 (1 + 2r )2 . Ası́
después de t años, nos queda
(
r )2t
S(t) = S0 1 +
2
(
r )nt
En general si el interés se compone n veces al año, obtenemos que: S(t) = S0 1 +
, donde
n
(
r )nt
lim S0 1 +
= S0 ert
n→∞
n
Volviendo al caso continuo, supongamos que es posible realizar depósitos o retiros además de la acumulación de intereses,
dividendos o ganancias de capital. Si se supone que los depósitos o retiros se realizan en montos constantes k, a plazo fijo,
entonces la ecuación (17), se reemplaza por:
dS
= rS + k
(19)
dt
donde k es positiva para depósitos y negativa para retiros. La ecuación (19) es lineal, con factor de integración e−rt de modo
que su solución general es
k
S(t) = Cert −
r
para satisfacer la condición inicial, se debe elegir C = S0 + kr . Entonces, la solución del problema es
S(t) = S0 ert +
k rt
(e − 1)
r
(20)
La primera parte corresponde a la parte de S(t) debida al rendimiento acumulado sobre la cantidad inicia S0 y el segundo
término es la parte debida al monto del depósito o retiro k.
• Poblaciones
Bajo condiciones ideales y en perı́odos cortos de tiempo, los modelos poblacionales obedecen a la misma ley de los materiales
radiactivos, ya que, cualquier población localmente y en un espacio de tiempo muy reducido tiene un crecimiento exponencial,
pero este modelo genera un margen de error bastante alto para t grande. A diferencia de los modelos radiactivos, en este
caso la constante k, puede ser positiva (crecimiento de la población).
Veamos un ejemplo.
Ejemplo 0.1.4. Un cultivo tiene una cantidad N0 de bacterias. pasada una hora la cantidad de bacterias presente es 32 N0 .
Si la rapidez de multiplicación de las bacterias, es proporcional al número de bacterias presentes en el instante t. Determine
el tiempo necesario para que el número de bacterias se triplique.
Solución: Sea N(t) el número de bacterias en el instante t, donde N(0) = N0 y N(1) = 23 N0 . Por el modelo presentado en
(11), la solución que se obtiene está dada por
N(t) = N0 ekt
donde k = ln(1.5) > 0. Luego, debemos buscar el tiempo τ en que N(τ) = 3N0 . Veamos
3N0 = N(τ) = N0 eτ ln(1.5) =⇒ τ =
ln 3
≈ 2.709511291 horas z
ln(1.5)
50
Estudiemos ahora un modelo mas eficiente para poblaciones.
• Modelo Demográfico (Ecuación Logı́stica o Ley de Verhulst)
Esta ecuación, se utiliza para describir el crecimiento de la población de una manera más precisa que la Ley de Malthus,
tomando en cuenta el decrecimiento de la población.
Para describir el modelo consideremos a P(t) como el tamaño de la población en el instante t. El modelo de crecimiento
exponencial comienza suponiendo que: dP
dt = kP, para cierto k > 0. En este modelo, la tasa especı́fica o relativa de
crecimiento (o disminución), definida por
( dP )
dt
(21)
P
se supone constante (igual a k). Es difı́cil encontrar casos reales de crecimiento exponencial durante largos perı́odos, por
ejemplo, por limitaciones del ambiente. Ası́, cabe esperar que la razón expresada por (21), disminuya a medida que P
aumenta. Luego, la hipótesis de que la tasa con que crece o decrece una población, sólo depende del número presente y no
de mecanismos dependientes del tiempo, se puede escribir como sigue
( dP )
dP
dt
= f(P)
ó
= Pf(P)
(22)
P
dt
La ecuación (22), se adapta a numerosos modelos demográficos de animales y se denomina Hipótesis de dependencia de
densidad.
Supongamos entonces que un medio es capaz de sostener, como máximo, una determinada cantidad C de individuos de
una población. A esta constante C, se le denomina Capacidad Máxima de Sustento. Entonces, f(C) = 0 y además,
supondremos que f(0) = r > 0.
La hipótesis mas sencilla, viene de suponer que f(P) es lineal, es decir,
f(P) = c1 P + c2
Si f(0) = r y f(C) = 0, tenemos que c2 = r y c1 = − Cr , luego, tenemos que f(P) = − Cr P + r. Por consiguiente, (22), se escribe
(
dP
r )
=P r− P
dt
C
(23)
de donde redefiniendo las constantes en (23), obtenemos
dP
= P (a − bP)
dt
(24)
y la ecuación (24), recibe el nombre de Ecuación Logı́stica o Ecuación de Verhulst.
Separando variables en la ecuación (24), nos queda que
dP
= dt
P(a − bP)
(
=⇒
Fracciones simples
1
a
P
+
b
a
a − bP
1
1
=⇒ ln |P(t)| − ln |a − bP(t)| = t + M =⇒ ln
a
a
=⇒
P(t)
= Neat
a − bP(t)
=⇒
despejando nos queda
P(t) =
(
)
dP = dt
P(t)
a − bP(t)
)
= at + aM
aNeat
aN
=
1 + bNeat
bN + e−at
donde N = eaM .
Si P(0) = P0 ̸=
a
b,
obtenemos que N =
P0
a−bP0
y por tanto, la solución nos queda expresada de la siguiente forma
P(t) =
Ahora, cuando t → ∞, tenemos que P(t) →
modelo.
a
b
aP0
bP0 + (a − bP0 )e−at
(25)
y si t → −∞, entonces, P(t) → 0. Veamos las gráficas asociadas a este
51
donde
a
2b
es el punto de inflexión de la gráfica de (25).
• Epidemias
Los problemas asociados a epidemias, son un claro ejemplo de las aplicaciones de la ecuación logı́stica, ya que, la diseminación de una enfermedad depende de los individuos portadores de un virus y también de los individuos no portadores.
Entonces, si x(t) representa al número de personas infectadas con un virus en el instante t y y(t) el número de personas sanas
en el instante t y la población consta de n individuos, tenemos que: x(t) + y(t) = n. Usualmente, las epidemias obedecen a
la siguiente ley:
“La velocidad de diseminación de una enfermedad, es proporcional tanto a la cantidad de individuos
infectados, como también a los no infectados”
Lo cual queda modelado por la siguiente ecuación
dx
= kxy
dt
(26)
dx
= kx(n − x)
dt
(27)
pero como y(t) = n − x(t), obtenemos de (26) que
Ejemplo 0.1.5. Suponga que un alumno es portador de un virus y regresa a su escuela, la cual posee una matrı́cula de 1000
estudiantes. Determine la cantidad de alumnos infectados 6 dı́as después, si se observa que al cuarto dı́a habı́an 50.
Solución: Sea x(t) el número de personas infectadas en el instante t y sabemos que el número total de estudiantes es 1000,
entonces, el problema que debemos resolver, según el modelo planteado en (27) está dado por
dx
= kx(1000 − x)
dt
sujeto a las condiciones iniciales x(0) = 1 y x(4) = 50. Entonces, separando variables en (28), nos queda
(
)
dx
1
1
1
= kdt
=⇒
+
dx = kdt
Fracciones simples 1000
x(1000 − x)
x 1000 − x
=⇒
1
x(t)
[ln |x(t)| − ln |1000 − x(t)|] = kt + C =⇒ ln
= 1000kt + 1000C
1000
1000 − x(t)
=⇒
x(t)
= MeKt ,
1000 − x(t)
donde M = e1000C y K = 1000k
despejando x(t), obtenemos que
x(t) =
1000eKt
1000MeKt
=⇒
x(t)
=
1 + MeKt x(0)=1
999 + eKt
y usando la otra condición inicial, nos queda
1000e4K
1000
=
=⇒ 1 + 999e−4K = 20
999 + e4K
1 + 999e−4K
(
)
19
1
19
=⇒ e−4K =
=⇒ K = − ln
= k0 > 0
999
4
999
50 = x(4) =
Entonces,
x(6) =
√
1000
1000 999
√
=
≈ 277 alumnos z
√
1 + 999e−6k0
999 + 193
(28)
52
• Reacciones Quı́micas
Supongamos que se combinan a gramos de la sustancia A, con b gramos de la sustancia B. Si para formar x(t) gramos de
la sustancia C, se necesitan N partes de A y M partes de B, los gramos de las sustancias A y B que quedan en el instante t,
son respectivamente
M
N
a−
x
y
b−
x
M+N
M+N
Según la Ley de Acción de Masas, la velocidad de reacción se aproxima a:
(
)(
)
M
N
dx
≈ a−
x
b−
x
dt
M+N
M+N
de donde podemos obtener
(
)(
)
M
N
dx
=k a−
x
b−
x
dt
M+N
M+N
(29)
introduciendo una constante de proporcionalidad k > 0. A la ecuación (29), se le denomina Reacción quı́mica de segundo
orden.
Ejemplo 0.1.6. Cuando se combinan dos sustancias quı́micas A y B se forma un compuesto C. La reacción entre ambas
es tal que, por cada gramo de A, se usan 4 gramos de B. Se observa, que a los 10 minutos se han formado 30 gramos del
producto C. Calcule la cantidad de C, en función del tiempo si la velocidad de la reacción es proporcional a las cantidades
de A y B que quedan y al principio hay 50 gramos de A y 32 gramos de B. ¿Qué cantidad del compuesto C hay a los 15
minutos? Analice la situación cuando t → ∞.
Solución: En este problema sólo plantearemos el modelo y le dejamos al lector la resolución de la ecuación diferencial.
Si por cada gramo de A, se usan 4 gramos de B, entonces,
(
dx
= k 50 −
dt
en virtud de (29), nos queda que
)(
)
1
4
x
32 − x
5
5
sujeta a las condiciones iniciales x(0) = 0 (ya que en el tiempo t = 0, no se han combinado las sustancias) y x(10) = 30 z
• Vaciado de Tanques
En hidrodinámica, la Ley de Torricelli establece que:
“La velocidad ν del flujo de agua a través de un agujero de bordes agudos en el fondo de un tanque, lleno
de agua hasta una altura (o profundidad) h, es igual a la velocidad de un objeto (en este caso una gota de
agua) que cae libremente desde una altura h”
Esto es justamente
ν=
√
2gh,
g = aceleración de gravedad
(30)
La expresión (30), se origina al igualar la energı́a cinética 12 mν2 , con la potencial mgh. Supongamos que un tanque está
parcialmente lleno de agua y se deja vaciar por gravedad, por un agujero en el fondo y queremos determinar la altura h en
el instante t.
√
Si el área transversal del agujero es A0 y √
la velocidad del agua que sale del fondo es ν = 2gh, el volumen de agua que
sale del tanque por unidad de tiempo es: A0 2gh. Entonces, si V(t) es el volumen del agua dentro del tanque en el instante
t, tenemos que
√
dV
= −A0 2gh
dt
Si el volumen V(t) = Aω h, en cualquier instante t, nos queda
dh
A0 √
=−
2gh
dt
Aω
(31)
Si Aω , no es constante, entonces depende de h, es decir Aω = A(h) y la ecuación (31) sigue funcionando. Cuando hay
fricción la ecuación (31), se transforma en
dh
A0 √
= −k
2gh
(32)
dt
Aω
donde 0 < k < 1 es la constante de fricción.
53
• Temperatura
Los problemas asociados a ganancia o pedida de calor a este nivel, generalmente son tratados por la Ley de Enfriamiento
de Newton. Dicha Ley establece que:
“La variación en la temperatura de un cuerpo en cualquier instante de tiempo t, es proporcional a la
diferencia entre la temperatura del cuerpo y la temperatura del medio ambiente”
Si T (t) es la temperatura del cuerpo en el instante t y Tm , es la temperatura del medio ambiente, obtenemos que la ley
queda representada por la ecuación
dT
= k(T − Tm )
(33)
dt
de donde es muy sencillo, obtener la solución
T (t) = Tm + Cekt
Observación 0.1.2. Es posible y fı́sicamente mas realista, conseguir problemas donde la temperatura del medio no sea
constante, en cuyo caso es probable que la ecuación diferencial que modela el fenómeno no sea de variables separables y
pueda resultar por ejemplo una ecuación lineal, pero claro está depende fuertemente de la función que modele la variación
de la temperatura del medio ambiente.
0.2
Aplicaciones que conducen a ecuaciones lineales
• Mezclas (Soluciones salinas)
Al mezclar dos soluciones salinas de distintas concentraciones, se da pie a una ecuación diferencial de primer orden, que
define la cantidad de sal que contiene la mezcla. Se supone que en el tanque no se crea ni se destruye sal, por tanto, las
variaciones en la cantidad de sal se deben únicamente al flujo de entrada y de salida
Si S(t) representa la cantidad de sal en el tanque en cualquier instante t, la rapidez con que cambia S(t) es la tasa neta
dada por
(
) (
)
dS
Tasa de entrada
Tasa de salida
=
−
(34)
de la sustancia
de la sustancia
dt
Ejemplo 0.2.1. Un tanque contiene 200 litros de un lı́quido en el cual se disuelven 30 gramos de sal (ver figura anexa).
Una salmuera que tiene un gramo de sal por litro se bombea al tanque con una rapidez de 4 litros por minuto; la solución
homogénea se bombea hacia afuera con la misma rapidez. Encuentre el número S(t) de gramos de sal que hay en el tanque
en un instante cualquiera.
Solución:
La tasa de entrada la podemos calcular como sigue:
gramo
litro
gramo
Tasa de entrada = 1
×4
=4
litro
minuto
minuto
Si S(t) es la cantidad de sal en el tanque en cualquier instante t, la tasa de salida es
S(t) gramo
litro
S(t) gramo
Tasa de salida =
×4
=
200 litro
minuto
50 minuto
Entonces la ecuación nos queda de la siguiente manera
dS
S(t)
=4−
dt
50
la cual es una ecuación lineal sujeta a la condición inicial S(0) = 30. Para encontrar a S(t) bastarı́a con resolver la ecuación
diferencial z
Ejemplo 0.2.2. En el instante t = 0, un tanque contiene Q0 lb de sal, disuelta en 100 gal de agua. Supóngase que en el
gal
sal
, con un gasto de r min
y que la mezcla que se homogeniza por agitación, se
tanque ingresa agua que contiene 41 lb de gal
drena del tanque con el mismo gasto. Formular el problema con valor inicial que describe este proceso de flujo. Encontrar
la cantidad de sal Q(t) presente en el tanque en cualquier instante de tiempo, ası́ como la cantidad QL que se encuentra
presente después d un tiempo muy largo. Si r = 3 y Q0 = 2QL , encontrar el tiempo T después del cual la concentración de
sal es 2% de QL o menor. Determinar además el gasto requerido para que el valor de T no exceda de 45 min.
54
Solución: Analicemos de forma análoga al anterior:
Tasa de entrada =
1 libra
galón
r libra
×r
=
4 galón
minuto
4 minuto
y además, dado que los gastos de entrada y salida son iguales, la cantidad de agua en el tanque permanece constante y como
la mezcla es homogénea es la misma concentración en cualquier lugar del tanque, entonces
Tasa de salida =
Q(t) libra
galón
rQ(t) libra
×r
=
100 galón
minuto
100 minuto
En consecuencia la ecuación diferencial está dada por:
dQ
r
rQ
= −
,
dt
4 100
Q(0) = Q0
Al considerar el problema en términos fı́sicos, podrı́a anticiparse que a la larga la mezcla presente en un principio en el tanque
libra
será sustituida prácticamente en su totalidad por la que ingresa cuya concentración es 14 galón
. Cabe esperar entonces, que
para un tiempo largo la cantidad de al en el tanque estarı́a cerca de 25 lb. También serı́a posible encontrar este valor para
QL , haciendo que Q ′ (t) = 0 en la EDO. Al resolver la ecuación, es sencillo verificar que
r
Q(t) = 25 + Ce− 100 t
y donde C = Q0 − 25, donde finalmente
r
r
Q(t) = 25(1 − e− 100 t ) + Q0 e− 100 t
Claramente, lim Q(t) = 25 = QL . Además, se puede inferir que Q(t) → 25 mas rápidamente cuando r se hace mas grande.
t→∞
Supóngase ahora que, r = 3 y que Q0 = 2QL = 50, entonces,
r
r
Q(t) = 25(1 − e− 100 t ) + 50e− 100 t =⇒ Q(t) = 25 + 25e−0.03t
Dado que 2% de 25 es 0.5, se desea encontrar el tiempo T en el cual Q(t) = 25.5 z
• Caı́da Libre y resistencia al aire
En ciertas circunstancias, un cuerpo de masa m que cae, se encuentra con una resistencia al aire que es proporcional a su
velocidad instantánea ν, es decir, Fr = kν, donde k es la constante de proporcionalidad. En este caso, si consideramos que
la dirección positiva es hacia abajo, tenemos que la fuerza neta Fn , está dada por Fn = P − Fr , donde P = mg es el peso.
Por otra parte, la segunda Ley de Newton, nos garantiza que Fn = m.a (masa × aceleración) y sabemos que la aceleración
es la derivada de la velocidad, entonces obtenemos que
m
dν
dν
k
= mg − kν =⇒
+ ν=g
dt
dt
m
la cual es una ecuación lineal.
• Circuitos en serie
Gustav Robert Kirchhoff (Königsberg, 12 de marzo de 1824 - Berlı́n, 17 de octubre de 1887) fue un fı́sico prusiano cuyas
principales contribuciones cientı́ficas estuvieron en el campo de los circuitos eléctricos, la teorı́a de placas, la óptica, la espectroscopı́a y la emisión de radiación de cuerpo negro. Kirchhoff, es responsable de dos conjuntos de leyes fundamentales, en la
teorı́a clásica de circuitos eléctricos y en la emisión térmica. Aunque ambas se denominan Leyes de Kirchhoff, probablemente
esta denominación es más común en el caso de las Leyes de Kirchhoff de la ingenierı́a eléctrica. Estas leyes se basan en la
conservación de la energı́a y la carga en los circuitos eléctricos y se usan para hallar corrientes y tensiones en cualquier punto
de un circuito y fueron descritas por primera vez por él en 1845. Ambas leyes de circuitos pueden derivarse directamente de
las ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracias a Georg Ohm su trabajo fue generalizado.
Es necesario definir ciertos componentes del circuito, antes de enunciar la ley de Kirchhoff. Veamos:
• la inductancia (L), es una medida de la oposición a un cambio de corriente de un inductor o bobina que almacena
energı́a en presencia de un campo magnético, y se define como la relación entre el flujo magnético (Φ) y la intensidad
de corriente eléctrica (i) que circula por la bobina y el numero de vueltas (N) de el devanado. Esta definición es de
poca utilidad porque es difı́cil medir el flujo abrazado por un conductor. En cambio, se pueden medir las variaciones
55
del flujo y eso sólo a través del voltaje inducido en el conductor por la variación del flujo. Con ello, llegamos a una
definición de inductancia equivalente pero hecha a base de cantidades que se pueden medir, esto es, la corriente, el
tiempo y la tensión:
∆i
VL = L
∆t
La inductancia siempre es positiva, salvo en ciertos circuitos electrónicos especialmente concebidos para simular inductancia negativa.
• La resistencia eléctrica de un objeto, es una medida de su oposición al paso de corriente. Descubierta por Georg
Ohm en 1827, la resistencia eléctrica tiene un parecido conceptual a la fricción en la fı́sica mecánica. La unidad de la
resistencia en el Sistema Internacional de Unidades es el ohmio (Ω). Su cantidad recı́proca es la conductancia, medida
en Siemens. Además, de acuerdo con la ley de Ohm la resistencia de un material puede definirse como la razón entre
la caı́da de tensión y la corriente en dicha resistencia, ası́:
R=
V
i
• la capacitancia o capacidad eléctrica, es la propiedad que tienen los cuerpos para mantener una carga eléctrica. La
capacitancia, también es una medida de la cantidad de energı́a eléctrica almacenada para un potencial eléctrico dado
y el dispositivo más común que almacena energı́a de esta forma es el condensador. La relación entre la diferencia de
potencial (o tensión) existente entre las placas del condensador y la carga eléctrica almacenada en éste, se describe
mediante la siguiente ecuación:
q
C=
V
En un circuito con el interruptor cerrado, la corriente en cualquier instante de tiempo se representa por i(t) y la carga
en el capacitor por q(t). Según la segunda Ley de Kirchhoff, el voltaje E(t) (Fuerza Electromotriz ) a través de un circuito
cerrado debe ser igual a la suma de las caı́das de voltaje en el mismo, es decir, el voltaje aplicado debe ser igual a la
suma de las caı́das de voltaje a través del inductor, el resistor y el capacitor.
Caı́das de voltaje
Unidades
•
•
•
•
•
•
E(t)
i(t)
q(t)
L
R
C
−→
−→
−→
−→
−→
−→
Voltios
Amperios
Coulombs
Henrys
Ohmios
Faradios
di
dt
• Resistor
−→ R i(t)
1
• Capacitor −→
q(t)
C
Relación i(t) ↔ q(t)
• Inductor
volt
amp
coul
h
Ω
f
i(t) =
−→
L
dq
dt
Entonces, la segunda Ley de Kirchhoff, queda fielmente expresada de la forma:
L
di
1
+ Ri + q = E(t)
dt
C
(35)
La ecuación (35), es una ecuación integro - diferencial para un circuito LRC, para la cual en este momento del curso
no disponemos de herramientas para resolverla (debemos esperar a ver Transformadas de Laplace). Entonces, por ahora,
debemos resolver circuitos en serie que sólo dependan del inductor - resistor o resistor - capacitor. Entonces:
Circuitos L ∼ R
L
di
+ Ri = E(t)
dt
Circuitos R ∼ C
R
1
dq
+ q = E(t)
dt
C
Ahora veamos un modelo proveniente de uno de los problemas mas famosos de la historia de la matemática, mas sin
embargo es un modelo no lineal.
56
• Problema de la Braquistocrona
El término Braquistocrona, proviene de los vocablos griegos braquistos, que significa el mas corto y cronos que significa tiempo. El problema consiste en encontrar la curva mas corta por la cual una partı́cula se deslizará sin fricción en el
tiempo mı́nimo desde un punto P hasta otro punto Q situado a un nivel inferior,
pero no directamente debajo del primero.
Este problema fue planteado por Johann Bernoulli en 1966 como un desafı́o a los matemáticos de se época. Entre quienes
hallaron soluciones correctas se cuentan el propio Johann, su hermano Jakob, Sir Isaac Newton, Gottfried Leibnitz y el
marqués de L’Hopital. Este problema es importante dentro de la matemática como uno de los precursores del cálculo de
variaciones.
Para resolver este problema tomar el origen en el punto superior P y considerar los ejes como en la figura. Entonces, es
posible demostrar que la curva de tiempo mı́nimo está dada por una función y = ϕ(x) que satisface la ecuación diferencial
(1 + y ′2 )y = k2
(36)
donde k2 es una constante positiva por determinar.
Entonces, responda las siguientes preguntas:
(a) Despeje y ′ de la ecuación (36). ¿Por qué es necesario tomar la raı́z positiva?
(b) Introduzca la nueva variable t, por medio de la relación: y = k2 sen2 t. Demuestre que la ecuación del inciso (a) asume
entonces la forma: 2k2 sen2 tdt = dx.
(c) Haciendo θ = 2t, demuestre que la solución de la ecuación anterior, para la cual x = 0 cuando y = 0 está dada por:
x=
k2
(θ − sen θ)
2
,
y=
k2
(1 − sen θ)
2
(37)
Las expresiones en (37), son las soluciones paramétricas de la ecuación (36) que pasa por (0, 0). Las gráficas de las
ecuaciones (37), se denominan cicloides.
57
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Apéndice 2
2014
Prof. Andrés Pérez
Ecuaciones de Clairaut y Lagrange
Antes de intentar resolver alguna ecuación de Clairaut o de Lagrange, se hace necesario estudiar algunos puntos importantes, para los efectos, de lograr tener clara la naturaleza de la respuesta esperada y poder dar una solución coherente y
razonada. Para ello, comenzaremos estudiando a la envolvente de una familia de curvas. Además, las soluciones de este tipo
de ecuaciones son las denominadas soluciones paramétricas, por consiguiente resulta conveniente manejar una teorı́a básica
de parametrizaciones de matemáticas III, de forma tal que la interpretación de dichas soluciones o la construcción de dichas
soluciones no resulte cuesta arriba.
0.3
Envolvente de una familia de curvas
Consideremos una ecuación de la forma
Φ(x, y, C) = 0
(38)
donde x e y son variables y C es un parámetro arbitrario.
Para cada valor del parámetro C, la ecuación (38), determina una curva en el plano xy y dando a C todos los valores
posibles, obtenemos una familia de curvas monoparamétrica.
Definición 0.3.1. Una curva L, se llama envolvente de una familia de curvas monoparamétrica, si en cada uno de sus
puntos toca una u otra curva de la familia.
Ejemplo 0.3.1. Si consideramos a la familia de curvas dada por las circunferencias (x − C)2 + y2 = r2 , con C ∈ R,
graficamente resulta sencillo determinar que las envolventes a esta familia están dadas por y = ±r.
Ahora bien, nos pudimos dar cuenta en el ejemplo anterior (ver Fig.2), que la envolvente a una familia de curvas no
necesariamente es única. Entonces, necesitamos generar un proceso que nos permita encontrar la o las envolventes a una
familia dada.
58
0.4
Busqueda de la ecuación de la envolvente de una familia dada
Consideremos a la familia de curvas dada en (8) y supongamos que esta familia tiene una envolvente cuya ecuación puede
escribirse de la forma y = φ(x), donde φ ∈ C1 (I), donde I es un intervalo abierto. Supongamos además que un punto M(x, y)
está sobre la envolvente, entonces, este punto también pertenece a cierta curva de (38), para algún valor de C, por tanto, el
parámetro C depende de la posición del punto, en consecuencia podemos escribir C = C(x, y). Luego, para todos los puntos
de la envolvente se verifica que
Φ(x, y, C(x, y)) = 0
(39)
Partiendo de la ecuación (39) de la envolvente, encontremos el coeficiente angular de la tangente a la envolvente en el
punto M(x, y), derivando (39) con respecto a x y considerando a y como función de x. Veamos
[
]
∂Φ ∂Φ ∂C
∂Φ ∂Φ ∂C dy
+
+
+
=0
∂x
∂C ∂x
∂y
∂C ∂y dx
o equivalentemente, tomando factor común a ΦC
′
[
Φx + y Φy + ΦC
]
∂C ∂C ′
+
y =0
∂x
∂y
(40)
Luego, el coeficiente angular de la tangente a la curva de la familia (38), en el punto M(x, y) se deduce de
Φx + y ′ Φy = 0
(41)
ya que C es constante en (38).
Podemos suponer que Φy ̸= 0, ya que, si Φy = 0, considerarı́amos a x como función de y (x = φ(y)). Ahora bien, puesto
que el coeficiente angular de la envolvente es igual al de la curva de la familia de las ecuaciones (40) y (41), se deduce que
[
]
∂C ∂C ′
ΦC
+
y =0
∂x
∂y
Pero como C(x, y) ̸= ctte en la envolvente, entonces
∂C ∂C ′
+
y ̸= 0
∂x
∂y
Entonces, para sus puntos es válida la ecuación
ΦC (x, y, C) = 0
(42)
Ası́, para determinar la envolvente se debe resolver el siguiente sistema en C
{
Φ(x, y, C) = 0
(43)
ΦC (x, y, C) = 0
Si eliminando C del sistema (43), obtenemos y = φ(x), donde φ ∈ C1 , siendo C = ctte en esta curva, entonces, y = φ(x) es
la ecuación de la envolvente.
Ejemplo 0.4.1. Consideremos nuevamente el ejemplo 0.3.1, entonces, debemos resolver el sistema
{
(x − C)2 + y2 = r2
−2(x − C) = 0
donde la segunda ecuación es la derivada con respecto a C de la primera. Luego, de la segunda obtenemos que x = C y
sustituyendo este valor en la primera nos queda que y = ±r, las cuales se verificaron gráficamente en el ejemplo 0.3.1.
59
Observación 0.4.1. Si y = φ(x), es el lugar geométrico de los puntos singulares de la familia (38), es decir, de los puntos
donde Φx = 0 y Φy = 0, entonces, las coordenadas de estos puntos también satisfacen el sistema (43).
En efecto, las coordenadas de los puntos singulares se pueden expresar en función del parámetro C de la ecuación (38), a
saber
x = λ(C) y y = µ(C)
luego, (38) nos queda
Φ(λ(C), µ(C), C) = 0
Derivando esta expresión, con respecto a C, obtenemos
Φx
dλ
dλ
+ Φy
+ ΦC = 0
dC
dC
y como estos puntos son singulares, tenemos que Φx = 0 = Φy , por tanto también se cumple (42).
Por consiguiente, el sistema (43), define a la envolvente, o bien a el lugar geométrico de los puntos singulares de (38), o
bien a la combinación de ambas. Entonces, resulta necesario determinar si los puntos que satisfacen (43) son de la envolvente
o son singulares.
Ejemplo 0.4.2. Hallar la envolvente de la familia de rectas
x cos α + y sen α − p = 0
donde α es un parámetro y p > 0 y fijo.
Solución: Derivando con respecto a α, obtenemos que
Dα [x cos α + y sen α − p = 0] =⇒ −x sen α + y cos α = 0 =⇒ x sen α = y cos α
(44)
de donde el sistema que debemos resolver está dado por
x cos α + y sen α = p
x sen α = y cos α =⇒ y = x sen α
cos α
sustituyendo la segunda en la primera, obtenemos que x = p cos α y sustituyendo esto en (44), nos queda que y = p sen α.
Por tanto,
x2 + y2 = (p cos α)2 + (p sen α)2 = p2
De donde la envolvente está dada por x2 + y2 = p2 .
Ejemplo 0.4.3. Hallar la envolvente y el lugar geométrico de los puntos singulares de la familia
2
(y − C)2 − (x − C)2 = 0
3
Solución: Derivando con respecto a C, obtenemos
60
2
DC [(y − C)2 − (x − C)2 = 0] =⇒ y − C − (x − C)2 = 0
3
por tanto el sistema está dado por
{
(y − C)2 − 23 (x − C)2 = 0
de donde
y − C − (x − C)2 =[ 0 =⇒ y − ]C = (x − C)2
2
nos queda que (x − C)3 x − C −
= 0, lo cual nos genera dos
3
2
soluciones: y = x (puntos singulares) y y = x − (envolvente).
9
0.5
Soluciones singulares de la Ecuaciones Diferenciales Ordinarias de primer
orden
Supongamos que la ecuación diferencial
(
dy
F x, y,
dx
)
(45)
=0
tiene como integral general (solución general) a la ecuación (38) y supongamos que esta familia de curvas tiene una envolvente.
Por consiguiente, en cada punto común la envolvente y cada curva de la familia tienen el mismo valor en las magnitudes
x, y, y ′ , pero las magnitudes x, y, y ′ , satisfacen (45), por tanto, la abscisa, la ordenada y el coeficiente angular de cada punto
de la envolvente, son también solución de (45). Entonces, la envolvente es también una solución de (45), pero no es en general
una curva de la familia (38), es decir, su ecuación no se puede deducir de (38), para algún valor de C, luego la envolvente es
una solución singular de (45).
Ejemplo 0.5.1. Hallar la o las solución(es) singular(es) de la ecuación
y2 (1 + (y ′ )2 ) = r2 ,
r>0
Solución: Despejando y ′ , obtenemos
√
r2 − y2
dy
y
=±
=⇒ ± √
dy = dx =⇒ (x − C)2 + y2 = r2
2
dx
y
r − y2
donde y = ±r no se obtienen de la general, pero resulta muy sencillo verificar que son soluciones de la E.D.O.
0.6
Ecuación de Clairaut
La ecuación de Clairaut, es una ecuación de la forma
dy
y=x
+ψ
dx
o equivalentemente
(
dy
dx
)
(46)
y = xy ′ + ψ (y ′ )
donde ψ es una función conocida de y ′ de clase C1 . Esta ecuación, se le atribuye al francés Alexis Claude Clairaut
1713 - 1765. La manera de obtener la integral general de la ecuación (46), es introducir un parámetro auxiliar. Para ello,
dy
consideraremos
= p, entonces, (46) nos queda
dx
y = xp + ψ(p)
(47)
Si derivamos la ecuación (47), con respecto a x, teniendo en cuenta que
p=p+x
dp
dp
+ ψ ′ (p)
dx
dx
dy
= p es una función de x, obtenemos
dx
61
o equivalentemente
dp
[x + ψ ′ (p)] = 0
dx
De donde se desprenden dos posibilidades
dp
=0
dx
x + ψ ′ (p) = 0
(48)
(49)
De (48), obtenemos que p = C, C ∈ R, por lo cual (47) se reescribe como
(50)
y = xC + ψ(C)
que desde el punto de vista geométrico representa una familia de rectas. De (49) encontramos que podemos escribir a p como
función de x, es decir, p = p(x). Si lo introducimos en (47), nos queda
(51)
y = xp(x) + ψ[p(x)]
la cual es fácil demostrar que satisface (46). Veamos, sabemos que
dy
dp
= p + [x + ψ ′ (p)]
=p
dx
dx
Ahora, introduciendo (51), en (46), obtenemos que en ambos lados de la ecuación (46) la expresión que queda es x + ψ(p).
La solución (51), no se puede obtener a partir de la integral general (50), para algún valor de C, por tanto, (51) es una
solución singular de (46) y se obtiene eliminando el parámetro p del sistema
{
y = xp + ψ(p)
x + ψ ′ (p) = 0
o equivalentenmente, eliminando C del sistema
{
y = xC + ψ(C)
x + ψ ′ (C) = 0
Luego la solución singular de Clairaut, determina una envolvente a la familia de rectas dada en (50).
Ejemplo 0.6.1. Halle la integral general y singular de la ecuación y = xy ′ + (y ′ )2 .
Solución: La ecuación diferencial planteada, es de la forma (46), con ψ(t) = t2 , luego introduciendo el parámetro auxiliar
y ′ = C, C ∈ R, obtenemos que la integral general está dada por
y = xC + C2
Derivando esta ecuación con respecto a C, nos queda
[
]
DC y = xC + C2 =⇒ x + 2C = 0
Por consiguiente el sistema que debemos resolver está dado por
y = xC + C2
x + 2C = 0 =⇒ x = −2C =⇒ y = −2C2 + C2 =⇒ y = −C2
Elevando al cuadrado la primera de las resaltadas, obtenemos que x2 = 4C2 , de donde
2
x2
4
= C2
y sustituyendo esta
expresión en la segunda de las resaltadas, nos queda que y = − x4 , la cual es la solución singular, ya que es imposible
obtenerla de la integral general.
62
Ejemplo 0.6.2. Hallar las integrales general y singular de
y = xy ′ + √
ay ′
1 + (y ′ )2
Solución: La E.D.O. planteada evidentemente tiene la forma (46), entonces, tomemos y ′ = C la cual nos indica que la
integral general es de la forma
aC
y = xC + √
(52)
1 + (C)2
Derivando (52) con respecto a C y considerando ψ(C) = √
[
aC
aC
,
1+(C)2
obtenemos
√
a 1 + C2 −
]
DC y = xC + √
1 + (C)2
=⇒ 0 = x +
1+
2
√aC
1+C2
C2
Simplificando esta última expresión se obtiene que
a
x = −√
(1 + C2 )3
Sustituyendo esta última expresión en (52), nos queda que
aC3
y= √
(1 + C2 )3
Ahora bien, elevando estas dos expresiones a la 2/3 y sumando los resultados, obtenemos que
x2/3 + y2/3 =
a2/3
a2/3 C2
+
= a2/3
2
1+C
1 + C2
Luego la solución singular es justamente el astroide dado por
x2/3 + y2/3 = a2/3
63
0.7
Ecuación de Lagrange
Una ecuación de Lagrange, es una ecuación de la forma
y = xφ(y ′ ) + ψ(y ′ )
(53)
donde φ y ψ, son funciones conocidas de y ′ de clase C1 . Esta ecuación se le atribuye a Joseph - Louis Lagrange 1736 1813.
Esta ecuación es lineal con respecto a x e y y además, es de hacer notar que la ecuación de Clairaut es una caso particular
de la ecuación de Lagrange, considerando el caso φ(y ′ ) ≡ y ′ . Análogamente, esta ecuación se resuelve introduciendo un
parámetro auxiliar p.
Consideremos entonces y ′ = p, luego la ecuación (??) se escribe como
y = xφ(p) + ψ(p)
(54)
Derivando a la ecuación (54), con respecto a x, obtenemos
p = φ(p) + xφ ′ (p)
dp
dp
dp
+ ψ ′ (p)
= φ(p) +
[xφ ′ (p) + ψ ′ (p)]
dx
dx
dx
o equivalentemente
p − φ(p) =
dp
[xφ ′ (p) + ψ ′ (p)]
dx
(55)
Si p = p0 , entonces, p0 − φ(p0 ) = 0, ya que dp
dx = 0. Ahora, la solución corresponde para cada valor de p = p0 , es decir,
dy
dx = p0 , que es una función lineal de x. Para hallar esta función, es suficiente sustituir en la ecuación (54), el valor p = p0 ,
la cual genera
y = xφ(p0 ) + ψ(p0 )
Si esta solución no se deduce de la solución general, para cualquier valor de p0 , esta serı́a la solución singular de la ecuación
(53).
Encontremos ahora la solución general. Para ello, escribamos la ecuación (55), considerando a x como función de p, de la
siguiente manera
dx
φ ′ (p)
ψ ′ (p)
−
x=
(56)
dp p − φ(p)
p − φ(p)
La ecuación (56), es entonces una ecuación diferencial lineal de x en p, cuya solución está dada por
x = ω(p, C)
(57)
64
Eliminando p, del sistema formado por las ecuaciones (54) y (57), dado por
{
y = xφ(p) + ψ(p)
x = ω(p, C)
obtenemos la integral general Φ(x, y, C) = 0 de la ecuación (53).
Ejemplo 0.7.1. Halle la integral general y la singular de la ecuación diferencial
y = x(y ′ )2 + (y ′ )2
Solución: Tomando y ′ = p, obtenemos que la E.D.O. se reescribe de la forma
y = xp2 + p2
Derivando esta última expresión con respecto a x, nos queda
p = p2 + 2xp
dp
dp
dp
+ 2p
=⇒ p − p2 = 2p [x + 1]
dx
dx
dx
(58)
Dado que p = p2 , cuando p = 0, 1, esto nos da dos soluciones lineales
y=0
y
y=x+1
las cuales determinaremos más adelante que tipo de soluciones son.
Para hallar la solución general debemos resolver la ecuación diferencial lineal en la variable x, que se obtiene de (58).
Veamos
dx
2p
2p
C2
−
=
=⇒
x
=
−1
+
dp p − p2
p − p2
(p − 1)2
de donde se obtiene que
√
C
x+1=
p−1
C2 p2
y y = (x + 1)p =
=
(p − 1)2
2
(
Cp
p−1
)2
(
)2
Cp
= C+
p−1
de donde obtenemos que
(
√
)2
y= C+ x+1
la cual es la solución general. Ahora bien, y = 0 no se puede obtener de la solución anterior para ningún valor de C, luego
y = 0 es la solución singular y y = x + 1, que se obtiene con C = 0, es una solución particular.
65
UNEXPO “ Antonio José de Sucre”
Vice-Rectorado “Luis Caballero Mejı́as”
Departamento de Ciencias Básicas
Matemáticas IV (11044)
Apéndice 3
2014
Prof. Andrés Pérez
Series de Potencias
0.8
Series de Potencias
Definición 0.8.1. Sea x una variable real. Una serie de potencias en x es una serie de la forma:
∞
∑
an xn = a0 + a1 x + a2 x2 + · · · + an xn + · · ·
n=0
donde ak ∈ R para todo k ∈ Z+ .
∑
Teorema 0.8.1. Si
an xn es una serie de potencias, entonces, se cumple una sola de las afirmaciones siguientes:
1. La serie converge solo para x = 0
2. La serie es absolutamente convergente para todo x
3. Existe un número positivo r, tal que la serie es absolutamente convergente para |x| < r y divergente para |x| > r
Ejemplos 0.8.1. Determine el radio de convergencia de las siguientes series de potencias
1)
∞
∑
n n
x
5n
2)
n=1
∞
∑
xn
n!
n=1
3)
∞
∑
n
x n!
4)
n=1
∞
∑
xn
√
n
n=1
Solución: Para el primer ejemplo, consideraremos el Criterio de la Raı́z n-ésima dado para series alternadas, a saber:
√
√
√
n
√
n n
n
n n
|x|
:=1 |x|
n
n
nn
lim
x
|x
|
=
lim
|x| = lim
=
lim
n
n
n→∞
n→∞ 5
n→∞
5
5
5 n→∞
5
Ahora bien, como queremos hallar el radio de convergencia, hacemos que este resultado sea menor que 1 (como lo indica el
criterio), entonces,
|x|
< 1 =⇒ |x| < 5 =⇒ −5 < x < 5
5
donde el radio de convergencia es 5 y el intervalo de convergencia es (−5, 5). Esta convergencia es absoluta, lo cual cumple
con el numeral 3 del Teorema.
Para el segundo ejemplo, podemos observar que hay un factorial, por tanto, tomaremos el criterio del cociente enunciado
para series alternadas. Veamos
lim
n→∞
xn+1
(n+1)!
xn
n!
= lim
n→∞
n!
xn+1
|x|
·
=0
= lim
n→∞ n + 1
xn
(n + 1)!
para cualquier x ∈ R. En consecuencia, el radio de convergencia es infinito y el intervalo de convergencia es R. Lo cual
cumple con el numeral del Teorema.
Para el tercer ejemplo, usaremos el mismo criterio que en el anterior. Veamos
lim
n→∞
xn+1 (n + 1)!
= |x| lim (n + 1)
n→∞
xn n!
la única forma de que este lı́mite converja es que de cero y esto ocurre sólo cuando x = 0. Lo cual cumple con el numeral 1
del Teorema.
66
Veamos ahora el ejemplo número 4. Consideremos el criterio de la raı́z n-ésima y por tanto,
v
u
√
u
*1
n
t
x
|x|
1
1
n
√ = lim √
lim
lim √ √ = |x| lim
= |x|
√ = |x| n→∞
n
√
n
n→∞
n→∞ n
n→∞
n
n
n
n
Como queremos que esta serie converja, hacemos que |x| < 1, lo cual nos da un radio de convergencia igual a 1 y el intervalo
de convergencia es (−1, 1). ¿Qué sucederá en la frontera de este intervalo?¿Será que la serie puede converger allı́?
∞
∑
1
√ ,
Para responder a estas interrogantes, consideremos a x = 1, dentro de la serie. Entonces, la serie nos queda:
n
n=1
∞
n
∑
(−1)
√ , la cual es
la cual sabemos es divergentes por series p. Ahora consideremos x = −1 en la serie y obtenemos:
n
n=1
∞
∑
xn
√ , es
condicionalmente convergente. Por consiguiente podemos concluir que el intervalo de convergencia de la serie
n
n=1
justamente [−1, 1).
Definición 0.8.2. Sea x una variable real y x0 un número real cualquiera. Una serie de potencias en x − x0 es una serie de
la forma:
∞
∑
an (x − x0 )n = a0 + a1 (x − x0 ) + a2 (x − x0 )2 + · · · + an (x − x0 )n + · · ·
n=0
donde ak ∈ R para todo k ∈ Z+
∑
Teorema 0.8.2. Si
an (x − x0 )n es una serie de potencias, entonces se cumple una sola de las afirmaciones siguientes
1. La serie converge solo para x = x0
2. La serie es absolutamente convergente para todo x
3. Existe un número positivo r, tal que la serie es absolutamente convergente para |x−x0 | < r y divergente para |x−x0 | > r
Ejemplos 0.8.2. Determine el radio de convergencia de las siguientes series de potencias
1)
∞
∑
(−1)n
n=0
1
(x − 3)n
n+1
2)
∞
∑
(−1)n
n=1
1 · 3 · 5 · · · (2n − 1)
(x − 5)n
3 · 6 · 9 · · · (3n)
Solución: Resolveremos solamente el ejemplo 1, el ejemplo 2 queda como ejercicio. Para este ejercicio, consideraremos
nuevamente el Criterio de la Raı́z n-ésima, veamos:
√
(−1)n (x − 3)n
1
lim n
= |x − 3|
= |x − 3|
:1
n→∞
n+1
√
n
lim n+1
n→∞
Entonces, como queremos que converja, tomamos |x − 3| < 1, de donde
−1 < x − 3 < 1 =⇒ 2 < x < 4 =⇒ x ∈ (2, 4)
Ahora bien, si x = 2, obtenemos la serie
∞
∑
n=1
1
, que es divergente por ser la cola de la armónica. Si tomamos x = 4, nos
n+1
∞
∑
(−1)n
, la cual es condicionalmente convergente. Por consiguiente el intervalo de convergencia es: (2, 4]
queda
n+1
n=1
0.8.1
Representación de funciones en series de potencias
∑
Se puede usar una serie de potencias
an xn para definir la función f cuyo dominio es el intervalo de convergencia de la
serie. Concretamente, para cada x en este intervalo, se define f(x) como la suma de la serie; es decir,
f(x) = a0 + a1 x + a2 x2 + · · · + an xn + · · ·
Si una función f está definida de esta manera, se dice que
∑
an xn es una representación en series de potencias de f(x).
67
Ejemplo 0.8.1. Encontrar una función f que este representada por la serie de potencias
1 − x + x2 − x3 + · · · + (−1)n xn + · · ·
Teorema 0.8.3. Sea
∑
an xn una serie de potencias con radio de convergencia r ̸= 0 y sea f la función definida por
f(x) = a0 + a1 x + a2 x2 + · · · + an xn + · · · =
∞
∑
an xn
n=0
para todo x en el intervalo de convergencia. Si −r < x < r, entonces
∞
∞
∑
∑
nan xn−1 = a1 + 2a2 x + 3a3 x2 + · · · + nan xn−1 + · · ·
Dx (an xn ) =
i ) f ′ (x) =
∫x
ii )
n=0
f(t) dt =
0
∞
∑
n=0
∫x
(an tn ) dt =
n=0 0
∞
∑
an n+1
x
n+1
n=0
= a0 x +
1
2
2 a1 x
+ 13 a2 x3 + · · · +
1
n+1
n+1 an x
+ ···
Ejemplo 0.8.2. Encontrar una representación en series de potencias para
Solución: Sabemos que.
(
Dx
(
)
1
1
=
D
−
. Entonces,
x
(1 + x)2
1+x
1
−
1+x
)
(
= −Dx
= −
∞
∑
1
1 − (−x)
(
)
= −Dx
Dx ((−1)n xn ) =
n=0
luego,
1
(1 + x)2
−
∞
∑
∞
∑
)
(−x)
n
(
= −Dx
n=0
(−1)n nxn−1 =
n=1
∞
∑
∞
∑
)
n n
(−1) x
n=0
(−1)n−1 nxn−1
n=1
∞
∑
1
=
(−1)n−1 nxn−1 .
(1 + x)2
n=1
Ejercicio 0.8.1. Encontrar una representación en series de potencias para ln(1 + x)
Ayuda: Derive al logaritmo, halle la serie de potencias para esa expresión y luego integre.
Ejercicio 0.8.2. Use los resultados del ejemplo anterior para hallar ln(1.1) con cinco cifras decimales de precisión.
Ejercicio 0.8.3. Encontrar una representación en series de potencias para arctan x
Ejercicio 0.8.4. Demostrar que ex tiene la representación en series de potencias
ex = 1 + x +
∫ 0.1
x2 x3
xn
+
+ ··· +
+ ···
2!
3!
n!
2
e−x dx.
Ejercicio 0.8.5. Calcular aproximadamente
0
0.8.2
Series de Taylor y Maclaurin
Sea f una función representada por una serie de potencia en x − x0 de manera que
f(x) =
∞
∑
an (x − x0 )n
n=0
=
a0 + a1 (x − x0 ) + a2 (x − x0 )2 + a3 (x − x0 )3 + · · ·
68
donde el dominio de f es un intervalo abierto que contiene a x0 . Podemos entonces hallar representaciones para f ′ (x), f ′′ (x),
etc, derivando los términos de la serie de f(x). Entonces,
∞
∑
f ′ (x) =
nan (x − x0 )n−1
n=1
a1 + 2a2 (x − x0 ) + 3a3 (x − x0 )2 + 4a4 (x − x0 )3 + · · ·
∞
∑
n(n − 1)an (x − x0 )n−2
=
f ′′ (x) =
n=2
2a2 + (3 · 2)a3 (x − x0 ) + (4 · 3)a4 (x − x0 )2 + · · ·
∞
∑
n(n − 1)(n − 2)an (x − x0 )n−3
=
f ′′′ (x) =
n=3
(3 · 2)a3 + (4 · 3 · 2)a4 (x − x0 ) + · · ·
=
y para todo k ∈ Z+
f
(k)
(x) =
∞
∑
n(n − 1) · · · (n − k + 1)an (x − x0 )n−k
n=k
además cada una de las series que se obtiene derivando tiene el mismo radio de convergencia de la serie original. Sustituyendo
x por x0 en cada una de estas representaciones en serie, se obtiene
f(x0 ) = a0 ,
f ′ (x0 ) = a1 ,
f ′′ (x0 ) = 2a2 ,
f ′′′ (x0 ) = (3 · 2)a3 ,
f(4) (x0 ) = (4 · 3 · 2)a4
y para todo entero positivo n
f(n) = n!an
o bien
an =
f(n)
n!
• Serie de Taylor para f(x) en x0
Si f es una función tal que
f(x) =
∞
∑
an (x − x0 )n
n=0
para todo x en un intervalo abierto que contiene a x0 , entonces f(n) (x0 ) existe para n ∈ Z+ y an =
f(x) =
f(n) (x0 )
por tanto,
n!
∞
∑
f(n) (x0 )
(x − x0 )n
n!
n=0
• Serie de Maclaurin para f(x)
Si f es una función tal que
f(x) =
∞
∑
an xn
n=0
para todo x en un intervalo abierto (−r, r), entonces f(n) (0) existe para n ∈ Z+ y an =
f(x) =
f(n) (0)
por tanto,
n!
∞
∑
f(n) (0) n
x
n!
n=0
Ejercicios 0.8.1. Encontrar las series de Maclaurin de las siguientes funciones
1) f(x) = sen x
2)
f(x) = cos x
3) f(x) = ex
4)
f(x) = ln(1 + x)
5) f(x) = arctan x
6)
f(x) = senh x
7) f(x) = cosh x
8)
f(x) = cos2 x