ECUACIONES LOGARITMICAS

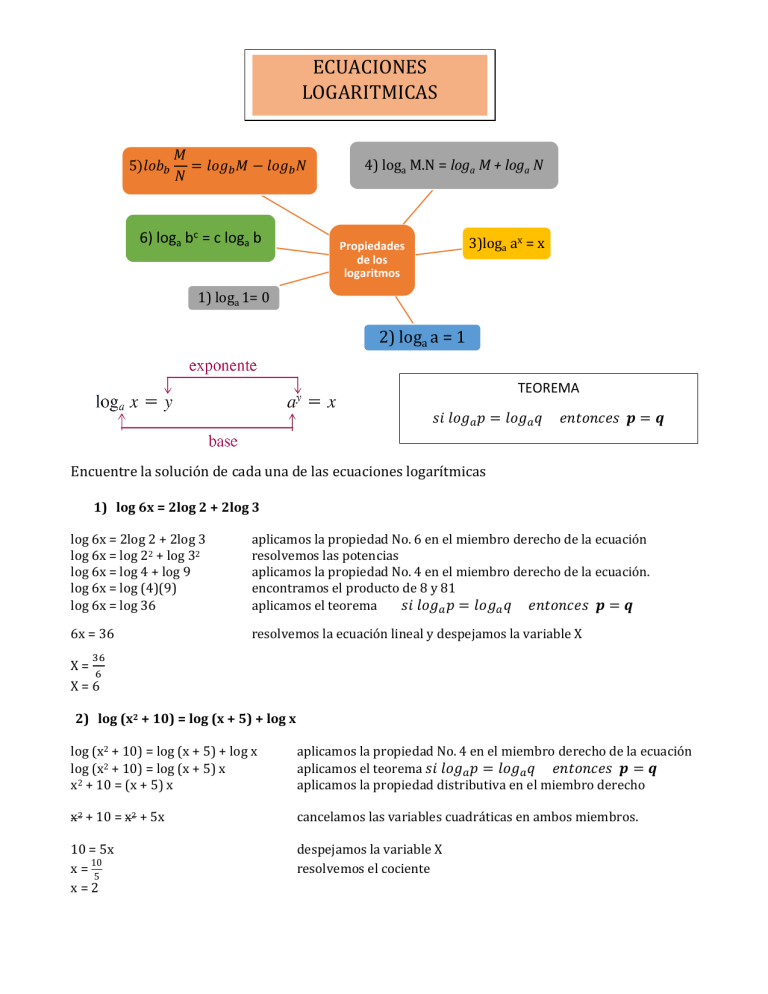
ECUACIONES
LOGARITMICAS
5)𝑙𝑜𝑏𝑏
𝑀
= 𝑙𝑜𝑔𝑏 𝑀 − 𝑙𝑜𝑔𝑏 𝑁
𝑁
6) loga bc = c loga b
4) loga M.N = loga M + loga N
3)loga ax = x
Propiedades
de los
logaritmos
1) loga 1= 0
2) loga a = 1
TEOREMA
𝑠𝑖 𝑙𝑜𝑔𝑎 𝑝 = 𝑙𝑜𝑔𝑎 𝑞
𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝒑 = 𝒒
Encuentre la solución de cada una de las ecuaciones logarítmicas
1) log 6x = 2log 2 + 2log 3
log 6x = 2log 2 + 2log 3
log 6x = log 22 + log 32
log 6x = log 4 + log 9
log 6x = log (4)(9)
log 6x = log 36
aplicamos la propiedad No. 6 en el miembro derecho de la ecuación
resolvemos las potencias
aplicamos la propiedad No. 4 en el miembro derecho de la ecuación.
encontramos el producto de 8 y 81
aplicamos el teorema
𝑠𝑖 𝑙𝑜𝑔𝑎 𝑝 = 𝑙𝑜𝑔𝑎 𝑞 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝒑 = 𝒒
6x = 36
resolvemos la ecuación lineal y despejamos la variable X
X=
36
6
X=6
2) log (x2 + 10) = log (x + 5) + log x
log (x2 + 10) = log (x + 5) + log x
log (x2 + 10) = log (x + 5) x
x2 + 10 = (x + 5) x
aplicamos la propiedad No. 4 en el miembro derecho de la ecuación
aplicamos el teorema 𝑠𝑖 𝑙𝑜𝑔𝑎 𝑝 = 𝑙𝑜𝑔𝑎 𝑞 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝒑 = 𝒒
aplicamos la propiedad distributiva en el miembro derecho
x2 + 10 = x2 + 5x
cancelamos las variables cuadráticas en ambos miembros.
10 = 5x
10
x= 5
x=2
despejamos la variable X
resolvemos el cociente
3) 𝑙𝑜𝑔 √𝑥 − 2 = 𝑙𝑜𝑔( 𝑥 + 2) − 𝑙𝑜𝑔 √𝑥 + 5
𝒍𝒐𝒈 √𝑥 − 𝟐 = 𝒍𝒐𝒈( 𝑥 + 𝟐) − 𝒍𝒐𝒈 √𝑥 + 𝟓
ecuación
𝑙𝑜𝑔 √𝑥 − 2 = 𝑙𝑜𝑔
√𝑥 − 2 =
(𝑥+2)
√𝑥+5
(𝑥+2)
√𝑥+5
aplicamos la propiedad No. 5 en el miembro derecho de la
aplicamos el teorema 𝑠𝑖 𝑙𝑜𝑔𝑎 𝑝 = 𝑙𝑜𝑔𝑎 𝑞
𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝒑 = 𝒒
realizamos un producto cruzado.
√𝑥 − 2 . √𝑥 + 5 = 𝑥 + 2
se realiza el producto de ambas raíces
√(𝑥 − 2)(𝑥 + 5) = 𝑥 + 2
se ubican cantidades subradicales bajo un mismo radical
2
(√(𝑥 − 2)(𝑥 + 5)) = (𝑥 + 2)2
se elevan al cuadrado ambos miembros de la ecuación
(𝑥 − 2)(𝑥 + 5) = (𝑥 + 2)2
se aplican productos notables en ambos miembros de la ecuación.
𝑥 2 + 3𝑥 − 10 = 𝑥 2 + 4𝑥 + 4
se intercambian términos en ambos miembros de la ecuación
𝑥 2 − 𝑥 2 + 3𝑥 − 4𝑥 = 10 + 4
se reducen términos semejantes
−𝑥 = 14
x = -14
multiplicando por ( - 1 )
4) Log x + log(x+3) = 2log(x+1)
se aplica la propiedad de la suma Prop. No 4
se aplica la propiedad No. 6 en el miembro derecho
se aplica el teorema 𝑠𝑖 𝑙𝑜𝑔𝑎 𝑝 = 𝑙𝑜𝑔𝑎 𝑞
𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝒑 = 𝒒
se resuelve los productos en ambos miembros
se resuelve la ecuación
5)
log (16−𝑥 2 )
log (3𝑥−4)
=2
el denominador de la fracción multiplica a 2
el dos pasa como exponente
se aplica el teorema 𝑠𝑖 𝑙𝑜𝑔𝑎 𝑝 = 𝑙𝑜𝑔𝑎 𝑞
se resuelve el cuadrado de 3x-4
16 − 𝑥 2 = 9𝑥 2 − 24𝑥 + 16
9𝑥 2 + 𝑥 2 − 24𝑥 + 16 − 16 = 0
10𝑥 2 − 24𝑥 = 0
𝑥(10𝑥 − 24) = 0
𝑥 = 0 10 𝑥 − 24 = 0
24 12
𝑥=0 𝑥=
=
10
5
se trasladan términos
se reducen términos semejantes
se aplica factor común
se igualan a cero
se despeja la variable x
𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝒑 = 𝒒