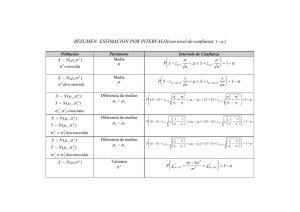
UNIVERSIDAD DE ORIENTE VICERRECTORADO ACADÉMICO CONSEJO DE ESTUDIOS DE POSTGRADO MAESTRÍA EN INGENIERÍA DE GAS Asignación N° 1 Estadística aplicada a la Ingeniería Elaborado por: Barreto Steevenson C.I: 19.415.309 Brito Aníbal C.I: 11.909.544 Campos Luis C.I: 12.575.982 Sánchez Fátima C.I: 20. 645.490 Facilitador: Profesor Luis Marquez (MSc.) Maturín, 19 de octubre de 2017 1.- Se pretende comparar la duración de tres tipos de pilas alcalinas de frecuente presencia en el mercado. Para ello se mide la duración (en horas) de cinco pilas de cada marca elegidas al azar, datos que se recogen a continuación: Marca 1 100 96 92 96 92 de las 2 76 80 75 84 82 pilas 3 108 100 105 102 100 Se pide: a) Variable respuesta, factor a estudiar, unidades experimentales, que modelo se debe plantear, cuántas variables se deben definir. ¿Cuáles son? b) ¿Cuál de las tres marcas dura más? Justifique su respuesta. c) ¿Qué se puede concluir acerca de la duración de estas tres marcas de pilas? d) Realizar comparaciones múltiples por los métodos de TUKEY y D.M.S ¿Se obtuvo el mismo resultado? e) Verifique el supuesto de normalidad e identifique si hay puntos atípicos. f) Verifique la igualdad de las varianzas. ¿Se puede usar la prueba de BARTLETT? ¿Por qué? g) Use la prueba de KRUSKAL-WALLIS para el análisis de varianza. ¿Es la misma conclusión de la parte c)? SOLUCIÓN: Parte a: Variable respuesta, factor a estudiar, unidades experimentales, que modelo se debe plantear, cuántas variables se deben definir. ¿Cuáles son? Variable respuesta: Duración en horas. Factor a estudiar: Marca de las pilas. Unidades experimentales: Uso de equipos de pruebas similares, iguales condiciones. Modelo: 𝑦𝑖𝑗 = µ𝑖 + ℇ𝑖𝑗 Variables: Se debe definir una variable, duración en horas. Detalle del modelo matemático para análisis de varianza de un factor: El modelo estadístico es: Para llevar a cabo el análisis requiere la construcción de la tabla análisis de varianza del modelo con un solo factor y efectos fijos, la cual se detalla a continuación: Al realizar la prueba de F y determinar el término 𝐹𝑜 , se procede a evaluar mediante tablas estadísticas el valor de 𝐹(𝛼,𝑎−1,𝑁−𝑎) . Las hipótesis que se plantean son: Una forma equivalente de escribir las hipótesis anteriores es en términos de los efectos de los tratamientos es: 𝐻𝑜 , deberá rechazarse y concluirse que hay diferencias en las medias de los tratamientos si: Parte b: ¿Cuál de las tres marcas dura más? Justifique su respuesta. Comparando la media de la duración de las baterías para las marcas a evaluar, La marca 3 se considera la de mayor duración, por presentar un valor superior en comparación con las otras medias de las dos marcas. La gráfica a continuación presenta los promedios de cada marca visualizándose que la marca3 presenta una duración de 103 horas. La evaluación de los datos por medio de un análisis de varianza, como el mostrado en el apartado c, justificaría si la marca 3 presenta la mayor duración, al validar si existen diferencias significativas entre la duración observada en cada marca de pila. Parte c: ¿Qué se puede concluir acerca de la duración de estas tres marcas de pilas? Para dar respuesta a ésta pregunta se procedió a la construcción del análisis de varianza de un solo factor de acuerdo a las ecuaciones indicadas anteriormente, para a igual a 3 y n igual a 5, N – a igual a 14: 𝑦𝑖𝑗 2 = 130034 𝑛 𝑆𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = ∑ 𝑖=1 𝑎 𝑦𝑖. 2 𝑦.. 2 − = 1445,74 𝑛 𝑁 𝑛 𝑆𝑆𝑇 = ∑ ∑ 𝑦𝑖𝑗 2 − 𝑖=1 𝑗=1 𝑦.. 2 = 1597,74 𝑁 𝑆𝑆𝐸 = 𝑆𝑆𝑇 − 𝑆𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = 152 𝑀𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = 𝑀𝑆𝐸 = 𝐹𝑜 = 𝑆𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 1445,74 = = 722,87 𝑎−1 2 𝑆𝑆𝐸 152 = = 12,66 𝑁−𝑎 12 𝑀𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 722,87 = = 57,09 𝑀𝑆𝐸 12,66 Se utilizó el software InfoStat para corroborar los cálculos y elaborar la tabla de análisis de varianza, los resultados se indican a continuación: Tabla 3. Resultados análisis de varianza para marca de pilas. Posteriormente se procedió a ubicar 𝐹(𝛼,𝑎−1,𝑁−𝑎) , donde: α es igual a 0,05 nivel de significancia fijado que fija el investigador a es igual a 3, a representa el número de tratamientos, en éste caso es el número de marcas de pilas. N, es el producto de n (número de observaciones o registros de la duración) y “a” el número de tratamientos. Se plantearon las siguientes hipótesis 𝐻𝑜 : 𝑙𝑎𝑠 𝑚𝑒𝑑𝑖𝑎𝑠 𝑑𝑒 𝑙𝑎 𝑑𝑢𝑟𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝑐𝑎𝑑𝑎 𝑚𝑎𝑟𝑐𝑎 𝑑𝑒 𝑝𝑖𝑙𝑎 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠 𝐻1 : 𝑎𝑙 𝑚𝑒𝑛𝑜𝑠 𝑢𝑛𝑎 𝑚𝑒𝑑𝑖𝑎 𝑑𝑒 𝑙𝑎 𝑑𝑢𝑟𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝑢𝑛𝑎 𝑚𝑎𝑟𝑐𝑎 𝑒𝑠 𝑑𝑖𝑓𝑒𝑟𝑓𝑒𝑛𝑡𝑒 De la tabla puntos porcentuales de la distribución F, se obtiene 𝐹(0,05,2,12) = 3,89 Se procedió a comparar 𝐹𝑜 y 𝐹(0,05,2,12) , determinándose lo siguiente: 𝐹𝑜 > 𝐹(0,05,2,12) Por lo tanto, y según lo indicado, la hipótesis nula (las medias de la duración de cada marca de pila son iguales) se rechaza, dando como conclusión que al menos la media de la variable duración (en horas) de una de las marcas de baterías es diferente a la de las otras marcas, o bien, el efecto de una de las marcas es diferente a cero. Parte d: Realizar comparaciones múltiples por los métodos de TUKEY y D.M.S ¿Se obtuvo el mismo resultado? Prueba de Tukey: Después de un análisis de varianza en el que se ha rechazado la hipótesis nula de la igualdad de las medias de los tratamientos, quieren probarse todas las comparaciones de las medias por pares: El procedimiento de Tukey hace uso de la distribución del estadístico del rango estudentizado: Para tamaños de las muestras iguales, la prueba de Tukey declara que dos medias son significativamente diferentes si el valor absoluto de sus diferencias muestrales excede: Donde: 𝑞𝛼 , es el estadístico del rango estudentizado a, es el número de tratamientos f, es el grado de libertad de los errores calculados en el análisis de varianza, para éste caso es 12. 𝑀𝑆𝐸 , es el cuadrado medio del error Aplicando las fórmulas indicadas para éste método se tiene: 12,66 12,66 𝑇0,05 = 𝑞0,05(3,12) × √ = 3,77 × √ = 5,99 5 5 El valor de 𝑞0,05(3,12) se obtiene de la tabla puntos porcentuales del estadístico del rango estudentizado (ver tabla) Se construye los intervalos de diferencia: |𝑦̅1. − 𝑦̅2. | = 15,62 ∗ |𝑦̅1. − 𝑦̅3. | = 7,98 ∗ |𝑦̅2. − 𝑦̅3. | = 23,6 ∗ Al comparar cada diferencia con el valor de 𝑇0,05 se concluye que los pares de medias son significativamente diferentes. Por otro lado, aplicando la prueba de Tukey con el software InfoStat (disponible en http://www.infostat.com.ar), se obtuvo los siguientes resultados: En conclusión los pares de medias de las marcas de las pilas son diferentes. Prueba de la diferencia media significativa LSD: Se aplica sólo después de que la prueba F en un análisis de varianza sea significativa en un 5%. Para diseños balanceados, caso en estudio, la fórmula a aplicar es: 𝐿𝑆𝐷 = 𝑡(𝛼,𝑁−𝑎) × √ 2 2𝑀𝑆𝐸 2 × 12,66 = 2,1788 × √ = 4,90 𝑛 5 Se construyen diferencias del tipo |𝑦̅𝑖 − 𝑦̅𝑗 | y se comparan con LSD calculado, se compara|𝑦̅𝑖 − 𝑦̅𝑗 | > 𝐿𝑆𝐷, las diferencias son significativas si se cumple la condición indicada. Para el ejercicio en estudio, se construyen los intervalos (similares a los construidos en la prueba de TUKEY y se comparan con LSD: |𝑦̅1. − 𝑦̅2. | = 15,62 ∗ |𝑦̅1. − 𝑦̅3. | = 7,98 ∗ |𝑦̅2. − 𝑦̅3. | = 23,6 ∗ Tolos los valores son mayores a 4,90 por tanto se concluye que hay diferencias significativas entre los pares de medias de las duraciones de las pilas. También se utilizó la prueba de LSD con el software InfoStat, obteniéndose los siguientes resultados: En conclusión se obtiene que los pares de medias de las duraciones de las marcas de las pilas son significativamente diferentes. En la aplicación de ambas pruebas y para él caso estudiado se obtiene los mismos resultados. En la gráfica generada por el software para ambas pruebas se observan las diferencias entre las medias de cada marca. Parte e: Verifique el supuesto de normalidad e identifique si hay puntos atípicos. Para la verificación del supuesto de normalidad se aplicó la prueba de Shapiro – Wilks, quién plantea lo siguiente: 𝐻𝑜 : 𝐿𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑎𝑙𝑒𝑎𝑡𝑜𝑟𝑖𝑎 𝑡𝑖𝑒𝑛𝑒 𝑢𝑛𝑎 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑐𝑖ó𝑛 𝑛𝑜𝑟𝑚𝑎𝑙 𝐻1 : 𝐿𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑎𝑙𝑒𝑎𝑡𝑜𝑟𝑖𝑎 𝑛𝑜 𝑡𝑖𝑒𝑛𝑒 𝑢𝑛𝑎 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑐𝑖ó𝑛 𝑛𝑜𝑟𝑚𝑎𝑙 Estadístico de prueba 𝑊𝑐 = 𝑏2 ∑𝑛 ̅)2 𝑖=1(𝑦𝑖 −𝑦 𝑏 = ∑𝑘𝑖=1 𝑎𝑖 × [𝑦(𝑛−𝑖,+1) − 𝑦𝑖 ], 𝑎𝑖 es el coeficiente tabulador. Se rechazará la hipótesis nula de normalidad si el estadístico Wc es menor que el valor crítico proporcionado por la tabla para el tamaño muestral y el nivel de significación dado, es decir, se rechaza la hipótesis nula 𝐻𝑜 : si 𝑊𝑐 < 𝑊𝑇 El desarrollo se realizó en Excel y software InfoStat, a continuación se presentan los resultados: Excel: InfoStat: 𝑊𝑇 se determina de las tablas estadísticas, para un nivel de significancia 𝑊(1−𝛼),𝑛 = 𝑊0,95,15 = 0,881 Finalmente, 𝑊𝑐 (0,90) > 𝑊𝑇 (0,881) Se concluye que se acepta la hipótesis nula, la variable aleatoria duración en horas tienen una distribución normal. Por otro lado, para la determinación de los puntos atípicos se verifica a través de la siguiente ecuación: 𝑑𝑖𝑗 = 𝑒𝑖𝑗 √𝑀𝑆𝐸 = 𝑦𝑖𝑗 − 𝑦̅𝑖. √𝑀𝑆𝐸 donde: 𝑒𝑖𝑗 , es el residual de la observación j – ésima, Para determinar los puntos atípicos se utilizó el diagrama de caja y bigotes (box-plot), es un gráfico que está basado en cuartiles y mediante el cual se visualiza la distribución de un conjunto de datos, éste gráfico suministra información sobre los valores mínimo y máximo, los cuartiles Q1, Q2 o mediana y Q3, y sobre la existencia de valores atípicos y la simetría de la distribución. Se procedió a graficar la caja de box-plot en infoStat, Se observa que para cada marca no hay puntos que estén por fuera de la caja. Parte f: Verifique la igualdad de las varianzas. ¿Se puede usar la prueba de BARTLETT? ¿Por qué? La prueba de BARTLETT se utiliza para verificar el supuesto de homogeneidad de las varianzas, si se viola éste supuesto, la prueba F sólo resulta afectada ligeramente en el modelo balanceado (mismo tamaño de la muestra en todos los tratamientos “a”) con efectos fijos. Sin embargo, en diseños no balanceados o en casos en que una de las varianzas es considerablemente más grande que las demás, el problema es considerable. Específicamente, si los niveles del factor que tienen las varianzas mayores corresponden también con los tamaños de las muestras más pequeños, el índice de error tipo 1 real, cuando el investigador no acepta la hipótesis nula (H0 siendo esta verdadera en la población, es mayor que lo previsto (o los intervalos de confianza tienen niveles de confianza reales más bajos que los que fueron especificados). Recíprocamente, si los niveles del factor con las varianzas mayores tienen también los tamaños de las muestras mayores, los niveles de significación son mucho menores que lo anticipado (los niveles de confianza son más altos). Ésta es una buena razón para escoger tamaños de las muestras iguales siempre que sea posible. Para los modelos con efectos aleatorios, las varianzas del error diferentes pueden introducir alteraciones significativas en las inferencias sobre los componentes de la varianza, incluso cuando se usan diseños balanceados. Cuando el supuesto de normalidad ha sido validada, (ya sea por el prueba de Shapiro–Wilks una gráfica QQ, Bartlett plantea el siguiente modelo matemático cuya distribución de muestreo es aproximada a la distribución “ji-cuadrado”, por medio de la siguiente expresión: Dónde: Las hipótesis a validar con esta prueba se basan en: 𝐻𝑜 : 𝜎1 2 = 𝜎2 2 = ⋯ … . = 𝜎𝑎 2 𝐻1 : 𝐴𝑙 𝑚𝑒𝑛𝑜𝑠 𝑢𝑛𝑎 𝜎𝑖 2 𝑒𝑠 𝑑𝑖𝑓𝑒𝑟𝑒𝑛𝑡𝑒 Se rechaza la hipótesis nula si se cumple la siguiente condición: 𝑋𝑜 2 > 𝑋(𝛼,𝑎−1) 2 El primer paso es determinar las varianzas para cada marca de pila con la aplicación del programa Infostat, cuyo resumen se presenta a continuación. Se sustituyen los valores de varianza, “a” igual a 3, n igual a 15 en las ecuaciones planteadas por Bartlett, obteniéndose el valor de 𝑋𝑜 2 : 𝑆𝑝 2 = 2 × [11,2 + 14,8 + 12] = 6,33 (15 − 3) 𝐶 = 1+ 1 3 1 × [ − ] = 1,236 3×2 2 12 𝑞 = 12 × 𝑙𝑜𝑔10 (6,33) − [2𝑙𝑜𝑔10 (11,2) + 2𝑙𝑜𝑔10 (14,8)] + 2𝑙𝑜𝑔10 (12,0) = 3,03 𝑋𝑜 2 = 2,3026 × 3,03 = 5,63 1,236 De las tablas estadísticas 𝑋(0,05,2) 2 = 5,99 2 Como 𝑋𝑜 2 < 𝑋(0,05,2) se acepta homogeneidad de las varianzas. la hipótesis nula, comprobando la Parte g: Use la prueba de KRUSKAL-WALLIS para el análisis de varianza. ¿Es la misma conclusión de la parte c)? En situaciones en las que el supuesto de normalidad no está justificado, el experimentador quizá quiera usar un procedimiento alternativo del análisis de varianza con la prueba F que no dependa de este supuesto. El estadístico de prueba es: Si no hay empates, esto es que no se repiten observaciones o su número de repetición es moderado, la anterior ecuación se simplifica a: 2 Si 𝑛𝑖 ≥ 5 H se distribuye aproximadamente como 𝑥𝑎−1 , por lo tanto, la hipótesis nula (los tratamientos no difieren) se rechaza si: 2 Para el caso en estudio 𝑥0,05,2 = 5,99, por tanto, 2 𝐻 > 𝑥0,05,2 ; 12,02 > 5,99 Se concluye que los tratamientos (marcas de las pilas) difieren, es la misma conclusión reportada en el apartado c. 2.- Se pretende comparar los cuentakilómetros de cuatro vehículos: El Renault Clio, el Renault Megane, el Ford Focus y Ford Mondeo. Para ello se realiza cinco recorridos con cada vehículo situando los cuentakilómetros a cero, y apuntando la distancia que marcan al final del recorrido. Los datos fueron los siguientes: Vehículo Renault Clio Renault Megane Ford Focus Ford Mondeo 1 63.5 64.1 65.9 64.9 RECORRIDO 2 63.2 64.2 65 65.2 3 62.3 63 63.9 64.1 4 65.6 64.2 66 65.9 5 65 64.9 65.8 67.9 Se pide: a) Identifique los elementos del experimento: Variable respuesta, factor(es), bloques, etc. Escriba detalladamente el modelo matemático. b) ¿Se puede concluir que los cuentakilómetros de los cuatro vehículos dan la misma precisión al medir distancias? c) ¿Es conveniente o no de incluir el bloque? SOLUCIÓN: Parte a: Identifique los elementos del experimento: Variable respuesta, factor(es), bloques, etc. Escriba detalladamente el modelo matemático. Variable de respuesta: Distancia recorrida en kilómetros. Factor: modelo del vehículo, rendimiento del vehículo; factor humano; tiempo Bloques: Para el caso en estudio se formó 5 bloques (recorridos) Tratamiento: (4) vehículos. Detalle del modelo matemático para diseño de bloques completamente aleatorizado: El modelo RCBD (Diseño de bloques completos aleatorizados); busca minimizar el error porcentual como fuera posible, es uno de los más utilizados. Las unidades de equipo de prueba son con frecuencia diferentes en sus características de operación y serian un factor de formación de bloques típicos; es decir; estudiar la influencia de un factor tratamiento (T) con i niveles en una variable de interés en presencia de una variable extraña, el factor bloque, B, que tiene j bloques. La formulación matemática del modelo de diseño en bloques completamente aleatorizados con un factor principal (factor tratamiento), T, con I niveles y un factor secundario (factor bloque), B, con J niveles o bloques es la siguiente: 𝑦𝑖𝑗 = 𝜇 + 𝜏𝑖 + 𝛽𝑗 + 𝜀𝑖𝑗 𝑖 = 1,2, … , 𝑎 𝑗 = 1,2, … , 𝑏 𝑏 𝑎 𝛽𝑗 = 0 𝜏𝑖 = 0 𝑖=1 𝑗 =1 El interés se encuentra en probar la igualdad de las medias de los tratamientos, por lo tanto, las hipótesis de interés son Una manera equivalente de escribir las hipótesis anteriores es en términos de los efectos de los tratamientos es, Para la comprobación de las hipótesis ya indicadas se requiere de la construcción de la siguiente tabla: 𝑆𝑆𝑇 = 𝑆𝑆𝑇𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 + 𝑆𝑆𝐸 + 𝑆𝑆𝐵 Se rechaza 𝐻𝑜 si 𝐹𝑜 > 𝐹𝛼,𝑎−1,(𝑎−1)(𝑏−1) Parte B Para el ejercicio en estudio se plantean las siguientes hipótesis: 𝐻𝑜 : 𝑁𝑜 𝑒𝑥𝑖𝑠𝑡𝑒 𝑑𝑖𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑎 𝑒𝑛𝑡𝑟𝑒 𝑙𝑜𝑠 𝑐𝑢𝑒𝑛𝑡𝑎 𝑘𝑖𝑙𝑜𝑚𝑒𝑡𝑟𝑜𝑠 𝑑𝑒 𝑐𝑎𝑑𝑎 𝑣𝑒ℎ𝑖𝑐𝑢𝑙𝑜 𝑒𝑛 𝑒𝑠𝑡𝑢𝑑𝑖𝑜 𝐻1 : 𝐸𝑥𝑖𝑠𝑡𝑒 𝑑𝑖𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑎 𝑒𝑛𝑡𝑟𝑒 𝑙𝑜𝑠 𝑐𝑢𝑒𝑛𝑡𝑎 𝑘𝑖𝑙𝑜𝑚𝑒𝑡𝑟𝑜𝑠 𝑑𝑒 𝑐𝑎𝑑𝑎 𝑣𝑒ℎ𝑖𝑐𝑢𝑙𝑜 𝑒𝑛 𝑒𝑠𝑡𝑢𝑑𝑖𝑜 Se realizan los cálculos en Excel, tomando como base todas las fórmulas indicadas en el modelo matemático para el análisis de varianza por la técnica diseño de bloques aleatorizados, se obtuvo o indicado en la tabla siguiente, se elige nivel de significancia igual a 0,05: Vehículo Renault Clio Renault Megane Ford Focus Ford Mondeo Yj Bloques Ȳj bloques Tratamiento o niveles (a) 4 bloques (b) 5 Numero total de observaciones (N) 20 1 63,5 64,1 65,9 64,9 258,4 64,6 2 63,2 64,2 65 65,2 257,6 64,4 RECORRIDO 3 62,3 63 63,9 64,1 253,3 63,325 4 65,6 64,2 66 65,9 261,7 65,425 5 65 64,9 65,8 67,9 263,6 65,9 Yi Ῡ Tra tami entos Tra tami entos 319,6 320,4 326,6 328 1294,6 64,73 63,92 64,08 65,32 65,6 64,73 𝑎 𝑏 𝑦𝑖𝑗2 𝑆𝑆𝑇 = 𝑖=1 𝑗 =1 5 4 𝑆𝑆𝑇 = 𝑖=1 𝑗 =1 𝑆𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜𝑠 𝑆𝑆𝑡𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜𝑠 𝑆𝑆𝑏𝑙𝑜 𝑞𝑢𝑒𝑠 Suma de los cuadrados totales 4 𝑦..2 𝑦𝑖𝑗2 − 𝑁 1 = 𝑏 1 = 5 1 = 𝑎 𝑦..2 − 𝑁 𝑎 𝑦𝑖2 − 𝑖=1 4 𝑦𝑖2 𝑖=1 𝑏 𝑦𝑗2 − 𝑗 =1 𝑆𝑆𝑇 = 𝑦..2 𝑁 𝑦..2 − 20 𝑦𝑖𝑗2 − 31,522 𝑖=1 𝑗 =1 𝑦..2 𝑁 Suma de los cuadrados de los tratamientos 10,918 𝑆𝑆 𝑦..2 20 5 Suma de los cuadrados de los bloques 𝑆𝑆 15,807 𝑆𝑆𝑇 = 𝑆𝑆𝑇𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 + 𝑆𝑆𝐸 + 𝑆𝑆𝐵 𝑆𝑆𝐸 = 𝑆𝑆𝑇 − 𝑆𝑆𝑇𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 − 𝑆𝑆𝐵 𝑆𝑆 𝑀𝑆𝑇𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 = 𝑆𝑆𝑇𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜 𝑎−1 𝑀𝑆 Suma de los cuadrados debida al error 4,797 Cuadrado medio de los tratamientos 3,64 𝑀𝑆𝐵𝑙𝑜𝑞𝑢𝑒𝑠 = 𝑆𝑆𝐵𝑙𝑜𝑞𝑢𝑒𝑠 𝑏−1 𝑀𝑆 𝑀𝑆𝐸 = Cuadrado medio de los bloques 3,95 𝑆𝑆𝐸 (𝑎 − 1)(𝑏 − 1) 𝑀𝑆 Cuadrado medio debidos al error 0,40 𝑜 = 𝑀𝑆𝑇𝑟𝑎𝑡𝑎𝑚𝑖𝑒𝑛𝑡𝑜𝑠 𝑀𝑆𝐸 Estadistico de pruebas 9,10 Por otro lado, se utilizó el software infoStats para corroborar los resultados obtenidos en la hoja Excel: Seguidamente se ubicó en las tablas estadísticas el valor de 𝐹0,05,3.12 = 3,49 Como 𝐹𝑜 > 𝐹0,05,3,12 se rechaza la hipótesis nula (la media de la variable recorrido en kilómetros son iguales), se concluye que al menos una media del recorrido de uno de los cuentakilómetros de un vehículo es diferente a otro cuentakilómetros de otro vehículo, por tanto, los cuentakilómetros no tienen la misma precisión. Parte c: ¿Es conveniente o no de incluir el bloque? Cuando la fuente de variabilidad perturbadora es conocida y controlable, puede usarse una técnica de diseño llamada formación de bloques para eliminar de manera sistemática su efecto sobre las comparaciones estadísticas entre los tratamientos. Para definir la inclusión o no del bloque se procede a evaluar a realizar el análisis de varianza sin la formación de bloques: Paso 1.- Determinación de los estadístico de los bloques SST 31,522 SSTratamiento SSE=SST– SSTratamiento 10,918 20,64 Paso 2.- Determinación de los cuadrados medios de los tratamientos y debido al error y Fo MStratamiento 3,693 MSE 1,2875 Fo 26 Paso 3.- Construcción de la tabla de análisis de varianza sin formación de bloques Fuente de variación suma de cuadrados Tratamientos Error Total 10,918 20,604 31,522 grados de medias de Fo libertad cuadrados 3 3,6393333 16 1,28775 2,826117906 19 Utilizando α=0,05 debe rechazarse la hipótesis nula si 𝑜 > 𝑎,𝑎−1,𝑁−𝑎 Tomando en consideración un valor de significancia de 5% (α=0,05) en conjunto con la tabla de puntos porcentuales de la distribución F(0,05). Se tiene que Fo > Fo;3;16 F(0,05);3;16= 3,24 Puesto que F (0,05)3,16 > Fo no se rechaza la hipótesis nula. Por lo tanto, es conveniente incluir el bloque para hacer el error experimental lo más pequeño posible; usando el RCBD, los bloques de prueba forman una unidad experimental homogénea, en la cual se puede comparar los tratamientos (vehículos); mejorando la precisión de las comparaciones entre los tratamientos al eliminar la variabilidad entre los bloques (recorridos). De no incluir en el análisis de varianza el bloque esto podría ocasionar un cálculo errado; por lo que se incrementa el error experimental; a tal magnitud de no detectar las diferencias entre las medias de los tratamientos. Por consiguiente el diseño de bloques aleatorizados minimiza lo suficiente la cantidad de ruido en los datos para que la diferencia entre los tratamientos (Vehículos) sea detectada. Se utiliza el software InfoStat para corroborar que es correcto rechazar la hipótesis nula, se aplica la prueba de diferencias mínimas significativas (DMS), a continuación se muestran los resultados: 3.- Un experimentador está estudiando el efecto de cinco posibles mezclas de material explosivo para la fabricación de dinamita. El material explosivo proviene de cinco orígenes distintos y es manipulado por cinco operarios para realizar las mezclas. Los datos que se recogen corresponden a la fuerza al explotar. ORIGEN 1 2 3 4 5 1 A 24 B 17 C 18 D 26 E 24 2 B 20 C 24 D 38 E 31 A 30 OPERARIOS 3 C 19 D 30 E 26 A 26 B 20 4 D 24 E 27 A 27 B 23 C 29 5 E 24 A 36 B 21 C 22 D 31 Se pide: a) Identificar los elementos del experimento. Escribir detalladamente el modelo matemático. b) Determinar si influyen todas las variables consideradas. ¿Considera que deba modificarse el modelo? c) Comprobar si la fuerza al explotar es, en media, la misma para las cinco mezclas. Parte a: Identificar los elementos del experimento. Escribir detalladamente el modelo matemático. Variable respuesta: Fuerza al explotar. Factor a estudiar: Origen del explosivo. Detalle del modelo matemático para diseño de cuadrados latinos: El diseño de cuadrado latino se usa para eliminar dos fuentes de variabilidad perturbadora; es decir, permite hacer la formación de bloques sistemática en dos direcciones. Por lo tanto, los renglones y las columnas representan en realidad dos restricciones sobre la aleatorización. En general, un cuadrado latino para p factores, o cuadrado latino pxp, es un cuadrado con p renglones y p columnas. El modelo es completamente aditivo; es decir, no hay interacción entre renglones, columnas y tratamientos. El modelo estadístico para el diseño de cuadrados latinos es: Se requiere la construcción de la tabla () para evaluar el estadístico Fo, de las tablas estadísticas de evalúa 𝐹𝛼,(𝑝−1),(𝑝−2)(𝑝−1) , y se plantean las siguientes hipótesis para el ejercicio: 𝐻𝑜 : 𝑙𝑎𝑠 𝑚𝑒𝑑𝑖𝑎𝑠 𝑑𝑒 𝑙𝑎 𝑓𝑢𝑒𝑟𝑧𝑎 𝑝𝑎𝑟𝑎 𝑒𝑥𝑝𝑜𝑡𝑎𝑟 𝑑𝑒 𝑙𝑎𝑠 𝑚𝑒𝑧𝑐𝑙𝑎𝑠 𝑠𝑜𝑛 𝑖𝑔𝑢𝑎𝑙𝑒𝑠 𝐻1 : 𝑎𝑙 𝑚𝑒𝑛𝑜𝑠 𝑢𝑛𝑎 𝑚𝑒𝑑𝑖𝑎 𝑑𝑒 𝑙𝑎 𝑓𝑢𝑒𝑟𝑧𝑎 𝑝𝑎𝑟𝑎 𝑒𝑥𝑝𝑙𝑜𝑡𝑎𝑟 𝑒𝑠 𝑑𝑖𝑓𝑒𝑟𝑒𝑛𝑡𝑒 La hipótesis nula se rechaza cuando 𝐹𝑜 > 𝐹𝛼,(𝑝−1),(𝑝−2)(𝑝−1) Tabla Parte b: Determinar si influyen todas las variables consideradas. ¿Considera que deba modificarse el modelo? Para el caso en estudio, se tiene un diseño 5x5, p es igual a 5,𝐹0,05,4,12 se selecciona 0,05 como nivel de significancia. Utilizando la herramienta infoStat, se obtuvieron los siguientes resultados: De la tablas estadísticas, 𝐹0,05,4,12 = 3,26 Como 𝐹0 > 𝐹0,05,4,12 se rechaza la hipótesis nula y se concluye que existen diferencias entre las medias de las fuerzas de explosión. En éste estudio se observa que tanto el origen de las mezclas como los operarios no tienen efecto (los valores de la prueba F son menores a el tabulado) sobre la variable fuerza de explosión, por tanto, no se considera el cambio de modelo, si el resultado hubiese sido que los valores de la prueba F sean mayores, deberá considerarse cambiar el diseño de cuadrado latinos a diseño factorial para estudiar el efecto e interacciones del origen de las mezclas y el cambio de operarios. Parte c: Comprobar si la fuerza al explotar es, en media, la misma para las cinco mezclas. Como 𝐹0 > 𝐹0,05,4,12 se rechaza la hipótesis nula y se concluye que existen diferencias entre las medias de las fuerzas de explosión. 4.- Un ingeniero diseña una batería para su uso en el motor de ciclomotores. Para ello dispone de tres tipos diferentes de material. Como considera que la temperatura es un factor influyente en la duración de la batería, decide diseñar el experimento combinando los tres materiales con tres temperaturas concretas: - 10⁰, 20⁰ y 50⁰. Así, una vez sometidas cuatro baterías de cada material a cada temperatura, las duraciones efectivas en horas de cada batería son las siguientes: 1 (-10⁰) 130 (-10⁰) 155 (50⁰) 70 (20⁰) 34 (-10⁰) 180 (20⁰) 80 (50⁰) 82 (20⁰) 40 (50⁰) 20 (-10⁰) 74 (20⁰) 75 (50⁰) 58 MATERIAL 2 (20⁰) 122 (20⁰) 126 (-10⁰) 150 (50⁰) 70 (50⁰) 25 (20⁰) 115 (-10⁰) 126 (50⁰) 58 (-10⁰) 159 (-10⁰) 188 (20⁰) 106 (50⁰) 45 3 (20⁰) 150 (20⁰) 174 (-10⁰) 138 (-10⁰) 110 (50⁰) 60 (50⁰) 96 (20⁰) 120 (-10⁰) 168 (-10⁰) 160 (20⁰) 139 (50⁰) 104 (50⁰) 82 Se pide: a) Identifique los elementos del experimento. Escribir detalladamente el modelo matemático. b) Estudiar si el tipo de material y la temperatura son factores determinantes en la duración de las baterías de ciclomotores. ¿Hay posibilidad de que un material sea más recomendado a una temperatura en concreto y no lo sea a otra distinta? c) Dibujar un gráfico de las duraciones medias con cada tratamiento. ¿Es coherente con los resultados del apartado b)?. Interpretar las interacciones con la ayuda de este gráfico. Nota: Antes de resolver, hay que organizar la tabla, para poder aplicar el diseño. Respuesta: Parte a: continuación se presenta los datos organizados que facilitaran la resolución del ejercicio: Material 1 2 3 Temperatura (-)10° 20° 50° 130 155 180 74 34 40 80 75 70 82 20 150 126 159 188 122 126 115 106 70 25 58 138 110 168 160 150 174 120 139 60 96 104 58 45 82 Parte a) Los elementos que intervienen en el experimento son: Tres (03) tipo de material de las baterías, temperatura del experimento, horas de duración del ensayo. De acuerdo a los datos presentado el análisis factorial con dos (02) se considera el modelo ideal para evaluar la influencia del material de la batería y la temperatura sobre el tiempo de duración de las baterías. El modelo estadístico lineal del diseño factorial a aplicar es: Por lo que su ecuación matemática es: 𝑆𝑆𝑇 = 𝑆𝑆𝑚𝑎𝑡𝑒𝑟𝑖𝑎𝑙 + 𝑆𝑆𝑇𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑎 + 𝑆𝑆𝑖𝑛𝑡𝑒𝑟𝑎𝑐𝑐𝑖ó𝑛 + 𝑆𝑆𝑒𝑟𝑟𝑜𝑟 Dónde: Los valores obtenidos serán tabulados en la tabla de análisis de varianza como se muestra a continuación: Los valores F0 determinados, seran comparadas con los los valores F de la tabla estadistística F para un nivel de significancia α del 0,05 que permiten aceptar o rechazar la hipótesis asumida durante el desarrollo del ejercicio.Para este caso, el valor F tabulado se ubica como F𝛼 (a-1)/(ab(n-1) en las tablas estadísticas. Parte B: Para evaluar si el tipo de material y la temperatura son significantes den la duración de las baterias, se procede a la apliación del análisis de varianza, bajo las siguientes hipótesis: Para el material: Para la temperatura Para la interacción entre ambos A continuación se presente las tabls excel con los valores calculados para cada término de la ecución matemática. Material 1 2 3 130 150 138 418 (-)10° 155 126 110 391 Y.j. 180 159 168 507 74 188 160 422 539 623 1738 576 Temperatura 20° 34 40 122 126 150 174 306 340 Y.j. 80 115 120 315 75 106 139 320 229 469 583 1281 70 70 60 200 50° 82 25 96 203 Y.j. 20 58 104 182 58 45 82 185 230 198 342 770 Y… 3789 Y˄2… Y˄2… /abn SST 14.356.521,00 398792,25 77.134,75 Cálculo del efecto de material SSmaterial: 1/bn= 0,0833333 Y˄2… Y1= 998 996.004,00 Y2= 1290 1.664.100,00 Y2= 1501 2.253.001,00 4.913.105,00 SSA= 10.633,17 Cálculo del efecto de la temperatura SStemperatura: 1/an= 0,0833333 Y˄2… Y1= 1738 3.020.644,00 Y2= 1281 1.640.961,00 Y2= 770 592.900,00 5.254.505,00 SSB= 39.083,17 Cálculo del efecto de la interacción SSinteracción: 1/n= 0,25 Y˄2… Y11= 539 290.521,00 Y12= 623 388.129,00 Y13= 576 331.776,00 Y21= 229 52.441,00 Y22= 469 219.961,00 Y23= 583 339.889,00 Y31= 230 52.900,00 Y32= 198 39.204,00 Y33= 342 116.964,00 1.831.785,00 SSBA 9.437,67 Por lo tanto: SSE= 17.980,75 El valor F tabulado se ubica como F𝛼 (a-1)/(ab(n-1), bajo la siguiente premisa: 𝑎 = 3; 𝑏 = 3; 𝑛 = 4; Por tanto el valor F para el efecto de los materiales y el efecto de las tempertura se aplica: 𝐹0.05 (2,27) y para el efecto de la interación de ambos se aplica 𝐹0.05 (4,27) , cuyos valores se presentan a continuación: 𝐹0.05 (2,27) = 4,21 𝐹0.05 (4,27) = 4,73 Conocidos los valores de F, es necesario determinar el valor de F0 que se obtiene con la aplicación matematica del anális de la varianza. Para este cálculo se utilizará el programa estadistico InfoStat (disponible en http://www.infostat.com.ar) , obteniéndose lo siguiente: Los valores calculados de F0 permiten inferir los siguiente: 1. Con respecto al efecto de material, el valor de 7,98 es mayor a al tabulado de 4,21, indicando que su interacción es significativa (rechazo de la hipótesis H0), el material tiene efecto en la duración de la batería. 2. De forma similar, el efecto de la temperatura es siginificativo en la duración de las baterias, debido a que el valor de Fo calculado de 29,34 es mayor al F tabulado (4,21). 3. En cuanto a la interacción de temperatura/material, los datos obtenidos indican el rechazo de la hipótesis H0, (3,54 calculado > 2,73 tabulado) por lo que su efecto tambien es significativo en la duración de las baterias. Con respecto al planteamiento sobre si hay posibilidad de que un material sea más recomendado o no a una temperatura en concreto o distinta, se aplicó en el programa InfoStat el procedimiento para determinar las medias de duración de baterías, considerando el material y la temperatura, como se muestra a continuación: En la anterior tabla se muestra que el material 2 presenta mayor duración para la temperatura de -10 con respecto a los demás materiales, por tanto, se recomienda el uso de éste material a la temperatura indicada. El mismo comportamiento lo refleja el material 3, cuyo valor de duración es mayor a los 20 grados. Sin embargo cuando la temperatura de experimentación aumenta de -10 a 20, la duración de la batería del material 3 permanece constante, mientras que el materiales 2 y 1 disminuyen, incluso de manera abrupta para este último. De lo antes expuesto se puede inferir que el material 3 es el ideal a ser recomendado por que la disminución de su tiempo de duración es menor tanto a -10 como 20 grados, sin descartar como posible sustituto el material 2. En cuanto al material 1, presenta los menores tiempo de duración, sobre en todas las temperaturas evaluadas con disminución al incrementarse la temperatura desde -10 grados, por lo que no se considera recomendable. Parte c: El grafico de duración media se presenta a continuación: El gráfico muestra los valores medios de la duración de las baterías para los tres tipos de materiales a las temperaturas de evaluación de -10, 20 y 50 grados. El comportamiento de las medias indica que todos los materiales presenta la mayor duración de batería sin importar el tipo de material, aunque. A la temperatura antes descrita, el material 2 refleja el mayor valor de duración de batería, sin embargo su disminución se ve afectada a 20 grados y presenta una fuerte disminución en la visa útil de la batería a la temperatura de 50. Con respecto al material 3, el mismo presenta un leve incremento de la duración de la batería al ser evaluada a 20 grados, lo que reafirma lo indicado en el punto b, en cuanto a su recomendación. Otro punto a considerar es el hecho que el material 2 presenta una tendencia lineal en comparación con las curvas del material 1 y el material 3, lo que infiere que la interacción de los efectos de material y temperatura es menor.