4-Soluciones

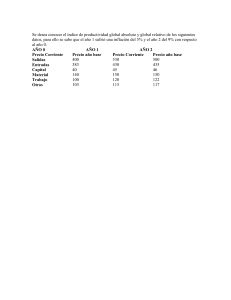
Soluciones a los ejercicios
MATEMATICA II UNAJ
Soluciones a los ejercicios
Linealización y extremos
2
b. 4 x  y  0 , f (1; 2)  4; 4
2
2
46. a. 2 x  y  4 , f (2; 2)  8; 4 ,
2
2
c. x  y  13 , f (3; 2) 
6 4
;
13 13
47. a. x  3 y  2 z  8 ; b.  x  y  2 ; c. 3 x  4 y  z  8
48. dV  7,5 cm3 , V  7,57525 cm3
49. a. L( R1 , R2 )  12 
9
4
( R1  20)  ( R2  30)
25
25
b. dR  0, 02ohms , R  0,0198ohms
50. a.
b.
 3;3 mínimo local
 2; 1 mínimo local
 2 2
 3 3
c.   ;  máximo local,  0; 0  punto de ensilladura
d.  0; 0  mínimo local, 1; 1 punto de ensilladura
e.
 2;1 mínimo local,  2; 1 máximo local;  0; 
f.
 0; 0  punto de ensilladura, 1; 1 ,  1;1
mínimos locales
1 
2 
g.  ;1 máximo local
h.
i.
 0; 0  punto de ensilladura
 k ;0 , con k entero puntos de ensilladura
j. 1;1 mínimo local

5 puntos de ensilladura
Soluciones a los ejercicios
MATEMATICA II UNAJ
51. En 1; 2  ,  1;0  hay mínimos locales.
1 
1 
1  
 1  
 y  1;  2 
 y  1;
 , máximo absoluto en 1;
2 
2 
2



52. Mínimo absoluto en 1; 

.
53. Mínimo absoluto en  4; 2  y en  4; 2  .
54. Máximo absoluto en  4;0  , mínimo absoluto en (0;1) .

55.  


38 1 
; 
3 3 
2 2 
 2
;
;
 , el más lejano es
3 3
 3
56. El punto más cercano es 
57.  2;0;1
2 
 2 2
;
;

.
3 3
3
