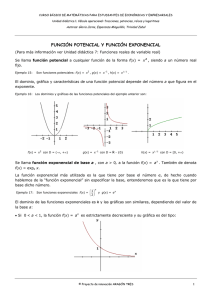
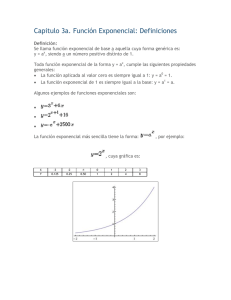
Módulo 13 Variación en procesos sociales Funciones exponenciales Funciones exponenciales Las funciones exponenciales se presentan en las siguientes formas: y = a · bx Donde: f(x) = a · bkx b se conoce como base; es un número positivo y distinto a 1. x es la variable independiente y se conoce como exponente. k es una literal, que siempre representa una constante. La función de Euler es un ejemplo de función exponencial; su expresión matemática es: y = ex La variable e es un número que suele llamarse número de Euler o constante de Napier. Es un número racional, es decir, no puede ser representado por un numeral decimal exacto ni por un decimal periódico. Su valor es e = 2.718281828459, sin embargo, sólo se expresa como 2.71. Gráfica de una función exponencial Al graficar una función, se realizan dos pasos: tabulación y localización de los puntos en el plano. Observa el siguiente ejemplo: Paso 1. Tabulación Para hallar la gráfica de una función exponencial primero tabulamos, es decir, sustituimos el valor de x para obtener el valor de y. En este caso, hay que elevar el número e al exponente que corresponde según el valor de x, por ejemplo: Si x vale −4 sustituimos en la función: con lo que se obtiene: y = ex y = (2.71)−4 Al realizar la operación, el resultado es: y = 0.01854 1 Módulo 13 Variación en procesos sociales Funciones exponenciales Las operaciones se pueden realizar con ayuda de una calculadora científica introduciendo el valor aproximado de e (2.71) o bien, directamente con la tecla ex. Para esta función la tabla que obtenemos es: x operaciones involucradas −4 e-4 = (2.71)−4 0.01854 e-2 = (2.71)−2 0.13616 e0 = (2.71)0 1.00000 e2 = (2.71)2 7.34410 −3 −2 −1 0 1 2 3 4 y e-3 = (2.71)−3 0.05024 e-1 = (2.71)−1 0.36900 e1 = (2.71)1 2.71000 e3 = (2.71)3 19.90251 e4 = (2.71)4 53.93580 Antes de realizar la gráfica, observa el comportamiento de los valores de y y x, y responde: •¿Qué ocurre con los valores de y cuando x adquiere valores negativos? •¿Qué ocurre con los valores de y cuando x adquiere valores positivos? •¿Qué ocurre en x = 0? En las funciones exponenciales: • Cuando x es negativa, los valores de y son muy pequeños. • Los valores de y van creciendo conforme x crece, pero poco y despacio. • Cuando x es igual 0, el valor de y es 1. • Cuando x es positiva, los valores de y son cada vez más grandes y crecen muy rápido. • Los valores de y son siempre positivos. 2 Módulo 13 Variación en procesos sociales Funciones exponenciales Paso 2. Localización de los puntos en el plano Se localizan los puntos en el plano cartesiano y se unen. La gráfica de la función exponencial siempre presenta la siguiente forma: y x Ejemplo de crecimiento exponencial ¿Has oído de fenómenos que crezcan muy rápido? Uno de ellos es la población. Cuando una población crece con rapidez, se dice que tiene un crecimiento exponencial. Un ejemplo de este tipo de fenómeno se encuentra en el crecimiento poblacional de los conejos: supongamos que tenemos un conejo macho y una hembra, y que producen cuatro crías (dos son machos y dos hembras), que a su vez producen ocho. Si continúa esta tasa de aumento, la próxima generación producirá 16 conejos, la próxima 32, la próxima 64, y así sucesivamente. Desde luego que en este modelo simple estamos suponiendo que el alimento es infinito y ¡que los conejos están muy libres! En ese caso, la función exponencial es: y = 2x Si a la ecuación anterior se designa C como el número de conejos y a t como el tiempo, la ecuación se expresaría: C = 2t 3 Módulo 13 Variación en procesos sociales Funciones exponenciales Al tabular y graficar esta función obtenemos: x y 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1,024 Crecimiento poblacional de los conejos En la tabla de valores y en la gráfica podemos ver cómo, efectivamente, los valores de y crecen muy rápido. Resolver funciones exponenciales con calculadora científica Si bien puedes utilizar cualquier calculadora científica, aquí te mostramos las formas de utilizar las funciones con la calculadora científica disponible en el sitio http://web2.0calc.es/. Para resolver operaciones de una función exponencial y = e, podemos utilizar el valor aproximado de e, o euler, que ya conoces (2.71), o bien, directamente con la tecla "e": En este ejemplo utilizaremos −4 como valor de x. Opción A. Utilizando el valor aproximado de e: 1. Escribe el valor de e (2.71). 2. Oprime la tecla “xy”, que sirve para elevar a cualquier potencia; en la pantalla aparecerá ^. 3. Teclea la potencia a la que deseas elevar, es este caso, −4. 4. Finalmente, oprime la tecla “=” para obtener el resultado. 4 Módulo 13 Variación en procesos sociales Funciones exponenciales −4 (2.71) Tecla para elevar a cualquier potencia. Opción B. Opción B. Utilizando la tecla “e”: 1. Presiona la tecla de la exponencial; en la pantalla aparecerá “exp”. 2. Escribe entre paréntesis el valor de x; en este caso escribimos −4. 3. Oprime la tecla “=” para obtener el resultado. En la pantalla de los cálculos, aparece "exp" al presionar la tecla de la exponencial. Entre paréntesis pondrás el valor de x. Tecla de la exponencial. Tu resultado está listo. ¡Prueba con diferentes valores! 5