Clase de funciones 2019

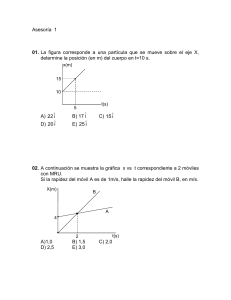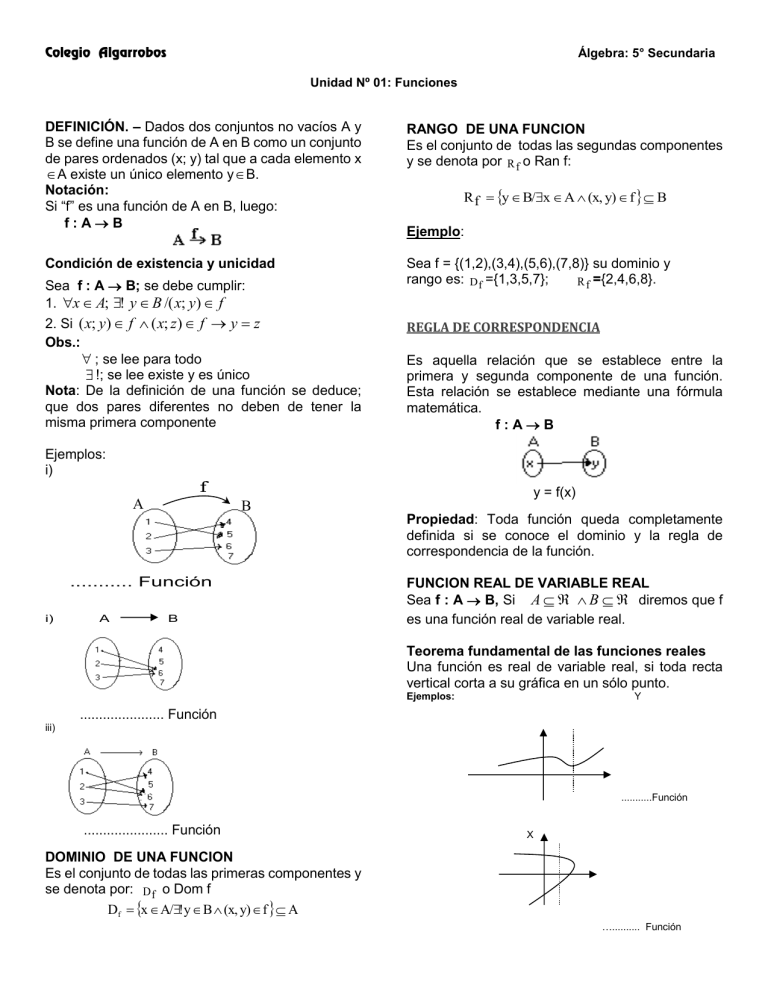
Colegio Algarrobos
Álgebra: 5° Secundaria
Unidad Nº 01: Funciones
DEFINICIÓN. – Dados dos conjuntos no vacíos A y
B se define una función de A en B como un conjunto
de pares ordenados (x; y) tal que a cada elemento x
 A existe un único elemento y  B.
Notación:
Si “f” es una función de A en B, luego:
f:AB
RANGO DE UNA FUNCION
Es el conjunto de todas las segundas componentes
y se denota por R f o Ran f:
Condición de existencia y unicidad
Sea f = {(1,2),(3,4),(5,6),(7,8)} su dominio y
rango es: D f ={1,3,5,7};
R f ={2,4,6,8}.
Sea f : A  B; se debe cumplir:
1. x  A; ! y  B /( x; y)  f
2. Si ( x; y)  f  ( x; z )  f  y  z
Obs.:
 ; se lee para todo
 !; se lee existe y es único
Nota: De la definición de una función se deduce;
que dos pares diferentes no deben de tener la
misma primera componente
R f  y  B/x  A  (x, y)  f   B
Ejemplo:
REGLA DE CORRESPONDENCIA
Es aquella relación que se establece entre la
primera y segunda componente de una función.
Esta relación se establece mediante una fórmula
matemática.
f:AB
Ejemplos:
i)
f
A
y = f(x)
B
Propiedad: Toda función queda completamente
definida si se conoce el dominio y la regla de
correspondencia de la función.
........... Función
i)
A
B
FUNCION REAL DE VARIABLE REAL
Sea f : A  B, Si A    B   diremos que f
es una función real de variable real.
Teorema fundamental de las funciones reales
Una función es real de variable real, si toda recta
vertical corta a su gráfica en un sólo punto.
Ejemplos:
Y
...................... Función
iii)
...........Función
...................... Función
X
DOMINIO DE UNA FUNCION
Es el conjunto de todas las primeras componentes y
se denota por: D f o Dom f
Df  x  A/!y  B  (x, y)  f   A
….......... Función
REGLA PRACTICA PARA CALCULAR EL
DOMINIO
1. Si la función es polinomial el dominio es el
conjunto de los números reales ( R ). Además si
la función polinomial es de grado impar, el rango
también es R.
función de y para luego analizar para que valores de
“y” la función está definida.
Ejemplo: Halle el rango de:
F ( x) 
3x  1
x2
Solución:
Ejemplo:
i) x - 2  0  x  2
i) F(x) = 6x +x + x + 3  DF = R
8
5
Luego: DF= R – {2}
3
ii) G(x) = x3 –2x2 +x +3  DG = R y RG = R
2. Si la función es racional : F(x) =
H ( x) ,
G ( x)
el dominio
ii) Rango: y  3x  1
x 2
 yx –2y = 3x – 1  yx – 3x = 2y –1
se obtiene como:
DF = R – { x/ G(x) = 0 }
 x(y-3) =2y – 1 
Ejemplos:
Como: y - 3  0  y  3
i)
F(x) =
2x  3
x2
ii)
G(x) =
x
x 9
 DF = R – { 2 }
 DF = R – { 3, -3 }
2
iii)
2y 1
y 3
Luego: RF = R – {3}
FUNCIONES ESPECIALES
1. FUNCIÓN CONSTANTE.
f(x) = c
f  (x,y)  RxR/y  c, "c" es constante)
H(x) = x2  5  DF = R
x  16
Donde D f =R; R f = {c}.
Observación: x2 + 16  0
3. Si la función es irracional: F(x) =
dominio se obtiene como:
x
Su gráfica es:
G (x) , el
Y
F(x)=c
c
DF = { x  R / G( x)  0 }
Ejemplos:
i) F(x) =
6x
Obs. 6 –x  0  6  x  x  6
Luego:
ii) G(x) =
DF =<-  ; 6]
2. FUNCIÓN LINEAL f  (x, y)  RxR/y  ax  b, a  0,
Donde: D f =R; R f =R.
Y
x3
x4
Obs. x - 4 >0  x > 4
Luego:
X
0
DF =<4; +  >
Nota: No existe una regla específica para el cálculo
del rango, sin embargo se recomienda despejar x en
X
3. FUNCIÓN RAIZ CUADRADA.– f(x)  x .
Donde: D f = R  ; R f = 0,  .
Problemas
01. Hallar ( a + b) para que:
A = {(2;5); (1;3); (b -2a; 3); (1; a2 – b2 );
(2; 2a + b)}
Una función
A) 0
4. FUNCIÓN VALOR ABSOLUTO– A la función f le
llamaremos función valor absoluto si su regla de
correspondencia es: f(x)=x 
donde: x  x, x  0,
 x, x  0.
D f = R ; R f = 0,  .
Y = f(x)
B) 1
C) 2
D) 3
E) 5
02. Sean f y g dos funciones definidas por:
F = { (2; a + b + c), (1; a-b-c), (2;8),(3; b+c),
(4;a), (1;2)}
G = { (x; y)  F / y – x = 1}
Entonces, el número de elementos de la
función G, es:
A) 1
B) 2
C) 3
D) 4
E) 5
03. Dado: F : A  B
F
Si: F(1) + F(2) + F(3) = 0,
1
a
Hallar
2
3
5. FUNCION CUADRÁTICA
F(x) = ax2 +bx + c, a  0
* v: Vértice
A) 3
2


V    b ; 4ac  b 
4a
 2a

b
c
3
E
B) –3
3
3
(a  b)  (b  c)  (a  c)
abc
C) 2
D) 6
E) 1
04. Dada la función:
x 2 ,
x3
x 1

 2
F(x)   x  4,  1  x  3
 x  3,
x  1



Si a>0 se tiene Si a<0, se tiene
Calcular: F[F(4)] + F[F(0)] + F(-2)
A) 15
B) 11
C) 13
D) 6
E) 9
05. Dada una función constante (F) que verifica:
DF= R
RF = [ 4ac  b2 ,  >
4a
2
4a
6. FUNCIÓN MÁXIMO ENTERO
Se simboliza por:
 
Regla de correspondencia:
F(x) = x ; donde x es el máximo entero no
 
 
mayor que x.
Si: n  x  n  1  x = n
 
Dominio: DF = R
Rango: RF = Z
3F(3)  5F(5)
1
4F(4)  2
DF = R
RF =<-  , 4ac  b ]
Halle: (F(2004))-F(2005)
A) 1
B) 4
C) 9
D)
2
E) 1/9
06. Calcular el dominio de la función ,
f(x)  8  x  8  x
A) [ -8, 8 ]
D) [ 2, 2 2 ]
B) [0, 8 ]
E) [4, 8]
C) [ 8, 16]
13. Si la función ganancia, en la editorial “ MI
ACADEMIA”, esta dada por:
G(x) = -3x2 + 96x + 552
Indicar como respuesta la suma de las cifras de
la ganancia máxima.
07. Hallar el dominio de la función:
2
x  x 2
1  2x
F(x) 
A) [-1; ½> U [2; +  >
A) 6
B) <-  ; -1] U < 1/2; 2]
C) < -  ; -1] U <1; 2]
B) 7
C) 4
D) 5
E) 7
14. Si f es una función definida por f(x) =
D) <-  ; -1> U <1/2; 2>
E) [-1;2]
4 ,
2
x 7
entonces el rango de f, es:
08. Si [a;b> - {c} con a < c < b es el dominio de la
A) <0; 4/7]
D) <-1;1>
B) <0; 1>
E) <1; 2>.
C) <1; 4/7]
2
función g(x) =
x x6
2
7x  x  12
15. Si la gráfica de: F(x) = -2x2 + 12x –10
Hallar el área de la región sombreada donde
V: Vértice de la pa
Entonces el valor de M = a + b + c , es:
A) -6
B) 5
C) -5
D) 4
E) 6
09. Determine el rango de:
2
F(x)  x  5
B) R+
C) [ 5; +  >
E) No se puede.
A) R
D) R – {5}
10. Sea F una función real, tal que:
2
A) 16 u2
C) 24 u2
E) 9 u2
B) 8 u2
D) 4 u2
16. En la figura adjunta se muestra la gráfica de f(x)
= ax2 +bx + c indicar el valor de verdad de las
siguientes afirmaciones:
F(x)  x ;  2  x  3
I. a. b < 0
el rango de F es:
A) [4;9]
C) [-4; 9]
B) <4;9]
D) [0; 4]
II. B < 0
III. C = 0
a) VVV b) FVV
c) VVF d) FVF e) VFV
E) [0;9]
11. Luego de hallar el dominio de la función:
G(x)  8  x 
1 
x3
1
x 2
17. Siendo F una función lineal tal que:
determine el número de valores enteros que la
verifican.
A) 2
B) 3
C) 4
D) 5
E) 6
12. Dada la función:
F(x)  2x  1 ; x  4;8]
x3
Determine su rango
A) < 3; 7>
C) <3; 7]
B) [3; 7]
D) [3; 7>
E) <-7; -3>
{ (n;n), (3;9), (-1;1)}  F
Halle el valor de: 2n2 +3
A) 35
B) 3
C) 53
D) -32
E) 21
18. Una bola se coloca en el punto P de la parábola
y = x2 – x – 6 cuya ordenada es 6. Se le deja
rodar por la parábola hasta que llegue a un
punto Q, cuya ordenada es -6, entonces la
distancia mínima horizontal recorrida por la bola
es:
A) 2
B) 3
C) 4
D) 5
E) 6
19. Si f es una función definida por f(x) = ax3 + b,
cuya gráfica se muestra en la figura adjunta.
Entonces el valor de T = a – b es:
26. Halle el área del triángulo que resulta de
interceptar las funciones
F( x) = 4 y G(x) = x  1  3
A) 5
C) 3
E) 0
B) 4
D) 2
A) 2
B) 3
C) 4
D) 5
E) 1
27. Sea “F” una función de proporcionalidad, tal que:
F(3) + F(5) = 64
20. Sea: f(x) = 3 + (-1)n
Donde n =  x  . Calcular el rango de la función
A) {2; 4}
B) { 1}
C) { 3}
D) R
E) N.A
Halle:
 3
 1 
F  4   F  4  
A) 16
B) 25
2
f(x) = 25  x  2 , entonces
el Dom(f)  Rang(f), es:
B) [-5;5]
E) [-3;3]
C) 36
D) 81
E) 10
29. La gráfica de la función:
21. Si f es una función definida por
A) [-5;2]
D) [-2;3]
2
2
y   2  x  bx  c
3
 
C) [-5;-2]
intercepta al eje “x” en los puntos ( -2;0) y (5; 0)
y al eje “y” en el punto ( 0; k); según esto,
calcular el valor de: ( b + c + k)
22. Dadas las funciones:
F = { (3;5); (4;9); (5;12) }
G = { (2;3); (5;4); (9; 3) }
B) –23/5
D) 46/3
A) 23/5
C) –46/3
Calcular:
T
A) 1
G(9)
30. Dada la función:
F = { (2; a + b), (b; b2 + 1), (2; 7), (b; 5)}
Halle ab + 30
F(G(2))  G(F(4))
B) 2
C) 3
D) 4
E) 5
A) 12
23. Hallar la suma de los elementos enteros del
dominio de la función
f(x) 
A) -2
B) -1
3
C) -3
D) 3
E) 0
B) [-7/2; 3]
D) <-  ;3]
25. Si f es una función definida por
2
(x  5x)3 (x  2) x
x  6x  11
, entonces el
dominio de f, es:
A) [0;5>
C) [5;  > U {0}
E) <-  ;5>
E) 50
31. Si f ( x)  ( x  1) 2  a entonces: f ( x)  f ( x  2)
x
x  10  3  x , entonces el dominio
f(x) =
de f, es:
2
D) 20
Será:
24. Si f es una función definida por
f(x) 
C) 45
2
x  2x  x
x 2
A) [-10; 3]
C) [-10;  >
E) [-9; 3]
B) 40
B) <-  ;0> U <5;  >
D) <5;  >
A) 4
B) 2
C) 1
D) -4
E) -2
3
x | x |
D) {0}
E) R
32. Halle el dominio de la función: f ( x) 
A) R – {0}
B) R+
C) R-
33. Determine el dominio de la función f, cuya regla
de correspondencia es:
x2
f ( x) 
3x  x 2
A) <-  ; 0> U <3; +  >
C) <-  ;0] U [3; +  >
E) R – {0}
B) <0;3>
D) [0;3]
34. Dada la función h( x)  12 , x  3;5] Indique su
6 x
40. Determine la suma del mayor y menor valor
entero que toma la función:
variación.
A) < 4; 12]
C) < 4;   >
E) <-4; 0]
35. Si
el
f ( x) 
B) < 4; 12 >
D)<12;   >
A) 21
rango
de
la
función:
2
f ( x) 
es  0;1 ,
| x | 1
B) 23
g ( x) 
A) <-1;1>
B) <-2; 2> - {1;-1}
C) <-  ; -3 ] U [3;   > D) <-  ; -3> U < 3;  >
E) <-3;3> - {1;-1}
36. Halle el rango de la función P( x)  x | x |
x
37. El
B) R – {0}
rango
de
C) {0; 2}
la
D) R
función
E) R-
cuadrática:
f ( x)  x 2  (a  1) x  7
es el intervalo [b;  , además f(1) = 12.
Halle el valor de a + b.
A) 5
B) 9
C) 6
C) 20
D) 11
4 x 
A) < -1; 1>
C) [-2; 2]
E) [-4;4]
E) 24
2
x 2
es:
B) <-2; 2>
D) [-4; 4] – {2; -2}
42. Señale el área generada por los gráficos de las
funciones f; g y el eje x en f(x) = px + q;
g(x) = -px + q; p; q  R   {0}
q2 2
A)
u
p
C)
E) 3
D) 22
41. El dominio de la función g de variable real con
regla de correspondencia
entonces el dominio es el conjunto
A) R+
20
; x  3;2 
x  4x  5
2
B) |p|u2
| p| 2
u
2
D)
| pq | 2
u
2
E) 2|pq|u2
43. La grafica de la función
38. Sea A1 + A2 + A3 = A4 en
F(x) = b - | x – a| es
Señale el valor del área S.
si f es lineal y g constante, hallar x.
A) 2
B) 4
C) 6
D) 5
A) 2ab
E) 8
B) ab
C) 3ab
D) 4
E) ab/2
44. Del gráfico de la función constante f,
f(x) = 5k + 3
39. Determine el rango de la expresión matemática
f ( x)  8  2 x  x 2  3
A) [3; 6]
D) <0; 3>
B) [0; 3]
E) <3;6>
C) [-2; 4]
Halle: 5 f (8)  2 f (0)
f (2)
A) 5
B) 2
C) 7
D) 0
E) 1
45. Halle el valor máximo de la función
f ( x)  2 x 2  x  1
A) 1/4
B) 3/8
C) 9/8
D) 9/4
E) 5/8
46. Determine el rango de la función:
x
f ( x) 
x2
A) [-1;1]
B) {1}
C) {0}
D) {1;-1}
E) R
47. Halle el área del triángulo que resulta de
interceptar las funciones
F( x) = 4 y G(x) = x  1  3
A) 2
B) 3
C) 4
D) 5
E) 1
48. Una compañía ha concluido que su utilidad está
dada por V(x)= 240x – x2 en soles, donde x
representa el número de unidades vendidas.
Hallar la máxima utilidad
A) 16 400
D) 13 200
B) 15 400
E) 12 400
C) 14 400
f ( x)  2  x  2  x
B) [0, 2 ]
C) [ 2, 4]
D) [ 2, 2 2 ]
A) p = $ 45  Gmáx = 1225
B) p = $ 40  Gmáx = $ 1250
C) p = $ 35  Gmáx = $ 2400
D) p = $ 30  Gmáx = $ 1655
E) N.A
53. Un obrero con 160 metros de alambrón desea
cercar una superficie de forma rectangular. Si
uno de los lados no necesita cerco, ¿cuáles
deben ser las dimensiones para que el área sea
máxima?. Dar como respuesta uno de los lados.
A) 60
B) 20
C) 80
D) 32
E) 50
54. Sean las funciones:
F(x) = 2x2 + 4x – 30
G(x) = -3x2 –6x + 24
Donde: b = min (F)
p = máx (G)
49. Calcular el dominio de la función,
A) [ -2, 2 ]
52. Un fabricante puede producir radios a un costo
de $10 cada uno y estima que son vendidos por
$x cada uno. Los usuarios compran
aproximadamente (80 – x) radios cada mes.
Halle el precio al cual debe vender cada radio
para obtener la máxima ganancia, y cuál es
ésta.
Hallar la distancia de M a N.
E) [4, 8]
N(n,p)
F
50. Un cañón situado en el punto (3, 0) dispara una
bala con una trayectoria y = x  3 . Si un avión
viaja por la recta y = 4, y la bala lo destruye.
Hallar el punto sobre el que fue el impacto.
G
M(a,b)
A) (4 ; 18)
D) (19; 4)
B) (19; 1)
C) (17; 2)
E) No llega a destruirlo
A) 21
51. Una liebre coja describe la trayectoria y = x2; un
perro que recorre la recta y = x la distingue y la
logra capturar. Hallar el punto donde ocurre la
captura, si sus coordenadas son positivas.
A) (1; 1)
D) (2; 2)
B) (1; 2)
E) (1/2; 1/2)
C) (2; 1)
B) 34
C) 59
D) 61
E) 93
55. Calcular el área del triángulo que resulta de
interceptar las funciones:
F(x) = 4
A) 2
;
B) 3
G(x) = |x - 1| + 3
C) 4
D) 5
E) 1