levietnagarciatres

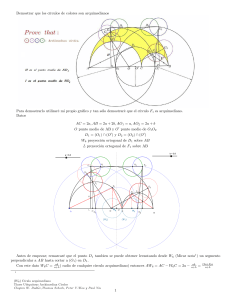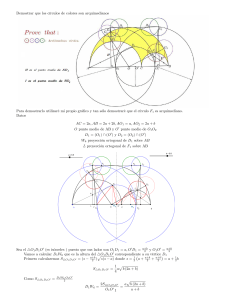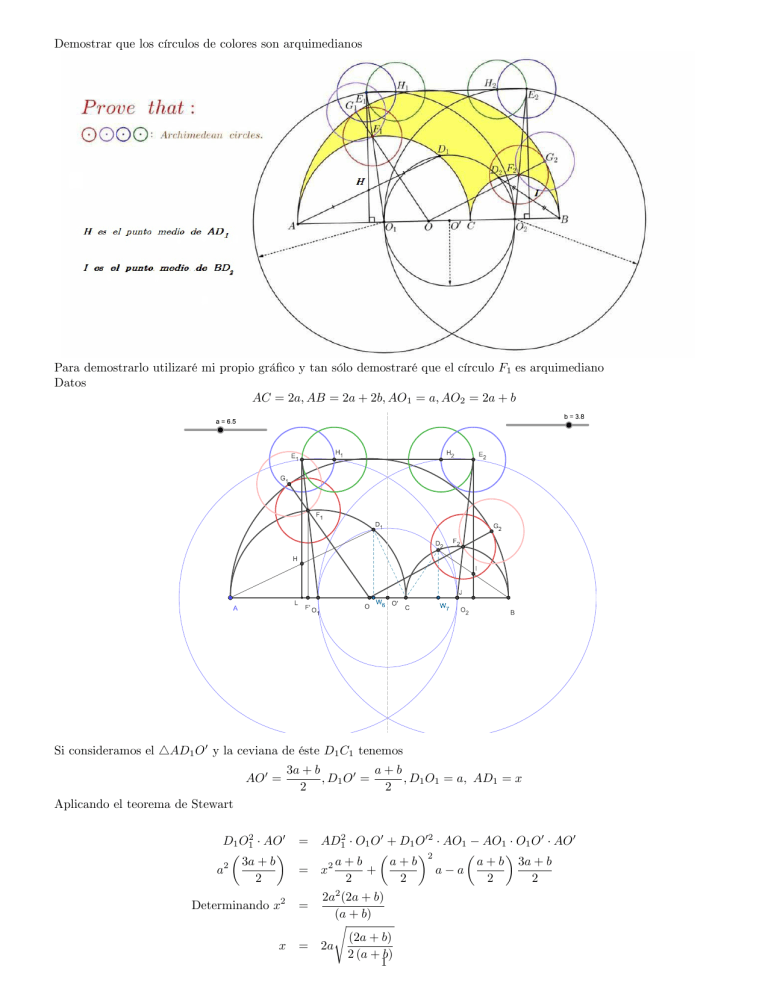
Demostrar que los círculos de colores son arquimedianos
Para demostrarlo utilizaré mi propio grá…co y tan sólo demostraré que el círculo F1 es arquimediano
Datos
AC = 2a; AB = 2a + 2b; AO1 = a; AO2 = 2a + b
Si consideramos el 4AD1 O0 y la ceviana de éste D1 C1 tenemos
AO0 =
3a + b
a+b
; D1 O 0 =
; D1 O1 = a; AD1 = x
2
2
Aplicando el teorema de Stewart
D1 O12 AO0
a2
3a + b
2
= AD12 O1 O0 + D1 O02 AO1
a+b
a+b
+
2
2
2
2a (2a + b)
(a + b)
s
(2a + b)
2a
2 (a + b)
1
= x2
Determinando x2
=
x =
2
a
a
AO1 O1 O0 AO0
a+b
2
3a + b
2
q
El 4AD1 C es rectángulo en D1 donde su hipotenusa AC = 2a y el cateto AD1 = 2a (2a+b)
2(a+b) tendremos pues
q
D1 C = AC 2
AD12
s
s
2a2 (2a + b)
b
= 2a
(a + b)
2 (a + b)
4a2
=
Si la proyección ortogonal de D1 sobre AB la denomino W6 entonces
q
q
(2a+b)b
p
b
2a
2a
2(a+b)
2(a+b)
a b (2a + b)
S4AD1 C
D1 W6 =
=
=
a
2a
a+b
Aplicando ahora a dicho triángulo el teorema del cateto tendremos
AW6
AD12
=
=
AC
y
W6 C
= AC
2a2 (2a+b)
(a+b)
2a
AW6 = 2a
=
a (2a + b)
a+b
a (2a + b)
ab
=
a+b
a+b
Como H es el punto medio del segmento AD1 .
4AD1 C O1 4AHO1 siendo la razón de semejanza para pasar del primero al segundo 21 ;por lo que
s
s
2a + b
1
1
b
1
; AO1 = AC = a; HO1 = D1 C = a
AH = AD1 = a
2
2 (a + b)
2
2
2(a + b)
Como también 4AD1 W6
O1 4AHL siendo la razón de semejanza para pasar del primero al segundo la.misma
p
a (2a + b) b
1
1
(2a + b) a
1
ab
HL = D1 W6 =
; AL = AW6 =
; LO1 = W6 C =
2
2(a + b)
2
2(a + b)
2
2(a + b)
Resaltemos que el segmento LO1 es la mitad del radio arquimediano. Sigamos
Consideramos 4O1 LE1 y 4O1 F 0 F1 rectángulos en L y F 0 respectivamente siendo F 0 la proyección ortogonal de F1 sobre
AB
a
4O1 LE1 4O1 F 0 F1 siendo la razón de semejanza para pasar del primero al segundo a+b
.Por lo que
F 0 O1 =
a
a2 b
ab
=
2(a + b) a + b
2(a + b)2
Como O1 F1 = a por Pitágoras
a4 b2
1
3ab + 2a2 + 2b2
= a2 (2a + b) (a + 2b)
4
4
4(a + b)
4
(a + b)
p
a
(2a + b) (a + 2b) (3ab + 2a2 + 2b2 )
2
2(a + b)
F 0 F12
= a2
F 0 F1
=
Vamos a calcular F 0 O
a2 b
Al ser F 0 O1 = 2(a+b)
2 ; entonces
AF 0 = AO1
Y como F 0 O = AO
a 3ab + 2a2 + 2b2
a2 b
=
2
2(a + b)2
2 (a + b)
F 0 O1 = a
a 3ab + 2a2 + 2b2
AF 0 = a + b
=
2
b 4ab + 3a2 + 2b2
2
2 (a + b)
2 (a + b)
Si consideramos ahora 4F1 F O rectángulo en F 0 por Pitágoras
0
OF12
0
2
=F O +F
0
F12
=
OF12
b2 4ab + 3a2 + 2b2
4
2
+
a2 (2a + b) (a + 2b) 3ab + 2a2 + 2b2
4(a + b)4
4 (a + b)
Calculando y factorizando
=
a2 + ab + b2
2
(a + b)
2
() OF1 =
2
a2 + ab + b2
a+b
Como OF1 + F1 G1 = OG1 = a + b …nalmente obtenemos que
F1 G 1 = a + b
a2 + ab + b2
ab
=
a+b
a+b
Lo que nos permite a…rmar que los círculos (F1 ) y (G1 ) son arquimedianos
Si ahora consideramos el punto E1 y trazamos por él una paralela al segmento AB y escogemos un punto H1 en dicha paralela
ab
es obvio que los circulos (E1 ) y (H1 ) son arquimedianos
tal que D(E1 ; H1 ) = 2D(L; O1 ) = a+b
Los círculos (H2 ) y (E2 ) son arquimedianos ya que son simétricos de (E1 ) y (H1 ) con respecto a la recta perpendicular a AB
que pasa por O0
Los otros círculos (F2 ) y (G2 ) también son arquimedianos
3