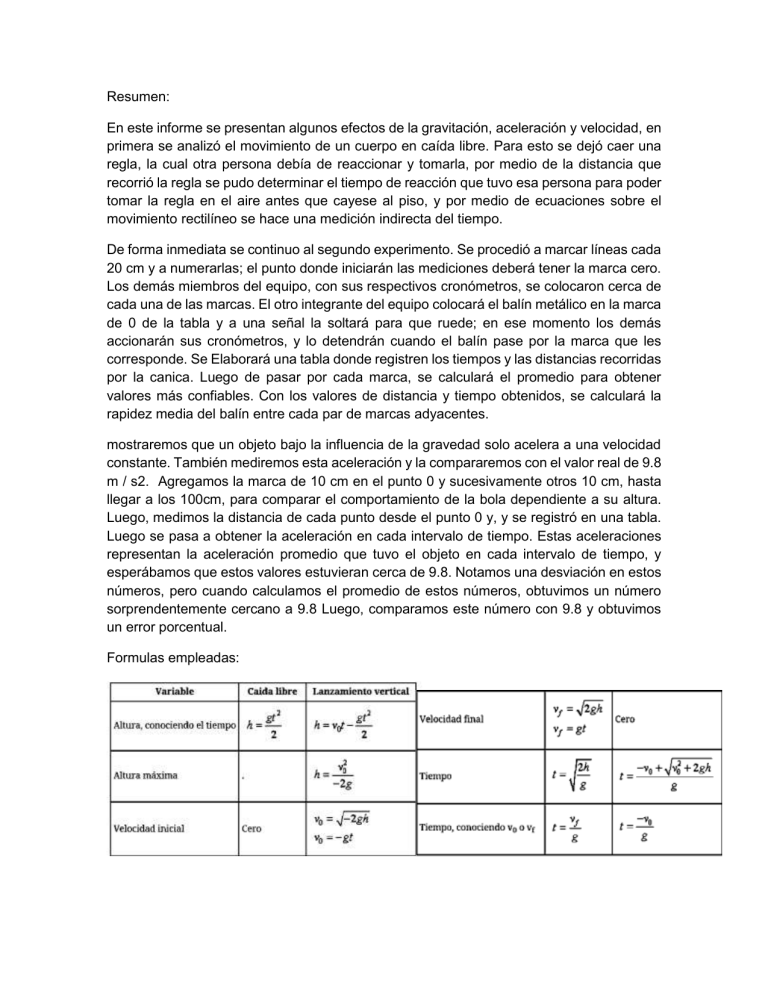
Resumen: En este informe se presentan algunos efectos de la gravitación, aceleración y velocidad, en primera se analizó el movimiento de un cuerpo en caída libre. Para esto se dejó caer una regla, la cual otra persona debía de reaccionar y tomarla, por medio de la distancia que recorrió la regla se pudo determinar el tiempo de reacción que tuvo esa persona para poder tomar la regla en el aire antes que cayese al piso, y por medio de ecuaciones sobre el movimiento rectilíneo se hace una medición indirecta del tiempo. De forma inmediata se continuo al segundo experimento. Se procedió a marcar líneas cada 20 cm y a numerarlas; el punto donde iniciarán las mediciones deberá tener la marca cero. Los demás miembros del equipo, con sus respectivos cronómetros, se colocaron cerca de cada una de las marcas. El otro integrante del equipo colocará el balín metálico en la marca de 0 de la tabla y a una señal la soltará para que ruede; en ese momento los demás accionarán sus cronómetros, y lo detendrán cuando el balín pase por la marca que les corresponde. Se Elaborará una tabla donde registren los tiempos y las distancias recorridas por la canica. Luego de pasar por cada marca, se calculará el promedio para obtener valores más confiables. Con los valores de distancia y tiempo obtenidos, se calculará la rapidez media del balín entre cada par de marcas adyacentes. mostraremos que un objeto bajo la influencia de la gravedad solo acelera a una velocidad constante. También mediremos esta aceleración y la compararemos con el valor real de 9.8 m / s2. Agregamos la marca de 10 cm en el punto 0 y sucesivamente otros 10 cm, hasta llegar a los 100cm, para comparar el comportamiento de la bola dependiente a su altura. Luego, medimos la distancia de cada punto desde el punto 0 y, y se registró en una tabla. Luego se pasa a obtener la aceleración en cada intervalo de tiempo. Estas aceleraciones representan la aceleración promedio que tuvo el objeto en cada intervalo de tiempo, y esperábamos que estos valores estuvieran cerca de 9.8. Notamos una desviación en estos números, pero cuando calculamos el promedio de estos números, obtuvimos un número sorprendentemente cercano a 9.8 Luego, comparamos este número con 9.8 y obtuvimos un error porcentual. Formulas empleadas:










