Fórmulas trigonométricas
Anuncio

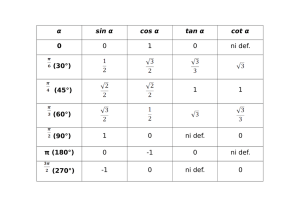
sin (A + B) = sinA cosB + sinB cosA sin (A – B) = sinAcosB – sinB cosA cos (A + B) = cosA cosB – sinA cosB cos (A – B) = cosA cosB + sinA sinB tan (A + B) = tanA + tanB 1 – tanA tanB tan (A – B) = tanA – tanB 1 + tanA tanB cot (A + B) = cotA + cotB - 1 cotA + cotB cot (A – B) = cotA + cotB + 1 cotA – cotB MULTIPLE ANGLE FORMULA sin 2A = 2sinA cosA cos 2A = cos2A – sin2A = 1 – 2sin2A = 2cos2A – 1 tan 2A = 2tanA 1 – tan2A cot 2A = cot2A – 1 2cotA HALF ANGLE FORMULAS sin A = 1 + cosA 2 2 cos A = 1 + cos2A 2 2 tan A = 1 – cosA 2 1 + cosA cot A = 1 + cosA 2 1 – cosA PYTHAGOREAN IDENTITIES sin2A + cos2A = 1 1 + cot2A = csc2A 1 + tan2A = sec2A ANGLE RELATIONSHIPS cos ( + ) = - cos cos ( - ) = - cos sin ( + ) = - sin sin ( - ) = sin tan ( + ) = tan tan ( - ) = - tan cot ( + ) = cot cot ( - ) = - cot sec ( + ) = - sec sec ( - ) = - sec csc ( + ) = - csc csc ( - ) = csc sin cos tan VALUES OF STANDARD ANGLES (30) (60) (45) (0) (180) (270)(360) (90) 0 /6 /3 /4 3/2 2 /2 ½ 0 -1 0 1 3/2 2/2 0 -1 0 1 0 3/3 ½ 2/2 1 1 3/3 3 sin (A + B) = sinA cosB + sinB cosA sin (A – B) = sinAcosB – sinB cosA cos (A + B) = cosA cosB – sinA cosB cos (A – B) = cosA cosB + sinA sinB tan (A + B) = tanA + tanB 1 – tanA tanB tan (A – B) = tanA – tanB 1 + tanA tanB cot (A + B) = cotA + cotB - 1 cotA + cotB cot (A – B) = cotA + cotB + 1 cotA – cotB MULTIPLE ANGLE FORMULA sin 2A = 2sinA cosA cos 2A = cos2A – sin2A = 1 – 2sin2A = 2cos2A – 1 tan 2A = 2tanA 1 – tan2A cot 2A = cot2A – 1 2cotA HALF ANGLE FORMULAS sin A = 1 + cosA 2 2 cos A = 1 + cos2A 2 2 tan A = 1 – cosA 2 1 + cosA cot A = 1 + cosA 2 1 – cosA PYTHAGOREAN IDENTITIES sin2A + cos2A = 1 1 + cot2A = csc2A 1 + tan2A = sec2A ANGLE RELATIONSHIPS cos ( + ) = - cos cos ( - ) = - cos sin ( + ) = - sin sin ( - ) = sin tan ( + ) = tan tan ( - ) = - tan cot ( + ) = cot cot ( - ) = - cot sec ( + ) = - sec sec ( - ) = - sec csc ( + ) = - csc csc ( - ) = csc sin cos tan VALUES OF STANDARD ANGLES (30) (60) (45) (0) (180) (270)(360) (90) 0 /6 /3 /4 3/2 2 /2 ½ 0 -1 0 1 3/2 2/2 0 -1 0 1 0 3/3 ½ 2/2 1 1 3/3 3







![Phoenix ED [Basics of Trigonometry] 9831333221 Page 1 y = tan x y](http://s2.studylib.es/store/data/008088045_1-5ae736332d368b28c47ea0fe1ab398d4-300x300.png)


