1 COLEGIO AXAYACATL SECUNDARIA 1º

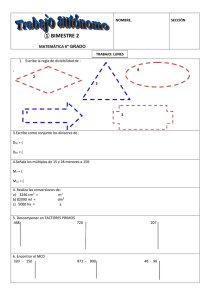
COLEGIO AXAYACATL
SECUNDARIA 1º
TEMARIOS 2DO BIMESTRE
2015-2016
Características de la entrega del temario.
TODOS LOS TEMARIOS DEBEN DE TENER LAS MISMAS CARACTERISTICAS
a)
b)
c)
d)
Podrán imprimirlos y deberá estar resuelto a mano, respetando la calidad.
Debe elaborarse una carátula que contenga tus datos personales y el de la asignatura.
Entrégalo en TU CARPETA DE TEMARIOS en perfectas condiciones.
El temario es derecho a examen y no se acepta ningún tipo de pretexto.
MATERIA: ESPAÑOL
PROF. RAFAEL CARMONA MARTÍNEZ
El presente temario es requisito indispensable para presentar examen bimestral y no necesariamente
implica puntos extra en la calificación final obtenida.
Lee, analiza y desarrolla los temas que se solicitan.
1.
2.
3.
4.
5.
6.
7.
Define qué es una monografía.
Menciona y explica cada una de las partes de la monografía.
Define qué es un párrafo.
Menciona y explica cada uno de los tipos de párrafo.
Explica qué es una descripción.
Explica cuáles son las principales características de la narrativa.
Menciona cuáles son los principales los géneros narrativos más importantes y explica cada uno
de ellos.
8. Define qué son los personajes.
9. Define qué es un narrador.
10. Explica la función de cada uno de los tipos de narrador.
11. Explica cómo está compuesta la estructura de los cuentos.
12. Desarrolla el concepto de noticia.
13. Teóricamente, explica cómo debe darse a conocer una noticia.
14. Explica qué es un debate y cuál es su principal función.
15. Menciona cuáles son los principales elementos que componen un debate. Explica la función de
cada uno de ellos.
16. Menciona y explica que elementos debemos analizar al realizar un análisis comparativo de
noticias.
MATERIA: GEOGRAFÍA DE MÉXICO Y DEL MUNDO
PROF. VICTOR HUGO RAMIREZ MORALES
1. Elabora un cuadro sinóptico sobre el uso de escalas (numérica/gráfica) en los mapas.
2. En una milimétrica representa lo siguiente:
a. Una bodega de superficie rectangular con un área de 100 metros cuadrados. Identifica de
color azul su barda perimetral.
b. Una habitación de superficie cuadrangular con un área de 16 metros cuadrados. Identifica
de color verde su barda perimetral.
c. Una habitación de superficie hexagonal con un área de 50 metros cuadrados. Identifica de
color café su barda perimetral.
Recuerda que es necesario indica la escala que diseñaste para representar cada superficie.
3. En un planisferio tamaño carta sin nombres y sin división política identifica TODOS los husos
horarios que existen en la superficie terrestre.
4. Elabora un mapa mental sobre la utilidad de la información geográfica de imágenes de satélite,
Sistema de Posicionamiento Global y Sistemas de Información Geográfica para el conocimiento
geográfico.
5. Elabora un mapa conceptual sobre la tectónica de placas y menciona la importancia de esta teoría
para el estudio de los movimientos sísmicos.
1
6. En un planisferio tamaño carta sin nombres y sin división política identifica las principales placas
tectónicas. Diseña una simbología adecuada para representar esta información.
7. En un mapa de la república mexicana tamaño carta sin nombres y sin división política identifica las
placas tectónicas que se encuentran en el territorio mexicano. Diseña una simbología adecuada
para representar esta información.
8. Elabora un mapa conceptual sobre las causas y consecuencias de los movimientos sísmicos.
9. Elabora un cuadro sinóptico sobre el vulcanismo y la sismicidad.
10. Define brevemente (2-4 líneas c/u) los siguientes conceptos:
a. Regiones sísmicas.
b. Regiones volcánicas.
c. Diversidad natural.
d. Relieve continental.
e. Relieve oceánico.
MATERIA: CIENCIAS I BIOLOGÍA
PROFESORA: ANDREA CAROLINA GODÍNEZ REYES
 Dibuja y escribe 1 ejemplo de alimentos que contengan carbohidratos.
 Dibuja y escribe 1 ejemplo de alimentos que contengan vitaminas y minerales.
 Dibuja y escribe 1 ejemplo de alimentos que contengan lípidos.
 Dibuja y escribe 1 ejemplo de alimentos que contengan Proteínas.
 Dibuja y escribe 1 ejemplo de animales que lleven a cabo una nutrición heterótrofa.
 Dibuja y escribe 1 ejemplo de animales que lleven a cabo una nutrición autótrofa.
 Responde a las siguientes preguntas:
 ¿Qué es la bulimia?
 ¿Qué es la anorexia?
 ¿En qué consiste la defensa Mecánica? Escribe dos ejemplos
 ¿En qué consiste la defensa Química? Escribe dos ejemplos
 ¿En qué consiste la defensa de Comportamiento? Escribe dos ejemplos
 ¿Qué es el mimetismo? Escribe dos ejemplos
 ¿Qué es el camuflaje? Escribe dos ejemplos
 Escribe dos alimentos convencionales
 Escribe dos alimentos no convencionales
 Escribe dos alimentos que sean comida rápida
 ¿Cuál es la función que realiza los cloroplastos?
 ¿Cuál es la función que realiza los estomas?
 ¿Cuál es la función que realiza la clorofila?
 En un esquema del aparato digestivo identifica los siguientes órganos utilizando los siguientes
colores:
- Rosa - Boca
- Verde - Esófago
- Amarillo - Estómago
- Rojo - Páncreas
- Morado - Vesícula Biliar
- Anaranjado - Intestino delgado
- Café - Intestino grueso
- Negro - Ano
1. Escribe la operación que permite conocer el índice de masa corporal
2. Resuelve el siguiente problema, para conocer el índice de masa corporal de Patricia
- Patricia tiene 14 años, su estatura es de 1.56 cm y pesa 54 kg. ¿Cuál es su índice de masa corporal?
(Realiza las operaciones)
2
MATERIA: MATEMÁTICAS
PROFA. AMADA
Recomendaciones generales: Procura prepararte para tu examen con anticipación, resuelve los
ejercicios que se te presentan en esta guía los cuales vienen acompañados de una pequeña explicación.
CRITERIOS DE DIVISIBILIDAD
Sirven para saber si un número es divisible entre otro sin necesidad de realizar la división.
Divisible significa que al dividirlo entre ese número el resultado es una división exacta con residuo
cero. Por ejemplo, 30 es divisible entre 5 porque al dividirlo entre 5 el residuo es cero 30 ÷ 5 = 6
Divisibilidad entre 2
Un número es divisible entre 2 si termina en 0 o cifra par.
Ejemplos:
2, 38, 94, 521 346, 40, ...
Divisibilidad entre 3
Un número es divisible entre 3 si la suma de todos sus dígitos es un múltiplo de 3.
Ejemplos:
36, 2 142, 42, 2 439, 717, 30 651 ...
Divisibilidad entre 5
Un número es divisible entre 5 si la última cifras es 5 ó 0.
Ejemplos:
35, 2 145, 400, 367 870, 85, ...
Divisibilidad entre 10
Un número es divisible entre 10 si termina en 0.
Ejemplos:
70, 234 140, 900, 7 870, 858 670 ...
Estos criterios son importantes dado que te facilitan el cálculo de la descomposición de factores que
a su vez sirven para reducir y simplificar fracciones.
Ejercicio
Coloca una X en la columna que corresponda
Número
Divisible Divisible Divisible Divisible
entre 2
entre 3
entre 5 entre 10
311 040
270
1 080
54
224
2 160
360
NÚMEROS PRIMOS Y COMPUESTOS
Los números primos son aquellos que sólo admiten dos divisores, la unidad y el mismo número: como
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, etc.
Los números compuestos son aquellos que admiten más de dos divisores como 4, 6, 8, 9, 10, 12, etc.
El número 1, sólo tiene un divisor, y se llama unitario o unidad.
FACTORIZACIÓN
3
Para descomponer números en factores primos puedes utilizar divisiones sucesivas entre números
primos, empezando por el número 2:, hasta tener como residuo cero.
Los factores primos de 60 se obtienen:
30
15
5
1
2 60
2 30
3 15
5 5
00
10
0
0
0
Observa que dividiste entre:
2, 2, 3, 5 y éstos son los factores primos, es decir:
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
Puedes facilitar el procedimiento colocando una línea vertical para indicar, las divisiones:
60
30
15
5
1
2
2
3
5
Factores primos
60 = 2 x 2 x 3 x 5
60 = 22 x 3 x 5
Ejercicio 1
Escribe en donde corresponda, los números primos y compuestos:
21, 16, 12, 30, 17, 24, 40, 29, 35, 56, 45, 46, 4, 14, 11, 51, 7, 28, 3, 46, 25, 31, 70
NÚMEROS PRIMOS
NÚMEROS COMPUESTOS
Ejercicio 2
Obtén la descomposición en factores de los siguientes números y escríbelos sobre la línea
correspondiente:
1)
75
2)
90
3) 5 2 5
4) 3 3 0
75 = _____________
90 = _____________
525 = ____________
330 = _____________
5) 6 4 8
6) 1 4 4
7) 1 5 0
8) 2 2 4
648 = ____________
144 = _____________
150 = ____________
224 = _____________
5) 3 2 4
6)
7) 4 7 0
8) 7 2 0
324 = ____________
15 = _____________
470 = ____________
720 = _____________
15
MÍNIMO COMÚN MÚLTIPLO
Se llama mínimo común múltiplo de dos o más números al menor de sus múltiplos comunes.
Se designa por las iniciales m.c.m.
4
Ejemplo:
El mínimo común múltiplo de 12 y 30 es:
12: 12, 24, 36, 48, 60, 72, . . . .
3: 30, 60, 90, 120, 150, . . .
Ve que el múltiplo común menor de 12 y 30 es 60; simbolizando tenemos:
m. c. m. ( 12 y 30 ) = 60
Una manera más sencilla para obtener el m.c.m. es obteniendo los factores primos con mayores
exponentes y multiplicarlos.
Ejemplo:
Obtén el mínimo común múltiplo de 12 y 30
12 2
30 2
6 2
15 3
3 3
5 5
1
1
12 = 22 x 3
30 = 2 x 3 x 5
Observa que los dos números tienen como factor común a 2
12 = 22 x 3
30 = 2 x 3 X 5
Este factor común difiere en el exponente y se elige al mayor exponente que es 2 2
Otro factor común es el 3, como tienen el mismo exponente se elige cualquier 3
12 = 22 x 3
30 = 2 x 3 x 5
Además hay un factor no común que es 5
12 = 22 x 3
30 = 2 x 3 x 5
Y para obtener el mínimo común múltiplo, se multiplica el factor común de mayor exponente, por los
factores no comunes.
m. c. m. ( 12, 30 ) = 22 x 3 x 5
= 4 x 3 x 5
m. c. m. ( 12, 30 ) = 60
Ejercicio 1
Calcula el m.c.m. de los siguientes números:
a) m.c.m. ( 9, 18 ) =
b) m.c.m. ( 18, 30, 24 ) =
c) m.c.m. ( 15, 65, 25 ) =
d) m.c.m. ( 20, 40, 60 ) =
f) m.c.m. ( 60, 45, 50 ) =
e) m.c.m. ( 50, 75, 100 ) =
Ejercicio 2
Resuelve los siguientes problemas
5
1. El número de días que han de transcurrir como mínimo para que tres agentes viajeros vuelvan a
coincidir en Guadalajara ya que el primero tarda en su recorrido 18 días, el segundo 15 días y el
tercero 8 días.
2. Los soldados de un regimiento pueden formar filas de dos en dos, de tres en tres, de cuarenta y ocho
en cuarenta y ocho, de ciento veinte en ciento veinte y de ciento veintiséis en ciento veintiséis, sin
que sobre ni falte ninguno. Cuántos soldados integran el regimiento?
MÁXIMO COMÚN DIVISOR
Se llama máximo común divisor de dos o más números al mayor de sus divisores comunes.
Se designa por las iniciales M. C. D.
Para calcular el M. C. D. de dos o más números, se descompone cada uno en sus factores primos.
Ejemplo:
Calcula el M. C. D. de los números 24, 48, 72 =
24
12
6
3
3
1
48
24
12
6
3
1
72
36
18
9
9
3
3
1
2
2
2
2
3
3
3
24 = 23 x 3
48 = 24 x 3
72 = 23 x 32
Los números tienen divisores comunes que son 2 y 3, posteriormente se elige el divisor común con
menor exponente los divisores comunes 23 y 3, que al tener el mismo exponente no presentan
problemas ya que cualquiera que se escoja es igual.
M.C.D. ( 24, 48, 72 ) = 23 x 3 = 8 x 3 = 24
Ejercicio 1
Calcula el M. C. D. de los siguientes números:
a) M. C. D. ( 15, 30 ) =
b) M. C. D. ( 24, 36, 48 ) =
c) M. C. D. ( 140, 160, 100 ) =
a) M. C. D. ( 60, 40, 30 ) =
b) M. C. D. ( 50, 75, 100 ) =
c) M. C. D. ( 40, 48, 72 ) =
Ejercicio 2
Resuelve los siguientes problemas:
1. Se tienen tres rollos de listón de 8m, 12m y 60m respectivamente. Si se deben cortar en tramos
iguales de la mayor medida posible, sin que falte o sobre listón ¿De qué medida tiene que ser cada
tramo? y ¿cuántos tramos resultarán de cada rollo?
2. Un ebanista quiere cortar una plancha de madera de 256 cm de largo y 96 cm de ancho, en
cuadrados lo más grandes posible. ¿Cuál debe ser la longitud del lado de cada cuadrado?
3. Diego cuenta con 12 juguetes, 36 chocolates y 48 dulces. Desea hacer unas cajas sorpresas iguales
que contengan lo mismo para sus amigos. ¿Cuál es la cantidad de cajas que puede formar?
6
4. Leticia tiene tres carretes con hilo cáñamo, uno de 30 cm, otro de 20 cm y el último de 80 cm y desea
cortarlos en tramos de igual medida sin que le sobre nada- ¿Cuál es el máximo tamaño que pueda
tener los trozos de cáñamo?
5. Pablo compró una canasta de 24 huevos y otra de 36 huevos. Para venderlos, Pablo debe
empacarlos en cajas pequeñas del mismo tamaño que contengan el mismo número de huevos. ¿Cuál
es el mayor número de huevos que puede empacar Pablo en cada caja, si no debe sobrar ni faltar
ninguno? ¿De cuántas cajas debe disponer?
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES COMUNES CON IGUAL DENOMINADOR
Sólo se suman o restan según sea el caso los numeradores y se anota el mismo denominador.
Recuerda siempre sacar enteros si la fracción es impropia o simplificar.
Siempre ten presente que para obtener los enteros necesitas realizar la división y para simplificar una
fracción a su mínima expresión, se dividirán sus dos términos sucesivamente por los divisores
comunes que tengan, hasta que resulte una fracción irreducible.
Ejemplo:
11 14 25



15 15 15
10
15
2
3
1 =1
Fracción impropia se debe sacar enteros
23 15
8
4



10 10 10 5
Simplificación
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES COMUNES CON DIFERENTE DENOMINADOR
Se obtiene el m.c.m. de los denominadores, el número obtenido será el denominador común, el m.c.m.
se divide entre el denominador de la primera fracción y el cociente obtenido se multiplica por el
numerador de esa fracción. El número obtenido se coloca como sumando en el numerador de la
fracción resultante y se procede igual para el resto de las fracciones; en la sustracción se siguen los
mismos pasos, sólo que los números obtenidos se restan.
Ejemplo:
2 x 5 = 10
Se multiplica
x
10
5
2
9



15
3
10
30
÷
15 3
15
5 1
1 1
Se divide
30 ÷ 15 = 2
5 2 9 10  20  27 57
 



15 3 10
30
30
27
=
30
10
3
5
1
2
5
5
3
m.c.m. (15, 3, 10) = 2 x 3 x 5 = 30
9
10
1 1
Ejemplo
44  35
11
7
9



10
8
40
40
10 8
2
7
5 4 2
5 2 2
5 1 5
1 1
m.c.m. (10,8) = 23 x 5 = 40
ADICIÓN Y SUSTRACCIÓN CON NÚMEROS MIXTOS
Se convierten los números mixtos a fracciones impropias (multiplicando el denominador de la fracción
por el entero y al producto obtenido se le suma el numerador), y se deja el mismo denominador de la
fracción del número mixto. Ejemplo:
1
6
136  156  76
368
17
52
19
+
+
=
=
=
3
6
8
24
24
2
3
4
8
3
–
4
1
27
7
27  14 13
=
–
=
=

2
2
4
4
4
5 +6 +3 =
6 3
8
=
24
1
3
15 15
1
4
3
Ejercicio 1
Resuelve las siguientes adiciones y sustracciones
3 2
1)
6
10
3



4
4
4
2)
2
13
8
7




15
15
15
15
3)
11
7


10
8
8)
9
4


5
8
4)
5
2
1



6
3
4
9)
4
3


12
16
5)
9
2


10
8
10)
7)
Ejercicio 2
Resuelve los siguientes problemas
10
1. El maestro de electricidad tenía
conexión y le ha quedado
7
2. Elisa compra
2

7
6)
1
m
2
4

7
4
1
2
+
+
3
9
9
5
6
–
2
1
5
=
6
4
9
=
10
de cable eléctrico. Lo usó para mostrar cómo se hace una
3
m, ¿cuánto cable utilizó en la conexión?
4
3
1
kg de papas,
kg de carne y
4
2
20
1
2
de tortillas, ¿Cuánto pesa todo junto?
5
3
4
8
3. De una pieza de tela de
tela queda sin vender?
1
m se vendieron 2 retazos de
2
1
my
2
3
m. ¿Qué cantidad de
4
4. En la Delegación Política Benito Juárez se realiza una competencia de ciclismo, en la que se tienen
65
que recorrer,
40
1
km y en la cual Eduardo lleva recorridos
4
para llegar a la meta?
5. El Satélite "Explore 40" tiene un peso de
3
km ¿Qué distancia le falta
4
28
4
toneladas y el Satélite" Anna l-B" pesa
de tonelada
25
125
¿Cuál es la diferencia de peso entre ambos satélites?
MATERIA: MATEMÁTICAS
PROF. LEOPOLDO MARTINEZ BEJAR
Representa en la recta numérica 10 sumas cualesquiera.
Representa en la recta numérica 10 restas cualesquiera.
Anota 10 sumas cualesquiera, que se compongan de 4 sumandos y 5 dígitos cada sumando; al terminar
estima su suma a millares y a centenas.
Redondea a centenas, decenas de millar, enteros y milésimos cada una de las siguientes cifras.
a)
b)
c)
d)
e)
2864556.122324
9856651.12331268
56458456.3559456
325545.545322
5454651256.564555
Trunca cada una de las siguientes cifras a millares y a enteros.
a)
b)
c)
d)
e)
2864556.122324
9856651.12331268
56458456.3559456
325545.545322
5454651256.564555
Realiza 5 ejemplos de cada una de las propiedades de la adición.
Realiza 5 ejemplos de cada una de las propiedades de la multiplicación.
Realiza cada una de las siguientes operaciones de números con signo.
1) -7+9=
6) 10-50=
11) -2-6=
2) -56+5=
7) 67-200=
12) -89-45=
3) -8+1=
8) 123-789=
13) -34-78=
4) -90+2=
9) 44-122=
14) -45-789=
5) -124+0=
10) 90-234=
15)-7-99=
16) -78-90+56-2+8=
21) (3)+(-2)-(7)-(-4)-(9)+(-2)=
17) 79+23-67-9-2+1=
22) (13)+(-12)-(17)-(-14)-(19)+(-12)=
18) -34-56+3+4-2-1=
23) (23)+(-22)-(27)-(-24)-(29)+(-22)=
19) 789-23-23-4+1+1-2=
24) (33)+(-32)-(37)-(-34)-(39)+(-32)=
20) 56+8+9+2-1-1-2-3-4=
25) (43)+(-42)-(47)-(-44)-(49)+(-42)=
26) 2+(4-5-7+(4-6)-8)-(4+3+4-5-7)+(-3-4-(5-8-8-(9-9+7+2+4)+4)+3)=
27) 1+(4-5-7+(7-7)-8)-(4+3+7-7-7)+(-3-7-(5-8-8-(9-9+7+6+6)+6)+7)=
28) 2+(3-3-3-(4-6)-3)-(3+3+3-3-3)+(-3-3-(5-8-3-(3-9+7+3+4)+3)+3)=
29) 4+(4-4-4+(4-4)-4)-(4+4+4-4-7)+(-4-4-(4-8-8-(4-4+7+4+4)+4)+4)=
30) 5+(4-5-5+(5-5)-5)-(54+3+4-5-5)+(-5-4-(5-5-8-(9-5+7+5+5)+4)+5)=
31) 6+(4-5-6+(6-6)-6)-(4+6+4-6-6)+(-6-4-(6-8-8-(6-6+7+6+6)+6)+6)=
9
32) 7+(7-7-7+(7-7)-7)-(4+3+4-7-7)+(-7-7-(7-7-7-(7-9+7+7+4)+7)+7)=
33) 8+(8-5-8+(8-6)-8)-(4+8+4-5-8)+(-8-8-(8-8-8-(8-8+7+8+8)+8)+8)=
34) 9+(9-5-9+(9-6)-9)-(4+3+4-5-9)+(-9-4-(9-7-9-(9-9+9+9+9)+9)+3)=
35) 2+(1-5-7+(4-6)-8)-(1+3+4-5-7)+(-3-4-(4-8-8-(9-9+7+2+4)+14)+3)=
36) 2+(4-5-7+(4-6)-8)-(4+3+4-5-7)+(-3-4-(5-7-8-(9-9+7+2+4)+4)+3)=
37) 2+(3-5-7+(4-6)-8)-(4+3+4-5-7)+(-3-4-(4-8-8-(9-9+7+2+4)+4)+3)=
38) 2+(3-5-7+(1-6)-8)-(5+3+4-5-7)+(-3-4-(4-7-8-(9-9+7+2+4)+4)+3)=
39) 5+(4-5-7+(4-6)-8)-(4+3+4-5-7)+(-3-4-(5-8-8-(9-9+7+2+4)+4)+3)=
40) 6+(4-5-7+(4-6)-8)-(4+3+4-5-7)+(-3-4-(5-7-8-(9-9+7+2+4)+4)+6)=
Realiza cada una de las siguientes ecuaciones.
1) (-4)+(x)=2
5) 8+(x)=-1
9) (x)+(-3)=-5.4
13) (x)+6=3
17) (-7)+(x)=6
21) 3/4x=1
25) 2/3x=1
29) x+2/3=2/3
33) 3/2+x=-5/4
37) x(-2/5)=4/15
41) 4x=-12
45) -2x=-6/5
49) 6x=-1/2
53) x:1/2=-3/4
2) (x)+(-4)=-7
3) x+7=-3
4) -5+x=-12
6) 5+(x)=-5
7) 5+x=9
8) x+9=-5
10) (x)+3=9.5
11) x+2=-8.5
12) -6+x=-2
14) (-10)+(x)=2
15) -3+x=7
16) x+10=-6
18) (-3)+(x)=-11
19) x+1=0
20) -8+x=-15
22) 5x=1
23) 1/6x=1
24) 7x=1
26) 5/4x=1
27) 1/4x=3/4
28) x+(-5/6)=-1/6
30) -1.75+x=-1.25 31) -2.4x+x=-3.1
32) x+(-2)=-3/4
34) x+(-2/3)=1/6 35) -3x=6
36) 3/4x=-3/8
38) 8x=-8/3
39) -3/2X=6
40) x(-3/4)=6/12
42) 2x=-2/3
43) 5x=15/4
44) -3x=-3/4
46) -5x=-10/3
47) 8x=-4
48)-2x=-8/5
50) x:3/5=1/2
51) 5/7:x=5/14
52) x:-2/3=-6/5
54) 4:x=-4/3
55) x:-2=-3/5
56) x:-3/4=-2
MATERIA: CULTURA DE LA LEGALIDAD
PROF. IGNACIO GÓMEZ TAGLE GUERRERO
I.
Lee cuidadosamente las siguientes afirmaciones y relaciona según corresponda:
Conforma su entorno para facilitar su vida y hacerla más confortable
1
SER CREATIVO
Es una consecuencia de su ser social y de su libertad.
2
SER POLITICO
Elabora códigos de expresión oral, corporal y de sonidos para
transmitir pensamientos e ideas.
Crea una relación de interdependencia con la naturaleza.
3
SER COMUNICATIVO
4
SER ECOLOGICO
Elabora formas de convivencia con la naturaleza para la mejor
administración de los recursos.
Necesitan de la interacción para la transmisión de valores y cultura
Desarrollan formas de relación, acuerdos, jerarquías para fines
públicos.
Observa, analiza y encuentra características y aplicaciones a su
entorno.
1.
2.
3.
4.
5.
II.
Completa:
La _________________________________ Garantiza los derechos y establece las obligaciones para los
mexicanos.
Es el resultado de ________________________ políticas, sociales y económicas en distintas etapas de la
historia del país.
Se considera como ____________________________ pues nadie, ni las autoridades están por encima de sus
mandatos, lineamientos y principios.
Fue publicada el ____________________________________ y es vigente a la fecha, pues no tiene límite de
tiempo por eso se dice que es __________________________.
Su carácter de ____________________ permite contemplar y adaptarse a las nuevas realidades.
10
6. Establece al país en una forma de gobierno _________________________________________, compuesta por
Estados __________________________________.
7. Las _________________________________ protegen los derechos fundamentales de cada individuo del país.
8. Consideran los principios de igualdad, libertad, seguridad jurídica que el Estado debe respetar, a
través de los ________________________________________.
III.
Señala el Artículo Constitucional que señala cada Garantía Individual.
Prohíbe la
esclavitud y los
títulos de nobleza
Derecho a la
Información
Libertad de
pensamiento
Derecho a la
Educación
Derecho a la
Intimidad (seguridad
y propiedad privada)
Libertad de
Tránsito
Derecho a la
Equidad
Libertad de Culto y
creencias
Libertad de
pensamiento e
imprenta
Preserva la igualdad
prohibiendo los
juicios en tribunales
especiales
MATERIA: MÚSICA
PROF. ELISEO PIOQUINTO MENDOZA
1.- Escala musical.
Tema 2.- Valores musicales.
Tema 3.-Armaduras de escalas con sostenidos.
Tema 4.- Armaduras de escalas con bemoles.
11
Tema 5.- Como está conformada una Orquesta Sinfónica.
PIANO
ARPA
VIOLINES
CORO
PERCUSIONES
ALIENTOS METAL
ALIENTOS MADERA
VIOLAS
DIRECTOR
CONTRABAJOS
CELLOS
Tema 6.-Instrumentos musicales.
Tema 7.- Música Barroca:
La música del periodo barroco es el género musical relacionado con una época cultural europea, que
abarca desde el nacimiento de la ópera en el siglo XVII (aproximadamente en1600) hasta la mitad
del siglo XVIII (aproximadamente hasta la muerte de Johann Sebastián Bach, en 1750).
Se trata de una de las épocas musicales más largas, fecundas, revolucionarias e importantes de la
música occidental, así como la más influyente. Su característica más notoria es probablemente el uso
del bajo continuo y el monumental desarrollo de la armonía tonal, que la diferencia profundamente de
los anteriores géneros modales.
Características
El género hoy llamado "barroco" se caracteriza estéticamente por la preeminencia de lo emocional
sobre lo racional, por el género vocal recitativo, en el cual el ritmo de la palabra determina el discurso
melódico -donde "la música ha de ser sirviente de la poesía"- y por un auge de la música instrumental
pura, es decir, sin relación con consideraciones ideológicas que se deriven de un texto, o funcionales
como en el caso de la música de danza.
En esta época se desarrollan la sonata, el Concerto Grosso y el ballet francés.
A diferencia de épocas anteriores, la música sacra y la música profana conviven armoniosamente,
formando parte de la profesión musical. La mayor permisividad estética lleva a que la interpretación
musical tienda a enriquecer las partes mediante una profusión de ornamentos y recursos expresivos.
12
Una característica importante fue que los detalles del arte en el Barroco no se aplicaron a la música. Se
buscó en un principio desechar las complicadas líneas melódicas de la polifonía renacentista para dar
lugar a la homofonía (más tarde la polifonía recuperará con Bach todo el esplendor que la había
caracterizado), dando de esta manera más fortaleza y protagonismo al texto, pues la música giraba en
torno a una sola melodía bien formada y acompañada por acordes, para que fuera "entendible" el texto.
Esto fue debido en gran parte a la corriente humanista.
Tienen gran importancia la teoría de los afectos, que considera a la música como creadora de
emociones, y la retórica, que transfiere conceptos de la oratoria tradicional a la composición del
discurso musical del Barroco.
El Barroco temprano (1600-1650)
Este período es conocido como el seicento: alrededor del año 1600 se destaca en la historia de la
música un compositor de inusual talento, Claudio Monteverdi. Fue un maestro de los dos géneros
entonces preponderantes: la prima prattica o el polifónico género madrigal y la seconda prattica o
recitativo de la música vocal solista. Compuso una de sus obras de Calahorra más famosas, el "Lamento
d'Arianna", tanto en versión polifónica como en versión para solista y bajo continuo. Monteverdi
y Antonio Vivaldi fueron los dos compositores estudiados más asiduamente por Johann Sebastian
Bach.
La seconda prattica, un subgénero de monodia acompañada, esto es, una o varias voces solistas y bajo
continuo, caracteriza la música de este período.
El Barroco medio (1650-1700)
El Barroco medio es el lapso comprendido entre 1650 y 1700; en él sobresalían el compositor
inglés Henry Purcell (1659 - 1695) y su contemporáneo alemán Johann Pachelbel (1653 - 1706).
El Barroco tardío (1700-1750)
El Barroco tardío va entre 1700 y 1750 (aproximadamente) y sus compositores característicos son: en
España Domenico Scarlatti, en Italia Antonio Vivaldi, en Inglaterra Georg Friedrich Händel, en
Alemania Johann Sebastian Bach y en Francia Jean Philippe Rameau.
Tema 8.- Música Gregoriana:
Historia
El origen del Canto Gregoriano y la liturgia
El nombre de canto gregoriano proviene del papa Gregorio I (590-604), quien introdujo importantes
modificaciones en la música eclesiástica utilizada hasta ese momento para la liturgia del rito romano.
Además de dichas modificaciones, fue autor de numerosas obras y melodías, como la Regula pastoralis,
el Libri quattuor dialogorum o diversas homilías.
La música en la liturgia cristiana existente hasta entonces tenía su origen en las sinagogas judías, por lo
que fue, al principio, exclusivamente vocal, sin la utilización de instrumentos musicales y con
predominio de la lengua helenística; para ello, un cantor solista, generalmente el sacerdote, dirigía los
rezos, que eran contestados por los asistentes a la celebración mediante la utilización de sencillos
motivos.
Poco a poco, en Occidente fue evolucionando, y se produjeron tres cambios importantes:



Apareció a finales del siglo VII un pequeño grupo de cantores elegidos que asumió el papel del
solista, la "schola"
La utilización del latín como lengua principal obligó a traducir los salmos utilizados hasta
entonces a prosa latina
La Iglesia Romana empezó a considerar como excesivo el empleo de los himnos en las funciones
litúrgicas, y se buscó más el carácter improvisatorio de los cánticos, de forma que fuesen más la
expresión libre de los sentimientos de los celebrantes.
Es en este marco donde encaja el Canto Gregoriano, como fuente de inspiración para la música
eclesiástica occidental, sobre todo en ciertas partes de la celebración eucarística, como el Introito,
el Ofertorio y la Comunión.
Son muy escasos los ejemplos de cantos escritos que han llegado hasta nosotros de los primeros siglos
del cristianismo, pero hay que destacar el Códice Alejandrino, un salterio del siglo V que contiene
trece de los cánticos empleados en el desarrollo de la liturgia. En esas obras se recogen los textos, pero
no la forma de entonar los cantos, por lo que la aparición de una rudimentaria forma de notación
musical en Hispania o en la Galia, durante el siglo IX, supuso un gran avance al respecto.
13
Tema 9.- Quintas:
Quintas de DO – SOL – RE –LA –MI –SI –FA
Quintas de RE –LA –MI –SI –FA –DO –SOL
Quintas de MI –SI –FA –DO –SOL –RE -LA
Quintas de FA –DO –SOL –RE –LA –MI –SI
Quintas de SOL –RE –LA –MI –SI –FA –DO
Tema 10.- Sonido y Ruido:
El ruido generalmente produce una sensación de estrés e irritamiento.
El sonido en tanto, es placentero y agradable de escuchar. Se asocia a la música y produce sensación de
relajo y bienestar.
14