PROBLEMA 2

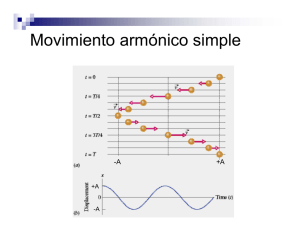
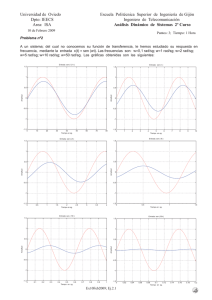
PROBLEMA 2
Una partícula que se mueve con un movimiento armónico simple recorre una distancia
total de 20 cm. en cada ciclo, y su máxima aceleración es de 50cm./s 2 . Encontrar: a) la
frecuencia angular y b) la máxima rapidez de la partícula
SOLUCION;
El sistema de unidades utilizado en el problema es el correspondiente al C.G.S.
a)
Si el ciclo consta de 20cm. nos indica que la amplitud es la siguiente;
Amplitud (A)=1/4 ciclo
A=1/4 20 = 5cm.
Como la aceleración total es igual a a = ω2 A , despejando correctamente de esta
fórmula la frecuencia angular (w) obtenemos el siguiente resultado;
ω2 = a/A = 50/5 = 10 rad/s
ω = 3.16 rad/s
b)
Mediante la derivada respecto al tiempo de la ecuación de la posición de un
movimiento armónico simple (x= A cos(w.t+ ∝) ) obtenemos la ecuación de la
velocidad que es la siguiente;
v = A w sen(w.t + ∝) Como lo que nos piden es la velocidad máxima el seno
debe tener su valor máximo, es decir, uno.
v = A ω = 5 3.16 = 15.8 cm /s
PROBLEMA 4
Una partícula que cuelga sobre un resorte ideal tiene una frecuencia angular de
oscilación ω0 = 2 rad/s. El resorte se cuelga del techo de un elevador, y cuelga sin
movimiento (respecto al elevador) conforme el elevador desciende con una rapidez
constante de 1.5 m/s. El elevador se para repentinamente. a) ¿Con qué amplitud oscilará
la partícula? b) ¿Cuál es la ecuación del movimiento de la partícula? (escoger la
dirección hacia arriba positiva).
SOLUCIÓN
a) Por ser V cte el sistema está en en equilibrio
Vmax = A w Ë 1.5 = A 2 Ë A = 0’75 m
b) Como t = 0 seg. Ë desplazamiento = 0 (sen 0 = 0) Ë va a ser función seno
y = -A sen wt Ë
y = -0.75 sen 2t
y = 0’75 sen (2t+π)
y = 0’75 cos (2t+π/2)
(Cualquiera de las tres)
Sen_ = Cos (_+π/2)
Sen_ = -Sen (_+π)
PROBLEMA 6
¿Cuál es el periodo de oscilación del agua en el tubo que se ve
en la figura si se desplaza inicialmente 6cm? La longitud total del
fluido del tubo es de 60 cm.
SOLUCION
Sabemos que cuando aparece una fuerza del tipo F = - Kx se producirá un movimiento
vibratorio armónico simple de frecuencia angular:
ω= K/M
con M la masa total del sistema.
En este caso F = m.g con m= area.(2y)ρ siendo y el desplazamiento desde la
posición de equilibrio (y = 3 cm).
Además la F lleva sentido contrario al desplazamiento ⇒
F = -A(2y)ρg =-(2Aρg)y = -Ky ⇒ K = 2Aρg
La masa total del sistema es M = L Aρ, por lo que la frecuencia angular vale
2g / L
ω=
K/M
= 2 Aρg / LAρ =
Teniendo en cuenta que L = 60 cm
Τ = 2π/ω = 2 π L / 2 g = 2 π 0.174 = 1.099 ≈ 1.1s
PROBLEMA 10
Una masa de 2 kg. sujeta aun resorte se impulsa por una fuerza externa F = 3cos2πt N.
Si la constante de la fuerza del resorte es 20 N/m, determinar a) el periodo y b) la
amplitud del movimiento. Suponer que no hay amortiguamiento.
SOLUCION
a) Comparando con la ecuación de la fuerza periódica F=Fo cos(wt), obtenemos el valor
de w: w=2π. A partir de w calculamos el periodo T:
2π 2π
T =
=
= 1s
w
2π
T=1s
b) Calculamos la amplitud utilizando la formula:
F0
A=
2
m2 w20 − w 2 + b2 w2
(
)
Suponiendo que no hay amortiguamiento y sabiendo el valor de w0 mediante la
fórmula:
wo =
A=
k
=
m
20
= 10 = 3.16 s-1
2
3
(
4 10
)
2
− 4π 2
= 5.088cm
⇒
A=5.008 cm