descargar documento

Matemáticas Financieras
Dr. Daniel A. Jaume
Prof. Gonzalo Molina
Esta versión: December 16, 2012
Contents
1 Valor tiempo del dinero
1.1 Introducción . . . . . . . . . . . . .
1.1.1 Funciones del dinero . . . .
1.1.2 Trueque . . . . . . . . . . .
1.1.3 Un esquema del surgimiento
1.2 Valor-tiempo del dinero . . . . . .
. . . . . .
. . . . . .
. . . . . .
del dinero
. . . . . .
. . . . . .
. . . . . .
. . . . . .
fiduciario
. . . . . .
2 Sistemas de capitalización simple
2.1 Sistema de capitalización simple . . . . . . . . .
2.2 Equivalencia de tasas . . . . . . . . . . . . . . . .
2.3 Equivalencia financiera de dos series de capitales
2.3.1 Tasa media . . . . . . . . . . . . . . . . .
2.3.2 Vencimiento medio . . . . . . . . . . . . .
3 Descuento
3.0.3
3.0.4
3.0.5
3.0.6
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
2
2
3
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9
9
16
19
27
32
Simple
36
Descuento simple . . . . . . . . . . . . . . . . . . . . . . . 37
Equivalencia de tasas de descuento simple. . . . . . . . . 40
Equivalencia entre tasas de descuento y de capitaliación
simples. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Equivalencia financiera revisada . . . . . . . . . . . . . . . 42
4 Sistemas de capitalización compuesta
4.1 Sistema de capitalización compuesta . . . .
4.2 Tasas . . . . . . . . . . . . . . . . . . . . .
4.2.1 Equivalencias de tasas compuestas .
4.2.2 Breve diccionario de tasas nominales
4.3 Equivalencia de capitales . . . . . . . . . . .
4.3.1 Tasa media . . . . . . . . . . . . . .
4.3.2 Vencimiento medio . . . . . . . . . .
4.4 Capitalización subperı́odica . . . . . . . . .
4.4.1 Convenio discreto o de truncamiento
4.4.2 Convenio exponencial o continuo . .
4.4.3 Convenio lineal . . . . . . . . . . . .
ii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
45
45
54
54
60
61
66
71
74
75
75
76
CONTENTS
5 Descuento
5.0.4
5.0.5
5.0.6
iii
compuesto
80
Equivalencia de tasas de descuento compuesto. . . . . . . 85
Equivalencia entre tasas de descuento y capitalización. . . 87
Descuento Racional . . . . . . . . . . . . . . . . . . . . . 89
6 Capitalización Continua
6.1 Capitalización continua . . . . . . . . . . . .
6.2 Equivalencia de capitales . . . . . . . . . . . .
6.3 Tasa media continua . . . . . . . . . . . . . .
6.4 Equivalencia entre tasas continuas y discretas
6.5 Vencimiento medio continuo . . . . . . . . . .
6.6 Descuento continuo . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
93
93
100
103
106
108
109
7 Composición de tasas
7.1 Rentabilidad real . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2 Efecto de las comisiones . . . . . . . . . . . . . . . . . . . . . . .
7.2.1 Efecto de las comisiones cobradas al principio de la operación . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.2 Efecto de las comisiones cobradas al final de la operación
7.3 Tasas negativas . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.1 Depreciación . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.2 Impuestos, seguros y comisiones varias . . . . . . . . . . .
7.3.3 Impuestos sobre la renta financiera y su efecto sobre la
rentabilidad. . . . . . . . . . . . . . . . . . . . . . . . . .
7.4 Tipo de cambio . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.5 Tasa de devaluación . . . . . . . . . . . . . . . . . . . . . . . . .
7.5.1 Tasas de devaluación . . . . . . . . . . . . . . . . . . . . .
7.6 ı́ndice de precios . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.7 Inflación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.8 Indexación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.9 Composición de tasa en el sistema continuo . . . . . . . . . . . .
111
111
114
8 Rentas
8.1 Rentas generales . . . . . . . . . . . . . . . . . . . . . . . . . .
8.2 Rentas constantes . . . . . . . . . . . . . . . . . . . . . . . . . .
8.3 Rentas vencidas o pospagables . . . . . . . . . . . . . . . . . .
8.4 Multiplicadores . . . . . . . . . . . . . . . . . . . . . . . . . . .
8.5 Métodos númericos . . . . . . . . . . . . . . . . . . . . . . . . .
8.5.1 Método de Newton-Raphson . . . . . . . . . . . . . . .
8.5.2 Método de la secante . . . . . . . . . . . . . . . . . . . .
8.6 Rentas prepagables . . . . . . . . . . . . . . . . . . . . . . . . .
8.7 Rentas perpetuas . . . . . . . . . . . . . . . . . . . . . . . . . .
8.7.1 Rentas perpetuas constantes vencidas (pospagables) . .
8.7.2 Rentas perpetuas constantes adelantadas (prepagables)
8.8 Rentas diferidas y anticipadas . . . . . . . . . . . . . . . . . . .
8.9 Rentas aritméticas . . . . . . . . . . . . . . . . . . . . . . . . .
155
155
158
159
168
170
170
175
178
183
183
186
187
190
.
.
.
.
.
.
.
.
.
.
.
.
.
114
116
118
119
122
122
125
133
133
141
147
153
153
iv
CONTENTS
8.10
8.11
8.12
8.13
8.14
Rentas geométricas . . . . . . . . . . . . .
Rentas variables en progresión geométrica
Inflación: su efecto sobre rentas . . . . . .
Otros tipos de rentas. . . . . . . . . . . .
Rentas a capitalización continua . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
201
201
210
214
214
9 Préstamos
9.1 Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2 Préstamos comerciales . . . . . . . . . . . . . . . . . . . . . . . .
9.3 Préstamos a interés sobre saldos . . . . . . . . . . . . . . . . . .
216
216
216
220
10 Préstamo francés
223
10.1 Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223
10.2 Usufructo y nuda propiedad . . . . . . . . . . . . . . . . . . . . . 232
10.3 Perı́odo de gracia . . . . . . . . . . . . . . . . . . . . . . . . . . . 238
10.4 CFT: costo financiero total. Efecto de impuestos, gastos y seguros 240
10.5 Cancelación anticipada total o parcial . . . . . . . . . . . . . . . 252
10.6 Adelanto de cuotas . . . . . . . . . . . . . . . . . . . . . . . . . . 254
10.7 Punitorios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
10.8 Préstamo francés a interes variable . . . . . . . . . . . . . . . . . 265
10.9 Inflación y su efecto sobre los préstamos . . . . . . . . . . . . . . 265
10.10Devaluación y su efecto sobre los préstamos . . . . . . . . . . . . 265
11 Préstamo alemán
266
11.1 Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 266
12 Préstamo americano
12.1 Introducción . . . . . . . . . .
12.2 Cuadro de Marcha . . . . . .
12.3 Variantes habituales . . . . .
12.3.1 Fondo de amortización
12.3.2 Fondo de amortización
. . . . .
. . . . .
. . . . .
en renta
en renta
. . . . . .
. . . . . .
. . . . . .
constante
variable .
A Variación proporcional
A.1 Variación proporcional directa. . . . . . . . .
A.2 Series de fracciones equivalentes. . . . . . . .
A.2.1 Reparto simple directo. . . . . . . . .
A.3 Variación proporcional inversa. . . . . . . . .
A.3.1 Reparto simple inverso: . . . . . . . .
A.4 Variación proporcional conjunta o compuesta.
A.4.1 Reparto compuesto. . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
273
273
278
279
280
281
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
284
284
286
288
290
291
293
293
B Relaciones recursivas
298
B.1 Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298
B.2 Relaciones recursivas lineales de primer orden a coeficientes constantes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 300
CONTENTS
B.3
B.4
B.5
B.6
B.7
Caso I: g (k) = cte. . . . . . . . . . . . . . . . . . . . . . . . . . .
Caso g 6= cte. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Caso g (k) es un polinomio . . . . . . . . . . . . . . . . . . . . . .
Caso III: g (k) es una función exponencial . . . . . . . . . . . . .
Caso IV: g (k) combinación de un polinomio y una función exponencial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B.8 Ejercitación general . . . . . . . . . . . . . . . . . . . . . . . . .
v
300
303
304
307
309
310
C Soluciones
312
C.1 Soluciones del capitulo 1 . . . . . . . . . . . . . . . . . . . . . . . 312
D Diccionarios de fórmulas
313
E Tabla de dı́as
314
vi
CONTENTS
Chapter 1
Valor tiempo del dinero
1.1
Introducción
El tema de este libro es el valor-tiempo del dinero: escencialmente un peso hoy
no vale lo mismo que un peso dentro de un año, en el sentido de la cantidad de
bienes y servicios que podemos adquirir es diferente. Esto se debe principalmente
a dos factores: el costo de oportunidad y la inflación.
Pero, ¿Qué es el dinero?
Definición 1.1 El dinero es todo aquello que constituye un medio de cambio o
de pago comúnmente aceptado.
Caracterı́sticas:
1. Carece de valor intrı́nseco: nos interesa porque podemos usarlo para adquirir
bienes y servicios.
2. El estado es el único que puede imprimirlo: moneda de curso legal.
3. No son sólo monedas y billetes:
(a) Monedas y billetes,
(b) Depósitos a la vista o cuentas corrientes (cheques y tarjetas débito)
y tarjetas de crédito,
(c) Bonos y acciones,
(d) Depósitos a plazos.
(e) Rentas (sueldos, jubilaciones, becas, etc.),
(f) Instrumentos financieros (futuros, opciones, seguros, etc.),
(g) Bienes (casas, autos, propiedades, muebles, etc.)
Los tipos de “dinero” listados arriba, están ordenado de más lı́quidos a menos
lı́quidos. Un valor es más lı́quido cuanto más fácil sea intercambiarlo por bienes
y servicios.
1
2
CHAPTER 1. VALOR TIEMPO DEL DINERO
1.1.1
Funciones del dinero
Las funciones que cumple el dinero son tres:
1. Es un depósito de valor.
2. Es una unidad de medida o cuenta.
3. Es un medio de cambio.
Decimos que el dinero es un depósito de valor pues nos permite transferir
poder adquisitivo espacial y temporalmente. El dinero que ganamos en un lugar
puede ser usado para adquirir bienes y servicios en otro lugar, y el dinero ganado
hoy puede ser intercambiado por bienes y servicios en algún momento del futuro.
Decimos que el dinero es una unidad de medida o cuenta pues es en
términos de dinero que se expresan los precios y las deudas. El dinero es el
patron con el que medimos las transacciones económicas.
Decimos que el dinero es un medio de cambio, todas las personas e instituciones aceptan intercambiar bienes y servicios por dinero.
Es claro que no todos los bienes conservan su valor el tiempo, por ejemplo las
manzanas recién cosechadas tienen claramente un valor (pueden ser intercambiadas por otros bienes y servicios), pero después de un tiempo es poco probable
que alguién acepte intercambiar sus bienes por lo que quede de nuestras viejas manzanas. Por otro lado si deseamos adquirir algún bien en algún punto
lejano a nuestro lugar de residencia, algunos bienes son más transportables que
otros, por ejemplo, es más fácil mover oro que sandias (considereando la relación
peso/valor).
Es claro que podrı́amos usar oro como depósito de valor, pero este es muy
incomodo como unidad de medida y cuenta, pues todos deberı́amos disponer
de equipos (balanzas) y conocimientos de metalurgı́a (pues el oro viene con
distintos grados de pureza), para poder intercambiar la cantidad adecuada de
oro por los bienes y servicios que deseamos adquirir.
1.1.2
Trueque
La mejor forma de entender las funciones del dinero es imaginar como era el
mundo antes de su aparición, lo que se conoce como economı́a de intercambio
o trueque. El dinero es una eficaz herramienta que surgió de manera natural a
medida que las sociedades fueron desarrollando economı́as cada vez más complejas. Las primeras sociedades tenı́an una economı́a de trueque: los bienes eran
intercambiados directamente por otros bienes. La principal desventaja de este
tipo de economı́as es que requiere de una doble coincidencia de deseos (temporal y espacial) para que dos agentes intercambien bienes. Por ejemplo, si yo
hoy tengo peras y deseo cuchillos, debo hallar (espacial) alguién que hoy quiera
peras y que hoy tenga cuchillos (temporal). Esto lleva de manera natural a:
1. una baja división del trabajo (poca especialización),
1.1. INTRODUCCIÓN
3
2. una economı́a sencilla: sólo se pueden hacer transacciones muy sencillas.
3. es dificı́l trasladar valor temporalmente, e inclusve espacialmente.
El dinero permite transacciones indirectas, y en este sentido es muy superior
al trueque, donde debe existir una doble coincidencias de deseos para realizar
intercambios.
1.1.3
Un esquema del surgimiento del dinero fiduciario
El dinero que no tiene valor intrı́nseco se denomina dinero fiduciario, ya que se
establece como dinero por decreto. Esto es lo normal en casi todos los paises de
mundo, aunque históricamente las economı́as utilizaron durante mucho tiempo
mercancı́as con valor intrı́nseco a modo de dinero: semillas de cacao, conchas
de mar, aceite de oliva, sal, plata, oro, etc.. Estos son ejemplos de lo que se
denomina dinero mercancı́a.
No es difı́cil de entender como surje un dinero mercancı́a como el oro: facilita
el intercambio (todo el mundo esta dispuesto a aceptarlo por su valor intrı́nseco),
es fácil de transportar (con respecto a la relación peso/valor) y además sirve para
trasladar valor en el tiempo al conservar generalmente su valor en el tiempo.
Es más dificil entender como surje el dinero fiduciario. ¿Qué hizo que la gente
comenzara a valorar algo que carece de valor intrı́nseco: esos pedazos de papel
que llamamos dinero? En realidad el proceso tomo varios siglos, pero se puede
resumir al siguiente esquema. En una economı́a que usa oro como dinero mercancı́a, la gente debe llevar consigo bolsas con oro. Para efectuar una transacción
comprador y vendedor deben concordar en el peso y la pureza del oro a ser intercambiado por el servicio o mercancı́a. Este proceso de pesado y verificación
de la pureza lleva su tiempo y requiere de conocimientos de metalurgı́a. Para
simplificar la operación y reducir sus costes el gobierno decide acuñar monedas
de oro de un peso y pureza conocidos. Están monedas son más fáciles de llevar
y usar que el oro en bruto. Al poco tiempo todo el mundo usa las monedas y
casi no circula oro sin acuñar. Luego, el gobierno y los bancos empiezan a emitir
certificados de oro: trozos de papel que dicen que Juan Perez tiene 12 kg. de oro
el banco tal o cual, o certificados de oro del gobierno que dicen, por ejemplo,
vale por medio kilo de oro. La gente empieza a aceptar estos papeles, y los van
a canjar por oro (al banco o al ayuntamiento). Una vez que la gente comienza a
verificar la veracidad de estas promesas de pago, y al ser más fáciles de guardar
y llevar, estos certificados se vuelven tan valiosos como el mismo oro y a la
larga nadie lleva oro, sino estos certificados oficiales respaldados por oro: los
certificados se convierten en el patron monetario. Ya solo resta un paso para el
surgimiento del dinero fiduciario: si nadie se molesta en canjear los billetes por
oro, el respaldo del oro deja de ser relevante. Mientras todo el mundo continue
aceptando los billetes de papel, estos tendrán valor y servirán de dinero.
4
CHAPTER 1. VALOR TIEMPO DEL DINERO
1.2
Valor-tiempo del dinero
La matemática financiera se ocupa de modelar el efecto del tiempo sobre el
valor nominal del dinero. Es lo que llamaremos el valor-tiempo del dinero. El
siguiente par de ejemplos clarifica la cuestión:
Ejemplo 1.2 Tener hoy $ 1.000 es mejor que tener (hoy) sólo $ 50.
Ejemplo 1.3 Es mejor tener $ 100 hoy que tener $ 100 dentro de un año.
De este par de ejemplos podemos concluir:
Conclusión 1.4 De dos montos disponibles al mismo instante de tiempo, preferimos el mayor.
Conclusión 1.5 De dos montos iguales disponibles en diferentes momentos,
preferimos el monto disponible antes.
Problema 1.6 En base a las conclusiones anteriores. ¿Qué es mejor? $ 100
hoy o $ 75 dentro de un año.
El problema surge al comparar montos distintos disponibles en diferentes
momentos del tiempo (donde el monto futuro es mayor que el monto presente):
¿Qué es mejor, $1.000 hoy, o $1.350 dentro de un año?
Todo depende del agente considerado y de su costo de oportunidad. El
costo de oportunidad hace referencia al hecho de que cada vez que optamos
por una cosa, hay un universo de alternativas que desechamos. La alternativa
desechada de mayor rendimiento es el costo de oportunidad en el que incurrimos
al tomar una decisión.
Volviendo a nuestro problema de decidir que es mejor, si $ 1.000 hoy o $
1.350 dentro de un año. Si el agente puede invertir los $ 1.000 de hoy y ganar
con certeza $ 500 extras al cabo de un año, a fin de año tendrá $ 1.500, lo que
es mejor que los $ 1 350. Para este agente $ 1.000 pesos hoy son mejores que
$ 1.350 dentro de un año (su costo de oportunidad es mayor que el rendimieno
ofrecido al agente). Para otro agente los $ 1.000 hoy son lo mismo que $ 1.350
dentro de un año, en el sentido de que el puede invertir estos $ 1.000 en alguna
otra opción de inversión y obtener la misma ganancia de $ 350 al cabo de un
año. Este agente es indiferente entre $ 1.000 hoy o $ 1.350 a fin de año. Para
finalizar, para un tercer agente $ 1.000 hoy es una peor inversión que recibir $
1.350 a fin de año, pues todas las otras alternativas de inversión que posee le
reportan al cabo de un año menos de $ 350 de ganancia.
En el análisis anterior la noción suyacente es la de equivalencia finaciera:
Definición 1.7 Dos capitales C1 y C2 , impuestos en momentos t1 y t2 , respectivamente, son financieramente equivalentes para un agente dado, si el
1.2. VALOR-TIEMPO DEL DINERO
5
agente es indiferente entre ellos: el valor del capital C1 al momento t2 es igual
a C2 (recı́procamente el valor del capital C2 al momento t1 es igual a C1 ):
C2 al momento t1
= C1
C1 al momento t2
= C2
C1
C2
t1
t2
(C1 , t1 )
equivalentes
(C2 , t2 )
Nota 1.8 Cada cantidad de dinero debe ser informada junto con el instante de
tiempo en que esta disponible, i.e., en matemáticas financieras (implı́citamente)
trabajamos con pares
(monto, tiempo)
Para medir el rendimiento de una inversión introducimos otro concepto fundamental ,la noción de tasa de interés. Recordemos que una tasa es una
medida de la magnitud relativa de cambio: Si una cantidad cambia de Ci a Cf
en un perı́odo de tiempo dado, la tasa de cambio es
t :=
Cf − Ci
.
Ci
Graficamente
t=
Ci
Cf −Ci
Ci
Cf
Cuando pasamos de Ci a Cf , podemos pensar que cada unidad pasa de 1 a
1 + t pues
(1 + t) Ci = Cf .
(1.1)
Ejemplo 1.9 Al invertir $ 1.000, obtenemos una ganancia de $ 1.350, tenemos
que la tasa de rendimiento asociada es
1.350 − 1.000
= 0, 35
1.000
Observe que la tasa es una magnitud adimensional, aunque implı́citamente
está asociada a una unidad de tiempo:
t=
el perı́odo de tiempo entre Ci y Cf .
Ejemplo 1.10 Continuando con el ejemplo anterior, si los $ 1.000 pasan a $
1.350, en un dı́a, o en un mes, o en un año, son tres situaciones muy distintas, aunque les corresponda la misma tasa. Por eso agregaremos la información
temporal y hablaremos de una tasa 0,35 diaria, o de una tasa 0,35 mensual, o
de una tasa 0,35 anual.
6
CHAPTER 1. VALOR TIEMPO DEL DINERO
t = 0.35
$1000
$1350
1 dı́a
t = 0.35
$1000
$1350
1 mes
t = 0.35
$1000
$1350
1 año
Definición 1.11 Un k-perı́odo de tiempo, es una unidad temporal que cabe k
veces el año.
Por ejemplo, un 12-perı́odo es un mes: 12 meses hacen un año, un 365perı́odo es un dı́a: pues en un año caben 365 dı́as, un 6-perı́odo es un bimestre:
6 bimestres hacen un año, etc.
k-perı́odo
1-perı́odo
2-perı́odo
3-perı́odo
4-perı́odo
6-perı́odo
12-perı́odo
52-perı́odo
360-perı́odo
365-perı́odo
tiempo
año,
semestre,
cuatrimestre,
trimestre,
bimestre,
mes,
semana,
dı́a comercial,
dı́a civil.
Nota 1.12 Observe que en t años entran
k·t
k-perı́odos,
por ejemplo, en 3 años hay 12 · 3 = 36 12-perı́odos, i.e., 36 meses; en 2.5 años
hay 52 · 2, 5 = 130 52-perı́odos, i.e., 130 semanas.
Definición 1.13 Una tasa k-perı́odica t, es una tasa t que actua sobre un
k-perı́odo, i.e., nos dice cuanto cambia una unidad en un k-perı́odo de tiempo.
Diremos que una tasa k-perı́odica capitaliza k veces en un año. También se
suele decir que la tasa tiene frecuencia de capitalización k. Por ejemplo una tasa
1.2. VALOR-TIEMPO DEL DINERO
7
mensual, capitaliza 12 veces en el año o, lo que es lo mismo, tiene frecuencia de
capitalización 12.
En el dı́a a dı́a, las tasas son informadas como porcentajes (i.e., numeradores
de cocientes de denominador 100) junto con una unidad temporal. Por ejemplo
una tasa mensual del 22,3 % hace referencia a una tasa 0, 223 12-perı́odica.
Para hallar la tasa asociada a una tasa tporcentual informada porcentualmente
hacemos
tporcentual
t=
100
En matemática financieras usaremos i(k) para denotar una tasa k-perı́odica.
Las más usadas son:
i
anual,
i(2)
semestral,
i(3)
cuatrimestral,
(4)
i
trimestral,
i(6)
bimestral,
i(12)
mensual,
i(52)
semanal,
i(360) diaria comercial,
i(365) diaria civil.
Nota 1.14 Observar que en lugar de i(1) para la tasa anual se usa simplemente
i.
Definición 1.15 Dados un capital original Co en un instante de tiempo to y
un capital final Cf en un instante de tiempo posterior tf . Llamaremos interés
I a la diferencia
I := Cf − Co
Si tf − to es un k-perı́odo, hay una tasa k-perı́odica asociada:
i(k) =
Cf − Co
Co
De donde se deduce una relación inmediata entre el interés I y la tasa k-perı́odica
i(k) :
I = Co i(k)
Sea i(k) la tasa k-perı́odica que podemos obtener, para cualquier capital C
disponible el dı́a de hoy podemos hallar un capital equivalente un k-perı́odo en
el futuro Cf o un k-perı́odo hacia el pasado Cp .
Cf =
1 + i(k) C
Cp
=
C
1 + i(k)
Cuando movemos un capital hacia el futuro en matemáticas financeras se habla
de capitalización. Mientras que si lo movemos hacia el pasado se habla de
actualización.
8
CHAPTER 1. VALOR TIEMPO DEL DINERO
Capitalización
Actualización
Cp
C
un k-perı́odo hacia el pasado
Cf
un k-perı́odo hacia el futuro
Pero tı́picamente debemos movermos más de un perı́odo, hacia atrás o hacia
adelante. Cuando debemos calcular los intereses de varios perı́odos surge un
interrogante natural: Los intereses de un perı́odo deben ser considerados o no
para el cálculo de los intereses del perı́odo siguiente. El cómo se hace esto recibe
el nombre de ley financiera.
Chapter 2
Sistemas de capitalización
simple
2.1
Sistema de capitalización simple
El sistema de capitalización simple es la ley financiera que establece que los
intereses generados en un perı́odo dado no son considerados para el cálculo de
los intereses del perı́odo siguiente.
Definición 2.1 Se llama capitalización simple a la ley financiera que establece que los intereses de cada perı́odo se calculan sobre el mismo capital
inicial o principal.
Dado un capital inicial C0 , una tasa de capitalización p-perı́odica i(p) y n
p-perı́odos tenemos que los intereses de cada perı́odo son iguales:
I1 = I2 = · · · = In = C0 i(p)
El interés total IT es, por definición, la suma de los intereses de cada uno de
los perı́odos considerados:
IT
n
X
:=
Ih
h=1
nC0 i(p)
=
Dado h ∈ {1, ..., n}, el capital acumulado hasta el momento h, es el capital
acumulado hasta el perı́odo anterior, h − 1, más los intereses generados:
Ch = Ch−1 + C0 i(p) ,
con la condición inicial C0 := Co (a la izquierda es capital a momento cero, a
la derecha tenemos el capital inicial u original). Por lo que usando la teorı́a de
9
10
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
relaciones recursivas ya desarrollada, caso g (k) = cte, con A = 1, concluimos
que:
Ch
= C0 + C0 i(p) h
= C0 1 + hi(p)
(2.1)
para 0 ≤ h ≤ n.
$
Cn
In
Cn−1
In−1
In−1
C3
IT
I3
I3
I3
I2
I2
I2
I2
I1
I1
I1
I1
I1
C0
C0
C0
C0
C0
C2
C1
C0
C0
0
1
2
3
n−1
n
tiempo
En particular
Cn = C0 1 + ni(p)
(2.2)
la cual es la fórmula habitual en la literatura.
Nota 2.2 Note que en la fórmula (2.2) existe una relación temporal entre los
2.1. SISTEMA DE CAPITALIZACIÓN SIMPLE
11
capitales Cn y C0 .
Esta en el futuro
(a la derecha)
del capital C0
z}|{
Cn
=
C0
|{z}
1 + ni(p)
Esta en el pasado
(a la izquierda)
del capital Cn
Nota 2.3 Se puede deducir de la formula (2.2) con un argumento inductivo: El
capital al final del primer perı́odo, C1 , es la suma de C0 , el capital al inicio del
perı́odo, más C0 i(p) , los intereses generados durante este perı́odo:
C1 = C0 + C0 i(p)
Similarmente C2 , el capital al final del segundo perı́odo, es la suma de C1 , el
capital al inicio del perı́odo, más C0 i(p) , los intereses generados durante este
perı́odo
C2 = C1 + C0 i(p)
pero como C1 = C0 + C0 i(p) , obtenemos
C2
= C0 + C0 i(p) + C0 i(p)
= C0 + 2C0 i(p)
Análogamente C3 , el capital al finalizar el tercer perı́odo, es la suma de C2 , el
capital al comienzo del perı́odo, más C0 i(p) , los intereses generados durante este
perı́odo:
C3 = C2 + C0 i(p)
y ya que C2 = C0 + 2C0 i(p) , obtenemos
C3 = C0 + 3C0 i(p)
De estas expresiones podemos inferir inductivamente que el capital acumulado
al momento n será
Cn = C0 + nC0 i(p)
(2.3)
i(k)
Cn−1
Cn
n−1
n
tiempo
(modificar dibujo)
La fórmulas (2.1) y (2.2) nos indican como se traslada un capital de un instante de tiempo dado a otro de forma financieramente equivalente. Por ejemplo,
12
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
a una tasa mensual del 1,2 %, $ 200 pesos son financieramente equivalentes a $
216,8 en 7 meses (usando capitalización simple):
216, 8 = 200 (1 + 7 · 0, 012)
Nota 2.4 En la fórmula (2.2) aparecen 4 variables relacionadas:
capital inicial
capital final
tiempo
tasa
C0
Cn
n
i(p)
Unas observaciones al respecto:
1. El problema tipo es: dadas tres magnitudes hallar la cuarta. Por lo que
tenemos problemas donde debemos hallar el capital final Cn (se les suele
llamar problemas de capitalización), una variación de este tipo de problemas es hallar el interés total generado. Problemas donde debemos hallar el
capital inicial C0 (se les suele llamar problemas de actualización). Problemas donde debemos hallar el tiempo n, y finalmente problemas donde
debemos hallar la tasa i(p) .
2. Dimensionalmente hablando, C0 y Cn son dinero. El tiempo y la tasa deben
ser dimensionalmente compatibles: si la tasa es k-perı́odica, el tiempo debe
estar dado en p-perı́odos, por ejemplo, si la tasa es mensual, n debe ser
una cantidad de meses. Similarmente si n es una cantidad de trimestres,
la tasa debe ser trimestral: una i(4) .
Ejemplo 2.5 Calcular el capital final o montante de $ 2.500.000 al 15 % anual,
colocado durante a) 20 dı́as, b) 3 meses, c) 4 cuatrimestres, d) 5 años, e) t pperı́odos.
Todo el problema es compatibilizar las unidades temporales de los intervalos
de tiempo y la tasa. Por ahora sólo podemos convertir los distintos perı́odos de
tiempo a años:
Ejemplo 2.6 a) 20 dı́as son
20
C20 dı́as = C 365
años
b) 3 meses son
3
12
3
C3 meses = C 12
20
365
años, por lo que al cabo de 20 dı́as tendremos
20
= 2.500.000 1 +
0, 15 = 2520547, 9452 pesos.
365
años, por lo que al cabo de 3 meses tendremos
3
0, 15 = 2593750 pesos.
años = 2.500.000 1 +
12
c) 4 cuatrimestres son
dremos
C4 cuatrimestres = C 34
4
3
años
años, por lo que al cabo de 4 cuatrimestres ten
4
= 2.500.000 1 + 0, 15 = 3.000.000 pesos.
3
2.1. SISTEMA DE CAPITALIZACIÓN SIMPLE
13
d) Al cabo de 5 años tendremos
C5 años = 2.500.000 (1 + 5 · 0, 15) = 4.375.000 pesos.
e) En general si tenemos t p-perı́odos, tenemos pt años, por lo que tendremos
t
t
Ct p−perı́odos = C k años = C0 1 + i
p
Ejemplo 2.7 Hoy extraemos del banco $ 281.300. ¿Cuál fue el capital original,
o principal, si nos han pagado una tasa mensual del 32% y el depósito fue
pactado a 15 meses?
Sabemos que
Cn = C0 1 + ni(p)
de donde
Cn
(2.4)
1 + ni(p)
y como hay compatibilidad temporal entre la tasa y la unidad temporal, ambas
son mensuales:
C0 =
C0
=
=
281.300
1 + 15 · 0, 32
48.500
i.e., debimos depositar hace 15 meses la suma de $ 48.500 a una tasa mensual
del 32% para poder extraer hoy $ 281.300.
Ejemplo 2.8 Determinar el interés total obtenido al depositar $ 15.000 a plazo
fijo por el término de 6 bimestres a una tasa bimestral del 14%.
Otra forma de definir el interés total: es la diferencia entre el capital final y
el capital inicial.
IT = Cfinal − Coriginal
Veamos que esta definición es equivalente a la dada previamente:
= Cn − C0
= C0 1 + ni(p) − C0
IT
= C0 ni(p)
(2.5)
Reemplazando
IT
=
15.000 · 6 · 0, 14
=
12.600
Esto nos dice que un plazo fijo de $ 15.000 a 6 bimestres, a una tasa bimestral
del 14% producen un interés total de $ 12.600.
14
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Ejemplo 2.9 Hallar el capital que produce unos intereses de $ 12.787,5 al cabo
de 75 dı́as, a una tasa diaria del 0,31%.
Del problema anterior sabemos que
IT = C0 ni(p)
(donde n es una cantidad de p-perı́odos). Luego
C0 =
IT
ni(p)
(2.6)
reemplazando
C0
12.787.5
75 · 0, 0031
55.000
=
=
Por lo tanto unos $ 55.000 producen un interés de $ 12.787,5 al cabo de 75
dı́as, a una tasa diaria del 0,31%.
Ejemplo 2.10 Depositamos en un banco $ 450.000 y al cabo de 18 meses nos
entregan $ 820.601,52. ¿Cuál es la tasa mensual que nos pagó el banco?
Como
Cn = C0 1 + ni(p)
tenemos que
i(p) =
Cn − C0
nC0
(2.7)
Luego
i(12)
=
=
820.601, 52 − 450.000
18 · 450.00
0.045753274
i.e., el banco nos pagó una tasa mensual del 4,5753274%.
Ejemplo 2.11 Durante cuantos dı́as hay que imponer un capital de $ 3.500.000
a una i(4) = 0, 2455, para obtener no menos de $ 5.100.000.
Como
Cn = C0 1 + ni(p)
de donde depejamos n
n=
Cn − C0
C0 i(p)
Ahora nosotros deseamos
9.100.000 ≤ 3.500.000 (1 + n · 0, 2455)
(2.8)
2.1. SISTEMA DE CAPITALIZACIÓN SIMPLE
15
luego
n ≥
≥
9.100.000 − 3.500.000
3.500.000 · 0, 2455
6.517311609
luego debemos imponer el capital al menos 7 dı́as.
Nota 2.12 El sistema de capitalización simple esta prácticamente en desuso.
En la actualidad la capitalización compuesta es el sistema más usado (en sus
versiones discreta y continua), el cual será estudiado en los capitulos subsiguientes.
Ejercicio 2.13 Calcular el capital final o montante que se obtendrá al colocar $
25.500 a 6 meses a una tasa anual del 12,5%. ¿A cuánto ascienden los intereses
totales?
Ejercicio 2.14 Calcular el montante que producirá un capital de $ 724.230,
colocado al 7% semestral durante 4 años.
Ejercicio 2.15 Determinar el interés obtenido por una empresa que efectuó un
depósito a plazo fijo por el término de 30 dı́as, con excedentes de fondos por $
80.000 a una tasa del 11 % anual.
Ejercicio 2.16 Obtenga los intereses totales que produce un capital de $ 22.300.000
impuestos al 3% trimestral durante 36 meses.
Ejercicio 2.17 Hallar el capital necesario para producir un interés de $ 1.030
en una colocación por un plazo de 50 dı́as en una entidad bancaria al 18 %
anual.
Ejercicio 2.18 Los intereses al cabo de un año, calculados según el año civil,
de un C capital ascienden a $ 784.720 ¿A cuánto ascenderán según el año
comercial (suponer i(360) = i(365) )?
Ejercicio 2.19 Hace 87 dı́as invertimos una cierta suma de dinero al 0,02%
diario a interés simple. Hoy nos entregan $ 75.420,50 ¿Cuál fue el monto invertido originalmente?
Ejercicio 2.20 Depositamos en un banco $ 150.000 y al cabo de 8 meses nos
entregan $ 160.672,50. ¿Cuál es la tasa de interés que nos pagó el banco?
Ejercicio 2.21 Un inversor reembolsará $ 499.500,50 por un depósito concertado a 90 dı́as por $ 300.700. Averiguar la tasa anual pactada.
Ejercicio 2.22 Hallar la tasa anual necesaria para que un depósito por $ 11.000
reditúe al inversor en 180 dı́as, la mitad de la colocación.
Ejercicio 2.23 ¿Cuál es la tasa de interés p-perı́odica que nos permite duplicar
el capital al cabo de n p-perı́odos?
16
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Ejercicio 2.24 ¿Cuánto tiempo es necesario que transcurra para triplicar un
capital al 5% bimestral?
Ejercicio 2.25 ¿Cuántos perı́odos son necesarios para duplicar un capital a
una tasa p-perı́odica i(p) ? Y para triplicarlo. Y para obtener un múltiplo dado.
Ejercicio 2.26 Una empresa con excedentes de fondos por $ 200.000 efectúa
dos colocaciones para cubrir necesidades futuras. Una durante 45 dı́as al 1,5%
mensual, y otra durante 15 dı́as al 1,25% mensual. Averiguar los importes de
los depósitos, sabiendo que las inversiones producen igual interés.
Ejercicio 2.27 Ud. posee $ 355.000. Decide invertilos en dos proyectos que le
pagarán respectivamente el 1,2 % bimestral y el 2,1% trimestral. Qué porcentaje
de sus ahorros debe invertir en cada proyecto, para recibir el mismo monto en
concepto de intereses al cabo de 6 meses. Si ahora deseamos que ambos proyectos
nos paguen los mismos intereses totales a lo largo de 1 año ¿cuánto deberemos
poner en cada uno de los proyectos?
Ejercicio 2.28 Un capital por $ 38.000 se impuso a interés simple durante 7
dı́as al 11,2%; luego el mismo capital por el término de 15 dı́as al 11,7%; y por
último se consiguió colocarlo 30 dı́as al 13,5%. Calcular el interés total y la tasa
real de la operación citada.
Ejercicio 2.29 Una empresa coloca excedentes de fondos en las siguientes alternativas:
1. Mercado de financiamiento oficial, $ 86.000 al 12%.
2. Mercado de financiamiento marginal, $ 72.000 al 18,5%.
Determinar el plazo de las colocaciones que le permiten percibir montos
iguales.
Ejercicio 2.30 Se desea saber cómo influirá una comisión de gastos fija sobre
el rendimiento de una inversión. A este efecto se nos comenta que, cualquiera
sea la inversión, la comisión ascenderá a $ 3.000. ¿Qué incidencia tendrá sobre nuestra inversión de $ 2.000.000 al 12%?, i.e., ¿Cuál es la tasa real de la
operación?. ¿Y si la inversión fuera de $ 500.000 al mismo tipo?
2.2
Equivalencia de tasas
Consideremos las siguientes operaciones: colocar $ 100 al 12% anual durante un
año, colocar los mismos $ 100 al 1% mesual también durante un año. Ambas
producen idéntico capital final o montante.
100 (1 + 0, 12) = 112 = 100 (1 + 12 · 0, 01) .
Este es un ejemplo de tasa equivalentes, uno de los conceptos fundamentales de
matemáticas financieras:
2.2. EQUIVALENCIA DE TASAS
17
Definición 2.31 Diremos que dos tasas i(p) y i(q) , son equivalentes, bajo una
ley financiera dada, si aplicadas a un mismo capital inicial, producen idéntico
capital final durante un mismo intervalo de tiempo, aunque tengan distinta frecuencia de capitalización (p 6= q).
ip
t años
C0
Cf
q
i
Ahora podemos deducir la ecuación fundamental de equivalencia de tasas
en el sistema de capitalización simple: Supongamos que un capital inicial C0 es
impuesto durante t años, donde t > 0 es un número real (no necesariamente
entero). La tasa p-perı́odica i(p) y la tasa q-perı́odica i(q) , con p, q ∈ Z+ , son
equivalentes si producen idéntico capital final:
C0 1 + tpi(p) = Cf = C0 1 + tqi(q) ,
Al simplificar nos queda
pi(p) = qi(q) .
Por lo tanto:
Proposición 2.32 Dados p, q ∈ Z+ , en el sistema de capitalización simple
dos tasas i(p) y i(q) , son financieramente equivalentes si cumplen la siguiente
relación de proporcionalidad:
pi(p) = qi(q) .
(2.9)
Ejemplo 2.33 ¿Cuál es la tasa mensual equivalente a una tasa trimestral del
7%?
Una tasa mensual es una i(12) , mientras que una trimestral es una i(4) (recordar que hay 4 trimestres en un año). Usando la ecuación (2.9) de equivalencias
de tasas:
12i(12)
=
12i(12)
4 · 0, 07
0, 28
=
12
= 0, 02333333 . . .
i(12)
i(12)
4i4 ,
=
Esto nos dice que es lo mismo poner $ 1.000 durante 6 meses a una tasa trimestral
del 7%, que ponerlos a una tasa mensual del 2.33333...%.
1000 (1 + 2 · 0, 07) = 1.140 = 1.000 (1 + 6 · 0, 02333333 . . .) ,
18
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
O que es lo mismo poner $ 500 durante 8 meses con cualquiera de estas dos
tasas:
8
500 1 + 0, 07 = 593.33333 . . . = 500 (1 + 8 · 0, 02333333 . . .)
3
Nota 2.34 Como muestra el ejemplo anterior y como puede concluirse de la
propia dedución de fórmula (2.9), la equivalencia de tasas en capitalización simple es independiente del intervalo de tiempo considerado: Si dos tasas producen
igual montante al cabo de t1 años, producirán igual montante al cabo de t2 años.
Ejercicio 2.35 Dada una i(2) = 0, 03, hallar la i(k) equivalente para k ∈ {1, 3, 4, 6, 12, 52, 360, 365}.
Ejercicio 2.36 Dada una tasa de interés anual del 25%. Hallar las tasas
subperı́odicas equivalentes, i.e., hallar i(k) equivalente a la tasa dada para
k ∈ {2, 3, 4, 6, 12, 52, 360, 365}. Expresar los resultados usando porcentajes.
Ejercicio 2.37 Demostrar que si i(365) y i(360) son equivalentes (a capitalización simple) entonces
72
i(365)
=
(360)
73
i
Ejercicio 2.38 Dados p, q ∈ Z+ , y un número real c > 0. Si
i(p) = c = i(q) ,
para cualquier C0 > 0 (dinero) y cualquier t > 0 (tiempo en años) demostrar
que
C0 1 + tpi(p) < C0 1 + tqi(q) ,
si y sólo si
p < q.
Es decir, dadas dos tasas de igual nominal, la que capitaliza con mayor frecuencia produce mayor montante.
Un problema habitual es comparar entre diferentes inversiones, y decidir cual
tiene mayor rendimiento. Consideremos las siguientes inversiones:
1. Invertir $ 1.000 nos da una ganacia de $ 250 al cabo de un mes.
2. Invertir $ 1.000 nos da una ganacia de $ 250 al cabo de un año.
3. Invertir $ 5.000 nos da una ganacia de $ 250 al cabo de un mes.
4. Invertir $ 900 nos da una ganacia de $ 450 al cabo de 2 meses.
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 19
Es facil concluir que la inversión 1 rinde más que la inversión 2 y que la
inversión 3, pero es más dificil decidir si rinde más o menos que la inversión
4. En general, lo mejor es comparar tasas de rendimiento de cada una de las
operaciones consideradas. La inversión 1 tiene una tasa mensual de rendimiento
(12)
t1
= 0, 25
mientras que la tasa de rendimiento de la inversión 4 es bimestral
(6)
t4 = 0, 5
(6)
Para decidir cual es mejor, hayamos la mensual equivalente a t2
6t4
(6)
=
12t4
(12)
6 · 0, 5
=
12t4
(12)
luego
(12)
t4
= 0, 25
Como ambas operaciones tienen el mismo rendimiento mensual (medido por sus
respectivas tasas mensuales de rendimiento)
(12)
t1
(12)
= 0.25 = t4
,
Decimos que ambas inversiones rinden lo mismo.
Ejercicio 2.39 Cuál inversión es mejor
1)
2)
Opción 1
$ 1.100 producen una ganacia
de $ 250 un mes.
$ 1.200 producen una ganacia
de $ 450 un año.
Opción 2
$ 850 producen una ganacia
de $ 460 en dos meses.
$ 6.500 producen una ganania
de $ 500 en 20 semanas
Ejercicio 2.40 ¿Qué oferta es más conveniente para una persona que desea
comprar una casa: $ 40.000 iniciales y $ 60.000 al cumplirse los 6 meses o $
60.000 iniciales y $ 40.000 al cumplirse el año? La tasa a usar es del 6% anual.
2.3
Equivalencia financiera de dos series de capitales
Una vez que sabemos calcular el equivalente financiero de un capital para distintos momentos, podemos verificar cuando dos series de capitales son financieramente equivalentes, este último es el segundo concepto fundamental de las
matemáticas financieras.
20
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Definición 2.41 Una serie de capitales A1 , A2 , . . . , An disponibles en los momentos ta1 , ta2 , . . . , tan , es equivalente a la serie de capitales B1 , B2 , . . . , Bm disponibles
en los momentos tb1 , tb2 , . . . , tbm , a una fecha focal f , para un agente dado (tasa),
bajo una ley financiera dada (sistema), si
n
X
Aj al momento f =
j=1
j=1
A1
Bj al momento f.
(2.10)
j=1
Pm
B1
m
X
Bj al momento f
B2
A2
B3
f
A3
Pn
j=1
Bm
An
Aj al momento f
El equivalente financiero de un capital dado, a la fecha focal f y a una tasa
p-perı́odica i(p) en el sistema de capitalización simple es
sgn(f −tj )
Aj al momento f = Aj 1 + |f − tj | i(p)
Nota 2.42 Definimos la función signo como:

 1 si x > 0
0 si x = 0
sgn (x) :=

−1 si x < 0
De donde, si f > tj (capitalización)
Aj al momento f = Aj 1 + (f − tj ) i(p)
si f = tj
Aj al momento f = Aj
y si f < tj (actualización)
Aj al momento f =
Aj
1 + (tj − f ) i(p)
En todas las fórmulas anteriores f y tj estan expresados en p-perı́odos, para que
sean compatibles con la tasa usada.
En particular para el sistema de capitalización simple tenemos que la definición
de equivalencia de capitales toma la forma
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 21
Definición 2.43 Una serie de capitales A1 , A2 , . . . , An disponibles en los momentos ta1 , ta2 , . . . , tan , es equivalente a la serie de capitales B1 , B2 , . . . , Bm disponibles
en los momentos tb1 , tb2 , . . . , tbm , a una fecha focal f , para una tasa p-perı́odica
i(p) , en el sistema de capitalización simple si
n
X
m
sgn(f −tbh )
sgn(f −taj ) X
Aj 1 + f − taj i(p)
.
=
Bh 1 + f − tbh i(p)
j=1
h=1
(2.11)
Nota 2.44 Es claro que despejar f de la ecuación (2.12) es casi siempre imposible, y son necesarios métodos numéricos para hallar f , en particular suele
ser útil usar soft mátematico como Matlab, Maple V, Mathematica, o Derive,
en cualquiera de sus versiones. (los valores de f1 y f2 se obtubieron con Maple
V Release 4, version 4.00c (1996), student edition).
El problema tı́pico (el cual no implica el uso de computadoras) es: dada una
serie de capitales, hallar una segunda serie financieramente equivalente. En el
sistema de capitalización simple, lo matemáticamente correcto es llevar todos los
capitales al origen de la serie conocida, porque no se deben usar los intereses en
los cálculos, lo cual no siempre es posible, ya que muchas veces desconoceremos
la fecha de origén de la operación.
Ejemplo 2.45 Debemos realizar 3 pagos, el primero de $ 400 dentro de tres
meses, el segundo de $ 300 dentro de 6 meses y último de $ 500 a los 9 meses.
Por razones de flujo de caja (disponibilidad de efectivo) queremos sustituir estos
3 pagos por 2: uno de $ 500 dentro de 5 meses y otro de monto a determinar
a los 10 meses. Se conviene una tasa de 2.5% mensual. Calcular el monto del
último pago usando la siguientes fechas focales: el origen, a los 6 meses, a los
10 meses.
Debemos igualar los valores de ambas operaciones a la fecha focal dada:
valor de la
valor de la
operación original = operación nueva
a la fecha focal f
a la fecha focal f
Fecha focal el origen: f = 0
22
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Serie (operación) nueva
fecha focal
C
$ 500
0
1
2
3
4
5
$ 400
6
7
8
$ 300
9
10
meses
$ 500
Serie (operación) original
Nota 2.46 Convendremos en dibujar las series originales debajo del eje temporal, y pondremos las series nuevas sobre el mencionado eje.
Tenemos que actualizar todos los capitales al momento cero:
300
500
400
+
+
1 + 3 · 0.025 1 + 6 · 0.025 1 + 9 · 0.025
=
1041.125854
=
500
C
+
1 + 5 · 0.025 1 + 10 · 0.025
C
444.4444445 +
,
1.25
de donde concluimos que
C = 745.8517624.
Fecha focal a los seis meses: f = 6
fecha focal
C
$ 500
0
1
2
3
$ 400
4
5
6
$ 300
7
8
9
10
meses
$ 500
Ahora debemos llevar todos los capitales a los seis meses, por lo que algunos
serán capitalizados (los que están disponibles antes de los 6 meses), otros serán
actualizados (los disponibles en fechas posteriores), y los disponibles a los 6
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 23
meses no cambian
400 (1 + 3 · 0.025) +
|
{z
}
Capitalización
+
300
|{z}
Sin cambios
500
1 + 3 · 0.025
{z
}
|
=
500 (1 + 0.025) +
1195.116279
=
512.500 +
C
1 + 4 · 0.025
Actualización
C
,
1.1
de donde
C = 750.877907
Ejemplo 2.47 Finalmente tomaremos como fecha focal a los 10 meses: f = 10.
fecha focal
C
$ 500
0
1
2
3
$ 400
4
5
6
7
8
$ 300
9
10
meses
$ 500
Todos los capitales, salvo C, deben ser capitalizados:
400 (1 + 7 · 0.025) + 300 (1 + 4 · 0.025) + 500 (1 + 0.025)
=
500 (1 + 5 · 0.025) + C
1312.5
=
562.500 + C,
de donde
C = 825.
Ejercicio 2.48 ¿Con qué cantidad se cancela hoy dı́a, un préstamo que se consiguió dos meses antes habiéndose firmado dos documentos; uno con valor nominal de $ 600 que vence en dos meses a partir de ahora y otro por $ 750 de
valor nominal y vencimiento a 5 meses del préstamo?. Suponga intereses del
20% anual. (Respuesta: $ 1 296.63).
Ejercicio 2.49 Una deuda de $ 2 000 con intereses del 5% anual vence en un
año. Si el deudor paga $ 600 a los 5 meses y $ 800 a los 9 meses. Hallar el saldo
de la deuda en la fecha de vencimiento. (Respuesta: $ 573.22).
Ejercicio 2.50 El señor X debe $ 500 con vencimiento en 2 meses, $ 1 000 con
vencimiento en 5 meses y $ 1 500 con vencimiento en 8 meses. Si desea saldar
las deudas mediante dos pagos iguales, uno con vencimiento en 6 meses y otro
con vencimiento en 10 meses. Determinar el importe de dichos pagos suponiendo
un interés del 6% anual, tomando como fecha focal la fecha del último pago: 10
meses.
24
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Problemas con almanaque
Ejercicio 2.51 El 10 de enero del corriente año se otorga un préstamo amparado con dos pagarés con vencimientos al 15 de marzo y al 3 de mayo, por
$ 1 300 y $ 800 respectivamente. Poco después, se conviene en cancelarlo con
tres pagos: el primero por $ 500 el 20 de febrero, el segundo por $ 1 000 el 30
de abril y el tercero el dı́a 10 de junio, ¿De qué cantidad es este último pago si
se cargan intereses del 30% mensual y se establece el 15 de marzo como fecha
de referencia?, ¿A cuánto asciende el monto del préstamo?.
Ejercicio 2.52 Sea desea sustituir el pago de 3 capitales de $ 12 725, $ 11
022 y $ 8 774, con vencimiento los dı́as 15 de mayo, 4 de junio y 25 de junio,
respectivamente, por uno único el dı́a 1 de junio; ¿a cuánto ascenderá el capital
si se aplica un 6% anual a la operación? Año civil. Fecha de operación: 15 de
mayo. (Respuesta: $ 32 516).
Ejercicio 2.53 Deseamos sustituir dos pagares de $ 14 500 y $ 12 300, con
vencimientos el 12 de abril y el 15 de junio, respectivamente, por otros tres de
igual monto, con vencimientos 10 de mayo, 10 de junio y 10 de agosto. Resolver
el problema usando:
fecha focal
8 de enero
12 de abril
10 de junio
10 de agosto
15 de septiembre
8 de enero
8 de enero
12 de abril
12 de abril
1)
2)
3)
4)
5)
6)
7)
8)
9)
tasa
1.2% mensual,
1.2% mensual,
1.2% mensual,
1.2% mensual,
1.2% mensual,
0.05% diario (365),
0.05% diario (360),
2.4% mensual,
0.6% mensual.
De la fórmula (2.11) es claro que en el sistema de capitalización simple dos
series de capitales pueden ser equivalentes para algunas fechas focales y para
otras no.
Ejemplo 2.54 Usando una tasa anual i = 0.45 (es decir una tasa del 45 %
anual), veamos a que fechas focales la serie de capitales: $ 130 000 hoy, $ 100
000 a los dos años y $ 150 000 a los 4 años, es equivalente a la serie de $ 350
000 a los 3 años y $ 400 000 a los 5 años.
El esquema de las series de capitales es
$ 350000
0
$ 130000
1
2
$ 100000
3
$ 400000
4
$ 150000
5
años
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 25
El valor de la serie de capitales: $ 130 000 hoy, $ 100 000 a los 2 años y $
150 000 a los 4 años, a la fecha focal f (en años) usando la tasa anual i = 0.45
es V1 (f ) :=
130000 (1 + 0.45 |f |)
sgn(f −2)
sgn(f )
+ 100000 (1 + 0.45 |f − 2|)
sgn(f −4)
+150000 (1 + 0.45 |f − 4|)
El valor de la serie de capitales: $ 250 000 dentro de 3 años y $ 450 000 dentro
de 5 años, a la fecha focal f (en años) usando la tasa anual i = 0.45 es V2 (f ) :=
sgn(f −3)
350000 (1 + 0.45 |f − 3|)
sgn(f −5)
+ 400000 (1 + 0.45 |f − 5|)
Por ejemplo, si escogemos como fecha focal dos años hacia adelante a partir de
hoy, f = 2, tenemos el siguiente flujo
f =2
$ 350000
0
$ 130000
1
2
$ 400000
3
$ 100000
4
5
años
$ 150000
De donde deducimos los siguientess valores para V1 y V2
V1 (2)
V2 (2)
=
sgn(2)
130000 (1 + 0.45 |2|)
+ 100000 (1 + 0.45 |2 − 2|)
+150000 (1 + 0.45 |2 − 4|)
sgn(2−4)
=
130000 (1 + 2 · 0.45) + 100000 +
=
425947.3684
sgn(2−3)
350000 (1 + 0.45 |2 − 3|)
350000
400000
=
+
1 + 0.45 1 + 3 · 0.45
= 411592.0763
=
sgn(2−2)
150000
1 + 2 · 0.45
sgn(2−5)
+ 400000 (1 + 0.45 |2 − 5|)
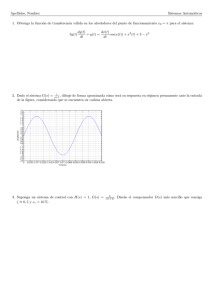
La siguente gráfica muestra los valores de las funciones V1 y V2 , en rojo la
primera y en azul punteada la segunda, para fechas focales entre 0 y 6 años.
Notar que las unidades del eje y son cientos de miles de pesos.
26
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
$ en 100000
V2 (f )
11
V1 (f )
10
9
8
7
6
5
4
3
2
1
f en años
0
f1
1
2
3
4
f2
5
6
Sólo existen dos fechas focales tales que
V1 (f ) = V2 (f ) ,
y ellas son (dadas en años)
f1
=
0.23877905,
f2
=
4.27194599.
Pues
V1 (0.23877905) = 283357.5590 = V2 (0.23877905) ,
y
V1 (4.27194599) = 851621.5493 = V2 (4.27194599) ,
(2.12)
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 27
Nota 2.55 En el sistema de capitalización simple, la equivalencia financiera
depende fuertemente de la fecha focal escogida.
2.3.1
Tasa media
Consideremos el siguiente ejemplo
Ejemplo 2.56 Ud. tiene $ 100.000 invertidos al 18% anual, $ 250.000 al 8%
semestral y % 75.000 al 2% mensual. ¿Qué tasa diaria deberı́a ofrecerle una
entidad financiera para que ud. coloque todo su capital, $ 425.000, en la misma?
Esto no es más que un problema de equivalencia financiera de capitales,
donde la incognita es una tasa (en principio, el tiempo también parece ser una
incognita, pero veremos que en sistema simple, este tipo de problemas es independiente del tiempo).
Poner dibujo!!!!!!!!!!!!!
Al cabo de t años, las inversiones originales generan la siguiente cantidad de
dinero
100.000 (1 + t · 0, 18) + 250.000 (1 + t · 2 · 0, 08) + 75.000 (1 + t · 12 · 0, 02)
La operación nueva genera al cabo de t años
425.000 1 + t · 365i(365)
si queremos que ambas produscan igual capital final, tenemos que
100.000 (1 + t · 0, 18)+250.000 (1 + t · 2 · 0, 08)+75.000 (1 + t · 12 · 0, 02) = 475.000 1 + t · 365i(365)
de donde
100.000 · 0, 18 + 250.000 · 2 · 0, 08 + 75.000 · 12 · 0, 02 = 425.000 · 365i(365)
Por lo que la tasa que buscamos, conocida como la tasa media diaria de la
operación, es
i(365)
=
=
100.000 · 0, 18 + 250.000 · 2 · 0, 08 + 75.000 · 12 · 0, 02
425.000 · 365
0, 000489927477841
Por lo tanto, la entidad financiera debe ofrecerle al menos un 0,0489927477841%
diario para que ud. reciba el mismo monto final. Veamos que efectivamente,
ambas operatorias producen el mismo ingreso. Por ejemplo en un año, sus inversiones originales le reportan $ 501.000 pues
100.000 (1 + 0, 18) + 250.000 (1 + 2 · 0, 08) + 75.000 (1 + 12 · 0, 02) = 501.000
Obtendrá la misma suma con la segunda operatoria
425.000 (1 + 365 · 0, 000489927477841) = 501.000
28
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Se invita al lector a calcular el ingreso de ambas operatorias a 2, 2,5, 3 y 5
años (o cualquier otro intervalo de tiempo), los ingresos producidos por ambas
operatorias deberian ser iguales (si no fuera el caso, ¡cometió un error!).
Es interesante comparar la tasa media de la operación, contra la tasa promedio de la misma. En este caso la tasa promedio diaria se consigue promediando
las tasas diarias equivalentes a las tasas originales
0, 18
= 0, 0004931506849
365
0, 16
(365)
(365)
365i2
= 2 · 0, 08
=⇒ i2
=
= 0, 0004383561643
365
0, 24
(365)
(365)
= 0, 0006575342465
365i3
= 12 · 0, 02 =⇒ i3
=
365
Luego la tasa promedio diaria de la operación es
(365)
365i1
(365)
i1
(365)
+ i2
= 1 · 0, 18
(365)
+ i3
=
3
=
=⇒
(365)
i1
=
0, 0004931506849 + 0, 0004383561643 + 0, 0006575342465
3
0, 0005296803651
En este caso se observa que la tasa promedio de la operación es ligeramente
superior a la tasa media de la misma.
La operación financiera anterior ocurre con relativa frecuencia, por lo que
amerita el desarrollo de fórmulas generales.
En general una serie n capitales Cj , con j = 1, . . . , n, colocados a las tasas
qj -perı́odicas i(qj ) , con j = 1, . . . , n, durante t años, es equivalente a una colocar
la suma de todos los capitales
C=
n
X
Cj
j=1
(p)
a la tasa media equivalente p-perı́odica imedia
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!!!!
n
X
(p)
Cj 1 + tqj i(qj ) = C 1 + tpimedia
j=1
de donde
n
X
j=1
Cj + t
n
X
(p)
Cj qj i(qj )
=
C + tCpimedia
Cj pj i(pj )
=
Cpimedia
j=1
n
X
(p)
j=1
despejando la tasa media obtenemos
n
X
(p)
imedia =
qj Cj i(qj )
j=1
pC
(2.13)
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 29
Nota 2.57 Observe que la fórmula para la tasa media de una serie de capitales
es independiente del tiempo t. Depende de los capitales Cj y de las tasas qj perı́odicas i(qj ) , con j = 1, . . . , n.
Si se observa con atención la fórmula anterior, se puede concluir que la tasa
media es un promedio pesado de las tasas p-perı́odicas equivalentes a las tasas
dadas:
n
X
Cj qj (qj )
(p)
i
imedia =
C p
j=1
qj (qj )
es la tasa p-perı́odica
p i
Cj
factores C , los cuales suman 1
donde cada factor
pesos son los
n
X
Cj
j=1
C
=
equivalente a la tasa i(qj ) , y los
n
1 X
Cj = 1
C j=1
Por lo que es inmediato que
qj (qj )
qj (qj )
(p)
min
i
≤ imedia ≤ max
i
1≤j≤n
1≤j≤n
p
p
En el caso del ejemplo 2.56 tenemos
qj (qj )
0, 18 2 · 0, 08 12 · 0, 02
min
i
= min
,
,
1≤j≤n
p
365
365
365
= min {0, 0004931506849, 0, 0004383561643, 0, 0006575342465}
=
max
1≤j≤n
qj (qj )
i
p
0, 0004383561643
0, 18 2 · 0, 08 12 · 0, 02
= max
,
,
365
365
365
= max {0, 0004931506849, 0, 0004383561643, 0, 0006575342465}
=
0, 0006575342465
y se verifica que
(p)
0, 0004383561643 ≤ imedia = 0, 000489927477841 ≤ 0, 0006575342465
(p)
Nota 2.58 Además, dados q1 , q2 ∈ Z, es evidente que las tasas medias imedia y
(q)
imedia (calculadas con respecto a una misma serie de capitales) son equivalentes:
n
X
(p)
pimedia =
Cj qj i(qj )
j=1
(q)
C
= qimedia
(2.14)
En general una serie de n capitales Cj , con j = 1, . . . , n, a las tasas qj perı́odicas i(qj ) , con j = 1, . . . , n, también tiene un tasa promedio p-perı́odica
30
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
asociada la cual no es otra cosa que el promedio de las tasas p-perı́odicas equivalentes a las tasas dadas:
n
(p)
ipromedio =
1 X qj (qj )
i
n j=i p
Para el ejemplo anterior la tasa mensual promedio es
1 1
4
(12)
ipromedio =
0, 07 + 0, 041 = 0, 00975
2 12
12
En este caso la tasa media, 0, 010925, resulta ser mayor que la tasa promedio,
0, 00975. La pregunta que surge de manera natural es ¿Existe alguna relación
entre tasa media y tasa promedio? Veremos que en realidad la tasa media (en
sistema simple) es un promedio pesado (o ponderado) de las tasas originales,
donde los pesos vienen dados por los tamaños relativos de los Cj respecto de C.
Por ejemplo, veremos que la tasa media y la tasa promedio coinciden en el caso
Cj = n1 C.
Dada una serie de operaciones consistentes de colocar n capitales Cj , con
j = 1, . . . , n, a las tasas qj -perı́odicas i(qj ) , con j = 1, . . . , n, si llamamos Cmin :=
min {C1 , . . . , Cn }, y Cmax := max {C1 , . . . , Cn }, como para todo j = 1, . . . , n
Cmin ≤ Cj ≤ Cmax
tenemos que
n
X
(p)
imedia
=
pC
n
X
qj Cj (qj )
=
i
p C
j=1
≥
Como
n
X
qj
j=1
qj Cj i(qj )
j=1
p
n
Cmin X qj (qj )
i
C j=1 p
(p)
i(qj ) = nipromedio
Tenemos que
Cmin (p)
i
C promedio
De manera similar se puede probar que
(p)
imedia ≥ n
(p)
imedia ≤ n
Cmax (p)
i
C promedio
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 31
Por lo que siempre se cumple que
n
Cmin (p)
Cmax (p)
(p)
i
≤ imedia ≤ n
i
C promedio
C promedio
de donde se deduce con facilidad que si C1 = C2 = · · · = Cn = C/n, entonces
(p)
(p)
imedia = ipromedio .
En el caso del ejemplo 2.56 tenemos
n
n
Cmin (p)
i
C promedio
Cmax (p)
i
C promedio
75.000
· 0, 0005296803651
425.000
= 0, 0002804190168
250.000
= 3·
· 0, 0005296803651
425.000
= 0, 0009347300559
=
3·
Ejercicio 2.59 Consideremos la siguiente modificación del ejemplo 2.56: Ud.
tiene $ 140.000 invertidos al 18% anual, $ 142.000 al 8% semestral y % 143.000
al 2% mensual. Se pide calcular: Tasa media diaria, tasa diaria mı́nima, tasa
(365)
min (365)
ipromedio , y 3 Cmax
diaria máxima, tasa promedio diarı́a, 3 CC
C ipromedio . Ordenar
estas cantidad de mayor a menor.
Ejemplo 2.60 Tenemos dos opciones de inversión: La primera es dividir el
capital en dos partes, colocando el 35% del mismo al 7% anual, y el 65% restante
al 4,1% trimestral. La segunda consite en colocar todo el capital al 1,25 mensual.
¿Cuál de las opciones es la más ventajosa?
En esta situación debemos comparar dos inversiones, una de las cuales involucra más de una tasa. Una forma de resolver este problema, es sustituir las
dos operaciones por una equivalente: Es decir, dado un intevalo de tiempo de
(12)
t años, queremos hallar una tasa media imedia 12-perı́odica (mensual), que nos
produzca la misma ganancia:
(12)
0.35C (1 + t · 0, 07) + 0.65C (1 + 4t · 0, 041) = C 1 + 12t · imedia
despejando
(12)
imedia =
0, 35 · 1 · 0, 07 + 0, 65 · 4 · 0, 041
= 0, 010925
12
Se puede observar que el valor de la tasa media (en el sistema de capitalización
simple) es independiente del tiempo. Ahora es claro que la segunda opción (no
dividir el capital) es la más conveniente:
(12)
i2
(12)
= 0, 0125 > 0, 010925 = imedia
En el fondo esto no es más que sustituir dos rectas (en t) por su suma, la cual
es a su vez una recta:
32
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
$
(12)
C(1 + t · imedia )
C
0.60C(1 + t · 0.07)
0.40C(1 + 4t · 0.041)
0.6C
0.4C
t (años)
Ejercicio 2.61 Tenemos $ 100.000 para invertir. Se nos presentan tres opciones. La primera es depositarlo todo en un banco que paga en 2,5% mensual.
La segunda en comprar $ 60.000 en bonos del estado que pagan un 8,2% trimestral y el resto en el banco al 1,8% mensual. La tercera consiste en comprar
obligaciones de empresas privadas: $ 30.000 en opciones de la empresa A, que
rinden un 21% semestral, $ 40.000 en opciones de la empresa B, que rinden
un 4,8% bimestral y el resto en opciones de la empresa C que rinden un 38,5%
anual. ¿Cuál de las opciones es la más ventajosa?
Ejercicio 2.62 Tenemos dos opciones de inversión: La primera es dividir el
capital en dos partes, colocando el 30% del mismo al 18% anual, y el 70%
restante al 6,5% trimestral. La segunda consite en colocar todo el capital al
0,5% semanal. ¿Cuál de las opciones es la más ventajosa?
Poner más ejercicios!!!!!!!!!!!!!!!!!!!!!!!!
2.3.2
Vencimiento medio
Este es un caso particular de equivalencia financiera, en el que sustituimos una
serie de capitales por un único pago igual a la suma algebraica de los capitales
involucrados.
Dada una tasa p-perı́odica y una fecha focal f , deseamos hallar la fecha m
en la cual podemos sustituir una serie de capitales C1 , C2 , . . . , Cn disponibles
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 33
en los momentos t1 , t2 , . . . , tn , por un único pago
C=
n
X
Cj
j=i
Dicha fecha focal es conocida como vencimiento medio:
n
X
sgn(f −tj )
sgn(f −m)
Cj 1 + |f − tj | i(p)
= C 1 + |f − m| i(p)
j=i
En la fórmula anterior los intervalos de tiempo son medidos en p-perı́odos, para
que sean compatibles con la tasa usada.
Falta poner ejemplos resueltos donde la incognita es un capital (?), o la tasa de interés.
Como se puede ver, usando capitalización simple, el vencimiento medio depende de cada una de las variables involucradas (salvo en casos excepcionales,
no hay simplificación de variables), y para calcular el valor de m tenemos que
analizar cada caso, y eventualmente necesitaremos emplear métodos númericos.
Razonando financieramente es intuitivo que el vencimiento medio se encuentra entre el primero y el último momento en que los capitales vencen, porque se
debe dar una compensación de intereses.
Ejemplo 2.63 Deseamos sustituir tres pagos, de $ 200, $ 300 y $ 500, con
vencimientos hoy, dentro de 6 meses y dentro de un año, respectivamente, por
único pago de $ 1000. Hallar el vencimiento medio para
fecha focal
hoy
hoy
6 meses
1 año
2 años
hoy
vencimiento medio
1)
2)
3)
4)
5)
6)
7)
tasa
2% mensual,
1% mensual,
1% mensual,
1% mensual,
32% anual,
1% diario comercial (360),
1% mensual.
Para resolver este problema planteamos la ecuación de equivalencia financiera
en general
sgn(f )
200 (1 + |f − 0| i)
+300 (1 + |f − 6| i)
sgn(f −6)
sgn(f −12)
+500 (1 + |f − 12| i)
1) fecha focal: f = 0, tasa: 2% mensual
200 +
500
300
+
1 + 6 · 0, 02 1 + 12 · 0, 02
871, 0829494
1.000
sgn(−m1 )
=
1.000 (1 + 0, 02 |m1 |)
=
(1 + 0, 02 |m1 |)
sgn(−m1 )
sgn(f −m)
= 1.000 (1 + |f − m| i)
34
CHAPTER 2. SISTEMAS DE CAPITALIZACIÓN SIMPLE
Como
871, 0829494
1000
entonces el exponente sgn (−m1 ) debe ser −1, y por lo tanto podemos asegurar
que m1 > 0,
871, 0829494
1
=
,
1000
1 + 0, 02m1
1 + 0, 02 |m1 | > 1 >
de donde
m1 = 7, 399814833 meses.
2) fecha focal: f = 0, tasa: 1% mensual
200 +
300
500
+
1 + 6 · 0, 01 1 + 12 · 0, 01
929, 4474394
1000
sgn(−m2 )
=
1.000 (1 + 0, 01 |m2 |)
=
(1 + 0, 01 |m2 |)
sgn(−m2 )
Como
929, 4474394
1.000
el exponente sgn (−m2 ) debe ser −1, y además podemos asegurar que vm2 > 0,
por lo tanto
929, 4474394
1
=
1.000
1 + 0, 01m2
1 + 0, 01 |m2 | > 1 >
de donde
m2 = 7, 590806926 meses.
Observando los resultados 1) y 2) vemos que en capitalización simple, el
vencimiento medio depende de la tasa usada.
3) fecha focal: f = 6, tasa: 1% mensual
500
1 + 6 · 0, 01
983, 6981132
1.000
200 (1 + 6 · 0, 01) + 300 +
=
1.000 (1 + 0, 01 |6 − m3 |)
=
(1 + 0, 01 |6 − m3 |)
sgn(6−m3 )
sgn(6−m3 )
Como
983, 6981132
1.000
el exponente sgn (6 − m3 ) debe ser −1, y además podemos asegurar que 6−m3 <
0, por lo tanto
871, 0829494
1
=
,
1.000
1 + 0, 02 (m3 − 6)
1 + 0, 01 |6 − m3 | > 1 >
de donde
vm3 = 7, 657204236 meses.
Observando los casos 2) y 3) podemos asegurar que el vencimiento medio depende de la fecha focal usada.
2.3. EQUIVALENCIA FINANCIERA DE DOS SERIES DE CAPITALES 35
7) f = m (fecha focal igual al vencimiento medio), tasa 1% mensual:
sgn(m)
200 (1 + |m| i)
+300 (1 + |m − 6| i)
sgn(m−6)
+500 (1 + |m − 12| i)
sgn(m−12)
Usando métodos númericos (y Maple V Release 4, version 4.00c (1996), student
edition):
m = 7, 711838862 meses.
Ejercicio 2.64 En el ejemplo anterior hallar m4 , m5 , y m6 .
Ejercicio 2.65 Se desea sustituir 12 pagos mensuales de $ 1.000, por un único
pago de $ 12.000. Suponer una tasa anual del 18,5%. Usar como fechas focales:
el origen, 6 meses, 1 año y el propio vencimiento medio.
Ejemplo 2.66 Si a los 7,46666666 meses se sustituyeron 3 pagos de $ 1.000,
a los cero, seis y doce meses, respectivamente, por un único pago de $ 3.000.
Utilizando una tasa del 5% mensual ¿Cuál fue la fecha focal usada?
Ejercicio 2.67 Si en el problema anterior sabemos que la sustitución fue a los
6 meses y se uso el origen como fecha focal.¿Cuál fue la tasa usada?
Poner más ejercicios!!!!!!!!!!!!!!
= 1.000
Chapter 3
Descuento Simple
En las operaciones comerciales habitualmente no se usa la actualización para
calcular el valor actual de un capital futuro. El método usado se conoce como
descuento (comercial). Este es el caso tı́pico de lo que ocurre con los cheques
a fechas. El poseedor de un cheque (documento, plazo fijo, etc.) el cual tiene un
nominal N , podrá hacerlo efectivo en t años (esta cantidad no tiene porque ser
entera), pero por algún motivo necesita dinero hoy (para pagar una deuda, por
una oportunidad de inversión, etc.). Entonces acude a un intermediaro finaciero
(banco, financiera, un “prestamista” en el peor de los casos), y cambia el cheque
por una suma en efectivo E, donde
E < N.
D
N
E
hoy
dentro de t años
La diferencia entre el E efectivo que recibe, y el nominal N del documento
entregado, recibe el nombre de descuento
D = N − E.
(3.1)
En esta operación se puede pensar que el intermediario financiero se ha
cobrado los intereses al principio de la operación. La tasa que se usa es llamada
tasa de descuento d, la cual tiene la particularidad que se aplica sobre el
nominal N .
36
37
3.0.3
Descuento simple
En el sistema de capitalización simple lo que nos descuentan por cada p-perı́odo
adelanto es
N d(p)
Supongamos que se quiere adelantar un documento de nominal N , unos n pperı́odos con un intermediario financiero que cobra una tasa de descuento pperı́odica d(p) . Si llamamos Ej al efectivo que recibiremos en el perı́odo j, tenemos la siguiente relación recursiva
Ej = Ej+1 − N d(p) j < n,
En = N
Donde la condición inicial es En = N (al momento n hacemos efectivo el documento, no necesitamos descontarlo).
d(k)
Dk
Dk+1
D1
D = D0
En = N
Ek
Ek+1
E1
E = E0
0
1
k
k+1
n
Usando la teorı́a de relaciones recursivas que hemos desarrollado concluimos
que la forma para el efectivo en el momento j, para j < n, es
Ej = h0 + jN d(p) ,
donde h0 es una constante que se ajusta usando la condición inicial En = N :
N
h0
= En = h0 + nN d(p)
=
1 − nd(p) N
luego
Ej = N 1 − (n − j) d(p) , para j ≤ n,
38
CHAPTER 3. DESCUENTO SIMPLE
en particular
E = E0 = N 1 − nd(p)
(3.2)
La cual es la ecuación fundamental del sistema de descuento simple para una
tasa de descuento p-perı́odica d(p) .
En términos de la tasa de descuento y el nominal, el descuento es
D = nN d(p)
(3.3)
Nota 3.1 Si n es suficientemente grande, el descuento comercial puede ser tan
grande que anule el efectivo
E = E0 = 0 = N 1 − nd(p) ,
(3.4)
Esto ocurre si
n=
Si n >
1
d(p)
1
.
d(p)
el efectivo es de hecho negativo.
Ejemplo 3.2 Se desea hacer efectivo hoy un cheque a 5 dı́as de nominal $ 1
.000. Qué efectivo recibiremos si acudimos a un banco que aplica un tasa de
descuento diario de 2,1%. ¿Cuántos dı́as hay que adelantar el documento para
que el efectivo sea nulo?
El efectivo que recibiremos se calcula con (3.4)
E = 1000 (1 − 5 · 0, 021) = 895
de donde
D = 1000 − 895 = 105
Finalmente
1
= 47, 619047619
0.021
i.e., si adelantamos un documento más de 47 dı́as lo único que nos dan son las
gracias (de hecho nos piden además del documento, ¡dinero extra!).
Observe que el valor actual de $ 1.000, calculado con una tasa efectiva diaria
del 2,1% es
1000
= 904, 98
C0 =
1 + 5 · 0, 021
nanulación =
Esto no es casualidad, si una tasa de descuento (simple) p-perı́odica d(p) es igual
(cómo número real) a una tasa (efectiva simple) p-perı́odica i(p)
d(p) = x = i(p)
y son aplicadas sobre un capital de nominal N disponible dentro de t años para
calcular su valor al dı́a de hoy
39
Poner dibu!!!!!!!!!!!!!!!!!!!!
tenemos que
N
(p)
=
C
>
E
=
N
1
−
tpd
0
1 + tpi(p)
Es claro que si E es no.positivo la desigualdad se cumple trivialmente pues
siempre C0 > 0. Si E > 0, entonces tpd(p) < 1. Y la desigualdad se deduce del
siguiente hecho: si 0 < ax < 1, entonces
1<
1
1 − (ax)
2
2
(Pues, si 0 < ax < 1, entonces 0 < (ax) < 1, y por lo tanto
2
0 < 1 − (ax) < 1
de donde deducimos que
1<
1
1 − (ax)
2
=
1
(1 − ax) (1 + ax)
que es la desigualdad requeridad). Lo que implica que
1
1
C0
=
=
2 >1
(p)
(p)
E
1 + tpi
1 − tpd
1 − (ax)
donde hacemos tp = a y d(p) = x = i(p) , y la condición tpd(p) < 1 garantiza que
0 < ax = tpd(p) < 1. De donde podemos deducir que C0 > E.
Ejercicio 3.3 ¿Cuál fue el descuento y el efectivo de una letra con vencimiento
a 3 meses si se aplicó una tasa de descuento del 4,5% mensual y su nominal
ascendı́a a $ 5.000?
Ejercicio 3.4 Sabiendo que el descuento sobre un cheque a 12 dı́as es de $ 230.
Calcular el nominal si la tasa de descuento diaria aplicada es del 5%.
Ejercicio 3.5 Se desea hacer efectivo hoy un cheque a 60 dı́as de nominal $
5.000. Que efectivo recibiremos si acudimos a un banco que aplica un tasa de
descuento diario de 1%. ¿Cuántos dı́as hay que adelantar un documento a esta
tasa para que efectivo sea nulo?
Ejercicio 3.6 Adelantamos 10 dı́as un cheque a fecha de nominal $ 3.500, y
nos entregan $ 3.150. ¿Cuál fue la tasa de descuento diario que nos aplicaron?
Poner más ejercicios!!!!!!!!
40
CHAPTER 3. DESCUENTO SIMPLE
3.0.4
Equivalencia de tasas de descuento simple.
Con respecto a las tasas de descuento surgen naturalmente dos preguntas, dada
una tasa de descuento q-perı́odica d(q) :
1. ¿Cuál es la tasa de descuento p-perı́odica equivalente?
2. ¿Cuál es la tasa efectiva p-perı́odica equivalente?
Por definición de equivalencia de tasas, dados un efectivo E, un nominal
N , un perı́odo de descuento de t años, y dos tasas descuento d(p) y d(q) , con
p, q ∈ Z, se dicen que son equivalentes si producen igual efectivo
N 1 − qtd(q) = E = N 1 − ptd(p) ,
de donde concluimos la ecuación fundamental de equivalencia de tasas de descuento simple
qd(q) = pd(p) .
(3.5)
d(p)
t años
E
N
(q)
d
Como antes, usaremos d, en lugar de d(1) , para designar una tasa de descuento anual
Ejemplo 3.7 Dada una tasa de descuento anual del 10% hallar la tasa d(p) ,
para k ∈ {2, 3, 4, 6, 12, 52, 360, 365}, equivalente.
Por ejemplo, la tasa de decuento cuatrimestral equivalente es
d
=
3d(3)
0, 10
=
3d(3) ,
de donde
d(3) = 0, 03333333 . . .
Ejercicio 3.8 Dada una tasa de descuento bimestral del 3,5% hallar la tasa
d(p) , para k ∈ {1, 2, 3, 4, 12, 52, 360, 365}, equivalente.
Poner más ejercicios!!!!
41
3.0.5
Equivalencia entre tasas de descuento y de capitaliación simples.
Por definición de equivalencia de tasas, dados un efectivo E, un nominal N , un
perı́odo de descuento de t años, y p, q ∈ Z, la tasa de capitalización p-perı́odica
i(p) y la tasa de descueno q-perı́odica d(q) , se dicen que son equivalentes si
producen igual efectivo
N
N 1 − qtd(q) = E =
1 + pti(p)
de donde llegamos a la relación fundamental de equivalencia entre tasas de
capitalización simple y de descuento simple
(3.6)
1 − qtd(q) 1 + pti(p) = 1.
Claramente esta equivalencia no es independiente del tiempo t considerado.
i(p)
t años
E
N
(q)
d
Ejemplo 3.9 Dada una tasa de descuento mensual del 8% hallar la tasa de
capitalización simple diaria (comercial) i(360) equivalente para una operación a
2 meses.
De (3.6)
2 (12) d
1 + 60i(360)
12
(1 − 2 · 0, 08) 1 + 60i(360)
1 − 12 ·
=
1.
=
1.
de donde
1
−1
0, 84
i(360) =
= 0, 0031746
60
Ejercicio 3.10 Completar la siguiente tabla de tasa equivalentes
1)
2)
3)
4)
5)
6)
7)
8)
9)
tasa 1
d(2) =?
d(2) =?
d(12) = 0, 023
d(12) = 0, 023
d(365) = 0, 01
d(360) =?
d(360) =?
d = 0, 18
d = 0, 18
tasa 2
i(6) = 0, 06
i(6) = 0, 06
i(4) =?
i(4) =?
i(360) = 0, 011
i(360) = 0, 035
i(360) = 0, 035
i =?
i =?
tiempo
3 meses,
10 meses,
6 meses,
6 dı́as,
¿? dı́as,
5 dı́as,
180 dı́as,
1 años
1/2 año.
42
CHAPTER 3. DESCUENTO SIMPLE
Poner más ejercicios
3.0.6
Equivalencia financiera revisada
Es posible usar descuento como ley financiera en la equivalencia financiara.
Tı́picamente esto se hace cuando la fecha focal f escogida no es posterior a
ninguno de los capitales de las series de capitales involucradas, pero en realidad
las única limitación que existe es lo que acuerden las partes involucradas. De
hecho se puede usar un sistema para capitalizar y otro para descontar, e inclusive
se puede usar una tasa para actualizar (o descontar) y otra para capitalizar. Aqui
un ejemplo.
Ejemplo 3.11 Debemos realizar 3 pagos, el primero de $ 400 dentro de tres
meses, el segundo de $ 300 dentro de 6 meses y el último de $ 500 a los 9 meses.
Por razones de flujo de caja (disponibilidad de efectivo) queremos sustituir estos
3 pagos por 2: uno de $ 500 dentro de 5 meses y otro de monto a determinar a
los 10 meses. Calcular el monto del segundo pago si
1)
2)
3)
4)
5)
6)
7)
fecha focal
en meses
f = 0 (hoy)
f =6
f =5
f =6
f =6
f =6
f =6
sistema usado
para actualizar
descuento
descuento
descuento
descuento
simple
descuento
simple
tasa usada
para actualizar
d(12) = 0, 03
d(12) = 0, 02
d(12) = 0, 02
d(12) = 0, 025
i(12) = 0, 025
d(12) = 0, 03
i(12) = 0, 05
sistema usado
capitalizar
—
descuento
descuento
simple
descuento
simple
descuento
tasa usada
para capitalizar
—
d(12) = 0, 02
d(12) = 0, 05
i(12) = 0, 025
d(12) = 0, 025
i(12) = 0, 02
d(12) = 0, 03
Debemos igualar lo valores a la fecha focal dada de ambas operaciones:
valor de la
valor de la
operación original = operación nueva
a la fecha focal f
a la fecha focal f
1) Fecha focal el origen: f = 0
Tenemos que descontar todos los capitales al momento cero:
400 (1 − 3 · 0, 03) + 300 (1 − 6 · 0, 03) + 500 (1 − 9 · 0, 03)
=
500 (1 − 5 · 0, 03) + C (1 − 10 · 0, 023)
975
=
425 + 0, 77C
de donde concluimos que
C = 714, 285714286
Por lo tanto el monto del segundo pago asciende a $ 714,28571 al usar como
fecha focal el origen y utilizar una tasa mensual de descuento comercial del 3%.
2) Fecha focal a los seis meses: f = 6
43
Ahora debemos llevar todos los capitales a los seis meses, usando descuento
400
+ 300 + 500 (1 − 3 · 0, 02) =
1 − 3 · 0, 02
1195, 5 =
500
+ C (1 − 4 · 0, 02)
1 − 1 · 0, 02
510, 2 + 0, 92C,
de donde
C = 744, 891304348
Por lo tanto el monto del segundo pago asciende a $ 744,8913 al usar como fecha
focal 6 meses y utilizar una tasa mensual de descuento comercial del 3%.
3) Fecha focal a los cinco meses: f = 5
Usaremos descuento, pero con diferentes tasas para descontar d(12) = 0.02 y
capitalizar d(12) = 0.05:
400
+ 300 (1 − 1 · 0, 02) + 500 (1 − 4 · 0, 02) = 500 + (1 − 5 · 0, 02) C
1 − 2 · 0, 05
1198, 4 = 500 + 0, 9C
de donde
C = 775, 55556
Por lo tanto el monto del segundo pago asciende a $ 775,55556 al usar como
fecha focal el 5to mes y utilizar una tasa mensual de descuento comercial del
2% para descontar y una tasa de descuento del 5% para capitalizar.
4) Fecha focal a los seis meses: f = 6
Usaremos descuento para actualizar, con tasa de decuento d(12) = 0, 025 y
sistema simple para capitalizar, con una tasa i(12) = 0, 025:
400 (1 + 3 · 0, 025) + 300 + 500 (1 − 3 · 0, 025)
=
500 (1 + 1 · 0, 025) + C (1 − 5 · 0, 025)
1192, 5
=
512, 5 + 0, 875C
de donde
C = 777, 142857143
Por lo tanto el monto del segundo pago asciende a $ 777,14286 usar como fecha
focal el 6to. mes y utilizar una tasa mensual de descuento comercial del 2,5%
para actualizar y una tasa (efectiva) simple del 2,5% para capitalizar.
7) Fecha focal a los seis meses: f = 6
Usaremos sistema simple para actualizar, con una tasa i(12) = 0, 05, y descuento para capitalizar, con tasa de decuento d(12) = 0, 03:
400
500
+ 300 +
1 − 3 · 0, 03
1 + 3 · 0, 05
=
1174, 3
=
de donde
C = 823, 55
500
C
+
1 − 1 · 0, 03 1 + 5 · 0, 05
C
515, 46 +
1, 25
44
CHAPTER 3. DESCUENTO SIMPLE
Por lo tanto el monto del segundo pago asciende a $ 823,55 al usar como fecha
focal el 6to. mes y utilizar una tasa (efectiva) simple mensual del 5% para
actualizar y una tasa de descuento mensual del 3% para capitalizar.
Ejercicio 3.12 Resolver los casos 5) y 6) del ejemplo anterior.
Ejercicio 3.13 El señor Y debe $ 600 con vencimiento en hoy, $ 10.000 con
vencimiento en 5 meses y $ 15.000 con vencimiento en 10 meses. Si desea saldar
las deudas mediante dos pagos iguales, uno con vencimiento en 6 meses y otro
con vencimiento en 12 meses. Determinar el importe de dichos pagos si
1)
2)
3)
4)
5)
6)
fecha focal
en meses
f = 0 (hoy)
f =6
f =6
f =6
f =6
f =0
sistema usado
para actualizar
descuento
descuento
descuento
simple
simple
simple
tasa usada
actualizar
d(12) = 0, 037
d(12) = 0, 037
d(12) = 0, 037
i(12) = 0, 037
i(12) = 0, 037
i(12) = 0, 037
sistema usado
capitalizar
—
descuento
simple
descuento
simple
simple
tasa usada
capitalizar
—
d(12) = 0, 037
i(12) = 0, 037
d(12) = 0, 037
i(12) = 0, 037
i(12) = 0,037
¿Cuál de las 6 operaciones propuestas es la más conveniente para el deudor?
¿Cuál es la más conveniente para el acreedor?
Nota 3.14 En el problema anterior, una cuestión importante es hallar las
fechas focales que minimizen (en el caso del deudor) o maximizen (en el caso del
acreedor) los pagos, dentro del rango de tiempo de la operación en cuestión. Por
ejemplo, al graficar los pagos en función de la fecha focal tenemos los siguientes
valores aproximados para los valores extremos para las operaciones 2) y 6)
2)
6)
fecha focal
de pago mı́nimo
f =0
f = 12
Pago mı́nimo
671.4375862
921.3632458
fecha focal
de pago máximo
f = 12
f =0
Pago máximo
1298.980462
1389.201350
De donde podemos concluir que, comparando entre 2) y 6), al deudor le conviene
proponer un esquema de pago como el planteado en 2) pero con el origen como
fecha focal, mientras que al acreedor le conviene proponer el esquema de pago
6), también con el origen como fecha focal.
Poner más ejercicios!!!!!!!!!!!
Chapter 4
Sistemas de capitalización
compuesta
4.1
Sistema de capitalización compuesta
En el capı́tulo anterior consideramos la ley financiera de capitalizacion simple
en la cual los intereses generados en un perı́odo dado no son considerados para
el cálculo de los intereses del perı́odo siguiente. En este capı́tulo estudiaremos
la ley financiera que surge al agregar al capital los intereses generados en un
perı́odo de tiempo dado para el cálculo de los intereses del perı́odo siguiente, es
lo que llamaremos capitalización compuesta.
Hoy en dı́a la capitalización compuesta es el sistema más usado por las
instituciones financieras, por ello que este capı́tulo es de suma importancia para
el estudio de la materia; aunque cada vez es más frecuente el uso del sistema de
capitalización continuo, el cual será estudiado en el capı́tulo siguiente.
Dado un capital inicial C0 , impuesto durante n p-perı́odos a una tasa pperiódica i(p) , deseamos obtener una expresión analı́tica para Cn , el capital
acumulado al momento n. Procederemos de manera inductiva observando en
detalle que ocurre en los primeros pasos, a fin de inferir una expresión para Cn .
Nota 4.1 Recordar que Ck es el capital disponible al momento k, es decir que
Ck es simultaneamente el capital al final del perı́odo k y el capital al inicio del
perı́odo k + 1.
(poner dibujo)
Usaremos la siguiente convención (coherente con el resto de la literatura).
Asi cuando hablemos de un capital al perı́odo k es equivalente a el capital al
momento k, es decir un capital al final de perı́odo k.
(poner dibujo)
El capital al final del primer perı́odo, C1 , es la suma de C0 , el capital al
45
46
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
inicio del perı́odo, más C0 i(p) , los intereses generados durante este perı́odo:
C1
= C0 + C0 i(p)
= C0 1 + i(p)
Similarmente C2 , el capital al final del segundo perı́odo, es la suma de C1 , el
capital al inicio del perı́odo, más C1 i(p) , los intereses generados durante este
perı́odo
C2
= C1 + C1 i(p)
= C1 1 + i(p)
pero como C1 = C0 1 + i(p) , obtenemos
C2 = C0 1 + i(p) 1 + i(p)
2
= C0 1 + i(p)
Análogamente C3 , el capital al finalizar el tercer perı́odo, es la suma de C2 , el
capital al comienzo del perı́odo, más C2 i(p) , los intereses generados durante este
perı́odo:
C3
= C2 + C2 i(p)
= C2 1 + i(p)
2
y ya que C2 = C1 1 + i(p) , obtenemos
3
C3 = C0 1 + i(p)
De estas expresiones podemos inferir inductivamente que el capital acumulado
al momento n será
n
Cn = C0 1 + i(p)
(4.1)
i(k)
Cn−1
Cn
n−1
n
tiempo
(modificar dibujo)
Ejemplo 4.2 Si depositamos $ 100 000 al 3 % mensual ¿Cuánto retiraremos
del banco al cabo de 18 meses?
El enunciado del ejemplo puede ser reformulado de la siguiente manera:
Capitalizar $ 100 000 durante 18 meses al 3 % mensual. Por lo cual podemos
4.1. SISTEMA DE CAPITALIZACIÓN COMPUESTA
47
usar la formula (4.1). En este caso
C0
=
$ 100 000
p
=
12
n
=
18 meses
luego
C18
18
=
100 000 (1 + 0.03)
=
170 243.306124
Recuerde que las tasas deben ser usadas en notacion decimal. Es decir, se debe
usar 0.03 en lugar de 3 %.
El método inductivo empleado para deducir la expresión (4.1) es propio de
las ciencias experimentales, y nos permite obtener una expresion plausible para
Cn , el capital acumulado hasta el momento n. Desde un punto de vista formal
no hay garantı́a de que la formula anterior sea correcta.
A través de un modelo recursivo podemos describir formalmente el funcionamieto de la capitalización compuesta. Esto nos permitirá usar la teorı́a de
recursividad desarrollada en el capı́tulo 2 para verificar la validez de la formula
(4.1).
Definición 4.3 Se llama capitalización compuesta a la ley financiera que
establece que los intereses generados en un perı́odo de tiempo dado son agregados
al capital al principio del mismo para el cálculo de los intereses del perı́odo
siguiente.
De acuerdo a la ley de capitalización compuesta, el capital al momento k + 1
es el capital al perı́odo k
Dado un capital inicial C0 , y una tasa de capitalización p-periódica i(p) ,
tenemos que el interés del n-ésimo p-perı́odo de tiempo es:
In = Cn−1 i(p) .
El capital acumulado hasta el momento n (la cantidad de p-perı́odos), es el
capital acumulado hasta el perı́odo anterior, el perı́odo n − 1, más los intereses
generados:
Cn
=
=
Cn−1 + Cn−1 i(p)
Cn−1 1 + i(p) ,
con condición inicial C0 = Co .
Usando la teorı́a
de relaciones recursivas desarrollada (caso g (n) = cte = 0,
con A = 1 + i(p) 6= 1 y B = 0) para resolver
Cn = Cn−1 1 + i(p)
C0 = Co
48
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
concluimos que:
n
Cn = C0 (1 + ip ) .
(4.2)
Cn
$
In
Cn−1
In−1
In−1
I3
I3
I3
I2
I2
I2
I2
I1
I1
I1
I1
I1
C0
C0
C0
C0
C0
IT
C3
C2
C1
C0
C0
0
1
2
3
n−1
n
tiempo
La fórmula (4.2) sirve para obtener capitales financieramente equivalentes
hacia el futuro.
(poner dibujo)
4.1. SISTEMA DE CAPITALIZACIÓN COMPUESTA
49
Pero también podemos usarla para obtener capitales financieramente equivalentes hacia el pasado
(poner dibujo)
para hacerlo basta despejar C0 de (4.2):
C0 =
Cn
n
1 + i(p)
Por ejemplo, a una tasa mensual del 1.2 %, $ 1 000 pesos dentro de un año son
financieramente equivalentes a $ 866.626222411 hoy pues:
12
1000 = Choy (1 + 0.012)
,
despejando obtenemos
Choy
=
Choy
=
1000
12
(1 + 0.012)
866.626222411.
Choy
1000
tiempo
dentro de 1 año
hoy
Nota 4.4 En la fórmula (4.2) aparecen 4 variables relacionadas:
capital inicial
capital final
tiempo
tasa
C0 ,
Cn ,
n,
i(p) .
Unas observaciones al respecto:
1. El problema tipo es: dadas tres magnitudes hallar la cuarta. Por lo que
tenemos problemas donde debemos hallar el capital final Cn (se les suele
llamar problemas de capitalización), una variación de este tipo de problemas es hallar el interés total generado. Problemas donde debemos hallar el
capital inicial C0 (se les suele llamar problemas de actualización). Problemas donde debemos hallar el tiempo n, y finalmente problemas donde
debemos hallar la tasa i(p) .
2. Dimensionalmente hablando, C0 y Cn son dinero. El tiempo y la tasa deben
ser dimensionalmente compatibles: si la tasa es p-perı́odica, el tiempo debe
estar dado en p-perı́odos, por ejemplo, si la tasa es mensual, n debe ser
una cantidad de meses. Similarmente si n es una cantidad de trimestres,
la tasa debe ser trimestral: una i(4) .
Nota 4.5 En Argentina habitualmente se usa TEA para designar la tasa efectica anual i, y TEM para designar la tasa efectiva mensual i(12) :
T EA
T EM
≡
≡
i
i(12)
50
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Ejemplo 4.6 Calcular el capital final o montante de $ 2 500 000 al 15 % anual,
colocado durante a) 20 dı́as, b) 3 meses, c) 4 cuatrimestres, d) 5 años, e) t kperı́odos.
Solución.
Todo el problema es compatibilizar las unidades temporales de los intervalos
de tiempo y la tasa. Por ahora sólo podemos convertir los distintos perı́odos de
tiempo a años:
20
años, por lo que al cabo de 20 dı́as tendremos
a) 20 dı́as son 365
20
C20 dı́as = C 365
b) 3 meses son
20
años
3
12
3
C3 meses = C 12
= 2500000 (1 + 0.15) 365 = 2 519 218.96888 pesos.
años, por lo que al cabo de 3 meses tendremos
3
años
= 2500000 (1 + 0.15) 12 = 2 588 895.19085 pesos.
c) 4 cuatrimestres son
dremos
C4 cuatrimestres = C 34
4
3
años, por lo que al cabo de 4 cuatrimestres ten4
años
= 2500000 (1 + 0.15) 3 = 3 012 107.46538 pesos.
d) Al cabo de 5 años tendremos
5
C5 años = 2500000 (1 + 0.15) = 5 028 392.96875 pesos.
e) En general si tenemos t k-perı́odos, tenemos
Ct k-perı́odos = C kt
t
k
años, por lo que tendremos
t
años
= C0 (1 + i) k .
Ahora resolveremos el resto de los problemas tipo, en cada caso, se da la
fórmula correspondiente.
Ejemplo 4.7 Hoy extraemos del banco $ 23 650.50. ¿Cuál fue el capital original
si nos han pagado una TEA del 18% y el depósito fue pactado de 6 meses?
Sabemos que
n
Cn = C0 1 + i(p) ,
de donde
C0
=
=
=
Cn
n
1 + i(p)
23650.50
(4.3)
1
(1 + 0.18) 2
21772.
Ejemplo 4.8 Determinar el interés total obtenido al depositar $ 5 000 a plazo
fijo por el término de 3 meses a una TEM 4.3%.
4.1. SISTEMA DE CAPITALIZACIÓN COMPUESTA
51
Por definición
IT = Cfinal − Coriginal
Es decir
n
= C0 1 + i(p) − C0
n
= C0 1 + i(p) − 1
IT
(4.4)
Reemplazando
IT
=
3
5000 (1 + 0.043) − 1
=
673.13
Ejemplo 4.9 Hallar el capital que produce unos intereses de $ 1 110 al cabo de
45 dı́as, a una tasa diaria del 0.25%.
Del problema anterior sabemos que
n
IT = C0 1 + i(p) − 1
(donde n es una cantidad de p-perı́odos). Luego
C0 =
1+
IT
n
(p)
i
−1
,
(4.5)
reemplazando
C0
=
=
1110
(1 + 0.0025)
9334.4
45
−1
Ejemplo 4.10 Depositamos en un banco $ 5 000 y al cabo de 30 meses nos
entregan $ 8 672.50. ¿Cuál es la TEM que nos pagó el banco?
Como
n
Cn = C0 1 + i(p) ,
tenemos que
r
(p)
i
=
n
Cn
− 1.
C0
Luego
r
i
12
i.e., una TEM del 1.18527%.
8672.50
−1
5000
= 0.018527,
=
30
(4.6)
52
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Ejemplo 4.11 Durante cuantos dı́as hay que imponer un capital de $ 3 000 a
una i(365) = 0.0078, para obtener no menos de $ 4 100.
Como
n
Cn = C0 1 + i(p) ,
tomando logaritmos a ambos lados
log Cn = n log 1 + i(p)
de donde depejamos
n=
log Cn − log C0
.
log 1 + i(p)
(4.7)
Ahora nosotros deseamos
4100 ≤ 3000 (1 + 0.0078)
n
como la función logaritmo es monótona creciente
log 4100 ≤ log 3000 + n log (1 + 0.0078) ,
luego
n
log 4100 − log 3000
log (1 + 0.0078)
≥ 40.204,
≥
luego debemos imponer el capital al menos 41 dı́as.
Nota 4.12 Una función f : R → R se dice monótona creciente sobre un intervalo I ⊂ dom (f ) si x < y impica que f (x) < f (y), con x, y ∈ I. Si además f
es diferenciable sobre el interior de I y f 0 > 0 en I (i.e., f 0 (x) > 0 para toda
x ∈ I), entonces f es monótona creciente. Por ejemplo
d
M
(log x) =
> 0, para x > 0
dx
x
donde M =
x > 0.
1
ln 10 .
Por lo tanto log es una función monótona creciente para
Ejercicio 4.13 Calcular el capital final o montante que se obtendrá al colocar
$ 25 500 a 6 meses a una TEA del 12.5 %. ¿A cuánto ascienden los intereses
totales?
Ejercicio 4.14 Calcular el montante que producirá un capital de $ 724 230,
colocado al 7 % semestral durante 4 años.
Ejercicio 4.15 Determinar el interés obtenido por una empresa que efectuó un
depósito a plazo fijo por el término de 30 dı́as, con excedentes de fondos por $
8000 a una tasa del 11 % anual.
4.1. SISTEMA DE CAPITALIZACIÓN COMPUESTA
53
Ejercicio 4.16 Obtenga los intereses totales que produce un capital de $ 230500
impuestos a una TEM del 1.23 % durante 4 meses.
Ejercicio 4.17 Hallar el capital necesario para producir un interés de $130 en
una colocación por un plazo de 50 dı́as en una entidad bancaria al 12 % anual.
Ejercicio 4.18 Hace 87 dı́as invertimos una cierta suma de dinero al 0.02% diario. Hoy nos entregan $ 75420.50 ¿Cuál fue el monto invertido originalmente?
Ejercicio 4.19 Depositamos en un banco $ 15000 y al cabo de 8 meses no
entregan $ 16672.20. ¿Cuál es la tasa de interés que nos pagó el banco?
Ejercicio 4.20 Un inversor reembolsará $ 4 995,50 por un depósito concertado
a 90 dı́as por $ 3 700. Averiguar la TEA pactada.
Ejercicio 4.21 Hallar la TEA necesaria para que un depósito por $ 11 000
reditúe al inversor en 180 dı́as, la mitad de la colocación.
Ejercicio 4.22 ¿Cuál es la tasa de interés k-perı́odica que nos permite duplicar
el capital en t k-perı́odos?
Ejercicio 4.23 ¿Cuánto tiempo es necesario que transcurra para triplicar un
capital al 5% bimestral?
Ejercicio 4.24 ¿Cuántos perı́odos son necesarios para duplicar un capital a
una tasa k-perı́odica i(k) ?
Ejercicio 4.25 Una empresa con excedentes de fondos por $ 20 000 efectúa
dos colocaciones para cubrir necesidades futuras. Una durante 45 dı́as al 1.5 %
mensual, y otra durante 15 dı́as a una TEM del 1.25%. Averiguar los importes
de los depósitos, sabiendo que las inversiones producen igual interés.
Ejercicio 4.26 Ud. posee $ 355 000. Decide invertilos en dos proyectos que le
pagaran respectivamente el 1.2 % bimestral y el 2.1 % trimestral. Qué porcentaje
de sus ahorros debe invertir en cada proyecto, para recibir el mismo monto en
concepto de intereses, es decir, a los 6 meses los intereses que le paga cada uno de
los proyectos deben ser iguales. Si ahora deseamos ambos proyectos nos paguen
los mismos intereses totales a lo largo de 1 año ¿cuánto deberemos colocar en
cada uno de los proyectos?
Ejercicio 4.27 Un capital por $ 3 800 se impuso a interés simple durante 7
dı́as al 11.2 % anual; luego el capital acumulado se impuso por el término de 15
dı́as al 11.7% anual; y por último se consiguió colocarlo 30 dı́as a una TEA 13.5
%. Calcular el interés total y la tasa real de la operación citada. (Respuesta: I
= $ 68.93, i = 12.73 %).
Ejercicio 4.28 Una empresa coloca excedentes de fondos en las siguientes alternativas:
54
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
1. Mercado de financiamiento oficial, $ 8 600 a una TEA del 12 %.
2. Mercado de financiamiento marginal, $ 7 200 al 18.5 % anual.
Determinar el plazo de las colocaciones que le permiten percibir montos
iguales. (Respuesta: n = 4.6667 años ≈ 4 años y 8 meses).
Ejercicio 4.29 Se desea saber cómo influirá una comisión de gastos fija sobre
el rendimiento de una inversión. A este efecto se nos comenta que, cualquiera
sea la inversión, la comisión ascenderá a $ 3 000. ¿Qué incidencia tendrá sobre
nuestra inversión de $ 2 000 000 al 12 % anual?, es decir, ¿Cuál es la tasa real
de la operación?. ¿Y si la inversión fuera de $ 500 000 al mismo tipo?
4.2
4.2.1
Tasas
Equivalencias de tasas compuestas
Tenemos las siguientes opciones de inversión: colocar $ 1.000 al x% anual durante
un año, o colocar los mismos $ 1.000 al y% mensual durante un año. Como nos
interesa tener un mayor capital final, la pregunta es ¿Qué opción de inversión
nos conviene?
Deduciremos ahora la ecuación fundamental de equivalencia de tasas en el
sistema de capitalización compuesto: Supongamos que un capital inicial C0 es
impuesto durante t años, donde t > 0 es un número real (pero no necesariamente
entero). La tasa p-perı́odica i(p) y la tasa q-perı́odica i(q) , con p, q ∈ Z+ , son
equivalentes si producen idéntico capital final:
i(p)
t años
C0
Cf
(q)
i
pt
qt
C0 1 + i(p)
= Cf = C0 1 + i(q)
Al simplificar nos queda
1 + i(p)
p
q
= 1 + i(q)
Acabamos de demostrar:
Proposición 4.30 Dados p, q ∈ Z+ , en el sistema de capitalización compuesta
dos tasas i(p) y i(q) , son financieramente equivalentes si cumplen la siguiente
relación:
p q
1 + i(p) = 1 + i(q)
(4.8)
4.2. TASAS
55
Ejemplo 4.31 ¿Cuál es la tasa mensual equivalente a una tasa trimestral del
7%?
Usando la ecuación (4.8) de equivalencia de tasas en capitazaliación compuesta para i(12) y i(4) :
12 4
1 + i(12)
= 1 + i(4)
despejando i(12)
i
(12)
q
=
12
q
i(12)
=
i(12)
=
12
1 + i(4)
4
−1
4
(1 + 0, 07) − 1
0, 02280912177
Esto nos dice que es lo mismo poner $ 1.000 durante 6 meses a una tasa trimestral
del 7 %, que ponerlos a una tasa del 2,280912177 % mensual
2
1000 (1 + 0, 07) = 1.144, 9 = 1.000 (1 + 0, 02280912177)
6
O que es lo mismo poner $ 500 (o cualquier otra suma) durante 8 meses (o
cualquier otro intervalo de tiempo) con cualquiera de estas dos tasas:
8
500 (1 + 0, 07) 3 = 598, 86199408 = 500 (1 + 0, 02280912177)
8
Nota 4.32 Como muestra el ejemplo anterior y como puede concluirse de la
propia dedución de fórmula (4.8), la equivalencia de tasas en capitalización
compuesta es independiente del intervalo de tiempo considerado: Si dos tasas
producen igual montante al cabo de t1 años, serán equivalentes y verificarán
(4.8). Por lo tanto producirán igual montante al cabo de t2 años, para cualquier
t2 6= t1 :
pt2
h
p i t2
C0 1 + i(p)
= C0 1 + i(p)
h
q it2
= C0 1 + i(q)
qt2
= C0 1 + i(q)
Similarmente, la equivalencia de tasas en capitalización compuesta es independiente del monto inicial usado.
Ejercicio 4.33 Dada una i(2) = 0, 03, hallar la i(k) equivalente para
k ∈ {1, 3, 4, 6, 12, 52, 360, 365}
Ejercicio 4.34 Dada una tasa de interés anual del 25 %. Hallar las tasas subperı́odicas equivalentes, i.e., hallar i(k) equivalente a la tasa dada para k ∈
{2, 3, 4, 6, 12, 52, 360, 365}. Expresar los resultados usando porcentajes.
56
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Ejercicio 4.35 Dados p, q ∈ Z+ , y un número real c > 0. Si
i(p) = c = i(q) ,
para cualquier C0 > 0 (dinero) y cualquier t > 0 (tiempo en años) demostrar
que
tp
tq
C0 1 + i(p)
< C0 1 + i(q)
,
si y sólo si
p < q.
Es decir, dadas dos tasas de igual nominal, la que capitaliza con mayor frecuencia produce mayor montante.
Ejercicio 4.36
Poner más ejercicios!!!!
Tasas nominales
Tı́picamente, al ciudadano promedio, una tasa del 0, 023 % diario, no le dice
mucho (no alcanza a percibir si es mucho o poco) una forma de lidiar con este
problema es calcular TEA equivalente: i = 0, 087564016. Pues una tasa anual del
8,7564016 % es más informativa que una tasa del 0, 023 % diario. Otra forma de
hacerlo es informar la tasas de manera seudo-anualizada: multipicando la tasa
por las veces que capitaliza en el año, en nuestro caso
0, 023% · 365 = 8, 395%
Esta costumbre informar las tasas efectivas de forma anual (multipicando la tasa
por las veces que capitaliza en un año), es lo que da origen a lo que se conoce
como tasas nominales. Estás son de caracter meramente informativo y deben
ser convertidas a tasas efectivas para poder usar las fórmulas ya deducidas.
Definición 4.37 Dada una tasa efectiva k-perı́odica i(k) , con k > 1, la tasa
nominal de capitalización k-perı́odica correspondiente es
J (k) = ki(k)
(4.9)
Nota 4.38 En Argentina la tasa nominal más usada es la tasa nominal de capitalización mensual: J (12) . Esta habitualmente recibe el nombre de tasa nominal
anual TNA.
Ejemplo 4.39 Hallar las tasas nominales asociadas a las siguientes tasas efectivas
1)
i(2) = 0, 04
2)
i(3) = 0, 12
3)
i(4) = 0, 025
4)
i(6) = 0, 012
(12)
5)
i
= 0, 076
6)
i(52) = 0, 003
7) i(360) = 0, 01
8) i(365) = 0, 002
4.2. TASAS
57
1) Usando la fórmula (4.9) la tasa nominal semestral (o de capitalización
semestral) asociada a la tasa efectiva semestral i(2) = 0, 04 es
J (2) = 2i(2) = 2 · 0, 04 = 0, 08
Tı́picamente las tasas nominales son expresadas en forma porcentual: la tasa
nominal semestral es del 8 %.
5) En este caso, queremos hallar la tasa nominal mensual J (12) asociada a
una tasa efectiva mensual i(12) = 0.076. Recordar que en Argentina la J (12) es
llamada T N A, tasa nominal anual. Usando la fórmula (4.9) la TNA asociada a
la tasa efectiva mensual i(12) = 0.076 es
T N A = J (12) = 12i(12) = 12 · 0.076 = 0.912
Es decir, una TNA del 91,2 % esta asociada (informa o hace referencia) a una
TEM del 7,6%.
Ejercicio 4.40 Hallar el resto de las tasas nominales asociadas a las tasas
efectivas dadas en el ejemplo anterior.
Ejemplo 4.41 Hallar la tasa efectiva asociada a una TNA del 21,5%.
Recordando que una TNA es una J (12) , tenemos que la tasa efectiva asocida
a una TNA es una i(12) (mensual). Usando la fórmula (4.9)
T N A = J (12) = 12i(12)
de donde
0, 215
J (12)
=
= 0, 017917
12
12
Ejercicio 4.42 Hallar las tasas efectivas asociadas a las siguientes tasas nominales
1)
J (2) = 31%
2)
J (3) = 18%
3)
J (4) = 25%
4)
J (6) = 12%
5) T N A = 41%
6)
J (52) = 46%
7) J (360) = 31%
8) J (365) = 10%
i(12) =
Ejemplo 4.43 Hallar la TNA equivalente a una tasa nominal trimestral del
18%.
Este ejercicio consta de tres pasos:
1. Hallar la tasa efectiva asociada a la J (4) : la tasa efectiva trimestral i(4) .
J (4)
=
i(4)
=
4i4 ,
0, 18
J (4)
=
= 0, 045
4
4
58
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
2. Hallar la tasa efectiva mensual (TEM) i(12) equivalente a la i(4) .
1 + i(12)
12
i(12)
=
4
1 + i(4)
q
4
12
1 + i(4 ) − 1
q
12
4
(1 + 0, 045) − 1
=
0, 01478
=
=
3. Hallar la TNA asociada a la i(12) encontrada.
J (12) = 12i(12) = 12 · 0, 01478 = 0, 17736
Luego, una TNA del 17,736% en equivalente a una tasa nominal trimestral
del 18%.
J (p)
Deseamos hallar
J (q)
1
i(p)
3
2
i(q)
Del ejemplo anterior es fácil deducir dos tasas nominales J (p) y J (q) son
equivalentes si
p q
J (p)
J (q)
1+
= 1+
(4.10)
p
q
Ejercicio 4.44 Hallar la TNA equivalente a una tasa nominal bimestral del
23,5%.
Ejercicio 4.45 Hallar la tasa nominal diaria (comercial) equivalente a una
TNA del 31,2%.
La principal ventaja (para los acreedores) de informar la tasa de forma nominal es que siempre es un número menor que la tasa efectiva anual equivalente:
Ejemplo 4.46 Un comercio cobra una TNA del 18%. ¿Cúal es la TEA que
realmente estamos pagando?
Primero calculamos la TEM asociada a la TNA:
i(12) =
0, 18
J (12)
=
= 0, 015
12
12
4.2. TASAS
59
luego calculamos la TEA equivalente a la TEM
12
(1 + i) =
1 + i(12)
12
i =
1 + i(12)
−1
=
(1 + 0, 015)
=
0, 19562
12
−1
Efectivamente, dada una tasa nominal J (k) , la TEA equivalente es
k
J (k)
(k)
= 1+
ieq J
−1
k
La cual, fijada k > 0, es una función
del valor de J (k) .
(k)
Ahora, verificar que ieq J
> J (k) , es equivalente a comprobar que
ieq J (k) − J (k) > 0
(4.11)
Consideremos la función f : R2 → R,
x k
−1−x
f (x, k) := 1 +
k
es claro que siempre que k > 1
f (0, k) = 0
∂f
x k−1
(x, k) =
1+
− 1 > 0, para toda x > 0
∂x
k
Básicamente, porque todas las funciones de la forma xα para α > 0, son estrictamente crecientes y como xk > 0 tenemos que 1 + xk > 1.
Por lo tanto, si k > 1, tenemos que
x k
− 1 − x > 0, para toda x > 0
f (x, k) = 1 +
k
de donde podemos concluir (4.11).
Nota 4.47 Aca estamos usando que si f es diferenciable y para algún a ∈ R se
cumple que
1. f (a) ≥ 0
2. f 0 (x) > 0 para todo x > a
Entonces podemos concluir que f (x) > 0 para todo x > a.
Ejercicio 4.48 Hallar la TEA equivalente a una J (k) = 30% para
k ∈ {2, 3, 4, 6, 12, 52, 360, 365, 8.760, 525.600}
Ejercicio 4.49 Hallar la TEA equivalente a una J (k) = 12% para
k ∈ {2, 3, 4, 6, 12, 52, 360, 365, 8.760, 52.5600}
poner más ejercicios!!!!!!!!!!!!
60
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
4.2.2
Breve diccionario de tasas nominales
Existe una multitud de expresiones que se usan para expresar una tasa nominal.
Por ejemplo para designar una J (3) del 23 % se suele decir:
1. 23 % nominal anual capitalizable trimestralmente.
2. 23 % nominal capitalizable trimestralmente.
3. 23 % nominal trimestral (forma empleada en este libro).
4. 23 % anual capitalizable trimestralmente.
5. 23 % anual a trimestre vencido (o simplemente 23 % ATV).
6. 23 % capitalizable trimestralmente.
7. 23 % trimestre vencido (o simplemente TV).
Siendo muy facil de confundir la última con una tasa efectiva.
Inclusive algunos autores hablan de tasas nominales no anuales. Por ejemplo
19 % semetral capitalizable bimestralmente
es una forma de referirse a una tasa bimestral, informada de manera semestral,
por lo que la tasa efectiva asociada a esta tasa nominal es
i(2) = 0, 095 =
0, 19
2
= 0, 19
3
6
En general una
tasa t % p-perı́odo capitalizable q-perı́odicamente
hace referencia a una tasa q-perı́odica, informada de maneral p-perı́odica:
i(q) =
t
(las veces que entra un q-perı́odo en un p-perı́odo)
100
donde generalmente
las veces que entra un q-perı́odo en un p-perı́odo =
p
q
Como ocurre en el siguiente ejemplo: una tasa del 20 % cuatrimestral capitalizable mensualmente, hace referencia a una tasa mensual
i(52) = 0, 2
3
= 0, 05
12
Pero este no siempre es el caso. Por ejemplo, una tasa de 15 % mensual
capitalizable semanalmente, hace referencia a una tasa semanal
i(52) = 0.15
1
= 0, 0375
4
4.3. EQUIVALENCIA DE CAPITALES
61
y no a
0.15
12
= 0.34615385
52
Como regla general, si no aparece la palabra nominal, la aparición de dos
unidades temporales asociadas a la tasa es un buen indicio de que la tasa que
nos estan informado es una tasa nominal, donde la unidad temporal menor, nos
indica la tasa efectiva a la que esta asociada la tasa nominal en cuestión.
4.3
Equivalencia financiera de dos o más series
de capitales en capitalización compuesta
Ya que sabemos calcular el equivalente financiero de un capital para distintos
momentos en capitalización compuesta, podemos verificar cuando dos series de
capitales son financieramente equivalentes con dicho sistema (recordamos que
éste es el segundo concepto fundamental de matemáticas financieras).
Una serie de capitales A1 , A2 , . . . , An disponibles en los momentos ta1 , ta2 , . . . , tan ,
es equivalente a la serie de capitales B1 , B2 , . . . , Bm disponibles en los momentos
tb1 , tb2 , . . . , tbm , a una fecha focal f , para un agente dado (tasa), bajo una ley
financiera dada (sistema) si
n
X
Aj al momento f =
j=1
j=1
A1
Bj al momento f
j=1
Pm
B1
m
X
Bj al momento t
B2
A2
B3
t
A3
Pn
j=1
Bm
An
Aj al momento t
(MODIFICAR DIBUJO!!!!!!!!!!!!!!!!!!!)
El equivalente financiero de un capital dado, a la fecha focal f y a una tasa
p-perı́odica i(p) en el sistema de capitalización compuesto es
f −taj
Aj al momento t = Aj 1 + i(p)
Donde el intervalo de tiempo entre t y taj es medido en p-perı́odos, para que sea
dimensionalmente compatible con la tasa i(p) usada.
62
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Nota 4.50 Si f ≥ taj , entonces debemos capitalizar el capital Aj desde taj hasta
f
f −taj
Aj al momento t = Aj 1 + i(p)
capitalización
Aj 1 + i(k)
Aj
taj
f −taj
f
Modificar dibujooooo!!!!!!!!!!!!!
Pero si f < taj , entonces debemos actualizar el capital Aj desde desde taj
hacia f
Aj al momento t
f −taj
= Aj 1 + i(p)
Aj
=
1 + i(p)
taj −f
actualización
Aj
ta −f
(1+i(k) ) j
Aj
taj
f
(MODIFICAR DIBUJO)
Proposición 4.51 Dada una tasa efectiva p-perı́odica i(p) , la serie de capitales
A1 , A2 , . . . , An disponibles en los momentos ta1 , ta2 , . . . , tan es financieramente
equivalente a la serie de capitales B1 , B2 , . . . , Bm disponibles en los momentos tb1 , tb2 , . . . , tbm , a la fecha focal f en el sistema de capitalización compuesta
si
n
m
f −taj
f −tbj
X
X
Aj 1 + i(p)
=
Bj 1 + i(p)
(4.12)
j=1
j=1
donde todos los datos temporales deben ser expresados en p-perı́odos.
Ejemplo 4.52 La señorita Viviana desea sustituir el siguiente esquema de pagos: $ 150.000 hoy, $ 150.000 a los dos años y $ 150.000 a los 4 años, por dos
pagos iguales, el primero al año, y el segundo a los 3 años. Hallar el nominal
de los montos a pagar usando una tasa anual i = 0, 35, y como fecha focal el
origen. Volver a resolver el problema usando como fechas focales 2 años y 4
años.
4.3. EQUIVALENCIA DE CAPITALES
C
0
C
1
$ 150000
63
2
3
$ 150000
4
5
años
$ 150000
El valor del primer esquema de pago: $ 150.000 hoy, $ 150.000 a los 2 años y
$ 150-000 a los 4 años, a la fecha focal f (en años) usando la tasa anual i = 0, 35
es
f −2
f
150.000 (1 + 0, 35) + 150.000 (1 + 0, 35)
f −4
+ 150.000 (1 + 0, 35)
,
El valor del segundo esquema de pago: $ x dentro de 1 año y $ x dentro de 3
años, a la fecha focal f (en años) usando la tasa anual i = 0, 35 es
f −1
x (1 + 0, 35)
f −3
+ x (1 + 0, 35)
Por ejemplo, usando como fecha focal el origen, f = 0, tenemos por (4.12)
150.000 +
150.000
2
(1 + 0, 35)
+
150.000
=
4
(1 + 0, 35)
277.464, 76
=
x
x
+
1 + 0, 35 (1 + 0, 35)3
1, 1471822848 x,
luego
x = 241.866, 20 pesos.
Si ahora usamos como fecha focal f = 2 años
2
150.000 (1 + 0, 35) + 150.000 +
150.000
2
(1 + 0, 35)
505679, 5267
x
1 + 0, 35
2, 090740741 · x
= x (1 + 0, 35) +
=
luego
x = 241.866, 20 pesos.
Hemos obtenido el mismo resultado con una u otra fecha focal (Se insta al
lector volver a calcular el monto de los nuevos pagos usando cualquier otra fecha
focal que se le ocurra, deberı́a obtener siempre x = 241.866.20 pesos).
El ejemplo anterior sugiere que la equivalencia financiera en capitalización
compuesta es independiente de la fecha focal elegida. Veamos que este siempre
es el caso.
Dada una tasa efectiva p-perı́odica i(p) , supongamos que la serie de capitales
A1 , A2 , . . . , An , disponibles en los momentos ta1 , ta2 , . . . , tan es financieramente
equivalente a la serie de capitales B1 , B2 , . . . , Bm , disponibles en los momentos
tb1 , tb2 , . . . , tbm , a la fecha focal f1 , bajo capitalización compuesta:
Al momento
n
X
j=1
Aj 1 + i(p)
f1 −tj
|
f1
{z
↓
=
}
m
X
l=1
f1 −tl
Bl 1 + i(p)
.
64
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Veamos que las mismas son equivalentes a cualquier otra fecha focal f2 6= f1
n
n
f2 −taj
X
X
Aj al momento f2 =
Aj 1 + i(p)
j=1
=
j=1
n
X
f2 −f1 +f1 −taj
Aj 1 + i(p)
j=1
=
n
X
f2 −f1 f1 −taj
Aj 1 + i(p)
1 + i(p)
j=1
=
1 + i(p)
n
f2 −f1 X
f1 −tj
Aj 1 + i(p)
j=1
|
n
X
{z
}
Aj al momento f1
j=1
=
1 + i(p)
m
f2 −f1 X
f1 −tbj
Bj 1 + i(p)
j=1
|
m
X
{z
}
Bj al momento f1
j=1
=
m
X
f2 −f1 f1 −tbj
Bj 1 + i(p)
1 + i(p)
j=1
=
=
m
X
j=1
m
X
f1 −tbj +f2 −f1
Bj 1 + i(p)
f2 −tbj
Bj 1 + i(p)
j=1
=
m
X
Bj al momento f2
j=1
Por lo tanto en capitalización compuesta se puede usar cualquier fecha como
fecha focal en la equivalencia financiera sin alterar el resultado final.
Ejemplo 4.53 Debemos realizar 3 pagos, el primero de $ 400 dentro de tres
meses, el segundo de $ 300 dentro de 6 meses y último de $ 500 a los 9 meses.
Por razones de flujo de caja (disponibilidad de efectivo) queremos sustituir estos
3 pagos por dos: uno de $ 500 dentro de 5 meses y otro de monto a determinar
a los 10 meses. Se conviene una tasa de 2,5% mensual.
Debemos igualar los valores a una fecha focal dada de ambas operaciones:
valor de la
valor de la
operación original = operación nueva
a la fecha focal f
a la fecha focal f
4.3. EQUIVALENCIA DE CAPITALES
65
Usando como fecha focal: f = 6 meses
fecha focal
C
$ 500
0
1
2
3
4
$ 400
5
6
$ 300
7
8
9
10
meses
$ 500
Debemos llevar todos los capitales a los seis meses, por lo que algunos serán
capitalizados (los que están disponibles antes de los 6 meses), otros serán actualizados (los disponibles en fechas posteriores), y los disponibles a los 6 meses
no cambian
C
500
3
= 500 (1 + 0, 025) +
400 (1 + 0, 025) + 300 +
3
4
(1 + 0, 025)
(1 + 0, 025)
C
1.195, 055956 = 512, 5 +
1, 10381289062
de donde
C = 753, 4140631
Ejercicio 4.54 Una deuda de $ 2.000 vence en un año. Si el deudor paga $
600 a los 5 meses y $ 800 a los 9 meses. Hallar el saldo de la deuda en la fecha
de vencimiento si la tasa convenida para la operación es una TEM del 2,85%.
Ejercicio 4.55 El señor Ignacio debe $ 25.000 con vencimiento en 2 meses,
$ 10.000 con vencimiento en 5 meses y $ 15.000 con vencimiento en 8 meses.
Si desea saldar las deudas mediante dos pagos iguales, uno con vencimiento en
6 meses y otro con vencimiento en 10 meses. Determinar el importe de dichos
pagos suponiendo una TNA del 26%.
Ejercicio 4.56 ¿Con qué cantidad se cancela hoy dı́a, un préstamo que se consiguió dos meses antes habiéndose firmado dos documentos; uno con valor nominal de $ 6.000 que vence en dos meses a partir de ahora y otro por $ 7.500
de valor nominal y vencimiento a 5 meses del préstamo?. Suponga intereses del
TEA de 20%.
Problemas con almanaque
Ejercicio 4.57 El 10 de enero del corriente año se otorga un préstamo amparado con dos pagarés con vencimiento al 15 de marzo y al 3 de mayo por $
1.300 y $ 800 respectivamente. Poco después, se conviene en cancelarlo con tres
pagos: el primero por $ 500 el 20 de febrero, el segundo por $ 1.000 el 30 de
abril y el tercero el dı́a 10 de junio, ¿De qué cantidad es este último pago si se
cargan intereses del 30% bimestral, ¿A cuánto asciende el monto del préstamo?
66
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Ejercicio 4.58 Sea desea sustituir el pago de 3 capitales de $ 12.725, $ 11.022
y $ 8.774, con vencimiento los dı́as 15 de mayo, 4 de junio y 25 de junio,
respectivamente, por uno único el dı́a 1 de junio; ¿a cuánto ascenderá el capital
si se aplica una TNA del 25,6% anual a la operación?.
Ejercicio 4.59 ¿Con qué cantidad se cancela hoy dı́a, un préstamo que se consiguió dos meses antes habiéndose firmado dos documentos; uno con valor nominal de $ 60.000 que vence en dos meses a partir de ahora y otro por $ 75.000
de valor nominal y vencimiento a 5 meses del préstamo?. Suponga una TEA
20%.
Ejercicio 4.60 Deseamos sustituir dos pagares de $ 145.000 y $ 123.000, con
vencimientos el 12 de abril y el 15 de junio, respectivamente, por otros tres de
igual monto, con vencimientos 10 de mayo, 10 de junio y 10 de agosto. Resolver
el problema usando:
1)
2)
3)
4)
5)
6)
7)
8)
9)
Ejercicio 4.61
4.3.1
tasa
TEA del 21%,
TNA del 21%,
TEM 1,8%,
2,2% efectiva bimestral,
2,2% nominal bimestral,
0,05% efectiva diaria civil (365),
0,05% efectiva diaria comercial (360),
2,4% efectiva trimestral,
2,4% nominal trimestral.
poner más ejercicios!!!!!!!!!!!
Tasa media
Consideremos el siguiente ejemplo
Ejemplo 4.62 Ud. tiene $ 130.000 invertidos al 18% anual, $ 150.000 al 8%
semestral y % 145.000 al 2% mensual por el término de 2 años. ¿Qué tasa diaria
(durante 2 años) deberı́a ofrecerle una entidad financiera para que ud. coloque
todo su capital, $ 425.000, en la misma?
Este no es más que un problema de equivalencia financiera de capitales,
donde la incognita es una tasa.
Poner dibujo!!!!!!!!!!!!!
Al cabo de 2 años, las inversiones originales generan el siguiente monto
2
4
24
130.000 (1 + 0, 18) + 150.000 (1 + 0, 08) + 145.000 (1 + 0, 02)
La operación nueva genera al cabo de 2 años
730
(365)
425.000 1 + imedia
= 618.308, 7451
4.3. EQUIVALENCIA DE CAPITALES
67
si queremos que ambas operaciones sean equivalentes, tenemos que
730
(365)
618.308, 7451 = 425.000 1 + imedia
de donde
(365)
imedia
r
=
=
618.308, 7451
−1
425.000
0, 000513692
730
Por lo que la tasa que buscamos, conocida como la tasa media diaria de la
(365)
operación es imedia = 0, 000513692.
Por lo tanto, la entidad financiera debe ofrecerle al menos un 0, 000513692%
diario. Con esta tasa ambas operatorias producen el mismo ingreso al cabo de
dos años. Veamos que para otros horizontes temporales estas operaciones dan
diferentes montos.
Ahora, al cabo de un año, las tasas originales producen
2
12
130.000 (1 + 0, 18) + 150.000 (1 + 0, 08) + 145.000 (1 + 0, 02)
= 512.255, 0603
mientras que con la segunda operatoria
365
425.000 (1 + 0, 000513692)
= 512.621, 9364
Por lo que se ve, que para tiempos inferiores a los dos años, estas operatorias
dan diferentes.
Por otro lado, al cabo de 5 años, las tasas originales producen
5
10
60
130.000 (1 + 0, 18) +150.000 (1 + 0, 08) +145.000 (1 + 0, 02)
= 1.096.996, 722
mientras que con la segunda operatoria
1825
425.000 (1 + 0, 000513692)
= 1.085.001, 189
Es interesante comparar la tasa media de la operación, contra la tasa promedio de la misma. En este caso la tasa promedio diaria se consigue promediando
las tasas diarias equivalentes a las tasas originales
365
1
(365)
(365)
1 + i1
= 1 + 0, 18
=⇒ i1
= (1 + 0, 18) 365 − 1 = 0, 000453567
365
2
(365)
(365)
2
1 + i2
= (1 + 0, 08)
=⇒ i2
= (1 + 0, 08) 365 − 1 = 0, 000421793
365
12
(365)
(365)
12
= (1 + 0, 02)
= (1 + 0, 02) 365 − 1 = 0, 000651257
1 + i3
=⇒ i3
Luego la tasa promedio diaria de la operación es
(365)
i1
(365)
+ i2
3
(365)
+ i3
=
=
0, 000453567 + 0, 000421793 + 0, 000651257
3
0, 0005088723333
68
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
En este caso se observa que la tasa promedio de la operación es superior a la
tasa media de la misma.
La operación financiera anterior ocurre con relativa frecuencia, por lo que
amerita el desarrollo de fórmulas generales.
En general dada una serie de operaciones consistente de colocar n capitales
Cj , con j = 1, . . . , n, a las tasas qj -perı́odicas i(qj ) , con j = 1, . . . , n, durante
t años, deseamos sustituir este conjunto de inversiones por una única inversión
por la suma total de los capitales involucrados
C=
n
X
Cj
j=1
que produzca el mismo rendimiento en t-años.
Cn
Cn 1 + i(pn )
pn t
C2
C2 1 + i(p2 )
p2 t
C1
C1 1 + i(p1 )
p1 t
hoy
dentro de t años
!
kt
n
P
(k)
Cj
1 + imedia
tiempo
n
P
!
Cj
j=1
j=1
(p)
La tasa media equivalente p-perı́odica imedia es la tasa que produce la
equivalencia financiera entre estas operaciones
n
X
tqj
tp
(p)
Cj 1 + i(qj )
= C 1 + imedia
j=1
de donde podemos despejar la tasa media equivalente
v
u X
u1 n
q j t
(p)
t
imedia (t) = pt
Cj 1 + i(qj )
−1
C j=1
(4.13)
Nota 4.63 Observe que la fórmula para la tasa media de una serie de capitales
en el sistema compuesto depende del tiempo t, los capitales Cj y de las tasas
qj -perı́odicas i(qj ) , con j = 1, . . . , n.
Usando un poco de Cálculo se puede probar que en el sistema compuesto la
tasa media tiende a la tasa más alta a medida que el horizonte temporal de la
operación tiende se hace más largo
 v

(
)
u X
n
qpj
u
1
q
t
(p)
j
t
lim i
(t) = lim  pt
−1
Cj 1 + i(qj )
− 1 = max
1 + i(qj )
t→∞ media
t→∞
1≤j≤n
C j=1
4.3. EQUIVALENCIA DE CAPITALES
69
i.e., para el ejemplo que venimos trabajando, a medida que aumentamos el
tiempo de la operación la tasa media diaria tiende 0, 000651257
(p)
imedia (2)
=
0, 000513692
(p)
imedia (5)
(p)
imedia (10)
(p)
imedia (100)
=
0, 000519720
=
0, 000530070
=
0, 000621801
..
.
=
0, 000651257
(p)
imedia (∞)
(p)
Nota 4.64 Además, dados p, q ∈ Z, es evidente que las tasas medias imedia y
(q)
imedia (calculadas con respecto a una misma serie de capitales) son equivalentes:
1+
(p)
imedia
p
v
u X
n
q
u
qj t 1
(q)
t
t
Cj 1 + i(qj )
= 1 + imedia
=
C j=1
(4.14)
Ejemplo 4.65 Tenemos dos opciones de inversión: La primera es dividir el
capital en dos partes, colocando el 60% del mismo al 7% anual, y el 40% restante
al 4.1% trimestral. La segunda consite en colocar todo el capital al 1.25 mensual.
¿Cuál de las opciones es la más ventajosa?
En esta situación debemos comparar dos inversiones, una de las cuales involucra más de una tasa. Usaremos tasa media para resolverla. Dado un intervalo
(12)
tiempo de t años, queremos hallar una tasa media imedia 12-perı́odica (mensual),
que nos produzca la misma ganancia:
t
4t
0.60C (1 + 0.07) + 0.40C (1 + 0.041)
12t
(12)
= C 1 + imedia
despejando
(12)
imedia =
q
12t
t
4t
0.60 (1 + 0.07) + 0.40 (1 + 0.041) − 1 = 0.00896666 . . . (4.15)
Claramente la tasa media resulta una función del tiempo. Podemos graficar
(12)
imedia (t) y verificar que
(12)
imedia (t) ≤ 0.0125 para todo t ≤ 78 años
70
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
tasa mensual
0.0150
0.0125
0.0100
0.0075
0.0050
0.0025
tiempo en años
0
50
100
150
200
78.51865948 años
Ahora es claro que la segunda opción (no dividir el capital) es la más conveniente si:
(12)
(12)
i2 = 0.0125 > imedia
En general no se puede despejar t de la expresión (4.15), por lo que se deben
usar métodos numéricos para hallar el tiempo de “equilibrio” (la cantidad de
años a la que somos indiferentes entre una o otra opción). Usando Maple student
edition, hallamos que para este ejemplo el tiempo de equilibrio es
t = 78.51865948 años
Ejercicio 4.66 Tenemos dos opciones de inversión: La primera es dividir el
capital en dos partes, colocando el 30 % del mismo al 18 % anual, y el 70 %
restante al 6.5 % trimestral. La segunda consite en colocar todo el capital al 0.5
% semanal. ¿Cuál de las opciones es la más ventajosa?
Ejercicio 4.67 Actualmente tenemos $ 25.000 en el banco A, que nos paga una
TEA del 13.5 %, $ 13.000 en LEBAC’s (letras del Banco Central) que pagan
una TNA del 15.7 % y $ 35.000 en bonos de la empresa B que pagan un 8.1%
semestral. Qué redimiento anual nos deberı́a ofrecer el banco C a tres años para
que depositemos en él todo nuestro capital.
Ejercicio 4.68 Actualmente disponesmos de $ 75.000 en acciones de una empresa de soft que historicamente han obtenido un redimiento del 8.1 % anual.
4.3. EQUIVALENCIA DE CAPITALES
71
Debido a la volatilidad del mercado decidimos partir nuestro capital en dos: en
bonos de bajo riesgo, que ofrecen un redimiento semestral de 2.4 %, y en una
compañia financiera que nos ofrece un rendimiento mensual del 1.3 %. ¿Qué
porcentaje de nuestros fondos debemos invertir en cada opción para obtener el
mismo rendimiento al cabo de un año que la inversión original?
Ejercicio 4.69 Tenemos $ 100.000 para invertir. Se nos presentan tres opciones. La primera es depositarlo todo en un banco que paga en 2,5% mensual.
La segunda en comprar $ 60.000 en bonos del estado que pagan un 8,2% trimestral y el resto en el banco al 1,8% mensual. La tercera consiste en comprar
obligaciones de empresas privadas: $ 30.000 en opciones de la empresa A, que
rinden un 21% semestral, $ 40.000 en opciones de la empresa B, que rinden
un 4,8% bimestral y el resto en opciones de la empresa C que rinden un 38,5%
anual. ¿Cuál de las opciones es la más ventajosa?
Ejercicio 4.70 Tenemos dos opciones de inversión: La primera es dividir el
capital en dos partes, colocando el 30% del mismo al 18% anual, y el 70%
restante al 6,5% trimestral. La segunda consite en colocar todo el capital al
0,5% semanal. ¿Cuál de las opciones es la más ventajosa?
Poner más ejercicios!!!!!!!!!!!!!!!!!!!!!!!!
4.3.2
Vencimiento medio
Este es un caso particular de la equivalencia financiera, en el que sustituimos una
serie de capitales por un único pago igual a la suma algebraica de los capitales
involucrados.
Definición 4.71 Dada una tasa p-perı́odica i(p) la fecha m a la cual la serie de
capitales C1 , C2 , . . . , Cn disponibles en los momentos t1 , t2 , . . . , tn es equivalente
a la suma algebraica, C, de dichos capitales
C=
n
X
Cj
j=i
se llama vencimiento medio de la serie considerada.
(Poner dibujo !!!!!!)
Como en el sistema compuesto la equivalencia financiera puede realizarse a
cualquier fecha focal sin alterar el resultado, tomando f = 0 en (4.12) tenemos
n
X
−tj
−m
Cj 1 + i(p)
= C 1 + i(p)
j=i
Aplicamos logarı́tmo en ambos miembros y obtenemos
log
n
X
j=1
−tj
Cj 1 + i(p)
= log C − m log 1 + i(p)
72
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Luego, despejamos m
log C − log
m=
n
X
j=1
Cj
1 + i(p)
tj
(4.16)
log 1 + i(p)
En la fórmula anterior los datos temporales se suponen expresados en p-perı́odos,
para que sean compatibles con la tasa i(p) usada.
Ejemplo 4.72 La señorita Marisa desea sustituir tres pagos, el primero de $
400, $ 300 el segundo y el último también de $ 300, con vencimientos hoy, dentro
de 6 meses y dentro de un año, respectivamente, por un único pago de $ 1.000.
Hallar el vencimiento medio para
1)
2)
3)
4)
5)
6)
7)
tasa
TEM del 4%
TEA del 18,5%
TNA del 14,8%
J (3) = 0, 14
i(3) = 0, 045
0,1% efectiva diaria comercial (360)
0,1% efectiva diaria civil (365)
1) Tasa: TEM del 4%,
log 1000 − log 400 +
m1
6
(1 + 0.04)
log (1 + 0.04)
=
=
300
+
!
300
12
(1 + 0.04)
4
Ejercicio 4.73 Hallar el resto de los vencimientos medios requeridos en el
ejemplo anterior.
Nota 4.74 Razonando financieramente es intuitivo que el vencimiento medio
se encuentre entre el primer y el último momento en que los capitales vencen,
pues se debe dar una compensación de intereses.
Ejemplo 4.75 Sustituir el siguiente esquema de pago: 4 cuotas semestrales de
$1.000, comenzando el dia de hoy, a una tasa i(2) del 15%; a) por un solo pago
al dı́a de hoy, b) por un solo pago dentro de 2 años.
En ambos casos se desea sustituir dicho esquema por un único pago. Para
ello recurriremos a la fórmula (4.12) y tomando como fecha focal a f = 0, nos
queda
1.000 +
1.000
1.000
1.000
C
+
+
=
t
2
3
(1 + 0, 15) (1 + 0, 15)
(1 + 0, 15)
(1 + 0, 15)
4.3. EQUIVALENCIA DE CAPITALES
73
(Poner Dibujo)
a) Se desea realizar el pago hoy, por lo tanto t = 0, entonces
1.000 +
1.000
1.000
1.000
+
+
3 = Ca
(1 + 0, 15) (1 + 0, 15)2
(1 + 0, 15)
donde se obtiene
Ca = 3.283, 225117
b) En este caso, t = 4
1.000 +
1.000
1.000
Cb
1.000
+
=
+
2
3
4
(1 + 0, 15) (1 + 0, 15)
(1 + 0, 15)
(1 + 0, 15)
despejando Cb
4
3
2
Cb = 1000 (1, 15) + 1000 (1, 15) + 1000 (1, 15) + 1000 (1, 15)
y obtenemos
Cb = 5.742, 38125
Con estos resultados es claro que si sustituimos dicho esquema por un solo
pago hoy dı́a de $ 4.000, la suma algebraica de las cuotas, pagarı́amos de más;
por el contrario si lo sustituimos por un pago de $ 4.000 dentro de dos años,
momento final del esquema, pagarı́amos de menos.
De hecho, dada una serie de capitales C1 , C2 , . . . , Cn disponibles en los momentos t1 < t2 < . . . < tn respectivamente, tenemos que
P
Cj al momento tn
z
}|
{
z }| {
<0
n
n
n
z }| { X
t − t j
X
X
(p) t1 −tj
(p) n
<
Cj <
Cj 1 + i
Cj 1 + i
|
{z
} j=i
{z
}
|
j=1
j=1
<1
>1
| P
{z
}
>0
Cj al momento t1
siempre que usemos una tasa positiva. Lo que demuestra que m ∈ (t1 , tn )
Ejercicio 4.76 El señor Nicolás desea sustituir 12 pagos mensuales de $ 1.000,
por un único pago de $12.000. Suponer una TEA del 18,5%. Hallar el vencimiento
medio.
Ejercicio 4.77 La señorita Ana acuerda con su acreedor sustituir el siguiente
esquema de pago: 3 pagos de $ 10.000, a los cero, seis y doce meses, respectivamente, por un único pago de $ 30.000 a los 7 meses. ¿Cuál fue la TNA
usada?
Ejercicio 4.78
poner más ejercicios!!!!!!!!!!!!
Nota 4.79 El problema de hallar la tasa que produce un esquema de vencimiento
medio dado, requiere el uso de métodos numéricos.
74
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
4.4
Capitalización subperı́odica
Hasta el momento no nos hemos preocupado por la discretitud del tiempo,
intrı́nseca de las fórmulas desarrolladas.
Ejemplo 4.80 Se deposita durante 6 meses y 19 dı́as unos fondos por $ 10 000
a una TEA del 19.5 %, ¿Cuál es el monto del capital acumulado?
Este tipo de situaciones se puede resolver de varias maneras. Una es convertir
el tiempo a años
6
10.000 (1 + 0, 195) 12
19
+ 365
= 10.000 (1, 195)
0,55205479452
= 11.033, 44778
donde
0, 55205479452 años = 6 meses y 19 dı́as
O conseguir una tasa diaria equivalente
(1 + 0, 195)
=
365
1 + i(365)
i(365)
=
0, 00048819087
y pasar todo el tiempo a dı́as:
10.000 (1 + 0, 00048819087)
199
= 11.019, 99522
Ahora, surjen de maneral natural una serie de preguntas asociadas a este
ejemplo:
1. ¿De donde surge la diferencia de $ 13,45456 entre ambos procedimientos
si conceptualmente son equivalentes?
2. ¿Por qué podemos usar exponentes no enteros en la fórmula de capitalización (discreta por naturaleza)?
3. ¿Cuál de los dos procedimientos es mejor?
4. ¿Existen otras formas de manejar estas situaciones?
Analizaremos esto con cierto grado de detalle en esta sección. Pero desde un
punto financiero, todo depende de lo que convengan las dos partes involucradas
en la operación financiera.
Hay unas tres formas generales de abordar el problema (la mayorı́a con una
que otra variante). Las que bautizaremos como convenios:
1. Convenio discreto o de truncamiento
2. Convenio lineal
3. Convenio Exponencial
4.4. CAPITALIZACIÓN SUBPERÍODICA
4.4.1
75
Convenio discreto o de truncamiento
Este es el sistema que habitualmente usan los bancos en Argentina para manejar
cajas de ahorro. La filosofı́a del sistema es que los intereses se capitalizan sólo
al final del perı́odo, y por lo tanto, dada una tasa p-perı́odica i(p) el capital
acumulado después de t p-perı́odos es igual al capital acumulado despues de btc
p-perı́odos
poner dibujo con la capitalización escalonada.
Por lo que la fórmula de capitalización toma la forma
btc
C0 1 + i(p)
Para el caso del ejemplo (4.80) tenemos que
Ca los 6 meses y 19 dı́as
b0.55205479452c
=
10.000 (1 + 0.195)
=
10 000 (1 + 0.195)
=
10 000
0
Esto muestra una de las desventajas del método discreto, la cual es más y más
evidente mientras menor sea la frecuencia de capitalización usada. Si utilizamos
tasas subperı́odicas equivalentes (i.e. tasas cuya frecuencia de capitalización sea
menor que la originalmente dada) este método se aproxima cada vez más al
resultado obtenido al usar exponentes no enteros. En la práctica se usa asociado
a tasas mensuales.
Ejemplo 4.81 Si depositamos $ 5 000 en una caja de ahorro que paga una
TEM del 1.2%. ¿Cuál será el monto acumulado al cabo de 9 meses y 26 dı́as?
Bueno, en este caso, como escencialmente las cajas de ahorro operan a sistema truncado, tenemos que el capital acumulado a los largo de 9 meses y 26
dı́as es
9
9+ 26
5 000 (1 + 0.012)b 30 c = 5 000 (1 + 0.012) = 5 566.6590
4.4.2
Convenio exponencial o continuo
Este es lo que hemos estado haciendo hasta ahora. Consiste en hacer caso omiso
de la discretitud temporal de las fórmulas. Una variante, es utilizar alguna tasa
subperı́odica equivalente, para capitalizar la parte subperı́odica. Ambas formas
deberı́an dar el mismo resultado. Entonces, por qué en el ejemplo (4.80) hubo
una diferencia de más de $ 13. La respuesta es sencilla: esa diferencia surge del
pésimo sistema que tenemos en matemáticas financieras para medir el tiempo:
las unidades no son claramente convertibles, por ejemplo
1. Un año tiene 12 meses y 365 dı́as. Cada mes tiene 30 dı́as, por lo que un
año deberı́a tener ¡360 dı́as!
76
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
2. Un año tiene 12 meses y cada mes tiene 4 semanas, luego un año tiene
48 semanas. Ahora como cada semana tiene 7 dı́as el año debe tener ¡336
dı́as!
3. Un mes tiene 4 semanas, y cada semana tiene 7 dı́as, luego todos los meses
tienen ¡28 dı́as!
4. En matemáticas financieras se usa que el año tiene 52 semanas, y como
cada semana tiene 7 dı́as, el año debe tener ¡364 dı́as!
No hay forma satisfactoria de solucionar esta ensalada. Un pobre intento de
solución es convenir en realizar todas las conversiones vı́a años. Por ejemplo 6
meses y 19 dı́as son unos
6 meses y 19 dı́as =
19
6
+
años = 0.55205479452 años
12 365
y una vez que tenemos anualizado el tiempo, convertir el mismo:
0.55205479452 años = 0.55205479452
365
dı́as = 201.5 dı́as
1
y con esta cantidad de dı́as operar:
10 000 (1 + 0.00048819087)
201.5
= 11033.44980
Lo que nos da un resultado mucho más próximo al original.
Este es el método de conversión temporal que los autores se atreven a recomendar.
Nota 4.82 Las conversiones entre meses, bimestres, trimestres, cuatrimestres,
semestres, años, lustros, decadas, siglos, etc. Funcionan a la perfección y de la
manera natural.
4.4.3
Convenio lineal
Este método es tı́picamente el usado en operaciones de crédito. Pues debido a la
convexidad de las funciones exponenciales, cualquier cuerda que une dos puntos
sobre una función convexa, queda por arriba de la función convexa, y vı́a el
lema de las tres cuerdas, es fácil demostrar que mientras más ”larga” (fijado
el punto de la izquierda) son las cuerdas consideradas, mayor es la diferencia
entre la cuerda y la función exponencial. Esto se traduce en un mayor capital
acumulado (en el caso de operaciones de crédito, es sinónimo de un pago mayor).
Todo convenio lineal trata de capitalizar de manera compuesta durante la
parte entera del perı́odo de tiempo y luego moverse a través de rectas (cuerdas)
en lugar de la función exponencial subyacente, por el lapso de tiempo que resta.
Poner dibujo con las tres cuerdas y numerarlas
1, 2, y 3 de acuerdo con el caso
Existen tres variantes del convenio lineal:
4.4. CAPITALIZACIÓN SUBPERÍODICA
77
1. Convenio lineal equivalente.
2. Convenio lineal proporcional.
3. Convenio lineal anualizado.
Y cada variante se puede obtener geométricamente (Proporcionalidad de
los lados homólogos de triángulos semejantes) o financieramente (obteneniendo
una tasa simple subperiodica adecuada “equivalente” o, mejor dicho, asociada
y utilizando sistema simple).
Convenio lineal equivalente
Este convenio coincide con el convenio exponencial. Simplemente se trata
de hallar la tasa simple subperı́odica equivalente para el lapso de tiempo correspondiente y utilizarla para capitalizar el capital acumulado durante la parte
no entera de tiempo.
Poner aqui dibujo
He aqui un ejemplo:
Ejemplo 4.83 Se pide un préstamo por $ 25 000 para remodelar la cocina del
quincho de una de nuestras casas de fin de semana. El banco nos cobra una TEM
del 3.4 % y utiliza convenio lineal equivalente. ¿Cuál es el monto que debemos
entregar para cancelar la deuda 5 meses y 9 dı́as más tarde?
Si usaramos convenio exponencial (y conversión anualizada del tiempo), deberı́amos entregar
25 000 (1 + 0.034)
9
5+ 365
12
1
= 29 842.77404
Ahora, para usar el convenio lineal equivalente, debemos hallar la tasa simple
diaria equivalente para 9 dı́as a la TEM del 3.4 %
9 12
(365)
1 + 9isimple
= (1 + 0.034) 365 1
(365)
isimple
=
0.00110468082556
Luego debemos entregar a los 5 meses y 9 dı́as la suma de
5
25 000 (1 + 0.034) (1 + 9 · 0.00110468082556) = 29 842.77404
Poner ejercicios?¡ o al final?
Convenio lineal proporcional
Dada una cantidad t de p-perı́odos, el convenio lineal proporcional conciste
en utilizar la cuerda que une los puntos
btc , Cbtc y dte , Cdte
Poner dibujo
78
CHAPTER 4. SISTEMAS DE CAPITALIZACIÓN COMPUESTA
Esto se puede hacer de dos formas, geométricamente (via semejanza de triangulos):
Cdte − Cbtc
x
=
t − btc
1
Por lo que
x = Cdte − Cbtc (t − btc)
Por lo que el
Ct
= Cbtc + Cdte − Cbtc (t − btc)
btc dte btc (p)
(p)
(p)
= C0
1+i
+ 1+i
− 1+i
(t − btc)
btc n
h
i
o
= C0 1 + i(p)
1 + 1 + i(p) − 1 (t − btc)
btc h
i
= C0 1 + i(p)
1 + (t − btc) i(p)
Financieramente, podemos llegar a la misma expresión calculando la tasa
(p)
simple p-periodica isimple equivalente a i(p) y luego capitalizando en sistema
simple Cbtc el capital acumulado hasta el momento dte por el tiempo que resta:
t − btc.
btc h
i
(p)
Ct = C0 1 + i(p)
1 + (t − btc) isimple
Esta dos fórmulas son iguales pues a un p-perı́odo ( p1 años) la equivalencia de
tasas intrasistemas nos da que la tasa simple equivalente es exactamente igual
a la tasa compuesta p-perı́odica i(p)
p p1
1 (p)
=
1 + i(p)
1 + p isimple
p
(p)
isimple
=
i(p)
Ejemplo 4.84 Si en el caso del ejemplo (4.83) el banco usará el convenio lineal
proporcional. ¿Cuánto deberı́amos pagar para cancelar la deuda a los 5 meses y
9 dı́as más tarde?
En este caso, debemos aplicar la formula anterior, convirtiendo los 9 dı́as a
meses via anualización
9 12
5
0.034
C5 meses y 9 dı́as = 25 000 (1 + 0.034) 1 +
365 1
= 29 846.26516
Convenio lineal anualizado
Es muy similar a la versión financiera del convenio lineal proporcional, pero
la equivalencia de tasas intrasistemas se plantea a un año
btc h
i
(p)
Ct = C0 1 + i(p)
1 + (t − btc) isimple
4.4. CAPITALIZACIÓN SUBPERÍODICA
79
(p)
donde isimple se obtiene a partir de
(p)
1 + pisimple
(p)
isimple
=
=
1 + i(p)
p
1 + i(p)
p
p
−1
Ejercicio 4.85 Si en el caso del ejemplo (4.83) el banco usará el convenio lineal
anualizado. ¿Cuánto deberı́amos pagar para cancelar la deuda a los 5 meses y 9
dı́as más tarde?
En este caso debemos debemos hallar primero la tasa simple mesual equibalente, a un año, a la TEM del 3.4 %
12
(p)
isimple
=
=
(1 + 0.034) − 1
12
0.041136818422
Luego, convirtiendo los 9 dı́as a meses via anualización
9 12
5
0.041136818422
C5 meses y 9 dı́as = 25 000 (1 + 0.034) 1 +
365 1
= 29 908.664243
En cada uno de los casos, la conversión del tiempo puede realizarse sin
anualizar, lo que cambia ligeramente los resultados.
Poner ejercicios!!!!
Chapter 5
Descuento compuesto
En las operaciones comerciales habitualmente no se usa la actualización para
calcular el valor actual de un capital futuro. El método usado se conoce como
descuento (comercial). Este es el caso tı́pico de lo que ocurre con los cheques
a fechas. El poseedor de un cheque (documento, plazo fijo, etc.) el cual tiene un
nominal N , podrá hacerlo efectivo en t años (esta cantidad no tiene porque ser
entera), pero por algún motivo necesita dinero hoy (para pagar una deuda, por
una oportunidad de inversión, etc.). Entonces acude a un intermediaro finaciero
(banco, financiera, un “prestamista” en el peor de los casos), y cambia el cheque
por una suma en efectivo E, donde
E < N.
D
N
E
hoy
dentro de t años
La diferencia entre el E efectivo que recibe, y el nominal N del documento
entregado, recibe el nombre de descuento
D = N − E.
(5.1)
En esta operación se puede pensar que el intermediario financiero se ha
cobrado los intereses al principio de la operación. La tasa que se usa es llamada
tasa de descuento d, la cual tiene la particularidad que se aplica sobre el
nominal N .
80
81
El sistema de descuento compuesto se caracteriza por calcular el descuento
con base en cada perı́odo.
Supongamos que se quiere adelantar un documento de nominal N , unos n
p-perı́odos con un intermediario financiero que cobra una tasa de descuento
compuesta p-perı́odica d(p) .
d( k)
Dj
Ej+1
Ej
j
j+1
perı́odo j + 1
El descuento compuesto en el perı́odo j + 1 se cobra al principio del perı́odo
j + 1, i.e., en el momento j, pero se calcula sobre el efectivo al final del perı́odo,
i.e., en el momento j + 1:
Dj = Ej+1 d(p)
Como el efectivo Ej que recibiremos en el momento j es igual al efectivo Ej+1 ,
disponible en el momento j + 1, menos el correspondiente descuento, el cual se
calcula sobre Ej+1 , tenemos la siguiente relación recursiva
Ej
En
=
=
Ej+1 − Ej+1 d(p) ,
N.
0 ≤ j < n,
Donde la condición inicial es En = N (al momento n hacemos efectivo el documento, no necesitamos descontarlo).
82
CHAPTER 5. DESCUENTO COMPUESTO
Dn−1
Dk+1
D
Dk
D0
D1
En−1
E0 = E
Ek+1
Ek
E1
1
k
N = En
n−1
k+1
n
tiempo
Esta última relación recursiva puede ser reescrita
(
1
Ej =
Ej+1 , 0 ≤ j < n,
1 − d(p)
En = N.
Observe que ambas relaciones recursiva están definidas sólo para los j ∈ Z tales
que
0≤j≤n
Esto obedece razones financieras. Hoy (j = 0), y no antes, queremos descontar
un documento que vence en n k-perı́odos. Por otro lado a partir del perı́odo n
el efectivo que recibiremos por nuestro documento es siempre el mismo:
Ej = N para j ≥ n
Usando la teorı́a de relaciones recursivas que hemos desarrollado, caso g (j) =
cte = 0, con
1
6= 1,
A=
1 − d(p)
concluimos que el la forma para el efectivo en el momento j, para 0 ≤ j ≤ n, es
Ej =
h0
1 − d(p)
j
donde h0 es una constante que se ajusta usando la condición inicial En = N :
N
=
h0
=
h0
n
1 − d(p)
n
1 − d(p) N
En =
luego
n−j
Ej = N 1 − d(p)
, para 0 ≤ j ≤ n,
83
en particular
n
E = E0 = N 1 − d(p)
Esto nos da la ecuación fundamental del sistema de descuento compuesto para
una tasa de descuento p-perı́odica, la cual nos permite calcular el efectivo E que
recibiremos al descontar un nominal N , unos n p-perı́odos con un intermediario
financiero que cobra una tasa de descuento compuesta p-perı́odica d(p) .
n
E = N 1 − d(p)
(5.2)
En términos de la tasa de descuento y el nominal, el descuento total compuesto es
n (5.3)
D = N 1 − 1 − d(p)
Nota 5.1 El descuento compuesto nunca anula al efectivo (siempre y cuando
la tasa de descuento sea razonable, i.e., d(p) ∈ (0, 1)). Como para todo n ∈ Z+
n n+1
1 > 1 − d(p) > 1 − d(p)
> 0,
y
lim
n→∞
1 − d(p)
n
= 0.
Tanto el efectivo, como el descuento son funciones exponenciales del tiempo de
descuento (ambas crecientes en j):
Ej
<
Ej+1
Dj
<
Dj+1
Mientras que el descuento total es creciente en n (tiempo total descontado):
n n+1 N 1 − 1 − d(k)
< N 1 − 1 − d(k)
Ejemplo 5.2 Se desea hacer efectivo hoy un cheque a 5 dı́as de nominal $ 1
000. Qué efectivo recibiremos si acudimos a un banco que aplica un tasa de
descuento diario del 2.1%. ¿Cuánto nos han descontado?
El efectivo que recibiremos se calcula con (5.2)
5
E = 1000 (1 − 0.021) = 899.32
de donde
D = 1000 − 899.32 = 100.68
Observe que el valor actual de $ 1000, calculado con una tasa efectiva diaria del
2.1% es
1000
C0 =
5 = 901.3
(1 + 0.021)
84
CHAPTER 5. DESCUENTO COMPUESTO
Ejemplo 5.3 ¿Cuántos dı́as hay que descontar un documento para obtener un
efectivo menor o igual a la mitad del nominal a una tasa de descuento d(360) =
0.01?
Como deseamos hallar el tiempo de descuento n, aplicando logaritmo en la
fórmula (5.2) obtenemos
log E = log N + n log 1 − d(p)
Luego
n=
log E − log N
log 1 − d(p)
(5.4)
En la cual remplazando los valores dados en el ejemplo quedarı́a
n
N
≤ N 1 − d(360)
2
de donde
n
≥
n
≥
n
≥
log N2 − log N
log (1 − 0.01)
log N − log 2 − log N
log (1 − 0.01)
log 2
−
log (1 − 0.01)
En particular
n≥−
log 2
= 68.968,
log (1 − 0.01)
i.e., si descontamos un documento 69 dı́as, el efectivo será prácticamente la
mitad del nominal.
Nota 5.4 El tiempo necesario para recibir una fracción dada del nominal, ab N ,
es independiente del nominal N , depende exclusivamente de la tasa de descuento
usada:
n
a
N = N 1 − d(p)
b
de donde
n=
log a − log b
log 1 − d(p)
Ejercicio 5.5 ¿Cuál fue el descuento y el efectivo de un cheque con vencimiento
a 3 meses si se aplicó una tasa de descuento del 4.5% mensual y su nominal
ascendı́a a $ 5000?
85
Ejercicio 5.6 El Sr. Ignacio desea adelantar 19 dı́as un documento de $ 4 580
de nominal. Tiene dos opciones: La primera es descontar el documento en el
Banco Gran J, que le cobra una tasa diaria de descuento del 0.75%. La segunda
es acudir a la Financiera ”Su Amiga Rosita”, institución que le cobra una tasa
de descuento del 23.9% mensual. ¿Donde debe el Señor Ignacio descontar su
documento?
Ejercicio 5.7 Sabiendo que el descuento sobre un cheque a 12 dı́as es de $ 230.
Calcular el nominal si la tasa de descuento diaria aplicada es del 5%.
Ejercicio 5.8 Se desea hacer efectivo hoy un cheque a 60 dı́as de nominal $
5 000. Qué efectivo recibiremos si acudimos a un banco que aplica un tasa de
descuento diario de 1.7%. ¿Cuántos dı́as hay que adelantar un documento a esta
tasa para el efectivo sea un tercio del nominal?
Ejercicio 5.9 La Srta. Mariela ha recibido $ 13 506.80 al descontar un cheque
12 dı́as en el Banco DAJ, institución que cobra un tasa diaria de descuento del
0.87%. ¿Cuál es el montante del cheque?
Ejercicio 5.10 El Señor Adrián recibió $ 1 235.50 al adelantar 7 dı́as un
cheque de $ 14 500. ¿Cuál es la tasa diaria de descuento que le aplicaron?
¿Qué tasa efectiva diaria transforman los $ 1 235.50 en $ 14 500?
Ejercicio 5.11 La señora Encarnación adelanto un documento y recibio 56 del
nominal del mismo. Si la institución financiera en la que operó le cobra una
tasa de descuento del 2.3 % diario. ¿Cuánto tiempo adelanto el documento?
Ejercicio 5.12 Completar la siguiente tabla de tiempos necesarios para obtener
la fracción dada del nominal, para las tasas de descuentos dadas:
p
q
1
2
1
3
2
3
1
4
3
4
3
5
4
5
d(365) = 0.05%
5.0.4
d(365) = 0.1%
d(365) = 0.5%
d(365) = 1%
d(365) = 5%
Equivalencia de tasas de descuento compuesto.
Con respecto a las tasas de descuento compuesto surgen las mismas preguntas
de siempre: dada una tasa de descuento p-perı́odica d(p)
1. ¿Cuál es la tasa de descuento q-perı́odica equivalente?
2. ¿Cuál es la tasa efectiva q-perı́odica equivalente?
86
CHAPTER 5. DESCUENTO COMPUESTO
La equivalencia de tasas se suele mirar de izquierda a derecha (del pasado
hacia el futuro). Esto funciona muy bien con las tasas efectivas, pero no asi
con las tasas de descuento. Es más natural plantear la equivalencia de tasas de
derecha a izquierda (del futuro hacia el pasado) para los sistemas de descuento:
Definición 5.13 Dos tasas de descuento compuestas d(p) y d(q) , con p, q ∈ Z,
se dicen que son equivalentes si aplicadas a un mismo nominal N durante un
mismo intervalo de t años producen el mismo descuento, y por lo tanto el mismo
efectivo, aunque tengan distinta frecuencia de descuento: p 6= q. Es decir
qt
pt
N 1 − d(q)
= E = N 1 − d(p)
A partir de la anterior definición deducimos la ecuación fundamental de
equivalencia de tasas de descuento compuesto
p
q (5.5)
1 − d(q) = 1 − d(p) .
d(p)
t años
E
N
(q)
d
Como antes, usaremos d, en lugar de d(1) , para designar una tasa de descuento anual
Nota 5.14 Observe que la equivalencia de tasas de descuento dada por (5.5)
es independiente del perı́odo de tiempo t considerado.
Ejemplo 5.15 Dada una tasa de descuento anual del 10% hallar la tasa d(k) ,
para k ∈ {2, 3, 4, 6, 12, 52, 360, 365}, equivalente.
Por ejemplo la tasa de descuento cuatrimestral equivalente es
3
1 − d = 1 − d(3)
de donde
d(3)
√
3
=
1−
=
1−
=
0.034511
√
3
1 − d,
1 − 0.1
Ejercicio 5.16 Dada una tasa de descuento bimestral del 3.5% hallar la tasa
d(k) equivalente, para k ∈ {1, 2, 3, 4, 12, 52, 360, 365}.
87
5.0.5
Equivalencia entre tasas de descuento y capitalización.
Dados dos capitales
C0 = E < N = Cn
separados temporalmente por t años
(Poner Dibujo)
Supongamos que la tasa de descuento q-perı́odica, d(q) , reduce N a E en t
años
qt
E = N 1 − d(q)
y que la tasa p-perı́odica, i(p) , transforma C0 en Cn en t años
pt
Cn = C0 1 + i(p)
Ahora tenemos
qt
N 1 − d(q)
= E = C0 =
Cn
1 + i(p)
pt =
N
1 + i(p)
pt
de donde llegamos a la relación fundamental de equivalencia entre tasas de
capitalización compuesta y de descuento compuesto
q p
1 − d(q)
1 + i(p) = 1.
(5.6)
Claramente esta equivalencia es independiente del tiempo t considerado.
i(p)
t años
E
N
(q)
d
Nota 5.17 despejando d(q) e i(p) de (5.6) obtenemos, respectivamente
s
1
(q)
p
d =1− q
1 + i(p)
s
(p)
i
=
p
1
q − 1
1 − d(q)
En particular, si tomamos q = p en (5.7)
d =
=
<
1−
1
1+i
i
1+i
i
(5.7)
(5.8)
88
CHAPTER 5. DESCUENTO COMPUESTO
Y, si q = p en (5.8)
i
1
−1
1−d
d
=
1−d
> d
=
Por lo tanto siempre la tasa efectiva equivalente es nominalmente mayor a la
tasa de descuento asociada (Insistimos: esto ocurre si ambas tasas tienen la
misma frecuencia o unidad temporal).
Ejemplo 5.18 Dada una tasa de descuento mensual del 8% hallar la tasa de
capitalización compuesta diaria (comercial) i(360) equivalente.
De (5.8) obtenemos que
s
(360)
i
=
1
360
1 − d(12)
s
=
=
12 − 1
1
360
(1 − 0.08)
0.0027833
12
−1
Ejemplo 5.19 Se desean encontrar las tasas de descuento d(52) , d(365) y d(12)
equivalentes a una TEM del 13%
Usando la fórmula (5.7) nos queda
s
d
(52)
=
=
1−
52
1
12
(1 + 0.13)
0.0278100474
de la misma manera calculamos d(365)
s
(365)
d
=
=
1−
365
1
12
(1 + 0.13)
0.0040100521
pero en cuanto a d(12) como tiene la misma frecuancia de capitalización que
nuestra TEM, el cálculo es mucho más sencillo
d(12)
1
1 + i(12)
1
= 1−
1 + 0.13
= 0.1150442478
=
1−
89
De los resultados obtenidos observamos que, para las tasas dadas:
d(12) = 0.1150442478 < 0.15 = i(12)
y, calculando las tasas equivalentes i(52) y i(365) a nuestra TEM
d(52)
=
0.0278100474 < 0.032778513 = i(52)
(365)
=
0.0040100521 < 0.004605486 = i(365)
d
lo cual coincide con el resultado de la nota anterior.
Ejercicio 5.20 Completar la siguiente tabla de tasas equivalentes compuestas
1)
2)
3)
4)
5)
6)
7)
8)
9)
5.0.6
tasa 1
d(2)
d(2)
d(12)
d(12)
d(365)
d(360)
d(360)
d
d
=
=
=
=
=
=
=
=
=
?
0.06
0.023
?
0.035
?
?
0.18
?
tasa 2
i(6)
i(6)
i(4)
i(4)
i(365)
i(365)
i(360)
i
i
=
=
=
=
=
=
=
=
=
0.06
?
?
0.023
?
0.035
0.035
?
0.18
Descuento Racional
La operación de descuento tı́pica asume conocidos en nominal N , la tasa de
descuento y el tiempo de adelanto, y se desea averiguar el efectivo E que se va
a recibir.
El descuento racional o matemático no es otra cosa que el uso de la actualización compuesta para el cálculo del efectivo: Dado un nominal N , una tasa
p-perı́odica i(p) y un intervalo de n p-perı́odos (que es el tiempo que deseamos
adelantar el documento) buscamos una cantidad de dinero Eracional tal que
n
Eracional 1 + i(p) = N
(5.9)
de donde
Eracional =
N
n
1 + i(p)
(PONER DIBUJO)
Por lo tanto el descuento es total es
Dracional
= N − Eracional
!
1
n
= N 1−
1 + i(p)
−n = N 1 − 1 + i(p)
(5.10)
90
CHAPTER 5. DESCUENTO COMPUESTO
Ejemplo 5.21 El señor Juan de desea hacer efectivo hoy un cheque a 5 dı́as de
nominal $ 1 000. Qué efectivo recibirá si acude al Banco Super J de San Luis,
el cuál usa descuento racional para adelantar documentos, cobrando una tasa
efectiva diaria i(365) del 2.1%. ¿A cuanto asciende el descuento que le realizan
al Sr. Juan?
Sólo hace falta usar (5.10)
=
−n 1 − 1 + i(k)
−5
1000 1 − (1 + 0.021)
=
98.696
Dracional
=
N
Es decir que al Sr. Juan le descuentan $ 98.70, por lo que recibe $ 901.30. Como
ya hicimos ver en el ejemplo (5.2), si la tasa que le cobran al Sr. Juan fuera de
descuento, recibirı́a
E = 899.32
pues el descuento (comercial) que le aplicarı́an es
D = 100.68
Ejercicio 5.22 ¿Cuál fue el descuento racional y el efectivo racional de un
cheque con vencimiento a 3 meses si se aplicó una tasa efectiva del 4.5% mensual
y su nominal ascendı́a a $ 5000?
Ejercicio 5.23 El Sr. Ignacio desea adelantar 19 dı́as un documento de $ 4
580 de nominal. Tiene dos opciones: La primera es descontar el documento
en el Banco Gran J, que le cobra una tasa diaria de descuento comercial del
0.85%. La segunda es acudir a la Financiera ”Su Amiga Rosita”, institución
usa descuento racional y cobra una tasa efectiva del 35.6% mensual. ¿Donde
debe el Señor Ignacio descontar su documento?
Ejercicio 5.24 Sabiendo que el descuento sobre un cheque a 12 dı́as es de $
230. Calcular el nominal si se aplica descuento racional y una tasa efectiva
diaria del 5%.
Ejercicio 5.25 Se desea hacer efectivo hoy un cheque a 60 dı́as de nominal $
5 000. Qué efectivo recibiremos si acudimos a un banco que aplica descuento
racional y una tasa efectiva diaria del 1.7%. ¿Cuántos dı́as hay que adelantar
un documento a esta tasa para el efectivo sea un tercio del nominal?
Ejercicio 5.26 La Srta. Mariela ha recibido $ 13 519.08 al descontar un cheque
12 dı́as en el Banco DAJ, institución que cobra un tasa diaria de descuento
racional del 0.87%. ¿Cuál es el montante del cheque?
Ejercicio 5.27 La señora Encarnación adelanto un documento y recibio 65 del
nominal del mismo. Si la institución financiera en la que operó le cobra una tasa
de descuento racional del 2.3 % diario. ¿Cuánto tiempo adelanto el documento?
91
Nota 5.28 Supngamos que deseamos descontar un documento por un nominal
N , unos n p-perı́odos a una tasa p-perı́odica r, el descuento comercial asociado
a ella
n
D (r) = N (1 − (1 − r) )
es siempre mayor que el descuento racional (actualización) asociado a la misma:
−n
Dracional (r) = N 1 − (1 + r)
Es decir
D (r) > Dracional (r)
(5.11)
Donde para resaltar que estamos observando el comportamiento de descuento en
cada sistema con respecto a la misma tasa, escribimos D (r) por D y Dracional (r)
por Dracional donde r es la tasa.
Verificar (5.11) es equivalente a comprobar que
D (r) − Dracional (r) > 0
(5.12)
Si r es una tasa razonable, i.e., r ∈ (0, 1), entonces
0<r<1
elevando al cuadrado (función monótona creciente)
0 < r2 < 1
luego, mutiplicando por −1
0 > −r2 > −1
y sumando 1
1 > 1 − r2 > 0
desarrollando la diferencia de cuadrados
1 > (1 − r) (1 + r) > 0
de donde conseguimos la desigualdad
1
>1−r
1+r
Ahora, como para cada n ∈ N, las funciones xn son monótonas crecientes
1
n
n > (1 − r)
(1 + r)
Luego, para toda r ∈ (0, 1) y para toda n ∈ N
1
n
n − (1 − r) > 0
(1 + r)
(5.13)
92
CHAPTER 5. DESCUENTO COMPUESTO
Por lo tanto
D(r) − Dracional (r)
n
−n
= N (1 − (1 − r) ) − N 1 − (1 + r)
1
n
= N
n − (1 − r)
(1 + r)
|
{z
}
>0 por (5.13)
>
0
lo que demuestra (5.12) para toda r ∈ (0, 1) y para toda n ∈ N.
Por lo tanto si un banco cobra un descuento comercial del 6.3% diario y
otra institución cobra un descuento racional del 6.3% diario, conviene realizar
el descuento del documento en la segunda institución.
Chapter 6
Capitalización Continua
6.1
Capitalización continua
En los ejercicios 4.48 y 4.49 del capı́tulo anterior, hallamos la TEA equivalente a
una tasa nominal fija a medida que aumentamos la frecuencia de capitalización
(las veces que capitaliza en el año). Los datos sugieren que a medida que p crece
la TEA asociada crece pero se mantiene acotada (si no ha resuelto los ejercicios
en cuestión, ¡hágalo ahora!)
Resolvamos un problema relacionado: Dada una tasa nominal J (p) , el capital
final acumulado al cabo de t años es
Ct = C0
J (p)
1+
p
pt
Si dejamos fijo el valor de la tasa nominal
J (p) = J, para todo p > 0,
tenemos que el capital final al cabo de t años se puede ver como una función de
p (la frecuencia de capitalización)
pt
J
Ct (p) = C0 1 +
p
Ahora, sicapitalizamos
cada vez más veces en el año, i.e., si hacemos crecer p,
p
J
el factor 1 + p crece pero se mantiene acotado por eJ . Por ejemplo si fijamos
93
94
CHAPTER 6. CAPITALIZACIÓN CONTINUA
J = 0.2 (20% nominal)
Frecuencia
“anual”
semestral
cuatrimestral
trimestral
bimestral
mensual
semanal
diario
por hora
..
.
p
1
2
3
4
6
12
52
365
8760
..
.
continuamente
∞
p
1 + 0.2
k
1 + 0.2
2
1 + 0.2
2 3
1 + 0.2
3 4
1 + 0.2
4 6
1 + 0.2
6
12
1 + 0.2
12 52
1 + 0.2
12 0.2 365
1 + 365
0.2 8760
1 + 8760
..
.
k
lim 1 + 0.2
k
k→∞
=
=
=
=
=
=
=
=
=
..
.
Valor
1.2
1.21
1.213629631
1.215506250
1.21742672
1.219391090
1.220934289
1.221335767
1.221399432
..
.
=
1.221402758
Pues
lim
k→∞
0.2
1+
k
k
= e0.2 = 1.221402758
A medida que p crece, la frecuencia de capitalización aumenta, disminuyendo
el tiempo entre dos capitalizaciones consecutiva. Cuando p tiende a infinito,
decimos que los intereses se capitalizan en forma instantánea. Esto se conoce
como capitalización continua.
Ahora el capital final al cabo de t años es
Ct = lim C0
p→∞
J
1+
k
pt
= C0 eJt
(6.1)
6.1. CAPITALIZACIÓN CONTINUA
95
$
C0 eJt
C0 1 +
(J 12 )
)
12
C0 1 +
C0 1 +
C0 1 +
(J 6 )
)
6
C0 1 +
6t
(J 4 )
4
4t
(J 3 )
3
3t
(J 2 )
2
2t
C0 (1 + J)t
C0
0
12
1
12
2
12
3
12
4
12
5
12
6
12
7
12
8
12
9
12
10
12
11
12
12
12
Años
Nota 6.1 Como la tasa efectiva usada en capitalización continua es nula:
lim
J
p→∞ k
=0
En capitalización continua sólo se utiliza la tasa nominal J.
Definición 6.2 Se denomina capitalización continua a la ley financiera por
la cuál un capital inicial C0 impuesto t años a una tasa nominal (anual) J
produce un capital final
Ct := C0 eJt
(6.2)
12t
96
CHAPTER 6. CAPITALIZACIÓN CONTINUA
$
J
C0 eJt
C0
Años
t
0
hoy
t años
Nota 6.3 Observe que en capitalización continua, el tiempo t en la fórmula
(6.2) siempre se debe colocar en años, para que sea dimensional compatible con
la tasa nominal continua J
Ejemplo 6.4 Calcular el montante que producirá un capital de $ 200.000 impuesto a capitalización continua durante 7 años a una tasa nominal continua
del 12%.
Sólo debemos aplicar la fórmula (6.2):
C7 = 200.000e0,12·7 = 463.273, 3954
Por lo que al cabo de 7 años dispondremos de $ 463.273,40.
Ejemplo 6.5 Calcular el montante que producirá un capital de $ 10.000 impuesto a capitalización continua durante 8 meses a una tasa nominal del 12%.
No es más que calcular
8
C 12
8
=
10000e0,12 12
=
10.833
Observe que debimos convertir los 8 meses a
fórmula de capitalización continua.
8
12
años para poder usarlos en las
6.1. CAPITALIZACIÓN CONTINUA
97
Ejemplo 6.6 Hoy extraemos del banco $ 17.251,75. ¿Cuál fue el capital original
si nos pagan una tasa nominal continua del 18,5% y el depósito fue pactado por
8 meses?
Sabemos que
Cn = C0 eJt
de donde
C0
= Cn e−Jt
(6.3)
=
17.251, 75e
=
15.250
8
−0,185 12
Luego el depósito original fue por $ 15.250.
Ejemplo 6.7 Determinar el interés total obtenido al depositar $ 5.000 a plazo
fijo por el término de 3 meses a capitalización continua con una tasa nominal
del 12,3%.
Por definición
IT = Cfinal − Coriginal
Es decir
IT
= C0 eJt − C0
= C0 eJt − 1
3
= 5000 e0,123 12 − 1
=
156, 13833
Por lo que el interés total obtenido es de $ 156,14.
Ejemplo 6.8 Hallar el capital que produce unos intereses de $ 1.110 al cabo de
45 dı́as, a una tasa nominal continua del 25%.
Del problema anterior sabemos que
IT = C0 eJt − 1
(6.4)
Luego
C0
=
=
=
IT
eJt − 1
1.110
(6.5)
45
e0,25 365 − 1
35.141, 71423
Por lo que el capital buscado es $ 35.141,71. Observe que se podrı́a haber usado
el año comercial
1.110
C0 = 0,25 45
= 34.652, 86508
360 − 1
e
En general este es un punto que debe ser aclarado en cada caso. Cuando no se
especifique el lector tiene libertad de usar uno o el otro.
98
CHAPTER 6. CAPITALIZACIÓN CONTINUA
Ejemplo 6.9 La señorita Viviana deposita en un banco $ 500.000 y al cabo de
30 meses le entregan $ 867.250. ¿Cuál es la tasa nominal que le pagó el banco
si éste usa capitalización continua?
Como
Cn = C0 eJt
tenemos que
J=
1 Cn
ln
t
C0
(6.6)
Luego
J
867.250
500.000
0, 2202876750
1
=
30
12
=
ln
i.e., una tasa nominal continua del 22,02876750%.
Ejemplo 6.10 Durante cuantos dı́as hay que imponer un capital de $ 3.000 a
una J = 23, 85%, para obtener no menos de $ 4.100.
Como
Cn = C0 eJt
tenemos que
t=
ln Cn − ln C0
J
(6.7)
Ahora, nosotros en realidad deseamos hallar el primer t, en dı́as tal que
t
4.100 ≤ 3.000e0,2385 365
como la función logaritmo es monótona creciente
ln 4.100 ≤ ln 3.000 + 0, 2385
t
365
luego
t ≥
≥
ln 4.100 − ln 3.000
0, 2385
478, 05769
365
Por lo tanto, debemos imponer el capital al menos 479 dı́as.
Ejercicio 6.11 Calcular el capital final o montante que se obtendrá al colocar
$ 25.500 a capitalización continua durante 3,5 años a una tasa nominal del
10,5%. ¿A cuánto ascienden los intereses totales?
6.1. CAPITALIZACIÓN CONTINUA
99
Ejercicio 6.12 Determinar el interés obtenido por la empresa RAL s.r.l., la
cual efectuó un depósito a plazo fijo por el término de 75 dı́as, con excedentes
de fondos por $ 80.000 a una tasa nominal del 11 % anual. Usar capitalización
continua.
Ejercicio 6.13 Obtenga los intereses totales que produce un capital de $ 5.300.500
impuestos a capitalización continua, a una tasa nominal del 18,33% durante 4
meses, 8 dı́as y 5 horas.
Ejercicio 6.14 Hallar el capital necesario para producir un interés de $ 1.500
en una colocación por un plazo de 150 dı́as en una entidad bancaria que capitaliza continuamente con una tasa nominal del 21,6%.
Ejercicio 6.15 Hace 187 dı́as el señor Nicolás invertió una cierta suma de
dinero al 35,2% nominal, a capitalización continua. Hoy le entregan $ 8.541.220,50
¿Cuál fue el monto que invertió originalmente?
Ejercicio 6.16 La señorita Viviana depositó en un banco $ 15.000 y al cabo de
8 meses le entregaron $ 15.672,20. ¿Cuál es la tasa de interés nominal que le
pagó el banco? Suponer capitalización continua.
Ejercicio 6.17 Un inversor reembolsará $ 4.995,50 por un depósito concertado
a 90 dı́as por $ 3.700. Averiguar la tasa nominal pactada si se usa capitalización
continua.
Ejercicio 6.18 Hallar la tasa nominal necesaria para que un depósito por $
11.000 reditúe al inversor en 180 dı́as, la mitad de la colocación usando capitalización continua.
Ejercicio 6.19 ¿Cuántos años son necesarios para duplicar un capital a una
tasa nominal J en capitalización continua?
Ejercicio 6.20 ¿Cuánto tiempo es necesario que transcurra para triplicar un
capital al 5% nominal capitalizable continuamente?
Ejercicio 6.21 ¿Cuál es la tasa de interés nominal que nos permite duplicar
el capital en t años usando capitalización continua?
Ejercicio 6.22 Una empresa con excedentes de fondos por $ 20.000 efectúa
dos colocaciones para cubrir necesidades futuras. Una durante 45 dı́as al 11,5%
nominal capitalizable continuamente, y otra durante 15 dı́as a una TEM del
3,25%. Averiguar los importes de los depósitos, sabiendo que las inversiones
producen igual interés.
Ejercicio 6.23 El señor Elias posee $ 355.000. Decide invertilos en dos proyectos que le pagarán respectivamente el 1,2 % bimestral y el 2,1% trimestral. Qué
porcentaje de sus ahorros debe invertir en cada proyecto, para recibir el mismo
monto en concepto de intereses a los 6 meses. Si ahora desea que ambos proyectos le paguen los mismos intereses totales al cabo de 1 año ¿Cuánto deberá poner
en cada uno de los proyectos?
100
CHAPTER 6. CAPITALIZACIÓN CONTINUA
Ejercicio 6.24 Un capital por $ 3.800 se impuso a capitalización continua durante 7 dı́as al 11,2% nominal anual; luego el capital acumulado se impuso a
capitalización compuesta por el término de 15 dı́as con una TNA del 25,7%
anual; y por último se consiguió colocarlo 30 dı́as a interés simple a una tasa
anual del 43,5%. Calcular el interés total y la tasa nominal continua equivalente
de la operación citada.
Delirio:
1
x+
p
− f (x)
f
f x+
1
p
1
p
J
= f (x) 1 +
p
= Jf (x)
tomando p −→ ∞ tenemos
f 0 (x) = Jf (x)
Luego
f (x) = CeJx
Si agregamos la condición inicial
f (0) = C0
tenemos que
f (x) = C0 eJt
6.2
Equivalencia de capitales
Dado un capital A disponible al momento t, en capitalización continua el valor
del mismo a la fecha focal f es:
A al momento f = AeJ(f −t)
pues si t < f , debemos capitalizar el capital A por f − t años
A al momento f = AeJ(f −t)
(PONER DIBUJO)
mientras que si t > f , debemos actualizar el capital A por t − f años:
A al momento f = Ae−J(t−f )
(PONER DIBUJO)
Esto nos permite concluir:
6.2. EQUIVALENCIA DE CAPITALES
101
Proposición 6.25 Dada una tasa nominal continua J, la serie de capitales
A1 , A2 , . . . , An disponibles en los momentos ta1 , ta2 , . . . , tan es financieramente
equivalente a la serie de capitales B1 , B2 , . . . , Bm disponibles en los momentos
tb1 , tb2 , . . . , tbm , a la fecha focal f en el sistema de capitalización continua si
n
X
J (f −ta
j)
Aj e
j=1
=
m
X
b
Bj eJ (f −tj )
j=1
donde todos los datos temporales deben ser expresados en años.
(PONER DIBUJO)
Ejemplo 6.26 La Sra. Yanina desea sutituir el siguiente esquema de pagos: $
50.000 hoy, $ 60.000 a los cinco años y $ 100.000 a los 10 años, por dos pagos
iguales, el primero al año, y el segundo a los 6 años. Hallar el nominal de los
montos a pagar usando una tasa nominal continua J = 13, 5%, y tomando como
fecha focal el dı́a de hoy. Resolver nuevamente el problema usando como fecha
focal f = 5 años.
El valor del primer esquema de pago: $ 50.000 hoy, $ 60.000 a los 5 años
y $ 100.000 a los 10 años, a la fecha focal f (en años) usando la tasa nominal
J = 13, 5% es
50.000e0,135f + 60.000e0,135(f −5) + 100.000e0,135(f −10)
El valor del segundo esquema de pago: $ x dentro de 1 año y $ x dentro de 6
años, a la fecha focal f (en años) usando la tasa la tasa nominal J = 13, 5% es
xe0,135(f −1) + xe0,135(f −6)
Por ejemplo, usando como fecha focal el origen, f = 0 tenemos
50.000 + 60.000e−0,675 + 100.000e−1,35 , = xe−0,135 + xe−0,81
50.000 + 30.549, 39 + 25.924, 03 = 1, 31857397791x
106.473, 41
= x
1, 31857397791
80.748, 91 = x.
i.e., los nuevos pagos serán de $ 80.748,91.
Ejercicio 6.27 Volver a calcular el monto de los nuevos pagos usando la otra
fecha focal propuesta o cualquier otra fecha focal que se le ocurra al lector.
Deberı́a obtener siempre x = 80.748, 91.
La equivalencia financiera en capitalización continua, al igual que en capitalización compuesta, es independiente de la fecha focal elegida.
102
CHAPTER 6. CAPITALIZACIÓN CONTINUA
Ejercicio 6.28 Verificar que este es el caso: comprobar que la equivalencia financiera en capitalización continua es independiente de la fecha focal elegida.
Ejemplo 6.29 Debemos realizar 3 pagos, el primero de $ 40.000 dentro de
tres meses, el segundo de $ 30.000 dentro de 6 meses y último de $ 50.000 a
los 9 meses. Por razones de flujo de caja (disponibilidad de efectivo) queremos
sustituir estos 3 pagos por dos: uno de $ 50.000 dentro de 5 meses y otro de
monto a determinar a los 10 meses. Se conviene una tasa del 25% nominal
continua.
Debemos igualar los valores a la fecha focal dada de ambas operaciones:
valor de la
valor de la
operación original = operación nueva
a la fecha focal f
a la fecha focal f
Usando como fecha focal: f = 6 meses
fecha focal
C
$ 500
0
1
2
3
4
$ 400
5
6
7
8
$ 300
9
10
meses
$ 500
Debemos llevar todos los capitales a los seis meses, por lo que algunos serán
capitalizados (los que están disponibles antes de los 6 meses), otros serán actualizados (los disponibles en fechas posteriores), y los capitales disponibles a los
6 meses no cambian
40.000e0,25· 12 + 30.000 + 50.000e0,25·(− 12 )
=
50.000e0,25 12 + Ce0,25·(− 12 )
42.580 + 30000 + 46.971
=
51.053 + 0, 920044414629C
3
3
1
4
de donde
C=
68.499
= 74.451
0, 920044414629
Por lo que el a los 10 meses deberemos pagar $ 74.451.
Ejercicio 6.30 Una deuda de $ 2.000 con una tasa nominal continua 18.5%
vence en un año. Si el deudor paga $ 900 a los 5 meses y $ 800 a los 9 meses.
Hallar el saldo de la deuda en la fecha de vencimiento.
6.3. TASA MEDIA CONTINUA
103
Ejercicio 6.31 El señor Denis debe $ 25.000 con vencimiento en 6 meses, $
10.000 con vencimiento en 15 meses y $ 18.500 con vencimiento en 18 meses.
Si desea saldar las deudas mediante dos pagos iguales, uno con vencimiento en
9 meses y otro con vencimiento en 18 meses. Determinar el importe de dichos
pagos suponiendo una tasa nominal del 31,5%.
Ejercicio 6.32 ¿Con qué cantidad se cancela hoy dı́a, un préstamo que consiguió dos meses atrás la Srta Noelia, habiendo firmado dos documentos; uno
con valor nominal de $ 6.000 que vence en dos meses a partir hoy y otro por
valor nominal de $ 7.500 y vencimiento a 10 meses del préstamo? Suponga
intereses continuos del 20,4%.
Problemas con almanaque
Ejercicio 6.33 El 15 de enero del corriente año se otorga un préstamo amparado con dos pagarés con vencimiento al 23 de marzo y al 23 de mayo por $
1.900 y $ 2.000 respectivamente. Poco después, se conviene en cancelarlo con
tres pagos: el primero por $ 500 el 22 de febrero, el segundo por $ 1.000 el 22 de
abril y el tercero el dı́a 22 de junio, ¿Cuál es el monto de este último pago si se
cargan intereses del 30% nominal? ¿A cuánto asciende el monto del préstamo?
Ejercicio 6.34 Sea desea sustituir el pago de 3 capitales de $ 12.725, $ 11.022
y $ 8.774, con vencimiento los dı́as 15 de mayo, 12 de junio y 29 de julio,
respectivamente, por uno único pago el dı́a 1 de julio; ¿A cuánto ascenderá el
capital si se aplica una tasa nominal continua del 26%?.
6.3
Tasa media continua
Como ya vimos, se le llama tasa media a la tasa que produce el mismo efecto
final que un grupo de tasas dadas actuando simultáneamente. Consideremos el
siguiente ejemplo:
Ejemplo 6.35 Ud. tiene $ 100.000 invertidos al 18%, $ 250.000 al 8% y %
75.000 al 2%, donde todas las tasas son nominales anuales continuas y todas
las inversiones son por 3 años. ¿Qué tasa nominal (anual) continua deberı́a
ofrecerle una entidad financiera para que ud. coloque todo su capital, $ 425.000,
en la misma (por tres años)?
Este no es más que un problema de equivalencia financiera, donde la incognita es una tasa (en principio, el tiempo también parece ser una incognita, pero
veremos que en sistema continuo, este tipo de problemas es independiente del
horizonte temporal).
Poner dibujo!!!!!!!!!!!!!
Planteemos la oparatoria a 3 años. Al cabo de 3 años, las inversiones originales generan la siguiente cantidad de dinero
100.000e0,18·3 + 250.000e0,08·3 + 75.000e0,02·3
104
CHAPTER 6. CAPITALIZACIÓN CONTINUA
La operación nueva genera al cabo de t años
425.000eJ·3
si queremos que ambas operaciones sean equivalentes, tenemos que
100.000e0,18·3 + 250.000e0,08·3 + 75.000e0,02·3 = 425.000eJ·3
Por lo que la tasa nominal continua J que buscamos, conocida como la tasa
media continua de la operación, es
J
=
=
1 100.000e0,18·3 + 250.000e0,08·3 + 75.000e0,02·3
ln
3
425.000
0, 36901324
Por lo tanto, la entidad financiera debe ofrecerle al menos una tasa nominal
continua del 0, 36901324 %. Esta tasa, produce igual rentabilidad en tres años
que a las otras tres inversiones en conjunto. Esto no ocurre a otras fechas.
A dos años tenemos que las tres inversiones en conjunto producen un montante de $ 1.217.318,74, pues
100.000e0,18·2 + 250.000e0,08·2 + 75.000e0,02·2 = 1.217.318, 74
mientras que si invertimos $ 425.000 al 36,901324% obtenemos un montante de
$ 889.016,40 pues
425.000e0,36901324·2 = 889.016, 3698
A tres años ambas inversiones producen el mismo montante $ 1.285.790,38
100.000e0,18·3 +250.000e0,08·3 +75.000e0,02·3 = 1285790.38 = 425.000e0,36901324·3
Mientras que a 7 años tenemos que las tres inversiones en conjunto producen
un montante de $ 1.652.915,623, pues
100.000e0,18·7 + 250.000e0,08·7 + 75.000e0,02·7 = 1.652.915, 623
mientras que si invertimos $ 425.000 al 36,901324% obtenemos un montante de
$ 5.626.156,741 pues
425.000e0,36901324·7 = 5.626.156, 741
En general, la serie de capitales Ck , con k = 1, . . . , n, los cuales hoy son
colocados a las tasas nominales continuas Jk , con k = 1, . . . , n, durante t años,
es equivalente a colocar hoy la suma de todos los capitales
C=
n
X
k=1
Ck ,
6.3. TASA MEDIA CONTINUA
105
a la tasa nominal continua media Jmedia durante t años, la cual realiza la igualdad en la siguiente ecuación:
n
X
Ck eJk t = CeJmedia
k=1
despejando la tasa media obtenemos
Jmedia
1
= ln
t
n
1 X
C k eJ k t
C
!
.
(6.8)
k=1
Nota 6.36 Observe que la fórmula para la tasa media en capitalización continua depende del tiempo t, los capitales Ck y de las tasas nominales Jk , con
k = 1, . . . , n.
Ejemplo 6.37 A la Señorita Noelia se le ofrecen dos opciones de inversión: La
primera es dividir el capital en dos partes, colocando el 70% del mismo al 8%
nominal anual, y el 30% restante al 12% nominal anual. La segunda consite en
colocar todo el capital al 10% nominal anual. ¿A que horizonte temporal una
opción es mejor que la otra?
Calculemos primero la tasa media de la primera operación. Dado un intervalo
tiempo de t años, queremos hallar una tasa Jmedia , que nos produzca la misma
ganancia:
0.70CeJ1 t + 0.30CeJ1 t = CeJmedia ·t
reemplazando y despejando
Jmedia =
1
ln 0.70e0.08t + 0.30e0.12t
t
Nuevamente la tasa media resulta una función del tiempo.
Podemos graficar Jmedia (t):
tasa
0.150
0.125
0.100
0.075
0.050
0.025
Jmedia (t)
0
20
40
60
42.36489302
80
100
120
140
160
180
200
Años
106
CHAPTER 6. CAPITALIZACIÓN CONTINUA
De la cual se puede ver que
Jmedia (t) ≤ 0.10 para todo t ≤ 42.36489302 años.
Ahora es claro que la segunda opción (no dividir el capital) es la más conveniente si:
t ≤ 42.36489302 años.
En general no se puede despejar t de la expresión (4.15), por lo cual se deben
usar métodos numéricos para hallar el tiempo de “equilibrio” (la cantidad de
años a la que somos indiferentes entre una o otra opción). Para este ejemplo,
usando Maple student edition, hallamos que el tiempo de equilibrio es
t = 42.36489302 años.
Ejercicio 6.38 Tenemos $ 100.000 para invertir. Se nos presentan tres opciones. La primera es depositarlo todo en un banco que paga en 10.8% nominal.
La segunda en comprar $ 65.000 en bonos del estado que pagan un 12% nominal
y el resto en el banco al 5% nominal. La tercera consiste en comprar obligaciones
de empresas privadas: $25.000 en opciones de la empresa A, que rinden un 14%,
$ 40.000 en opciones de la empresa B, que rinden un 10% y el resto en opciones
de la empresa C que rinden un 9% anual. ¿Cuál de las opciones es la más ventajosa a 10 años? ¿Existe un tiempo de equilibrio en el cual seamos indiferentes
entre las tres opciones?
Ejercicio 6.39 Al señor Gonzalo se le ofrecen dos opciones de inversión: La
primera es dividir el capital en dos partes, colocando el 35% del mismo al 18%
nominal, y el 65% restante al 6,5% nominal. La segunda consiste en colocar
todo el capital al 9,4% nominal. ¿Cuál de las opciones es la más ventajosa a 5
años? ¿Cuál es el tiempo de equilibrio?
PONER MÁS EJERCICIOS!!!!!!!!!!!!!!! !
6.4
Equivalencia entre tasas continuas y discretas
A la señorita Georgina se le ofrecen dos opciones: Imponer su capital a una TEA
del 12% o imponerlo a una tasa nominal continua del 11,5%. ¿Cuál opción es
mejor? Si dispusieramos de fórmula para convertir tasas continuas en discretas
y viceversa podrı́amos responder esta pregunta (Si es verdad, hay otras formas
de resolver el problema). Esto se puede lograr facilmente aplicado la definición
de equivalencia de tasas: La tasa efectiva p-perı́odica i(p) (discreta) y la tasa
nominal continua J, son financieramente equivalentes si aplicadas un capital
inicial C0 , durante t años, producen idéntico capital final Cf :
pt
C0 eJt = Cf = C0 1 + i(p)
6.4. EQUIVALENCIA ENTRE TASAS CONTINUAS Y DISCRETAS
107
i(k)
t años
C0
Cf
J
De donde llegamos a la relación fundamental de equivalencia entre tasa discretas y continuas
Proposición 6.40 La tasa efectiva p-perı́odica i(p) (discreta) y la tasa nominal
continua J, son financieramente equivalentes si
p
eJ = 1 + i(p)
(6.9)
Nota 6.41 Depejando de la última expresión obtenemos
J = p ln 1 + i(p)
i(p)
= e
1
pJ
−1
(6.10)
(6.11)
Además, como se puede apreciar de las fórmulas anteriores, esta equivalencia
de tasas es independiente del tiempo.
Para responder a la pregunta que se esta haciendo Georgina, calculemos la
tasa nominal continua equivalente a una TEA del 12%
J = ln (1 + 0, 12) = 0, 1133286853
Por lo tanto es mejor la otra inversión.
A modo confirmatorio, calculemos la TEA equivalente a la J = 0.115:
i(p) = e0.115 − 1 = 0.12187 > 0, 12
Ejercicio 6.42 Hallar la tasa nominal continua equivalente a una TNA del
18%.
Ejercicio 6.43 Hallar la tasa nominal continua equivalente a una i(p) = 0.02
con
p ∈ {1, 3, 4, 6, 12, 52, 360, 365}.
Ejercicio 6.44 Dada una J = 0.30, hallar la i(p) equivalente para
p ∈ {1, 3, 4, 6, 12, 52, 360, 365}.
Ejercicio 6.45 Hallar la tasa nominal continua equivalente a una nominal
trimestral (J (4) ) del 24%.
Ejercicio 6.46
Poner más ejercicios
108
CHAPTER 6. CAPITALIZACIÓN CONTINUA
6.5
Vencimiento medio continuo
Dada una tasa nominal continua J, deseamos hallar el vencimiento medio m,
en el cual podemos sustituir una serie de capitales C1 , C2 , . . . , Cn disponibles en
los momentos t1 ≤ t2 ≤ . . . ≤ tn , por un único pago
C=
n
X
Ck .
k=1
Como en el sistema continuo la equivalencia financiera puede realizarce a
cualquier fecha focal sin alterar el resultado, eligiendo f = 0 tenemos
n
X
Ck e−Jtk = Ce−Jm
k=1
Luego
1
m=
J
ln C − ln
n
X
!
−Jtk
Ck e
(6.12)
k=1
Razonando financieramente es intuitivo que el vencimiento medio se debe hallar
entre t1 y tn , pues debe haber una compensación de intereses.
Ejemplo 6.47 El Señor Paul desea sustituir tres pagos, de $ 4.000, $ 3.000 y
$ 3.000, con vencimientos hoy, dentro de 6 meses y dentro de un año, respectivamente, por un único pago de $ 10.000. Hallar el vencimiento medio para las
siguientes tasas nominales
1)
2)
3)
4)
tasa nominal
4%
8%,
31%,
42%
1) Tasa nominal del 4%,
6
ln 10.000 − ln 4000 + 3.000e−0.04 12 + 3.000e−0.04
vmedio
=
=
0.04
0.4465537 años,
i.e., prácticamente 163 dı́as.
Ejercicio 6.48 Hallar el resto de los vencimientos medios requeridos en el
ejemplo anterior.
Ejercicio 6.49 La empresa González s.r.l. de desea sustituir 6 pagos bimestrales de $ 150.000 , por un único pago de $900.000. Suponer una tasa nominal
del 24.5%. Hallar el vencimiento medio.
6.6. DESCUENTO CONTINUO
109
Ejercicio 6.50 La fábrica de pastas La Nona, S.A. sutituyó el siguiente esquema de pagos:3 pagos de $ 75.000, hoy, a los seis y doce meses, respectivamente, por un único pago de $ 225.000 dentro de 8 meses. ¿Cuál fue la tasa
nominal continua usada?
Ejercicio 6.51
6.6
PONER MÁS EJERCICOS
Descuento continuo
En ésta sección demostraremos que en capitalización continua actualizar y descontar son la misma operación.
Las tasas de descuento no suelen informarse de manera anual, pues tı́picamente
son muy altas pero, a fin de poder desarrollar el descuento continuo, las introduciremos.
Dada una tasa de descuento p-perı́odica d(p) , la tasa de descuento nominal
correspondiente es
H (p) = pd(p)
Por ejemplo la tasa de descuento nominal equivalente a una tasa efectiva de
descuento diario d(365) del 1,1% es
H (365) = 365d(365) = 365 · 0, 011 = 4, 015
i.e., una tasa nominal de descuento del 401,5%.
Ahora, dada una tasa de descuento nominal que descuenta p veces en el año,
tenemos que el efectivo E correspondiente a descontar un nominal N durante t
años es
pt
H (p)
E =N 1−
p
Si ahora fijamos la tasa nominal
H (p) = H para todo p ∈ Z+
y pensamos al efectivo como una función de p
pt
H
E (p) = N 1 −
p
al hacer tender p hacia ∞ obtenemos el siguiente efectivo
E
=
lim E (p)
pt
H
= lim N 1 −
p→∞
p
p→∞
= N e−Ht
Poner dibujo!!!!!!
110
CHAPTER 6. CAPITALIZACIÓN CONTINUA
Luego
N = EeHt
de donde podemos deducir que actualizar y descontar son la misma operación
en capitalización continua (por eso los libros de finanzas suelen hablar siempre
de descuento).
Chapter 7
Composición de tasas
7.1
Rentabilidad real
Hay muchas situaciones donde debemos tener en cuenta más de una tasa para
poder tomar una decisión financieramente acertada. Por ejemplo, cuando la
inflación es grande, cuando se opera con monedas de diferentes naciones, cuando
se cobran comisiones, cuando se pagan impuestos, etc.
Consideremos la siguiente situación
Ejemplo 7.1 Disponemos de $ 250.000. Hoy el dólar cuesta $ 4,15, además el
banco con el que operamos nos paga una tasa en dólares del 6,3 %. Por otro
lado, se estima que la tasa de devaluación anual del peso respecto del dólar será
del 3,7 %. Si compramos dólares, y los depositamos en este banco por 2 años,
¿Cuál será nuestra rentabilidad en pesos?
La respuesta no es simplemente sumar ambas tasas:
6, 3% + 3, 7% = 10%
Veamos en detalle la operación para obtener la tasa real de rendimiento:
1. Primero compramos 60.240,96 dólares, pues cómo cada dólar nos cuesta
$ 4, 15:
$ 250.000
= U $ 60.240, 96386
4, 15
2. Luego capitalizamos por dos años la cantidad de dólares que adquirimos
a la tasa en dólares que nos ofrecen:
2
U $ 60.240, 96386 (1 + 0.067) = U $ 68.583, 67467
3. Luego usamos la tasa anual de devaluación del peso con respecto al dólar
para hallar el precio del dólar frente al peso dentro de dos años:
2
4, 15 (1 + 0, 037) = 4, 46278
111
112
CHAPTER 7. COMPOSICIÓN DE TASAS
4. Luego usamos el tipo de cambio que acabamos de encontrar para obtener
una suma en pesos:
U $ 68.583, 67467 · 4, 46278 = $ 306.073, 94436
5. Por lo que la tasa de rendimiento anual en pesos es la tasa que convierte
$ 250.000 en $ 306.073, 94436 en dos años:
$ 306.073, 94436 = $ 250.000 (1 + r)
2
Por lo que la tasa anual de rendimiento es
r = 10, 6479 %
Dibu: del esquema de la operación
Si observamos en detalle la operación anterior podemos ver la relación entre
las tasas originales y la tasa real de rendimiento del 10, 6479 % :
2
306.073, 94436
=
250.000 (1 + r)
68.583, 67467 · 4, 46278
=
250.000 (1 + r)
2
=
250.000 (1 + r)
2
=
250.000 (1 + r)
=
250.000 (1 + r)
68.583, 67467 · 4, 15 (1 + 0, 037)
2
60.240, 96386 (1 + 0, 067) · 4, 15 (1 + 0, 037)
250.000
2
2
(1 + 0, 067) · 4.15 (1 + 0, 037)
4, 15
2
2
2
2
Cancelando, obtenemos
2
2
=
(1 + r)
0, 067 + 0, 037 + 0, 067 · 0, 037
=
r
0, 106479
=
r
(1 + 0, 067) (1 + 0, 037)
2
Por lo tanto, si tenemos más de una tasa actuando simultáneamente, el efecto
conjunto no es la mera suma de las tasas (en el sistema compuesto).
Además, el ejemplo anterior muestra que si bien las tasas actúan de manera
simultánea sobre un capital, no hay pérdida de generalidad en suponer que las
tasas actúan secuencialmente.
Poner dibujo?????
(p )
(p )
(p )
Definición 7.2 Dadas unas n tasas efectivas i1 1 , i2 2 , . . . , in n , llamaremos
tasa real r(p) a la tasa p-perı́odica que produce un efecto equivalente sobre
un capital inicial C0 durante un perı́odo de tiempo de t años que la aplicación
(p ) (p )
(p )
simultánea de las tasas i1 1 , i2 2 , . . . , in n :
C0
n Y
k=1
(p )
1 + ik k
pk t
pt
= C0 1 + r(p)
(7.1)
7.1. RENTABILIDAD REAL
113
De la definición se puede deducir la ecuación fundamental para el cálculo de
tasas reales
(p )
(p )
(p )
Proposición 7.3 Dadas unas n tasas efectivas i1 1 , i2 2 , . . . , in n de aplicación
simultánea, la tasa real p-perı́odica r(p) asociada a las mismas satisface:
n Y
(p )
1 + ik k
pk
p
= 1 + r(p)
(7.2)
k=1
Ejemplo 7.4 Compramos un propiedad inmobiliaria por $ 350.000. Se espera
que el valor de las propiedades de la zona aumenten a un ritmo del 5% anual.
Además, a causa de la inflación, se espera que los inmuebles aumenten a un
15% anual. ¿Cuál es el rendimiento anual “real” de la inversión?
La respuesta no es 20 % anual, el efecto es compuesto:
350000 (1 + 0.05) (1 + 0.15)
=
350000(1 + 0.05 + 0.15 + 0.0075)
{z
}
|
=
350000 (1 + 0, 2075)
esta es la tasa real
la tasa “real” es del 20. 75 % anual. Observe que habrı́amos obtenido el mismo
resultado usando la fórmula fundamental de tasas reales (7.2):
1+r
=
(1 + 0.05) (1 + 0.0075)
r
=
0, 2075
Ejemplo 7.5 Siguiendo con los ejemplos inmobiliarios, decidimos comprar un
salón comercial aledaño al centro por unos $ 750.000. Estimamos que la inflación anual rondará el 0,45 % mensual por los próximos 5 años. Además,
como la ciudad está en expansión, el costo de las locales comerciales está aumentando a un 4 % semestral. Finalmente la apertura de un supermercado y la
creación de una escuela, ambos en las inmediaciones del local están aumentando
el valor de los inmuebles de la zona en un 3 % anual. ¿Cuál es la tasa redimiento
trimestral de nuestra inversión?¿Cuál será el valor (aproximadamente) del local
al cabo de 4 años?
Hallar la tasa de rendimiento no es más que aplicar la fórmula (7.2)
1 + r(4)
4
= (1 + 0.0045)
12
2
(1 + 0.04) (1 + 0.03)
de donde
r(4) = 0.04129983381
Por lo que la tasa de rendimiento trimestral de nuestra inversión es del 4,129983381%.
El valor estimado de la propiedad al cabo de 4 años será de $ 1.228.755,79488
pues
12
750.000 (1 + 0, 04129983381) = 1.228.755, 79488
114
CHAPTER 7. COMPOSICIÓN DE TASAS
Ejercicio 7.6 Compramos una casa en un barrio por $ 85.000. Por efecto de
la inflación el valor de las propiedades sube un 0,52% mensual. Y debido a la
inaguración de un parque público las propiedades de la zona están aumentando
su valor un 3,5% anualmente. ¿Cuál es el valor de mercado de nuestra casa
pasados 8 años?
Ejercicio 7.7 Compramos un propiedad inmobiliaria por $ 550.500. Se espera
que el valor de las propiedades de la zona aumenten a un ritmo del 6,1% anual.
Además, a causa de la inflación, se espera que aumenten a un 7% anual. ¿Cuál
es el rendimiento anual real de la inversión?
Ejercicio 7.8 En mayo de 2008, compramos un camión en $ 730.700, para
alquilarselo a una empresa minera que nos paga mesualmente el 1,82% del valor
del vehı́culo. A causa de la inflación el precio de este tipo de vehı́culos sube en
promedio un 8,7 % anual. ¿Cuál es el rendimiento de la inversión a mayo de
2010?
Ejercicio 7.9 Un banco nos ofrece un préstamo a una tasa del 24,7% anual,
más un seguro del 0,8% mensual, más el impuesto varios que son del orden del
2,73% trimestral. ¿Cuál es la tasa diaria real del préstamo?
Ejercicio 7.10
7.2
PONER MÁS EJERCICOS
Efecto de las comisiones
Es esta sección analizaremos el efecto de las comisiones sobre la rentabilidad de
las inversiones. En lı́neas generales, las comisiones disminuyen la rentabilidad
de una inversión.
Las comisiones pueden ser cobradas de varias formas. Pueden ser un monto
fijo, un porcentaje de la inversión inicial, porcentaje de la ganancias, o una
combinación de los anteriores. Similarmente, las comisiones, pueden se cobradas
al principio o al final de la operación.
Una inversión por un monto Cinicial , la cual produce al cabo de t años, un
monto Cfinal , tiene una tasa de rendimiento p-perı́odica tal que
pt
Cfinal − Cinicial
Cinicial 1 + i(p)
=
Cinicial
PONER DIBUJO!!!!!!!!!!!
7.2.1
Efecto de las comisiones cobradas al principio de la
operación
Este es el caso más habitual. Analizaremos por separado el efecto de las comisiones de monto fijo y las comisiones porcentuales (sobre la inversión inicial).
7.2. EFECTO DE LAS COMISIONES
115
Comencemos con las comisiones de monto fijo. Si se invierte un capital C0
durante n p-perı́odos, a una tasa i(p) , pero nos cobran una comisión fija c tenemos que la cantidad efectivamente invertida es C0 − c y lo que recibiremos
es
n
Cfinal = (C0 − c) 1 + i(p)
(7.3)
poner dibujo!!!!!!!!!!!!!!!!!!!!!!
La tasa p-perı́odica real r(p) es la que transforma en n p-perı́odos nuestra
inversión C0 en Cfinal
n
Cfinal = C0 1 + r(p)
(7.4)
Igualando (7.3) y (7.4)
n
n (C0 − c) 1 + i(p) = 1 + r(p)
Obtenemos la siguiente expresión
s
c
n
(p)
1+i
1−
= 1 + r(p)
C0
(7.5)
de donde resultan obvias las siguientes observaciones:
1. El rendimiento real es menor que el rendimiento declarado: r(p) < i(p) .
2. El impacto de la comisión fija depende de el monto invertido inicialmente
C0 y del horizonte temporal de la inversión. Fijada n, Mientras más grande
sea la inversión inicial, menor será la diferencia entre r(p) y i(p) . Similarmente, Fijada C0 , mientras mayor sea el horizonte temporal (n) de la
operación, menor será la diferencia entre r(p) y i(p) . Esto se puede expresar sucintamente:
r(p) % i(p) , cuando n → ∞ o cuando C0 → ∞
donde % indica que la convergencia es monótona creciente.
PONER 4 O 5 EJERCICIOS!!!!!!!!!!!!!!!!!
Ahora analizaremos las comisiones porcentuales. En este caso, el comisionista cobra un porcentaje fijo t sobre la inversión realizada. Por lo si se invierte
un capital C0 durante n p-perı́odos, a una tasa i(p) , pero nos cobran C0 t en conceptos de comisión. luego que la cantidad efectivamente invertida es C0 (1 − t)
y lo que recibiremos es
n
Cfinal = C0 (1 − t) 1 + i(p)
(7.6)
poner dibujo!!!!!!!!!!!!!!!!!!!!!!
116
CHAPTER 7. COMPOSICIÓN DE TASAS
Al igual que antes la tasa p-perı́odica real r(p) es la que transforma al cabo
de n p-perı́odos nuestra inversión C0 en el capital Cfinal
n
Cfinal = C0 1 + r(p)
(7.7)
Igualando (7.6) y (7.7)
n n
(1 − t) 1 + i(p) = 1 + r(p)
Obtenemos la siguiente expresión
p
1 + i(p) n (1 − t) = 1 + r(p)
(7.8)
(7.9)
de donde resultan obvias las siguientes observaciones:
1. El rendimiento real es menor que el rendimiento declarado: r(p) < i(p) .
2. El impacto de la comisión porcentual no depende de el monto invertido
inicialmente C0 , pero si depende del horizonte temporal de la inversión.
Mientras mayor sea el horizonte temporal (n) de la operación, menor será
la diferencia entre r(p) y i(p) . Esto se puede expresar sucintamente:
r(p) % i(p) , cuando n → ∞
poner 4 o 5 ejercicios!!!!!!!!!!!!!!!!
7.2.2
Efecto de las comisiones cobradas al final de la operación
Comencemos con las comisiones de monto fijo. Si se invierte un capital C0 durante n p-perı́odos, a una tasa i(p) , pero nos cobran una comisión fija c tenemos
que la cantidad efectivamente recibida al final de la inversión es Cfinal = Cn − c
donde
n
Cn = C0 1 + i(p)
(7.10)
poner dibujo!!!!!!!!!!!!!!!!!!!!!!
La tasa p-perı́odica real r(p) es la que transforma al cabo de n p-perı́odos
nuestra inversión C0 en Cfinal = Cn − c
n
Cfinal = Cn − c = C0 1 + r(p)
(7.11)
Reemplazando (7.10) en (7.11)
n
n
C0 1 + i(p) − c = C0 1 + r(p)
Obtenemos la siguiente expresión
n
n
c
1 + i(p) −
= 1 + r(p)
C0
de donde resultan obvias las siguientes observaciones:
(7.12)
7.2. EFECTO DE LAS COMISIONES
117
1. El rendimiento real es menor que el rendimiento declarado: r(p) < i(p) .
2. El impacto de la comisión fija depende de el monto invertido inicialmente
C0 y del horizonte temporal de la inversión. Fijada n, Mientras más grande
sea la inversión inicial, menor será la diferencia entre r(p) y i(p) . Similarmente, Fijada C0 , mientras mayor sea el horizonte temporal (n) de la
operación, menor será la diferencia entre r(p) y i(p) . Esto se puede expresar sucintamente:
r(p) % i(p) , cuando n → ∞ o cuando C0 → ∞
PONER 4 O 5 EJERCICIOS!!!!!!!!!!!!!!!!!
Ahora analizaremos las comisiones porcentuales. En este caso hay dos variantes, pues la comisión se puede cobrar sobre el monto final total, o sobre la
ganacia obtenida.
Consideremos el caso donde el comisionista cobra un porcentaje fijo t sobre
el monto final Cfinal . Si se invierte un capital C0 durante n p-perı́odos, a una tasa
i(p) , nos cobran Cfinal t en conceptos de comisión. Luego la cantidad de dinero
que efectivamente se recibe es Cfinal (1 − t) donde
n
Cn = C0 1 + i(p)
(7.13)
poner dibujo!!!!!!!!!!!!!!!!!!!!!!
Al igual que antes la tasa p-perı́odica real r(p) es la que transforma al cabo
de n p-perı́odos nuestra inversión C0 en el capital que efectivamente recibimos
Cfinal = Cn (1 − t)
n
Cfinal = Cn (1 − t) = C0 1 + r(p)
(7.14)
Reemplazando (7.13) y (7.14)
n
n
1 + i(p) (1 − t) = 1 + r(p)
Esta expresión coincide con (7.8) por lo que para el inversor es lo mismo que
la comisión porcentual la cobren sobre la inversión inicial que sobre el capital
final, i.e. al final de la operación recibe la misma cantidad de dinero:
n
C0 (1 − t) 1 + i(p)
Nota 7.11 Observemos que si el comisionista cobra una comisión porcentual t,
recibe C0 t al principio de la operación (momento 0)si la comisión la cobra sobre
la inversión inicial al principio de la operación, mientras que recibe Cn t al final
de la operación (momento n)si la comisión la cobra sobre el monto final. Si bien
son sumas distintas de dinero, son financieramente equivalentes a la tasa i(p) :
n
C0 t 1 + i(p) = Cn t
pues Cn = C0 1 + i(p)
n
.
118
CHAPTER 7. COMPOSICIÓN DE TASAS
Analizaremos ahora el caso donde el comisionista cobra el porcentaje t sobre
las ganancias obtenidas por el inversor:
ganacias = Cfinal − Cinicial
Si se invierte un capital C0 durante n p-perı́odos, a una tasa i(p) , y nos cobran
una comisión porcentual t sobre las ganacias, en lugar de recibir
n
Cn = C0 1 + i(n)
recibimos
Cfinal
= Cn − (Cn − C0 ) t
= C0 1 + i(n) (1 − t) + t
(7.15)
Luego la tasa de rentabilidad real p-periodica para el inversionista, r(p) , es aquella que transforma al cabo de n p-perı́odos la inversión inicial C0 en el monto
final Cfinal
n
Cfinal = C0 1 + r(p)
(7.16)
Igualando (7.15) y (7.16)
n
n
C0 1 + i(n) (1 − t) + t = C0 1 + r(p)
Obtenemos la siguiente expresión
n
n
1 + i(n) (1 − t) + t = 1 + r(p)
(7.17)
de donde resultan obvias las siguientes observaciones:
1. El rendimiento real es menor que el rendimiento declarado: r(p) < i(p) .
2. El impacto de la comisión porcentual no depende de el monto invertido
inicialmente C0 , pero si depende del horizonte temporal de la inversión.
Mientras mayor sea el horizonte temporal (n) de la operación, menor será
la diferencia entre r(p) y i(p) . Esto se puede expresar sucintamente:
r(p) % i(p) , cuando n → ∞
poner 4 o 5 ejercicios!!!!!!!!!!!!!!!!
7.3
Tasas negativas
Si bien en la deducción de la fórmula de capitalización compuesta
n
Cn = C0 1 + i(p)
7.3. TASAS NEGATIVAS
119
no hay ninguna restricción sobre los valores que puede tomar la tasa p-perı́odica
i(p) , hasta ahora hemos asumido que la tasa es positiva. Es decir, matemáticamente,
la tasa i(p) puede ser nula o inclusive negativa. Pero
¿Cuál es el significado financiero de una tasa no-positiva?
Para empezar, si i(p) = 0 (no hay costo de oportunidad), no hay matemáticas
financiera y todo se trivializa. $ 100 hoy son equivalentes a $ 100 pesos dentro
de quince años, y a $ 100 hace 6 años.
El caso i(p) < 0 tiene un significado financiero: corresponde a depreciaciones,
el pago de impuestos, seguros, comisiones y servicios varios.
7.3.1
Depreciación
La mayorı́a de los bienes que adquirimos comienzan a perder valor ni bien están
en nuestras manos (por el desgaste que produce el uso, por la acción de los
elementos naturales, o inclusive por obsolecencia).
Definición 7.12 La depreciación es la pérdida de valor que sufren los activos
fijos (como edificios, maquinaria, mobiliario, equipos de computo, vehı́culos,
etc.) a lo largo de su vida útil, haciendo que la misma resulte limitada.
No daremos un tratamiento completo del tema y nos limitaremos a presentar el método de depreciación de porcentaje fijo, el cual corresponde a usar
capitalización compuesta con una tasa negativa.
La idea es simple, utilizaremos una tasa fija a lo largo de la vida útil del
activo fijo en cuestión, para ir reduciendo el valor del mismo, perı́odo a perı́odo
de acuerdo con la tasa de deprecicación dada. Veamos un ejemplo
Ejemplo 7.13 Una Universidad compra una camioneta todo terreno por unos $
215.000 para su el departamento de Geologı́a. Se sabe que la tasa de depreciación
para este tipo de vehı́culos es del 5,5 % anual. ¿Cuál es el valor del vehı́culo al
cabo de 5 años?
Una tasa de depreciación del 5,5% anual, nos dice que el bien en cuestión
pierde el 5,5% de su valor en un año, si a principio de año el bien valı́a $ 215.000,
al final del año valdrá $ 203.175 pues
{z }
|215.000
−
Valor del bien
a principios del año
|
215.000 · 0, 055
|
{z
}
= 215.000 (1 − 0, 055) = 203.175
Valor pérdido
al cabo de un año
{z
Valor al final del año
}
PONER DIBU!!!!!!!!!!!!
Al siguiente año, la situación es similar, pero ahora el valor del bien a principios del año es $ 203.175, luego, al finalizar el segundo año, el valor del bien
será de $ 193.016,25, pues
2
203.175−203.175·0, 055 = 203.175 (1 − 0, 055) = 215.000 (1 − 0, 055) = 193.016, 25
120
CHAPTER 7. COMPOSICIÓN DE TASAS
Porner dibujoooo!!!!!!!!!!
Ahora es claro que al final del tercer año el valor del bien será de $ 183.365,4375
pues
3
215.000 (1 − 0, 055) = 183.365, 4375
Finalmente es claro que el valor de la camioneta al cabo de 5 años será $
162.030,7725 pues
5
215.000 (1 − 0, 055) = 162.030, 7725
Proposición 7.14 Dado un activo fijo de valor C0 y la tasa p-perı́odica i(p) de
depreciación del mismo, el valor del activo fijo al cabo de t años es
pt
(7.18)
Ct = C0 1 − i(p)
PONER DIBU!!!!!!!!!!!!!!!!
Nota 7.15 La tradición establece que las tasas (en matemáticas financiera) son
siempre informadas de forma positiva, por lo que el signo de las misma, queda
explı́cito en las fórmulas. Cuando digamos que una tasa es negativa, en realidad
queremos decir que usaremos la fórmula (7.18).
Ejemplo 7.16 En abril de 2006, compramos un auto en $ 36.700. Sabemos que
los vehı́culos de este tipo se deprecian (pierden valor) a una tasa del 4,5% anual.
En mayo de 2008 decidimos vender el auto ¿Qué precio debemos cobrar?
Han pasado 25 meses desde la compra del auto, por lo que teniendo encuenta
la deprecicación su precio será de $ 33.343,13 pues
1
2+ 12
36.700 (1 − 0, 045)
|
{z
= 33.343, 1343
}
factor de depreciación
Consideremos ahora el efecto de la inflación.
Ejemplo 7.17 En abril de 2006, compramos un auto en $ 36.700. Sabemos que
los vehı́culos de este tipo se deprecian (pierden valor) a una tasa del 4,5% anual.
Pero a causa de la inflación suben un 18% anual. En mayo de 2008 decidimos
vender el auto ¿Qué precio debemos cobrar?
Han pasado 25 meses desde la compra del auto, su precio será
efecto de la inflación
36.700 (1 − 0, 045)
{z
|
1
2+ 12
z
}|
{
2+ 1
(1 + 0, 18) 12
=
}
factor de depreciación
1
36.700(1−0, 045 + 0, 18 + (−0, 045) · 0, 18)2+ 12
{z
}
|
esta es la tasa real
1
2+ 12
=
36.700 (1 + 0.1269)
=
47.071, 78
7.3. TASAS NEGATIVAS
121
Es decir, nuestra compra a rendido un 12,69%, por lo que al cabo del 25 meses
(gracias a la inflación), el auto “vale más” de lo que pagamos originalmente
aunque tenga más de dos años de uso.
Del ejemplo anterior resulta claro que la fórmula para hallar la tasa real
cuando actúan de manera simultánea un grupo de tasas no cambia si alguna(s)
de las tasas consideradas es negativa. Pero por razones didácticas la reestableceremos:
(p )
(p )
(p )
Proposición 7.18 Dada una serie de n tasas efectivas i1 1 , i2 2 , . . . , in n y
(q ) (q )
(q )
una serie de m tasas negativas i1 1 , i2 2 , . . . , imm de aplicación simultánea,
(p)
llamaremos tasa real a la tasa p-perı́odica r que produce un efecto equivalente
sobre un capital inicial C0 durante un perı́odo de tiempo de t años:
C0
n Y
k=1
(p )
1 + ik k
m pk t Y
(qj )
1 − ij
qj t
pt
= C0 1 + r(p)
j=1
De donde podemos deducir la ecuación fundamental para el cálculo de tasas
reales
n m pk Y
q
p
Y
(q ) j
(p )
1 + ik k
1 − ij j
= 1 + r(p)
(7.19)
k=1
j=1
Nota 7.19 De la fórmula anterior resulta claro que la tasa real que producen
una serie de tasas aplicadas simultáneamente no depende del tiempo, ni los
montos iinvolucrados, sólo depende de las tasas.
Ejercicio 7.20 Hace 3 años compramos un camión en $ 730.000, para alquilarselo
a una empresa minera que nos paga mesualmente el 2,82% del valor del vehı́culo.
Sabemos que los vehı́culos de este tipo se deprecian a una tasa del 6,5% anual . Pero a causa de la inflación suben en promedio 8% anual. ¿Cuál es el
rendimiento de la inversión?
Ejercicio 7.21 La señorita Viviana adquirió un automóvil por unos $ 65.000
para ser utilizado como taxi. Si al cabo de 5 años lo vende por $ 45.000.
1. ¿Cuál es la tasa mensual de depreciación que usó?
2. Si ahora consideramos que la inflación anual fue del 12 %, ¿Cuál es la
tasa anual de depreciación usada?
Ejercicio 7.22 Una empresa adquiera un centro de copiado (all-in-one) por
unos $ 12.500. Cuál es el valor del mismo al cabo de 3 años si
1. La tasa de depreciación de este equipo es del 1,5 % mensual.
2. Si además consideramos que la inflación es del 5 % anual.
Ejercicio 7.23
Poner más ejercicios!!!!!!!!!!!!
122
7.3.2
CHAPTER 7. COMPOSICIÓN DE TASAS
Impuestos, seguros y comisiones varias
Las tasas impositivas, los seguros y las comisiones porcentuales también actuan
como tasas negativas, i.e., debemos usar la fórmula (7.18).
Ejemplo 7.24 El señor Elias adquirió un auto por $ 70.000, a fin de utilizarlo
como remis. El estima que la inversión le rinde un 35 % anual. A lo cual le
debe descontar el 2 % mensual en concepto de impuestos municipales y un 5 %
anual para el pago del seguro obligatorio. ¿Cuál es el rendimiento diario real de
la inversión?
Se nos está pidiendo que hallemos la tasa real diaria de la operación, la cual
se puede calcular facilmente usando (7.19):
1 + r(365)
365
r(365)
12
=
(1 + 0.35) (1 − 0.02)
=
0.000017476
(1 − 0.05)
i.e., el rendimiento diario de la inversión del Sr. Elias es del 0,0017476% diario.
Ejercicio 7.25 Compramos una casa en un barrio por $ 75.000. Por efecto de
la inflación el valor de las propiedades suben un 0.52% mensual. Pero debido a
la contaminación creciente de un rio aledaño, las propiedades de la zona están
disminuyendo su valor un 3% anualmente. ¿Cuál es el valor de mercado de
nuestra casa pasados 5 años?
Ejercicio 7.26 Compramos un propiedad inmobiliaria por $ 550.500. Se espera
que el valor de las propiedades de la zona aumenten a un ritmo del 6,1% anual.
Además, a causa de la inflación, se espera que aumenten a un 7% anual. Si
descontamos el impuesto inmoviliario, el cual es del 1,1% anual. ¿Cuál es el
rendimiento anual real de la inversión?
Ejercicio 7.27 En mayo de 2001, compramos un camión en $ 73.700, para
alquilarselo a una empresa minera que nos paga mesualmente el 0,82% del valor
del vehı́culo. Sabemos que los vehı́culos de este tipo se deprecian a una tasa
del 6,5% anual . Pero a causa de la inflación suben en promedio 8% anual.
Si descontamos los impuestos que pagamos, los cuales son del orden del 2,1%
anual, cual es el rendimiento de la inversión a mayo de 2008.
Ejercicio 7.28
7.3.3
Poner más ejercicios
Impuestos sobre la renta financiera y su efecto sobre
la rentabilidad.
Si bien hoy por hoy en la Argentina no se cobran impuestos sobre los intereses
ganados por depósitos, ni operaciones de bolsa, es de esperar que en un futuro
no muy lejando dicho impuesto se implemente
7.3. TASAS NEGATIVAS
123
Nota 7.29 Uno de los autores sostiene que es inmoral que se cobre i.v.a. y no
se cobre impuesto sobre la renta financiera.
Los impuestos sobre los intereses ganados pueden ser implementados de diferentes maneras. Analizaremos primero el caso en que los impuestos se cobran
perı́odo a perı́odo.
Si imponemos un capital C0 a una tasa p-perı́odica i(p) durante unos n pperı́odos, sabemos que los intereses ganados durante el perı́odo k son
Ik = Ck i(p)
Sea τ la tasa impositiva que el gobierno aplica sobre los intereses ganados
en un p-perı́odo. Por lo que perı́odo a perı́odo, el estado se queda con
Ik τ
ingresando a la cuenta del inversionista
Ikgravado = Ik − Ik τ = Ck i(p) (1 − τ )
en lugar de Ik = Ck i(p) . Esto nos lleva a la siguiente relación recursiva
gravado
Ck+1
= Ckgravado + Ckgravado i(p) (1 − τ ) = Ckgravado (1 +
i(p) − i(p) τ )
| {z }
tasa real después
de impuestos
Por lo que, con la condición inicial C0 = inversión. Tenemos que el capital
acumulado al cabo de n p-perı́odos es
n
Cngravado = C0 1 + i(p) (1 − τ )
(7.20)
y la tasa de rendimiento real p-perı́odica es
r(p) = i(p) (1 − τ )
(7.21)
Poner dibujo!!!
Ejemplo 7.30 Un banco nos ofrece por nuestros depósitos una tasa del 16 %
anual. Pero debemos pagar en concepto de impuestos sobre los interéses un
5.5%, en cada capitalización. ¿Cuál es la tasa anual real que recibimos?
En nuestro caso la tasa real después de impuestos es
r = 0, 16 (1 − 0, 055) = 0, 1512
i.e., nuestra inversión en realidad nos rinde un 15,12% anual.
Poner ejercicios
124
CHAPTER 7. COMPOSICIÓN DE TASAS
Otra forma de cobrar impuestos sobre los intereses ganados en depósitos,
consiste de aplicar una tasa impositiva τ sobre el interés tot al ganado por el
inversionista. Si imponemos un capital C0 a una tasa p-perı́odica durante unos
n p-perı́odos, sabemos que los intereses totales ganados están dados por
n
IT = C0 ((1 + i) − 1)
Sobre este monto el estado cobra la tasa impositiva τ
ITgravado
=
=
IT (1 − τ )
n
C0 1 + i(p) − 1 (1 − τ )
Por lo que el capital que recibiremos será
= C0 + ITgravado
n
h
n
i
o
= C0 1 + 1 + i(p) − 1 (1 − τ )
n
o
n
= C0 1 + i(p) (1 − τ ) + τ
Cngravado
Por lo que la tasa real p-perı́odica satisface
n n
1 + r(p) = 1 + i(p) (1 − τ ) + τ
(7.22)
la cual claramente depende de la duración de la inversión.
Ejemplo 7.31 El banco Holandés nos ofrece por nuestros depósitos una tasa del
3.5 % mensual. Pero debemos pagar en concepto de impuestos sobre los intereses
un 12 % sobre los intereses totales ganados. ¿Cuál es la tasa mensual real de
rendimiento si la operación es pactada a 6 meses?¿Cambia el rendimiento real
si la operación hubiera sido pactada a 18 meses?
No hay más que aplicar (7.22). Averiguemos el rendimiento real mesual por
el depósito a 6 meses
1 + r(12)
6
r(12)
6
=
(1 + 0, 035) (1 − 0, 12) + 0, 12
=
0, 03110296367
En cambio, el rendimiento a los 18 meses es
1 + r(12)
18
r(12)
18
(1 − 0, 12) + 0, 12
=
(1 + 0, 035)
=
0, 03172824625
Este ejemplo muestra algo que ya dijimos, que el rendimiento real después
de impuestos sobre los intereses totales depende de la duración de la operación.
7.4. TIPO DE CAMBIO
125
De hecho, cuando n se hace cada vez más grande la tasa real se aproxima a la
nominal, pues
q
n
r(p) = n 1 + i(p) (1 − τ ) + τ − 1
y tomando lı́mite cuando n tiende a infinito
q
n
(p)
lim r = lim n 1 + i(p) (1 − τ ) + τ − 1 = i(p)
n→∞
n→∞
También se puede probar siempre que la si τ < 100 %, la convergencia es
monótona creciente: a más tiempo, mayor rendimiento real.
Nota 7.32 En ambos casos, es financieramente evidente que el rendimiento
después de impuestos debe ser menor que el rendimiento nominal:
r(p) < i(p)
Ejercicio 7.33 Un banco nos ofrece por nuestros depósitos una tasa mensual
del 1,2%. Pero debemos pagar en concepto de impuestos sobre los intereses un
4,5% anual. ¿Cuál es el rendimiento mensual real de nuestra inversión?
Poner 4 o 5 ejercicios más!!!!!!!!!!!
7.4
Tipo de cambio
En esta sección estudiaremos con algún detalle el funcionamiento de las operaciones finacieras que involucren más de una moneda. En nuetro camino
descubriremos que las tasas además de tener una unidad temporal asociada,
también tienen asociadas una unidad monetaria. Otra noción importante será
el tipo de cambio entre dos monedas, el cual especifica el precio de una moneda
en términos de la otra (en un momento dado).
Ejemplo 7.34 Estamos interesados en invertir $ 500.000 por el término de 1
año. Se nos ofrecen dos opciones:
1. Realizar un depósito a plazo fijo en dólares el cual paga una tasa del 6,7
% anual.
2. Realizar un plazo fijo en pesos a una tasa del 15,5 % anual.
¿Cuál es la mejor inversión? La respuesta depende fuertemente de la variación
en el valor del dólar frente al peso.
Para empezar la tasa del 6,7 % anual en dólares sólo puede ser aplicada a
montos en dólares. Por lo tanto debemos convertir a dólares nuestros $ 50 000.
Supongamos que el tipo de cambio vendedor hoy es
$ 4.3 por dólar
126
CHAPTER 7. COMPOSICIÓN DE TASAS
¿Qué significa esto? Un tipo de cambio vendedor de $ 4.3 por dólar nos indica que
debemos pagar 4.3 pesos por cada dólar que deseemos adquirir. Si disponemos
de $ 50 000, podemos comprar
50 000 $
= 11 627.91 U$S
4.3 $/U$S
Depósitando estos U$S 11 627.91 a la tasa en dólares del 6.7 % anual, al cabo
de un año tendremos
11 627.91 (1 + 0.067) = 12 406.98 U$S
Mientras que si depositamos nuestros $ 50 000 al 15.5 % anual obtendremos
50 000 (1 + 0.155) = 57 750 $.
¿Cuál inversión es mejor? Como ya dijimos, esto depende del precio comprador
del dólar frente al peso al cabo de un año. Ahora, ¿Qué significa un tipo comprador de 4.10 pesos por dólar? Es el precio al que nos compran los dolares, por
cada dólar que entreguemos, recibiremos $ 4.10.
1. Si al cabo de un año el precio del dólar comprador es de 4.3 pesos por
dólar, los U$S 12 406.98 equivaldrán a
12406.98 U$S · 4.3 $/U$S = 53 350.01 $.
Por lo que serı́a una mejor inversión realizar el depósito en pesos.
2. Si al cabo de un año el precio del dólar comprador 4.74 pesos por dólar,
los U$S 12 406.98 equivaldrán a
12 406.98 U$S 4.75 $/US$ = 58 933.14 $.
Por lo que serı́a una mejor inversión hacer el depósito en dólares.
Una pregunta interesante es:
¿A qué tipo de cambio comprador futuro serı́amos indiferentes entre ambas
inversiones?
El tipo de cambio de “equilibrio” es el que transforma U$S 12 406.98 en $
57 750:
tipo de cambio $/U$S =
57 750 $
= 4.654639 $/U$S
12 406.98 U$S
Esto nos dice que si el tipo de cambio comprador futuro es superior a 4.654639 $/U$S,
entonces conviene comprar relizar el déposito en dólares, y si el tipo de cambio
comprador futuro es inferior a 4.654639 $/U$S, conviene realizar el depósito en
7.4. TIPO DE CAMBIO
127
pesos (El problema es que nadie sabe a ciencia cierta cual será el valor del tipo
de cambio futuro).
Hemos estado usando de manera intuitiva lo que se conoce como forma
directa de expresar los tipos de cambio, la cuál es de hecho es la utilizada
Argentina, asi como en la mayorı́a de los paı́ces del mundo. En este caso, el
tipo de cambio indica cuantas unidades de moneda nacional son necesarias para
comprar una unidad de moneda extranjera.
La cotización de una moneda se suele representar en dos precios. El menor
precio, representa el precio comprador, o de demanda (bid). Se denomina
comprador porque es el precio que las casas de cambio nos pagan al comprarnos
las divisas. El precio más alto es el precio vendedor, o de oferta (offer). Se
denomina vendedor porque es el precio que las casas de cambio nos cobran al
vendernos las divisas.
El estándar internacional ISO 4217 fue creado por la ISO con el objetivo de
definir códigos de tres letras para todas las monedas del mundo. Esto elimina las
confusiones causadas por algunos nombres de divisas como dólar, franco, peso o
libra, que son utilizados en numerosos paı́ses pero tienen tipos de cambio muy
diferentes. Las dos primeras letras del código son las dos letras del código del
paı́s de la moneda según el estándar ISO 3166-1 y la tercera es normalmente la
inicial de la divisa en sı́. La siguiente tabla contiene los códigos de las monedas
más usadas en Argentina
Código
ARS
AUD
BOB
BRL
CAD
CLP
CNY
EUR
GBP
ILS
INR
JPY
MXN
PEN
PYG
USD
UYU
ZAR
Moneda
Peso argentino
Dolar australiano
Boliviano
Real
Dolar canadiense
Peso chileno
Yuan renminbi
Euro
Libra esterlina
Nuevo shéquel israelı́
Rupia india
Yen japonés
Peso mexicano
Nuevo sol peruano
Guaranı́ paraguayo
Dolar estadounidense
Peso Uruguayo
Rand sudafricano
Paı́s
Argentina
Australia
Bolivia
Brasil
Canadá
Chile
China
Eurozona
Gran Bretaña
Israel
India
Japón
México
Perú
Paraguay
USA
Uruguay
Sudáfrica
Agregar sı́mbolos a la tabla!!!!!!!!!!!
Utilizaremos tanto el estandar ISO 4217 como los sı́mbolos habituales para
las monedas de mayor circulación.
128
CHAPTER 7. COMPOSICIÓN DE TASAS
Definición 7.35 Dadas dos monedas XXX y Y Y Y , llamaremos tipo de cambio vendedor XXX/Y Y Y al momento t al precio en XXX que debemos
pagar para adquirir una unidad de la moneda Y Y Y . El cual será simbolizado
XXX/Y Y Y
vt
Similarmente llamaremos tipo de cambio comprardor XXX/Y Y Y al momento t al precio en XXX que nos pagan al vender una unidad de la moneda
Y Y Y . El cual será simbolizado
XXX/Y Y Y
ct
Ejemplo 7.36 Si hoy el tipo de cambio vendedor del peso (argentino) con respecto al dólar es
3.15 $/U $S
entonces hoy debemos entregar 3.15 pesos para obtener un dólar.
Ejemplo 7.37 Si el 11 de agosto de 1999 el tipo de cambio comprador del yen
(moneda de Japón) con respecto al dolar fue de
110 U/U $S
entonces el 11 de agosto de 1999 necesitabamos nos entregaban U 110 por cada
dólar que vendı́amos.
Ejemplo 7.38 El la pizzarra de una casa de cambio vemos el tipo de cambio
entre el peso y el euro
4.77/4.82 $/e
en este caso el menor es el tipo de cambio comprador, y el mayor es el tipo
de cambio vendedor. Es decir, si hoy queremos comprar un euro en esta casa
de cambios deberemos entregar 4.82 $. En cambio si deseamos vender un euro,
recibiremos 4.77 $.
Nota 7.39 Se llama spread es la diferencia entre el precio comprador y el
vendedor. Por ejemplo, si la cotización EUR/USD es 1.2025/1.2028, entonces
el spread es EUR 0.0003. El spread suele variar de acuerdo al lugar donde se
realice el cambio y de acuerdo al monto. Usualmente los particulares recurren a
las casas de cambio para cambiar pequeñas cantidades de divisas. Los inversores,
en cambio, realizan transacciones de mayores cantidades de divisas en otras
instituciones que ofrecen un menor spread, o en las mismas casas de cambio o
bancos, pero a un menor spread.
Ejemplo 7.40 Si hoy entregamos 594 coranas suecas (SEK en código ISO
4217) para adquirir 100 USD, ¿Cuál es el tipo de cambio vendedor SEK/USD?
594 SEK
= 5.94 SEK/USD
100 USD
Es decir necesitamos entregar 5.94 coronas suecas por cada dólar.
SEK/USD
choy
=
7.4. TIPO DE CAMBIO
129
U/£
Ejemplo 7.41 Por ejemplo si choy = 207 U/£ tenemos que £ 300 (libras
esterlinas, moneda de Gran Bretaña) nos permiten adquirir
300 £ · 207 U/£ = 42 849 U
$/£
Ejemplo 7.42 Si vhoy = 6.11 $/£ (i.e., hacen falta $ 6.11 para adquirir una
libra esterlina), entonces $ 17 000 nos permiten adquirir
1
= 2 782.32406 £.
6.11 $/£
17000 $
Aqui, podemos considerar que
1
6.11 $/£
£/$
vhoy =
Ejemplo 7.43 Si hoy en una casa de cambios el tipo de cambio comprador
AUD/INR (AUD es el código ISO 4217 para el dólar australiano y INR es el
código ISO 4217 para la rupia indú) es
AUD/INR
choy
= 267.5 AUD/INR
¿Cuál es hoy el tipo de cambio comprador INR/AUD?
Un momento de reflexión nos indica que
INR/AUD
choy
=
1
AUD/INR
choy
Esta relación se cumple en general
XXX/Y Y Y
ct
XXX/Y Y Y
vt
=
=
1
Y Y Y /XXX
ct
1
Y Y Y /XXX
vt
Otro momento de reflexión nos permite ver que los tipos de cambios son transitivos: Dadas tres monedas,
AAA/BBB
=
AAA/BBB
=
ct
vt
AAA/CCC CCC/BBB
ct
AAA/CCC CCC/BBB
vt
vt
ct
Remarcamos que ambas ecuaciones requieren que todos los tipos de cambios
sean a la misma fecha.
Ejemplo 7.44 En la pizarra de una casa de cambio leemos:
845.23/865.7
6.89/6.99
.../...
CLP/ARS
ARS/GBP
CLP/GBP
donde CLP es peso chileno, ARS es peso argentino y GBP es la libra esterlina
(Gran Bretaña). Completar la tabla.
130
CHAPTER 7. COMPOSICIÓN DE TASAS
No hay más que la trasitividad de los tipos de cambios:
CLP/GBP
choy
CLP/ARS ARS/GBP
choy
= choy
=
845.23 CLP/ARS · 6.89 ARS/GBP
=
5 823.637 CLP/GBP
por lo que hoy, en esta casa de cambios debemos entregar 5 823.637 pesos
chilenos por cada libra esterlina que adquiramos.
Ejercicio 7.45 Con 400 dólares canadiense hoy se puede adquirir U$S 390, o
3063 dólares de Hong Kong, o U 39390 (yenes), o 9165 rublos. ¿Calcular los
diferentes tipos cambios?
Ejercicio 7.46 La siguiente tabla brinda los tipos de cambio (comprador) entre
el peso y diferentes monedas al dı́a XX
Moneda (Paı́s o Zona)
Euro (Eurozona)
Kuna (Croacia)
Rublo (Rusia)
Libra esterlina (Inglaterra)
Franco Suizo
Real (Brasil)
Peso (Chile)
Guaranı́ (Paraguay)
Boliviano (Bolivia)
Peso (Uruguay)
Nuevo peso (México)
Dólar (USA)
Dólar (Canada)
Yen (Japón)
Rupee (India)
Renimbi (China)
Shekel (Israel)
Rand (Sudáfrica)
Dirham (Marruecos)
Sı́mbolo
e
£
U$S
U
Tipo $/X abril 2008
5.18
0.686
0.1341
6.21
3.241
1.86
0.0069
0,000725
0.419
0,1573
0.299
3.14
3.08
0.0311
0.07536
0.4484
0.8921
0.3981
0.43175
Tipo $/X abril 20XX
3.70
1. Con $ 5000 ¿Cuántos X podemos adquirir? (reemplaze X, por cada una
de las monedas de la tabla)
2. Si estamos en Argentina y disponemos de 1 450 300 rublos, ¿Cuántos X
podemos adquirir? (reemplaze X, por cada una de las monedas de la tabla)
poner unos cuantos ejercicos más...
al estilos d elos ejemplos.
Ejercicio 7.47
7.4. TIPO DE CAMBIO
131
Dados un par de monedas XXX y Y Y Y , si tenemos un capital inicial de C0
unidades de una moneda XXX, y deseamos invertirlo a una tasa denominada
en moneda Y Y Y , p-perı́odica, durante t años
(p)
iY Y Y
el rendimiento de la inversión en términos de la moneda de origen XXX, deY Y Y /XXX
pende de los tipos de cambio Y Y Y /XXX vendedor al inicio v0
y el
XXX/Y Y Y
tipo de cambio XXX/Y Y Y comprador al cabo de t años ct
:
tp
XXX/Y Y Y
(p)
Y Y Y /XXX
ct
,
(7.23)
1 + iY Y Y
Ct = C0 v0
{z
}
|
Convierte
XXX en YYY
|
|
{z
Calcula en rendimiento en YYY
}
{z
Convierte YYY en XXX
}
La cual llamaremos primera forma para capitalización compuesta bi-monetaria.
Ejemplo 7.48 Hace tres años disponı́amos de $ 250 000, y los invertimos en
obligaciones de una empresa holandesa que nos ofrecián un rendimiento del
9.7% anual. El tipo de cambio vendedor fue de 3.95 $/e. Hoy el tipo de cambio
comprador es 5.196 $/e ¿Cuál fue el rendimiento en pesos de la operación?
Para hallar el capital en pesos acumulado al dı́a de hoy, sólo necesitamos
aplicar la fórmula de capitalización compuesta bi-monetaria (primera forma)
tp
(p)
EU R/ARS
ARS/EU R
Choy = Chace tres años vhace tres años 1 + iEU R
ct
ARS/EU R
Pero nosotros no tenemos vhace tres años , si el tipo de cambio recı́proco. Por lo
tanto
1
1
EU R/ARS
vhace tres años = ARS/EU R
=
= 0.253164556962 e/$
/
3.95
$/e
v
hace tres años
Ahora
Choy
3
=
250 0000 $ · 0.253164556962 e/$
/ (1 + 0.097) · 5.196 $/e
=
434 142.14 $.
Asi el rendimiento de la operación (los intereses totales) son
rendimiento =
Cf − Co
=
434 142.14 $ − 250 000 $
=
184 142.14 $.
Ejercicio 7.49 En octubre de 2006, compramos U 12 500 000 en obligaciones
de una empresa japonesa denominadas en yenes que ofrecı́an un rendimiento
$/U
del 4.25% anual. Hoy el tipo de cambio comprador es choy = 0.02987. ¿Cuántos
pesos tenemos hoy?
132
CHAPTER 7. COMPOSICIÓN DE TASAS
Ejercicio 7.50 El tipo de cambio entre el dólar y el real es de 1.7 reales por
dólar. Si la tasa de interés en dólares es del 5.5% anual y la tasa de interés en
reales es del 8.8% anual ¿Cuál será dentro de {6 meses, 1 año, 5 años} el tipo
de cambio futuro de equilibrio entre ambas monedas.
poner 3 o 4 ejercicos más????????????
Nota 7.51 Como precio que es, el tipo de cambio cumple un importante papel como orientador de recursos. Si bien existe una gran cantidad de pares de
monedas para construir tipos de cambio, casi siempre se publica la relación de
las monedas respecto al dólar de Estados Unidos. Otras monedas que se suelen utilizar como referencia son el euro (Comunidad Económica Europea) y el
yen (Japón). En 2007 el 95% de las operaciones con modedas extranjeras en la
República Argentina fue realizada en dólares, el 4% en euros y el restante 1%
en unas 56 monedas distintas. En lo que se refiere a la distribución del volumen
operado por monedas en el año 2008, el dólar estadounidense mantuvo su liderazgo frente al resto de las monedas, principalmente en las entidades financieras.
En estas últimas se verificó que el 95% del total operado con clientes se concentró en dólares estadounidenses, el 4% en euros y el 1% restante en otras 59
diferentes monedas. En cambio, en las casas y agencias de cambio, la participación de la moneda estadounidense agrupa un poco menos del 85% del total,
subiendo las participaciones de euros y reales a 12% y el 3%, respectivamente.
Otras monedas muy usadas en Argentina (por razones geográficas) son el peso
chileno, el peso uruyuayo, y el guaranı́ (moneda de Paraguay).
Nota 7.52 Se pueden utilizar diferentes convenciones para expresar el tipo de
cambio. En el mercado forex, se utiliza una simbologı́a de pares de monedas.
Cada divisa está representada por tres letras, por ejemplo USD representa al
Dólar estadounidense, EUR al euro, JPY al yen japonés, MXN al peso mexicano, y ARG al peso argentino. Un par de monedas se puede formar con
cualquier par de divisas, por ejemplo USDEUR o USDMXN. Las primeras
tres letras representan la moneda base. USDJPY = 107 indica que hacen falta
107 Yenes para comprar un Dólar. Es decir, el precio de la primera divisa en
términos de la segunda. Existen otras dos formas de representar el tipo de cambio. La forma directa y la forma indirecta. La forma directa es la mas utilizada,
y en este caso el tipo de cambio indica cuantas unidades de moneda nacional
son necesarias para comprar una unidad de moneda extranjera (Usada en Argentina). Por ejemplo, si leemos en un periódico argentino que el tipo de cambio
del real es 1.82, nos indica que se deben pagar 1.82 pesos para obtener un real.
La forma indirecta es utilizada en Inglaterra, y también en Australia, Nueva
Zelanda y Canadá.
7.5. TASA DE DEVALUACIÓN
7.5
7.5.1
133
Tasa de devaluación
Tasas de devaluación
En algunos paı́ses, se utiliza un único tipo de cambio, y lo que se cobra es la una
comisión porcentual, esto ocurre por ejemplo en España
CHEQUEAR!!!!!!!!!!!!!!!.
Ejemplo 7.53 La señora Eliana, se encuentra de vacaciones en Barcelona, y
decide cambiar unos $ 15 000 por euros para ir de compras. En el banco, la
cotización era del peso era 0.32 e/$, además el banco cobra una comisión del
1.56 % sobre las operaciones con divisas. ¿Cuál es el monto de euros que recibio
la señora Eliana?
En principio la cuenta es sencilla:
15 000 $ · 0.32 e/$ = 4 800 e
Y sobre este monto, el banco le cobra una comisión del 0.56 %:
4 800 (1 − 0.0156) = 4 725.12 e
Por lo que la señora Eliana podrá gastar unos 4 725.12 e.
Ejemplo 7.54 Una empresa Española debe cancelar una deuda en dólares para
lo cual acude a un intermediario financiero y cambia e 2 500 000. Si la cotización del dólar era 0.78 e/U $ y el intermediario cobra una comisión del 0.8
%, ¿Cuántos dólares obtuvo la empresa?
De nuevo la cuenta es sencilla:
2 500 000 e
= 3 205 128.205 U $
0.78 e/U $
Sobre esta suma el intermediario finaciero cobra su comisión:
3 205 128.205 U $ · (1 − 0.008) = 3 179 487.179
Por lo que la empresa recibe 3 179 487.179 U$ por sus 2 500 000 e
En general, en los sistemas de cambio con precio único, además del tipo
de cambio, debemos tener en cuenta las comisiones correspondientes, las cuales
pueden variar de institución a institución, y dentro de una misma casa de cambios podemos encontrar variaciones en las comisiones de acuerdo con el par de
monedas involucradas y el tipo de operación (compra o venta de divisas).
Existe una correspondencia entre los sistema de tipo de cambio único con
comisión, y los sistemas con tipo comprador y tipo vendedor.
Ejemplo 7.55 Encuentre el tipo comprador del banco en el que operó la señora
Eliana y el tipo vendedor de la institución financiera donde opero la empresa
española
134
CHAPTER 7. COMPOSICIÓN DE TASAS
El tipo comprador ce/$ que estamos buscando, es el precio en euros al que
le reciben los pesos a la señora Eliana. Si entrego $ 15 000 y recibio 4 725.12 e
tenemos que
4 725.12 e
ce/$ =
= 0.315008 e/$
15 000 $
Recordamos que ce/$ da el precio en euros al que el banco compra el peso
argentino: vamos al banco (español) con una moneda extranjera (en este caso
pesos) y deseamos moneda local ( en este caso euros). Para hallar la relación
entre ambos tipos de cambio observamos que
15 000 $ · ce/$ = 4 725.12 e = 15 000 $ · 0.32 e/$ (1 − 0.0156)
Por lo que
ce/$ = 0.32 e/$ (1 − 0.0156)
Similarmente en el caso de la empresa. El tipo vendedor v e/U $ que estamos
buscando es el precio en euros al que venden los dólares. La empresa entregó e
2 500 000 y recibió 3 205 128.205 U$, por lo que
v e/U $ =
2 500 000 e
= 0.786290322701 e/$
3 179 487.179 U $
Recordamos que v e/$ da el precio en euros al que la institución financiera vende
los dólares. Para hallar la relación entre ambos tipos de cambio observamos que
3 179 487.179 U $ · v e/$
e/$
3 205 128.205 U $ · (1 − 0.008) · v
2 500 000 e
· (1 − 0.008) · v e/$
0.78 e/U $
de donde obtenemos
v e/$ =
=
2 500 000 e
=
2 500 000 e
=
2 500 000 e
0.78 e/U $
(1 − 0.008)
Dados un par de monedas XXX e Y Y Y , denotaremos por
XXX/Y Y Y
ct
(σ c , σ v )
al tipo de cambio único con comisiones σ c para las operaciones de compra de
moneda Y Y Y (pagando con moneda XXX) y σ v para las operaciones de venta
de divisas Y Y Y (cobrando en moneda XXX). A veces escribiremos simplemente
XXX/Y Y Y
ct
especialmente si las tasas de las comisiones son claras del contexto. Si ambas
comisiones son iguales usaremos:
XXX/Y Y Y
ct
(σ)
7.5. TASA DE DEVALUACIÓN
135
De los ejemplos anteriores podemos deducir que:
ce/$
XXX/Y Y Y
= ct
v e/$
=
(1 − σ c )
XXX/Y Y Y
ct
(1 − σ v )
Estas relaciones nos permiten convertir un tipo de cambio en el otro.
dados un par de monedas XXX e Y Y Y , y un tipo de cambio unicosi unaEl
análisis anterior también se puede hacer en términos de la tasa de devaluación
anual de una moneda frente a otra.
Poner 4 o 5 ejercicos de cada tipo...inclusive algunos hallando las comisiones
Introdujimos los tipos de cambio unicos pues nos permiten definir de manera
natural la noción de tasa de devaluación.
XXX/Y Y Y
Definición 7.56 Dadas dos monedas XXX e Y Y Y , sea c0
(σ c0 , σ v0 )
XXX/Y Y Y
el tipo de cambio único al comienzo de un perı́odo de t años, y ct
(σ ct , σ vt )
el tipo de cambio unico al final del mismo, la tasa de devaluación p-perı́odica
de la moneda XXX respecto de la moneda Y Y Y es la tasa p-perı́odica
que realiza la igualdad
XXX/Y Y Y
c0
(p)
1 + δ XXX/Y Y Y
pt
XXX/Y Y Y
= ct
(7.24)
Ejemplo 7.57 Si hace un año el tipo de cambio del peso frente al euro fue
$/e
chace un año = 4.3 $/e
y el tipo de cambio hoy es
$/e
choy = 4.75 $/e
Hallar la tasa de devaluación anual del peso respecto del euro.
Por lo tanto la tasa de devaluación anual del peso frente al euro fue
$/e
=
δ $/e
=
chace un año 1 + δ $/e
$/e
choy
$/e
=
=
$/e
choy − chace un año
$/e
chace un año
4.75 $/e − 4.3 $/e
4.3 $/e
0.104651162791
i.e., una tasa de devaluación anual del 10.4651162791%.
136
CHAPTER 7. COMPOSICIÓN DE TASAS
Ejercicio 7.58 La siguiente tabla contiene los tipos de cambio entre el peso y
diferentes monedas de mayo de 2008:
Paı́s o Zona
Eurozona
Croacia
Rusia
Inglaterra
Suiza
Brasil
Peso (Chile)
Guaranı́ (Paraguay)
Boliviano (Bolivia)
Peso (Uruguay)
Nuevo peso (México)
Dólar (USA)
Dólar (Canada)
Yen (Japón)
Rupee (India)
Renimbi (China)
Shekel (Israel)
Rand (Sudáfrica)
Dirham (Marruecos)
Moneda
Euro
Kuna
Rublo
Libra esterlina
Franco Suizo
Real
Sı́mbolo
e
£
U$S
U
Cambio $/e mayo 2008
4.98
0.788
0.1421
6.25
3.01
2.1
0.0059
0,000725
0.556
0,1432
0.305
3.05
2.98
0.0298
0.067
0.434
0.8921
0.3071
0.4300
1. Completar la tabla anterior con las cotizaciones de las diferentes monedas
(si aún existen) al dı́a de hoy.
2. Hallar la tasa de devaluación mensual del peso frente a las diferentes monedas dadas.
3. Dar la lista de monedas con respecto a las cuales el peso se depreció (ordenar de mayor a menor depreciación).
4. Dar la lista de monedas con respecto a las cuales el peso se apreció (ordenar de mayor a menor).
5. Dar la lista de monedas con respecto a las cuales el peso no varió.
Dados un par de monedas XXX y Y Y Y , si tenemos un capital inicial de C0
unidades de una moneda XXX, y deseamos invertirlo a una tasa denominada
(p)
en moneda Y Y Y , p-perı́odica iY Y Y , durante t años. Queremos ver cual es el
efecto de la devaluación de la moneda XXX con respecto a la moneda Y Y Y
sobre el rendimiento de la inversión en términos de la moneda XXX. Si la tasa
de devaluación estimada de la moneda XXX con respecto a la moneda Y Y Y
(q)
en los próximos t años es δ XXX/Y Y Y (una tasa q-perı́odica) y el tipo de cambio
Cambio $/e hoy
7.5. TASA DE DEVALUACIÓN
137
XXX/Y Y Y
único al inicio de la operación fue c0
Ct
= C0
(1 − σ v0 )
XXX/Y Y Y
c0
(p)
1 + iY Y Y
pt
(σ c0 , σ v0 ) tenemos que
XXX/Y Y Y
c0
(q)
1 + δ XXX/Y Y Y
qt
(1 − σ ct )
pt qt
(p)
(q)
= C0 (1 − σ v0 ) 1 + iY Y Y
1 + δ XXX/Y Y Y
(1 − σ ct )
reordenado podemos obtener la segunda forma para capitalización compuesta
bi-monetaria
pt qt
(p)
(q)
Ct = C0 1 + iY Y Y
1 + δ XXX/Y Y Y
(1 − σ v0 ) (1 − σ ct )
A partir de la cual podemos obtener una expresión para la rentabilidad real
k-perı́odica r(k) de la operación
1 + r(k)
k
p q
1
(p)
(q)
= 1 + iY Y Y
1 + δ XXX/Y Y Y [(1 − σ v0 ) (1 − σ ct )] t
Ambas fórmulas dependen de la comisión sobre las compras de divisas σ ct al final
del perı́odo de t años. Para la mayorı́a de las aplicaciones se puede suponer que
σ ct = σ c0 , pues no suelen haber grandes variaciones en las comisiones cobradas.
Ejemplo 7.59 ¿Cuál es el rendimiento a un año de $ 50 000, en bonos italianos
que pagan un 6.7% anual, sabiendo que la tasa de devaluación del peso respecto
del euro será del 10.4% anual y que la comisión por la compra o venta de divisas
suele ser del 2.5 %?
Aplicando la segunda forma de capitalización compuesta bi-monetaria:
Cf
2
1 + δ $/e (1 − σ)
=
C0 1 + i$/e
=
50 000 (1 + 0.067) (1 + 0.10465) (1 − 0.025)
=
55 990.2915
2
Además podemos hallar la tasa anual real de rendimiento en pesos
1+r
=
2
(1 + ie ) 1 + δ $/e (1 − σ)
=
(1 + 0.067) (1 + 0.104) (1 − 0.025)
=
0.11980583
de donde se puede apreciar el fuerte efecto de la comisiones sobre la rentabilidad.
Ahora veamos un ejemplo más complicado
De aqui para abajo hay que arreglar las cosas
para que vayan en el nuevo lenguaje... verificar los
ejemplos y poner unos ejercicios extras!!!!!!!!!!!!!!
138
CHAPTER 7. COMPOSICIÓN DE TASAS
Ejemplo 7.60 Tenemos U$S 35 000, y los invertimos en pesos por 95 dı́as a
una tasa diaria del 0.35% en pesos. Si hoy el tipo de cambio es 0.3 U$S/$,
y se estima que dentro de 95 dı́as el tipo de cambio será 0.26 U$S/$. ¿Cuál
será el rendimento en dólares de la operación? ¿Cuál es la tasa mensual real en
dólares?
Primero calculamos la tasa devaluación del dolar respecto del peso
( 95 años)
dU365
$S/$
=
=
0.27 − 0.3
0.3
−0.1 .
Las tasas de devaluación negativas, indican una apreciación de la primera moneda respecto de la segunda, en este caso del dólar frente al peso, en estos casos
se suele hablar de una tasa de apreciación.
El rendimento de la operación en dólares es
Cf
=
35000 (1 + 0.0035)
=
43899.68 .
95
(1 − 0.1)
Hay muchas formas de obtener la tasa diaria real en dólares, por ejemplo despejando la tasa en la fórmula de capital final:
95
(365)
43899.68 = 35000 1 + rdólares
,
de donde
(365)
rdólares
r
43899.68
−1
35000
0.00238768 .
95
=
=
95
Otra consiste en pasar la tasa de devaluación 365
años-perı́odica a diaria y
aplicar la fórmula para hallar la tasa real
95
95
(365)
1 + i( 365 años)
=
1 + dU $S/$
95
(365)
(1 − 0.1) =
1 + dU $S/$
,
de donde
(365)
dU $S/$
=
=
√
95
1 − 0.1 − 1
−0.001108443282 .
Luego la tasa diaria real en dólares es
(365)
rdólares
(365)
(365)
= i(365) + dU $S/$ + i(365) dU $S/$
=
0.0035 − 0.001108443282 + 0.0035 (−0.001108443282)
=
0.00238768
7.5. TASA DE DEVALUACIÓN
139
Ejemplo 7.61 Se supone que la tasa de devaluación mensual del peso respecto
del dolar será del 0.5%, durante los próximos dos años. Si disponemos de $ 100
000, y los queremos invertir en obligaciones a 9 meses de una empresa dada,
denominadas en dólares, las cuales pagan un 2.5% trimestral. ¿Cuál será el
montante en pesos? ¿Cuál será la TEA de rendimiento?
Para calcular el montante solo debemos usar la fórmula de capitalización
compuesta bi-moneraria
Cf
3
=
100000 (1 + 0.025) (1 + 0.005)
=
112633.13
9
La tasa de rendimiento a 9 meses es
9
i( 12
años)
=
=
112633.13 − 100000
10000
0.12633129727
La TEA equivalente es (calculada a 9 meses)
9
9
(1 + i) 12 = 1 + i( 12
años)
de donde
i
r
9
9
1 + i( 12
años)
12
=
−1
q
9
12
(1 + 0.12633129727) − 1
=
0.17189365443
=
Ejercicio 7.62 Cuál es el rendimiento a un año de $20 000, en bonos españoles
que pagan un 7.2% anual, sabiendo que la tasa de devaluación anual del peso
respecto del euro será del 8.5%.
Ejercicio 7.63 Tenemos $ 35 000, y los invertimos en reales por 65 dı́as a una
tasa diaria del 0.25%. Si hoy el tipo de cambio es 2.4 reales/$, y se estima que
dentro de 95 dı́as el tipo de cambio será 0.28 reales/$. ¿Cuál será el rendimento
en pesos de la operación? ¿Cuál es la tasa diaria en pesos?
Ejercicio 7.64 Se supone que la tasa de devaluación mensual del euro respecto
del dolar será del -1.1%, durante los próximos dos años. Si disponemos de U$S
100 000, y los invertirmos en obligaciones a 9 meses de una empresa, denominadas en euros, las cuales pagan un 1.58% bimestral. ¿Cuál será el montante
en dólares? ¿Cuál será la TEA de rendimiento en dólares?
Ejercicio 7.65 Supongase que hace 9 meses, ud. diponı́a de e 10 000, y los
invirtio en Argentina (en pesos) a una TNA del 14.6%. Si el tipo de cambio hace
nueve meses era 3.95 $/e y hoy es 4.52 $/e. ¿Cuál fue la TNA de rendimiento
en euros?.
140
CHAPTER 7. COMPOSICIÓN DE TASAS
Nota 7.66 Regı́menes Cambiarios: se refiere al modo en que el gobierno de
un paı́s maneja su moneda con respecto a las divisas extranjeras y como se
regulan las instituciones del mercado de divisas. El régimen cambiario influye
decisivamente en el valor del tipo de cambio y en las fluctuaciones del mismo.
Existes tres regı́menes básicos, que se explican a continuación: el tipo de cambio
flotante (libre o sucia), el tipo de cambio fijo y el régimen de crowling-peg.
Tipo de Cambio Flotante: Este régimen suele denominarse también de tipo
de cambio libre o flexible. Bajo tipo de cambio flotante, el tipo de cambio se determina sin intervención del gobierno en el mercado de divisas. Es decir, que el
tipo de cambio es el resultado de la interacción entre la oferta y la demanda de
divisas en el mercado cambiario. En ningún paı́s existe el régimen de flotación
pura, debido a la gran volatilidad cambiaria y a los efectos en la economı́a real.
Es por esto, que los bancos centrales suelen intervenir en el mercado cambiario
para evitar las fuertes fluctuaciones del tipo d e cambio. Cuando el Banco Central interviene ofreciendo o demandando divisas, el régimen se denomina de
flotación sucia. En ese caso, a pesar de que haya un régimen de tipo de cambio
libre, en la práctica el valor del tipo de cambio se mantiene estable en el tiempo.
Tipo de Cambio Fijo: En este caso, el valor de la moneda se fija con respecto a otra moneda, a una canasta de monedas, o a otra medida de valor,
por ejemplo el oro. En los paı́ses latinoamericanos ha sido usual que el tipo de
cambio esté fijo con respecto al dólar. Los tipos de cambio fijos son criticados
porque, al ser un precio rı́gido, pueden generar rigideces y desequilibrios en la
economı́a. El tipo de cambio ha sido usualmente utilizado como un ancla nominal. En una economı́a abierta, los precios de los bienes transables no pueden
ser muy diferentes de los precios internacionales de estos bienes. La fijación del
tipo de cambio, puede ser útil para disminuir la inflación. Esto se ve reforzado
debido a que, si existe una fuerte convicción de que el compromiso de mantener
el tipo de cambio se va a cumplir, se pueden eliminar las expectativas de devaluación. La experiencia histórica de los paı́ses con poca influencia en el mercado
internacional de divisas indica que los tipos de cambio fijos funcionan durante
un cierto perı́odo de tiempo atenuando la inflación, pero los desequilibrios que se
generan se van acumulando con el tiempo, por lo que la salida del tipo de cambio
fijo suele ir acompañada de otros fenómenos, como fuertes depreciaciones de la
moneda, pérdidas de depósitos bancarios y salidas de capitales. Estos fenómenos
suelen influir negativamente en la tasa de crecimiento (devaluación en México
1994 ( Efecto Tequila), devaluación Argentina en Diciembre de 2001).
Crawling Peg: Bajo un sistema de Crowling Peg, el tipo de cambio se ajusta
de modo progresivo y controlado de acuerdo a una tasa como la inflación o la
tasa de interés, o una combinación de las mismas, o bien de acuerdo a un cronograma establecido por el gobierno, como lo fue la famosa “Tablita Cambiaria”
en Argentina. La principal caracterı́stica del Crowling Peg es que el tipo de cambio se ajusta con pequeñas variaciones porcentuales, en vez de hacerlo mediante
grandes devaluaciones.
7.6. ÍNDICE DE PRECIOS
7.6
141
ı́ndice de precios
Definición 7.67 def de canasta
Definición 7.68 Se llama ı́ndice de precios a un indicador que tiene por
objeto medir las variaciones, a través del tiempo, en los precios de un conjunto
definido de bienes y servicios (canasta) a través de un promedio ponderado (o
pesado) de los mismos.
Cada paı́s tiene un servicio estadı́stico encargado de elaborar distintos incides
de precios. En Argentina, es el INDEC (Instituto Nacional de Estadı́sticas y
Cencos), a través del Centro de Estadı́sticas e Censos. El INDEC elabora varios
ı́ndices de precios, entre ellos:
1. IP C: Índice de Precios al Consumidor. Este ı́ndice mide la variación
de precios minoristas de un conjunto de bienes y servicios que representan
el consumo de hogares representativos de un perı́odo especı́fico.
2. IP IM : Índice de Precios Internos al por Mayor. Este ı́ndice mide la
variación promedio de los precios a los cuales el productor, el importador
directo o el comerciante mayorista coloca sus productos en el mercado
argentino (sin importar el paı́s de origen de los productos)
3. IP BP : Índice de Precios Básicos al Productor. Este ı́ndice mide la
variación promedio de los precios a los cuales el productor local vende su
producción, sin importar a que mercado.
4. IP IB: Índice de Precios Internos Básicos al por Mayor. Este ı́ndice
es similar al IP IM , sólo que los precios considerados no incluyen el impuesto al valor agregado: IVA, los impuestos a los combustibles e internos.
5. ICC: Índice del Costo de la Construcción. Este ı́ndice mide la variación
promedio que experiementa el costo de la construcción privada de los edificios destinados a vivienda. Para ello mensualmente se valorizan los elementos necesarios para la construcción de modelos de vivienda que se
consideran representativos de un perı́odo base y una región determinada.
Esta información, y mucho más, se puede hallar en la página del INDEC
http://www.indec.mecon.ar/
Ejercicio 7.69 Se deja como ejercicio que el lector descargue de la pagina del
INDEC la tabla con el IPC histórico.
Todo ı́ndice de precios mide como evolucionan en promedio los precios de una
dada canasta de bienes y/o servicios, pero no cuánto vale dicha canasta. Cuando
un ı́ndice sube, refleja una disminución del poder de compra del dinero en función
de los precios medios de la canasta de bienes y servicios en cuestión, cuando baja,
refleja un aumento del poder de compra del dinero en estos términos. Por eso
142
CHAPTER 7. COMPOSICIÓN DE TASAS
se elije un perı́odo base, generalmente el año que se determina la estructura de
ponderaciones del ı́ndice, y se le asigna al valor base de 100.
Por ejemplo el IPC base 1999=100 mide la evolución de los precios de los
bienes y servicios que consumen los hogares residentes en el aglomerado Gran
Buenos Aires. El conjunto de bienes y servicios cuyos precios son recopilados
para el cálculo del IPC constituye la canasta del ı́ndice, que es representativa de
los gastos de consumo de los hogares residentes en la Ciudad de Buenos Aires
y en 24 partidos del Gran Buenos Aires (GBA). El IPC no considera todos
los gastos de los consumidores que tienen que ver con el mantenimiento de su
nivel de vida. Excluye, por ejemplo, los pagos de intereses y amortizaciones de
préstamos, y los impuestos no incluidos en los precios de los bienes.
Con el transcurso del tiempo, el conjunto de bienes y servicios considerados
en los ı́ndices de precios pueden ir perdiendo representatividad. Los hogares van
cambiando su estructura de consumo: dejan de consumir determinados bienes o
servicios o los reemplazan por otros; los productores van modificando los tipos de
bienes que ofrecen; cambian las caracterı́sticas de las viviendas que se construyen
y en las técnicas empleadas en la construcción de las mismas, ect. Por estos
cambios los ı́ndices van perdiendo su capacidad para representar la realidad
y se vuelve necesario modificar su base. Por ejemplo el IPC base 1974=100
consideraba sólo los hogares residentes en el GBA cuyo tamaño oscilaba entre 2
y 7 miembros, que percibieran un ingreso familiar entre $ 250 y $ 2 500 (pesos
ley 18.188 de 1970) y cuyo jefe de hogar fuera una asalariado de la industria o el
comercio. Con el transcurso del tiempo, esa población dejó de ser representativa
del conjunto de los hogares del GBA: hacia 1980, sólo el 20% de los hogares
del GBA reunı́a esas caracterı́sticas. Por eso en la revisión de 1988 del IPC
la población de referencia fue ampliada para incluir los hogares de 2 o más
miembros, sin importar su nivel de ingresos, ni el perfil del jefe del hogar. El
IPC se empezó a elaborar en 1914, y su base de cálculo fue actualizada 7 veces
desde entonces (1914, 1943, 1960, 1974, 1988, 1999 y 2008).
Un ı́ndice de precios puede ser usado para calcular la inflación o deflación
de un perı́odo de tiempo, y el valor real de un monto nominal a un momento
dado para un sector determinado de la economı́a.
Definición 7.70 DEFINICION DE INFLACION
Ejemplo 7.71 Calcular la inflación del mes de enero de 2008.
Para hallar inflación de un mes dado, calculamos la tasa de variación entre
IPC de mes anterior, y el IPC del mes en cuestión:
π 2002
=
=
=
enero
diciembre
IP C2008
− IP C2007
diciembre
IP C2007
204.37 − 202.49
202.49
0.00922844
7.6. ÍNDICE DE PRECIOS
143
Una inflación del 0.922844% (¿!). Esto quiere decir en promedio los bienes y
servicios aumentaron casi un 1% en enero de 2008, esto no implica que no haya
productos que aumentaron más y otros que aumentaron menos.
Ejercicio 7.72 Completar la siguiente tabla con la inflación mensual de 20XX
20
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
Mes
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
Octubre
Noviembre
Diciembre
tasa de inflación
Ejemplo 7.73 Calcular la inflación anual para el consumidor promedio durante el año 2002.
Para hallar inflación de un año, calculamos la tasa de variación entre IPC
de diciembre el año anterior, y el IPC de diciembre año en cuestión:
π 2002
=
=
=
diciembre
diciembre
IP C2002
− IP C2001
diciembre
IP C2001
137.57 − 97.60
97.60
0.40953
La inflación del 2002 fue casi un 41%.
Ejercicio 7.74 Completar la siguiente tabla con la inflación anual de 1997 a
144
CHAPTER 7. COMPOSICIÓN DE TASAS
2009. De una estimación (personal) para la inflación de 2010
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
Años
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
tasa de inflación
Ejemplo 7.75 Calcular la inflación anual para la construcción durante el año
2002.
Para hallar inflación de un año, calculamos la tasa de variación entre ICC
de diciembre el año anterior, y el ICC de diciembre año en cuestión:
π construcción
2002
=
=
=
diciembre
diciembre
ICC2002
− ICC2001
diciembre
ICC2001
134.2 − 95
95
0.41263
Por lo que la inflación para la construcción fue ligeramente superior a la inflación para el consumidor medio.
Ejemplo 7.76 Hallar la inflación total desde mayo de 2003 hasta marzo de
2004.
Para hallar inflación de un perı́odo de tiempo dado, calculamos la tasa de
variación entre IPC de mes anterior al inicio del perı́odo, y el IPC del último
mes del perı́odo de tiempo en cuestión:
π mayo de 2003 a marzo de 2004
=
=
=
marzo
abril
IP C2004
− IP C2003
abril
IP C2003
144.20 − 141.07
141.07
0.022188
Ejercicio 7.77 Calcular la inflación del mes de octubre de 2001.
Ejercicio 7.78 Calcular la inflación del mes de junio de 2006.
7.6. ÍNDICE DE PRECIOS
145
Ejercicio 7.79 Hallar la inflación total desde julio de 2000 hasta septiembre
de 2005.
Ejercicio 7.80 Hallar la inflación total desde agosto de 2004 hasta enero de2006.
Ejercicio 7.81 Si la inflación del més de febrero de 2008 fue del 0.9% ¿Cuanto
febrero
?.
vale el IP C2008
Al tener en cuenta la inflación se suele hablar de valores nominales y valores
reales.
Definición 7.82 Un valor nominal es una cantidad dada de dinero a una
fecha determinada.
Por ejemplo $ 500 pesos hoy, $ 100 000 el 16 de ocubre de 1995, etc.
Definición 7.83 Dada una canasta de bienes y servicios, cada valor nominal
tiene asociado un valor real igual a la cantidad de canastas que se pueden
adquirir con el nominal dado.
Ejemplo 7.84 En enero de 1996 ganaba $ 860, en enero de 2008 gané $ 2 750.
En principio parece que en enero de 2008 estoy ganando tres veces más. ¿Es esto
correcto?.
En términos nominales si, pero en términos reales, i.e., en términos de la
cantidad de bienes y servicios que puedo adquirir, el razonamiento anterior es
completamente erróneo. Para analizar el poder adquisitivo de un valor nominal
en el tiempo, hay que considerar cuantas canastas de bienes se pueden adquirir
con ese nominal en el momento en cuestión:
enero
En enero de 1996 gané $ 860 y cada canasta costaba IP C1996
= 100.9494.
Por lo que podı́a adquirir
860
= 8.5191 canastas.
100.9494
Es decir: $ 860 en enero de 1996 tenı́an un valor real de 8.5191 canastas.
enero
En enero de 2008 gané $ 2 750 y cada canasta costaba IP C2008
= 204.37.
Por lo que podı́a adquirir
2750
= 13.456 canastas.
204.37
Es decir: $ 2 750 en enero de 2008 tenı́an un valor real de 13.456 canastas.
Por lo que en términos reales, en enero de 2008 podı́a consumir casi un 60%
más que en enero de 1996, y no tres veces más (200%). Es decir, estoy mejor,
pero no tanto como se podı́a creer en un principio.
Por lo tanto cuando hablemos de términos reales, debemos pensar en la
cantidad de canastas que podemos adquirir.
146
CHAPTER 7. COMPOSICIÓN DE TASAS
Para realizar una analisis dimensional debemos considerar que el IPC tiene
como unidades
$
canastas
Los IPC sirven para mover en el tiempo el poder adquisitivo real de un
nominal de dinero.
Ejemplo 7.85 En julio de 2001, ganabamos $ 1 500 por mes. Suponiendo que
nuestros ingresos se mantienen constantes en términos reales, cuanto ganabamos
en octubre de 2007.
De nuevo la solución pasa por hallar el número de canastas. En julio de 2001,
ganabamos $ 1 500, y una canasta de bienes “costaba”
julio
IP C2001
= 98.86
Por lo que podı́a adquirir
1500
= 15.173 canastas
98.86
Ahora, en octubre de 2007 cada canasta costaba
octubre
IP C2007
= 198.93
Mantener costante los ingresos en términos reales, significa que debo ser capaz
de adquirir la misma cantidad de canastas. Por lo que en octubre de 2007 debo
ganar
15.173 · 198.93 = 3018.4 pesos
Ejercicio 7.86 En febrero de 2003, pague $ 2 por un café con medialunas en el
buffet de la Universidad. ¿Cuánto deberı́a costar aproximadamente ese mismo
café con medialunas en octubre de 2007?
Ejemplo 7.87 El 15 de agosto de 2007 compramos una heladera por $ 2 100,
cuanto hubieramos pagado (aproximadamente) en febrero de 2003 por la misma
heladera (suponiendo que los precios de los electrodomésticos evolucionaron al
ritmo del IPC).
Simplemente debemos ver cuantas canastas son equivalentes al precio de la
heladera.
En agosto de 2007 una canasta costaba
agosto
IP C2007
= 196.01
Por lo tanto el costo de la heladera era equivalente a
2100
= 10.714 canastas.
196.01
7.7. INFLACIÓN
147
Por lo tanto hacen falta 10.714 canastas para comprar la heladera, i.e., esta
heladera cuesta en términos reales 10.714 canastas, cualquiera sea el momento
del tiempo. Como en febrero de 2003 cada canasta costaba
febrero
IP C2006
= 172.80
En febrero de 2003 habrı́amos necesitado aproximadamente
10.714 · 172.80 = 1851.40 pesos
para comprar la misma heladera.
SECCIÓN SOBR ELA CONSTRUCCIÓN DE
INDICERS DE PRECIOS... PROPONER QUE
EL ALUMNO CONSTRUYA SU PROPIO INDICE DE PRECIOS.
Ejercicio 7.88 En julio de 2007 compré mi primer auto (0 Km) por $ 42 700.
¿Cuánto hubiera pagado (aproximadamente) en agosto de 2002 por un auto
similar?
Ejercicio 7.89 Al pedir préstados $ 2 500 el 1ero. de enero de 2002, nos comprometimos a devolver el montante más unos intereses reales de 8% anual.
¿Cuánto debemos devolver el 1ero. de enero de 2004?
Ejercicio 7.90 Nuestra madre nos prestó a principio de julio de 2003 $ 20 000,
a principios de abril de 2005 le devolvemos a nuestra santa madre los $20 000
que gentilmente nos présto. ¿Cuánto deberı́amos haberle devuelto por lo menos
a la pobre santa?
Ejercicio 7.91 Continuación del ejercicio (7.105) de la sección anterior:
1. Calcule la inflación entre marzo de 2001 y abril de 2008.
2. ¿Cuál fue el porcentaje nominal de aumento de su sueldo?
3. Dar la TEM nominal de aumento de su sueldo.
4. Si en abril de 2008 Ud. ganó $ 2 130, ¿Cuál fue su sueldo en marzo de
2001?
7.7
Inflación
Suponga cuando cumplio 20 años, su padre le regala $ 1000 en bonos del estado
que pagan un 13% anual y vencen en 45 años. Si bien ahora ud. no puede usar
el dinero, cuando venzan, los bonos rendiran $ 244 641.40 pues
45
1000 (1 + 0.13)
= 244641.4019 ,
148
CHAPTER 7. COMPOSICIÓN DE TASAS
La mala noticia es que todo costará mucho más caro. Por ejemplo, si los precios
de los bienes y servicios suben también a un 13% anual cuando ud. tenga 65
años, i.e., 45 años después de recibir los bonos, podrá comprar ”lo mismo” que
podı́a comprar con $ 1000 cuando tenı́a 20 años. En esta situación se dice que
un sentido “real”, no se ha ganado ningún interés.
El ejemplo anterior muestra que si deseamos tomar decisiones financieramente adecuadas a largo plazo, debemos tener en cuenta la inflación, y no sólo
los intereses.
Definamos pues, que entenderemos por inflación
Definición 7.92 Llamaremos inflación a la tasa con que varı́a el nivel de precios de una canasta dada de bienes y servicios de una economı́a a lo largo de un
perı́odo de tiempo determinado. Una tasa de inflación p-perı́odica será denotada
π (p)
Observe que esta definición de tasa de inflación es un poco más amplia que la
habitual: aumento porcentual del nivel de precios en un perı́odo dado de tiempo.
En el caso de ser positiva nuestra tasa de inflación, ambas nociones coinciden.
Pero nuestra inflación puede ser negativa, es lo que se conoce como deflación:
reducción porcentual del nivel de precios.
Al tener en cuenta la inflación se suele hablar de tasas nominales y tasas
reales. La tasa de interés nominal es la tasa efectiva denominada en pesos, o
cualquier otra moneda. El aumento del poder adquisitivo es la tasa de interés
real. Usaremos i para denotar tasas nominales y r para denotar tasas reales.
Nota 7.93 En esta sección la término nominal tiene un sentido diferente del
usado anteriormente. Para evitar confusiones recalcamos que todas las tasas
usadas serán efectivas.
Ejemplo 7.94 Suponga que dispone de $ 1 000 hoy, y que además la canasta
de bienes y servicios básica cuesta hoy $ 245. Si el banco le paga una TEA
del 9.5% (una tasa nominal) y inflación esperada del 6.1% anual. ¿Cuál es el
rendimiento real a un año que le ofrece el banco?
Hoy tiene $ 1000, y como la canasta de bienes y servicios hoy cuesta $ 245,
hoy su poder adquisitivo real es de
1000
= 4.0816
245
canastas de bienes y servicios.
Al cabo de un año sus $ 1 000 se transforman en $1 095 pues
1000 (1 + 0.095) = 1095.
Mientras que una canasta de bienes y servicios pasa a costar
245 (1 + 0.061) = 259.95,
7.7. INFLACIÓN
149
Por lo que su poder adquisitivo al cabo de un año es
1095
= 4.2123
259.95
Luego la tasa de interés real es la que convierte nuestro poder adquisitivo de
4.0816 canastas en 4.2123 canastas al cabo de un año:
4.0816 (1 + r)
=
r
=
r
=
4.2123
4.2123
−1
4.0816
0.032022
La tasa real es del 3.2022% anual, y no del 3.4% = 9.5% − 3.1%, como se podrı́a
haber supuesto.
Volvamos a plantear el problema anterior en términos generales: al comienzo
de un perı́odo de t años, se dispone de una cantidad C de dinero y el costo de
la canasta de bienes y servicios básicos es b, si nos pagan una tasa nominal i(p)
y la inflación esta dada por una tasa π (p) , tenemos que la tasa real r(p) es la
que tranforma el poder aquisitivo al inicio del perı́odo en el poder adquisitivo
al final del mismo
pt
pt
C 1 + r(p)
C
(p)
=
1+r
pt
b
b 1 + π (p)
Simplificando y reordenando llegamos a famosa fórmula de Fisher
1 + r(k) 1 + π (k) = 1 + i(k) .
(7.25)
O despejando la tasa real
i(k) − π (k)
.
(7.26)
1 + π (k)
La fórmula de Fisher es independiente del perı́odo de tiempo considerado, el
monto disponible C y el precio b de la canasta de bienes y servicios básicos.
r(k) =
Nota 7.95 De la forma despejada de la fórmula de Fisher se puede ver que
cuando la tasa de inflación es baja, la diferencia entre la tasa nominal y la tasa
de inflación da una buena aproximación para la tasa real.
Ejemplo 7.96 ¿Cuál es la tasa de interés real anual si la tasa nominal es una
TEA del 12.9% y la tasa de inflación es del 7.3% al año?
Usando la fórmula de Fisher:
(1 + r) (1 + 0.073) = 1 + 0.129,
de donde
r
1 + 0.129
−1
1 + 0.073
= 0.05219
=
150
CHAPTER 7. COMPOSICIÓN DE TASAS
Ejemplo 7.97 El Sr. Elias cobrará una beca de $ 10.000 dentro de 6 meses.
Si la inflación mensual estimada es del 1,7 % mensual. ¿Cuál es el valor en
términos del poder adquisitivo al dı́a de hoy de esos $ 10.000 dentro de 6 meses?
Llamemos p0 al precio de la canasta de bienes y servicios al dı́a de hoy. El
precio de la canasta de bienes y servicios dentro de 6 meses será
p6 = p0 (1 + 0, 017)
6
Con $ 10.000 podemos comprar dentro de 6 meses la siguiente cantidad de
canastas:
$10.000
$10.000
=
6
p6
p0 (1 + 0, 017)
Para comprar hoy la misma cantidad de canastas necesitamos una cantidad x
de dinero tal que
x
10.000
=
6
p0
p0 (1 + 0, 017)
de donde concluimos que
x=
10.000
(1 + 0, 017)
6
= 9038, 040487
Esto nos indica que con $ 10.000, dentro de 6 meses, podremos comprar aproximadamente lo mismo que hoy podrı́amos comprar con $ 9.038,040487.
Ejemplo 7.98 El Sr. Adrián guardo $ 5.000 es un lugar secreto, y luego se
olvido de donde habia puesto el dinero. Al cabo de 5 meses los encontro en el
bolsillo de un viejo saco. Si la inflación mensual durante esos 5 meses fue
inflación mensual
π1
π2
π3
π4
π5
tasa porcentual
1, 8
2, 3
3.1
1.9
2.5
Se pide
1. Calcular el valor de estos $ 5.000, en términos de pesos de hace 5 meses.
2. Calcular el poder de compra de estos $ 5000, hace 5 meses en términos de
pesos de hoy.
Con estos $ 5.000 disponibles ahora, podemos adquirir lo mismo (casi lo
mismo) que con $ 4.458,5 hace 5 meses pues
$ 5.000
(1 + π 1 ) (1 + π 2 ) (1 + π 3 ) (1 + π 4 ) (1 + π 5 )
=
=
=
$ 5.000
(1 + 0, 018) (1 + 0, 023) (1 + 0, 031) (1 + 0, 019) (1 + 0, 0
$ 5.000
1, 12145054517
$ 4.458, 51136
7.7. INFLACIÓN
151
Es decir, $ 5.000 hoy valen (aproximadamente) lo mismo que $ 4.458,5 pesos
de hace 5 meses.
Por otro lado, con $ 5.000 hace 5 meses el Sr. Adrián podı́a comprar bienes
y servicios equivalentes (aproximadamente) a los que puede adquirir hoy con $
5.607,25 pues
$ 5.000 (1 + π 1 ) (1 + π 2 ) (1 + π 3 ) (1 + π 4 ) (1 + π 5 ) = $ 5.000·1, 12145054517 = $ 5.607, 252726
Es decir,los $ 5.000 de hace seis meses son equivales, i.e.,tienen el mismo poder
de compra, que $ 5.607,25 pesos de hoy.
Los ejemplos anteriores nos dicen que si queremos saber el valor en términos
de pesos de hoy, o pesos constantes (expresión que significa: pesos con el
mismo poder de compra que el peso hoy) de una cantidad futura de dinero,
debemos actualizarlos a la tasa de inflación dada (si es conocida). En general,
dada una tasa de inflación p-perı́odica π (p) , el valor al dı́a de hoy de un capital
C disponible dentro de t años es
C
1 + π (p)
pt
(7.27)
Correspondientemente, si queremos saber el valor en pesos de hoy de una cantidad pasada de dinero, debemos capitalizarlos a la tasa de inflación dada (si es
conocida). En general, dada una tasa de inflación p-perı́odica π (p) , el valor al
dı́a de hoy de un capital C disponible hace de t años es
pt
C 1 + π (p)
(7.28)
Ejercicio 7.99 ¿Cuál es la tasa de interés real mensual si la tasa nominal es
una TEM del 1.9% y la tasa de inflación mensual es 1.4%?
Ejercicio 7.100 ¿Cuál es la tasa de interés real anual si la tasa nominal es
una TEM del 0.9% y la tasa de inflación mensual es 1.2%?
Ejercicio 7.101 ¿Cuál es la tasa de interés real anual si la tasa nominal es
una tasa efectiva trimestral del 10% y la tasa de inflación diaria es del 0.04%?
Ejercicio 7.102 Si un banco nos paga una TEA del 25.5% y la inversión rinde
en términos reales sólo un 5.6% al año, ¿Cuál es la tasa anual de inflación?
Ejercicio 7.103 Al sacar un préstamo, el banco A nos cobra una TEM fija
del 2.3%, mientras que el banco B, nos cobra una tasa efectiva mesual variable:
π (12) + 0.011. Se pide decidir donde conviene obtener un crédito si
1. La inflación anual se estima en 8%.
2. La inflación anual se estima en un 21%.
3. Hallar la tasa de inflación de equilibrio: la tasa de inflación esperada que
nos hace indiferentes entre el banco A y el banco B.
152
CHAPTER 7. COMPOSICIÓN DE TASAS
Ejercicio 7.104 En la siguiente tabla se da
un año dado
Mes
1) Enero
2) Febrero
3) Marzo
4) Abril
5) Mayo
6) Junio
7) Julio
8) Agosto
9) Septiembre
10) Octubre
11) Noviembre
12) Diciembre
la tasa de inflación mes a mes de
Tasa
1.1%
2.3%
0.7%
0.5%
0.8%
0.95%
1.2%
1.4%
1.7%
1.6%
2.1%
2.5%
Se pide
1. Hallar la tasa de inflación anual y la mesual equivalente a esta.
2. Hallar la tasa de inflación mensual promedio. Comparar con la tasa mesual
hayada en el item anterior.
3. Si un banco paga un 2.5% mensual, cual es la tasa real que paga el banco
cada mes.
4. Calcular el rendimiento nominal y real de colocar $ 5 000 en dicho banco
desde el 1ero de enero hasta el 31 de agosto.
5. Si un televisor costó $ 1 870 en Noviembre, ¿Cuánto costaba en abril?
6. En enero un obrero cobraba $ 750 al mes, si en diciembre este mismo
obrero cobraba $ 875. ¿En términos reales esta mejor o peor?. Dar el tasa
de variación real del sueldo del obrero.
7. Si deseamos obtener una retabilidad real del 8% anual, de cuanto debe ser
la tasa anual nominal de rendimiento de una inversión.
8. Otro banco se compromete brindar una rentabilidad real de 1.5% mensual.
¿Cuáles son las tasas mensuales que ofrece?. Dar la TEA real que ofrece
el banco.
9. En que banco conviene invertir nuestros ahorros cada mes, ¿y de manera
anual?
10. Ud en enero de este saco un préstamo de $ 10 000. Le cobran un 12% anual
y debe devolver el nominal más los intereses en enero del año siguiente.
¿Cuál fue la tasa real del préstamo?
7.8. INDEXACIÓN
153
Ejercicio 7.105 En marzo de 2001 su sueldo mensual le alcanzaba para comprar 1 Televisor y medio. En Abril de 2008 su sueldo le alcanza para comprar
2.1 Televisores.
1. ¿Cuál fue el porcetaje de aumento de su sueldo?.
2. Suponiendo que su sueldo aumentó un porcentaje fijo cada mes, ¿Cuál fue
la TEM de aumento?
3. ¿Las tasas anteriores son reales o nominales?
poner más ejercicios.... del estilo de
los últimos ejemplos
Ejercicio 7.106
Nota 7.107 La inflación (positiva) tiene causas muy complejas y variadas de
acuerdo con las polı́ticas económicas implementadas en cada paı́s. Sin embargo
un fénomeno común a todos los procesos inflacionarios es un aumento del circulante (monedas y billetes) sin el aumento equivalente en la producción de bienes
y servicios. Cuando aumenta el circulante, la gente tiene más dinero en sus bolsillos para gastar, lo que aumenta la demanda de bienes y servicios en general, si
esto no se corresponde con un aumento de la oferta, los precios inevitablemente
suben.
La deflación (inflación negativa), es un fenónemo menos habitual. La última
deflación en USA se dio en 1955 y en Argentina hubo deflación en 1999 (−1.810449933%),
en 2000 (−0.7337073802%), y en 2001 (−1.543427822%). Las deflaciones prolongadas (uno o más años) son sı́ntoma de perı́odos de contracción econónica
(depresión).
7.8
Indexación
7.9
Composición de tasa en el sistema continuo
Dadas un grupo n de tasas nominales (positiva o negativa) J1 , J2 , . . . , Jn de
aplicación simultánea, cuyas tasas efectivas p-perı́odicas asociadas son
(p)
ik =
(p)
(p)
Jk
pk
(p)
El error que cometemos al usar i1 + i2 + · · · + in intuitivamente disminuye
al aumentar la frecuencia de capitalización:
(p)
(p)
i1 + i2 + · · · + in(p) ≈ a la tasa real
si p es grande.
154
CHAPTER 7. COMPOSICIÓN DE TASAS
Dadas n tasas nominales J1 , . . . , Jn de aplicación simultánea sobre un capital
C0 por unos t años. Consideremos como evoluciona nuestra aproximación
pt
Jn
J1
C0 1 +
+ ··· +
p
p
a medida que aumentamos la frecuencia de capitalización:
pt
J1
Jn
lim C0 1 +
+ ··· +
p→∞
p
p
=
pt
J1 + · · · + Jn
lim C0 1 +
p→∞
p
= C0 e(J1 +···+Jn )t
Poner dibujo!!!!
Esto sugiere que en capitalización continua la aplicación de simultánea de
dos o más tasas equivale a sumar las mismas: Dadas n tasas nominales continuas
J1 , . . . , Jn todas de aplicación simultánea sobre un capital C0 , el capital total
acumulado al cabo de t años es
Ct = C0 e(J1 +···+Jn )t
Esta nos permite demostrar formalmente la fórmula (7.1). Dado un grupo
(p) (p)
(p)
de n tasas efectivas p-perı́odicas i1 , i2 , . . . , in que actúen simultáneamente
sobre un capital C0 . El capital Ct acumulado al cabo de t años se puede obtener,
al plantear la situación en capitalización compuesta. Para hacer esto convertimos
las tasas efectivas compuestas en tasas nominales continuas equivalentes:
p
(p)
1 + ik
= eJk para k ∈ {1, . . . , n}
de donde
p
(p)
Jk = ln 1 + ik
para k ∈ {1, . . . , n}
Luego
Ct
= C0 e(J1 +···+Jn )t
p
p
(p)
ln 1+i1
+···+ln(1+i(p)
t
n )
= C0 e
pt
pt
(p)
· · · 1 + i(p)
= C0 1 + i1
n
Poner ejercicios!!!!! al menos unos 4 o 5.
Chapter 8
Rentas
8.1
Rentas generales
A lo largo del resto del libro utilizaremos capitalización compuesta como ley
financiera por defecto, salvo que explı́citamente se diga lo contrario. Esto se
corresponde uso predominante en Argentina del sistema compuesto.
El siguiente ejemplo muestra la situación tı́pica que deseamos analizar ahora
Ejemplo 8.1 Se obtiene de un banco un préstamo por $ 125.000 a pagar en
10 años, en cuotas mesuales consecutivas e iguales, pagando la primera dentro
de un mes. Si el banco nos cobra una TEM del 0,34 %, ¿cuál es el monto de la
cuota mensual que debemos pagar?
$ 125.000 =
120
X
k=1
C
(1 + 0, 0034)
0
k
C
C
C
C
C
1
2
3
119
120
Hoy
En todo préstamo lo que debemos pagar debe ser financieramente equivalente
al desembolso del préstamo (a la tasa pactada). Para hallar el monto que se debe
pagar al banco cada mes es conveniente plantear la correspondiente equivalencia
financiera. Trabajaremos con capitalización compuesta, y como da lo mismo usar
155
156
CHAPTER 8. RENTAS
una u otra fecha focal, usaremos el origen como tal:
$ 125.000 =
C
C
C
+
+ ··· +
120
(1 + 0, 0034) (1 + 0, 0034)2
(1 + 0, 0034)
de donde podemos despejar C
C=
125.000
1
1
1
+ ··· +
+
2
120
(1 + 0, 0034) (1 + 0, 0034)
(1 + 0, 0034)
Es claro que serı́a muy útil disponer de una fórmula para calcular
1
1
1
+
+ ··· +
120
(1 + 0, 0034) (1 + 0, 0034)2
(1 + 0, 0034)
(que no sea realizar los 120 cocientes y luego sumarlos).
La situación del ejemplo anterior, con alguna variación, es suficientemente
frecuente en la actividad económica (sueldos, alquileres, seguros, préstamos,
servicios, etc.) como para desarrollar fórmulas adecuadas para el manejo de
sucesiones de capitales disponibles a lo largo del tiempo.
Definición 8.2 Una renta (finita) es una sucesión de n capitales C1 , C2 , . . . , Cn ,
llamados términos, disponibles a los momentos t1 < t2 < · · · < tn (estamos
asumiendo que n es un entero positivo).
De una renta tı́picamente nos interesa calcular VA (to ), su valor actual a
un momento to dado, y V F (tf ), su valor final a un momento tf dado, con
to ≤ t1 < · · · < tn ≤ tf
Capitalización
to
VA (to )
C1
C2 C3
C4
Cn−1
Cn
t1
t2
t4
tn−1
tn
t3
VF (tf )
tf
Actualización
Dada una tasa de interés p-perı́odica i(p) , el valor actual (al momento to ) de
una renta consistente de n capitales C1 , C2 , . . . , Cn disponibles a los momentos
t1 < t2 < · · · < tn (usando p-perı́odos para medir el tiempo), es igual a la suma
8.1. RENTAS GENERALES
157
de los valores actuales al momento to de cada uno de los términos que componen
la renta
VA (to )
=
=
n
X
k=1
n
X
k=1
to −tk
Ck 1 + i(p)
Ck
t −to
1 + i(p) k
(8.1)
(8.2)
(8.3)
Ya que todas las diferencias to − tk , con k ∈ {1, . . . , n}, no positivas.
Similarmente, el valor final de la renta al momento tf es igual a la suma
de los valores (capitalizados) al momento tf de cada uno de los términos de la
renta
n
tf −tk
X
VF (tf ) =
Ck 1 + i(p)
(8.4)
k=1
en este caso todas las diferencias tf − tk , con k ∈ {1, . . . , n}, son no negativas.
Al capitalizar el valor actual VA (to ) de la renta al momento to durante tf −to
p-perı́odos a la tasa p-perı́odica i(p) obtenemos el valor final V !F (tf ) de la renta
!
n
tf −to
to −tk tf −to
X
VA (to ) 1 + i(p)
=
Ck 1 + i(p)
1 + i(p)
k=1
=
=
n
X
k=1
n
X
to −tk tf −to
Ck 1 + i(p)
1 + i(p)
tf −tk
Ck 1 + i(p)
k=1
= VF (tf )
Obviamente, si actualizamos VF (tf ) unos tf − to p-perı́odos obtenemos el valor
actual
VF (tf )
t −to = VA (to )
1 + i(p) f
Esto nos dice que si hallamos una expresión para el valor actual de una renta,
automáticamente diponemos de una expresión para el valor final de la misma y
viceversa.
Nota 8.3 Una notación más precisa serı́a
n
X
to −tk
V A to , t1 , . . . , tn , C1 , . . . , Cn , n, i(p) =
Ck 1 + i(p)
k=1
pero en general, como los valores de t1 , . . . , tn , C1 , . . . , Cn , n, i(p) serán claros del
contexto preferimos usar simplemente V A (to ) o inclusive sólo V A (si también
es claro del contexto el valor de to ).
158
CHAPTER 8. RENTAS
Es claro que para encontrar fórmulas que simplifiquen el cálculo de (8.3) y
(8.4), tanto la sucesión de capitales como la sucesión de momentos deben poseer
ambas cierta regularidad.
La regularidad en la sucesión de momentos se consigue al imponer que la
distancia temporal entre dos términos consecutivos (entre los momentos a los
que se imponen los mismos) se mantenga constante a lo largo de la renta:
tk+1 − tk = cte para 1 ≤ k ≤ n − 1.
En la mayorı́a de los casos esta distancia temporal será un mes, pero puede ser
una cantidad cualquiera, pero fija, de p-perı́odos (por ejemplo 15 dı́as, mes y
medio, un trimestre, etc.) donde p esta dado por la frecuencia de capitalización
de la tasa efectiva i(p) que actua sobre la renta.
Con respecto a la regularidad sobre los montos de los términos, estudiaremos cuatro casos: constantes, variables en progresión aritmética y variables en
progresión geométrica.
8.2
Rentas constantes
Consideremos una renta de n términos a una tasa p-perı́odica i(p) . Analizaremos
el caso donde todos los términos (capitales) de la renta son iguales
C1 = C2 = · · · = Cn = C
de ahi el nombre de rentas constantes.
Actualización
V A (to )
to
C
C
C
C
C
1
2
3
n−1
n
Con esta regularidad (8.3) se puede reescribir
V A (to ) = C
n
X
k=1
1
1+
t −to
i(p) k
(8.5)
Si consideremos que la sucesión temporal de las imposiciones tiene un paso
constante unitario de un p-perı́odo (por ejemplo, si la tasa es mensual, tenemos
una sucesión de meses)
tk+1 − tk = 1 p-perı́odo, para 1 ≤ k ≤ n − 1
o lo que es lo mismo
tk = t1 + (k − 1) para 1 ≤ k ≤ n − 1
8.3. RENTAS VENCIDAS O POSPAGABLES
159
Luego la ecuación (8.5) toma la forma
V A (to )
=
=
C
C
n
X
k=1
n
X
k=1
1
1+
t −to
i(p) k
1 + i(p)
1
t1 +k−to −1
(Recordar que to está medido en p-perı́odos).
8.3
Rentas vencidas o pospagables
El modelo de rentas que vamos a estudiar ahora se corresponde perfectamente
con situaciones tales como el cobro de un sueldo, o el pago de algunos servicios
(luz, gas, etc.). Primero se trabaja o brinda el servicio, y luego se realizan las
imposiciones correspondientes (pagos o cobros). Es decir, las imposiciones se
hacen al final del cada perı́odo. Por este motivo estas rentas reciben el nombre
de rentas vencidas o pospagables (En Argentina y Latinoamérica en general
se habla de rentas vencidas, en España de rentas pospagables).
El valor actual corresponde calcularlo un perı́odo de tiempo antes de la
imposición del primer capital:
to = t1 − 1
Esto es claro a partir del ejemplo del cobro de un sueldo: uno comienza a trabajar
en el momento to y recién recibe el primer pago en el momento
t1 = to + 1
El compromiso asumido en la operación financiera comienza en to .
El valor final, por otro lado, corresponde calcularlo al mismo momento de la
imposición del último capital, ya que en ese momento términa el compromiso
asumido:
tf = tn
Comenzaremos analizando la situación to = 0 y por lo tanto
t1 = 1, t2 = 2, . . . , tn = n
V A(to )
Actualización a la tasa i(p)
C
C
C
C
C
C
0
1
1 p-perı́odo
2
3
n−2
n−1
n
Inicio
Final
160
CHAPTER 8. RENTAS
En este caso la ecuación (8.6) toma la forma
V A (0) = C
n
X
k=1
1
1 + i(p)
V F (n) = V A(0) 1 + i(p)
n
Actualización
V A(0)
0
k .
V F (n)
C
C
C
C
C
C
1
2
3
n−2
n−1
n
Capitalización
Ahora todo el problema se reduce a encontrar un fórmula cerrada para la
expresión
n
X
k=1
1
1 + i(p)
k .
Usando el hecho que (8.6) es una serie geométrica, por (B.6)
n
X
k=1
1
1 + i(p)
k
=
=
=
n−1
X
1
1
(p)
1 + i k=0 1 + i(p) k
1
n
1−
1 + i(p)
1
1
1 + i(p)
1−
1 + i(p)
−n
1 − 1 + i(p)
i(p)
(8.6)
8.3. RENTAS VENCIDAS O POSPAGABLES
V A(0) =
n
X
161
C
k
k=1
0
(1+i(p) )
C
C
C
C
C
1
2
3
n−1
n
V F (n) =
n
X
C 1 + i(p)
k
k=1
Ahora podemos dar la fórmula para calcular el valor actual de una renta
constante vencida (o pospagable) de n términos de monto C a una tasa i(p) que
comienza en el momento 0 y términa en el momento n:
−n
1 − 1 + i(p)
(8.7)
V A (0) = C
i(p)
A partir de (8.7) podemos obtener, como ya señalamos, una expresión para el
valor final de una renta vencida al momento tf = tn = n
n
n
1 + i(p) − 1
(p)
V F (n) = V A (0) 1 + i
=C
(8.8)
i(p)
Nota 8.4 Se debe notar que la última fórmula se puede deducir a partir de
la teorı́a de relaciones recursivas. Consideremos una renta de n términos constantes de monto C a una tasa p-perı́odica i(p) , impuestos consecutivamente
con un paso temporal de un p-perı́odo. Sea V F (k) valor “final” acumulado de
la renta después de imponer el k-ésimo término (con k ∈ {1, . . . , n})
Es claro que el valor final (k + 1)-ésimo es igual al valor final k-ésimo, más
los intereses generados, más el término (k + 1)-ésimo de la renta
V F (k + 1) = V F (k) 1 + i(p) + C
La solución de esta relación recursiva es
V F (k)
=
=
k
1 − 1 + i(p)
h0 (1 + k) + C
1 − 1 + i(p)
k
1 + i(p) − 1
k
h0 (1 + k) + C
i(p)
k
162
CHAPTER 8. RENTAS
donde h0 es una constante que podemos ajustar usando alguna condición inicial.
En nuestro caso es claro que
V F (1) = C
luego
C
= V F (1)
1
1 + i(p) − 1
= h0 (1 + k) + C
i(p)
(p)
+C
= h0 1 + i
1
lo que implica que h0 = 0. Luego
k
1 + i(p) − 1
V F (k) = C
para k ≥ 1
i(p)
Otra condición inicial adecuada resulta del hecho que V F (0) = 0 (no se ha
realizado ninguna imposición al momento cero).
En los problemas de rentas tı́picamente aparecen 4 variables C, i(p) , n y V A
o V F según el caso. El problema tipo es dadas tres de ellas calcular el valor de
la cuarta. Después de un momento de reflexión (y tal vez una cuantas pruebas)
vemos que si n > 5, en general, es imposible despejar i(p) de la fórmula (8.7) o la
fórmula (8.8). Esto implica el uso de métodos númericos para hallar la tasa i(p)
aplicada en una renta dada. Más adelante daremos una breve introducción a los
métodos numéricos de Newton-Raphson y de la secante, pero desde ya queremos
dejar asentado que no nos openemos al uso de soft especı́fico (Maple, Matlab,
Excel, Derive, etc.) o al uso de calculadoras financieras o cientı́ficas para hallar
la tasa asociada a un esquema de renta.
Ejemplo 8.5 Terminemos de resolver el ejemplo (8.1)
Todos los meses, por los próximos 10 años, debemos pagar $ 1.270,32 pues
C
=
=
=
125.000
1
1
1
+
+ ··· +
120
(1 + 0, 0034) (1 + 0, 0034)2
(1 + 0, 0034)
125.000
1 − (1 + 0, 0034)
0, 0034
$1.270, 32
−120
Ejemplo 8.6 Un programa de televisión anuncia un premio $ 300.000, consistente un sueldo fijo a mes vencido de $ 2.500 mensuales durante 10 años.
¿Realmente el premio consiste de $ 300.000?. Si la tasa que ud. puede conseguir
es del 0,85% mensual, que prefiere, el esquema de sueldos o $ 200.000 en efectivo
(en caso de ganar el concurso correspondiente).
8.3. RENTAS VENCIDAS O POSPAGABLES
163
Todo lo que necesitamos saber es el valor actual de este esquema de pagos a
la tasa que ud. puede conseguir:
V A(hoy) = 2.500
1 − (1 + 0, 0085)
0, 0085
−120
= 187.602, 16
Esto nos dice que el premio de “$ 300.000” en realidad hoy vale $ 187.602,16, y
por lo tanto si hoy nos ofrecen $ 200.000 en efectivo deberı́amos aceptarlos (esta
oferta es aún más conveniente si incluimos en el análisis la inflación esperada).
Ejemplo 8.7 Si ud. toma los $ 200.000 del premio y los depósita al 0,85%
mensual, ¿Cuál es el monto que puede retirar del banco mes a mes por los
próximos 10 años?
Poner dibujo!!!!!!!!!!!!!!!!!!!! poner dibujo Rent10!!!
Ahora, lo que conocemos es el valor actual de una renta (vencida) constante
mensual de 120 términos y deseamos saber el importe C de los términos. A
partir de
−n
1 − 1 + i(p)
V A (0) = C
i(p)
podemos despejar fácilmente C:
C=
En particular
C=
V A (0) i(p)
−n
1 − 1 + i(p)
200.000 · 0.0085
1 − (1 + 0.0085)
−120
(8.9)
= 2665.21458
Ejemplo 8.8 Si ud toma los $ 200.000 del premio los depósita al 0,85% mensual, ¿Durante cuánto tiempo podrá extraer mensualmente $ 2.500?
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!
En este caso, de la expresión
C=
V A (0) i(p)
−n
1 − 1 + i(p)
deseamos hallar n. Primero acomodamos un poco las cosas de manera tal que
podamos aplicar logaritmos (este es el procedimiento usual para despejar alguna
variable que aparece en un exponente)
−n
C − V A (0) i(p) = C 1 + i(p)
C − V A (0) i(p)
C
log C − V A (0) i(p) − log C
−n
1 + i(p)
= −n log 1 + i(p)
=
164
CHAPTER 8. RENTAS
de donde obtenemos
log C − log C − V A (0) i(p)
n=
log 1 + i(p)
(8.10)
En particular
n=
log 2.500 − log (2.500 − 200.000 · 0, 0085)
= 134.62001
log (1 + 0, 0085)
Por lo que podriamos retirar $ 2.500 por 134 meses (11 años y dos meses), y al
finalizar aún nos sobrarı́a un poco de dinero en la cuenta (¿Cuánto?).
Ejemplo 8.9 Don Máximo puede ahorrar al final de cada mes $700. La tasa
que puede conseguir es del 0,75% mensual. ¿Cuál es el monto acumulado del
que dispondrá Don Máximo al cabo de 3 años?
poner dibujo!!!!!!!!!!!!!!!!!!!
En este caso debemos hallar el valor final de una renta. Como no sabemos
exactamente cuanto depositará Don Máximo al final de cada mes (pueden ser
$ 700, o $ 754, o $ 800), calcularemos dos valores finales, uno suponiendo que
mes a mes deposita $ 700 y el otro suponiendo que mes a mes deposita $ 800. El
capital acumulado por Don Máximo estará entre estos dos valores. Comencemos
con la renta de $ 700:
60
V F (60) = 700
(1 + 0.0075)
0.0075
−1
= 700 · 75, 4241369253 = 52.796, 89585
Ahora calculemos el valor final de la renta de $ 800
60
V F (60) = 800
(1 + 0.0075)
0.0075
−1
= 800 · 75, 4241369253 = 63.339, 30954
Es decir, Don Máximo dispondrá al cabo de 5 años de un capital entre $
52.796,90 y $ 63.339.31.
Nota 8.10 El ejemplo anterior muestra porque los factores
−n
n
1 − 1 + i(p)
1 + i(p) − 1
y
i(p)
i(p)
suelen ser llamados multiplicadores. Ellos dan el valor actual (al momento
0) y el valor final (al momento n), respectivamente, de una renta unitaria
(C = $ 1), de n términos consecutivos con paso unitario p-perı́odico (iniciada
al momento 1 y finalizada al momento n) a una tasa p-perı́odica i(p)
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!!!!!!
El nombre de multiplicador proviene del siguiente hecho obvio: el valor actual y el valor final de cualquier renta constante de término C (de n términos
consecutivos con paso unitario p-perı́odico, iniciada al momento 1 y finalizada
al momento n, a una tasa p-perı́odica i(p) ) se calcula mutiplicado C por el correspondiente multiplicador.
8.3. RENTAS VENCIDAS O POSPAGABLES
165
Ejemplo 8.11 Ud desea comprarse un LED de 64”. Cuanto debe ahorrar (al
menos) mes a mes durante los próximos 3 años si el LED cuesta unos $ 26.000,
y la tasa que ud puede conseguir es del 0,4% mensual.
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!!!!!!
En este caso, tenemos una renta de la que conocemos una cota inferior para
el valor valor final de la renta: este no debe ser inferior a $ 26.000, y queremos
determinar el valor de los términos C de la renta
n
1 + i(p) − 1
26.000 ≤ V F (n) = C
i(p)
de donde debemos despejar C
C=
V F (n) i(p)
26.000i(p)
n
n
≥
1 + i(p) − 1
1 + i(p) − 1
(8.11)
por lo tanto en nuestro caso
C≥
26.000 · 0, 004
(1 + 0, 004)
36
−1
= 672, 91079
Por lo que deberemos ahorrar cada mes al menos $ 672,92.
Ejemplo 8.12 Suponga que ud puede ahorrar $ 550 cada mes, y los puede
depositar a un 0,37% mensual. ¿Cuánto tiempo deberá ahorrar para poder comprarse un auto que cuesta unos $ 32.000?
Poner Dibujo!!!!!!!!!!!!!!!!
En este caso, tenemos una renta de la que conocemos una cota inferior para
el valor valor final de la renta: este no debe ser inferior a $ 32.000, y queremos
un n tal que
n
1 + i(p) − 1
32.000 ≤ V F (n) = C
i(p)
despejemos n de la igualdad
V F (n) i(p)
+1
C
log V F (n) i(p) + C − log C
n
1 + i(p)
= n log 1 + i(p)
=
de donde obtenemos
n=
log V F (n) i(p) + C − log C
log 1 + i(p)
En particular, si realizamos el despeje de n partiendo de la desigualdad
log 32.000i(p) + C − log C
n≥
log 1 + i(p)
(8.12)
166
CHAPTER 8. RENTAS
de donde obtenemos
n≥
log (32.000 · 0.0037 + 550) − log 550
= 52.79162
log (1 + 0.0037)
Es decir necesitamos ahorrar al menos 53 meses.
Nota 8.13 Observe (8.7) calcula el valor actual de la renta dada un p-perı́odo
antes de la imposición del primer capital. Por ejemplo si tenemos un renta
bimestral cuyo primer término esta disponible en el mes 5, la fórmula (8.7) nos
da el valor actual de la renta (una cantidad de dinero) al mes 3.
Nota 8.14 El n que aparece en las fórmulas anteriores coincide siempre con el
número de términos de la renta, y como veremos más adelante no tiene porque
coincidir con el perı́odo al que es impuesto el último término.
Las dos observaciones anteriores son importantes a la hora de entender cabalmente el siguiente ejemplo.
Ejemplo 8.15 Ud. esta ahorrando $ 250 al final de cada mes para su jubilación.
En este momento tiene 30 años y espera jubilarse a los 65 años. Después de
retirarse espera vivir hasta los 85 años. ¿Cuánto podrá retirar mes a mes del
banco una vez que se jubile si este le paga una TNA del 6.2%?
En este problema tenemos dos rentas relacionadas: el valor final de la primera
es el valor actual de la segunda.
PONER DIBUJO!!!!!!!!!!!!!!!!!!!!!!!!
Comenzaremos calculando el valor final de la primer renta o renta de ahorro
35·12
0.062
−1
1+
12
= 373039.91
V Fahorro = 250
0.062
12
Esta cantidad de dinero es el valor actual de la renta de jubilación
V Fahorro = V Ajubilación
donde esta igualdad se da a los 420 meses (dentro de 35 años, es decir cuando
tenga 75 años). La segunda renta comienza en el perı́odo 421 y términa en el
perı́odo 660 por lo que el número de términos es
660 − 421 + 1 = 240 = 20 · 12
Ahora
373039.91 = V Ajubilación
−20·12
0.062
1− 1+
12
= Cjubilación
0.062
12
8.3. RENTAS VENCIDAS O POSPAGABLES
167
de donde
Cjubilación = $ 2 715.79
Lo cual no parecı́a tan mal en 2001, pero ya en 2010 era es mucho.
Nota 8.16 Uno de los autores sostiene que la edad mı́nima de jubilación para
el año 2030 rondará los 75 años (para los hombres). También sostiene que las
mujeres deberı́an jubilarse a la misma edad que los hombres.
Ejercicio 8.17 Al comprar una casa se nos ofrecen las siguientes alternativas:
1. Pago al contado hoy de $ 180 000.
2. 120 pagos mensuales de $ 3000 comenzando a pagar dentro de un mes.
¿Cuál es más conveniente para nosotros si la tasa que podemos conseguir es
una TEA del 9%?
Ejercicio 8.18 Su hijo se va a la universidad. Cuánto debe depositarle en diciembre si ud. desea que él pueda extraer $ 850 cada mes durante el resto del
año que viene. Suponer que el banco le paga una TNA del 7.5%.
Ejercicio 8.19 Si su capacidad de ahorro es de $ 650 por mes y puede obtener
una TEA 6.4%. ¿Cuántos meses le tomará formar un capital de al menos $ 50
000?. Suponer que ud deposita el dinero a fin de mes.
Ejercicio 8.20 Ud. desea comprar una moto que cuesta $ 15 000. Si ud. puede
invertir sus ahorros a una TNA del 10%. ¿Cuánto deberá ahorrar por mes para
poder comprar la moto en 18 meses? Suponer que ud deposita el dinero a fin de
mes.
Ejercicio 8.21 Ud ha estado ahorrando al final de cada año $ 3 000 durante
los últimos 15 años en un banco que le paga una TNA del 9.2%. ¿Cuanto podrá
retirar mensualmente durante los próximos 5 años?
Ejercicio 8.22 Ud esta ahorrando $ 350 al final de cada mes para su jubilación.
En este momento tiene 35 años y espera jubilarse a los 65 años. Después de
retirarse espera vivir hasta los 82 años. ¿Cuánto podrá retirar mes a mes del
banco una vez que se jubile si este le paga una TEA del 5%?
Ejercicio 8.23 Como ud. es argentino, sabe que la jubilación que obtenga no
será mucho. Por lo que decide que cuando cumpla 40 años, depositará $ 5 000
en una cuenta de ahorro y cada mes, agregará unos $ 250 a la misma, hasta
que cumpla 65 años. Después esperará hasta 68 años, y luego se dará la gran
vida por unos dos años. ¿Cuánto deberá sacar mes a mes para que la vida loca
le dure hasta los 70 años? Suponer una TEM 0.49%.
Ejercicio 8.24 Don Máximo puede ahorrar al final de cada mes entre 700 y
800 pesos. La tasa que puede conseguir es del 0,85% mensual. ¿Cuál es el monto
acumulado del que dispondrá Don Máximo al cabo de 4 años?
Poner más ejercicios, 2 o 3 de cada
tipo y un par más de rentas relacionadas.
Ejercicio 8.25
168
CHAPTER 8. RENTAS
8.4
Multiplicadores
Ahora estudiaremos un poco el comportamiento de los multiplicadores de valor
actual y de valor final:
−n
n
1 − 1 + i(p)
1 + i(p) − 1
y
i(p)
i(p)
Demostraremos que ambos son crecientes en n y monótonos en i(p) (el primero
es decreciente y el segundo creciente).
Recordemos que los multiplicadores son expresiones compactas de ciertas
sumas (potencialemente largas) que nos dan el valor actual y el valor final de
una renta vencida o pospagable unitaria (C = $ 1) de n términos iniciada en el
momento 0. De hecho el valor actual es

−n
n
 1 − 1 + i(p)
X
1
si i(p) 6= 0
k = 
i(p)
(p)
k=1 1 + i
n
si i(p) = 0
Además (usando L´Hostipal)
1 − 1 + i(p)
i(p)
i(p) →0
−n
lim
−n−1
=n
= lim n 1 + i(p)
i(p) →0
Una observación similar vale para el multiplicador de valor final

n
n k  1 + i(p) − 1
X
si i(p) 6= 0
1 + i(p) =
(p)
i

k=1
n
si i(p) = 0
y similarmente
lim
i(p) →0
n
n−1
1 + i(p) − 1
= lim n 1 + i(p)
=n
(p)
i
i(p) →0
De aqui en más consideremos tasas positivas: i(p) > 0. Bajo este supuesto es
evidente ( financieramente) que para cada n ≥ 2
1 − 1 + i(p)
i(p)
−n
n
1 + i(p) − 1
<n<
i(p)
(8.13)
Esto es ası́ pues al dı́a de hoy, cada término vale menos de un peso (de hecho
mientras mayor sea la tasa i(p) más chico es el valor actual de cada uno de los
términos), y sumar n cantidades más chicas que uno obtenemos menos que n:
1 − 1 + i(p)
i(p)
−n
=
n
X
k=1
1
k < n
1 + i(p)
|
{z
}
<1
8.4. MULTIPLICADORES
169
Por otro lado, el valor de cada término al momento n es mayor que un peso
(de hecho mientras mayor sea la tasa i(p) , más grande es valor al momento n
de cada uno de los términos), y sumar n cantidades cada una mayor que uno,
salvo la última la cual es igual a uno, nos da más que n:
n
n
n−k
1 + i(p) − 1 X =
1 + i(p)
>n
(p)
i
{z
}
k=1 |
>1 si k<n
Poner dibujo!!!!!!!!!!!!!!!!!!!!!
Siguiendo en esta lı́nea de pensamiento, es financieramente obvio que fijado
n, el multiplicador
−n
1 − 1 + i(p)
i(p)
(p)
(p)
es una función estrictamente decreciente de i(p) : si i1 < i2
−n
−n
(p)
(p)
1 − 1 + i1
1 − 1 + i2
>
(p)
(p)
i1
i2
entonces
Esto es fácil de ver en las correspondientes expresiones abiertas, pues el valor
(p)
(p)
actual de cada uno de los términos es menor a la tasa i2 que a la tasa i1 :
para cada 1 ≤ k ≤ n
1
1
k > k
(p)
(p)
1 + i1
1 + i2
luego
−n
(p)
1 − 1 + i1
(p)
i1
=
>
=
n
X
1
k
(p)
k=1 1 + i1
n
X
1
k
(p)
k=1 1 + i2
−n
(p)
1 − 1 + i2
(p)
i2
Por otro lado, fijado n, el multiplicador
n
1 + i(p) − 1
i(p)
(p)
(p)
es una función creciente estrictamente creciente de i(p) : si i1 < i2
n
n
(p)
(p)
1 + i1
−1
1 + i2
−1
<
(p)
(p)
i1
i2
entonces
170
CHAPTER 8. RENTAS
(p)
pues el valor al momento n de cada uno de los términos es mayor a la tasa i2
(p)
que a la tasa i1 : para cada 1 ≤ k ≤ n
(p)
1 + i1
k
k
(p)
< 1 + i2
Similarmente, fijada i(p) , ambos multiplicadores son funciones estrictamente crecientes de n, pues simplemente sumamos más términos.
8.5
8.5.1
Métodos númericos
Método de Newton-Raphson
El método de Newton-Raphson (o simplemente Newton) es uno de los métodos
numéricos más efectivos para resolver el problema
f (x) = 0
Este método funciona muy bien para funciones dos veces diferenciables. Sea p
una raı́z de la ecuación anterior:
f (p) = 0
y supongamos que tenemos una aproximación pk de la raı́z p:
pk ≈ p
por lo que se puede esperar (por la continuidad de f ) que
f (pk ) ≈ 0
Newton-Raphson nos dice que podemos obtener una mejor aproximación partiendo de pk y realizando la siguiente iteración:
pk+1 = pk −
f (pk )
f 0 (pk )
(8.14)
Poner dibujo.
Si bien ni la deducción, ni la convergencia del método son difı́ciles de probar,
remitimos al lector interesado a [?].
Para nuestro caso particular, dada una renta pospagable de valor actual o
inicial V A, de n términos de montante C, deseamos hallar la tasa p-perı́odica
i pactada (no usaremos i(p) pues recargarı́amos de notación las fórmulas de la
sección las cuales de por si son un poco abtrusas).
Poner dibujo
Ahora
−n
VA=C
1 − (1 + i)
i
8.5. MÉTODOS NÚMERICOS
171
Para poder usar Newton, debemos colocar las cosas de la forma f (x) = 0, lo
cual se logra al definir
−n
1 − (1 + i)
−VA
i
El método de Newton requiere la derivada de f respecto de la tasa de interés
h
i
−n−1
−n
ni
(1
+
i)
−
1
−
(1
+
i)
df (i)
f 0 (i) =
=C
di
i2
f (i) = C
En la iteración necesitaremos el cociente f (i) /f 0 (i):
−n
f (i)
f 0 (i)
1 − (1 + i)
−VA
i
h
i
−n−1
−n
ni (1 + i)
− 1 − (1 + i)
C
=
C
=
=
i2
VA
−n
1 − (1 + i) −
i i
C
−n
−n−1
(1 + i) + ni (1 + i)
−1
n
V A (1 + i)
n
(1 + i) − 1 −
i
C
i
ni
n
1+
− (1 + i)
1+i
Luego como la fórmula de iteración es
ik+1 = ik −
f (ik )
, para k ≥ 0
f 0 (ik )
tenemos que


ik+1 = 1 +
1+

n
V A (1 + ik )
n
ik − (1 + ik )

C
 ik
nik
n
1+
− (1 + ik )
1 + ik
(8.15)
esta fórmula recursiva genera una sucesión que converge a la raı́z p buscada. El
criterio habitual de parada, es fijar un nivel de tolerancia ε, y parar cuando el
factor de corrección ff0(i(ikk)) es menor en valor absoluto que ε:
n
V A (1 + ik )
n 1 +
ik − (1 + ik )
C
|ik+1 − ik | = ik < ε
nik
n
1+
− (1 + ik )
1 + ik
Notación 8.26 Aquı́, vı́a algebra obtenemos una fórmula que nos permite plantear
la tabla de Newton-Raphson con sólo tres columnas. Generalmente la tabla de
Newton-Raphson tiene cinco columnas: k, ik , fk , fk0 y ffk0 . La forma general es
k
la usada en rentas prepagables.
172
CHAPTER 8. RENTAS
Ejemplo 8.27 El Sr. Daniel tomó un préstamo por $ 20.000 a devolver en 24
cuotas mensuales consecutivas de $ 2.500. ¿Qué tasa mensual esta pagando?
Utilizaremos Newton para hallar una aproximación de la tasa mensual asociada a esta renta. Fijaremos un nivel de tolerancia
ε = 0, 00000001 = 1 · 10−8
Es decir, pararemos cuando el término de corrección sea menor que ε. Para
facilitar la presentación construimos la siguiente tabla:
f (ik )
f 0 (ik )
0, 052367249
0, 038181752
0, 014096162
0, 001376066
0, 000011411
7, 74082 · 10−10
−
k
ik
0
1
2
3
4
5
0, 01
0, 062367249
0, 100549001
0, 114645163
0, 116021229
0, 116032642
Donde
0, 062367249
=
0, 100549001
=
f (i0 )
= 0, 01 + 0, 052367249
f 0 (i0 )
f (i1 )
= 0, 062367249 + 0, 038181752
i2 = i1 − 0
f (i1 )
i1 = i0 −
y asi sucesivamente. La tasa mensual que buscamos es
i = 0, 116032642
pues
f (i5 ) −10
< 1 · 10−8 = ε
f 0 (i5 ) = 7, 74082 · 10
Comprobemos que esta tasa funciona bien:
−24
2.500
1 − (1 + 0, 116032642)
0, 116032642
= 20.000, 0000947
Un problema no trivial con el método de Newton es la elección de una buena
semilla i0 , tanto para garantizar la convergencia del mismo, como para reducir
el número de interaciones. Un buen criterio ad hoc para nuestro problema es
comprobar que la semilla i0 satisfaga
−n
1 − (1 + i0 )
VA
≈
C
i0
En el ejemplo del Sr. Daniel V A/C = 8, y si escogemos i0 = 0, 01, obtenemos
−24
1 − (1 + 0, 01)
0, 01
= 21, 2433872576
8.5. MÉTODOS NÚMERICOS
173
mientras que si hubieramos elegido i0 = 0, 10
−24
1 − (1 + 0, 15)
0, 15
= 6, 43377144806
lo que nos indica i0 = 0, 10 es una mejor semilla para realizar las iteraciones.
Usando esta semilla necesitamos 3 iteraciones para alcanzar el nivel de precisión
deseado:
f (ik )
f 0 (ik )
0, 014546475
0, 001473075
1, 30917 · 10−5
1, 01861 · 10−9
−
k
ik
0
1
2
3
0, 1
0, 114546475
0, 116019550
0, 116032642
En el caso de tener como dato el valor final de la renta V F , las fórmulas
anteriores deben ser modificadas pues debemos partir de
n
(1 + i) − 1
i
Dada una renta pospagable de valor final V F , de n términos de montante C, si
deseamos hallar la tasa p-perı́odica i para poder usar Newton, debemos colocar
las cosas de la forma f (x) = 0, lo cual se logra al definir
VF =C
n
(1 + i) − 1
−VF
i
El método de Newton requiere la derivada de f
f (i) = C
n−1
f 0 (i) = C
ni (1 + i)
En la iteración necesitaremos el cociente
n
− [(1 + i) − 1]
i2
f (i)
f 0 (i) (término
de corrección):
n
f (i)
f 0 (i)
(1 + i) − 1
−VF
i
n−1
n
ni (1 + i)
− [(1 + i) − 1]
C
i2
VF
n
i
(1 + i) − 1 −
C
i
n−1
n
ni (1 + i)
− [(1 + i) − 1]
VF
n
i
(1 + i) − 1 −
C
n−1
ni
1 + ni (1 + i)
− (1 + i)
C
=
=
=
Por lo tanto la relación recursiva buscada es:
VF
n
1+
ik − (1 + i)
C
ik+1 = ik +
n−1
n ik
1 + nik (1 + ik )
− (1 + ik )
(8.16)
174
CHAPTER 8. RENTAS
(para las personas de poca fe, en la nota ?? al final de esta sección está la
correspondiente deducción)
Ejemplo 8.28 El Sr. Ignacio desea ahorrar unos $ 14.000 para comprase un
telivisor LED de 40” y un home-theater con Blue-ray. Para tal fin deposita a
principio de cada mes $ 600. Si al cabo de 18 meses a juntado suficiente dinero,
cual fue la tasa que obtuvo del banco.
Lo primer que debemos hacer es hallar una semilla adecuada. En este caso
buscamos que
n
(1 + i0 ) − 1
VF
≈
C
i0
Ahora V F/C = 23, 3333333. Probamos con i0 = 0, 5:
18
(1 + 0, 5)
0, 5
−1
= 2.953, 78376
lo cual claramente está muy lejos del valor buscado. Ahora, ¿tenemos que subir
o bajar la tasa semilla para lograr una mejor aproximación? La respuesta es
n
sencilla, debido a la monotonı́a del multiplicador (1+i)i −1 , como la primera
apróximación fue por exceso, debemos probar con una tasa más pequeña. Veamos
que ocurre con i0 = 0, 05
18
(1 + 0, 05)
0, 05
−1
= 28, 13238467
la cual es una mejor aproximación inicial. Ahora usando la fórmula iterativa
(8.16) obtenemos la siguiente tabla
f (ik )
f 0 (ik )
−0, 01828357
−0, 002077465
−2, 37185 · 10−5
−3, 04451 · 10−9
−
k
ik
0
1
2
3
0, 05
0, 03171643
0, 029638966
0, 029615247
donde hemos usado como criterio de parada ε = 1 · 10−8 .
Comprobemos que esta tasa da una buena aproximación de la tasa buscada
en este problema:
18
600
(1 + 0, 029615247)
0, 029615247
−1
= 14.000, 0003835
Poner 6 a 10 ejercicios, una mitad con VA y la
otra con VF
8.5. MÉTODOS NÚMERICOS
8.5.2
175
Método de la secante
El método de secante, es una variación del método de Newton, que se aplica
para resolver el problema
f (x) = 0
cuando se desea evitar el uso de la derivada de la función con la que vamos
a trabajar (ya sea porque la derivada es compleja, ya sea porque no se sabe
derivar). Por ejemplo, la derivada de una función relativamente simple, suele
ser compleja, por ejemplo
d x2 cos x2 ln x3
= 2 cos x2 ln x3 − 2x3 sin x2 ln x3 + 3x cos x2
dx
volviendo tedioso el uso de Newton-Raphson.
El método de la secante se deriva a partir del método de Newton, sustituyendo la derivada por la aproximación de esta que produce el uso de una
secante
Poner dibujo... mirar Burden pag 59
Si bien en general su convergencia es más lenta que la del método de Newton
(lo que se suele traducir en varios renglones más en las tablas correspondientes),
funciona muy bien para funciones convexas continuas (como suele ser el caso en
Matemáticas financieras).
Sean pk y pk+1 aproximaciones de la raı́z p del problema f (p) = 0. El
Método de la secante nos dice que podemos obtener una mejor aproximación
pk+2 y realizando la siguiente iteración:
pk+2 = pk+1 −
f (pk+1 ) (pk+1 − pk )
f (pk+1 ) − f (pk )
(8.17)
para k ≥ 0, la cual se puede obtener a partir de la grafica ?????????? o de la
fórmula iterativa de Newton usando la aproximación de la derivada
f 0 (pk ) ≈
f (pk+1 ) − f (pk )
pk+1 − pk
Ni la deducción, ni la convergencia del método son difı́ciles de probar. Remitimos al lector interesado a [?].
A diferencia del Newton, necesitamos dos semillas para comezar la iteración,
y la elección de un buen par de semillas i0 e i1 , garantiza la convergencia del
método y reduce el número de interaciones.
Para nuestro caso particular, dada una renta pospagable o vencida de valor
actual V A, y n términos de montante C, deseamos hallar la tasa p-perı́odica i
pactada.
Poner dibujo
Ahora
−n
VA=C
1 − (1 + i)
i
176
CHAPTER 8. RENTAS
Para poder usar el método de la secante, debemos colocar las cosas de la forma
f (x) = 0, lo cual se logra al definir
−n
f (i) = C
1 − (1 + i)
i
−VA
Ejemplo 8.29 El Sr. Daniel tomó un préstamo por $ 20.000 a devolver en 24
cuotas mensuales consecutivas de $ 2.500. ¿Qué tasa mensual esta pagando?
Utilizaremos el método de la secante para hallar una aproximación de la tasa
mensual asociada a esta renta. Fijaremos un nivel de tolerancia
ε = 0.00000001 = 1 · 10−8
Para hallar un par de semillas adecuadas el mismo criterio ad hoc que usamos
en Newton funciona: comprobar que la semilla i0 satisfaga
−n
1 − (1 + i0 )
VA
≈
C
i0
Como V A/C = 8, eligiendo i0 = 0, 10, tenemos que
1 − (1 + 0, 1)
0, 1
−24
≈ 8, 985
lo que nos indica i0 = 0, 10 una buena semilla para realizar las iteraciones, pero
necesitamos una segunda semilla ¿Cómo podemos escogerla? Una buena opción
es tomar la segunda semilla como una corrección de la primera en la dirección
que corresponde, en este caso, i0 = 0, 10 nos da 8, 985 (aproximadamente), la
segunda raı́z deberı́a movernos hacia 8, como el multiplicador
1 − (1 + i)
i
−n
es una función decreciente de i (si n se mantiene constante), la segunda semilla
deberı́a ser mayor a 0, 10, por ejemplo, podemos tomar i1 = 0, 11. Usando estas
semillas necesitamos 5 iteraciones para alcanzar el nivel de precisión deseado:
k
ik
f (ik )
0
1
2
3
4
5
0, 1
0, 11
0, 115468622
0, 116012535
0, 116032575
0, 116032643
2461, 86005
870, 3414445
78, 73376828
2, 797850786
0, 009371666
1, 11977 · 10−6
f (ik ) − f (ik−1 )
−1591, 518606
−791, 6076762
−75, 9359175
−2, 78847912
−0, 009370546
Por lo que la tasa buscada es
i(12) = 0, 116032643
f (ik ) (ik − ik−1 )
f (ik ) − f (ik−1 )
−
−0, 005468622
−0, 000543912
−2, 00404 · 10−5
−6, 73528 · 10−8
−8, 04861 · 10−12
8.5. MÉTODOS NÚMERICOS
177
El método de la secante funciona igual de bien en los casos donde deseamos
hallar la tasa en una relación de valor final:
n
VF =C
(1 + i) − 1
i
Dada una renta pospagable de valor final V F , y n términos de montante C,
si deseamos hallar la tasa p-perı́odica i que satisface la igualdad anterior, colocamos las cosas de la forma f (x) = 0, lo cual se logra al definir
n
g (i) = C
(1 + i) − 1
−VF
i
y aplicamos el método de la secante a g
ik = ik−1 −
g (ik−1 ) (ik−1 − ik−2 )
g (ik−1 ) − g (ik−2 )
Ejemplo 8.30 El Sr. Ignacio desea ahorrar unos $ 14.000 para comprase un
telivisor LED de 40” y un home-theater con Blue-ray. Para tal fin deposita a
principio de cada mes $ 600. Si al cabo de 18 meses a juntado suficiente dinero,
cual fue la tasa que obtuvo del banco.
Lo primer que debemos hacer es hallar un par de semillas adecuadas. En
este caso buscamos que
n
VF
(1 + i) − 1
≈
C
i
Ahora V F/C = 23, 3333333. Veamos que ocurre con i0 = 0, 05
18
(1 + 0, 05)
0, 05
−1
= 28, 13238467
n
Para hallar la segunda semilla por la monotonı́a del multiplicador (1+i)i −1 (el
cual es creciente en i, si mantenemos constante n), como la primera apróximación
fue por exceso, debemos probar con una tasa más pequeña. La cual posiblemente
nos de una mejor aproximación, por ejemplo i1 = 0, 02. Ahora usando la fórmula
iterativa que el método de la secante nos da, obtenemos la siguiente tabla:
k
ik
g (ik )
g (ik ) − g (ik−1 )
g (ik ) (ik − ik−1 )
g (ik ) − f (ik−1 )
0
1
2
3
4
5
0, 05
0, 02
0, 028575894
0, 029670281
0, 029614934
0, 029615244
2879, 430804
−1152, 612573
−130, 4412944
6, 948273059
−0, 039127869
−1, 16511 · 10−5
−4032, 043377
1022, 171278
137, 3895674
−6, 987400928
0, 039116217
−0, 008575894
−0, 001094387
5, 5347 · 10−5
−3, 09931 · 10−7
−9, 23156 · 10−11
178
CHAPTER 8. RENTAS
donde hemos usado como criterio de parada ε = 1 · 10−8 . Comprobemos que
esta tasa es una buena aproximación de la tasa buscada en este problema:
18
600
(1 + 0, 029615244)
0, 029615244
−1
= 14.000, 0000051
Poner 6 a 10 ejercicios, una mitad con VA y la
otra con VF..... o decir, rehacer los ejercicios de
Newton Raphson
8.6
Rentas prepagables
Las rentas vencidas (pospagables) no describen de manera satisfactoria el flujo
de fondos que originan operaciones financieras como los alquileres y los seguros.
Se paga el alquiler y luego se ocupa el inmueble. El valor actual de la renta
resulta natural calcularlo al momento que se impuso el el primer capital, que
es el momento en el cual se inicia la operción. Por otro lado, el valor final de
la renta debe ser calculado un perı́odo después del pago del último término.
La propiedad no esta disponible (para el propietario) sino hasta después de un
perı́odo del momento del pago del último término.
Con los seguros ocurre lo mismo: el compromiso comienza al momento de
realizarse el primer pago y se extiende un perı́odo más alla del último pago.
En ambos casos podemos asumir que las imposiciones se realizan al comienzo
de cada perı́odo, de ahi el nombre de rentas prepagables. En latinoamérica
se le suele llamar rentas adelantadas, nosotros preferimos llamar ası́ a otro
tipo de rentas, en esto seguimos el uso habitual en España.
Poner dibu!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Dada una renta prepagable constante de de n términos de montante C
disponibles a los momentos 0, 1, 2, . . . , n − 1 (p-periodos) y una tasa p-perı́odica
i(p) es claro que
V Aprepagable (0) = V Apospagable (−1) 1 + i(p)
Por lo tanto
1 − 1 + i(p)
V Aprepagable (0) = C
i(p)
−n 1 + i(p)
(8.18)
Mientras que el valor final es
V Fprepagable (n) = V Fpostpagable (n − 1) 1 + i(p)
Por lo tanto
n
1 + i(p) − 1 (p)
V Fprepagable (n) = C
1
+
i
i(p)
(8.19)
8.6. RENTAS PREPAGABLES
179
Ejemplo 8.31 Una empresa de seguros nos cobra una prima de $ 185 por mes
por un seguro contra todo riego para automotores. Sabiendo el valor actual de
un año de seguro se corresponde con el 5% del valor del vehı́culo, calcular el
precio del vehı́culo. Suponer una TNA del 8,3%.
poner dibu!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Para hallar el valor del vehı́culo necesitamos el valor actual de la renta constante prepagable
V Aprepagable (0)
0, 083
1− 1+
12
= 185
0, 083
12
= 2.108, 75
−12
0, 083
1+
12
Por lo tanto el automóvil vale
$ 42.174, 95 = 20 · 2.108, 75
En general los esquemas de ahorro también se adecuan al esquema de rentas
prepagables ya que la mayorı́a de la gente ahorra a principio de mes.
Ejemplo 8.32 La Sra. Agustina, deposita a principio de mes $ 350 en una
cuenta de ahorro que paga una TEM del 0,5%. Hace ya 4 años y 5 meses que
la Sra. Agustina comenzó a ahorrar. ¿Cuál es el monto del que ahora dispone?
Poner dibu!!!!!!!!!!!!!!!!
No hay más que aplicar la fórmula (8.19) con n = 4 · 12 + 5 = 53
53
V Fprepagable (53) = 350
(1 + 0, 005)
0, 005
−1
(1 + 0, 005) = 21.285, 8420266
La Sra. Agustina dispone de $ 21.285,84.
Ejemplo 8.33 Ud. ha empezado a ahorrar $ 1.450 cada mes para comprarse
un dpto. que cuesta unos $ 145.000. En este momento tiene 40 años, cuantos
años tendrá cuando pueda comprar el dpto. Suponga que puede obtener TEA del
0,5%. ¿Y con una TEM del 0,8%?
En este caso, buscamos un n que nos garantize que el valor final de la renta
no sea inferior a $ 145.000: debemos despejar n de la fórmula (8.19)
n
1 + i(p) − 1 V Fprepagable (n) = C
1 + i(p)
(p)
i
n
V Fprepagable (n) i(p)
(p)
+
1
=
1
+
i
C 1 + i(p)
180
CHAPTER 8. RENTAS
de donde
log V Fprepagable (n) i(p) + C 1 + i(p) − log C 1 + i(p)
n=
log 1 + i(p)
Reemplazando V Fprepagable (n) por $ 145.000, y el signo = por ≥
n≥
log [145.000 · 0, 005 + 1.4501 + 0, 005] − log 1.450 (1 + 0, 005)
= 80, 9628061817
log (1 + 0, 005)
por lo que al cabo de 6 años y 9 meses dispondrá de los fondos necesarios
(en realidad tendrá $ 145.080). Por otro lado si consigue una TEM del 0,7%
necesitará
n≥
log [145.000 · 0, 007 + 1.450 (1 + 0, 007)] − log 1.450 (1 + 0, 007)
= 75, 65812128
log (1 + 0, 007)
Necesitará 6 años y 4 meses para reunir los fondos necesarios.
Nota 8.34 Para hacer un análisis a largo plazo necesitamos introducir de una
u otra forma los efectos de la inflación. Los modelos de rentas variables (sobre
todo las variables en forma geométrica) serán el marco adecuado para incluir la
inflación.
Ejemplo 8.35 El valor actual de una renta constante prepagable es de $ 20.000.
Si la renta constaba de 24 pagos mensuales de $ 3.500 ¿Cuál es la tasa aplicada
a la operación?
En general, suele ser imposible despejar i(p) de las fórmulas (8.18) y (8.19),
por lo que debemos volver a recurrir a Newton-Raphson. En este caso, a partir
de (8.18) debemos obtener una función de i (usaremos i en lugar de i(p) ) cuyas
raı́ces nos den la solución del problema. Esto se logra definiendo
−n
1 − (1 + i)
(1 + i) − V A
i
El esquema iterativo de Newton-Raphson requiere de la derivada de la función
g:
h
i
−n−1
−n
−n
ni
(1
+
i)
−
1
−
(1
+
i)
1 − (1 + i)
dg (i)
= C
+ C (1 + i)
di
i
i2
h
i
C
−n
= 2 (1 + i) (ni + 1) − 1
i
y el esquema iterativo toma la forma
g (i) = C
g (ik )
, para k ≥ 0
g 0 (ik )
ik+1
= ik −
ik+1
1 − (1 + ik )
(1 + ik ) − V A
ik
= ik −
h
i
C
−n
(1
+
i
)
(ni
+
1)
−
1
k
k
i2k
−n
C
(8.20)
8.6. RENTAS PREPAGABLES
181
La semilla adecuada para iniciar la iteración es una i tal que
VA
1 − (1 + i)
≈
C
i
−n
(1 + i)
Sabemos que 20.000/3.500 ≈ 5, 7, comencemos con i = 0.5 tenemos
1 − (1 + 0, 5)
0, 5
−24
(1 + 0, 5) = 2.9998
Como este valor esta por debajo de 5,7 podemos obtener una mejor semilla
usando una tasa más chica, por ejemplo tomando i = 0, 2
1 − (1 + 0, 2)
0, 2
−24
(1 + 0, 2) = 5, 9245
Fijando un nivel de tolerancia ε = 1 · 10−5
k
0
1
2
3
ik
0, 2
0, 209071425
0, 209447107
0, 209447708
g (ik )
735, 8385805
28, 18093889
0, 044909815
g 0 (ik )
−81116, 09903
−75012, 64964
−74773, 74137
g (ik ) /g 0 (ik )
−0, 009071425
−0, 000375682
−6, 00609 · 107
La tasa buscada parece ser i = 0, 209447708, veamos que tan buena aproximación es:
−24
3.500
1 − (1 + 0, 209447708)
0, 209447708
(1 + 0, 209447708) = 19.999, 99983
(La semilla i0 = 0, 5 requiere de 11 renglones en la tabla anterior para hallar
esta misma tasa).
Ejemplo 8.36 El valor final de una renta constante prepagable es de $ 2.000.000.
Si la renta constaba de 24 pagos mensuales de $ 2.000 ¿Cuál es la tasa aplicada
en la operación?
En este caso, a partir de (8.19) debemos obtener una función de i cuyas
raices nos den la solución del problema. Esto se logra definiendo
n
g (i) = C
(1 + i) − 1
(1 + i) − V F
i
El esquema iterativo de Newton-Raphson requiere de la derivada de la función
dg (i)
di
= C
=
1 − (1 + i)
i
−n
n−1
+ C (1 + i)
C
n
[(1 + i) (ni − 1) + 1]
i2
ni (1 + i)
n
− [(1 + i) − 1]
i2
182
CHAPTER 8. RENTAS
y el esquema iterativo toma la forma
−n
C
ik+1 = ik −
1 − (1 + ik )
(1 + ik ) − V F
ik
C
n
[(1 + ik ) (nik − 1) + 1]
i2k
(8.21)
La semilla adecuada para iniciar la iteración es una i tal que
n
VF
(1 + i) − 1
≈
(1 + i)
C
i
Sabemos que 2.000.000/2.000 = 1000, comencemos con i = 0.5 tenemos
24
(1 + 0, 5)
0, 5
−1
(1 + 0, 5) ≈ 50499
Como este valor esta por arriba de 400, podemos obtener una mejor semilla
usando una tasa más chica, por ejemplo tomando i = 0, 25
24
(1 + 0, 25)
0, 25
(1 + 0, 25) ≈ 1053
Fijando un nivel de tolerancia ε = 1 · 10−5
k
0
1
2
3
ik
0, 25
0, 246827725
0, 24674453
0, 246744475
g (ik )
107582, 3681
2681, 905985
1, 783717507
g 0 (ik )
33913317, 89
32236330, 33
32193459, 29
g (ik ) /g 0 (ik )
0, 003172275
8, 31951 · 10−5
5, 54062 · 10−8
La tasa buscada parece ser i = 0, 246744475. Veamos que tan buena aproximación es:
24
2.000
(1 + 0, 246744475)
0, 246744475
−1
(1 + 0, 246744475) = 2.000.008, 86852
(La semilla i0 = 0, 5 requiere de 8 renglones en la tabla anterior para hallar esta
misma tasa).
Ejercicio 8.37 Un empresa que alquila maquinaria para movimientos de suelo
desea saber cuanto debe cobrar al mes como mı́nimo para amortizar el costo de
adquisición de una máquina en 5 años. La misma costó $ 300.000. Suponer una
TEM del 0,7%.
Ejercicio 8.38 Si en el problema anterior decidimos tener en cuenta los gastos
de mantenimiento y operación, los cuales ascienden a $ 50.000 al año ¿Cuánto
debe cobrar ahora como mı́nimo?
8.7. RENTAS PERPETUAS
183
Ejercicio 8.39 En cuanto tiempo amortizamos la compra de un camión que
costó $ 650.000 si lo alquilamos a $ 3.500 por mes. Suponer una TEA del 10,7%.
Poner más ejercicios!!! y con al menos
4 sobre tasas (dos para usar VA y dos para usar
VF)
Ejercicio 8.40
8.7
Rentas perpetuas
Hay un número de situaciones que generan un flujo infinito de fondos:
1. Depósitar una suma de dinero, y retirar solamente los intereses generados.
2. Los presupuestos de ciertas agencias del estado.
3. Los dividendos provenientes de acciones de una compañia.
4. Las rentas inmobiliarias (los ingresos que produce una propiedad al ser
alquilada), etc.
Llamaremos rentas perpetua a toda renta que conste de una sucesión
infinita de términos.
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Este tipo de rentas no tiene un valor final (no tiene mucho sentido hablar de
una cantidad infinita de dinero disponible más alla del fin de los tiempos), pero
es posible calcular su valor actual (si la tasa es positiva, ya que el aporte de los
términos muy lejanos tiende a cero).
8.7.1
Rentas perpetuas constantes vencidas (pospagables)
Analizaremos el caso de una renta constante perpetua vencida: el compromiso
comienza en el momento 0 (cero) y no tiene fecha de finalización, los términos se
imponen a perı́odo vencido (t1 = 1), y la renta esta sujeta a una tasa p-perı́odica
i(p) (dimensionalmente compatible con la unidad temporal usada para medir los
perı́odos entre imposiciones). Es claro que
V A (0)
=
∞
X
k=1 1
∞
X
= C
C
+ i(p)
k
1
k
1 + i(p)
1
1
= C
(p)
1
1+i
1−
1 + i(p)
C
= (p)
i
k=1
184
CHAPTER 8. RENTAS
Esta es la fórmula fundamental de rentas perpetuas
V A (0) =
C
i(p)
(8.22)
Nota 8.41 En la deducción anterior hemos usado la conocida fórmula para la
suma de una serie geométrica:
∞
X
ark−1 = a
k=1
1
si |r| < 1
1−r
con
0<a=r=
1
<1
1 + i(p)
siempre que i(p) > 0.
Veamos un ejemplo sencillo:
Ejemplo 8.42 El estado se compromete a entregar todos los meses (a mes
vencido) la suma de $ 15.000 a una fundación sin fines de lucros. ¿Cuál es el
valor actual de dicha renta? si la fundación puede depositar sus excedentes al
1.3% mensual.
Poner dibu!!!!!!!!!!!!!!!!
Sólo debemos aplicar la fórmula (8.22):
V A (0) =
15.000
= 1.153.846, 15385
0, 013
Este es el valor actual de la renta perpetua.
Si la institución recibiera estos fondos y los depósitara al 1.3%, de aqui en
adelante, podrı́a retirar al final de cada mes la suma de $ 15.000 por toda la
eternidad:
1.153.846, 15385 · 0.013 = 15.000
Nota 8.43 Esto nos permite interpretar financieramente el valor actual de una
renta perpetua, vencida, p-perı́odica, constante de término C, a una tasa i(p) :
es la suma de dinero que se debe depositar a la tasa i(p) para retirar al final de
cada p-perı́odo la suma C.
Ejemplo 8.44 El Sr. Máximo desea que su hija Viviana reciba al final de cada
mes la suma de $ 4.500 por el resto de sus dı́as, para lo cual realizará un depósito
a una T EM del 0,81%, de manera tal que al final de cada mes los la Srta. Viviana pueda retirar los intereses generados por el mismo. ¿Cuánto debe depositar
hoy el señor Máximo?
8.7. RENTAS PERPETUAS
185
Es claro que se debe cumplir que
depósito · 0, 0081 = $ 4.500
de donde
$ 4.500
= $ 555.555, 55556
0, 0081
Observe que esto origina una renta perpetua vencida mensual de $ 4.500 para
la Srta. Viviana y que los $ 555.555,55556 pueden ser visto como (y de hecho
son) el valor actual de la misma.
depósito =
Nota 8.45 He aquı́, otra deducción para el valor actual de una renta constante
perpetua vencida (o pospagable). Recordando que
−n
n
X
1 − 1 + i(p)
C
=C
(p) k
i(p)
k=1 1 + i
y que
∞
X
k=1
C
1+
i(p)
lim
k = n→∞
n
X
k=1
C
1 + i(p)
k
tenemos que
−n
1 − 1 + i(p)
C
V A (0) = lim C
= (p)
(p)
n→∞
i
i
Nota 8.46 En la fórmulas de valor actual para rentas perpetuas constantes
vencidas que hemos desarrollado aparecen tres variables: V A, C e i(p) . Por lo
que es claro que hay tres problemas tipo (dadas dos de estas, hallar la tercera)
Ejemplo 8.47 El señor Juan recibe como herencia $ 250.000 en bonos a perpetuidad que pagan anualmente el 6 % vencido en concepto de intereses, ¿Cuánto
recibirá año tras año el Sr. Juan?
En este caso, por (8.22) o mejor aún recuriendo a la interpretación financiera
de rentas perpetuas vencidas, tenemos que
$250.000 · 0.06 = $ 15.000
Por lo que el Sr. Juan recibirá la suma de $ 15.000 al comienzo de cada año por
el resto de su vida.
Ejemplo 8.48 Qué tasa de interés hace que el valor actual de una renta perpetua, vencida, trimestral, de $ 25.000 sea de $ 750.000.
Por (8.22)
$ 750.000 =
de donde
i(4) =
Ejercicio 8.49
$ 25.000
i(4)
$ 25.000
= 0, 0333333
$ 750.000
PONER EJERCICIOSSSSSSS!!!!!!!!!!!!!!!!!!!!
186
CHAPTER 8. RENTAS
8.7.2
Rentas perpetuas constantes adelantadas (prepagables)
Algunos flujos infinitos de fondos se adaptan mejor a las rentas perpetuas adelantadas, como es el caso de los alquileres.
Ejemplo 8.50 Nos ofrecen un salon comercial por $ 370.000. Sabemos que es
posible alquilarlo por unos $ 2.600 mensuales. Si la tasa que podemos conseguir
por nuestros ahorros es una TEM 0.65% ¿El local está sobrevalorado o es un
buen negocio adquirirlo? ¿Cuál es el precio correcto del inmueble?
¿Cómo estimar el valor de la propiedad? Esencialmente un alquiler puede
ser modelado como un flujo infinito de fondos. El valor actual de ese flujo infinito de capitales nos puede dar una idea del valor de la propiedad (insistimos,
esta es una primera estimación del valor de una propiedad, hay todo una serie
de factores que deben ser incluidos en el análisis, para que el mismo sea serio, por ejemplo: inflación estimada, desarrollo urbanı́stico probable de la zona,
crecimiento demográfico de la ciudad, situación polı́tica, y un largo etc.).
Volviendo al problema, ambas preguntas se responden calculando el valor
actual de la renta a perpetuidad que produce la propiedad. He aqui el flujo de
fondos:
poner dibu!!!!!!!!!!!!!!!!!!!!!
Como se puede apreciar, la fórmula (8.22) nos dá el valor del flujo infinito
de fondos un perı́odo antes de la imposición del primer término de la renta (el
primer alquiler)
2600
= 400.000
V A (−1)perpetuo =
0, 0065
pero nosotros deseamos el valor al momento de la operación (momento 0)
V A (0) = V A (−1)perpetuo (1 + 0, 0065) = 402600
Por lo tanto, comprar el local es una buena inversión (en el sentido que no
produce pérdida de capital). El precio correcto (para Ud., es decir, a la tasa
i(12) = 0, 0065) es $ 402.600. Si el precio del local es superior a este monto, el
local esta sobrevalorado (para ud.) y obtendrı́a un rédito mayor depositando sus
fondos al 0,65% mensual. Si el precio del local es inferior a $ 402.600, entonces
entonces es una buena inversión, pues obtendrá un flujo de fondos superior con
los alquileres que depósitando sus fondos al 0,65% mensual (suponemos que esta
es la mejor tasa que ud. puede conseguir).
Nota 8.51 He aquı́ una deducción para el valor actual de una renta constante
perpetua adelantada (prepagable). Recordando que el valor actual de una renta
de este tipo de n términos es
n−1
X
k=0
C
1 + i(p)
k = C
1 − 1 + i(p)
i(p)
−n 1 + i(p)
8.8. RENTAS DIFERIDAS Y ANTICIPADAS
187
y que
∞
X
k=1
C
1 + i(p)
lim
k = n→∞
n
X
k=1
C
1 + i(p)
k
tenemos que
1 − 1 + i(p)
V A (0) = lim C
n→∞
i(p)
C = (p) 1 + i(p)
i
−n 1 + i(p)
de donde obtenemos la fórmula para el valor actual de una renta constante, pperı́odica, perpetua y adelantada (o prepagable), de término C a una tasa i(p) :
V A (0) =
C (p)
1
+
i
i(p)
Ejercicio 8.52 El estado se compromete a entregar todos los meses (a mes
vencido) la suma de $ 50.000 a una fundación sin fines de lucros. ¿Cual es el
valor actual de dicha renta? Suponer una TEA del 11%.
Ejercicio 8.53 Un campo se alquila anualmente por $ 140.000 (pagaderos a fin
de año). Si la TEA del mercado es 9.2% ¿Cuál es el valor de dicha propiedad?
Ejercicio 8.54 Nos ofrecen un salon comercial por $ 470.000. Sabemos que es
posible alquilarlo por unos $ 17.500 mensuales. Si la tasa que podemos conseguir
por nuestros ahorros es una TEM del 0,85% ¿El salón está sobrevalorado? ¿Cuál
deberı́a ser (apróximadamente) su precio?
Ejercicio 8.55 Determinar el valor de un local comercial, es cual está alquilado
a $ 12.100 por mes. Suponer un TNA del 18.9%.
Poner más ejercicios!!!!!!!!!!!!!!!!!!!!!
8.8
Rentas diferidas y anticipadas
Comenzemos con las rentas diferidas o con perı́odo de gracia. Estas rentas
aparecen de forma natural en ciertas operaciones crediticias, del estilo ”lleve
hoy y comience a pagar recién en octubre”. En estas operaciones, la primera
cuota esta diferida una cierta cantidad de tiempo hacia el futuro. Consideremos
el siguiente ejemplo
Ejemplo 8.56 La señora Mariela compró hoy en su tienda habitual ropa por
unos $ 7.000, aprovechando la promoción “llevé hoy y comience a pagar en 3
meses”. Si la operación fue pactada a 6 cuotas iguales, concecutivas y mensuales,
a una tasa del 2% mensual, ¿Cuál es el monto de las cuotas?
188
CHAPTER 8. RENTAS
Poner dibujo
El problema puede ser resuelto de varias formas. Utilizando la teorı́a de
rentas postpagables, tenemos que
−6
C
1 − (1 + 0, 02)
0, 02
es el valor de la renta dentro de dos meses.
Poner dibujo!!!!!!!!!!!!!!!!!!!
Si actualizamos un par de meses este monto tendremos
−6
7.000 = C1
1 − (1 + 0, 02)
0, 02
1
2
(1 + 0, 02)
donde podemos despejar C1
C1
2
=
7.000 (1 + 0, 02)
=
1.300, 16779
0, 02
−6
1 − (1 + 0, 02)
Es decir, la señora Mariela deberá abonar 6 cuotas de $ 1.300,17. Siendo la
primer cuota abonada a los 3 meses de realizada la compra.
También podemos resolverlo usando la noción de renta prepagable. En dicho
caso, el valor de la renta al momento de realizar el primer pago es
−6
C2
1 − (1 + 0, 02)
0, 02
(1 + 0, 02)
Poner dibujo!!!!!!!!!!!!!!!!!
Este monto al actualizarlo 3 meses debe ser igual al valor de la compra
−6
7.000 = C2
1 − (1 + 0, 02)
0, 02
(1 + 0, 02)
1
3
(1 + 0, 02)
Resulta obvio que ambos planteos son equivalentes:
C1 = C2
Una tercera forma de resolver este problema es capitalizar la deuda por
2 meses (3 meses), y considerar la renta postpagable (prepagable) cuyo valor
actual es este monto
−6
2
7.000 (1 + 0, 02) = C3
1 − (1 + 0, 02)
0, 02
De nuevo, pasando dividiendo el factor de capitalización de la derecha, resulta
obvio que
C1 = C3
8.8. RENTAS DIFERIDAS Y ANTICIPADAS
189
(usando prepagables obtenemos:
3
7.000 (1 + 0, 02) = C4
1 − (1 + 0, 02)
0, 02
−6
(1 + 0, 02)
de donde resulta obvio que C2 = C4 y por lo tanto C4 = C1 ).
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!
Al perı́odo de tiempo que media desde la concertación de la operación financiera y el primer pago se le suele llamar diferimiento o perı́odo de gracia. Preferimos enfocarnos en usar equivalencia financiera y la teorı́a de rentas
postpagables (o prepagables) en lugar de desarrollar fórmulas ad hoc.
Claramente, el valor final de una renta diferida no necesita de nuevas fórmulas,
y se calcula usando el valor final de una renta pospagable o prepagable según
sea el caso.
Poner 5 o 6 ejercicios.
Se llama rentas anticipadas, a las rentas cuyo valor final se debe calcular
2 o más perı́odos después de impuesto el último término de la renta. Dicho
perı́odo de tiempo recibe el nombre de anticipo.
Poner dibujo
Un ejemplo de las mismas son los planes (cı́rculos de ahorro) para adquirir
un automotor, desde el último pago, hasta la entrega efectiva del vehı́culo suelen
pasar 2 o 3 meses.
Ejemplo 8.57 Ud. adhirió a un plan de ahorro “80 cuotas sin interés” para
adquirir un 0 km. Después de pagar las 80 cuotas mensuales de $ 799 del plan
correspondiente a un ”supercar” cuyo valor de mercado es de $ 63.000, ud recibió
su 0 km 3 meses después. Si la tasa de mercado a la que ud podı́a acceder era
del 0.7 % mensual ¿Cuánto le costo realmente el vehı́culo?
Simplemente debemos calcular el valor de la renta 3 meses después de realizado el último pago. De nuevo, este problema se puede resolver de varias fomas.
En este caso haremos las cuentas pensando que la renta es pospagable. El valor
final de la renta al momento de realizar el último pago de $ 799 es
80
799
(1 + 0, 007)
0, 007
−1
= 85.294, 44174
luego debemos capitalizar este monto por 3 meses
80
799
(1 + 0, 007)
0, 007
−1
3
(1 + 0, 007) = 87.098.19256
Es decir, si hubiera ahorrado $ 799 por mes en el banco, ahora se podrı́a comprar
el ”supercar” y además le sobrarı́an unos $ 24.100. De todas formas este análisis
no es del todo completo y sólo funciona cuando la inflación es baja y economı́a
se mantiene estable.
190
CHAPTER 8. RENTAS
Ejercicio 8.58 Volver a hacer las cuentas para el ejemplo anterior usando las
fórmulas de rentas prepagables. Deberı́a obtener el mismo resultado.
El valor actual de una renta anticipada no requiere de mayor análisis, pues
corresponde a usar el valor actual de la renta (pospagable o prepagable según
corresponda).
Poner 4 o 5 ejercicios uno modificando el ejemplo
del auto para abarcar los planes 80/20.
8.9
Rentas aritméticas
El siguiente ejemplo muestra el tipo de situaciones que deseamos analizar.
Ejemplo 8.59 El Sr. Daniel se compromete a cumplir el siguiente esquema de
12 pagos mensuales con el Sr. Ignacio. Un primera cuota de $ 100, una segunda
cuota de $ 140, una tercera cuota $ 180 y asi sucesivamente hasta la cuota doce
¿Cuál es el monto de la cuota 9? Suponiendo una TEM del 1,2%. ¿Qué cantidad
deberı́a entregarle hoy el Sr. Daniel al Sr. Ignacio para sustituir este esquema
de pago? ¿Podrá comprarse el Sr. Ignacio una PS3 al cabo de un año con estos
fondos? (el precio de una PS3 es $ 3.200).
Este es un ejemplo de una renta variable, donde la variación sigue una ley
determinada.
Actualización
V A(0)
0
100
140
180
500
540
580
100 + 0 · 40
100 + 1 · 40
100 + 2 · 40
100 + 10 · 40
100 + 11 · 40
100 + 12 · 40
1
2
3
10
11
12
V F (12)
Capitalización
Las fórmulas que desarrollamos en la sección anterior para el cálculo del valor
actual y final de una renta no son útiles para resolver este problema. Necesitamos
desarrollar fórmulas que nos permitan sumar expresiones de la forma
V A (0) =
C + 40
100
C + 2 · 40
C + (12 − 1) 40
+
+
3 + ··· +
12
1 + 0.012 (1 + 0.012)2
(1 + 0.012)
(1 + 0.012)
8.9. RENTAS ARITMÉTICAS
191
Definición 8.60 Dados dos números reales a y b, se llama progresión o
sucesión aritmética finita a toda sucesión finita de n términos de la forma
{a + b (k − 1)}1≤k≤n := a, a + b, a + 2b, . . . , a + (n − 1) b
Llamaremos progresión o sucesión aritmética infinita a toda sucesión de
la forma
{a + b (k − 1)}k≥1 := a, a + b, a + 2b, a + 3b, . . .
Al número a se le llama término inicial, y al número b se le llama paso o
diferencia común.
Nota 8.61 Si bien progresión y sucesión son sinónimos en matemáticas. La
segunda hace incapie en el orden, mientras que la primera enfatiza el hecho
de que la sucesión en cuestión tiene una ley de formación fija, en particular
se suele hablar de progresión aritmética (suma fija) y progresión geométrica
(multiplicación fija).
Toda progresión aritmética finita puede ser escrita de forma recursiva:
a1 = a
ak+1 = ak + b para 1 ≤ k ≤ n − 1.
Lo mismo ocurre con las sucesiones aritméticas infinitas:
a1 = a
ak+1 = ak + b para k ≥ 1.
De hecho, de acuerdo con la teorı́a de relaciones recursivas que desarrollamos
en el capı́tulo 2 la forma de la solución de estas relaciones recursivas es
ak = a + (k − 1) b
Ejemplo 8.62 Los siguientes son ejemplos de progresiones y sucesiones aritméticas
1. 1, 2, 3, 4, 5, . . . sucesión aritmética de término inicial a = 1 y paso b = 1.
2. 2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32 progresión aritmética finita de término
inicial a = 2 y paso b = 3.
3. 4, 2, 0, −2, −4, −6, . . .
4. 1, 1 + π, 1 + 2π, 1 + 3π, . . .
√ √ √ √ √
5. 2, 2 2, 3 2, 4 2, 5 2
6. {1 + 2k}1≤k≤14
7. {−3 − 2k}k≥0
192
CHAPTER 8. RENTAS
8.
9.
a1
ak+1
=
=
−3
ak + 2
para 1 ≤ k ≤ 10.
a1
ak+1
=
=
0
ak + 5
para k ≥ 1
Es fácil ver que
2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32
es una progresión aritmética: la diferencia entre dos términos consecutivos se
mantiene constante:
5 − 2 = 8 − 5 = · · · = 29 − 28 = 32 − 29 = 3 = b
Mientras que el valor el primer término nos da el valor de a
a=2
La forma general de la progresión aritmética es
ak = 2 + 3 (k − 1) para 1 ≤ k ≤ n
Para hallar n utilizamos el valor del último término:
2 + 3 (n − 1) = 32
de donde deducimos que n = 11 y por lo tanto la progresión aritmética buscada
es
ak = 2 + 3k para 1 ≤ k ≤ 11
Pasar de forma recursiva a la forma explı́cita de una progresión/sucesión
aritmética y viceversa no presenta dificultad:
a1 = 7
⇐⇒
ak = 7−4 (k − 1) para 1 ≤ k ≤ 11.
ak+1 = ak + −4 para 1 ≤ k ≤ 11.
Ejercicio 8.63 Hallar el término inicial, el paso común y la forma general de
cada uno de los items que restan del ejemplo (12.3).
Ahora podemos responder a una de las preguntas planteadas en el ejemplo
(8.59): ¿Cuál es el monto de la cuota 9?
La progresión aritmética que representa la renta dada en el ejemplo (8.59)
es
Ck = 100 + 40 (k − 1)
por lo que el monto de la cuota 9 es $420 pues
C9 = 100 + 40 (9 − 1) = 420
Las rentas variables en progresión aritmética, son aquellas rentas cuyos
términos forman una progresión aritmética, i.e.:
C1 = C
(8.23)
Ck+1 = Ck + b para 1 ≤ k ≤ n − 1.
8.9. RENTAS ARITMÉTICAS
193
Actualización
V A(0)
0
C1
C2
C3
Cn−2
Cn−1
Cn
C+0·b
C + 1 · 40
C+2·b
C + (n − 3) · b
C + (n − 2) · b
C + (n − 1) · b
1
2
3
n−2
n−1
n
V F (n)
Capitalización
De nuevo, calcular el valor actual de este tipo de rentas no es más que
sumar el valor actual de cada uno de los términos involucrados. Supongamos
que tenemos una sucesión de n capitales sujetos a una ley aritmética como la
expreseda en (8.23), sobre la que actua una tasa p-perı́odica i(p) . Supongamos
que los términos están disponibles a los p-perı́odos 1, 2, . . . n . El valor actual de
este tipo de renta es
V A (0)
C
C +b
C + 2b
C + (n − 1) b
n
+
2 +
3 + · · · +
(p)
(p)
1 + i(p)
1 + i(p)
1+i
1+i
!
−n
1 − 1 + i(p)
b
1
2
n−1
+
= C
+
2 + · · · +
n−1
i(p)
1 + i(p)
1 + i(p)
1 + i(p)
1 + i(p)
=
Ahora, todo el problema se reduce a encontrar una fórmula cerrada para la
suma
m
X
k
1
2
3
m
= + 2 + 3 + ··· + m
(8.24)
rk
r
r
r
r
k=1
Hay varias formas de hallar esta suma.
La suma de la izquierda en (8.24) es una suma por filas, sumando por columnas podemos obtener una expresión cerrada
1
1
=
r
r
2
1
1
=
+
r2
r2
r2
3
1
1
1
=
+
+
r3
r3
r3
r3
..
..
..
..
..
..
..
..
.
.
.
.
.
.
.
.
1
1
1
m
=
+
+
+ ··· +
rm
rm
rm
rm
1
1
1
m
X
1 1 − rm−1
1 1 − rm−2
1 1 − rm
k
+
+
+
... +
=
1
1
1
rk
r
r2
r3
k=1
1−
1−
1−
r
r
r
1
rm
1
1 1− r
1
rm
1−
r
194
CHAPTER 8. RENTAS
de donde para 1 ≤ k ≤ m
1
r
1
1
1 1 − rm−k−1
=
−
1
rk
r − 1 rk
rm+1
1−
r
Por lo que
m
X
k
rk
m
X
1
r
1
−
r − 1 rk
rm+1
k=1
r
1
1
m
1
1
=
+ 2 + 3 + · · · + m − m+1
r−1 r
r
r
r
r
m
r
m
r −1
=
−
r − 1 rm (r − 1) rm+1
=
k=1
Otra forma de hallar una fórmula para esta suma, consite en repetir el truco
que se usó para sumar la serie geométrica:
S
=
rS
=
2
3
m−1
m
1
+ 2 + 3 + · · · + m−1 + m
r
r
r
r
r
2
3
m−1
m
1 + + 2 + · · · + m−2 + m−1
r
r
r
r
y luego restar
rS − S
(r − 1) S
(r − 1) S
(r − 1) S
2 1
3
2
m
m−1
m
= 1+
−
− 2 + ··· +
− m−1 − m
+
2
m−1
r
r
r
r
r
r
r
1
1
1
1
m
= 1 + + 2 + 3 + · · · + m−1 − m
r
r
r
r
r
1
1− m
r − m
=
1
rm
1−
r
1 rm − 1
m
=
− m
rm−1 r − 1
r
De donde obtenemos
m
X
k
1 rm − 1
m
=
− m
2
k
m−1
r
r
r (r − 1)
(r − 1)
(8.25)
k=1
Existe una tercera forma de obtener una forma cerrada para la suma
la cual se basa en la siguiente observación
x
d
xk = kxk
dx
X
k
rk
8.9. RENTAS ARITMÉTICAS
195
la cual es válida para cualquier x real si k es un entero mayor o igual que 1.
Luego
m
X
m
X
d
xk
dx
k=1
!
m
d X k
x
= x
dx
k=1
m−1 d
x
= x
x
dx
x−1
kxk
=
k=1
= x
x
xm − 1
mxm−1 (x − 1) − (xm − 1)
+x
2
x−1
(x − 1)
!
Lo que nos lleva (después de un poco de álgebra) a la siguiente expresión
m
X
xm+2
1
m+1
k
kx =
+ m+1
m−
2
x
x
(x − 1)
k=1
En particular haciendo x = 1/r, obtenemos
m
X
k
1
m (r − 1)
m
=
r
−
1
−
2
rk
rm
rm−1 (r − 1)
k=1
Ahora como
2
n−1
1
+
2 + · · · +
n−1
(p)
1+i
1 + i(p)
1 + i(p)
es de la forma
Pm
k
k=1 r k
con
r
=
1 + i(p)
m
=
n−1
Al usar (8.25)Tenemos que
n−1
X
k=1
k
1 + i(p)
k
=
=
!
n−1
1 + i(p)
−1
n−1
−
n−1
i(p)
1 + i(p)
i(p) 1 + i(p)
n−1
1 + i(p)
−1
1
n−1
−
n−2
2
n−1
(p)
(p)
(p)
1+i
i
i
1 + i(p)
1 + i(p)
De donde podemos concluir que
−n
1 − 1 + i(p)
b
V A (0) = C
+
n−1
(p)
i
i(p) 1 + i(p)
!
n−1
1 + i(p)
−1
n−1
−
i(p)
1 + i(p)
(8.26)
196
CHAPTER 8. RENTAS
En la literatura de matemáticas financieras suelen aparecer también la siguientes expresiones para el valor actual de una renta aritmética
−n 1 − 1 + i(p)
b
nb
V A(0) =
C + (p) + nb − (p)
(8.27)
i(p)
i
i
n
−n
1 + i(p) − ni(p) − 1
1 − 1 + i(p)
+b
(8.28)
= C
2
n
i(p)
i(p)
1 + i(p)
las cuales son equivalentes (8.26).
Por ejemplo
!
−n
n−1
1 − 1 + i(p)
1 + i(p)
−1
b
n−1
V A (0) = C
+
−
n−1
i(p)
i(p)
1 + i(p)
i(p) 1 + i(p)
!
−n
−(n−1)
1 − 1 + i(p)
1 − 1 + i(p)
b
n
1
n +
n
= C
+ (p)
−
(8.29)
i(p)
i
i(p)
1 + i(p)
1 + i(p)
!
−n
−n
1 − 1 + i(p)
1 − 1 + i(p)
b
n
n
+ (p)
−
= C
i(p)
i
i(p)
1 + i(p)
−n 1 − 1 + i(p)
b
nb
=
C
+
+
nb
− (p)
i(p)
i(p)
i
Para hallar el valor final de una renta aritmética sólo necesitamos recordar que
n
V F (n) = V A (0) 1 + i(p)
luego tenemos que
n
n
nb 1 + i(p)
1 + i(p) − 1
b
V F (n) =
C + (p) + nb −
i(p)
i
i(p)
(8.30)
Ejercicio 8.64 Demostrar que la expresión (8.28) es equivalente a la expresión
(8.26).
Nota 8.65 Las fórmulas obtenidas corresponden a una renta postpagable, si
desea obtener las correspondientes fórmulas para rentas prepagables, se deben
realizar las correspondientes modificaciones en las deduciones anteriores, las
cuales no deberı́an ser difı́ciles de realizar por parte del lector.
Ahora podemos responder a las restantes preguntas que se nos plantearon en
el ejemplo (8.59). El Sr. Daniel deberı́a entregar hoy al Sr. Ignacio $ 3 493.35,
el valor actual de la renta (recordar C = 100, TEM 1.2 %, b = 40 y n = 12)
−n 1 − 1 + i(p)
b
nb
V A(0) =
C
+
+
nb
− (p)
(p)
(p)
i
i
i
−12 1 − (1 + 0.012)
40
12 · 40
=
100 +
+ 12 · 40 −
0.012
0.012
0.012
= 3493.35
8.9. RENTAS ARITMÉTICAS
197
Por otro lado, el Sr. Ignacio (si va ahorrando el dinero a una TEM del 1.2%)
juntará al cabo de un año la suma de $ 4 030.96 (más que suficiente como para
comprarse la PS3), pues
n
n
nb 1 + i(p)
1 + i(p) − 1
b
C + (p) + nb −
V F (12) =
i(p)
i
i(p)
12
12
(1 + 0.012) − 1
40
12 · 40 (1 + 0.012)
=
100 +
+ 12 · 40 −
0.012
0.012
0.012
= 4030.9619181
Nota 8.66 En las fórmulas (8.26) y (8.30) aparecen 5 variables:V A o V F, C, b, i(p)
y n. Las tres primeras no presentan dificultad, pero las dos últimas: i(p) y n,
al no ser posible despejarlas, requieren de métodos númericos, Newton-Raphson
para la primera, tanteo para la segunda (pues n debe ser entero, si se permite n
continuo se deberá usar Newton-Raphson).
Ejemplo 8.67 (Continuación del ejemplo (8.59)) De cuanto debe ser el incremento si el Sr. Ignacio desea juntar $ 5.000 al cabo de 12 meses.
En este caso, deseamos averiguar el valor de b (recordar C = 100, TEM 1.2
%, b =?, n = 12 y V F (12) = 5000)
5000
= V F (12)
n
1 + i(p) − 1
1 + i(p)
= C
+
b
i(p)
i(p)
12
−1
!
n−1
1 + i(p)
−1
n−1
−
i(p)
1 + i(p)
=
(1 + 0.012)
100
0.012
1 + 0.012
+b
0.012
=
1282.4552015 + 68.7126679184 · b
12−1
(1 + 0.012)
0.012
−1
12 − 1
−
1 + 0.012
!
Por lo tanto
b = 54.1027573389
Es decir, el Sr. Daniel debe aumentar las cuotas en $ 54.11 cada mes.
Ejemplo 8.68 (Continuación del ejemplo (8.59)) De cuánto debe ser el término
inicial para que el valor actual de la renta sea del $ 3.600.
En este caso la incognita es C (recordar C =?, TEM 1.2 %, b = 40, n = 12
y V A (0) = 3600)
3600
=
V A (0)
=
1 − 1 + i(p)
C
i(p)
=
1 − (1 + 0.012)
C
0.012
−n
+
b
i(p) 1 + i(p)
−12
=
+
n−1
!
n−1
1 + i(p)
−1
n−1
−
i(p)
1 + i(p)
12−1
40
0.012 (1 + 0.012)
11.1141448677 · C + 2381.9390949
12−1
(1 + 0.012)
0.012
−1
12 − 1
−
1 + 0.012
!
198
CHAPTER 8. RENTAS
Por lo tanto
C = 109.595557697
Lo que implica que el Sr. Daniel pagarle al Sr. Ignacio $ 109.60 el primer mes,
y luego ir incrementando en $ 40 cada cuota hasta la cuota 12.
Ejemplo 8.69 (Continuación del ejemplo (8.59)) Al Sr. Ignacio le ofrecen una
PS3 en $ 2.150, ¿Cuando podrá comprar la PS3?
La incognita ahora es el tiempo n necesario para juntar al menos $ 2.150
(recordar C = 100, TEM 1.2 %, b = 40, n =? y V F (n) ≥ 2150). Como ya
dijimos, no se puede despejar n de las fórmulas (8.26) y (8.30).
Resolveremos este problema de dos formas. Primero, asumiendo que n debe
ser entero, basta usar tanteo. Una buena semilla para comenzar el tanteo (y
Newon Raphson, si fuera el caso) puede ser obtenida a partir del hecho que
n
X
a + b (k − 1)
=
an + b
n
X
(k − 1)
k=1
k=1
=
(a − b) n + b
n (n + 1)
2
luego como a = C = 100 y b = 40 buscamos n tal que
2150 ≈ (100 − 40) n + 40
n (n + 1)
2
Para n = 5 tenemos que
60 · 5 + 40
5 (5 + 1)
= 900
2
para n = 8
8 (8 + 1)
= 1920
2
por lo que podemos usar como semilla para iniciar el tanteo n = 8 :
8
8
(1 + 0, 012) − 1
40
8 · 40 (1 + 0, 012)
V F (8) =
100 +
+ 8 · 40 −
0, 012
0, 012
0, 012
= 1981, 7057
60 · 8 + 40
Si usamos n = 9
9
V F (9)
=
=
(1 + 0, 012) − 1
0, 012
2425, 4861
100 +
9
40
9 · 40 (1 + 0, 012)
+ 9 · 40 −
0, 012
0, 012
Por lo tanto, El sr. Ignacio podrá comprarse la PS3 al final del 9no. perı́odo.
Poner dibujos!!!!!!!!!!!!!!!!!!!!!!!!!!!
8.9. RENTAS ARITMÉTICAS
199
Para comenzar usaremos
Por lo que aplicaremos Newton-Raphson para
n
1 + i(p) − 1
1 + i(p)
f (n) = C
+
b
i(p)
i(p)
!
n−1
1 + i(p)
−1
n−1
−
− V F (n)
i(p)
1 + i(p)
Por lo tanto
0
f (n) =
b
C
+
2
(p)
i(p)
i
!
1 + i(p)
n
b
ln 1 + i(p) − (p)
i
Para aplicar Newton-Raphson completamos la siguiente tabla, donde hemos
establecido como criterio de parada ε = 0.01, y una buena semilla para la raı́z
puede ser obtenida a partir del hecho que
n
X
a + b (k − 1)
=
k=1
an + b
n
X
(k − 1)
k=1
=
(a − b) n + b
n (n + 1)
2
luego como a = C = 100 y b = 40 buscamos n tal que
2150 ≈ (100 − 40) n + 40
n (n + 1)
2
Para n = 5 tenemos que
60 · 5 + 40
5 (5 + 1)
= 900
2
para n = 8
60 · 8 + 40
8 (8 + 1)
= 1920
2
la cual podemos usar como semilla
k
0
1
2
3
4
5
6
7
8
nk
f (nk )
f 0 (nk )
nk+1 = nk −
f (nk )
f 0 (nk )
|nk − nk+1 |
200
CHAPTER 8. RENTAS
Ejercicio 8.70 Un programa de televisión anuncia un premio $ 300 000, consistente 60 pagos mensuales, el primero de sólo $ 212, el segundo de $ 364, el
tercero de $ 516, y asi sucesivamente hasta el último pago a los 60 meses de $
9 180. Si la tasa que ud. puede conseguir es del 0.85 % mensual se pide:
1. ¿Realmente el premio consiste de $ 300 000?
2. ¿Qué prefiere, el esquema de pagos o $ 150 000 en efectivo?
3. De cuanto deberı́a ser el incremento mensual en el pago para que el valor
actual del esquema de pagos sea de $ 150 000.
4. De cuanto deberı́a ser el pago inicial para que el valor actual del esquema
de pagos sea de $ 150 000.
5. ¿A partir de que mes los pagos superan los $ 5 000?
Ejemplo 8.71
1. ¿Cuál es el valor final de este esquema de pagos?
2. En cuanto tiempo la suma de los nominales de los pagos superarán los $
150 000.
3. ¿Cuál es la tasa a la que somos indiferentes entre el esquema de pagos y
los $ 150 000 en efectivo?
4. ¿Cuál es número mı́nimo de pagos que deben hacerse con este esquema de
pagos para que su valor actual sea de al menos $ 150 000?
Ejercicio 8.72 Ud comienza ahorrando $ 1, al siguiente mes ahorra $ 2, al
siguiente $ 4, y asi sucesivamente. Si Usted gana $ 4 500 por mes, ¿cuántos
meses pasarán hasta que el nivel de ahorro requido por este esquema supere sus
ingresos? Si le pagan una TNA del 13.3 % ¿Cuánto habrá ahorrado hasta ese
momento?
Ejercicio 8.73 Cuanto debe depositar en diciembre para que su hijo pueda retirar a principios de enero $ 650, pero como estima que este año habrá una
inflación de al menos un 1% mensual, ud. desea que al siguiente mes pueda
retirar un 1.5% más, y ası́ sucesiamente hasta fin de año. Suponer que le pagan
una TEM del 0.85%.
Ejercicio 8.74 Suponga que usted tiene un contrato por 5 años con una empresa, ésta le ofrece tres opciones: 60 sueldos mensuales de $ 8 000, o 5 pagos
anuales de $ 90 000 comenzando hoy, o un único pago de $ 300 000 hoy. Ud
estima que la inflación promedio de los próximos 5 años será del 8% anual,
y que puede obtener una TEA del 10.5% para sus ahorros. Sabiendo esto, que
esquema de pago le resulta más atractivo.
Ejercicio 8.75 Ud. empieza a ahorrar unos $ 350 por mes, pero como esta
conciente de la inflación, ud. incrementa cada mes lo ahorrado en un 0.5%.
Además al comienzo de cada año aumenta en $ 100 la cantidad ahorrada a
diciembre del año anterior. Suponiendo una TEM del 0.9%, ¿Cuánto tendrá
ahorrado en 5 años?
8.10. RENTAS GEOMÉTRICAS
Ejercicio 8.76
201
Poner más ejercicios!!!!!!!!!!!!!!!!!
8.10
Rentas geométricas
8.11
Rentas variables en progresión geométrica
Consideremos el siguiente ejemplo
Ejemplo 8.77 El Sr. Daniel se compromete a cumplir el siguiente esquema de
12 pagos mensuales con el Sr. Ignacio. Un primera cuota de $ 100, una segunda
cuota de $ 110, una tercera cuota $ 121 y asi sucesivamente hasta la cuota doce.
¿Cuál es el monto de la cuota 9? Suponiendo una TEM del 1,2%. ¿Qué cantidad
deberı́a entregarle hoy el Sr. Daniel al Sr. Ignacio para sustituir este esquema
de pago? ¿Podrá comprarse el Sr. Ignacio una PS3 al cabo de un año con estos
fondos? (el precio de una PS3 es $ 3 200).
Este es un ejemplo de una renta variable, donde la variación sigue una ley
determinada: los términos de la renta forman una progresión geométrica
Actualización
V A(0)
0
C1
C2
C3
C10
C11
C12
100
100 · 1.1
(100 · 1.1)2
100 · (1.1)9
100 · (1.1)10
100 · (1.1)11
1
2
3
10
11
12
V F (12)
Capitalización
Necesitamos desarrollar fórmulas que nos permitan sumar expresiones de la
forma
V A (0) =
100
1.1 · 100
1.12 · 100
1.112 · 100
+
+
+
·
·
·
+
n
3
1 + 0.012 (1 + 0.012)2
(1 + 0.012)
(1 + 0.012)
Para esto estudiaremos las progresiones y las sucesiones aritméticas
Definición 8.78 Dados dos números reales a y r, se llama progresión geométrica
a toda sucesión finita de n términos de la forma
k
ar 0≤k≤n−1 := a, ar, ar2 , . . . , arn−1
202
CHAPTER 8. RENTAS
Si la sucesión es infinita, preferiremos llamarle sucesión geométrica
k
ar k≥0 := a, ar, ar2 , ar3 , . . .
Habitualmente al número a se le llama término inicial, y al número r se le llama
razón (común).
Nota 8.79 Toda progresión geométrica puede ser escrita de forma recursiva:
a1 = a
ak+1 = rak para 1 ≤ k ≤ n − 1.
Lo mismo ocurre con las sucesiones geométricas:
a1 = a
ak+1 = rak para k ≥ 1.
De hecho, de acuerdo con la teorı́a de relaciones recursivas que desarrollamos
en el capı́tulo 2 la forma de la solución de estas relaciones recursivas es
Ck = ark−1
Ejemplo 8.80 Los siguientes son ejemplos de progresiones y sucesiones geométricas
1. 2, 4, 8, 16, 32, . . . es una sucesión geométrica de término inicial a = 2 y
razón r = 2.
2. 2, −6, 18, −54, 162, −486, 1458, −4374 es una progresión geométrica de término
inicial a = 2 y razón r = −3.
1 1 1 1 1
3. 1, , , , , , . . .
2 4 8 16 32
4. 1, π, π 2 , π 3 , . . .
√
√
√
5. 2, 2, 23 , 4, 25 .
3
.
6.
5k 0≤k≤14
7.
n
o
k
2 (−1.5)
.
k≥0
8.
9.
a1
ak+1
=
=
−3
2ak
para 1 ≤ k ≤ 10.
a1
ak+1
=
=
0
5ak
para k ≥ 1
8.11. RENTAS VARIABLES EN PROGRESIÓN GEOMÉTRICA
203
Es fácil ver que
2, −6, 18, −54, 162, −486, 1458, −4374
es una progresión geométrica: la razón entre dos términos consecutivos se mantiene
constante:
18
−54
162
−486
1458
−4374
−6
=
=
=
=
=
=
= −3 = r
2
−6
18
−54
162
−486
1458
Mientras que el valor el primer término nos da el valor de a
a=2
La forma general de la progresión aritmética es
ak = 2 (−3)
k−1
para 1 ≤ k ≤ n
Para hallar n utilizamos el valor del último término:
2 (−3)
n−1
= −4374
de donde deducimos que n = 8. El signo sólo nos dice la paridad del término,
para el cálculo del n no hace falta considerarlo:
2 (−3)
n
n−1
=
−4374
n−1
=
4374
2 (−1) 3
lo que nos dice que n es par (pues si fuera impar tendrı́amos −2 · 3n−1 = 4374
lo que es absurdo).
Por lo tanto la progresión geométrica buscada es
ak = 2 · (−3)
k−1
para 1 ≤ k ≤ 8
Si la progresión/sucesión esta dada de forma recursiva
a1 = −7
ak+1 = −4ak para 1 ≤ k ≤ 11.
podemos conseguir su expresión cerrada aplicando la teorı́a de relaciones recursivas como se explica en la nota (8.79):
ak = −7 (−4)
(k−1)
para 1 ≤ k ≤ 11.
Ejercicio 8.81 Hallar el término inicial, el paso común y la forma general de
cada uno de los items que restan del ejemplo (8.80).
Ahora podemos responder a una de las preguntas planteadas en el ejemplo
(??): ¿Cuál es el monto de la cuota 9?
204
CHAPTER 8. RENTAS
La progresión geométrica que representa la renta dada en el ejemplo (??) es
Ck = 100 · 1.1k−1
por lo que el monto de la cuota 9 es
C9 = 100 · 1.18 = 214.358881
Las rentas variables en progresión geométrica, son aquellas rentas cuyos
términos forman una progresión geométrica, i.e.:
Ck+1 = rCk para k ≥ 0
(8.31)
Actualización
V A(0)
0
C1
C2
C3
Cn−2
Cn−1
Cn
C
rC
r2 C
rn−3 C
rn−2 C
rn−1 C
1
2
3
n−2
n−1
n
V F (n)
Capitalización
Supongamos que tenemos una sucesión de n capitales sujetos a una ley
geométrica como la expreseda en (8.31), sobre la que actua una tasa p-perı́odica
i(p) . Supongamos que los términos están disponibles a los p-perı́odos 1, 2, . . . n .
El valor actual de este tipo de renta no es otra cosa que la suma de los valores
actuales (al momento 0) de cada uno de los términos
V A (0)
=
=
=
=
C
rC
r2 C
rn−1 C
n
+
+
+
·
·
·
+
2
3
1 + i(p)
1 + i(p)
1 + i(p)
1 + i(p)
r
r2
rn−1
+
1+
+
·
·
·
+
n−1
2
1 + i(p)
1 + i(p)
1 + i(p)
rn
n
1−
1 + i(p)
C
r
1 + i(p) 1 −
1 + i(p)
−n
1 − rn 1 + i(p)
C
1 + i(p) − r
C
1 + i(p)
!
8.11. RENTAS VARIABLES EN PROGRESIÓN GEOMÉTRICA
de donde
−n
rn 1 + i(p)
−1
V A (0) = C
r−i−1
205
(8.32)
Por lo que el valor final es
(p)
V F (n) = V A (0) 1 + i
n
rn − 1 + i(p)
=C
r−i−1
n
(8.33)
La situación tı́pica es que la razón geométrica tome la forma
r =1+t
donde t es una tasa (de efectiva si es positiva, y de descuento si es negativa). La
fórmulas anteriores quedan
−n
1 + i(p)
−1
V A (0) = C
t−i
n
n
(1 + t) − 1 + i(p)
V F (n) = C
t−i
n
(1 + t)
(8.34)
(8.35)
Mientras que si la razón geometrica es un factor de actualización
r=
1
−1
= (1 + t)
1+t
las fórmulas anteriores son
−n
(1 + t) 1 + i(p)
−1
1
−
i
−
1
1+t
n
−n
(1 + t) − 1 + i(p)
C
1
1+t − i − 1
V A (0)
= C
(8.36)
V F (n)
=
(8.37)
Nota 8.82 Las fórmulas obtenidas corresponden a una renta postpagable, para
rentas prepagables se deben realizar las correspondientes modificaciones, las cuales
no deberı́an ser difı́ciles de realizar por parte del lector.
Ahora podemos responder a las restantes preguntas que se nos plantearon
en el ejemplo (??). El Sr. Daniel deberı́a entregar hoy al Sr. Ignacio $ 1 954.38,
el valor actual de la renta (recordar C = 100, TEM 1.2%, r = 1.1 y n = 12)
V A(0)
−n
−1
rn 1 + i(p)
= C
r−i−1
−12
1.112 (1 + 0.012)
−1
= 100
1.1 − 0.012 − 1
= 1954.38296033
206
CHAPTER 8. RENTAS
Por otro lado, el Sr. Ignacio (si va ahorrando el dinero a una TEM del 1.2%)
juntará al cabo de un año la suma de $ 2 255.15 (lo cual no es suficiente como
para comprarse la PS3), pues
n
rn − 1 + i(p)
V F (12) = C
r−i−1
12
1.112 − (1 + 0.012)
= 100
1.1 − 0.012 − 1
= 2255.15199151 = 1954.38296033 · 1.01212
Nota 8.83 En las fórmulas de la (8.32) a la (8.37) aparecen 5 variables:V A
o V F, C, n, r o t, y i(p) . Las dos primeras no presentan dificultad, pero las
dos últimas: r o t, y i(p) , al no ser posible despejarlas, requieren de métodos
númericos (Newton-Raphson) para estimar sus valores. Mientras que n es despejable de las fórmulas de valor inicial pero no de las fórmulas de valor final.
Ejemplo 8.84 (Continuación del ejemplo (??)) De cuanto debe ser la cuota
inicial si el Sr. Ignacio desea comprarse la PS3 (i.e. desea juntar al menos $ 3
200 al cabo de 12 meses).
En este caso, deseamos averiguar el valor de C (recordar TEM 1.2 %, r = 1.1,
n = 12 y V F (12) = 3200)
3200
= V F (12)
n
rn − 1 + i(p)
= C
r−i−1
12
1.112 − (1 + 0.012)
= C
1.1 − 0.012 − 1
= 22.5515199152C
Por lo tanto
C = 141.897309451
Es decir, el primer pago del Sr. Daniel debe ser de $ 141.90. Con este pago
inicial el Sr. Ignacio junta al cabo de 12 meses la suma de $ 3 200.06, i.e. se
puede comprar la PS3 y le sobran 6 centavos.
Ejemplo 8.85 (Continuación del ejemplo (??)) Sabemos que el valor actual
de la renta que le paga el Sr. Daniel al Sr. Ignacio es de $ 1 954.38 (recordar
C = 100, TEM 1.2%, r = 1.1 y n = 12). Ahora nos preguntamos cuanto deberı́a
durar la renta si el valor actual de la misma queremos que sea al menos $ 2 900.
En este caso buscamos un n tal que
−n
−1
rn 1 + i(p)
≥ 2900
V A(0) = C
r−i−1
8.11. RENTAS VARIABLES EN PROGRESIÓN GEOMÉTRICA
207
En este caso hay que ser cuidadosos, si r − i − 1 < 0, al realizar el pasaje
de términos la desigualdad se da vuelta. Como en nuetro caso r − i − 1 =
1.1 − 0.012 − 1 = 0.098 > 0 esto no ocurre.
−n
rn 1 + i(p)
Ejemplo 8.86 (Continuación del ejemplo (??)) Como acabamos de ver, en 12
meses el Sr. Ignacio no alcanza a ahorrar lo necesario para comprarse la PS3.
¿Cuántos meses deberı́a durar este esquema de pagos para que el Sr. Ignacio
pueda comprarse su preciada PS3?
En este caso buscamos un n tal que
rn − 1 + i(p)
C
r−i−1
n
≥ 3200
de donde
Ejemplo 8.87 (Continuación del ejemplo (8.59)) De cuánto debe ser el término
inicial para que el valor actual de la renta sea del $ 3 600.
En este caso la incognita es C (recordar C =?, TEM 1.2 %, b = 40, n = 12
y V A (0) = 3600)
3600
=
V A (0)
=
1 − 1 + i(p)
C
i(p)
=
1 − (1 + 0.012)
C
0.012
−n
+
b
i(p) 1 + i(p)
−12
=
+
n−1
!
n−1
1 + i(p)
−1
n−1
−
i(p)
1 + i(p)
12−1
40
0.012 (1 + 0.012)
11.1141448677 · C + 2381.9390949
12−1
(1 + 0.012)
0.012
−1
12 − 1
−
1 + 0.012
Por lo tanto
C = 109.595557697
Lo que implica que el Sr. Daniel pagarle al Sr. Ignacio $ 109.60 el primer mes,
y luego ir incrementando en $ 40 cada cuota hasta la cuota 12.
Ejemplo 8.88 (Continuación del ejemplo (8.59)) Al 5to mes, al Sr. Ignacio le
ofrecen una PS3 en $ 2 150, ¿Cuando podrá comprar la PS3?
!
208
CHAPTER 8. RENTAS
La incognita ahora es el tiempo n (recordar C = 100, TEM 1.2 %, b = 40,
n =? y V F (n) ≥ 2150), necesario para juntar al menos $ 2 150. Como ya
dijimos, no se puede despejar n de las fórmulas (8.26) y (8.30). Por lo que
aplicaremos Newton-Raphson para
!
n−1
1 + i(p)
−1
n−1
−
− V F (n)
i(p)
1 + i(p)
n
1 + i(p) − 1
1 + i(p)
+ b (p)
f (n) = C
(p)
i
i
Por lo tanto
0
f (n) =
b
C
+
2
(p)
i
i(p)
!
1 + i(p)
n
b
ln 1 + i(p) − (p)
i
Para aplicar Newton-Raphson completamos la siguiente tabla, donde hemos
establecido como criterio de parada ε = 0.01, y una buena semilla para la raı́z
puede ser obtenida a partir del hecho que
n
X
a + b (k − 1)
=
k=1
an + b
n
X
(k − 1)
k=1
=
(a − b) n + b
n (n + 1)
2
luego
2150 ≤ (100 − 40) n + 40
n (n + 1)
2
la raı́z
k
nk
f (nk )
f 0 (nk )
nk+1 = nk −
f (nk )
f 0 (nk )
|nk − nk+1 |
0
1
2
3
4
5
6
7
8
Ejemplo 8.89 Un programa de televisión anuncia un premio $ 300 000, consistente un sueldo fijo a mes vencido de $ 2 500 mensuales durante 10 años.
¿Realmente el premio consiste de $ 300 000?. Si la tasa que ud. puede conseguir
es del 0.85% mensual, y la inflación mensual estimada es del 0.7%. mensual.
8.11. RENTAS VARIABLES EN PROGRESIÓN GEOMÉTRICA
209
Como antes sólo debemos calcular el valor actual del esquema de sueldos.
Debemos usar la fórmula (8.36) ya que la inflación actua como un factor de
actualización (ver nota ([?]) :
−120
V A (0) = 2500
(1 + 0.007)
1
1+0.007
−120
(1 + 0.0085)
− 0.0085 − 1
−1
= 136427.76
Al tener en cuenta la inflación, inclusive es mejor que nos den la “mitad” del
premio en efectivo que en 120 mensualidades (suponiendo una tasa de inflación
anual constante del 8,7 %, si la inflación es mayor, el valor actual del premio
inclusive será menor.
Observe que si hubieramos usado la tasa de inflación como una tasa de
descuento, hubieramos cometido un error, pero uno pequeño:
120
V A (0) = 2500
−120
(1 − 0.007) (1 + 0.0085)
−0.007 − 0.0085
−1
= 136147.74
Por eso a veces en estos tipos de problemas se suele pensar la tasa de inflación
como una tasa de descuento (este error disminuye a medida que aumentamos la
frecuencia de capitalización ¿Por qué?).
Ejemplo 8.90 Ud. empieza a ahorrar unos $ 450 por mes, pero como esta
conciente de la inflación, ud. incrementa cada mes lo ahorrado en un 1%.
Suponiendo una TEM del 1.1%, ¿Cuánto tendrá ahorrado en dos 2 años?
Sólo debemos calcular el valor final de una renta geométrica
24
V F (24) = 450
24
(1 + 0.01) − (1 + 0.011)
0.01 − 0.011
= 13733.08263
Ejemplo 8.91 Si la inflación anual estimada para los próximos 2 años es del
9.5% anual, ¿Cuál es el valor real (en pesos de hoy) de los $ 11 063.86 que
tendremos en dos años?
Simplemente hay que deflactar los $ 11 063.86 dos años a la tasa anual de
inflación
11063.86
2 = 9927.38
(1 + 0.095)
i.e., con los $ 11 063.86 podrá comprar dentro de dos años, más o menos lo
mismo que podrı́a aquirir hoy con $ 9 927.38.
0.007591534
450
1 + 0.007591534
: 11355. : 10080.0 : −77. 623
24
24
1+0.001
− (1 + 0.011)
1+0.007591534
1+0.001
1+0.007591534 − 0.011 − 1
210
CHAPTER 8. RENTAS
Ejercicio 8.92 Ud comienza ahorrando $ 1, al siguiente mes ahorra $ 2, al
siguiente $ 4, y asi sucesivamente. Si Usted gana $ 4 500 por mes, ¿cuántos
meses pasarán hasta que el nivel de ahorro requerido por este esquema supere
sus ingresos? Si le pagan una TNA del 13.3 % ¿Cuánto habrá ahorrado hasta
ese momento?
Ejercicio 8.93 Cuánto debe depositar en diciembre para que su hijo pueda retirar a principios de enero $ 650, pero como estima que este año habrá una
inflación de al menos un 1% mensual, ud. desea que al siguiente mes pueda
retirar un 1.5% más, y ası́ sucesiamente hasta fin de año. Suponer que le pagan
una TEM del 0.85%.
Ejercicio 8.94 Suponga que usted tiene un contrato por 5 años con una empresa, ésta le ofrece tres opciones: 60 sueldos mensuales de $ 8 000, o 5 pagos
anuales de $ 90 000 comenzando hoy, o un único pago de $ 300 000 hoy. Ud
estima que la inflación promedio de los próximos 5 años será del 8% anual,
y que puede obtener una TEA del 10.5% para sus ahorros. Sabiendo esto, que
esquema de pago le resulta más atractivo.
Ejercicio 8.95 Ud. empieza a ahorrar unos $ 350 por mes, pero como esta
conciente de la inflación, ud. incrementa cada mes lo ahorrado en un 0.5%.
Además al comienzo de cada año aumenta en $ 100 la cantidad ahorrada a
diciembre del año anterior. Suponiendo una TEM del 0.9%, ¿Cuán
Ejercicio 8.96 }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
tendrá ahorrado en 5 años?
8.12
Inflación: su efecto sobre rentas
En esta sección estudiaremos el efecto de la inflación sobre las rentas. Caracterizaremos el efecto de la inflación sobre el valor actual de una renta, y
estudiaremos como diseñar una renta constante en poder adquisitivo.
Comenzaremos con el efecto de la inflación sobre el valor actual de una renta
vencida constante de n términos.
Dada una operación financiera con un horizonte temporal de t años (tiempo
que resta para la finanlización de la misma). Supongamos que disponemos de
una estimación de la inflación para los próximos t años, dada por la una tasa
p-perı́odica de inflación esperada π (p) . La inflación socaba el poder adquisitivo
del dinero, por lo tanto, ajusta hacia abajo el valor actual de cualquier flujo de
fondos futuro. La forma de realizar esta corrección es expresar todos los capitales
en pesos constantes (al dı́a de hoy). Como ya vimos, el valor en pesos de hoy
(pesos constantes) de una capital C disponible dentro de t años es
C
1 + π (p)
pt
8.12. INFLACIÓN: SU EFECTO SOBRE RENTAS
211
Por lo que el flujo de fondos de una renta vencida constante de n términos de
capital C se traduce a una renta geométrica cuyos terminos son de la forma
C
1 + π (p)
k , con k = 1, . . . , n
Poner dibujo!!!!!!!!!!!!!!!!!!!!!!!!!!!
De aqui que el valor actual de la renta sujeta a una tasa efectiva i(p) y a una
inflación esperada π (p) se puede calcular usando (8.36)
−n
1 + π (p) 1 + i(p)
−1
V A (0) = C
−1
(p)
(p)
1+π
−i −1
Ejemplo 8.97 Analicamos de nuevo el ejemplo del programa de televisión,
agregando la inflación esperada para los próximos 10 años (ejemplo 8.6): Un
programa de televisión anuncia un premio $ 300.000, consistente un sueldo fijo
a mes vencido de $ 2.500 mensuales durante 10 años. ¿Realmente el premio
consiste de $ 300.000? Si la tasa que ud. puede conseguir es del 0,85% mensual
y ud. estima que la inflación mensual de los próximos 10 años sera del 0,75%
mensual, que prefiere, el esquema de sueldos o $ 200.000 en efectivo (en caso
de ganar el concurso correspondiente).
Habiamos calculado que el valor actual de la renta de sueldos considerando
la tasa del 0,85% mensual y sin tener en cuenta la inflación era de $ 187.602,16.
Ahora veamos la corrección a la baja que debemos hacer al tener encuenta la
inflación:
−120
V A(hoy) = 2.500
[(1 + 0, 0075) (1 + 0, 0085)]
(1 + 0, 0075)
−1
−1
− 0, 0085 − 1
= $133.632, 619721
Esto nos dice que el premio de “$ 300.000” en realidad hoy vale un aproximado de $ 13.3632,6, y por lo tanto si hoy le ofrecen $ 200.000 en efectivo
deberı́a aceptarlos gustoso.
La estimación de la inflación futura o esperada esta fuera del alcance de este
libro, y en general la supondremos dada (aunque advertimos al lector que esta
no es una tarea menor).
Nota 8.98 El análisis anterior es bastante incompleto, cada vez que se trabaja con una variable macroeconómica futura (como la inflación) se debe hacer
al menos lo que se conoce como análisis de sensibilidad. Además estimar la
inflación es un arte difı́cil, y hasta los mejores analistas suelen cometer errores groseros. En materia de predicción del comportamiento de varias variables
macroeconómicas aún nos falta un largo camino por recorrer y las técnicas actuales no son del todo satisfactorias. De todas formas informamos al lector que
podrá encontrar algunas técnicas para realizar estimaciones para la inflación
futura y análisis de sensibilidad en libros (o cursos) de evaluación de proyectos
de inversión, econometrı́a, o finanzas.
212
CHAPTER 8. RENTAS
Ejemplo 8.99 El gobierno dona a una entidad sin fines de lucro $ 60.000, en
tres cuotas mensuales y consecutivas, depositando la primera a principios del
mes que viene. Deseamos estimar el valor actual de la misma, estimando que la
inflación mensual será
π 1 2, 7%
π 2 1, 8%
π 3 3, 1%
y que la entidad puede obtener una TEM del 2,4% por sus depósitos.
Hay tres formas de resolver este problema, cada una dará un resultado diferente, pero como hablamos de estimaciones, no hay razones para preferir uno al
otro.
El primer método consiste simplemente de sumar el valor actualizado y deflactado de cada término
V A (0)
=
20.00
20.000
20.000
+
+
(1 + 0, 024) (1 + 0, 027) (1 + 0, 024)2 (1 + 0, 027) (1 + 0, 018) (1 + 0, 024)3 (1 + 0, 027) (
19.474, 2
19.129, 86
18554, 66
+
+
3
(1 + 0, 024) (1 + 0, 024)2
(1 + 0, 024)
19.017, 77 + 18.243, 66 + 17.280, 38
=
54.541, 80
=
=
El segundo método consiste en tomar una inflación mensual promedio
(12)
π media =
0, 027 + 0, 018 + 0, 031
= 0, 0253333333
3
para usar luego la fórmula de valor actual geométrico
V A (0)
=
=
20.000
[(1 + 0, 0253333333) (1 + 0, 024)]
(1 + 0, 0253333333)
55.850, 88
−1
−3
−1
− 0, 024 − 1
Un tercer método consiste en hallar la tasa mensual equivalente, i.e., la que
satisface
3
1 + π (12) = (1 + 0, 027) (1 + 0, 018) (1 + 0, 031)
de donde
π (12)
=
p
3
1, 077896066 − 1
=
0, 02531889851
y volver a usar la fórmula de valor actual geométrico
V A (0)
=
=
20.000
[(1 + 0, 02531889851) (1 + 0, 024)]
(1 + 0, 02531889851)
55.851, 64
−1
−3
−1
− 0, 024 − 1
8.12. INFLACIÓN: SU EFECTO SOBRE RENTAS
213
En cualquier caso, podemos decir que el valor actual de esta renta, considerando
la inflación esperada, ronda los $ 55.000.
Ahora veremos como diseñar una renta con poder adquisitivo constante.
Supongamos que deseamos una renta (vencida) de n términos, cada uno de los
cuales debe tener el mismo poder adquisitivo que un capital C hoy. Para hacer
esto necesitamos tener una estimación de la inflación a lo largo del horizonte
temporal de la renta.
poner dibujo!!!!!!!!!!!!!!!!!!!
Si estimamos la inflación en π (p) la renta deberá tener términos forma
k
C 1 + π (p)
para 1 ≤ k ≤ n
pues el valor al dı́as de hoy de cada uno de estos términos es C. Por lo que
podemos aplicar la teorı́a de rentas geométricas, donde la fórmula que mejor se
ajusta es la (8.34)
n
−n
1 + π (p)
1 + i(p)
−1
V A (0) = C
(p)
(p)
π −i
Ejemplo 8.100 Cuánto debemos depositar hoy, principios de diciembre, para
que nuestro hijo pueda retirar a principios de cada mes el año que viene el equivalente a $ 850 de hoy, si usted estima que durante el próximo año la inflación
mensual rondrá en el 3.5%. La tasa que podemos obtener por nuestros ahorros
es una TEM del 1.5%.
El flujo de fondos de esta renta es
poner dibujo!!!!!!!!!!!!
Para averiguar cuanto debemos depositar debemos calcular el valor actual
de la misma, para lo cual no hay más que aplicar la fórmula que acabamos de
desarrollar
12
V A (0)
=
=
−12
(1 + 0, 035) (1 + 0, 015)
0, 035 − 0, 015
11.213, 1498
850
−1
Por lo que debemos depositar a principios de diciembre aproximadamente $
11.213 para que nuestro vástago tenga una nivel de vida constante (equivalente
a $ 850 de hoy) durante el año que viene (¡más vale que apruebe todos los
parciales!).
Nota 8.101 Unas palabras de advertencia: hoy por hoy, con el desarrollo que
tiene la economı́a, estimar la inflación futura (a largo plazo) es virtualmente
imposible. Basta chequear los pronósticos contra la inflación medida efectivamente. Por lo que se debe ser muy cuidadoso con los análisis a largo plazo, y
de una u otra forma, hay que incorporar el riesgo. La parte de la matemática
financiera que se ocupa del riesgo, será motivo de un segundo volumen dentro
de muchos, muchos años.
214
CHAPTER 8. RENTAS
8.13
Otros tipos de rentas.
8.14
Rentas a capitalización continua
En esta sección desarrollaremos fórmulas para manejar rentas a capitalización
continua. Comencemos con la las rentas pospagables o vencidas. El valor actual
de una renta constante vencida (o pospagable) de n términos de monto C a
una tasa nominal continua J que comienza en el momento 0 y términa en el
momento n, midiendo el tiempo en p-perı́odos es
poner dibujo
V A (0) =
n
X
n
k
Ce−J p = C
1 − e−J p
J
ep − 1
k=1
Similarmente
n
V F (n) = V A (0) eJt = C
eJ p − 1
J
ep − 1
poner un par de ejemplos
Ejercicio 8.103 poner unos ejercicios
Ejemplo 8.102
El valor actual de una renta prepagable constante de n términos de montante
C disponibles a los momentos 0, 1, 2, . . . , n − 1 (p-perı́odos) a una tasa nominal
continua J es
n
1 − e−J p Jp
e
V A (0)prepagable = C J
ep − 1
Mientras que el valor final es
n
V F (n)prepagable = C
eJ p − 1
J
p
J
ep
e −1
poner dibujo!!!!!!!!!!!!!
poner un par de ejemplos
Ejercicio 8.105 poner unos ejercicios
Ejemplo 8.104
El valor actual de una renta aritmética pospagable a interés continuo no es
más que sumar el valor actual de cada uno de los términos involucrados. Supongamos que tenemos una sucesión de n capitales sujetos a una ley aritmética como
la expreseda en (8.23), sobre la que actua una tasa nominal anual continua J.
Supongamos que los términos están disponibles a los p-perı́odos 1, 2, . . . n .
poner dibujo!!!!!!!!!!!!!!!!!!!!!
8.14. RENTAS A CAPITALIZACIÓN CONTINUA
215
El valor actual de esta renta es
V A (0)
1
2
3
n
= Ce−J p < + (C + b) e−J p + (C + 2b) e−J p + · · · + (C + (n − 1) b) e−J p
n
n−1
1
2
1
1 − e−J p
= C J
+ be−J p e−J p + 2e−J p + · · · + (n − 1) e−J p
ep − 1
Como
m
X
1 rm − 1
k
m
=
− m
2
k
m−1
r
r
r (r − 1)
(r − 1)
k=1
tenemos que
1
2
e−J p + 2e−J p + · · · + (n − 1) e−J
n−1
p
=
1
eJ
n−2
p
n−1
n−1
eJ p − 1
1
2 − J n−1 J 1
e p e p −1
eJ p − 1
Luego
V A (0) = C

−J n
p
J n−1
p
−J n
p
n−1 e
−1
(n − 1) e

+ b e−J p 2 −
1
1
eJ p − 1
e −1
eJ p − 1
1−e



J
p
poner un par de ejemplos
Ejercicio 8.107 poner unos ejercicios
Ejemplo 8.106
Supongamos que tenemos una sucesión de n capitales sujetos a una ley
geométrica sobre la que actua una tasa nominal anual continua J. Supongamos
que los términos están disponibles a los p-perı́odos 1, 2, . . . n .
poner dibujo!!!!!!!!!!!!!!!!!!!!!
El valor actual de este tipo de renta no es otra cosa que la suma de los valores
actuales (al momento 0) de cada uno de los términos
V A (0)
1
2
3
n
1
−J p
= Ce
= C
1 − rn e−J p
1
1 − re−J p
n
1 − rn e−J p
1
eJ p − r
Por lo que el valor final es
n
V F (n) = C
eJ p − r n
1
eJ p − r
poner un par de ejemplos
Ejercicio 8.109 poner unos ejercicios
Ejemplo 8.108
n
= Ce−J p + rCe−J p + r2 Ce−J p + · · · + rn−1 Ce−J p
n−1
2
1
1
= Ce−J p 1 + re−J p + r2 e−J p + · · · + rn−1 e−J p
Chapter 9
Préstamos
9.1
Introducción
En mayor o menor medida todos sabemos que es un préstamo. Igual damos la
siguiente definición para establecer un marco común de referencia:
Definición 9.1 Se llama préstamo a la operación financiera consistente en
la entrega de una cantidad dada de dinero (C0 ), llamado principal (o deuda),
por parte de una persona (fı́sica o jurı́dica), llamado prestamista o acreedor,
a otra persona (fı́sica o jurı́dica), llamado prestatario o deudor, quién se
compromete a amortizar el principal
Nota 9.2 Se llama amortizar al proceso financiero mediante el cual se cancela, generalmente de manera gradual, una deuda por pagos perı́odicos, lo cuales
pueden ser iguales o diferentes.
De todo el espectro posible de esquemas de reembolsos de préstamos slo
estudiaremos dos variantes, de acuerdo a como son cobrados los intereses:
1. Préstamos comerciales: son los préstamos donde se aplica la tasa directamente sobre el capital inicial (durante el perı́odo de tiempo pactado para
el préstamo) y el monto de las cuotas del reembolso se calculan dividiendo
este monto por el número de términos
2. Préstamos a interés sobre saldos: son los préstamos donde la tasa se
aplica sobre, lo que se conoce como, capital pendiente (que es el dinero
que efectivamente se debe después de cada pago).
9.2
Préstamos comerciales
En la Argentina el sistema de préstamo comercial es usado principalmente por
pequeños comercios y algunas instituciones financieras (conocidad precisamente
216
9.2. PRÉSTAMOS COMERCIALES
217
con ese nombre: financieras). El mayor inconveniente deudor (tambin llamado
préstatario) con estos sistemas es que no reconocen los pagos parciales efectuados, lo que lleva a que no exista equivalencia financiera (a la tasa declarada)
entre el total financiado (o monto prstado) y el flujo de capitales que amortiza
la deuda.
Analicemos la siguiente situacin:
Ejemplo 9.3 Una tienda anuncia que sólo cobra un recargo del 20% anual sobre
las compras en cuotas. Ud. realiza una compra por $ 1.000, y desea pagarla en
12 cuotas mensuales y consecutivas. La dueña de la tienda le plantea el siguiente
esquema de pago: “Son $ 1.000, más un recargo del 20%, nos da $ 1.200, ahora
lo dividimos por el número de cuotas lo que nos da doce cuotitas mensuales de
$ 100”.
Del ejemplo es claro que los elementos que conforman un préstamo comercial
son:
1. Importe del préstamo (o deuda): C0 .
2. Tasa de interés (directa) p-perı́odica cobrada: δ (p) .
3. Duración de la operación (expresada en años): t
4. Número de cuotas: n
5. Monto de cada uno de los pagos: a
El monto de cada uno de los n pagos es determinado por la expresión
pt
C0 1 + δ (p)
a :=
(9.1)
n
Por ejemplo, esta fue la cuenta que hizo la dueña de la tienda del ejemplo
anterior
1.000 (1 + 0, 2)
1.200
a=
=
= $ 100
12
12
Si consideramos la renta generada
y calculamos su valor actual con la tasa
√
mensual equivalente i(12) = 12 1 + 0.2 − 1 = 0, 0153094705, obtenemos
100
1 − (1 + 0, 0153094705)
0, 0153094705
−12
= $ 1088, 65075816
Lo cual nos da la primera advertencia: a la tasa declarada la renta generada y el
desembolso del préstamo (o deuda) no son financieramente equivalentes. Veamos
que siempre ocurre que el valor actual de la renta es mayor que el desembolso
del préstamo (o monto de la deuda).
Por razones claridad (y sin pérdida de generalidad), podemos suponer que
el número de cuotas n coincide con la cantidad de q-perı́odos que caben en
218
CHAPTER 9. PRÉSTAMOS
t años (la duración de la operación) para algún q de los habituales, i.e., q ∈
{1, 2, 3, 4, 6, 12, 52, 360, 365}. De hecho, as ocurre casi siempre en las operaciones
a pr’estamo comercial. Por ejemplo 12 cuotas en un año nos dice que las cuotas
son mensuales, mientras que 12 cuotas en 3 años nos dice que las cuotas son
trimestrales, 9 cuotas en año y medio nos indica que las cuotas son bimestrales.
Por lo tanto asumiremos que
frecuencia de los subperı́odos × tiempo en años
=
números de cu
qt = n
(p)
Dada δ , la tasa de interés (directa) p-perı́odica cobrada, calculamos la
tasa directa q-perı́odica asociada
r
p
(q)
δ = q 1 + δ (p) − 1
Con ambas tasa podemos calcular a pues
qt
pt
C0 1 + δ (q)
C0 1 + δ (p)
=
a=
n
n
Ahora, el valor actual de la renta asociada es siempre mayor que C0 :
−qt
1 − 1 + δ (q)
a
> C0
δ (q)
Para corroborarlo basta con hacer unas cuentas
−n
−qt
1 − 1 + δ (q)
1 − 1 + δ (q)
= a
a
δ (q)
δ (q)
−n
n
C0 1 + δ (q) 1 − 1 + δ (q)
=
n
δ (q)
n
(q)
−1
C0 1 + δ
=
(q)
n
δ{z
|
}
>n
>
C0
(1+x)n −1
x
Recordar que el multiplicador
> n si n > 1 y x > 0 ver 8.13.
(q)
Por otro lado, la tasa q-perı́odica i
a la cual la renta de n términos a
tiene un valor actual de C0 es siempre mayor que la tasa directa q-perı́odica δ (q)
equivalente a la tasa (directa) declarada pues
−qt
−qt
1 − 1 + δ (q)
1 − 1 + i(q)
a
> C0 = a
i(q)
δ (q)
9.2. PRÉSTAMOS COMERCIALES
219
de donde obtenemos que
−qt
1 − 1 + δ (q)
δ (q)
1 − 1 + i(q)
>
i(q)
−qt
de donde se puede concluir que
i(q) > δ (q)
Recordar que este multiplicador, fijado n, es una función estrictamente decreciente de la tasa (ver seccin 8.4.
Verifiquemos que la tasa declarada es menor que la tasa efectiva real en el
ejemplo que venimos trabajando. Primero encontramos la tasa efectiva mensual
(real) de la renta generada por el esquema de pagos, i.e., la tasa i12 que verifica:
−12
1 − 1 + i(12)
= 1.000
100
i(12)
Cómo ya sabemos, es necesario usar métodos númericos (Newton-Raphson o
secante) para hallarla:
i(12) = 0, 0292285407616 > 0, 0153094705 = δ (12)
Lo que nos una tasa anual
i = 0, 412998984 > 0, 2 = δ
Finalmente los términos de la renta tendrián que ser de $ 91,86 para que a
la tasa declarada el valor actual de la renta sea $ 1.000, pues
1.000 · 0, 0153094705
−12
1 − (1 + 0, 0153094705)
= $91, 8568229987
Ejercicio 9.4 El Sr. Nicolás solicita un préstamo de $ 15.000 en su obra social,
la cual utiliza el sistema comercial y cobra una tasa anual del 26.5 %. Plantear
el préstamos para 12, 18, 24, 36, y 60 meses (cuotas mensuales). En cada caso
dar el valor actual de la renta generada y averiguar la tasa real que cobra la
obra social.
Ejercicio 9.5 La Srta. Jésica compro unos zapatos en la zapaterı́a top del momento. Los zapatos cuestan $ 650. Gonzalo, el vendedor, le dice “no te preocupes
querida, los podes pagar en 6 cuotitas mensuales de $ 120”. Si la tienda usa interés directo ¿Cuál es el interés directo semestral cobrado?.
Ejercicio 9.6 A la Srta. Jésica le es más facil pagar pagar $ 30 cada semana,
en lugar de los $ 120 por mes. El dueño de la tienda acepta sin ninguna queja
¿Por qué? (Calcular la tasa real de ambas operaciones o el valor actual de cada
una de las rentas generadas).
Agregar más ejercicios.
220
CHAPTER 9. PRÉSTAMOS
9.3
Préstamos a interés sobre saldos
Los elementos que componen un préstamo a interés sobre saldos son:
1. C0 el importe del préstamo (llamado principal o deuda).
2. n número de cuotas en las que se devolverá el préstamo más los intereses
generados.
3. a1 , a2 , . . . , an sucesión de términos amortizativos, son lo pagos acordados que el prestatario realiza a fin de cancelar el préstamo más los intereses
generados.
4. t0 , t1 , t2 , . . . tn sucesión de plazos en los que el dinero cambia de manos.
t0 es el momento en el cual el préstamista le entrega la cantidad C0 al
prestatario. El resto de los tiempos corresponden a la sucesión de términos
amortizativos (los pagos realiza el prestario).
5. i1 , i2 , . . . , in la sucesión de intereses que se aplican en cada uno de los
perı́odos:
ik corresponde al interés cobrado en el perı́odo k
recordar que el perı́odo k comienza en el momento tk−1 y termina en el
momento tk .
PONER DIBU>!!!!!!!!!!!!!!!!!!!!!!!!
En un préstamo tı́pico, dada C0 , la sucesión de tiempos t0 , t1 , t2 , . . . tn y la
sucesión de intereses a ser aplicados i1 , i2 , . . . , in , el problema es determinar el
monto de los pagos que deberá abonar el prestatario, los cuales deben generar
un flujo de fondos financieramente equivalente a la candidad prestada C0 :
a2
an
a1
+
+ ··· +
C0 =
1 + i1
(1 + i1 ) (1 + i2 )
(1 + i1 ) (1 + i2 ) · · · (1 + in )
n
X
ah
(9.2)
=
h
Y
h=1
(1 + ik )
k=1
Cada término amortizativo ah tiene en principio dos componentes: una destinada a cancelar los intereses generados en el correspondiente perı́odo, y la otra
a destinada a disminuir el monto de la deuda, las cuales reciben los nombres de
cuota de interés y cuota de capital (o de amortización) respectivamente
Cuota de interés
Se encarga de cancelar
los intereses
ah
|{z}
=
z}|{
Ih
+
Ah
|{z}
Término amortizativo
Cuota de capital
Es lo que efectivamente
Se encarga ir cancelando
paga el prestatario
el capital adeudado
(9.3)
9.3. PRÉSTAMOS A INTERÉS SOBRE SALDOS
221
De la definición de cuota de interés se deduce
Ih
=
(saldo al pricipio del periodo anterior) por (el interés del perı́odo)
(9.4)
=
(saldo al momento h − 1) ih
(9.5)
Por definición de cuota de capital, si deseamos alguna vez cancelar el préstamo,
debe ocurrir que
C0 = A1 + A2 + · · · + An
(9.6)
El monto adeudado al momento h es conocido como capital pendiente Ch ,
es la cantidad de dinero que se debe luego de pagar el término amortizativo ah .
Como perı́odo a perı́odo se deben cancelar los intereses generados, para cada
1 ≤ h ≤ n se cumple que
Ch := C0 − A1 − A2 − · · · − Ah = Ah+1 + Ah+2 + · · · + An
(9.7)
de donde se deduce con facilidad la siguiente relación recursiva
Ch = Ch−1 − Ah
(9.8)
Otra forma recursiva de para calcular el capital pendiente al momento h resulta
de la siguiente observación: lo que se debe al momento h debe ser igual a lo que
se debı́a en el perı́odo anterior h − 1, capitalizado al perı́odo h, menos el pago
realizado:
Ch = Ch−1 (1 + ih ) − ah
(9.9)
También podemos calcular el capital pendiente al momento h actualizando todos
los pagos que restan por realizar
Ch =
n
X
j=h
aj
j
Y
(9.10)
(1 + ik )
k=h
Ahora podemos reescribir la ecuación (9.4) para la cuota de interés en
términos del capital pendiente al perı́odo anterior
Ih = Ch−1 ih
(9.11)
Nota 9.7 Esta es la razón por la cual decimos que estos sistemas de préstamos
cobran los intereses sobre saldos.
Se llama total amortizado al perı́odo h a la suma de las cuotas de amortización pagadas hasta el momento h
M h = A1 + A2 + · · · + Ah
(9.12)
Por lo tanto, para todo momento h (entre 0 y n) se debe cumplir que la suma
entre el capital pendiente y el total mortizado debe ser igual al capital prestado
C0 = Ch + Mh
222
CHAPTER 9. PRÉSTAMOS
Aqui se está implı́cito que M0 = 0.
Si los intereses cobrados al prestamista permanecen constantes:
i1 = i2 = · · · = in = i
el cálculo del monto de cada uno de los términos amortizativos se simplifica al
suponer constante alguna de la partes de (9.3):
an = In + An
esto da origen a tres tipos de préstamos dentro de los que cobran los intereses
sobre saldos.
1. Préstamo Francés: en este caso se dejan constantes los términos amortizativos ah (los pagos a realizar).
2. Préstamo Alemán: en este caso se dejan constantes las cuotas de capital
Ah .
3. Préstamo Americano: en este caso se dejan constantes las cuotas de
interés Ih .
Existen una gran cantidad de variantes, variables y situaciones que modifican
este esquema inical de préstamo a interés sobre saldo. Las principales (pero no
las únicas) son:
1. Perı́odo de gracia.
2. Efectos de los impuestos.
3. Efectos de gastos varios: costos administrativos, honorarios varios (para
peritos, notarios, escribanos, por nombrar algunos), etc.
4. Efectos de los seguros.
5. Adelanto de cuotas y cancelación anticipada.
6. Efecto de eventuales atrasos (mora) y los punitorios correspondientes.
7. Efecto de la inflación.
8. Efecto de la devaluación o apreciación de las monedas involucradas en la
operación (directa o indirectamente).
Analizaremos el efecto de las mismas con cierto grado de detalle para el
préstamo francés, pues este es el sistema más usado en nuestro Argentina.
Chapter 10
Préstamo francés
10.1
Introducción
Recordemos que como hipótesis inicial de trabajo vamos a suponer que la tasa
de interés cobrada por el prestamista (acreedor) es constante a lo largo de todo
el préstamo, lo cual nos permitirá aplicar las fórmulas desarrolladas para rentas
constantes.
El sistema francés es el más habitual en Argentina, ya que son constantes
cada uno de los pagos que realiza el prestatario
a1 = a2 = · · · = an = a
(10.1)
lo cual es lo preferido por la mayorı́a de la población (por algún motivo psicológico más alla de los conocimientos de los autores).
Los elementos que componen un tı́pico préstamo francés son:
1. C0 el capital préstado (deuda).
2. i la tasa de interés cobrada por el prestamista.
3. a la cuota de amortización.
4. n la cantidad de pagos que debe realizar el prestatario.
poner dibu!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Para simplificar la notación supondremos que la tasa aplicada y los perı́odos
a los que son impuestos cada uno de los capitales son temporalmente compatibles
(si las cuotas son mensuales, el interés es mensual, y en general si las cuotas son
p-perı́odicas, la tasa considerada será p-perı́odica).
Como en todo préstamo a interés sobre saldos, el capital préstado debe ser
financieramente equivalente al valor actual de la renta generada por la sucesión
de términos amortizativos, la primera relación que tenemos es
223
224
CHAPTER 10. PRÉSTAMO FRANCÉS
−n
1 − (1 + i)
i
de donde podemos despejar el valor de la cuota de amortización
C0 = a
a=
C0 i
(10.2)
(10.3)
−n
1 − (1 + i)
Es claro que si los términos de amortizativos son constantes, tenemos que la
sucesión de cuotas de interés es estrictamente decreciente
I1 > I2 > · · · > In ,
(pues perı́odo a perı́odo el saldo adeudado va decreciendo) y la sucesión de
cuotas de amortización debe ser estrictamente creciente:
A1 < A2 < · · · < An .
PONER DIBU
Para un análisis completo de cualquier esquema de préstamo, debemos tener
fórmulas para calcular el resto de las cantidades significativas: cuotas de interés
y amortización, capital pendiente y total amortizado.
Sabemos que
Ah = Ch − Ch−1
Aplicando la fórmula (9.9) obtenemos la siguiente relación recursiva entre los
capitales pendientes de dos perı́odos consecutivos
Ch = Ch−1 (1 + i) − a
(10.4)
Si escribimos la recursión para los perı́odos h y h − 1
Ch
= Ch−1 (1 + i) − a
Ch−1
= Ch−2 (1 + i) − a
Restado estas ecuaciones obtenemos




Ch − Ch−1 = Ch−1 − Ch−2  (1 + i)
| {z }
|
{z
}
Ah
Ah−1
de donde se deduce la siguiente relación recursiva entre las cuotas de amortización en sistema francés
Ah = Ah−1 (1 + i) para 2 ≤ h ≤ n
(10.5)
cuya solución general es
h−1
Ah = A1 (1 + i)
(10.6)
10.1. INTRODUCCIÓN
225
Para conocer el valor de todas las cuotas de amortización sólo necesitamos
calcular el valor de A1
A1 = C0 − C1 = C0 − [C0 (1 + i) − a] = a − C0 i
(10.7)
En particular, usando (10.3) y (10.7)
A1
C0 i
−n − C0 i
1 − (1 + i)
i
= C0
n
(1 + i) − 1
=
de donde obtenemos
n
(1 + i) − 1
i
Para hallar el capital pendiente Ch además de la fórmula recursiva (10.4)
pod emos usar las fórmulas (9.7) y (9.10).
Método restropectivo: considerando el flujo de fondos hasta el momento
h, de las ecuaciones (9.7), (10.6) y (10.3) se tiene
C 0 = A1
Ch
= C0 − A1 − A1 (1 + i) − · · · − A1 (1 + i)
h−1
h
(1 + i) − 1
i
h
(1 + i) − 1
= C0 − C0
n
(1 + i) − 1
= C 0 − A1
n
= C0
(1 + i) − (1 + i)
n
(1 + i) − 1
h
(10.8)
poner dibujo
Método prostectivo: considerando el flujo de fondos del momento h en
adelante, de las ecuaciones (9.10) y (10.6) se tiene
Ch
h
h+1
= A1 (1 + i) + A1 (1 + i)
n−h
h
= A1 (1 + i)
(1 + i)
+ · · · A1 (1 + i)
n−1
−1
i
Para calcular el total amortizado usamos (9.12), (10.6) y (10.3):
Mh
=
A1 + A1 (1 + i) + · · · + A1 (1 + i)
=
A1
(10.9)
h−1
h
=
(1 + i) − 1
i
h
(1 + i) − 1
C0
n
(1 + i) − 1
(10.10)
Para calcular la cuota de interés basta usar (9.11) y (10.8) o (10.9):
n
Ih = Ch−1 i = C0
h−1
(1 + i) − (1 + i)
n
(1 + i) − 1
i
(10.11)
226
CHAPTER 10. PRÉSTAMO FRANCÉS
Ejemplo 10.1 Ud. acude a un banco y pide un préstamo de $ 25.000 a devolver
en 5 años en cuotas mensuales, por el método francés. La TNA que le cobra el
banco es del 22,5%.
Primero calcularemos el valor del termino amortizativo (lo que ud. debe
pagar mes a mes), de acuerdo con (10.3)
a =
=
0, 225
25.000
12
−12·5
0, 225
1− 1+
12
697, 59862786
i.e., ud. debe pagar unos $ 697,60 cada mes, comenzando un mes después de
que el banco le entregara los $ 25.000.
Para calcular el calor de una cuota de capital primero calculamos el valor
de la primera cuota de capital y luego usamos (10.6). Por ejemplo para hallar
el valor de la cuota de capital A41 calculamos A1
A1 = a − C0 i = 697, 59862786 − 25.000
0, 225
= 228, 84862786
12
y luego A41
40
A41 = A1 (1 + i)
0, 225
= 228, 84862786 1 +
12
40
= 481, 11974739
El mismo resultado se puede obtener de un sólo paso usando
Ah = C0
i
h−1
(1 + i)
n
(1 + i) − 1
(10.12)
de donde
A41
0, 225
40
0, 225
12
= 25.000 1+
= 481, 11974739
60
12
0, 225
1+
−1
12
Para calcular el valor de una cuota de interés dada, por ejemplo la cuota I37 ,
usamos (10.11)
60 37−1
0, 225
0, 225
− 1+
1+
0, 225
12
12
= 250, 932833256
I37 = 25.000
60
12
0, 225
1+
−1
12
Podemos calcular el capital pendiente en cualquier momento usando (10.8)
60
23
1 + 0.225
− 1 + 0.225
12
12
C23 = 25000
= 18494.0299904
60
−
1
1 + 0.225
12
10.1. INTRODUCCIÓN
227
El total amortizado hasta el perı́odo 23 es
M23 = C0 − C23 = 6505, 9700096
Hubieramos obtenido lo mismo usando (10.10)
23
0, 225
1+
−1
12
M23 = 25.000 = 6505, 9700096
60
0, 225
1+
−1
12
Ejercicio 10.2 La Srta. Noelia saco un préstamo a sola firma de $ 2.500 en la
financiera ”Su amigo Adrián”, la cual trabaja con sistema frances y cobra una
TNA del 42,7 %. El prestamo dura 1 año y se conviene realizar el reembolso del
mismo en 12 cuotas mensuales. Se pide:
1. ¿Cuánto es el monto de los términos amortizativos?
2. ¿A cuánto ascienden las cuotas de amortización A1 , A6, y A11 ?
3. ¿Cuál es el monto de las cuotas de interés I1 e I8 ?
4. ¿A cuánto asciende el capital pendiente C8 ?
5. ¿En qué momento el capital pendiente es inferior a $ 1.000?
6. ¿A cuánto asciende el total amortizado M3 ?
7. ¿En que momento el total amortizado supera los $ 1500?
Ejercicio 10.3 Una empresa acude a un banco y pide préstados $ 2.000.000.
Se conviene una TEM del 1,04 %. Si se usa sistema francés, el préstamo dura
3 años, y la cuotas son bimestrales.
1. ¿Cuánto es el monto de los términos amortizativos?
2. ¿A cuánto ascienden las cuotas de amortización A1 , A10, y A18 ?
3. ¿Cual es el monto de las cuotas de interés I5 e I14 ?
4. ¿A cuánto asciende el capital pendiente C6 ?
5. ¿En que momento el capital pendiente es inferior a $ 1.000.000?
6. ¿A cuánto asciende el total amortizado M12 ?
7. ¿En que momento el total amortizado supera los $ 1.500.000 ?
Ejercicio 10.4 El Sr. Juan paga cada mes la suma de $ 3.174,18 para cancelar
un préstamo a sistema francés que obtuvo del Banco Cooperativo de la Paz.
Sabiendo que la tasa de la operación es una TEA del 19,5662 % y que la misma
fue pactada a 5 años, se pide
228
CHAPTER 10. PRÉSTAMO FRANCÉS
1. Monto del préstamo solicitado por el Sr. Juan.
2. ¿A cuánto ascienden las cuotas de amortización A1 , A30, y A60 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I20 e I40 ?
4. ¿A cuánto asciende el capital pendiente al final de cada año, tomando año
por medio (C12 , C24 , C36 , C48 y C60 )?
5. ¿A partir de que cuota el capital pendiente es inferior a la mitad del monto
del préstamo solicitado?
6. ¿A cuánto asciende el total amortizado a principio de cada año (M0 , M12 ,
M24 , M36 y M48 )?
7. ¿A partir de que cuota el total amortizado supera los dos tercios del monto
del préstamo solicitado?
Ejercicio 10.5 La Sra. Melina desea renovar la cocina de su departamento,
para lo cual solicita un prestamo personal a una TNA del 30 %, el cual reembolsará en 36 cuotas mensuales de $ 1.061,9. Se pide
1. Monto del préstamo solicitado por la Sra. Melina.
2. ¿A cuánto ascienden las cuotas de amortización A1 , A12 , A24, y A36 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I6 e I18 ?
4. ¿A cuánto asciende el capital pendiente al final de cada año (C12 , C24 , y
C36 )?
5. ¿A partir de que cuota el capital pendiente es inferior a un cuarto del
monto del préstamo solicitado?
6. ¿A cuánto asciende el total amortizado a principio de cada año (M0 , M12 ,
M24 , y M36 )?
7. ¿A partir de que cuota el total amortizado supera la mitad del monto del
préstamo solicitado?
Ejercicio 10.6 Ud. trabaja en el departamento financiero de una empresa de
venta de productos para el hogar. La empresa tiene como eslogán ”la cuota más
baja del mercado”. Acaban de entrar al catálogo los siguientes productos
Código
Producto
Precio de lista
Precio contado
1102
1303
1304
1505
1755
Super phone
Multiprocesadora A
Microondas Wave
Heladera Mamut
Cocina Leñita
2.299,99
399,99
649,99
3.799,99
1.599,99
1.999,99
324,99
619,99
3.499,99
1.299,99
Valor de
la cuota
Ud. debe fijar el monto y el número de cuotas mensuales de cada uno de los
productos de acuerdo con las siguientes directivas:
Número
de cuotas
10.1. INTRODUCCIÓN
229
1. La cuota no debe superar los $ 75 ni ser inferior a $ 20.
2. El número de cuotas debe ser el menor posible.
3. Ud. debe usar las siguientes tasas dependiendo del número n de cuotas del
plan
Para
TEA
1) 1 ≤ n ≤ 12 35 %
2) 12 < n ≤ 24 38.5 %
3) 24 < n ≤ 36 43.7 %
4) 36 < n ≤ 48 48.5 %
5) 48 < n ≤ 60 55.8 %
6)
n > 60
65.7 %
Ejercicio 10.7 Calcular la cantidad de cuotas mensuales necesarias para saldar
una deuda de $ 500.000.000, si se sabe que la tasa convenida es una TNA del
18 % y el monto de cada cuota es de $ 7.535.426,69.
Ejercicio 10.8 El Sr. Gonzalo desea solicitar un préstamo de $ 20.000. Cómo
su presupuesto es limitado, sólo puede pagar cuotas mensuales no mayores de $
600. El Banco local ofrece las siguientes tasas fijas para préstamos convenidos
a diferentes plazos:
TEA
Plazo
21 %
1 año
23 %
2 años
26,5 % 3 años
28,7 % 5 años
32,8 % 10 años
Si el Sr. Gonzalo desea tomar el préstamo de menor duración posible, ¿Qué
plazo escogerá?
Ejercicio 10.9 Un banco otorga préstamos a una TEM del 1,2 %. Se sabe que
la cuota de amortización 55 de un préstamo es de $ 717,57, y que la cuota de
interés 54 es de $ 867,74. Calcular el desembolso del préstamo y el número de
cuotas (sistema francés).
Ejercicio 10.10 Un banco otorga préstamos a una TEM del 2,5 %. Se sabe
que la cuota de amortización 30 de un préstamo es de $ 225,72, y que la cuota
de interés 32 es de $ 248,15. Calcular el desembolso del préstamo y el número
de cuotas (sistema francés).
poner más ejercicios!!!!!!!!!!! 2 más
de cada caso!!!
Ejercicio 10.11
Los prestamos suelen ser informados mediante la confección de lo que se
conoce como cuadro de marcha o de amortización. Hay muchas formas
de llenar un cuadro de marcha en cualquier sistema de préstamo. Generalmente
230
CHAPTER 10. PRÉSTAMO FRANCÉS
constan de 6 columnas (al menos), y tantas filas como perı́odos tenga el préstamo
(más una para el momento inicial). De izquierda a derecha, las columnas corresponden: a los perı́odos (de 0 a n), término amortizativo ah , cuota de interés Ih ,
cuota de amortización o capital Ah , total amortizado Mh , y capital pendiente
Ch .
Los datos necesarios para llenar cualquier cuadro de marcha de un préstamo
dado, son los mismos que se necesitan para confeccionar un préstamo:
1. C0 el capital préstado.
2. i la tasa que se cobra.
3. n la cantidad de perı́odos que dura el préstamo.
Ahora damos el esquema genérico para completar un cuadro de marcha, los
números entre paréntesis indican el orden que usan los autores para llenar el
cuadro (el cuál, repetimos, no es el único).
n
0
1
2
3
4
..
.
n−1
n
a
(2)
(2)
(2)
(2)
a
a
a
a
..
.
(2)
(2)
a
a
Ih
Ah
Mh
-
-
-
I1 = C0 i
I2 = C1 i
(11) I3 = C2 i
(15) I4 = C3 i
A1 = a − I1
A2 = a − I2
(12) A3 = a − I3
(16) A4 = a − I4
(5) M1 = A1
M 2 = M 1 + A2
(13) M3 = M2 + A3
(17) M4 = M3 + A4
Ch
C0
(6) C1 = C0 − A1
(10) C2 = C1 − A2
(14) C3 = C2 − A3
(18) C4 = C3 − A4
..
.
..
.
..
.
..
.
In−1 = C n−2 i
In = C n−1 i
An−1 = a − I n−1
An = a − I n
Mn−1 = M n−2 +An−1
Mn = M n−1 +An = C 0
Cn−1 = C n−2 −An−1
Cn = C n−1 −An = 0
(3)
(7)
(4)
(8)
(9)
(1)
Nota 10.12 Algunas observaciones
1. Una vez calculado el término amortizativo, se llena toda la segunda columna.
2. La columna de las cuotas de interés debe ser decrececiente.
3. La columna de las cuotas de capital debe ser creciente (de forma geométrica
con razón (1 + i))
4. La columna del total amortizado debe ser estrictamente creciente comenzando en 0 (cero) y finalizando en C0 .
5. La columna del capital pendiente debe ser estrictamente decreciente comenzando en C0 y terminando en 0 (cero).
En general, si se redondea a dos cifras, las dos últimas condiciones no se
cumplen. En dicho caso si el error no supera una cota preestablecida (por ejemplo
para este libro: 5 centavos) se considera correcto. Si el error fuera mayor se
debe aumentar la cantidad de decimales considerados. Los autores recomiendan
trabajar al menos con 5 (cinco) decimales.
10.1. INTRODUCCIÓN
231
Ejemplo 10.13 Hacer el cuadro de marcha de un préstamo francés a 6 meses
por $ 5.000, a una TEM del 1,2%.
n
0
1
2
3
4
5
6
a
Ih
Ah
Mh
868, 6812195
868, 6812195
868, 6812195
868, 6812195
868, 6812195
868, 6812195
60
50, 29582537
40, 47520064
30, 53672841
20, 47899452
10, 30056782
808, 6812195
818, 3853941
828, 2060188
838, 1444910
848, 2022249
858, 3806516
808, 6812195
1.627, 066614
2.455, 272632
3.293, 417123
4.141, 619348
5.000
Ch
5000
4.191, 318781
3.372, 933386
2.544, 727368
1.706, 582877
858, 3806516
0
Algoritmo 10.14 A continuación damos el algoritmo para llenar el cuadro de
marcha francés
Paso 1: Cálculo del término amortizativo:
a=
C0 i
−n
1 − (1 + i)
=
5000 · 0, 012
1 − (1 + 0, 012)
−6
= 868, 68
Paso 2: Llenado de la primera fila:
1. Cálculo de la cuota de interés I1
I1 = C0 i = 5000 · 0, 012 = 60
2. Cálculo de la cuota de capital A1
A1 = a − I1 = 868, 6812195 − 60 = 808, 6812195
3. Cálculo del total amortizado M1
M1 = M0 + A1 = A1 = 808, 6812195
(Recordar que hemos tomado M0 = 0)
4. Cálculo del capital pendiente C1
C1 = C0 − A1 = 5000 − 808, 6812195 = 4191, 318781
Paso 3: Mientras h ≤ n, una vez completada la fila h − 1, llenar la fila h :
1. Cálculo de la cuota de interés Ih
Ih = Ch−1 i
2. Cálculo de la cuota de capital Ah
Ah = a − I h
232
CHAPTER 10. PRÉSTAMO FRANCÉS
3. Cálculo del total amortizado Mh
Mh = Mh−1 + Ah
4. Cálculo del capital pendiente Ch
Ch = Ch−1 − A1
Nota 10.15 Es claro que el uso de una planilla de cálculo facilita la confección
de cualquier cuadro de marcha. Por lo que se recomienda su uso siempre que
sea posible.
Ejercicio 10.16 Hacer el cuadro de marcha para un préstamo francés a 12
años por $ 10.000.000, para el cual se han pactado 12 pagos anuales consecutivos
y una TEA del 23%.
Ejercicio 10.17 Escoger al menos tres de los préstamos planteados en los ejercicios del (10.2) al (10.10) y realizar el correspondiente cuadro de marcha
10.2
Usufructo y nuda propiedad
Consideremos la siguiente situación
Ejemplo 10.18 La Sra. Rosa sacó un préstamo a sistema francés por $15.000
a pagar en 60 cuotas mensuales iguales y consecutivas de $ 485,30 a una TEM
del 2,5 %. A los 18 meses la Sra. Rosa recibe una herencia por $ 750.000 por lo
que decide dejar a su marido y cancelar su deuda. La situación del mercado a
cambiado y la tasa vigente para estas operaciones a los 18 meses de tomado el
(12)
préstamo es una im = 1, 1 % mensual.
En primer lugar, la Sra. Rosa debe a los 18 meses la suma de $ 12.530,76
pues
60
C18
=
=
15.000
(1 + 0, 025)
− (1 + 0, 025)
60
(1 + 0, 025)
12.530, 76473
18
−1
Pero a los 18 meses, para el acreedor (préstamista) es mejor seguir recibiendo la
renta que le origina el préstamo concedido que los $ 12.530,76 que le devolverı́a
(12)
la Sra. Rosa pues a la tasa que ahora puede pretar dinero (im = 0, 011) el
valor actual de la renta que espera recibir es de $ 16.252,54 pues
V A(18)
=
=
1 − (1 + 0, 011)−(60−18)
0, 011
16.252, 53866
485, 30
10.2. USUFRUCTO Y NUDA PROPIEDAD
233
Si el contrato firmado por la Sra. Rosa le permite al préstamista ejercer el
derecho a recibir lo que se llama valor actual de mercado del préstamo
convenido, entonces la Sra. Rosa, deberá desembolsar $ 16.252,54 para cancelar
el préstamo a los 18 meses de otorgado
Observe que si la tasa de mercado fuera del 3,2%:
i(12)
m = 0, 032
Entonces el valor de mercado a los 18 meses del préstamo tomado por la Sra.
Rosa es $ 11 126.26 pues
V A(18)
=
=
1 − (1 + 0, 032)−(60−18)
0, 032
11.126, 26066
485, 30
En este caso el préstamista prefiere que la Sra. Rosa le devuelva $ 12.530,76 en
lugar del valor de mercado del préstamo.
En general, dado un préstamo por C0 , convenido a n perı́odos, a una tasa
pactada i (dimensionalmente compatible con la unidad temporal de los n perı́odos).
Si nos encontramos en un momento cualquiera k (fecha de valoración), 0 ≤ k ≤
n − 1, los términos amortizativos pendientes
ak+1 , . . . , an
representan para el acreedor (prestamista) un derecho de cobro futuro y para
el deudor (prestatario) una obligación de pago. Si al momento k se quisiera
cancelar anticipadamente la deuda, el prestatario (deudor) deberı́a entregar en
principio Ck , el capital pendiente al momento k.
Sin embargo, puede ocurrir que las condiciones del mercado hayan cambiado
desde el momento en que se concertó la operación al dı́a de hoy. En este sentido,
para determinar si esta cancelación resulta o no conveniente para el acreedor
(préstamista), serı́a necesario valorar los términos amortizativos pendientes con
un nuevo criterio, ajustado a las condiciones actuales del mercado, esto es, valorarlos a la tasa im que puede obtener hoy el préstamista en el mercado.
Esto es importante pues el acreedor (titular del capital pendiente) puede
transferir total o parcialmente los derechos de los préstamos por él concedidos.
Definición 10.19 Dado un préstamo por C0 , convenido a n perı́odos, a una
tasa pactada i (dimensionalmente compatible con la unidad temporal de los n
perı́odos). El valor al momento 0 ≤ k ≤ n − 1 de la sucesión de términos
amortizativos
ak+1 , . . . , an
a una tasa im dada, recibe el nombre de valor actual de mercado del préstamo
al momento k
n
X
ah
V AMk (im ) =
(10.13)
h−k
h=k+1 (1 + im )
234
CHAPTER 10. PRÉSTAMO FRANCÉS
Representa la cantidad que el deudor tendrá que pagar para cancelar su
deuda o, desde el punto de vista del prestamista, lo que deberı́a recibir por
transferir los derechos futuros que el préstamo supone, en las condiciones actuales del mercado.
Criterio 10.20 Suponiendo que el préstamista por contrato tiene la facultad
de ejercer el derecho a recibir el valor actual de mercado del préstamo por
él concedido. Si el prestatario desea cancelar anticipadamente el préstamo. El
prestamista ejercerá el derecho cada vez que
im > i
donde im es la tasa de mercado al momento de la cancelación anticipada, mientras que i es la tasa a la que fue otorgado el préstamo.(¿Por qué?).
Nota 10.21 En los contratos, siempre se deja establecido el método para calcular la tasa de mercado, por ejemplo: la tasa de referencia del Banco Central
más un punto porcentual, o el promedio de las TNA de los bancos de la plaza,
etc.
En un sentido estricto, el préstamista o acreedor recibe dos rentas del prestatario
o deudor: la renta de las cuotas de amortización y la renta de las cuotas de interés. Por lo que el puede transferir los derechos sobre una o ambas rentas a un
tercero, esto da origén a los conceptos de usufructo y nuda propiedad.
Definición 10.22 Dado un préstamo por C0 , convenido a n perı́odos, a una
tasa i (dimensionalmente compatible con la unidad temporal de los n perı́odos).
El valor al momento 0 ≤ k ≤ n − 1 de la sucesión de cuotas de interés
Ik+1 , . . . , In
a una tasa im dada, recibe el nombre de usufructo al momento k
Uk (im ) =
n
X
Ih
h−k
h=k+1 (1 + im )
(10.14)
El usufructo representa el “fruto” (rédito, ganacia o utilidad) pendiente al
momento k que el préstamista obtendrá por haber otorgado el préstamo.
Definición 10.23 Dado un préstamo por C0 , convenido a n perı́odos, a una
tasa i (dimensionalmente compatible con la unidad temporal de los n perı́odos).
El valor al momento 0 ≤ k ≤ n − 1 de la sucesión de cuotas de amortización
Ak+1 , . . . , An
a una tasa im dada, recibe el nombre de nuda propiedad al momento k
Nk (im ) =
n
X
Ah
h−k
h=k+1
(1 + im )
(10.15)
10.2. USUFRUCTO Y NUDA PROPIEDAD
235
La nuda propiedad es el valor actual de la parte de la propiedad (dinero) al
momento k que el préstamista ha cedido (temporalmente) al prestario.
Como para cada k se cumple que
ak = Ak + Ik
es claro que
V AMk (im ) = Uk (im ) + Nk (im )
(10.16)
La fórmulas anteriores son generales y funcionan para cualquier préstamo a
interés sobre saldos. Pero toman formas particulares en cada sistema.
Dado un préstamo por C0 , por sistema francés, convenido a n perı́odos, a
una tasa pactada i (dimensionalmente compatible con la unidad temporal de
los n perı́odos). El valor actual de mercado al perı́odo k, 1 ≤ k ≤ n − 1, a la
tasa de mercado im (con la misma unidad temporal que i) es
V AM Fk (im )
n
X
=
a
h=k+1
(1 + im )
n−k
X
1
= a
h−k
h
(1 + im )
h=1
Entonces
−(n−k)
V AM Fk (im )
= a
1 − (1 + im )
im
(10.17)
−(n−k)
= C0
1 − (1 + im )
i
1 − (1 + i)−n
im
(10.18)
El usufructo y la nuda propiedad son un poco más complicados de calcular.
El usufructo en sistema francés al perı́odo k es
U Fk (im )
=
n
X
Ih
h−k
h=k+1
(1 + im )
n
=
C0 i
n
X
(1 + im )
h=k+1
k
=
h−1
(1 + i) − (1 + i)
n
(1 + i) − 1
C0 i (1 + im )
n
(1 + i) − 1
h−k
n
X
(1 + i)
h=k+1
(1 + im )
h−1
n
h
−
(1 + i)
!
h
(1 + im )
Por lo tanto

n
U Fk (im ) = C0
i
(1 + i)
n
(1 + i) − 1 (1 + im )n−k
 (1 + i )n−k − 1

m
−

im


k−n
1+i
− 1
1 + im


im − i

(10.19)
236
CHAPTER 10. PRÉSTAMO FRANCÉS
Mientras que la nuda propiedad en sistema francés es
N Fk (im )
=
n
X
Ah
h=k+1 (1
n
X
+ im )
= A1
h−k
(1 + i)h−1
h−k
(1 + im )
n−k
1+i
1−
1 + im
= A1 (1 + i)k
im − i
h=k+1
(10.20)
de donde podemos concluir
N Fk (im ) = C0 (1 + i)k
i
(1 + i)n − 1
1−
1+i
1 + im
im − i
n−k
(10.21)
Concideremos ahora el siguiente ejemplo
Ejemplo 10.24 La financiera ”Su amigo Adrián” desea abrir una nueva sucursal. Por lo que necesita fondos por $ 2.500.000. En este momento dispone de
$ 1.150.000 en efectivo para invertir. Como no desea descapitalizarse, el resto
de los fondos planea obtenerlos vendiendo con un 10 % de descuento el usufruto
de los siguientes préstamos que ha concedido
h
1)
2)
3)
C0
$ 2.000.000
$ 1.000.000
$ 400.000
(12)
ih
0,015
0,008
0,01
nh
120
60
36
Hoy: kh
23
45
20
Suponer que la tasa de mercado es
i(12)
m = 0, 007
El problema nos pide calcular
1
2
3
U F23
(0.007) + U F45
(0.007) + U F20
(0.007) (1 − 0.1)
Ahora usando (10.19) y recordando que C01 = 2.000.000, i = 0, 015, n = 120,
1
k = 23 e im = 0, 007, tenemos que U F23
(0, 007) es igual a


23−120
1 + 0.015
1 + 0.015
120 
−
120−23
2000000 · 0.015
1 + 0.015
−1
1 + 0.007
1 + 0.007 
 (1 + 0.007)

−


120
0.007
0.007 − 0.015


(1 + 0.015) − 1 1 + 0.007
Por lo tanto
1
U F23
(0, 007) = 1.304.204, 826
10.2. USUFRUCTO Y NUDA PROPIEDAD
237
De manera similar calculamos
2
U F45
(0, 007)
=
18.574, 76627
3
U F20
=
16.333, 33841
(0, 007)
Por lo tanto
1
2
3
U F23
(0.007) + U F45
(0.007) + U F20
(0.007) (1 − 0.1) = 1.339.112, 931
de los cuales utiliza $ 1.350.000, sobrandole $ 10.887,07.
También podemos calcular el valor de mercado de cada uno de los préstamos
considerados, por ejemplo
−(n−k)
1
V AM F23
(0.07)
= C0
i
1 − (1 + im )
1 − (1 + i)−n
im
−(120−23)
=
=
1 − (1 + 0, 007)
0, 015
1 − (1 + 0, 015)−120
0, 007
2.531.216, 584
2.000.000
Ejercicio 10.25 Calcular el valor de mercado de los restantes préstamos
La nuda propiedad del primer préstamo es
n−k
1+i
1−
i
1 + im
1
N F23
(0.007) = C0 (1 + i)k
n
(1 + i) − 1
im − i
120−23
1 + 0, 015
1−
0, 015
1 + 0, 007
= 2.000.000(1 + 0, 015)k
120
(1 + 0, 015) − 1
0, 007 − 0, 015
= 1.227.011, 758
Y se verifica que (10.16)
1
1
U23
(0, 007) + N F23
(0, 007)
=
1
V AM F23
(0, 007)
1.304.204, 826 + 1.227.011, 758
=
2.531.216, 584
Ejercicio 10.26 Calcular la nuda propiedad de los préstamos restantes y verificar que se cumple(10.16).
Ejercicio 10.27 Ud. es trabaja para la financiera “”Pedro, su mejor amigo”.
El gerente desea saber cual es el valor actual de la siguiente cartera de préstamos
h
1)
2)
3)
4)
$
$
$
$
C0
2.500.000
1.500.000
3.400.000
5.050.000
(12)
ih
0,021
0,012
0,011
0,018
nh
120
60
36
120
Hoy: kh
32
22
16
75
238
CHAPTER 10. PRÉSTAMO FRANCÉS
Suponer que la TEM de mercado al dı́a de hoy es del 1 %. El gerente quiere la
información desglosada: capital pendiente, valor actual de mercado, usufructo y
nuda propiedad.
Ejercicio 10.28 Volver a realizar el ejercicio anterior, suponiendo que la tasa
de mercado es una TEM del 1,8 %
10.3
Perı́odo de gracia
Definición 10.29 Diremos que existe un perı́odo de gracia de duración d ≥ 2
cuando existen d perı́odos de tiempo entre el desembolso del préstamo y el pago
del primer término amortizativo.
Los perı́odos de gracias no modifican sustancialmente el esquema de préstamo.
Su único efecto sobre las fórmulas dadas hasta ahora es la sustitución de C0 por
d−1
C0 (1 + i) . Pues tomar un préstamo hoy por C0 a la tasa i, y comenzar a
pagarlo al momento d es financieramente equivalente a tomar un préstamo por
d−1
C0 (1 + i)
en el momento d − 1, a la misma tasa i (ambos con la misma
catidad de cuotas).
Nota 10.30 PONER DIBU
Por razones de completitud daremos las fórmulas asociadas, las cuales son
d−1
las mismas que antes, pero cambiando C0 por C0 (1 + i)
y teniendo en cuenta
un pequeño ajuste sobre los subı́ndices.
Término amortizativo:
a=
C0 i (1 + i)
d−1
−n
1 − (1 + i)
Sigue valiendo que la relación recursiva entre las cuotas de amortización
Ah = Ah−1 (1 + i)
por lo cual
h−1
Ah = A1 (1 + i)
Debemos notar ahora que A1 está disponible en el momento d, A2 en el momento
d + 1, y en general
Ah está disponible en el momento d + h − 1
Una observación similar vale para el resto de las cantidades significativas
Ih , Ch y Mh están disponibles en el momento d + h − 1
El valor de A1 es
A1
=
a − C0 i (1 + i)
=
C0
d−1
d−1
i (1 + i)
n
(1 + i) − 1
10.3. PERÍODO DE GRACIA
239
El capital pendiente es
n
d−1
Ch = C0 (1 + i)
(1 + i) − (1 + i)
n
(1 + i) − 1
h
El total amortizado es
h
Mh = C0 (1 + i)
d−1
(1 + i) − 1
n
(1 + i) − 1
Finalmente la cuota de interés es
n
d−1
Ih = Ch−1 i = C0 (1 + i)
h−1
(1 + i) − (1 + i)
n
(1 + i) − 1
i
Ejemplo 10.31 Un banco nos ofrece un préstamo de $ 20 000 a 5 años, a pagar
en cuotas mensuales consecutivas he iguales por el método francés. La TNA
que nos cobran es del 18%. Nos ofrecen 3 meses de gracias. Se pide calcular:
a, A23 , I18 , M50 , y C30 . Confeccionar el cuadro de marcha.
Término amortizativo:
a=
C0 i (1 + i)
d−1
−n
1 − (1 + i)
=
20000 ·
0.18
12
1− 1+
0.18 3−1
12
0.18 −60
12
1+
= 512.22
Ahora confeccionaremos el cuadro de marcha
n
0
1
2
3
..
.
h
0
1
a
512.22
..
.
Ih
309.675
..
.
Ah
203.1525
..
.
Mh
203.1525
..
.
Ch
20000
20300
20604.5
20401.3475
..
.
Ejemplo 10.32 Nota 10.33 PONER DIBU
Ejercicio 10.34 Calcular el resto de datos requeridos en el problema anterior
y terminar el cuadro de marcha.
Ejercicio 10.35 Una empresa recibe un préstamo por $ 5 000 000 para la compra de un nuevo equipo de producción, la empresa espera amortizar el prestamo
con las ganacias que le reporte la nueva maquinaria, por lo que solicita un
perı́odo de gracia de 6 meses, el cuál le es otorgado. El préstamo es acordado
por sistema francés, a pagar en 3 años en cuotas cuatrimestrales con una TEA
del 19.5%. Calcular: a, A5 , I9 , M6 , y C2 . Confeccionar el correspondiente cuadro
de marcha.
240
10.4
CHAPTER 10. PRÉSTAMO FRANCÉS
CFT: costo financiero total. Efecto de impuestos, gastos y seguros
En todo préstamo (legal) existen varios factores que influyen sobre la rentabilidad real que obtendrá el acreedor o préstamista, y sobre el costo real para el
prestatario o deudor (conocido como CFT, costo financiero total, en Argentina, ver nota 10.36). En los préstamos a tasa fija los principales factores
son: impuestos, seguros, comisiones y gastos operativos.
Como marco de trabajo supongamos un préstamo a interés sobre saldos por
C0 , a una tasa i, pactado a n perı́odos. Por ahora no especificaremos el sistema.
Efecto de los impuestos
Los impuestos pueden impactar sobre ambos agentes: prestamista y prestatario.
Pero en general el agente con más poder transfiere la carga impositiva al otro
agente en el contrato, por lo que tı́picamente el prestatario (deudor) es quien
términa pagando los impuestos asociados a un préstamo.
El estado suele cobrar impuestos cada vez que el dinero cambia de manos,
por lo que habrá una serie de impuestos iniciales (sellados, impuestos provinciales varios, etc) los cuales son cobrados al momento de otorgar el préstamo.
Llamaremos G a la suma de estos. Además el estado cobra otros impuestos en
cada cuota de amortización, los cuales pueden constar de una suma fija g (sellados) y un par de tasas impositivas: τ A y τ I las cuales actuan sobre la cuota de
capital Ah y la cuota de interés Ih , las cuales tı́picamente suelen ser constantes
a lo largo de un préstamo. Por lo que si consideramos los impuestos, el deudor
en lugar de C0 recibirá
C0d = C0 − G
y en lugar de pagar cada perı́odo ah , debe entregar
adh = Ah (1 + τ A ) + Ih (1 + τ I ) + g, para 1 ≤ h ≤ n
Por ejemplo en Argentina, el estado cobra IVA (impuesto sobre el valor agragado) sobre las cuotas de interés: τ I = 21%; y no cobra (aún) impuestos sobre
las cuotas de capital: τ A = 0%.
Efecto de los seguros
Agregaremos ahora el efecto de los seguros. Tı́picamente todo préstamo
obliga al deudor o préstatario a tomar uno o varios seguros (de vida, contra incendios, contra todo riesgo, etc) en favor del préstamista o acreedor. El
seguro impacta directamente sobre el préstatario (deudor). Eventualmente el
préstatario deberá pagar al momento inicial el costo de contratar el seguro, esta
suma de dinero debe ser agregada a la suma G. Luego, perı́odo a perı́odo, deberá
pagar, eventualmente, un costo fijo el cual se agrega a g, más un costo variable
dado por una tasa σ, la cual se cobra sobre el capital pendiente.
Al tener en cuenta el efecto de los seguros sobre el préstatario (deudor),
tenemos que en lugar de C0 recibirá
C0d = C0 − G
10.4. CFT: COSTO FINANCIERO TOTAL. EFECTO DE IMPUESTOS, GASTOS Y SEGUROS241
donde ahora G no sólo incluye los impuestos iniciales, sino también costo inicial
de contratar un seguro. Por otro lado en lugar de pagar cada perı́odo ah , debe
entregar
adh = Ah (1 + τ A ) + Ih (1 + τ I ) + σCh + g, para 1 ≤ h ≤ n
ahora g no sólo incluye los impuestos perı́odicos (sellados), si los hubira, sino
también costo cualquier costo fijo mensual asociados a la la contratación de un
seguro.
Efectos de los gastos operativos
El efecto de los gastos operativos impacta siempre sobre ambos agentes.
En el caso del prestatario (deudor), representa el costo (certificados, gastos de
otorgamiento, honorarios de peritos y notarios, gastos de evaluación, costo de
apertura y mantenimiento de una cuenta, etc) en los que se incurre para tomar
el préstamo y realizar los pagos perı́odicos. La suma de estos costos iniciales
debe ser agregada a G. Por otro lado pagar cada cuota le costará al prestatario
una cantidad g (costo de mantenimiento de cuenta, costo de traslado para pagar
cada cuota, etc).
Al agregar a nuestro análisis el efecto de estos gastos operativos, el prestatario
recibirá en lugar de C0 la suma de
C0d = C0 − G
(10.22)
donde G es la suma de todos los montos que el prestatario debe pagar al momento inicial: impuestos, seguros y gastos. Finalmente, en cada perı́odo en lugar
de ah el prestatario deberá desembolsar
adh = Ah (1 + τ A ) + Ih (1 + τ I ) + σCh + g, para 1 ≤ h ≤ n
(10.23)
donde g es la suma de todos los montos que el deudor de pagar perı́odicamente:
sellados (imopuestos), cargos fijos de seguros, mantenimiento de cuenta, etc.
En el caso del prestamista, llamaremos GP al costo operativo inicial en el que
incurre por otorgar el préstamo (horas hombre, formularios, publicidad y gastos
operativos generales). Además el cobro de cada término amortizativo tiene un
costo operativo g que representa el costo de impresión y envı́o de las facturas,
horas hombre, etc.
Al considerar estos factores, el préstamista deberá desembolsar en lugar de
C0 la suma de
(10.24)
C0p = C0 + GP
Mientras que en cada perı́odo, recibirá la suma de
aph = ah − gp , para 1 ≤ h ≤ n
(10.25)
Teniendo en cuenta esta información surgen las siguientes preguntas
¿Cuál es la tasa que realmente términa pagando el préstatario (CFT)?
¿Cuál es la tasa real que términa ganando el prestamista?
242
CHAPTER 10. PRÉSTAMO FRANCÉS
Nota 10.36 El Banco Central de la República Argentina, BCRA, llama costo
financiero total CFT, a la tasa rd que términa pagando el préstatario. El
Costo Financiero Total (CFT) es la principal variable que se debe tener en
cuenta al elegir un préstamo personal, prendario o hipotecario, ya que es el
mejor indicador del costo global que deberá afrontar el cliente.
Si bien la tasa informada por cada institución financiera es una variable
importante a la hora de elegir un préstamo, cuando se eligen alternativas de
financiación es mejor comparar los CFT, ya que una tasa más baja no significa
un CFT más bajo, pues al incluir los costos adicionales en los cálculos, puede
ocurrir que la institución que ofrece una tasa más baja tenga un CFT mayor.
El BCRA establece que el CFT se debe expresar en forma de tasa efectiva anual, en tanto por ciento con dos decimales. Además ha decretado que los bancos
están obligados a exponer en pizarras, colocadas en sus sucursales, información
sobre tasas de interés de las lı́neas de crédito ofrecidas como ası́ también el
CFT.
Similarmente, cuando los bancos hacen publicidad de sus créditos deben adjudicarle al CFT mayor o igual importancia -en términos de tamaño y tiempoque la asignada a la TNA, la cantidad de cuotas y/o su importe. Para el caso
de operaciones pactadas a tasa variable, el CFT se calcula en base a la tasa
vigente al momento de su concertación, y deberá quedar claro que este costo se
modificará cada vez que varı́e la tasa de interés.
La tasa real rd del préstamo para el prestatario (deudor) es la tasa que
produce la equivalencia finaciera entre lo que efectivamente recibe C0d y el valor
actual de la renta generada con los términos que realmente paga: ad1 , ad2 , . . . , adn
C0d =
n
X
adh
h
h=1
(1 + rd )
(10.26)
Similarmente, la tasa real rp del préstamo para el prestamista (acreedor)
es la tasa efectiva que realiza la equivalencia financiera entre el capital que
efectivamente deseembolsa C0p y la renta que efectivamente recibe, i.e., la renta
de términos ap1 , ap2 , . . . , apn
C0p =
n
X
h=1
aph
(1 + rp )
h
(10.27)
Es claro que siempre se cumple que
C0d < C0 < C0p
y que para cada 1 ≤ h ≤ n
aph < ah < adh
De las desigualdades anteriores se puede concluir que la tasa real rd que paga
el deudor o prestatario es siempre mayor que la tasa declarada i, y que la tasa
real rp que gana el acreedor o préstamista es siempre menor que i:
rp < i < rd
(10.28)
10.4. CFT: COSTO FINANCIERO TOTAL. EFECTO DE IMPUESTOS, GASTOS Y SEGUROS243
Como (recordar que adh > ah )
n
X
ah
h=1
(1 + i)
h
= C0 >
C0d
=
n
X
h=1
adh
(1 + rd )
h
>
n
X
ah
h
h=1
(1 + rd )
Por la monotonı́a de las funciones potenciales, podemos concluir que
1
1
>
1+i
1 + rd
de donde es fácil deducir que i < rd .
Similarmente, como (recordar que aph < ah )
n
X
ah
h
h=1
(1 + i)
= C0 < C0p =
n
X
aph
h
h=1
(1 + rp )
<
n
X
ah
h
h=1
(1 + rp )
de donde se deduce que rp < i.
Las fórmulas (10.26) y (10.27) toman formas particulares en cada sistema
de préstamo. Veamos como son en el sistema francés.
Analizaremos primero lo que ocurre con el deudor en un préstamo por sistema francés por un monto C0 , a una tasa efectiva i, pactado a n perı́odos
(tasa y perı́odos dimensionalmente compatibles). Consideraremos los términos
que efectivamente debe desembolsar el préstatario:
adh = Ah (1 + τ A ) + Ih (1 + τ I ) + σCh + g, para 1 ≤ h ≤ n
donde g es el agregado de todas las sumas fijas que se le cobran perı́odo a perı́odo
al préstatario (sellados, costos fijos por seguros, mantenimiento de cuenta, etc).
Por lo tanto
C0d
=
=
n
X
h=1
n
X
adh
(1 + rd )
h
Ah (1 + τ A ) + Ih (1 + τ I ) + σCh + g
h
(1 + rd )
h=1
Recordando que en el sistema francés
C0 i
n
(1 + i) − 1
A1
=
Ah
Ih
= A1 (1 + i)
n
h−1
= A1 (1 + i) − (1 + i)
Ch
= A1
h−1
n
h
(1 + i) − (1 + i)
i
tenemos que C0d es igual la suma de las siguientes partes
244
CHAPTER 10. PRÉSTAMO FRANCÉS
C0d = amortización + interés + seguros + gastos
donde
parte amortizativa
parte de interés
= A1 (1 + τ A )
= A1 (1 + τ I )
n
h−1
X
(1 + i)
h
h=1
n
X
(1 + rd )
n
h
(1 + rd )
h=1
parte de los seguros
h−1
(1 + i) − (1 + i)
n
n
h
σA1 X (1 + i) − (1 + i)
h
i
(1 + rd )
=
h=1
parte de los gastos fijos
=
g
n
X
h=1
1
(1 + rd )
h
Ahora como
n
h−1
X
(1 + i)
h
h=1
(1 + rd )
h
n 1 X 1+i
1+i
1 + rd
h=1
n
1+i
1−
1 1+i
1 + rd
1+i
1 + i 1 + rd
1−
1 + rd
n
1+i
1−
1 + rd
rd − i
=
=
=
y
n
X
h=1
−n
1
(1 + rd )
h
=
1 − (1 + rd )
rd
Obtenemos la siguiente expresión
1+i
1−
1
+
i
1
+ rd
C0d = A1 τ A − τ I − σ
i
rd − i
n
1 − (1 + r )−n
σ
d
n
+g
+ A1 (1 + i) 1 + τ I +
i
rd
(10.29)
Como es claro de la fórmula anterior, debemos usar Newton-Raphson o
método de la secante para hallar la tasa rd que efectivamente paga el prestatario
o deudor. Por eso damos la expresión para la derivada respecto de rd que se debe
usar en el esquema de Newton-Raphson:
n
n 
 1+i
1+i
n
1−
 1+i 
1 + rd
1 + rd

− A1 (1 + i)n 1 + τ I + σ + g
A1 τ A − τ I − σ
−
2
 (1 + rd ) (rd − i)

i
i
(rd − i)
(10.30)
n (1 +
10.4. CFT: COSTO FINANCIERO TOTAL. EFECTO DE IMPUESTOS, GASTOS Y SEGUROS245
Esperamos que con el siguiente ejemplo el lector pueda sacar algo en limpio.
Ejemplo 10.37 La Srta. Georgina desea sacar un préstamo personal por $
5.000 a sistema francés, a pagar en un año de forma mensual. Ella acude a
dos Bancos: Banco del Sur y Banco del Norte. En la siguiente tabla a recogido
toda la información relevante:
Items
TEM
Gastos de otorgamiento y evaluación
Gastos de Apertura de cuenta
Gastos de mantenimiento de cuenta
Seguro mensual sobre saldo
Sur
1,1%
$ 200
$ 25
$7
0,5%
Norte
1,35%
Sin cargo
$ 45
Sin cargo
0,65%
La Srta. Georgina quiere saber el CFT de cada una de las opciones. Para lo
cual hay que tener en cuenta que el estado nacional cobra IVA del 21% sobre las
cuotas de interés y el estado provincial cobra un impuesto al inicio (”sellados”)
del 1.5% del monto solicitado.
Los gastos iniciales en los que incurrirı́a la Srta. Georgina son
Items
Gastos de otorgamiento y evaluación
Gastos de Apertura de cuenta
Primera cuota de seguro
Sellados provinciales
G (suma de los gastos iniciales)
Sur
$ 200
$ 25
$ 25
$ 75
$ 325
Norte
Sin cargo
$ 45
$ 32.5
$ 75
$ 152.5
Otros datos relevantes para el préstamo de la Stra. Georgina son
Items
i (TEM)
τA
τ I (IVA)
σ (seguros)
g (gastos fijos mensuales)
Sur
0,011
0
0,21
0,005
$7
Norte
0,0135
0
0,21
0,0065
Sin cargo
A continuación daremos los cuadros de marcha de las dos opciones (este paso
no es necesario en general, pero clarifica la exposición) y el cálculo del CFT.
Cuadro de marcha del préstamo del Banco Sur (en este cuadro se hicieron
las cuentas con 5 decimales, pero se volcaron los resultados con dos decimales a
fin de simplificar la lectura del cuadro).
246
CHAPTER 10. PRÉSTAMO FRANCÉS
Seguro
σCh
h
a
Ah
Ih
Ih (1 + τ I )
Ch
0
1
2
3
4
5
6
7
8
9
10
11
12
447,06
447,06
447,06
447,06
447,06
447,06
447,06
447,06
447,06
447,06
447,06
447,06
392,06
396,37
400,73
405,14
409,59
414,10
418,65
423,29
427,91
432,62
437,38
442,19
55
50,69
46,33
41,92
37,46
32,96
28,40
23,80
19,14
14,43
9,68
4,86
66,55
61,33
56,06
50,72
45,33
39,88
34,37
28,79
23,16
17,47
11,71
5,89
5000
4607,94
4211,58
3810,85
3405,71
2996,12
2582,02
2163,37
1740,11
1312,19
879,57
442,19
−2, 4 · 10−11
Mh
23,04
21,06
19,05
17,03
14,98
12,91
10,82
8,70
6,56
4,40
2,21
−1, 2 · 10−13
0
392,06
788,42
1189,15
1594,29
2003,88
2417,98
2836,63
3259,89
3687,81
4120,43
4557,81
5000
Térm
real
gastos
fijos
325
7
7
7
7
7
7
7
7
7
7
7
7
488
485
482
479
476
473
470
467
464
461
458
455
Usaremos Newton-Raphson para hallar el CFT de cada opción. Para realizar
el cálculo del CFT del Banco Sur necesitaremos las calcular las contantes
1 + 0.011
1+i
= 392, 0556788 0 − 0.21 − 0.005
A1 τ A − τ I − σ
i
0.011
= −262, 4990977
σ
0.005
n
12
A1 (1 + i) 1 + τ I +
+ g = 392, 0556788 (1 + 0.011)
1 + 0.21 +
+7
i
0.011
= 751, 1444981
Luego la función f del esquema de Newton-Raphson es
1−
f (rk ) = −262, 4990977
1 + 0, 011
1 + rk
rd − 0, 011
12
−12
+751, 1444981
1 − (1 + rk )
rk
−4675
y su derivada es
12
12 
1 + 0, 011
1 + 0, 011
1−
 12

1 + rk
1 + rk


0
−
f (rk ) = −262, 4990977 
−751, 1444981
2
 (1 + rk ) (rk − 0, 011)

(rd − 0, 011)

Por lo que podemos conseguir el siguiente esquema iterativo, donde hemos
usado como criterio de parada un nivel de corrección de 0,0001 y como semilla
una tasa un poco mayor a la tasa del préstamo, en este caso usamo i0 = 0, 015.
−12−
12 (1 + rk )
rk
10.4. CFT: COSTO FINANCIERO TOTAL. EFECTO DE IMPUESTOS, GASTOS Y SEGUROS247
k
ik
f (ik )
f 0 (ik )
0
1
2
3
0, 015
0, 030161925
0, 031284399
0, 031289944
481, 0656965
31, 12811474
0, 152256433
−31728, 53642
−27731, 70231
−27460, 95625
f (ik )
f 0 (ik )
0, 015161925
0, 001122474
5, 54447 · 10−6
−
Vale la pena destacar que usando métodos un poco más sofisticados se
pueden hallar otras tasas que igualan C0d con la renta de los adh , las mayorı́a
de ellas son compejas, pero no todas (no es sorprendente desde el punto de vista
matemático que existan varias tasas y que la mayorı́a sean complejas).
x1
= −1, 780945411
x2
= −1, 684774678 − 0, 3795459427 i
x3
= −1, 684774678 − 0, 3795459427 i
x4
= −1, 418029169 − 0, 6693482554 i
x6
= −1, 418029169 + 0, 6693482554 i
x7
= −1, 040854227 − 0, 7996930283 i
x8
= −1, 040854227 + 0, 7996930283 i
x9
= −0, 6372049230 − 0, 7358225463 i
x9
= −0, 6372049230 + 0, 7358225463 i
x10
= −0, 2920477297 − 0, 4821554719 i
x11
= −0, 2920477297 + 0, 4821554719 i
x12
=
0, 03128994420
La pregunta importante es, con cual debemos quedarnos. Bueno, son faciles
de descartar las soluciones complejas. Como estamos buscando una tasa positiva,
también es facil descartar las tasas negativas. Además la tasa que buscamos debe
ser mayor que la declarada por el banco. Con un poco de suerte, sólo habrá una
tasa entre i y 1, y esa es la tasa que buscamos, la cual es la que habitualmente
nos brindará Newton-Raphson si usamos como raı́z la tasa declarada por el
banco o una ligeramente mayor.
Como ya se explico el CFT es una tasa efectiva anual, de hecho, el CFT del
Banco Sur, para este préstamo es la TEA equivalenta a la tasa mensual real:
12
CF T =
1 + r(12)
−1
=
(1 + 0, 03128994420)
=
0, 447336105
12
−1
Por lo que el CFT para la Srta. Georgina en el Banco Sur es del 44,7336105%.
Mientras que la TEA equivalente a la tasa declara por el banco es del 14,0286196%
pues
12
i = (1 + 0, 011) − 1 = 0, 140286196
248
CHAPTER 10. PRÉSTAMO FRANCÉS
Por otro lado el cuadro de marcha del préstamo del Banco Norte es:
h
a
Ah
Ih
Ih (1 + τ I )
Ch
0
1
2
3
4
5
6
7
8
9
10
11
12
454,13
454,13
454,13
454,13
454,13
454,13
454,13
454,13
454,13
454,13
454,13
454,13
386,63
391,85
397,14
402,50
407,93
413,44
419,02
424,68
430,41
436,22
442,11
448,08
67,50
62,28
56,99
51,63
46,20
40,69
35,11
29,45
23,72
17,91
12,02
6,05
81,67
75,36
68,96
62,47
55,90
49,23
42,48
35,63
28,70
21,67
14,54
7,32
5.000
4.613,37
4.221,53
3.824,39
3.421,89
3.013,96
2.600,52
2.181,50
1.756,82
1.326,41
890,19
448,08
0,00
Seguro
σCh
29,99
27,44
24,86
22,24
19,59
16,90
14,18
11,42
8,62
5,79
2,91
0,00
Mh
0
386,63
778,47
1.175,61
1.578,11
1.986,04
2.399,48
2.818,50
3.243,18
3.673,59
4.109,81
4.551,92
5.000,00
gastos
fijos
152,5
0
0
0
0
0
0
0
0
0
0
0
0
Término
real adh
505,29
501,65
497,95
494,21
490,42
486,58
482,68
478,73
474,73
470,67
466,56
462,40
Usaremos Newton-Raphson para hallar el CFT del Banco Norte. Como
antes, calculamos primero in par de constantes
A1
1+i
τA − τI − σ
i
=
=
n
A1 (1 + i)
σ
1 + τI +
+g
i
=
=
1 + 0, 0135
386, 6276444 0 − 0, 21 − 0, 0065
0, 0135
−269, 858936
0, 0065
12
386, 6276444 (1 + 0, 0135)
1 + 0, 21 +
+7
0, 0135
775, 1485007
Luego la función f del esquema de Newton-Raphson para operación con el
Banco Norte es
1−
f (rk ) = −269, 858936
1 + 0, 0135
1 + rk
rd − 0, 0135
12
−12
+775, 1485007
1 − (1 + rk )
rk
−4.847, 50
y su derivada
12
12 
1 + 0, 0135
1 + 0, 0135
1−
 12

1 + rk
1 + rk


f 0 (rk ) = −269, 858936 
−
+775, 1485007
2
 (1 + rk ) (rk − 0, 0135)

(rd − 0, 0135)

Por lo que podemos conseguir el siguiente esquema iterativo, donde hemos
usado como criterio de parada un nivel de corrección de 0,0001 y como semilla
−12−
12 (1 + rk )
rk
10.4. CFT: COSTO FINANCIERO TOTAL. EFECTO DE IMPUESTOS, GASTOS Y SEGUROS249
una tasa un poco mayor a la tasa del préstamo, en este caso usamos i0 = 0, 015.
k
ik
f (ik )
f 0 (ik )
0
1
2
3
0, 015
0, 028642582
0, 029542582
0, 029546147
442, 7907442
25, 87845723
0, 101704077
−32456, 52095
−28753, 8384
−28528, 19155
f (ik )
f 0 (ik )
0, 013642582
0, 0009
3, 56504 · 10−6
−
El CFT del Banco Norte, es la TEA equivalenta a la tasa mensual real
obtenida por Newton-Raphson:
CF T
12
=
=
(1 + 0, 029546147)
=
0, 4182240266
(12)
1 + rd
−1
12
−1
Por lo que el CFT para la Srta. Georgina en el Banco Sur es del 41,82240266%.
Mientras que la TEA equivalente a la tasa declara por el banco es del 17,4586585%
pues
12
i = (1 + 0, 0135) − 1 = 0, 174586585
El siguiente cuadro resume toda la información relevante para tomar una
decisión:
TEM
TEA
TNA
(12)
rd
CFT
Sur
1.1 %
14,0286196%
13,2%
3,128994420%
44,7336105%
Norte
1.35 %
17,4586585 %
16.2 %
2,9546147%
41,82240266%
De esta manera, aunque el Banco Sur declare una tasa más baja, el efecto de
los restantes costos hace que la opción más conveniente para la Srta. Georgina
sea el Banco Norte. Se debe notar, que en ambos casos, al tener en cuenta todos
los factores la tasa que efectivamente paga la Srta. Georgina, la tasa efectiva
(12)
mensual que real para el deudor rd , es muy superior a la tasa i(12) declarada
por los bancos.
Ejemplo 10.38 Una empresa acude a un banco y pide préstados $ 500 000.
Se conviene una TEM del 1.04%. Si se usa sistema francés, el préstamo dura
1 año, a pagar en cuotas mensuales. Los gastos de otorgamiento son de $ 250
más un sellado de $ 100. Es estado cobra unos impuestos sobre los préstamos
del 0.5% del monto otorgado. Sobre las anualidades el estado cobra un impuesto
250
CHAPTER 10. PRÉSTAMO FRANCÉS
del 1%, y un sellado de $ 5. El costo interno de otorgamiento para el banco es
de $ 500, y cobrar cada anualidad le cuesta $ 35. ¿Cualés son las tasas reales
de la operación?
Primero calcularemos el monto que efectivamente recibe la empresa:
= C0 (1 − t0 ) − s0
c0
C
=
500000 (1 − 0.005) − (250 + 100)
=
497150
Mientras que el banco desembolsa
C0
=
C0 + c0
=
500000 + 500
=
500500
Los términos amortizativos que debe pagar la empresa son (a = $ 44 536.7466196):
b
a =
=
=
=
a (1 + t) + s
a (1 + 0.01) + 5
500000 · 0.0104
1 − (1 + 0.0104)
44987.1140858
−12
(1 + 0.01) + 5
mientras que los que recibe el banco son
a
=
a−c
=
44 536.7466196 − 35
=
44531.7466196
La tasa real que debe pagar la empresa es (deudor) la que produce
c0
C
1 − 1 + idr
= b
a
idr
−n
1 − 1 + idr
497150 = 44987.1140858
idr
−12
1 − 1 + idr
11.0509422554 =
idr
−12
Lo que nos da una tasa
idr = 0.0129089158023
usando métodos númericos. Es decir la tasa que realmente paga la empresa es
del 1.2908916 % mensual (y no la del 1.04% que le dice el banco).
10.4. CFT: COSTO FINANCIERO TOTAL. EFECTO DE IMPUESTOS, GASTOS Y SEGUROS251
Por otro lado la tasa que realmente gana el banco es la que produce
−n
1 − (1 + iar )
iar
C0
=
a
500500
=
44531.7466196
11.2391729046
=
1 − (1 + iar )
iar
1 − (1 + iar )
iar
−12
−12
Al resolver númericamente, obtenemos
iar = 0.0102238824627
La tasa que realmente gana el banco es del 1.02238824627% mensual (y no la
del 1.04%).
Nota 10.39 Recomendaciones del Banco Central de la República Argentina para contratar un préstamo:
1. La tasa de interés no es el único dato a tener en cuenta para elegir un
préstamo. Al costo de la tasa deben sumarse los gastos adicionales y los
seguros, de lo que resulta el Costo Financiero Total (CFT). El CFT es
la verdadera carga financiera de un préstamo y es el dato en base al cual
deben compararse las ofertas de las distintas entidades.
2. Se puede optar entre una tasa de interés que se mantenga estable a lo
largo del préstamo (tasa fija) o que varı́e periódicamente (tasa variable).
En este último caso, el cliente debe conocer cuál será el parámetro para
ajustarla.
3. Si la entidad percibe gastos de administración, se debe analizar cuál es el
costo y cómo se aplica (en porcentaje de la cuota, en porcentaje del saldo
de deuda o un monto fijo, etc.).
4. También debe analizarse, siguiendo iguales criterios, si la entidad cobra
gastos de otorgamiento.
5. Si el préstamo incluye la contratación de un seguro de vida, se debe analizar
de qué forma es cobrado por la entidad. Según la ley, el cliente tiene derecho a elegir entre tres diferentes aseguradoras.
6. Si el tomador del préstamo es consumidor final deberá pagar el IVA sobre
los intereses abonados cada mes, lo que impactará en la cuota.
7. Si el préstamo contempla la posibilidad de una cancelación anticipada,
parcial o total, es conveniente conocer cuál es su costo.
8. Algunas entidades financieras obligan a contratar productos adicionales
junto con el préstamo (cajas de ahorro, cuentas corrientes, tarjetas de
crédito). A la hora de decidir, su costo debe añadirse al de la cuota.
252
CHAPTER 10. PRÉSTAMO FRANCÉS
9. Muchas entidades financieras ofrecen ventajas para sus clientes con ”cuentassueldos”. Estos beneficios deben contemplarse en la comparación con otras
entidades.
10. Todas las condiciones informadas por la entidad financiera al momento
de ofrecer el préstamo deben figurar en el contrato. Es importante revisarlo minuciosamente, con el fin de evitar firmar cláusulas sobre las que el
cliente no tiene conocimiento.
Ejercicio 10.40 Hacer el cuadro de marcha (para el prestatario) del préstamo
anterior (agregar las siguientes columnas: tasas, gastos fijos, b
a; a continuación
de la columna de cuotas de capital).
Ejercicio 10.41 Un banco le ofrece un préstamo de $ 50 000 a una TEA del
21% por sistema francés, a pagar en 5 años en cuotas mensuales consecutivas.
Los gastos de otorgamiento son de $ 350 más un sellado de $ 150. Es estado
cobra unos impuestos sobre los préstamos del 1.5% del monto otorgado. Sobre las
anualidades el estado cobra un impuesto del 5%, y un sellado de $ 10. Además el
costo mensual del seguro obligatorio es de $ 39. El costo interno de otorgamiento
para el banco es de $ 300, y cobrar cada anualidad le cuesta $ 25. ¿Cuáles son
las tasas reales de la operación?
10.5
Cancelación anticipada total o parcial
Cancelación parcial: una variante que perminten ciertos contratos es adelantar una cantidad cualquiera de capital, no sólo una cantidad entera de cuotas.
En general si se dispone de una cierta cantidad de dinero al momento t + f ,
donde f es una fracción de perı́odo, todo lo que hay que hacer es cancelar los
intereses generados y descontar del capital pendiente el resto del dinero. Por lo
que el nuevo capital pendiente será
e = Ct (1 + i)f − adelanto
C
Para recalcular el préstamo debemos pactar una tasa y un perı́odo de tiempo,
lo habitual es mantener la tasa original, y mantener la cantidad de pagos que
restaban por realizar.
Ejemplo 10.42 En el caso del préstamo de la empresa, supongamos ahora que
a lo 2 años 7 meses y 19 dı́as decide adelantar $ 410 000, pues el contrato le
permite realizar cancelaciones parciales.
Bueno, sólo debemos calcular la deuda actual
e
C
f
= Ct (1 + i) − adelanto
19
=
2676421.769 (1 + 0.015) 30 − 410000
=
2291778.32
10.5. CANCELACIÓN ANTICIPADA TOTAL O PARCIAL
253
y ahora recalculamos el préstamo para con
i
=
n
e
= n−t+1
0.015
=
84 − 31 + 1
=
54
Por ejemplo, la cuota de amortización ahora será
a
=
=
=
e
Ci
−e
n
1 − (1 + i)
2291778.32 · 0.015
1 − (1 + 0.015)
62224.94690
−54
La cancelación total no es más que un caso particular de la cancelación
parcial. Si en el momento t + f , decidimos cancelar el préstamo, entonces
adelanto = Ct (1 + i)
f
Ejercicio 10.43 Ud. pide un préstamo a un banco de $ 80 000 para arreglar
la cocina de su casa (¡menuda cocina!). Pacta con el banco pagar en cuotas
mensuales por el término de 6 años a una TEA del 24.3%. A los 4 años, 9
meses y 7 dı́as ud. decide adelantar $ 5500.
1. Recalcular el préstamo.
2. Recalcular el prétamo usando n = 6 meses.
Compensación por adelantos
Puede ocurrir que la situación económica sea tal que el adelanto de capital
pérjudique al préstamista. Esto ocurre cuando la tasa actual ia que puede
obtener el préstamista es más baja que la tasa convenida i
ia < i.
En dicho caso el préstamista puede solicitar (si ası́ el contrato lo estipulara) una
compensación. La forma sencilla de hacer esto es actualizar el flujo de fondos
futuro a la tasa actual.
Ejemplo 10.44 Volviendo al caso del préstamo de la empresa, supongamos
ahora que a los 2 años 7 meses y 19 dı́as decide adelantar $ 410 000, pero la
tasa actual que cobra puede ganar el banco es una TEM del 0.85%. Recalcular
el préstamo:
254
CHAPTER 10. PRÉSTAMO FRANCÉS
En este caso, debemos usar la nueva tasa para actualizar el flujo de pagos y
hallar lo que llamaremos deuda compensada
#
"
−n+t+1
1 − (1 + ia )
a
deuda compensadat+f =
1+
1−f
ia
(1 + ia )
!
−84+31+1
73562.43293
1 − (1 + 0.0085)
=
1+
1− 19
0.0085
(1 + 0.0085) 30
=
3145402.862
Nota 10.45 PONER DIBU
Ahora le decontamos a la deuda
Nota 10.46 Poner dibu
10.6
Adelanto de cuotas
Adelanto de cuotas: es la opción que a veces (dependiendo del contrato) tiene
el prestatario de pagar antes de la fecha de vencimiento las cuotas de capital.
Según el contrato firmado, la cuotas adelantadas corresponden a uno u otro
extremo del esquema de pago.
Llamaremos adelanto inverso, al contrato que le da la opción al prestatario
de adelantar cuotas de capital comenzando la última An , siguiendo con la An−1
y ası́ sucesivamente.
Llamaremos adelanto directo, al contrato que le da la opción al prestatario
de adelantar las sucesivas cuotas de capital, comenzado con la siguiente que le
toque amortizar, más los intereses generados hasta el momento.
En ambos caso, una vez efectivizado el adelanto de las cuotas se recalcula
el préstamo con el nuevo capital pendiente, la misma tasa o una nueva (si
correspondiera) y el número de perı́odos que corresponda o un nuevo (si fuese
posible repactar el número y la frecuencia de los perı́odos de amortización). En
general el adelanto de cuotas esta excento de gastos e impuestos.
Desarrollaremos las fórmulas necesarias con un ejemplo
Ejemplo 10.47 Una empresa pide un préstamo por $ 3 500 000 para construir
un nuevo salón de ventas. Pacta con el banco un prestamo fránces mensual a
una tasa TEM del 1.5% por el término de 7 años. Transcurrido 2 años y 7
meses, y debido un aumento significativo en las ventas, la empresa dispone de $
410 000 para adelantar cuotas de capital. Si el contrato firmado es de adelanto
inverso, ¿cuántas cuotas puede adelantar la empresa? ¿Qué monto necesitaria
para adelatar las últimas 10 cuotas?
Debemos hallar k tal que
n
X
h=k
Ah ≤ adelanto <
n
X
h=k−1
Ah
(10.31)
10.6. ADELANTO DE CUOTAS
255
Recordando que
Ah = A1 (1 + i)
h−1
tenemos que
A1
n
X
(1 + i)
h−1
≤ adelanto < A1
h=k
k−1
A1 (1 + i)
(1 + i)
(1 + i)
k−1
h−1
(1 + i)
h=k−1
n−k
X
h=0
n−k+1
A1 (1 + i)
n
X
h
k−2
n−k+1
X
k−2
(1 + i)
≤ adelanto < A1 (1 + i)
(1 + i)
h
h=0
−1
i
n−k+2
≤ adelanto < A1 (1 + i)
Como
A1 = C0
−1
i
i
n
(1 + i) − 1
tenemos
C0
k−1 h
k−2 h
i
i
(1 + i)
(1 + i)
n−k+1
n−k+2
(1
+
i)
−
1
≤
adelanto
<
C
(1
+
i)
−
1
0
n
n
(1 + i) − 1
(1 + i) − 1
de donde
h
k−1
(1 + i)
(1 + i)
n−k+1
n
i
−1
(1 + i) − (1 + i)
≤
k−1
≤
h
i
adelanto
n
k−2
n−k+2
[(1 + i) − 1] < (1 + i)
(1 + i)
−1
C0
adelanto
n
n
k−2
[(1 + i) − 1] < (1 + i) − (1 + i)
C0
por lo que
(1 + i)
k−1
n
≥ (1 + i) −
adelanto
n
k−2
[(1 + i) − 1] > (1 + i)
C0
Luego
n
n
log (1 + i) −
k≥
adelanto
C0
n
[(1 + i) − 1]
o
+1>k−1
log (1 + i)
(10.32)
En particular
84
log (1 + 0.015) −
k≥
410000
3500000
84
(1 + 0.015)
log (1 + 0.015)
lo que equivale a
k ≥ 79.136 > k − 1
Por lo que
k = 80
−1
+1>k−1
256
CHAPTER 10. PRÉSTAMO FRANCÉS
Es decir, con $ 410 000 la empresa puede adelantar las últimas 5 cuotas de
capital, desde A80 hasta A84 :
número de cuotas adelantadas = n − k + 1
(10.33)
Para comprobarlo, calculamos
A79
A80
A81
A82
A83
A84
=
=
=
=
=
=
67275, 9487
68285, 08793
69309, 36425
70349, 00471
71404, 23978
72475, 30338
y observamos que
84
P
Ah = 351823, 0001
h=80
mientras que
84
P
Ah = 419098, 9488
h=79
Ahora veremos que ocurre de aqui en adelante (estamos en el mes 31: 2 años
y 7 meses después de desembolsado el préstamo).
Lo primero que necesitamos saber es cuanto debemos ahora:
deuda actual = capital pendiente−la suma de las cuotas de capital adelantadas
Es decir, si al momento t adelantamos las cuotas de capital Ak , Ak+1 , . . . , An ,
el nuevo capital pendiente será
n
ft = Ct − P Ah
C
(10.34)
h=k
Haciendo las sustituciones correspondientes
ft
C
=
=
=
k−1 h
n
t
i
(1 + i)
(1 + i) − (1 + i)
n−k+1
−
C
(1
+
i)
−
1
0
n
n
(1 + i) − 1
(1 + i) − 1
nh
i
h
io
C0
n
t
k−1
n−k+1
(1 + i) − (1 + i) − (1 + i)
(1 + i)
−
(10.35)
1
n
(1 + i) − 1
h
i
C0
k−1
t
(1 + i)
− (1 + i)
n
(1 + i) − 1
C0
Ahora, con $ 410 000 la empresa puede adelantar las últimas 5 cuotas en el
momento 31, por lo que
g
C
31
=
C31 −
84
P
Ah
h=80
=
2676421.769 − 351823.0001
=
2324598.7689
10.6. ADELANTO DE CUOTAS
257
Lo mismo puede ser obtenido usando
3500000
80−1
31
ft =
(1
+
0.015)
−
(1
+
0.015)
= 2324598.7689
C
84
(1 + 0.015) − 1
Este monto es la deuda actual, y debemos recalcular el préstamo, tomando como
monto inicial los $ 2 324 598.7689, usando la tasa y la cantidad de perı́odos que
convengan las partes (tı́picamente se mantiene la tasa original y la cantidad de
perı́odos que se usa es la natural: los que restan:
número de
número
número de
número de
perı́odos =
total
cuotas
− términos −
que faltan
perı́odos
pagados
adelantadas
Es decir
n
e :=
número de
perı́odos = n − t − (n − k + 1) = k − t − 1
que faltan
Por ejemplo en este caso
n
e = 80 − 31 − 1 = 48
Por lo que si mantenemos la tasa, y la cantidad de perı́odos, la empresa debe
pagar por los próximos 48 meses la suma de
i
ft
e
a = C
−e
n
1 − (1 + i)
0.015
g
= C
31
−48
1 − (1 + 0.015)
0.015
= 2324598.7689
−48
1 − (1 + 0.015)
= 68285.0879255
Lo cual es menos que el término
a = 73562.43293
que originalmente debı́a pagar mes a mes la empresa.
Para hallar el monto necesario para adelantar las últimas 10 cuotas de capital
usamos
n
P
Ah = adelanto
(10.36)
h=k
donde
k = n + 1 − el número de cuotas que se quieren adelantar
En nuestro caso
k = 84 + 1 − 10 = 75
(10.37)
258
CHAPTER 10. PRÉSTAMO FRANCÉS
Como
n
P
Ah = C 0
h=k
k−1 h
i
(1 + i)
n−k+1
(1 + i)
−1
n
(1 + i) − 1
tenemos que
k−1
h
i
(1 + i)
n−k+1
(1 + i)
−1
n
(1 + i) − 1
adelanto = C0
(10.38)
En particular
75−1
adelanto = 3500000
(1 + 0.015)
84
(1 + 0.015)
−1
(1 + 0.015)
84−75+1
− 1 = 678406, 332592
El lector puede comprobar que efectivamente es da la suma de las últimas 10
cuotas de capital.
Ejemplo 10.48 En la misma situación de ejemplo anterior, pero ahora el contrato estipula que el adelanto de las cuotas de capital debe ser directo.
En este caso el dato: “Transcurrido 2 años y 7 meses”, es crucial, pues nos
dice estamos en el mes 31 y que la primera cuota que tenemos para adelantar
es la A32 . En general si estamos en el momento t, la primer cuota que podemos
adelantar es la At+1 . Ahora el problema es hallar k tal que
k
X
Ah ≤ adelanto <
h=t+1
k+1
X
Ah
(10.39)
h=t+1
de donde
k
X
A1
h−1
(1 + i)
≤
h=t+1
t
A1 (1 + i)
adelanto < A1
k+1
X
h−1
(1 + i)
h=t+1
k−t−1
X
h
(1 + i)
≤
adelanto < A1 (1 + i)
t
h=0
t
h
(1 + i)
h=0
k−t
A1 (1 + i)
k−t
X
(1 + i)
i
−1
k−t+1
≤
adelanto < A1 (1 + i)
t
(1 + i)
Luego
(1 + i)
k−t
≤
i
adelanto
k−t+1
+ 1 < (1 + i)
t
A1
(1 + i)
sustituyendo A1
n
k−t
(1 + i)
≤
(1 + i) − 1 adelanto
k−t+1
+ 1 < (1 + i)
t
C0
(1 + i)
i
−1
10.6. ADELANTO DE CUOTAS
259
Luego
log
k≤
n
(1 + i) − 1 adelanto
+
1
t
C0
(1 + i)
+t<k+1
log (1 + i)
(10.40)
En particular
"
log
k≤
84
− 1 410000
+1
31
3500000
(1 + 0.015)
(1 + 0.015)
log (1 + 0.015)
#
+ 31 < k + 1
lo que equivale a
k ≤ 42.347 < k + 1
Por lo que
k = 42
Es decir, con $ 410 000 la empresa puede adelantar 11=42-31 cuotas: de la A32
a la A42 , pues
números de cuotas adelantadas =k − t
Para comprobarlo, calculamos
A32
A33
A34
A35
A36
A37
A38
A39
A40
A41
A42
A43
=
=
=
=
=
=
=
=
=
=
=
=
33416, 10639
33917, 34799
34426, 10821
34942, 49983
35466, 63733
35998, 63689
36538, 61644
37086, 69569
37642, 99613
38207, 64107
38780, 75568
39362, 46702
y observamos que
42
P
Ah = 396424, 0417
h=32
mientras que
43
P
h=32
Ah = 435786, 5087
(10.41)
260
CHAPTER 10. PRÉSTAMO FRANCÉS
Observe que en general
k
X
Ah
k
X
=
h=t+1
A1 (1 + i)
h−1
h=t+1
t
=
A1 (1 + i)
k−t−1
P
h
(1 + i)
h=0
k−t
(1 + i)
−1
i
k−t
−1
t (1 + i)
C0 (1 + i)
n
(1 + i) − 1
t
=
A1 (1 + i)
=
Ahora debemos recalcular el préstamo. Lo primero que se debe averiguar es
el monto de la deuda pendiente:
deuda actual = capital pendiente−las suma de las cuotas de capital adelantadas
Es decir, si al momento t adelantamos las cuotas de capital At+1 , At+2 , . . . , Ak ,
el nuevo capital pendiente será
k
ft = Ct − P Ah
C
(10.42)
h=t+1
Haciendo las sustituciones correspondientes
n
ft
C
k−t
t
−1
(1 + i) − (1 + i)
t (1 + i)
− C0 (1 + i)
n
n
(1 + i) − 1
(1 + i) − 1
nh
i
h
io
C0
n
t
t
k−t
(1 + i) − (1 + i) − (1 + i) (1 + i)
−1
n
(1 + i) − 1
h
i
C0
n
k
(1
+
i)
−
(1
+
i)
(10.43)
n
(1 + i) − 1
= C0
=
=
Ahora, con $ 410 000 la empresa puede adelantar las próximas 11 cuotas en
el momento 31, por lo que
g
C
31
=
C31 −
42
P
Ah
h=32
=
2676421.769 − 396424.0417
=
2279997.7273
Lo mismo puede ser obtenido usando
ft =
C
3500000
84
(1 + 0.015)
−1
(1 + 0.015)
84
42
− (1 + 0.015)
= 2279997.7273
Este monto es la deuda actual, y debemos recalcular el préstamo, tomando como
monto inicial los $ 2 279 997.7273, usando la tasa y la cantidad de perı́odos que
10.6. ADELANTO DE CUOTAS
261
convengan las partes (tı́picamente se mantiene la tasa original y la cantidad de
perı́odos que se usa es la natural: los que restan
número de
número
número de
número de
perı́odos =
total
cuotas
− términos −
que faltan
perı́odos
pagados
adelantadas
Es decir
n
e := n − t − (k − t) = n − k
Por ejemplo en este caso
n
e = 84 − 42 = 42
Por lo que si mantenemos la tasa, y la cantidad de perı́odos, la empresa debe
pagar por los próximos 42 meses la suma de
i
ft
e
a = C
−e
n
1 − (1 + i)
0.015
g
= C
31
−42
1 − (1 + 0.015)
0.015
= 2279997.7273
−42
1 − (1 + 0.015)
= 73562.43293
= a
pues el adelanto directo de t cuotas de capital equivale a moverse moverse t
renglones (filas) sobre el cuadro de marcha.
Para hallar el monto necesario para adelantar las próximas 10 cuotas de
capital si estamos en el momento t usamos
k
P
Ah = adelanto
(10.44)
h=t+1
donde
k = t + el número de cuotas que se quieren adelantar
(10.45)
En nuestro caso
k = 31 + 10 = 41
Como
k
P
k−t
Ah = C0 (1 + i)
(1 + i)
−1
n
(1 + i) − 1
t
h=k
tenemos que
k−t
t
adelanto = C0 (1 + i)
(1 + i)
−1
n
(1 + i) − 1
(10.46)
262
CHAPTER 10. PRÉSTAMO FRANCÉS
En particular
41−31
31
adelanto = 3500000 (1 + 0.015)
(1 + 0.015)
(1 + 0.015)
84
−1
−1
= 357643.286
El lector puede comprobar que efectivamente esto es lo que da la suma de las
próximas 10 cuotas de capital.
Ejercicio 10.49 Ud. pide un crédito por $ 65 000 a 10 años para ampliar su
casa. El banco utiliza sistema fránces, con una TNA 23% a pagar mensualmente.
Transcurridos 4 años y 3 meses, ud. recibe una herencia de $ 15 000 y decide
adelantar cuotas de capital con la misma.
1. ¿Cuántas cuotas puede adelantar si el contrato firmado es de adelanto
inverso?
2. ¿Cuántas cuotas puede adelantar si el contrato firmando es de adelanto
directo?
3. ¿Cuánto necesita para adelantar 20 cuotas? Suponer adelanto directo.
4. ¿Cuánto necesita para adelantar 15 cuotas? Suponer adelanto inverso.
5. En cada caso recalcule el préstamo (usando la tasa dada y la cantidad de
perı́odos natural)
6. Recalcule el préstamo si se pacta a 36 meses a una tasa TEM 1.3%
Ejemplo 10.50 Volviendo al ejemplo de la empresa, y suponiendo que el contrato permite el adelanto directo de cuotas de capital, que ocurre si la fecha de
adelanto es 2 años, 7 meses y 18 dı́as.
Hay varias maneras de lidiar con esta situación, la más simple de todas es actualizar el adelanto los 18 dı́as, y prodecer como antes. En general si disponemos
de una cantidad dada de dinero y deseamos saber cuantas cuotas de capital
podemos adelantar al momento t + f , donde f es una fracción (menor que uno)
de perı́odo, es equivalente a diponer de
adelanto
(1 + i)
f
pesos
al momento t.
Nota 10.51 PONER DIBU
Ahora el problema es hallar k tal que
k
X
h=t+1
Ah ≤
adelanto
f
(1 + i)
<
k+1
X
h=t+1
Ah
10.6. ADELANTO DE CUOTAS
263
y de los desarrollos anteriores
"
#
n
(1 + i) − 1 adelanto
log
+1
t
f
(1 + i)
C0 (1 + i)
k≤
+t<k+1
log (1 + i)
(10.47)
En nuestro caso, tenemos que f = 18 dı́as, esto nos permite adelantar hasta la
cuota
!
84
(1 + 0.015) − 1
385983.966119
log
18 + 1
31
(1 + 0.015)
3500000 (1 + 0.015) 30
k≤
+ 31 < k + 1
log (1 + 0.015)
: 41. 644de donde
k ≤ 41.644 < k + 1
por lo tanto
k = 41
Es decir, ahora podemos adelantar 10 cuotas: k − t = 41 − 31.
El cálculo de cuanto se necesita para pagar un determinado número de cuotas
al momento t + f , se reduce al caso ya tratado: simplemente hay que actualizar
al momento t el adelanto:
adelanto
(1 + i)
f
k−t
= C0 (1 + i)
t
(1 + i)
−1
n
(1 + i) − 1
donde
k = t + el número de cuotas que se quieren adelantar.
Observe que lo anterior corresponde a recalcular la deuda al momento t + f ,
realizar el adelanto y luego actualizar al momendo t y proceder como antes (a
fin de mantener las fechas de pagos pactadas originalmente):
1. Cálculo de la deuda al momento t + f : debemos capitalizar Ct , capital
pendiente al momento t, hasta el momento t + f y restar el adelanto:
f
Nueva deuda al momento t + f = Ct (1 + i) − adelanto.
2. Para mantener las fechas de pago, lo más sencillo es actualizar la nueva
deuda, llevandola al momento t, de esta manera podremos aplicar las
fórmulas ya desarrolladas
Nueva deuda
f
Ct (1 + i) − adelanto
adelanto
al momento t + f
= Ct −
=
f
f
actualizada al
(1 + i)
(1 + i)
momento t
264
CHAPTER 10. PRÉSTAMO FRANCÉS
Ejercicio 10.52 Un comercio pide préstado por sistema francés $ 110 000, a
pagar en 3 años en cuotas trimestrales. La TAE acordada es de un 22%. Al año
y dos meses, los socios dueños del comercio deciden adelantar 4 cuotas. Hacer
los calculos correspondientes (suponiendo primero sistema directo de adelanto
de cuotas, y luego sistema inverso).
Ejercicio 10.53 Un amigo suyo hace tres años y 22 dı́as pidio un préstamo por
$ 18 000 a pagar en 5 años por sistema fránces a una TEM del 2.3%. Como está
convencido de que el interés que le cobran es muy alto y además ayer ganó $ 4
500 en el casino, decide ir mañana a la financiera y adelantar cuantas cuotas de
capital pueda. El desconfı́a un poco de la financiera, por lo que le pide a ud. que
le saque las cuentas. Ud le pregunta si puede adelantar cuotas de forma directa
o inversa, pero el responde que no sabe, por lo que decide hacer las cuentas para
los dos casos.
10.7
Punitorios
Cuando se toma un préstamo, cada una de las cuotas de amortización tiene un
intervalo de tiempo durante el cual el deudor debe efectivizar su pago (por ejemplo, del 1ero al 10mo de cada mes). Superada la fecha lı́mite para realizar el pago
de una cuota de amortización, el acreedor tiene derecho a aplicar punitorios
sobre la/s cuotas adeudadas. Los punitorios son los cargos (fijos y variables)
que el acreedor aplica sobre las cuotas que atrasadas. Dependiendo el tipo de
préstamo, y el contrato firmado, a la tercera (o 5ta) cuota impaga el acreedor
procede a reclamar la deuda por vı́a judicial (intimando al garante, ejecutando
la prenda o hipoteca, relizando un embargo sobre los bienes o sueldos del deudor,
etc.).
En general, como la término k-ésimo de amortización tiene dos partes: la
cuota de amortización o de capital, y la cuota de interés
ak = Ak + Ik
y la mora consta de una catidad m de dı́as.
Cómo se cobran los punitorios:
1. Pueden existir multas, y gastos de cobranza M
l
2. tenemos una sucesión de tasas punitorias sobre el capital pA
h h=1 , y una
l
sucesión de tasas punitorias sobre los intereses de pIh h=1 y una sucesión
l−1
de tiempos (th )h=1 que marca los plazo de apliación de cada una de las
tasas punitorias
3. Un monto fijo por dı́a p
Ahora esta el tema del tiempo de mora. Supongamos que ud. debe pagar
sus cuotas del 1ero al 10mo de cada mes, y ud paga el 14 ¿En cuántos dı́as de
10.8. PRÉSTAMO FRANCÉS A INTERES VARIABLE
265
mora incurrio? Uno tiene la tendencia a pensar que son 4 dı́as. Pero depediendo
del contrato firmado, puede ser que consideren que lleva 14 dı́as de mora. El
primero lo llamaremos mora natural y al segundo mora bancaria.
Asi la deuda despues de m dı́as de mora es
M +mp+Ak
Y
Σth ≤m
1 + pA
h
th
1 + pA
x+1
m−Σth
+Ik
Y
1 + pIh
th
1 + pIx+1
m−Σth
Σth ≤m
Ejemplo 10.54
10.8
Préstamo francés a interes variable
10.9
Inflación y su efecto sobre los préstamos
10.10
Devaluación y su efecto sobre los préstamos
Chapter 11
Préstamo alemán
11.1
Introducción
Los elementos que componen un tı́pico préstamo alemán son:
1. C0 el capital préstado.
2. i la tasa de interés cobrada por el prestamista.
3. A cuota de amortización.
4. n la cantidad de términos amortizativos a pagar.
En este tipo de préstamo se mantiene constante la cuota de amortización:
A1 = A2 = · · · = An = A
Por lo tanto
C0 =
n
X
A = nA
k=1
de donde podemos despejar el valor de la cuota de amortización
A=
C0
n
(11.1)
Es claro que si las cuotas de amortización son constantes, entonces las cuotas
de interés forman una sucesión estrictamente decreciente
I1 > I2 > · · · > In ,
al igual que la sucesión de términos de amortizativos:
a1 > a2 > · · · > an .
266
11.1. INTRODUCCIÓN
267
Nota 11.1 PONER DIBU
Para un análisis completo debemos tener fórmulas para calcular el resto de
las cantidades significativas: términos amortizativos, cuotas de interés, capital
pendiente y total amortizado.
Sabemos que
A = Ch−1 − Ch
de donde es fácil deducir la siguiente relación recursiva entre los capitales pendientes de todo préstamo alemán:
Ch = Ch−1 − A
tenemos que
C0
(n − h)
(11.2)
n
lo que nos dice que el capital pendiente forma una renta aritmética decreciente
de término inicial C0 y paso −A. Observe que a mitad del préstamo (en h = n/2)
se debe exáctamente la mitad (esto no ocurre nunca en el sistema francés ¿por
qué?).
Para calcular la cuota de interés basta recordar
Ch = C0 − hA =
Ih = iCh−1 = i
C0
(n − h + 1)
n
(11.3)
Nuevamente obtenemos una renta aritmética decreciente de término inicial C0 i
y paso −Ai
El total amortizado es también muy fácil de expresar:
Mh = hA = h
C0
n
(11.4)
Lo que nos da una renta aritmética creciente de término inicial A, y paso A.
Un poco más complejo resulta el cálculo de los términos amortizativos. Sabemos que al final del perı́odo h el término amortizativo es igual a los intereses
generados durante el perı́odo h más la cuota de amortización:
ah
= Ch−1 i + A
=
(C0 − (h − 1) A) i + A
= C0 i + (1 + i − hi)A
C0
=
(1 + (n − h + 1) i)
n
(11.5)
(11.6)
Por lo tanto, recordando (11.1)
ah = A + (n − h + 1) iA = C0 i + A − (h − 1) Ai
(11.7)
de donde resulta claro que los términos amortizativos en un préstamo alemán
forman una renta aritmética decreciente de término inicial C0 i + A y paso −Ai.
268
CHAPTER 11. PRÉSTAMO ALEMÁN
Ejemplo 11.2 Ud. acude a un banco y pide un préstamo de $ 24 000 a devolver
en 5 años en cuotas mensuales, por el sistema alemán. La TNA que le cobra el
banco es del 18%.
Primero calcularemos el valor de la cuotas de amortización usando (11.1)
A
24000
60
400
=
=
i.e., ud. cancela $ 400 cada mes del capital adeudado.
Ahora podemos dar las expresiones para el resto de las cantidades significativas. Comencemos con los términos amortizativos, según (11.7)
0.18
ah = 400 1 − (60 − h + 1)
12
Asi, como Ai = 6 y
a1 = 400 (1 + 60 · 0.015) = 760
tenemos que
a2
a3
a4
=
=
=
..
.
754
748
742
a59
a60
=
=
412
406
El capital pendiente al perı́odo h, dado por (11.2), es
Ch = C0 − hA = 24000 − 400h
Por ejemplo, el capital pendiente a los 12, y a los 30 meses es
C12
=
19200
C30
=
12000
El total amortizado viene dado por
Mh = hA
Por ejemplo, a los 15 y a los 45 meses es
M15
=
15 · 400 = 6000
M45
=
45 · 400 = 18000
La cuota de interés correspondiente será
Ih
=
Ch−1 i
=
(24000 − 400 (h − 1)) 0.015
=
366 − 6h
11.1. INTRODUCCIÓN
269
Por ejemplo, la cuota de capital a los 30 y 48 meses es
I30
=
186
I48
=
78
Ejercicio 11.3 La Srta. Noélia saco un préstamo a sola firma de $ 2 500 en la
financiera ”Su amigo Adrián”, la cual trabaja con sistema alemán y cobra una
TNA del 38.6 %. El prestamo dura 1 año y se conviene realizar el reembolso del
mismo en 12 cuotas mensuales. Se pide:
1. ¿Cuánto es el monto de las distintas cuotas de maortización?
2. ¿A cuánto ascienden los términos amortizativos a1 , a6, y a11 ?
3. ¿Cuál es el monto de las cuotas de interés I1 e I8 ?
4. ¿A cuánto asciende el capital pendiente C8 ?
5. ¿En qué momento el capital pendiente es inferior a $ 1 000?
6. ¿A cuánto asciende el total amortizado M3 ?
7. ¿En que momento el total amortizado supera los $ 1 500?
Ejercicio 11.4 Una empresa acude a un banco y pide préstados $ 2 000 000.
Se conviene una TEM del 1.04 %. Si se usa sistema alemán, el préstamo dura
3 años, y la cuotas son bimestrales.
1. ¿Cuánto es el monto de las cuotas de amortización?
2. ¿A cuánto ascienden los términos amortizativos a1 , a10, y a18 ?
3. ¿Cual es el monto de las cuotas de interés I5 e I14 ?
4. ¿A cuánto asciende el capital pendiente C6 ?
5. ¿En que momento el capital pendiente es inferior a $ 1 000 000?
6. ¿A cuánto asciende el total amortizado M12 ?
7. ¿En que momento el total amortizado supera los $ 1 500 000 ?
Ejercicio 11.5 El Sr. Juan paga cada mes los interes generados por un préstamo
que obtuvo del Banco Cooperativo de Oeste, más una suma fija de $ 550 para
cancelar capital. Sabiendo que la tasa de la operación es una TEA del 22.5 % y
que la misma fue pactada a 5 años, se pide
1. Monto del préstamo solicitado por el Sr. Juan.
2. ¿A cuánto ascienden los términos amortizativos a1 , a30, y a60 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I20 e I40 ?
270
CHAPTER 11. PRÉSTAMO ALEMÁN
4. ¿A cuánto asciende el capital pendiente al final de cada año (C12 , C24 ,
C36 , C48 y C60 )?
5. ¿A partir de que cuota el capital pendiente es inferior a la mitad del monto
del préstamo solicitado?
6. ¿A cuánto asciende el total amortizado a principio de cada año (M0 , M12 ,
M24 , M36 y M48 )?
7. ¿A partir de que cuota el total amortizado supera los dos tercios del monto
del préstamo solicitado?
Ejercicio 11.6 La Sra. Florencia desea renovar la cocina de su departamento,
para lo cual solicita un prestamo personal a tres anños, a una TNA del 30 %,
el cual reembolsará por sistema alemán cancelando cada mes $ 300 de capital.
Se pide
1. Monto del préstamo solicitado por la Sra. Florencia.
2. ¿A cuánto ascienden los términos amortizativos a1 , a12 , a24, y a36 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I6 e I18 ?
4. ¿A cuánto asciende el capital pendiente al final de cada año (C12 , C24 , y
C36 )?
5. ¿A partir de que cuota el capital pendiente es inferior a un cuarto del
monto del préstamo solicitado?
6. ¿A cuánto asciende el total amortizado a principio de cada año (M0 , M12 ,
M24 , y M36 )?
7. ¿A partir de que cuota el total amortizado supera la mitad del monto del
préstamo solicitado?
Los datos necesarios para llenar el cuadro de marcha de un préstamo alemán
dado, son los mismos que siempre se necesitan para confeccionar un préstamo:
1. C0 el capital préstado.
2. i la tasa que se cobra.
3. n la cantidad de perı́odos que dura el préstamo.
Ahora damos el esquema genérico para completar un cuadro de marcha, los
números entre paréntesis indican el orden que usa el autor para ir llenado el
11.1. INTRODUCCIÓN
271
cuadro (el cual no es único).
n
0
1
2
3
4
..
.
a
(4) a1 = A + I1
(8) a = A + I2
(12) a = A + I3
(16) a = A + I4
..
.
Ih
A
Mh
-
-
-
I1 = C0 i
I2 = C1 i
(11) I3 = C2 i
(15) I4 = C3 i
..
.
n−1
n
a = A + In−1
a = A + In
In−1 = C n−2 i
In = C n−1 i
(5) M = A
M2 = M1 + A
(13) M3 = M2 + A
(17) M4 = M3 + A
Ch
C0
(6) C1 = C0 − A
(10) C2 = C1 − A
(14) C3 = C2 − A
(18) C4 = C3 − A
..
.
..
.
..
.
A
A
Mn−1 = M n−2 +A
Mn = M n−1 +A = C 0
Cn−1 = C n−2 −A
Cn = C n−1 −A = 0
(3)
(2)
(7)
(2)
(2)
(2)
A
A
A
A
(9)
(1)
Nota 11.7 Algunas observaciones
1. Una vez calculada la cuota de amortización, se llena toda la cuarta columna.
2. La columna de las cuotas de interés debe ser aritmeticamente decrececiente.
3. La columna de las terminos amortizativos debe ser decreciente aritméticamente,
4. La columna del total amortizado debe ser estrictamente creciente comenzando en 0 (cero) y finalizando en C0 .
5. La columna del capital pendiente debe ser estrictamente decreciente comenzando en C0 y terminando en 0 (cero).
En general, si se redondea a dos cifras, las dos últimas condiciones no se
cumplen. En dicho caso si el error no supera una cota preestablecida (por ejemplo
para este libro: 5 centavos) se considera correcto. Si el error fuera mayor se debe
aumentar la cantidad de decimales considerados. El autor recomienda trabajar
al menos con tres decimales.
Ejemplo 11.8 Hacer el cuadro de marcha de un préstamo alemán a 6 meses
por $ 5000, a una TEM del 1.2%.
n
0
1
2
3
4
5
6
a
Ih
Ah
Mh
893, 3333333
883, 3333333
873, 3333333
863, 3333333
853, 3333333
843, 3333333
60
50
40
30
20
10
833, 3333333
833, 3333333
833, 3333333
833, 3333333
833, 3333333
833, 3333333
833, 3333333
1666, 666667
2500
3333, 333333
4166, 666667
5000
Ch
5000
4166, 666667
3333, 333333
2500
1666, 666667
833, 3333333
0
Nota 11.9 Es claro que el uso de una planilla de cálculo, como excel, fácilita
la confección de cualquier cuadro de marcha. Por lo que se recomienda su uso
siempre que sea posible.
272
CHAPTER 11. PRÉSTAMO ALEMÁN
En todo préstamo a interés sobre saldos el valor actual de la renta de los
términos amortizativos es igual al capital préstado. En el sistema francés esto
es obvio (¿Por qué?), pero en el resto de los sistemas (alemán y américano)
esta afirmación necesita ser verificada. Veamos que este es el caso en el sistema
alemán.
El valor actual de los términos amortizativos de un préstamo alemán por
C0 , a una tasa i, convenido a n perı́odos (usando (11.7)) es
n
X
h=1
ah
(1 + i)
n
X
C0 i + A − (h − 1) Ai
=
h
h
(1 + i)
h=1
Ahora, la expresión anterior corresponde es exactamente el valor actual de una
renta aritmética (8.27)
−n
V Aaritmética (0) =
1 − (1 + i)
i
nb
b
C + + nb −
i
i
donde
C
= C0 i + A
b = −Ai
Por lo tanto, recordando que A = C0 /n
n
X
−n
ah
h
h=1
(1 + i)
=
1 − (1 + i)
i
=
1 − (1 + i)
i
−Ai
n (−Ai)
C0 i + A +
+ n (−Ai) −
i
i
−n
(C0 i + A − A − nAi) + nA
|
{z
}
=0
= C0
Ejercicio 11.10 Hacer el cuadro de marcha para un préstamo alemán a 12
años por $ 10 000 000, para el cual se han pactado 12 pagos anuales consecutivos
y una TEA del 23%.
Ejercicio 11.11 Escoger al menos tres de los préstamos planteados en los ejercicios del (12.3) en adelante y realizar el correspondiente cuadro de marcha.
Chapter 12
Préstamo americano
12.1
Introducción
El sistema americano se suele usar cuando se otorgan préstamos muy grandes,
como los que habitualmente otorgan los organismos internacionales (BID, FMI,
Banco Mundial, etc.) a diferentes paı́ses o empresas. Además nos da el esquema
básico para el análisis de las obligaciones y los bonos.
Los elementos que componen un tı́pico préstamo americano son:
1. El capital préstado: C0 .
2. La tasa de interés cobrada por el prestamista: i.
3. La cantidad de términos amortizativos a pagar: n.
Nota 12.1 Como siempre, suponemos que existe compatibilidad dimensional
entre la frecuencia de capitalización de la tasa i y la distancia temporal entre
dos términos amortizativos consecutivos, i.e., si la tasa usada es mensual, los
pagos son mensuales. Similarmente, si los pagos son trimestrales, la tasa debe
ser trimistral. Usamos esta convención para no sobrecargar notacionalmente las
fórmulas del sistema americano que deduciremos a continuación.
El sistema americano se caracteriza por mantener constante la cuota de
interés, i.e. de las dos componentes de cada término amortizativo ah = Ih + Ah
en el sistema americano se mantiene constante Ih . ¿Cómo se logra esto? pues
muy sencillo: debiendo siempre lo mismo. Como inevitablemente la primera
cuota de interés debe ser I1 = C0 i tenemos que
C0 i = I1 = I2 = · · · = In = I
273
(12.1)
274
CHAPTER 12. PRÉSTAMO AMERICANO
i
an
C0
C0
a1
a2
I
0
I
1
2
an−1
a3
I
I
n−1
3
I
n
Por lo tanto todas las cuotas de amortización deben ser todas nulas, salvo
la última, la cual debe ser igual al monto prestado a fin de cancelar la deuda:
0
si 1 ≤ h ≤ n − 1 ,
Ah =
(12.2)
C0 si h = n.
Por esta razón los términos amortizativos son todos iguales, salvo el último:
C0 i
si 1 ≤ h ≤ n − 1,
ah =
(12.3)
(1 + i) C0 si h = n.
Similarmente el capital pendiente siempre es igual a C0 , salvo al final, pues
siempre debe ocurrir que Cn = 0 (pues se debe cancelar el préstamo)
C0 si 1 ≤ h ≤ n − 1,
Ch =
(12.4)
0
si h = n.
Por otro lado el total amortizado es siempre nulo, salvo en la última cuota:
0
si 1 ≤ h ≤ n − 1,
Mh =
(12.5)
C0 si h = n.
Ejemplo 12.2 La República Argentina decide solicitar al BID un préstamo por
unos U$ 4.700.000.000 para financiar la construcción de una nueva central nuclear. Ud. como representante oficial de Argentina negocia con el BID y acuerda
que el préstamo será a sistema americano, a 5 años, y a una tasa del 4.8% nominal trimestral (J (4) ).
Primero calcularemos el valor de la cuotas de interés usando (12.2)
I
=
4.700.000.000
=
$ 20.400.000
0, 048
4
12.1. INTRODUCCIÓN
275
i.e., al final de cada trimestre la República Argentina debe pagar al BID la suma
de U$ 20.400.000.
Ahora podemos calcular el resto de las cantidades significativas asociadas
con el préstamo. Comenzaremos con las cuotas de amortización. Según (12.3)
$0
si 1 ≤ h ≤ 19,
Ah =
$ 1.700.000.000 si h = 20.
Ahora, según (12.4) los términos amortizativos son
$ 20.400.000
si 1 ≤ h ≤ 19,
ah =
$ 1.720.400.000 si h = 20.
El capital pendiente al perı́odo h, dado por (12.5), es
$ 1.700.000 si 1 ≤ h ≤ 19,
Ch =
$ 0
si h = 20.
El total amortizado según (12.6) viene dado por
$0
si 1 ≤ h ≤ 19,
Mh =
$ 1.700.000.000 si h = 20.
Dado un préstamo americano por C0 , a una tasa i, convenido a n perı́odos,
comprobaremos que el valor actual de la renta de los términos amortizativos del
mismo es exáctamente C0 . Usando (12.4) tenemos
n
X
ah
h
h=1
(1 + i)
=
=
n
X
h=1
n
X
h=1
I
h
+
C0
n
(1 + i)
h
+
C0
n
(1 + i)
(1 + i)
C0 i
(1 + i)
−n
=
1 − (1 + i)
C0
C0 i
+
n
i
(1 + i)
−n
−n
C0 1 − (1 + i)
+ C0 (1 + i)
=
C0
=
Ejercicios Propuestos
Ejercicio 12.3 La Srta. Noelia saco un préstamo a sola firma de $ 25.000 en
la financiera “Su amigo Adrián”, la cual trabaja con sistema americano y cobra
una TNA del 58,6 %. El préstamo dura 5 años y se conviene realizar el pago de
los intereses cuatrimestralmente. Se pide:
1. Monto de las distintas cuotas de amortización.
2. ¿A cuánto ascienden los términos amortizativos a1 , a6, y a15 ?
276
CHAPTER 12. PRÉSTAMO AMERICANO
3. ¿Cuál es el monto de las cuotas de interés I1 , I7 e I15 ?
4. ¿A cuánto asciende el capital pendiente C8 y el C15 ?
5. ¿A cuánto asciende el total amortizado M4 y el M15 ?
Ejercicio 12.4 Un paı́s sudamericano pide U$ 500.000.000 al FMI para construir una autopista. Se pacta el prétamo por sistema americano a una TEA del
4,5 %. El préstamo dura 10 años y se conviene realizar el pago de los intereses
trimestralmente. Se pide:
1. Monto de la cuota de interés.
2. Monto de las distintas cuotas de amortización.
3. ¿A cuánto ascienden los términos amortizativos a7 , a25, y a60 ?
4. ¿A cuánto asciende el capital pendiente C30 y el C51 ?
5. ¿A cuánto asciende el total amortizado M4 y el M43 ?
Ejercicio 12.5 Una empresa acude a un banco y pide préstados $ 20.000.000.
Se conviene una TEM del 1.3 %. Si se usa sistema americano, el préstamo dura
3 años, y la cuotas son trimestrales, se pide
1. ¿Cuánto es el monto de las cuotas de amortización?
2. ¿A cuánto ascienden los términos amortizativos a1 , a10, y a12 ?
3. ¿Cual es el monto de las cuotas de interés I5 e I12 ?
4. ¿A cuánto asciende el capital pendiente C8 y el C12 ?
5. ¿A cuánto asciende el total amortizado M1 y el M12 ?
Ejercicio 12.6 La Sra. Melina desea renovar la cocina de su departamento,
para lo cual solicita un prestamo personal a tres años, a una TNA del 35 %, el
cual reembolsará por sistema americano, pagando intereses bimestralmente. Si
la primera cuota que paga la Sra Melina asciende a $ 450. Se pide
1. Monto del préstamo solicitado por la Sra. Melina.
2. ¿A cuánto ascienden los términos amortizativos a1 , a12 , y a18 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I6 e I18 ?
4. ¿A cuánto asciende el capital pendiente al final de cada año (C6 , C12 , y
C18 )?
5. ¿A cuánto asciende el total amortizado al principio de cada año (M0 ,
M12 , y M18 )?
12.1. INTRODUCCIÓN
277
Ejercicio 12.7 El Gobierno de la Provincia de San Luis desea construir una
red de subterráneos en la ciudad Capital de la Provincia. Para lo cual solicita
al BID un préstamo a 15 años, a una TEA del 3 %. Este préstamo se pacta
a sistema americano, con pago cuatrimestral de intereses. Si el 7mo término
amortizativo asciende a U$ 8.500.000. Se pide
1. Monto del préstamo solicitado por la provincia de San Luis.
2. ¿A cuánto ascienden los términos amortizativos a1 , a20 , y a45 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I32 e I45 ?
4. ¿A cuánto asciende el capital pendiente al final de cada año (C3 , C6 ,
. . . ,C45 )?
5. ¿A cuánto asciende el total amortizado al principio de cada año (M0 , M3 ,
. . . ,M44 )?
Ejercicio 12.8 La Sra. Viviana desea realizar una series de mejoras en una
estancia de su propiedad, para lo cual solicita un préstamo para la inversión
agropecuaria a 5 años, a una TNA del 5,5 %, el cual reembolsará por sistema
americano, pagando intereses trimestralmente. Si la primera cuota asciende a
$ 15.000. Se pide
1. Monto del préstamo solicitado por la Sra. Viviana.
2. ¿A cuánto ascienden los términos amortizativos a1 , a12 , y a20 ?
3. ¿Cual es el monto de las cuotas de interés I1 , I11 e I20 ?
4. ¿A cuánto asciende el capital pendiente al final de cada año (C4 , C8 , C12 ,
C16 , y C20 )?
5. ¿A cuánto asciende el total amortizado al principio de cada año (M0 , M4 ,
M8 , M12 , M16 , y M20 )?
Ejercicio 12.9 Una empresa de soft desea realizar una series de mejoras en sus
instalaciones, para lo cual solicita un préstamo para pymes al Banco Nación.
Se pacta un préstamo de $ 2.000.000 a 3 años, por sistema americano con pago
bimestral de intereses. Si el monto del 3er término amortizativo es de $ 12.500.
Se pide
1. ¿Cuál es la TAE cobrada por el banco?.
2. ¿A cuánto ascienden los términos amortizativos a1 , a9 , y a18 ?
3. ¿Cuál es el monto de las cuotas de interés I1 , I11 e I18 ?
4. Monto de las cuotas de amortización.
5. ¿A cuánto asciende el capital pendiente al final de cada año (C6 , C12 , y
C18 )?
278
CHAPTER 12. PRÉSTAMO AMERICANO
6. ¿A cuánto asciende el total amortizado al principio de cada año (M0 , M6 ,
y M12 )?
Datos para ejercicios
• Centarl nuclar $ 4.000.000.000 de euros
• Parque eólico $ 1.500.000.000 de dolares
• 5 km de oleodocto o gasoducto U$ 2.500.000
• Plataforma petrolera marı́tima: entre U$ 800 y U$ 1.200 millones.
• central hidroelectrica U$ 11.000.000.000
• Autopista: de 1 a 2 millones de km, por montaña de 3 a 4 millones.
• fábrica de urea $ 1.000 millones de dolares (en tierra del fuego)
• minerı́a $ 30.000 millones dolares una mina de potasio en mendoza. 45
millones de dolares minas de salitre de litio y potasio en la puna
• aeropuerto de 15 a 17 millones de dólares
• Hospitales
• Universidades
• satelite
• avion Boing 737 de 75 a 110 millones de dolares, 747 unos 355 millones,
767 de 160 a 200 millones.
12.2
Cuadro de Marcha
Los datos necesarios para llenar el cuadro de marcha de un préstamo americano,
son los mismos que siempre se necesitan para confeccionar un préstamo:
1. C0 el capital préstado.
2. i la tasa que se cobra.
3. n la cantidad de perı́odos que dura el préstamo.
Ahora damos el esquema genérico para completar un cuadro de marcha
americano, los números entre paréntesis indican el orden que usan los autores
para ir llenando el cuadro (hay varias recetas para completar un cuadro de
marcha americano, se insta al lector a desarrollar una).
Nota 12.10 Algunas observaciones
1. Una vez calculada la cuota de interés, se llena toda la segunda columna.
12.2. CUADRO DE MARCHA
n
0
1
2
3
..
.
n−1
n
a
(4)
(4)
(4)
(4)
(5)
a1
a2
a3
279
Ih
—
= I1
= I2
= I3
..
.
An
—
(1)
(1)
(1)
I1
I2
I3
—
= C0 i
= C0 i
= C0 i
(2)
(2)
(2)
A1
A2
A3
..
.
an−1 = In−1
an
= In + C0
(1)
(1)
Mh
—
= 0
= 0
= 0
(6)
(6)
(6)
..
.
In−1 = C0 i
In
= C0 i
(2)
(3)
Ch
M1
M2
M3
(0)
= 0
= 0
= 0
(8)
(8)
(8)
..
.
An−1 = 0
A1
= C0
(6)
(7)
Mn−1 = 0
Mn
= C0
C0
C1
C2
C3
= C0
= C0
= C0
..
.
(8)
(9)
Cn−1 = C0
Cn
= 0
Table 12.1: Cuadro de marcha de un préstamo americano
2. Salvo la segunda columna, correspondiente a la cuota de interés, el resto
de las columnas se caracteriza por ser constantes para todos los perı́odos
salvo el último.
3. Como siempre, el último capital pendiente debe ser nulo, mientras que el
último total amortizado debe ser igual al monto original de la deuda, C0 .
Ejemplo 12.11 Hacer el cuadro de marcha de un préstamo americano a 6
meses por $ 5.000, a una TEM del 1.2%.
n
0
1
2
3
4
5
6
a
Ih
Ah
Mh
60
60
60
60
60
5.060
60
60
60
60
60
60
0
0
0
0
0
5.000
0
0
0
0
0
5.000
Ch
5.000
5.000
5.000
5.000
5.000
5.000
0
Ejercicio 12.12 Hacer el cuadro de marcha para un préstamo americano a 12
años por $ 10.000.000, para el cual se han pactado 12 pagos anuales consecutivos
y una TEA del 28%.
Ejercicio 12.13 Hacer el cuadro de marcha para un préstamo americano a
20 años por U$ 100.000.000, para el cual se ha pactado un esquema de pagos
cuatrimestrales y una TEA del 13,5%.
Ejercicio 12.14 Hacer el cuadro de marcha para un préstamo americano a 5
años por U1.000.000.000 (U, yenes, moneda oficial de Japón), para el cual se
han pactado 10 pagos semestrales consecutivos y una TNA del 8.7%.
Ejercicio 12.15 Hacer el cuadro de marcha de al menos 3 de los préstamos
(ejercicios) de la sección anterior.
280
CHAPTER 12. PRÉSTAMO AMERICANO
12.3
Variantes habituales
12.4
Fondo de amortización en renta constante
Una variante habitual en los préstamos amenricanos consiste en la constitución
de un fondo, con el objetivo de acumular hacia el final de la operación una
fracción o el total del capital adeudado
En lugar de desarrollar fórmulas para cada caso, prefirimos presentar una
serie de ejemplos, modelarlos, y usar las fórmulas que ya tenemos para calcular
las magnitudes requeridas.
Ejemplo 12.16 La empresa Vichu s.r.l. desea comenzar a producir hongos
secos. Para lo cual solicita un préstamo por $ 10.000.000 al KK Bank. El
préstamo es pactado a 5 años por sistema americano a una tasa nominal bimestreal
del 18%. Atendiendo al ciclo de producción, se acuerda que el pago de los intereses será bimestral. La empresa por su parte, a fin de garantizar el pago
del préstamo al cabo de los 5 años decide crear, a partir del 3er trimestre de
adquirido el préstamo, un fondo de amortización en la financiera Chichocash
con el objetivo de acumular fondos por el 75% del capital adeudado. ¿Cuánto
debe depositar trimestre a trimestre la empresa Vichu s.r.l. si la financiera Chichocash le paga una tasa de interés trimestral del 1.2 %? ¿Cuál es el capital
pendiente contable al comienzo del 2do trimestre? ¿y a los 3 años?
Poner dibujoooooooo!!!!!!!!!!!!
Comenzemos averiguando cuanto debe depositar la empresa Vichu s.r.l. para
acumular $ 7.500.000 dentro de 5 años. Estamos suponiendo que trimestre a
trimestre, comenzando en el 3er. trimestre, y términando en el 15vo., la empresa
depositará una suma fija (renta constante). Se espera que el valor final de esta
renta sea $ 7.500.000.
poner dibujo
Pero esto ya sabemos como se calcula:
18
$ 7.500.000 = C
(1 + 0, 012)
0, 012
−1
Luego
C = 375.770, 8171
Por lo que la empresa Vichu s.r.l. deberá depositar cada trimestre (a partir de
3ero.) $ 375.770,82.
Ahora vamos a encontrar el capital pendiente al comienzo del 2do. trimestre.
Esto es muy sencillo, pues como no se ha realizado ningún depósito y el préstamo
es a sistema americano, el capital pendiente es simplemente $ 10.000.000.
Hallar el capital pendiente al los tres años requiere de un poco más de
análisis. Debemos calcular el total acumulado hasta los tres años en el fondo de
12.4. FONDO DE AMORTIZACIÓN EN RENTA CONSTANTE
281
amortización y restarlo de los $ 10.000.000 que se adeaudan.
10
CC3 años = 10.000.000 − 375.770, 8171
(1 + 0, 012)
0, 012
−1
Por lo que el capital pendiente contable al cabo de 3 años es
CC3 años = $ 6.032.743, 922
Insistimos en llamarlo capital pendiente contable, pues es la deuda contable de
la empresa (la diferencia entre lo que se debe y lo ahorrado). Al banco se le
deben aún los $ 10.000.000.
poner de 10 a 13 ejércicios!!!!!!!!!!!!! al menos 2
por cada variante
12.4.1
Fondo de amortización en renta variable
Procederemos igual que antes, presentaremos un ejemplo, lo modelaremos, y
después usaremos las fórmulas que ya tenemos para calcular las magnitudes
requeridas.
Ejemplo 12.17 Ud. solicitó un préstamo (para desarrollar un emprendimiento
gastronómico) por $ 1.000.000 al Banco Supercredito. El préstamo es pactado
a 10 años por sistema americano con pago trimestral de intereses, a una i(4)
del 4,5%. Al cabo de 5 años, Ud. decide crear un fondo de amortización en
el Dirichlet Bank con el objetivo de acumular fondos afin de poder afrontar el
pago del capital adeudado. Ud. deposita inicialmente $ 4.000, al siguiente mes
$ 4.300, al siguiente $ 4.600 y ası́ sucesivamente (él último depósito lo realiza
un mes antes de la cancelación del préstamo) ¿A cuánto asciende el último
depósito?¿De cuánto dispone en el Dirichlet Bank el dı́a que debe cancelar el
préstamo, si el banco le paga una tasa de interés mensual 0.8 %? ¿Cuál es el
capital pendiente contable al comienzo del 4to. año? ¿y al comienzo del 8vo.
año?
Poner dibujoooooooo!!!!!!!!!!!!
Comenzaremos averiguando cuanto acumuló en el Dirichlet Bank. Del enunciado del problema podemos ver que sus depósitos generan una renta aritmética,
con un paso de $ 100 y 59 términos.
El monto del último depósito es de $ 21.400 pues
4.000 + 58 · 300 = 21.400
Por otro lado, el total acumulado hasta al periodo 119 es de $ 900.982,611.
59
59
300
59 · 300 (1 + 0, 008)
(1 + 0, 008) − 1
4.000 +
+ 59 · 300 −
V F (59) =
0, 008
0, 008
0, 008
= 900.982, 611
282
CHAPTER 12. PRÉSTAMO AMERICANO
Luego debemos capitalizar un mes esta cantidad de dinero:
900.982, 611 (1 + 0, 008) = 908190.4719
Por lo que ud dispondrá de $ 908.190,4719 en el Dirichlet Bank para afrontar el
pago de préstamo (le faltan unos $ 91.809,5281 los cuales deberá conseguirlos o
tenerlos!)
poner dibujo
Ahora vamos a encontrar el capital pendiente contable al comienzo del 4to.
año. Esto es muy sencillo, pues como no se ha realizado ningún depósito y
el préstamo es a sistema americano, el capital pendiente es simplemente $
1.000.000.
Hallar el capital pendiente al comienzo del 8vo. año, al igual que antes,
requiere de un poco más de análisis. Debemos calcular el total acumulado en el
fondo de amortización y restarselo al $ 1.000.000 que se adeaudan.
El capital acumulado en el fondo de amortización de los 5 a los 8 años es de
$ 373.442,280 pues
36
(1 + 0, 008) − 1
V F (36) =
0, 008
= 373.442, 280
36
300
36 · 300 (1 + 0, 008)
4.000 +
+ 36 · 300 −
0, 008
0, 008
Por lo que el capital pendiente contable es de $ 626.557,720 pues
CC8 años = 1.000.000 − 373.442, 280 = 626.557, 720
Insistimos, el capital pendiente contable, es la deuda contable de la empresa
(la diferencia entre lo que se debe y lo ahorrado). Al banco aún se le debe $
1.000.000.
poner de 10 a 13 ejércicios!!!!!!!!!!!!! (dos para
cada variante...poner algunos con rentas geometricas
Appendix A
Variación proporcional
A.1
Variación proporcional directa.
Dadas dos variables x e y, diremos que la variable y es directamente proporcional a la variable x si para alguna constante k ∈ R se cumple que
y = kx,
la constante k suele ser llamada constante de proporcionalidad (directa).
Observemos que si duplicamos la variable x, se duplica el valor de la variable
y (similarmente, si la variable x reduce su valor a la mitad, lo propio ocurre con
la variable y), por ejemplo si
y = 3x
entonces
x=
y=
1
3
2
6
4
12
8
24
es decir
x0
kx0 = y0
−→
−→
x1 = 2x0
y1 = kx1 = k (2x0 ) = 2kx0 = 2y0
y ambas cambian al mismo ritmo:
x1
2x0
2kx0
2y0
y1
=
=2=
=
= .
x0
x0
kx0
y0
y0
En general:
x0
kx0 = y0
−→
−→
x1 ,
y1 = kx1 ,
kx1
y1
x1
=
= .
x0
kx0
y0
Esto no es otra cosa que la conocida “regla de tres simples directa”.
283
284
APPENDIX A. VARIACIÓN PROPORCIONAL
Ejercicio A.1 Tres lı́neas de producción producen 15.500 pañales descartables
por hora, si agregamos dos lı́neas de producción adicionales. Cuantos pañales
descartables serán producidos en una hora.
Ejercicio A.2 Cuatro personas ejecutaron un trabajo por el cual cobraron $
16.500. ¿Cuánto le corresponde a cada uno si una de las personas trabajo 14
dı́as, otra 12 dı́as, otra 10 dı́as y la última trabajó 7 dı́as?
Ejercicio A.3 Si un automóvil recorre 100 km con 6.5 litros de gasolina. ¿Qué
distancia recorrerá con 25 litros (bajo las mismas condiciones de velocidad y
resistencia al avance)?
Ejercicio A.4 Un campamento militar con 300 hombres tiene provisiones para
35 dı́as. Si se quiere que las provisiones duren 12 dı́as más, ¿cuántos hombres
habrá que retirar del campamento?
Ejercicio A.5 Un restaurant, de una ciudad turı́stica, necesita 5 personas para
servir 850 almuerzos durante cualquier dı́a de la temporada baja. Durante la
temporada alta se estima que el número de almuerzos diarios a servir sube a
12.500. ¿Cuántas personas más deberá contratar?
Ejercicio A.6 Bajo ciertas condiciones, la distancia de frenado (con las ruedas
trabadas) es directamente proporcional al cuadrado de la velocidad. En un accidente un vehı́culo deja unas huellas de rayado (o patinaje) de 51 m. El conductor
declara que conducı́a a 55 km/h. Se sabe que a 60 km/h un auto de las caracterı́sticas del vehı́culo siniestrado deja unas huellas de rayado de 19 m de
longitud. ¿A qué velocidad se desplazaba el auto antes de comenzar a frenar?
Ejercicio A.7 Dadas unas condiciones de luz, el tiempo necesario para lograr
una buena fotografı́a es directamente proporcional al cuadrado del número f
de la lente de la camara (este número indica la dimensión de la abertura del
diafragma). Los valores habituales de difragma son: f /1.4, f /2, f /2.8, f /4,
f /5.6, f /8, f /11, f /16 y f /22. En esta escala, cada abertura permite el paso
de la mitad de luz que la anterior. Si con una abertura f /11 y sol brillante se
1
segundos de exposición. Bajo las mismas
logra una buena fotografı́a con
125
condiciones de luz, llenar el cuadro de tiempo de exposiciones para diferentes
aberturas:
f /x
segundos
f /1.4
f /2
f /2.8
f /4
f /5.6
f /8
1
f /11
125
f /16
f /22
A.2. SERIES DE FRACCIONES EQUIVALENTES.
A.2
285
Series de fracciones equivalentes.
Llamaremos serie de fracciones equivalentes una expresión de la forma
α2
αn
α1
=
= ··· =
=λ
β1
β2
βn
con αi β i 6= 0 para i = 1, 2, . . . , n (i.e., son todos no nulos). También diremos que
la serie de números α’s son proporcionales a la serie de números β’s. El valor
común λ se llama razón de proporcionalidad. La expresión anterior se puede
reescribir como n ecuaciones (relaciones de proporcionalidad):
αi = λβ i , para i = 1, 2, . . . , n.
Multiplicando las igualdades anteriores por n números reales ki , para i =
1, 2, . . . , n:
ki αi = λki β i , para i = 1, 2, . . . , n.
Al sumar las igualdades anteriores obtenemos
n
X
ki αi = λ
i=1
n
X
ki β i .
i=1
Si la expresión anterior es no nula, podemos obtener una nueva fracción equivalente a las dadas
n
X
ki αi
i=1
n
X
= λ.
(A.1)
ki β i
i=1
Dado un par de series numéricas proporcionales, el procedimiento anterior nos
permite generar una infinidad de nuevas fracciones equivalentes.
Notación A.8 Usaremos la notación de sumatoria habitual:
n
X
αi := α1 + α2 + · · · + αn .
i=1
Ejemplo A.9 Por ejemplo las siguientes fracciones son equivalentes
3
6
=
,
5
10
entonces, también son equivalentes a las dadas
9
3
6
15
= =
=
,
15
5
10
25
Además, podemos generar otras fracciones equivalentes con diferente razón de
proporcionalidad. Por ejemplo a partir de
9
3
=
15
5
286
APPENDIX A. VARIACIÓN PROPORCIONAL
obtenemos
9
15
18
= =
6
3
5
entre otras.
Ejemplo A.10 En general si
a
c
=
b
d
entonces las siguientes son equivalentes a las anteriores
a±c
a
c
ma + nc
= = =
b±d
b
d
mb + nd
para cualesquiera valores de m y n. Además podemos formar las siguientes fracciones equivalentes con razón de proporcionalidad diferente
a+c
b+d
=
,
a−c
b−d
entre otras.
Ejercicio A.11 Hallar 5 fracciones equivalentes a las dadas, y generar 3 pares
adicionales de fracciones equivalentes (con razones de proporcionalidad diferentes)
2
a
=
.
7
2+b
Estas relaciones simplifican la resolución de ciertas ecuaciones
Ejemplo A.12 Resolver
2
5
=
3+x
3−x
Por la relación (A.1) cualesquiera de estas fracciones es equivalente a la fracción
que se obtiene al sumar numerador con numerador y denominador con denominador:
2+5
7
2
=
=
3+x
(3 + x) + (3 − x)
6
Ahora es más fácil despejar x
2
3+x
=
2
=
12
7
=
12
−3
7
9
−
7
7
6
7
(3 + x)
6
3+x
= x
= x
A.2. SERIES DE FRACCIONES EQUIVALENTES.
287
Ejercicio A.13 Resolver
2−x
x
=
2+x
1−x
Ejercicio A.14 Resolver
x−2
1+x
=
x
x+4
Ejercicio A.15 Resolver
a
c
=
,
b+x
b−x
x
a−x
2)
=
,
b+x
c−x
1)
x+a
x+b
=
,
x
x−b
x+a
x
4)
=
.
x
x−b
3)
El reparto proporcional es la distribución de una cantidad atendiendo a
un criterio de proporcionalidad con respecto a una o varias series de números.
Este puede ser simple o compuesto, directo o inverso, dependiendo de la cantidad de series de números involucradas y su relación de proporcionalidad con
la cantidad a repartir. En lo que sigue supondremos siempre que el reparto se
hace entre n agentes, por lo que las series de números tendrán longitud n.
A.2.1
Reparto simple directo.
Es cuando la serie de datos es proporcional a la serie de incógnitas.
• Datos
1. Cantidad a repartir: Q.
2. Serie de números con respecto a la cual se hace el reparto proporcional: α1 , α1 , . . . , αn .
• Incógnitas
1. Cantidades a ser repartidas: x1 , x1 , . . . , xn .
• Relaciones:
1. Se debe repartir Q, i.e.:
n
X
xi = Q.
i=1
2. Las series de las α’s y de las x’s deben ser directamente proporcionales:
xi = λαi para i = 1, 2, . . . , n
288
APPENDIX A. VARIACIÓN PROPORCIONAL
Sumando estas ecuaciones podemos expresar la constante de proporcionalidad en función de la cantidad a repartir Q y la serie de los α’s
n
X
xi
=
i=1
n
X
λαi
i=1
n
X
Q = λ
αi ,
i=1
de donde
λ=
Q
.
α1 + . . . + αn
Lo que nos permite escribir
x2
xn
Q
x1
=
= ... =
=
α1
α2
αn
α1 + . . . + αn
Ejemplo A.16 Un emprendimiento agrı́cola reportó unas ganancias netas de
$ 875 000. Esta cantidad debe ser repartida entre 5 socios, los cuales aportaron
$ 15 000, $ 17 000, $ 38 000, $ 51 000 y $ 25 000 respectivamente. ¿Cuánto
recibe cada socio?
Solución: Es claro que quien más aportó, más debe recibir. Estamos en un
caso de reparto proporcional simple directo. Tenemos entonces que
Q =
875000
=
x1 + x2 + x3 + x4 + x5 ,
x1
=
15000λ,
x2
=
17000λ,
x3
=
38000λ,
x4
=
51000λ,
x5
=
25000λ,
donde
875000
x1 + x2 + x3 + x4 + x5
=
= λ.
15000 + 17000 + 38000 + 51000 + 25000
146000
Por lo tanto
x1
=
89.897, 26 $
x2
=
101.883, 56 $
x3
=
227.739, 73 $
x4
=
305.650, 68 $
x5
=
149.828, 77 $
A.3. VARIACIÓN PROPORCIONAL INVERSA.
A.3
289
Variación proporcional inversa.
Dadas dos variables x e y, diremos que la variable y es inversamente proporcional a la variable x si para alguna k ∈ R
yx = k,
donde k recibe el nombre de constante de proporcionalidad (inversa).
Observe que si duplicamos la variable x el valor de la variable y debe reducirse
a la mitad
x0
−→
x1 = 2x0 ,
y0 x0 = k
−→
y1 x1 = k ⇒ y1 =
k
1
k
=
= y0
x1
2x0
2
y ambas variables cambian a ritmos recı́procos
k
k
x1
kx1
1
2x0
y0
x0
x0
=
=
=
= y1 .
2=
=
=
k
k
x0
x0
kx0
y1
y0
x1
2x0
lo que implica que
y1
1
=
y0
2
En general:
x0 −→ x1 ,
y0 x0 = k −→ y1 x1 = k,
k
x1
kx1
y0
x0
=
=
=
=
k
x0
kx0
y1
x1
Esto no es otra cosa que la conocida “regla de
1
y1 .
y0
tres simple inversa”.
Ejemplo A.17 Tres albañiles levantan una pared en 4 dı́as, ¿Cuanto tardarán
5 albañiles?
Se puede suponer que más albañiles terminaran el trabajo en menos dı́as, asumiendo que todos los albañiles tienen la misma productividad y no hay efectos de
interferencia, podemos suponer una proporcionalidad inversa, lo cual es razonable (hasta cierto punto), entre los dı́as de obra y la cantidad de obreros
(dı́as de obra) (número de albañiles) = k
Para determinar k, utilizamos las condiciones iniciales:
(4 dı́as de obra) (3 albañiles) = k
luego
k = 12 (dı́as de obra) (albañiles)
290
APPENDIX A. VARIACIÓN PROPORCIONAL
Ahora, si disponemos de 5 albañiles
dı́as de obra =
12 (dı́as de obra) (albañiles)
= 2.4 (dı́as de obra)
(5 albañiles)
Es decir 5 albañiles deberı́an terminar la obra en 2 dı́as, 9 horas y 36 minutos.
Ejercicio A.18 Dos grifos (surtidores) iguales llenan una piscina con agua en
14 horas. ¿Cuánto tiempo se empleará en llenar la piscina si usamos otros 5
grifos iguales?
Ejercicio A.19 Un libro tiene 550 páginas de 285 cm2 cada una. Se desea
reeditarlo usando páginas A4 (197 mm por 210 mm). Si el tipo de letra usado
es el mismo, ¿cuántas páginas tendrá la nueva edición?
Ejercicio A.20 Una rueda dentada de 40 dientes engrana con otra de 52 dientes. Si la primera rueda gira a 75 rpm (revoluciones por minuto), ¿A cuántas
rpm gira la segunda?
A.3.1
Reparto simple inverso:
Es cuando la serie de datos es inversamente proporcional a la serie de incógnitas.
• Datos
1. Cantidad a repartir: Q.
2. Serie de números con respecto a la cual se hace el reparto proporcional
inverso: α1 , α2 , . . . , αn .
• Incógnitas
1. Cantidades a ser repartidas: x1 , x1 , . . . , xn .
• Relaciones:
1. Se debe repartir Q, i.e.:
n
X
xi = Q.
i=1
2. Las series de las α’s y de las x’s deben ser inversamente proporcionales:
αi xi = λ para i = 1, 2, . . . , n
o de manera equivalente
xi = λ
1
para i = 1, 2, . . . , n
αi
A.3. VARIACIÓN PROPORCIONAL INVERSA.
291
Sumando estas n ecuaciones se puede deducir el valor de λ en función de los
datos
n
X
xi
=
i=1
n
X
λ
i=1
n
X
Q = λ
i=1
Por lo tanto
λ=
1
αi
1
αi
Q
1
1
+ ... +
α1
αn
Esto nos permite escribir
α 1 x1 = α 2 x2 = . . . = α n xn =
Q
,
1
1
+ ... +
α1
αn
o equivalentemente
x1
x2
xn
Q
=
= ... =
=
.
1
1
1
1
1
+ ... +
α1
α2
αn
α1
αn
Ejemplo A.21 Para fomentar la productividad una empresa decide repartir
un bono de $ 1 000 entre 4 empleados de acuerdo con el tiempo que tardan
en realizar una determinadad tarea. Si los tiempos son 45 minutos, 1 hora 5
minutos, 2 horas y 2 horas 15 minutos. ¿Cuánto recibe cada empleado?
Solución: Quién tarda menos en hacer la tarea es más productivo y por lo
tanto debe recibir una mayor parte del bono. Estamos en un caso de reparto
proporcional inverso. Llevando todos los tiempos a minutos tenemos que
Q =
1000
= x1 + x2 + x3 + x4 ,
45x1
= λ,
65x2
= λ,
120x3
= λ,
135x4
= λ,
Lo cual puede ser reescrito como
x1
x2
x3
x4
=
=
=
,
1
1
1
1
45
65
120
135
de donde
x1 + x2 + x3 + x4 + x5
1000
=
= λ.
1
1
1
1
749
+
+
+
45 65 120 135
14040
292
APPENDIX A. VARIACIÓN PROPORCIONAL
Por lo tanto
A.4
x1
=
416.56 $,
x2
=
288.38 $,
x3
=
156.21 $,
x4
=
138.85 $.
Variación proporcional conjunta o compuesta.
Dadas dos series de variables y1 , y2 , . . . , yn y x1 , x2 , . . . , xm diremos que satisfacen una relación de proporcionalidad conjunta o compuesta si
n
Y
yi = k
i=1
m
Y
xj .
j=1
donde k recibe el nombre de constante de proporcionalidad conjunta.
Notación A.22 Usaremos la notación de productoria habitual:
n
Y
αi := α1 α2 · · · αn .
i=1
A.4.1
Reparto compuesto.
Es cuando hay más de una serie de datos los cuales tienen una relación de
proporcionalidad conjunta con la serie de incognitas.
• Datos
1. Cantidad a repartir: Q.
2. m series de números con respecto de las cuales el reparto es directamente proporcional:
αk1 , αk2 , . . . , αkn , para k = 1, 2, . . . , m.
3. t series de números con respecto de las cuales el reparto es inversamente proporcional:
β j1 , β j2 , . . . , β jn , para j = 1, 2, . . . , t
• Incognitas:
Cantidades a ser repartidas: x1 , x2 , . . . , xn .
• Relaciones:
A.4. VARIACIÓN PROPORCIONAL CONJUNTA O COMPUESTA.
293
1. Se debe repartir Q, i.e.:
n
X
xi = Q
i=1
2. Las series son conjuntamente proporcionales:
xi
t
Y
β ji = λ
j=1
m
Y
αki , para i = 1, 2, . . . , n
k=1
Observe que hemos planteado una ecuación para cada agente.
Clarificar que en esta ecuación se fija el agente
y se mueven las series.!!!!!!!!!!!!!!!
Estas últimas relaciones pueden ser reescritas a modo de fracciones equivalentes:
t
t
t
Y
Y
Y
x2
β j2
xn
β jn
x1
β j1
j=1
m
Y
=
αk1
k=1
j=1
m
Y
j=1
= ... =
m
Y
αk2
k=1
= λ,
αkn
k=1
o, de manera equivalente
x2
xn
x1
= λ,
= m
= ... = m
m
Y
Y
Y
k
k
k
α1
α2
αn
k=1
t
Y
j=1
β j1
k=1
t
Y
k=1
t
Y
β j2
j=1
β jn
j=1
de donde se puede deducir que la constante de proporcionalidad λ es
Q
m
Y
λ=
n
X
k=1
i=1
t
Y
,
αki
β ji
j=1
Ejemplo A.23 El departamento de matemáticas de una universidad divide su
presupuesto anual de $ 289.000 entre tres áreas. Las áreas que atienden más
alumnos son las que reciben más presupuesto: el A1 atiende 230 alumnos, el
A2 atiende 720 alumnos, y el A3 atiende 173 alumnos. Por otro lado a fin de
equilibrar las áreas, mientras mayor es el número de miembros de un área, menor
debe ser su parte de presupuesto anual: el A1 tiene 12 docentes, el A2 tiene 21
docentes, y el A3 tiene 15 docentes. Por otro lado las áreas más productivas
294
APPENDIX A. VARIACIÓN PROPORCIONAL
(número de trabajo publicados) reciben más presupuesto: el A1 tiene 13 trabajos
publicados este año, el A2 tiene 6 trabajos publicados, y el A3 tiene 35 trabajos
publicados. ¿Cuánto recibe cada área?
Solución: Es claro estamos en un caso de reparto proporcional compuesto.
Series directamente proporcionales a las cantidades a repartir x1 , x2 , y x3 :
1. Número de alumnos: 230, 720, y 173.
2. Número de trabajos publicados: 13, 6, y 35.
Serie inversamente proporcional a las cantidades a repartir
1. Cantidad de docentes en el área: 12, 21, y 15
Tenemos entonces que
Q =
=
donde
λ=
289000
x1 + x2 + x3 ,
12x1
=
230 ∗ 13 ∗ λ,
21x2
=
720 ∗ 6 ∗ λ,
15x3
=
173 ∗ 35 ∗ λ.
x1 + x2 + x3
289000
=
.
36059
230 ∗ 13 720 ∗ 6 173 ∗ 35
+
+
42
12
21
15
Por lo tanto
x1
=
83873.24 $,
x2
=
69246.51 $,
x3
=
135880.25 $.
Regla de compañı́a
Se denomina ası́ al sistema de reparto proporcional compuesto de beneficios
entre socios. Principalmente se tiene en cuenta dos factores:
1. El tiempo durante el que ha estado invertido un capital.
2. La cantidad de capital invertido.
Ambas variables son directamente proporcionales a la cantidad a repartir.
Ejercicio A.24 Una fábrica produce 5 000 camisas en 4 dı́as utilizando 25
trabajadoras. ¿Cúantas camisas se producirán en 3 dı́as con 32 trabajadoras?.
Si se necesitan producir 18 000 camisas en 9 dı́as, ¿Cuántas trabajadoras se
necesitan?. Si hay una huelga y sólo trabajan 7 empleadas, ¿Cuántos dı́as serán
necesarios para producir 3 000 camisas?
A.4. VARIACIÓN PROPORCIONAL CONJUNTA O COMPUESTA.
295
Ejercicio A.25 Un grupo de 5 cosechadores, trabajando 6 horas diarias, levantan la cosecha de una finca en 3 dı́as. ¿Cuántos cosechadores se necesitarán
para levantar la cosecha en no más de dos dı́as, trabajando 8 horas diarias?
Ejercicio A.26 Un campamento militar con 250 hombres, tiene provisiones
para 30 dı́as a razón de 3 comidas diarias por hombre. Si se suman 53 hombres,
¿cuantos dı́as durarán las provisiones si cada hombre come sólo dos veces por
dı́a?
Ejercicio A.27 Tres profesores de inglés de un instituto impartieron clases
particulares a un grupo de ejecutivos de una empresa. El instituto cobro $ 15
000 por el servicio. El instituto se queda con el 15 %, y reparte el resto en
función del número de dı́as y las horas diarias de clases. El primer profesor
trabajó 2 horas diarias durante 40 dı́as, el segundo, una hora diaria durante 20
dı́as, y el tercero trabajó 3 horas diarias durante 30 dı́as. ¿A cuánto ascienden
los honorarios de cada uno?
Ejercicio A.28 Tres productos P1 , P2 , y P3 , tardan 3, 4 y 5 horas, respectivamente, para ser fabricados. Se sabe que el costo de fabricación de cada uno
de los productos es directamente proporcional al tiempo empleado. Sabiendo que
cuesta $ 1500 fabricar el producto P2 ,¿Cuánto cuesta fabricar los otros productos? Si el costo de un cuarto producto de caracterı́sticas similares es $ 2 100,
¿Cuánto tiempo se emplea para fabricarlo?
Ejercicio A.29 Una empresa de transporte utiliza un cuadro tarifario directamente proporcional al peso del paquete, y a la distancia entre el origen y el
destino del mismo. Sabemos el costo de enviar un paquete de 5 kg, una distancia
de 150 km es: $ 12. ¿Cuánto costará enviar un paquete de 8 kg, 90 km? Si nos
cobraron $ 35 por enviar un paquete 30 km ¿Cuánto pesaba el mismo? Si nos
costó $ 10 enviar un paquete de 15 kg ¿A que distancia lo mandamos?.
Ejercicio A.30 Una empresa fabrica 5 productos, los cuales le proporcionan
los mismos ingresos. Se producen 320 unidades diarias del producto P1 , 220
unidades diarias del producto P2 , 110 unidades diarias del producto P3 , 420
unidades diarias del producto P4 , y 52 unidades diarias del producto P5 . ¿Qué
precios relativos les corresponden a cada uno de los productos?
Ejercicio A.31 Para ser socio de una compañı́a de seguros hay que aportar
$ 500 000. Este año la compañı́a reportó una ganancia neta de $ 1 250 600,
sabiendo que son 5 socios, que los dos primeros colocaron el capital durante
el mismo tiempo, el tercero coloco el capital el triple del tiempo que los dos
primeros, y los que restan colocaron el capital la mitad del tiempo que el tercero
¿Cuánto le tocada a cada uno?
Ejercicio A.32 Una empresa reportó una ganancia anual neta de $ 17 000
000. Los socios tiene como regla, ahorrar el 18% de las ganancias, y repartir el
resto. Si son 9 socios, de los cuales 3 son socios fundadores, lo cuales aportaron
296
APPENDIX A. VARIACIÓN PROPORCIONAL
$ 250 000 hace tres años al fundar la empresa. Dos años atras, se agregaron
2 socios más, quienes contribuyeron con $ 300 000 (lo que ayudo a financiar
una expanción de la empresa). Hace un año atras se agregaron otros dos socios
quienes aportaron $ 1 000 000 y $ 150 000 (los que fueron usados para informatizar la empresa). Hace 6 meses se incorparon el resto de los socios, quienes
aportaron $ 300 000 cada uno (lo que fue usado para abrir una nueva sucursal
en Brasil). ¿Cuánto le toca a cada uno de los socios?.
Ejercicio A.33 Una empresa repartirá proporcionalmente un premio de $ 80
000 entre sus cuatro gerentes regionales. A fin de fomentar las ganancias, mientras más ventas tenga una región mayor será el premio. A fin de fomentar la
productividad, mientras menor sea la cantidad de personal, mayor será el premio. A fin de fomentar la lealtad a la empresa, mientras más antigüedad, mayor
será el premio, y a fin de fomentar una polı́tica de austeridad, mientras menores
sea los gastos de la sucursal, mayor será la parte del premio que reciben. Los
datos están arreglados en la siguiente tabla
Sucursal
Sucursal
Sucursal
Sucursal
Norte
Sur
Este
Oeste
Ventas en $
7 560 050
6 890 300
4 230 650
12 560 890
Personal
15
13
8
16
Antiguedad en años
5
8
9
4
Gastos en $
1 950 000
2 150 000
2 500 000
3 000 500
¿Cuánto recibe cada uno de los gerentes?
Ejercicio A.34 La cantidad de pintura necesaria para pintar una columna
cilı́ndrica varı́a conjuntamente con el radio y la altura de la columna. Compare la cantidad de pintura necesaria para pintar una columna de 7 m de alto y
60 cm de radio, con la cantidad de pintura necesaria para pintar una columna
de 9 m de alto y 50 cm de radio.
Appendix B
Relaciones recursivas
B.1
Introducción
El siguiente ejemplo ilustra la situación tı́pica que queremos resolver.
Ejemplo B.1 Una persona realiza un depósito a plazo fijo de $ 10.000 por 6
meses. El banco le paga una tasa del 1,25 % mensual. ¿Cuánto tendrá al final
del sexto mes?.
Solución: Denotaremos con fk al monto acumulado hasta el mes k. Es claro
que el monto fk acumulado hasta el mes k, depende del monto acumulado hasta
el mes anterior: fk−1 . La relacción es
fk
= fk−1 + 0, 125fk−1
=
(B.1)
(1 + 0, 0125) fk−1
Además sabemos que
f0 = 10.000
(B.2)
Luego:
f1
f2
f3
f4
f5
f6
=
=
=
=
=
=
(1 + 0, 0125) 10.000
(1 + 0, 0125) 10.125
(1 + 0, 0125) 10.251, 5625
(1 + 0, 0125) 10.379, 7070312
(1 + 0, 0125) 10.509, 4533691
(1 + 0, 0125) 10.640, 8215362
=
=
=
=
=
=
10.125
10.251, 5625
10.379, 7070312
10.509, 4533691
10.640, 8215362
10.773, 8318054
Es decir, tendrá $ 10.773,83.
Tı́picamente trabajaremos con funciones a valores reales cuyo dominio es Z.
Dada
f :Z→R
para cada k ∈ Z, denotaremos
fk := f (k)
297
298
APPENDIX B. RELACIONES RECURSIVAS
Nota B.2 La siguiente figura muestra la posición de cada uno de los fk en
la recta. Observe que el 1er. perı́odo comienza en el cero y términa en el uno,
y en general el k−ésimo perı́odo empieza en el momento k − 1 y términa en
el momento k, i.e., cada intervalo o perı́odo recibe el nombre de su extremo
derecho.
f0
f1
f2
f3
fk−1
fk
fk+1
0
1
2
3
k−1
k
k+1
1er perı́odo
k-ésimo perı́odo
La ecuación (B.1) es un ejemplo de una relación recursiva. La ecuación
(B.2) es un ejemplo de condiciones iniciales.
Definición B.3 Decimos que una función f : A → R, con A ⊂ Z, se define
recursivamente siempre que
B algún conjunto finito de valores, generalmente el primero o los primeros, se
especifiquen, los que llamaremos condiciones iniciales,
R los valores restantes de la función están definidos en término de valores previos. Una fórmula que hace esto recibe el nombre de fórmula o relación
recursiva.
Ejemplo B.4 Las siguientes son ejemplos de relaciones recursivas:
1. fk+1 − fk = 3, con k ∈ Z+ y f0 = 2
2. senkfk + cos (k − 1) fk−1 + sen (k − 2) fk−2 = 0, con k ∈ Z+
Definición B.5 Una solución de una relación recursiva es toda función que
satisfaga la relación de recurrencia en cuestión.
Ejemplo B.6 La función
k (k − 1)
+C
2
donde C es una constante arbitraria, es una solución de la relación recursiva
fk =
fk+1 − fk = k,
pues para k ∈ Z
fk+1 − fk
=
=
=
(k + 1) k k (k − 1)
−
2 2 k2 + k − k2 − k
2
k
B.2. RELACIONES RECURSIVAS LINEALES DE PRIMER ORDEN A COEFICIENTES CONSTANTES.299
B.2
Relaciones recursivas lineales de primer orden a coeficientes constantes.
Básicamente trabajaremos con relaciones recursivas de la forma
a1 fk+1 + a0 fk = g (k)
donde a1 , a2 son constantes no nulas arbitrarias, y g una función, g : Z → R.
Nosotros analizaremos los siguientes casos: cuando g es un polinomio en k, o
una función exponencial en k, o una combinación lineal de un polinomio en k
con una exponencial en k.
Ejemplo B.7 La relaciones recursivas con la que trabajaremos serán de similares a
1. 2fk+1 + 5fk = 2k,
1
2. − (fk − fk−1 ) = fk + k 2 ,
2
1
3
3. 6fk+1 + fk = e−k ,
4
3
4. k 3 − fk = 3k − fk+1 .
Ejemplo B.8 Todos los meses ud. ahorra $ 550, los cuales deposita en una
cuenta de ahorro que le paga el 0,5 % de interés mensual. Hallar la relación
recursiva que describe la situación:
La relación recursiva es
fk = 1, 005fk−1 + 550
con la condición inicial
f0 = 550
B.3
Caso I: g (k) = cte.
Esta es la situación más simple. Queremos resolver la relación recursiva
a1 fk+1 + a0 fk = c
(B.3)
donde a1 , a2 , y c son constantes arbitrarias, con a1 6= 0. La relación anterior
puede reescribirse
fk+1 = Afk + B
donde
A
= −
B
=
a0
a1
c
a1
300
APPENDIX B. RELACIONES RECURSIVAS
Ahora usaremos el método inductivo para conjeturar la forma de la solución:
f1
=
Af0 + B
f2
=
Af1 + B
=
A (Af0 + B, ) + B
=
A2 f0 + B (1 + A)
=
Af2 + B
=
=
A A2 f0 + B (1 + A) + B
A3 f 0 + B 1 + A + A2
..
.
=
Afk−1 + B
=
Ak f0 + B 1 + A + · · · + Ak−1
f3
fk
Ahora hay dos situaciones: A = 1 o A 6= 1. Si A = 1 es claro que
fk = f0 + kB
Por otro lado, si A 6= 1, la expresión
1 + A + · · · + Ak−1
es una serie geométrica de razón A, para la cuál es facil hallar una versión
cerrada: llamemos S a la suma de la serie
S = 1 + A + A2 + · · · + Ak−2 + Ak−1
(B.4)
multipliquemos ambos miembros por A
AS = A + A2 + A3 + · · · + Ak−1 + Ak
(B.5)
Si hacemos (B.4) menos (B.5) obtenemos
S − AS
=
S
=
1 − Ak
1 − Ak
1−A
(B.6)
Por lo tanto si A 6= 1 la solución de la relación recursiva (B.3) debe ser
fk = Ak f0 + B
1 − Ak
.
1−A
Resumiendo, el método inductivo sugiere que la solución de la relación recursiva
(B.3) debe ser de la forma

 k
1 − Ak
si A 6= 1,
A
f
+
B
0
fk =
(B.7)
 f + kB 1 − A
si A = 1.
0
B.3. CASO I: G (K) = CT E.
301
Para probarlo debemos usar inducción dos veces: una para A 6= 1, y otra
para A = 1. Haremos la primera (la otra queda como tarea para el lector).
Verificaremos que si A 6= 1, y fk es una solución de la relación recursiva (B.3),
1 − Ak
entonces fk tiene la forma fk = Ak f0 + B
.
1−A
Paso base: k = 1 esto no es más que la fórmula de recursión:
f1 = Af0 + B = A1 f0 + B
1 − A1
1−A
Hipótesis inductiva: supongamos que la relación recursiva es cierta para k−1,
i.e.:
1 − Ak−1
fk−1 = Ak−1 f0 + B
1−A
Ahora veamos que ocurre lo propio para k
fk
= Afk−1 + B
1 − Ak−1
k−1
+B
= A A
f0 + B
1−A
A − Ak
+1
= Ak f0 + B
1−A
= Ak f0 + B
1 − Ak
.
1−A
Ejemplo B.9 Todos los meses la srta. Viviana ahorra $ 550, y los deposita en
una cuenta de ahorro que le paga el 0,5 % de interés mensual. Hace 8 meses
que comenzo a ahorrar. ¿Cuánto tiene ahorrado?¿Cuantos meses más deberá
ahorrar para poder comprarme un televisor de LED de 42” que cuesta $ 8.500?
Ya hemos hallado la relación recursiva que describe esta situación:
fk = 1, 005fk−1 + 550
f0 = 550
Como A = 1, 005 6= 1 y B = 550, por (B.7) tenemos que
fk
=
1 − 1, 005k
1 − 1, 005
k
550 · 1, 005 + 110.000 1, 005k − 1
=
110.550 · 1, 005k − 110.000
=
550 · 1, 005k + 550
Por lo tanto, a los 8 meses la srta. Viviana tendrá (pesos)
f8 = 110.550 · 1, 0058 − 110.000 = 5.050, 1637
302
APPENDIX B. RELACIONES RECURSIVAS
Para averiguar cuantos meses más deberá ahorrar para tener por lo menos $
8.500, debemos plantear la siguiente desigualdad donde la incógnita es k
8.500 < fk = 110.550 · 1, 005k − 110.000
Es decir
118.500
< 1, 005k
110.550
como el logaritmo es una función monótona creciente, al tomar logaritmos de
ambos lados no se altera el sentido de la desigualdad anterior:
118.500
< k log (1, 005)
log
110.550
por lo tanto
118.500
log
110.550
14, 92370427 =
log (1, 005)
<k
luego, la srta. Viviana deberá ahorrar 15 meses para juntar al menos $ 8.500.
Es decir, faltan 7 meses para que se pueda comprar el televisor.
Ejercicio B.10 Resolver las siguientes relaciones recursivas
1. 3fk+1 − 6fk = 1, con f0 =
2
.
3
2. fk+1 − 3fk = 2, con f2 = 17.
Ejercicio B.11 Los costos mensuales de un proyecto de construcción de tres
años de duración guardan la siguiente relación: los costos totales de cada mes
son los costos del mes anterior más $ 12.000. La inversión inicial fue de $
20.000. ¿Cuál será el costo del penúltimo mes de vida del proyecto? ¿En qué
mes los costos mensuales superan los $ 100.000?
B.4
Caso g 6= cte.
En general si g es una función, tenemos que cualquier solución f de la relación
recursiva
a1 fk+1 + a0 fk = g (k)
(B.8)
tiene la forma
fk = hk + pk
donde hk es la solución de la relación de recursiva homogénea (lo que significa
igualada a cero) asociada a (B.8):
a1 fk+1 + a0 fk = 0
B.5. CASO G (K) ES UN POLINOMIO
303
y pk es una solución particular de (B.8). Es decir que pk debe satisfacer la
relación recursiva
a1 pk+1 + a0 pk = g (k)
La función pk debe ser de la misma clase que g, i.e., si g es un polinomio de
grado n, la solución particular pk también, si g es una función exponencial de
base a, lo mismo ocurre con pk . La solución particular pk se haya por el método
de los coeficientes indeterminados.
Observe que una solución fk de la forma fk = hk + pk satisface la relación
recursiva (B.8):
a1 fk+1 + a0 fk
= a1 (hk+1 + pk+1 ) + a0 (hk + pk )
=
(a1 hk+1 + a0 hk ) + (a1 pk+1 + a0 pk )
=
0 + (a1 pk+1 + a0 pk )
= g (k)
B.5
Caso g (k) es un polinomio
Estudiaremos la relación recursiva
a1 fk+1 + a0 fk = Pn (k)
(B.9)
donde
Pn (k) = αn k n + αn−1 k n−1 + · · · + α1 k + α0
i.e., Pn (k) es un polinomio en k de grado n.
Primero hallamos la solución homogénea asociada, usando el método desarrollado anteriormente:
a1 hk+1 + a0 hk
=
hk+1
donde
A=−
La solución homogénea asociada es
k
A h0
hk =
h0
0
= Ahk
a0
a1
si A 6= 1,
si A = 1.
Para hallar la solución particular asociada a (B.9) proponemos una solución
particular pk de la forma
β n k n + β n−1 k n−1 + · · · + β 1 k + β 0 si A 6= 1,
pk =
k β n k n + β n−1 k n−1 + · · · + β 1 k + β 0
si A = 1.
donde los β’s son constantes a determinar.
304
APPENDIX B. RELACIONES RECURSIVAS
Ejemplo B.12 Resolver la siguiente relación recursiva:
2fk+1 − 3fk
=
4k 2 + 1,
f0
=
5.
(B.10)
La ecuación homogénea asociada es
2hk+1 − 3hk = 0
la cual reescribiremos
hk+1 =
Como
3
hk
2
3
6= 1, la solución homogénea asociada es
2
k
3
hk =
h0
2
3
Como g es un polinomio de grado 2 y 6= 1, debemos proponer como solución
2
partı́cular
pk := β 2 k 2 + β 1 k + β 0
Ahora
4k 2 + 1
2fk+1 − 3fk
h
i
2
= 2 β 2 (k + 1) + β 1 (k + 1) + β 0 − 3 β 2 k 2 + β 1 k + β 0
=
= −β 2 k 2 + (4β 2 − β 1 ) k + (2β 2 + 2β 1 − β 0 ) .
Como dos polinomios a corficientes reales son iguales si, y sólo si sus coeficientes
son iguales, podemos determinar los β’s resolviendo el sistema

−
β2 = 4

−
β 1 + 4β 2 = 0

−β 0 + 2β 1 + 2β 2 = 1
De donde
−41
β0
=
β1
= −16
β2
= −4
Por lo tanto la solución de (B.10) es de la forma
fk = h0
k
3
− 4k 2 − 16k − 41
2
B.5. CASO G (K) ES UN POLINOMIO
305
Donde resta por determinar el valor de h0 . Usaremos la condición inicial para
ajustar el valor de h0 :
5 = f0 = h0 − 41,
lo que implica que h0 = 46, por lo tanto la solución de (B.10) es
k
3
− 4k 2 − 16k − 41.
fk = 46
2
En el siguiente ejemplo abordaremos el caso A = 1.
Ejemplo B.13 Resolver la relación recursiva
fk+1 − fk
=
2k − 3,
f1
=
4.
La ecuación homogénea asociada es
hk+1 − hk = 0
Luego la solución homogénea asociada es constante:
hk = h0
Observe que si proponemos una solución particular de la forma
pk = β 1 k + β 0
tenemos que
2k − 3
=
fk+1 − fk
=
(β 1 (k + 1) + β 0 ) − (β 1 k + β 0 )
=
β1
Lo cual es imposible, pues esta ecuación debe ser válida para todo k.
Como g es un polinomio de grado 1 y A = 1, debemos proponer como
solución particular
pk = k (β 1 k + β 0 ) .
Ahora
2k − 3
=
fk+1 − fk
=
[(k + 1) (β 1 (k + 1) + β 0 )] − [k (β 1 k + β 0 )]
=
2β 1 k + (β 1 + β 0 ) .
De donde
β0
= −4,
β1
=
1,
306
APPENDIX B. RELACIONES RECURSIVAS
Por lo tanto la solución de (B.10) es de la forma
fk = h0 + k (k − 4) .
Ahora usaremos la condición inicial para ajustar el valor de h0 :
4 = f1 = h0 − 3,
lo que implica que h0 = 7, por lo tanto la solución de (B.10) es
fk = 7 + k (k − 4) .
Nota B.14 La idea de usar k β n k n + β n−1 k n−1 + · · · + β 1 k + β 0 , en lugar
de β n k n +β n−1 k n−1 +· · ·+β 1 k+β 0 , si A = 1, viene de la técnica introducida por
Liouville para hallar una nueva solución a una ecuación diferencial ordinaria,
a partir de una solución conocida.
B.6
Caso III: g (k) es una función exponencial
El tipo de relación recursiva que deseamos resolver es
a1 fk+1 + a0 fk = cbk ,
con b > 0, b 6= 1.
La solución homogénea asociada se calcula como antes. La solución particular
es
βbk ,
si A 6= b,
pk =
βkbk , si A = b.
donde A = − aa10 , y el coeficiente β es hallado usando el método de los coeficientes
indeterminados.
Ejemplo B.15 Resolver la relación recursiva
fk+1
=
4fk + 3 2k , con k ≥ 1,
f0
=
1.
La relación recursiva homogénea asociada es
fk+1 − 4fk = 0,
por lo tanto la solución homogénea asociada es
hk = h0 4k .
Como A = − (−4) 6= 2, la solución particular debe ser de la forma
pk = β2k .
B.6. CASO III: G (K) ES UNA FUNCIÓN EXPONENCIAL
307
Usando el método de los coeficientes indeterminados
3 · 2k
= pk+1 − 4pk
= β2k+1 − 4β2k
= −2β2k .
Luego
3
β=− .
2
Por lo tanto la solución general es
3
fk = h0 4k − 2k .
2
Ahora ajustamos el valor de h0 para que se satisfaga la condición inicial:
3
1 = f0 = h0 − ,
2
luego
h0 =
Por lo tanto
5
.
2
5 k 3 k
4 − 2 .
2
2
fk =
Ejemplo B.16 Resolver la relación recursiva
fk+1 − 3fk
=
12 · 3k , con k ≥ 1,
f0
=
2.
La solución homogénea asociada es
hk = h0 3k .
Como A = − (−3) = 3, la solución particular asociada debe ser de la forma
pk = βk3k .
Usando el método de los coeficientes indeterminados
12 3k
= pk+1 − 3pk
= β (k + 1) 3k+1 − 3βk3k
= β3k+1 ,
de donde
β = 4.
Por lo tanto la solución general es de la forma
fk = h0 3k + 4k3k .
308
APPENDIX B. RELACIONES RECURSIVAS
Usando la condición inicial, ajustamos el valor de h0
2 = f0 = h0 .
Luego la solución general es
fk = 2 · 3k + 4k3k .
Ejercicio B.17 Resolver las siguientes relaciones recursivas
1. 3fk+1 − 6fk = 3 · 2k , con f0 =
2. 3fk+1 − fk =
2
.
3
1
, con f2 = 5.
3k
Ejercicio B.18 Ud. invierte $ 180 000. Esa inversión de duplica cada año,
pero ud. retira al cabo del primer año $ 10 000, del segundo año $ 20 000, del
tercero $ 40 000, del cuarto $ 80 000, etc. Establecer una relación recursiva que
describa el problema. ¿Cuanto tendrá al cabo del 7mo. año?
B.7
Caso IV: g (k) combinación de un polinomio
y una función exponencial
Ahora resolveremos relaciones recursivas de la forma
a1 fk+1 + a0 fk = Pn (k) + cbk ,
(B.11)
donde
Pn (k) = αn k n + αn−1 k n−1 + · · · + α1 k + α0 ,
es un polinomio de grado n, y b > 0 y b 6= 1. De nuevo todo el problema es
hallar una solución particular, pues la homogénea asociada no ofrece dificultad.
La solución particular propuesta debe ser de la misma clase que g

si A ∈
/ {1, b} ,
 β n k n + β n−1 k n−1 + · · · + β 1 k + β 0 + βbk ,
k β n k n + β n−1 k n−1 + · · · + β 1 k + β 0 + βbk , si A = 1,
pk =

β n k n + β n−1 k n−1 + · · · + β 1 k + β 0 + βkbk ,
si A = b.
donde A = − aa01 .
Ejercicio B.19 Resolver las siguientes relaciones recursivas:
fk+1 − 2fk = 3 · 4k + 4k,
1.
f0 = 4.
(
2 k
3 + k − 1,
fk+1 − fk =
2.
5
f1 = 4.
fk+1 − 3fk = 4 · 3k − 2k,
3.
f0 = 2.
B.8. EJERCITACIÓN GENERAL
B.8
309
Ejercitación general
Ejercicio B.20 Decidir si la funciones propuestas son o no solución de las
relaciones recursivas dadas (c reprsenta una constante abitraria)
1
2
3
4
6
7
8
9
10
11
Función propuesta
fk = 3
fk = c
fk = −3 · 5k
fk = c3k
fk = 2ck
fk = k
fk = c + k (k + 1)
c
fk =
1 + ck
1 k+1
fk =
3
+1
2
fk = 3 2k+1 − 1
Relación recursiva
fk − fk−1 = 0,
fk − fk−1 = 0,
fk = 5fk−1 ,
fk = 3fk−1 ,
fk = cfk−1 ,
fk+1 − fk = 1,
fk+2 − fk+1 = 2k + 3,
fk = 3fk − 1,
fk
fk+1 =
,
1 + fk
fk + 2fk−1 − 1 = 0.
Ejercicio B.21 Hallar la solución de cada una de las siguientes relaciones
recursivas
fk+1 − fk = 1,
1.
f0 = 4.
(
2fk+1 − fk
=
f0
=
2.
3.
fk+1
f0
=
=
−2fk ,
4.


 1 fk+1 − 4 fk
3
3
4.


f0
=
6,
2
.
3
=
4fk − fk+1
f1
=
=
1,
2.
(
4fk+1 − fk
=
f3
=
3,
1
.
2
5.
6.
fk+1 + fk
f0
(
fk+1 − 3fk
=
f0
=
7.
8.
3,
1
.
2
=
=
3k + 1,
2.
5k 2 ,
1
.
2
310
APPENDIX B. RELACIONES RECURSIVAS
fk+1
f1
fk+1 − fk
f2
2fk+1 − 2fk
f3
=
=
3k − 1,
0.
(
2fk+1 + 3fk
=
f0
=
5 · 2k ,
1
.
2
9.
10.
11.
12.
fk + 4k,
0.
2k 2 + k,
1.
=
=
fk+1 − 2fk
f0
=
=
6 · 2k ,
1.
fk+1 + 3fk
f1
=
=
2 · 4k − k,
0.
(
3fk − fk−1
=
f1
=
1
,
3k
0.
3fk + fk+1
=
f0
=
1
,
3k
2.
2fk−1 − fk
f1
=
=
4k−1 − 3k + 8,
4.
13.
14.
15.
(
16.
17.
=
=
Ejercicio B.22 Una persona tiene hoy $ 40 000 y a partir de la segunda semana gasta cada semana la tercera parte de lo que tenı́a la semana anterior.
¿Cuántas semanas tarda en tener menos de $ 10? ¿Cuántas semanas tarda en
gastar todo su capital?.
Ejercicio B.23 Una compañı́a de seguros ofrece a sus inversionista el siguiente
esquema de pagos: cada año el inversionista tendrá un acumulado igual a 5/4
de lo que tenı́a el año anterior, pero le descuentan cada año una doceava parte
del total acumulado. ¿Cuánto tendrá al cabo de 8 años una persona que invierte
$ 3 000 000? ¿Cuánto tiempo tardará en duplicar su capital un inversionista
cualquiera?
Ejercicio B.24 Se invierten hoy $ 6 000 000. Está inversión rinde un 12%
trimestralmente, i.e., cada trimestre se agrega el 12% del capital acumulado
hasta el trimestre anterior. Al comienzo del segundo trimestre se agregan $ 25
000, al comienzo del tercero $ 30 000, del cuarto $ 35 000, y ası́ sucesivamente.
Además al finalizar cada trimestre se retiran $ 75 000. ¿Cuál será el total acumulado al cabo de 5 años? ¿Cuánto tiempo tardará en triplicar su capital el
inversionista?
Appendix C
Soluciones
C.1
Soluciones del capitulo 1
(8.37)
311
Appendix D
Diccionarios de fórmulas
312
Appendix E
Tabla de dı́as
313
Bibliography
[1] Dumrauf, Guillermo L., 2006, Finanzas Corporativas. Alfaomega, México.
[2] Joseph W. Kitchen, 1992, Cálculo. McGraw Hill. México.
[3] Joanna Place, 2005. Análisis básico de bonos. Ensayos 72. Centro de estudios
monetarios latinoamericanos. México. http://www.cemla.org/ensayos.htm
314
Index
equivalentes
fracciones, 3
proporcional
directamente, 1
reparto
proporcional, 5
simple directo, 5
315