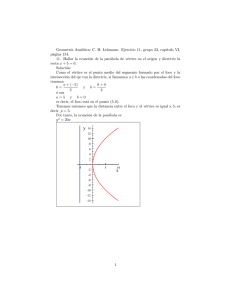
Semana 3 y 4

Taller de Matemáticas III Taller de Matemáticas III 1 Universidad CNCI de México Semana 3 y 4
Taller de Matemáticas III Semana 3 y 4
Temario 1. La parábola 1.1. Caracterización geométrica 1.1.1. La parábola como lugar geométrico 1.1.2. Elementos asociados con la parábola 1.2. Ecuación ordinaria de la parábola 1.2.1. Parábola horizontal y vertical con vértice en el origen 1.2.1.1. Obtención de los elementos de una parábola con vértice en el origen a partir de su ecuación 1.2.1.2. Obtención de la ecuación de una parábola con vértice en el origen a partir de sus elementos 1.3. Ecuación ordinaria de la parábola con vértice fuera del origen 1.3.1. Parábola horizontal y vertical con vértice fuera del origen 1.3.1.1. Obtención de los elementos de una parábola con vértice fuera del origen a partir de su ecuación 1.3.2.2. Obtención de la ecuación ordinaria de una parábola con vértice fuera del origen a partir de algunos de sus elementos mínimos necesarios 1.4. Ecuación general de la parábola 1.4.1. Conversión de la forma ordinaria de la ecuación de una parábola con vértice fuera del origen a su forma general 1.4.2. Conversión de la forma general de la ecuación de una parábola con vértice fuera del origen a su forma ordinaria 2. La Elipse 2.1. Caracterización Geométrica 2.1.1. La Elipse como lugar geométrico 2.1.2. Elementos asociados con la elipse 2.1.3. Formas de trazo a partir de la definición 2.2. Ecuación ordinaria de la elipse 2.2.1. Elipses horizontales y verticales con centro en el origen 2.2.1.1. Obtención de los elementos de una elipse con centro en el origen a partir de su ecuación 2.2.1.2. Obtención de la ecuación ordinaria de una elipse con centro en el origen a partir de sus elementos mínimos necesarios 2.3. Ecuación ordinaria de la elipse con centro fuera del origen 2.3.1. Elipse horizontal y vertical con centro fuera del origen 2.3.1.1. Obtención de los elementos de una elipse con centro fuera del origen a partir de su ecuación 2 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
2.3.1.2. Obtención de la ecuación ordinaria de una elipse con centro fuera del origen a partir de algunos de sus elementos mínimos necesarios 2.4. Ecuación general de la elipse 2.4.1. Conversión de la forma ordinaria de la ecuación de una elipse con centro fuera del origen a su forma general 2.4.2. Conversión de la forma general de la ecuación de una elipse con centro fuera del origen a su forma ordinaria 3 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Seman
na 3 Sesión 9 Los ttemas a revvisar el día d
de hoy son:: 1. La parrábola 1.1. Caaracterizaciión geométtrica 1
1.1.1. La pa
rábola como lugar geo
ométrico 1
1.1.2. Eleme
entos asociaados con la parábola 1.2. Eccuación ord
dinaria de laa parábola
1
1.2.1. Paráb
bola horizon
ntal y vertical con vértice en el origen 1. La parábola 1.1.. Caracterizzación geom
métrica Ejem
mplo: Cocinaa solar paraabólica La co
ocina parabólica constaa de un discco que refle
eja y conccentra la luzz del sol en un punto fiijo en el cuaal la comiida se cocin
na. Alcan
nza temperraturas de h
hasta 300 grados en se
eco, pued
de hervir 1 1 litro de agua en 10 minutos y 2
adem
más cocina ssin emitir CO . ¿Cóm
mo crees qu
ue se calientta la comidaa? uerda que laa parábola se clasifica como una sección có
ónica porqu
ue proviene
e del Recu
cortee de un cono con dos ccapas a travvés de un plano. Este tipo de figura cónica puedes encontrarlo aplicado a
en diferentes ámbitos de
e tu vida cotidiana, por ejemp
plo, las lucees de los automóviles tienen una pantalla con form
ma parabólicca, la anten
na parabólicca, la cocin
na parabólicca, en la arrquitectura:: los puen
ntes colganttes, los tún
neles, los arrcos; en la n
naturaleza: el arcoíris,, montañas; en los deportes, la trayectoria de las pelo
otas y balones al ser lan
nzados, etc.. En este tema veerás un anáálisis detallaado de los diferentes tipos de eccuaciones d
de la parábola, así como su representación gráficca y cómo
o ésta depende de los comp
ponentes que la integrran. Pero, antes de ccomenzar, ¿¿cuáles son las caracteerísticas con
n las que see identifica una pará
ábola en el p
plano carteesiano? 1.1.1
1. La parábola como lu
ugar geomé
étrico v
la forma de la cocina solarr, esta form
ma se puedee representtar en el plano Has visto carte
esiano advirrtiendo algu
unas caractterísticas paarticulares p
para ser ideentificada co
omo tal. 4 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
La parábola en el plano cartesiano se define como el lugar geométrico de los puntos en éste, cuya distancia a un punto fijo llamado foco es la misma que su distancia a una recta fija del plano llamada directriz. Cocina solar parabólica
¿En qué influye esta forma para ser considerada como
una cocina?
El punto donde se encuentra ubicada la olla se le llama
foco, hacia éste caen rebotados todos los rayos solares
que se dirigen al interior de la parábola.
¿A qué se le llama directriz de una parábola?
1.1.2. Elementos asociados con la parábola D
P1
D1
D2
P2
F V
D4
D5
D6
D1P1 = P 1F
D2P2 = P 2F
D3P3 = P 3F
P3 D3
S
P 4
P 5
P6
DnPn = P nF (si Pn está en la curva de la parábola) DV = V F
F: foco de la parábola.
D: recta fija, directriz.
S: eje de la parábola, recta que contiene al foco y es
perpendicular ( ⊥) a la directriz.
V: vértice , punto medio entre el foco y la directriz.
a: distancia dirigida de V a F, a = VF
P: parámetro de la parábola, DF = P = ¦2a¦ 5 Universidad CNCI de México Al hacer un análisis sobre el lugar geométrico de la
parábola, se logran definir sus elementos característicos
como sigue :
T
Taller de
e Matemááticas IIII Semana 3 y 4
En donde
d
de ma
anera general, los elementtos que
cara
acterizan a la parábola
p
son:
F: Foco,
F
punto po
or donde pas
sa el lado rec
cto y se
encu
uentra a una distancia “a” de
el vértice.
D: Directriz,
D
recta
a fija perpend
dicular al eje focal, a
una distancia “a” del
d vértice.
S: Eje
E focal, recta que contiene al foco
o y es
perp
pendicular (⊥) a la directriz.
V: Vértice,
V
punto medio entre el foco y la directriz,
d
gene
eralmente sus
s coordenadas
s son (h, k).
L y R:
R puntos extremos del Lad
do Recto
LR: Lado Recto, es
e la distancia que pasa por el foco,
pendicular al ejje focal. Su longitud es de 4a.
4
perp
a: dis
stancia dirigid
da de V a F, a = VF
P: pa
arámetro de la
a parábola, DF
F = P = │2a│
Prácctica 31 A partir de la siguiente imagen traza en el plano
o una paráb
bola que le correspond
da e identtifica sobre la misma lo
os elemento
os que la co
omponen. ordinaria de
e la parábola 1.2. Ecuación o
Ejem
mplo: • ¿Cómo le hacen paara construiir los arcos sin que se caiga la p
piedra? • ¿Cómo h
hacen para obtener la misma forma precisa cada vezz? 6 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
El ser humano, para realizar estructuras como las del ejemplo anterior requiere de la forma analítica (ecuación) de la cónica, de tal manera que pueda construir réplicas idénticas y precisas de una misma. En seguida harás un estudio analítico de la ecuación de la parábola, se diferencia y caracteriza porque una de sus variables, y no ambas, está elevada al cuadrado. Ejemplo: Grafica la siguiente ecuación: 3x2 = y Para la tabulación se determinan los valores de “x” y se obtienen los de “y”. y = 3x2
Valores
de “x”
Valores
de “y”
-3
27
-2
12
-1
3
0
0
1
3
2
12
3
27
¿Acaso todas las parábolas son iguales siempre? 1.2.1. Parábola horizontal y vertical con vértice en el origen Existen diferentes tipos de parábolas, las hay verticales, horizontales y oblicuas; en esta sesión comienzas a estudiar las parábolas horizontales. 7 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Parábolas Horizontales
Para determinar una parábola horizontal con vértice
en el origen en el plano cartesiano, necesitas
verificar que su eje focal coincida con el eje de las
“x”, y su vértice coincidente con el origen (0, 0). (Ver
gráfica)
Supón una parábola con el foco sobre el eje positivo
de las ejes “x”. Si recuerdas la definición de la
parábola como lugar geométrico, la distancia de un
punto de la directriz M a un punto de la parábola P es
la misma que la distancia de P al foco F.
Entonces, si aplicas lo anterior en las fórmulas
correspondientes, obtendrás la ecuación ordinaria de
la parábola con vértice en el origen, eje focal sobre el
eje de las “x” y a > 0.
De lo anterior concluyes que d1 = d2, por lo tanto, MP = PF, es decir: Como M = (–a, y), P = ( x , y) y F = ( a, 0), sustituye sus valores en la fórmula de la distancia: Eleva al cuadrado ambas partes de la igualdad:
Desarrolla los cuadrados:
Recuerda que:
Despeja “y”:
Como a = p/2, entonces:
( [ x − (−a)] + ( y − y) ) = (
2
2
2
( x − a) 2 + ( y − 0) 2
)
2
(x + a)2 = (x – a)2 + y2
(x + a)2 = x2 + 2ax + a2
x2 + 2ax + a2 = x2 – 2ax + a2 + y2
y2 = 4ax
y2 = 2px
La ecuación de una parábola en la forma canónica con vértice en el origen y foco en (a, 0) es: y2 = 4ax Análisis de la ecuación: Con base en la ecuación canónica de la parábola y2 = 4ax que ya obtuviste, puedes deducir lo siguiente: 8 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
1. Su gráfica es simétrica respecto al eje “x”, es decir, si el
punto P1(x, y) satisface su ecuación, entonces el punto
P2(x, –y) también; significa que los dos puntos están en la
gráfica.
2. Si y ≠ 0, entonces y2 será siempre un número positivo,
por lo que se deduce que tanto el valor de “a” como el de
“x” deben tener el mismo signo. Si a > 0, entonces “ x”
sólo podrá tener por valor números positivos, es decir,
el dominio de la relación es el intervalo donde x ≥ 0, y el
rango es el conjunto de los número reales, ya que: y = ± 4ax
• Grafica la siguiente ecuación: y 2 = 16x
De la ecuación ordinaria y 2 = 4ax:
4 a = 16
a = 4
a > 0
Para la tabulación se determinan los valores
de x ≥ 0 y se obtienen los de “y”
F (4, 0)
y2 = 16x
Valores
de “x”
Valores
de “y”
5
8.9
4
8
3
6.9
2
5.7
1
4
0
0
Como puedes ver, en este
caso la parábola es
horizontal abierta a la
derecha.
¿Todas las parábolas
abren hacia la derecha?
Si haces un nuevo análisis de la ecuación canónica de la parábola y2 = 4ax, puedes deducir lo siguiente: 9 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
1. Su gráfica es simétrica respecto al eje “x”, es decir, si el
punto P1(–x, y) satisface su ecuación, entonces el punto
P2(–x, –y) también; significa que los dos puntos están en
la gráfica.
2. Si y ≠ 0, entonces y2 será siempre un número positivo,
por lo que se deduce que tanto el valor de “a” como el de
“x” deben tener el mismo signo. Si a < 0, entonces “x”
sólo podrá tomar valores negativos, es decir, el
dominio de la relación es el intervalo (– ∞, 0], y el rango
es el conjunto de los número reales, ya que: y = ± 4ax
Podrás notar que según las dos condiciones anteriores, la
parábola resulta una curva abierta hacia la izquierda que se
extiende infinitamente hacia arriba y hacia abajo. (ver figura)
Práctica 32 Grafica la siguiente ecuación: y2 = –9x De la ecuación ordinaria y2 = 4ax: Para la tabulación se determinan los valores de x ≤ 0 y se obtienen los de “y”. Parábolas Verticales
Como sabes PF = PM y si aplicas la fórmula de la distancia, obtienes lo siguiente: x2 = 4ay
a) La gráfica es simétrica con respecto al eje “y”.
b) Si x ≠ 0, entonces “x” es siempre positivo, por lo que “a” y “y” deben tener el mismo signo.
Si a < 0, su gráfica se extiende abajo, ya que el
valor de “y” será un número negativo o cero.
Rango ≤ 0, y el dominio es el conjunto de los
números reales.
Si a > 0, su gráfica se extiende arriba, ya que el
valor de “y” será un número positivo o cero.
Rango ≥ 0, y el dominio es el conjunto de los
números reales.
Práctica 33 Grafica la siguiente ecuación: x2 = 16y De la ecuación ordinaria y2 = 4ax: Para la tabulación se determinan los valores de y ≥ 0 y se obtienen los de “x”. 10 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Sesión 10 Los ttemas a revvisar el día d
de hoy son:: 1.2.1.1. O
Obtención d
de los elem
mentos de un
na parábolaa con vértice en el origen a partir de su
u ecuación
1.2.1.2. O
Obtención d
de la ecuación de una parábola co
on vértice een el origen a partir de su
us elemento
os 1.2.1
1.1. Obtencción de los e
elementos de una parrábola a parrtir de su eccuación mplo. Ejem
¿Quéé diferenccia observvas entre los chorros de aguaa de las imágenes? ¿Cuáál crees que q
sea el e objetivo de provocar una cierta c
formaa a los cho
orros de aggua? El retto en este ttema, para continuar ccon el análissis de la parábola, consiste en obtener los elementos d
de la misma a partir dee su ecuació
ón; como yaa lo has visto, los eleme
entos que iintegran a la parábola son: V: vértice
co
F: foc
D: dirrectriz
S: eje
e focal
LR: la
ado recto
L y R: puntos extrremos del Lado Recto
stancia dirigid
da de V a F. a = VF
a: dis
p: parámetro de la
a parábola, AF
A =P
Ya que la paráb
bola que esstás trabajaando tiene vértice en el origen, ssus coorden
nadas son V(0, 0). ¿Será ¿
posib
ble represeentar med
diante coorrdenadas a
al resto dee los elem
mentos que iintegran a una parábo
ola? 11 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Parábolas horizontales
Parábolas verticales
• Como la distancia dirigida del vértice al foco es
la constante “a”, puedes deducir que las
coordenadas del foco corresponden a F(a, 0).
• Como la distancia dirigida del vértice al foco es
la constante “a”, puedes deducir que las
coordenadas del foco corresponden a F(0, a).
• A partir de la definición de la directriz de la
parábola, la distancia dirigida del vértice a ésta
es la misma distancia que la del foco al vértice.
Por lo tanto, la directriz está dada por x= –a.
• A partir de la definición de la directriz de la
parábola la distancia dirigida del vértice a ésta
es la misma distancia que la del foco al vértice.
Por lo tanto, la directriz está dada por y= –a.
• El parámetro P es la distancia de la recta
directriz al foco, y al tomar los datos anteriores
se concluye que P = 2a.
• El parámetro P es la distancia de la recta
directriz al foco, y al tomar los datos anteriores
se concluye que P = 2a.
• ¿Qué ocurre con el lado recto?
Parábolas Horizontales Recuerda que el segmento de recta que es perpendicular al eje focal y pasa por el foco se llama Lado Recto y su longitud es: LR = │4a │ ¿Por qué? ¿Cuáles son los puntos donde el lado recto cruza a la parábola? Si el foco está en (a, 0), sustituye “a” en la ecuación ordinaria de la parábola con vértice en el origen (y2 = 4ax). Entonces si x = a, y2 = 4a(a) y2 = 4a2 y = ± 2a Las coordenadas de los puntos extremos del lado recto son: R (2a, a) y L(–2a, a). A partir de la fórmula de la distancia: d = ( x2 − x1 )2 + ( y2 − y1 ) 2
LR = (a − a)2 + [2a − (−2a)]2
LR = (4a)2 = 4a
LR = 4a = 2 p
¿Y qué ocurre con las parábolas verticales? 12 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Parábolas Verticales Recu
uerda nuevaamente quee el segmento de rectta que es perpendicul
p
lar al eje fo
ocal y pasa por el foco
o se llama Laado Recto yy su longitud
d es: LR = │ 4a │ Si el foco está een (0, a). Para que conozcas los puntos don
nde el lado recto cruzaa a la parábola se susstituye “a” en la ecuaación ordinaria de la parábola co
on vértice en el 2
origeen (x = 4ay). x2 = 4
Entonces si y = aa, 4a(a) 2
x = 4
4a2 x = ± 2a Las ccoordenadas de los pun
ntos extrem
mos del lado
o recto son: R (2a, a) y L(–2a, a). A partir de la fórmula de la distancia: d = ( x2 − x1 ) 2 + ( y2 − y1 ) 2
LR = ( −2a − 2a ) 2 + [a − a ]2
LR = (−4a ) 2 = 4a
LR = 4a = 2 p
Prácctica 34 de la parábo
ola que forman los cho
orros de aggua de la im
magen Deteermina los eelementos d
cuya ecuación eestá dada po
or: x2 = –– 28y 13 Universsidad CNCI dde México T
Taller de
e Matemááticas IIII Semana 3 y 4
1.2.1
1.2. Obtención de la e
ecuación de una paráábola con vértice en eel origen a p
partir de su
us elemento
os Ejem
mplo: e los ¿El uso de la forma paarabólica en ntes se trata t
solam
mente de una puen
cuesttión estéticca? El tema a tratarr en esta seesión consisste en la ob
btención de la ecuación de la parábola partir de suss elementoss, caso conttrario al tem
ma anterior.. con vvértice en eel origen a p
Sabráás que no ees una cuesttión puramente estéticca el hecho
o de que loss puentes te
engan form
ma arqueadaa, en los puentes de arrco en com
mpresión, un
na piedra cllave en el m
medio del aarco distribu
uye el peso al resto dell puente, traabajan tran
nsfiriendo ell peso propio del puen
nte y las so
obrecargas de d uso haccia los apoyyos extremo
os de la luzz (distancia libre entree pilares dee uno de suss vanos), mediante la ccomprensió
ón del arco, proporcion
nando mayo
or resistenccia y duració
ón. Existen puentess romanos,, como el de la d su imaggen, en Méérida, que a pesar de antiggüedad sigguen siend
do útiles en e la actuaalidad. ¿Cóm
mo harías para p
consttruir una réplica ré
de esste puente?? t caso si s se cono
ocen sus dimensione
es, se pueede generrar la ecuación En tal correespondientee a la formaa parabólicaa del puente
e y hacer un
na réplica. mplo: Ejem
Encontraar la ecuació
ón de la parábola y sus elemento
os si la direcctriz de la m
misma es x == –5 . Solucción: La diirectriz es una u línea reecta perpen
ndicular al eje de las “x”, “ y por d
definición, el e eje focall se encuen
ntra sobre eel mismo ejje. Por lo taanto logras identificar que se trata de una p
parábola ho
orizontal. Los elementos que tienees que con
nsiderar so
on los que respectan
n a la parábola horizzontal: • V(0,
V 0), F(a, 0), x= – a, P = 2a,
L = 4a = 2 p
• R(a, 2a) y L(a,
L –2a) LR
14 Universsidad CNCI dde México T
Taller de
e Matemááticas IIII Semana 3 y 4
Del dato: d
x = –5, – observaas que por ser éste negativo, la parábola sse abre hacia la derecha. Por lo tanto a = 5 De ahí puedes o
obtener tan
nto la ecuacción como ssus elementtos faltantees si sustituyyes el valorr de “a”. Con eel dato quee obtuviste aa= 5 , sustitúyelo en caada uno de llos siguientes elementtos: • V(0
0, 0)
• F(a
a, 0) = F (5, 0)
• x = – a, x = –5
• P = |2a| = |2(–5)| = | –10| = 10
R = 4 a = 2 p = 2 (10 ) = 20
• LR
• R(2
2a, a) y L(–2a
a, a) / R(–10,, 5) y L(10, 5)
Y la
a ecuación de
e la parábola horizontal con
n
vérrtice en el orig
gen es: y2 = 4ax
y2 = 4 (5)x
y2 = 20
0x
Prácctica 35 Si la longitud del arco cen
ntral es de 1,991 m y la altura de d las torres es de 28
83 m. Deteermina la eccuación del arco centraal del puente. A
Akashi Kaikyyo Puen
nte colgantee más largo del mundo
o, con 1991 m de longittud. 15 Universsidad CNCI dde México T
Taller de
e Matemááticas IIII Semana 3 y 4
Sesión 11 Los ttemas a revvisar el día d
de hoy son:: 1.3. Ecuaación ordinaria de la p
parábola con vértice fu
uera del oriigen 1
1.3.1. Paráb
bola horizon
ntal y vertical con vértice fuera deel origen 1.3.1
1.1. Obtenciión de los elementos de una paráb
bola con vértice fuera deel origen a p
partir de su ecuación 1.3.2
2.2. Obtenciión de la ecuación ordinaria de un
na parábola con vértice fuera del o
origen a parttir de algun
nos de sus elemen
ntos mínimo
os necesario
os 1.3. Ecuación o
ordinaria de
e la parábola con vérticce fuera de
el origen Te has preguntado algunaa vez, ¿qué factores influyyen para que la luna sse pueda ver desde la Tierra en un
na forma deeterminadaa, la cual únmente ess llamada faase? comú
Por eejemplo, si se considerra a la Tierrra como el punto de reeferencia; ees decir, com
mo el origeen, la fase lu
unar, con fo
orma parabó
ólica se enccuentra con vértice fueera del orige
en. ¿Cuá
ál será la ecuación ordinaria que le correesponda a la forma de la fasse lunar cono
ocida como creciente? La paarticularidad de la ecu
uación ordiinaria de la paarábola con
n vértice fuera f
del origen o
es que se adjuntan
n como eleementos claave de la ma, a sus co
oordenadass, dadas por V(h, k), mism
así como c
otros elementoss que la componen, en el caso de laa fase lunarr sabes que se logra graciias a la posición entre el sol, la tiierra y la luna,, así como al factor de la distancia y sus respeectivos tam
maños, dan
ndo forma así a un espectáculo nattural asomb
broso visto desde la Tierrra. 1.3.1
1. Parábolaa horizontall y vertical ccon vértice fuera del o
origen La cu
uestión aho
ora es: ¿quéé ecuación rrepresenta a una pará
ábola con vvértice fuerra del origeen? 16 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Parábolas Horizontales Supón una parábola con vértice fuera del origen como la de la figura. Ya que es más práctico trabajar con una parábola con vértice en el origen como lo has estado haciendo hasta el momento, entonces toma el vértice de la parábola como el origen, si haces eso y trazas unos ejes perpendiculares ficticios sobre el vértice, como los de la figura, observarás que dichos ejes están recorridos respecto al origen una distancia “h” sobre el eje de las “x” y una distancia “k” sobre el eje de las “y”. ¿Qué has hecho? Eso que acabas de hacer se le llama una traslación de ejes. Pero, ¿cómo validarlo? La traslación de los ejes coordenados ocurre solamente si: a) Los nuevos ejes son paralelos, respectivamente, a los ejes originales. b) Las coordenadas del nuevo origen sean (h, k) respecto al sistema original. c) Las coordenadas de cualquier punto P antes de la traslación sean (x, y) y después de la misma sean (x’, y’). Si observas bien la gráfica, se puede determinar que la ecuación de trasformación queda como sigue: x = h + x’
y = k + y’
o
o
x’ = x – h
y’ = y – k
A partir de estas fórmulas se puede obtener la ecuación
ordinaria de una parábola con vértice fuera del origen
V(h, k).
Si se considera una parábola como la de la figura, con
eje focal paralelo al eje de las “x”, abierta a la derecha y
con vértice en V(h, k), al hacer la traslación de ejes y al
tomar el vértice de la parábola como el nuevo origen, su
ecuación ordinaria corresponde a (y’)2 = 4ax’.
Ahora, como y’ = y – k
y
x’ = x – h, se sustituyen
en la ecuación anterior y se obtiene:
(y – k)2 = 4a (x – h)
Ecuación ordinaria de la parábola con vértice fuera
del origen y eje focal paralelo al eje de las “x”.
17 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Ejemplo: obtén la ecuación ordinaria de la parábola cuya gráfica se representa en el siguiente plano cartesiano. A partir de la gráfica es posible identificar el vértice y foco de la parábola, el vértice se compone de las coordenadas (4, 2) y el foco de (2, 2). Si observas la gráfica y su comportamiento puedes deducir que se trata de una parábola horizontal abierta hacia la izquierda, cuya ecuación ordinaria correspondiente es del tipo: (y – k)2 = 4a (x – h) Ahora, una vez obtenido el vértice y la distancia dirigida “a” de la parábola, se sustituyen en la ecuación anterior para establecer la ecuación de la parábola en su forma ordinaria. Por lo tanto si h = 4, k = 2 y a = –2, entonces: (y – 2)2 = –8(x – 4) Práctica 36 Traza la gráfica que le corresponde a la ecuación ordinaria de la parábola dada por (y + 5)2 = 6(x – 3) Parábolas Verticales ¿Cuál será la forma ordinaria de la ecuación si la parábola con vértice fuera del origen tiene su eje focal paralelo al eje de las “y”? y
y’
En este caso, recuerda que la fórmula que le
corresponde a una parábola vertical con vértice en el
origen es del tipo: x2 = 4ay, según el traslado de ejes,
la ecuación ordinaria correspondiente a la parábola
con vértice fuera del origen sería: (x’)2 = 4ay’.
F(h, k+a)
Ahora, ya sabes que x’ = x – h y que y’ = y – k,
entonces, al sustituirlos en la fórmula anterior resulta:
Foco
D
a
V
h
k
0
x
(x – h)2 = 4a(y – k)
Ecuación ordinaria de la Parábola con vértice fuera
del origen y eje focal paralelo al eje de las “y”.
18 Universidad CNCI de México x’
T
Taller de
e Matemááticas IIII Semana 3 y 4
Ejem
mplo: obtén la ecuació
ón de la parrábola cuyaa gráfica se representaa en el sigu
uiente plano
o cartesiano
o. A part
rtir de la gráfic
ca es posible identificar el vértice
v
de la
a parábola, el cual se compone de
e las
coord
denadas (–2, 4) y su distanc
cia dirigida a= –1.1.
–
Al ob
bservar la grráfica y su comportamient
c
to es
posiblle deducir que
e se trata de una parábola ve
ertical
abiertta hacia ab
bajo, cuya ecuación
e
ord
dinaria
corres
spondiente es del tipo:
(x – h)2 = 4a (y – k)
Ahora
a, una vez ob
btenido el vértice y la disttancia
dirigid
da “a” de la parábola, se
e sustituyen en la
ecuac
ción anterior para
p
establece
er la ecuación de la
paráb
bola en su form
ma ordinaria.
Por lo
o tanto si h = –2
2, k = 4 y a = –1.1,
–
entonces
s:
(x + 2)2 = –4.4(y – 4)
Prácctica 37 Ejem
mplo 2: traza la gráficaa que le corrresponde aa la ecuació
ón ordinariaa de la parábola dadaa por (x + 1)2 = 8(y + 2).. 1.3.1
1.1. Obtencción de los elementos de una paarábola con
n vértice fueera del origgen a partiir de su ecu
uación Ejem
mplo: Tiro all Blanco ¿Cóm
mo hacen los capittanes de los barco
os de gueerra para acertar a un objettivo cuando
o lanzan un misil? ¿Ten
ndrán buen tino? A un
na distancia considerab
ble y a simp
ple vista nin
ngún capitáán sería cap
paz de atinaarle a un objetivo o
si lanzara un misil desd
de su barco. Para loggrarlo neceesita de alggunos instrumentos dee medición, de la velo
ocidad en laa que viaja, de la distaancia a la que se encu
uentra el objetivo, o
ettc. Ademáss, una de las cosas más impo
ortantes qu
ue se consideran es laa trayectoriia del misil cuando sale disparado
o del barco
o, la cual se sabe que es parabóliica. ¿Cómo
o se podría escribir la ecuación ordinaria o
d
de la trayecctoria para
abólica del misil lanzzado por el e barco? Considera C
que conoccemos la altura a
máxiima alcanza
ada por el m
misil, la disttancia que recorrió, ettc. 19 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Es posible determinar los elementos de una parábola con vértice fuera del origen si se conoce su ecuación ordinaria o la gráfica que le corresponde, si ésta se encuentra de manera nítida. De cualquiera de los dos datos que te proporcionen, lo primero que debes obtener es “h” y “k” ; es decir, las coordenadas del vértice y la distancia dirigida “a” de las cuales dependen la mayoría de los elementos de la parábola. Parábolas Horizontales Ya has visto una parábola con vértice V(h, k) y cómo hay una estrecha dependencia entre la ecuación y su gráfica; ahora, ¿cuáles son los elementos que componen a la parábola y que producen tales efectos? En el caso de las parábolas horizontales, cuyo vértice
es V(h, k), el eje focal es paralelo al eje de las “x” y la
distancia dirigida del vértice al foco es “a”, por lo tanto
la distancia sobre el eje de las “x” desde el origen
hasta el foco es “h + a”, y la distancia sobre el eje de
las “y” desde el origen hasta el foco es solamente “k”,
por lo que, las coordenadas del foco son: F(h + a, k).
Con respecto a la ecuación de la directriz:
se iguala a cero y resulta:
ahora, como
al sustituirlo en la ecuación resulta:
y al despejar “x” queda:
x’ = –a
x’ + a = 0
x’ = x – h
x– h+ a = 0
x=h–a
Ahora se procede a obtener las coordenadas de los puntos extremos del lado recto junto con su longitud, para dicho cálculo se toman los elementos necesarios: el foco (h + a, k) y la ecuación: (y – k)2 = 4a(x – h). El foco es considerado porque, si observas bien la gráfica, el lado recto pasa sobre éste, quiere decir que las coordenadas del lado recto toman el mismo valor en “x”. Entonces, para conocer sus puntos se sustituye x = a + h en la ecuación ordinaria de la parábola con vértice fuera del origen (y – k)2 = 4a(x – h). Entonces si x = a + h, (y – k)2 = 4a(x – h) Se sustituye: (y – k)2 = 4a(a + h – h) Se simplifica: (y – k)2 = 4a2 Se aplica la raíz cuadrada: (y – k) =± 2a Se despeja “y”: y = k ± 2a Las coordenadas de los puntos extremos del lado recto son: L(a + h, k + 2a) y R (a + h, k – 2a). 20 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
A partir de la fórmula de la distancia: d = ( x2 − x1 ) 2 + ( y2 − y1 ) 2
LR = [(a + h) − (a + h)]2 + [(k − 2a) − (k + 2a)]2
LR = (a + h − a − h) 2 + (k − 2a − k − 2a) 2
LR = (−4a) 2 = 4a = 2 p
Por ejemplo: • Para obtener los elementos de una parábola con ecuación determinada se realizan los siguientes pasos: Si la ecuación de la parábola es: (y – 2)2 = (x + 5), lo primero a obtener son los elementos “h”, “k” y “a”, luego, a través de estos, obtener el resto de los elementos, ya que en su mayoría dependen de al menos uno de ellos. Entonces a través de la ecuación dada se deduce que se trata de una parábola horizontal, por lo tanto, al tomar la ecuación ordinaria de la parábola con vértice fuera del origen: 2
(y – k) = 4a(x – h) y de la ecuación proporcionada en este ejemplo: (y – 2)2 = (x + 5) Al igualar término a término cada uno de los elementos de la ecuación se obtiene: 4a = 1 (x– h) = ( x + 5) (y – k)2 = (y – 2)2 y – k = y – 2 a = ¼ – h = 5 – k = – 2 h = –5 k = 2 Los elementos obtenidos son h = –5, k = 2 y a = ¼. Ahora, sólo queda sustituir en cada forma los elementos que se requieran para obtener el resto. Ya que el valor de la distancia dirigida “a” es positivo se deduce que la parábola se abre a la derecha y la forma de la ecuación directriz es x = h – a. 21 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Elementos faltantes: F: foco
D: directriz
LR: lado recto
L y R: puntos extremos del LR
P: parámetro
F(h+a, k)
x=h–a
LR = 4a = 2 p
L(h + a, k + 2a) y R(h + a, k – 2a)
P = DF = | 2a |
Los datos h = –5, k = 2 y a = ¼ se sustituyen en las siguientes fórmulas:
F(h + a, k)
x=h–a
LR = 4 a = 2 p
L(h + a, k + 2a) y R(h + a, k – 2a)
P = DF = | 2a |
Parábolas Verticales F(–5 + ¼, 2)
x = –5 – ¼
LR = 4 a = 4 ( 1 4 ) = 1
L[–5 + ¼, 2 + 2(1/4)]
R[–5 + ¼, 2 – 2(1/4)]
P =| 2(1/4)|
F(–4.75, 2)
x = –5.25
LR = 1
L (–4.75, 2.5)
R(–4.75, 1.5)
P = ½ = 0.5
Obtención de los elementos de la parábola
En el caso de las parábolas verticales, cuyo vértice
es V(h, k), el eje focal paralelo al eje de las “y” y la
distancia del vértice al foco es “a”, por lo tanto las
coordenadas del foco son: F(h, k + a).
Con respecto a la ecuación de la directriz:
se iguala a cero y resulta:
ahora, como
al sustituirlo en la ecuación resulta:
y al despejar “y” queda
y’ = –a
y’ + a = 0
y’ = y – k
y–k+a=0
y=k–a
Las coordenadas de los puntos extremos del lado
recto y la longitud del lado recto se desarrollan a
detalle en la siguiente diapositiva.
Si observas bien la gráfica, el lado recto pasa por el foco, en este caso, el foco se encuentra sobre la recta paralela al eje de las “y”, por lo tanto las coordenadas de los puntos extremos del lado recto tendrán la misma ordenada, (k + a). Entonces si y = k + a, (x – h)2 = 4a(y – k) (x – h)2 = 4a(k + a – k) (x – h)2 = 4a2 x – h = ± 2a x = h ± 2a Las coordenadas de los puntos extremos del lado recto son: L (h+2a, k+a) y R(h–2a, k+a). 22 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
A partir de la fórmula de la distancia: 2
2
d = ( x2 − x1 ) + ( y2 − y1 ) 2
2
LR = [( k + a ) − ( k + a )] + [(h − 2 a ) − ( h + 2a)]
2
LR = (k + a − k − a ) + ( h − 2 a − h − 2a)
2
2
LR = ( − 4 a) = 4 a = 2 p Para obtener los elementos de una parábola dada la ecuación se realizan los siguientes pasos: Si la ecuación de la parábola es: (x + 5)2 = –3.2(y – 2), lo primero a obtener son los elementos “h”, “k” y “a”, y a través de estos el resto de los elementos, ya que en su mayoría dependen de al menos uno de ellos. Entonces a través de la ecuación dada, se deduce que se trata de una parábola vertical, por lo tanto, al tomar la ecuación ordinaria de la parábola con vértice fuera del origen: 2
(x – h) = 4a(y – k) y de la ecuación proporcionada en este ejemplo: (x + 5)2 = –3.2(y – 2) Al igualar término a término cada uno de los elementos de la ecuación se obtiene: (x – h)2 = (x + 5)2 4a = –3.2 (y – k) = (y – 2) x – h = x + 5 a = –0.8 – k = – 2 – h = 5 k = 2 h = –5 Los elementos obtenidos son h = –5, k = 2 y a = –0.8. Ahora, sólo queda sustituir en cada forma los elementos que se requieran para obtener el resto. Ya que el valor de la distancia dirigida “a” negativo se deduce que la parábola se abre hacia abajo y la forma de la ecuación directriz es y = k – a. 23 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Elementos faltantes: F: foco
D: directriz
LR: lado recto
L y R: puntos extremos del LR
P: parámetro
F(h, k + a)
y=k–a
LR = 4a = 2 p
L(h+2a, k+a) y R(h –2a, k + a)
P = DF = | 2a |
Los datos h = –5, k = 2 y a = –0.8 se sustituyen en las siguientes fórmulas:
F(h, k + a)
F(–5, 2 – 0.8)
F(–5, 1.2)
y = 2 – (– 0.8)
LR = 4 a = 4 ( − 0 . 8 ) = 3 . 2
y=k–a
LR = 4 a = 2 p
L(h + 2a, k + a) y R(h – 2a, k + a)
y = 2.8
LR = 3.2
L[–5 + 2(–0.8), 2 + (–0.8)]
R[–5 – 2(–0.8), 2+ (–0.8)]
P = | 2(–0.8) |
P = DF = | 2a |
L (–6.6, 1.2)
R(–3.4, 1.2)
P = 1.6
Una vez que se obtuvieron los elementos que componen a la parábola con vértice fuera del origen tanto en su forma vertical como horizontal, se puede concluir que: Parábola Horizontal
Elementos:
F: foco
D: directriz
S: eje focal
V: vértice
LR: lado recto
L y R: puntos extremos del LR
a: distancia dirigida
P: parámetro
Parábola Vertical
F(h + a, k)
x=h–a
Paralelo al eje de las “x”
V(h, k)
LR = 4a = 2 p
F(h, k + a)
y=k–a
Paralelo al eje de las “y”
V(h, k)
LR = 4a = 2 p
L(h+a, k+2a) y R(h+a, k–2a)
L(h+2a, k+a) y R(h–2a, k+a)
1.3.1.2. Obtención de la ecuación ordinaria de la parábola con vértice fuera del origen a partir de alguno de sus elementos mínimos necesarios Es posible determinar la ecuación ordinaria de una parábola con vértice fuera del origen si se conocen al menos algunos de sus elementos mínimos; por ejemplo, si se conocen el foco y el vértice, los puntos extremos del lado recto, la directriz y el foco, etc., y viceversa. Puesto que los elementos mínimos necesarios se pueden obtener a partir de los datos que se proporcionan, ¿cuáles son esos elementos mínimos necesarios? Los elementos mínimos necesarios para determinar la ecuación ordinaria de una parábola con vértice fuera del origen son: los componentes del vértice (h, k), la distancia dirigida “a” y el eje focal. 24 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
De cualquier dato que te proporcionen, lo primero que debes obtener son los elementos mínimos necesarios y luego, a partir de estos, construir la ecuación ordinaria correspondiente de la parábola sustituyendo los valores básicos. Ejemplo: obtén la ecuación ordinaria y grafica la parábola cuya directriz es x – 6 = 0 y cuyo vértice está en (0,3). Ya que el vértice está en (0, 3) y que la forma general del vértice es (h, k) se deduce que: h = 0 y que k = 3 Obtenidos estos valores sólo falta determinar la distancia dirigida “a” y el eje focal. Ahora, de la ecuación de la directriz x – 6 = 0, se despeja “x”, de lo que resulta: x = 6 Como la directriz corta al eje “x”, se deduce que su eje focal es paralelo a dicho eje, de lo que se concluye que se trata de una parábola horizontal. Al conocer la ecuación de la directriz x = h – a y del dato proporcionado x = 6 se sustituyen h = 0 y x = 6, 6 =0 – a de lo que resulta: a = –6 Ahora sí, mediante los elementos mínimos necesarios es posible obtener la ecuación ordinaria correspondiente. Como se mencionó, el eje focal es paralelo al eje “x”, la parábola es horizontal y la forma ordinaria de la ecuación es del tipo: (y – k)2 = 4a(x – h). Luego, ya sabes que el vértice es (0, 3) y la distancia dirigida es a = –6, por lo tanto, al sustituir en la ecuación resulta: (y – 3)2 = 4(–6)(x – 0) (y – 3)2 = –24x 25 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
¿Qué importancia podrían tener los parámetros
“h”, “k” y “a” en una parábola?
Para responder a tal pregunta es necesario hacer
distintas pruebas con dichos parámetros y comparar
los resultados.
Supón una parábola con vértice fijo en (–6, –3) y en
el cual varía el parámetro “a” asignando valores
distintos cada vez.
Por ejemplo, ¿cómo es la gráfica si a = ½?
¿cómo si a = 1?
¿cómo si a = 1½?
¿cómo si a = 2?
etc.
¿Qué ocurre gráficamente cuando el parámetro
“a” se incrementa o disminuye?
• Obtén los puntos extremos del lado recto de dos
de las parábolas de la gráfica y determina las
diferencias.
y
6
5
Si observas bien la gráfica, cuando el parámetro “a”
disminuye, la parábola se hace más pequeña, mientras
que cuando “a” se incrementa la parábola se hace más
grande.
4
3
a=1
1
-8
-7
-6
-5
-4
a=1
2
V(- 4, 2)
-3
-2
-1
0
V(1, 2)
1
2
3
4
-2
V(-6, -3)
a=1
5
x
Ahora, ¿qué ocurre si varías el vértice de la parábola
fuera del origen y fijas un determinado valor al
parámetro “a”?
-1
-3
-4
-5
V(1, -5)
-6
-7
-8
V(0, -8.5)
Ciertamente que la gráfica de la parábola es la misma
pero ubicada en diferentes lugares en el plano conforme
a su vértice, y en este caso, como “a” es positivo, la
parábola se abre a la derecha o hacia arriba.
-9
-10
-11
-12
26 Universidad CNCI de México • Determina la ecuación de cada una de las parábolas
que se encuentran en el plano de la imagen.
Taller de Matemáticas III Semana 3 y 4
Práctica 38 Instrucciones: determina la ecuación ordinaria de la parábola con vértice fuera del origen de la forma que proyecta el agua lanzada por un bombero y obtén los elementos faltantes a partir de la ecuación Considera al bombero como el punto de referencia y crea
el plano cartesiano a partir de él. La posición del
bombero respecto al fuego depende de la forma
parabólica del agua y de la presión con la cual es
lanzada.
El agua alcanza una altura máxima de 2 metros y la
distancia del bombero al punto más alto que alcanza el
agua es de 5 metros, además que el punto (– 2, 1)
pertenece a la parábola.
27 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Sesión 12 Los ttemas a revvisar el día d
de hoy son:: 1.4. EEcuación ge
eneral de laa parábola
1.4.1. Conveersión de la forma ordiinaria de la ecuación de una paráb
bola con vértice fuera del origen aa su forma general 1.4.2. Conveersión de la forma general de la eccuación de una parábo
ola con vértice fuera del origen aa su forma ordinaria eneral de laa parábola
1.4. EEcuación ge
¿Quéé tipo de forma producce el delfín aal saltar? Si el delfín es capaz c
de producir salto
os al nadarr, ¿su h
habilidad lee permitirá escapar fáccilmente de
e las reedes de los pescadoress? Has d
de saber qu
ue los delfin
nes produceen esos tipo
os de saltoss como exprresión de alegría o como juego, pero, lameentablemen
nte los delfines son in
ncapaces dee escapar de d las redes de los cazzadores. Ah
hora, ¿creess que se pueeda represeentar mateemáticamen
nte la form
ma del salto de un delfíín? A traavés de la ecuación de una parábo
ola en su fo
orma ordinaaria es posib
ble, pero, ¿ccómo se pu
uede representar la forma fo
geneeral de la ecuación dee una paráb
bola dada en e su form
ma ordinaria
a? Recu
uerda que la ecuación de cualquier gráfica en su form
ma general es represen
ntada mediante la igu
ualdad a ceero, para lograr lo anterior en un
na ecuación
n ordinaria de la parábola, es necesario dessarrollar loss cuadradoss de la mism
ma y simpliificar orden
nando sus términos. Has notado qu
ue al pasarr de una ecuación e
a otra, se ejjerce sobree la mismaa una transsformación,, a lo que see le conocee como convversión de una forma de la ecuacción a otra,, y esto se realiza en ffunción del requerimie
ento de unaa o de la ottra, según ssea el caso. Preciisamente, ¿¿qué es lo q
que ocurre een tal conveersión? 1.4.1
1. Conversió
ón de la fo
orma ordinaaria de la ecuación de
e
e una paráb
bola con vé
értice fueraa del origen
n a su formaa general Para realizar la cconversión mencionad
da anteriorm
mente, se to
oman los do
os casos possibles de laa parábola y en paralelo se dessarrollan haasta lograr el objetivo
o de obtener su convversión al tip
po de formaa general. 28 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
A partir de la forma ordinaria de la parábola se desarrolla lo siguiente: Horizontal es:
(y – k)2 = 4a(x – h)
y2 – 2ky + k2 = 4ax – 4ah
2
y – 2ky – 4ax + (k2 + 4ah) = 0
Desarrolla los cuadrados
Iguala a cero
Vertical es:
(x – h)2 = 4a(y – k)
x2 – 2hx + h2 = 4ay – 4ak
2
x – 2hx – 4ay + (h2 +4ak) = 0
Ejemplo: Supón que la ecuación de la forma del salto del delfín es (x – 3)2 = –12(y – 4), ¿Cuál es la ecuación general de la forma parabólica que produce el delfín al saltar? Desarrolla los cuadrados:
Iguala a cero:
Simplifica:
(x – 3)2 = –12(y – 4)
x2 – 6x + (–3)2 = – 12y + 48
x2 – 6x + 12y + 9 – 48 = 0
x2 – 6x + 12y – 39 = 0
Además de haber obtenido la ecuación general de la parábola que forma el delfín al saltar, puedes deducir a través de la ecuación que se trata de una parábola vertical, ya que la variable lineal en este caso es la “y”, y por ser la distancia dirigida “a” negativa, la parábola se extiende hacia abajo. Lo anterior es correcto ya que como sabes, el delfín efectúa un salto que forma una parábola con las características obtenidas a través de la ecuación. Práctica 39 Dada la ecuación de la parábola con vértice fuera del origen en su forma ordinaria (y + 7)2 = 32(x – 6), conviértela a su forma general y traza su gráfica. 29 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
1.4.2
2. Conversión de la forrma generaal de la ecuaación de un
na parábolaa con vértice
e fuera dell origen a su
u forma ord
dinaria Ejem
mplo: Paracaaídas Se ceelebra un concurso c
so
obre la fab
bricación de
e paracaídas, se pide realizaar 10, 000 ejemplaress de paracaídas p
como el de la imaagen. A laa empresa que logre terrminar loss 10, 000
0 paracaídas en el menor tiempo po
osible se le
e entreegará una ccantidad de 100 billonees de euros.. Si tú estás trab
bajando en una empreesa de gran
n presttigio, y tu jefe te pide p
colaborar en el e
proyecto, pero,, al iniciar se encuenttran con un
n gran problema: ¿cómo obtener o
una ecuación
n que representee las dimen
nsiones del paracaídass de la
a imagen? En el e ejemplo anterior lograste iden
ntificar la forma f
del paracaídas, p
y seguram
mente coinccides en que se trata d
de una paráábola, ya qu
ue la forma de la paráb
bola es verttical y se prresenta abiierta hacia abajo, por lo que pue
edes conclu
uir que el ttipo de ecuación ordin
naria que lee correspond
de es: (x – h
h)2 = 4a(y – k) Ya ap
prendiste a convertir lla ecuación de una parábola con vértice fueera del orige
en de su fo
orma ordinaaria a su forrma general, ahora, ¿q
qué ocurre ssi tienes el caso contra
ario?, ¿cóm
mo convierttes la ecua
ación de un
na parábola
a con vértiice fuera d
del origen de d su form
ma general a
a su forma ordinaria?
ma abreviada de resolvver cualquieer tipo de cconversión de la Para determinar una form
ecuación de parábola con vértice fueera del origgen de su forma f
ordin
naria a su forma f
geneeral y viceveersa, es neccesario conssiderar los d
dos posibless casos de p
parábolas que se pued
den presenttar, parábollas horizonttales y paráábolas vertiicales. Fo
orma generral
Horizontal
y2 – 2ky – 4a
ax + (k2 + 4a
ah) = 0
Vertical
x2 – 2hx – 4ay + (h
( 2 + 4ak) = 0
La ecuación y2 – 2ky – 4ax + (k2 + 4ah) = 0,
porr ejemplo,
y + (h2 + 4ak)) = 0,
La ecuación x2 – 2hx – 4ay
por ejemplo,
Se abre
a
hacia el semieje
s
“x” po
ositivo (si a > 0).
0
Se abre
a
hacia el semieje
s
“x” ne
egativo (si a< 0).
0
Se abre hacia el
S
e semieje “y” positivo
p
(si a > 0).
S abre hacia el
Se
e semieje “y” negativo
n
(si a<
< 0).
Aho
ora, al hacer D = –2k, E= –4
4a, y
F = k2 + 4ah, la ecuación resulta:
Ahora, al hacerr D = –2h, E= –4a,
A
–
y
F = h2 + 4ak, la
a ecuación res
sulta:
y2 + Dy + Ex + F = 0
Form
ma general de la
a ecuación de la
a parábola horiz
zontal
30 Universsidad CNCI dde México x2 + Dx + Ey + F = 0
Fo
orma general de
e la ecuación de
e la parábola ve
ertical
T
Taller de
e Matemááticas IIII Semana 3 y 4
De lo
o obtenido aanteriormente se conccluye que: Ecua
ación
C
Constantes
D EyF
D,
Pa
arábola Horizontal
y2 + Dy + Exx + F = 0
D = –2kk, E= –4a, y F = k2 + 4ah
h
Pa
arábola Verttical
x2 + Dx + Eyy + F = 0
D = –2h
h, E= –4a, y F = h2 +4ak
Ejem
mplo: Convvierte la ecuación de la parábolaa a su form
ma ordinariaa, cuya form
ma generall está 2
dadaa por: y – 6y – 12x – 39
9 = 0. Solucción: Se id
dentifica térrmino a térm
mino la ecuación propo
orcionada ccon la ecuacción generaal que le corresponde. y2 – 6
6y – 12x – 3
39 = 0 y2 + Dy ++ Ex + F = 0 –6 = D
–12 = E
–39 = F
si D =–
–2k
si E = –4a
si F = k2 + 4ah
sustituyes
s –6 = –2k
sustituyes
s –12 = –4a
sustituyes
s –39 = 32 + 4(3)h
4
y obtienes:
y obtienes:
y obtienes:
k= 3
a= 3
h= – 4
Por lo tanto all sustituir los l valores que obtuvviste en la ecuación ordinaria de d la parábola con vé
értice fueraa del origen y horizontaal resulta: (y – kk)2 = 4a (x –– h) (y – 3
3)2 = 12 (x ++ 4) Prácctica 40 Paraguas Conssiderando que al paragguas de la im
magen que tiene formaa parabólicaa le corresp
ponde la eccuación general, x2 – – 10x – 8y + 39 = 0,, conviértela a su forma ordinaaria y repreeséntala en el plano caartesiano. 31 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Semana 4 Sesión 13 Los temas a revisar el día de hoy son: 2. La Elipse 2.1. Caracterización Geométrica 2.1.1. La Elipse como lugar geométrico 2.1.2. Elementos asociados con la elipse 2.1.3. Formas de trazo a partir de la definición 2.2. Ecuación ordinaria de la elipse 2.2.1. Elipses horizontales y verticales con centro en el origen 2. La elipse 2.1. Caracterización geométrica ¿Qué forma identificas que tienen en común las imágenes anteriores? ¿A través de qué características lograrías describir su forma? Recuerda que la elipse se clasifica como una sección cónica porque proviene del corte de un cono con dos capas a través de un plano. Este tipo de figura cónica puedes encontrarla aplicada en diferentes ámbitos de tu vida cotidiana; por ejemplo, la forma del balón de fútbol americano, la forma de una sandía, la trayectoria de la Tierra al orbitar alrededor del Sol, cámaras secretas, los pétalos de un girasol, los arcos semielípticos, etc. En este bloque verás un análisis detallado de los diferentes tipos de ecuaciones de la elipse, así como su representación gráfica y cómo ésta depende de los componentes que la integran. Pero, antes de comenzar, ¿cuáles son las características con las que se identifica una elipse en el plano cartesiano? 32 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
2.1.1. La elipse como lugar geométrico En el ejemplo inicial has logrado identificar la forma elíptica de las imágenes, esta forma se puede representar en el plano cartesiano advirtiendo algunas características particulares para ser identificada como tal. La elipse en el plano cartesiano se define como el lugar geométrico de los puntos tales que la suma de su distancia a dos puntos fijos llamados focos es una constante positiva, la cual siempre es mayor que la distancia entre dichos puntos fijos. Ciertamente, como en todo lugar geométrico, entre los elementos que integran la elipse hay algunos que son clave, debido a que condicionan la forma. En el caso de la elipse, ¿qué factores o elementos hacen posible la elaboración gráfica de una elipse? 2.1.2. Elementos asociados con la elipse Al hacer un análisis sobre el lugar geométrico de la elipse, se logran definir sus términos característicos como sigue: F y F’: focos
C: centro
L: eje focal
V y V’: vértices
(L y R) y (L’ y R’): puntos extremos
VV’: eje mayor = 2a BB’: eje menor = 2b
LR y L’R’: lado recto e: excentricidad En donde de manera general, los elementos que caracterizan a la elipse son: 33 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
C: centro de la elipse, es el punto medio del segmento
de recta cuyos puntos extremos son los vértices.
F y F’: Los puntos F y F’ son los puntos fijos
denominados focos.
L: eje focal, es la recta que pasa por donde están los
focos.
V y V’: vértices, son los puntos de intersección de la
elipse con su eje focal.
VV’: eje mayor, es el segmento de recta cuyos puntos extremos son los vértices de la elipse.
BB’: eje menor, es el segmento de recta que pasa por el centro de la elipse y que es perpendicular al
eje focal.
LR y L’R’: lado recto, es el segmento de recta perpendicular al eje focal que pasa por uno de sus focos
y cuyos puntos extremos están sobre la elipse.
e: la excentricidad de una elipse es su grado de “achatamiento”.
2.1.3. Formas de trazo a partir de la definición Ya conoces la forma, la definición y los elementos que componen a una elipse; ahora, ¿cómo trazarías una si utilizas un trozo de hilo y un lápiz? Si tomas la definición de la elipse puedes lograr deducir el
siguiente método para trazarla, ¡inténtalo!
1.
Corta un hilo de la medida que tú elijas, este hilo
representa una longitud 2a, después ata sus
extremos a dos puntos fijos: F1 y F2 sin tensarlos .
2.
Tensa el hilo con la punta de un lápiz, como se
muestra en la figura. El lápiz trazará en su movimiento
una elipse con focos en los puntos F1 y F2, ya que la
suma de las distancias, de la punta del lápiz a cada
uno de los focos, es constante; es decir, es igual a 2a
(la medida que elegiste).
F1
¿Será posible trazarla también con un compás?
F2
¿Cómo trazar una elipse con un compás? A partir también de la definición de la elipse, puedes deducir el siguiente método para trazarla con una regla y un compás, para eso tienes que ubicar un conjunto de puntos como se indica a continuación: 1. Traza una línea horizontal y sobre ella marca el centro de la elipse C. 2. A partir de este punto y con la ayuda del compás, traza sus vértices V y V’, ubicados a la misma distancia del centro. 3. Con una abertura menor del compás marca los focos F y F’. 4. Considera un punto P cualquiera situado sobre la línea horizontal; luego abre el compás en una distancia igual a V’P. 34 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
5 Coloca eel compás een el foco F’’ y traza loss dos arcos,, arriba y deebajo de la línea 5.
recta (eje mayor). 6 Toma co
6.
omo centro el foco F, y procede de
e igual manera que en el paso 5. 7 Coloca aahora el com
7.
mpás en el foco F’ co
on una aberrtura igual aa VP y traza dos arcos, arrriba y abajjo del eje m
mayor, de iggual modo traza dos aarcos pero aahora toma a FF como centtro. Los p
puntos de in
ntersección
n de los arco
os son desiggnados por P1, P2, P3 y P4, y se traata de los puntos p
de la elipse. Al repetir esste proceso
o para cualq
quier punto
o Q sobre el e eje mayo
or, se pueede localizaar los pun
ntos Q1, Q2, Q3 y Q4 sobre lla elipse, y así sucesivamente. puntos que localizaste con el méttodo anterior únelos ccon una líneea continuaa y así Los p
obtieenes el trazo
o de la elipsse. El método desccrito se justtifica ya qu
ue las distan
ncias V’P y y PV sumaan 2a, cond
dición uerdo con laa definición.. neceesaria para fformar la elipse de acu
Prácctica 41 ue componeen a la elipse en la siguiente imageen. Identtifica los eleementos qu
de la elipse para A traavés de estte ejemplo puedes ver como las personas se sirven d
crearr instrumen
ntos que en este caso sson para enttretenerse yy divertirse. 35 Universsidad CNCI dde México T
Taller de
e Matemááticas IIII Semana 3 y 4
2.2. Ecuación o
ordinaria de
e la elipse Ejem
mplo: Jitomaate Huaje Con el fin de op
ptimizar el espacio, ¿ccuál es la mejo
or manera de d acomod
dar los jitom
mates en una caja como la de la figura? Consid
dera que todo
os los jitomaates deben ser guardad
dos en el mism
mo sentid
do: parado
os, acostados o cruzaados. En el ejemplo anterior a
con
nsideraste la l forma de
el jitomate para saberr la posición
n que mo te habráás dado cueenta, el jito
omate más convenía a fin de optiimizar espaacios, y com
tienee forma elííptica, y diicha formaa tiene opcciones diferentes de ser presen
ntada, obliccua, horizon
ntal o verticcalmente, claro, siemp
pre en funciión del punto de referrencia que sse toma. Para resolver ell problema de la posicción más faavorable para optimizaar espacios en el acom
modo de los jitomatess, es importtante conocer sus dim
mensiones, ya que ésttas se utilizzan en el cáálculo del área á
y del volumen. v
Conociendo C
las dimenssiones ento
onces, hacees las prueb
bas necesarrias para co
onocer los espacios qu
e
ue ocupan een las diferentes posicciones de acomodo a
y al comparrarlas deducces las quee optimizan
n mejor esp
pacio. Existe una man
nera más rápida y práctica de
e obtener el volumen
n del jitom
mate… ¿quieeres saber de qué se s trata? Lo lograríaas si conocieras la eecuación qu
ue le correesponde al jjitomate. EEntonces surge la pregu
unta: ¿Cuá
ál será la forma de la eecuación con la que se pudiera disstinguir a u
una elipse? En seeguida haráás un estudio analítico de la ecuación de la eelipse, que como en ell caso de laas otras cónicas, es la fo
orma más ssimple de re
epresentar ssu lugar geo
ométrico. 1. Elipse ho
orizontal y vvertical con
n centro en el origen 2.2.1
Elipsses horizonttales Para determinar la ecuació
ón ordinariaa de la elipsse con centrro en el origgen y horizo
ontal, es neecesario creear una a paartir de su d
definición, e
estableciend
do lo siguien
nte: • Primero coloca
a el centro en el origen del plano
artesiano, de tal manera qu
ue el eje mayo
or VV’
ca
qu
ueda determinado sobre el eje de las “x”.
• Ahora, conside
era “c” como
o la distancia
a del
ce
entro de la elipse a cada un
no de los foco
os; de
ta
al modo que s us coordenad
das quedan as
sí:
F(c, 0) y F’(–c, 0).
Por fines prá
ácticos, toma la expresió
ón 2a
• P
co
omo la distanc
cia constante de la que habla la
de
efinición.
36 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
NOTA: Si observas con atención, cuando el punto P se encuentra en la misma posición que el punto B, la longitud de la línea recta roja es exactamente la mitad de la longitud total; es decir, la constante "a". Ahora, si consideras todas las constantes "a", "b" y "c" identificarás que entre ellas forman un triángulo rectángulo en el cual la constante "a" se encuentra en el lugar de la hipotenusa, y las constantes "b" y "c" en el de los catetos. Si el punto P(x, y) es un punto cualquiera de la elipse y si tomas como referencia la definición, obtienes:
FP + F’P =2a
La distancia FP está dada por:
FP = ( x − c) 2 + ( y − 0) 2
La distancia F’P está dada por:
F ' P = ( x + c) 2 + ( y − 0) 2
FP + F ' P = 2a
Sustituyes lo anterior en la fórmula FP + F’P =2a y resulta:
( x − c)2 + ( y − 0)2 + ( x + c)2 + ( y − 0)2 = 2a
Acomodas la igualdad:
Elevas al cuadrado ambos lados de la igualdad:
[ (x − c) + y ] = [2a −
2
Desarrollas los binomios al cuadrado:
2
2
( x + c)2 + y2
]
2
( x − c)2 + y2 = 4a2 − 4a ( x + c)2 + y2 + (x + c)2 + y2
Nuevamente desarrollas cuadrados:
Igualas a cero:
( x − c)2 + y2 = 2a − ( x + c)2 + y2
x2 − 2cx + c2 + y2 − 4a2 + 4a (x + c)2 + y2 − x2 − 2cx − c2 − y2 = 0
− 4cx − 4a2 + 4a (x + c)2 + y2 = 0
Divides todo entre 4:
− cx − a2 + a ( x + c)2 + y2 = 0
Acomodas la igualdad:
Elevas al cuadrado ambos lados de la igualdad:
Desarrolla los cuadrados:
Desarrolla el binomio al cuadrado:
Iguala a cero la ecuación:
Simplifica:
Factoriza y obtén el factor común:
[cx + a ]
2 2
[
cx + a2 = a ( x + c)2 + y2
= a ( x + c) + y
2
2
]
2
c 2 x 2 + 2 a 2 cx + a 4 = a 2 ( x + c ) + a 2 y 2
2
c 2 x 2 + 2 a 2 cx + a 4 = a 2 x 2 + 2 a 2 cx + a 2 c 2 + a 2 y 2
c 2 x 2 + 2 a 2 cx + a 4 − a 2 x 2 − 2 a 2 cx − a 2 c 2 − a 2 y 2 = 0
c 2 x 2 + a 4 − a 2 x 2 − a 2c 2 − a 2 y 2 = 0
− x 2 (a 2 − c 2 ) + a 2 (a 2 − c 2 ) − a 2 y 2 = 0
La suma de las distancias del P(x, y) a los focos es 2a, y
ésta debe ser mayor que el segmento de recta FF’, es decir:
2a > 2c, por lo que se obtiene que a > c. A su vez que a2 >
c2, de lo que se obtiene a2 – c2 > 0.
Según la gráfica de la imagen b2 = a2 – c2, en donde b > 0,
lo aplicas a la ecuación anterior y te queda:
Divides todo entre a2b2
− x 2b 2 + a 2b 2 − a 2 y 2 = 0
x2 y2
+
=1
a2 b2
37 Universidad CNCI de México Ecuación ordinaria de una elipse
horizontal con centro en el origen.
Taller de Matemáticas III Semana 3 y 4
Análisis de la ecuación: Con base en la ecuación canónica de la elipse con centro en el origen y horizontal que ya obtuviste, puedes deducir lo siguiente: x 2 y 2
+
=1
a2 b2
1. Su gráfica es simétrica respecto al eje “x”; es decir, si el punto P1(x, y) satisface su ecuación, entonces el punto P2(x, –y) también, significa que los dos puntos están en la gráfica. 2. Su gráfica es simétrica respecto al eje “y”; es decir, si el punto P1(x, y) satisface su ecuación, entonces el punto P2(–x, y) también, significa que los dos puntos están en la gráfica. 3. Si su gráfica es simétrica respecto al eje “x” y respecto al eje “y”, entonces tiene simetría respecto al origen. 4. El dominio de la elipse son los valores que puede tomar la variable independiente “x” en la ecuación, para obtenerlo despeja “y” de la ecuación b
ordinaria de la elipse con centro en el origen que obtuviste, y = ± a2 − x2
a
2
2
2
2
por lo tanto a – x ≥ 0 de tal modo que a ≥ x y resulta –a ≤ x ≤ a. 5. El rango de la elipse son los valores que puede tomar la variable dependiente “y” en la ecuación, para obtenerlo despeja “x” de la ecuación ordinaria de la 2
x = ± ba b 2 − y por elipse con centro en el origen que obtuviste, lo tanto b2 – y2 ≥ 0 de tal modo que b2 ≥ y2 y resulta –b ≤ y ≤ b. Podrás notar que según las dos condiciones anteriores, la elipse horizontal con centro en el origen está acotada por ±a en el eje de las “x” y por ±b en el eje de las “y”. Práctica 42 Ejemplo: x2 y2
+
=1
Grafica la siguiente ecuación: 64 25
Elipses verticales Para determinar la ecuación ordinaria de la elipse con centro en el origen y vertical, se siguen pasos similares a los que realizaste para obtener la ecuación de la elipse con centro en el origen y horizontal. • Primero coloca el centro en el origen del plano
cartesiano, de tal manera que el eje mayor VV’
queda determinado sobre el eje de las “y”.
• Ahora, considera “c” como la distancia del
centro de la elipse a cada uno de los focos; de
tal modo que sus coordenadas quedan así:
F(0, c) y F’(0, –c).
• Por fines prácticos, toma la expresión 2a como
la distancia constante de la que habla la
definición.
38 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Si el punto P(x, y) es un punto cualquiera de la elipse y si tomas como referencia la definición, obtienes: FP + F’P =2a La distancia FP está dada por:
FP = ( x − 0) 2 + ( y − c) 2
La distancia F’P está dada por:
F ' P = ( x − 0) 2 + ( y + c ) 2
Sustituyes lo anterior en la fórmula FP + F’P =2a y resulta:
FP + F ' P = 2a
( x − 0)2 + ( y − c)2 + (x − 0)2 + ( y + c)2 = 2a
Acomodas la igualdad:
x2 + ( y − c)2 = 2a − x2 + ( y + c)2
Procedes de la misma manera que como lo hiciste con la elipse horizontal hasta llegar a encontrar la
ecuación ordinaria de la elipse con centro en el origen y vertical.
x2 y2
+
=1
b2 a2
Ecuación ordinaria de una elipse
vertical con centro en el origen.
Análisis de la ecuación: Con base en la ecuación canónica de la elipse con centro en el origen y vertical que ya obtuviste, puedes deducir lo siguiente: x 2 y 2
+
=1
b2 a2
1. Su gráfica es simétrica respecto al eje “x”, es decir, si el punto P1(x, y) satisface su ecuación, entonces el punto P2(x, –y) también; significa que los dos puntos están en la gráfica. 2. Su gráfica es simétrica respecto al eje “y”, es decir, si el punto P1(x, y) satisface su ecuación, entonces el punto P2(–x, y) también; significa que los dos puntos están en la gráfica. 3. Si su gráfica es simétrica respecto al eje “x” y respecto al eje “y”, entonces tiene simetría respecto al origen. 4. El dominio de la elipse son los valores que puede tomar la variable independiente “x” en la ecuación, para obtenerlo despeja “y” de la ecuación a
ordinaria de la elipse con centro en el origen que obtuviste, y = ± b2 − x2
b
2
2
2
2
por lo tanto b – x ≥ 0 de tal modo que b ≥ x y resulta –b ≤ x ≤ b. 5. El rango de la elipse son los valores que puede tomar la variable dependiente “y” en la ecuación, para obtenerlo despeja “x” de la ecuación ordinaria de la 2
x = ± ba a 2 − y por elipse con centro en el origen que obtuviste, lo 2
2
2
2
tanto a – y ≥ 0 de tal modo que a ≥ y y resulta –a ≤ y ≤ a. Podrás notar que según las dos condiciones anteriores, la elipse vertical con centro en el origen está acotada por ±b en el eje de las “x” y por ±a en el eje de las “y”. Práctica 43 x2 y 2
+
=1
Grafica la siguiente ecuación: 16
64
39 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Sesión 14 Los ttemas a revvisar el día d
de hoy son:: 2.2.1.1. Obtención de los elem
mentos de u
una elipse co
on centro een el origen a partir de su
u ecuación
2.2.1.2. Obtención de la ecuacción ordinarria de una eelipse con ceentro en el origen a paartir de sus elementos mínimos neecesarios 1.1. Obtencción de los e
elementos de una elip
pse a partir de su ecuación 2.2.1
Ejem
mplo: ¿Se p
podría comunicar un ssecreto a distancia enttre tanta geente en unaa galería com
mo la de laa imagen? Una galería com
mo la de la imagen an
nterior estáá diseñada con forma elíptica, ¿ccómo será posible com
municar seccretos aquí?? En dicha ssala se prod
duce un efeccto de refle
exión; es deecir, una peersona que se coloquee en uno de
e los focos d
de la elipse puede escu
uchar lo qu
ue dice la otra personaa ubicada en el otro fo
oco, sin quee en otros p
puntos de laa sala se esscuche lo qu
ue dice. ¿Súp
per interesaante no? Para P
constrruir una gaalería con tal forma los arquitectos requieren de laa ecuación de la form
ma construid
da, en estee caso de laa ecuación de la elipse y sobre todo t
de loss elementoss clave para producir tal efecto; es decir, de d los focoss. ¿Cómo see podrán ob
btener los eelementos d
de la elipse y en especiial los focoss? Las características de la gráfica y de la ecuaación de laa elipse deependen de los elem
mentos que la componen, por taal motivo es importaante conoceerlos y sab
ber la influeencia que tiene cada u
uno de ellos con su gráffica y ecuacción. Si reccuerdas los elementos que integraan a una eliipse son: 40 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
F y F’: focos
C: centro
L: eje focal
V y V’: vértices
(L y R) y (L’ y R’): puntos extremos
VV’: eje mayor = 2a
BB’: eje menor = 2b
LR y L’R’: lado recto
e: excentricidad
a> b
¿Será posible representar mediante coordenadas a los elementos que integran a una elipse?
Ya que la elipse que estás trabajando tiene centro en el origen, sus coordenadas son C(0, 0).
Elipses horizontales
Elipses verticales
• Como la distancia del centro a cualquiera de
los focos es la constante “c”, y por ser el eje
focal coincidente con el eje de las “x”, puedes
deducir que las coordenadas de los focos
corresponden a F(c, 0) y F’(–c, 0)
• Como la distancia del centro a cualquiera de los
focos es la constante “c”, y por ser el eje focal
coincidente con el eje de las “y”, puedes deducir
que las coordenadas de los focos corresponden
a F(0, c) y F’(0, –c)
• Al ser los vértices de la elipse los puntos
extremos del eje mayor, y la distancia del
origen a cada vértice está dada por la
constante “a”, además que éste se encuentra
sobre el eje de las “x”, entonces las
coordenadas de los vértices corresponden a
V(a, 0) y V’(–a, 0)
• Al ser los vértices de la elipse los puntos
extremos del eje mayor, y la distancia del
origen a cada vértice está dada por la
constante “a”, además que éste se encuentra
sobre el eje de las “y”, entonces las
coordenadas de los vértices corresponden a
V(0, a) y V’(0, –a)
• Si la distancia del centro a uno de los puntos
extremos del eje menor de la elipse es la
constante “b”, y estos se encuentran sobre el
eje de las “y”, entonces las coordenadas de los
puntos extremos del eje menor de la elipse
corresponden a B(0, b) y B’(0, –b)
• Si la distancia del centro a uno de los puntos
extremos del eje menor de la elipse es la
constante “b”, y estos se encuentran sobre el
eje de las “x”, entonces las coordenadas de los
puntos extremos del eje menor de la elipse
corresponden a B(b, 0) y B’(–b, 0)
¿Qué ocurre con la longitud del lado recto y sus puntos extremos?
41 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Elipses horizontales
Recuerda que el segmento de recta que es perpendicular al eje focal y pasa por el foco se llama lado
recto, ¿cuál es su longitud?
Para conocer su longitud es necesario conocer las coordenadas de sus puntos extremos, si uno de los
focos se encuentra en (±c, 0), sustituye “c” en la ecuación ordinaria de la elipse con centro en el origen .
x2 y2
+
=1
a2 b2
c2 y2
+
=1
a2 b2
y2
c2
= 1− 2
2
b
a
2
b (a 2 − c 2 )
y2 =
a2
Sustituye x = c:
Despeja “y”:
Simplifica:
Ordenada cuando x = c:
Por lo tanto las coordenadas que le corresponden a
los puntos extremos del lado recto de la elipse con
centro en el origen y horizontal son:
L(c, ba ) y R (c,− ba )
b2 2
(a − c 2 )
a2
b
y=±
a2 − c2
a
2
y=
Aplicas el teorema
de Pitágoras a2 =b2 + c2:
b 2
b
a
b2
y=±
a
y=±
Simplifica:
2
L' (−c, ba ) y R ' (−c,− ba )
2
2
¿Y qué pasa con la longitud del lado recto?
Para obtener la longitud del
lado recto se calcula la distancia
que existe entre sus puntos
extremos, si tomas cualesquiera
de los pares de puntos extremos
se obtiene el lado recto:
La longitud del eje mayor,
es la distancia de V(a, 0) a
V’(–a, 0) de la elipse:
La longitud del eje menor,
es la distancia de B(0, b) a
B’(0, –b) de la elipse:
d = ( x2 − x1 ) 2 + ( y2 − y1 ) 2
d = ( x2 − x1 ) 2 + ( y2 − y1 ) 2
VV ' = (−a − a) 2 + (0 − 0) 2
BB' = (0 − 0) 2 + (−b − b) 2
L(c, ba ) y R (c,− ba )
VV ' = (−2a) 2
BB' = (−2b) 2
d = ( x2 − x1 ) 2 + ( y2 − y1 ) 2
VV ' = 4a 2
BB' = 4b 2
VV ' = 2a
BB' = 2b
2
2
LR = (c − c) 2 + (− ba − ba ) 2
2
LR = (−2 ba ) 2
2
2
LR = 4
LR = 2
b4
a2
La excentricidad de la elipse es la razón de sus ejes determinados
por la longitud de su eje mayor y la distancia entre sus focos.
b2
a
e=
2c
c
⎯
⎯→e =
2a
a
Elipses Verticales De la misma manera como obtuviste las coordenadas del lado recto y su longitud para una elipse con centro en el origen y horizontal, lo puedes hacer para una elipse vertical. La diferencia es que los focos en una elipse vertical son F(0, c) y F’(0, –c). Entonces y = c ahora sustitúyelo en la ecuación. 42 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Sustituye
e y = c:
Desp
peja “x”:
Sim
mplifica:
x2 y2
+
=1
b2 a2
x2 c2
+
=1
b2 a2
x2
c2
=
−
1
b2
a2
2
b (a 2 − c 2 )
x2 =
a2
b2 2
(a − c 2 )
a2
b
x=±
a2 − c2
a
Simplifica:
Ordena
ada cuando y = c:
b 2
b
a
b2
y=±
a
y=±
Por lo tanto
t
las coordenadas que
e le correspond
den a
los pun
ntos extremos
s del lado rectto de la elipse
e con
centro en el origen y horizontal so
on:
x=
Aplicas el teorema
de Pitágoras
P
a2 =b
b 2 + c 2:
L( ba , c) y R(− ba , c)
2
L' ( ba ,−c) y R' (− ba ,−c)
2
¿Y qué pasa
a con la long
gitud del lado recto?
2
2
Prácctica 44 A paartir de la ecuación e
prroporcionad
da obtén lo
os elementtos que com
mponen a dicha elipse. 1 x 2 y 2
1)
+ 36 = 1
81
x 2 y 2
2 144
2)
+ 499 = 1
2.2.1
1.2. Obten
nción de la ecuación d
de una elipsse con centtro en el orrigen a parttir de sus e
elementos m
mínimos ne
ecesarios Ejem
mplo: Balone
es en los de
eportes n los deporttes de fútbol soccer y de fútbol aamericano se intercam
mbian Imaggina que en
los b
balones, perro las reglass de juego n
no. ¿Cómo resultará el partido paara cada juggador y parra los árbitrros? 43 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
¡Qué caos provocaría intercambiar los balones de fútbol en las canchas! Cada uno está diseñado para un uso específico, el balón de fútbol americano específicamente rompe el viento por su forma elíptica puntiaguda y es más fácil manejarlo con las manos, difícil sería hacerlo rodar con los pies. Como ves, la forma de cada objeto, fenómeno o situación tiene su utilidad particular, ya te imaginas lo que provocaría intercambiar balones, lo mismo causaría confundir las ecuaciones de la circunferencia con la de la elipse por ejemplo; es importante saber distinguirlas y conocer los elementos que componen a cada una y que las hace ser únicas. En esta sesión aprenderás algo nuevo y muy interesante, ya que has aprendido a identificar los elementos que componen a la elipse te bastará conocer los elementos mínimos necesarios para lograr determinar su ecuación ordinaria. ¿Cuáles son los elementos mínimos necesarios para determinar y graficar la ecuación ordinaria de la elipse? Ejemplo: Determina la ecuación de la elipse y el resto de los elementos que la componen si uno de sus vértices es V(0, –12) y su excentricidad es de e = 0.83. Además traza la gráfica de la ecuación. Solución: Para determinar la ecuación de la elipse los elementos necesarios son las constantes “a” y “b”. Para encontrarlas, primero analiza los elementos proporcionados arriba, V(0, –12) ¿qué característica observas? Exacto, como la abscisa de las coordenadas del vértice es igual a cero, entonces se deduce que el vértice se encuentra sobre el eje de las “y”, y que por lo tanto se trata de una elipse vertical. Por lo que la ecuación ordinaria que le corresponde a una elipse ordinaria es del tipo: x2 y2
+
=1
b2 a2
Además que las fórmulas de los vértices para una elipse vertical son de la forma: V(0, a) y V’(0, –a). Y como ya lo sabes, a > 0 entonces, al observar las coordenadas del vértice proporcionado V(0, –12) y las fórmulas de las coordenadas de los vértices deduces que a = 12. Solamente falta obtener la constante “b” para determinar la ecuación de la elipse. El segundo dato que proporcionan es la excentricidad, como ya sabes, la excentricidad es la misma razón para una elipse horizontal así como para una elipse vertical: e = c / a. Entonces, si e = 0.83, sustituyes este valor junto con el valor de la constante “a” en la fórmula de la excentricidad y obtienes lo siguiente: 0.83 = c / 12, por lo tanto c = 10. 44 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Muy bien, la constante “b” no la obtuviste directamente, pero sí lograste obtener la constante “c”, dato importante por medio del cual puedes obtener la constante “b”. ¿De qué manera? Recuerda que la relación entre las tres constantes “a”, “b” y “c”, se da a través del teorema de Pitágoras, determinadas de la siguiente manera: a2 = b2 + c2 , ahora, como la constante que buscas es la “b”, entonces despejas de la ecuación a “b” y te queda: b2 = a2 – c2, ahora sólo tienes que sustituir los valores de las constantes “a” y “c” en la ecuación despejada. De tal manera que te queda así: 2 b = a2 − c2 ⎯
⎯→ b 2 = (12) 2 − (10) 2 ⎯
⎯→ b 2 = 144 − 100 ⎯
⎯→ b 2 = 44 ⎯
⎯→ b = 44 ⎯
⎯→ b = 6.63
Ahora sí, ya tienes las constantes “a” y “b” para poder determinar la ecuación ordinaria de la elipse con centro en el origen y vertical, de tal manera que te queda de la siguiente manera: x 2 y 2
+
=1
44 144
La solución no termina aquí, puesto que además hay que encontrar el resto de los elementos que componen a la elipse, tienes ya una gran ventaja, conoces a las tres constantes “a” y “b” y “c”, las cuales son indispensables para obtenerlos. Entonces, si a = 12, b = 6.63 y c = 10, los elementos que componen a la elipse con centro en el origen son: F y F’: focos
V y V’: vértices
B y B’: puntos extremos eje menor
L y R: puntos extremos del LR
L’ y R’: puntos extremos del L’R’
VV’: longitud del eje mayor
BB’: longitud del eje menor
FF’: longitud entre los focos
LR y L’R’: longitud del lado recto
e: excentricidad
F(0, c) y F’(0, –c)
V(0, a) y V’(0, –a)
B(b, 0) y B(–b, 0)
F(0, 10) y F’(0, –10)
V(0, 12) y V’(0, –12)
B(6.63, 0) y B(–6.63, 0)
2a
2b
2c
L'(3.66,−10) y R'(−3.66,−10)
2(12) = 24
2(6.63) = 13.26
2(10) = 20
L(b2 a , c) y R(− b2 a , c)
L' (b2 a ,−c) y R' (− b2 a ,−c)
L(3.66,10) y R(−3.66,10)
LR = 7 . 33
LR = 2 ba
2
e = 0.83
e = c/a
Y su respectiva gráfica queda como sigue: 45 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Prácctica 45 Tablaa de billar e
elíptica Sabía
as que… En la
a tabla de biillar elíptica
a debes teneer cuidado d
de no da
añar el paño y evitar que la bola ccaiga al suelo. Adem
más de que los rebotes se realizan
n mantenien
ndo la igu
ualdad de á
ángulos de iincidencia yy de reflexión. Por las caracteríísticas geom
métricas de la elipse si la una bola passa por un fo
oco, también la trayeectoria de u
bola pasará porr el otro foco
o. Supó
ón que la tabla de billar elíptica dee la imagen
n tiene uno de sus foco
os en (80, 0) y su eje menor m
mide 60. A traavés de esttos datos determina d
la ecuación ordinaria de la elipse. 46 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Sesión 15 Los temas a revisar el día de hoy son: 2.3. Ecuación ordinaria de la elipse con centro fuera del origen 2.3.1. Elipse horizontal y vertical con centro fuera del origen 2.3.1.1. Obtención de los elementos de una elipse con centro fuera del origen a partir de su ecuación 2.3.1.2. Obtención de la ecuación ordinaria de una elipse con centro fuera del origen a partir de algunos de sus elementos mínimos necesarios 2.3. Ecuación ordinaria de la elipse con centro fuera del origen Estructuras del Vaticano ¿Alguna vez te has preguntado por qué la plaza San Pedro en Roma tiene tal forma? En los temas anteriores has aprendido a determinar la ecuación de una elipse con centro en el origen y su representación gráfica en sus distintas formas. No todas las elipses tienen su centro en el origen, cuando pasa eso, se habla de una elipse con centro fuera del origen. ¿Cómo ocurre esto? Por ejemplo, si se considera la Basílica de San Pedro como el origen o punto de referencia, ¿cuál será la ecuación ordinaria que le corresponda a la forma de la plaza de San Pedro en el Vaticano? La particularidad de la ecuación ordinaria de la elipse con centro fuera del origen es que se adjuntan como elementos clave de la misma a sus coordenadas, dadas por C(h, k), así como otros elementos que la componen, en el caso de la plaza de San Pedro, fue construida considerando dichos elementos. 47 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
2.3.1. Elipse horizontal y vertical con centro fuera del origen La cuestión ahora es: ¿qué ecuación representa a una elipse con centro fuera del origen? Elipses Horizontales Supón una elipse con centro fuera del origen como la
de la figura. Ya que es más práctico trabajar con una
elipse con centro en el origen como lo has estado
haciendo hasta el momento, entonces toma el centro de
la elipse como el origen, si haces eso y trazas unos ejes
perpendiculares ficticios sobre el centro, como los de la
figura, observarás que dichos ejes están recorridos
respecto al origen una distancia “h” sobre el eje de las
“x” y una distancia “k” sobre el eje de las “y”.
Recuerda que la traslación de los ejes coordenados
ocurre solamente si:
a) Los nuevos ejes son paralelos respectivamente a los
ejes originales.
b) Las coordenadas del nuevo origen sean (h, k)
respecto al sistema original.
c) Las coordenadas de cualquier punto P antes de la
traslación sean (x, y) y después de la misma sean
(x’, y’).
Si observas bien la gráfica, se puede determinar que la ecuación de trasformación queda como sigue: x = h + x’
y = k + y’
o
o
x’ = x – h
y’ = y – k
A partir de estas fórmulas se puede obtener la ecuación
ordinaria de una elipse con centro fuera del origen
C(h,k).
Si se considera una elipse como la de la figura, con eje
focal paralelo al eje de las “x” y con centro en C(h, k), al
hacer la traslación de ejes y al tomar el centro de la
elipse como el nuevo origen, su ecuación ordinaria
corresponde a ( x ' ) 2 ( y ' ) 2
a2
+
b2
=1
Ahora, como y’ = y – k
y
x’ = x – h, se sustituyen
en la ecuación anterior y obtienes:
( x − h)2 ( y − k )2
+
=1
a2
b2
Ecuación ordinaria de la elipse con centro fuera del
origen y eje focal paralelo al eje de las “x”
48 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Por ejemplo: 1) Obtén la ecuación ordinaria de la elipse cuya gráfica se representa en el siguiente plano cartesiano. A partir de la gráfica es posible identificar el centro de
la elipse, cuyas coordenadas son (4, –6), además la
distancia del centro al vértice es de 8 unidades y la
distancia del centro al foco es de 7 unidades.
Si observas la gráfica y su comportamiento, podrás
deducir que se trata de una elipse horizontal, cuya
ecuación ordinaria es del tipo:
( x − h) 2 ( y − k ) 2
+
=1
a2
b2
Ahora, una vez obtenido el centro deduces que h = 4
y que k = –6. Luego, a partir de las longitudes
anteriores, deduces que a = 8 y c = 7, para obtener el
valor de la constante “b” utilizas el teorema de
Pitágoras como sigue: b2 = a2 – c2, de lo que se
obtiene: b = 3.87.
Por lo tanto si h = 4, k = –6, a = 8 y b = 3.87,
entonces:
( x − 4) 2 ( y + 6) 2
64
+
15
=1
2) Traza la gráfica que le corresponde a la ecuación ordinaria de la elipse dada por: ( x − 5) 2 ( y + 7) 2
+
=1
9
64
La ecuación proporcionada corresponde al tipo de elipse vertical, por lo tanto la ecuación de base es: ( x − h)2 ( y − k )2
+
=1
b2
a2
A partir de ambas ecuaciones se igualan término a
término sus componentes:
x– h= x –5
y– k = y + 7
b2 = 9
a2 = 48
h= 5
k = –7
b= 3
a= 8
Por lo que el centro corresponde a C(5, –7) la
longitud del semieje mayor es de 8 unidades, y la
longitud del semieje menor es de 3 unidades.
Al graficar, a partir del centro se miden 3 unidades a
la derecha e izquierda y 8 unidades hacia arriba y
hacia abajo.
49 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Prácctica 46 Obtéén la ecuación ordinaria de la form
ma elíptica d
de la plaza d
de San Pedro a partir d
de los datos siguientess y considerra que se traata de una elipse horizzontal: La plaza
p
de San
n Pedro fue construida entre
e
1656 y
1667
7 con el fin de crear un
n sitio capazz de acoger
gran
ndes congreg
gaciones de fieles. En esta plaza el
Papa
a ofrece algunas celeb
braciones solemnes que
reún
nen a multitud
des como las audiencias
a
pú
úblicas.
Sus dimensiones
s alcanzan lo
os 320 metross de largo y
240 metros de ancho
a
y en los acontecim
mientos más
desttacados del Vaticano
V
la Plaza de Sa
an Pedro ha
llega
ado a alberga
ar más de 300.000 persona
as.
El arquitecto
a
Be
ernini utilizó para la estru
uctura de la
Plazza de San Pedro una arquitectura oblicua que
imprresiona como
o un único grupo
g
arquite
ectónico que
circu
unda la Basílic
ca.
Para
a resolver el ejercicio, su
upón que la distancia
d
del
centtro de la plaza
a de San Ped
dro a la Basílicca es de 200
metrros.
2.3.1
1.1 Obtención de los e
elementos d
de una elipsse con centtro fuera deel origen a p
partir de su
u ecuación S
Sistema Sola
ar ¿Te haas preguntaado alguna vvez cómo nos movemo
os respecto al sol? ¿Qué inffluencia ejeerce dicho m
movimiento
o sobre nueestro planeta Tierra? 50 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Durante más de 2,000 años se creyó que los planetas se movían en órbitas circulares alrededor de la Tierra, según el denominado modelo aristotélico; hasta que en el siglo XVII se demostró que en realidad las órbitas que describen los planetas son elípticas y que lo hacen en torno al Sol, en donde el Sol ocupa el lugar de uno de los focos. ¿Cómo se podría escribir la ecuación ordinaria de la órbita elíptica del Plantea Tierra? Es posible determinar los elementos de una elipse con centro fuera del origen si se conoce su ecuación ordinaria o la gráfica que le corresponde, si ésta se encuentra proporcionada de manera clara. De cualquiera de los dos datos que te proporcionen, lo primero que tienes que hacer es obtener los elementos de las coordenadas del centro y las longitudes del semieje mayor y menor, de las cuales dependen la mayoría de los elementos de la elipse. La distancia cambiante originada por la órbita elíptica de la Tierra con respecto al Sol da origen a las cuatro hermosas estaciones del año que se producen en la Tierra. Sabías que… Los vértices de la trayectoria elíptica por la que se desplaza la Tierra alrededor del Sol, se denomina Afelio, que corresponde a la posición más lejana del Sol, y Perihelio, que es el punto más cercano. Elipses Horizontales Ya has visto una elipse con centro C(h, k) y como hay una estrecha dependencia entre la ecuación y su gráfica; ahora, ¿cuáles son los elementos que componen a la elipse y que producen tales efectos? 51 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
En el caso de las elipses horizontales, cuyo centro es
C(h, k), el eje focal es paralelo al eje de las “x” y la
distancia del centro a cualquiera de los focos es “c”, por
lo tanto la distancia sobre el eje de las “x” desde el
origen hasta el foco es “h c”, y la distancia sobre el
eje de las “y” desde el origen hasta el foco es
solamente “k”, por lo que, las coordenadas de los
focos son:
F(h + c, k) y F’(h – c, k)
Respecto a los vértices, es semejante, la distancia del
centro a cada vértice es de “a”, ahora, la distancia
sobre el eje de las “x” del origen a cada vértice es “h
a” y la distancia sobre el eje de las “y” a partir del
origen es “k”. Por lo tanto las coordenadas de los
vértices de la elipse con C(h, k) son:
V( h + a, k) y V’(h – a, k)
De la misma manera procedes para obtener las
coordenadas del eje menor B(h, k + b) y B’(h, k – b).
Ahora se procede a obtener las coordenadas de los puntos extremos del lado recto junto con su longitud, para dicho cálculo se toman los elementos necesarios: uno de los focos (h + c, k) y la ecuación: ( x − h) 2 ( y − k ) 2
+
=1
a2
b2
el foco es considerado porque, si observas bien la gráfica, el lado recto pasa sobre éste, quiere decir que las coordenadas del lado recto toman el mismo valor de la abscisa. Entonces, para conocer sus puntos se sustituye x = c + h en la ecuación ordinaria de la elipse con centro fuera del origen. (c + h − h ) 2 ( y − k ) 2
+
=1
a2
b2
2
2
Simplificas: ( y − k ) = 1 − c
b2
a2
2
b (a 2 − c 2 )
2
Recuerda b2 = a2 – c2: ( y − k ) =
a2
2
b4
Aplicas la raíz cuadrada: ( y − k ) = a 2
Sustituyes x = c + h
Despejas “y”: y − k = ± ba ⎯
⎯→ y = ±
2
b2
+k
a
L(h + c, k + ba ) y R(h + c, k − ba )
2
2
L' (h − c, k + ba ) y R' (h − c, k − ba )
2
52 Universidad CNCI de México 2
¿Y qué pasa con la longitud del lado recto?
Taller de Matemáticas III Semana 3 y 4
Para obtener la longitud del
lado recto se calcula la distancia
que existe entre sus puntos
extremos, si tomas cualesquiera
de los pares de puntos extremos
se obtiene el Lado Recto:
La longitud del eje mayor, es la distancia de V(h+a, k) a
V’(h–a, k) de la elipse: d = ( x − x ) 2 + ( y − y ) 2
2
1
2
1
VV ' = [( h − a ) − ( h + a )] + ( k − k ) 2
2
VV ' = ( −2 a ) 2
VV ' = 4 a 2
L ( h + c, k + ) y
b2
a
VV ' = 2 a
R (h + c, k − ba )
2
La longitud del eje menor, es la distancia de B(h, k+b) a
B’(h, k–b) de la elipse:
d = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2
d = ( x2 − x1 ) 2 + ( y2 − y1 )2
BB ' =
LR = [(h + c) − (h + c)] + [(k − ba ) − (k + ba )]
2
LR = (−2 ba )
2
2
2
2
BB ' =
( − 2b ) 2
4b 2
BB ' = 2 b
4
2
( h − h ) 2 + [( k − b ) − ( k + b )] 2
BB ' =
LR = 4 ba2
LR = 2 ba
2
La excentricidad de la elipse es la razón de sus ejes determinados
por la longitud de su eje mayor y la distancia entre sus focos.
2c
c
e=
⎯
⎯→ e =
2a
a
Por ejemplo: 1) Para obtener los elementos de una elipse determinada su ecuación, se realizan los siguientes pasos: ( x − 16) 2 ( y + 7) 2
+
=1
Si la ecuación de la elipse es: 26 14 , lo primero que debes obtener son los elementos “h”, “k”, “a” y “b”, luego, a través de estos puedes obtener el resto de los elementos, ya que en su mayoría dependen de al menos uno de ellos. Entonces a través de la ecuación dada, deduces que se trata de una elipse horizontal, por lo tanto, si tomas la ecuación ordinaria de la elipse con centro fuera del origen: ( x − h) 2 ( y − k ) 2
( x − 16) 2 ( y + 7) 2
+
=
1
+
=1
y la ecuación proporcionada en este ejemplo: a2
b2
26
14
Igualas término a término cada uno de los elementos de la ecuación y obtienes: x – h = x – 16 h = 16 y – k = y + 7 k = –7 2
a = 26 a = 5.1 2
b = 14 b = 3.7 Muy bien, los elementos obtenidos son h = 16, k = –7, a = 5.1 y b = 3.7. Ahora, sólo falta obtener el valor de la constante “c”, recuerda que la relación que existe entre las constantes “a”, “b” y “c” es a través de la fórmula del teorema de Pitágoras a2 = b2 + c2, por lo tanto c2 = a2 – b2 de lo que resulta c = 3.46. 53 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
F y F’: focos
V y V’: vértices
B y B’: puntos extremos eje menor
L y R: puntos extremos del LR
L’ y R’: puntos extremos del L’R’
VV’: longitud del eje mayor
BB’: longitud del eje menor
FF’: longitud entre los focos
LR y L’R’: longitud del lado recto
e: excentricidad
F(h+c, k) y F’(h–c, k)
V(h+a, k) y V’(h–a, k)
B(h, k+b) y B(h, k–b)
L(h + c, k + b2 a) y R(h + c, k − b2 a)
L' (h − c, k + b2 a) y R' (h − c, k − b2 a)
2a
2b
2c
LR = 2
b2
a
e = c/a
Sólo queda sustituir en cada fórmula los
elementos obtenidos para obtener el resto.
F(19.46, –7) y F’(12.54, –7)
V(21.1, –7) y V’(10.9, –7)
B(16, –3.3) y B(16, –10.7)
h = 16, k = –7, a = 5.1, b = 3.7 y c = 3.46
L (19 .46, − 4.32 ) y R (19 .46, - 9.68)
L' (12.54, − 4.32) y R' (12.54, - 9.68)
2(5.1) = 10.2
2(3.7) = 7.4
2(3.46) = 6.92
LR = 5.4
e = c/a = 3.46/ 5.1 = 0.68
Elipses Verticales En el caso de las elipses verticales, cuyo centro es C(h, k),
el eje focal es paralelo al eje de las “y” y la distancia del
centro a cualquiera de los focos es “c”, por lo tanto la
distancia sobre el eje de las “y” desde el origen hasta el
foco es “k c”, y la distancia sobre el eje de las “x” desde
el origen hasta el foco es solamente “h”, por lo que, las
coordenadas de los focos son:
F(h, k+c) y F’(h, k – c).
Respecto a los vértices, la distancia del centro a cada
vértice es de “a”, ahora, la distancia sobre el eje de las “y”
del origen a cada vértice es “k a” y la distancia sobre el
eje de las “x” a partir del origen es “h”. Por lo tanto las
coordenadas de los vértices de la elipse con C(h, k) son:
V( h, k+a) y V’(h, k – a)
De la misma manera procedes para obtener las
coordenadas del eje menor B(h+b, k) y B’(h – b, k).
Ahora se procede a obtener las coordenadas de los puntos extremos del lado recto junto con su longitud, para dicho cálculo se toman los elementos necesarios: uno de los focos (h, k+c) y la ecuación: ( x − h) 2 ( y − k ) 2
+
=1
2
2
b
a
el foco es considerado porque, si observas bien la gráfica, el Lado recto pasa sobre éste, quiere decir que las coordenadas del lado recto toman el mismo valor de la abscisa. Entonces, para conocer sus puntos se sustituye y = k + c en la ecuación ordinaria de la elipse con centro fuera del origen. 54 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
( x − h) 2 (k + c − k ) 2
+
=1
b2
a2
2
2
Simplificas: ( x − h ) = 1 − c
2
b
a2
2
b (a 2 − c 2 )
2
Recuerda b2 = a2 – c2: ( x − h ) =
a2
4
2
b
Aplicas la raíz cuadrada: ( x − h ) = a 2
Sustituyes y = k+c
Despejas “y”: x − h = ± ba ⎯
⎯→ x = h ±
2
b2
a
L(h + ba , k + c) y R(h − ba , k + c)
2
2
L' (h + ba , k − c) y R' (h − ba , k − c)
2
2
¿Y qué pasa con la longitud del lado recto?
Para obtener la longitud del
lado recto se calcula la distancia
que existe entre sus puntos
extremos, si tomas cualesquiera
de los pares de puntos extremos
se obtiene el Lado Recto:
La longitud del eje mayor, es la distancia de V(h, k+a) a V’(h, k
– a) de la elipse:
d = ( x2 − x1 ) 2 + ( y 2 − y1 ) 2
VV ' = ( h − h ) 2 + [( k − a ) − ( k + a )]2
VV ' = ( −2 a ) 2
VV ' = 4 a 2
L(h +
b2
a
R(h −
2
, k + c) y
VV ' = 2 a
, k + c)
b
a
La longitud del eje menor, es la distancia de B(h+b, k) a B’(h–b, k)
de la elipse:
d = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2
d = ( x2 − x1 )2 + ( y2 − y1 )2
BB ' = [( h − b ) − ( h + b )] 2 + ( k − k ) 2
LR = [(h − ba ) − (h + ba )]2 [(k + c) − (k + c)]2 +
2
2
BB ' =
LR = (−2 ba )2
2
4
2
( − 2b ) 2
4b 2
BB ' = 2 b
LR = 4 ba2
LR = 2 ba
BB ' =
La excentricidad de la elipse es la razón de sus ejes determinados
por la longitud de su eje mayor y la distancia entre sus focos.
2c
c
e=
⎯
⎯→ e =
2a
a
Por ejemplo: 1) Para obtener los elementos de una elipse determinada su ecuación se realizan los siguientes pasos: ( x − 9) 2 ( y − 5) 2
+
=1
28 , lo primero que debes obtener son Si la ecuación de la elipse es: 10 los elementos “h”, “k”, “a” y “b”, luego, a través de estos puedes obtener el resto de los elementos, ya que en su mayoría dependen de al menos uno de ellos. Entonces a través de la ecuación dada deduces que se trata de una elipse vertical, por lo tanto, si tomas la ecuación ordinaria de la elipse con centro fuera del origen: ( x − h) 2 ( y − k ) 2
( x − 9) 2 ( y − 5) 2
+
=
1
+
=1
y la ecuación proporcionada en este ejemplo: b2
a2
10
28
Igualas término a término cada uno de los elementos de la ecuación y obtienes: x – h = x – 9 h = 9 y – k = y – 5 k = 5 b2 = 10 b = 3.16 a2 = 28 a = 5.3 55 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Muy bien, los elementos obtenidos son h = 9, k = 5, a = 5.3 y b = 3.16. Ahora, sólo falta obtener el valor de la constante “c”, recuerda que la relación que existe entre las constantes “a”, “b” y “c” es a través de la fórmula del teorema de Pitágoras a2 = b2 + c2, por lo tanto c2 = a2 – b2 de lo que resulta c = 4.2. F y F’: focos
V y V’: vértices
B y B’: puntos extremos eje menor
L y R: puntos extremos del LR
L’ y R’: puntos extremos del L’R’
VV’: longitud del eje mayor
BB’: longitud del eje menor
FF’: longitud entre los focos
LR y L’R’: longitud del lado recto
e: excentricidad
F(h, k+c) y F’(h, k – c)
V(h, k+a) y V’(h, k – a)
B(h+b, k) y B’(h – b, k)
L(h + b2 a , k + c) y R(h − b2 a , k + c)
L' (h + b2 a , k − c) y R' (h − b2 a, k − c)
2a
2b
2c
LR = 2
b2
a
e = c/a
F(9, 9.2) y F’(9, 0.8)
V(9, 10.3) y V’(9, –0.3)
B(12.16, 5) y B’(5.84, 5)
Sólo queda sustituir en cada fórmula los
elementos obtenidos para obtener el resto.
L (10 .9, 9 .2 ) y R ( 7 .1, 9 .2 )
L' (10.9, 0.8) y R' (7.1, 0.8)
h = 9, k = 5, a = 5.3, b = 3.16 y c = 4.2
2(5.3) = 10.6
2(3.2) = 6.4
2(4.2) = 8.4
LR = 3.8
e = c/a = 4.2/ 5.3 = 0.8
Una vez que se obtuvieron los elementos que componen a la elipse con centro fuera del origen tanto en su forma vertical como horizontal, se puede concluir que: Elementos:
Elipse Horizontal
F y F’: focos
F(h+c, k) y F’(h–c, k)
F(h, k+c) y F’(h, k – c)
V y V’: vértices
V(a+h, k) y V’(h–a, k)
V(h, k+a) y V’(h, k – a)
L: eje focal
Paralelo al eje de las “x”
Paralelo al eje de las “y”
B y B’: puntos extremos eje menor
B(h, k+b) y B(h, k–b)
L y R: puntos extremos del LR
L(h + c, k + b a) y R(h + c, k −b a)
L’ y R’: puntos extremos del L’R’
L' (h − c, k + b2 a) y R' (h − c, k − b2 a)
2
B(h+b, k) y B(h – b, k)
2
L(h + b2 a , k + c) y R(h − b2 a , k + c)
L' (h + b2 a , k − c) y R' (h − b2 a, k − c)
VV’: longitud del eje mayor
2a
2a
BB’: longitud del eje menor
2b
2b
FF’: longitud entre los focos
2c
LR y L’R’: longitud del lado recto
e: excentricidad
2c
LR = 2 ba
2
e = c/a
LR = 2 ba
2
e = c/a
56 Universidad CNCI de México Elipse Vertical
Taller de Matemáticas III Semana 3 y 4
2.3.1.2. Obtención de la ecuación ordinaria de la elipse con centro fuera del origen a partir de alguno de sus elementos mínimos necesarios Es posible determinar la ecuación ordinaria de una elipse con centro fuera del origen si se conocen al menos algunos de sus elementos mínimos; por ejemplo, si se conocen uno de sus focos, uno de sus vértices y el centro, los puntos extremos del lado recto, uno de sus focos y el centro, etc., y viceversa; puesto que los elementos mínimos necesarios se pueden obtener a partir de los datos que se proporcionan. ¿Cuáles son esos elementos mínimos necesarios? Los elementos mínimos necesarios para determinar la ecuación ordinaria de una elipse con centro fuera del origen son: los componentes del centro (h, k), y las constantes “a” y “b”. De cualquier dato que te proporcionen, lo primero que tienes que hacer es obtener los elementos mínimos necesarios y luego, a partir de estos, construir la ecuación ordinaria correspondiente de la elipse sustituyendo los valores básicos. Práctica 47 Obtén la ecuación ordinaria y grafica la elipse cuya longitud del eje menor es 16, uno de sus puntos extremos es L(4.4, 9) su centro está en (–2, 3) y su eje focal paralelo al eje de las “y”. 57 Universidad CNCI de México T
Taller de
e Matemááticas IIII Semana 3 y 4
Sesión 16 Los ttemas a revvisar el día d
de hoy son:: 2.4. Ecuaación generral de la elip
pse 2
2.4.1. Conve
ersión de la forma ordinaria de la ecuación de una elipse con centro fueraa del origen a su forma general 2
2.4.2. Conv
ersión de laa forma gen
neral de la ecuación de una elipse con centro fueraa del origen a su forma ordinaria
eneral de laa elipse 2.4. EEcuación ge
Ejem
mplo: Pétalo
os elípticos Obseerva las dos imágenes: ¿Te p
produce alggún efecto eel contemplarlas? ¿Algu
unos de esttos dos tipo
os de floress te atrae m
más que la o
otra, te has preguntado por qué?? q según Rudolf Arnheim las fo
ormas tieneen un deteerminado efecto e
Has de saber que ológico sobrre quien lass contemplaa, efecto qu
ue se derivaa de sus cualidades prropias psico
expreesivas. Segú
ún él la líneea horizontaal comunicaa estabilidaad, la vertical es símbo
olo de infinitud, la líneea recta siggnifica deciisión, fuerzza, estabilid
dad, mientrras que la curva indicca dinamism
mo, flexibilid
dad, el círcu
ulo comunica equilibriio y dominio y la elipse por su paarte, al conttar con dos vértices comunica inquietud e ineestabilidad.. ¿Será
á cierto tod
do eso? ¿Tú
ú qué dices?? Los pétalos del d
girasoll tienen forma f
elíp
ptica, ¿te comunicarron inquie
etud?, indep
pendientem
mente de lo que pudierran comuniccar. pueda repreesentar matemáticamente la form
ma del péta
alo del girassol? ¿Creees que se p
58 Universsidad CNCI dde México Taller de Matemáticas III Semana 3 y 4
Sabías que… Rudolf Arnheim fue un psicólogo y filósofo nacido en Berlín, Alemania en 1904. Realizó importantes contribuciones para la comprensión del arte visual y otros fenómenos estéticos. A través de la ecuación de una elipse en su forma ordinaria es posible representar matemáticamente la forma del pétalo del girasol; pero, ¿Cómo se puede representar la forma general de la ecuación de una elipse dada en su forma ordinaria? Recuerda que la ecuación de cualquier gráfica en su forma general es representada mediante la igualdad a cero, para lograr lo anterior en una ecuación ordinaria de la elipse, es necesario desarrollar los cuadrados de la misma y simplificar ordenando sus términos. Te has dado cuenta que al pasar de una ecuación a otra, se ejerce sobre la misma una transformación, a lo que se le conoce como conversión de una forma de la ecuación a otra, y esto se realiza en función del requerimiento de una o de la otra, según sea el caso. Precisamente ¿qué es lo que ocurre en tal conversión? 2.4.1. Conversión de la forma ordinaria de la ecuación de una elipse con centro fuera del origen a su forma general Para realizar la conversión mencionada anteriormente, se toman los dos casos posibles de la elipse y en paralelo se desarrollan hasta lograr el objetivo de obtener su conversión al tipo de forma general. Entonces, la forma ordinaria de la elipse: Horizontal
Vertical
Desarrolla los cuadrados
Iguala a cero
( x − h) 2 ( y − k ) 2
+
=1
a2
b2
b 2 x 2 − 2b 2 hx + b 2 h 2 + a 2 y 2 − 2 a 2 ky + a 2 k 2 = a 2 b 2
( x − h)2 ( y − k ) 2
+
=1
b2
a2
a 2 x 2 − 2 a 2 hx + a 2 h 2 + b 2 y 2 − 2b 2 ky + b 2 k 2 = a 2 b 2
b 2 x 2 − 2b 2 hx + a 2 y 2 − 2 a 2 ky + b 2 h 2 + a 2 k 2 − a 2 b 2 = 0
a 2 x 2 − 2 a 2 hx + b 2 y 2 − 2b 2 ky + a 2 h 2 + b 2 k 2 − a 2 b 2 = 0
Ejemplo: Supón que la ecuación ordinaria de la forma del pétalo del girasol del primer ejemplo es la siguiente: ( x − 3) 2 ( y − 1) 2
+
=1
9
1
¿Cuál es la ecuación general de la forma elíptica del pétalo? 59 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Multiplica todo por 25:
Desarrolla los cuadrados:
Iguala a cero:
Simplifica:
(x −3)2 ( y −1)2
+
=1
9
1
(x −3)2 + 9( y −1)2 = 9
x2 −6x + 9 +9y2 −18y +9 −9 = 0
x2 −6x + 9y2 −18y + 9 = 0
Práctica 48 Dada la ecuación de la elipse con centro fuera del origen en su forma ordinaria conviértela a su forma general y traza su gráfica. ( x + 4) 2 ( y − 9) 2
+
=1
8
12
2.4.2. Conversión de la forma general de la ecuación de una elipse con centro fuera del origen a su forma ordinaria ¿Alguna vez has escuchado hablar del Litotriptor? ¿Sabes para qué sirve y por qué tiene forma elíptica? Recuerda que los segmentos de recta que unen los focos de una elipse con un punto cualquiera ubicado en ella, forman ángulos iguales con la recta tangente a la elipse que pasa por dicho punto. 60 Universidad CNCI de México Taller de Matemáticas III Semana 3 y 4
Debido a esta propiedad, si se coloca una fuente de luz o sonido en uno de los focos de un reflector, cuya superficie haya sido generada por la revolución de una elipse alrededor de su eje mayor, todas las ondas reflejadas pasarán por el otro foco. Dicha propiedad se usa en medicina con el aparato llamado litotriptor para deshacer cálculos renales, este aparato utiliza un reflector de ultrasonido. Para usarlo se coloca el reflector de tal modo que la fuente sonora se ubique en uno de los focos y el cálculo renal en otro; las ondas se concentran en el tumor para hacerlo vibrar y posteriormente desintegrarlo. ¡Qué tal! Vale la pena conocer la elipse y sus propiedades ¿no?, pues como en este caso hay muchos otros por los cuales hay que estar agradecidos de su estudio. Ya aprendiste a convertir la ecuación de una elipse con centro fuera del origen de su forma ordinaria a su forma general, ahora, ¿qué ocurre si tienes el caso contrario?, ¿Cómo conviertes la ecuación de una elipse con centro fuera del origen de su forma general a su forma ordinaria? Para determinar una forma abreviada de resolver cualquier tipo de conversión de la ecuación de la elipse con centro fuera del origen de su forma ordinaria a su forma general y viceversa, es necesario considerar los dos posibles casos de elipses que se pueden presentar, elipses horizontales y elipses verticales. Forma General
Horizontal
b 2 x 2 + a 2 y 2 − 2b 2 hx − 2 a 2 ky + b 2 h 2 + a 2 k 2 − a 2b 2 = 0
Ahora, al hacer A=b2 B=a2, D=–2b2h, E=–2a2k
y F = b2h2+a2k2 – a2b2, la ecuación resulta:
Ahora, al hacer A=a2 B=b2, D=–2a2h, E=–2b2k
y F = a2h2+b2k2 – a2b2, la ecuación resulta:
Ax2 + By2 + Dx + Ey + F = 0
Ax2 + By2 + Dx + Ey + F = 0
Forma general de la ecuación de la elipse
horizontal
Forma general de la ecuación de la elipse
vertical
61 Universidad CNCI de México Vertical
a 2 x 2 + b 2 y 2 − 2a 2 hx − 2b 2 ky + a 2 h 2 + b 2 k 2 − a 2b 2 = 0
Taller de Matemáticas III Semana 3 y 4
De lo obtenido anteriormente se concluye lo siguiente: Ecuación
Elipse Horizontal
Elipse Vertical
Constantes A, B, D, E y F
Ax2 + By 2 + Dx + Ey + F = 0
A=b2
B=a2
D= –2b2h
E= –2a2k
F = b2h2+a2k2–a2b2
Ax2 + By 2 + Dx + Ey + F = 0
A=a2
B=b2
D= –2a2h
E= –2b2k
F = a2h2+b2k2 – a2b2
Para identificar si la elipse es horizontal o vertical, puedes usar el siguiente criterio: • Si A > B, entonces se trata de una elipse vertical. • Si A < B, entonces se trata de una elipse horizontal. Práctica 49 Convierte la ecuación de la elipse a su forma ordinaria, cuya forma general está dada por: 9x2 + 16y2 – 36x + 96y + 36 = 0. Convierte las siguientes ecuaciones de elipses con centro fuera del origen proporcionadas en su forma general a su forma ordinaria y traza su gráfica. 20x2 + 18y2 – 280x + 180y + 1070 = 0 62 Universidad CNCI de México