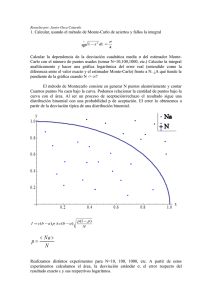
2. Repetir el problema anterior con el método de muestreo

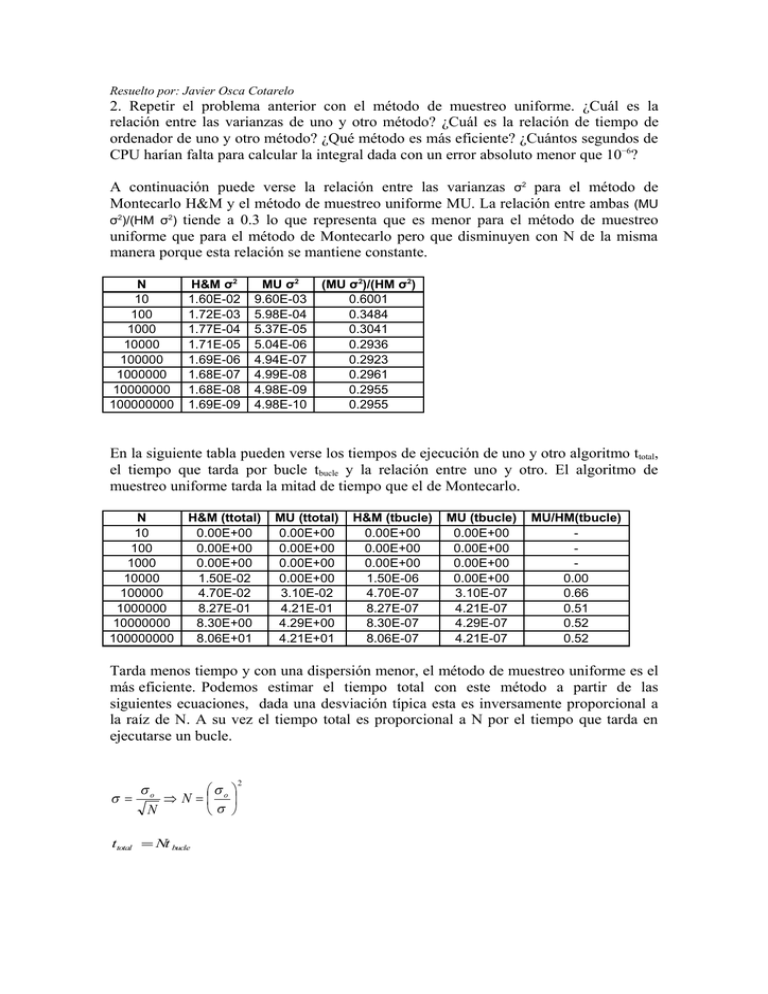
Resuelto por: Javier Osca Cotarelo
2. Repetir el problema anterior con el método de muestreo uniforme. ¿Cuál es la
relación entre las varianzas de uno y otro método? ¿Cuál es la relación de tiempo de
ordenador de uno y otro método? ¿Qué método es más eficiente? ¿Cuántos segundos de
CPU harían falta para calcular la integral dada con un error absoluto menor que 10−6?
A continuación puede verse la relación entre las varianzas σ2 para el método de
Montecarlo H&M y el método de muestreo uniforme MU. La relación entre ambas (MU
σ2)/(HM σ2) tiende a 0.3 lo que representa que es menor para el método de muestreo
uniforme que para el método de Montecarlo pero que disminuyen con N de la misma
manera porque esta relación se mantiene constante.
N
10
100
1000
10000
100000
1000000
10000000
100000000
H&M σ2
1.60E-02
1.72E-03
1.77E-04
1.71E-05
1.69E-06
1.68E-07
1.68E-08
1.69E-09
MU σ2
9.60E-03
5.98E-04
5.37E-05
5.04E-06
4.94E-07
4.99E-08
4.98E-09
4.98E-10
(MU σ2)/(HM σ2)
0.6001
0.3484
0.3041
0.2936
0.2923
0.2961
0.2955
0.2955
En la siguiente tabla pueden verse los tiempos de ejecución de uno y otro algoritmo ttotal,
el tiempo que tarda por bucle tbucle y la relación entre uno y otro. El algoritmo de
muestreo uniforme tarda la mitad de tiempo que el de Montecarlo.
N
10
100
1000
10000
100000
1000000
10000000
100000000
H&M (ttotal)
0.00E+00
0.00E+00
0.00E+00
1.50E-02
4.70E-02
8.27E-01
8.30E+00
8.06E+01
MU (ttotal)
0.00E+00
0.00E+00
0.00E+00
0.00E+00
3.10E-02
4.21E-01
4.29E+00
4.21E+01
H&M (tbucle)
0.00E+00
0.00E+00
0.00E+00
1.50E-06
4.70E-07
8.27E-07
8.30E-07
8.06E-07
MU (tbucle)
0.00E+00
0.00E+00
0.00E+00
0.00E+00
3.10E-07
4.21E-07
4.29E-07
4.21E-07
MU/HM(tbucle)
0.00
0.66
0.51
0.52
0.52
Tarda menos tiempo y con una dispersión menor, el método de muestreo uniforme es el
más eficiente. Podemos estimar el tiempo total con este método a partir de las
siguientes ecuaciones, dada una desviación típica esta es inversamente proporcional a
la raíz de N. A su vez el tiempo total es proporcional a N por el tiempo que tarda en
ejecutarse un bucle.
σ
σ 
σ = o ⇒ N = o
N
σ 
ttotal = Nt bucle
2
La constante σo la podemos calcular a partir de la regresión lineal de la desviación
estándar frente a la inversa de la raíz cuadrada de N. Con este resultado y las anteriores
ecuaciones se calcula el tiempo total.
Método de muestreo uniforme σvsN
1.20E-01
-1/2
y = 0.3081x - 0.0012
R2 = 0.9955
1.00E-01
σ
8.00E-02
6.00E-02
4.00E-02
2.00E-02
0.00E+00
0
0.05
0.1
0.15
0.2
0.25
N-1/2
σ
1.00E-06
N
9.49E+10
ttotal(s)
39953
ttotal(h)
11.1
Código del algoritmo de muestreo uniforme.
program ejer2
!Librerias
use util
implicit none
!Parametros
integer,parameter :: nexperiment=8;
real (kind=double),parameter :: a=0,b=1;
!Funciones
real (kind=double) :: f
!indices
integer :: i,j
!variables
integer :: na,nloops
real :: total,etime,starttime(2),endtime(2)
real (kind=double) :: u,v,p,Area,Error,muestra
nloops=1;
do i=1,nexperiment
total=etime(starttime)
Area=0.0_double;
Error=0.0_double;
nloops=nloops*10;
do j=1,nloops
call random_number(u)
muestra=f(a+(b-a)*u)
Area=Area+muestra
Error=Error+muestra*muestra
end do
Area=Area/dble(nloops)
Error=sqrt((Error/dble(nloops)-Area*Area)/dble(nloops))
Area=(b-a)*Area
Error=(b-a)*Error
total=etime(endtime)
write(*,*), nloops,Area,Error,endtime(1)-starttime(1)
end do
end program ejer2
0.3
0.35
function f(x)
!Librerias.
use util
implicit none
!in/out
real (kind=double) :: x,f
f=sqrt(1-(x*x))
end function
Código del algoritmo de Montecarlo (mismo que el ejercicio nº 1)
program ejer1
!Librerias
use util
implicit none
!Parametros
integer,parameter :: nexperiment=8;
real (kind=double),parameter :: a=0,b=1,c=1;
!Funciones
real (kind=double) :: f
!indices
integer :: i,j
!variables
integer :: na,nloops
real :: total,etime,starttime(2),endtime(2)
real (kind=double) :: u,v,p,Area,Error
nloops=1;
do i=1,nexperiment
total=etime(starttime)
na=0.0_double;
nloops=nloops*10;
do j=1,nloops
call random_number(u)
call random_number(v)
if ( f(a+(b-a)*u)> c*v ) na=na+1
end do
p=dble(na)/dble(nloops)
Area=c*(b-a)*p
Error=sqrt(p*(1-p)/dble(nloops))*c*(b-a)
total=etime(endtime)
write(*,*), nloops,Area,Error,endtime(1)-starttime(1)
end do
end program ejer1
function f(x)
!Librerias.
use util
implicit none
!in/out
real (kind=double) :: x,f
f=sqrt(1-(x*x))
end function f