α - SMIE

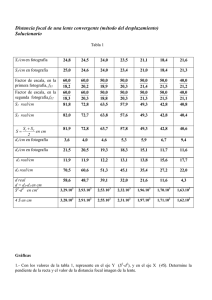
ESTIMACIÓN DE DAÑO POR FATIGA EN PLATAFORMAS MARINAS DE ACERO
ALEJANDRO RUIZ SIBAJA, SERGIO OLLER MARTÍNEZ, ALEX H. BARBAT
Universitat Politècnica de Catalunya
c/Gran Capitán s/n
Barcelona 08034, España
tel: 34.93.401.56.69
fax: 34.93.401.10.48
email: [email protected]
RESUMEN
En este trabajo se presenta un nuevo modelo constitutivo para estimar el crecimiento de daño por fatiga en
plataformas marinas fijas. El modelo se basa en un tratamiento de la mecánica del daño continuo (MDC). Se muestra
la teoría necesaria para evaluar la degradación en la resistencia del material por efecto de la fatiga ocasionada por
carga cíclica. La técnica permite reproducir la evolución en el tiempo de la respuesta no lineal de la estructura. Se
incluye una aplicación numérica en dos dimensiones para una plataforma fija sometida a carga de oleaje. Se
presentan las curvas de daño y deterioro de la resistencia.
SUMMARY
In this paper a new constitutive model to obtain the damage growth due to fatigue in fixed offshore platforms is
presented. The model is based on a continuum damage mechanics (CDM) treatment. It shows the basic theory to
evaluate deterioration in material strength by fatigue effects caused by cyclic loading. This formulation permits to
reproduce temporal evolution of non-linear structural response. Finally examples are included for a fixed offshore
platform subjected to wave load. It shows damage history and strentgh deterioration curves.
INTRODUCCIÓN
Más de un cuarto del petróleo de la Tierra y más del 15% del gas natural se encuentran bajo el mar. La extracción de
hidrocarburos desde instalaciones costa afuera ha incrementado las demandas sobre la integridad estructural de las
plataformas marinas de acero que se utilizan para tal fin. Particularmente, en el entorno marino, se ha encontrado
que es necesario diseñar las estructuras contra un posible daño por fatiga. La naturaleza del daño por fatiga que
ocurre en las plataformas marinas de acero tiene su origen, principalmente, en el crecimiento de grietas de fatiga.
Esto se debe a que las conexiones tubulares son regiones de alta concentración de esfuerzos y altos esfuerzos
residuales. Además en estas zonas es común la presencia de defectos en la soldadura (Byers et al, 1997; Dover,
1991). El estudio de la fatiga requiere el comprender que este no es un fenómeno asociado al concepto clásico de
plasticidad y/o daño y que la rotura se produce bajo cargas que están aún en el intervalo elástico del comportamiento
del material. Concretamente tiene lugar una pérdida de resistencia en función del número de ciclos que induce a un
rebase posterior de la resistencia máxima, provocando así un problema de plasticidad y/o daño secundario.
Las roturas de fatiga son especialmente peligrosas porque no suelen presentar indicios de fallo inminente, más bien,
este se produce de modo repentino y sin observar deformaciones plásticas de conjunto. Se trata pues de roturas
frágiles que se caracterizan por presentar zonas bien diferenciadas: una de textura lisa con muestra de rotura dúctil y
otra de textura gruesa rugosa más brillante que es donde se localiza la rotura final al rebasar la resistencia máxima,
disminuida por el fenómeno de fatiga (Dowling, 1999; Forrest, 1962). La estimación de la vida por fatiga es difícil
ya que la práctica de la ingeniería convencional se basa en curvas esfuerzo-log(N ) y alguna regla de acumulación de
daño. Por lo general esta aproximación se traduce en el uso de la regla de Palmgren-Miner. Esta regla proporciona
información sobre el número de ciclos hasta la falla, Nf, para una amplitud de esfuerzos determinada. Un defecto
conocido de este método es el hecho observado de que el daño por fatiga no siempre crece en forma lineal con el
número de ciclos aplicados.
En su lugar, la parte principal de la vida en servicio puede agotarse sin ninguna manifestación de reducción en la
resistencia. De forma que el daño se vuelve evidente y crece en forma visible sólo hacia el final del tiempo de vida.
Una segunda objeción ocurre cuando se tienen cargas cíclicas con amplitudes variables. En tal situación la regla de
Palmgren-Miner pronostica el mismo valor de daño acumulado sin tomar en cuenta el orden de aparición de las
diferentes amplitudes, hecho que es contrario a las observaciones experimentales (Committee, 1982; Kutt y Bieniek,
1988).
La aproximación alternativa se basa en el crecimiento de la grieta y recurre a la mecánica de la fractura. Esta técnica
modela la situación fí sica de forma más cercana, y su principal objetivo es encontrar la resistencia residual en un
cuerpo, en función del tamaño de una grieta existente. Para esto se basa en una medida de la energía liberada, lo que
conduce al desarrollo de un criterio de fractura para determinar el crecimiento de la grieta en cuestión. De esto se
deduce que este método está limitado a aquellos casos en los cuales se conozcan la orientación y el tamaño de una
grieta existente. Además la teoría no está bien desarrollada para el caso tridimensional y carece de una base de datos
suficiente que confirme los resultados de pruebas controladas con las condiciones de campo (Dover, 1991; Jubran y
Coffer, 1991).
De lo anterior se desprende la necesidad de desarrollar una aproximación totalmente nueva para la predicción del
comportamiento ante fatiga de un material virgen. Idealmente, esta aproximación debe ser completamente
independiente de la dimensión límite de la grieta y de los parámetros empíricos que se utilizan para pronosticar el
crecimiento de grietas microscópicas. Esta descripción hace pensar que la estructura teórica mecánica de las
formulaciones inelásticas continuas, como la plasticidad y el daño, es apropiada para el tratamiento del daño por
fatiga. En el apartado siguiente se propone un modelo para el estimar el crecimiento de daño por fatiga mediante la
mecánica del daño continuo (MDC), tal modelo se basa en las propiedades termodinámicas de acumulación de daño
con lo cual se abate el grado de empirismo presente en las metodologías descritas en este apartado. Además, el
modelo propuesto permite introducir el fenómeno de pérdida de resistencia de los metales producido por los efectos
combinados de fatiga, plasticidad y daño.
MODELO DE DAÑO POR FATIGA PROPUESTO
En un trabajo anterior se presentaron las teorías inelásticas de plasticidad y daño que resuelven el problema del
comportamiento del material una vez que se abandona el régimen elástico (Ruiz Sibaja et al, 1999). Ambas teorías
permiten estudiar el cambio de resistencia que sufre un punto del sólido por efectos inelásticos, pero no son sensibles
al efecto de las cargas cíclicas. No obstante su formulación básica permite incorporar los fenómenos de pérdida de
resistencia por efectos instantáneos, acoplados con los efectos cíclicos. Cada punto del sólido, sigue una ley
constitutiva elasto-plástica con daño, es decir plasticidad con degradación de rigidez (Lubliner et al, 1989; Luccioni
et al, 1996; Oller, 1991). Así, la evolución de los esfuerzos depende de la variable libre de deformación del
componente y del grupo de variables internas plásticas y de daño. Esta teoría trata en conjunto los fenómenos de
acumulación de deformación permanente mediante la teoría de plasticidad y de degradación de rigidez mediante la
teoría de daño.
Modelo de daño plástico
El modelo de daño plástico se basa en la hipótesis de la aditividad entre la parte elástica Ψ e y la parte plástica Ψ p .
Esto ocurre en la configuración referencial para un cierto campo de entropía η, una temperatura θ y una deformación
elástica de Green Eeij = Eij – Epij - Eθij, tal que estas dos últimas actúan como variables libres del problema (Green y
Naghdi, 1964; Lubliner et al, 1989; Luccioni et al, 1996; Oller, 1991)
(
)
(
Ψ = Ψ e Eije , d ,θ + Ψ p α p ,θ
[
]
)
( 1)


ρ2
e 0
0
p
p
(
)

Ψ = 1− d
E ij C ijkl E kl + Ψ α , θ  − θ η
0
2
m


(
)
( 2)
Considerando la segunda ley de la termodinámica, desigualdad de Clasius-Duhem (Lubliner, 1972; Lubliner, 1990;
Malvern, 1969)
Ξ=
. p
S ij : E ij
0
( 3)
.
− Ψ−
m
J
θ m0
q i ∇θ ≥ 0
resulta la siguiente defi nición de esfuerzo y entropía
S ij = m 0
( )
∂Ψ e
∂Ψ
0
e
E kl
; η=
= (1 − d )ρ 2 Cijkl
∂θ
∂Eije
( 4)
donde m 0 es la densidad del material, E eij, Eij, E pij, E θij, son los tensores de deformación elástico, total, plástico y
térmico, respectivamente, d ini ≤ d ≤ 1 es la variable de daño mecánica, C 0 ijkl el tensor constitutivo del material en
estado virgen, S ij el tensor de esfuerzos para un punto y ρ 2 la variable de regradación del material.
Función de discontinuidad plástica F y potencial plástico G
Se definen funciones homogéneas de primer grado en los esfuerzos, de la forma
(
) (
(
)
)
F S ij , α p ,θ = f S ij ,θ − K S ij , α p ,θ = 0
(
) ( )
G S ij , α p = g S ij = cte .
( 5)
( 6)
donde f ( Sij, θ ) y g ( Sij) son funciones de esfuerzo y potencial equivalente, respectivamente, K(Sij, α, θ ) es el
umbral de resistencia y α p son las variables internas del modelo plástico (Lubliner et al, 1989; Luccioni et al, 1996;
Oller, 1991).
Evolución del f lujo plástico y de las variables internas
Se adopta la forma clásica para la definición de las variables internas. Esto es
. p
E ij
. p
α
.
=λ
(
∂G
∂S ij
( 7)
) ( )
.
.
∂G
= λ H S ij , α p = λ h p
ij ∂S
ij
( 8)
en donde λ es el factor de consistencia plástica y H una función escalar de argumentos tensoriales (Lubliner et al,
1989; Luccioni et al, 1996; Oller, 1991).
Función de discontinuidad de daño
Se defi nen, al igual que en plasticidad, funciones homogéneas de primer grado en los esfuerzos. Esto es
(
)
(
)
(
)
G D S ij , d ,θ = Sσ S ij ,θ − f c S ij , d ,θ = 0
( 9)
donde Sσ (Sij, θ ) es la función de daño en el espacio dañado, fc ( Sij, d, θ ) es el umbral de resistencia de daño y d es la
variable interna del modelo de daño (Lubliner et al, 1989; Luccioni et al, 1996; Oller, 1991).
Regla de evolución de las variables internas de daño
En general se escribe:
.
.
d mec = µ
∂G D
∂ Sσ
( 10)
donde µ es el factor de consistencia de daño y G D la función umbral de daño (Lubliner et al, 1989; Luccioni et al,
1996; Oller, 1991).
Ley constitutiva tangente
A partir de las condiciones de consistencia, resulta la variación temporal del esfuerzo, que puede escribirse en la
siguiente forma
.
e
S ij = Cijkl
.
p
E kl − Cijkl
. p
.θ
s
E kl − Cijkl E kl
( 11)
donde
s
0
C ijkl
= (1 − d ) C ijkl
1 ∂G D
e
s
Cijkl
= Cijkl
−
(1 − d ) ∂Sσ
 ∂S
 σ
0
 ∂S rs
( 12)
 0 
C  S
 rsij  kl


( 13)
( )
2
p
s
Cijkl
= Cijkl
− h p S kl
ij
ρ
( 14)
 ∂F

∂F
e


−
C mnkl
∂S mn ∂S mn


θ
s
Cijkl = Cijkl −
∂F
∂G
∂F
∂
G
p
−
hr )tu
+
C mnrs
(
∂S tu ∂S mn
∂S rs
∂α rp
p
Cijrs
∂G
∂S rs
( 15)
De esta forma se ha descrito la ley constitutiva tangente para un modelo de plasticidad con daño afectado por
temperatura. A continuación se describe la forma en que se incluye el fenómeno de fatiga dentro de esta estructura
teórica.
Formulación del modelo de daño por fatiga
Se define sólo el caso de fatiga isotérmica sin regradación. El tratamiento que se presenta difiere considerablemente
de aquel introducido por Chaboche (1974), pues aquí no se define la evolución de la variable interna de daño en
función del número de ciclos. En su lugar, se formula una función que modifica el umbral de discontinuidad
(fluencia plástica o daño), y a través de esta se provoca una evolución implícita de las variables internas de los
modelos inelásticos de plasticidad o daño. Consiste en introducir el efecto del número de ciclos en la función de
discontinuidad plástica y de daño, exigiendo el cumplimiento simultáneo de las mismas
(
)
( )
(
)
f S ij


 − K S ij , α p = 0
f S ij − K S ij , α p ⋅ f red (N , S med , R ) = 0 ⇒ 

 f red (N , S med , R ) 
( )
( 16)
(
(
)
)
f ′ S ij , N , R − K S ij , α p = 0
( 17)
( )
Sσ S ij


( 18)
 − f c S ij , d = 0
Sσ S ij − f c S ij , d ⋅ f red (N , S med , R ) = 0 ⇒ 

 f red (N , S med , R ) 
( )
(
)
(
)
(
(
)
)
Sσ′ S ij , N , R − f c S ij , d = 0
( 19)
La función fred ( N, Smed, R ) hace sensible los modelos de plasticidad y daño al fenómeno de fatiga, N es el número de
ciclos actual, R = Smin / Smax es el factor de reversión de los esfuerzos y Smed el esfuerzo medio (Figura 1).
S
Smax
Smed
t
Smin
T
Figura 1 – Evolución del esfuerzo en un punto
De esta forma, la ley constitutiva tangente para un problema de fatiga isotérmico queda escrita como
.
.
t
S ij = Cijkl
E kl
( 20)
donde
∂G ∂f ′ e
C
∂S rs ∂Smn mnkl
t
e
C ijkl = C ijkl −
∂F
∂G  ∂f ′  s
∂G
 C mnrs
−
h
+
p tu
p
∂S tu  ∂S mn 
∂S rs
∂α
s
C ijrs
( )
en esta expresión
( 21)
1  ∂Sσ′
e
s

Cijkl
= Cijkl
−
(1 − d )  ∂S rs0
 0 
C  S
 rsij  kl


( 22)
También se define la variable de deterioro global en función de la disipación normalizada, esto es
( ) (
) ( ) ( ( ))
.
 r S ij
1 − r S ij 
q = Ξm f S ij = Ξ p + Ξd 
+

gc
 gf

( 23)
en donde r( Sij) adopta el valor de 1 para tracción pura y de 0 para compresión pura, Ξ p , Ξ d son las disipaciones
producidas por el problema plástico y de daño respectivamente, g f , g c son los límites máximos de energía que puede
disipar un punto al fi nal del proceso de deterioro total. Debe observarse que esta definición obliga al cumplimiento
simultáneo de las condiciones de consistencia plástica y de daño. También se puede ver que el proceso mecánico que
se ha descrito anteriormente permite acoplar fenómenos dependientes o no del tiempo y del número de ciclos. Por lo
tanto el camino para alcanzar una determinada resistencia, resulta de la composición de otros dos definidos en
espacios independientes (Figura 2).
Sσ= Sσ(K,fc,fred)
ruta 1
ruta 2
N
q=q(αp,d)
Figura 2 – Distintas rutas para converger a un punto del espacio de esfuerzo equivalente
En la Figura 2 también se observa esquemáticamente la evolución de la variable de daño global, luego de ocurrir un
número de ciclos y haber entrado en plasticidad o daño.
Curvas de Wöhler
Las curvas S - N, o curvas de Wöhler (Figura 3), se obtienen experimentalmente tras someter a distintas probetas a
estados cíclicos de carga, generalmente de tracción-compresión, flexión y torsión. Posteriormente se representa en
ordenadas los valores de esfuerzo (usualmente el máximo) y en abscisas el número de ciclos necesarios para romper
la pieza. De esta manera se establece la relación de pérdida de resistencia en función del número de ciclos de carga.
Por regla general, después de varios millones de ciclos de carga la curva S – N se vuelve prácticamente horizontal
(Partón, 1990). La definición de la carga se realiza mediante su período T, su relación de amplitudes ∆S = Smax – Smin
y su relación de reversión R = Smin / Smax.
Las curvas de Wöhler permiten definir la función fred(N, Smed, R) de disminución de resistencia por fatiga. Como se
ve en la definición básica de estas curvas, puede ocurrir una disminución de resistencia del material, aún para puntos
del sólido sometidos a cargas por debajo del límite elástico. Se denomina NF al número de ciclos que necesita un
punto del sólido sometido a un esfuerzo Sf, para alcanzar el umbral del comportamiento elástico.
Smax
S0f
Sf
Slim(R=-1)
Nlim≈107
NF
Figura 3 – Curva de Wöhler y resistencia máxima en un punto
Particularización de la función de reducción fred(N, Smed, R) para el acero
A continuación se presentan las expresiones que describen la evolución de la resistencia del material para el acero.
En el estado virgen, es decir, para N = 0 ciclos, la resistencia es Smax = S 0 f, y a su vez esta corresponde al umbral de
resistencia instantáneo para un problema no cíclico. Se propone que cuando N → ∞ se alcanza el límite de resistencia
a la fatiga
R 
 1
S lim = S of 
+

 1.26 3.3 
( 24)
a través de una evolución de la resistencia máxima de la forma
(
S max = S f0 exp − A (log N )α
)
( 25)
Imponiendo Slim = Smax (N=Nlim=107 ) , se obtiene el límite de resistencia a la fatiga
(
)
 1
R 
 = S f0 exp − A (log N )α → A = −
S lim = S f0 
+
1.26 3.3 
 1
R 

ln 
+
1.26 3.3 
( 26)
7α
Con el objeto de ajustar las curvas de Wöhler se adopta α = 4( 22R ), tal como se describe en (Suero y Oller, 1998).
De esta manera, se definen las curvas de resistencia límite a la fatiga para el acero a partir de sus características
(Suero y Oller, 1998), de lo cual resultan las siguientes aproximaciones
S f (N = 0) = S 0f
(
)
S f (N < N F ) = S f0 exp − B 1 (log N ) β = S f0 f red (N , S med , R ) > S max ( N )
( 27)
( 28)
(
S f (N = N F ) = S f0 exp − A (log N )α
(
)
( 29)
)
S f (N F ≤ N ≤ N lim ) = S f = S f0 exp − B 1 (log N ) β = S f0 f red (N , S med , R )
(
)
S f (N ≥ N lim ) = S f = S f0 exp − B 2 (log N ) β = S f0 f red (N , S med , R )
( 30)
( 31)
en donde
B1 = −
 S apli
ln  0
 Sf




(log N F ) β
, B2 = −
S

lim 

ln  0 
 Sf 
( 32)
( 7) β
1/ α
 

 
  ln  S apli  
 0  
 
 Sf 
− 1 
2R

⋅ C , N F = log 7
β = 42
  ln  1 + R  
  1.26 3.3  

 
( )







( 33)
en estas expresiones Sapli representa el nivel de esfuerzo aplicado en el punto de análisis.
APLICACIÓN NUMÉRICA
La estructura considerada para el ejemplo de aplicación es del tipo que se acostumbre para operaciones de
perforación en aguas someras (Figura 4). El sistema cuenta con elementos tubulares estructurados en forma de torre.
Figura 4 – Modelo de plataforma marina
La plataforma tiene una altura de 42.50 m y está desplantada en una profundidad de agua de 37.50 m. Los elementos
tubulares constituyen las dos piernas y un sistema de arriostramientos en “K”. El diámetro exterior de las piernas, los
elementos de arriostramiento y los espesores correspondientes se indican en la Tabla 1.
Tabla 1 – Diámetros y espesores de los elementos tubo del modelo estructural
Elemento
Arriostramiento
Arriostramiento
Arriostramiento
Arriostramiento
Arriostramiento
Arriostramiento
Pierna
Pierna
Pierna
Pierna
D (cm)
60.960
60.960
66.040
66.040
76.200
76.200
154.940
154.940
154.940
154.940
tw (cm)
1.270
2.540
1.270
1.588
1.588
2.220
3.490
1.588
3.175
1.905
2
5
4
4
r
D
3
3
2
2
tw
1
secciones de integración
2
1
j
1
×
i
×
elemento cuadrático de 3
nodos
k
Figura 5 – Elemento tubo cuadrático de 3 nodos en el plano
La estructura se discretizó en 42 elementos viga-tubo, con tres grados de libertad por nodo (dos desplazamientos
lineales y giro), y dos elementos masa con dos grados de libertad (dos desplazamientos lineales), lo que hace un total
de 44 elementos (Figura 4). Los elementos viga-tubo de tres nodos constan de dos puntos de integración de Gauss.
Cada uno de estos tiene cinco secciones de integración (Figura 5).
Las masas concentradas reproducen los pesos de la cubierta más el del equipo industrial. El modelo dinámico de la
torre cuenta con 73 nodos. La longitud característica promedio de los elementos viga-tubo resultó de 377.00 cm. El
estado del material se revisó en los puntos de integración de Gauss de cada barra (ABAQUS, 1999). Se consideró
que la base del sistema está empotrada en el lecho marino.
Se usaron las siguientes propiedades físicas del material: Es = 2.1 × 106 kg/cm2, σ 0 s = 2500.00 kg/cm2, νs = 0.29, ρs
= 7.5 × 10-5 kg/cm3. El peso total estimado para los elementos de la torre fue de 7.4556 × 106 kg, sin incluir pilotes y
conductores. Este peso se concentró en la cubierta superior de la estructura, debido a que las fuerzas de oleaje son
más pronunciadas en esa zona de la plataforma. Estas fuerzas se modelaron considerando la teoría de oleaje de
amplitudes pequeñas y aceptando que el flujo es irrotacional y no viscoso. De manera que puede describirse según la
ecuación de Morison (Brebbia y Walker, 1979; Dean y Dalrymple, 1998):
F = Cm ρ
.
.
π D 2 ..
1
U x + CD ρ U x U x
4
2
( 34)
Evidentemente esta es una aproximación conservadora ya que en realidad, deberá considerarse la interacción entre la
ola y la estructura cuando la velocidad y la aceleración del movimiento estructural sean del mismo orden de
magnitud que el de las partículas de agua.
Sin embargo, teniendo en mente que el principal objetivo de este trabajo es el desarrollo de un procedimiento de
análisis de fatiga, esta aproximación de la configuración de la carga sirve como una ilustración. Se consideró la
acción de un oleaje con altura de ola H = 100 cm, longitud L = 3903.23 cm y período T = 5.0 s, y coeficientes de
Morison: Cm = 1.05 y CD = 1.20.
El análisis se hizo para un tiempo total de 25 años, aplicando la carga durante un período de tiempo suficiente para
que se desarrollen los esfuerzos máximos y se estabilice la respuesta del sistema. A partir de ese momento se
continúa con la acción de los máximos de la carga, de forma que se reproducen los efectos de la misma durante el
intervalo de análisis.
Solamente son necesarios los extremos de los procesos de carga de oleaje, debido a que el curso de acción entre
extremos consecutivos no se considera importante (Agerskov y Pedersen, 1992). Esto hace posible el uso de un
algoritmo rápido de cálculo de fatiga basado en la mecánica del daño continuo. En la Figura 6, se muestra la
respuesta en desplazamientos para los primeros 120 s de carga de oleaje. Esta condición de carga origina la
degradación en los arriostramientos del nivel más inferior de la plataforma (elementos 29 y 30).
desplazamientos en la cubierta superior
1.50E+01
desplazamientos (cm)
1.00E+01
5.00E+00
0.00E+00
0.00E+00
2.00E+01
4.00E+01
6.00E+01
8.00E+01
1.00E+02
-5.00E+00
-1.00E+01
respuesta dinámica
-1.50E+01
tiempo (s)
Figura 6 – Desplazamientos en la cubierta superior
1.20E+02
daño en el elemento 29
3.50E-01
sección 1
sección 2
sección 3
3.00E-01
daño
2.50E-01
2.00E-01
1.50E-01
1.00E-01
5.00E-02
0.00E+00
0.00E+00
1.00E+08
2.00E+08
3.00E+08
4.00E+08
5.00E+08
6.00E+08
7.00E+08
8.00E+08
tiempo (s)
Figura 7 – Evolución del daño en el elemento 29
En la Figura 7, se muestra la evolución del daño para el elemento 29 del modelo estructural. Se advierte que el
proceso de deterioro tiene lugar en las secciones 1, 2 y 3 del segundo punto de integración del elemento. Esta
situación indica presencia de degradación en más del 50% de las secciones de la pared del tubo en esa zona. La
sección más solicitada es la 1, ya que en esta el proceso de deterioro comienza a los 1696 días y alcanza un valor de
0.31 a los 25 años de aplicación de la carga.
disminución de la resistencia en el elemento 29
3000
resistencia (kg/cm2)
2500
2000
1500
1000
sección 1
sección 2
sección 3
500
0
0.00E+0 1.00E+0 2.00E+0 3.00E+0 4.00E+0 5.00E+0 6.00E+0 7.00E+0 8.00E+0
0
8
8
8
8
8
8
8
8
tiempo (s)
Figura 8 – Disminución de la resistencia en el elemento 29
En las secciones 2 y 3, el daño se presenta a los 3331 y 5826 días, con valores de daño, respectivamente, de 0.25 y
0.13 al final de la vida útil de la estructura. En la Figura 8 se presenta la disminución de la resistencia en las
secciones 1, 2 y 3. Se observa que la reducción alcanza valores de 1724, 1870 y 2185 kg/cm2 en cada una de estas
secciones. Estas disminuciones representan el 69%, 75% y 87% de la resistencia original.
daño en el elemento 30
1.40E-01
1.20E-01
sección 1
sección 2
daño
1.00E-01
8.00E-02
6.00E-02
4.00E-02
2.00E-02
0.00E+00
0.00E+0 1.00E+0 2.00E+0 3.00E+0 4.00E+0 5.00E+0 6.00E+0 7.00E+0 8.00E+0
0
8
8
8
8
8
8
8
8
tiempo (s)
Figura 9 – Evolución del daño en el elemento 30
En las secciones 1 y 2 del elemento 30, también se desarrolla deterioro por acción de la carga cíclica de oleaje. El
daño en estas secciones, comienza a los 4507 y 7526 días, respectivamente (Figura 9). Al término de 25 años, la
degradación alcanza valores de 0.12 y 0.06. La resistencia en las secciones 1 y 2 desciende hasta valores de 2192 y
2362 kg/cm2, esto es, 88% y 94% de la resistencia inicial (Figura 10).
disminución en la resistencia del elemento 30
2550
resistencia (kg/cm2)
2500
2450
2400
2350
2300
sección 1
sección 2
2250
2200
2150
0.00E+ 8.00E+ 1.60E+ 2.40E+ 3.20E+ 4.00E+ 4.80E+ 5.60E+ 6.40E+ 7.20E+ 8.00E+
00
07
08
08
08
08
08
08
08
08
08
tiempo (s)
Figura 10 – Disminución de la resistencia en el elemento 30
CONCLUSIONES
A partir de los resultados obtenidos, se destaca la capacidad del modelo propuesto para proporcionar información
interesante, acerca del comportamiento de las componentes estructurales de la plataforma de ejemplo. Permite el
cálculo de la degradación de los miembros, bajo la acción de los numerosos ciclos de carga de oleaje. Al mismo
tiempo, registra la concentración del daño debido a la redistribución de los esfuerzos en los elementos estructurales.
Los resultados presentados proporcionan una base para determinar la región de comportamiento inelástico de la
plataforma. Una vez que se detecta la zona de la estructura afectada por la fatiga, puede calcularse la vida restante de
los elementos afectados. Así, el modelo propuesto también puede incorporarse en una estrategia de inspección y
reparación de la plataforma marina.
Para la estructura estudiada se observa que la zona de deterioro se presenta en los arriostramientos en “K”, en el nivel
más inferior de la plataforma. Esto ocurre debido a que el colapso progresivo de esta estructura es gobernado por el
colapso de sus componentes más próximas al fondo del mar. Esta situación controla la capacidad resistente de la
plataforma marina ante la acción del oleaje.
En síntesis, la plataforma marina se comporta de manera semejante a una viga empotrada cuya sección más débil está
próxima al sitio de empotre. Este es el comportamiento que se observa con frecuencia en plataformas marinas fijas
(Sudati y Prates, 1997).
RECONOCIMIENTO
Esta publicación es parte de un trabajo de investigación que se está desarrollando con apoyo de una beca crédito del
Consejo Nacional de Ciencia y Tecnología.
REFERENCIAS
ABAQUS Version 5.8-16 (1999), “Theory Manual”, Hibbitt, Karlson and Sorensen, Inc.
Agerskov, H. and Pedersen, N. T. (1992), “Fatigue Life of Offshore Steel Structures Under Stochastic Loading”,
Journal of Structural Engineering ASCE, 118(8):2101-2117.
Brebbia, C. E. and Walker, S. (1979), “Dynamic Analysis of Offshore Structures”, Newness-Butterworths.
Byers, W. G., Marley, M. J., Mohammadi, J., Nielsen, R. J., and Sarkani, S. (1997), “Fatigue Reliability
Reassessment Applications: State of the Art Paper”, Journal of Structural Engineering ASCE, 123(3):277-285.
Chaboche, J. L. (1974), “Une Loi Différentielle d’Endommagement de Fatigue Avec Acumulation Non Linéaire”,
Revue Française de Mécanique, 50-51.
Committee on Fatigue and Fracture Reliability of the Committee on Structural Safety and Reliability of the
Structural Division (1982), “Fatigue Reliability: Variable Amplitude Loading”, Journal of Structural Engineering
ASCE, 108(ST1):47-69.
Dean, R. G. and Dalrymple, R. A. (1998), “Water Mechanics for Engineers and Scientist”, Prentice-Hall.
Dover, W. D. (1991), “Chapter 15: Fatigue Behaviour of Offshore Structures”, Volume II of “Offshore Structures”,
Krieger Publishing Co.
Dowling, N. E. (1999), “Mechanical Behavior of Materials”, Prentice-Hall.
Forrest, P. G. (1972), “Fatiga de los Metales”, Ediciones Urmo.
Green, A. and Naghdi, P. (1964), “A General Theory of an Elastic-Plastic Continuum”, Arch. Rational Mech.
Anal., 18:19-281.
Jubran, J. S. and Cofer, W. F. (1991), “Ultimate Strength Analysis of Structural Components Using the
Continuum Damage Mechanics Approach”, Computers & Structures, 39(6):741-752.
Kutt, T. V. and Bieniek, M. P. (1988), “Cumulative Damage and Fatigue Life Prediction”, AIAA Journal,
26(2):213-219.
Lubliner, J. (1972), “On Thermodynamics Foundations of Non-Linear Solid Mechanics”, Int. Journal Non-Linear
Mechanics, 7:237-254.
Lubliner, J., Oliver, J., Oller, S. and Oñate, E. (1989), “A Plastic-Damage Model for Concrete”, Int. J. Solids and
Struct., 25(3):299-326.
Lubliner, J. (1990), “Plasticity Theory”, Macmillan Publishing.
Luccioni, B., Oller, S. and Danesi, R. (1996), “Coupled Plastic-Damage Model”, Comp. Methods Appl. Mech.
Engng., 129:81-89.
Malvern, L. (1969), “Introduction to the Mechanics of a Continuous Medium”, Prentice-Hall.
Oller, S. (1991), “Modelización Numérica de Materiales Friccionales”, Monografía CIMNE, 3.
Partón, V. Z. (1990), “Mecánica de la Destrucción. De la Teoría a la Práctica”, Mir.
Ruiz Sibaja, A., Oller, S. y Barbat, A. H. (1999), “Estimación de Daño por Carga Cíclica en Plataformas Marinas
de Acero”, XII Congreso Nacional de Ingeniería Sísmica, Morelia, Michoacán.
Sudati Sagrilo, L. V. e Prates de Lima, E. C. (1997), “Um Procedimento Simplificado para Análise de
Confiabilidade Estrutural de Plataformas Marítimas Fixas”, Revista Internacional de Métodos Numéricos para
Cálculo y Diseño en Ingeniería, 13(2):149-163.
Suero, A. y Oller, S. (1998), “Tratamiento del Fenómeno de Fatiga Mediante la Mecánica de Medios Continuos”,
Monografía CIMNE, 45.