Mercados a futuro - U

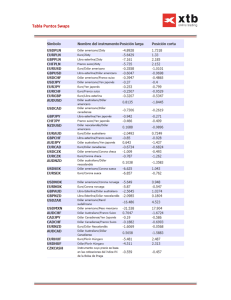
Derivados Lineales
Gabriel Cuevas R.
Historia y evolución de los mercados



Trueque: no existen transacciones monetarias y los
productos se intercambian directamente en el mismo
momento.
Cash markets: Intercambio de bienes mediante un
medio de pago. Exigen la presencia física de los
productos.
Spot markets: no es necesaria la presencia física de
los productos.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward markets





Las transacciones se efectúan a través de contratos
para un producto específico que estipulan la entrega
del producto en una fecha futura predeterminada.
El pago coincide con la fecha de entrega del producto.
Los mercados forward permitieron cubrir los riesgos
de cambio en los precios inherente al tiempo que
separa la producción de la venta.
Los contratos no son estandarizados, son hechos a la
medida.
Esta basado en la confianza entre las partes, porque
puede generarse un fuerte incentivo a no cumplir.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward markets
Operaciones forward:
 Consisten en operaciones a futuro entre dos partes,
pero que no requieren de un mercado organizado
(over-the-counter OTC).
 Lo anterior hace que sean flexibles, porque no están
limitadas por las normas que rigen un mercado a
futuro.
 Tiene dos fases:
1. Se celebra el contrato. Se fija precio, cantidad, calidad, fecha y
lugar de entrega.
2. Se realiza la entrega del producto y el pago.

En una operación forward existe separación temporal
entre ambas fases.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward markets
Operaciones forward:
 Una de las partes toma una posición larga (long
position):
–

La otra parte (contraparte) toma una posición corta
(short position):
–


Acuerda comprar el underlying (subyacente) en una cierta fecha
futura por un cierto precio.
Acuerda vender el underlying en la misma fecha por el mismo
precio.
La ganancia de una parte implica la pérdida de la
contraparte.
Los contratos sobre moneda extranjera son muy
comunes (Forward Foreign Exchange).
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward markets
Operaciones forward:
 Tradition Closing Run 17/05/2012:
CLP/USD SWAP OBS ( LOCAL PRICES)
TENOR


Días
BID
MID
OFFER
7
0,48
0,53
0,58
14
1,02
1,07
1,12
1 meses
35
2,60
2,65
2,70
2 meses
64
4,55
4,65
4,75
3 meses
96
6,50
6,60
6,70
4 meses
127
8,05
8,15
8,25
5 meses
155
9,35
9,45
9,55
6 meses
188
10,40
10,50
10,60
9 meses
280
14,25
14,35
14,45
12 meses
368
18,25
18,50
18,75
18 meses
553
27,25
27,75
28,25
24 meses
733
36,00
36,50
37,00
Bid: el mercado está dispuesto a comprar.
Offer: el mercado está dispuesto a vender.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward markets
Ejemplo 1:
 Un procesador intermedio debe entregar una oferta
en una licitación. Para no correr riesgo, puede fijar el
precio de la materia prima a través de un forward.
 En el caso de mercados competitivos, los
procesadores operan con bajos márgenes. Si el
costo de la materia prima es importante, una pequeña
variación en su precio puede eliminar su utilidad.
 Si fija el precio de la materia prima con un forward
¿qué pasa si no gana la licitación?
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Tipo de cambio Forward
Disponer hoy de US$100:
Invertir a un plazo d y tasa r* recibiendo:
d 

*
100  1  r 

360 

Cambiar a pesos hoy (S CLP/USD) e invertir a tasa r plazo
d recibiendo:
d 

100  S  1  r 

360 

IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Tipo de cambio Forward
Si contrato hoy una tasa de cambio Forward F para un
plazo d, para evitar arbitraje entonces,
d
d
100  (1  r 
)  F  100  S  (1  r 
)
360
360
d
(1  r 
)
360
F  S
d
*
(1  r 
)
360
*
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward Foreign Exchange


Ejemplo 2:
Nos ofrecen comprarnos en 1 año más, 1 millón de
dólares en 530 millones de pesos (short position).
US$-1.000.000
¿Aceptamos?
0
1
$530.000.000
Si las tasas a 1 año son:
rCLP = 6.0% y rUSD = 5,0%
y además el tipo de cambio spot es 530, entonces
VP  
IN4302
1,0  530
530

 MM $  4,8
(1  5%)
(1  6%)
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward Foreign Exchange


Ejemplo 3:
Contrato Forward de US$1.000 a 60 días con un tipo
de cambio fijado en F=27,0 USD/UF.
NF
VP 
(1  rUSD )
N: Nominal en USD
d: Días
rUSD: Tasa d días en USD
VP 
1.000  27,0
(1  5,5%)
IN4302
60
360

d
360

N S
(1  rUF )
d
360
F: Tipo Cambio Futuro
S: Tipo cambio Spot
rUF: Tasa d días en UF
1.000  26,230
(1  4,5%)
60
360
 UF 5,54
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward markets
Ejemplo 4:
 Suponga que el precio Spot del oro es US$300 por
onza y la tasa libre de riesgo a 1 año es 5%. ¿Cuál
debería ser el precio forward del oro?
 Caso 1:
–

Precio Forward es de US$340 por onza.
Caso 2:
–
Precio Forward es de US$300 por onza.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Mercados a futuro




Los mercados forward mantenían como característica
esencial el hecho de ser mercados donde se
efectuaban exclusivamente transacciones físicas.
Lo anterior comenzó a limitar el crecimiento de los
mercados en la medida que para efectuar una
transacción es necesario que coincidan las
necesidades de compradores y vendedores en el
tiempo y espacio.
La solución a este problema fue la evolución desde
los contratos forward a los contratos futuros.
La diferencia más importante es que no se transa un
producto específico sino contratos futuros.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Mercados a futuro
Contratos a futuro:
 Son compromisos para recibir o entregar una
cantidad estándar de un bien, en una determinada
fecha y de acuerdo a ciertos términos y condiciones
reglamentadas por el organismo central de
administración de la bolsa, a un precio que se
establece en el presente y en el lugar físico fijado para
la realización de estas transacciones.
 No hay intercambio de bienes ni de dinero en el
momento de tomar el compromiso.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Mercados a futuro
Contratos a futuro:
 Tienen como objetivo controlar el riesgo precio. No
hay interés en la entrega física.
 Tiene dos fases:
1. Contratación del futuro (ej. Venta)
2. Contratación contraria (compra)

La contratación contraria (compra del contrato
futuro, posición larga) cancela la posición inicial en el
mercado (venta de contrato futuro, posición corta).
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Diferencias entre futuros y forwards
Futuros
 Son papeles
 Se transan en bolsa
 Son estandarizados
 Son más líquidos
 Menores costos
 Requieren márgenes
 Son marked-to-market
 Poseen mayores
garantías
IN4302
Forwards
 Involucran una
transacción física
 Son más flexibles
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Contratos futuros
Financieros:
 Tasas de interés
 Tipos de cambio
 Bonos
 Índices
IN4302
Commodities:
 Metales
 Petróleo
 Maíz
 Soya
 Harina
 Azúcar
 Café
 Ganado vivo
 etc.
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Aspectos legales y operatoria
Básicamente intervienen tres tipos de personas u
organizaciones:



El cliente
El broker
La Cámara de Compensación
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Tipos de clientes
Especuladores:
 Son aquellos que participan en estos mercados
asumiendo los riesgos asociados a la variación de
precios, con la esperanza de obtener una ganancia
Hedgers:
 Tienen por objetivo minimizar el riesgo de sus
operaciones de compra o venta a ser realizadas en
fechas futuras
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Cámara de compensación de
Mercado Futuro


Es el organismo de la bolsa que actúa como
contraparte del comprador y del vendedor, y que
garantiza el cumplimiento de los contratos.
Se encarga de saldar diariamente todos los contratos
abiertos
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Mecanismos de seguridad




Cámara de compensación
Márgenes
Seguimiento de mercado
Límites a las fluctuaciones diarias de precio
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ejemplo: Cobertura (Hedge)
En junio de un año determinado, un productor de trigo sabe
que obtendrá su cosecha en noviembre, y quiere asegurar el
precio que obtendrá por la venta.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ejemplo: Cobertura perfecta
JUNIO
NOVIEMBRE
RESULTADO
BOLSA
FISICO
VENDE FUTURO
10.000 QQ
10.000 QQ
F(J/N) = 6,35 US$/QQ
P(J) = 6,15 US$/QQ
VALOR = US$ 63.500
VALOR = US$ 61.500
INVERSION = 0
BASE = P(J)-F(J/N) = -0,20
COMPRA FUTURO
VENDE
10.000 QQ
10.000 QQ
F(N/N) = 5,00 US$/QQ
P(N) = 5,00 US$/QQ
VALOR = US$ 50.000
VALOR = US$ 50.000
INVERSION = 0
BASE = P(N)-F(N/N) = 0,00
+13.500
-11.500
DIFERENCIA EN LA BASE = +0,20
RESULTADO FINAL = +2.000
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ejemplo: Se mantiene la base
JUNIO
OCTUBRE
BOLSA
FISICO
VENDE FUTURO
10.000 QQ
10.000 QQ
F(J/N) = 6,35 US$/QQ
P(J) = 6,15 US$/QQ
VALOR = US$ 63.500
VALOR = US$ 61.500
INVERSION = 0
BASE = P(J)-F(J/N) = -0,20
COMPRA FUTURO
VENDE
10.000 QQ
10.000 QQ
F(O/N) = 5,50 US$/QQ
P(O) = 5,30 US$/QQ
VALOR = US$ 55.000
VALOR = US$ 53.000
INVERSION = 0
BASE = P(O)-F(O/N) = -0,20
RESULTADO
+8.500
-8.500
DIFERENCIA EN LA BASE = 0,00
RESULTADO FINAL = 0
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ejemplo: Riesgo en la base
JUNIO
OCTUBRE
RESULTADO
BOLSA
FISICO
VENDE FUTURO
10.000 QQ
10.000 QQ
F(J/N) = 6,35 US$/QQ
P(J) = 6,15 US$/QQ
VALOR = US$ 63.500
VALOR = US$ 61.500
INVERSION = 0
BASE = P(J)-F(J/N) = -0,20
COMPRA FUTURO
VENDE
10.000 QQ
10.000 QQ
F(O/N) = 5,50 US$/QQ
P(O) = 5,20 US$/QQ
VALOR = US$ 55.000
VALOR = US$ 52.000
INVERSION = 0
BASE = P(O)-F(O/N) = -0,30
+8.500
-9.500
DIFERENCIA EN LA BASE = -0,10
RESULTADO FINAL = -1.000
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ejemplo: Bolsas de Futuros



http://www.lme.co.uk/
http://www.cbot.com/
http://www.nymex.com/index.aspx
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
¿Por qué existen los mercados de futuros si
podríamos usar sólo forwards?

Contratos forward tienen riesgo de no pago.
– La bolsa (clearing house) elimina los riesgos de la contraparte garantizando los pagos.
– La bolsa se protege a si misma demandando márgenes y ajustes diarios.
– Ejemplo: Supongamos que el 14 de Junio una persona toma una posición larga de 100
onzas a través de un contrato futuro que vence el 1 de Julio. El valor futuro actual es de
US$450/onza.
14-Jun
15-Jun
16-Jun
17-Jun
20-Jun
21-Jun
22-Jun
23-Jun
24-Jun
27-Jun
28-Jun
29-Jun
30-Jun
01-Jul
Precio
Futuro
450
449
455
450
452
449
445
440
445
450
460
465
470
475
Cambio Valor
Futuros
0
-100
600
-500
200
-300
-400
-500
500
500
1,000
500
500
500
Margen
Inicial
0
1,900
2,500
1,500
2,200
1,700
1,300
1,500
2,500
2,500
3,000
2,500
2,500
2,500
Retiro de
Dinero
-2,000
0
500
-500
200
0
-700
-500
500
500
1,000
500
500
2,500
Margen
Final
2,000
1,900
2,000
2,000
2,000
1,700
2,000
2,000
2,000
2,000
2,000
2,000
2,000
0
Onzas=100; Margen inicial=US$2,000; Margen Mantención=1,500
¿Podría un contrato forward eliminar el riesgo de la contraparte a través de ajustes diarios?
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Protección usando futuros

Una empresa que sabe que venderá un activo en el futuro
puede protegerse tomando una “short position” (short
hedge).
– Si el precio del activo baja, la empresa pierde en la venta del activo pero
gana en su contrato futuro (y viceversa)

Sin embargo, existe numerosas razones por las cuales el
desarrollo de resguardos usando contratos futuros no
funciona a la perfección en la práctica, por ejemplo:
– El activo a ser protegido no es exactamente el mismo que el activo en el
contrato futuro.
– Existe incertidumbre con la fecha exacta de venta.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
¿Por qué las empresas se protegen usando
forwards o futuros?

El valor presente neto de una transacción de protección en
un mercado de futuros activos es igual a cero (o
ligeramente negativo).

Si hedging es irrelevante en mercados perfectos, debemos
entender como los mercados reales difieren de los
mercados perfectos para encontrar la respuesta:
– Impuestos: pérdida de beneficios tributarios
– Bancarrota o financial distress:
• Caer en bancarrota tiene importantes costos de transacción.
• Si una empresa está cerca de bancarrota, tendrá incentivos para especular
usando futuros.
– Los tenedores de acciones no tienen nada que perder. Los que están asumiendo el
riesgo son los tenedores de la deuda.
– Información imperfecta sobre la administración de la empresa.
– Falta de diversificación.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Forward Rate Agreemtents
Definición:
 Es un contrato donde dos instituciones (contrapartes)
acuerdan hoy que una cierta tasa se aplicará a un
cierto monto nocional, por un cierto período de
tiempo, y a partir de una fecha específica.
Ejemplo: FRA 3x6
 Hoy 01/06/12 acordamos que recibo tasa UF + 7,5%
sobre un nocional de 1.000 UF entre el 01/09/12 y el
01/12/12. En el fondo fijo hoy la tasa de un depósito a
plazo de 90 días, que comienza en 90 días más.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Mecánica de un FRA
El contrato de seguro de tasas puede representarse con el
siguiente gráfico
tiempo
01/06/12
01/09/12
92 días
IN4302
01/12/12
91 días
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Flujos de caja de un FRA
De acuerdo al ejemplo, entregamos a la contraparte 1.000UF el
01/09/12 y cobraríamos el 01/12/12 el monto final del depósito
91 

1.000  1  7,5% 
  1.018,96
360 

-1.000 UF
1.018,96 UF
tiempo
01/06/12
01/09/12
IN4302
01/12/12
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Flujos de caja de un FRA
Por otro lado, la contraparte tomará el principal y lo depositará a la
tasa a 90 días vigente en el mercado el 01/9/12 (r90). Los flujos de la
contraparte serán entonces:
+1.000 UF
-1.000*(1+r90*91/360) UF
tiempo
01/06/12
01/09/12
IN4302
01/12/12
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Compensando el FRA
El día 01/09/12 se conocerá la tasa r90, y en vez de esperar 3 meses el FRA
típicamente se cancelará por compensación esa fecha:
tiempo
01/06/12
01/09/12
01/12/12
1.018,96
C  1.000 
91 

1  r90 

360 

IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
FRA y los swaps de tasas
La compensación que se paga al comienzo del período puede
escribirse como
91 
91 


1

r

1

7
,
5
%





90
360
360
  1.000  

C  1.000  
91 
91 


1  r90 

1  r90 

360 
360 


Lo que equivale decir que:
1.000
91
C
 7,5%  r90 
91 
360

1

r



90
360


Es decir en este ejemplo estamos intercambiando tasa fija por tasa
flotante y compensando al comienzo del período
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Equivalencia entre FRAs y Swaps
FRAs son entonces equivalentes a un swap de tasas de un solo
período
01/06/12
01/09/12
01/12/12
Pagos pueden ocurrir en cualquiera de estas dos fechas. Lo estándar
es que ocurran al comienzo del período.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
P&L (ex-post) del FRA
Compensación del FRA
7.5
5.0
2.5
UF
0.0
-2.5 5%
6%
7%
8%
9%
10%
11%
-5.0
-7.5
-10.0
-12.5
Tasa de 90 días
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Sin embargo ex-ante...
Cambiamos...
-1.000 UF
01/06/12
01/09/12
1.012,78
1.015,33
1.017,89
1.020,44
1.023,00
1.025,56
01/12/12
Por...
-1.000 UF
IN4302
1.018,75 UF
Departamento de Ingeniería Industrial
Universidad de Chile
2012
¿Cuándo se demanda un FRA?

Eliminar riesgo tasa de repricing
– Asegurar hoy tasas para pasivos frente a una potencial alza de tasas
– Asegurar hoy tasas para inversiones futuras frente a una potencial
caída de tasas


Cubrir riesgos de swaps
Alterar duración de la cartera sin cambiar el balance:
– Equivalente a incorporar un pasivo y un activo a un plazo mayor

Tomar posición frente a una visión de mercado
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Swaps de Tasas de Interés
Definición: Es un acuerdo entre dos contrapartes para
intercambiar flujos de cajas en el futuro de acuerdo a una fórmula
predeterminada.
Swaps de tasas tipo “Plain Vanilla” es el más común. Institución B se
compromete a pagar a A interés sobre un nocional por un
determinado número de períodos, y por su parte A se
compromete a pagar a B en las mismas fechas un tasa flotante
que se irá fijando en el futuro de acuerdo a un estándar acordado.
Ejemplo:
Un swap a dos años entre A y B, en el que se intercambia TAB 90 días por una
tasa fija de UF+5,8%, sobre un nocional de 200.000 UF, a partir del 01 de
junio de 2012, con pagos trimestrales.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Mecánica del swap de tasas
TAB 90 días
01-Jun-12
01-Sep-12
01-Dic-12
01-Mar-13
01-Jun-13
01-Sep-13
01-Dic-13
01-Mar-14
UF+ 5,8%
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Flujos del swap (Nocional de 200.000UF)
Fecha
Días Intervalo
22-jun-12
Tasa Fija
Tasa TAB 90
5,80%
5,40%
Flujo (UF)
Pierna Fija
Flujo (UF)
Pierna
Flotante
Flujo (UF)
Fijo - Flotante
22-sep-12
92
5,80%
5,40%
2.964,44
2.760,00
204,44
22-dic-12
91
5,80%
5,70%
2.932,22
2.730,00
202,22
22-mar-13
90
5,80%
5,50%
2.900,00
2.850,00
50,00
22-jun-13
92
5,80%
5,30%
2.964,44
2.811,11
153,33
22-sep-13
92
5,80%
5,90%
2.964,44
2.708,89
255,56
22-dic-13
91
5,80%
6,30%
2.932,22
2.982,78
-50,56
22-mar-14
90
5,80%
6,10%
2.900,00
3.150,00
-250,00
22-jun-14
92
5,80%
6,10%
2.964,44
3.117,78
-153,33
Suponiendo una realización determinada de las Tasas TAB90 hasta
Jun 2014
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Swap de tasas: transformando un pasivo


Suponga que la institución A en el ejemplo anterior tiene un crédito a
2 años a TAB 90 días + 1,15%, y quisiera cambiar a un crédito a tasa
fija.
La institución B ofrece pagarle TAB 90 días vs. una tasa de 6,5% en
un swap a dos años:
TAB90+1,15% Institución
TAB90
A
Institución
B
6,5%
El efecto neto para A es pagar una tasa fija. ¿De cuánto?
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Intermediarios de swaps

Suponga que la institución B es un intermediario
TAB90+0,85%
Institución
TAB90
A
Institución
B
Intermediaria
6,5%
6,4%
B deberá encontrar otra contraparte
con necesidades opuestas (i.e. que
requiera transformar un crédito a
tasa fija, en uno a tasa variable)
IN4302
TAB90
Institución
7,3%
C
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ejemplo Contrato
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Market Makers

En la práctica es poco probable que 2 compañías contacten a una
institución financiera al mismo tiempo y deseen tomar posiciones
opuestas en el mismo swap.

Instituciones financieras actúan como “market makers” de swaps.

Esto significa que ellos están preparados para entrar en un swap
sin tener necesariamente la posición opuesta con otra contraparte.

Los market makers deben cuantificar cuidadosamente y realizar el
hedge de los riesgos que están tomando.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Tasa del Swap

Los swaps de transan de acuerdo a la tasa fija (swap rate). Esta cambia
día a día de acuerdo a las expectativas de mercado.
Ejemplo:

Fuente: Bloomberg

IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Tasa del Swap

Curva USD fijo-flotante:

Fuente: Bloomberg
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Tasa del Swap


Al igual que los derivados mencionados previamente, al momento de
iniciar un contrato, el valor presente de un swap es cero.
Esto quiere decir que al comienzo del contrato el valor presente de la
pierna flotante debe ser igual al valor presente de la pierna fija.
VP(Flotante) = VP(Fija)


Normalmente las tasas swap se construyen con futuros de tasas para
la parte corta de la curva mientras que en la parte larga de la curva las
tasas swap son definidas por la oferta y demanda del mercado.
En el cado de la curva swap fijo-flotante es USD. Normalmente se
utilizan las tasas LIBOR para la parte corta. Los futuros de Eurodollar
para la parte media y la parte larga es definida por las expectativas de
largo plazo.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Precios IRS CLP

Tradition Chile 01/06/2012
IRS CLP vs Camara
Implied
1 Yr
Forward
Tenor
3m
6m
9m
1Y
1,5Y
2Y
3Y
4Y
5Y
6Y
7Y
8Y
9Y
10Y
15Y
Bid
4,81
4,80
4,72
4,62
4,60
4,53
4,65
4,84
4,95
5,06
5,13
5,19
5,24
5,29
5,33
Mid
4,83
4,82
4,74
4,64
4,62
4,55
4,67
4,86
4,97
5,08
5,15
5,21
5,26
5,31
5,35
Offer
4,85
4,84
4,76
4,66
4,64
4,57
4,69
4,88
4,99
5,10
5,17
5,23
5,28
5,33
5,37
Prev
4,86
4,84
4,76
4,66
4,63
4,57
4,68
4,84
4,95
5,04
5,09
5,15
5,20
5,24
5,27
∆bp
-0,03
-0,02
-0,02
-0,02
-0,01
-0,02
-0,01
+0,02
+0,02
+0,04
+0,06
+0,06
+0,06
+0,07
+0,08
Inflation
20Y
5,35
5,37
5,39
5,29
+0,08
3,08%
12Y
5,31
5,33
5,35
5,25
+0,08
IN4302
2,87%
2,58%
2,72%
2,89%
2,95%
3,04%
3,05%
3,05%
3,06%
3,10%
3,08%
2,29%
2,99%
3,43%
3,18%
3,48%
3,10%
3,03%
3,21%
3,45%
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Precios IRS CLF

Tradition Chile 01/06/2012
IRS UF vs Camara
Bid
2,70
2,30
2,20
1,70
1,62
1,90
1,88
1,89
1,94
1,96
2,02
2,08
2,11
2,12
2,18
Mid
2,80
2,35
2,25
1,72
1,64
1,92
1,90
1,91
1,96
1,98
2,04
2,10
2,13
2,14
2,20
Offer
2,90
2,40
2,30
1,74
1,66
1,94
1,92
1,93
1,98
2,00
2,06
2,12
2,15
2,16
2,22
Prev
3,05
2,20
2,15
1,82
1,62
1,82
1,84
1,86
1,92
1,94
2,00
2,06
2,09
2,10
2,16
∆bp
-0,25
+0,15
+0,10
-0,10
+0,02
+0,10
+0,06
+0,05
+0,04
+0,04
+0,04
+0,04
+0,04
+0,04
+0,04
20Y
2,20
2,22
2,24
2,18
+0,04
12Y
2,14
2,16
2,18
2,12
+0,04
Tenor
3M (local)
6M (local)
9M (local)
1Y (local)
1,5Y
2Y
3Y
4Y
5Y
6Y
7Y
8Y
9Y
10Y
15Y
maturity
September 7, 2012
December 7, 2012
March 8, 2013
June 7, 2013
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Precios IRS

BID: es la tasa fija a la cual el market maker pagará la pierna fija y
recibirá tasa flotante en un contrato swap.

OFFER: es la tasa fija a la cual el market maker recibirá la pierna
fija y pagará tasa flotante en un contrato swap.

La tasa de mercado corresponde al MID.

El valor inicial de un swap es 0, descontado a MID, por lo que el
market maker siempre genera un spread inicial.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Valoración de Swaps

A medida que avanza el tiempo, el swap tiene un valor (mark to market)
que puede ser positivo o negativo.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Valoración de Swaps


Como ya se mencionó, el valor del swap puede calcularse como el
resultado de la valorización de un bono a tasa fija y un bono a tasa
flotante.
El valor de un bono a tasa fija se puede calcular como:
n
VP Fija   
i 1

ci
P

1  ri ti 1  rn tn
Por su parte, un bono a tasa flotante se calcula como:
VP Flotante 

P  1  k 
1  r1 t1
Donde k es la tasa flotante fijada en el último pago y r1 es la tasa al
próximo pago de cupón.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Valoración de Swaps

Por lo tanto, para un inversionista o empresa que recibe tasa fija y
paga flotante se tiene que el valor del swap es:
VP(Swap)=VP(Fija)-VP(Flotante)

Análogamente, para un inversionista o empresa que recibe tasa
flotante y paga fija se tiene que:
VP(Swap)=VP(Flotante)-VP(Fija)


Ejemplo:
Supongamos que una institución financiera tiene un swap donde paga
LIBOR de 6 meses y recibe fija de 8% anual (Considere composición
semianual, 30/360). Sobre un nocional de MM USD 100. Las fechas
restantes de pago son 3, 9 y 15 meses. Las tasas LIBOR para estos
plazos son 10%, 10,5% y 11% respectivamente. La LIBOR de 6 meses
en el último pago fue de 10,2%.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Valoración de Swaps

Calculando el valor del bono a tasa fija:
VP Fija  
4.000.000
 10% 
1 

2



3
2
12

4.000.000
 10,5% 
1 

2


9
2
12

104.000.000
 11% 
1 

2


15
2
12
 98.578.914
Calculando el valor del bono a tasa flotante:
 10,2% 
100.000.000  1 

2 

VP Flotante 
 102.567.098
3
2
 10%  12
1 

2 


Por lo tanto, el valor del swap es:
VPSwap   3.988.184
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Duración de los Swaps



Cada una de las piernas del swap tiene una duración distinta:
Para el caso de la pierna a tasa fija, la duración es equivalente a un
bono.
Para el caso de la pierna flotante, la duración es equivalente al plazo
del siguiente cupón conocido (tal como los bonos a tasa flotante).
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Duración de los Swaps



Por lo tanto:
Si recibimos tasa fija y pagamos flotante, obtenemos una ganancia
cuando las tasas bajan y una pérdida cuando las tasas suben. Es
decir, estamos largos en duración.
Por el contrario, si recibimos tasa flotante y pagamos tasa fija.
Estamos cortos en duración. Es decir, obtenemos una ganancia
cuando las tasas suben y una pérdida cuando las tasas bajan.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Duración de las piernas del swap


Pierna Fija: Igual que un bono
Pierna Flotante: como un FRN
01-Jun-12
01-Sep-12
rN
N
IN4302
01-Dic-12
01-Mar-13
01-Jun-13
01-Sep-13
01-Dic-13
01-Mar-14
Duración es equivalente al
plazo del siguiente cupón
(ya conocido)
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ventajas Comparativas

¿Por qué los swaps son tan utilizados?

Usualmente se argumenta que esto se debe a que algunas empresas
tienen ventajas comparativas para financiarse a tasa fija, mientras que
otras empresas tienen ventaja en el mercado de tasa flotante.

Para obtener financiamiento, tiene entonces sentido recurrir al
mercado donde se tenga una ventaja comparativa.

Como resultado de esto, algunas empresas pueden terminar pidiendo
prestado a tasa fija, cuando en verdad querían flotante (y viceversa).
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ventajas Comparativas





Ejemplo:
Supongamos que ahora tenemos 2 empresas extranjeras con
diferentes clasificaciones de riesgo que desean pedir prestado US$10
MM. La empresa 1 es AAA, mientras que la empresa 2 es BBB. Las
tasas a las que se pueden financiar ambas son:
La diferencia entre las tasas a las que pueden acceder las empresas 1
y 2 es mayor en el mercado de tasa fija que en el de tasa variable (1,2%
vs 0,7%).
• La empresa 1 tiene una ventaja comparativa en el mercado de tasa
fija,
mientras que la empresa 2 tiene una ventaja comparativa en el
mercado de tasa flotante.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ventajas Comparativas

Para facilitar el análisis, supongamos que ambas empresas pueden
ponerse en contacto directamente (el que exista un intermediario
financiero no cambia los resultados).

Supongamos además que la empresa 1 desea financiarse a tasa
flotante mientras que la empresa 2 necesita fija.

Ambas entran en un swap: la empresa 2 se compromete a pagarle a la
empresa 1 una tasa fija de 9,95% a cambio de 6M LIBOR (sobre el
nocional de US$10 MM.
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Ventajas Comparativas


Como resultado, tenemos que:
La empresa 1:
–
–
–
–

La empresa 2:
–
–
–
–



Paga 10% a sus prestamistas.
Recibe 9,95% de la empresa 2.
Paga LIBOR a la empresa 2.
Pago Neto = LIBOR + 0,05%.
Paga LIBOR + 1% a sus prestamistas.
Recibe LIBOR de la empresa 1.
Paga 9,95% a la empresa 1.
Pago Neto = 10,95%.
El swap mejora la tasa de ambas empresas en 0,25%.
La ganancia total del acuerdo es 1,2% - 0,7% = 0,5% (la diferencia entre las
tasas fijas que ven ambas empresas menos la diferencia en las tasas
flotantes).
¿Por qué los spreads entre las tasas pueden ser diferentes en los distintos
mercados de tasas?
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Demanda por swaps

Contratar seguro de tasa para varios períodos sucesivos.

Tener acceso a mercados de tasa fija cuando sólo se ofrecen tasas variables.

Disminuir costo financiamiento.

Alterar la sensibilidad a tasas.

Manejar riesgo de tasas sin alterar la composición de los activos y pasivos.

Administrar riesgos de carteras de derivados de tasa.

Especular sobre la trayectoria de tasas
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Cross Currency Swap

Es un contrato en el cual se realiza un intercambio de principal e
intereses en una moneda y se recibe un principal e intereses en
otra moneda.

Se debe especificar el principal en cada una de las monedas.

En este caso se pueden dar más combinaciones:
Fijo – Fijo
Flotante – Flotante
Fijo – Flotante
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Precios CCS Libor 6M / Cámara

Tradition Chile 01/06/2012
6 Mth Libor vs Camara
Tenor
Bid
Mid
Offer
Prev.
∆bp
6M
28,00
33,00
38,00
33,00
0,00
1Y
53,00
58,00
63,00
48,00
10,00
2Y
68,00
73,00
78,00
73,00
0,00
3Y
70,00
75,00
80,00
75,00
0,00
4Y
81,00
86,00
91,00
86,00
0,00
5Y
90,00
95,00
100,00
95,00
0,00
6Y
92,00
97,00
102,00
97,00
0,00
7Y
99,00
104,00
109,00
104,00
0,00
8Y
108,00
113,00
118,00
113,00
0,00
9Y
116,00
121,00
126,00
121,00
0,00
10Y
118,00
123,00
128,00
123,00
0,00
15Y
122,00
127,00
132,00
127,00
0,00
20Y
124,00
129,00
134,00
129,00
0,00
12Y
121,00
126,00
131,00
126,00
0,00
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Precios CCS Libor 3M / Cámara

Tradition Chile 01/06/2012
3 Mth Libor vs Camara
Tenor
Bid
Mid
Offer
Prev
∆bp
6M
49,00
54,00
59,00
54,00
0,00
1Y
74,00
79,00
84,00
69,00
10,00
2Y
86,00
91,00
96,00
91,00
0,00
3Y
86,00
91,00
96,00
91,00
0,00
4Y
95,00
100,00
105,00
100,00
0,00
5Y
103,00
108,00
113,00
108,00
0,00
6Y
105,00
110,00
115,00
110,00
0,00
7Y
112,00
117,00
122,00
117,00
0,00
8Y
121,00
126,00
131,00
126,00
0,00
9Y
128,00
133,00
138,00
133,00
0,00
10Y
130,00
135,00
140,00
135,00
0,00
15Y
134,00
139,00
144,00
139,00
0,00
20Y
136,00
141,00
146,00
141,00
0,00
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012
Riesgo de Crédito



Si la contraparte entra en default,
existirá una pérdida si el valor del swap
para la institución financiera es
positivo y no habrá efecto alguno en el
caso que el valor sea negativo.
Las pérdidas potenciales en un swap
son menores que en un crédito, debido
a que el valor del swap, usualmente es
mucho menor que el de un crédito.
Las pérdidas potenciales en un cross
currency swap son mayores que en un
interest rate swap, debido a que los
principales se intercambian (por lo que
un CCS puede tener un valor mayor
que un IRS).
IN4302
Departamento de Ingeniería Industrial
Universidad de Chile
2012