guia_ndeg_5_iv2015_func - SED | Colegio San Esteban

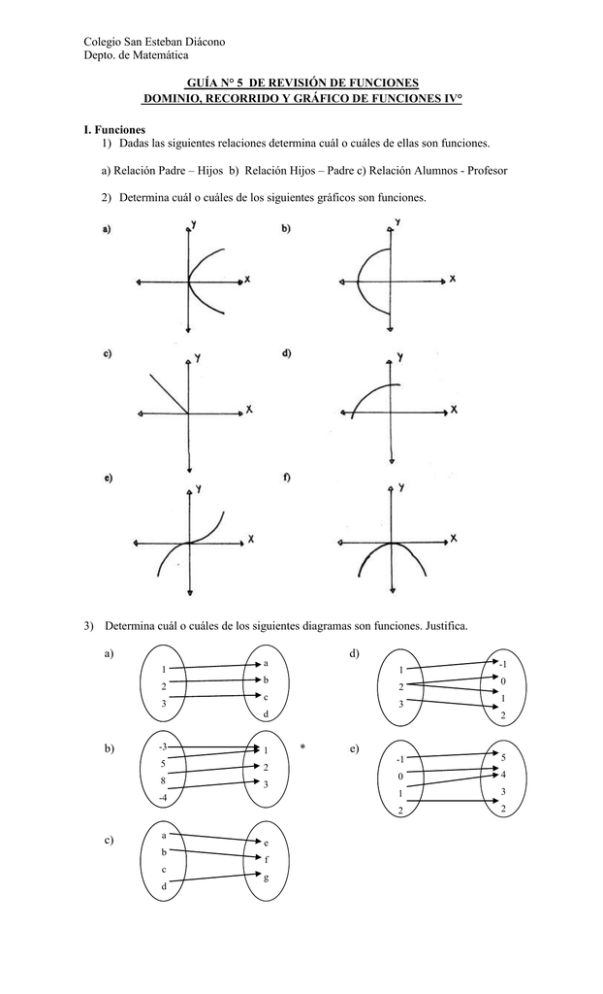
Colegio San Esteban Diácono
Depto. de Matemática
GUÍA N° 5 DE REVISIÓN DE FUNCIONES
DOMINIO, RECORRIDO Y GRÁFICO DE FUNCIONES IV°
I. Funciones
1) Dadas las siguientes relaciones determina cuál o cuáles de ellas son funciones.
a) Relación Padre – Hijos b) Relación Hijos – Padre c) Relación Alumnos - Profesor
2) Determina cuál o cuáles de los siguientes gráficos son funciones.
3) Determina cuál o cuáles de los siguientes diagramas son funciones. Justifica.
a)
1
2
3
d)
a
1
b
2
c
3
d
b)
-3
1
5
2
8
3
-4
c)
a
b
c
d
e
f
g
-1
0
1
2
*
e)
-1
5
0
4
1
3
2
2
Colegio San Esteban Diácono
Depto. de Matemática
4) Dadas las siguientes funciones, encuentra el dominio:
a)
c)
e)
4
x6
x 1
h( x )  2
x 9
2
j ( x)  2
x 1
f ( x) 
b)
g ( x)  x  10
d)
i ( x)  x 2  2 x  7
f)
k ( x)  6 
3
x 1
5) Determina algebraicamente el recorrido de las siguientes funciones.
a)
c)
x 1
x
b)
g ( x) 
h( x)  1  x 2
d)
i ( x)  3 x  8
f ( x) 
x 1
2x  1
6) Grafica las siguientes funciones y encuentra el dominio y recorrido.
a) f(x) = 3x + 2
b) g(x) = x2 + 3
7)
f : R  R , tal que f ( x)  5x  3 . Calcula:
1
f (0) 
a) f   
b)
5
 1
f  0,3 
d) f    
e)
 2
Sea
c)
3
f 
5
f 2  f (1)

f)
3  f (5)
Colegio San Esteban Diácono
Depto. de Matemática
8) Sea
g : R  R , tal que g ( x)  x 2  1 . Determina las preimágenes de los siguientes
valores:
a) g ( x)
 15
21
d) g ( x ) 
4
2
x
 2
9) Sea h( x )   2
 x

a)
Calcula:
i. h(100) 
g ( x)  3
1
g ( x) 
9
b)
e)
si x  0
c)
g ( x)  1
.
si x  0
ii. h(1) 
iii. h(5) 
*Grafica la función y encuentra dominio, codominio y recorrido
Respuestas:
1)
a) No
b) Si
c) Si
a) No
b) No
c) Si
d) Si
e) Si
a) Si
b) Si
c) No
d) No
e) Si
2)
f) Si
3)
4)
e)
Dom f    6
Dom h    3,3
a)
Re c f    
1
a)
b)
d)
Dom g  x   / x  10
Dom i  
e) Dom k  x   / x  1
5)
6)
a)
b)
b)
1 
Re c g     
2
c)
Re c i  
Colegio San Esteban Diácono
Depto. de Matemática
7)
1
a) f    2
5
e) f  0,3  
b) f 0  3
9
2
f)
f 2  f 1 3

3  f 5
22
 3
c) f    0
5
11
 1
d) f     
2
 2
8)
a) x1  4 , x2  4
d) x1 
b) x1  2 , x2  2
5
5
, x2  
2
2
e) x1 
c) x  0
10
10
, x2  
3
3
9) a)
i)
ii) h 1  
h100  10
iii) h5  5
3
2
7
 3
iv) h    
8
 2
e)
II.- Función cuadrática
1.-
En cada una de las funciones cuadráticas, indica el sentido de su concavidad, calcula los
ceros de la función y determina su intersección con el eje Y.
a) y  x 2  8x  12
b) f  x   x 2  4x  5
c) y  2x 2
d) f  x   3x 2  6x
e) y  x 2  1
f) y  x2  25
2.- Calcula las coordenadas del vértice, valor máximo o mínimo de cada una de las
siguientes funciones cuadráticas.
a)
y  x 2  8x  9
d)
y  2x 2  18
e)
y  x 2  6x
x2
y
 3x
2
b)
c)
y  3x 2  6x  2
3.- Determina para cada una de las siguientes funciones cuadráticas los intervalos reales en los
cuales son crecientes o decrecientes.
a)
d)
y  3 x  2  4 b) y  2x 2  5x  6
c) y  x 2  5x  6
y  x 2  7x e) y  4x 2  8x  3 f) y  1  x 2
2
4.- Un fabricante determina que el ingreso obtenido por la producción y venta de x artículos
está dado por la función R(x) = 350 -0,25x2.
a) Calcula el ingreso cuando se vende 100 artículos.
b) Si el ingreso obtenido es 120.000, determina la cantidad de artículos vendidas.
5.- Un proyectil se lanza directamente hacia arriba desde el suelo. Después de transcurridos
t segundos su distancia en metros por encima del suelo está dado por la función
d(t) = 144t – 16t2.
a) ¿Después de cuántos segundos estará el proyectil a128m del suelo?
b) ¿En qué momento toca el suelo el objeto?
c) Dibuja en gráfico para la función.
Colegio San Esteban Diácono
Depto. de Matemática
6.- El número de millas M que cierto automóvil puede recorrer con un galón de gasolina, con una
rapidez de v millas por hora, está dado por la función:
𝑀=
−1
30
5
𝑣 2 + 𝑣,
para
2
0 < 𝑣 < 70
a) Calcula el número de millas que el automóvil puede recorrer con un galón de gasolina,
para 𝑣 = 20 millas por hora.
b) Si el automóvil recorrió 45 millas, determina su rapidez.
7.- Un objeto lanzado verticalmente hacia arriba logra una altura de acuerdo a la función
h(t) = 18t - 3t2 ( h en metros, t en segundos).
a) ¿Cuánto demora en alcanzar la altura máxima?
b) ¿Cuál es la altura máxima?
8.- Los registros de te1moperaturas entre las 0 y 24 horas en una zona rural se ajustan a la
función
T(x) =
−
1
(𝑥
12
− 12)2 + 10 donde T es la temperatura en grados Celsius y x es la
hora que se registró.
a) ¿Cuál fue la temperatura máxima?
b) ¿A qué hora se registró?
c) ¿A qué hora la temperatura fue de 7° Celsius?
Respuestas
1.-
a) Hacia arriba ; ceros de la función 𝑥1 = 2 𝑥2 = 6 ; intersección con el y
(0,12)
b) Hacia abajo; ceros de la función 𝑥1 =- 1 𝑥2 =5; intersección con el eje y (0,5)
c) Hacia arriba; ceros de la función 𝑥1 =𝑥2 = 0; intersección con el eje y (0,0)
d) Hacia abajo; ceros de la función 𝑥1 =0 𝑥2 =2; intersección con el eje y (0,0)
e) Hacia arriba; ceros de la función 𝑥1 =1 𝑥2 =-1;intersección con el eje y(0-1)
f) Hacia arriba; ceros de la función 𝑥1 =√−25 𝑥2 =−√−25; intersección con el eje y (0,25).
2.-
a) V(4, -25) ; Mínimo -25 b) V(3,-9) Mínimo -9 c) V(1,5) Mínimo 5
9
9
2
2
d) V(o,-18) e) V(3, ) Máximo
3.-
5
5
4
4
a)Creciente]−∞, −2[ Decreciente ]−2, ∞[ b) creciente]− , ∞[ decreciente ]−∞, − [
5
c) creciente
]−∞, 52[decre𝑐𝑖𝑒𝑛𝑡𝑒 ] , ∞[ d)Creciente]−7/2, ∞[ decreciente]−∞, −7/2[
2
e) creciente]1∞, [ decreciente ]−∞, 1[ f) creciente ]0, ∞[ decreciente]−∞, 0[
4.-
a) 32.500 u. m.
b) x1 = 600
5.-
a) En 1 seg. y a los 8 seg.
b)
6.- a) 110/3 millas
7.- a) 3 seg.
8.- a) 12 grados Celsius
o x2 = 800
9 seg.
b) 45 o 35 millas por hora
b) 27 m.
b) 10 horas
c) 6 hrs. y a las 18 hrs.
Colegio San Esteban Diácono
Depto. de Matemática