Presentación de PowerPoint

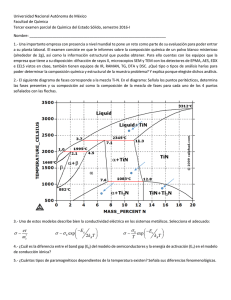
ECUACIONES
DIFERENCIALES
PRÁCTICA
ECUACIONES DIFERENCIALES
Contenido
- EJEMPLOS DE ED Y SOLUCIONES.
- EL COMANDO dsolve. RESOLUCIÓN DE PROBLEMAS DE CONDICIÓN
INICIAL.
- CAMPOS DE DIRECCIONES.
- TRAYECTORIAS ISOCLINAS.
- ED EN VARIABLES SEPARADAS.
COMANDOS PARA LA DERIVACIÓN
» syms x
» diff(f,x)
Halla la función derivada de f respecto a x.
» diff(f,x,n)
Halla la función derivada enésima de f respecto a x.
» Df
Representa simbólicamente la derivada de f.
Para derivadas sucesivas D2, D3, etc.
EJEMPLOS DE ED Y SOLUCIONES
1. Sea la ecuación
m y´´ = -m g + k y´
Comprobar que
y(t) = A + B exp(k t / m) + m g t / k
es una solución de dicha ED
SOLUCIÓN
1º. Definir simbólicamente y(t).
2º. Sustituir en la ED
» syms t y k m g A B
» y = A + B*exp(k*t/m) + m*g/k*t;
» a=m*diff(y,t,2)-k*diff(y,t)+m*g
a =1/m*B*k^2*exp(k*t/m)k*(B*k/m*exp(k*t/m)+m*g/k)+m*g
» simplify(a)
ans =0
2. Comprobar que la función
u(x,t) = exp( -Π2 c2 t / l2 ) sen( Π x / l)
es solución de la ecuación del calor
ut(x,t)= c2 uxx(x,t)
» syms u t c x l
» u='exp(-pi^2*c^2*t/l^2)*sin(pi*x/l)';
» diff(u,t)-c^2*diff(u,x,2)
ans =0
El comando dsolve. Resolución de PCI
El comando dsolve permite resolver explícitamente algunas ED,
incluso sin declarar simbólicas a las variables involucradas.
-Resolver la ED
y'=1+y^2
» dsolve('Dy=1+y^2')
ans =tan(t+C1)
-Obtener la solución local con la CI (0,1)
» dsolve('Dy=1+y^2','y(0)=1')
ans =tan(t+1/4*pi)
-Representar dicha solución local
» ezplot('tan(t+pi/4)',[-pi/4,pi/4]), hold on, plot(0,1,'*r')
tan(t+ π/4)
9
8
7
6
5
4
3
2
1
0
-0.6
-0.4
-0.2
0
t
0.2
0.4
0.6
- Resolver la ED
y' = - y - 2 t
» dsolve('Dy=-y-2*t')
ans =-2*t+2+exp(-t)*C1
- Obtener la solución local con la CI (-2,1)
» dsolve('Dy=-y- 2*t','y(-2)=1')
ans =-2*t+2-5*exp(-t)/exp(2)
- Representar dicha solución local
» ezplot('-2*t+2-5*exp(-t)/exp(2)',[-4,3]), hold on,
plot (-2,1,'*g')
-2 t+2-5 exp(-t)/exp(2)
2
0
-2
-4
-6
-8
-10
-12
-14
-16
-4
-3
-2
-1
0
t
1
2
3
Algunas ED resolubles no pueden ser resueltas por
MATLAB.
EJEMPLO.
y'=-2t-y+cos(y)
» dsolve('Dy=-2*t-y+cos(y)')
Warning: Explicit solution could not be found.
>In C:\MATLABR11\toolbox\symbolic\dsolve.m at
line 326
ans = [ empty sym ]
Si el comando dsolve no puede obtener explícitamente
la solución, entonces el propio dsolve ofrece la solución
en la forma implícita.
EJEMPLO.
y'=y^2(1-y)
» dsolve('Dy=y^2*(1-y)')
Warning: Explicit solution could not be found;
implicit solution returned.
> In C:\MATLABR11\toolbox\symbolic\dsolve.m at
line 292
t+1/y-log(y)+log(-1+y)+C1=0
Resolver la ED
con la CI
y''=-y+ cos(2x)
y(0)=1, y'(0)=0.
» y=dsolve('D2y=-y+ cos(2*x) ','y(0)=1','Dy(0)=0','x')
y = (1/2*sin(x)+1/6*sin(3*x))*sin(x)+(1/6*cos(3*x)1/2*cos(x))*cos(x)+4/3*cos(x)
Notar el efecto del comando simplify
» simplify(y)
ans = -2/3*cos(x)^2+4/3*cos(x)+1/3
Significado geométrico de y'=f(x,y).
Dada la ED y'=f(x,y), si y(x) es solución y (x0,y0) es un punto de
la gráfica de y(x), entonces la pendiente de dicha solución en
(x0,y0) es y' (x0) que es igual a f (x0,y0).
Así pues, para conocer la pendiente de la solución que pasa
por (x0,y0) no hace falta conocer dicha solución; basta con
calcular f (x0,y0).
Si esto se hace con todos los puntos del plano, tendremos las
pendientes de las soluciones que pasan por cada punto del
plano.
Naturalmente, en la práctica es imposible hacer esto con todos
los puntos del plano, pero nada nos impide hacerlo con tantos
puntos como queramos, configurando un dibujo que se llama
campo de direcciones de la ED.
CAMPOS DE DIRECCIONES
Sea n=1 y sea y'(x)=f(x,y(x)).
Para construir el CAMPO DE DIRECCIONES de la ED,
por cada punto (x,y) de una red de puntos de R^2 se dibuja
un segmento o vector de pendiente f(x,y).
Para el estudio gráfico de las soluciones de una ED sin
haberla resuelto, usaremos un programa en el que
intervienen los comandos
meshgrid y quiver,
que permite dibujar el campo de direcciones.
Los vectores a considerar para obtener el campo de
direcciones serán (1, y') .
EJEMPLO. Construir el campo de direcciones de
la ED
y'=x
» f=inline('x', 'x','y')
» paso=0.5;iz=-3;der=3;
» [x,y]=meshgrid(iz:paso:der,iz:paso:der)
» [n,m]=size(x)
» dx=ones(n,m)
» z=f(x,y)
» dy=z
» quiver(x,y,dx,dy)
4
3
2
1
0
-1
-2
-3
-4
-3
-2
-1
0
1
2
3
4
Representar además la solución particular que
cumple la CI y(0)=0.
» hold on, quiver(x,y,dx,dy)
» dsolve('Dy=x','y(0)=0', 'x')
» ezplot('1/2*x^2',[-2.5,2.5]), hold on, plot(0,0,'*g')
1/2 x 2
3
2.5
2
1.5
1
0.5
0
-2.5
-2
-1.5
-1
-0.5
0
x
0.5
1
1.5
2
2.5
Ejercicio.
1. Construir el campo de direcciones de
y'=-x/y
2. Representar además la solución particular
que cumple la CI
y(1)=1.
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
0
-0.2
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
(-x 2+2)1/2
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0.4
0.6
0.8
1
x
1.2
1.4
1.6
TRAYECTORIAS ISOCLINAS
Dada la ED y'=f(x,y) , se llaman curvas de nivel o isoclinas a
las obtenidas al imponer la condición
y'=k
Método de las isoclinas.
Es una variante de las ideas antes descritas. Los puntos del
plano por los que pasa una solución con pendiente k, son los
puntos de la curva de ecuación f(x,y)=k (isoclina de pendiente
k).
Dibujando las distintas isoclinas se obtiene una representación
similar a la del campo de direcciones.
Puede tener interés identificar la isoclina para la pendiente 0
pues las soluciones tendrán generalmente un máximo o un
mínimo al pasar por esta isoclina.
Representar las isoclinas de la ED
y' = x + y^2
Representar el gráfico de contorno (curvas de nivel
o isoclinas) de la superficie
z = x + y^2
» [x,y]=meshgrid(0:0.05:3,-2:0.05:2);
» z=x+y.^2;
» isoclinas=contour(x,y,z,20)
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
0.5
1
1.5
2
2.5
3
Representar las isoclinas de la ED
y' = x^2 + y^2
» [x,y]=meshgrid(-4:0.05:4);
» z=x.^2+y.^2;
» isoclinas=contour(x,y,z,20)
4
3
2
1
0
-1
-2
-3
-4
-4
-3
-2
-1
0
1
2
3
4
EJERCICIO.
Representar las isoclinas de la ED
y' = 2x- y
¿Qué tipo de curvas son dichas isoclinas?
Representar las isoclinas correspondientes a
k=0, y k=2.
¿Qué particularidad tiene la correspondiente
a k=2?
Construir el campo de direcciones y las curvas de nivel
de la ED
y'=sin(x)+y
» f=inline('sin(x)+y', ‘x','y')
» paso=0.5;iz=-3;der=3;
» [x,y]=meshgrid(iz:paso:der,iz:paso:der)
» [n,m]=size(x)
» dx=ones(n,m)
» z=f(x,y)
» dy=z
» hold on, contour(x,y,z,20),quiver(x,y,dx,dy)
4
3
2
1
0
-1
-2
-3
-4
-3
-2
-1
0
1
2
3
4
Ecuaciones en variables separadas
y'=f(x)h(y)
y(x0)=y0
dy/h(y)=f(x)dx , si 1/h=g, entonces g(y)dy=f(x)dx
Integrando G(y)=F(x)+c (Solución general)
c=G(y0)-F(x0)
G(y)=F(x)+G(y0)-F(x0) (Solución particular)
Resolver el siguiente PCI
y' = -2 x y,
y(0)=2
Representar la solución.
f(x)=-2x, h(y)=y
» syms F G x y c
» f='-2*x'; g='1/y';
» x0=0;y0=2;
» F=int(f); G=int(g);
» sol=solve(G-F-c,y)
solución general
» c=solve(subs(sol,x0,'x')-y0,c);
» y=subs(sol,c,'c')
solución particular
» ezplot(y,[-2,2]), hold on, plot (0,2,'+r')
sol =exp(-x^2+2*c) solución general
y =exp(-x^2+log(2)) solución particular
exp(-x2+log(2))
2
1.5
1
0.5
0
-2
-1.5
-1
-0.5
0
x
0.5
1
1.5
2
Resolver el siguiente PCI
y' = -2 x y
y(0) = 2
usando el comando dsolve.
» dsolve('Dy=-2*x*y','y(0)=2','x')
y =2*exp(-x^2)
Resolver el PCI
y'=sen(x)(y-1)
y(0)=2
» syms F G x y X Y
» f='sin(x)'
» g='1/(y-1)'
» F=int(f,x,0,X)
» G=int(g,y,2,Y)
» sol=solve(G-F,Y)
solución particular
» F =-cos(X)+1
» G =log(Y-1)
» sol =exp(-cos(X)+1)+1
Resolver
ycos(x)dx-(1+y^2)dy=0, y(0)=1.
Despejando
y'=ycos(x)/(1+y^2)
» y= dsolve('Dy=y*cos(x)/(1+y^2) ', 'x')
y =-i*(-lambertw(exp(2*sin(x)+2*C1)))^(1/2)
Teniendo en cuenta que Lambertw(x)=w cumple
que w*exp(w)=x,
lo que se obtiene es
y^2*exp(y^2)=K*exp(2*sin(x))
Resolver ycos(x)dx-(1+y^2)dy=0, y(0)=1.
Separando las variables
» solve('int(cos(x),x)-int((1+y^2)/y,y)')
» ans =asin(1/2*y^2+log(y)),
es decir, sin(x)=log(y)+1/2*y^2+c (solución general)
» c=simple(sym('solve(subs(x=0,y=1,sin(x)=
log(y)+1/2*y^2+ c),c)'))
» c =-1/2,
es decir, la solución particular es
sen(x)=log(y)+1/2(y^2-1)
Aplicar herramientas del MATLAB para
resolver los siguientes ejercicios.
a ) y' + y 2 sin (x) = 0
b) 4 xy dx + ( x 2 + 1)dy = 0
c) xy ' = y + ( x 2 − y 2)
d ) ( x − y ) dy = ( x + 3 y ) dx
e) ( x 2 + 1) dy = ( y 2 + 1) dx, y (0) = 1 / 2
f ) (1 + ex ) y y ' = ey, y (0) = 0
Nota. MATLAB se vale de una colección de “funciones básicas elementales” más
amplia que la nuestra, con la cual nos puede dar una mayor cantidad de respuestas en
forma cerrada. Una de estas funciones es w(z)=Lambertw(z) definida implícitamente
por
Lambertw(z)*exp(Lambertw(z))=z
La definición de cualquier función especial MatLab puede ser
consultada invocando en la línea de comandos help+nombre de función, por ejemplo
>>help lambertw
LAMBERTW Lambert's W function.
W = LAMBERTW(X) is the solution to w*exp(w) = x.
W = LAMBERTW(K,X) is the K-th branch of this multi-valued function.
Reference: Robert M. Corless, G. H. Gonnet, D. E. G. Hare,
D. J. Jeffrey, and D. E. Knuth, "On the Lambert W Function",
Advances in Computational Mathematics, volume 5, 1996, pp. 329-359.
Also available from:
http://pineapple.apmaths.uwo.ca/~rmc/papers/LambertW/index.html
Overloaded methods
help sym/lambertw.m