Amplificador Sumador Inversor

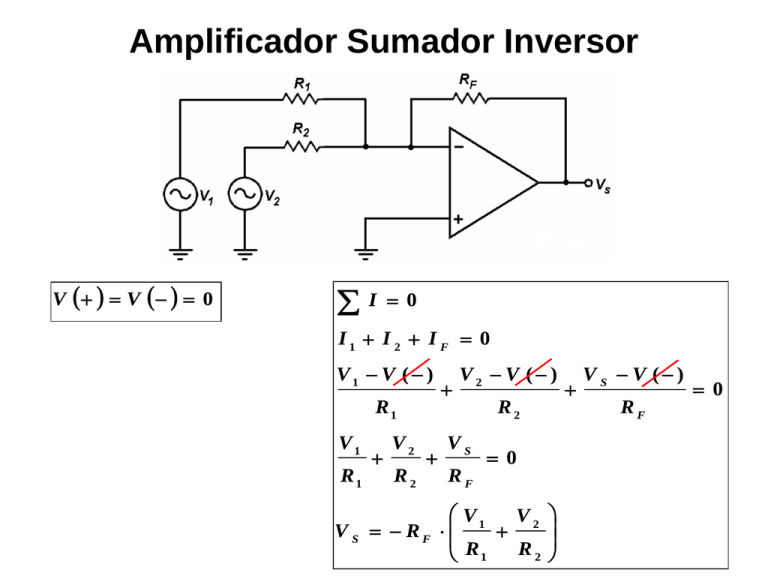
Amplificador Sumador Inversor
V    V    0
V    V    0

I  0
I1  I 2  I F  0

I  0
V1  V (  )
I1  I 2  I F  0
V1  V (  )

V2  V ( )
R1
V1
R1

V2
R2
R1
R2

VS
RF
 0

V2  V ( )
R2
VS
V S VV1 (  V
) 2


 0

 0
RF1
R2
RF
R
V
V 
V S   R F   1  2 
R2 
 R1

V S  V ( )
RF
 0
Si R 1  R 2  R
 V1 V 2 

V S   R F  


R
R
1 
 1
VS  
RF
R
 V 1  V 2 
Si R 1  R 2  R  R F
VS  
RF
RF
 V 1  V 2 
V S   V 1  V 2 
De esta manera se tiene un amplificador sumador
inversor de ganancia unitaria
Si R 1  R 2  R
VS  
RF
R
 V 1  V 2 
Si R F 
1
R
2
 R 1
V S      V 1  V 2 
 2  R
 V1  V 2 
VS  

2


De esta manera se tiene un amplificador inversor de
promedio o promediador
Amplificador Sumador No Inversor
 I ( )  0
IA  IB  0
VS

V ( )
RA
RA

V ( )
0
RB
 VS  RA  RB

V (  )  
 R  R
R
B
A
 A
V ( ) 
VS  RB
RA  RB
 I    0
I1  I 2  0
V1  V (  )

V2  V ( )
R1
V1

R2
V ( )
R1
 0
R1

V2

V ( )
R2
R2
 V 1  R 2  V 2  R1
V (  )  
R1  R 2

V ( ) 
V 1  R 2  V 2  R1
R1  R 2
 0
  R1  R 2

  R  R
2
  1




Si R 1  R 2 y R A  R B ( n  1 ),
donde n es el número
de entradas del amplificad
or, en nuestro caso
son 2, por lo tanto n  2 :
VS
 R1
 V 1  V 2   
 2 R1
 
R  ( 2  1) 
 1  B

 

RB
 

VS
1
 V 1  V 2       2 
2
V S  V 1  V 2 
De esta manera se tiene un amplificador sumador no
inversor de ganancia unitaria.
Si R 1  R 2 y R A  0 , tenemos
VS 
VS 
:
 R1 
  1  0 

 2 R1 
V 1  V 2   
V1  V 2
2
De esta manera se tiene un amplificador no inversor de
promedio o promediador.
Bibliografía:
• Amplificadores Operacionales y Circuitos integrados Lineales
(Quinta Edición).
Páginas: 52 – 57, 67 y 68.
Autor: Robert F. Coughlin.
• Teoría de Circuitos y dispositivos electrónicos (Octava Edición)
Páginas: 719 – 722.
Autor: Boylestad Nashelsky.
• Principios de Electrónica (Sexta Edición).
Páginas: 710 – 712.
Autor: Albert Paul Malvino.