Tema 1 Estadística 2010 WEB

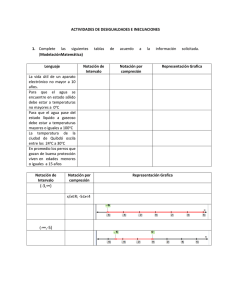
1.
2.
Tema 1
Estadística descriptiva
en variables
unidimensionales
Carlos Montes. Estadística uc3m.
1. Definiciones y notación
Definiciones y notación
Construcción de tablas estadísticas
2.1.- Datos sin agrupar
2.2.- Datos agrupados
3. Representaciones gráficas
3.1.- Datos cualitativos
3.2.- Datos cuantitativos
3.2.1.- Sin agrupar
3.2.2.- Agrupados
4.- Medidas características de una distribución
4.1.- Generalidades
4.2.- Medidas de tendencia central
4.3.- Medidas de dispersión
4.4.- Medidas de forma
4.4.1.- Asimetría
4.4.2.- Apuntamiento o curtosis
4.5.- Resumen: diagrama de caja (Box-Plot)
5.- Transformaciones
5.1.- Lineales
5.2.- No lineales
1. Definiciones y notación
• Caracteres: rasgos o cualidades de los
elementos de la población.
• Población: conjunto de elementos
objeto de estudio que presentan
características comunes.
• Elementos o individuos: unidades que
constituyen la población.
– Variables cualitativas, categóricas o
atributos.
• No toman valores numéricos
• Su realización concreta es una cualidad o
modalidad.
– Variables cuantitativas: toman valores
numéricos.
• Discretas: toman valores enteros.
• Continuas: toman valores en un intervalo.
1. Definiciones y notación
-
La cantidad de información
aportada por ambos tipos de variables
es muy distinta
Variables cualitativas
sin
Variables cuantitativas
n
de
or
n
de
or
1. Definiciones y notación
• Rango o recorrido de una variable:
diferencia entre el mayor y el menor
valor de ésta.
No confundir con el rango intercuartílico, que
se verá más adelante.
escalas de intervalos
+
razones o escalas de cociente
0 como ausencia de la característica
Carlos Montes. Estadística uc3m.
1. Definiciones y notación
• Frecuencia
– absoluta (f): el número de veces que
aparece cada dato de la variable.
– total (n): número total de datos de
la variable (suma de frecuencias
absolutas).
– relativa (fr): cociente entre
frecuencia absoluta y frecuencia total.
1. Definiciones y notación
– acumulada: supuesta la ordenación de
los datos de menor a mayor, la
frecuencia acumulada de xi es la suma
de frecuencias hasta el valor xi.
•Absoluta (F)
•Relativa (Fr)
La frecuencia acumulada relativa de un dato
es el cociente entre
la frecuencia acumulada absoluta de un dato
y la frecuencia total.
1. Definiciones y notación
1. Definiciones y notación
ej: 3, 2 ,3, 3, 4 ,5 ,3, 6, 3 ,6
(n=10)
Propiedades de las frecuencias relativas
xi
fi
Fr
F
Fr
2
1
0,1
1
0,1
3
5
0,5
6
0,6
4
1
0,1
7
0,7
5
1
0,1
8
0,8
6
2
0,2
10
1
f r ( xi ) ≥ 0 ∀xi
f r ( xi + x j ) = f r ( xi ) + f r ( x j )
n
∑ f (x ) = 1
i =1
r
i
Carlos Montes. Estadística uc3m.
2. 1.- Datos sin agrupar
2.2.- Datos agrupados
Los datos se presentan agrupados
en clases o intervalos
Los datos se presentan en 2 columnas:
Valores / Frecuencias absolutas
• Amplitud de un intervalo: diferencia entre
el extremo superior e inferior del mismo.
•Marca de clase (mj): punto medio
de cada intervalo o clase,
valor representativo de todos los datos
del intervalo.
El número de clases r debe oscilar entre 5 y
20; a menudo se escoge el entero más
próximo a n
3.1.- Datos cualitativos
3.2.1.- Datos cuantitativos sin agrupar
Peso
78
55
81
47
57
52
53
58
63
81
77
70
83
70
82
75
69
Pictogramas
Diagrama de tallo y hojas
1
3
6
7
7
(2)
7
4
4|7
5|23
5|578
6|3
6|
7|00
7|578
8|1123
Carlos Montes. Estadística uc3m.
3.2.2.- Datos cuantitativos agrupados
Base: amplitud del intervalo
Altura: proporcional, de manera que
las áreas de los rectángulos sean
proporcionales a las frecuencias
Carlos Montes. Estadística uc3m.
3.2.2.- Datos cuantitativos agrupados
4.1.- Medidas características:
Generalidades
4.2.- Medidas de tendencia central
Media aritmética
Son aquellas que nos permiten resumir los
rasgos fundamentales de la distribución:
x + x + ... + xn
x= 1 2
=
n
Tendencia central o centralización:
indican el valor medio de los datos.
Dispersión: indican la variabilidad de los
datos.
Forma:
Simetría
Apuntamiento
Concentración
4.2.- Medidas de tendencia central
Propiedades de la media aritmética x =
n
1)
n
i =1
i =1
n
2)
x′ =
∑ ( xi + k )
i =1
n
n
3)
x = ∑ x j fr ( x j )
x′ =
∑ kx
i =1
n
i
=k
=
Para datos en clases:
x = ∑ m j fr (m j )
n
∑ xi
n
n
i
n
Error de agrupamiento
Carlos Montes. Estadística uc3m.
4.2.- Medidas de tendencia central
n
∑x
i =1
i
n
Mediana
i =1
∑x
n
n
(sumatorio extendido
al nº de valores
distintos de la variable)
n
n
i
i
n
Para datos discretos agrupados:
∑ ( x − x ) = ∑ x − ∑ x = nx − nx = 0
i
∑x
+
= kx
∑k
n
n
=
∑ xi
n
n
+
nk
= x+k
n
Valor de la variable estadística
que divide en dos partes iguales
la distribución de frecuencias
4.2.- Medidas de tendencia central
4.2.- Medidas de tendencia central
Datos sin agrupar
Supuesta serie ordenada:
* nº impar de datos: valor central
* nº par de datos: media aritmética
de los valores centrales
Moda
Es el valor más frecuente de la
distribución
Datos agrupados: centro del intervalo mediano
(xa, xb)
En datos agrupados tomamos como moda
la marca de clase del intervalo
con mayor densidad de frecuencia
f r ( x < xa ) < 0,5
f r ( x > xb ) ≥ 0,5
Carlos Montes. Estadística uc3m.
4.3.- Medidas de dispersión
Miden la proximidad entre los valores de la
variable y las medidas de centralización
Propiedades de la varianza
1)Es una cantidad acotada y positiva
Varianza
S2 =
4.2.- Medidas de dispersión
2) La varianza NO se ve afectada por los
cambios de origen (transformaciones aditivas)
∑ ( xi − x ) 2
n
n
S 2 = ∑ ( x j − x )2 fr ( x j )
n
Sx =
2
Para datos discretos agrupados:
(sumatorio extendido
al nº de valores
distintos de la variable)
Sy =
2
∑ (x − x)
2
i
y = x+k
n
n
∑(y
i
− y)2
n
n
=
∑ (x + k − x − k)
i
n
n
2
=
∑ (x − x)
i
n
n
2
= Sx
2
4.2.- Medidas de dispersión
4.2.- Medidas de dispersión
3) La varianza SÍ se ve afectada por los
cambios de escala
(transformaciones multiplicativas)
Fórmula de cálculo
Sx =
∑ (x − x)
2
Sy =
2
Sx =
2
2
i
y = kx
n
n
∑(y
i
− y)2
=
n
n
∑ (kx − kx )
i
n
n
2
=
k 2 ∑ ( xi − x ) 2
n
n
= k 2Sx
∑x
2
j
n
n
fj
− x2
 ∑ xi 2

 n
2
 n −x 


2
Carlos Montes. Estadística uc3m.
4.3.- Medidas de dispersión
Desviación típica
Sx =
∑ (x − x)
Desigualdad de Tchebychev:
entre la media y k veces la desviación típica
existe como mínimo el
2
i
n
100 (1 −
n
Para datos discretos agrupados:
Sx =
∑ (x
n
j
4.3.- Medidas de dispersión
− x )2 f r ( x j )
(sumatorio extendido
al nº de valores
distintos de la variable)
Carlos Montes. Estadística uc3m.
1
)%
2
k
de los datos (k³2)
1
300
)=
= 75%
2
2
4
1
800
x ± 3s 100(1 − 2 ) =
= 89%
3
9
x ± 2 s 100(1 −
4.3.- Medidas de dispersión
Coeficiente de variación
Es una medida de dispersión relativa.
CV =
s
• 100 x ≠ 0
/x/
Nos permite:
1) Comparar la dispersión entre distribuciones.
2) Evaluar la representatividad de la media.
CSR =
4.3.- Medidas de dispersión
Cuantiles
Son los valores de la variable
que dividen la distribución en c partes iguales.
Cuartiles (Q)
Quintiles (K)
Percentiles (p)
Para calcular un cuantil
nos fijamos en su frecuencia acumulada.
/x/
• 100 x ≠ 0
s
4.3.- Medidas de dispersión
c=4
c=5
c=100
n⋅i
c
4.4.1- Asimetría
Coeficiente de asimetría (CA)
Rango intercuartílico (RI)
CA = g1 =
∑ (x − x
i
3
)
n
ns 3
g1=0 Distribución simétrica
Es la diferencia
entre los percentiles 75 y 25
(o entre los cuartiles 3 y 1)
g1>0 Distribución asimétrica positiva
o asimétrica a derechas
g1<0 Distribución asimétrica negativa
o asimétrica a izquierdas
Carlos Montes. Estadística uc3m.
4.4.1- Asimetría
4.4.2- Apuntamiento o curtosis
Otras medidas de asimetría:
Indica el mayor o menor agrupamiento de los datos
en torno a la media
x − Mo
s
x − Med
s
Como referencia se toma el apuntamiento
de la distribución normal, que cumple
∑ (x − x)
4
=3
i
0,4
Mean,Std. dev.
0,1
ns 4
0,3
0,2
0,1
0
-5
-3
-1
1
3
5
∑ (x − x)
CAp =
i
ns 4
4.4.2- Apuntamiento o curtosis
Mean,Std. dev.
0,1
0,3
0,2
0,1
0
-5
-3
-1
1
3
Representación gráfica de una distribución,
construida para mostrar
sus características principales
y señalar los posibles datos atípicos.
5
2
CAp>0: leptocúrtica
1,6
(en el ejemplo: 3,21)
0,8
−3
4.5- Diagrama de caja
0,4
CAp=0: mesocúrtica
4
1,2
M
0,4
im
ín
o
M
im
áx
o
Cu
a
s
le
i
rt
0
3,7
4,2
4,7
5,2
5,7
6,2
6,7
1,5
LI= Q1-1,5(Q3-Q1)
LS= Q3+1,5(Q3-Q1)
LIE= Q1-3(Q3-Q1)
LSE= Q3+3(Q3-Q1)
1,2
CAp<0: platicúrtica
(en el ejemplo: -0,9)
0,9
0,6
0,3
0
0
Carlos Montes. Estadística uc3m.
0,2
0,4
0,6
0,8
1
4.5- Diagrama de caja
5.1- Transformaciones lineales
Media
Q1
Q3
Diagrama de caja
y = a + bx
y = a + bx
S y = / b / Sx
47
57
67
77
87
Peso
Q2
5.2- Transformaciones no lineales
Se trata de aplicar a la variable una
transformación h(x) tal que la nueva variable
y=h(x) sea aproximadamente simétrica
y=x
2
y= x
y = ln x
y= 1
x
Comprime la escala en los valores bajos
y la expande en los valores altos
Adecuada para distribuciones
asimétricas negativas
Comprime la escala en los valores altos
y la expande en los valores bajos
Adecuada para distribuciones
asimétricas positivas
Carlos Montes. Estadística uc3m.
Los coeficientes de asimetría y curtosis
no se alteran por ser adimensionales