Cap雲tulo 2 Integral triple

Cap¶³tulo 2
Integral triple
2.1
La integral triple en un rect¶
angulo
2.1.1 De¯nici¶
on.- Llamaremos rect¶angulo tridimensional de R3 a todo paralelep¶³pedo en R3 de la forma I = [a; b] £ [c; d] £ [e; f ]. Denotaremos por ¹(I) el volumen
del paralelep¶³pedo ( es decir, (b ¡ a)(d ¡ c)(f ¡ e) ).
2.1.2 De¯nici¶
on.- Sea I = [a; b] £ [c; d] £ [e; f ] un rect¶angulo acotado contenido
3
en R . Se llama partici¶on de I a todo conjunto de la forma P = P1 £ P2 £ P3 , donde
P1 es una partici¶on del intervalo [a; b], P2 es una partici¶on del intervalo [c; d] y P3 es
una partici¶on del intervalo [e; f ].
17 Observaci¶
on: Sean las particiones P1 = fx0 ; x1 ; : : : ; xn g, P2 = fy0 ; y1 ; : : : ; ym g
y P3 = fz0 ; z1 ; : : : ; zp g. Entonces P es la partici¶on
P = P1 £ P2 £ P3 = f(x0 ; y0 ; z0 ); (x0 ; y0 ; z1 ); : : : ; (xi ; yj ; zk ); : : : ; (xn ; ym ; zp )g
y est¶a formada por (n + 1)(m + 1)(p + 1) puntos de R3 que descomponen al paralelep¶³pedo I en nmp subparalelep¶³pedos
Iijk = f(x; y; z) 2 R3 : xi¡1 · x · xi yj¡1 · y · yj zk¡1 · z · zk g
para 1 · i · n 1 · j · m 1 · k · p, que denominaremos subrect¶angulos de la
partici¶on.
Se veri¯ca:
n;m;p
¹(I) =
X
¹(Iijk )
i=1;j=1;k=1
2.1.3 De¯nici¶
on.- Se dice que la partici¶on Q = Q1 £ Q2 £ Q3 de I, es m¶as ¯na que
P = P1 £ P2 £ P3 si Pi ½ Qi , i = 1; 2; 3.
22
18 Observaci¶
on: Los comentarios hechos sobre las particiones de R2 se extienden
sin di¯cultad a las particiones en R3 .
2.1.4 De¯nici¶
on.- Sea f : I 7
¡! R una funci¶on acotada y P una partici¶on de I.
Para cada subrect¶agulo Iijk de P sean:
mijk = inf ff (x; y; z) : (x; y; z) 2 Iijk g
Mijk = supff (x; y; z) : (x; y; z) 2 Iijk g
Los n¶
umeros
L(P; f ) =
n;m;p
P
mijk ¹(Iijk )
U (P; f ) =
i=1;j=1;k=1
n;m;p
P
Mijk ¹(Iijk )
i=1;j=1;k=1
se denominan, respectivamente, suma superior y suma inferior de la funci¶on f respecto de la partici¶on P.
2.1.5 Proposici¶
on.- Sea P(I) el conjunto de todas las particiones de I. Entonces:
1. Para toda P 2 P(I), se tiene L(f; P ) · U(f; P ).
2. Si P; Q 2 P(I) y Q es m¶as ¯na que P , se tiene:
L(f; P ) · L(f; Q)
U(f; Q) · U (f; P )
3. Si P; Q 2 P(I), se tiene: L(f; P ) · U(f; Q).
4. supfL(f; P ) : P 2 Pg · inf fU(f; P ) : P 2 Pg
19 Observaci¶
on: Como consecuencia de las propiedades anteriores, el conjunto de
sumas inferiores de f est¶a acotado superiormente y el conjunto de sumas superiores
lo est¶a inferiormente, por tanto, estos conjuntos tendr¶an, respectivamente, extremo
¹ y U.
superior y extremo inferior, que denotaremos por L
2.1.6 De¯nici¶
on.- Sean I = [a; b]£[c; d]£[e; f ] y f : I 7
¡! R una funci¶on acotada.
¹
¹ = U se
Se dice que f es integrable en I si L = U. En tal caso, el n¶
umero I = L
denomina integral de f en I y se representa por
ZZZ
f (x; y; z) dxdydz
I
o, m¶as brevemente, por
RRR
I
f.
Ejemplos:
² La funci¶on f : I 7
¡! R, de¯nida por f (x; y; z) = k, para todo (x; y; z) 2 I, es
RRR
integrable y I kdxdy = k¹(I).
23
² La funci¶on f : [0; 2] £ [1; 4] £ [0; 1] 7
¡! R de¯nida por
8
< 0
f (x; y) = :
si x 2 Q, y 2 Q y z 2 Q
1; en los dem¶as casos
no es integrable.
20 Observaci¶
on: Si I es de la forma I = [a; b] £ [c; d] £ [e; f ] con a = b, c = d ¶o
e = f diremos que es un subrect¶angulo degenerado de R3 . Si f : I 7
¡! R es una
RRR
funci¶on acotada en I, entonces es integrable y se tiene que I f = 0, ya que para
cualquier partici¶on de I, el volumen de cada subrect¶angulo es 0.
En lo sucesivo, trabajaremos con rect¶angulos no degenerados.
2.1.7 Proposici¶
on.- (Criterio de integrabilidad de Riemann). Sea f : I 7
¡! R
acotada. Entonces f es integrable si, y s¶olo si, para cada ² > 0 existe una partici¶on
P de I tal que
U (f; P ) ¡ L(f; P ) < ²:
2.1.8 De¯nici¶
on.- (Sumas de Riemann). Sean I = [a; b]£[c; d]£[e; f ] y f : I 7
¡! R
una funci¶on acotada. P una partici¶on de I y fIijk : i = 1 : : : n; j = 1 : : : m; k =
1 : : : pg el conjunto de todos los subrect¶angulos de P. Llamaremos elecci¶
on en P a
todo conjunto de puntos de I de la forma
E = feijk 2 Iijk : i = 1 : : : n; j = 1 : : : m; k = 1 : : : pg
y suma de Riemann asociada a la terna f; P; E al n¶
umero:
S(f; P ; E) =
n;m;p
X
f (eijk )¹(Iijk )
i=1;j=1;k=1
21 Observaci¶
on: Est¶a claro que para toda P 2 P y todo conjunto E se tiene
L(f; P ) · S(f; P ; E) · U (f; P ).
2.1.9 Proposici¶
on.- Sean I = [a; b] £ [c; d] £ [e; f ] y f : I 7
¡! R una funci¶on
acotada y P una partici¶on de I. Entonces f es integrable en I si, y s¶olo si existe un
n¶
umero real A tal que para cada ² > 0 existe una partici¶on P² 2 P tal que para
toda partici¶on Q m¶as ¯na que P² y para cualquier elecci¶on E en Q se cumple:
jS(f; Q; E) ¡ Aj < ²
Adem¶as, si f es integrable en I, se veri¯ca que
RRR
I
f = A.
22 Observaci¶
on: El resultado anterior signi¯ca, en particular, que si la funci¶on es
integrable en I, entonces las sumas de Riemann de la funci¶on tienden a la integral
cuando el di¶ametro de la partici¶on, es decir el volumen de los subrect¶agulos de la
partici¶on, tiende a cero.
24
4 Propiedades: Si f y g son funciones integrables en I,
1. Tambi¶en lo son f + g y tf; t 2 R y se cumple:
ZZZ
(f + g) =
I
ZZZ
ZZZ
f+
I
ZZZ
tf = t
I
g
I
ZZZ
f
I
2. Si f (x; y; z) ¸ 0 para todo (x; y; z) 2 I, entonces
RRR
I
f ¸ 0.
3. Si f (x; y; z) · g(x; y; z) para todo (x; y; z) 2 I, entonces
RRR
I
f·
RRR
I
g.
4. Si m = inf ff (x; y; z) : (x; y; z) 2 Ig y M = supff (x; y; z) : (x; y; z) 2 Ig,
entonces:
ZZZ
f (x; y; z) dxdydz · M ¹(I)
m ¹(I) ·
I
5. ¹(I) =
RRR
I
dxdydz.
6. Si el rect¶angulo I se subdivide en dos subrect¶angulos I1 e I2 , de forma que I1 [I2 =
I y la intersecci¶on de ambos es un rect¶angulo de R2 , entonces f es integrable en
I si, y s¶olo si, lo es en I1 y en I2 . En ese caso,
ZZZ
f=
I
ZZZ
f+
I1
ZZZ
f
I2
7. Si f es integrable en I tambi¶en lo es jf j y se cumple:
j
ZZZ
I
fj ·
ZZZ
I
jf j:
2.1.10 Proposici¶
on.- Sean I = [a; b] £ [c; d] £ [e; f ] y f : I 7
¡! R una funci¶on
continua. Entonces:
1. f es integrable en I.
2. Existe un punto (»; ´; ³) 2 I tal que f (»; ´; ³)¹(I) =
RRR
I
f.
23 Observaci¶
on: La parte 2) de la proposici¶on anterior se conoce como Teorema
del Valor Medio para integrales triples.
Si f es integrable en I, se llama valor medio de f en I al valor:
1 ZZZ
f dxdydz
¹(I)
I
Si f es continua en I, el teorema anterior garantiza que este valor medio se alcanza
en alg¶
un punto.
25
Contenido cero.
2.1.11 De¯nici¶
on.- Se dice que un subconjunto B ½ R3 tiene contenido cero ,
( abreviadamente, c(B) = 0) si para cada ² > 0 existe un n¶
umero ¯nito de rect¶an3
gulos acotados de R , I1 : : : Ip , tal que:
² B½
²
p
P
1
p
S
Ik
k=1
¹(Ik ) · ².
24 Observaci¶
on: Los rect¶angulos considerados en la de¯nici¶on anterior pueden ser
cerrados o de otro tipo ( es decir, conteniendo o no a su frontera). La medida de
estos subrect¶agulos de R3 es su volumen, por tanto, intuitivamente, un conjunto de
contenido cero es aquel que encierra o de¯ne un volumen nulo.
Ejemplos:
² Un conjunto ¯nito de puntos de R3 tiene contenido cero.
² Un segmento en R3 tiene contenido cero.
² Un rect¶angulo de R2 tiene contenido cero en R3 .
² Los conjuntos de R2 proyectables en x, o proyectables en y, tienen contenido cero
en R3 .
² Un rect¶angulo no vac¶³o de R3 no tiene contenido cero.
5 Propiedades: 1. Si B ½ C y C tiene contenido cero, entonces B tiene contenido
cero.
2. Si B1 ; : : : ; Bq tienen contenido cero, B =
q
S
Bk tiene contenido cero.
k=1
3. Si B tiene contenido cero, entonces B es un conjunto acotado de R3 .
2.1.12 Proposici¶
on.- Si f : [a; b] £ [c; d] 7
¡! R es continua, entonces su gr¶a¯ca, es
decir el conjunto B = f(x; y; f (x; y)) : (x; y) 2 [a; b] £ [c; d]g, tiene contenido cero.
Ejemplos:
² El conjunto f(x; y; z) 2 R3 : x2 + y 2 + z 2 = 1g ( esfera) tiene contenido cero ( por
ser uni¶on de dos conjuntos de contenido cero).
² El conjunto f(x; y; z) 2 R3 : x2 + y 2 = 1; 1 · z · 5g (cilindro acotado) tiene
contenido cero.
26
² El conjunto f(x; y; z) 2 R3 : x2 + y 2 = z 2 ; 1 · z · 5g (tronco de cono acotado)
tiene contenido cero.
2.1.13 Proposici¶
on.- Sean I = [a; b] £ [c; d] £ [e; f ], f : I 7
¡! R una funci¶on
acotada y B = f(x; y; z) : f no es continua en (x; y; z)g. Si B es un conjunto de
contenido cero, entonces f es integrable en I.
25 Observaci¶
on: Sin embargo, el rec¶³proco de esta proposici¶on no es verdadero,
existen funciones integrables cuyo conjunto de puntos de discontinuidad no tiene
contenido cero.
2.2
Integral triple en un conjunto acotado
En esta secci¶on vamos a extender el concepto de integral triple a conjuntos m¶as
generales del espacio y a caracterizar los conjuntos del espacio a los que se les puede
asignar un volumen ¯nito.
2.2.1 De¯nici¶
on.- Sea f : S 7
¡! R una funci¶on de¯nida y acotada sobre un conjunto acotado S contenido en R3 . Sea I un intervalo que contiene a S. Se denomina
funci¶on caracter¶³stica o prolongaci¶on caracter¶³stica de f a I, a la funci¶on f~I : I 7
¡! R,
de¯nida por:
8
< f (x; y; z)
f~I (x; y; z) = :
0;
si (x; y; z) 2 S
si (x; y; z) 2 I ¡ S
2.2.2 De¯nici¶
on.- La funci¶on f de la de¯nici¶on anterior se dice que es integrable
en S si, y s¶olo si, su prolongaci¶on caracter¶³stica f~ es integrable. En tal caso, se
de¯ne:
ZZZ
ZZZ
f (x; y; z) dxdydz =
f~I (x; y; z) dxdydz
S
I
26 Observaci¶
on: Resulta f¶acil probar que la de¯nici¶on anterior es independiente
del rect¶angulo I considerado, con la u
¶nica condici¶on de que contenga al conjunto S.
(Pensadlo).
Vamos a caracterizar ahora qu¶e conjuntos del espacio tiene un volumen ¯nito ;
a estos es a los que podemos extender el concepto de integral triple:
2.2.3 Proposici¶
on.- Sea S un subcjunto acotado de R3 ; la funci¶on id¶enticamente 1
en S es integrable en dicho conjunto si, y s¶olo si, F r(S) es un conjunto de contenido
cero en R3 .
2.2.4 De¯nici¶
on.- Un s subconjunto S de R3 se denomina medible Jordan ( o
simplemente medible) si es acotado y F r(S) tiene contenido cero. En ese caso se
RRR
de¯ne el volumen del conjunto S como: ¹(S) = S dxdydz.
27
27 Observaci¶
on: Los conjuntos medibles del espacio son, por tanto, los conjuntos
acotados a los que es posible asignar un volumen. Entre ¶estos, los que consideraremos
con m¶as frecuencia son los siguientes:
² Regi¶on proyectable en x-y: son los conjuntos de la forma
S = f(x; y; z) : (x; y) 2 D;
'1 (x; y) · z · '2 (x; y)g
siendo D un conjunto proyectable en x o en y, y '1 y '2 funciones reales continuas
en D.
² Regi¶on proyectable en y-z: son los conjuntos de la forma
S = f(x; y; z) : (y; z) 2 D;
Ã1 (y; z) · x · Ã2 (y; z)g
siendo D un conjunto proyectable en y o en z, y Ã1 y Ã2 funciones reales continuas
en D.
² Regi¶on proyectable en z-x: son los conjuntos de la forma
S = f(x; y; z) : (x; z) 2 D;
Á1 (x; z) · y · Á2 (x; z)g
siendo D un conjunto proyectable en x o en z y Ã1 y Ã2 funciones reales continuas
en D.
² Regi¶on proyectable en x-y-z: son los conjuntos que son proyectables tanto en x-y
como en y-z como en z-x.
28
² Regi¶on proyectable: aquella que se puede descomponer como uni¶
on de un n¶
umero
¯nito de regiones proyectables de los tipos anteriores.
6 Propiedades: En general, son las mismas que en el primer apartado, pero referidas ahora a un conjunto medible Jordan cualquiera S. La propiedad de sumabilidad
de la integral respecto del dominio ( propiedad 6) ), es la u
¶nica que presenta alguna
diferencia; se expresa ahora en la siguiente forma: Si el conjunto S se subdivide en
dos conjuntos medibles Jordan S1 y S2 , de forma que S1 [ S2 = S y la intersecci¶on
de ambos es un conjunto de contenido cero, entonces f es integrable en S si, y s¶olo
si, lo es en S1 y en S2 . En ese caso,
ZZZ
f=
S
ZZZ
f+
S1
ZZZ
f
S2
2.2.5 Proposici¶
on.- Sea f : S 7
¡! R una funci¶on de¯nida y acotada sobre un
conjunto medible Jordan S, contenido en R3 . Si el conjunto de puntos de discontinuidad de la funci¶on f en int(S) tiene contenido cero, entonces f es integrable en
S. (>Por qu¶e?).
2.3
Reducci¶
on de la integral triple a integrales simples iteradas.
2.3.1 De¯nici¶
on.- Sea
S = f(x; y; z) : a · x · b; g1 (x) · y · g2 (x); '1 (x; y) · z · '2 (x; y) g
donde g1 y g2 son funciones continuas en [a,b] y '1 , '2 son continuas en D = f(x; y) :
a · x · b; g1 (x) · y · g2 (x)g, y f : S 7
¡! R una funci¶on acotada. Si para cada
(x; y) 2 D la funci¶on fx;y : ['1 (x; y); '2 (x; y)] 7
¡! R de¯nida por fx;y (z) = f (x; y; z)
es integrable en ['1 (x; y); '2 (x; y)], tiene sentido la funci¶on g : D 7
¡! R de¯nida
R '2 (x;y)
por g(x; y) = '1 (x;y) f (x; y; z)dz. Si, a su vez, existe la integral iterada en y-x de la
funci¶on g, entonces se denomina integral iterada o sucesiva de la funci¶
on f respecto
de z-y-x a:
Z
b
a
Z
g2 (x)
(
Z
'2 (x;y)
(
g1 (x)
f (x; y; z)dz)dy)dx:
'1 (x;y)
De manera an¶aloga se de¯nen las otras integrales iteradas (respecto de z-x-y, respecto
de y-z-x, de y-x-z, de x-y-z y de x-z-y).
Vamos a enunciar un teorema que permite el c¶
alculo efectivo de integrales
triples, reduciendo ¶estas al c¶alculo de integrales simples iteradas.
2.3.2 Teorema.- (Teorema de Fubini.) Sea S una regi¶on proyectable en x-y como
la dada en la de¯nici¶on anterior, f : S 7
¡! R una funci¶on de¯nida y acotada en S,
continua en int(S). Entonces:
29
1. f es integrable en S.
2. Existe la integral iterada de f respecto de z,y,x.
3.
RRR
S
f (x; y; z) dxdydz =
R b R g2 (x) R '2 (x;y)
a ( g1 (x)
(
f (x; y; z)dz)dy)dx:
'1 (x;y)
Nota: Se tiene un resultado an¶alogo si la regi¶on S es proyectable en y-z o en z,-x.
2.3.3 Proposici¶
on.- Como consecuencia del teorema anterior se tienen los dos resultados siguientes:
1. Sea S una regi¶on como la del teorema, y para cada x 2 [a; b], sea A(x) el a¶rea
de la secci¶on que en S produce el plano X = x. Entonces, se puede calcular el
R
volumen de S por medio de: ab A(x)dx.( Este resultado se conoce como principio
de Cavalieri, o c¶alculo del volumen por secciones).
2. Sea S una regi¶on como la del teorema y f : S 7
¡! R una funci¶on de¯nida y
acotada en S, continua en int(S). Si la funci¶on f depende s¶olo de la variable x y
para cada x 2 [a; b] denotamos por A(x) el a¶rea de la secci¶on que en S produce
el plano X = x, entonces:
ZZZ
S
f=
Z
b
f (x)A(x)dx
a
( Este resultado se conoce como c¶alculo de la integral por secciones. Tr¶atese de
demostrar, a partir del teorema de Fubini).
28 Observaci¶
on: Se obtiene un resultado an¶alogo ( considerando ahora las secciones que en S producen los planos Y = y) si la regi¶on S es proyectable con
conjunto D proyectable en y y si la funci¶on f depende s¶olo de la variable y. Igualmente si D es proyectable en z y la funci¶
on f depende s¶olo de la variable z. ( Enunciar
dichos resultados)
2.4
Cambio de variable
Coordenadas curvil¶³neas
Igual que ocurre en el plano, una importante clase de problemas f¶³sicos y de ingenier¶³a est¶an relacionados con sistemas o s¶olidos en el espacio con simetr¶³a esf¶erica, y
otros con simetr¶³a axial. En estos casos ( adem¶as de en otras muchas ocasiones) el
sistema de coordenadas cartesianas rectangulares no es el m¶as adecuado para abordar estos problemas. Resulta necesario, igual que en R2 , de¯nir otros sistemas de
coordenadas curvil¶³neas, entre los que vamos a destacar el de coordenadas esf¶ericas
y el de coordenadas cil¶³ndricas.
30
En estos casos, las nuevas coordenadas vendr¶
an dadas por funciones '(u; v; w)
3
3
de¯nidas de abiertos de R en R , cumpliendo id¶enticas condiciones que las correspondientes funciones en R2 . De nuevo, el cambio de coordenadas va a transformar
el reticulado rectangular del espacio en un nuevo reticulado en el que las im¶agenes
de los planos paralelos a los ejes van a ser super¯cies en R3 , llamadas super¯cies coordenadas, que se cortan en curvas alabeadas ( es decir, no necesariamente planas),
llamadas curvas coordenadas. Dichas curvas se obtienen como imagen de las rectas
paralelas a los planos coordenados.
2.4.1 De¯nici¶
on.- Sea U un subconjunto abierto de R3 . Una funci¶on vectorial
':U 7
¡! R3 se llama cambio de coordenadas en U si veri¯ca las tres propiedades
siguientes:
1. ' es de clase C 1 en U.
2. ' es inyectiva en U.
= 0 para cada (u; v; w) 2 U .
3. El determinante jacobiano J' (u; v; w) 6
29 Observaci¶
on: Las propiedades 1) y 3) establecen que la funci¶on ' es una aplicaci¶on abierta [Proposici¶on 1.5.6, Laguna-Mariju¶an], es decir, que transforma los
abiertos de U ( y en particular el propio U) en abiertos de '(U); la propiedad 2)
establece adem¶as que ' es biyectiva de U en '(U ), y '¡1 es una funci¶on de clase
C 1 ('(U )), en virtud del Teorema de la funci¶on inversa (proposici¶on 5.1.5, LagunaMariju¶an). Por u
¶ltimo, como consecuencia de la regla de la cadena, si a 2 U ,
1
J' (a) = J ¡1 ('(a)) .
'
Todo lo anterior indica que '¡1 es tambi¶en un cambio de coordenadas en '(U).
Ejemplos:
² Cambios lineales de coordenadas
Uno de los cambios m¶as sencillos es el de¯nido por una matriz (3 £ 3) A, no
singular ( es decir, con det(A) 6
= 0). Si consideramos la base can¶onica en R3 ,
las columnas de la matriz constituyen una base en R3 y las correspondientes
curvas coordenadas vendr¶³an dadas por rectas en la direcci¶on de estos dos vectores. En ese caso, cada rect¶angulo R en el sistema U V W se tansformar¶³a en un
paralelep¶³pedo, y la relaci¶on entre sus vol¶
umenes vendr¶³a dada por:
¹('(R)) = j det(A)j ¹(R)
² Coordenadas cil¶³ndricas
Sea U = f(r; µ; z) : r > 0; 0 < µ < 2¼; z 2 Rg y
' de¯nida por:
'(r; µ; z) = (r cos µ; r sen µ; z):
31
La imagen '(U ) es el conjunto R3 ¡ f(x; 0; z) : x ¸ 0g, la funci¶on ' es un cambio
de coordenadas de U en '(U) y
¯
¯
¯ cos µ
¯
J' (r; µ; z) = ¯¯ ¡r sen µ
¯
¯
0
¯
sen µ 0 ¯¯
¯
r cos µ 0 ¯¯ = r
¯
0
1 ¯
El signi¯cado de las nuevas coordenadas es el siguiente:
{ r mide la distancia de la proyecci¶on del punto (x; y; z) sobre el plano z = 0 al
origen de coordenadas.
{ µ mide el a¶ngulo formado por el semieje OX positivo y la proyecci¶
on del vector
de coordenadas (x; y; z) sobre el plano z = 0.
{ z es la correspondiente coordenada del punto (x; y; z).
Las super¯cies coordenadas son cilindros de eje OZ ( para r constante), semiplanos
que pasan por el eje OZ y son perpendiculares al plano XY ( para µ constante) y
planos paralelos al plano XY ( para z constante).
Las curvas coordenadas son, en este caso: circunferencias centradas en el eje OZ
y paralelas al plano XY (para r constante y z constante), rectas paralelas al eje
OZ (para r constante y µ constante), y semirrectas paralelas al plano XY que
pasan por el eje OZ (para µ constante y z constante).
² Coordenadas esf¶ericas.
Sea U = f(½; µ; Ã) : ½ > 0; 0 < µ < 2¼; 0 < Ã < ¼g y ' de¯nida por:
'(½; µ; Ã) = (½ sen à cos µ; ½ sen à sen µ; ½ cos Ã):
32
La imagen '(U ) es el conjunto R3 ¡ f(x; 0; z) : x ¸ 0g, la funci¶on ' es un cambio
de coordenadas de U en '(U) y
¯
¯
sen (µ) sen (Ã)
cos(Ã)
¯ cos(µ) sen (Ã)
¯
¯
J' (½; µ; Ã) = ¯ ¡½ sen (µ) sen (Ã) ½ sen (µ) cos(Ã)
0
¯
¯ ½ cos(µ) cos(Ã)
½ cos(µ) sen (Ã) ¡½ sen (Ã)
¯
¯
¯
¯
¯ = ¡½2 sen Ã
¯
¯
¯
El signi¯cado de las nuevas coordenadas es el siguiente:
{ ½ mide la distancia de cada punto del espacio al origen de coordenadas en el
espacio XYZ:
x2 + y 2 + z 2 = ½2
{ µ mide el a¶ngulo formado por el semieje OX positivo y la proyecci¶
on del vector
de coordenadas (x; y; z) sobre el plano z = 0.
{ Ã mide el a¶ngulo formado por el semieje OZ positivo y el vector de coordenadas
(x; y; z).
Las super¯cies coordenadas son esferas centradas en el origen, semiplanos que
pasan por el eje OZ y son perpendiculares al plano XY y semiconos circulares
con v¶ertice en el origen y cuyo eje coincide con el eje OZ.
Las curvas coordenadas son, en este caso, las circunferencias con centro en el eje
OZ y paralelas al plano z = 0 (para ½ constante y à constante); semicircunferencias con centro en el origen y situadas en planos con a¶ngulo µ constante (para
µ constante y ½ constante) y semirrectas que parten del origen de coordenadas
(para µ constante y à constante).
2.4.2 Proposici¶
on.- Sea U un subconjunto abierto de R3 y ' : U 7
¡! R3 una
funci¶on de clase C 1 (U ). Si S es un conjunto medible con S [ F r(S) ½ U y ' es un
cambio de coordenadas en int(S), entonces:
1. '(S) es medible en R3 .
33
2. F r('(S)) ½ '(F r(S)).
Si adem¶as ' es un cambio de coordenadas en U, se tiene que
F r('(S)) = '(F r(S)):
30 Observaci¶
on: En las condiciones de la proposici¶on anterior y si ' s¶olo es un
cambio de coordenadas en el interior de S, no tiene por qu¶e existir funci¶on inversa
de '(S) en S sino s¶olo de int(S) en '(int(S)) ( que es abierto).
La proposici¶on anterior nos ser¶a de utilidad para determinar los dominios de
integraci¶on al realizar un cambio de variables en una integral.
Teorema del cambio de variable
2.4.3 Teorema.- Sea U un subconjunto abierto de R3 , S un conjunto medible con
S [ F r(S) ½ U y ' : U 7
¡! R3 una funci¶on de clase C 1 (U) que es un cambio de
coordenadas en int(S). Si f : '(S) 7
¡! R es una funci¶on acotada cuyo conjunto de
puntos de discontinuidad en '(S) es de contenido cero, entonces:
1. f es integrable en '(S).
2. (f ± ')jJ' j es integrable en S.
3.
RRR
'(S)
f (x; y; z) dxdydz =
RRR
S (f
± ')(u; v; w)jJ' (u; v; w)j dudvdw.
[Lang, An¶alisis Matem¶atico, pg. 431]
31 Observaci¶
on: Signi¯cado \geom¶etrico" del Jacobiano del cambio de coordenadas.
Si el cambio de coordenadas es lineal, es decir, dado por una matriz no singular A,
el teorema de cambio de variable aplicado a la funci¶on id¶enticamente 1 indica que:
¹('(S)) = j det(A)j¹(S)
puesto que en ese caso el jacobiano del cambio de coordenadas es det(A). Puesto
que toda funci¶on de clase C 1 se puede aproximar localmente por una transformaci¶on
lineal, se puede considerar el jacobiano del cambio de coordenadas como un factor
de la variaci¶on local de volumen del recinto de integraci¶on al ser transformado.
El siguiente resultado es una consecuencia del teorema del cambio de variable
y permite calcular de forma r¶apida algunas integrales:
2.4.4 Proposici¶
on.- Sea f (x; y; z) una funci¶on de¯nida en un conjunto medible D
3
de R :
34
1. Si D es sim¶etrico respecto del plano x = 0 y f (x; y; z) = f (¡x; y; z), para
(x; y; z) 2 D (es decir, es una funci¶on par respecto de la variable x) entonces:
ZZZ
f (x; y; z) dx dy dz = 2
D
ZZ
f (x; y; z) dx dy dz;
D1
donde D1 = f(x; y; z) 2 D; x ¸ 0g.
2. Si D es sim¶etrico respecto del plano x = 0 y f (x; y; z) = ¡f (¡x; y; z), para
(x; y; z) 2 D (es decir, es una funci¶on impar respecto de la variable x) entonces:
ZZZ
f (x; y; z) dx dy dz = 0:
D
32 Observaci¶
on: Se obtienen resultados an¶alogos si el conjunto D es sim¶etrico
respecto del plano y = 0 ( respectivamente z = 0) y la funci¶on es impar ( caso de
integral nula) o par respecto de la variable y (respectivamente z) en D.
2.4.5 Proposici¶
on.- Sea f (x; y; z) una funci¶on de¯nida en un conjunto medible D
3
de R . Si D es sim¶etrico respecto de los tres planos coordenados y f (x; y; z) es una
funci¶on par respecto de las tres variables, entonces:
ZZZ
f (x; y; z) dx dy dz = 8
D
ZZZ
D1
donde D1 = f(x; y; z) 2 D; x ¸ 0 y ¸ 0 z ¸ 0g.
35
f (x; y; z) dx dy dz;
2.5
Ejercicios
1. Demostrar, utilizando sumas superiores e inferiores, que :
(a) La funci¶on f : I 7
¡! R, de¯nida por f (x; y; z) = k, para todo (x; y; z) 2 I, es
RRR
integrable y I kdxdydz = k¹(I).
(b) La funci¶on f : [0; 2] £ [1; 4] £ [0; 1] 7
¡! R de¯nida por
f (x; y; z) =
8
< 0
si x 2 Q, y 2 Q y z 2 Q
: 1; en los dem¶
as casos
no es integrable.
2. Sean D1 = f(x; y; z) 2 R3 : x > yg y D2 = f(x; y; z) 2 R3 : x < y g;
sea I = [¡1; 1] £ [¡1; 1] £ [¡1; 1] y f (x; y; z) de¯nida en I por:
f (x; y; z) =
(
x2
si x 2 I \ D1
sen (x2 + y 2 ) si x 2 I \ D2
Justi¯car por qu¶e f es integrable en I.
3. Sean f : [a; b] 7
¡! R, g : [c; d] 7
¡! R y h : [e; f ] 7
¡! R, funciones integrables y
Á(x; y; z) = f (x)g(y)h(z). Demostrar que Á es integrable en I = [a; b] £ [c; d] £
RRR
R
R
R
[e; f ] y que I Á = ( ab f )( cd g)( ef h).
4. Sea I = [0; 1] £ [0; 2] £ [0; 3]; demostrar que 0 ·
RRR
2
I (x
+ y 2 + z)dx dy dz · 48.
5. Sean f ,g : I 2 R3 7
¡! R tales que g(~x) ¸ 0 y m · f (~x) · M para todo ~x 2 I.
(a) Demostrar que existe k 2 [m; M ] tal que
RRR
I
fg = k
RRR
I
g.
(b) Demostrar que si adem¶as f es continua, existe x~0 2 I tal que
RRR
f (x~0 ) I g.
RRR
I
fg =
6. Demostrar que si I = [0; 1] £ [0; 3] £ [0; 5], entonces
ZZZ
I
2 +y 2
(ex+y ¡ 1)ex
log(1 + z 2 )dxdydz ¸ 0:
7. Sea D = f(x; y; z) 2 R3 : x2 + (y ¡ 1)2 · 1; ¡1 · z · 1g y f (x; y; z) = (y ¡ 1)3 .
>se tiene la siguiente igualdad:
ZZZ
f =2
D
ZZZ
f
D1
con D1 = f(x; y; z) 2 D : y > 1g? Si es as¶³, demostrarlo, y si no, encontrar el
valor de la integral.
36
8. Dibujar los recintos y calcular:
R 1 nR p1¡x2
Ra
o
0 dz] dy dx
hR p
i
o
a
2 + y 2 dz dy dx
(b)
z
x
0
(
" p
#
)
p
R 1 R 1¡x2 R 1¡x2 ¡y2 p
2
2
2
(c) 0 0
x + y + z dz dy dx
0
(a)
p
0
¡ 1¡x2
p
n
R 2 R 2x¡x2
0
0
[
; 8 a2 ; ¼8 ))
(Sols: ¼a
2 9
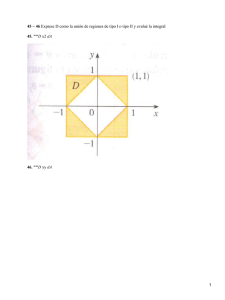
9. Si D es el dominio de integraci¶on limitado por los planos coordenados y el plano
x + y + z = 1 , calcular:
ZZZ
dx dy dz
D (x + y + z + 1)3
(Sol: ln2
¡
2
5
)
16
10. Si D es el dominio de integraci¶on de¯nido por 0 < b2 < x2 + y 2 + z 2 < a2 ,
calcular:
ZZZ
dx dy dz
p 2
x + y2 + z 2
D
(Sol:2¼(a2 ¡ b2 ))
11. Si D es el dominio de integraci¶on limitado por x2 + y 2 = 2z y z = 2, calcular:
ZZZ
(x2 + y 2 ) dx dy dz
D
(Sol:16¼=3)
12. Si D= f(x; y; z)= x > 0 ; x2 + y 2 + (z ¡ 1)2 < 1 ; 4z 2 > 3(x2 + y 2 )g calcular:
ZZZ
x2 dx dy dz
D
n
13. Si D= (x; y; z)= 0 < z < x2 + y 2
ZZZ
0·y·
q
o
p
2x ¡ x2 calcular:
zy x2 + y 2 dx dy dz
D
14. Encontrar una f¶ormula abreviada para resolver integrales del tipo
ZZZ
f (x) dx dy dz
A
donde A es un s¶olido tal que sus secciones por planos x =cte tienen a¶reas conocidas. (Se supone que A es del tipo x,y,z).
Como aplicaci¶on si A= f(x; y; z)=x2 + y 2 + z 2 · R2 ; x2 + y 2 + z 2 · 2Rxg, calcular:
ZZZ
x2 dx dy dz
A
37
n
o
p
15. Si D= (x; y; z)= x2 + y 2 · z · 3 calcular:
ZZZ q
x2 + y 2 + z 2 dx dy dz
D
n
2
16. Si D= (x; y; z)= xa2 +
y2
b2
+
z2
c2
p
(Sol:¼(27=2)(2 2 ¡ 1))
o
¡ 1 · 0 calcular:
ZZZ
q
e
2
2
x2
+ y2 + z2
a2
b
c
dx dy dz
D
(Sol:4¼abc(e ¡ 2))
17. Hallar el volumen total del espacio comprendido entre el cono 2(x2 +y 2 )¡z 2 = 0
p
(Sol:4¼a3 ( 2 ¡ 1)=3)
y el hiperboloide x2 + y 2 ¡ z 2 = ¡a2 . (z ¸ 0)
18. Hallar el volumen determinado por el paraboloide
z = 2 + 2x + 2y
x2 + y 2 = z
y el plano
(Sol:8¼)
19. Si V es la parte com¶
un al paraboloide 2az ¸ x2 +y 2 y a la esfera x2 +y 2 +z 2 · 3a2
demostrar sin efectuar c¶alculos, es decir, mediante alg¶
un cambio de variables, que
ZZZ
(xy + xz + yz) dx dy dz = 0
V
20. Si D es el interior del elipsoide
ZZZ
4x2 + 9y 2 + 36z 2 = 36
calcular:
(2x + 3y + 6z)2 dx dy dz
D
(Sol: 864¼
)
5
(Nota: Recu¶erdese el ejercicio 19 )
21. Calcular el volumen del cuerpo engendrado por un tri¶
angulo rect¶angulo is¶osceles
variable, uno de cuyos catetos est¶a constantemente en una vertical ¯ja, y el otro
es una cuerda variable de una circunferencia horizontal que pasa por su pie.
3
(Sol: 16R
)(R=radio de la circunferencia)
9
22. Calcular el volumen com¶
un al elipsoide y al paraboloide el¶³ptico de ecuaciones:
x2 y 2 z 2
+ 2 + 2 =1
a2
b
c
x2 z 2
y
+ 2 =
2
a
c
b
(Sol: 5¼
(3 ¡
12
38
p
5)abc)
23. Hallar el promedio integral p de los cuadrados de la distancia al origen para los
puntos del interior de la esfera x2 + y 2 + z 2 = 36. Estudiar si existe un punto ~c
del interior de la esfera con jj~cjj2 = p
24. Sea M el conjunto acotado limitado por los planos x = 0; y = 0; z = 0;
y = 1; x + z = 1: Calcular el volumen de g(M) donde
g(x; y; z) = (e2z + e2y ; e2x ¡ e2z ; x ¡ y)
25. Calcular:
donde
ZZZ
(x + y + z) x2 y 2 z 2 dx dy dz
X
X = f(x; y; z)=x ¸ 0; y ¸ 0; z ¸ 0; x + y + z · 1g
1
(Sol: 10¤7!
)
26. Evaluar, con un cambio de variable adecuado
ZZZ
R
(x + y + z)(x + y ¡ z)(x ¡ y ¡ z) dx dy dz
siendo R el tetraedro limitado por
x+y¡z =0
x + y + z = 0;
x ¡ y ¡ z = 0;
2x ¡ z = 1
27. Se considera un s¶olido V tal que su volumen viene dado por la integral
Z
2¼
0
"Z
¼¡©0
©0
"Z
2
2
( sen ©)¡1
#
#
½ sen © d½ d© dµ
donde sen ©0 = 1=2.
Expresa anal¶³ticamente, en coordenadas cartesianas qui¶en es V, dib¶
ujalo y calcula
su volumen de dos maneras diferentes de la dada y de las coordenadas cartesianas.
(Nota: Expresa ½2 sen 2 © en coordenadas cartesianas.)
39