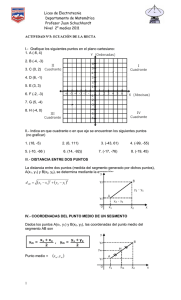
17. Sistemas Coordenados

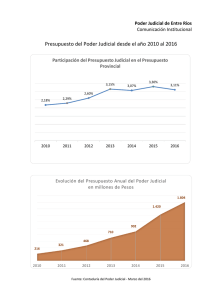
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
MATEMÁTICAS BÁSICAS
SISTEMAS COORDENADOS
SISTEMA COORDENADO UNIDIMENSIONAL
Existe una correspondencia biyectiva o biunívoca entre el conjunto de los números reales y el de los
puntos de una recta. A esta recta que tiene un origen, un sentido y en donde se pueden ubicar todos los
números reales se le conoce como sistema coordenado unidimensional. Gráficamente esto es:
P4
-5
P1
-4
-3
P2
-2
-1
0
P3
1
La notación habitual para localizar un punto es:
2
3
4
5
x
P(x ) . Por ejemplo, para ubicar los puntos
P1 (−2.6), P2 (0.5), P3 (4.7 ), P4 (−5) , simplemente se localiza su respectivo valor en la numeración y se le
marca.
Se define como abscisa de un punto a la distancia del origen al punto en magnitud y signo.
La distancia dirigida (dd ) que existe de un punto
inicial:
P1 a un P2 viene dada por el valor final menos el
dd = P2 − P1 .
La distancia (d ) entre dos puntos
absoluto, esto es:
P1 y P2 está dada por el valor final menos el inicial pero en valor
d = P2 − P1 .
Es decir, la diferencia que existe entre distancia dirigida y distancia entre dos puntos es que en la primera se
toma en cuenta el signo y su magnitud, y en la segunda sólo se toma su magnitud. Se mide en unidades (u ).
Ejemplo.
Encontrar la distancia dirigida y la distancia entre los siguientes pares de puntos:
()
1) P1 3 y
Solución:
P2 (−6)
dd = −6 − 3 = −9 u . y d = − 6 − 3 = − 9 = 9 u.
1
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
2)
P1 (− π)
Autor: Dr. José Manuel Becerra Espinosa
 35 

 6 
y P2  −
Solución:
35
≈ 5.8333
6
dd = −5.8333 − (−3.14159) = −2.69 u .
−π ≈ −3.14159
y
−
d = − 5.8333 − (− 3.14159 ) = − 2.69 = 2.69 u .
SISTEMA COORDENADO BIDIMENSIONAL
Es un sistema formado por dos ejes numéricos perpendiculares donde su origen es el punto en que se
cruzan.
Se genera estableciendo una correspondencia biunívoca entre los puntos de un plano y los elementos de
todas las parejas ordenadas de números reales. Esto quiere decir que se genera un plano a partir de una
infinidad de puntos.
y
5
4
Cuadrante II
Cuadrante I
3
(-, +)
(+, +)
2
1
-5
-4
-3
-2
-1
-1
1
2
3
4
5
-2
Cuadrante III
(-, -)
-3
Cuadrante IV
-4
(+, -)
-5
Se forman cuatro regiones llamadas cuadrantes.
El eje horizontal ( x ) recibe el nombre de eje de las abscisas.
El eje vertical ( y ) recibe el nombre de eje de las ordenadas.
Para ubicar un punto en el plano se utiliza la siguiente notación: P (x , y )
Ejemplo.
Ubicar los siguientes parejas ordenadas en el plano:
 8

P1 (2 ,4 ), P2  − , − 2  , P3 (− 1,1), P4 (3,− 4 ), P5 (− 5, π ), P6 (0 ,2 ), P7 (4.5,0 )
 3

Solución:
2
x
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
y
5
P1 (2,4)
4
P5 (-5, π)
3
P6 (0,2)
2
P3 (-1,1)
-5
-4
-3
-2
P7 (4.5,0)
1
-1
-1
1
2
3
4
5
x
-2
P2 (-2.66,-2)
-3
-4
P4 (3,-4)
-5
Ejemplos.
Dados los siguientes conjuntos, obtener el producto cartesiano correspondiente:
1) A = {1, 2 ,3 }, B = { 0 ,1, 2 }
Solución.
El conjunto solución a este producto cartesiano son nueve puntos discretos formado por las parejas
ordenadas. A × B = { (1,0 ) ,(1,1),(1, 2 ),(2 ,0 ),(2 ,1),(2 , 2 ),(3,0 ),(3,1),(3, 2 ) }
Gráficamente esto es:
y
5
4
3
2
1
-5
-4
-3
-2
-1
-1
1
2
3
4
5
x
-2
-3
-4
-5
2) A = { x
{
1 ≤ x ≤ 3, x ∈ R } , = B = y
0 ≤ x ≤ 2, y ∈ R }
Solución.
El conjunto solución a este producto cartesiano es una superficie plana de forma rectangular limitada
tanto en x como en y . Gráficamente esto es:
3
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
y
5
4
3
2
1
-5
-4
-3
-2
-1
-1
1
2
3
4
5
x
-2
-3
-4
-5
{
3) A = x
x ∈ R }, = B = { y
y ∈R }
Solución.
El conjunto solución a este producto cartesiano es una superficie plana ilimitada tanto en x como en
Gráficamente esto es:
y.
y
5
4
3
2
1
-5
-4
-3
-2
-1
-1
1
2
3
4
5
x
-2
-3
-4
-5
Como puede deducirse, el sistema coordenado bidimensional está constituido por el producto cartesiano
×R.
de los números reales (en x ) por los números reales (en y ), es decir, R2= R×
SISTEMA COORDENADO TRIDIMENSIONAL
Es un sistema formado por tres ejes numéricos perpendiculares donde su origen es el punto en que se
cruzan.
Se forma estableciendo una correspondencia biunívoca entre los puntos de un espacio y los elementos
de todas las ternas ordenadas de números reales. Esto quiere decir que se genera un volumen a partir de
una infinidad de puntos.
4
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
z
P(x1, y1, z1)
y
z1
y1
x
x1
Se forman ocho regiones llamadas octantes.
El eje x recibe el nombre de eje de las abscisas.
El eje y recibe el nombre de eje de las ordenadas.
El eje z recibe el nombre de eje de las cotas.
Para ubicar un punto en el espacio se utiliza la siguiente notación: P (x , y , z ) , es decir de forma similar
que en un plano.
DISTANCIA ENTRE DOS PUNTOS
Sean P1 ( x1 , y1 ) y P2 (x 2 , y 2 ) dos puntos cualesquiera en el plano:
y
P(x2, y2)
y2
d
y2-y1
P(x1, y1)
y1
x1
x2
x
x2-x1
Al formarse un triángulo, se observa que los catetos son las diferencias de ordenadas y de abscisas.
Ahora, recordando el teorema de Pitágoras expuesto en la unidad II: c 2 = a 2 + b 2 y aplicándolo se tiene:
d 2 = (x2 − x1 )2 + ( y 2 − y1 )2
despejando d se obtiene la fórmula para encontrar la distancia entre dos puntos:
5
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
(x2 − x1 )2 + ( y2 − y1 )2
d=
Ejemplos.
Obtener la distancia entre los siguientes pares de puntos:
1) P1 (4 , − 5) y P2 (7 , − 1)
Solución.
d=
(7 − 4)2 + (− 1 − (− 5))2
= 3 2 + 4 2 = 9 + 16 = 25 = 5 u .
2) P1 (−6 , − 11) y P2 (1,13 )
Solución.
d=
3)
(1 − (− 6))2 + (13 − (− 11))2
1 7
P1  ,− 
4 4
y
= 7 2 + 24 2 = 49 + 576 = 625 = 25 u .
 3 15 
P2  − ,− 
 8 8
Solución.
2
2
2
2
25 1
 3 1   15  7  
 5  1
d =  − −  +  − −  −   =  −  +  −  =
+
=
64 64
 8 4   8  4 
 8  8
(
)
(
2 ,π y P2 − 5 ,−0.170
4) P1
Solución.
Utilizando tres cifras decimales:
d=
26
26
=
u.
64
8
)
(− 2.236 − 1.414)2 + (− 0.170 − 3.141)2
(− 3.676)2 + (− 3.311)2
=
= 13.512 + 10.962
= 24.474 ≈ 4.947 u .
Ejemplo.
Si los puntos
P1 (−2 ,− 2 ) , P2 (1,3)
y P3 (5 , − 3) son los vértices de un triángulo, obtener su perímetro.
y
5
4
P1 (1,3)
3
2
1
-5
-4
-3
P2 (-2,-2)
-2
-1
-1
1
2
3
4
5
x
-2
-3
-4
-5
6
P3 (5,-3)
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
la distancia entre
P1
y
P2
es: d1 =
(1 − (− 2 ))2 + (3 − (− 2 ))2
la distancia entre
P1
y
P3
es: d 2 =
(5 − 1)2 + (− 3 − 3)2
= 3 2 + 5 2 = 9 + 25 = 34
= 4 2 + (− 6 )2 = 16 + 36 = 52
es: d 3 = (5 − (− 2 )) + (− 3 − (− 2 )) =
Por tanto, el perímetro viene dado por la suma de sus tres lados:
la distancia entre
P2
y
2
P3
2
7 2 + (− 1)2 = 49 + 1 = 50
P = d1 + d 2 + d 3 = 34 + 52 + 50 ≈ 5.83 + 7.21 + 7.07 ≈ 20.11 u .
Ejemplo.
Sea el punto
P1 (4,− 3)
y el punto
P2 (x ,10 ) , obtener la abscisa de P2
de tal manera que la distancia
que los separe sea 15 unidades.
Solución.
Sustituyendo los datos en la fórmula se tiene:
15 =
(x − 4)2 + (10 − (− 3))2
=
(x − 4)2 + 132
(x − 4)2 + 169
=
despejando x se tendrán dos soluciones de x 2 :
15 2 = (x − 4)2 + 169 ⇒
x1 ≈ 11.48
y
P1 (11.48 ,10 )
225 − 169 = (x − 4)2 = 56 ⇒ x − 4 = ± 56
x2 ≈ −3.48 ,
y el punto
por lo que los puntos buscados son aproximadamente:
P1 (− 3.48 ,10 )
En el espacio, la fórmula de distancia entre dos puntos se deduce de forma similar que en dos
dimensiones, considerando que la distancia es un segmento de recta que pertenece a un plano. Esto es,
si se tienen los puntos P1 ( x1 , y1 , z1 ) y P2 ( x 2 , y 2 , z 2 ) , la distancia que los separa es:
d=
(x2 − x1 )2 + ( y2 − y1 )2 + (z 2 − z1 )2
Gráficamente, es:
z
y
P1 (x1, y1, z1)
z1
d
z2
P2 (x2, y2, z2)
y2
y1
x1
x
x2
7
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
Ejemplo.
Obtener la distancia entre los puntos: P1 (2 , − 7 ,5) y P2 (−8 , − 11, 2 )
Solución.
d=
(− 8 − 2)2 + (− 11 − (− 7))2 + (2 − 5)2
=
(− 10)2 + (− 4)2 + (− 3)2
= 100 + 16 + 9 = 125 u.
DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA
Dividir un segmento dirigido en una razón dada significa segmentarlo en partes de forma tal que se
encuentren las coordenadas de un punto P ( x , y ) que satisface la comparación entre dos magnitudes.
En general, si la razón es de la forma r =
ejemplo, si r =
a
, implica que el segmento se divide en a + b partes. Por
b
7
, el segmento se divide en 11 partes iguales.
4
Sean los puntos P1 ( x1 , y1 ) y P2 (x 2 , y 2 ) , así como el segmento de recta que los une:
y
P2(x2, y2)
y2-y
P(x,y)
x2-x
y-y1
P1(x1, y1)
x-x1
x
Sea un punto P ( x , y ) que pertenezca al segmento. Si se forman los triángulos mostrados, se observa
que son semejantes. Esto es:
x − x1
y − y1
=r
=r
y
x2 − x
y2 − y
donde r es la razón de proporcionalidad de semejanza.
Si se despeja x de la primera ecuación se tiene:
x − x1 = r (x2 − x )
x − x1 = r x2 − r x
x + x r = x1 + rx2
x (1 + r ) = x1 + r x2 , que implica:
8
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
x=
x1 + r x2
1+ r
y=
y1 + r y 2
1+ r
análogamente se puede encontrar que:
expresiones que sirven para obtener las coordenadas de un punto que divide a un segmento en una razón dada.
En el caso particular en que se trate del punto medio, r vale r =
x=
x1 + x2
2
1
= 1 , y las ecuaciones se convierten en:
1
y=
y
y1 + y2
2
Ejemplos.
Obtener las coordenadas de un punto P ( x , y ) que divida al segmento de recta que se forma al unir los
siguientes pares de puntos en la razón dada:
1) P1 (4 , − 3), P2 (9 ,5), r =
3
2
Solución.
3
(9) 4 + 27 35 35
2
2 = 2 =
x=
=
=7;
3
3
5
5
1+
1+
2
2
2
 9
Por lo tanto, el punto buscado es: P  7 , 
 5
4+
2) P1 (− 2 ,8), P2 (7 , − 4 ), r =
y=
3
(5) − 3 + 15 9 9
2
2 = 2 =
=
3
3
5 5
1+
1+
2
2
2
−3+
4
5
Solución.
4
(7 ) − 2 + 28 18 18
5
5 = 5 =
x=
=
=2;
4
4
9
9
1+
1+
5
5
5
 8
Por lo tanto, el punto buscado es: P  2, 
 3
−2+
y=
4
(− 4) 8 − 16 24 24 8
5
5 = 5 =
=
=
4
4
9
9 3
1+
1+
5
5
5
8+
Ejemplo.
Encontrar el punto medio del segmento de recta unido por los puntos A (−8,5 ) y B (3, − 6 )
Solución.
Aplicando las fórmulas del punto medio:
x=
−8 + 3 −5
5 + (−6) −1
 5 1
=
=
; y=
. El punto es: P  − , −  .
2
2
2
2
 2 2
9
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
Ejemplo.
Hallar las coordenadas de dos puntos P1 ( x1 , y1 ) y P2 (x 2 , y 2 ) , que dividan al segmento que une a los
puntos k (3, − 1) y B (9,7 ) en tres partes iguales.
Solución:
El primer punto está al final del primer tercio, es decir a razón uno a dos:
1
(9) 3 + 9 15 15
2 = 2 =
2
x=
=
=5;
1
3
1
3
1+
1+
2
2
2
 5
el primer punto buscado es: P1  5, 
 3
3+
y=
r=
1
:
2
1
(7 ) − 1 + 7 5 5
2
2 = 2 =
=
1
1
3 3
1+
1+
2
2
2
−1+
El segundo punto está al final del segundo tercio, es decir a razón dos a uno: r =
2
(9) 3 + 18 21 21
1
1 = 1 =
x=
=
=7;
2
2
3
3
1+
1+
1
1
1
3+
el segundo punto buscado es:
y=
2
:
1
2
(7 ) − 1 + 14 13 13
1
1 = 1 =
=
2
2
3
3
1+
1+
1
1
1
−1 +
 13 
P2  7 , 
 3
Ejemplo.
Sabiendo que el punto P (9, 2 ) divide al segmento que determina la unión de los puntos P1 (6 ,8) y
P2 (x 2 , y 2 ) en la razón r =
3
, hallar las coordenadas de P2 .
7
Solución.
x=
x1 + r x2
, despejando x 2 :
1+ r
x(1 + r ) − x1
r
y(1 + r ) − y1
procediendo de forma similar se obtiene: y 2 =
r
x (1 + r ) = x1 + rx2 ⇒ rx2 = x(1 + r ) − x1 ⇒ x2 =
sustituyendo en ambas expresiones:
 3
 10 
91 +  − 6 9  − 6
7
7
x2 = 
=  
=
3
3
7
7
 3
 10 
21 +  − 8 2  − 8
7
7
y2 = 
=  
=
3
3
7
7
90
48
−6
48
7
= 7 =
= 16
3
3
3
7
7
20
− 36
−8
− 36
7
= 7 =
= −12
3
3
3
7
7
10
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
Por lo tanto, el punto buscado es: P2 (16 , − 12 )
Ejemplo.
Hallar las coordenadas de un punto P ( x , y ) que divida al segmento unido por los puntos P1 (−4 , − 10 ) y
P2 (12 ,6 ) en las siguientes razones:
1
7
a)
r=
g)
r= −
b) r =
1
6
h)
8
9
r= −
c)
23
24
r=1
i) r = − 1
d) r =
j)
11
10
r= −
16
15
e) r =
500
2
k) r = −
f) r = 0
600
2
y establecer una conclusión del comportamiento de los puntos con respecto a las relaciones.
Solución:
Al ser fijos P1 y P2 , las fórmulas
x=
y1 + r y 2
x1 + r x2
y y=
se aplican fácilmente a todas las
1+ r
1+ r
relaciones dadas puesto que las coordenadas no cambian.
Procediendo repetidamente se obtienen los siguientes puntos de división:
Pa (− 2, − 8)
Pb (3.52, − 2.47)
Pc (4, − 2)
Pd (4.38, − 1.61)
Pe (11.93, 5.93)
Pf (4, − 10 )
Pg (− 5.14, − 11.14)
Ph (− 372, − 378)
Pi (No existe)
Pj (252, 246)
Pk (12.05, 6.05)
A partir de los resultados, se puede concluir que:
•
•
•
•
r = 0 , el punto P (x , y ) se ubica en P1
A medida que r va creciendo P ( x , y ) se desplaza hacia P2
En su punto medio r vale 1
Cuando r es negativa, el punto se ubica en su prolongación hacia abajo alejándose hasta que llega
a r = −1 donde es infinito y cambia de sentido. Al seguir decreciendo, tiende a P2 .
Con
Geométricamente, lo anterior se puede representar como:
11
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
y
12
Pj
8
P2 (12,6)
r < -1
Pk
Pe
4
-8
-4
4
Pb
8
r >1
16
x
Pc
Pd
-4
Pa
-8
0<r<1
P1 (4,-10)
Pf
Pg
-12
Ph
-1<r<0
Pi
no existe, pero geometricamente implica ∞
En el espacio, las fórmulas división de un segmento en una razón dada se deduce de forma similar que
en dos dimensiones ya que el segmento puede ser parte de un plano que une dichos puntos. Esto es, si
se tienen los puntos P1 ( x1 , y1 , z1 ) , P2 ( x 2 , y 2 , z 2 ) como extremos de un segmento y una razón r , el
punto que lo divide se puede encontrar por medio de:
x=
x1 + r x2
;
1+ r
y=
y1 + r y2
;
1+ r
Gráficamente, es:
12
z=
z1 + z x2
1+ r
Sistemas coordenados
Facultad de Contaduría y Administración. UNAM
Autor: Dr. José Manuel Becerra Espinosa
z
y
P1 (x1, y1, z1)
z1
P (x, y, z)
z2
P2 (x2, y2, z2)
y2
y1
x1
x
x2
Ejemplo.
Obtener las coordenadas de un punto P (x , y , z ) que divida al segmento de recta que se forma al unir los
puntos P1 (−5, − 6 ,11) y P2 (8 , − 1, − 4 ) con la razón r =
14
.
5
Solución.
14
(8) − 5 + 112 87 87
5
5 = 5 =
x=
=
14
14
19 19
1+
1+
5
5
5
14
14 −44
− 6 + (− 1) − 6 −
5
5 = 5 = − 44
y=
=
14
14
19
19
1+
1+
5
5
5
14
56 −1
11 + (− 4) 11 −
5
5 = 5 =− 1
z=
=
14
14
19
19
1+
1+
5
5
5
1
 87 44
,−
,− 
Por lo tanto, el punto buscado es: P 
 19 19 19 
−5+
APLICACIONES
La utilidad de los sistemas coordenados es especial en la Geografía, la Topografía y en la Aeronáutica,
principalmente a través de la utilización de mapas y en radares. Por ejemplo, se puede determinar la
posición de algún objeto, utilizando un sistema coordenado teniendo el eje y , hacia el Norte y el eje x ,
hacia el Este. Esto define las coordenadas de un punto, que puede ser una casa, una ciudad, un avión,
una montaña, etc.
13
Facultad de Contaduría y Administración. UNAM
Sistemas coordenados
Autor: Dr. José Manuel Becerra Espinosa
Los sistemas coordenados también sirven para conocer el punto en que se encuentran dos móviles que
se desplazan en direcciones distintas a una misma velocidad. O bien conocer la distancia de dos objetos
si están inmóviles.
Los sistemas coordenados son esenciales para realizar mapas precisos, pero hay algunas sutilezas. Por
ejemplo, la superficie esférica aproximada de la Tierra no se puede representar sobre un mapa plano sin
que haya distorsión. A unas cuantas decenas de kilómetros, el problema es muy poco notorio, pero a una
escala de cientos o miles de kilómetros, la distorsión aparece necesariamente. Se puede hacer una
variedad de representaciones aproximadas y cada una implica un tipo algo diferente en la distorsión de
forma, área o distancia1.
Tanto la figura como la escala pueden tener consecuencias importantes en procesos de Ingeniería. Por
ejemplo, las conexiones triangulares maximizan la rigidez, las superficies lisas disminuyen la turbulencia
y los recipientes esféricos minimizan el área de la superficie para cualquier volumen o masa dada.
Cambiar el tamaño de objetos manteniendo la misma forma puede tener efectos profundos debido a la
geometría de la escala: el área varía como el cuadrado de las dimensiones lineales, y el volumen lo hace
como el cubo.
1
Un tipo común de mapa exagera las áreas aparentes de las regiones cercanas a los polos (por ejemplo, Groenlandia y Alaska),
mientras que otros tipos específicos representan de manera engañosa la distancia más corta entre dos lugares, o aun qué punto es
adyacente a qué otro.
14