5,4b = r 4 5446 5,44,6 ba −=⋅+

r
r
1. Hallar el producto escalar de los vectores a = (−6,4) y b = (4,5) .
Solución.
Por estar definidos en la base canónica:
r r
a o b = (− 6,4) o (4,5) = (− 6 ) ⋅ 4 + 4 ⋅ 5 = −4
El producto escalar de dos vectores puede ser negativo. La información que se obtiene del signo
del producto escalar es:
r r
a o b > 0 ⇒ El ángulo entre los vectores es agudo
r r
a o b < 0 ⇒ El ángulo entre los vectores es obtuso
r
r
r r
r
r
2. Halla a o b si a = (2,−4) , b = 2 y el ángulo que forman los vectores a a y b es de 60º.
Solución.
Teniendo en cuenta el tipo de datos que nos dan, el producto escalar lo hacemos por la
definición.
r r r r
a o b = a ⋅ b ⋅ cos α
Siendo α el ángulo que forman los vectores.
r r
El módulo de a : a = a 12 + a 22 = 2 2 + (− 4 )2 = 20
r r r r
1
a o b = a ⋅ b ⋅ cos α = 20 ⋅ 2 ⋅ cos 60º = 4 5 ⋅ = 2 5
2
r
r
3. Hallar el producto escalar y el ángulo que forman los vectores v(3,4) y w = (−4,3) .
Solución.
r r
v o w = (3,4) o (−4,3) = 3 ⋅ (−4) + 4 ⋅ 3 = 0
r
v ≠ 0
r r
r r
Si v o w = 0 ∧  r
⇒ v⊥ w
w
0
≠


Si son perpendiculares, el ángulo que forman es de 90º
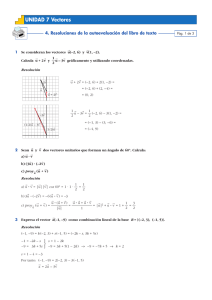
4. Calcular los ángulos y la longitud de los lados del triángulo ABC, sabiendo que las
coordenadas de sus vértices son los puntos A(0,0), B(1,3) y C(4,2).
Solución.
Para calcular el ángulo correspondiente a un vértice es preciso tomar los vectores con origen en
dicho vértice.
)
AB
AB
 ⇒ Â :
 ⇒ 180º −A
AC
CA 
Vectores necesarios:
r r
AB = b − a = (1 − 0, 3 − 0 ) = (1, 3) ⇒ BA = (− 1, − 3)
r r
AC = c − a = (4 − 0, 2 − 0) = (4, 2) ⇒ CA = (− 4, − 2)
r r
BC = c − b = (4 − 1, 2 − 3) = (3, − 1) ⇒ BA = (− 3, 1)
Ángulos:
AB o AC
(1, 3) o (4, 2) =
1⋅ 4 + 3 ⋅ 2
10
2
2
cos  =
=
=
=
⇒ Â = arccos
= 45º
2
2
(1, 3) ⋅ (4, 2) 12 + 3 2 ⋅ 4 2 + 2 2
10 ⋅ 20
AB ⋅ AC
cos B̂ =
BA o BC
BA ⋅ BC
=
(− 1, − 3) o (3,. − 1)
(− 1, − 3) ⋅ (3,. − 1)
=
(− 1) ⋅ 3 + (− 3)⋅ (− 1)
(− 1)2 + (− 3)2 ⋅ 3 2 + (− 1)2
=
0
10 ⋅ 10
Teniendo en cuenta el valor de la suma de los ángulos de en un triángulo:
)
Ĉ = 180º − A + B̂ = 160º −(45º +90º ) = 45º
(
)
1
= 0 B̂ = 0º
Lados:
Lado(AB) = AB = (1, 3) = 12 + 3 2 = 10
Lado(AC) = AC = (4, 2 ) = 4 2 + 2 2 = 20
Lado(BC) = BC = (3,. − 1) = 3 2 + (− 1)2 = 10
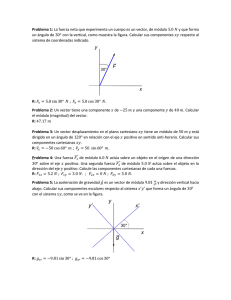
5. Hallar un punto B de la perpendicular a OX que pasa por A(2, 1) de tal forma que, los
vectores de posición de ambos puntos formen entre sí un ángulo de 30º.
Solución.
Se pide determinar las coordenadas de un punto y para ello nos dan dos datos:
• El punto B, por pertenecer a la perpendicular a OX que pasa por A
(x = 2), tendrá la forma (2, y).
• El ángulo (α) que forman los vectores de posición de los puntos es
de 30º, por aplicación la definición de producto escalar de dos
vectores:
r r
aob
cos α = r r
a⋅b
r
 a = OA = (2, 1)
Siendo:  r
b = OB = (2, y )
Aplicando la expresión analítica del producto escalar.
a 1 ⋅ b1 + a 2 ⋅ b 2
cos α =
a 12 + a 22 ⋅ b12 + b 22
cos 60 =
2 ⋅ 2 + 1⋅ y
2 +1 ⋅ 2 + y
Multiplicando en cruz para ordenar:
2
2
2
1
=
2
2
(
4+y
5 ⋅ 4 + y2
)
5 ⋅ 4 + y 2 = 8 + 2y
Elevando al cuadrado para eliminar la raíz y ordenando el resultado se obtiene una ecuación de segundo
grado.
(
)
2
 5 ⋅ 4 + y 2  = (8 + 2 y )2




(
)
5 ⋅ 4 + y 2 = 64 + 32 y + 4 y 2
 y = 16 + 10 3
y 2 − 32 y − 44 = 0 : 
 y = 16 − 10 3
Existen dos posibles puntos B, que cumplen las condiciones propuestas:
B = 2, 16 + 10 3 ó B′ = 2, 16 − 10 3
(
)
(
)
(
)
(
)
r
r
6. Comprueba que el ángulo formado por los vectores v = 3 − 1, 3 + 1 y w = 3 + 1, 3 − 1
es de 60º.
Solución.
r r
vo w
3 − 1, 3 + 1 o 3 + 1, 3 − 1
3 −1 ⋅ 3 + 1 + 3 + 1 ⋅ 3 −1
cos α = r r =
=
=
vow
2
2
2
2
3 − 1, 3 + 1 o 3 + 1, 3 − 1
3 −1 + 3 +1 ⋅
3 + 1 + 3 −1
(
(
=
( 3 )2 − 2
)(
)
( )( ) ( )( )
) (
) ( ) ( ) ( ) ( )
( 3 )2 − 12 + ( 3 )2 − 12
4
4 1
=
= =
2
2
2
8⋅ 8 8 2
3 + 12 + ( 3 ) + 2 3 + 12 ⋅ ( 3 ) + 2 3 + 12 + ( 3 ) − 2 3 + 12
cos α =
1
2
α = ar cos
2
1
= 60º
2
r
7. Las componentes de a son
( r3, 1) . Sabiendo que forma un ángulo de 60º con br
y tienen
igual módulo, calcular las componentes de b .
Solución.
r
Se pide calcular las componentes de un vector b = (b1 , b 2 ) que cumpla dos condiciones:
2
r r
1. a = b :
3 + 12 = b12 + b 22
b 12 + b 22 = 4
r r
3 ,1 o (b1 , b 2 ) 1
3b 1 + b 2
aob r r
2. cos 60 = r r : a = b = 2 : cos 60 =
: =
: 3b 1 + b 2 = 2
2⋅2
2
4
a⋅b
( )
( )
Cada una de las condiciones genera una ecuación por lo que se puede plantear un sistema.
2
2
 b + b 2 = 4
S: 1
 3b1 + b 2 = 2
El sistema, se resuelve por sustitución (lo más sencillo es despejar b1 de la 2ª ecuación y sustituir
en la primera).
b1 =
2 − b2
3
 2 − b2
: 
3

2

 + b 22 = 4 :


(2 − b 2 )2
3
+ b 22 = 4 :
2 2 − 4b 2 + b 22 + 3b 22
=4
3
b = −1
4b 22 − 4b 2 − 8 = 0 :  2
 b2 = 2
Conocido b2 se calcula b1.
r
2 − (− 1)
3

b 2 = −1 ⇒ b 1 =
=
= 3 : b = 3 ,−1

2 − b2 
3
3
b1 =
:
r
2−2
3 
b 2 = 2 ⇒ b1 =
= 0 : b = (0,2 )

3
(
)
r
r
8. Calcular s de modo que a (1, s ) y b(− 3, s ) sean perpendiculares.
Solución.
Si el producto escalar de dos vectores no nulos es cero, los vectores son perpendiculares.
r r
r r
a ⊥ b ⇔ aob = 0
r r
a o b = (1, s ) o (− 3, s ) = 0
1 ⋅ (−3) + s ⋅ s = 0
s2 − 3 = 0
s=± 3
9. Hallar las componentes de un vector unitario y perpendicular al segmento AB , siendo
A(−1, 2) y B(−3, −4).
Solución.
El vector unitario de AB se obtiene dividiendo las componentes del vector por su módulo, y se
( )
denomina vector normalizado AB n .
AB n =
AB
AB
r r
AB = b − a = (− 3,−4 ) − (− 1,2) = (− 2,−6 )
AB =
(− 2,−6) = 
= 40 = 2 10
−2
− 6   −1
−3 
=

,
,

 

± 2 10  ± 2 10 ± 2 10   ± 10 ± 10 
− 1 − 3   − 10 − 3 10 
=
,
,
Unitario de igual dirección y sentido

10 
10 10   10
AB n =

AB n = 

(− 2)2 + (− 6)2
3
AB
′
n
 −1
− 3   10 3 10 
=
= 
,
,
Unitario de igual dirección y sentido opuesto
 
10 
 − 10 − 10   10
El vector perpendicular al unitario (ortonormal), y en general, el vector perpendicular a uno
conocido, se obtiene intercambiando las componentes de posición y a una de signo (a cualquiera).
 −3
 3
1 
−1 
 ó AB on = 

AB on = 
,
,



 10 10 
 10 10 
r
r
10. Dados los vectores a = (1,4 ) y b = (6,2) , determina el ángulo que forma la bisectriz de estos
vectores con el eje OX.
Solución.
El ángulo que forma la bisectriz a los dos vectores con el eje OX (α) es la media aritmética del
ángulo que forma cada vector con el eje OX.
El ángulo que forma un vector con el eje OX es el ángulo que forma con su vector
r
representativo ( i = (1, 0) ).
Si denominamos α1 y α2 a los ángulos que forma cada vector con OX:
r r
aoi
(1, 4) o (1, 0) =
1 ⋅1 + 4 ⋅ 0
1
cos α 1 = r r =
=
: α 1 = arccos
2
2
2
2
(
)
(
)
1,
4
⋅
1,
0
17
a⋅i
1 +4 ⋅ 1 +0
r r
aoi
(6, 2) o (1, 0) =
6 ⋅1 + 2 ⋅ 0
6
cos α 2 = r r =
=
: α 2 = arccos
(1, 4) ⋅ (1, 0) 6 2 + 2 2 ⋅ 12 + 0 2
40
a⋅i
α=
1
17
6
40
≈ 75'96º = 75º58'
≈ 18'43º = 18º 26'
α 1 + α 2 75º58'+18º 26'
=
= 47º12'
2
2
11. Deseamos trazar la tangente desde un punto A a una circunferencia. Sabiendo que las
coordenadas de A son (−3, 4) y que la circunferencia está centrada en el origen de ordenadas y es de radio
unidad, calcular las coordenadas del punto de tangencia P(x, y).
Solución.
El punto buscado P(x, y) forma dos vectores, el OP y el
AP . Del primero conocemos su módulo por ser el radio de la
circunferencia, y su posición relativa respecto al segundo, son
perpendiculares, por ser radio ( OP ) y tangente ( AP ). Cada una de
estas condiciones permite plantear un sistema de dos ecuaciones con
dos incógnitas.
OP = (x, y ) ⇒ OP = x 2 + y 2 = 1 : x 2 + y 2 = 1
OP ⊥ AP ⇒ OP o AP = 0
r r
AP = p − a = (x − (− 3), y − 4) = (x + 3, y − 4)
OP o AP = (x, y ) o (x + 3, y − 4) = 0
x ⋅ (x + 3) + y ⋅ (y − 4) = 0 : x 2 + 3x + y 2 − 4 y = 0

 x 2 + y 2 = 1
x2 + y2 =1
:
 2

x + y 2 + 3x − 4 y = 0 1 + 3x − 4 y = 0
El sistema se resuelve por sustitución, de la segunda ecuación:
3x + 1
y=
4
Se sustituye en la 1ª
4
2
(3x + 1) 2
 3x + 1 
2
 = 1 : x +
x + 
= 1 : 16x 2 + 9x 2 + 6x + 1 = 16 : 25x 2 + 6x − 15 = 0
16
 4 
Resolviendo la ecuación de segundo grado:

−3+8 6
+1

 −3+8 6 4+6 6 
4+6 6
25

 x 1 = − 3 + 8 6 : y1 =
,
=
⇒ P1 = 


25
4
25
25
25 


−3−8 6

+1
 −3−8 6 4−6 6 

−3−8 6
4−6 6
25

x
=
:
y
=
=
⇒ P2 = 
,
2
2



25
4
25
25
25



2
Se obtienen dos posibles puntos, tal y como muestra la figura.
r
r
12. Dados los vectores u = (1,−1) y v = (−1,2) hallar:
r
r
a) La proyección de u sobre v .
r
r
b) El vector proyección de u sobre v .
Solución.
r r
r uov
a.
Por definición: proy v u = r
v
r (1,−1) o (−1,2) 1 ⋅ (−1) + (−1) ⋅ 2 − 3
proy v u =
=
=
(− 1,2)
5
(− 1)2 + 2 2
r
r
r
Si denominamos ω al vector proyección de u sobre v :
r
r r
ω = proy v u ⋅ v N
r
r
Siendo v N el vector normalizado de v .
r
r
v
(− 1,2 ) =  − 1 , 2 
vN = r =


v
(− 1)2 + 2 2  5 5 
b.
r
r
r
r
Conocido v N , y la proyección de u sobre v , se calcula ω .
r
r r
− 3  −1 2   3 − 6 
= ,
ω = proy v u ⋅ v N =
⋅ 
,


5  5 5  5 5 
13. Hallar el área de un triángulo de vértices A(1, 3), B(3, 6) y C(7, 2).
1


El área de cualquier triángulo  A = base × altura 
2


se puede obtener como aplicación del producto escalar. Si en
el triángulo de la figura se toma como base la longitud del
segmento AC, la altura será el valor absoluto de la proyección
del segmento AB sobre la dirección ortogonal (perpendicular)
al segmento AC .
Área ABC = AC ⋅ proy AC
ORT
AB
r r
AC = c − a = (7 − 2, 2 − 3) = (5, − 1) : AC = 5 2 + (− 1)2 = 26
Sí AC = (5, − 1) ⇒ AC ORT = (1, 5)
r r
AB = b − a = (3 − 1, 6 − 3) = (2, 3)
proy AC
ORT
AB =
AB o AC ORT
=
AC ORT
5
(2, 3) o (1, 5) =
(1, 5)
2 ⋅1 + 3 ⋅ 5
12 + 5 2
=
17
26
Área ABC = AC ⋅ proy AC
ORT
AB =
1
17
17 2
26 ⋅
=
u
2
2
26
r
r
r r
r
r
r
r
14. Si {u 1 , u 2 } es una base ortonormal y a = −2u 1 + a 2 u 2 ; b = 5u 1 − 3u 2 , hallar a2 para que el
r r
producto escalar de a o b = 6 .
Solución.
Los vectores que forman una base ortonormal son perpendiculares entre si y de módulo unidad,
por lo tanto, los productos escalares por ellos mismos son la unidad y los productos cruzados entre ellos
son nulos.
r r
r r
r r
u 1 o u 1 = u 2 o u 2 = u 1 ⋅ u 1 ⋅ cos 0 = 1 ⋅1⋅1 = 1
r r
r r
r r
u 1 o u 2 = u 2 o u 1 = u 1 ⋅ u 2 ⋅ cos 90 = 1 ⋅1 ⋅ 0 = 0
r r
r
r
r
r
r r
r r
r r
r r
a o b = (− 2u 1 + a 2 u 2 ) o (5u 1 − 3u 2 ) = −10u 1 o u 1 + 6u 1 o u 2 + 5a 2 u 2 o u 1 − 3a 2 u 2 o u 2 =
= −10 ⋅1 + 6 ⋅ 0 + 5a 2 ⋅ 0 − 3a 2 ⋅1 = −10 − 3a 2 = 6 : a 2 =
−16
3
r
r
3 4
 4 3
15. Probar que los vectores u 1 =  ,−  y u 2 =  ,  forman una base ortonormal, Hallar
5
5


5 5
r
las coordenadas de vector v = (2,−1) respecto de dicha base.
Solución.
Una base ortonormal esta formada por vectores perpendiculares de módulo unidad.
2
Módulos:
2
r
3
 4
u1 =   +  −  =
5
 5
2
9 16
+
= 1 =1
25 25
2
r
16 9
4
3
u2 =   +  =
+
= 1 =1
25 25
5
5
r r
 3 4   4 3  3 4  4  3 12 12
−
=0
Perpendiculares ⇔ u 1 o u 2 = 0 :  ,−  o  ,  = ⋅ +  −  ⋅ =
 5 5   5 5  5 5  5  5 25 25
Los vectores forman una base ortonormal ó canónica.
r
r
r
Para expresar v en función de u 1 y u 2 hay que buscar dos números reales (α, β) tales que:
r
r
r
v = α ⋅ u1 + β ⋅ u 2
(2,−1) = α ⋅  3 ,− 4  + β ⋅  4 , 3 
5
5
 5 5
Descomponiendo la igualdad por componentes se llega a un sistema de dos ecuaciones con dos
incógnitas.
3
4

 1ª : 2 = 5 α + 5 β  3α + 4β = 10
α = 2
:
(solución ) : 

4
3 − 4α + 3β = −5
β =1
 2 ª : −1 = − α + β 
5
5

Por lo tanto:
r
r
r
v = 2u 1 + u 2
6
r
r
16. Probar que si v = (cos α,− sin α ) y u = (sin α, cos α ) son perpendiculares y unitarios.
Solución.
Una base ortonormal esta formada por vectores perpendiculares de módulo unidad.
Módulos:
r
v =
(cos α )2 + (− sin α )2
r
u =
(sin α )2 + (cos α )2
= cos 2 α + sin 2 α = 1 = 1
= sin 2 α + cos 2 α = 1 = 1
r r
Perpendiculares ⇔ v o u = 0 : (cos α,− sin α ) o (sin α, cos α ) = 0
cos α ⋅ sin α + (− sin α ) ⋅ cos α = 0
Los vectores forman una base ortonormal ó canónica.
17. Probar que los puntos A(1,7),B(4,6),C(4,-2),D(6,2) pertenecen a una circunferencia de centro
O(1,2).
Solución.
Si los puntos A, B, C y D pertenecen a la circunferencia de centro O será por que todos ellos
están a igual distancia de O y por lo tanto, los módulos de los segmentos que determinan los puntos con el
punto O serán iguales.
OA = OB = OC = OD
r r
OA = a − o = (1 − 1, 7 − 2) = (0, 5) ⇒ OA = 0 2 + 5 2 = 25 = 5
r r
OB = b − o = (4 − 1, 6 − 2) = (3, 4) ⇒ OB = 3 2 + 4 2 = 25 = 5
r r
OC = c − o = (4 − 1, − 2 − 2) = (3, − 4) ⇒ OC = 3 2 + (− 4 )2 = 25 = 5
r r
OD = d − o = (6 − 1, 2 − 2) = (5, 0) ⇒ OD = 5 2 + 0 2 = 25 = 5
Todos los puntos están a cinco unidades de O, por lo tanto, pertenecen a la circunferencia de
centro O y radio 5
(
)
18. Dados los puntos A − 3 ,1 , B(5,−4), C(− 5,3) calcular el ángulo que forman AB y AC .
Solución.
El ángulo entre vectores se calcula como aplicación del producto escalar. Si denominamos α al
ángulo que forman AB con AC :
cos α =
AB o AC
AB ⋅ AC
r r
AB = b − a = 5 − − 3 , − 4 − 1 = 5 + 3 , − 5
r r
AC = c − a = − 5 − − 3 , 3 − 1 = − 5 + 3 , 2
( ( )
( ( )
Sustituyendo
cos α =
=
(5 +
(5 +
)(
3 , − 5) ⋅ (− 5 +
53 + 10 3 ⋅ 32 − 10 3
)
)
) = (5 + 3 )⋅ (− 5 + 3 )+ (− 5)⋅ 2
3 , 2)
(5 + 3 )2 + (− 5)2 ⋅ (− 5 + 3 )2 + 2 2
3, − 5 o − 5 + 3, 2
−32
) (
) (
=
≈ −0'996 ⇒ α = arcos (− 0'996) ≈ 174'86º = 174º52'
r
r
19. Hallar el valor de a para que los vectores z = (3,4) y w = (a ,−2) formen un ángulo de 45º.
Solución.
Aplicando la definición de ángulo entre dos vectores se despeja el parámetro a. Si denominamos
r
r
α al ángulo que forman los vectores z y w :
7
r r
zow
cos α = r r
z⋅w
cos 45º =
(3,4 ) o (a,−2)
(3,4) ⋅ (a ,−2 )
2
3 ⋅ a + 4 ⋅ (− 2)
=
2
3 2 + 4 2 ⋅ a 2 + (− 2 )2
:
2
3a − 8
=
2
5⋅ a 2 + 4
:
Multiplicando en cruz se obtiene una ecuación irracional que se resuelve elevando al cuadrado
los dos miembros.
5 a 2 + 4 ⋅ 2 = 2 ⋅ (3a − 8)
2
5 2a 2 + 8 = 6a − 16
:
2
5 2  2a 2 + 8  = (6a )2 − 2 ⋅ 6a ⋅16 + 16 2


50a 2 + 200 = 36a 2 − 192a + 256 :
:
:
(
 5 2a 2 + 8  = (6a − 16)2




)
25 2a 2 + 8 = 36a 2 − 192a + 256
14a 2 + 192a − 56 = 0 :
7a 2 + 96a − 28 = 0
Resolviendo la ecuación de segundo grado se obtienen los posibles valores del parámetro a.
a=
− 96 ± 96 2 − 4 ⋅ 7 ⋅ (− 28)
2⋅7
=
− 96 ± 100  a = 2
7
:
14
a = −14
r r
r
20. Hallar un vector unitario en la misma dirección y sentido que el vector z = 4 i − 3 j . Hallar
otro igual pero en sentido opuesto.
Solución.
r
Si denominamos u al vector unitario en la misma dirección y sentido:
r
r z
(4, − 3) = (4, − 3) =  4 , − 3 
u= r =


z
5 5 
25
4 2 + (− 3)2
r
r
El vector de sentido opuesto (ω) será el vector opuesto a u (el mismo pero de signo cambiado)
r
r
 4 −3  −4 3
ω = − u = − ,
, 
=
5 5   5 5
r r
r
21. Hallar un vector de módulo 10 en la dirección de a = 4 i + 3 j .
Solución.
r
r
Si denominamos u al vector unitario en la misma dirección que a y de módulo 10:
r
r
u = 10 a N
r
r
Donde a N es el vector a normalizado (de módulo la unidad).
r
r
r
(4, 3) = 10 (4, 3) = (8, 6)
a
u = 10 a N = 10 r = 10
5
a
4 2 + 32
r
r
22. Dados los vectores u = (4,−3) y v = (1, m ) . Calcula el valor de m para que:
r r
a) Angulo formado entre u y v sea de 60º
r
r
r r
b) u + 2 v sea perpendicular a 2u − v
Solución.
a. Si llamamos α al ángulo que forman los vectores:
r r
uov
cos α = r r
u⋅v
cos 60º =
2
(4, − 3) o (1, m )
+ (− 3)2 ⋅ 12 + m 2
4
Multiplicando en cruz para ordenar:
8 − 6m = 5 1 + m 2
8
=
4 − 3m
5 1+ m
2
=
1
2
Elevando al cuadrado para quitar la raíz y ordenando se obtiene una ecuación de 2º grado.
(8 − 6m )2 = 5 2 
1 + m 2 


2
(
8 2 − 2 ⋅ 8 ⋅ 6m + 6 2 m 2 = 25 1 + m 2
64 − 96m + 36m = 25 + 25m
2
)
2
11m 2 − 96m + 39 = 0
m=
− (− 96) ±
(− 96)2 − 4 ⋅11⋅ 39
2 ⋅11
=
96 ± 50 3 48 ± 25 3
=
22
11
r
r
r r
b. u + 2 v sea perpendicular a 2u − v
Solución.
Si dos vectores son perpendiculares, su producto escalar es cero.
r
r
u + 2v = (4, − 3) + 2(1, m ) = (4 + 2 ⋅1, − 3 + 2 ⋅ m ) = (6, − 3 + 2m )
r r
2u − v = 2(4, − 3) − (1, m ) = (2 ⋅ 4 − 1, 2 ⋅ (− 3) − m ) = (7, − 6 − m )
(6, − 3 + 2m ) o (7, − 6 − m ) = 0
6 ⋅ 7 + (−3 + 2m ) ⋅ (−6 − m ) = 0
42 + 18 − 9m − 2m 2 = 0
− 2m 2 − 9m + 60 = 0 : m =
− (− 9) ±
(− 9)2 − 4 ⋅ (− 2) ⋅ 60
2 ⋅ (− 2)
=
9 ± 149
−4
r
r
r r
r
r
r
r
23. Hallar el producto escalar de los vectores a = 2u − 3v y b = 3u + 2v sabiendo que u y v
r
r
forman 30º y que u = 4 y v = 5 .
Solución.
r r
r r
r
r
r r
r r
r r
r r
a o b = (2u − 3v ) o (3u + 2v ) = 2 ⋅ 3u o u + 2 ⋅ 2u o v − 3 ⋅ 3v ⋅ u − 3 ⋅ 2 v o v
r r r r
Teniendo en cuenta que el producto escalar es conmutativo (u o v = v o u ) y efectuando las
operaciones numéricas.
r r
r r
r r
r r
a o b = 6⋅u o u −5⋅u o v −6⋅vo v
r r
r r
Los productos escalares u o u y v o v , se resuelven por la definición.
r r r r
r2
u o u = u ⋅ u ⋅ cos 0º = u 
r r r r
r 2  r r
r2
r r
r2
v o v = v ⋅ v ⋅ cos 0º = v  : a o b = 6 ⋅ u − 5 ⋅ u ⋅ v ⋅ cos 30º −6 ⋅ v
r r r r
u o v = u ⋅ v ⋅ cos 30º 

Sustituyendo por sus valores:
r r
a o b = 6 ⋅ 4 2 − 5 ⋅ 4 ⋅ 5 ⋅ cos 30º −6 ⋅ 5 2 = −54 − 50 3
24. Calcula a y b para que los vectores
v
u = 5 . (1 punto)
Solución.
Si
r
v
v = (− 2, a ) y u = (b,1) formen 60º y además
v
u = 5 ⇒ b 2 + 12 = 5 ⇒ b 2 + 12 = 5 ⇒ b = ± 4 = ±2
Si los vectores forman 60º, deben cumplir:
r r
(−2, a )⋅ (b, 1) = − 2b + a = 1
vou
cos 60º = r r =
u⋅v
(− 2 )2 + a 2 ⋅ 5 20 + 5a 2 2
ordenando
− 4b + 2a = 20 + 5a 2
9
•
Si b = 2: − 8 + 2a = 20 + 5a 2 elevando al cuadrado (− 8 + 2a )2 =  20 + 5a 2 


2
64 − 32a + 4a 2 = 20 + 5a 2 ordenando a 2 + 32a − 24 = 0
resolviendo:
x=
− 32 ± 32 2 − 4 ⋅1 ⋅ (− 24)
2 ⋅1
− 32 ± 4 70 = −16 + 2 70
=
2
= −16 − 2 70
=
Por tanto, dos posibles soluciones son:
r
v = − 2, − 16 + 2 70
ó
r
v = − 2, − 16 − 2 70
•
(
)
∧
r
u = (2, 1)
(
)
∧
r
u = (2, 1)
Si b = −2: 8 + 2a = 20 + 5a 2 elevando al cuadrado (8 + 2a )2 =  20 + 5a 2 


2
64 + 32a + 4a 2 = 20 + 5a 2 ordenando a 2 − 32a − 24 = 0
resolviendo:
x=
− (− 32) ±
(− 32)2 − 4 ⋅1⋅ (− 24)
2 ⋅1
=
32 ± 4 70 = 16 + 2 70
=
2
= 16 − 2 70
Por tanto, las otras dos posibles soluciones son:
r
v = − 2, 16 + 2 70
∧
ó
r
v = − 2, 16 − 2 70
∧
(
)
r
u = (− 2, 1)
(
)
r
u = (− 2, 1)
r
r
25. Dados los vectores v = (1, − 1) u = (2, x ) . Calcular x para que dichos vectores formen 45º.
Solución.
Por aplicación del producto escalar de vectores. Si denominamos α al ángulo que forman los
vectores:
r r
vou
cos α = r r
v⋅u
2
1 ⋅ 2 + (− 1) ⋅ x
=
:
2
12 + (− 1)2 ⋅ 2 2 + x 2
Multiplicando en cruz, ordenando y simplificando:
cos 45 =
(1,−1) o (2, x )
(1,−1) ⋅ (2, x )
:
2
=
2
2−x
2 ⋅ 4+ x2
4+ x2 = 2− x
Elevando al cuadrado para quitar la raíz:
2
 4 + x 2  = (2 − x )2 : 4 + x 2 = 2 2 − 2 ⋅ 2 ⋅ x + x 2 : 4x = 0 : x = 0




10
( )
(
)
r
r
r
26. Dados los vectores a 3 , 1 , b = − 3 , 1 , c = (1, − 2) Calcular:
r
r
a) El ángulo que forma a y b
r
b) Las coordenadas de un vector perpendicular a c de modulo 2
r
r
c) La proyección del vector a sobre c
r
r
d) El vector proyección de b sobre a
Solución.
a.
Por aplicación del producto escalar de vectores. Si denominamos α al ángulo que forman los
vectores.
r r
aob
cos α = r r
a⋅b
cos α =
b.
c.
d.
( 3,1)o (−
( 3,1) ⋅ (−
)=
3 ⋅ (− 3 )+ 1 ⋅1
3 ,1)
( 3 )2 + 12 ⋅ (− 3 )2 + 12
3 ,1
=
− 2 −1
−1
=
: α = arccos
= 120º
2
4
2
r
r
Si denominamos u al vector perpendicular a c de nódulo 2:
r
r
c Ort  c = (1,−2) 
r
(2,1) =  4 , 2 
u = 2 r = r
 = 2⋅


c
c Ort = (2,1)
12 + (− 2)2  5 5 
r
proy cr a
r r
aoc
= r =
c
( 3,1)o (1,−2) =
(1,−2 )
3 ⋅1 + 1 ⋅ (− 2)
12 + (− 2)2
=
3−2
5
r
r r
r
r
proy ar b = proy ar b ⋅ a n , siendo a n ≡ Vector a normalizado (de módulo unidad).
r
r b o ar
− 3 ,1 o 3 ,1 − 3 ⋅ 3 + 1 ⋅1 − 2
r
proy a b = r =
=
=
= −1
2
a
2
3 ,1
2
− 3 +1
r
 3 1
r
3 ,1
a
an = r =
=
, 
 2 2
a
2
2


3 +1
(
)( )
( )
( )
( )
( )
Sustituyendo en la expresión:
r
 3 1 
3 1 
proy ar b = −1 ⋅ 
,  = −
,−
 2 2  2
2 

 
r
r
r r
27. Se tienen los vectores v = (4,0 ) , u = (1,5) . Calcular el ángulo que forman los vectores u + v
r r
y u−v .
Solución.
Si denominamos α al ángulo que forman los vectores:
(ur + vr ) o (ur − vr )
cos α = r r
(u + v ) ⋅ (ur − vr )
r r
u + v = (1,5) + (4,0) = (5,5)
r r
u − v = (1,5) − (4,0 ) = (−3,5)
cos α =
(5, 5) o (− 3, 5)
(5, 5) ⋅ (− 3, 5)
=
5 ⋅ (− 3) + 5 ⋅ 5
52 + 52 ⋅
(− 3)2 + 5 2
α = arccos
=
17
≈ 76º
17
11
10
50 ⋅ 34
=
10
1700
=
17
17
28. Calcular los valores de m y de n para que los vectores
r 1
 r  −1 
u =  , m  , v =  n, 
3

 6 
a) Sean unitarios
b) Sean ortogonales.
r r
r r
c) Si m = n = 1, calcular las proyecciones de u en v y de v en u
Solución.
a.
Vector unitario ≡ modulo unidad.
2
r
1
1 8
8
8
1
u =   + m2 =1 :
+ m 2 = 12 : m 2 = 1 − = : m = ±
=±
9
9 9
9
3
3
2
r
1
1 35
35 ± 35
 −1 
u = n2 +  =1 : n2 +
= 12 : n 2 = 1 −
=
: n=±
=
6
36
36
36
36
6
 
b.
Si dos vectores son ortogonales, forman 90º, y por tanto, su producto escalar es cero.
r r
1
−1
1
  −1 
u o v = 0 :  , m  o  n,  = 0 : ⋅ n + m ⋅
= 0 : m − 2n = 0
3
6
3   6 
Ecuación homogénea con infinitas soluciones. Para obtener una cualquiera de sus soluciones
basta con dar un valor a una de las incógnitas y calcular la otra mediante la ecuación.
Si n = 1 ⇒ m = 2
c.
r  1  r  −1 
u =  , 1 , v = 1, 
3 
 6 
 1   −1 
1
1
−1

r r  , 1 o 1,
⋅1 + 1 ⋅
r
3
6
u
o
v




3
6
6
proy vr u = r =
=
=
=
2
v
1
 −1 
 −1 
1+
1,

12 +  
36
 6 
6
 
 1   −1 
1
−1

r r  , 1 o 1,
⋅1 + 1 ⋅
r
3
6
u
o
v

 

6 =
proy ur v = r =
= 3
2
u
1 
1
2
 , 1
  +1
3 
 3
1
6 =
1
+1
9
1
6 =
37
36
1
6 =
10
9
1
6 = 1 = 37
37
37
37
6
1
6 = 1 = 10
20
10 2 10
3
r
r
r
r
r r
29. Dos vectores a y b son tales que: a = 10 ; b = 5 6 ; a + b = 20 . Hallar su producto
escalar, el ángulo que forman entre ellos y los ángulos que forman cada uno de ellos con el vector suma.
Solución.
r r
Producto escalar a o b
El problema se resuelve a partir de la definición de módulo de un vector.
r
r r
u = + uou
( )
Aplicando la definición al módulo de la suma y operando el producto escalar:
r r
r r r r
r r r r r r r r
a +b = + a + b o a +b = aoa +aob+boa + bob
( )( )
Teniendo en cuenta que el producto escalar es conmutativo y que el producto escalar de un
vector por si mismo es el módulo del vector elevado al cuadrado:
r r r r
a ob = boa
r r r r
r r
r2
a o a = a ⋅ a ⋅ cos 0 = a ⋅ a ⋅1 = a
12
r r r r
r r
r2
b o b = b ⋅ b ⋅ cos 0 = b ⋅ b ⋅1 = b
Nota: El ángulo que forma un vector con el mismo es cero.
Sustituyendo en la definición de módulo
r r
r2
r r r2
a+b = a +2aob+ b
Elevando los dos miembros al cuadrado, se despeja el producto escalar de los vectores
r r r2
r r2 r2
a+b = a +2aob+ b
( )2  = 75
r r 1r r2 r2 r2 1
a o b =  a + b − a − b  =  20 2 − 10 2 − 5 6
2
 2
Ángulos.
r
r
Primero se calcula el ángulo entre a y b (α) como aplicación del
producto escalar, conocido este se calcula el ángulo entre uno de ellos y el vector
suma (por ejemplo α1), por último el ángulo α2 se calcula teniendo en cuenta que
α = α1 + α2.
r r
aob
75
6
cos α = r r =
: α = arccos
≈ 52,2º
4
a ⋅ b 10 ⋅ 5 6
( )
r r r
r r r r r2 r r
a o a + b a o a + a o b a + a o b 10 2 + 75 175 7
7
cos α1 = r r r = r r r = r r r =
=
= : α1 = arccos ≈ 29º
10 ⋅ 20
200 8
8
a ⋅ a+b
a ⋅ a+b
a ⋅ a+b
α 2 = α − α1 = 52,2º −29º = 23,2º
r r r
r r r
30. Si a , b y c son tres vectores de igual módulo y c = a + b , calcular el producto escalar de
r r
los vectores a y b , y el ángulo que forman.
Solución.
Si denominamos α al ángulo que forman los vectores:
r r
aob
cos α = r r
a⋅b
r r
El producto escalar a o b se obtiene de la definición de módulo de la suma en función en función
de los módulos de los vectores.
Aplicando la definición de módulo al módulo de la suma y operando el producto escalar:
r r
r r r r
r r r r r r r r
a + b = a + b o a + b = a oa +a ob + boa + bob
( )( )
Teniendo en cuenta que el producto escalar es conmutativo y que el producto escalar de un
vector por si mismo es el módulo del vector elevado al cuadrado:
r r r r
r r r r
r r
aob = boa ⇒ aob+ boa = 2aob
r r r r
r r
r2
a o a = a ⋅ a ⋅ cos 0º = a ⋅ a ⋅1 = a
r r r r
r r
r2
b o b = b ⋅ b ⋅ cos 0º = b ⋅ b ⋅1 = b
Sustituyendo en la definición de módulo de la suma:
r r
r2
r r r2
a+b = a +2aob+ b
Elevando los dos miembros al cuadrado, se despeja el producto escalar de los vectores.
13
r r r2
r r2 r2
a+b = a +2aob+ b
r r 1r r 2 r2 r 2
aob =  a +b − a − b 
2

r r r
r r r
El módulo de la suma se puede obtener del enunciado. Si c = a + b ⇒ c = a + b (si dos
r r r
vectores son iguales, sus módulos también lo son), y como a = b = c , se puede concluir:
r r r
a+b = a
Sustituyendo en la expresión del producto escalar:
r r 1r2 r2 r 2
1 r2
aob =  a − a − b  = − a
2
2

r
Si en la expresión del ángulo entre vectores sustituimos todo en función del módulo de a :
1 r 2  − 1 ar 2
r r r r
a o b a o b = − a 
1
2
2
cos α = r r = 
= r r =−
r r
2
a⋅a
a⋅b 

a = b


1
α = arccos − = 120º
2
r r r
r r r
Si c = a + b y a = b = c , los tres vectores forman un triángulo equilátero
31. Sea el triángulo de vértices A(2, 3), B(1, 0) y C(3, 4). Calcular:
Módulo de AB
Ángulo de AB con AC
Proyección de AB sobre el eje x
Proyección de AB sobre AC
i.
ii.
iii.
iv.
Vector unitario en la dirección de AC
v.
Vector proyección de AB sobre AC
Área del triángulo
Determina el valor de a para que el vector (a, −1) sea ortogonal al vector BC
Valor de a para que el punto (a, 2) forme con B y C un triángulo de área 4 unidades
cuadradas.
Solución.
r r
AB = b − a = (1 − 2,0 − 3) = (− 1,−3) ; AB = (− 1)2 + (− 3)2 = 10
vi.
vii.
viii.
ix.
i.
ii.
Se denominamos α al ángulo que forman los vectores:
− 1 ⋅1 + (− 3) ⋅1
AB o AC 
AB = (− 1,−3)
 (− 1,−3) o (1,1)
cos α =
=
=
=
=
r r
10 ⋅ 2
AB ⋅ AC AC = c − a = (3 − 2,4 − 3) = (1,1)
10 ⋅ 12 + 12
cos α =
iii.
−4
20
: α = arccos
−4
20
= 170,5º
r
El representante del eje OX es el vector unitario i = (1,0)
r
AB o i (− 1,−3) ⋅ (1,0)
r
proy i AB = r =
= −1 ⋅1 + (− 3) ⋅ 0 = −1
1
i
14
iv.
v.
proy AC AB =
AB o AC
=
AC
−4
2
= −2 2
Vector unitario o normalizado. AC N =
AC
=
AC
(1,1) = 
2
1
1 

,


2
 2
vi.
 1
1 
 = (− 2,−2)
proy AC AB = proy AC AB ⋅ AC N = −2 2 ⋅ 
,

2
 2
vii.
Área (ABC) =
AB ⋅ AC'
2
 AC = (1,1)  (− 1,−3) o (− 1,1) − 1 ⋅ (− 1) + (− 3) ⋅1 2
=
= = 1u 2
=
=
2
2
2
AC' = (− 1,1)
viii.
Si dos vectores son perpendiculares, su producto escalar es cero.
(a,−1) o BC = 0 : (a,−1) o (2,4) = 0 : a ⋅ 2 + (−1) ⋅ 4 = 0 : a = 2
ix.
A(a, 2); B(1, 0); C(3, 4)
AB = (1 − a ,0 − 2) = (1 − a ,−2 )

 (1 − a ,−2) o (− 2,3 − a )
Área (ABC) =
=  AC = (3 − a ,4 − 2) = (3 − a ,2)  =
=
2
2


AC' = (− 2,3 − a )


(1 − a ) ⋅ (− 2) + (− 2) ⋅ (3 − a ) 4a − 8
+ : a = 4
4a − 8
=
=
= 4:
= ±4 : 4a − 8 = ±8 : 
2
2
2
− : a = 0
AB ⋅ AC'
15