Guía teórica - U

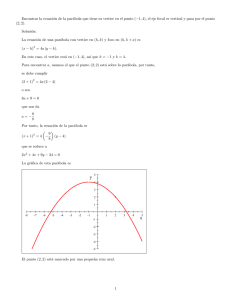
Liceo auto-gestionado Manuel Barros Borgoño
Matemáticas
Profesor: Joaquín Díaz.
Guía teórica
I) RAÍCES – FUNCIÓN RAÍZ CUADRADA
Definición 1: si n es un entero par positivo y a es un real no negativo, entonces √ es el único real b,
no negativo, tal que = ೙
√ = ⇔ = , ≥ 0
೙
⬚
Definición 2: si n es un entero impar positivo y a es un real cualquiera, entonces √ es el único real b
tal que = ೙
√ = ⇔ = , ∈ ೙
⬚
Observaciones:
•
•
Si n es un entero impar positivo y a es un real negativo, entonces √ NO ES REAL
೙
La expresión √ , con a real, se puede expresión como una potencia de exponente fraccionario.
೙
√ = ೙
ೖ
೙
•
Por último, es importante entender la unicidad de la raíz:
= ||
Ejemplo:
−3 =¿ ?
En este caso existe mentalmente dos opciones, 3 y -3. La respuesta correcta es 3, debido a que la raíz es
una función que trabaja solo con números positivos, y además se refiere a un único positivo (no
confundir con el hecho de “sacar raíces” en una ecuación o encontrar el número que al cuadrado me del
número dentro de la raíz).
Propiedades de las raíces:
Si √ y √ están bien definidas en los reales (esto es, respetan con las definiciones anteriores), se
cumplen las siguientes propiedades:
೙
೙
√ ∙ √ = √ ∙ •
Multiplicación de raíces de igual índice.
•
División de raíces de igual índice.
•
Potencia de una raíz.
•
Raíz de una raíz
•
Amplificación y simplificación del orden de una raíz.
೙
೙
೙
೙
√ = ೙
√
೙
√ =
೙
•
√ = √ ೙
√ =
೙ ೘
೙
√ ೘೙
√ , ∈ , ∈ ೘೙
Producto de raíces de distinto índice.
√ = ೙
=
√ ∙ √ =
೙
೘
⁄
= √ ೘೙
√ ∙ , , ∈ ೘೙
•
Factor de una raíz como factor sub-radical.
∙ √ = √ , ∈ ೙
•
೙
Racionalización:
racionalizar el denominador de una fracción consiste en transformarla en una fracción
equivalente cuyo denominador no contenga ninguna raíz.
Caso 1:
Fracciones de la forma
√
Caso 2:
Fracciones de la forma
√
√
II) ECUACIÓN DE SEGUNDO GRADO Y FUNCION CUADRATICA
Una ecuación de segundo grado es una ecuación que puede llevar la forma + + = , con a, b
y c coeficientes reales y ≠ 0.
El cálculo de las soluciones o raíces de esta ecuación, se realiza aplicando la siguiente formula:
=
− ± √ − Si y son soluciones de la ecuación esta se puede escribir como:
− ∙ − = 0
De la misma forma, si y son soluciones (o raíces) de la ecuación de segundo grado + + = 0
entonces siempre se cumple que:
1) + = −
2) ∙ =
FUNCIÓN CUADRÁTICA
A la función de segundo grado = + + , siendo a, b, c números reales y ≠ 0 se le
denomina función cuadrática.
La representación gráfica de una función cuadrática es una parábola, simétrica respecto a una recta
paralela al eje de las ordenadas (eje y). Dicha recta recibe el nombre de eje de simetría.
Concavidad: es la abertura que tiene la parábola.
Si > 0, la concavidad de la parábola está
orientada hacia arriba
Si < 0 la concavidad de la parábola está
orientada hacia abajo
Intersección con el eje Y
La parábola asociada a la función = + + siempre intersecta al eje de las ordenadas (Eje Y) en
=
Los ceros de la función:
Los ceros (o raíces) de la función cuadrática son los valores para los que = 0.
Discriminante
La expresión − 4 se denomina discriminante, pues determina la naturaleza de las raíces de la
ecuación cuadrática asociada a la función = + + .
Si − > Si − = Si − < La parábola intersecta al eje x en
dos puntos, por lo tanto tiene 2
soluciones (raíces distintas)
La parábola es tangente al eje x,
por lo tanto tiene sus soluciones
idénticas (una única solución
real)
La parábola no intersecta al eje
x, no tiene solución real.
Eje de simetría:
El eje de simetría de una parábola es una recta que divide a esta curva en dos “ramas” congruentes.
Eje de simetría:
=
+ 2
O
=
−
2
Vértice de la parábola:
El vértice de la parábola es un punto de intersección de esta con su eje de simetría.
− 4−
= ! ,
"
2
4