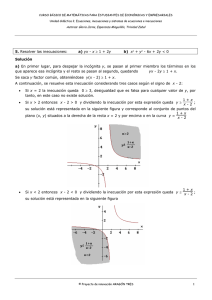
− > − ≥ − − > ⇒ − > − ≥ − − ≥ − − < −

Unidad 2: Inecuaciones y sistemas de inecuaciones
RESOLUCIÓN DE LOS EJERCICIOS BÁSICOS
a) ࢞૛ − ૜ሺ૛࢞ − ૞ሻ ≤ ሺ࢞ − ૚ሻሺ࢞ + ૛ሻ + ૠ
1. Resuelve y representa las soluciones de las inecuaciones:
࢞ା૛
૜
b)
−
૛࢞ା૝
૚૙
c)
−
૜ሺ࢞ି૚ሻ
−
૛
d)
>
૛࢞ି૜
૝
૜
૝
≥
࢞ି૜
૝
−
࢞ା૚
૛
࢞ା૛
૞
૝࢞ < 1 − ቀ࢞ + ቁ
૚
૛
a) ‫ ݔ‬ଶ − 3ሺ2‫ ݔ‬− 5ሻ ≤ ሺ‫ ݔ‬− 1ሻሺ‫ ݔ‬+ 2ሻ + 7 ⇒ ‫ ݔ‬ଶ − 6‫ ݔ‬+ 15 ≤ ‫ ݔ‬ଶ + ‫ ݔ‬+ 8 ⇒ 15 − 8 ≤ ‫ ݔ‬+ 6‫ ⇒ ݔ‬7 ≤ 7‫⇒ ݔ‬
Solución
଻
଻
≤ ‫ ⇒ ݔ‬1 < ‫ ; ݔ‬la solución de la inecuación es ሺ૚, +∞ሻ
௫ାଶ
ଷ
b)
8 > 2‫⇒ ݔ‬
ଶ௫ାସ
ଵ଴
c)
−
଼
ଶ
−
ଶ௫ିଷ
ସ
>
ଷ
ସ
1
ସ௫ା଼
−
଺௫ିଽ
>
௫ାଶ
2
ସ௫ା଼
−
ଵଶ
⇒
ଵଶ
ଽ
ଵଶ
⇒ 4‫ ݔ‬+ 8 − 6‫ ݔ‬+ 9 > 9 ⇒ 8 > 6‫ ݔ‬− 4‫⇒ ݔ‬
> ‫ ⇒ ݔ‬2 > ‫ ; ݔ‬la solución de la inecuación es ሺ−∞ , ૛ሻ
௫ିଷ
ସ
≥
௫ାଵ
ଶ
−
ହ
ଶ଴
⇒
ହ௫ିଵହ
ଶ଴
≥
ଵ଴௫ାଵ଴
ଶ଴
−
ସ௫ା଼
ଶ଴
⇒ 4‫ ݔ‬+ 8 − 5‫ ݔ‬+ 15 ≥
≥ 10‫ ݔ‬+ 10 − 4‫ ݔ‬− 8 ⇒ −‫ ݔ‬+ 23 ≥ 6‫ ݔ‬+ 2 ⇒ 23 − 2 ≥ 6‫ ݔ‬+ ‫ ⇒ ݔ‬21 ≥ 7‫ ⇒ ݔ‬3 ≥ ‫ ; ݔ‬la solución de
la inecuación es ሺ−∞, ૜]
d)
ଷሺ௫ିଵሻ
−
ଶ
ଷሺ௫ିଵሻ
ଶ
−
ସ
ଷ
−
4‫ < ݔ‬1 − ቀ‫ ݔ‬+ ଶቁ
଼௫
ଶ
< −
ଵ
ଶ
ଶ௫
ଶ
ଵ
3
⇒
ଷሺ௫ିଵሻ
−
ଶ
4‫ < ݔ‬1 − ‫ ݔ‬− ଶ
࢞
ଷሺ௫ିଵሻ
−
ଶ
4‫ < ݔ‬ଶ − ‫⇒ ݔ‬
ଵ
૝
, +∞ሻ
૜
< 5, un alumno procede así:
-4/3
Multiplica por x la inecuación: ૝ < 5࢞
2. Para resolver
⇒
⇒ 3‫ ݔ‬− 3 − 8‫ < ݔ‬1 − 2‫ ⇒ ݔ‬−3 − 1 < 8‫ ݔ‬− 3‫ ݔ‬− 2‫ ⇒ ݔ‬−4 < 3‫⇒ ݔ‬
< ‫ ; ݔ‬la solución de la inecuación es ሺ−
૝
ଵ
Divide por 5 y obtiene la solución:
¿Este razonamiento es correcto?
૝
૞
<‫ݔ‬
Solución
Matemáticas CCSS II
Página 1 de 6
Unidad 2: Inecuaciones y sistemas de inecuaciones
El primer paso es falso en general ya que x puede ser positivo o negativo.
•
Si x es positivo el signo de la inecuación no cambia de sentido
•
Si x es negativo el signo de la inecuación cambia de sentido
૜ሺ࢞ − ૛ሻ + ૠ < ‫ ݔ‬+ 2ሺ‫ ݔ‬− 5ሻ
3. Comprueba que no hay ningún número que verifique esta inecuación
Se quitan los paréntesis en la desigualdad: 3‫ ݔ‬− 6 + 7 < ‫ ݔ‬+ 2‫ ݔ‬− 10 y se simplifica 3‫ ݔ‬+ 1 < 3‫ ݔ‬−
Solución
10 ⇒ 1 < −10
Esta desigualdad es falsa y por lo tanto no hay ningún número que verifique la inecuación.
4. Halla los números naturales cuyo triple más seis unidades es mayor que su doble más
cinco unidades.
Solución
Sea x un número natural cualquiera de los pedidos.
El triple menos 6 será: 3x-6
El doble más 5 será: 2x+5
La inecuación planteada será: 3‫ ݔ‬− 6 > 2‫ ݔ‬+ 5
⇒
3‫ ݔ‬− 2‫ > ݔ‬5 + 6 ⇒ ‫ > ݔ‬11
Los números naturales mayores que 11 satisfacen las condiciones del problema.
a) ࢞૛ + ࢞ − ૟ ≥ ૙
5. Resuelve las inecuaciones:
b) ࢞૛ − ࢞ + ૝ ≤ ૞࢞ − ૝
Solución
a) Se resuelve la ecuación ‫ ݔ‬ଶ + ‫ ݔ‬− 6 = 0 . Las soluciones son: x=2 y x=-3
Factorizando el polinomio queda: ሺ‫ ݔ‬− 2ሻሺ‫ ݔ‬+ 3ሻ ≥ 0
Se divide la recta en los intervalos:
ሺ−∞, −3ሻ, ሺ−3,2ሻ, ሺ2, +∞ሻ
ሺ−4 − 2ሻሺ−4 + 3ሻ = ሺ−6ሻሺ−1ሻ = 6 ≥ 0 ; el primer intervalo es solución.
Se toma un valor para x del primer intervalo, por ejemplo x=-4 y se sustituye:
Se repite el proceso con un valor para x del segundo intervalo, por ejemplo x=0; y se sustituye,
ሺ0 − 2ሻሺ0 + 3ሻ = ሺ−2ሻ · 3 = −6 ≤ 0; por lo tanto el 2º intervalo no es solución.
Para el siguiente intervalo tomamos x=3 y sustituimos, ሺ3 − 2ሻሺ3 + 3ሻ = 1 · 6 = 6 ≥ 0, por lo tanto
el tercer intervalo también es solución.
−∞
-3
2
+∞
(x+5)
−
+
+
(x-2)
−
−
+
(x+5)(x-2)
+
−
+
La solución de la inecuación es: ሺ−∞, −૜] ∪ [૛, +∞ሻ
b) ‫ ݔ‬ଶ − ‫ ݔ‬+ 4 ≤ 5‫ ݔ‬− 4 ⇒ ‫ ݔ‬ଶ − ‫ ݔ‬+ 4 − 5‫ ݔ‬+ 4 ≤ 0 ⇒ ‫ ݔ‬ଶ − 6‫ ݔ‬+ 8 ≤ 0.
Las soluciones de la ecuación ‫ ݔ‬ଶ − 6‫ ݔ‬+ 8 = 0 son x=2 y x=4 , con lo que la inecuación queda
ሺ‫ ݔ‬− 2ሻሺ‫ ݔ‬− 4ሻ ≤ 0 y la recta real se dividida en los intervalos: ሺ−∞, 2ሻ, ሺ2 , 4ሻ, ሺ4, +∞ሻ . Se estudian los signos de cada factor en los diferentes intervalos
Matemáticas CCSS II
Página 2 de 6
Unidad 2: Inecuaciones y sistemas de inecuaciones
−∞
2
4
+∞
(x-2)
−
+
+
(x-4)
−
−
+
(x-2)(x-4)
+
−
+
La solución de la inecuación es el intervalo [2 , 4].
࢞ሺ࢞ା૚ሻ
6. Resuelve gráficamente la inecuación
૛
Solución
௫ሺ௫ାଵሻ
ଶ
≤ 5−‫ݔ‬
≤૞−࢞
⇒ ‫ ݔ‬ଶ + ‫ ≤ ݔ‬10 − 2‫࢞ ⇒ ݔ‬૛ + ૜࢞ − ૚૙ ≤ ૙
Se representa gráficamente ya función ‫ ݔ = ݕ‬ଶ + 3‫ ݔ‬− 10,
su gráfica es una parábola de vértice V(-3/2, -49/4) y
la ecuación ‫ ݔ‬ଶ + 3‫ ݔ‬− 10 = 0 ; son x=-5 y x=2.
cuyos puntos de corte con el eje X son las soluciones de
ሺ−∞, −5ሻ, ሺ−5,2ሻ, ሺ2, +∞ሻ , la función queda por debajo
De los tres intervalos en que queda dividido el eje X:
de eje X, es decir es negativa en el intervalo ሺ−5,2ሻ, code la inecuación es el intervalo [−૞, ૛]
mo debemos incluir las raíces del polinomio, la solución
࢞ି૞
7. Resuelve las siguientes inecuaciones:
a)
b)
c)
≥૙
࢞ା૛
࢞૛ ା૞࢞
࢞ି૜
૛࢞ି૜
࢞ି૚
≤ 0
<1
Solución
dividir la recta en los intervalos: ሺ−∞, −2ሻ, ሺ−2, 5ሻ, ሺ5, +∞ሻ y estudiaremos los signos del nu-
a) Calculando las raíces del numerador y denominador: x-5=0 y x+2=0 ⇒ x= 5 y x=-2, podemos
merador y denominador en cada intervalo
−∞
-2
5
+∞
(x-5)
−
+
+
(x+2)
−
−
+
(x-5)/(x+2)
+
−
+
La solución de la inecuación es: ሺ−∞, −૛ሻ ∪ [૞, +∞ሻ
Matemáticas CCSS II
Página 3 de 6
Unidad 2: Inecuaciones y sistemas de inecuaciones
b) Calculando los valores que anulan numerador y denominador: ‫ ݔ‬ଶ + 5‫ݔ = ݔ‬ሺ‫ ݔ‬+ 5ሻ = 0 y
‫ ݔ‬− 3 = 0 se obtiene x=0, x=-5 y x=3. Tendremos la recta dividida en los intervalos: ሺ−∞, −5ሻ,
ሺ−5,0ሻ, ሺ0,3ሻ, ሺ3, +∞ሻ. Se estudian los signos en cada intervalo.
−∞
-5
0
+∞
(x+5)
−
+
+
+
x
−
−
+
+
−
−
+
+
−
+
−
(x-3)
−
x(x+5)/(x-3)
La solución de la inecuación es: ሺ−∞, −૞] ∪ [૙, ૜ሻ
ଶ௫ିଷ
3
ଶ௫ିଷ
2‫ିݔ‬ଷ
−
௫ିଵ
ଶ௫ିଷି௫ାଵ
c) Pasando 1 al primer miembro y efectuando la operación indicada, transformamos la inecuación
௫ିଵ
⇒
< 1 en una como las anteriores:
௫ିଶ
௫ିଵ
௫ିଵ
– 1<0 ⇒
< 0 . Si x=1, x=2 son las raíces, se tiene
−∞
1
௫ିଵ
<0 ⇒
௫ିଵ
2
௫ିଵ
<0
+∞
(x-2)
−
+
+
(x-1)
−
−
+
(x-2)/(x-1)
+
−
+
La solución de la inecuación es el intervalo ሺ૚, ૛ሻ.
૜࢞ − ૛ሺ࢞ − ૚ሻ
૞ − ૜࢞
≤ ૝ሺ࢞ − ૚ሻ
≥ ૝ሺ૚ − ࢞ሻ
8. Resuelve y representa gráficamente la solución de los sistemas:
a) ൜
b)
‫ ۓ‬૜࢞ + ૞ < ૛
ۖ࢞ା૚ ࢞ି૚ ࢞
+
> ૛
૜
૞
‫࢞ ۔‬ା૚
ۖ
+૚≤࢞
‫ ە‬૜
࢞
Solución
a) Se resuelve cada inecuación del sistema
3‫ ݔ‬− 2ሺ‫ ݔ‬− 1ሻ
൜
5 − 3‫ݔ‬
⇒ቄ
6
‫ݔ‬
≤
≥
≤
≥
3‫ ݔ‬
2
⇒ቄ
−1
‫ݔ‬
4ሺ‫ ݔ‬− 1ሻ
3‫ ݔ‬− 2‫ ݔ‬+ 2
⇒ቄ
4ሺ1 − ‫ݔ‬ሻ
5 − 3‫ݔ‬
≤
≥
‫ݔ‬
−1
≤
≥
4‫ ݔ‬− 4
2+4
⇒ቄ
4 − 4‫ݔ‬
4‫ ݔ‬− 3‫ݔ‬
≤
≥
4‫ ݔ‬− ‫ ݔ‬
4−5
La solución de la primera inecuación es [2, +∞ሻ y de la segunda [−1. +∞ሻ.
-1
22
2
La solución del sistema es [2, +∞ሻ ∩ [−1. +∞ሻ = [૛, +∞ሻ
Matemáticas CCSS II
Página 4 de 6
Unidad 2: Inecuaciones y sistemas de inecuaciones
‫ ۓ‬3‫ ݔ‬+ 5 < ଶ
ۖ௫ାଵ ௫ିଵ ௫
+
> ଶ
ଷ
ହ
‫ ۔‬௫ାଵ
ۖ
+1≤‫ݔ‬
‫ ە‬ଷ
௫
b)
⇒
‫ݔ‬
൝‫ݔ‬
2
<
>
≤
⇒
−2
−5/19
‫ݔ‬
6‫ ݔ‬+ 10
൝15‫ ݔ‬+ 15 + 10‫ ݔ‬− 10
‫ݔ‬+1+3
-2 2
<
>
≤
‫ݔ‬
6‫ ݔ‬
3‫ݔ‬
⇒
5‫ݔ‬
൝19‫ݔ‬
4
<
>
≤
−10
−5 2‫ݔ‬
2
-5/19
5
, +∞൰ ∩ ሺ−∞, −2] = ∅
19
La intersección de los intervalos solución de cada inecuación:
ሺ−∞, −2ሻ ∩ ൬−
El sistema de inecuaciones no tiene solución
9. Resolver gráficamente la inecuación ૜࢞ − ૛࢟ ≤ ૝
Solución
De la inecuación dada pasamos a la igualdad 3‫ ݔ‬− 2‫ = ݕ‬4, se despeja
tamos la función.
‫ = ݕ‬ଶ ‫ ݔ‬− 2 y represenଷ
Dicha recta divide el plano en dos semiplanos uno de los cuales es la solución.
(0, 0) y sustituyendo en la inecuación se obtiene 3 · 0 − 2 · 0 = 0 ≤ 4 una desigualdad cierta, por lo
Para determinar cuál de ellos es, se toma un punto que no esté en la recta, por ejemplo el origen
que el semiplano que contiene ese punto es la solución de la inecuación, en caso de ser falsa la
desigualdad el otro semiplano será la solución.
x
0
4
y
-2
4
࢞+࢟
࢞+࢟
b) ൞
࢟
࢞
10. Resolver gráficamente los siguientes sistemas:
૞࢞ + ૛࢟
a) ൝૛࢞ − ࢟ − ૟
࢟
Solución
≥ ૚૙
≤ ૙
≤ ૜
≥
≤
≤
≤
૟
૚૛
ૡ
ૢ
a) Resolvemos cada inecuación por separado, y representamos la parte del plano que es solución
de cada inecuación. Para ello se representan gráficamente cada una de las rectas: ‫ = ݕ‬− ‫ ݔ‬+ 5,
‫ = ݕ‬2‫ ݔ‬− 6 , ‫ = ݕ‬3.
Matemáticas CCSS II
ହ
ଶ
Página 5 de 6
Unidad 2: Inecuaciones y sistemas de inecuaciones
Se representa en los mismos ejes, la parte del plano que es solución de cada inecuación y la solución al sistema es la parte del plano común a dichas regiones.
b) Procediendo de la misma forma, la solución del sistema de inecuaciones es la región del plano
coloreada.
Matemáticas CCSS II
Página 6 de 6