para DESCARGAR el documento. - Docencia en Matemática Aplicada

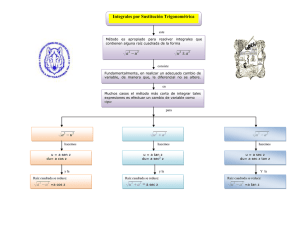
1
ADOLFO CHAPUZ BENITEZ PRESENTA:
MÉTODO DE SUSTITUCIÓN TRIGONOMÉTRICA parte I
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
2
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
3
Sobre el autor.
Adolfo Chapuz Benítez
Lic. En Matemáticas en la Universidad Juárez Autónoma De Tabasco
Profesor desde el año 1999 de matemáticas en el Instituto Tecnológico Superior De Comalcalco en
Tabasco, México
http://www.comoaprendomatematicas.com
Dedico este trabajo primeramente a Cristo Jesús, a Él sea toda lo gloria, toda la honra y toda la
alabanza. Él es el camino, y la verdad, y la vida Juan 14:6
A mi esposa Guillermina, a mis hijas Dulce y Regina, por quienes me esfuerzo para que tengan una
vida llena de bendiciones.
A mis padres Felipe y Valentina. Los mejores.
A mis hermanos: Nena, Mini, Sandra, Richard, Marbe e Ingrid. Inigualables.
A todos mis alumnos. De todo corazón.
Esto es para todos.
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
4
Contenido:
1.- Ejemplo General De la Forma
x2  a2
2.- Ejemplo General De la Forma
x2  a2
3.- Ejemplo General De la Forma
a2  x2
4.- Cinco ejemplos diversos
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
5
Introducción.
Uno de los métodos de integración clásicos es el llamado Método De Sustitución
Trigonométrica.
Este se usa para calcular integrales que involucran expresiones del tipo:
x2  a2 ,
x2  a2
a2  x2
donde a es una constante.
Para cada una de estas expresiones existe una sustitución específica que nos ayuda a
que la raíz cuadrada involucrada desaparezca y la integral que se quiera calcular sea
más fácil de encontrar.
Además de la sustitución, se le asocia un triángulo que nos va a servir para poder
regresar a nuestra variable original.
Las sustituciones las usamos de acuerdo a la siguiente tabla:
TIPO DE EXPRESION
SUSTITUCIÓN
ADECUADA
x2  a2
x  a tan
dx  a sec2 d
x2  a2
x  a sec
dx  a sec tand
a2  x2
x  asen
dx  a cos d
Antes de empezar con nuestros ejemplos, debo decirte que necesitamos de algunas
integrales que vamos a suponer que ya calculamos, éstas se pueden consultar en los
ejercicios vistos en la sección de Integrales trigonométricas. Estas integrales son las
siguientes:
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
6
I.-
 secd  lnsec  tan   c
II.-
 cscd   lncsc  cot    c
III.IV.-
 sec d  2 sec tan  2 ln sec  tan   c
1
3
1
 tand  lnsec   c
I.- EJEMPLO GENERAL DE LA FORMA
1.-

x2  a2
x 2  a 2 dx
Desarrollo: En este caso queremos calcular la integral en forma general porque
vamos a trabajar para cualquier valor de a y usamos el primer tipo de sustitución
porque es una SUMA de cuadrados.
x  a tan
dx  a sec2 d
Aquí aprovechamos igual para observar como la raíz cuadrada se cancela de manera
automática. De hecho este mismo procedimiento es el que debes aplicar cada vez que
quieras resolver una integral de este tipo. Así que pon mucha atención, porque no será
necesario repetirlo, sino simplemente aplicar el resultado ya obtenido.
Simplificamos
x2  a2 
x2  a2 :
a tan 2  a 2
 a 2 tan 2   a 2  a 2 tan 2   1  a 2 sec 2 
sec2 
 a 2  sec 2   a sec
2
2
Conclusión: x  a  a sec
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
7
Ahora, calculamos la integral:

x 2  a 2 dx   a seca sec 2 d
 a 2  sec3 d
1
1

 a 2  sec tan   ln sec  tan    c
2
2



x 2  a 2 dx 
a2
a2
sec tan   ln sec  tan    c
2
2
a2
a2
sec tan  ln sec  tan   c
2
2
Resultado previo.
Hasta este punto la integral ya está resuelta, solo debemos regresar a la variable
original x, usando el siguiente triángulo, que solo es válido para esta sustitución
x  a tan .
De aquí, obtenemos tan 
x
opuesto

,
a adyacente
con esto construimos nuestro triángulo
rectángulo:
x2  a2
Cateto opuesto

x
a
Cateto adyacente
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
8
Observando el triángulo, tenemos que:
tan 
x
, cos  
a
a
y sec  
x2  a2
x2  a2
. Ahora sólo basta sustituir en la
a
integral anterior.

x 2  a 2 dx 
a2
a2
sec tan   ln sec  tan    c
2
2

a 2  x 2  a 2
2 
a
 x  a 2  x 2  a 2 x 
   ln 
 c
 a  2 
a
a 



a 2  x x 2  a 2
2 
a2

x x 2  a 2 a 2  x 2  a 2  x 
 ln
c

2
2 
a

 a2  x2  a2  x 
  ln 
c
 2 

a



Por lo tanto, tenemos que:

x 2  a 2 dx 
x x 2  a 2 a 2  x 2  a 2  x 
 ln
c

2
2 
a

Todos Los Derechos Reservados
www.comoaprendomatematicas.com
9
II.- EJEMPLO GENERAL DE LA FORMA
x2  a2
Desarrollo:
x  a sec
dx  a sec tand
Simplificamos
x2  a2 
x2  a2 :
a sec 2  a 2
 a 2 sec 2   a 2  a 2 sec 2   1  a 2 tan 2 
tan 2 
 a 2  tan 2   a tan
2
2
Conclusión: x  a  a tan 
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
10
Ahora, calculamos la integral, sustituyendo lo que acabamos de obtener:

x 2  a 2 dx   a tan  a sec tan d 
 a 2  tan 2  secd


 a 2  sec 2   1 secd
 a 2  sec3 d  a 2  secd
1
1

 a 2  sec tan   ln sec  tan    a 2 ln sec  tan    c
2
2


a2
a2
sec tan   ln sec  tan    a 2 ln sec  tan    c
2
2

a2
a2
sec tan   ln sec  tan    c
2
2
Tenemos el resultado provisional de la integral en términos de 

x 2  a 2 dx 
a2
a2
sec tan  ln sec  tan   c
2
2
Resultado previo.
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
11
Hasta este punto la integral ya está resuelta en términos de  , solo debemos
regresar a la variable original x, usando el siguiente triángulo, que solo es válido para
esta sustitución x  a sec .
De aquí, obtenemos sec 
x hipotenusa

,
a adyacente
con esto construimos nuestro triángulo
rectángulo:
Cateto opuesto
x
x2  a2

a
Cateto adyacente
Observando el triángulo, tenemos que:
sec 

x
opuesto

, tan 
a
adyacente
x 2  a 2 dx 
x2  a2
. Ahora sólo basta sustituir en
a
a2
a2
sec tan  ln sec  tan   c
2
2
,
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
12

x 2  a 2 dx 
a 2  x  x 2  a 2
 
2  a 
a
2
2
 a2  x
  ln   x  a
 2 a
a



1
a2  x  x2  a2
x x 2  a 2  ln 
2
2 
a

c


x 2  a 2 dx 
1
a2  x  x2  a2
x x 2  a 2  ln 
2
2 
a

c



c


Conclusión:

Todos Los Derechos Reservados
www.comoaprendomatematicas.com
13
III.- EJEMPLO GENERAL DE LA FORMA
a2  x2
Desarrollo:
x  asen
dx  a cos d
Simplificamos
a2  x2 :
a 2  x 2  a 2  asen   a 2  a 2 sen 2  a 2 1  sen 2   a 2 cos 2 
2
cos 2 
 a 2  cos 2   a cos 
2
2
Conclusión: a  x  a cos 
Ahora calculamos la integral:
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
14

a 2  x 2 dx   a cos  a cos d 
 a 2  cos 2 d
1 1

 a 2    cos(2 ) d
2 2

1
1
 a 2  d  a 2  cos(2 )d
2
2

a2
a2  1

   sen2   c
2
2 2


a2
a2
  sen2  c
2
4

a2
a2
  2 sen cos    c
2
4
a2
a2
   sen cos   c
2
2
Tenemos el resultado provisional de la integral en términos de 

Resultado previo.
a2
a2
a  x dx    sen cos   c
2
2
2
2
Hasta este punto la integral ya está resuelta en términos de  , solo debemos
regresar a la variable original x, usando el siguiente triángulo, que solo es válido para
esta sustitución x  asen .
De aquí, obtenemos sen 
x
opuesto

,
a hipotenusa
con esto construimos nuestro triángulo
rectángulo:
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
15
a
x
Cateto opuesto

a2  x2
Cateto adyacente
Observando el triángulo, tenemos que:
x
a
sen 
x
a,
cos  
adyacente
a2  x2

. Ahora sólo basta sustituir en:
Hipotenusa
a
  sen1  

a 2  x 2 dx 
a2
a2
  sen cos   c
2
2

a 2  x 2 dx 
2
2
2
a2
 x a  x a x
sen 1     
c
2
a
a 2 a
a2
 x x 2

sen 1   
a  x2  c
2
a 2
Y finalmente tenemos:

a2
 x x 2
a  x dx  sen1  
a  x2  c
2
a 2
2
Todos Los Derechos Reservados
2
www.comoaprendomatematicas.com
16
Ejemplos diversos:
NOTA: EN ESTOS EJEMPLOS VAMOS A USAR LAS SIGUENTES EXPRESIONES
QUE HEMOS OBTENIDO ANTERIORMENTE PARA AHORRAR UN POCO DE
ESPACIO Y TIEMPO EN LAS EXPLICACIONES.
1. x 2  a 2  a sec
2. x 2  a 2  a tan
3. a 2  x 2  a cos 
1.-

x2  3
dx
x
Desarrollo:
Primero identificamos el valor de a :
a2  3  a  3 .
x  3 tan  y
dx  3 sec2 d .Entonces recordemos que hemos obtenido con
anterioridad la siguiente expresión:
x 2  a 2  a sec , así que sólo vamos a sustituir
el valor de a :
Tenemos que
x2  3  3 sec y debemos sustituir en la integral.
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
17

x2  3
3 sec 
dx  
3 sec2 d
x
3 tan 
sec3 
 3
d
tan 
sec2  sec 
 3
d
tan 
 3
tan   1sec d
 3
tan  sec  sec d
2
tan 
1
sec 
cos 
1
cos 



sen
tan 
cos sen
sen
cos 
2
tan 
 csc 
tan 2  sec 
sec 
 3
d  3 
d
tan 
tan 
 3  tan  sec  d  3  csc d

x2  3
dx  3  tan sec d  3 ln csc   cot    c
x
Simplificamos el integrando de la primera integral:
tan sec 
sen
1
sen


cos  cos  cos 2 
u  cos 
du   send
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
18
Ahora usamos cambio de variable.

x2  3
du
dx   3  2  3 ln csc   cot    c
x
u
  3  u  2 du  3 ln csc   cot    c
 u 1 
  3 ln csc   cot    c
  3 

1




3
 3 ln csc   cot    c
u

3
 3 ln csc   cot    c
cos 
x2  3
3
dx 
 3 ln csc   cot    c
x
cos 
Resultado previo.
Ahora regresamos a la variable x, nos basamos en la sustitución con que empezamos
x  3 tan  tan 
x
opuesto
:

3 adyacente
x2  3
Cateto opuesto

x
3
Cateto adyacente
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
19
Observando el triángulo, tenemos que:
tan  
cos  

3
x
sen 
, cot  
x
3
3
x2  3
, sec  
x
x2  3
, csc  
x2  3
.
x
x2  3
Ahora sólo basta sustituir en la integral anterior.
3
x2  3
3
dx 
 3 ln csc   cot    c
x
cos 
 x2  3
3 
 3 sec   3 ln 

c


x
x


 3  x2  3 
x2  3
c
 3
 3 ln 


x
3


 3  x2  3 
c
 x  3  3 ln 


x


2

 3  x2  3 
x2  3
2
c
dx  x  3  3 ln 


x
x
Conclusión.


Todos Los Derechos Reservados
www.comoaprendomatematicas.com
20
2.-

x 2  25
dx
x
Desarrollo:
Aquí usamos x  5 sec y
dx  5 sec tand al sustituir estas expresiones nos
ayudan a simplificar la parte que tiene el radical.
x 2  25  5 tan

.Entonces tenemos lo siguiente:
x 2  25
5 tan
dx  
5 sec tand
x
5 sec
sec   1  tan 2 
2
sec   1  tan 2 
2
 5 tan 2 d
 5 sec 2   1d
 5 sec 2 d  5 d
 5 tan  5  c

x 2  25
dx  5 tan  5  c
x
Resultado previo.
Hasta este punto la integral ya está resuelta, solo debemos regresar a la variable
original x, usando el siguiente triángulo, que solo es válido para esta sustitución con la
que iniciamos x  5 sec .
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
21
De aquí, obtenemos sec 
x hipotenusa

,
5 adyacente
con esto construimos nuestro triángulo
rectángulo:
x
x 2  25
Cateto opuesto

5
Cateto adyacente
Observando el triángulo, tenemos que:
sec 
x
x
opuesto

,   arc sec( ) tan 
5
5
adyacente

x 2  25
dx  5 tan  5  c
x

x 2  25
dx  5 tan   5  c
x
5
x 2  25
. Ahora sólo basta sustituir en
5
x 2  25
x
 5arc sec( )  c
x
5
Conclusión:

x 2  25
x 2  25
dx  5
 5arc sec( x / 5)  c
x
x
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
22
3.-

16  x 2
dx
x
Desarrollo: a  16, a  4
2
x  4sen
dx  4 cosd
Hemos obtenido previamente que:
Así que

a 2  x 2  a cos 
16  x 2  4 cos  .
16  x 2
4 cos 
4 cos d 
dx  
x
4 sen
 4
cos 2 
d
sen
 4
1  sen  d
 4
1
sen 2
d  4 
d
sen
sen
2
sen
 4  cscd  4  sen d
 4 ln csc  cot    4 cos   c

16  x 2
dx  4 ln csc  cot    4 cos   c
x
Resultado previo.
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
23
Hasta este punto la integral ya está resuelta en términos de  , solo debemos
regresar a la variable original x, usando el siguiente triángulo, que solo es válido para
esta sustitución x  4sen .
De aquí, obtenemos sen 
x
opuesto

,
4 hipotenusa
con esto construimos nuestro triángulo
rectángulo:
4
x
Cateto opuesto

16  x 2
Cateto adyacente
Observando el triángulo, tenemos que:
x
4,
sen 
cos  
tan 
cot  
csc 
1
4

sen x
adyacente
16  x 2

Hipotenusa
4
opuesto
x

adyacente
16  x 2
16  x 2
x
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
24
Ahora sólo basta sustituir en:

16  x 2
dx  4 ln csc  cot    4 cos   c
x

4
16  x 2
16  x 2
dx  4 ln  
x
x
x

 4  16  x 2
 4 ln 

x

2

  4 16  x  c

4


  16  x 2  c


Conclusión:

 4  16  x 2
16  x 2
dx  4 ln 

x
x

Todos Los Derechos Reservados

  16  x 2  c


www.comoaprendomatematicas.com
25
Ejemplo 4.-

x
3  x4
dx
Primero hacemos un cambio de variable: u  x , du  2 xdx y transformamos nuestra
2
integral original en términos de u .

x
3 x
4
dx 
1
2 xdx

2 3  x2
 
2

1
du

2 3  u2
En este punto es donde aplicamos la sustitución trigonométrica.
2
Desarrollo: a  3, a  3
u  3sen
du  3 cos d y

x
3 x
3  u2 
dx 
4
1
2 xdx

2 3  x2

1
du

2 3  u2

1
3 cos d

2
3 cos 

1
d
2
 
2

3 cos 
1
du

2 3  u2
1
  c
2
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
26

x
1
dx    c
2
3 x
Resultado previo.
4
Ahora vamos a regresar a la variable original x:
u  3sen
sen 
 u 

 3
u
3
  arcsen
Pero como u  x , entonces
2

 x2 
  arcsen  , por lo tanto:
 3
 x2 
1
  c
dx  arcsen
2
3
3  x4


Conclusión.
x
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
27
Ejemplo 5.-
x2

x 2 100
dx
Desarrollo:
a 2  100, a  10
x  10 sec  x 2  100 sec2 
dx  10 sec tand
Además:

x 2  100  10 tan
100 sec 2 
10 sec tan d 
dx  
10 tan 
x 2  100
x2
 100 sec3 d
1
1

 100 sec  tan   ln sec   tan    c
2
2


x2
x  100
2
dx 
100
100
sec  tan  
ln sec   tan    c
2
2
Resultado previo.
Solo debemos regresar a la variable original x, usando el siguiente triángulo, que solo
es válido para esta sustitución con la que iniciamos x  10 sec .
Todos Los Derechos Reservados
www.comoaprendomatematicas.com
28
De aquí, obtenemos sec 
x hipotenusa

,
10 adyacente
con esto construimos nuestro triángulo
rectángulo:
Cateto opuesto
x
x 2  100

10
Cateto adyacente
Observando el triángulo, tenemos que:
sec 


opuesto
x

, tan 
10
adyacente
x2
x 2  100
x 2  100
. Ahora sólo basta sustituir en
10
dx  50 sec tan  50 ln sec  tan   c
2
 x
 x  x  100 
 
dx

50

50
ln



 10
10
 10 
x 2  100


x2
x 2  100 
c

10

 x  x 2  100 
1
2
c
 x x  100  50 ln 


2
10


Conclusión

 x  x 2  100 
1
2

c
dx

x
x

100

50
ln


2
10
x 2  100


x2
Todos Los Derechos Reservados
www.comoaprendomatematicas.com