Práctico 5 - Universidad de la República

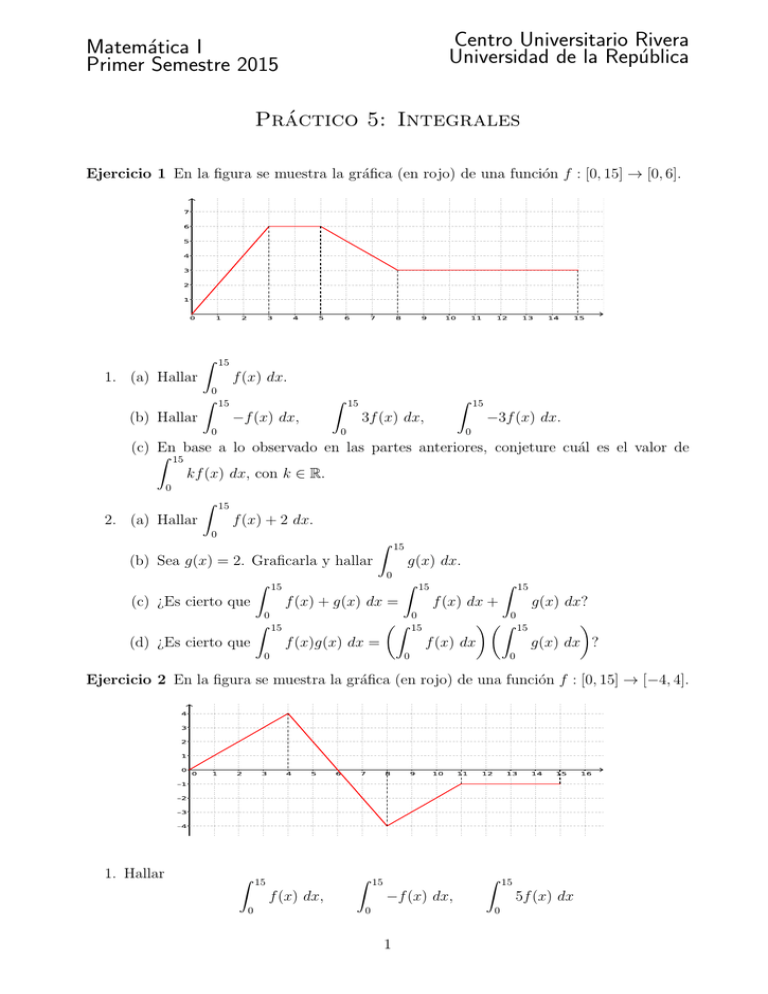
Centro Universitario Rivera
Universidad de la República
Matemática I
Primer Semestre 2015
Práctico 5: Integrales
Ejercicio 1 En la figura se muestra la gráfica (en rojo) de una función f : [0, 15] → [0, 6].
Z
15
1. (a) Hallar
f (x) dx.
0
Z
15
Z
−f (x) dx,
(b) Hallar
15
Z
0
0
0
15
−3f (x) dx.
3f (x) dx,
(c) Z
En base a lo observado en las partes anteriores, conjeture cuál es el valor de
15
kf (x) dx, con k ∈ R.
0
Z
15
f (x) + 2 dx.
2. (a) Hallar
0
Z
15
g(x) dx.
(b) Sea g(x) = 2. Graficarla y hallar
0
15
Z
Z
(c) ¿Es cierto que
f (x) + g(x) dx =
0
Z
Z 15
(d) ¿Es cierto que
f (x)g(x) dx =
0
15
Z
15
f (x) dx +
g(x) dx?
0
0
Z 15
15
f (x) dx
g(x) dx ?
0
0
Ejercicio 2 En la figura se muestra la gráfica (en rojo) de una función f : [0, 15] → [−4, 4].
1. Hallar
Z
15
Z
Z
−f (x) dx,
f (x) dx,
0
15
0
5f (x) dx
0
1
15
2. Indicar las opciones correctas, justificando mediante el cálculo de las integrales.
Z 15
f (x) dx =
0
(a)
(b)
(c)
(d)
(e)
R6
0
R6
0
R8
0
R8
0
R8
0
f (x) dx +
R 15
f (x) dx −
R 15
f (x) dx +
R 15
f (x) dx −
R4
f (x) dx +
6
6
8
8
R4
8
f (x) dx.
f (x) dx.
f (x) dx.
f (x) dx +
R 15
4
f (x) dx.
R 15
f (x) dx + 4 f (x) dx.
Z 15
4 + f (x) dx =
3. Indicar la opción correcta:
0
15
Z
f (x) dx.
(a) 4 +
0
Z
(b) 4 × 15 +
15
f (x) dx.
0
Z
15
f (x) dx.
(c) 4
0
Ejercicio 3
1. Sea f : R → R, f (x) = 6. Para cada valor de x ∈ R, calcular
Z x
F (x) =
f (t) dt.
0
Graficar F (x) y estudiar su crecimiento.
2. Sea f : R → R, f (x) = −6. Para cada valor de x ∈ R, calcular
Z x
F (x) =
f (t) dt.
0
Graficar F (x) y estudiar su crecimiento.
3. Sea f : R → R, f (x) = 7x . Para cada valor de x ∈ R, calcular
Z x
F (x) =
f (t) dt.
0
Graficar F (x) y estudiar su crecimiento.
4. ¿Qué relación observa entre el signo de f y el crecimiento de F ?
Ejercicio 4 Sea f la función cuyo gráfico aparece en el ejercicio 2 y sea
Z x
F (x) =
f (t) dt
0
2
1. Hallar F (0), F (1), F (6) y F (15).
2. Hallar el valor mı́nimo m y el valor máximo M que la función F toma en el intervalo
[0, 15].
3. ¿Cuántas raı́ces tiene F ?
4. Bosquejar el gráfico de F .
Ejercicio 5 Sea f la función cuya gráfica se presenta en el ejercicio 1.
Para x ∈ [0, 15], definimos
Z x
f (t) dt.
F (x) =
0
1. Hallar el valor que toma F en x = 5.
2. Hallar el valor mı́nimo que alcanza la función F .
3. Hallar el valor máximo que alcanza la función F .
4. Hallar x tal que F (x) = 4.
5. Hallar F 0 (3).
6. Bosquejar el gráfico de F .
Ejercicio 6
Z
x
1. Sea f una función constante: f (x) = 7 y sea F (x) =
f (t) dt.
1
(a) Hallar F (x). Comparar F 0 (x) con f (x).
Rb
(b) Calcular a f (t) dt y comparar con F (b) − F (a).
(c) Sea G otra primitiva de f . Calcular G(b) − G(a) y comparar con el resultado de
la parte anterior.
Z x
2. Sea f una función lineal: f (x) = 2x − 2 y sea F (x) =
f (t) dt.
1
(a) Hallar F (x). Comparar F 0 (x) con f (x).
Rb
(b) Calcular a f (t) dt y comparar con F (b) − F (a).
(c) Sea G otra primitiva de f . Calcular G(b) − G(a) y comparar con el resultado de
la parte anterior.
Ejercicio
7 Calcular lasZ derivadas de las siguientes funciones:
Z x√
3
t2 − t + 1 dt,
sen3 (t) + t2 dt
0
x
Ejercicio 8 Calcular primitivas de las siguientes funciones:
1
1
1
a) 3x2 − 6x + 8,
b) √ ,
c) + 2 + e2x ,
x x
x
d) ex+2 − 1,
e) 2x2 − e−3x ,
f ) 2sen(3x).
3
Ejercicio 9 Hallar una función f tal que:
1. sea primitiva de la función g(x) = 6x2 + x y se anule en x = 2.
2. f 00 (x) = 3x2 − ex − 2 y f 0 (0) = f (0) = 1.
Ejercicio 10 Calcular:
R2
1. −1 6x2 dx
R4
2. 5 2x5 dx
Rπ
3. 0 12sen(x) dx
R1
4. −1 3et dt
R −1
5. −2 (2t2 + 4t − 1) dt
Rπ
6. −π (5sen(t) + cos(t)) dt
Ejercicio
Z 2 11 Calcular
(2x2 − ex )dx,
a)
b)
−1
Z
d)
1
2
4
Z
1
1
1
+ 2 dx,
x x
Z
e)
0
√
1/ 2
π
Z
1
√ dx,
x
sen (2x)dx,
c)
0
1
dx,
1 + x2
Z
f)
1
2
1
1
−
dx.
e2x x
Ejercicio 12 Hallar el área comprendida entre el gráfico de f y el eje Ox en el intervalo
indicado:
a) f (x) = x3 + 1 en [−2, 1] b) f (x) = cos(x) en [0, π/2]
c) f (x) = ex + 2 en [0, 1].
Ejercicio 13 Calcular el área de las siguientes regiones:
1. La región limitada entre las gráficas de f y g sobre el intervalo [0, 2] siendo f (x) =
x(x − 2) y g(x) = x2 .
2. La región acotada que se encuentra encerrada entre los gráficos de ex , e−x y las rectas
y = 0, x = −1 y x = 2.
Ejercicio 14 Tengo que embaldosar parte de un patio de 20m de largo por 10m de ancho.
El dueño quiere que el piso sea la superficie bajo el gráfico de la parábola
y=−
x2
+ 20
5
en el primer cuadrante, tomando una esquina del jardı́n como el origen, el ancho como el eje
horizontal y el largo como el vertical. El resto del espacio ser reservado a cesped y canteros
para plantas.
Pedı́ dos presupuestos. Alberto Álvarez contestó que la obra costará $88000. Mientras
que en Baldosas Baez me dicen que tienen un costo fijo de transporte de $6000 y luego $600
por metro cuadrado.
¿Cuál de las dos opciones es la más barata?
4