GENERALIDADES DE LA GEOMETRÍA

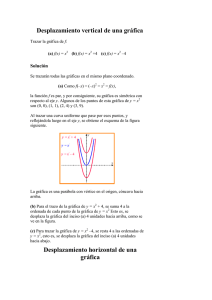
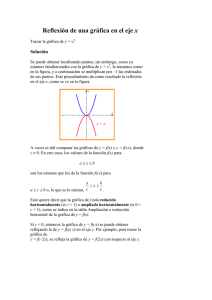
GENERALIDADES DE LA GEOMETRÍA
Unidad 1. El dibujo técnico en el plano
La geometría nos permite medir áreas y volúmenes, es útil en la preparación
de diseños, e incluso en la fabricación de artefactos mecánicos.
1
¿QUÉ ENCONTRAREMOS EN ESTE DOCUMENTO?
Conceptos básicos ........................................................................................... 3
Para qué nos sirve la Geometría en los planos ................................................... 3
Elementos básicos y geometría plana ................................................................ 4
Procedimientos para el trazado de polígonos y elementos tangentes .................. 9
Cómo construir trazados de polígonos regulares ............................................... 9
Cómo construir trazados de elementos tangentes ........................................... 16
Escala ............................................................................................................ 20
Características dimensionales en los planos ................................................... 20
Qué es escala ................................................................................................. 21
Tipos de escala ............................................................................................... 22
Líneas utilizadas en el dibujo ........................................................................... 24
Aplicaciones de las líneas en el plano .............................................................. 24
Convensiones para líneas ocultas ................................................................... 30
Enlaces de interés .......................................................................................... 32
Dónde podemos encontrar más información.................................................... 32
2
Conceptos básicos
Para qué nos sirve la Geometría en los planos
La geometría es un aspecto fundamental, en el cual
se basan las manifestaciones de dibujo de
ingeniería, a partir de ella se estructuran las
expresiones gráficas que se plasman en los planos
técnicos, por lo que es indispensable conocer los
conceptos básicos que de ella se derivan.
Para construir una representación gráfica de un
objeto por medio del dibujo técnico, es muy
importante conocer y dar un correcto uso a las
construcciones geométricas básicas.
Se abordara de forma general los
aspectos relevantes de la
geometría enfocados a facilitar
la interpretación de
representaciones gráficas.
3
Elementos básicos y geometría plana
Elementos básicos
El Punto
El punto se define como el mínimo lugar geométrico,
el punto no pose dimensiones.
Línea recta
La línea recta se define como la trayectoria
generada por un punto en movimiento en una misma
dirección.
Línea curva
Si el punto en movimiento cambia continuamente de
dirección la línea generada es una línea curva.
El Plano
El plano es una superficie bidimensional que carece
de espesor y se limita por su largo y ancho.
Existen diferentes tipos de
geometría pero en este caso
estudiaremos la geometría
plana.
La geometría plana se centra en el estudio de
las figuras planas, que solo tienen dos
dimensiones y que por lo tanto, se
encuentran y operan en un plano,
los
elementos básicos con que se suele trabajar
son los polígonos y las circunferencias.
4
Polígonos
Un polígono es una figura geométrica plana cerrada por segmentos de línea. Un polígono
tiene los siguientes elementos: Lados, vértices, ángulos y diagonales.
Los polígonos se dividen en regulares e irregulares, en los polígonos regulares todos los
lados y ángulos son iguales, en caso contrario es irregular.
Según el número de lados los polígonos se clasifican en:
 Descripción de algunas clases de polígonos
Triángulo
Un triángulo, es un polígono determinado
por tres rectas. Los puntos de
intersección de las rectas son los vértices
y los segmentos de recta determinados
son los lados del triángulo. Un triángulo
tiene 3 ángulos interiores, 3 lados y 3
vértices.
Los triángulos se pueden clasificar por la
relación entre las longitudes de sus lados
o por la amplitud de sus ángulos.
5
Clasificación de los triángulos por la longitud de los lados
 Triángulo equilátero, si sus tres lados tienen la misma longitud (los tres ángulos
internos miden 60 grados).
 Triángulo isósceles, si tiene dos lados de la misma longitud. Los ángulos que se
oponen a estos lados tienen la misma medida.
 Triángulo escaleno, si todos sus lados tienen longitudes diferentes (en un
triángulo escaleno no hay dos ángulos que tengan la misma medida).
Clasificación de los triángulos por la amplitud de sus ángulos
 Triángulo rectángulo, si tiene un ángulo interior recto (90°).
 Triángulo obtusángulo, si uno de sus ángulos interiores es obtuso (mayor de
90°); los otros dos son agudos (menores de 90°).

Triángulo acutángulo, cuando sus tres ángulos interiores son menores de 90°.
6
Algunas propiedades de los ángulos de los triángulos
 Los tres ángulos internos de un triángulo miden 180°.
 La suma de las longitudes de dos de sus lados es siempre mayor que la longitud del
tercer lado.
 El valor de la paralela media de un triángulo (recta que une dos puntos medios de dos
lados) es igual a la mitad del lado paralelo.
 Para cualquier triángulo se verifica el Teorema del seno que establece: Los lados de
un triángulo son proporcionales a los senos de los ángulos puestos.
𝑎
𝑏
𝑐
=
=
𝑠𝑒𝑛 (𝛼 )
𝑠𝑒𝑛 (𝛽)
𝑠𝑒𝑛(𝛾)
Para cualquier triángulo se verifica el Teorema del coseno que demuestra que: El
cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el
doble del producto de estos lados por el coseno del ángulo comprendido.
𝑎2 = 𝑏 2 + 𝑐 2 − 2𝑏𝑐 . cos(𝛼)
𝑏 2 = 𝑎2 + 𝑐 2 − 2𝑎𝑐 . cos(𝛽)
𝑐 2 = 𝑎2 + 𝑏 2 − 2𝑎𝑏 . cos(𝛾)
Para cualquier triángulo rectángulo, cuyos catetos miden a y b, y cuya hipotenusa mida c,
se verifica el Teorema de Pitágoras:
𝑎2 + 𝑏 2 = 𝑐 2
7
Cuadrilátero
Un cuadrilátero es un polígono que tiene
cuatro lados es decir está definido por 4
segmentos de línea. Los cuadriláteros
pueden tener distintas formas en función
de la longitud de sus lados, pero todos
ellos tienen cuatro vértices y dos
diagonales.
Los cuadriláteros se caracterizan por que
la suma de sus 4 ángulos internos es
igual a 360º.
Círculo y circunferencia
El circulo es una figura geométrica plana delimitada por una
circunferencia de radio r, todos los puntos del circulo estar
se ubican a una distancia menor o igual que r partiendo del
centro como referencia.
Es importante mencionar que la circunferencia es la línea
que encierra el círculo. Aunque ello hace que compartan
características comunes como el centro, el radio y el
diámetro.
Para calcular el área de un circulo simplemente multiplicamos el cuadrado de su radio por
el numero π (3,1416), aunque como existe una relación entre el radio, el diámetro y la
longitud de la circunferencia el área se puede expresar en sus términos.
𝐴 = 𝜋. 𝑟 2
𝐴=
𝐴=
En función del radio (r)
𝜋 . 𝑑2
4
En función del diámetro (d), r = d/2
𝐶2
4. 𝜋
En función de la longitud de la
circunferencia máxima (C), pues la longitud
de dicha circunferencia es:
8
Procedimientos para el trazado de
polígonos y elementos tangentes
Cómo construir trazados de polígonos regulares
En el diseño de una máquina es posible definir las secciones de las
piezas en función de alguna necesidad específica o finalidad de la pieza,
esto implicará entonces que al plasmar el dibujo, este contenga múltiples
secciones que se representen por medio de polígonos.
Para facilitar la interpretación de un
dibujo dentro de un plano técnico y
conocer como se construyen,
analizaremos los procedimientos para
construir algunos polígonos.
9
Trazar un cuadrado
longitud del lado (a)
Procedimiento:
conociendo
la
1. Trace una recta AB con longitud a,
como base del cuadrado.
2. Desde los extremos de A y B, trace
dos perpendiculares a la recta AB.
3. Con centro en A y B trace dos arcos
con radio a que corten las
perpendiculares para ubicar los
vértices del cuadrado.
4. Una los cuatro puntos y dibuje el
cuadrado pedido.
Trazar un cuadrado conociendo su
diagonal (d)
Procedimiento:
1. Trazar dos rectas r y s perpendiculares
entre sí.
2. Se traza la bisectriz del ángulo formado
por las dos rectas r y s.
3. Sobre la bisectriz se lleva la diagonal AC
de longitud d.
4. Desde el punto C se trazan paralelas a
las rectas r y s.
5. Utilizando estos puntos, se construye el
cuadrado.
10
Trazar un rectángulo conociendo la
longitud de sus lados (a y b).
Procedimiento:
1. Trazar dos rectas de longitud a y b con
origen común en A y perpendiculares
entre sí.
2. Desde
el
otro
extremo
del
lado a (punto B) se traza un arco de
radio b.
3. Desde el punto D (extremo del lado b)
se traza un arco de radio igual al
lado a.
4. Se unen los cuatro puntos y se obtiene
el rectángulo.
Trazar un rombo conociendo una
diagonal (d) y la longitud de su lado (a).
Procedimiento:
1. Trazar una recta horizontal AC de
longitud d.
2. Con centro en A y C trazar arcos con
radio a, los puntos de intersección son
los puntos B y D.
3. Unir los extremos de la diagonal A y C,
con los puntos hallados B y D para
obtener el rombo.
11
Trazar
un
romboide,
dadas
las
longitudes de las diagonales (a y b) y el
ángulo (m)
Procedimiento:
1. Dadas las diagonales a y b, y el ángulo
m.
2. Trace la recta AB de longitud a, halle
su centro O.
3. Trace la recta CD que pase por O y
con ángulo m partiendo de la
horizontal.
4. Haciendo centro en O y con radio igual
a b/2 trace un arco que corte la recta
CD.
5. Se trazan las rectas correspondientes
que unan los puntos AC, CB, BD y DA.
Trazar de un pentágono regular inscrito
en una circunferencia dada
Procedimiento:
1. Trazar dos rectas perpendiculares PD y
OQ que pacen por el centro O.
2. Ubicar el punto medio de OQ y ubicar M,
trazar la recta desde P que pase por M
(recta PM).
3. Con centro en M trazar una
circunferencia de radio MO que corte la
recta PM, ubicar los puntos R y S.
4. Con centro en P y radios PR, PS, trazar
arcos que corten la circunferencia dada
para hallar los vértices del pentágono.
5. Unir los vértices
pentágono.
para
dibujar
el
12
Trazar
un
pentágono
regular
conociendo la longitud de su lado AB
Procedimiento:
1. Trazar el lado AB y hallar su mediatriz
para ubicar el punto M.
2. En uno de los extremos de la línea AB
(se escoge el punto B), se traza una
perpendicular de longitud AB y se halla
el punto N.
3. Con centro en M y radio MN, se traza
un arco y se halla el punto O.
4. Con radio MO se trazan arcos desde A
y B. Se obtiene D.
5. Desde D, se traza un arco de radio AB.
Se obtiene E y C.
6. Se unen los puntos A, B, C, D y E. Se
obtiene el pentágono.
Trazar un Hexágono regular conociendo
el lado que está inscrito en una
circunferencia de radio igual al lado
Procedimiento:
1. Trazar una circunferencia de radio AB.
2. Desde los puntos A y D se trazan
arcos con el radio AB.
3. Se unen los puntos A, B, C, D, E y F
obteniendo el hexágono regular.
13
Trazar un heptágono conociendo la
longitud de su lado AB
Procedimiento:
1. Trazar de forma horizontal la recta AB.
2. Con radio AB trazar arcos con centro
en A y B, hallar el punto 1.
3. Trazar dos perpendiculares a la recta
AB, una que pase por 1 y la otra por
B.
4. Trazar la bisectriz del ángulo formado
por las líneas imaginarias A1 y AB,
esta bisectriz corta la perpendicular en
2.
5. Con radio A2, trazar un arco que corte
la perpendicular que pasa por 1en el
punto O.
6. Desde O, con un radio AO, se traza
una circunferencia. A partir de B se
lleva 7 veces el lado AB.
7. Se unen todos los puntos y se obtiene
el heptágono.
14
Trazar un octógono
longitud de su lado AB
Procedimiento:
conociendo
la
1. Trazar horizontalmente el lado AB y
trazar su mediatriz.
2. En el punto B, se traza
perpendicular de longitud AB.
una
3. Se une el punto A con el punto 1.
Corta a la mediatriz en 2.
4. Haciendo centro en O, y radio OA, se
traza la circunferencia.
5. Sobre la circunferencia hallada se
trazan los vértices partiendo de B.
6. Se unen todos los puntos y se obtiene
el octógono.
15
Cómo construir trazados de elementos tangentes
Para realizar un plano donde se
incluyen contornos de superficies
cilíndricas, es muy importante
conocer
los
diferentes
procedimientos para trazar las
tangencias entre los elementos del
dibujo, para ello se analizaran
algunos ejemplos claves donde se
describen los procedimientos y se
describen gráficamente.
Trazar un arco tangente a las líneas AB – AC
que forman un ángulo recto dado un radio R
Procedimiento 1:
Procedimiento 1
1. Trace desde el punto A, un arco de
radio R, que intercepte las dos líneas en
el los puntos de tangencia T.
Procedimiento 2
2. Desde estos puntos de tangencia T y
con radio R, trace arcos que se cortan
en O.
3. Con centro en O y con radio R, Dibuje
el arco tangente requerido.
Procedimiento 2 (método general):
1. Dibuje líneas paralelas a una distancia
R de las líneas AB y AC.
2. En el punto donde se cortan ubique el
centro O.
3. Con centro en O y radio R, dibuje el
arco tangente requerido.
16
Trazar un arco tangente a dos líneas AB –
AC que forman un ángulo agudo u obtuso
dado un radio R.
Ángulo agudo
Procedimiento:
1. Dibuje líneas paralelas a una distancia
R de las líneas AB y AC.
2. En el punto donde se cortan ubique el
centro O.
Ángulo obtuso
3. Desde O construir perpendiculares a las
líneas AB – AC y ubicar los puntos de
tangencia T.
4. Con centro en O y radio R, dibuje el
arco tangente requerido entre los
puntos de tangencia.
17
Trazar un arco tangente a otro arco de
radio G y a una línea recta AB
Procedimiento:
1. Dibuje una línea paralela
distancia R de la línea AB.
a
una
2. Trace un arco con centro en O y con
radio G+R, este arco debe cortar la
línea paralela a AB en el punto C.
3. Trace un línea desde el punto C hasta
O para ubicar el punto de tangencia T1
y trace una recta perpendicular a AB
desde C para obtener le punto de
tangencia T2.
4. Con centro en C y radio R, dibuje el
arco tangente requerido entre los
puntos de tangencia.
Trazar un arco tangente con radio R a
dos arcos con centros en O y S.
Procedimiento:
1. Dados dos arcos con centro en O y S, u
el radio requerido R.
2. Dibuje arcos paralelos a los arcos
dados con centros en O y S, a una
distancia R de ellos, la intersección de
los arcos C es el centro del arco
requerido.
3. Dibuje las líneas CO y CS, para hallar
los puntos de tangencia T.
4. Con centro en C y radio R dibuje el arco
requerido entre los punto de tangencia
T.
18
Trazar un arco tangente envolvente de
radio HK a dos arcos con centros en A y
B, y con radios R y r.
Procedimiento:
1. Con centro en A trace un arco de radio
HK-r (HK menos r) y con centro en B
trace el arco HK-R, estos arcos se
cortan en el punto G.
2. Trace las líneas GA y GB y extiéndalas
hasta encontrar los puntos de tangencia
T.
3. Dibuje el arco requerido con centro en
G y radio HK entre los puntos de
tangencia.
19
Escala
Características dimensionales en los planos
En el proceso de creación de planos técnicos, los
dibujos se plasman sobre formatos de dimensiones
normalizadas, esto implica que las características
dimensionales de los objetos se tengan que ajustar
al tamaño de los formatos, es decir, se hace
indispensable el uso de las escalas para poder
representar con claridad los objetos en el papel,
dado que muchas veces el objeto es muy grande y
no cabe en el formato o por el contrario es muy
pequeño y sobra espacio.
El instrumento que se utiliza
para hacer este tipo de
dimensionamiento es el
escalimetro
20
Qué es escala
Es la relación que existe entre la dimensión lineal de un elemento representado en el
dibujo y la dimensión real del mismo elemento.
La escala expresa el número de veces que el dibujo se ha reducido o ampliado con
respecto al tamaño natural o real del objeto; el denominador indica las partes en que se
divide el total y el numerador la parte o partes que hemos tomado para plasmas el
dibujo.
Escala = (Tamaño del dibujo/Tamaño del objeto)
21
Tipos de escala
Escala natural
La escala natural tiene una relación 1:1, es
decir, las dimensiones del dibujo son las
mismas dimensiones reales del elemento.
Escala de ampliación
La escala de ampliación es una escala
mayor a la escala natural, las escalas de
ampliación se designan de la siguiente
manera X: 1, lo que indica que las medidas
del dibujo son mayores a las del objeto
real.
Escala de reducción
La escala de reducción es una escala
menor que la escala natural, las escalas de
reducción son muy comunes dada su
utilidad para plasmar en los formatos
dibujos de gran dimensión, su designación
es 1:X, donde X representa el número de
reducción.
22
Indicaciones importantes
•
Cuando se representa un objeto y se utiliza una escala de ampliación muy grande, se
recomienda adicionar vista de tamaño natural del objeto, mostrando únicamente sus
contornos, con el objetivo de ampliar la información plasmada en el dibujo.
•
En cualquier caso la escala a seleccionar depende de la complejidad del objeto a representar;
esta debe ser lo suficientemente grande para permitir la interpretación clara y fácil de la
información representada.
•
Cuando detalles muy finos no se pueden dimensionar completamente en la representación
principal, se emplea un dibujo adyacente en una vista de detalle (o sección) y en una escala
mayor para dar claridad sobre los detalles.
23
Líneas utilizadas en el dibujo
Aplicaciones de las líneas en el plano
En la práctica del dibujo normalizado se requiere el uso
de diferentes tipos de líneas estandarizados que tienen
aplicaciones específicas. Los diferentes tipos de líneas
se conocen como alfabeto de líneas y difieren por las
características de su trazo y espesor.
En la siguiente imagen y tabla
se pueden observar los
diferentes tipos de líneas
empleadas en el dibujo y sus
aplicaciones.
24
Letra
Nombre
A
Línea visible
Descripción
Línea
gruesa
continua
Ejemplo
25
Espesor
0,6mm
Aplicaciones
Contornos visibles
Letra
Nombre
B1
Línea de cota
B2
Línea de
extensión
B3
Línea de
selección
Descripción
Línea
fina
Espesor
Aplicaciones
0,3mm
Líneas imaginarias, de
cotas, de proyección, de
referencia, achurados, de
sección, líneas de ejes
cortos.
Espesor
Aplicaciones
0,6mm
Líneas de vistas parciales
o interrumpidas, secciones
continua
Ejemplo
Letra
C
Nombre
Línea corta de
interrupción
Descripción
Línea
continua
fina
a
mano
alzada y continua
fina en zigzag.
Ejemplo
26
Letra
Nombre
D
Líneas oculta
Descripción
Línea
segmentos
Espesor
Aplicaciones
0,3mm
Líneas ocultas o invisibles
Espesor
Aplicaciones
0,3mm
Líneas de centros o de
ejes de simetría
a
Ejemplo
Letra
E1
Nombre
Descripción
Línea de eje
Línea fina
cadena
E2
de
Línea de cadena
Ejemplo
27
Letra
F
Nombre
Línea de plano de
corte
Descripción
Espesor
Aplicaciones
Línea fina de
cadena y con
cambio
de
sección
0,3mm
Líneas de corte de planos
Espesor
Aplicaciones
0,3mm
Líneas
de
piezas
adyacentes,
posiciones
extremas o alternas de
piezas móviles.
Ejemplo
Letra
G
Nombre
Línea fantasma
Descripción
Línea fina de
cadena con doble
guion.
Ejemplo
28
Notas importantes
Espesores
Aunque como se mencionó, sólo se emplean dos espesores de líneas, gruesas y
delgadas, estas deben guardar una relación de 2:1 y el espesor final solo lo define el
tamaño del y clase de dibujo.
Orden de prioridad de líneas coincidentes
También es importante mencionar que en un solo dibujo se pueden encontrar diferentes
tipos de líneas, es decir existe la necesidad de jerarquizar los diferentes tipos de líneas o
dicho de otra forma dar orden de prioridad de las líneas coincidentes, para ello se
establece el siguiente orden de prioridad:
 Las líneas visibles de contornos.
 Las líneas ocultas o invisibles.
 Planos de corte.
 Las líneas de eje y líneas de simetría.
 Líneas centroide.
 Líneas de proyección para cotas.
29
Convenciones para líneas ocultas
En el trazado de líneas ocultas existen ciertas reglas que permiten establecer cuando un
trazo esta correcto o incorrecto. Para abordar el tema se empleará la siguiente figura
donde se analizarán casos específicos identificados con literales en la proyección
ortogonal:
30
Convenciones
Descripción
A
sin espacio
Las líneas ocultas deben comenzar o terminar desde las demás líneas.
Es decir el primer trazo empieza justo en la línea visible.
B
unión de
esquinas
Las líneas que se interceptan deben formar un ángulo agudo en el punto
exacto donde se interceptan.
C
con espacio
Cuando una línea oculta sea continuación de una línea visible deberá
comenzar con un espacio.
D
unión
Cuando hay una triple unión de líneas ocultas esta intersección debe
tener un punto común.
E
unión
Cuando las líneas ocultas se interceptan se crea un vértice.
F
comenzar el
arco en una
línea de eje
Los arcos de líneas ocultas comienzan su trazo desde las líneas de ejes.
G
no cruzar la
línea solida
Cuando una línea oculta se intercepte con una línea visible, la línea
oculta se traza de tal forma que quede un espacio a cada lado de la
visible, es decir no se cruzan.
H
No cruzar
Las líneas ocultas no se cruzan y siempre se debe dar prioridad a la
línea más cercana al observador
31
Enlaces de interés
Dónde podemos encontrar más información
 Geometría.
http://www.escolar.com/menugeom.htm
http://es.wikipedia.org/wiki/Geometr%C3%ADa
 Polígonos.
http://es.wikipedia.org/wiki/Pol%C3%ADgono_regular
http://www.educacionplastica.net/poligonos.htm
 Trazados paso a paso.
http://www.euskalnet.net/ibiguri/
 Líneas.
http://dibujotecnico.ramondelaguila.com/normalizacion/lineasnormalizadas.htm
 Escala.
http://es.wikipedia.org/wiki/Escala_%28cartograf%C3%ADa%29#Representaci.
C3.B3n
32