Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1

Unidad 1
Integrales Indefinidas
1.1 Diferenciales
1.1.1 Aproximaciones
1.1.2 Anti derivada
1.2 Integración
1.2.1 Formulas
1.2.2 Integrales Inmediatas
1.2.3 Cambio de variable
1.3 Métodos de integración
1.3.1 Por partes
1.3.2 Por sustitución
1.3.3 Por fracciones parciales
1.1.
Diferencial
1.1.1 Aproximaciones
“La derivada de una función con respecto a una variable es el límite del
incremento de la función entre el incremento de la variable, cuando el
incremento de la variable tiende a cero”
Se expresa:
𝑑𝑦
△𝑦
Derivada = 𝑑𝑥 = lim (△𝑥 )
△→0
DIFERENCIALES
La diferencial de una función es el producto de la derivada de la función por el incremento
de la variable independiente, es decir: dy = y’*△ 𝑥
dy significa “la diferencia de la función y”
y’es la derivada de la función
△ x es el incremento de la variable independiente
du
1. d(c) = 0dx
8. d(sen u) = cosu.du
15. d(arccos u) = √1−
2. d(x) = 1dx
9. d(cos u) = senu.du
16. d(arctan u) =
3. d(u + v + w) = du + dv + dv
10. d(tan u) = 𝑠𝑒𝑐 2 u. du
4. d(c.u) = c.du
11. d(cot u) = - 𝑐𝑠𝑐 2 u.du
18. d(arcsec u) =
5. d(u.v) = u.dv + v.du
12. d(sec u) = tanu . secu. du
19. d(arccsc u) =
2
6. d(𝑢 ) = n. 𝑢
𝑢
7. d(𝑣 ) =
𝑛−1
𝑣.𝑑𝑢−𝑢.𝑑𝑣
𝑣𝑐
du
13. d(csc u) = cotu . cscu . du
du
14. d(arcsen u) = √1−
𝑢2
𝑢2
du
1+ 𝑢2
du
17. d(arc cot u) = 1+ 𝑢2
20. d(ln u) =
du
𝑢√𝑢2 −1
du
𝑢√𝑢2 −1
du
𝑢
log 𝑒
21. d(log u) =
u
22. d(𝑒 𝑢 ) = 𝑒 𝑢 . 𝑑𝑢
. 𝑑𝑢
Ejemplos
Encuentre la diferencial de las siguientes funciones que se indican.
1. Sea la función 𝑦 = 𝑥 4
Su derivada es 𝑦′ = 4𝑥 3
Su diferencial se expresa así: 𝑑𝑦 = 4𝑥 3 △ 𝑥
2. Calcular la diferencial de 𝑦 = 6𝑥 3 − 𝑥 + 3
La derivada de 𝑓(𝑥) 𝑜 𝑦 ′ = 18x 2 − 1
La diferencial 𝑑𝑦 = (18𝑥 2 − 1)𝑑𝑥
3. Calcular la diferencial de 𝑦 = √1 − 3x
3
La derivada es 𝑓′(𝑥) = 2√1−3x
3dx
La diferencial es 𝑑𝑦 = 2√1−3x
4. Calcular la diferencial de la función y = 3𝑥 2 para x=4 y el △ 𝑥 + 0.2
Su derivada es y’= 6x
La diferencia es dy = 6x△ 𝑥 como x = 4
y △ 𝑥 = 0.2
El valor numérico de la diferencia es: dy = 6(4)(0.2)
dy = 4.8
1.1.2 Anti derivadas
Definición: A una función F se le llama ANTIDERIVADA de una función f, si F’(x) = f(x).
A la operación de calcular la anti derivada (primitiva) de una función se le llama
integración y se representa con el símbolo ∫ que es la inicial de la palabra suma.
Si F(x) es una función primitiva de f(x) se expresa:
∫ 𝑓(𝑥)𝑑𝑥 = 𝐹(𝑥) + 𝑐
La expresión ∫ 𝑓(𝑥)𝑑𝑥 es la anti derivada de f(x), donde:
 ∫ 𝑠𝑖𝑔𝑛𝑜 𝑑𝑒 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑐𝑖𝑜𝑛, 𝑠𝑒 𝑙𝑒𝑒 "𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑙 𝑑𝑒"
 f(x) integrando
 dx diferencial de la variable
 F(x) función primitiva
 C constante de integración
Ejemplos
Si derivamos las funciones
𝑓(𝑥) = 𝑥 2 ,
Obtendremos para cada caso 𝑓′(𝑥) = 2𝑥,
𝑔(𝑥) = 𝑥 2 + 5,
𝑔′(𝑥) = 2𝑥,
ℎ(𝑥) = 𝑥 2 − 20
ℎ′(𝑥) = 2𝑥
Se observa que as derivadas de las funciones f(x), g(x) y h(x) es la misma función 2x, para
cualquier numero c ∈ ⎕ que se le agregue a la función 𝑥 2 .
Entonces tendremos que la anti derivada de ∫ 2𝑥 𝑑𝑥 = 𝑥 2 + 𝑐 donde c ∈ ⎕
1.2 Integración
1.2.1 Formulas de integrales
Como vimos anteriormente, que a la operación de calcular la anti derivada (primitiva) de
una función se le llama integración, es decir que la derivación y la integración son
operaciones inversas, ello nos permite obtener las formulas de la integración
directamente de las fórmulas de derivación.
Fórmulas para integrales inmediatas elementales
1) ∫ 𝑑𝑥 = 𝑥 + 𝑐
2) ∫ 𝑘𝑑𝑥 = 𝑘∫ 𝑑𝑥 = 𝑘𝑥 + 𝑐
La integral del producto de una constante por una función es igual a la constante
por la integral de la función.
3) ∫ [𝑓(𝑥) + 𝑔(𝑥)]𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 + ∫ 𝑔(𝑥)𝑑
La integral de la suma de un número finito de funciones es igual a la suma
algebraica de las integrales de las funciones.
4) ∫ [𝑓(𝑥) − 𝑔(𝑥)]𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 − ∫ 𝑔(𝑥)𝑑
La integral de la resta de un número finito de funciones es igual a la resta
algebraica de las integrales de las funciones.
5) ∫ 𝑥 𝑛 𝑑𝑥 =
6) ∫
𝑑𝑥
𝑥
𝑥 𝑛+1
𝑛−1
+ 𝑐 (𝑛 ≠ −1)
= ln 𝑥 + 𝑐
7) ∫ 𝑠𝑒𝑛𝑥𝑑𝑥 = − cos 𝑥 + 𝑐
8) ∫ 𝑐𝑜𝑠𝑥𝑑𝑥 = 𝑠𝑒𝑛𝑥 = 𝑐
9) ∫ 𝑡𝑎𝑛𝑥𝑑𝑥 = ln|𝑠𝑒𝑛𝑥| + 𝑐 = − ln|𝑐𝑜𝑠𝑥| + 𝑐
10) ∫ (sec 𝑥 tan 𝑥) = sec 𝑥 + 𝑐
11) ∫ (csc 𝑥 cot 𝑥)𝑑𝑥 = − csc 𝑥 + c
12) ∫ sec xdx = ln|sec 𝑥 + 𝑡𝑎𝑛𝑥| + 𝑐
13) ∫ sin2 𝑥𝑑𝑥 = tan 𝑥 + 𝑐
14) ∫ cot 𝑥𝑑𝑥 = ln|𝑠𝑒𝑛𝑥| + 𝑐
15) ∫ csc 𝑥𝑑𝑥 = − ln|𝑐𝑠𝑐𝑥 + 𝑐𝑜𝑡𝑥| + 𝑐
16) ∫ csc 2 𝑥𝑑𝑥 = − cot 𝑥 + 𝑐
𝑎𝑥
17) ∫ 𝑎 𝑥 𝑑𝑥 = ln 𝑎 + 𝑐 donde a > 0
18) ∫ 𝑒 𝑥 𝑑𝑥 = 𝑒 𝑥 + 𝑐
1.2.2 integraciones inmediatas.
Aplicando las formulas anteriores, obtendremos la integral de las siguientes funciones.
a) ∫ 1𝑑𝑥 = 1 ∫ 𝑑𝑥 = 𝑥 + 𝑐 Aplicando formula 1
b) ∫ 4𝑑𝑥 = 4∫ 𝑑𝑥 = 4(𝑥 + 𝑐) = 4𝑥 + 𝑐 a Aplicando formula 2 donde x = 4
c) ∫ 3𝑥𝑑𝑥 = 3∫ 𝑥𝑑𝑥 Aplicando primeramente la fórmula 2 de ahí, = 3∫ 𝑥1 𝑑𝑥
aquí aplicaremos la fórmula 5 de la potencia donde n = 1 entonces
𝑥2
∫ 3𝑥𝑑𝑥 = 3( ) + 𝑐
2
d) ∫ 4𝑠𝑒𝑛𝑥𝑑𝑥 = 4∫ 𝑠𝑒𝑛𝑥𝑑𝑥 = 4(−𝑐𝑜𝑠𝑥 + 𝑐) = −4𝑐𝑜𝑠𝑥 + 𝑐 Aplicando formula 2
y7
e) ∫ 5𝑒 𝑥 𝑑𝑥 = 5∫ 𝑒 𝑥 𝑑𝑥 = 5𝑒 𝑥 + 𝑐 Aplicando formulas 2 y 18
1.2.3 Integración por cambio de variable
Existen integrales indefinidas que no se pueden resolver usando la fórmula de integración
inmediata del tema anterior, lo que se tiene que hacer es un ‘’cambio de variable’’, para
ello retomaremos las fórmulas de integración directas y las transformaremos al caso
general quedando de las siguiente manera.
Formulario de integración
1. ∫ 𝑢𝑛 𝑑𝑢 =
2. ∫
𝑑𝑢
𝑢
𝑢𝑛+1
𝑛+1
+ 𝑐, 𝑛 ≠ −1
= 𝑙𝑛𝑢 + 𝑐
3. ∫ 𝑒 𝑢 𝑑𝑢 = 𝑒 𝑢 + 𝑐
4. ∫ 𝑎𝑢 𝑑𝑢 =
𝑎𝑢
ln 𝑎
+𝑐
5. ∫ 𝑠𝑒𝑛 𝑢 𝑑𝑢 = − cos 𝑢 + 𝑐
6. ∫ 𝑐𝑜𝑠 𝑢 𝑑𝑢 = 𝑠𝑒𝑛 𝑢 + 𝑐
7. ∫ sec 2 𝑢 𝑑𝑢 = tan 𝑢 + 𝑐
8. ∫ csc 2 𝑢 𝑑𝑢 = − cot 𝑢 + 𝑐
9. ∫ 𝑠𝑒𝑐 𝑢 tan 𝑢 𝑑𝑢 = sec 𝑢 + 𝑐
10. ∫ 𝑐𝑠𝑐 𝑢 cot 𝑢 𝑑𝑢 = − csc 𝑢 + 𝑐
11. ∫ 𝑡𝑎𝑛 𝑢 𝑑𝑢 = ln|sec 𝑢| + 𝑐
12. ∫ 𝑐𝑜𝑡 𝑢 𝑑𝑢 = ln|𝑠𝑒𝑛 𝑢| + 𝑐
13. ∫ 𝑠𝑒𝑐 𝑢 𝑑𝑢 = ln|sec 𝑢 + tan 𝑢| + 𝑐
14. ∫ 𝑐𝑠𝑐 𝑢 𝑑𝑢 = ln|csc 𝑢 − cot 𝑢| + 𝑐
15. ∫ sen2 𝑢 cos 𝑢 𝑑𝑢 =
sen+1 𝑢
𝑛+1
+𝑐
Ejemplo
1. Calcule la siguiente integral indefinida usando la formula (1).
Esta fórmula se utiliza cuando en la integral aparece un paréntesis con exponente
diferente de -1, en donde u será lo que se encuentre dentro del paréntesis.
∫ (2𝑥 + 1)4 2𝑑𝑥 =
Solución.

∫ (2𝑥 + 1)4 2𝑑𝑥 =


Primeramente
identificamos quien
es “u”
Después derivamos
𝑢 = 2𝑥 + 1
𝑑𝑢
=2
𝑑𝑥
𝑑𝑢 = 2𝑑𝑥
𝑑𝑢
= 𝑑𝑥
2
Se despeja el
diferencial dx
Ahora haremos el cambio de variable sustituyendo u y dx
𝑢 = 2𝑥 + 1
Entonces encontraremos que:
4
∫ (2𝑥 + 1) 2𝑑𝑥
𝑑𝑥 =
𝑑𝑢
2
𝑑𝑢
)
2
= ∫ 𝑢4 𝑑𝑢
= ∫ 𝑢4 (
= 𝑎𝑝𝑙𝑖𝑐𝑎𝑛𝑑𝑜 𝑙𝑎 𝑓𝑜𝑟𝑚𝑢𝑙𝑎(1). ∫ 𝑢𝑛 𝑑𝑢 = (
=(
𝑢4+1
)+𝑐
4+1
𝑢5
=
+𝑐
5
= Volver a cambiar u
=
(2𝑥 + 1)5
+𝑐
5
𝑢𝑛+1
) + 𝑐, 𝑛 ≠ −1
𝑛+1
2. Calcula la siguiente integral indefinida usando la fórmula (2). Esta fórmula se utiliza casi
siempre cuando en la integral aparece un división, en donde u será lo que se encuentre en
el denominador.
∫
𝑥
𝑑𝑥 =
−2
5𝑥 2
Solución.

∫
𝑥
𝑑𝑥 =
5𝑥 2 − 2


Primeramente
identificamos quien
es “u”
Después derivamos
𝑢 = 5𝑥 2 − 2
𝑑𝑢
= 10𝑥
𝑑𝑥
𝑑𝑢 = 10𝑑𝑥
𝑑𝑢
= 𝑑𝑥
10𝑥
Se despeja el
diferencial dx
Encontramos entonces que :
𝑢 = 5𝑥 2 − 2
y
𝑑𝑢
𝑑𝑥 = 10𝑥
Ahora haremos el cambio de variable sustituyendo u y dx
∫
𝑥
𝑑𝑥
−2
5𝑥 2
=∫
𝑥 𝑑𝑢
(
)
𝑢 10𝑥
= 𝑎𝑝𝑙𝑖𝑐𝑎𝑛𝑑𝑜 𝑝𝑟𝑜𝑝𝑖𝑒𝑑𝑎𝑑 𝑑𝑒 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒𝑠 𝑦 𝑒𝑙𝑖𝑚𝑖𝑛𝑎𝑛𝑑𝑜 𝑥
=
1 𝑑𝑢
∫
10 𝑢
=aplicando la formula (2). ∫
1
ln 𝑢 + 𝑐
10
= Volver a cambiar u
=
=
1
ln(5𝑥 2 − 2) + 𝑐
10
𝑑𝑢
𝑢
= ln 𝑢 + 𝑐
1.3 METODOS DE INTEGRACION
1.3.1 Por Partes
Si queremos resolver integrales que contienen productos como:
∫ 𝑥𝑠𝑒𝑛𝑥𝑑𝑥, ∫ 𝑥𝑒 𝑥 𝑑𝑥, ∫ 𝑠𝑒𝑛(ln 𝑥)𝑑𝑥
Podemos usar el método de integración por partes, el cual se te presenta a continuación.
METODO DE INTEGRACION POR PARTES
Con el método de integración por partes podemos integrar funciones que pueden
expresarse como un producto de una función de la derivada de otra.
La fórmula de integración por partes se deduce de la derivada de un producto de dos
funciones
[𝑓(𝑥)𝑔(𝑥)]′ = 𝑓(𝑥)𝑔(𝑥)′ + 𝑔(𝑥)𝑓′(𝑥)
∫[𝑓(𝑥)𝑔(𝑥)]′ = ∫[𝑓(𝑥)𝑔(𝑥)′ + 𝑔(𝑥)𝑓 ′ (𝑥)]𝑑𝑥
𝑓(𝑥)𝑔(𝑥) = ∫𝑓(𝑥)𝑔(𝑥)′ 𝑑𝑥 + ∫𝑔(𝑥)𝑓′(𝑥)𝑑𝑥
Esta última ecuación se puede reacomodar en la forma:
∫ 𝑓(𝑥)𝑔′ (𝑥)𝑑𝑥 = 𝑓(𝑥)𝑔(𝑥) − ∫ 𝑔(𝑥)𝑓′(𝑥)𝑑𝑥
La fórmula anterior∫ 𝑓(𝑥)𝑔′ (𝑥)𝑑𝑥 = 𝑓(𝑥)𝑔(𝑥) − ∫ 𝑔(𝑥)𝑓′(𝑥)𝑑𝑥 resulta ser mas fácil de
recordar si hacemos el cambio de literales 𝑢 = 𝑓(𝑥) → 𝑑𝑢, = 𝑓 ′ (𝑥)𝑑𝑥; 𝑣 = 𝑔(𝑥) → 𝑑𝑣 =
𝑔′ (𝑥)𝑑𝑥 quedándonos de la siguiente manera:
∫ 𝑢𝑑𝑦 = 𝑢𝑣 − ∫ 𝑣𝑑𝑢
La integración por partes con frecuencia se utiliza cuando contiene logaritmos, funciones
trigonométricas inversas y productos.
Ejemplo.
Encuentra la integral ∫ 𝑥𝑒 𝑥 ∗ 𝑑𝑥
Solución:
Para este ejemplo nos apoyaremos de la siguiente elección adecuada para u y dv.
Tomando u = x de la integral, entonces el dv viene siendo la parte que nos queda en el
integrado, es decir, dv = 𝑥𝑒 𝑥 ∗ 𝑑𝑥, el du es igual a la derivada de x multiplicada por el
diferencial de x, a la v es la integral de 𝑒 𝑥 con respecto a x, lo anterior lo podemos resumir
en el siguiente cuadro:
𝑢 = 𝑥 → 𝑑𝑢 = 1𝑑𝑥
𝑑𝑣 = 𝑒 𝑥 𝑑𝑥 → ∫ 𝑑𝑣 = ∫ 𝑒 𝑥 𝑑𝑥
𝑣 = ∫ 𝑒 𝑥 𝑑𝑥 = 𝑒 𝑥
Sustituyendo en la formula ∫ 𝑢𝑑𝑣 = 𝑢𝑣 − ∫ 𝑣𝑑𝑢 tenemos:
∫ 𝑥𝑒 𝑥 𝑑𝑥 = 𝑥𝑒 𝑥 − ∫ 𝑒 𝑥 (1𝑑𝑥)
= 𝑥𝑒𝑥 − ∫ 𝑒𝑥 𝑑𝑥
= 𝑥𝑒 𝑥 − 𝑒 𝑥 + 𝑐
𝑒 𝑥 (𝑥 − 1) + 𝑐
Como podemos observar fue mucho más fácil integrar ∫ 𝑒 𝑥 𝑑𝑥 que ∫ 𝑥𝑒 𝑥 𝑑𝑥, lo cual
quiere decir, que la elección para u y dv fueron correctas.
Ejemplo.
1. Resuelva la integral ∫ ln 𝑥 𝑑𝑥.
Solución
La elección adecuada para u y dv la podemos poner así:
𝑢 = ln 𝑥 → 𝑑𝑢 =
1
𝑑𝑥
𝑑𝑥 =
𝑥
𝑥
Sustituyendo en la fórmula de integración por
partes tenemos:
𝑑𝑣 = 𝑑𝑥 → ∫ 𝑑𝑣 = ∫ 𝑑𝑥
𝑣 = ∫ 𝑑𝑥 = 𝑥
∫ ln 𝑥 𝑑𝑥 = (ln 𝑥)(𝑥) − ∫ 𝑥
= 𝑥 ln 𝑥 − ∫ 𝑑𝑥
= 𝑥 ln 𝑥 − 𝑥 + 𝑐
= 𝑥 (ln 𝑥 − 1) + 𝑐
𝑑𝑥
𝑥
2
2. Obtenga la integral ∫ 𝑥 3 𝑒 𝑥 𝑑𝑥
Solución
La ecuación adecuada para u y dv la podemos poner así:
𝑢 = 𝑥 2 → 𝑑𝑢 = 2𝑥𝑑𝑥
2
2
𝑑𝑣 = 𝑥 3 𝑒 𝑥 𝑑𝑥 → ∫ 𝑑𝑣 = ∫ 𝑥 3 𝑒 𝑥 𝑑𝑥
𝑣=
1
2
= 𝑒𝑥
2
Por lo tanto tenemos:
1
1 2
1
2
2
2
2
∫ 𝑥 3 𝑒 𝑥 𝑑𝑥 = 𝑥 2 𝑒 𝑥 − ∫ ( 𝑒 𝑥 ) (2𝑥𝑑𝑥) = 𝑥 2 𝑒 𝑥 − ∫ 𝑥𝑒 𝑥 𝑑𝑥 → (1)
2
2
2
3. Por el método de integración por partes resuelva la integral ∫ sen2 𝑥 𝑑𝑥
Solución.
Sean 𝑢 = 𝑠𝑒𝑛 𝑥 y 𝑑𝑣 = 𝑠𝑒𝑛 𝑥𝑑𝑥, entonces 𝑑𝑢 = cos 𝑥𝑑𝑥 𝑦 𝑣 = ∫ 𝑠𝑒𝑛 𝑥𝑑𝑥 = − cos 𝑥. Ahora bien
sustituyendo en la fórmula de integración por partes tenemos:
∫ 𝑢𝑑𝑣 = 𝑢𝑣 ∫ 𝑣𝑑𝑢
∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥 = −𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥 − ∫(−𝑐𝑜𝑠𝑥)(𝑐𝑜𝑠𝑥)𝑑𝑥 → ∫ sen2 𝑥𝑑𝑥 − 𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥 + ∫ cos 2 𝑥𝑑𝑥 → (7)
De la identidad trigonométrica sen2 𝑥 + cos 2 𝑥 = 1 despejamos cos 2 𝑥, quedando
cos2 𝑥 = 1 − sen2 𝑥 sustituyendo esta última igualdad en la ecuación (7) tenemos:
∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥 = −𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥 + ∫(1 − 𝑠𝑒𝑛 𝑥) 𝑑𝑥 y simplificando el lado derecho de esta igualda tenemos
∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥 = −𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥 + ∫ 𝑑𝑥 − ∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥 = −𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥 + 𝑥 − ∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥
Ahora bien nos vuelve a parecer la misma integral pero ahora con el signo contrario, por lo que si la
despejamos, obtendremos el resultado de dicha integral.
2 ∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥 = −𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥 + 𝑥
∫ 𝑠𝑒𝑛2 𝑥𝑑𝑥 =
𝑥 − 𝑠𝑒𝑛𝑥 𝑐𝑜𝑠𝑥
+𝑐
2
1.3.2 por sustitución trigonométrica
Existen casos de funciones racionales que pueden ser resueltas su integral con este método por sustitución
trigonométrica:
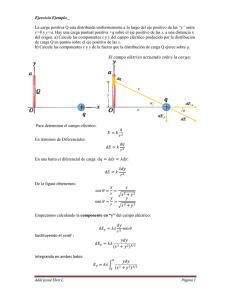
Como es ∫
𝑑𝑥
𝑥 2 +4
Se puede construir un triángulo rectángulo como:
En este caso x/2 = tan⎕ con 𝑑𝑥 = 2 sec 2 ⎕d⎕
√𝑥 2 +4
2
= sec 𝜃 por lo que √𝑥 2 + 4 = 2𝑠𝑒𝑐𝜃
Elevando al cuadrado 𝑥 2 + 4 = 4𝑠𝑒𝑐 2 ⎕
Sustituyendo la integral original:
∫
𝑑𝑥
2 sec 2 θdθ 1
𝜃
=∫ 2
= ∫ 𝑑𝜃 = + 𝑐
+4
2 sec 2 θ
2
2
𝑥2
Despejado de la primera relación: ⎕ = tan−1 (𝑥/2) por lo tanto:
La integral queda determinada por: ∫
𝑑𝑥
𝑥 2 +4
=∫
2 sec2 θdθ
22 sec2 θ
1
= ∫ 𝑑𝜃 =
2
𝜃
2
1
𝑥
2
2
= tan−1 ( ) + 𝑐
Sin embargo existen funciones relacionales que no pueden ser resultas su integral como la anterior por lo
que se requiere utilizar el método por sustitución trigonométrica. Entonces se basa en √𝑢 2 ± 𝑎2 , la cual
puede estar directa o en forma racional y a partir del Teorema de Pitágoras se le pueden asignar estos
valores a los catetos y a la hipotenusa de un triángulo rectángulo, dependiendo de cada caso, con respecto a
un ángulo 𝜃.
Aplicamos el método por sustitución trigonométrica en tres casos:
CASO I
𝑢
√𝑎2 − 𝑢2 = 𝑎 𝑐𝑜𝑠𝜃 𝑐𝑜𝑛 𝑢 = 𝑎 𝑠𝑒𝑛𝜃, donde 𝑠𝑒𝑛𝜃 = 𝑎
CASO II
𝑢
√𝑎2 + 𝑢2 = 𝑎 𝑠𝑒𝑐𝜃 𝑐𝑜𝑛 𝑢 = 𝑎 𝑡𝑎𝑛𝜃, donde 𝑡𝑎𝑛𝜃 = 𝑎
CASO III
𝑢
√𝑢2 − 𝑎2 = 𝑎 𝑡𝑎𝑛𝜃 𝑐𝑜𝑛 𝑢 = 𝑎 𝑠𝑒𝑐𝜃, donde 𝑠𝑒𝑐𝜃 = 𝑎
Dependiendo de cada caso se debe utilizar alguna de estas fórmulas:
∫ √𝑎2 − 𝑢2 hágase 𝑢 = 𝑎 𝑠𝑒𝑛𝜃
∫ √𝑎2 + 𝑢2 hágase 𝑢 = 𝑎 𝑡𝑎𝑛𝜃
∫ √𝑢2 − 𝑎2 hágase 𝑢 = 𝑎 𝑠𝑒𝑐𝜃
*donde u es una función y a es un número*
Además será necesario aplicar algunas identidades trigonométricas bastante útiles a la hora de sacarles raíz
cuadrada a un valor.




cos 2 𝜃 = 1 − sen2 𝜃
sec 2 𝜃 = 1 + 𝑡𝑎𝑛𝜃
tan2 𝜃 = sec 2 𝜃 − 1
cot 2 𝜃 = csc 2 𝜃 − 1

sen2 𝜃 =

2
cos 𝜃 =
1−𝑐𝑜𝑠2𝜃
2
1+𝑐𝑜𝑠2𝜃
2
Ejemplo
1. Integra la función radical aplicando el caso I: ∫ √𝑎2 − 𝑢2 hágase 𝑢 = 𝑎 𝑠𝑒𝑛𝜃
Por lo que 𝑥 + 3𝑠𝑒𝑛𝜃𝑑𝜃
Por lo tanto:
∫
𝑑𝑥
𝑥 2 √9
−
𝑥2
=∫
3𝑐𝑜𝑠𝜃
(3𝑐𝑜𝑠𝜃)2 √9
=∫
=∫
=∫
− (3𝑐𝑜𝑠𝜃)2
3𝑐𝑜𝑠𝜃
3𝑠𝑒𝑛2 𝜃√9
− 9𝑠𝑒𝑛2 𝜃
𝑑𝜃
𝑑𝜃
𝑐𝑜𝑠𝜃
(3𝑠𝑒𝑛2 𝜃)3√1 − 𝑠𝑒𝑛2 𝜃
𝑑𝜃
𝑐𝑜𝑠𝜃
1
𝑑𝜃 = ∫ csc 2 𝜃𝑑𝜃
2
9𝑠𝑒𝑛 𝜃𝑐𝑜𝑠𝜃
9
1
= − 𝑐𝑜𝑡𝜃 + 𝑐
9
Puesto que la sustitución era 𝑥 = 3𝑠𝑒𝑛𝜃 donde a la hipotenusa se le asigna el valor de 3.
Por el teorema de Pitágoras, se tiene que el lado adyacente es √9 − 𝑥 2 . Por lo tanto se tiene:
𝑐𝑜𝑡𝜃 =
𝑐𝑜𝑠𝜃 √9 − 𝑥 2
=
𝑠𝑒𝑛𝜃
𝑥
Ahora se sigue que: ∫
𝑑𝑥
𝑥 2 √9−𝑥 2
1
1 √9−𝑥 2
9
9
= − 𝑐𝑜𝑡𝜃 + 𝑐 == −
𝑥
+𝑐
2. Integra la función radical aplicando el caso II
∫ √𝑎2 + 𝑢2 hagase 𝑢 = 𝑎 tan 𝜃
Hallar ∫
𝑑𝑥
√9+4𝑥 2
3
3
2
2
Sea 𝑥 = 𝑡𝑎𝑛𝜃, entonces 𝑑𝑥 = sec 2 𝜃𝑑𝜃, y √9 + 4𝑥 2 = 3𝑠𝑒𝑐𝜃
Solución:
∫
𝑑𝑥
𝑥√9 +
4𝑥 2
=∫
3
sec 2 𝜃𝑑𝜃
2
3
( 𝑡𝑎𝑛𝜃) (3𝑠𝑒𝑐𝜃)
2
=
1
1
∫ csc 𝜃𝑑𝜃 = ln(𝑐𝑠𝑐𝜃 − 𝑐𝑜𝑡𝜃) + 𝑐
3
3
1
√9 + 4𝑥 2 3
= ln (
− )+𝑐
3
𝑥
𝑥
3. integra la función radical aplicando el caso III
∫ √𝑢2 − 𝑎2 hágase 𝑢 = 𝑎 𝑠𝑒𝑐𝜃
Integra la siguiente función con 𝑥 = 5𝑠𝑒𝑐𝜃 donde 𝑠𝑒𝑐𝜃 =
𝑥
𝑥
𝑦 𝑑𝑥 = 5𝑠𝑒𝑐𝜃𝑡𝑎𝑛𝜃𝑑𝜃.
∫
√𝑥 2 − 25
√(5𝑠𝑒𝑐𝜃)2 − 25
𝑑𝑥 = ∫
(5𝑠𝑒𝑐𝜃𝑡𝑎𝑛𝜃)𝑑𝜃
𝑥
5𝑠𝑒𝑐𝜃
= ∫ √25 sec 2 𝜃 − 25 𝑡𝑎𝑛𝜃𝑑𝜃 = ∫ √sec 2 𝜃 − 1 𝑡𝑎𝑛𝜃𝑑𝜃
= 5 ∫ 𝑡𝑎𝑛2 𝜃𝑑𝜃 = 5 ∫(sec 2 𝜃 − 1) 𝑑𝜃 = 5(𝑡𝑎𝑛𝜃 − 𝜃) + 𝑐
𝑥 2
1
𝑥
Por ultimo como 𝑥 = 𝑠𝑒𝑐𝜃 y 𝑡𝑎𝑛𝜃 = √sec 2 𝜃 − 1 = √( ) − 1 = √𝑥 2 − 25 y 𝜃 = sec −1 ( ) + 𝑐. Ahora se
5
5
5
tiene que:
∫
√𝑥 2 − 25
√𝑥 2 − 25
𝑑𝑥 = 5(𝑡𝑎𝑛𝜃 − 𝜃) + 𝑐 = ∫
𝑑𝑥 + 𝑐
𝑥
𝑥
1.3.3 Por fracciones parciales
El método por fracciones parciales consiste en reducir un cociente de polinomios en fracciones más simples,
es decir, se trata de encontrar la suma de que fracciones da como resultado la fracción dada que permitan
obtener de manera inmediata una integral.
Caso I
Integre las funciones racionales ∫
𝑑𝑥
𝑥 2 −1
y∫
5𝑥
𝑥 2 −𝑥−6
𝑑𝑥 utilizando el método de fracciones parciales.
Solución:
A cada factor lineal, 𝑎𝑥 + 𝑏, del denominador de una fracción racional propia (que el denominador se puede
descomponer), le corresponde una fracción de la forma
𝐴
𝑎𝑥+𝑏
, siendo A una constante a determinar.
𝑑𝑥
1) ∫ 2
𝑥 −1
Para resolverla, primero se factoriza el denominador como una diferencia de cuadrados:
𝑥 2 − 1 = (𝑥 + 1)(𝑥 − 1)
Después se descompone la función racional a integrar en suma de fracciones donde hay que
obtener los numeradores, desarrollando como se muestra a continuación:
1
𝐴
𝐵
𝐴(𝑥 − 1) + 𝐵(𝑥 + 1) 𝐴𝑥 − 𝐴 + 𝐵𝑥 + 𝐵 (𝐴 + 𝐵)𝑥 − 𝐴 + 𝐵
=
+
=
=
=
𝑥2 − 1 𝑥 + 1 𝑥 − 1
(𝑥 + 1)(𝑥 − 1)
(𝑥 + 1)(𝑥 − 1)
(𝑥 + 1)(𝑥 − 1)
Por ser una igualdad, se tiene que 1 = (A + B)x – A + B, de donde se deduce el sistema de
ecuaciones:
𝐴+𝐵 =0
−𝐴 + 𝐵 = 1
Aplicando el método de reducción, se obtiene el resultado:
𝐴+𝐵 =0
−𝐴 + 𝐵 = 1
0 + 2𝐵 = 1
2𝐵 = 1
𝐵=½
Se sustituye el valor de B en
𝐴+𝐵 =0
𝐴+½=0
𝐴=0−½
𝐴 = −½
La integral original se reescribe como:
𝑑𝑥
𝐴
𝐵
∫ 𝑥 2−1 = ∫ 𝑥 2+1 𝑑𝑥 ∫ 𝑥 2−1 𝑑𝑥, sustituyendo los valores de A y B y utilizando la ∫
𝑥
𝑑𝑢
𝑢
= ln 𝑢 + 𝑐 y a la
identidad del logaritmo natural ln 𝑥 − ln 𝑦 = ln( ) se llega al resultado:
𝑦
∫
∫
𝑑𝑥
−1/2
1/2
1
1
1
𝑥−1
=∫ 2
𝑑𝑥 ∫ 2
𝑑𝑥 = − ln(𝑥 + 1) + ln(𝑥 − 1) = ln (
)+𝑐
𝑥2 − 1
𝑥 +1
𝑥 −1
2
2
2
𝑥+1
𝑑𝑥
1
𝑥−1
= ln (
)+𝑐
−1 2
𝑥+1
𝑥2
Caso II
Integre las integrales siguientes ∫
8
(𝑥−2)2
𝑥
𝑑𝑥 y ∫
𝑑𝑥 utilizando la técnica de fracciones
(𝑥+302
parciales.
Solución.
A cada factor lineal, ax+b, que figure n veces en el denominador de una fracción racional propia, e
corresponde la sima de n fracciones de la forma:
𝐴1
𝐴2
𝐴𝑛
+
+ ⋯+
(𝑎𝑥 + 𝑏) (𝑎𝑥 + 𝑏)2
(𝑎𝑥 + 𝑏)𝑛
Siendo 𝐴1 , 𝐴2 , … , 𝐴𝑛 constantes a determinar.
8
1) ∫
𝑑𝑥
(𝑥−2)2
La fracción en este caso se descompone en:
8
𝐴
𝐵
𝐴(𝑥 − 2) + 𝐵 𝐴𝑥 − 2𝐴 + 𝐵
=
+
=
=
2
2
(𝑥 − 2)
𝑥 − 2 (𝑥 − 2)
(𝑥 − 2)2
(𝑥 − 2)2
Por ser una igualdad, se tien 8 = 𝐴𝑥 − 2𝐴 + 𝐵, donde se deducen las ecuaciones lineales:
𝐴=0
−2𝐴 + 𝐵 = 8
Se sustituye el valor de A = 0
−2𝐴 + 𝐵 = 8
−2(0) + 𝐵 = 8
𝐵=8
La integral original se reescribe:
∫
8
𝐴
𝐵
𝑑𝑥 = ∫
𝑑𝑥 + ∫
𝑑𝑥
(𝑥 − 2)2
𝑥−2
(𝑥 − 2)2
Sustituyendo los valores de A y B, simplificando y utilizando la formula ∫ 𝑢𝑛 𝑑𝑢 =
𝑢𝑛+1
𝑛+1
+ 𝑐 se llega
al resultado:
∫
8
0
8
8
−8
𝑑𝑥 = ∫
𝑑𝑥 + ∫
𝑑𝑥 = ∫
𝑑𝑥 = ∫
+𝑐
2
2
2
(𝑥 − 2)
𝑥−2
(𝑥 − 2)
(𝑥 − 2)
𝑥−2
∫
8
−8
𝑑𝑥 =
+𝑐
(𝑥 − 2)2
𝑥−2
Unidad II
2.1 Sumas de Riemann.
2.1.1 Propiedades.
2.1.2 Notación.
2.2 Teorema Fundamental del cálculo.
2.2.1 integral definida
2.1.2 Calculo de áreas y volúmenes.
2.1 Sumas de Riemann
2.1.1 Aproximación del área bajo la curva.
El método de aproximación consiste en aproximar el área de la región acotada(R) comprendida
entre la gráfica de una función f, definida en un intervalo cerrado [ a , b ] con una característica tal
que para todo valor x en el intervalo (𝑎 ≤ 𝑥 ≤ 𝑏) la función 𝑓(𝑥) ≥ 0; es decir es positiva.
La longitud del intervalo se obtiene restando los límites del intervalo, en este caso la longitud △
𝑥=
𝑏−𝑎
𝑛
donde a y b son los limites inferiores y superiores respectivamente del intervalo [a, b] y
“n” es el número de sub intervalos en que se desea dividir el intervalo original.
Riemann construyo dos tipos de rectángulos, algunos los construyo bajo la curva a los que llamo
rectángulos inscritos; la suma de las áreas de estos rectángulos son nombradas dumas inferiores.
Otros están por encima de la curva cuya suma de áreas es llamada áreas superiores.
2.1.2 Propiedades y notación de la suma de Riemann
Si llamamos 𝐴1 , 𝐴2 , … , 𝐴𝑛 a cada una de las áreas de los rectángulos, la sumatoria de las áreas se
representa por:
𝑛
∑ 𝐴𝑖 = 𝐴1 + 𝐴2 + ⋯ + 𝐴𝑛
𝑖=1
Donde los símbolos “n” representan el número de rectángulos que se tomen, ya sean inscritos
(inferiores) o circunscritos (superiores). La letra “i” es llamado el índice de la sumatoria, indica el
número de términos que se debe de sumar. Así mismo, el símbolo Σ es la letra S mayúscula del
alfabeto griego llamada “sigma”.
Las sumas de las áreas inferiores y superiores las representamos como:
Sumas de áreas inferiores = ∑𝑛𝑖=1 𝑓(𝑚𝑖) △ 𝑥
Sumas de aras inferiores = ∑𝑛𝑖=1 𝑓(𝑀𝑖) △ 𝑥
Donde 𝑚𝑖 y 𝑀𝑖 representa el valor mínimo o máximo de la función en cada sub intervalo y △ 𝑥 =
𝑏−𝑎
𝑛
2.2. TEOREMA FUNDAMENTAL DE CÁLCULO
2.2.1 integral definida
El área de una región limitada por un intervalo [ a , b ], se puede ver como una integral definida,
donde si tenemos a 𝑦 = 𝑓(𝑥) como una función continua en el intervalo cerrado [ a , b ], se tiene
que el área de la región limitada por la función 𝑦 = 𝑓(𝑥), el eje “x” y las rectas verticales 𝑥 = 𝑎 y
𝑥 = 𝑏 viene dada por el número real:
𝑏
𝐴𝑟𝑒𝑎 = ∫ 𝑓(𝑥)𝑑𝑥
𝑎
Si tenemos una función “f(x)” continua en un intervalo [a , b] y F(x) como la anti derivada de “f(x)”
en [a,b], entonces:
𝑏
∫ 𝑓(𝑥)𝑑𝑥 = 𝐹(𝑏) − 𝐹(𝑎)
𝑎
Este resultado es la Regla de Barrow y nos relaciona la integral definida (y por tanto el cálculo de
áreas) y a teoría de la integración (como cálculo de primitivas o anti derivadas).
Para calcular integrales definidas, se realiza lo siguiente:



Calculamos una primitiva de f.
Evaluamos la primitiva en los límites inferior “a” e inferior “b”.
Realizamos la diferencia del valor obtenido en b menos el obtenido en a.
Ejemplo:
1. Determine el valor de la integral definida por los límites de integración 𝑎 = 1 y 𝑏 = 2 de la
función 𝑓(𝑥) = 𝑥 2 − 3, utilizando el Teorema Fundamental del Cálculo.
𝑏
∫ 𝑓(𝑥)𝑑𝑥 = 𝐹(𝑏) − 𝐹(𝑎)
𝑎
Solución:
Solo basta con sustituir los valores de los límites de integración 𝑎 = 1 y 𝑏 = 2 en la anti derivada
de la función, para después simplificar mediante las operaciones correspondientes.
Anti derivada de f(x)
2
∫ (𝑥 2 − 3)𝑑𝑥 = [
1
=[
𝑥3
− 3𝑥 + 𝑐]
3
(2)3
(1)3
− 3(2) + 𝑐] − [
− 3(1) + 𝑐]
3
3
8
3
1
3
= [ − 6 + 𝑐] − [ − 3 + 𝑐]
=
8
1
−6+𝑐− +3−𝑐
3
3
=−
2
3
2. Utilizando el teorema fundamental del cálculo resolver la siguiente integral definida:
2
2
∫ 2𝑥𝑒 𝑥 𝑑𝑥 =
0
Solución:
Utilizando un cambio de variable, digamos que 𝑢 = 𝑥 2 y 𝑑𝑢 = 2𝑥, entonces:
2
2
2
2𝑥𝑒 𝑢 𝑑𝑢
2
∫ 2𝑥𝑒 𝑑𝑥 = ∫
= ∫ 𝑒 𝑢 𝑑𝑢 = 𝑒 𝑢 {
0
2𝑥
0
0
0
𝑥2
2 2
2
2
= 𝑒 𝑥 { = 𝑒2 − 𝑒0 = 𝑒4 − 1
0
Por lo que:
2
2
∫ 2𝑥𝑒 𝑥 𝑑𝑥 = 𝑒 4 − 1
0
3. Utilizando el teorema fundamental del calculo resolver las siguientes integrales
definidas de funciones trigonométricas.
𝜋
1) ∫0 (3 − 𝑠𝑒𝑛𝑥)𝑑𝑥 =
Solución:
𝜋
𝜋
∫ (3 − 𝑠𝑒𝑛𝑥)𝑑𝑥 = (3𝑥 + cos 𝑥) { = 3𝜋 + cos 𝜋 − [3(0) + cos(0)]
0
0
= 3𝜋 − 1 − [0 + 1]
3𝜋 − 2
𝜋
2) ∫0 𝑥𝑐𝑜𝑠𝑥𝑑𝑥 =
Solución:
Integrando por partes:
𝑈=𝑥
𝑣 = ∫ cos 𝑥𝑑𝑥
𝐷𝑢 = 𝑑𝑥
𝑑𝑣 = 𝑠𝑒𝑛 𝑥
𝜋
𝜋
∫ 𝑥𝑐𝑜𝑠𝑥𝑑𝑥 = (𝑥𝑠𝑒𝑛𝑥 + 𝑐𝑜𝑠𝑥) { =
0
0
= (𝜋𝑠𝑒𝑛𝜋 + 𝑐𝑜𝑠𝜋) − (0𝑠𝑒𝑛(𝑜) + cos(0))
= (𝜋(0) − 1) − (0 + 1)
= −2
2.2.2 cálculo de áreas y de volúmenes
El problema del cálculo de áreas bajo la curva ha sido estudiando desde hace muchos
años. Quizás los griegos fueron los primeros que lo trataron un poco más formalmente,
usando los elementos de la integral definida. Más adelante se hizo intervenir el concepto
de la anti derivada, que en el siglo XVII, Newton y Leibniz utilizaron para calcular áreas.
Este concepto evoluciono hasta llegar a lo que se conoce como el teorema fundamental
del cálculo (TFC).
EL TEOREMA FUNDAMENTAL DEL CALCULO (TFC)
Si f es continua en [a,b] y F es la antiderivada de la f en el intervalo, donde F’(x) = f(x).
𝑏
Entonces ∫𝑎 𝑓(𝑥)𝑑𝑥 = 𝐹(𝑏) − 𝐹(𝑎)
Ejemplo
1. Calcula el área bajo la curva de 𝑓(𝑥) = 𝑥 2 en el intervalo [0 , 2]
Solución:
Sustituyendo en la formula
𝑏
∫ 𝑓(𝑥)𝑑𝑥 = 𝐹(𝑏) − 𝐹(𝑎)
𝑎
2
𝑥3 2
(2)2 (0)2 8 2
∫ 𝑥 2 𝑑𝑥 = [ ] =
−
= 𝑢
3 0
3
3
3
0
Otra manera de representar el resultado es:
2
2 3 𝑢2 , 2. 6𝑢2 la 𝑢2 representa unidades de areas
𝜋
2. Calcula e área bajo la curva de 𝑓(𝑥) = 3𝑠𝑒𝑛𝑥 en el intervalo [𝑜, ]
2
Solución:
𝜋
∫ 3𝑠𝑒𝑛𝑥𝑑𝑥 = 3[−𝑐𝑜𝑠𝑥] 2
0
0
𝜋
2
𝜋
= 3 (−𝑐𝑜𝑠 ( ) − (−𝑐𝑝𝑠(0)) = 3(0 + 1) = 3
2
Por lo tanto es 3𝑢2
5
3. determine el valor de ∫1 𝑒 𝑥 𝑑𝑥
Solución:
Redondear en centésimas
5
5
∫ 𝑒 𝑥 𝑑𝑥 = [𝑒 𝑥 ] = 𝑒 5 − 𝑒 1 = 148.41 − 2.71 = 145.69𝑢2
1
1
CALCULO DE VOLUMENES
En este curso solamente se utilizara cuando se gira alrededor del eje “x”.
Si está girando en el eje “x” la fórmula
para calcular el volumen es:
Si está girando en el eje “y” la fórmula
para calcular el volumen es:
𝑏
𝑏
𝑣 = 𝜋 ∫ [𝑓(𝑥)]2 𝑑𝑥
𝑣 = 𝜋 ∫ [𝑓(𝑦)]2 𝑑𝑦
𝑎
𝑎
Ejemplo
1. calcula el volumen del solido de revolución que se forma al girar alrededor del eje “x” la
función 𝑓(𝑥) = 2 en el intervalo [-2 , 3]
Solución:
3
𝑣 = 𝜋∫
[2]2
3
3
𝑑𝑥 = 𝜋 ∫ 4𝑑𝑥 = 4𝜋 ∫ 𝑑𝑥
−2
−2
𝑣 = 4𝜋[𝑥]
−2
3
= 4𝜋(3 − (−2))
−2
𝑣 = 4𝜋(5) = 20𝜋 𝑢3
2. Calcula el volumen que se obtiene al girar la función 𝑓(𝑥) = 𝑥 en el intervalo [0 , 4]
Solución:
4
𝑣 = 𝜋∫
[𝑥]2
0
=
64
3
0
4
(4)3 (0)3
𝑥3 4
𝑑𝑥 = ∫ 𝑥 𝑑𝑥 = [ ] = (
−
)
3 0
3
3
0
−3=
64
3
𝑢3
2
ó
1
21 2 𝑢3
ó
21.3𝑢3