24 Análisis de Relaciones.

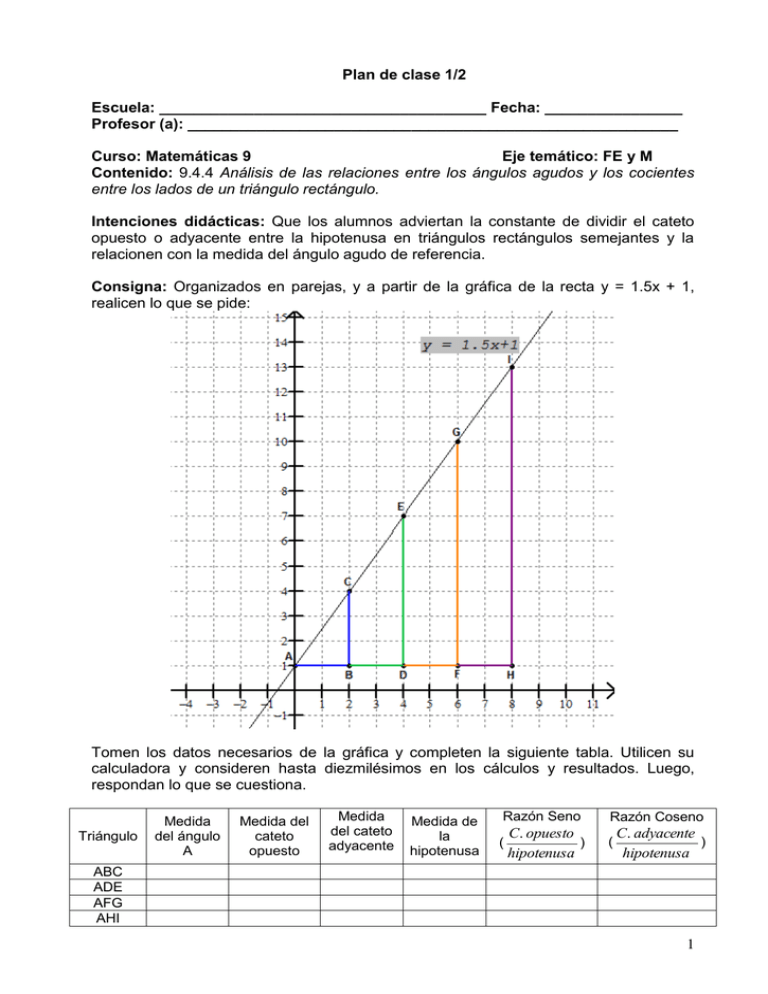
Plan de clase 1/2
Escuela: ______________________________________ Fecha: ________________
Profesor (a): _________________________________________________________
Curso: Matemáticas 9
Eje temático: FE y M
Contenido: 9.4.4 Análisis de las relaciones entre los ángulos agudos y los cocientes
entre los lados de un triángulo rectángulo.
Intenciones didácticas: Que los alumnos adviertan la constante de dividir el cateto
opuesto o adyacente entre la hipotenusa en triángulos rectángulos semejantes y la
relacionen con la medida del ángulo agudo de referencia.
Consigna: Organizados en parejas, y a partir de la gráfica de la recta y = 1.5x + 1,
realicen lo que se pide:
Tomen los datos necesarios de la gráfica y completen la siguiente tabla. Utilicen su
calculadora y consideren hasta diezmilésimos en los cálculos y resultados. Luego,
respondan lo que se cuestiona.
Triángulo
Medida
del ángulo
A
Medida del
cateto
opuesto
Medida
del cateto
adyacente
Medida de
la
hipotenusa
Razón Seno
(
C. opuesto
)
hipotenusa
Razón Coseno
(
C. adyacente
)
hipotenusa
ABC
ADE
AFG
AHI
1
a) ¿Cómo es el resultado de la razón seno en los cuatro triángulos?
___________________ ¿Y el de la razón coseno? _________________________
¿A qué creen que se deba esto?________________________________________
__________________________________________________________________
b) Con una calculadora científica, obtengan el seno y el coseno de los cocientes
obtenidos. ¿Los resultados coinciden con la medida del ángulo A?______________
¿Por qué? __________________________________________________________
Consideraciones previas
La idea central es que los alumnos concluyan que todos los cocientes que resultan de
dividir, por ejemplo, el cateto opuesto entre la hipotenusa son constantes. Este cociente
constante, con ayuda de una calculadora, puede servir para obtener el valor del ángulo
de la recta y a la inversa, conociendo el valor del ángulo se puede obtener el valor del
cociente constante.
Prever que los estudiantes lleven calculadora científica a la clase y el profesor las
tablas con los valores de las razones trigonométricas de seno y coseno. En ambos
casos, se sugiere que el profesor explique su uso para obtener la medida del ángulo a
partir del cociente del cateto opuesto o adyacente y la hipotenusa.
La discusión de las respuestas al inciso a es muy importante y se espera que los
alumnos se den cuenta de que se trata de triángulos semejantes y a eso se debe que
todos los cocientes que resultan de dividir, por ejemplo, el cateto opuesto entre la
hipotenusa son constantes. Esto mismo sucede con las otras razones.
Con respecto al inciso b, se espera que puedan determinar que sen(0.8320) es
aproximadamente 56° y lo mismo que para el cos(0.5547) es aproximadamente 56°.
Observaciones posteriores:
1. ¿Cuáles fueron los aspectos más exitosos de la sesión?
________________________________________________________________
________________________________________________________________
________________________________________________________________
2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase?
________________________________________________________________
________________________________________________________________
________________________________________________________________
3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso
para usted.
Muy útil
Útil
Uso limitado
Pobre
2
Plan de clase 2/2
Escuela: ___________________________________ Fecha: _________________
Profesor (a): ________________________________________________________
Curso: Matemáticas 9
Eje temático: FE y
M
Contenido. 9.4.4 Análisis de las relaciones entre los ángulos agudos y los cocientes
entre los lados de un triángulo rectángulo.
Intenciones didácticas: Que los alumnos reflexionen acerca de la relación que existe
entre las razones trigonométricas de un ángulo y las de su complemento.
Consigna: Organizados en equipos, contesten lo que se plantea enseguida.
1. ¿Cuánto suman los ángulos M y N en el triángulo rectángulo que aparece
abajo?________
2. ¿Qué nombre reciben esos ángulos?________________
3. Calculen los valores de las razones de los ángulos M y N.
sen M =
cos M =
10
tan M =
8
sen N =
cos N =
6
tan N =
4. ¿Qué relación existe entre el seno de un ángulo y el coseno de sus
complemento?_____________________________________________________
_________________________________________________________________
5. Si el seno de un ángulo de 30 grados es igual a 0.5, ¿a qué es igual el coseno de
un ángulo de 60 grados?____________________________
6. ¿A qué es igual el producto de la tangente de un ángulo de 30 grados por la
tangente de un ángulo de 60 grados?__________________
Consideraciones previas: En este momento es importante que los alumnos recuerden
que los ángulos agudos de un triángulo rectángulo siempre son complementarios
(suman 90º) y dejarlos que exploren con diferentes triángulos rectángulos para
3
responder la última pregunta. También es importante que concluyan que: el seno de un
ángulo es igual al coseno de su complemento y que la tangente de un ángulo es
recíproco o inverso multiplicativo a la tangente de su complemento.
Se les puede dejar como tarea el problema que se enuncia más abajo. La finalidad es
que indaguen la manera de obtener la medida que falta. Al revisarla es importante que
vean la necesidad de recurrir al teorema de Pitágoras para obtenerla.
Escriban las razones trigonométricas (seno, coseno, tangente) para el siguiente
triángulo rectángulo.
Observaciones posteriores:
1. ¿Cuáles fueron los aspectos más exitosos de la sesión?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase?
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso
para usted.
Muy útil
Útil
Uso limitado
Pobre
4